Numerical Modelling of Flat Slabs with Different Amounts of Double-Headed Studs as Punching Shear Reinforcement
Abstract
1. Introduction
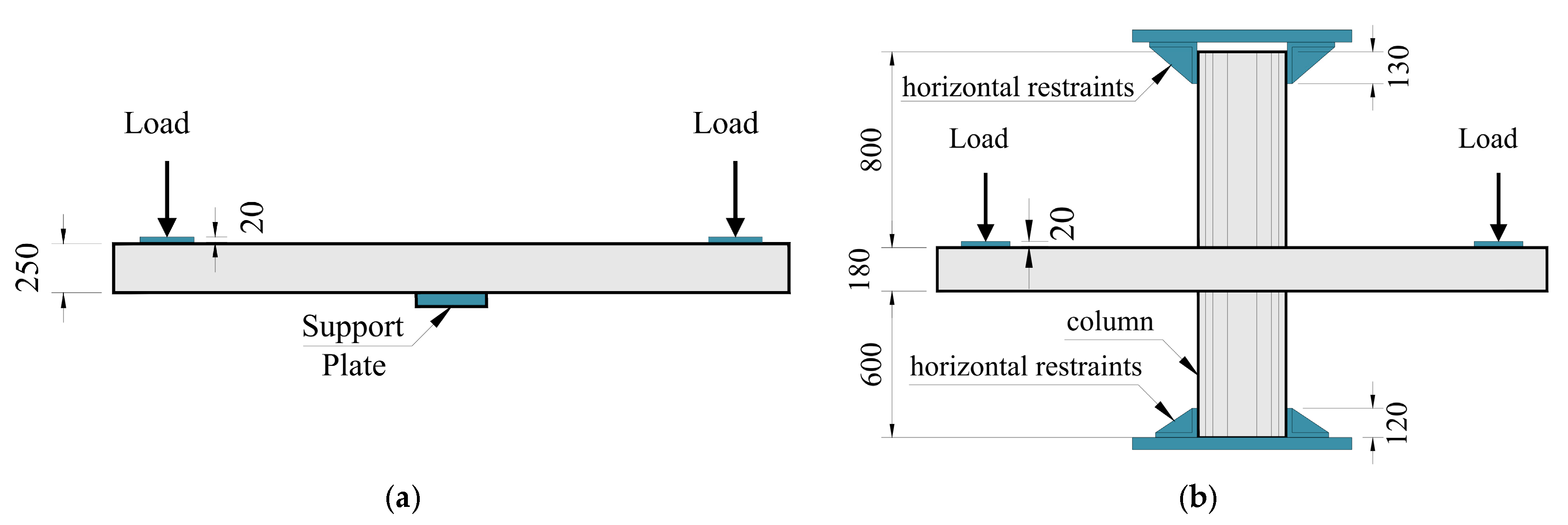
2. Selected Experimental Tests
3. Modelling Strategies
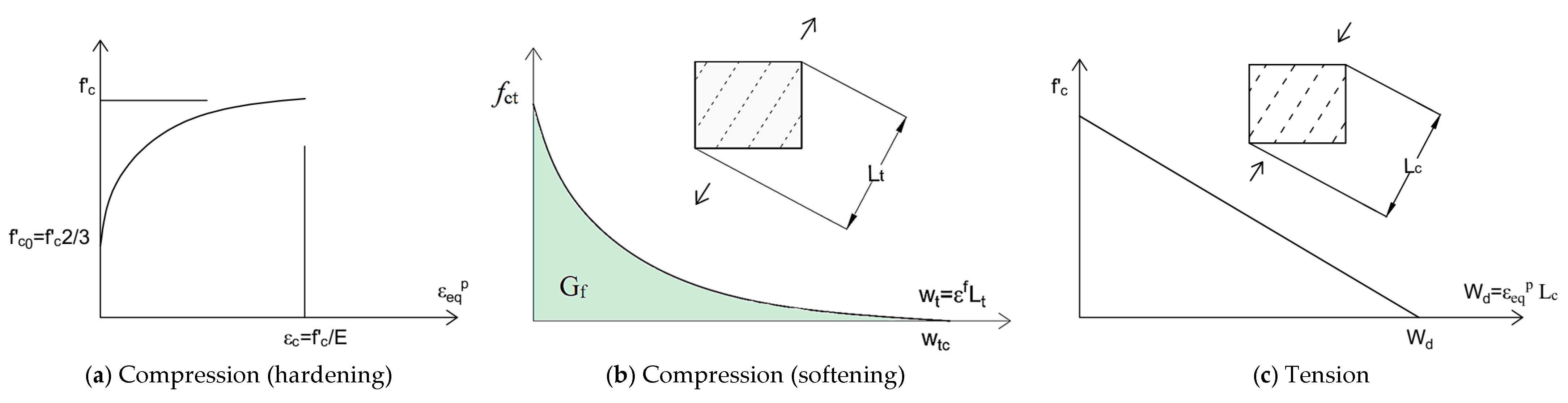
3.1. Constitutive Material Models
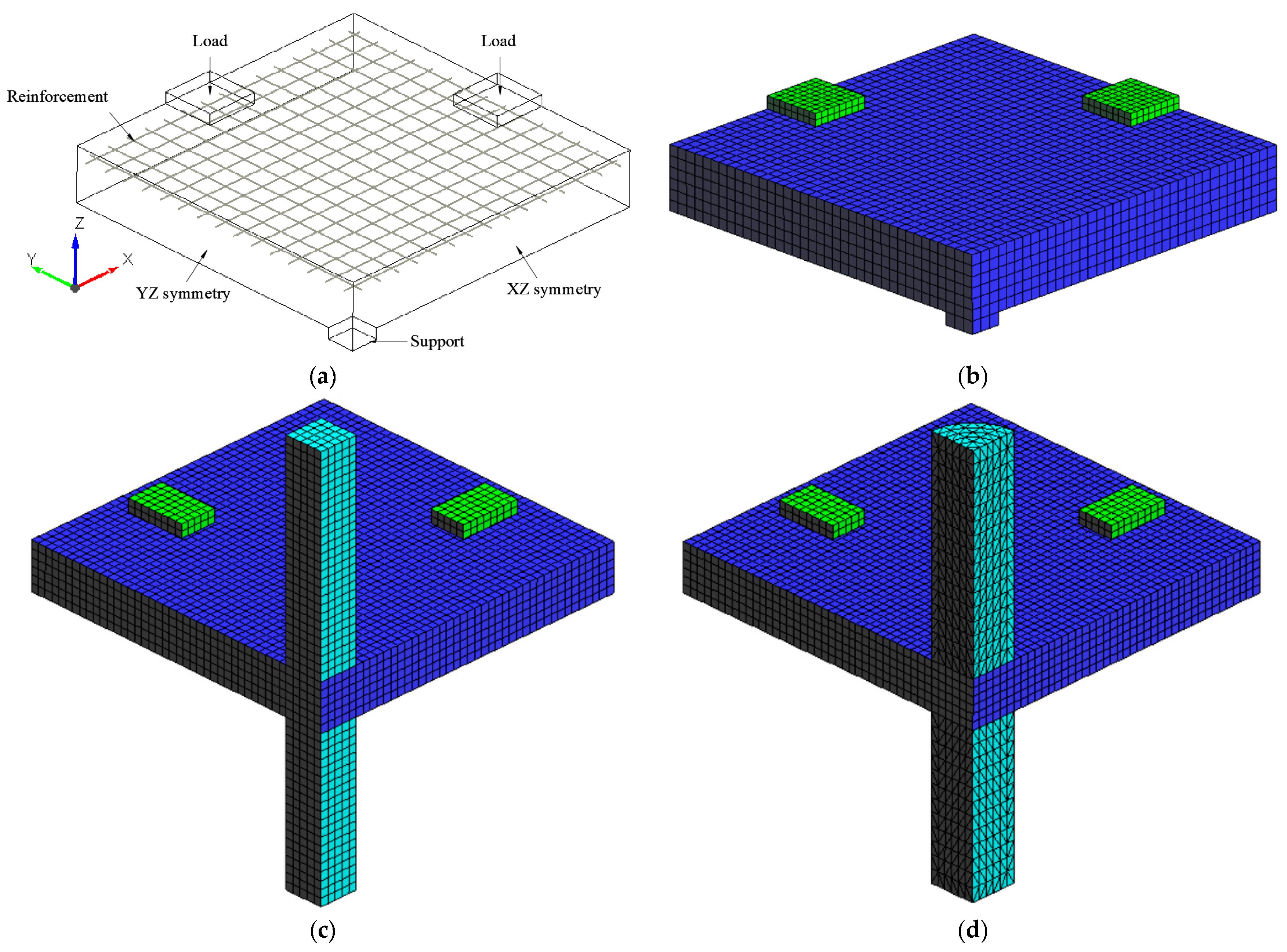
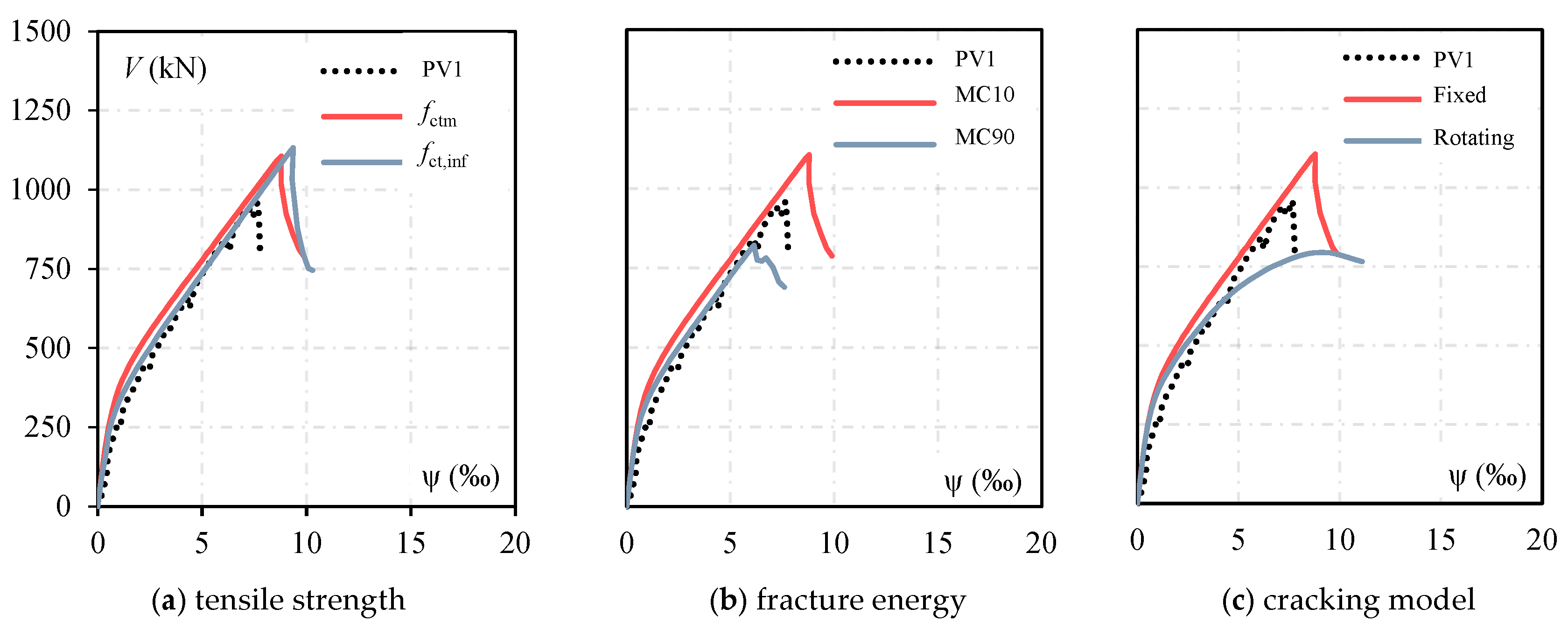
3.2. Preliminary Simulations
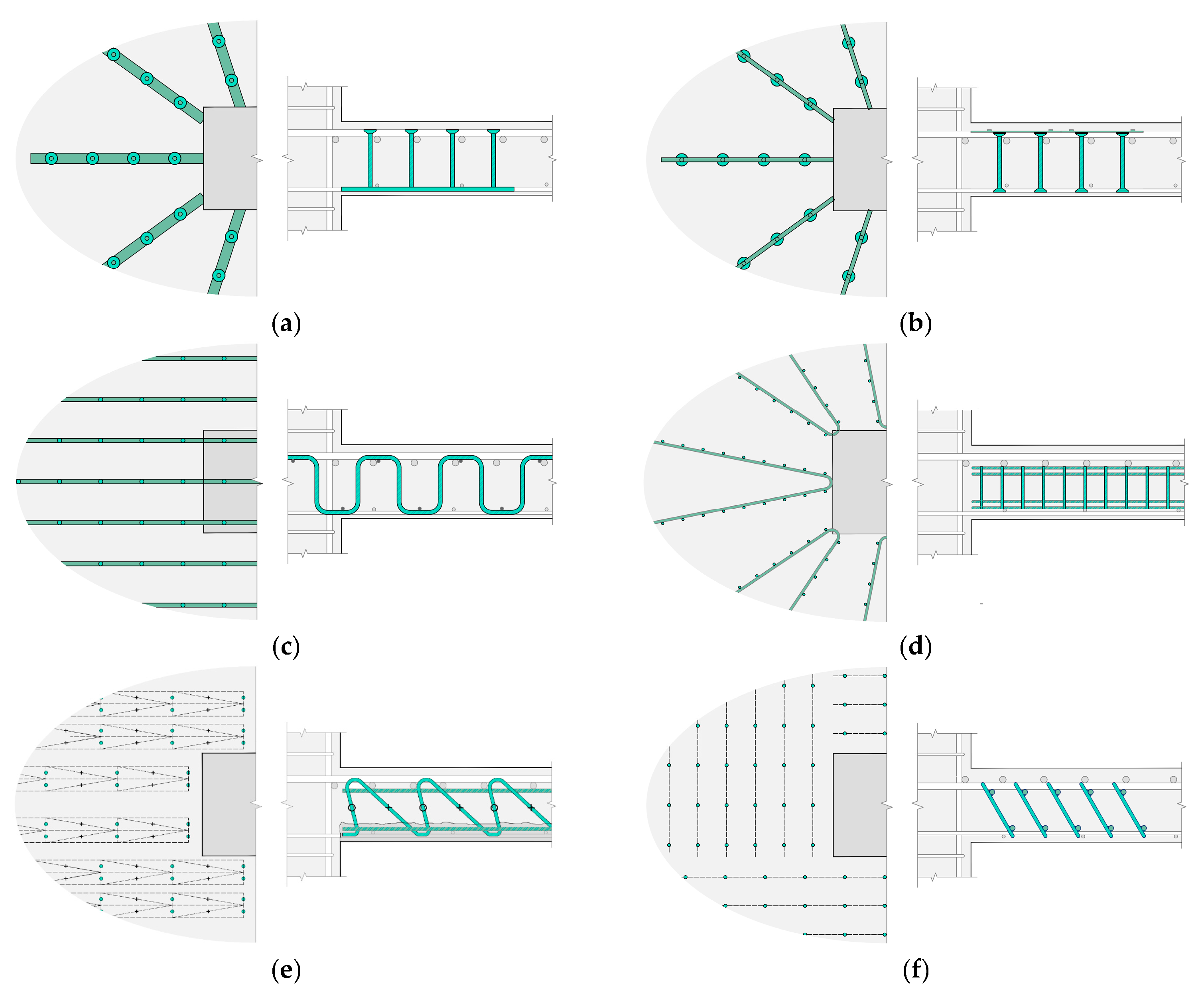
3.3. Simulations of Slabs with Shear Reinforcement
4. Results and Discussions
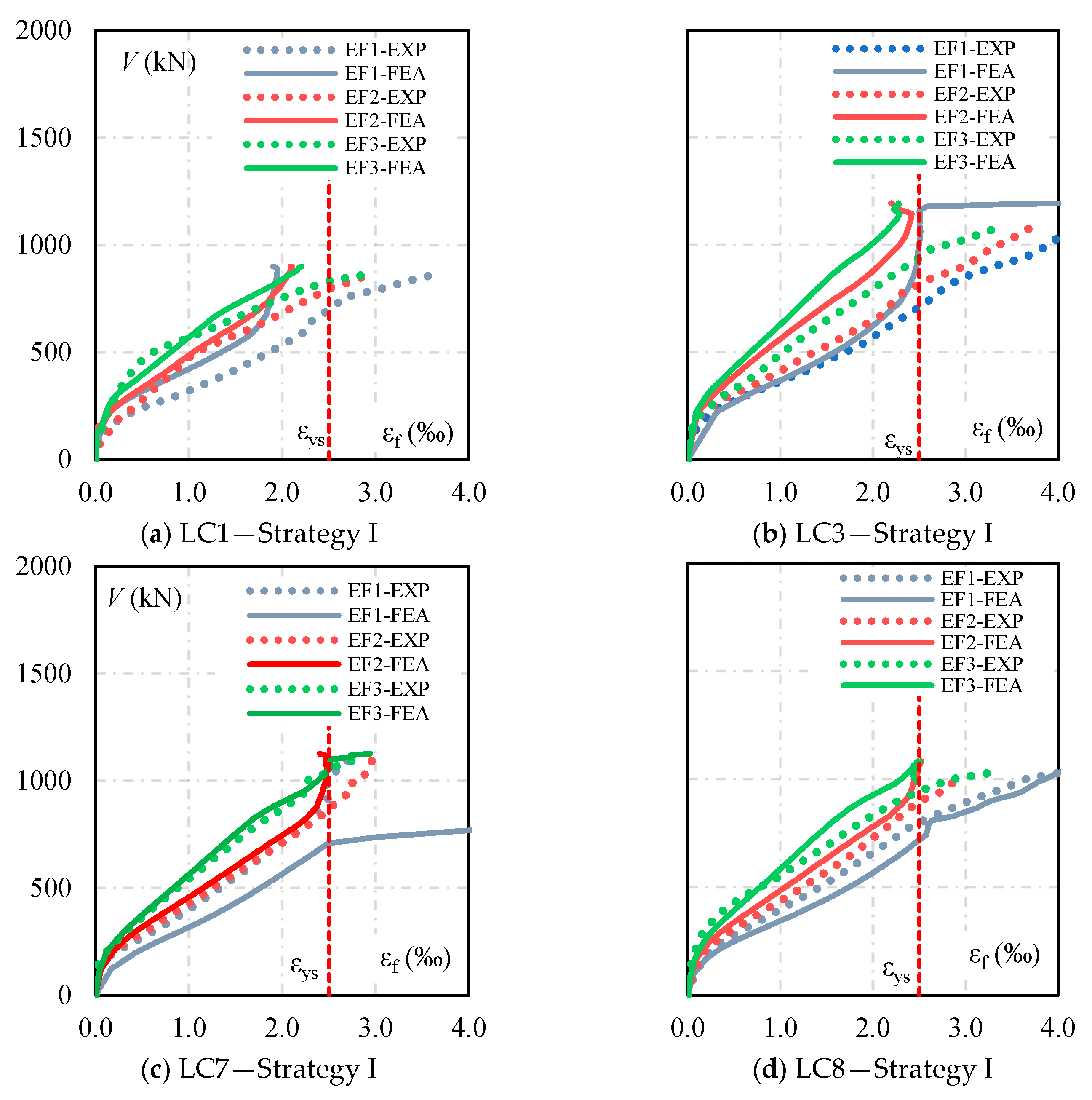
4.1. Load–Rotation Curves
4.2. Strains in Flexural and Shear Reinforcement
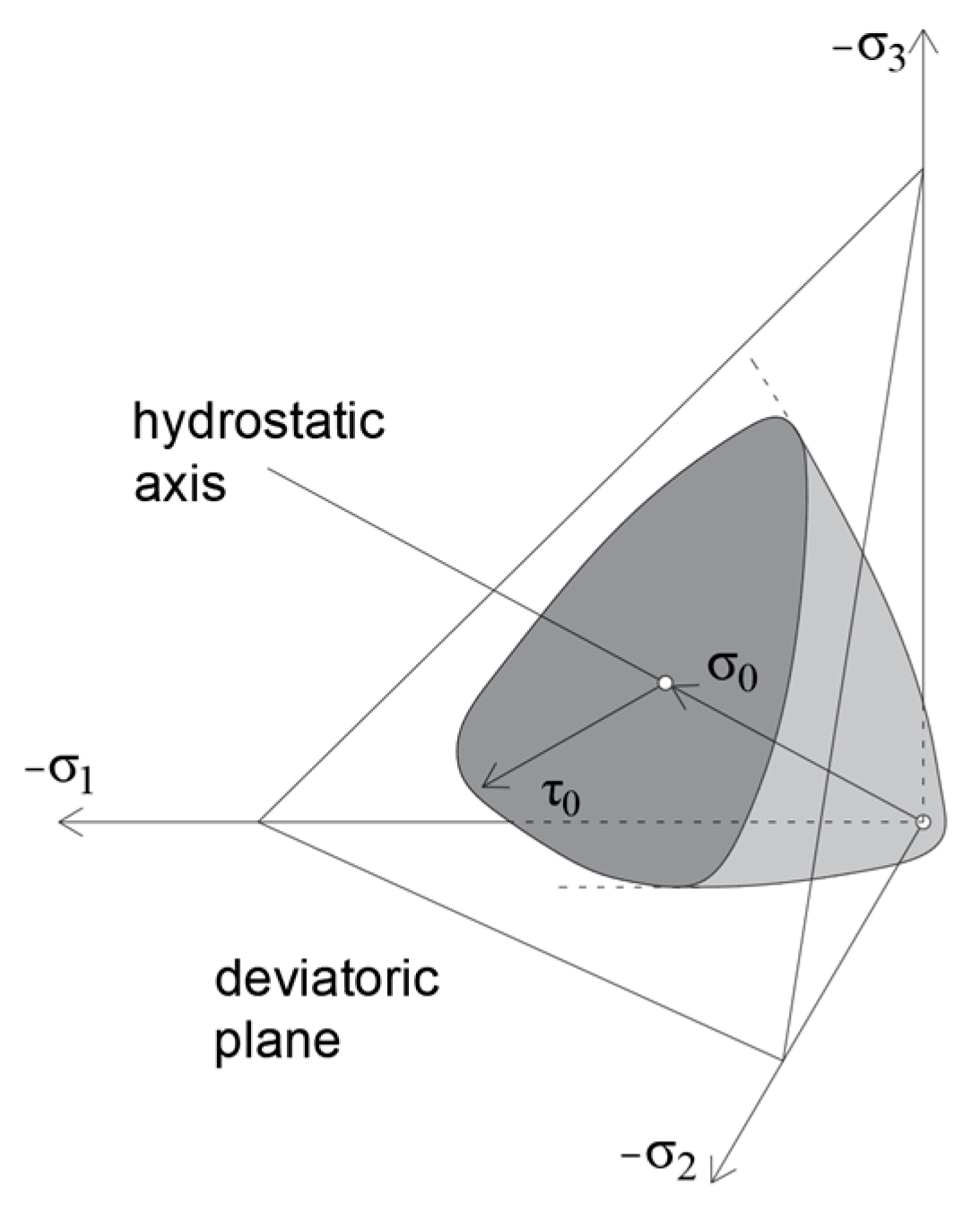
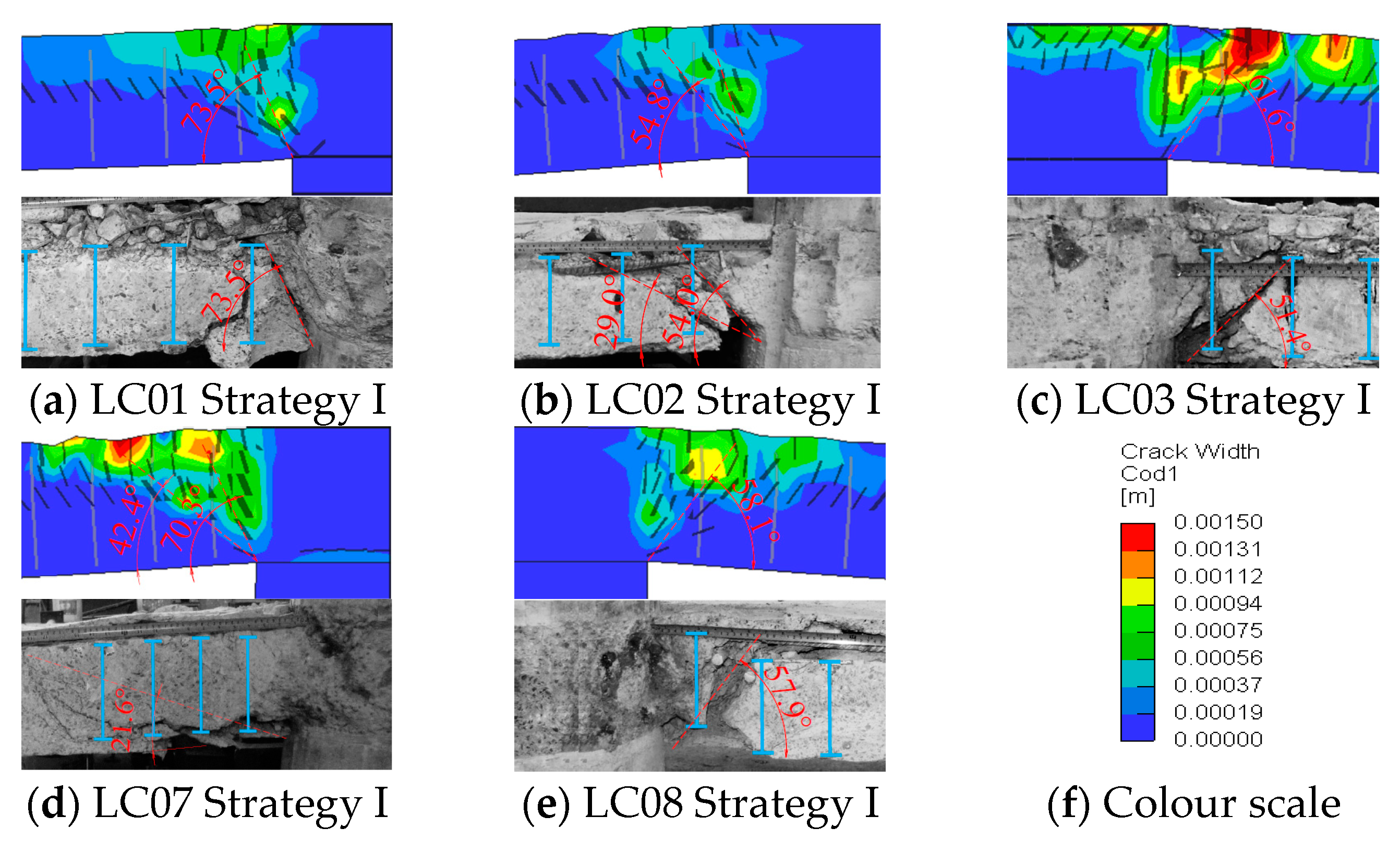
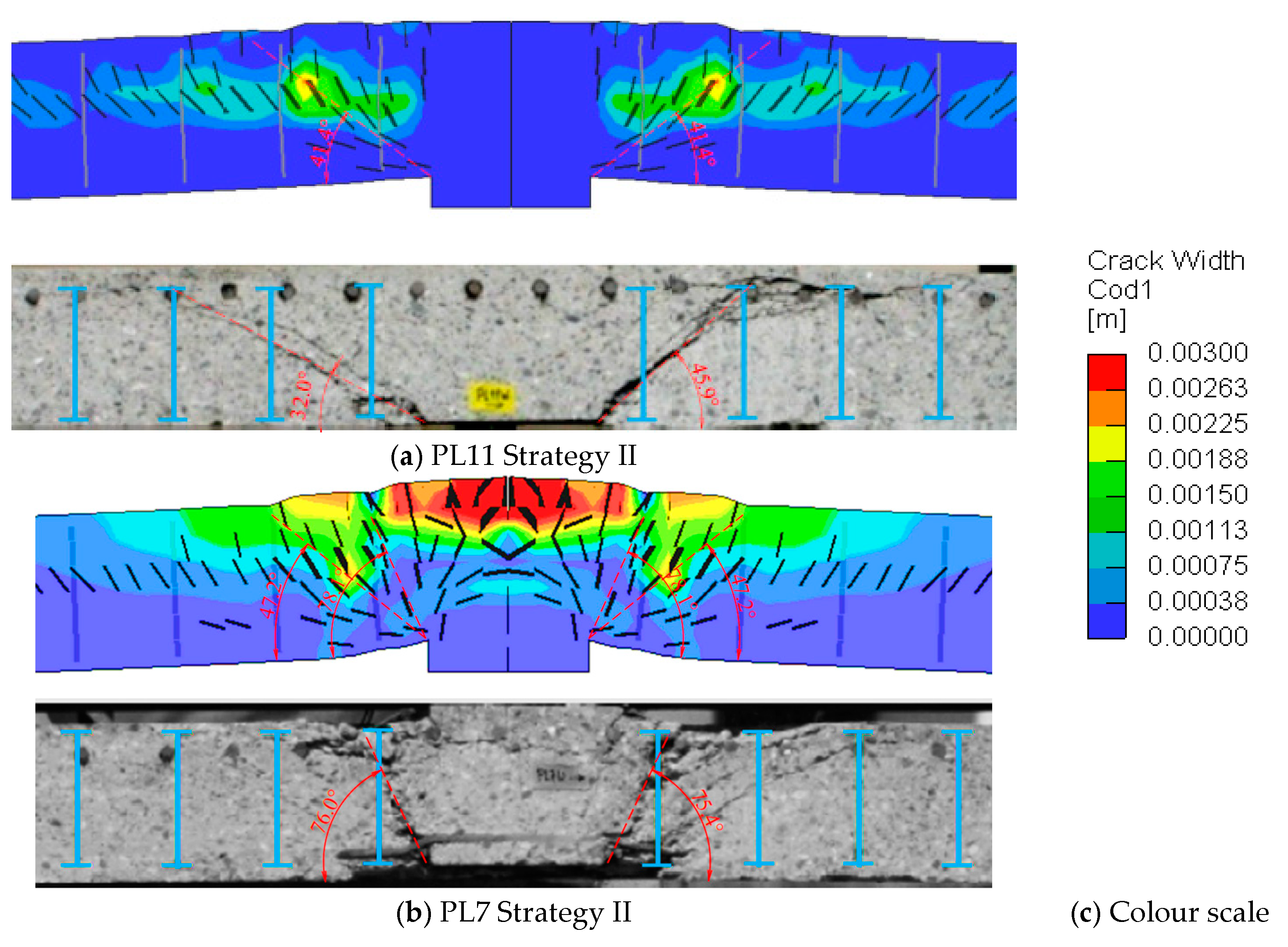
4.3. Failure Surface
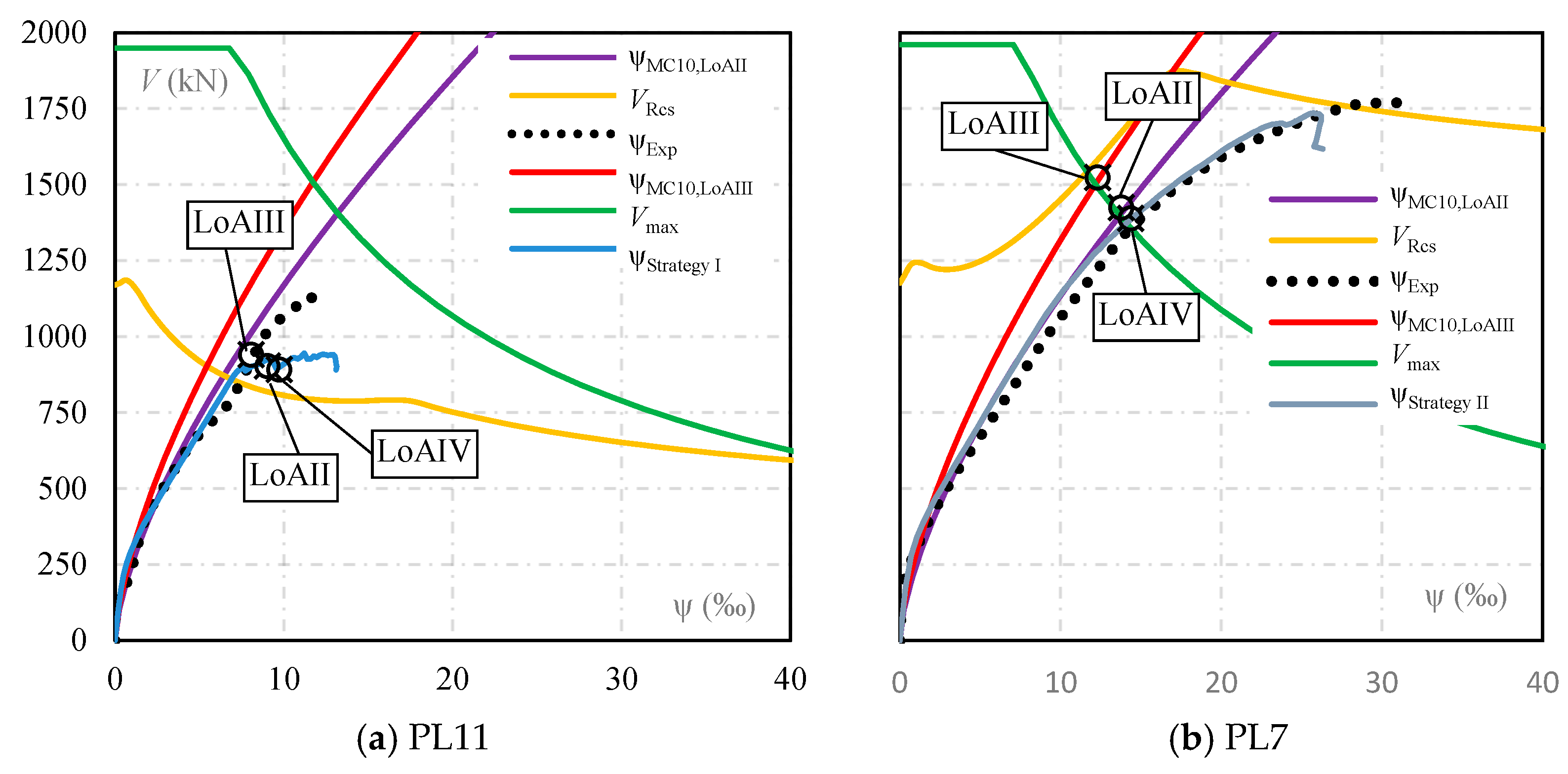
4.4. Comparison with Fib Model Code 2020
- VRcs is the punching resistance within the shear-reinforced zone;
- is the punching resistance of a slab without shear reinforcement;
- is the resistance provided by the punching shear reinforcement;
- Vout is the punching resistance outside the shear-reinforced zone;
- Vmax is the maximum punching resistance of a slab–column connection.
- is the stress in the shear reinforcement.
- ksys is assumed as 2.8 for studs with heads larger or equal to three times the bar diameter.
- fb is the bond strength, assumed as 3 MPa for corrugated studs.
5. Conclusions
- The flexural and shear reinforcement were modelled using truss elements, assuming a perfect bond between concrete and steel. The NLFE models generally captured flexural response aspects of the slab–column connections, such as load–rotation behaviour, cracking patterns, and flexural reinforcement strains. However, in terms of punching shear, the comparison between numerically predicted strains in the studs and experimental measurements showed poor correlation, indicating limitations in how the NLFE models represent the shear transfer mechanisms.
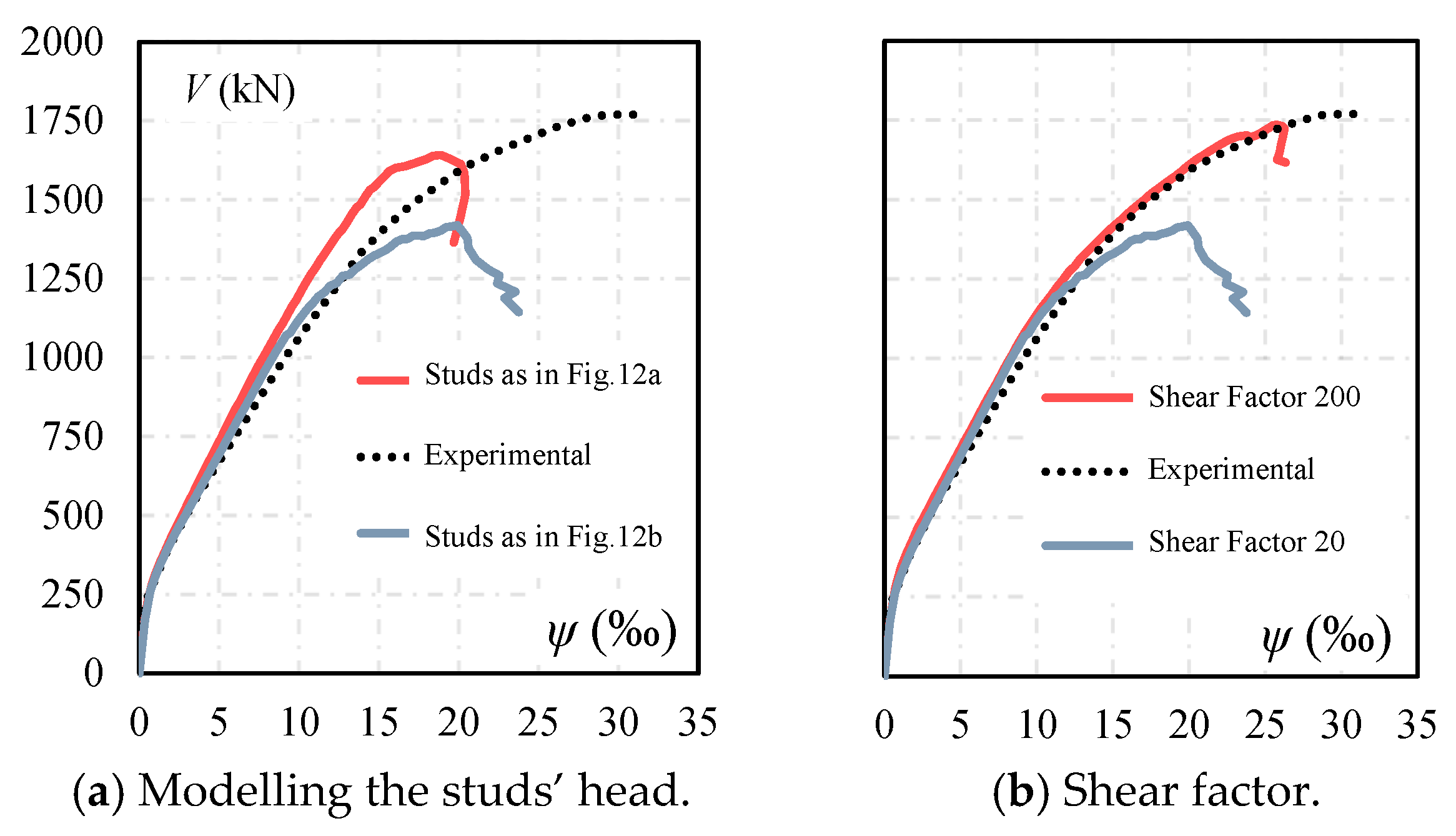
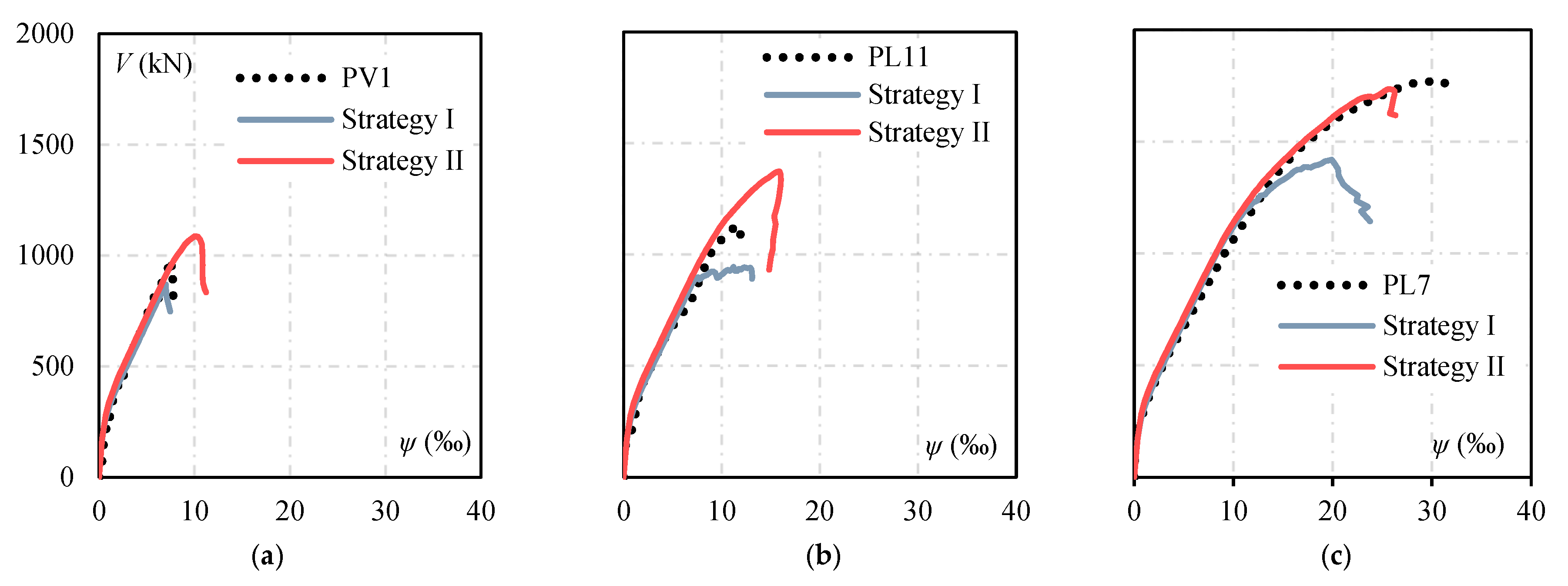
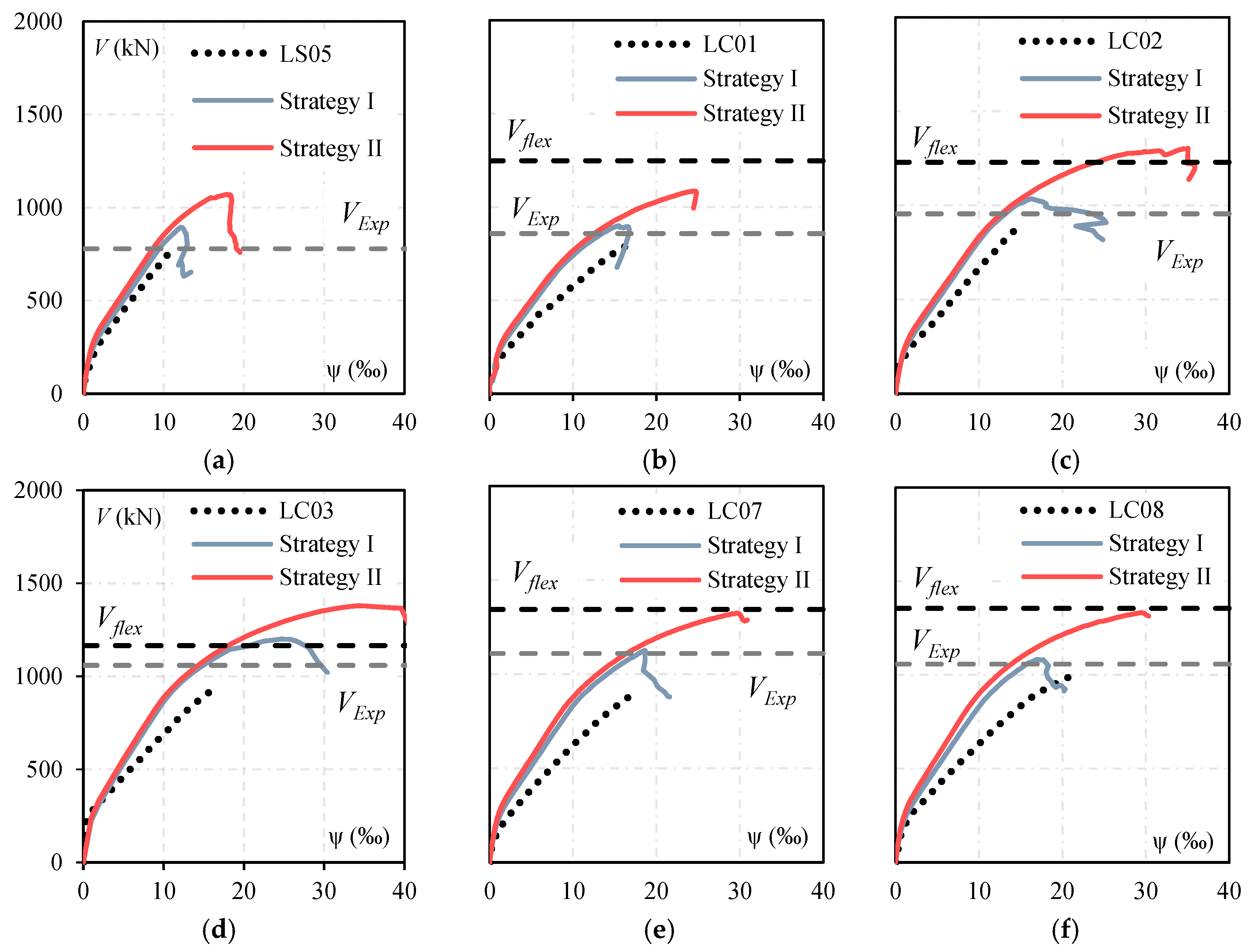
- The shear factor (SF) significantly influenced the numerical results, particularly for slabs with high shear reinforcement ratios. Strategy I, in which SF was assumed as 20, provided reasonable estimates for slabs with low-to-moderate reinforcement. In contrast, with SF assumed as 200, Strategy II better captured the behaviour and resistance of slabs with high shear reinforcement ratios, such as PL7. Finally, the computational effort required to solve slabs with Strategy II was mainly governed by the iterative method and mesh size rather than by the chosen SF value. Therefore, adopting SF = 200 did not impose significant practical limitations on structural engineering applications.
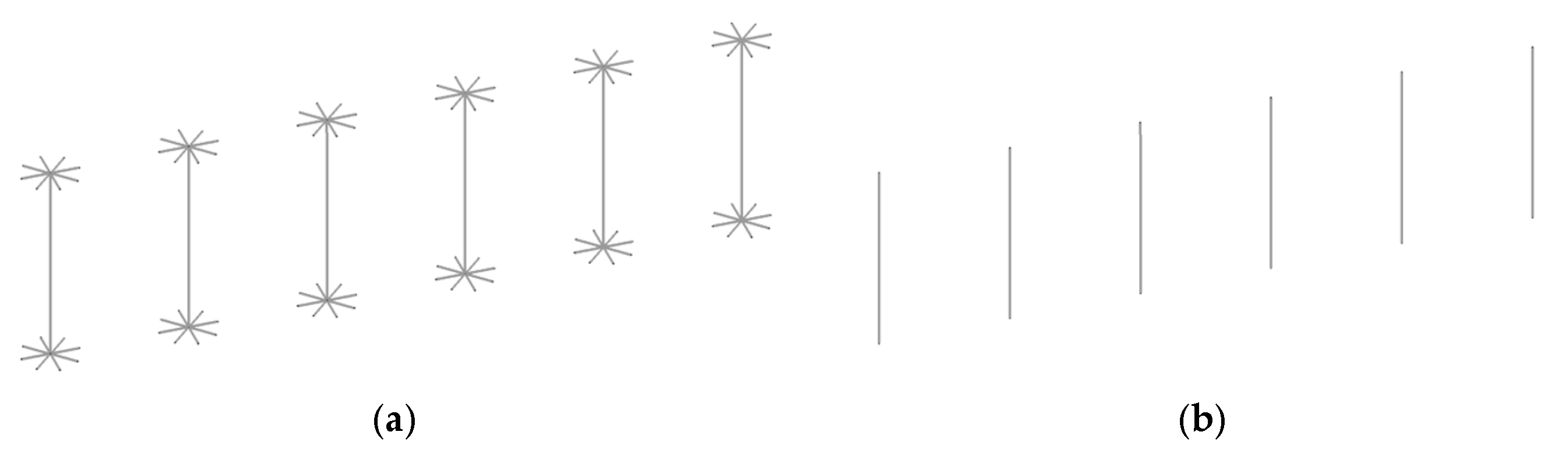
- The modelling of double-headed studs significantly affected numerical results. Simulations that explicitly represented the stud heads led to higher punching resistance estimates than those that ignored them. However, it also altered the slabs’ stiffness, leading to discrepancies in the numerical load–rotation response. These results emphasise the importance of adequately representing the geometry of the studs to enhance accuracy while maintaining realistic structural behaviour. Moreover, these results indicate that the methodologies assessed in this paper are insufficient for detailed investigations into the punching shear failure mechanisms and the activation process of the shear reinforcement.
- Assuming a perfect bond between the shear reinforcement and concrete led to reasonable punching shear strength estimates. However, it did not accurately capture the development of strains in the shear reinforcement. Softening the perfect bond assumption would introduce an additional modelling complexity, as it would require a constitutive bond–slip model, which would demand additional calibration and computational effort. The perfect bond was adopted to balance accuracy and usability in practical engineering applications. Nevertheless, further studies are recommended to evaluate the impact of bond–slip models on the numerical response and resistance of slabs with different amounts of shear reinforcement.
- The punching shear strength estimates for the selected slabs obtained using the fib Model Code were conservative compared to the experimental results and with the NLFEA. It was also observed that increasing complexity from LoA II to LoA IV did not consistently improve the accuracy of strength estimates. These results suggest potential limitations in the levels of approximation adopted by the fib Model Code to estimate the punching shear strength of slabs with shear reinforcement. Further investigation is required to determine whether these discrepancies arise from inherent constraints in the theoretical model or uncertainties in the numerical modelling process.
- The NLFEA methodologies presented in this paper demonstrated a strong correlation with experimental results. They effectively evaluated the punching shear strength and structural response of slabs incorporating varying amounts of double-headed studs as punching shear reinforcement. These findings support the methodologies’ applicability for structural engineering issues, potentially offering more reliable strength estimates than simplified methods outlined in design codes. Future research should focus on bond–slip models to improve strain predictions in shear reinforcement, examine the impact of slab continuity and boundary conditions in practical structural scenarios, and assess the benefits of utilising LoA IV methodology for achieving more consistent strength estimates in the fib Model Code 2020.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notation
| d | Effective depth of the slab. |
| dv | Shear resisting effective depth of the slab. |
| dg | Maximum size of aggregate. |
| fc | Compressive strength of concrete. |
| fcm | Mean compressive strength of concrete. |
| fctm | Mean tensile strength of concrete. |
| fct,inf | Lower bound value of the tensile strength of concrete. |
| ft | Tensile strength of concrete. |
| fy | Yield strength of the flexural reinforcement. |
| fyw | Yield strength of the shear reinforcement. |
| Gf | Concrete fracture energy. |
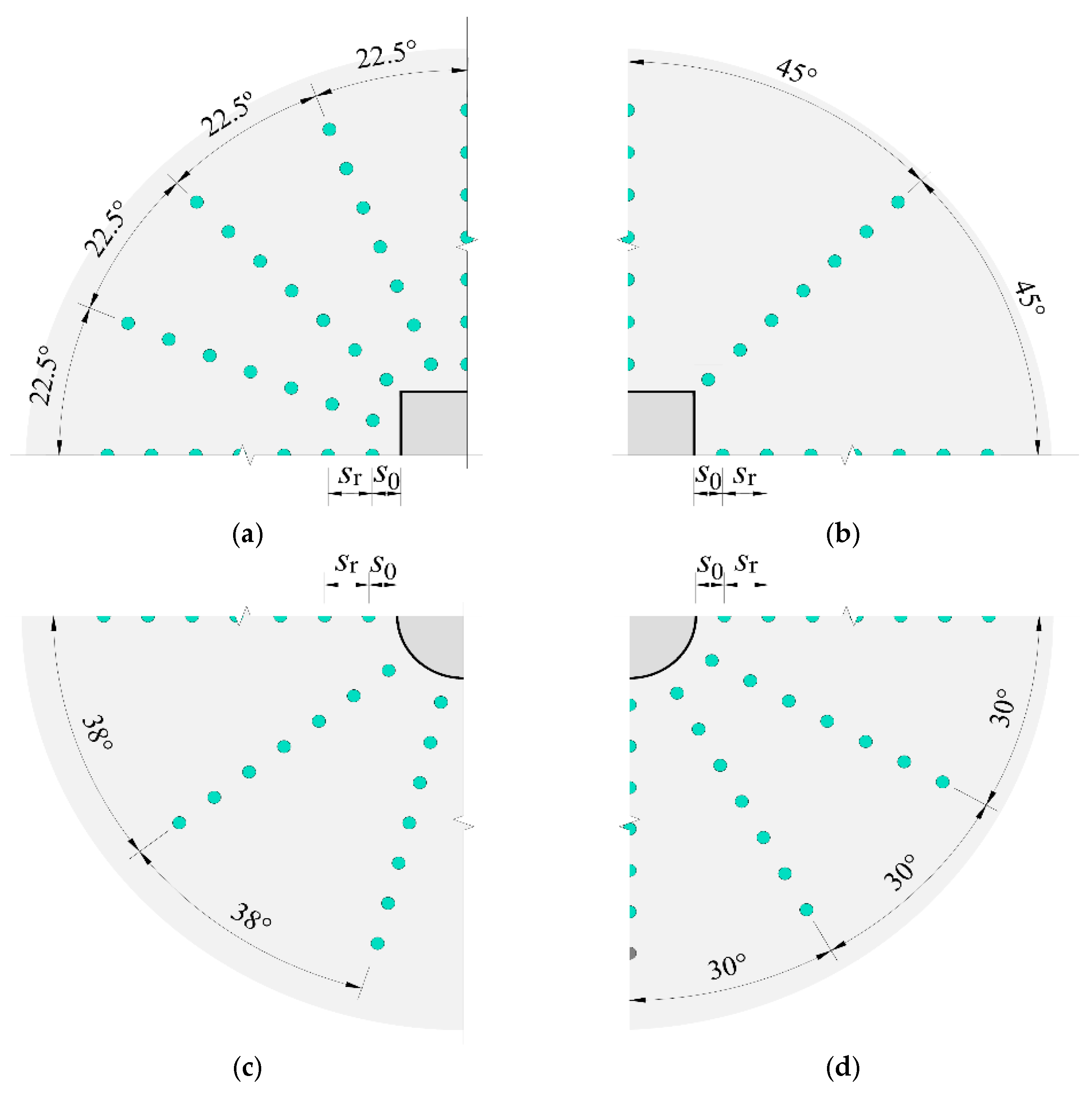
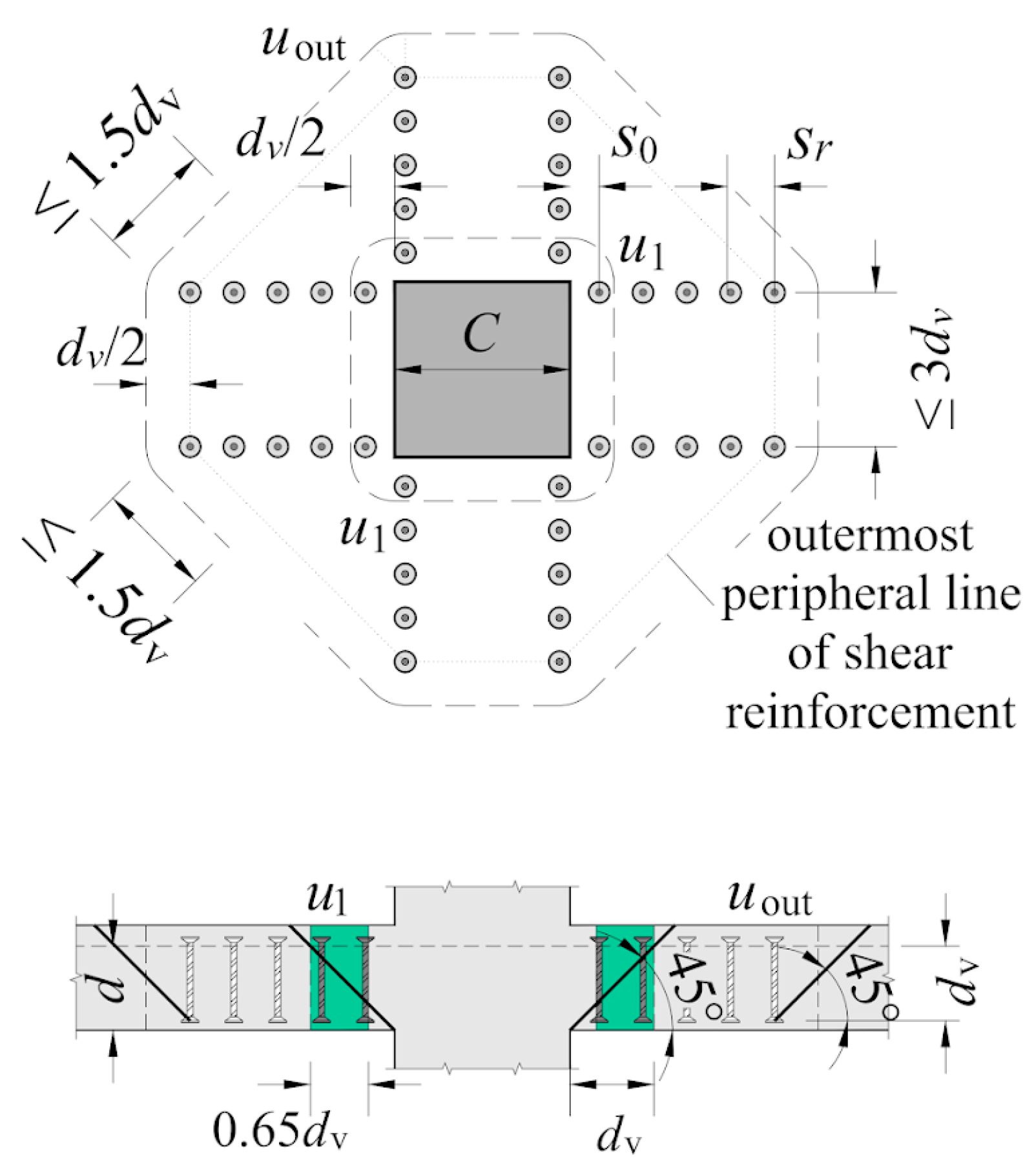
| s0 | Distance from column face to first layer of shear reinforcement. |
| sr | Radial spacing of shear reinforcement. |
| st | Tangential spacing of shear reinforcement. |
| st,max | Maximum value of st (generally in outer perimeter of shear reinforcement). |
| u1 | Length of control perimeter for calculation of VRc and VRcs. |
| uout | Length of control perimeter for calculation of Vout. |
| uout,ef | Effective value of uout respecting the limits of st,max. limited by fib Model Code 2010 as st,max ≤ 1.5∙dv. |
| Asw | Sum of the cross-sectional area of all shear reinforcement within the zone bounded by 0.35∙dv and dv from the edge of the supported area (see Figure 20). |
| Asw/perim. | Area of shear reinforcement per perimeter. |
| C | Diameter of a circular column, case of slabs type LC, or the side length of a square column, for all the other slabs. |
| Es | Modulus of elasticity of flexural reinforcement, presented in Table 3. |
| ρflex | Flexural reinforcement ratio. |
| Øw | Diameter of the shear reinforcement. |
| ψ | Rotation of the slab. |
| Ec | Concrete modulus of elasticity. |
| ν | Poisson ratio. |
| Es | Steel modulus of elasticity. |
| V | Load carrying capacity of the model. |
| Vflex | Expected flexural load capacity. |
| Vexp | Experimental observed load capacity. |
| Vexp | Computational observed load capacity. |
| εys | Limit deformation for steel rebars. |
References
- Birkle, G.; Dilger, W.H. Influence of slab thickness on punching shear strength. ACI Struct. J. 2008, 105, 180–188. [Google Scholar] [CrossRef]
- Ferreira, M.P.; Melo, G.S.; Regan, P.E.; Vollum, R.L. Punching of reinforced concrete flat slabs with double-headed shear reinforcement. ACI Struct. J. 2014, 111, 363–374. [Google Scholar] [CrossRef]
- Einpaul, J.; Brantschen, F.; Fernández Ruiz, M.; Muttoni, A. Performance of punching shear reinforcement under gravity loading: Influence of type and detailing. ACI Struct. J. 2016, 113, 827–838. [Google Scholar] [CrossRef]
- Hegger, J.; Sherif, A.G.; Kueres, D.; Siburg, C. Efficiency of various punching shear reinforcement systems for flat slabs. ACI Struct. J. 2017, 114, 631–642. [Google Scholar] [CrossRef]
- Kueres, D.; Schmidt, P.; Hegger, J. Two-parameter kinematic theory for punching shear in reinforced concrete slabs with shear reinforcement. Eng. Struct. 2019, 181, 216–232. [Google Scholar] [CrossRef]
- Regan, P.E.; Samadian, F. Shear reinforcement against punching in reinforced concrete flat slabs. Struct. Eng. 2001, 79, 24–31. [Google Scholar]
- Eligehausen, R.; Cook, R.A.; Appl, J. Behavior and Design of Adhesive Bonded Anchors. ACI Struct. J. 2006, 103, 822–831. [Google Scholar]
- Park, H.-g.; Ahn, K.-s.; Choi, K.-k.; Chung, L. Lattice Shear Reinforcement for Slab-Column Connections. ACI Struct. J. 2007, 104, 294–303. [Google Scholar] [CrossRef]
- Lips, S.; Fernández Ruiz, M.; Muttoni, A. Experimental investigation on punching strength and deformation capacity of shear-reinforced slabs. ACI Struct. J. 2012, 109, 889–900. [Google Scholar] [CrossRef][Green Version]
- Furche, J.; Schmidt, P. Orthogonal arrangement of effective lattice punching shear reinforcement. In Proceedings of the fib Symposium—CONCRETE Innovations in Materials, Design and Sructures, Krakow, Poland, 27–29 May 2019. [Google Scholar]
- Ferreira, M.; Filho, M.P.; Lima, N.; Oliveira, M. Influence of the flexural and shear reinforcement in the concrete cone resistance of headed bars. Eng. Struct. 2021, 248, 113212. [Google Scholar] [CrossRef]
- Trautwein, L.M.; Bittencourt, T.N.; Gomes, R.B.; Bella, J.C.D. Punching Strength of Flat Slabs with Unbraced Shear Reinforcement. ACI Struct. J. 2011, 108, 197–205. [Google Scholar] [CrossRef]
- Schmidt, P.; Ungermann, J.; Hegger, J. Contribution of concrete and shear reinforcement to the punching shear resistance of column bases. Eng. Struct. 2021, 245, 112901. [Google Scholar] [CrossRef]
- Ferreira, M.d.P.; Oliveira, M.H.; Melo, G.S.S.A. Tests on the punching resistance of flat slabs with unbalanced moments. Eng. Struct. 2019, 196, 109311. [Google Scholar] [CrossRef]
- Ghali, A.; Youakim, S.A. Headed studs in concrete: State of the art. ACI Struct. J. 2005, 102, 657–667. [Google Scholar] [CrossRef]
- ABNT NBR 6118; Design of Concrete Structures—Procedures. Brazilian Association of Technical Standards: Rio de Janeiro, Brazil, 2014.
- Comité Euro-International du Béton. CEB-FIP Model Code 1990; Thomas Telford: London, UK, 1993. [Google Scholar]
- Pereira Filho, M.J.M.; Freitas, M.V.P.D.; Santos, D.F.A.D.; Nascimento, A.; Ferreira, M. Slabs strengthened for punching shear with post-installed steel and CFRP connectors. IBRACON Struct. Mat. J. 2019, 12, 445–478. [Google Scholar] [CrossRef]
- Fédération Internationale du Béton. fib Model Code for Concrete Structures 2020; Fédération Internationale du Béton: Lausanne, Switzerland, 2023. [Google Scholar]
- Muttoni, A. Punching shear strength of reinforced concrete slabs without transverse reinforcement. ACI Struct. J. 2008, 105, 440–450. [Google Scholar] [CrossRef]
- Fernández Ruiz, M.; Muttoni, A. Applications of the critical shear crack theory to punching of R/C slabs with transverse reinforcement. ACI Struct. J. 2009, 106, 485–494. [Google Scholar] [CrossRef]
- Marí, A.; Cladera, A.; Oller, E.; Bairán, J.M. A punching shear mechanical model for reinforced concrete flat slabs with and without shear reinforcement. Eng. Struct. 2018, 166, 413–426. [Google Scholar] [CrossRef]
- Wang, Y.; Gu, Y.; Liu, J. A domain-decomposition generalised finite difference method for stress analysis in three-dimensional composite materials. Appl. Math. Lett. 2020, 104, 106226. [Google Scholar] [CrossRef]
- Kabir, H.; Aghdam, M.M. A robust Bézier based solution for nonlinear vibration and post-buckling of random checkerboard graphene nanoplatelets reinforced composite beams. Compos. Struct. 2019, 212, 184–198. [Google Scholar] [CrossRef]
- Silva Mamede, N.F.; Pinho Ramos, A.; Faria, D.M.V. Experimental and parametric 3D nonlinear finite element analysis on punching of flat slabs with orthogonal reinforcement. Eng. Struct. 2013, 48, 442–457. [Google Scholar] [CrossRef]
- Navarro, M.; Ivorra, S.; Varona, F.B. Parametric computational analysis for punching shear in RC slabs. Eng. Struct. 2018, 165, 254–263. [Google Scholar] [CrossRef]
- Navarro, M.; Ivorra, S.; Varona, F.B. Parametric finite element analysis of punching shear behaviour of RC slabs reinforced with bolts. Comput. Struct. 2020, 228, 106147. [Google Scholar] [CrossRef]
- Beutel, R. Durchstanzen Schubbewehrter Flachdecken im Bereich von Innenstützen. Ph.D. Thesis, RWTH Aachen, Aachen, Germany, 2003. [Google Scholar]
- Genikomsou, A.S.; Polak, M.A. Finite-element analysis of reinforced concrete slabs with punching shear reinforcement. J. Struct. Eng. 2016, 142, 04016129. [Google Scholar] [CrossRef]
- Setiawan, A.; Vollum, R.L.; Macorini, L.; Izzuddin, B.A. Numerical modelling of punching shear failure of reinforced concrete flat slabs with shear reinforcement. Mag. Concr. Res. 2021, 73, 1205–1224. [Google Scholar] [CrossRef]
- Marques, M.G.; Liberati, E.A.; Pimentel, M.J.; de Souza, R.A.; Trautwein, L.M. Nonlinear finite element analysis (NLFEA) of reinforced concrete flat slabs with holes. Structures 2020, 27, 1–11. [Google Scholar] [CrossRef]
- Mendes, R.P.; Mesquita, L.C.; Ferreira, M.P.; Trautwein, L.M.; Marvila, M.T.; Marques, M.G. Numerical Evaluation of the Punching Shear Strength of Flat Slabs Subjected to Balanced and Unbalanced Moments. Buildings 2024, 14, 985. [Google Scholar] [CrossRef]
- Kueres, D.; Schmidt, P.; Hegger, J. Punching shear behavior of reinforced concrete flat slabs with a varying amount of shear reinforcement. Struct. Concr. 2019, 21, 235–246. [Google Scholar] [CrossRef]
- Červenka, V.; Jendele, L.; Červenka, J. ATENA Program Documentation Part 1 Theory; Červenka Consulting s.r.o.: Prague, Czech Republic, 2016; p. 282. [Google Scholar]
- Červenka, J.; Papanikolaou, V.K. Three-dimensional combined fracture–plastic material model for concrete. Int. J. Plast. 2008, 24, 2192–2220. [Google Scholar] [CrossRef]
- Belletti, B.; Damoni, C.; Hendriks, M.A.N.; de Boer, A. Analytical and numerical evaluation of the design shear resistance of reinforced concrete slabs. Struct. Concr. 2014, 15, 317–330. [Google Scholar] [CrossRef]
- Shu, J.; Plos, M.; Zandi, K.; Johansson, M.; Nilenius, F. Prediction of punching behaviour of RC slabs using continuum nonlinear FE analysis. Eng. Struct. 2016, 125, 15–25. [Google Scholar] [CrossRef]
- Fédération Internationale du Béton. Fib Model Code for Concrete Structures 2010; Fédération Internationale du Béton: Lausanne, Switzerland, 2013. [Google Scholar]
- Sanabria Diaz, R.A.; de Oliveira, L.H.B.; Trautwein, L.M.; de Almeida, L.C.; dos Santos, A.C. Aspects of finite element modeling of punching shear behavior of reinforced concrete flat slabs. Lat. Am. J. Solids Struct. 2018, 15, e120. [Google Scholar] [CrossRef]
- Hendriks, M.A.N.; Roosen, M. Guidelines for Non-Linear Finite Element Analysis of Concrete Structures; Rijkswaterstaat Technical Document (RTD), Report RTD:1016-1:2022; Rijkswaterstaat: Utrecht, The Netherlands, 2022. [Google Scholar]
- Cervenka, V.; Cervenka, J.; Pukl, R.; Sajdlova, T. Prediction of shear failure of large beams based on fracture mechanics. In Proceedings of the International Conference on Fracture Mechanics of Concrete and Concrete Structures, Berkeley, CA, USA, 28 May–1 June 2016. [Google Scholar]
- Cervenka, V.; Cervenka, J.; Rymes, J. Numerical simulation of concrete structures—From research to engineering application. Struct. Concr. 2024, 25, 751–772. [Google Scholar] [CrossRef]
- Simões, J.T.; Fernández Ruiz, M.; Muttoni, A. Validation of the Critical Shear Crack Theory for punching of slabs without transverse reinforcement by means of a refined mechanical model. Struct. Concr. 2018, 19, 191–216. [Google Scholar] [CrossRef]






| Slab | c (mm) | d (mm) | ρflex (%) | ρw (%) | fcm (MPa) | fy (MPa) | Shear Reinforcement | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No. of Studs Per Perimeter | Øw (mm) | No. of Perimeters | s0 (mm) | sr (mm) | fyw (MPa) | Asw/perim. (mm²) | ||||||||
| PV1 | 260 | 210 | 1.50 | 0 | --- | 34.0 | 709 | --- | --- | --- | --- | --- | --- | --- |
| PL7 | 260 | 197 | 1.59 | 0.93 | H | 35.9 | 583 | 16 | 14.0 | 7 | 80 | 160 | 519 | 2463.0 |
| PL11 | 260 | 201 | 1.56 | 0.23 | L | 34.2 | 554 | 8 | 10.0 | 7 | 80 | 160 | 592 | 628.3 |
| LC1 | 270 | 143 | 1.48 | 0.61 | M | 47.8 | 557 | 10 | 10.0 | 6 | 70 | 100 | 573 | 785.4 |
| LC2 | 360 | 140 | 1.52 | 0.50 | M | 46.9 | 557 | 10 | 10.0 | 6 | 70 | 100 | 573 | 785.4 |
| LC3 | 450 | 142 | 1.49 | 0.42 | M | 48.9 | 557 | 10 | 10.0 | 6 | 70 | 100 | 573 | 785.4 |
| LC7 | 360 | 144 | 1.47 | 0.62 | M | 49.0 | 557 | 10 | 10.0 | 7 | 55 | 100 | 573 | 785.4 |
| LC8 | 360 | 144 | 1.47 | 0.60 | M | 48.1 | 557 | 12 | 10.0 | 6 | 70 | 100 | 573 | 942.5 |
| LS5 | 300 | 143 | 1.48 | 0 | --- | 50.5 | 557 | --- | --- | --- | --- | --- | --- | --- |
| Tensile strength | * | fib Model Code 2010 [37] |
| fib Model Code 2010 [37] | ||
| Fracture energy | fib Model Code 2010 [37] | |
| CEB-FIP Model Code 1990 [16] | ||
| Crack model | --- | Fixed |
| --- | Rotating |
| Concrete | |
| Crack model | Fixed |
| fcm (MPa) | Experimental (see Table 1) |
| fct,inf (MPa) | fib Model Code 2010 [38] (see Table 2) |
| Gf (N/m) | CEB-FIP Model Code 1990 [17] (see Table 2) |
| Ec (GPa) | fib Model Code 2010 [38] (see Table 2) |
| Steel | |
| fy (MPa) | Experimental (see Table 1) |
| Es (GPa) | 200 |
| Concrete | Strategy I | Strategy II |
| Crack model | Fixed | Fixed |
| fc (MPa) | fcm,Exp | fcm,Exp |
| ft (MPa) | fct,inf (see Table 3) | fct (see Table 3) |
| Gf (N/m) | MC90 (see Table 3) | MC90 (see Table 3) |
| Ec (GPa) | MC10 (see Table 3) | MC10 (see Table 3) |
| Shear factor | 20 | 200 |
| Steel | Strategy I | Strategy II |
| fy (MPa) | fy,Exp | fy,Exp |
| Es (GPa) | 200 | 200 |
| Slab | VExp (kN) | VFEA (kN) | VMC10.LoAII (kN) | VMC10.LoAIII (kN) | VMC10.LoAIV (kN) | VExp/ | VExp/ | VExp/ | VExp/ |
|---|---|---|---|---|---|---|---|---|---|
| VFEA | VMC10.LoAII | VMC10.LoAIII | VMC10.LoAIV | ||||||
| PL7 | 1773.0 | 1736.3 | 1400.0 * | 1500.0 * | 1375.0 * | 1.02 | 1.27 | 1.18 | 1.26 |
| PL11 | 1176.0 | 940.6 | 870.0 | 905.0 | 863.0 | 1.25 | 1.35 | 1.30 | 1.09 |
| LC01 | 858.4 | 894.7 | 775.0 | 712.0 | 700.0 | 0.96 | 1.11 | 1.21 | 1.28 |
| LC02 | 955.7 | 1027.1 | 815.0 | 820.0 | 785.0 | 0.93 | 1.17 | 1.17 | 1.31 |
| LC03 | 1076.2 | 1201.2 | 863.0 | 895.0 | 875.0 | 0.90 | 1.25 | 1.20 | 1.37 |
| LC07 | 1110.4 | 1068.3 | 845.0 | 820.0 | 810.0 | 1.04 | 1.31 | 1.35 | 1.32 |
| LC08 | 1058.9 | 1083.8 | 912.0 | 938.0 | 870.0 | 0.98 | 1.16 | 1.13 | 1.25 |
| Mean | 1.01 | 1.28 | 1.27 | 1.31 | |||||
| CoV | 0.11 | 0.12 | 0.12 | 0.11 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maués, F.P.; Ferreira, M.P.; Díaz, R.A.S.; Liberati, E.A.P.; Trautwein, L.M.; Santos, J.P.B. Numerical Modelling of Flat Slabs with Different Amounts of Double-Headed Studs as Punching Shear Reinforcement. Buildings 2025, 15, 960. https://doi.org/10.3390/buildings15060960
Maués FP, Ferreira MP, Díaz RAS, Liberati EAP, Trautwein LM, Santos JPB. Numerical Modelling of Flat Slabs with Different Amounts of Double-Headed Studs as Punching Shear Reinforcement. Buildings. 2025; 15(6):960. https://doi.org/10.3390/buildings15060960
Chicago/Turabian StyleMaués, Frederico P., Mauricio P. Ferreira, Rafael A. S. Díaz, Elyson A. P. Liberati, Leandro M. Trautwein, and João P. B. Santos. 2025. "Numerical Modelling of Flat Slabs with Different Amounts of Double-Headed Studs as Punching Shear Reinforcement" Buildings 15, no. 6: 960. https://doi.org/10.3390/buildings15060960
APA StyleMaués, F. P., Ferreira, M. P., Díaz, R. A. S., Liberati, E. A. P., Trautwein, L. M., & Santos, J. P. B. (2025). Numerical Modelling of Flat Slabs with Different Amounts of Double-Headed Studs as Punching Shear Reinforcement. Buildings, 15(6), 960. https://doi.org/10.3390/buildings15060960