Model with GA and PSO: Pile Bearing Capacity Prediction and Geotechnical Validation
Abstract
1. Introduction
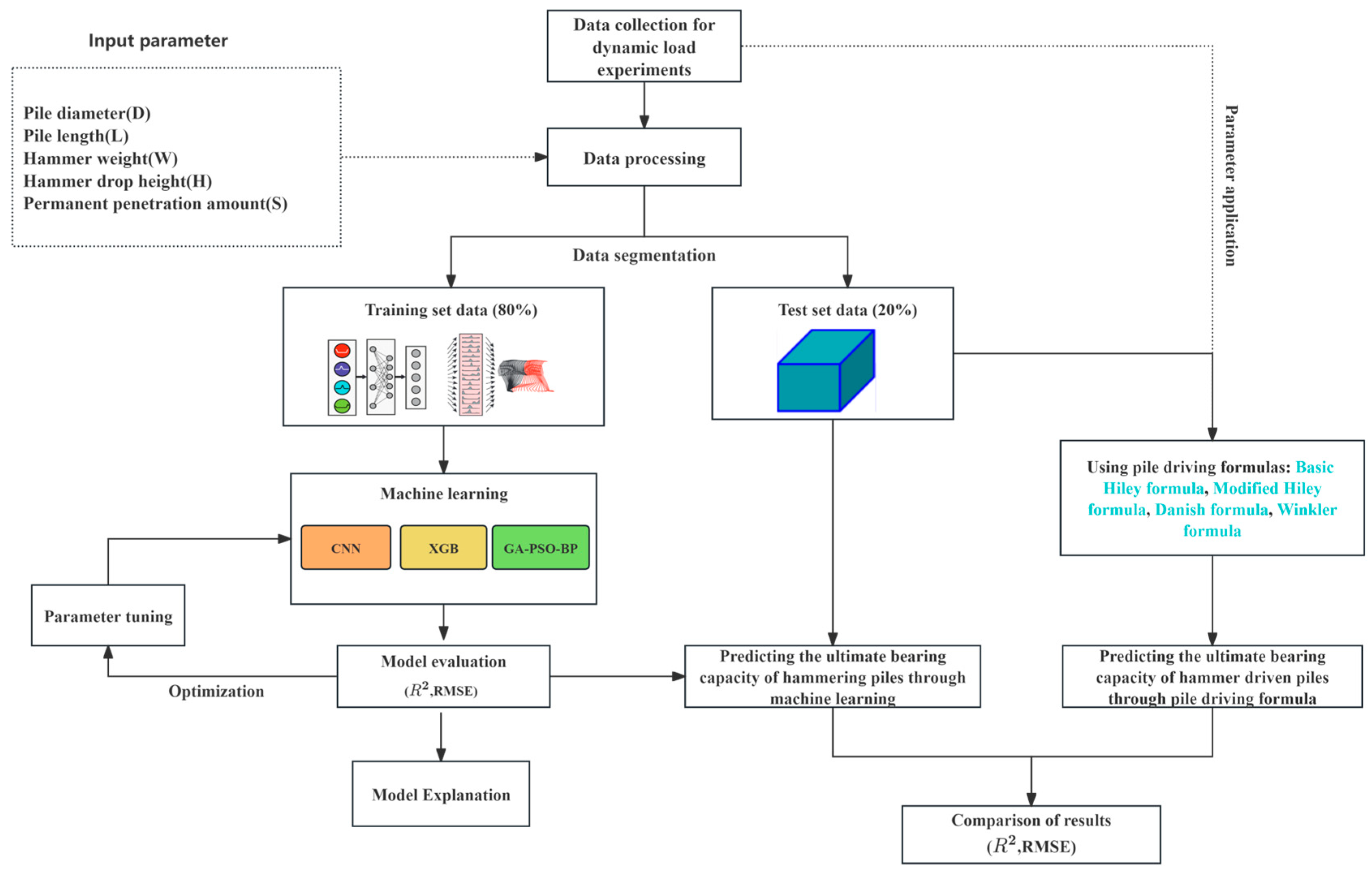
2. Methodology
2.1. Pile Dynamic Load Test
2.2. CNN (Convolutional Neural Network)
- Convolution and Feature Extraction: The core operation in CNN is the convolution process, where the input data (e.g., an image) is convolved with a set of filters (kernels) to extract local features.
- Activation Function: After convolution, a nonlinear activation function such as ReLU (Rectified Linear Unit) is applied to introduce nonlinearity.
- Pooling and Dimensionality Reduction: The pooling layer is used to downsample the feature maps, typically through max pooling or average pooling.
- Fully Connected Layer and Backpropagation: After convolution and pooling, the data is flattened into a vector and passed through fully connected layers to make predictions. The network learns to minimize the error using backpropagation, updating weights using the gradient descent method.
2.3. XBG (EXtreme Gradient Boosting)
- Model Initialization: The process starts with an initial model, usually a constant value, such as the mean of the target variable.
- Gradient Computation: In each iteration, the gradient of the loss function with respect to the current model is computed.
- Adding New Trees: A new decision tree is fit to the negative gradient (or residuals) from the previous model. This tree aims to correct the errors by learning from the gradients.
- Regularization and Final Prediction: To prevent overfitting, XGB incorporates regularization terms into the objective function, which balances the model’s complexity and accuracy.
2.4. BPNN (Back Propagation Neural Network)
- Model Initialization: The BPNN begins with an initial set of weights, which are typically initialized randomly. The input data is then passed through the network layer by layer. Each neuron computes its output by taking a weighted sum of its inputs, adding a bias term, and applying an activation function.
- Error Calculation and Backpropagation: The error between the predicted output y and the actual target value is calculated using a loss function, typically Mean Squared Error (MSE). Backpropagation involves calculating the gradient of the error with respect to each weight by applying the chain rule of differentiation.
- Weight Update: After the error gradients are computed, the weights are adjusted using gradient descent to minimize the error.
2.5. Pile Driving Formulas
2.6. Methodological Distinctions: A Machine Learning Approach Versus Conventional Analysis
3. Data Preparation and Experimental Configuration
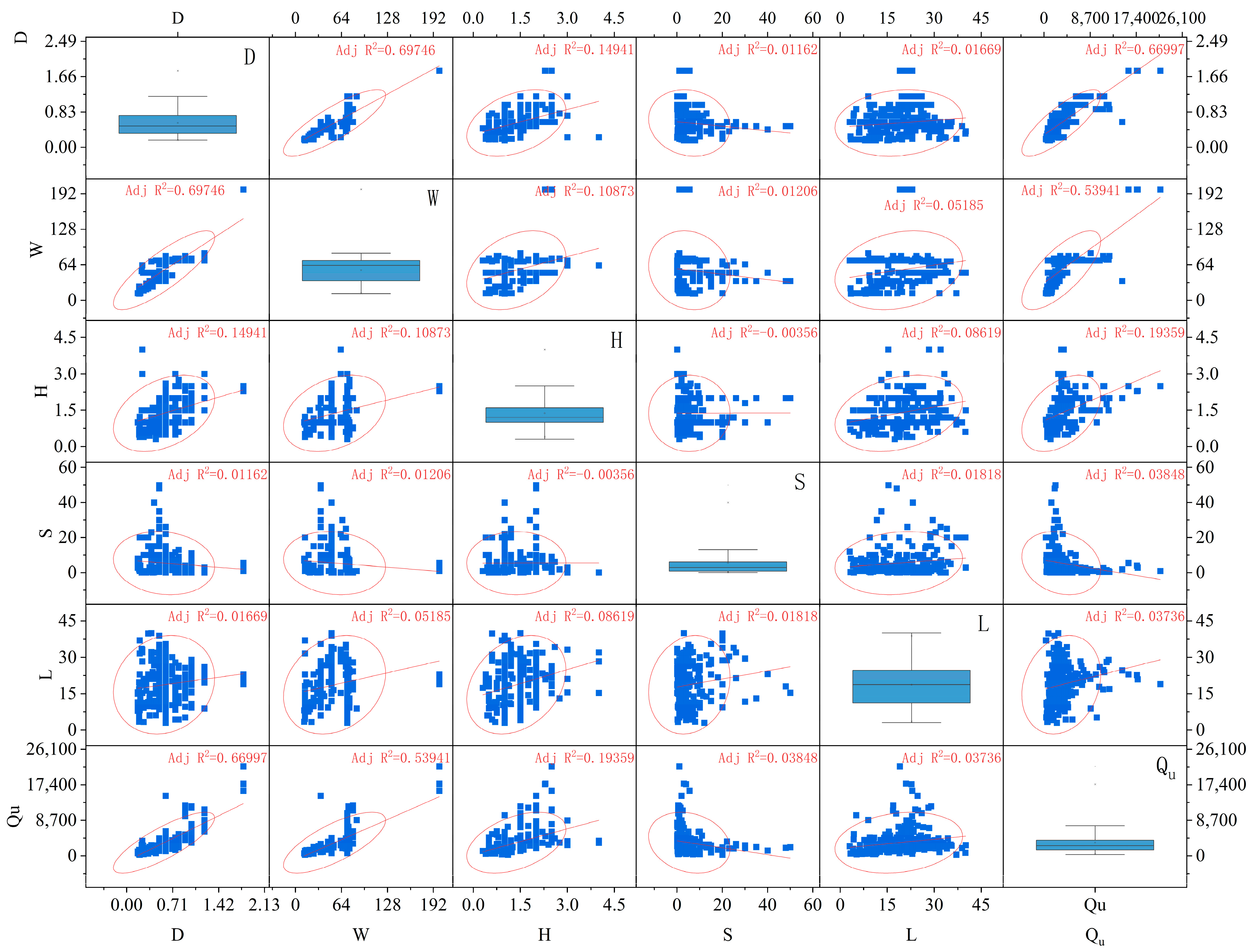
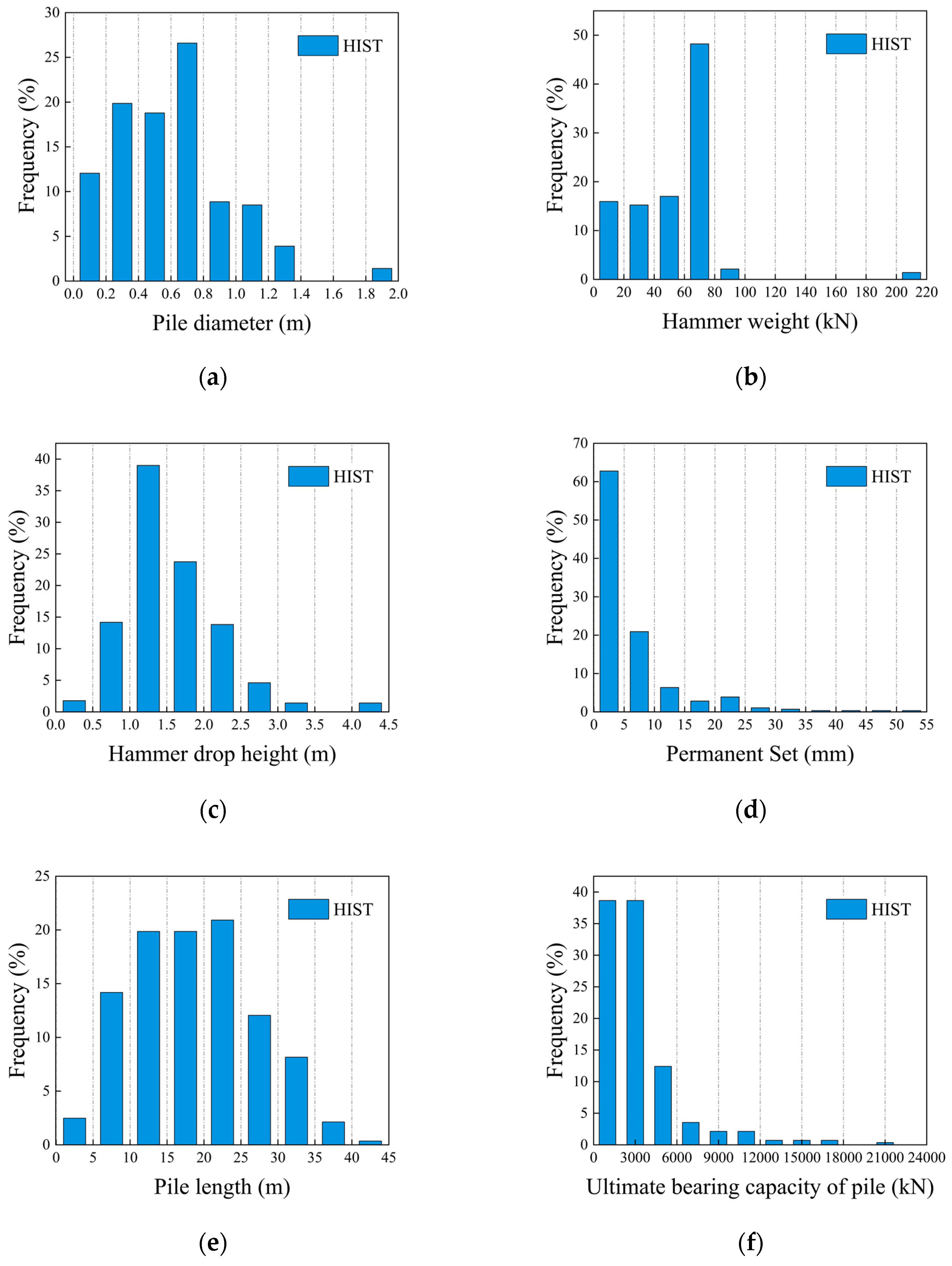
3.1. Data Preparation
3.2. Data Preprocessing
3.3. Performance Metrics
3.4. Explanatory Approach
4. Results
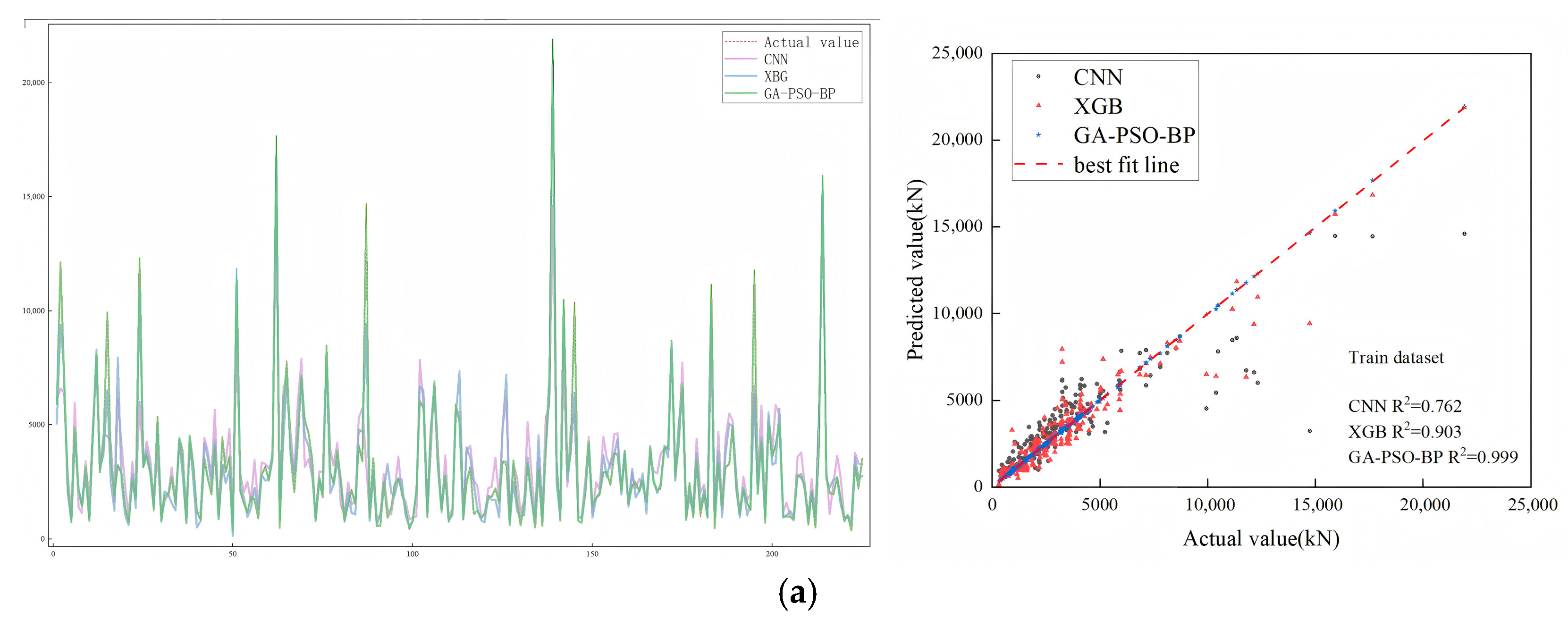
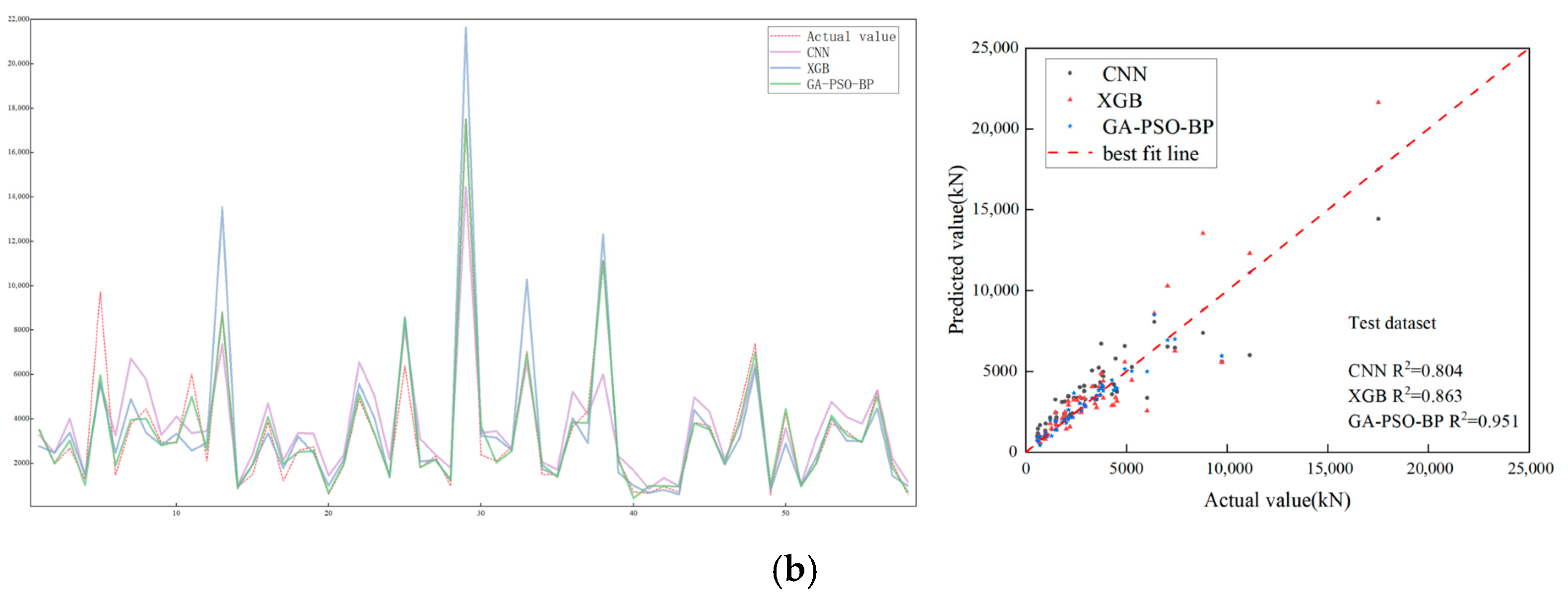
4.1. Comparison of Performance Among AI-Based Prediction Models
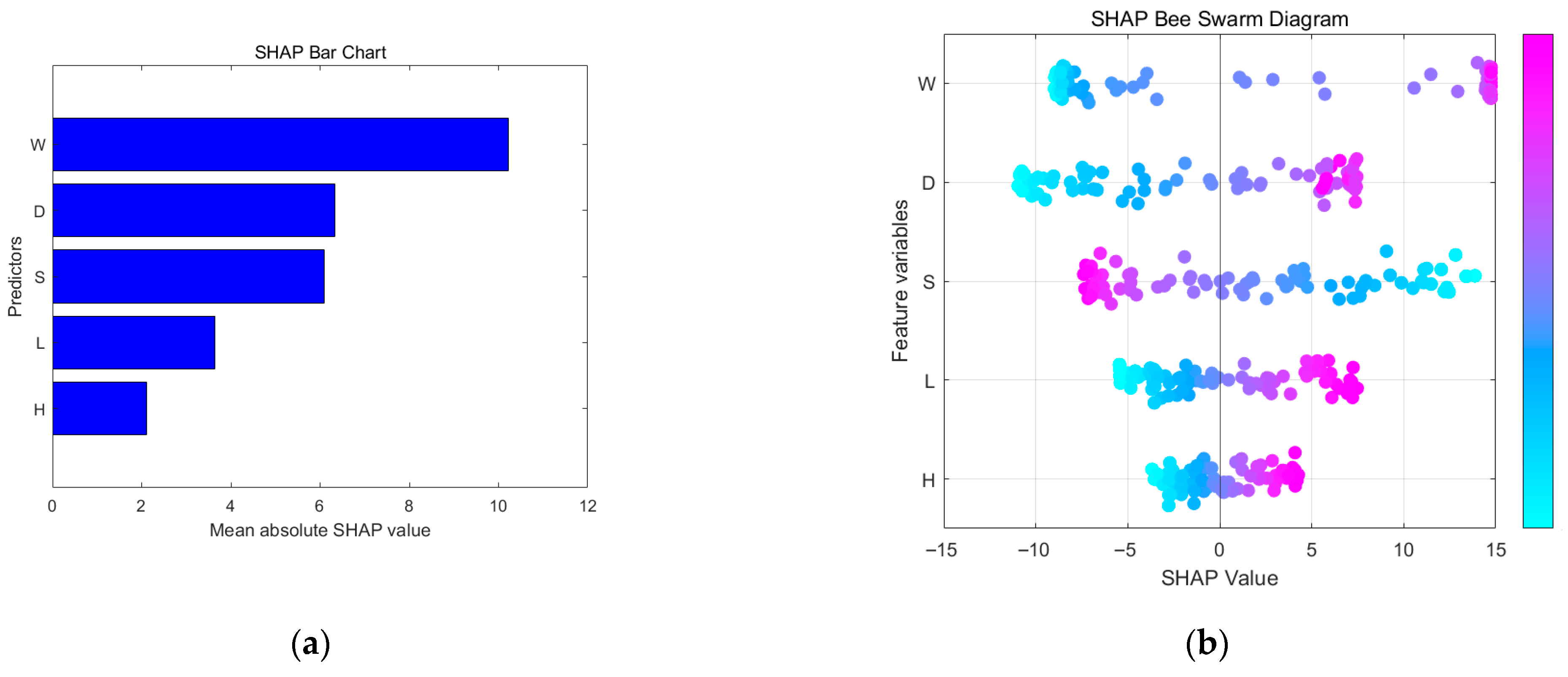
4.2. Analysis of Variable Significance in AI-Based Prediction Models
4.3. The Variable Importance Analysis of Prediction Models Based on Artificial Intelligence
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Supplementary Data Section
- The core operation in CNN is the convolution process, where the input data (e.g., an image) is convolved with a set of filters (kernels) to extract local features. Mathematically, the convolution operation can be represented as:where I is the input image, K is the kernel, and (x, y) represents the location of the filter in the image. This process helps detect basic features such as edges and textures.
- After convolution, a nonlinear activation function such as ReLU (Rectified Linear Unit) is applied to introduce nonlinearity. The ReLU activation function is mathematically expressed as:This step enables the network to learn complex patterns by modeling nonlinear relationships.
- The pooling layer is used to downsample the feature maps, typically through max pooling or average pooling. For example, max pooling can be represented aswhere X is the region in the feature map being pooled. Pooling reduces the spatial dimensions of the data, retaining the most important features while improving computational efficiency and reducing overfitting.
- After convolution and pooling, the data is flattened into a vector and passed through fully connected layers to make predictions. The network learns to minimize the error using backpropagation, updating weights using the gradient descent method. The gradient of the loss function L with respect to the weights W is computed aswhere is the loss for the i-th training example, and N denotes the total number of examples. This allows the network to iteratively adjust the weights to improve performance.
- Model Initialization: The process starts with an initial model, usually a constant value, such as the mean of the target variable. This can be expressed aswhere L is the loss function, is the true value, and h m(x) is the initial prediction (usually the mean of the target values).
- Gradient Computation: In each iteration, the gradient of the loss function with respect to the current model is computed. The gradient at each step is given bywhere is the gradient for the i-th data point, and is the model at iteration m.
- Adding New Trees: A new decision tree is fit to the negative gradient (or residuals) from the previous model. This tree aims to correct the errors by learning from the gradients, and the update rule is given bywhere is the newly trained tree, and is the learning rate that controls the step size.
- Regularization and Final Prediction: To prevent overfitting, XGB incorporates regularization terms into the objective function, which balances the model’s complexity and accuracy. The final model is given bywhere is a regularization term for the tree k, typically penalizing the complexity of the model (e.g., the number of leaf nodes).
- 9.
- Model Initialization: The BPNN begins with an initial set of weights, which are typically initialized randomly. The input data is then passed through the network layer by layer. Each neuron computes its output by taking a weighted sum of its inputs, adding a bias term, and applying an activation function:where is the activation of the j-th neuron, are the weights, are the inputs, is the bias term, and f is the activation function.
- 10.
- Error Calculation and Backpropagation: The error between the predicted output y and the actual target value is calculated using a loss function, typically Mean Squared Error (MSE):Backpropagation involves calculating the gradient of the error with respect to each weight by applying the chain rule of differentiation. The weight updates are computed as
- 11.
- Weight Update: After the error gradients are computed, the weights are adjusted using gradient descent to minimize the error. The weight update rule is
References
- Meyerhof, G.G.; Asce, F. Bearing Capacity and Settlement of Pile Foundations. J. Geotech. Eng. Div. ASCE 1976, 102, 197–228. [Google Scholar] [CrossRef]
- Yin, J.; Bai, X.; Yan, N.; Sang, S.; Cui, L.; Liu, J.; Zhang, M. Dynamic Damage Characteristics of Mudstone around Hammer Driven Pile and Evaluation of Pile Bearing Capacity. Soil Dyn. Earthq. Eng. 2023, 167, 107789. [Google Scholar] [CrossRef]
- Alwalan, M.F.; El Naggar, M.H. Analytical Models of Impact Force-Time Response Generated from High Strain Dynamic Load Test on Driven and Helical Piles. Comput. Geotech. 2020, 128, 103834. [Google Scholar] [CrossRef]
- Alkroosh, I.; Nikraz, H. Predicting Pile Dynamic Capacity via Application of an Evolutionary Algorithm. Soils Found. 2014, 54, 233–242. [Google Scholar] [CrossRef]
- Zhang, R.; Xue, X. A Novel Hybrid Model for Predicting the End-bearing Capacity of Rock-socketed Piles. Rock Mech. Rock Eng. 2024, 57, 10099–10114. [Google Scholar] [CrossRef]
- Maizir, H.; Suryanita, R.; Jingga, H. Estimation of Pile Bearing Capacity of Single Driven Pile in Sandy Soil Using Finite Element and Artificial Neural Network Methods. Int. J. Appl. Phys. Sci. 2016, 2, 50002–50003. [Google Scholar] [CrossRef]
- Kordjazi, A.; Pooya Nejad, F.; Jaksa, M.B. Prediction of Ultimate Axial Load-Carrying Capacity of Piles Using a Support Vector Machine Based on CPT Data. Comput. Geotech. 2014, 55, 91–102. [Google Scholar] [CrossRef]
- Alkroosh, I.S.; Bahadori, M.; Nikraz, H.; Bahadori, A. Regressive Approach for Predicting Bearing Capacity of Bored Piles from Cone Penetration Test Data. J. Rock Mech. Geotech. Eng. 2015, 7, 584–592. [Google Scholar] [CrossRef]
- Jahed Armaghani, D.; Shoib, R.S.N.S.B.R.; Faizi, K.; Rashid, A.S.A. Developing a Hybrid PSO–ANN Model for Estimating the Ultimate Bearing Capacity of Rock-Socketed Piles. Neural Comput. Appl. 2017, 28, 391–405. [Google Scholar] [CrossRef]
- Wang, B.; Moayedi, H.; Nguyen, H.; Foong, L.K.; Rashid, A.S.A. Feasibility of a Novel Predictive Technique Based on Artificial Neural Network Optimized with Particle Swarm Optimization Estimating Pullout Bearing Capacity of Helical Piles. Eng. Comput. 2020, 36, 1315–1324. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Harandizadeh, H.; Momeni, E.; Maizir, H.; Zhou, J. An Optimized System of GMDH-ANFIS Predictive Model by ICA for Estimating Pile Bearing Capacity. Artif. Intell. Rev. 2022, 55, 2313–2350. [Google Scholar] [CrossRef]
- Yong, W. A New Hybrid Simulated Annealing-Based Genetic Programming Technique to Predict the Ultimate Bearing Capacity of Piles. Eng. Comput. 2021, 37, 2111–2127. [Google Scholar] [CrossRef]
- Prayogo, D.; Susanto, Y.T.T. Optimizing the Prediction Accuracy of Friction Capacity of Driven Piles in Cohesive Soil Using a Novel Self-Tuning Least Squares Support Vector Machine. Adv. Civ. Eng. 2018, 2018, 6490169. [Google Scholar] [CrossRef]
- Borthakur, N.; Dey, A.K. Evaluation of Group Capacity of Micropile in Soft Clayey Soil from Experimental Analysis Using SVM-Based Prediction Model. Int. J. Geomech. 2020, 20, 04020008. [Google Scholar] [CrossRef]
- Harandizadeh, H.; Toufigh, M.M.; Toufigh, V. Application of Improved ANFIS Approaches to Estimate Bearing Capacity of Piles. Soft Comput. 2019, 23, 9537–9549. [Google Scholar] [CrossRef]
- Harandizadeh, H.; Jahed Armaghani, D.; Khari, M. A New Development of ANFIS–GMDH Optimized by PSO to Predict Pile Bearing Capacity Based on Experimental Datasets. Eng. Comput. 2021, 37, 685–700. [Google Scholar] [CrossRef]
- Dehghanbanadaki, A.; Khari, M.; Amiri, S.T.; Armaghani, D.J. Estimation of Ultimate Bearing Capacity of Driven Piles in C-φ Soil Using MLP-GWO and ANFIS-GWO Models: A Comparative Study. Soft Comput. 2021, 25, 4103–4119. [Google Scholar] [CrossRef]
- Momeni, E.; Dowlatshahi, M.B.; Omidinasab, F.; Maizir, H.; Armaghani, D.J. Gaussian Process Regression Technique to Estimate the Pile Bearing Capacity. Arab. J. Sci. Eng. 2020, 45, 8255–8267. [Google Scholar] [CrossRef]
- Momeni, E.; Nazir, R.; Jahed Armaghani, D.; Maizir, H. Application of Artificial Neural Network for Predicting Shaft and Tip Resistances of Concrete Piles. Earth Sci. Res. J. 2015, 19, 85–93. [Google Scholar] [CrossRef]
- Moayedi, H.; Moatamediyan, A.; Nguyen, H.; Bui, X.-N.; Bui, D.T.; Rashid, A.S.A. Prediction of Ultimate Bearing Capacity through Various Novel Evolutionary and Neural Network Models. Eng. Comput. 2020, 36, 671–687. [Google Scholar] [CrossRef]
- Pham, T.A.; Tran, V.Q.; Vu, H.-L.T.; Ly, H.-B. Design Deep Neural Network Architecture Using a Genetic Algorithm for Estimation of Pile Bearing Capacity. PLoS ONE 2020, 15, e0243030. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.; Kumar, D.R.; Khatti, J.; Samui, P.; Grover, K.S. Prediction of Bearing Capacity of Pile Foundation Using Deep Learning Approaches. Front. Struct. Civ. Eng. 2024, 18, 870–886. [Google Scholar] [CrossRef]
- Pham, T.A.; Ly, H.-B.; Tran, V.Q.; Giap, L.V.; Vu, H.-L.T.; Duong, H.-A.T. Prediction of Pile Axial Bearing Capacity Using Artificial Neural Network and Random Forest. Appl. Sci. 2020, 10, 1871. [Google Scholar] [CrossRef]
- Yaychi, B.M.; Esmaeili-Falak, M. Estimating Axial Bearing Capacity of Driven Piles Using Tuned Random Forest Frameworks. Geotech. Geol. Eng. 2024, 42, 7813–7834. [Google Scholar] [CrossRef]
- Amjad, M.; Ahmad, I.; Ahmad, M.; Wróblewski, P.; Kamiński, P.; Amjad, U. Prediction of Pile Bearing Capacity Using XGBoost Algorithm: Modeling and Performance Evaluation. Appl. Sci. 2022, 12, 2126. [Google Scholar] [CrossRef]
- Esmaeili-Falak, M.; Benemaran, R.S. Ensemble Extreme Gradient Boosting Based Models to Predict the Bearing Capacity of Micropile Group. Appl. Ocean Res. 2024, 151, 104149. [Google Scholar] [CrossRef]
- Nguyen, H.; Cao, M.-T.; Tran, X.-L.; Tran, T.-H.; Hoang, N.-D. A Novel Whale Optimization Algorithm Optimized XGBoost Regression for Estimating Bearing Capacity of Concrete Piles. Neural Comput. Appl. 2023, 35, 3825–3852. [Google Scholar] [CrossRef]
- Moayedi, H.; Jahed Armaghani, D. Optimizing an ANN Model with ICA for Estimating Bearing Capacity of Driven Pile in Cohesionless Soil. Eng. Comput. 2018, 34, 347–356. [Google Scholar] [CrossRef]
- Yago, G.; Verri, F.; Ribeiro, D. Use of Machine Learning Techniques for Predicting the Bearing Capacity of Piles. Soils Rocks 2021, 44, e2021074921. [Google Scholar] [CrossRef]
- Kardani, N.; Zhou, A.; Nazem, M.; Shen, S.-L. Estimation of Bearing Capacity of Piles in Cohesionless Soil Using Optimised Machine Learning Approaches. Geotech. Geol. Eng. 2020, 38, 2271–2291. [Google Scholar] [CrossRef]
- Zhou, T. Developing a Machine Learning-Driven Model That Leverages Meta-Heuristic Algorithms to Forecast the Load-Bearing Capacity of Piles. J. Artif. Intell. Syst. Model. 2023, 1, 1–14. [Google Scholar] [CrossRef]
- Liu, Q.; Cao, Y.; Wang, C. Prediction of Ultimate Axial Load-Carrying Capacity for Driven Piles Using Machine Learning Methods. In Proceedings of the 2019 IEEE 3rd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 March 2019. [Google Scholar]
- Yousheng, D.; Keqin, Z.; Zhongju, F.; Wen, Z.; Xinjun, Z.; Huiling, Z. Machine Learning Based Prediction Model for the Pile Bearing Capacity of Saline Soils in Cold Regions. Structures 2024, 59, 105735. [Google Scholar] [CrossRef]
- Dadhich, S.; Sharma, J.K.; Madhira, M. Prediction of Ultimate Bearing Capacity of Aggregate Pier Reinforced Clay Using Machine Learning. Int. J. Geosynth. Ground Eng. 2021, 7, 44. [Google Scholar] [CrossRef]
- Sun, Z.; Liu, F.; Han, Y.; Min, R. Prediction of Ultimate Bearing Capacity of Rock-Socketed Piles Based on GWO-SVR Algorithm. Structures 2024, 61, 106039. [Google Scholar] [CrossRef]
- Cao, Y.; Ni, J.; Chen, J.; Geng, Y. Rapid Evaluation Method to Vertical Bearing Capacity of Pile Group Foundation Based on Machine Learning. Sensors 2025, 25, 1214. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Li, H.; Li, Y.; Liu, H.; Chen, Y.; Ding, X. Application of Deep Learning Algorithms in Geotechnical Engineering: A Short Critical Review. Artif. Intell. Rev. 2021, 54, 5633–5673. [Google Scholar] [CrossRef]
- Karakaş, S.; Taşkın, G.; Ülker, M.B.C. Re-Evaluation of Machine Learning Models for Predicting Ultimate Bearing Capacity of Piles through SHAP and Joint Shapley Methods. Neural Comput. Appl. 2024, 36, 697–715. [Google Scholar] [CrossRef]
- Ouyang, W.; Li, G.; Chen, L.; Liu, S.-W. Machine Learning-Based Soil–Structure Interaction Analysis of Laterally Loaded Piles through Physics-Informed Neural Networks. Acta Geotech. 2024, 19, 4765–4790. [Google Scholar] [CrossRef]
- Abdulkadirov, R.; Lyakhov, P.; Nagornov, N. Survey of Optimization Algorithms in Modern Neural Networks. Mathematics 2023, 11, 2466. [Google Scholar] [CrossRef]
- Rausche, F.; Moses, F.; Goble, G.G. Soil resistance predictions from pile dynamics. J. Soil Mech. Found. Div. 1972, 98, 917–937. [Google Scholar] [CrossRef]
- Rausche, F.; Goble, G.G.; Likins, G.E., Jr. Dynamic determination of pile capacity. J. Geotech. Eng. 1985, 111, 367–383. [Google Scholar] [CrossRef]
- Hannigan, P.J.; Goble, G.G.; Thendean, G.; Likins, G.E.; Rausche, F. Design and Construction of Driven Pile Foundations—Volume I (Report No. FHWA-HI-97-013); Federal Highway Administration: Washington, DC, USA, 1998. Available online: https://rosap.ntl.bts.gov/view/dot/58200 (accessed on 20 October 2025).
- ASTM D4945; Standard Test Method for High-Strain Dynamic Testing of Piles. ASTM International: West Conshohocken, PA, USA, 1989.
- EN ISO 22476-1; Geotechnical Investigation and Testing—Field Testing—Part 1: Electrical Resistivity and High-Strain Dynamic Testing of Piles. International Organization for Standardization (ISO): Geneva, Switzerland, 2012.
- Paikowsky, S.G.; Hart, L.J. Development and Field Testing of Multiple Deployment Model Pile (MDMP) (Report No. FHWA-RD-99-194); Federal Highway Administration: Washington, DC, USA, 2000. Available online: https://highways.dot.gov/sites/fhwa.dot.gov/files/FHWA-RD-99-194.pdf (accessed on 20 October 2025).
- Prakash, S.; Sharma, H.D. Pile Foundations in Engineering Practice; John Wiley & Sons: Hoboken, NJ, USA, 1991. [Google Scholar]
- Pessoa, A.D.; Sousa, G.C.L.D.; Araujo, R.D.C.D.; Anjos, G.J.M.D. Artificial Neural Network Model for Predicting Load Capacity of Driven Piles. Res. Soc. Dev. 2021, 10, e12210111526. [Google Scholar] [CrossRef]
- Momeni, E.; Nazir, R.; Jahed Armaghani, D.; Maizir, H. Prediction of Pile Bearing Capacity Using a Hybrid Genetic Algorithm-Based ANN. Measurement 2014, 57, 122–131. [Google Scholar] [CrossRef]
- Antwarg, L.; Miller, R.M.; Shapira, B.; Rokach, L. Explaining Anomalies Detected by Autoencoders Using Shapley Additive Explanations. Expert Syst. Appl. 2021, 186, 115736. [Google Scholar] [CrossRef]
- Wang, J.-C.; Yu, J.; Shiguo, M.; Gong, X. Hammer’s Impact Force on Pile and Pile’s Penetration. Mar. Georesour. Geotechnol. 2016, 34, 409–419. [Google Scholar] [CrossRef]

| Equation Title | Equation Representation | Formula Annotation | Units | Description |
|---|---|---|---|---|
| Hiley | : Hammer efficiency : Ram weight S: Permanent penetration per : Pile weight | : Unitless : kN h: m S: m : Unitless : kN | No parameter tuning on the test set; constants are empirically determined from training data and may vary by soil conditions. | |
| Winkler | K: Empirical correction factor (dimensionless) | : kN S: m K: Unitless | This formula uses an empirical factor K, adjusted for soil conditions and pile type. | |
| Danish | C: Elastic compression term (m) l: Pile length A: Pile cross-sectional area : Elastic modulus of pile material | : Unitless : kN h: m S: m C: m l: mA: : Mpa | This formula improves on Hiley by considering pile length and material stiffness (via ) to better estimate bearing capacity. | |
| Modified Hiley | M: Ram weight X: Hammer drop height Q: Elastic compression of the pile-soil system | E: Mpa M: kN X: m S: m : kN | This modified formula improves prediction accuracy by considering pile material stiffness. | |
| Modified Danish | E: Hammer efficiency | E: Mpa : kN h: m S: m : kN | This formula refines the elastic compression term to better match observed pile behavior during driving. |
| Model | XGB | CNN | GA-PSO-BPNN |
|---|---|---|---|
| Control parameter | n_estimators = 300 learning_rate = 0.001 max_depth = 10 | Input Layer Shape: [32, 1, 5, 1] Convolutional Layer Filters: 32, Kernel size: [10, 1] Pooling Layer Pool size: [1, 10], Stride: 10 Adam optimizer, Learning rate: 0.004 | population size = 450 = 2.286, = 1.714 genetic operation size = 25 |
| Model | MAPE | RMSE | MAE | |||||
|---|---|---|---|---|---|---|---|---|
| TR | TE | TR | TE | TR | TE | TR | TE | |
| CNN | 0.762 | 0.804 | 0.325 | 0.381 | 1520.31 | 1390.90 | 867.72 | 998.94 |
| XGB | 0.903 | 0.863 | 0.210 | 0.239 | 945.87 | 1350.07 | 521.52 | 836.15 |
| GA-PSO-BPNN | 0.999 | 0.951 | 0.013 | 0.135 | 39.28 | 660.13 | 27.41 | 328.51 |
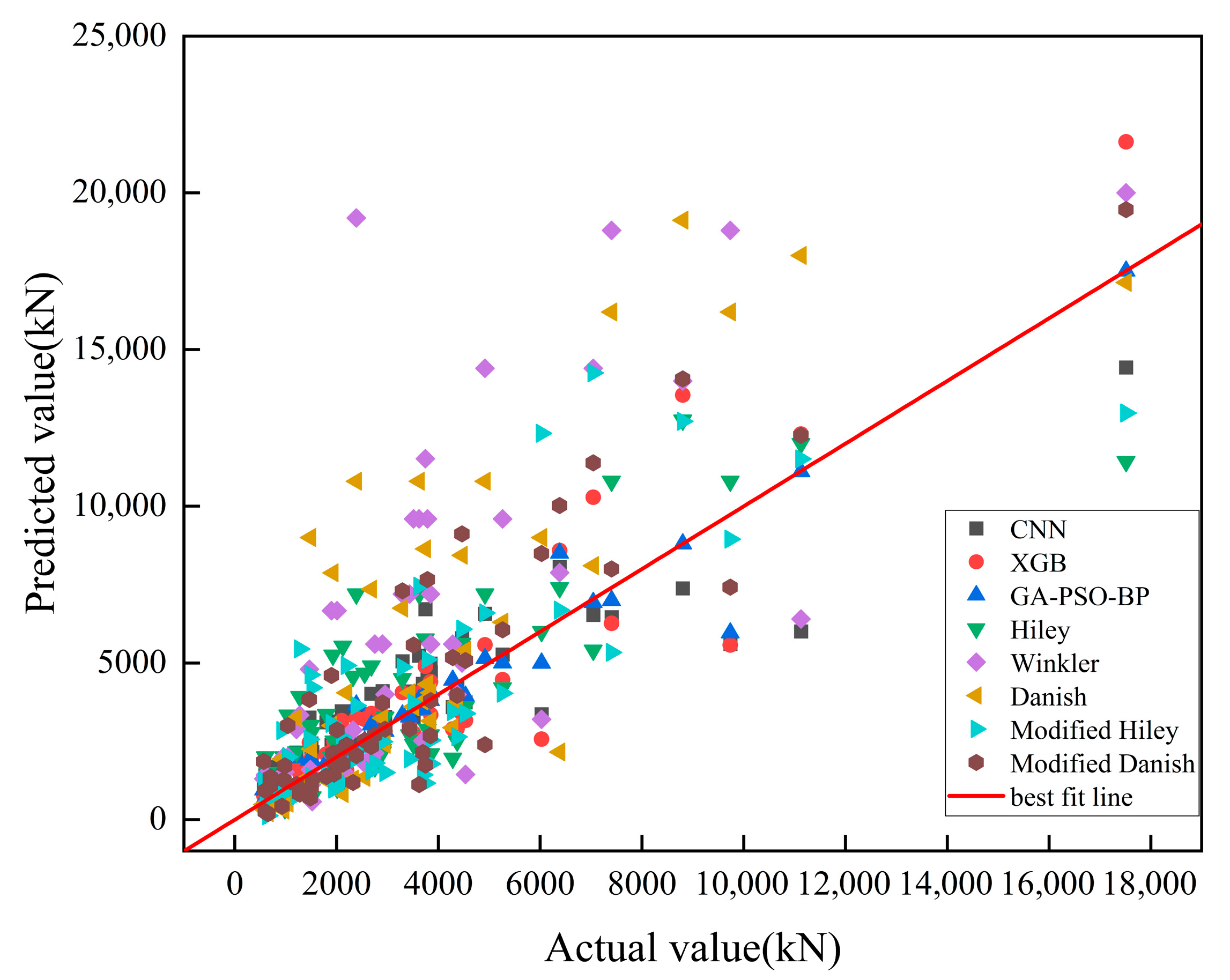
| Model | MAPE | RMSE | MAE | |
|---|---|---|---|---|
| CNN | 0.804 | 0.381 | 1390.9 | 998.49 |
| XGB | 0.863 | 0.239 | 1350.07 | 836.15 |
| GA-PSO-BPNN | 0.951 | 0.135 | 660.13 | 328.51 |
| Hiley | 0.588 | 0.615 | 1890.48 | 1460.69 |
| Winkler | −0.863 | 0.901 | 4240.56 | 2748.28 |
| Danish | −0.286 | 0.681 | 3342.23 | 2043.95 |
| Modified Hiley | 0.515 | 0.523 | 2051.78 | 1415.28 |
| Modified Danish | 0.638 | 0.456 | 1773.24 | 1211.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, H.; Li, Z.; Xu, Q.; Sang, Q.; Zheng, R. Model with GA and PSO: Pile Bearing Capacity Prediction and Geotechnical Validation. Buildings 2025, 15, 3839. https://doi.org/10.3390/buildings15213839
Jin H, Li Z, Xu Q, Sang Q, Zheng R. Model with GA and PSO: Pile Bearing Capacity Prediction and Geotechnical Validation. Buildings. 2025; 15(21):3839. https://doi.org/10.3390/buildings15213839
Chicago/Turabian StyleJin, Haobo, Zhiqiang Li, Qiqi Xu, Qinyang Sang, and Rongyue Zheng. 2025. "Model with GA and PSO: Pile Bearing Capacity Prediction and Geotechnical Validation" Buildings 15, no. 21: 3839. https://doi.org/10.3390/buildings15213839
APA StyleJin, H., Li, Z., Xu, Q., Sang, Q., & Zheng, R. (2025). Model with GA and PSO: Pile Bearing Capacity Prediction and Geotechnical Validation. Buildings, 15(21), 3839. https://doi.org/10.3390/buildings15213839






