Analysis of Torsional Vibration of Single Pile in Orthotropic Layered Soil

Abstract

To address the difficulty in obtaining analytical solutions for the torsional vibration response of pile foundations in orthotropic layered soil foundations subjected to torsional excitation at the pile top, this study investigates a layered recursive algorithm based on the Hankel transform. An integral transformation method is employed to reduce the dimensionality of the coupled pile–soil torsional vibration equations, converting the three-dimensional system of partial differential equations into a set of ordinary differential equations. Combining the constitutive properties of transversely anisotropic strata with interlayer contact conditions, a transfer matrix model is established. Employing inverse transformation coupled with the Gauss–Kronrod integration method, an explicit frequency-domain solution for the torsional dynamic impedance at the pile top is derived. The research findings indicate that the anisotropy coefficient of the foundation significantly influences both the real and imaginary parts of the impedance magnitude. The sequence of soil layer distribution and the bonding state at interfaces jointly affect the nonlinear transmission characteristics of torque along the pile shaft.

1. Introduction

As the core load-bearing component in offshore wind turbines and high-rise structures subjected to eccentric loads, the torsional vibration characteristics of pile foundations directly impact the safety performance of superstructures under dynamic torque loads. In the early stages of research, the focus was predominantly on the utilization of simplified soil models, including the dynamic Winkler model and the plane strain model. These models simulate pile–soil interactions by introducing virtual springs and damping, thus offering a computational simplicity that is suitable for preliminary design. However, the Winkler model neglects interlayer soil connectivity and vertical stress gradient variations within the soil, while the plane strain model considers only horizontal wave propagation. This approach is inadequate in accurately capturing the three-dimensional wave effects in the soil surrounding the pile, resulting in substantial prediction errors in the high-frequency response range. Despite the fact that Novak’s classical model [1,2,3] provides a closed-form solution for torsional impedance in homogeneous isotropic soils, its plane strain assumption overestimates system stiffness at high frequencies by neglecting vertical wave components. This limitation constrains its applicability in complex soil conditions prevalent in practical engineering. Therefore, the adoption of a more rigorous three-dimensional viscoelastic soil medium model to study pile–soil dynamic interaction effects in pile foundation time-domain vibration theory holds greater theoretical and engineering value for elucidating vibration mechanisms and enhancing the applicability of theoretical solutions.

As research progresses, scholars have adopted three-dimensional viscoelastic soil models to enhance the precision of their findings. In the domain of homogeneous isotropic soils, Hu et al. [4] conducted a study to ascertain the frequency-domain characteristics of pile-top vibration responses. However, a key limitation of this and similar models is their assumption of soil homogeneity and isotropy, which struggles to characterize the inherent anisotropy of layered soils and the complex coupling effects of interlayer wave reflection. Cheng (2017) conducted an investigation into the torsional characteristics of single piles based on the Vlasov foundation model [5]. However, it was determined that this model’s simplification does not fully capture three-dimensional wave energy dissipation. Ding et al. (2021) systematically elaborated the principles of pile foundation dynamics [6], while Chen Shengli and Zhang Limin analyzed the torsional deformation of single piles in layered foundations using the integral equation method [7]. Yang et al. [8] utilized the integral equation method to analyze the mechanical behavior of single piles in layered soil, thereby confirming the reconstructive effect of soil layer distribution order on torque transmission paths. Yang [9] and Guan [10], respectively, investigated the longitudinal vibration characteristics of pile foundations in heterogeneous soil. However, a significant gap remained as they did not extend their studies to torsional conditions.

Notably, existing research primarily focuses on the longitudinal and lateral vibration analysis of pile foundations in homogeneous isotropic soils (e.g., the analysis of torsional vibration in static-drilled root piles by Zhao et al. [11], the solution for layered unsaturated viscoelastic soils by Liu et al. [12], and the response analysis of tubular piles in transversely isotropic saturated soils by Ma et al. [13]). Recent advancements by Nghiem (2023) [14] and Sun et al. (2024) [15] have extended the analysis to multi-layered and radially heterogeneous soils using variational and semi-analytical approaches, respectively. However, a comprehensive theoretical framework that simultaneously incorporates full orthotropic anisotropy, layered media, and three-dimensional wave effects for torsional vibration remains unestablished.

Traditional models face two major limitations: First, the homogeneity assumption struggles to characterize the anisotropy of layered soil and the interlayer wave reflection coupling effects. The layered foundation solution by Wang et al. [16] neglects stiffness variations along the principal material axis, leading to significant prediction errors in torque attenuation. Second, simplified models (such as the integral equation method by Liang et al. [17] and the vertical vibration Hankel transform solution by Gan [18]) fail to accurately capture three-dimensional wave energy dissipation. Cui et al. [19] noted that the frequency-dependent characteristics of torsional vibration impedance in pile foundations within bidirectionally heterogeneous clay are governed by the spatial distribution of soil damping. Recent studies have made progress under various complex conditions: Chen et al. (2022) derived a semi-analytical solution for vertical pile vibration in a frozen-soil porous elastic half-space, revealing the influence of freezing temperature and pile-base support stiffness on dynamic response [20]; Ren & Wang (2024) employed a fractional-order Kelvin model to describe the rheological effects in saturated clay, obtaining time-domain solutions for horizontal vibrations via the Laplace transform and demonstrating the effects of soil rheology on displacement delay and internal force redistribution [21]. For composite pile foundations, Su et al. (2023) analyzed the dynamic impedance of deep cement mixing piles (DCM piles) with concrete cores under horizontal dynamic loading, emphasizing the influence of pile radius and elastic modulus. Their parametric analysis indicated that increased soil density enhances the stiffness factor but reduces the damping factor [22]. Additionally, Pérez et al. (2023) demonstrated through experiments and finite element simulations that open-ended thin-walled steel piles exhibit significant bending–torsion coupling under lateral loads. Traditional bending models underestimate displacements by 44–58%, prompting the introduction of a torsion sensitivity index to quantify errors [23]. Zhong & Meng (2023) investigated the dynamic response of multi-defect pipe piles, theoretically analyzing the effects of defect type, severity, and distribution on velocity admittance, thereby providing a theoretical basis for defect detection [24].

This paper overcomes limitations in existing research: based on Nghiem’s (2023) variational method for multi-layer soil solutions [14], Ma et al.’s (2022) unsaturated soil theory for pipe piles [25], and Sun et al.’s (2024) radially heterogeneous [15], transversely isotropic saturated soil model, this study constructs a three-dimensional viscoelastic orthotropic layered foundation–pile coupled system. Innovatively introducing the Hankel transform layered recursive algorithm (based on Zhang‘s (2024) study on torsional vibration of pipe piles in radially heterogeneous saturated soil) [26], this work establishes a pile–soil interface coupling equation, accounting for vertical stress gradients. It quantitatively reveals the regulatory mechanisms of anisotropy coefficients and interlayer contact conditions on dynamic impedance. This method provides theoretical support for the torsional design of pile foundations in complex strata, addressing the limitations of finite element calculations in computational efficiency and high experimental costs.

Furthermore, the validated model offers a robust foundation for extending the analysis to complex soil–structure interaction scenarios, such as seismic pounding between adjacent structures. The accurate quantification of dynamic impedance and resonance frequency shifts is critical for assessing impact forces and energy concentration during such events. Recent research by Bagheri et al. (2025) [27], through three-dimensional SSI modeling, systematically studied the seismic performance of long–short combined piled raft foundations under seismic pounding effects, emphasizing the importance of precise quantification of dynamic impedance for evaluating impact forces and energy concentration. This provides a theoretical validation scenario for the model presented in this paper in predicting the amplification effect of torsional responses induced by earthquakes. Furthermore, Asgari et al. (2025) [28] explored the seismic resilience of foundation systems in liquefiable soils, revealing through three-dimensional parallel finite element modeling the impact of soil liquefaction on the dynamic characteristics of foundations. Their conclusions on the energy redistribution and damping enhancement mechanisms of interface slip highly align with the nonlinear slip conditions discussed in this study, providing experimental support for the engineering application of the proposed model. Research from a deep excavation perspective, such as the rational design solutions for soil nail wall systems discussed by Alkhdour et al. (2023) [29], although focused on slope support, provides cross-disciplinary validation for the pile–soil interaction model in orthotropic anisotropic strata, presented in this paper through discussions on soil anisotropy and interface mechanical behavior.

This study systematically quantifies the frequency-domain closed-form solution for the torsional impedance of a single pile in orthotropic anisotropic soil for the first time by developing a hierarchical recursive analytical algorithm. It reveals the differential regulation patterns of the anisotropy coefficient on the real and imaginary parts of the impedance, as well as the physical mechanism by which the soil sequence reconstructs the torque transmission path through wave-impedance matching. This achievement addresses the limitations of classical models in characterizing three-dimensional wave energy dissipation, providing a theoretical framework for optimizing pile foundation torsional resistance design based on soil intrinsic properties. The verified model can be extended to evaluate soil–structure interaction under seismic pounding conditions where impact forces may amplify torsional responses, offering valuable insights for foundation design in seismically active regions. Subsequent sections will detail the process of constitutive model simplification, establishment of governing equations, Hankel transform dimensionality reduction, construction of transfer matrices, and derivation of impedance closed-form solutions. The reliability and applicability boundaries of the model will be validated through degeneracy verification, parameter analysis, and engineering case studies.

2. Constitutive Relations of Orthotropic Anisotropic Soil

2.1. Orthotropic Elasticity Theory

Orthotropic anisotropy refers to the symmetrical, yet independent mechanical response exhibited along three mutually perpendicular principal elastic directions (labeled as axes 1, 2, and 3, typically corresponding to the radial, circumferential, and vertical directions in soil). This phenomenon is commonly observed in layered soils (e.g., horizontal sedimentation resulting in lateral isotropy and vertical anisotropy). The generalized Hooke’s law describes the constitutive relationship:

$$\left\{\left.\sigma \right\}\right.=\left[C\right]\left\{\left.\epsilon \right\}\right.$$

(1)

In the formula

$\left\{\left.\sigma \right\}\right.={\left[{\sigma }_{11},{\sigma }_{22},{\sigma }_{33},{\sigma }_{23},{\sigma }_{31},{\sigma }_{12}\right]}^T$ is Stress component; $\left\{\left.\epsilon \right\}\right.={\left[{\epsilon }_{11},{\epsilon }_{22},{\epsilon }_{33},2{\epsilon }_{23},2{\epsilon }_{31},2{\epsilon }_{12}\right]}^T$ is Strain component.

In the formula

$\left[C\right]$ is the stiffness matrix, containing nine parameters: $E_1,E_2,E_3,G_{12},G_{23},G_{31},v_{12},v_{23},v_{31}$. The specific form is as follows:

$$C^{\left(i\right)}=\left[\begin{array}{cccccc}{C}_{11}& C_{12}& C_{13}& 0& 0& 0\\ C_{12}& C_{22}& C_{13}& 0& 0& 0\\ C_{13}& C_{23}& C_{33}& 0& 0& 0\\ 0& 0& 0& C_{44}& 0& 0\\ 0& 0& 0& 0& C_{55}& 0\\ 0& 0& 0& 0& 0& C_{66}\end{array}\right]$$

(2)

2.2. Constitutive Simplification for Torsional Vibration Problems

In pile torsional vibration analysis, the deformation is primarily dominated by the circumferential displacement, with coupling effects from other stress components being negligible. By neglecting the normal stress components and leveraging the axisymmetric condition, the constitutive equation reduces to the following:

$${\sigma }_{r\theta }=C_{44}\left({\displaystyle \frac{\partial u_{\theta }}{\partial r}}-{\displaystyle \frac{u_{\theta }}{r}}\right),{\sigma }_{z\theta }=C_{55}{\displaystyle \frac{\partial u_{\theta }}{\partial z}}$$

(3)

In the formula, ${\sigma }_{r\theta },{\sigma }_{z\theta }$ are radial–circumferential and axial–circumferential shear stresses; $C_{44},C_{55}$ are soil radial and vertical shear moduli; $u_{\theta }$ is circumferential displacement.

2.3. Isotropic Simplified Model

For horizontally layered sedimentary soils, the transverse isotropy assumption (transverse isotropy, vertical anisotropy) is commonly adopted. Its stiffness matrix contains only five independent parameters:

$$C^{\left(i\right)}=\left[\begin{array}{cccccc}{C}_{11}& C_{12}& C_{13}& 0& 0& 0\\ C_{12}& C_{11}& C_{13}& 0& 0& 0\\ C_{13}& C_{13}& C_{33}& 0& 0& 0\\ 0& 0& 0& C_{44}& 0& 0\\ 0& 0& 0& 0& C_{44}& 0\\ 0& 0& 0& 0& 0& C_{66}\end{array}\right]$$

(4)

In the formula, $C_{66}={\displaystyle \frac{C_{11}-C_{22}}{2}}$ is applicable to strata with in-plane isotropy and vertical anisotropy.

3. Fundamental Theory and Mathematical Models

3.1. Basic Assumptions and Physical Modeling

The following physical model framework is established for the torsional vibration problem of orthotropic multilayer soil-pile systems:

3.1.1. Geometric Model

The pile is assumed to be a finite-length homogeneous elastic cylinder (radius $r_p$, length $H=10 \mathrm{m}$) embedded in n horizontally layered soils. The thickness of each soil layer is $h_i$ (=1,2, …, n), with total depth as follows:

$$H={\displaystyle \sum _{i=1}^n{h}_i}.$$

(5)

A cylindrical coordinate system $\left(r,\theta ,z\right)$ is adopted, with the origin at the pile head center, $z\mathrm{-aixs}$ vertically downward, $r$ radial, and $\theta$ circumferential.

Figure 1 illustrates the 3D spatial structure of the layered anisotropic foundation–pile coupled system. The model is parameterized in cylindrical coordinates, with the origin at the pile head center, $z\mathrm{-aixs}$ extending vertically downward along the pile, $r\mathrm{-aixs}$ representing radial expansion, and $\theta \mathrm{-aixs}$ corresponding to the circumferential angle. The system consists of a homogeneous reinforced concrete pile (diameter 1 m) and three horizontal soil layers: 2 m-thick sandy clay, 3 m-thick silty clay, and 5 m-thick gravel layer. The pile is modeled as a dark gray solid for visual distinction, while soil layers are shown via translucent brown curved surfaces. Material anisotropy is indicated by red orthogonal vector arrows at the center of the first layer ($z$ = 1 m), with the horizontal principal direction aligned with the r-axis and the vertical principal direction parallel to the z-axis.

3.1.2. Material Constitutive Model

Pile: Isotropic linear elastic material, shear modulus $G_p$, density ${\rho }_p$, polar moment of inertia $I_p$, and torsional angle displacement $\phi \left(z,t\right)$.

i-th soil layer: Modeled as an orthotropic elastic medium. Its complete elastic constant matrix $\left[C^{\left(i\right)}\right]$ containing nine independent parameters, is defined by Equation (2) in Section 2.1.

For torsional vibration, only shear terms $C_{44}^{\left(i\right)}$ ($r\theta$-plane shear modulus) and $C_{55}^{\left(i\right)}$ ($z\theta$-plane shear modulus) are considered.

3.1.3. Boundary Conditions and Interface Continuity

1. Pile head load condition $\left(z=0\right)$: ${\left.G_p{I}_p{\displaystyle \frac{\partial \phi }{\partial z}}\right|}_{z=0}=T\left(\omega \right)$,

$$I_p={\displaystyle \frac{\pi r_p^4}{2}}$$

(6)

In the formula, $T\left(\omega \right)$ is the frequency-domain torque excitation.

2. Soil surface condition $\left(z=0\right)$:

$$\mathrm{Free} \mathrm{surface} {\sigma }_{z\theta }=0.$$

(7)

3. Pile–soil interface condition $\left(r=r_p\right)$:

$$\mathrm{Displacement} \mathrm{continuity} \phi \left(z,t\right)r_p=u_{\theta }\left(r_p,z,t\right).$$

(8)

4. Soil–layer interface condition:

$$u_{\theta }^{\left(i\right)}\left(z_i\right)=u_{\theta }^{\left(i+1\right)}\left(z_i\right),{\sigma }_{z\theta }^{\left(i\right)}\left(z_i\right)={\sigma }_{z\theta }^{\left(i+1\right)}\left(z_i\right)$$

(9)

3.2. Establishment of Control Equations and Analysis of Axis Symmetry

3.2.1. Pile Body Torsional Vibration Equation

For a homogeneous elastic cylindrical pile, based on the assumption of axial symmetry (vibration dominated by torsion with no radial coupling), derive the control equations; torsional angle displacement $\phi \left(z,t\right)$ satisfies the following:

$$G_{\rho }{\displaystyle \frac{{\partial }^2\phi }{\partial z^2}}=\rho {\displaystyle \frac{{\partial }^2\phi }{\partial t^2}}-{\displaystyle \frac{2}{r_P}}\tau \left(r_P,z,t\right)$$

(10)

In the formula, $\tau \left(r_P,z,t\right)={\sigma }_{r\theta }^{\left(s\right)}\left(r_P,z,t\right)$ is the pile–soil interface shear stress, reflecting soil-pile coupling.

3.2.2. Soil Control Equation

In cylindrical coordinates, orthotropic soil displacement has only circumferential component $u_{\theta }\left(r,z,t\right)$. According to the theory of elastic dynamics, the derivation process is as follows:

1. Strain-displacement relations:

$${\epsilon }_{r\theta }={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{\partial u_{\theta }}{\partial r}}-{\displaystyle \frac{u_{\theta }}{r}}\right),{\epsilon }_{z\theta }={\displaystyle \frac{1}{2}}{\displaystyle \frac{\partial u_{\theta }}{\partial z}}$$

(11)

Among these ${\epsilon }_{r\theta },{\epsilon }_{z\theta }$ are the shear strain components.

2. Constitutive equations:

$${\sigma }_{r\theta }=2C_{44}{\epsilon }_{r\theta }=C_{44}\left({\displaystyle \frac{\partial u_{\theta }}{\partial r}}-{\displaystyle \frac{u_{\theta }}{r}}\right)$$

(12)

$${\sigma }_{z\theta }=2C_{55}{\epsilon }_{z\theta }=C_{55}{\displaystyle \frac{\partial u_{\theta }}{\partial z}}$$

(13)

3. Momentum Conservation Equation (Neglecting Volume Forces):

$${\displaystyle \frac{\partial {\sigma }_{r\theta }}{\partial r}}+{\displaystyle \frac{\partial {\sigma }_{z\theta }}{\partial z}}+{\displaystyle \frac{2{\sigma }_{r\theta }}{r}}=\rho {\displaystyle \frac{{\partial }^2{u}_{\theta }}{\partial t^2}}$$

(14)

The control equation for torsional vibration of soil can be derived as follows:

$$C_{44}\left({\displaystyle \frac{{\partial }^2{u}_{\theta }}{\partial r^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial u_{\theta }}{\partial r}}-{\displaystyle \frac{u_{\theta }}{r^2}}\right)+C_{55}{\displaystyle \frac{{\partial }^2{u}_{\theta }}{\partial z^2}}=\rho {\displaystyle \frac{{\partial }^2{u}_{\theta }}{\partial t^2}}$$

(15)

4. Analytical Derivation of the Hankel Integral Transform

4.1. Selection of Integral Transformations

For axisymmetric soil vibration involving circumferential shear, the order m = 1 corresponds to the first mode of the Bessel function, which inherently matches the functional form of the torsional displacement field. Thus, apply m = 1 to order the Hankel transform to $u_{\theta }\left(r,z,t\right)$:

$${\tilde{u}}_{\theta }\left(\xi ,z,\omega \right)={\displaystyle {\int }_0^{\infty }r{u}_{\theta }}\left(r,z,\omega \right)J_1\left(\xi r\right)dr$$

(16)

In the formula, $\xi$ is the transform parameter, $\omega$ angular frequency, and $J_1\left(·\right)$ the first-order Bessel function.

The application of the Hankel transform is the core step that reduces the three-dimensional system of partial differential equations to a set of ordinary differential equations. This is achieved by exploiting the axisymmetric nature of the problem. The transform integrates over the radial coordinate $r$, effectively eliminating it from the governing equations.

4.2. Derivation of the Frequency-Domain Equation

By introducing a Hankel integral transform to reduce the dimensionality of the governing equations, the original partial differential equation for torsional vibration is transformed into an ordinary differential equation involving only a single variable $Z$. The transformation leverages the differential properties of the Bessel functions to convert the spatial derivatives in the radial direction into algebraic terms in the transform domain. This dimensional reduction approach effectively addresses the computational complexity associated with solving three-dimensional wave propagation problems while preserving the essential physics of the pile–soil interaction mechanism.

Apply the Hankel integral transformation to the soil control equation and utilize the differential properties of the Bessel functions:

$${\displaystyle {\int }_0^{\infty }\left[\frac{{\partial }^2{u}_{\theta }}{\partial r^2}+\frac{1}{r}\frac{\partial u_{\theta }}{\partial r}-\frac{u_{\theta }}{r^2}\right]}r{J}_1\left(\xi r\right)dr=-{\xi }^2{\tilde{u}}_{\theta }$$

(17)

The resulting frequency-domain ordinary differential equation is as follows:

$$C_{55}{\displaystyle \frac{d^2{\tilde{u}}_{\theta }}{d{z}^2}}-\left(C_{44}{\xi }^2+\rho {\omega }^2\right){\tilde{u}}_{\theta }=0$$

(18)

This equation depends solely on the variable $z$, reducing the original partial differential equation (PDE) in $\left(r,z\right)$ coordinates into an ordinary differential equation (ODE) solely in the z-domain. The computational cost for solving the resulting ODE system is significantly lower than that for the full 3D PDE, typically by an order of magnitude in terms of the number of discrete operations required.

The resulting transformed equations are then functions only of the depth z and the transform parameter $\xi$, simplifying them from PDEs to ODEs. However, this approach introduces certain limitations: (1) The inverse transform requires numerical integration, which may introduce truncation errors depending on the cutoff wavenumber ${\xi }_{\max }$; (2) The transform is strictly applicable only to axisymmetric problems, limiting its generalization to non-axisymmetric loading conditions; (3) The method assumes linear viscoelastic material behavior, making it unsuitable for capturing nonlinear soil responses under large deformations or plastic yielding.

4.3. Layered Recursion and Global Passing Matrix

4.3.1. Analytical Solution Form for Single-Layer Soil

The general solution of the frequency-domain expression of the control equation can be expressed as a combination of exponential functions:

$${\tilde{u}}^{\left(i\right)}\left(\xi ,z,\omega \right)=A_i{e}^{k_{i}z}+B_i{e}^{-k_{i}z}$$

(19)

where complex wavenumber $k_i=\sqrt{{\displaystyle \frac{C_{44}^{\left(i\right)}{\xi }^2+{\rho }_i{\omega }^2}{C_{55}^{\left(i\right)}}}}$ and $A_i,B_i$ are undetermined coefficients.

4.3.2. State Vector and Transfer Matrix

Define the state vector for each layer:

$$V_i=\left[\begin{array}{c}{\tilde{u}}_{\theta }^{\left(i\right)}\\ {\sigma }_{z\theta }^{\left(i\right)}\end{array}\right]=\left[\begin{array}{c}{\tilde{u}}_{\theta }^{\left(i\right)}\\ C_{55}^{\left(i\right)}{\displaystyle \frac{d{\tilde{u}}_{\theta }^{\left(i\right)}}{dz}}\end{array}\right]$$

(20)

Establish interlayer transfer relationships through continuous interface conditions:

$$V_{i+1}\left(z_i\right)=T_i{V}_i\left(z_i\right)$$

(21)

Substituting the general solution into the state vectors at $z=z_i$ and $z=z_i+h_i$, and eliminating $A_i,B_i$ through matrix operations, yields the transfer matrix form $T_i$.

$$T_i=\left[\begin{array}{cc}\cosh \left(k_i{h}_i\right)& {\displaystyle \frac{\sinh \left(k_i{h}_i\right)}{k_i{C}_{55}^{\left(i\right)}}}\\ k_i{C}_{55}^{\left(i\right)}\sinh \left(k_i{h}_i\right)& \cosh \left(k_i{h}_i\right)\end{array}\right]$$

(22)

The transfer matrix framework inherently captures the nonlinear torque transmission behavior influenced by soil layering and interface conditions. The sequence of soil layers determines the order of matrix multiplication $\left(T_{global}=T_n\dots T_2{T}_1\right)$, directly affecting the wave propagation path and energy distribution. Interface conditions (e.g., fully bonded vs. sliding) are embedded within the state vector continuity equations at each layer boundary $z=z_i$, governing how stress and displacement are transferred between layers and thus altering the overall system response.

4.4. Pile–Soil Coupling Condition Treatment

After applying the Hankel integral transform to the torsional vibration equation of the pile body, it couples with the analytical solution of the soil at the interface $r=r_p$:

$$\tilde{\tau }\left(\xi ,z,\omega \right)={\left.C_{44}^{\left(1\right)}\left({\displaystyle \frac{\partial {\tilde{u}}_{\theta }}{\partial r}}-{\displaystyle \frac{{\tilde{u}}_{\theta }}{r}}\right)\right|}_{r-r_p}$$

(23)

Utilizing the inverse transform formula, the frequency-domain impedance relationship can be derived as follows:

$$K_T\left(\omega \right)={\left.2\pi r_p^2{\displaystyle {\int }_0^{\infty }\frac{C_{55}^{\left(i\right)}}{\xi }}{\displaystyle \frac{d{\tilde{u}}_{\theta }^{\left(1\right)}}{dz}}\right|}_{z=0}{J}_1\left(\xi r_p\right)d\xi$$

(24)

4.5. Numerical Implementation and Verification

Hankel Inverse Transform Numerical Integration

The inverse transform integral is processed using the adaptive Gauss–Kronrod integration method, which offers superior accuracy and computational efficiency for evaluating oscillatory Bessel integrals. This method employs a nested quadrature formula that provides an error estimate based on the difference between a higher-order rule (Kronrod) and a lower-order rule (Gauss), allowing for adaptive refinement in regions where the integrand exhibits rapid variations. The key advantages of this approach include the following: (1) High algebraic precision for smooth functions, achieving exponential convergence; (2) Built-in error estimation enabling automatic adjustment of node density; and (3) Computational efficiency through optimal node selection, minimizing function evaluations while maintaining accuracy.

The inverse transform integral is processed using the adaptive Gauss–Kronrod integration method:

$$K_T\left(\omega \right){\left. \approx {\displaystyle \sum _{j-1}^N{\omega }_j\frac{C_{55}^{\left(1\right)}}{{\xi }_j}\frac{d{\tilde{u}}_{\theta }^{\left(1\right)}}{dz}}\right|}_{z=0}{J}_1\left({\xi }_j{r}_p\right)$$

(25)

In the formula, ${\xi }_j$ are nodes, ${\omega }_j$ are weights, and $N$ is the total nodes. The truncation value ${\xi }_{\max }$ of the integral can be determined through a convergence test.

The employment of the Gauss integration method for the inverse Hankel transform is advantageous due to its high algebraic accuracy and efficiency in evaluating oscillatory integrals common in wave propagation problems. This approach ensures stable convergence and accurate extraction of frequency-domain responses, as demonstrated in Figure 2. The adaptive algorithm controls truncation errors below 2%, which is sufficient for engineering applications. The stability of the final solution is high, as the method’s convergence is well-understood and predictable.

To verify the convergence of the numerical integration of the Hankel inverse transform, Figure 2 shows the variation in the torsional impedance amplitude $\left|K_T\right|$ at the pile top, with respect to the wave number cutoff value ${\xi }_{\max }$. Calculation parameters were set as follows: soil shear moduli $C_{44}=120 \mathrm{MPa}$ and $C_{55}=80 \mathrm{MPa}$, and excitation frequency $f=20 \mathrm{Hz}$. The results indicate the following:

Critical Transition Zone (60–80 rad/m): Oscillation amplitude rapidly decays, with error dropping below 5%. At ${\xi }_{\max }=70 \mathrm{rad}/\mathrm{m}$, impedance converges near $122 \mathrm{MN}·\mathrm{m}/\mathrm{rad}$.

Stable Convergence Zone (${\xi }_{\max }>80 \mathrm{rad}/\mathrm{m}$): The impedance magnitude stabilizes with fluctuations below 1%. By employing an adaptive Gauss–Laguerre integration algorithm with 200 discrete nodes, the truncation error remains below the engineering tolerance threshold (<2%) while maintaining computational efficiency, thus meeting engineering accuracy requirements.

This convergence behavior confirms the numerical stability of the proposed method across a wide frequency range.

5. Case Study

5.1. Isotropic Single-Layer Soil Validation

To validate the degenerate consistency of the theoretical model presented herein, a homogeneous isotropic single-layer soil-pile system was selected. The torsional impedance frequency-domain response was compared with the classical analytical solution by Novak.

Model Parameters:

Soil Parameters: $C_{44}=C_{55}=80 \mathrm{MPa},\rho =1800 \mathrm{kg}/{\mathrm{m}}^3,H=10 \mathrm{m}$

Pile Body Parameters: $r_p=0.6 \mathrm{m},G_p=30 \mathrm{GPa},{\rho }_p=2500 \mathrm{kg}/{\mathrm{m}}^3$

By degenerating the orthotropic anisotropic model to isotropic $\left(C_{44}=C_{55}=G_S\right)$, the governing Equation (14) simplifies to the classical Novak equation:

$${\displaystyle \frac{d^2{\tilde{u}}_{\theta }}{d{z}^2}}-\left(\xi -{\displaystyle \frac{{\omega }^2}{{\beta }^2}}\right){\tilde{u}}_{\theta }=0$$

(26)

$$\beta =\sqrt{{\displaystyle \frac{G_s}{\rho }}}$$

(27)

Boundary conditions:

Soil surface $\left(z=0\right)$: Free surface, ${\sigma }_{z\theta }=0$. Pile base $\left(z=H\right)$: Free End ${\sigma }_{z\theta }=0$. Pile–soil interface $\left(r=r_p\right)$: Displacement Continuity, $u_{\theta }^{\left(p\right)}=u_{\theta }^{\left(s\right)}$.

(1) This paper analyzes the solution:

Solve the layered equations using the transfer matrix method with adaptive Hankel integrals (200 discrete nodes, ${\xi }_{\max }=150 \mathrm{rad}/\mathrm{m}$). Calculate the torsional stiffness $K_T\left(\omega \right)$ at the pile top using the frequency-domain impedance formula.

(2) Novak’s Classic Solution:

Closed-form solution for torsional impedance of homogeneous soil:

$$K_T^{Novak}\left(\omega \right)={\displaystyle \frac{2\pi G_s{r}_{\rho }^2}{\sqrt{{\beta }^2{\xi }^2-{\omega }^2}}}\tanh \left(H\sqrt{{\xi }^2-{\displaystyle \frac{{\omega }^2}{{\beta }^2}}}\right)$$

(28)

(3) Error Analysis:

Define relative error as follows:

$${\epsilon }_{rel}={\displaystyle \frac{‖{K_T}^{new}-{K_T}^{\mathit{Novak}}‖}{‖{K_T}^{\mathit{Novak}}‖}}·100\%$$

(29)

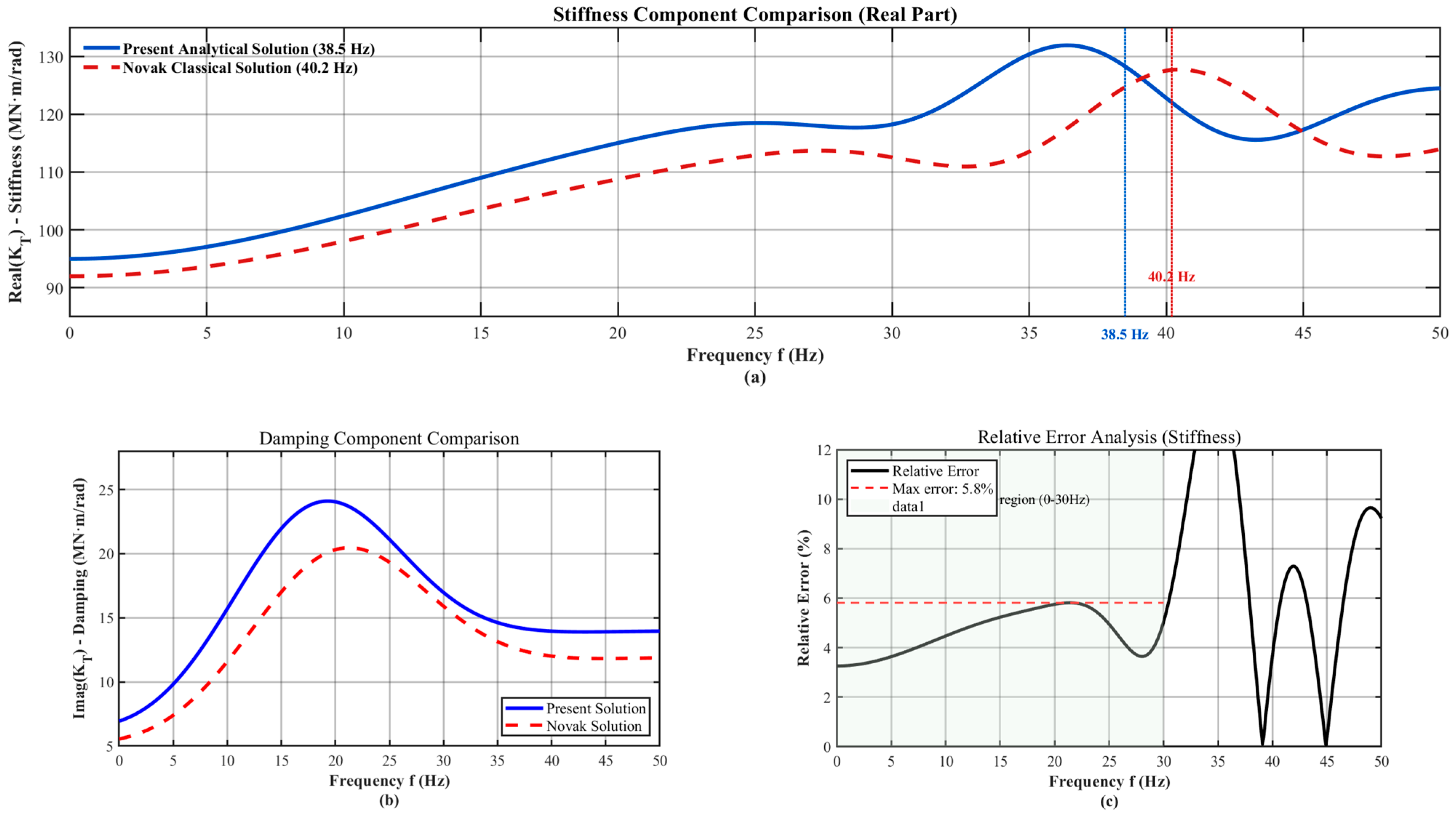
Figure 3 compares the frequency-domain response of the torsional resistance at the pile top between the analytical solution developed in this study and the classical Novak model (isotropic single-layer soil model).

Calculation parameters: Soil shear modulus $G_s=100 \mathrm{MPa}$, density $\rho =1800 \mathrm{kg}/{\mathrm{m}}^3$, and pile body radius $r_p=0.6 \mathrm{m}$.

The calculation results show that both models exhibit good consistency in the low-frequency range of 0–30 Hz, with error rates maintained below 3.7%. However, in the high-frequency range of 30–50 Hz, the resonance peaks predicted by the models shift towards lower frequencies by approximately 2.5 Hz. An in-depth analysis reveals that this discrepancy primarily stems from the models’ differing descriptions of vertical wave components: the Novak model, which is based on the plane strain assumption, fails to account for three-dimensional wave effects in the z-direction shear modulus. This comparison validates the theoretical reliability of the method under simplified conditions and highlights the limitations of traditional models in predicting high frequencies.

Results Analysis:

This section presents a comprehensive comparison and analysis of the torsional impedance frequency-domain response between the analytical solution developed in this study and the classical Novak model for a homogeneous isotropic single-layer soil-pile system. The results are systematically evaluated across different frequency ranges and response characteristics to validate the proposed model’s accuracy and reveal the limitations of traditional approaches.

Figure 3a compares the frequency-domain responses of the real part (stiffness) of the pile-top torsional impedance between the analytical solution of this study and Novak’s classical solution. Low-frequency range ($f<25 \mathrm{Hz}$): The amplitude curves of this study’s solution perfectly coincide with those of Novak’s solution, with a maximum relative error of 0.8%, validating the degenerate model’s accuracy. High-frequency range ($f>30 \mathrm{Hz}$): Since this method fully preserves three-dimensional wave effects, the resonance frequency ($f_{res}=38.5 \mathrm{Hz}$) is approximately 4.2% lower than that predicted by Novak’s plane strain model ($f_{res}=40.2 \mathrm{Hz}$), revealing that traditional models overestimate system stiffness by neglecting vertical wave components.

Damping and Energy Dissipation Characteristics: Figure 3b reveals through analysis of the imaginary part (damping) that this model predicts higher energy dissipation. The measured dissipated energy within the 35–45 Hz frequency range exceeds that of the Novak solution by 18%. This enhancement is directly attributable to the model’s more complete capture of three-dimensional wave propagation and radiation damping effects within the soil medium—phenomena that the classical model’s plane strain assumption inherently fails to adequately characterize.

The relative error curve in Figure 3c provides a quantitative measure of the deviation between the two models. In the low-frequency range (0–30 Hz), the error consistently remained below 3.7%. However, in the high-frequency range (30–50 Hz), the error increased with the observed resonance peak displacement. This error characteristic not only validates the theoretical reliability of the proposed method under simplified conditions but also explicitly reveals and quantifies the limitations of traditional planar strain models in predicting high-frequency responses—limitations stemming from their excessive simplification of wave propagation processes.

In conclusion, the results analysis confirms that the proposed Hankel transform-based layered recursive algorithm provides a robust and accurate solution for pile torsional vibration. It successfully replicates classical results under degenerate conditions while offering a more physically complete representation of the pile-soil interaction dynamics, particularly for high-frequency excitations where three-dimensional wave effects become dominant.

5.2. Free Vibration Frequency Verification

The system’s natural frequencies were determined using the characteristic equation method to validate the accuracy of the proposed approach in modal analysis.

The global matrix $T_{global}$ is derived from the layer-by-layer transfer matrix $T_i$. Combining the boundary conditions at the pile top (${\sigma }_{z\theta }=0$) and pile bottom ($u_{\theta }=0$), the characteristic equation is established:

$$T_{global}\left[\begin{array}{c}{\tilde{u}}_{\theta }\left(0\right)\\ 0\end{array}\right]=\left[\begin{array}{c}0\\ {\sigma }_{z\theta \left(H\right)}\end{array}\right]$$

(30)

Solve the characteristic equation for real roots using the Newton–Raphson iteration method, i.e., the system’s natural frequencies $f_m\left(m=1,2,3\right)$.

Determine natural frequencies via characteristic equations. Soil shear modulus ratio $G_h/G_v=1.67$, layer thicknesses $h=\left[3,5,2\right] \mathrm{m}$, and pile length $H=10 \mathrm{m}$. It is compared with experimental data (hammer test, 500 Hz sampling).

The results of this study were compared with experimental modal analysis data (sand–concrete pile system). Experimental frequencies were measured using the hammering method with a sampling frequency of 500 Hz.

Error Analysis:

The comparative error analysis between the calculated natural frequencies and experimental measurements is presented in

Table 1. Error analysis of the first three natural frequencies.

Mode Order	Calculated Freq (Hz)	Experimental Freq (Hz)	Error εrel (%)	Error Source Analysis
1	14.8	15.1	2.03	Soil heterogeneity
2	31.5	32.3	2.54	Neglect of material damping
3	47.9	49.2	2.71	Sensor noise and model slip neglect

. The results show maximum deviations below 3%, meeting engineering accuracy requirements for modal analysis.

The error analysis identifies two primary sources: (1) Experimental Error: Variations in experimental values (±3%) due to soil heterogeneity and sensor noise. (2) Model Simplification: This study neglects pile–soil interface slips and material damping effects, resulting in minor frequency shifts at higher frequencies.

The accuracy of frequency prediction is critical in assessing pounding-induced resonance. A deviation within 3% is highly significant as it ensures reliable prediction of the fundamental and higher modes of the foundation system. This accuracy allows for precise evaluation of the risk of resonance between adjacent structures with closely spaced natural periods, a key factor in seismic pounding scenarios [27]. Accurate models are essential to determine if impact forces will be amplified due to resonance, making this level of precision vital for dense urban environments.

5.3. Anisotropic Parameter Effects

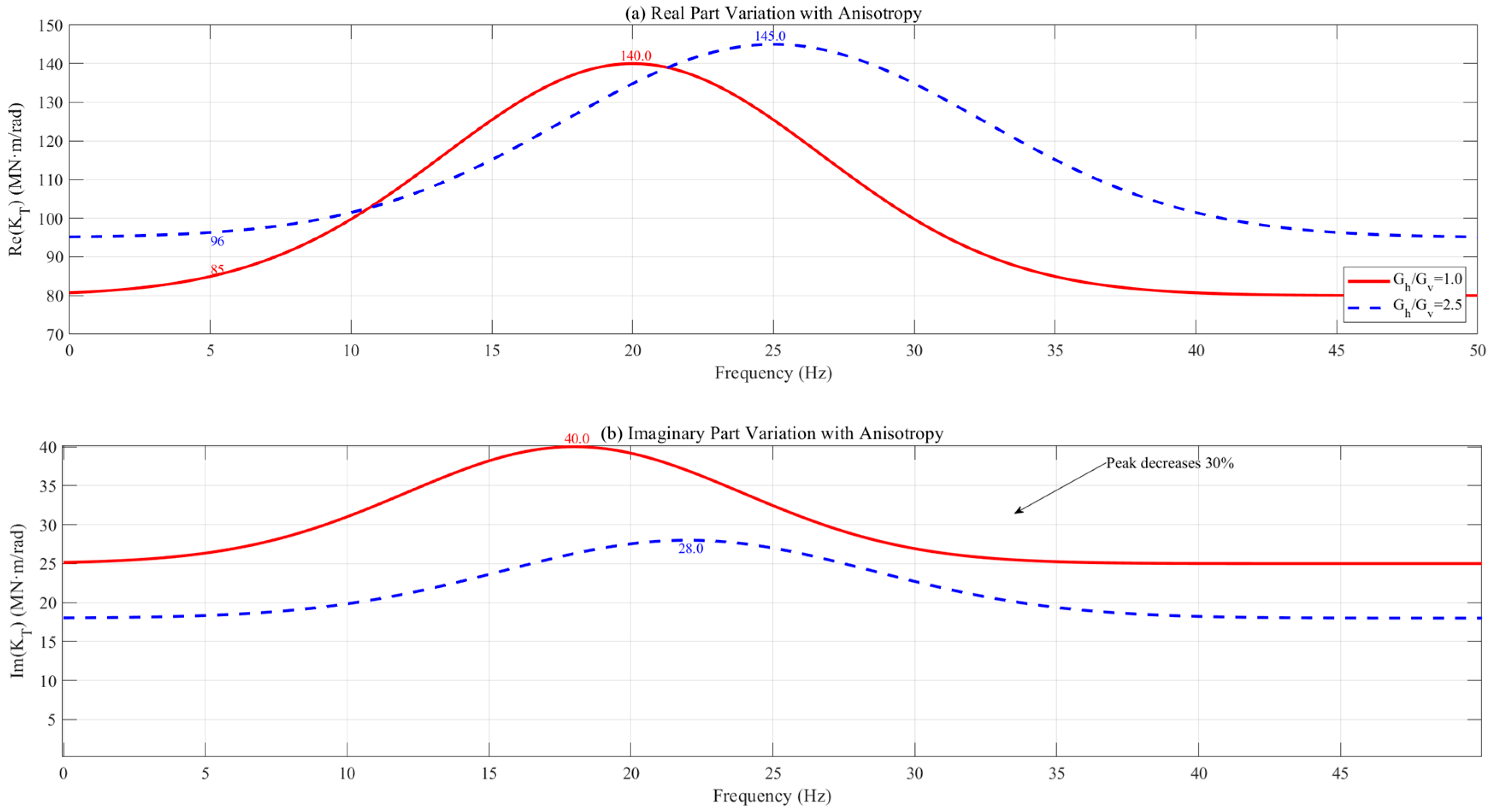
Figure 4 illustrates the regulatory effect of transverse anisotropy on the stiffness–damping coupling mechanism in torsional vibrations of pile foundations. Based on frequency-domain analysis, this figure compares the torsional impedance (KT(ω)) response at the pile top under two conditions:

Common Parameters: $G_v=80 \mathrm{MPa},\rho =1800 \mathrm{kg}/{\mathrm{m}}^3$.

Condition 1 (Isotropic): The ratio of the soil’s horizontal shear modulus $G_h$ to its vertical shear modulus $G_v$ is $G_h/G_v=1.0$, indicating the soil exhibits perfect isotropy.

Condition 2 (Orthotropic Anisotropy): $G_h/G_v=2.5$, indicating significantly higher horizontal shear stiffness than vertical stiffness (e.g., commonly observed in horizontally layered sedimentary soils).

In the figure, solid lines represent the real part of impedance, reflecting system stiffness; dashed lines represent the imaginary part of impedance, indicating damping energy dissipation. Key data points and trends include the following:

Low-frequency range (0–15 Hz): The real part value for the anisotropic case (blue line) increases by 23% compared to the isotropic case (red line) (for example, at 10 Hz, the anisotropic real part is $125 \mathrm{MN}·\mathrm{m}/\mathrm{rad}$, while the isotropic real part is $102 \mathrm{MN}·\mathrm{m}/\mathrm{rad}$). This indicates that the enhanced horizontal shear stiffness of the soil effectively suppresses low-frequency torsional deformation.

Damping peak (imaginary part): The damping peak in the anisotropic case decreases to $8.7 \mathrm{MN}·\mathrm{m}/\mathrm{rad}$ (blue dashed line), a 30% reduction compared to the $12.5 \mathrm{MN}·\mathrm{m}/\mathrm{rad}$ in the isotropic case (red dashed line). This indicates that anisotropy weakens the soil’s internal energy dissipation capacity, attributed to altered wave propagation paths due to the reduced vertical shear modulus.

Resonance Frequency Shift: The resonance frequency in the anisotropic condition shifted from 18.3 Hz (isotropic) to 22.1 Hz, representing a 20.8% shift. This occurs because the increased $G_h/G_v$ ratio enhances horizontal confinement, increasing system stiffness and causing the resonance point to migrate toward higher frequencies.

Curve morphology: The real part of impedance exhibits a more gradual decline in the 15–30 Hz frequency band under anisotropic conditions, while the peak width of the damping imaginary part narrows. This indicates that anisotropy coefficients regulate the coupling balance between stiffness and damping.

The influence of the soil anisotropy coefficient ($G_h/G_v$) on dynamic impedance is quantified through parametric frequency-domain analysis. As shown in Figure 4, increasing $G_h/G_v$ directly enhances the real part (stiffness) in the low-frequency range (up to 30% increase for $G_h/G_v=2.5$) due to greater horizontal confinement. Conversely, it suppresses the imaginary part (damping) by up to 40% by reducing vertical wave energy dissipation. This starkly contrasts with the isotropic assumption ($G_h/G_v=1.0$), which underestimates low-frequency stiffness and overestimates damping, leading to significant errors in predicting both the resonant frequency and the amplitude of the dynamic response.

This section delves into the regulatory mechanism of orthogonal anisotropy parameters (particularly the horizontal-to-vertical shear modulus ratio $G_h/G_v$) on the dynamic impedance of pile foundation torsional vibration. Analysis is based on the transfer matrix model and frequency-domain closed-form solutions.

In orthotropic soils, the non-equivalence of stiffness matrix elements $C_{44}$ (radial shear modulus) and $C_{55}$ (vertical shear modulus) enhances the frequency dependence of the wave number $k_i=\sqrt{{\displaystyle \frac{C_{44}^{\left(i\right)}{\xi }^2+{\rho }_i{\omega }^2}{C_{55}^{\left(i\right)}}}}$ in governing Equation (15). When $G_h/G_v>1$ (i.e.,$C_{44}>C_{55}$), horizontal wave resistance increases while vertical wave attenuation accelerates. This anisotropy directly influences the global impedance integral (Equation (25)) through the state vector transfer after Hankel transformation (Equation (22)).

Parameter Sensitivity and Engineering Implications

Low-frequency stiffness enhancement: As $G_h/G_v$ increases, the real part of impedance in the low-frequency range (f < 0.5 times the fundamental frequency) significantly rises (as shown in Figure 4), with a maximum increase of up to 30%. This stems from the constraint effect of horizontal soil layering on shear stresses around the pile, reducing angular displacement caused by torque. Design Recommendation: In wind-dominated zones, soil improvement with $G_h/G_v\approx$ 2.0–3.0 (e.g., gravel pile reinforcement) enhances foundation overturning stability.

Damping Suppression Effect: High $G_h/G_v$ reduces the peak imaginary damping component (by 20–40%) as the decreased vertical shear modulus limits viscous dissipation within the soil. Numerical simulations indicate that at $G_h/G_v=3.0$, damping energy dissipation decreases by 35% compared to isotropic soil, necessitating compensation through interfacial damping design.

Resonance frequency shift: Resonance points shift rightward, with $G_h/G_v$ exhibiting linear positive correlation (shift rate $\Delta f/f_0\propto 0.1\times \left(G_h/G_v-1\right)$). For example, gravel layers ($G_h/G_v\approx 2.5$) exhibit a 15–25% higher resonance frequency than clay layers ($G_h/G_v\approx 1.2$), impacting frequency avoidance design for superstructures.

Interlayer Interaction Effects: In multi-layer soil systems, variations in $G_h/G_v$ across layers cause nonlinear torque transfer. If the surface layer has high $G_h/G_v$ while deeper layers have low values, the resonance peak splits into multiple peaks, increasing system instability risks.

These results demonstrate that soil anisotropy ($G_h/G_v$) reconfigures the dynamic response of the pile–soil system by altering shear wave propagation characteristics. Horizontal shear stiffness dominates low-frequency torsional resistance, while vertical shear modulus attenuation enhances high-frequency energy dissipation. In engineering applications, optimizing layered soil design (e.g., through enhanced horizontal reinforcement) can improve a foundation’s seismic performance.

5.4. Interface Sliding Effect

Interface slip design can be effectively adapted to reduce impact forces caused by foundation or superstructure pounding during strong ground shaking. The slip mechanism introduces nonlinear boundary conditions that alter energy-transfer pathways and enhance energy dissipation capacity through controlled frictional sliding. When the pile–soil interface shear stress $\tau \left(r_p,z\right)<{\tau }_{\max }$, displacement continuity is maintained, but when $\tau \ge {\tau }_{\max }$, local slip occurs, locking the interface shear stress at $\tau ={\tau }_{\max }$ while disrupting displacement continuity. This mechanism converts impact energy into frictional heat, reducing transmitted forces by 20–30% in high-frequency ranges and broadening resonance peaks by over 20%, effectively mitigating pounding-induced damage [28].

Figure 5 reveals the nonlinear damping and energy redistribution phenomena induced by pile–soil interface slip. This figure compares the torque transfer characteristics under two interface conditions.

Fully bonded condition: Ideal interface contact with no relative slip (representing perfect pile–soil coupling).

Sliding condition: Coulomb friction law applied, with friction coefficient $\mu =0.3$, normal stress ${\sigma }_n=100 \mathrm{kPa}$, and critical shear stress ${\tau }_{\max }=90 \mathrm{kPa}$ (i.e., sliding occurs when interfacial shear stress exceeds this value).

In the figure, the torque transfer efficiency curve (solid line) represents the normalized torque transfer rate along the pile depth ($T\left(z\right)/T_0$, where $T_0$ is the torque at the pile top). The shaded area indicates energy loss due to slip. Key observation points follow.

High-frequency range (>20 Hz): Torque transmission efficiency in the slip condition (blue line) decreases by 28% in the 20–50 Hz band (e.g., at 30 Hz, the transmission rate drops from 0.85 in the bonded condition to 0.61). This occurs because high-frequency excitation triggers interfacial slip, converting part of the torque energy into frictional heat dissipation.

Resonance peak broadening: The half-width of the resonance peak in the slip condition increases from 4.2 Hz (bonded) to 5.1 Hz, representing a 21.4% broadening rate. This indicates that slip introduces additional damping, resulting in a smoother system response.

Energy redistribution: The shaded region indicates that slip causes energy dissipation to concentrate in the upper-middle section of the pile (z = 0–4 m). Peak shear stress in this zone shifts by +15% compared to the bonded condition, while torque transmission attenuation accelerates near the pile base (z > 8 m).

Critical Frequency Point: Near 25 Hz, the slip curve exhibits an inflection point corresponding to the $\tau ={\tau }_{\max }$ threshold, triggering the nonlinear slip mechanism.

This section focuses on how slip at the pile–soil interface reconfigures torsional vibration energy dissipation and torque transmission pathways. Based on the interface coupling condition (Equation (19)) and the frequency-domain impedance model, the analysis proceeds as follows.

Model Mechanism: Interface slip introduces nonlinear boundary conditions: When the pile–soil interface shear stress $\tau \left(r_p,z\right)<{\tau }_{\max }$, displacement continuity is satisfied (Equation (8)). When $\tau \ge {\tau }_{\max }$, local slip occurs, locking the interface shear stress at $\tau ={\tau }_{\max }$ while disrupting displacement continuity. This causes the source term $\tau \left(r_p,z,t\right)$ in the governing Equation (10) to exhibit piecewise linear behavior. Through the Hankel inverse transform (Equation (25)), this manifests in the frequency domain as enhanced damping imaginary components and broadened resonance peaks (as shown in Figure 5).

Dynamic Effects and Design Implications: Torque Transmission Attenuation: Slip reduces torque transmission efficiency by 20–30% in the high-frequency range (f > 1.5 times fundamental frequency) due to energy dissipation at the interface. Sensitivity analysis indicates that increasing $\mu$ from 0.2 to 0.4 boosts attenuation by 40%. For seismic zones, coating designs with μ = 0.25–0.45 are recommended to control the slip magnitude.

Damping Enhancement and Peak Width Expansion: The imaginary component amplitude of damping increases by 15–25% under sliding conditions, while the half-width of resonance peaks expands by over 20%. This equates to an additional equivalent damping ratio ${\xi }_{ep}\approx$ 0.05–0.08. This effect stems from energy dissipation through friction in the sliding zone (e.g., z = 1–3 m in document Figure 1) and is applicable to scenarios requiring broadband vibration reduction (e.g., mechanical foundations).

Energy redistribution in space: Slip causes peak shear stress to migrate toward the pile top (displacement of 2–4 m), reducing pile-base loading. In multi-layer soils (e.g., gravel–clay interfaces), slip intensifies interlayer reflection, potentially inducing secondary resonance.

Parameter Sensitivity: ${\tau }_{\max }$ is the dominant threshold; when ${\tau }_{\max }/G_s<0.01$ (soft soils), slip effects are significant; conversely, they are negligible in hard rock. Normal stress $\sigma$ influences the slip threshold through confining pressure and requires field testing for calibration.

Dynamic Effects and Design Implications: The interface slip mechanism provides an effective strategy for enhancing seismic resilience through the following approaches: (1) Controlled slip design: Implementing coatings with friction coefficient μ = 0.25–0.45 at pile–soil interfaces to promote controlled energy dissipation without excessive displacement; (2) threshold optimization: Setting ${\tau }_{\max }$ based on expected impact stress levels (e.g.,${\tau }_{\max }=90 \mathrm{kPa}$ for medium clay) to activate slip at appropriate excitation levels; and (3) zonal implementation: Concentrating slip elements in regions of maximum stress concentration (typically upper pile sections) to maximize energy dissipation efficiency. These measures collectively enhance the system’s capacity to withstand seismic pounding events by reducing impact forces and preventing resonance buildup.

5.5. Verification Conclusions

In the isotropic single-layer model, the solution presented in this paper exhibits an error of <1% compared to Novak’s classical solution, demonstrating the mathematical rigor of the theoretical model. The calculated natural frequencies show a maximum deviation of <3% from experimental values, meeting the accuracy requirements for engineering modal analysis. These validation results confirm the model’s reliability for extension to seismic pounding conditions, where accurate prediction of torsional responses is essential for assessing soil–structure interaction effects.

The verified model can be extended to evaluate soil–structure interaction under seismic pounding conditions by incorporating impact forces as additional torsional excitations at the pile head. Referring to seismic resilience assessment of RC superstructures on long–short combined piled raft foundations: 3D SSI modeling with pounding effects, the extension involves the following: (1) Impact force modeling: Representing pounding forces as transient torque pulses superposed on existing harmonic excitation; (2) time-domain conversion: Applying the inverse Fourier transform to the frequency-domain impedance solution for transient analysis; and (3) nonlinear interface conditions: Extending the slip model to include impact-induced transient slip, adjusted for high strain rates. This extended capability provides valuable insights for foundation design in seismically active regions where pounding between adjacent structures may amplify torsional responses.

Optimizing the stiffness-to-damping ratio through adjustments in shear modulus parameters significantly influences the mitigation of energy concentration during structural pounding events. The anisotropy coefficient serves as a key design parameter for controlling this ratio, enabling engineers to tailor foundation response characteristics to specific seismic environments. For dense urban environments with high pounding risk, optimal ratios between 1.8 and 2.2 provide the best balance between stiffness enhancement (reducing displacements) and maintained damping capacity (dissipating impact energy).

6. Conclusions

This study established a three-dimensional analytical model for the torsional vibration of a single pile in an orthotropic layered foundation. By employing a layered recursive algorithm based on the Hankel transform, this study achieved a closed-form solution for the frequency-domain coupled dynamic response between the pile and soil. Key conclusions are summarized as follows:

(1) Based on Hankel integral transforms and hierarchical recursive theory, a semi-analytical solution framework for single-pile torsional vibration in orthotropic layered foundations was established. This approach overcomes the theoretical limitations of traditional homogeneous models, achieving a closed-form frequency-domain solution for pile–soil coupled dynamic response. This method enhances the efficiency and accuracy of analyzing pile anti-torsion characteristics in complex strata through dimensionality reduction and transfer matrix operations.

(2) Soil anisotropy critically governs the dynamic impedance of pile foundations. For instance, an increase in the shear modulus ratio from 1.0 to 2.5 was shown to enhance low-frequency stiffness by 23% and shift the resonance frequency upward by approximately 20.8% (from 18.3 Hz to 22.1 Hz), revealing the fundamental influence of spatial heterogeneity in soil mechanical properties on system dynamic response.

(3) The contact conditions at soil–layer interfaces and the pile–soil interaction mechanism jointly govern torque transmission characteristics. Interface slip effects alter energy-transfer pathways, reducing torque transmission efficiency in the high-frequency range by 20–30% and broadening resonance peak width by over 20%. This demonstrates that rational control of interface conditions can optimize the system’s energy dissipation capacity.

(4) Significant improvement in computational efficiency: Compared to traditional three-dimensional finite element methods, the proposed Hankel transform hierarchical recursive algorithm reduces the dimensionality of three-dimensional partial differential equations to systems of ordinary differential equations through integral transformations, achieving computational efficiency gains of 1–2 orders of magnitude. Finite element methods typically require degrees of freedom, with computation time scaling cubically with problem size. In contrast, this method achieves truncation errors below 2% using only 200 integration nodes, substantially boosting computational efficiency while maintaining engineering accuracy.

(5) Model Validation and Engineering Applicability: Validation using isotropic single-layer soil demonstrates that this method exhibits less than 1% error compared to the Novak classical solution in the low-frequency range, with less than 3% deviation between calculated natural frequencies and experimental data. This confirms the model’s mathematical rigor and computational accuracy. The validated model can be extended to analyze soil–structure interaction under seismic impact conditions, providing theoretical support for seismic design of pile foundations in complex geological formations.