Numerical Simulation of Heat Transfer in Layered-Plate Heat Exchangers for High-Temperature Cement Cooling

Abstract

Cement is a widely used construction material, but its high temperature after milling can lead to issues such as gypsum dehydration, cement agglomeration, and increased slump, all of which negatively affect concrete performance. Existing cement heat exchangers have several limitations, such as low efficiency, high energy consumption, and strict processing precision requirements. This study introduces a novel layered-plate heat exchanger and analyzes its cooling performance using ANSYS Fluent 2024 R1 software. The results indicated that increasing the height of the cooling unit group significantly improved cooling efficiency from 7.83% at 1 m to 35.99% at 10 m. When the cooling unit group height was maintained constant, adding fins and increasing the cooling water flow rate were key methods to improve cooling efficiency. At a 10 m height, adopting 100 mm (F-1) and 200 mm (F-2) fin spacings and increasing the cooling water usage of over 90t/h can reduce the temperature of 130 °C cement powder to below 80 °C, with a cooling efficiency exceeding 38.47%. This study offers an effective method for lowering the temperature of freshly milled cement, providing theoretical support for cement manufacturers to effectively address the issue of high-temperature cement.

1. Introduction

Cement is a crucial building material that plays an essential role in urban infrastructure development. Global cement production reached approximately four billion tons in 2024 [1]. During the cement grinding process, the impact and friction between grinding bodies inside the mill, along with their interaction with the lining plate, generate a significant amount of heat, leading to an elevated cement temperature [2]. Additionally, factors such as the large size of the mill, the characteristics of the input materials, and seasonal variations can further increase the temperature of cement as it exits the mill [3,4]. When the cement temperature reaches 90–120 °C, the crystallization water in the added gypsum is partially lost, leading to the dehydration of natural gypsum and the formation of hemihydrate compounds [5,6,7]. High cement temperatures can increase the water demand for standard consistency and reduce the setting time of cement paste [8]. Moreover, excessively high cement temperatures can compromise the safety of equipment such as mills and separators; increase the energy consumption of grinding systems; shorten the service life of machinery; and negatively affect cement storage, packaging, and transportation [9]. As a key cementitious material in concrete, cement plays a decisive role in both the workability of fresh mixtures and the mechanical performance of hardened concrete [10,11]. However, excessively high cement temperatures can impair its compatibility with raw materials and admixtures, leading to reduced slump and increased viscosity in the fresh mix. Consequently, newly milled cement must be cooled to a specified temperature before storage or sale [4,9].

Heat exchangers are devices that facilitate the transfer of thermal energy between two or more fluids at different temperatures, thereby enabling efficient energy conversion and utilization [12,13]. These devices are widely used in industries such as petroleum refining, metallurgy, and power generation, where they contribute to enhanced energy efficiency and reduced production costs [14,15]. Numerical simulation, a fundamental tool in modern engineering and scientific research, has been extensively applied across various fields, including energy systems, aerospace, chemical engineering, materials science, and environmental engineering [16]. In the field of powder heat exchange, due to its advanced computational fluid dynamic (CFD) capabilities, ANSYS Fluent has become a vital tool for studying and optimizing heat transfer processes [17]. This software effectively simulates complex heat transfer and flow phenomena, including particle–fluid interactions, multiphase flow dynamics, and radiative heat transfer. Accurate numerical simulations enable the prediction of critical parameters in heat exchange processes, such as temperature distributions [18], heat transfer rates [19], and pollutant emissions [20].

In current engineering practice, freshly milled cement is typically cooled using screw lift coolers, water spraying on the grinding mill cylinder, and in-mill spray cooling. While these methods can achieve a certain degree of cooling, they face several practical limitations. For example, screw lift coolers require enhanced heat transfer efficiency and reduced energy consumption, while their complex structure can complicate maintenance. Similarly, water spraying on the grinding mill cylinder is limited in heat transfer capacity, particularly in large-scale grinding mills. And may adversely affect the working environment. In-mill spray cooling requires precise control of water volume, and the management and maintenance of the spray nozzles present additional challenges.

To address these challenges, this study introduces a novel layered-plate heat exchanger specifically designed for powder heat exchange applications, such as cement powder cooling. It began with the structural design and 3D modeling of the heat exchanger using SolidWorks software. After the heat transfer process in the heat exchanger was analyzed, its design was initial optimized. Subsequently, ANSYS Fluent software was used to investigate the effects of structural and operational parameters on the cooling efficiency of the heat exchanger, enabling further structural optimization. This study offers an effective method for lowering the temperature of newly milled cement, mitigating temperature-related changes in cement and concrete properties. It provides theoretical support for cement manufacturers to effectively address the issue of high-temperature cement.

2. Model Description

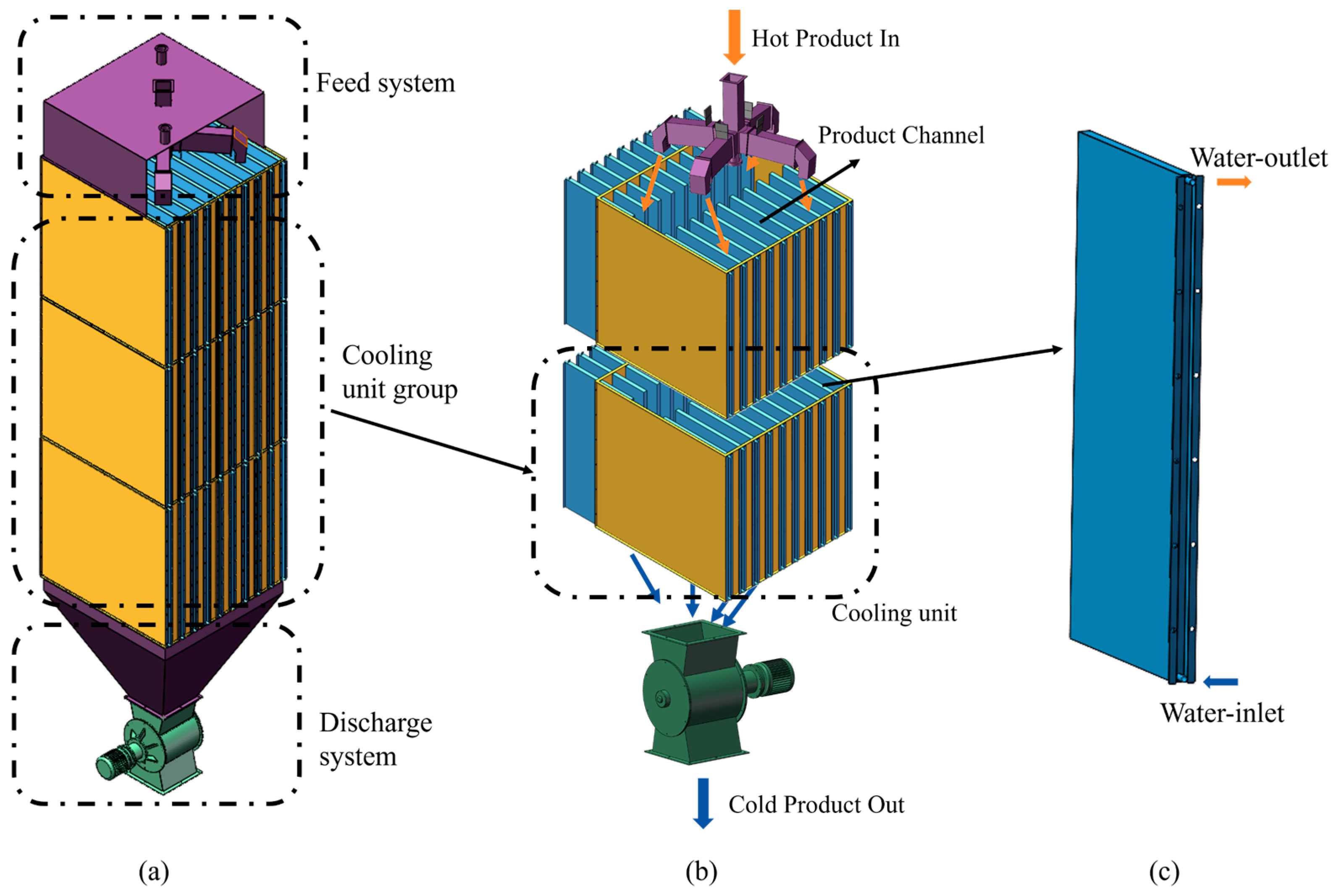
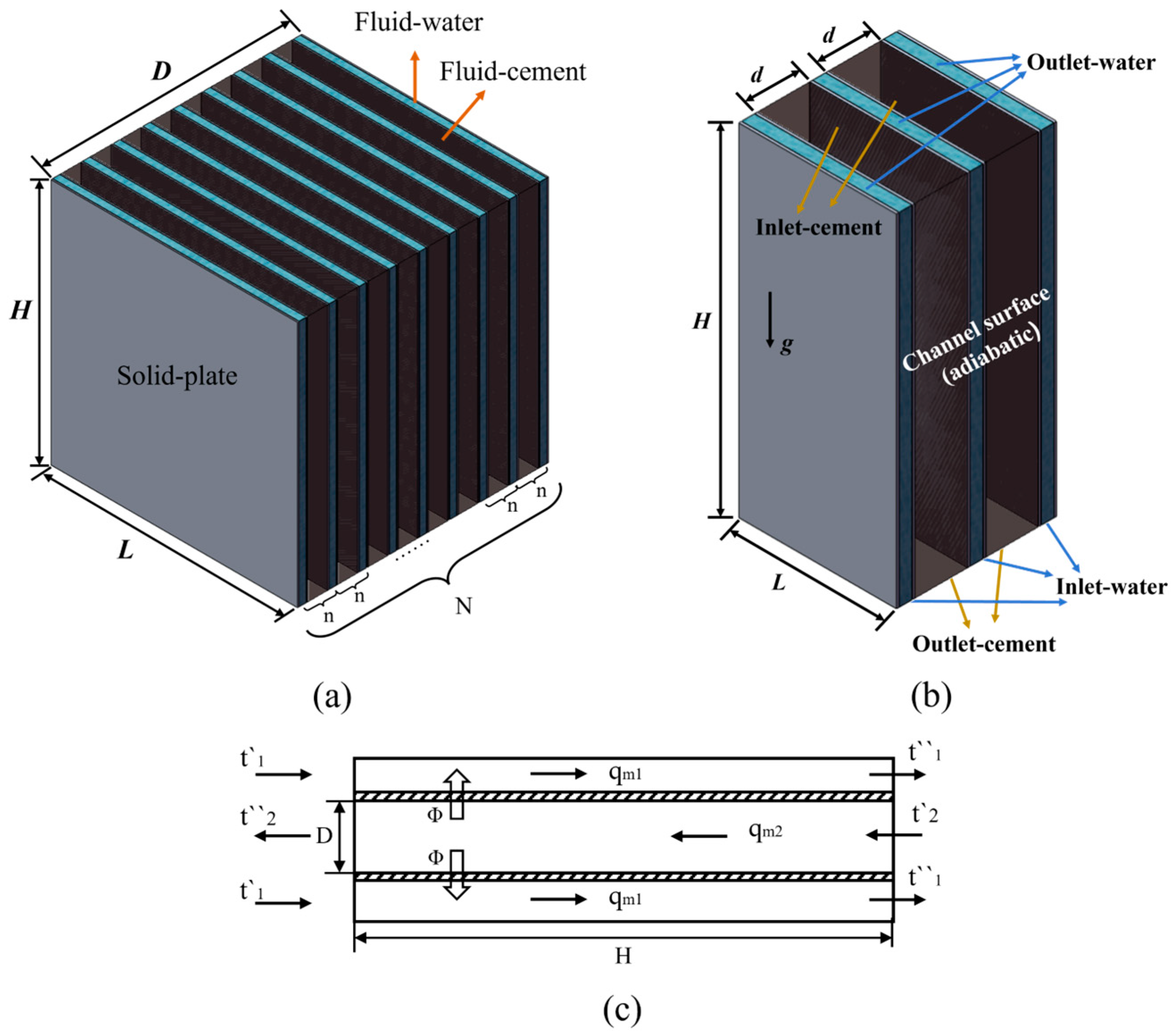
2.1. Geometric Model Construction

To accurately simulate the proposed layered-plate heat exchanger, this study utilized SolidWorks 2021 software to construct its geometric model. As shown in Figure 1a, the heat exchanger comprises three main components: the feeding system, the cooling unit group, and the discharge system. The cooling unit group consisted of multiple interconnected cooling units. Each cooling unit included a shell and several cooling plates (Figure 1b). Both sides of the shell contained cavities, and the cooling plates were assembled into the interior of the shell through these cavities. Uniform spacing was maintained between adjacent cooling plates to form 17 product channels. The cooling plates were secured to the shell via flanges, and the cooling units were interconnected through flange connections. This design simplified both fabrication and maintenance while allowing flexible adjustment of the cooling unit group to meet different operational requirements. Figure 1c shows the structure of the cooling plate. It was hollow to facilitate the flow of cooling water. A water inlet and outlet were installed at the lower and upper ends of the cooling plate, respectively, while flanges were secured on both sides of the plate.

In the layered-plate heat exchanger, the coordinated operation of the feeding and discharge systems ensured a stable load and flow rate of high-temperature cement powder in the product channels, promoting uniform flow and effective heat exchange. Figure 1b illustrates the flow path of high-temperature cement powder. Newly milled high-temperature cement powder was uniformly distributed into each product channel via an air-conveyed inclined chute. Within the channels, heat was transferred from the high-temperature powder to the cooling water through the cooling plates, effectively cooling the powder. After cooling, the powder was evenly discharged via a divided wheel device for subsequent storage or sale.

2.2. Physical Model Construction

The coordinated operation of the feeding and discharge systems maintained a stable flow rate and uniform distribution of high-temperature cement powder within the cooling unit group. As shown in Figure 2a, the computational domain constructed in this study includes only the section of the cooling unit group involved in heat transfer. Therefore, in the following text, references to the inlet, outlet, and cooling efficiency specifically denote those of the cooling unit group. The computational domain consisted of multiple cooling cycles, with H, D, and L representing the height, width, and length of the cooling unit group, respectively. Figure 2b provides a detailed view of a single cooling cycle, where d represents product channel width. Figure 2c illustrates the heat transfer mechanism within a cooling cycle, clarifying the thermal interactions occurring in the cooling units. For simulation purposes, this study used the cooling cycle depicted in Figure 2b as the computational model. High-temperature cement powder entered the product channels from the top and flowed downward along the outer walls of the cooling plates. Then, it was discharged at the bottom at a constant flow rate. Meanwhile, cooling water flowed upward along the inner walls of the cooling plates at a constant flow rate, exiting from the top of the plates. The sides of the product channels and cooling plates were considered as adiabatic boundaries. The counter-current flow between the high-temperature powder and cooling water across the cooling plates enabled effective heat exchange.

The particle size of finished cement powder is primarily in the range of 10–30 μm, and the powder is highly dense within the cooling channels, with a volume fraction of approximately 90%. The average inter-particle spacing and interaction scale are much smaller than the characteristic dimensions of the channel, resulting in frequent particle collisions and interactions. Consequently, at the channel scale, the cement powder can be treated as a continuous medium. Therefore, in this study, the cement powder is modeled as a fluid to simplify calculations while maintaining reasonable accuracy. The fluid domains of the cement powder and cooling water, as well as the solid domain of the cooling plates, are modeled separately and coupled at the interfaces. The thermal resistance at the cement–plate interface impedes heat transfer from the cement to the cooling plates.

The structural and operational parameters of the layered-plate heat exchanger significantly influenced its cooling efficiency. These structural parameters included the height of the cooling unit group, the material of the cooling plates, the width of the product channels, the addition of fins, and the shape of the cooling plates. Meanwhile, the operational parameters included the treatment capacity of high-temperature cement powder and the consumption of cooling water. Therefore, this study focuses on investigating the effects of these factors on the cooling efficiency of the cooling unit group.

The following assumptions were adopted in this study:

• The cement powder flow maintained a full-load state within the product channels.
• Assuming a maximum temperature difference of 100 °C and emissivity of 0.91 and 0.96 for cement and water, the radiative heat fluxes are estimated to be approximately 926 W/m² and 977 W/m², respectively. Compared with the convective heat flux on the order of 10⁵ W/m², radiative heat transfer is negligible in this system.
• Thermal contact resistance between particles and the potential effects of interstitial air layers on heat transfer were not considered.
• The initial temperature of the cement powder flow was uniform, and local thermal equilibrium was achieved at the interface between solid particles and pores.
• The physical properties of the materials were considered to be constant.
• The conductive heat flux along the plate length is estimated using a thermal conductivity of 500 W/(m·°C), a plate length of 10 m, and a thickness of 2 mm, assuming a maximum temperature difference of 100 °C. The resulting axial heat flux is approximately 10 W/m². Compared with the convective heat flux on the order of 10⁵ W/m², the axial conductive heat transfer is negligible in this system.
• Heat dissipation due to viscous dissipation is disregarded.
• No heat losses occurred in the cooling unit group throughout the process.

2.3. Boundary Conditions

Figure 2a shows the dimensions of the cooling unit group. Its width (D) and length (L) were both 1.5 m, while its height (H) varied from 1 m to 10 m. The model applied three groups of boundary conditions: inlet, outlet, and wall. The inlet was configured as a velocity inlet, with the velocity determined by the inlet area and the mass flow rate of the material. The outlet was defined as a pressure outlet with a pressure of 0 Pa. No-slip boundary conditions were applied to all wall surfaces. In addition, transient simulations were employed in this study to capture the full operational process of the heat exchanger, from start-up to steady-state, allowing the observation of temporal variations in flow and temperature. Moreover, when flow and heat transfer are strongly coupled, transient simulations generally achieve convergence more easily than steady-state simulations.

To achieve convergence of the fluid flow, species transport, and energy conservation equations within the computational domain, this study used the SIMPLE (Semi-Implicit Method for Pressure-Linked Equations) algorithm for pressure–velocity coupling. The residuals for continuity, velocity, turbulent kinetic energy, and the dissipation rate were set to 10⁻³, whereas the residual for the energy equation was set to a more stringent value of 10⁻⁶.

The properties of the materials used in the simulations are detailed in

Table 1. Properties of materials used in simulations.

Material	Density (kg/m3)	Specific Heat (J/(kg·°C))	Thermal Conductivity (W/(m·°C))	Viscosity (kg/(m·s))	Initial Temperature °C
Cement	1200	841	0.3	1.72 × 10−5	130
Water	995.6	4180	0.615	7.972 × 10−4	30

.

2.4. Governing Equations

During the cooling of high-temperature cement powder in the layered-plate heat exchanger, the primary physical processes were material flow and heat transfer. This study employed ANSYS Fluent 2024 R1 software to perform numerical simulations of the cooling process. To comprehensively analyze the cooling mechanisms within the powder heat exchanger, this study solved the governing differential equations for mass conservation, momentum conservation, and energy conservation.

The governing equations for mass conservation, momentum conservation, and energy conservation are presented in Equations (1)–(3), respectively [21].

$${\displaystyle \frac{\partial \rho }{\partial t}}+\nabla \left(\rho \overrightarrow{\nu }\right)=S_m,$$

(1)

where $\overrightarrow{\nu }$ is the flow velocity in m/s, and ρ is the material density in kg/m³.

$${\displaystyle \frac{\partial }{\partial t}}\left(\rho \overrightarrow{\nu }\right)+\nabla ·\left(\rho \overrightarrow{\nu }\overrightarrow{\nu }\right)=-\nabla P+\nabla \left(\stackrel{̿}{\tau }\right)+\rho \overrightarrow{g}+\overrightarrow{F}.$$

(2)

The first term on the right-hand side of Equation (2) represents the force derived from the pressure gradient, the second term is the force from stress, and the third term is the force of gravity. The first term on the left-hand side of the equation represents the rate of change in fluid velocity, and the second term denotes the transfer of fluid momentum. Here, p is the static pressure in Pa, $\overrightarrow{g}$ is the gravitational acceleration in m/s², $\overrightarrow{F}$ represents external body forces in kg/(m²·s²), and $\stackrel{̿}{\tau }$ is the stress tensor in Pa, defined in Equation (3):

$$\stackrel{̿}{\tau }=\mu \left[\left(\nabla \overrightarrow{\nu }+{\nabla \overrightarrow{\nu }}^T\right)-{\displaystyle \frac{2}{3}}\nabla ·\overrightarrow{\nu }I\right],$$

(3)

where μ is the molecular viscosity in kg/(m·s²), and I is the identity tensor. The second term on the right-hand side of Equation (2) accounts for the effect of volume dilation.

$${\displaystyle \frac{\partial }{\partial t}}\left[\rho \left(e+{\displaystyle \frac{{\nu }^2}{2}}\right)\right]+\nabla ·\left[\rho \nu \left(h+{\displaystyle \frac{{\nu }^2}{2}}\right)\right]=\nabla ·\left(k_e\nabla T-{\sum }_j{h}_j{\overrightarrow{J}}_j+{\stackrel{̿}{\tau }}_e\overrightarrow{\nu }\right)+S_h.$$

(4)

The first three terms on the right-hand side of Equation (4) represent energy transfer due to thermal conduction, species diffusion, and viscous dissipation, respectively. S_h denotes volumetric heat sources, while e and h represent the total energy per unit mass and enthalpy of species j, respectively. Meanwhile, k_e denotes the effective thermal conductivity in W/(m·°C), and ${\overrightarrow{J}}_j$ represents the diffusion flux of species j.

In this simulation, the heat transfer rate output Q was calculated using Equation (5):

$$Q={\displaystyle \frac{C_P·M·\left(T_{in}-T_{out}\right)}{l}},$$

(5)

where C_p is the specific heat capacity in J/(kg·°C), and M is the mass flow rate in kg/s.

This study employed the SST (Shear Stress Transport) k–ω turbulence model to simulate flow behavior. In this model, the kinematic viscosity coefficient ($v_t$) is not a constant and is defined by Equation (6). The governing equations for turbulent kinetic energy (k) and the turbulent dissipation rate per unit mass (ω) are shown in Equations (7) and (8), respectively [22,23].

$$v_t={\displaystyle \frac{a_{1}k}{max\left(a_1,S{F}_2\right)}},$$

(6)

$${\displaystyle \frac{\partial \left(\rho k\right)}{\partial t}}+{\displaystyle \frac{\partial \left(\rho u_{i}k\right)}{\partial x_i}}={\tilde{P}}_k-{\beta }^{*}\rho k\omega +{\displaystyle \frac{\partial }{\partial x_i}}\left[\left(\mu +{\sigma }_k{\mu }_t\right){\displaystyle \frac{\partial k}{\partial x_i}}\right],$$

(7)

$${\displaystyle \frac{\partial \left(\rho \omega \right)}{\partial t}}+{\displaystyle \frac{\partial \left(\rho u_i\omega \right)}{\partial x_i}}=\alpha {\displaystyle \frac{1}{{\nu }_t}}{\tilde{P}}_k-\beta \rho {\omega }^2+{\displaystyle \frac{\partial }{\partial x_i}}\left[\left(\mu +{\sigma }_{\omega }{\mu }_t\right){\displaystyle \frac{\partial \omega }{\partial x_i}}\right]+2\left(1-F_1\right)\rho \sigma {\omega }_2{\displaystyle \frac{1}{\omega }}{\displaystyle \frac{\partial k}{\partial x_i}}{\displaystyle \frac{\partial \omega }{\partial x_i}}.$$

(8)

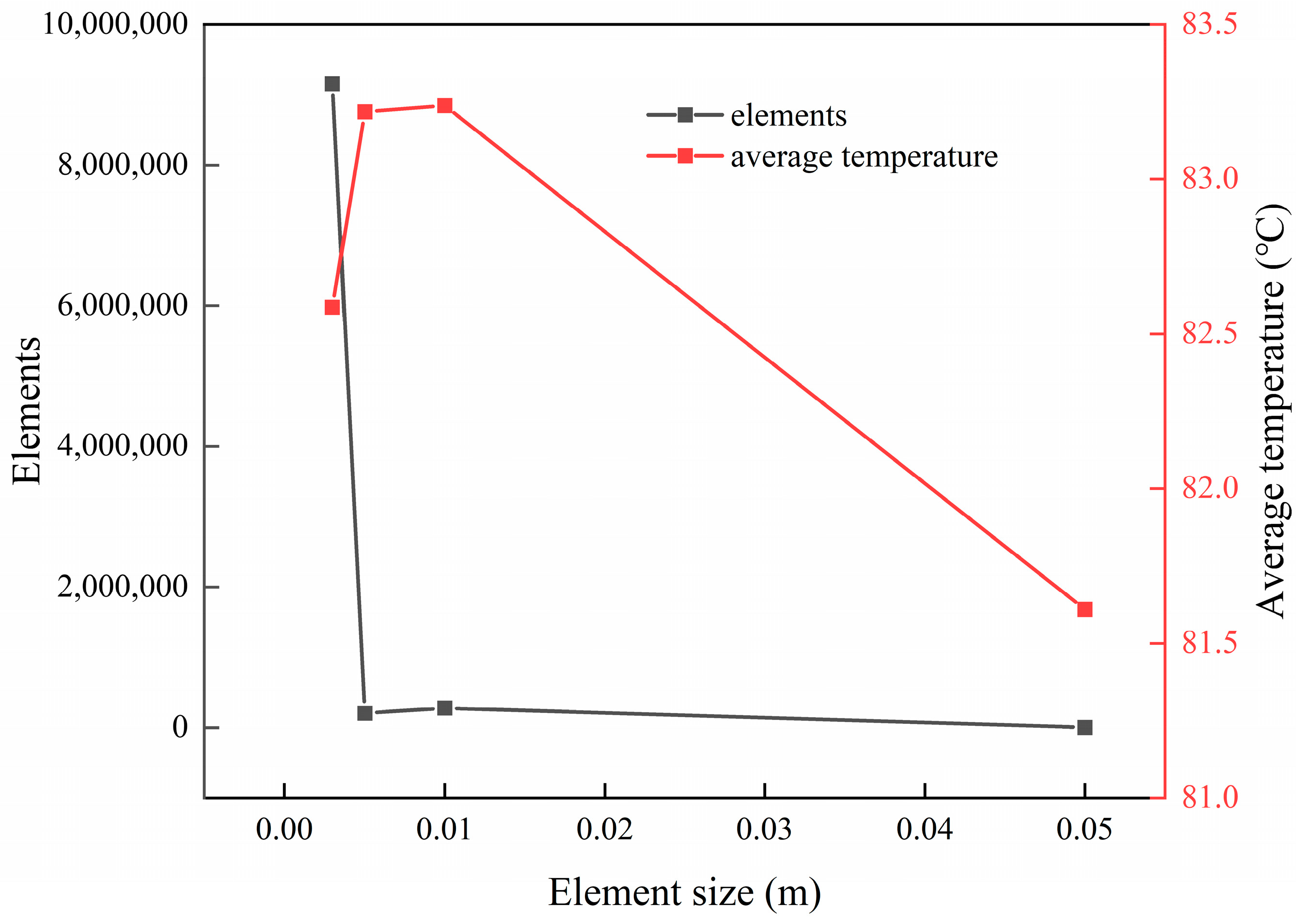
2.5. Grid Independence Test

In finite element analysis, finer mesh discretization generally improves computational accuracy. However, increasing the number of mesh elements significantly raises computational costs, and beyond a certain point, further refinement yields negligible improvements in accuracy. Therefore, mesh independence verification is essential to ensure sufficient accuracy while minimizing computational effort. In this study, a progressive mesh refinement approach was employed, comparing convergence behavior and heat transfer results. When further refinement resulted in stable convergence and variations in the results of less than 1%, the solution was considered mesh-independent.

For the simulations, a swept meshing strategy was used, and four mesh sizes (0.05 m, 0.01 m, 0.005 m, and 0.003 m) were tested. As shown in Figure 3, meshes of 0.05 m and 0.01 m failed to converge. Although the outlet temperature difference between the 0.01 m and 0.005 m meshes was less than 1%, the 0.01 m mesh was still unsuitable. In contrast, both 0.005 m and 0.003 m meshes achieved stable convergence with outlet temperature differences below 1%. Considering both computational accuracy and efficiency, a mesh size of 0.005 m was selected.

Furthermore, the turbulence parameter for the cement phase was evaluated, yielding a Y⁺ value of approximately 124, which falls within the recommended range of 30–300 for wall functions. Hence, the use of the SST k–ω turbulence model with wall function treatment is both reasonable and reliable.

3. Results and Discussion

3.1. Influence of the Structural Parameters of the Cooling Unit Group on Cooling Efficiency

Modifications to the structure of the cooling unit inevitably alter the flow pattern of the material, thereby affecting the heat exchange process. In this study, ANSYS Fluent simulation software was used to comprehensively analyze the effects of the structural parameters of the cooling unit group on cooling efficiency. These parameters included the height of the cooling unit group, the material of the cooling plates, the width of the product channels, the addition of fins, and the shape of the cooling plates. For these analyses, the cement powder treatment capacity was set to 120 t/h, and the cooling water consumption was set to 60 t/h, reflecting typical operational conditions in cement production facilities. Unless otherwise specified, the product channel width (d) was maintained at the standard setting of 100 mm.

Under the conditions of this study, the inlet velocities of the cement and water phases were 0.016 m/s and 0.03 m/s, corresponding to Reynolds numbers of approximately 2.03 × 10⁵ and 1.47 × 10³, respectively. The turbulence intensities at the inlets were 3.44% for the cement phase and 6.27% for the water phase, with characteristic lengths of approximately 0.18 m and 0.039 m. The inlet temperatures were set to 130 °C for the cement phase and 30 °C for the water phase. The SST k–ω turbulence model was employed due to its proven capability to accurately predict flow in near-wall regions as well as in areas prone to separation and recirculation. The cement phase is treated as a continuous medium at the macroscopic scale, and its high Reynolds number indicates that the overall flow and heat transfer are dominated by turbulence. The SST k–ω model is well-suited for this condition, as it effectively captures both near-wall and free-shear flow development, making it a reasonable and reliable choice for the present study.

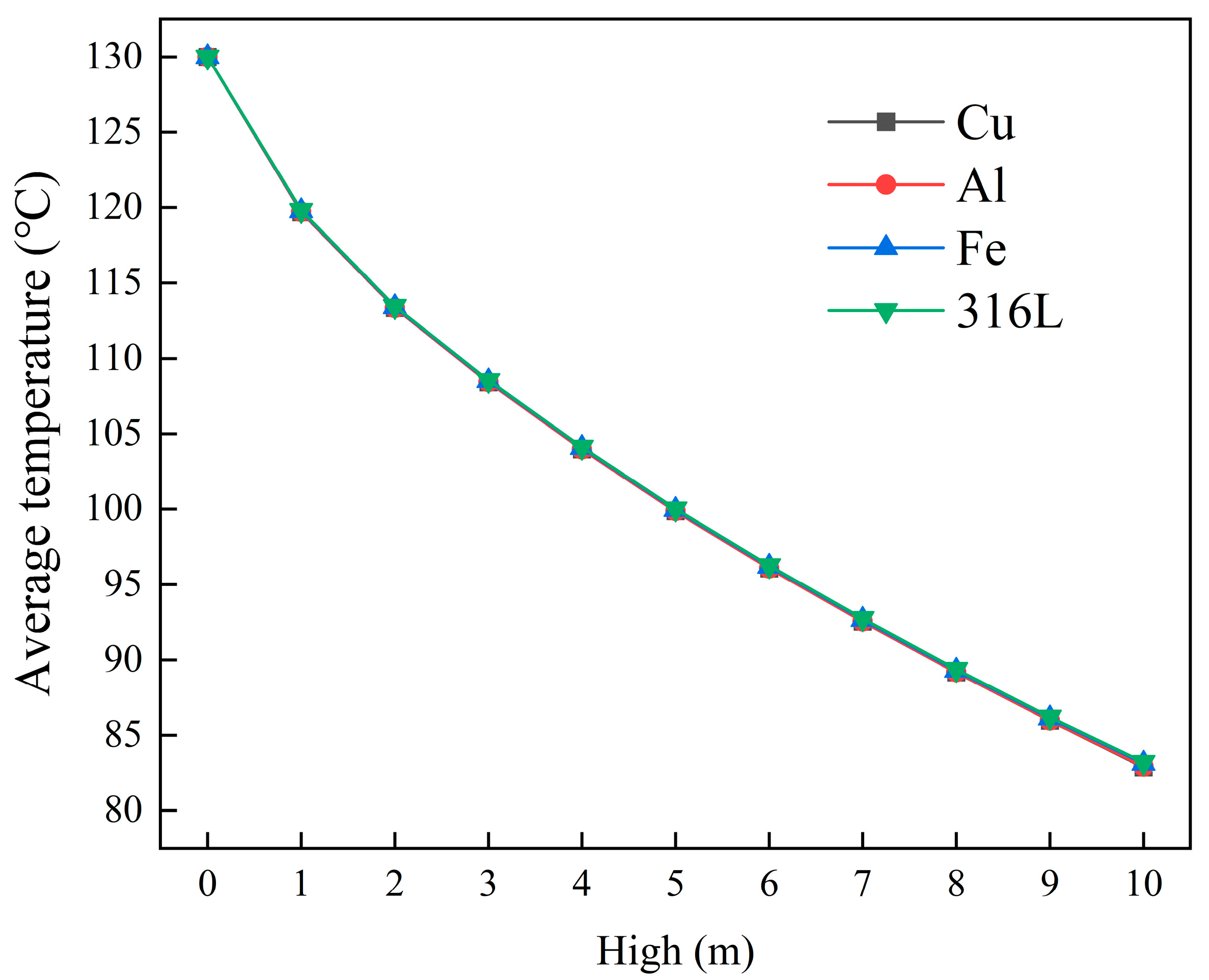
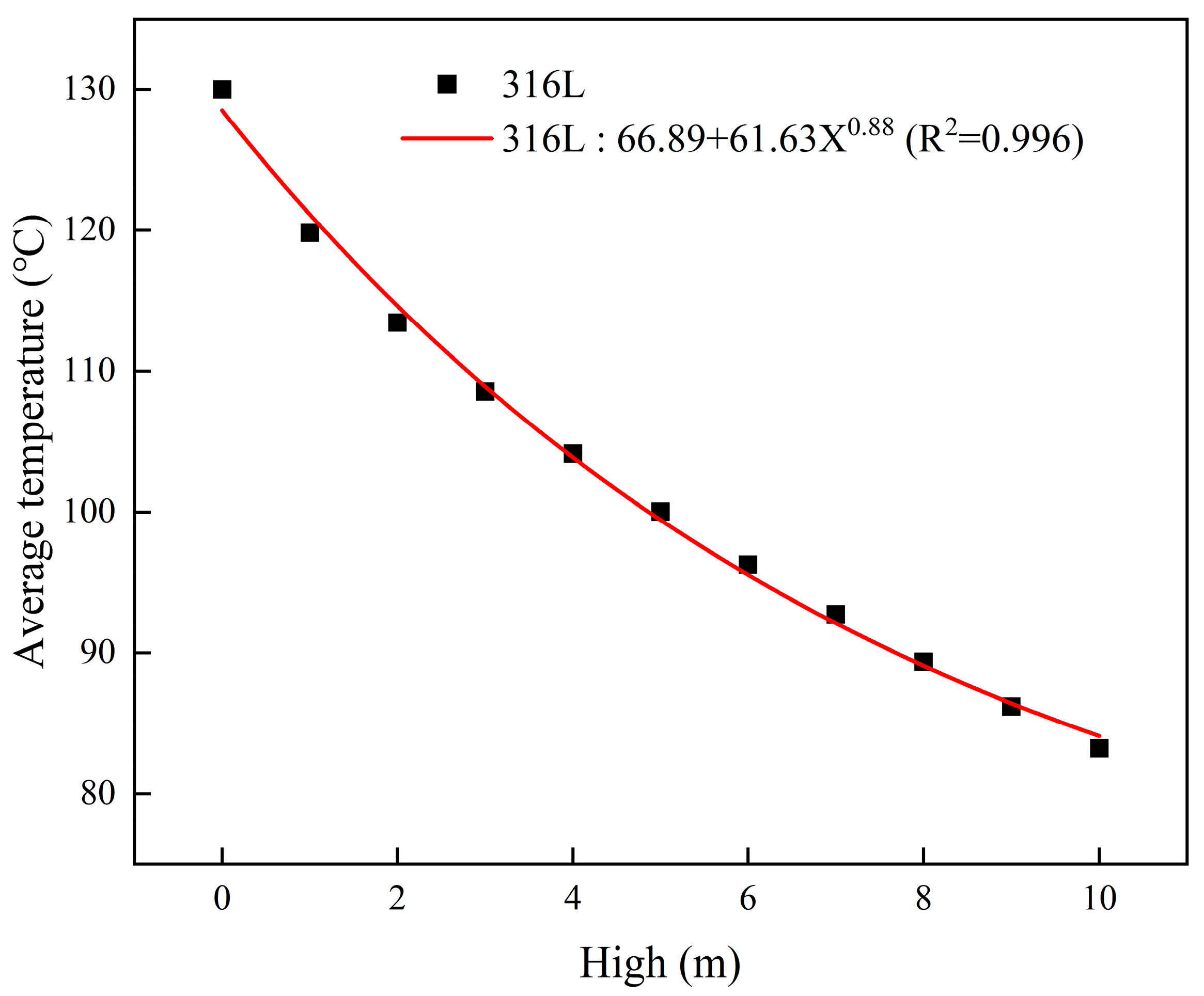
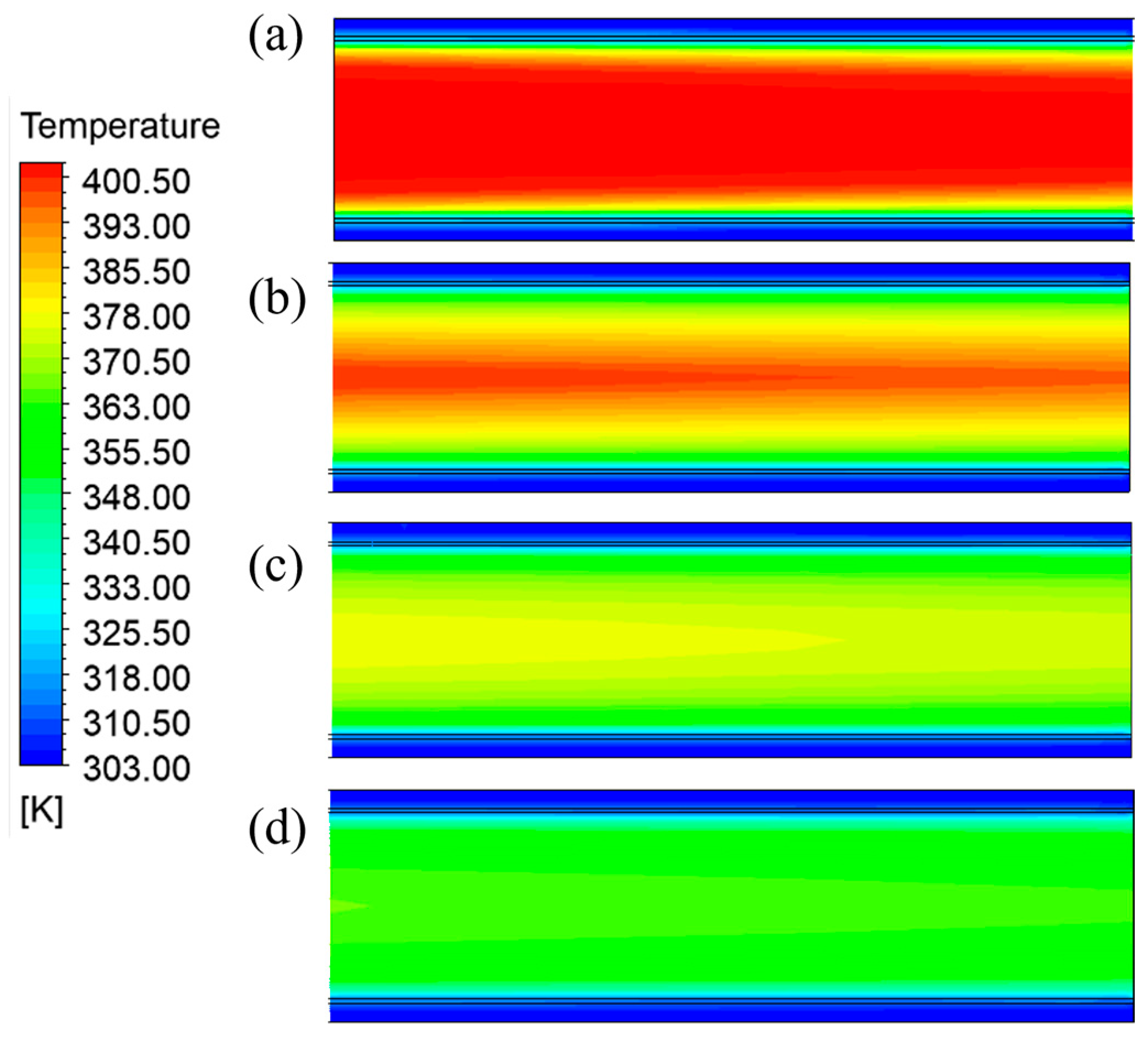
3.1.1. Influence of Cooling Unit Group Height and Cooling Plate Material on Cooling Efficiency

Figure 4 presents the simulation results for the average outlet temperature of the cement powder flow across 10 different heights of the cooling unit group and 4 different types of cooling plate materials.

Table 2. Characteristics of cooling plate materials.

Materials	Density (kg/m3)	Specific Heat (J/(kg·°C))	Thermal Conductivity (W/(m·°C))	R-Value Per Unit Area (m2·°C/W)	Abrasion Resistance	Corrosion Resistance
Cu	8978	381	387.6	5.2 × 10−6	Bad	Fine
Al	2710	902	236	8.5 × 10−6	Bad	Fine
Fe	7870	455	81.1	2.5 × 10−5	Fine	Bad
316L	7980	500	15.1	1.3 × 10−4	Excellent	Excellent

shows the characteristics of these materials. As the height of the cooling unit group increased, the average outlet temperature of the cement powder flow decreased. In contrast, variations in cooling plate material exhibited minimal impact on the average outlet temperature. Increasing the height of the cooling unit group extended the residence time of high-temperature cement powder, facilitating effective heat exchange between the cement powder and cooling water, thus improving overall cooling efficiency. Figure 5 presents the fitted relationship between the heat exchanger height and the average outlet temperature of cement when 316L stainless steel is used as the cooling plate material. The results indicate that when the height exceeds 10 m, the outlet temperature continues to decrease, and the cooling efficiency further improves. As the height increases, the temperature of the cement powder gradually approaches that of the cooling water, with the system’s cooling efficiency reaching its maximum and eventually plateauing. Additionally, the thermal resistance values of the different cooling plate materials remained on the order of 10⁻⁴ (m²·°C)/W or above (Table 2), indicating that changing the cooling plate material had a minimal impact on heat transfer efficiency.

Figure 6 shows the temperature distribution across the central cross-section of the cement powder flow, measured within 0.5 m of the outlet, across different heights of the cooling unit group equipped with cooling plates constructed from 316L stainless steel. High-temperature regions were concentrated in the center of the product channels, decreasing radially toward the cooling plates. This radial temperature gradient indicated effective heat transfer. As the height of the cooling unit group increased, the area of high-temperature regions significantly decreased, indicating improved cooling efficiency. This finding supported the conclusion that the height of the cooling unit group had a greater impact on temperature control compared to material selection, as previously illustrated in Figure 4.

Table 3. Average outlet temperatures of the cement powder flow across different heights of the cooling unit group and various types of cooling plate materials.

High (m)	Average Outlet Temperature (°C)
	Cu	Al	Fe	316L
1	119.697	119.714	119.774	119.816
4	103.977	103.980	104.074	104.134
7	92.540	92.546	92.665	92.740
10	82.882	82.931	83.132	83.218

presents the average outlet temperatures of the cement powder flow across different heights of the cooling unit group equipped with cooling plates constructed from 316L stainless steel. Cooling efficiency improved as the cooling unit group height increased: 7.83% at 1 m, 19.90% at 4 m, 28.66% at 7 m, and 35.99% at 10 m.

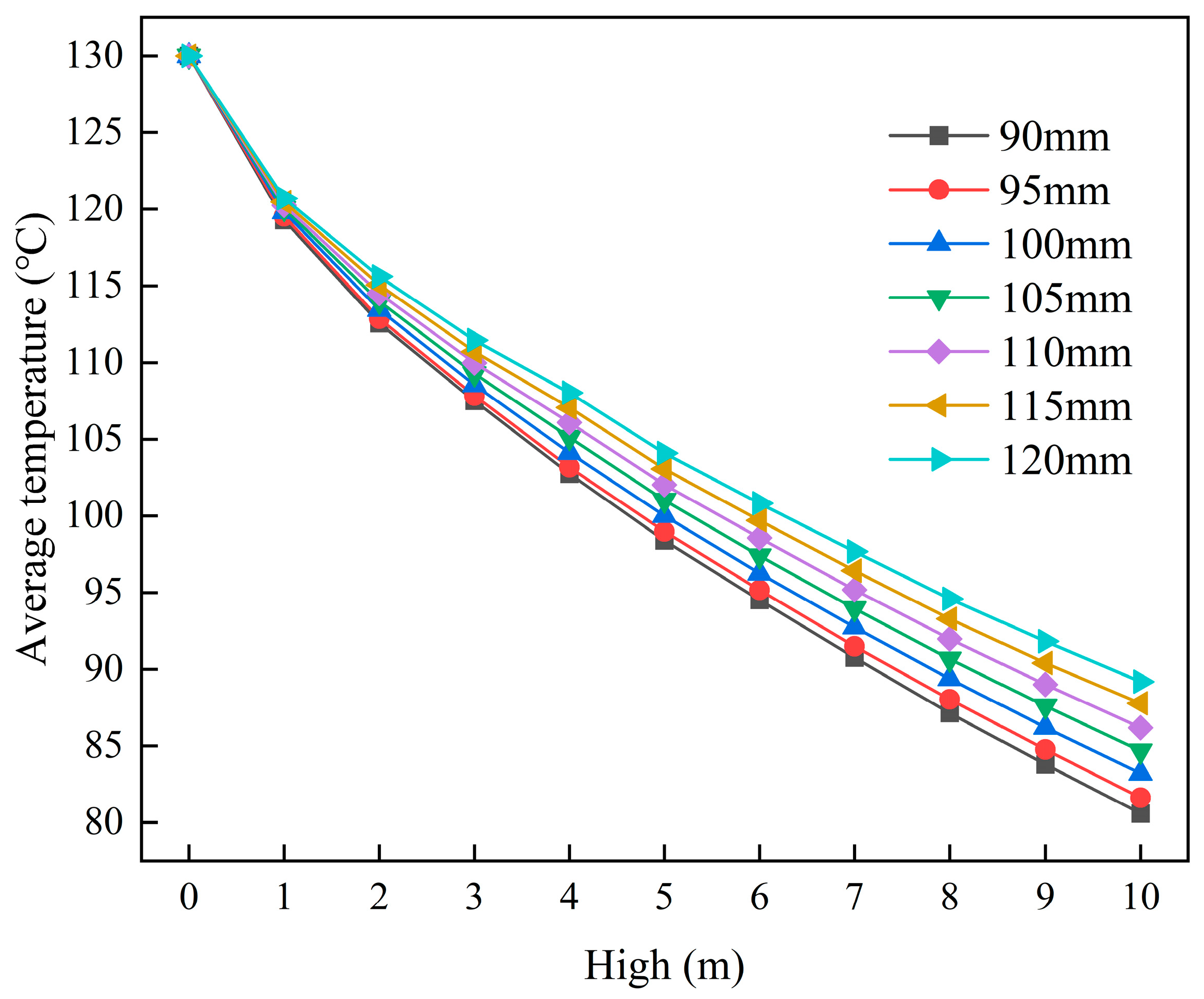
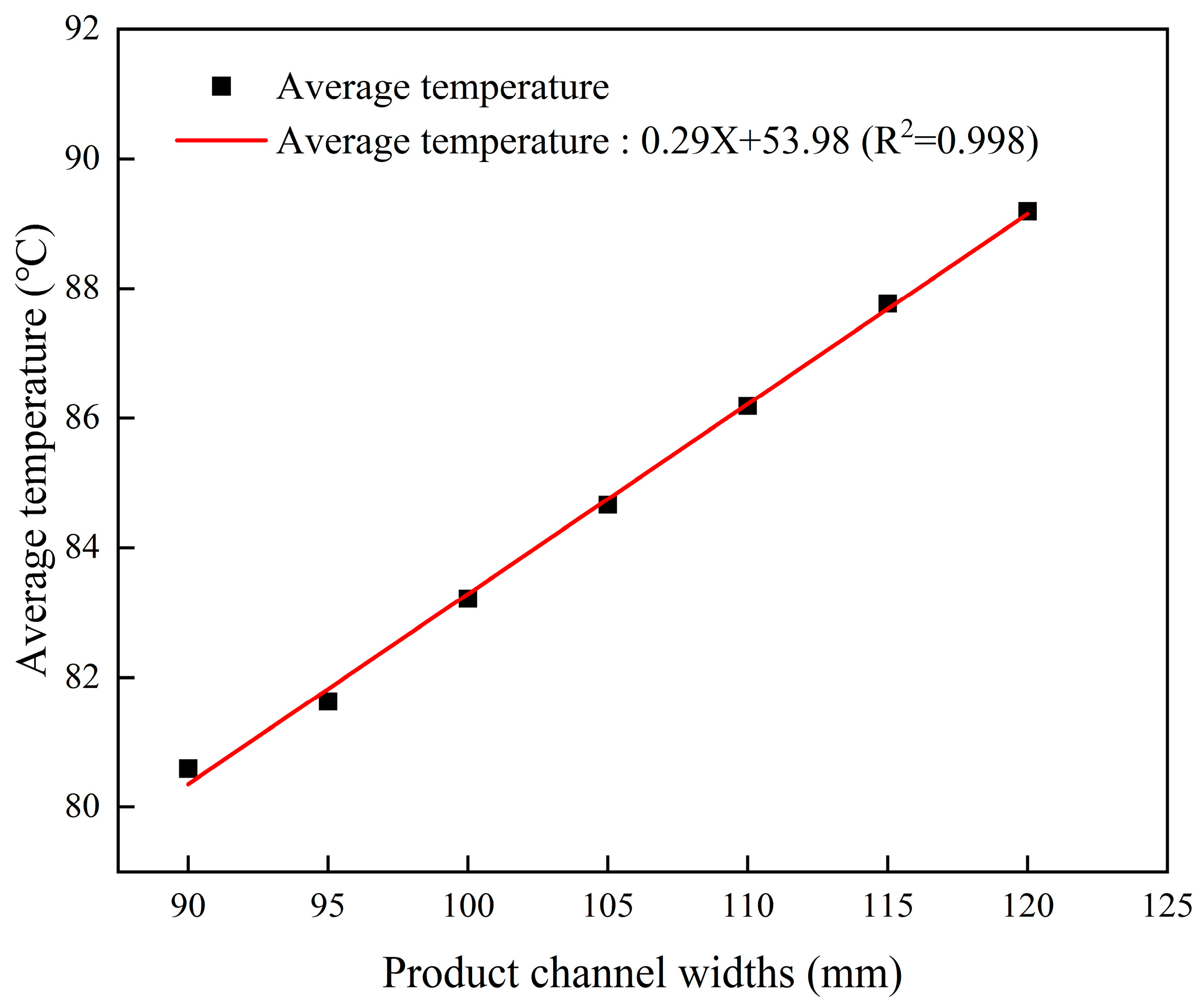
3.1.2. Influence of Product Channel Width on Cooling Efficiency

The effects of varying product channel widths on cooling efficiency were investigated using cooling plates constructed from 316L stainless steel. Figure 7 presents simulation results depicting the average outlet temperatures of the cement powder flow across 10 different heights of the cooling unit group and 7 different widths (d) of the product channel. Figure 7 reveals a negative relationship between product channel width and cooling efficiency: as the channel width increases, cooling efficiency tends to decrease. Figure 8 presents the fitted correlation between material channel width and the average outlet cement temperature at an exchanger height of 10 m. When the number of product channels and the cement powder treatment capacity were maintained constant, increasing the channel width expanded the inlet area. This expansion slightly reduced the feed velocity and increased the residence time of cement powder, which was expected to enhance cooling efficiency. However, a wider channel promoted the formation of a thicker boundary layer near the cooling plate surface, increasing the thermal resistance of the cement powder flow.

Table 4. Average outlet temperatures of the cement powder flow across different cooling unit group heights and product channel widths.

High (m)	Average Outlet Temperature (°C)
	90 mm	95 mm	100 mm	105 mm	110 mm	115 mm	120 mm
1	119.280	119.533	119.816	120.047	120.249	120.465	120.708
4	102.765	103.176	104.134	105.126	106.089	107.075	108.027
7	90.767	91.497	92.741	93.953	95.176	96.430	97.666
10	80.595	81.630	83.218	84.668	86.188	87.768	89.188

presents the average outlet temperatures of the cement powder flow across different cooling unit group heights and product channel widths. At a cooling unit group height of 10 m, the cooling efficiencies for the product channel widths of 90, 100, 110, and 120 mm were 38.00%, 35.99%, 33.70%, and 31.39%, respectively.

In Fluent, by setting the reference temperature in the Reference Values to the inlet temperature of the cement powder, the local convective heat transfer coefficient can be obtained with respect to this reference. As shown in

Table 5. Surface convective heat transfer coefficient under different product channel widths.

Widths	90 mm	95 mm	100 mm	105 mm	110 mm	115 mm	120 mm
hSurf (W/(m2·°C))	53.23	51.86	50.44	49.31	47.99	46.96	45.96

, within the channel width range of 90–120 mm, the surface heat transfer coefficient decreases with increasing channel width, resulting in higher outlet temperatures for the cement powder. This behavior can be attributed to two main factors. First, widening the channel reduces the surface-to-volume ratio, decreasing the heat transfer area available per unit volume and thus lowering the convective heat transfer capability at the wall. Second, a wider channel increases the thickness of the material layer, which enhances the thermal resistance between the central region and the wall, thickens the thermal boundary layer, and leads to insufficient cooling. Consequently, both the average wall heat transfer coefficient and the wall heat flux density decrease.

Figure 9 illustrates the temperature distribution across the central cross-section of the cement powder flow, measured within 0.5 m of the outlet and at a cooling unit group height of 10 m, across different product channel widths. The high-temperature region expanded as product channel width increased. Table 4 presents the average outlet temperatures of the cement powder flow across different cooling unit group heights and product channel widths. At a cooling unit group height of 10 m, the cooling efficiencies for the product channel widths of 90, 100, 110, and 120 mm were 38.00%, 35.99%, 33.70%, and 31.39%, respectively. This progressive decrease in efficiency was attributed to multiple factors.

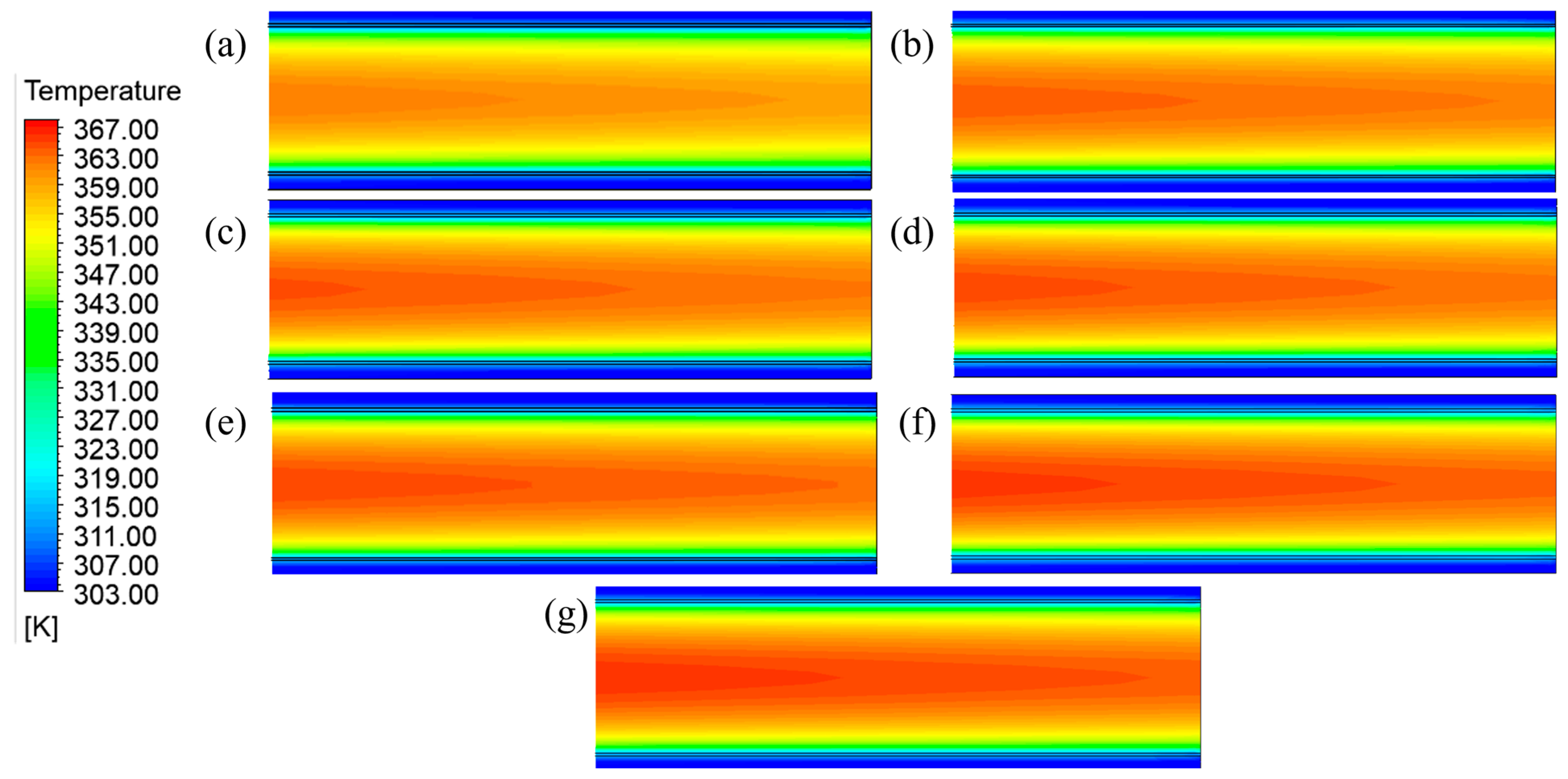
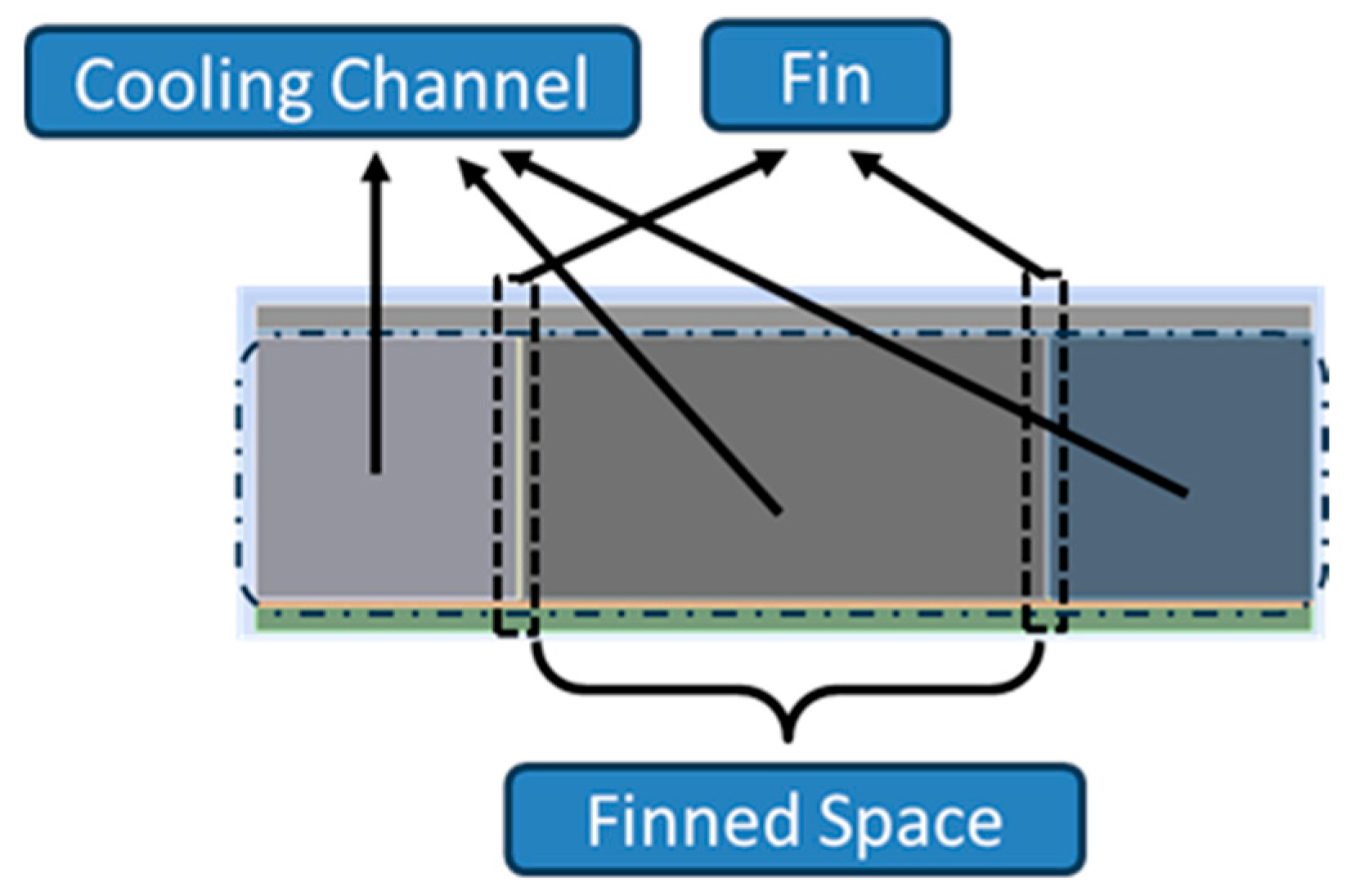
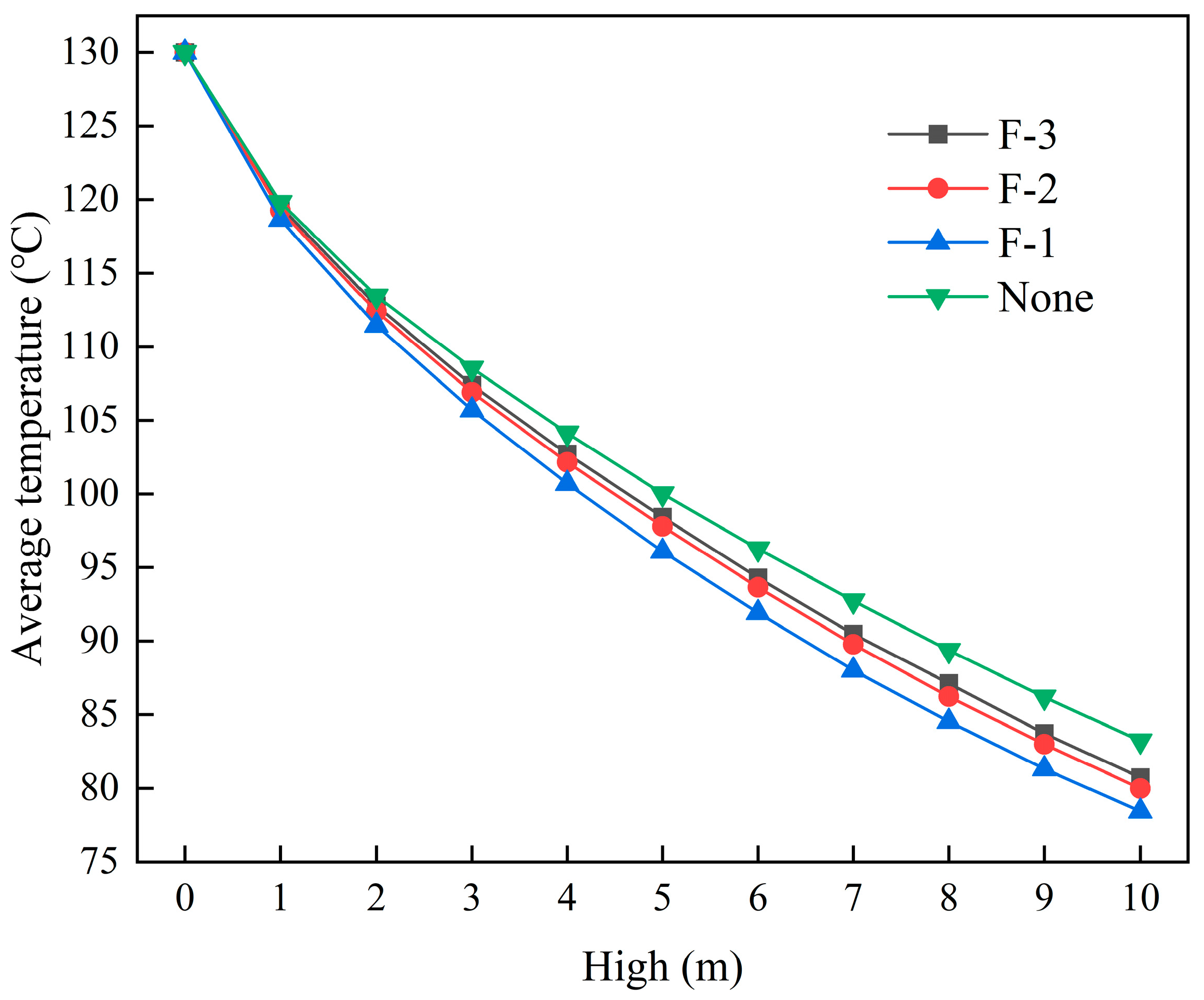
3.1.3. Influence of Adding Fins on Cooling Efficiency

The effect of incorporating fins within the product channel on cooling efficiency was investigated using cooling plates constructed from 316L stainless steel. As illustrated in Figure 10, the fins are attached to both sides of the cooling plates, dividing the product channel into multiple sub-channels. Three fin spacings were analyzed: 100 mm (F-1), 200 mm (F-2), and 300 mm (F-3), respectively. A reference condition without fins was also included. Figure 11 presents the simulation results for the average outlet temperatures of the cement powder flow across different cooling unit group heights and fin configurations. The results indicated that the incorporation of fins significantly improved cooling efficiency, as it increased the surface area available for heat transfer and enhanced the disruption of the boundary layer around the fins, thereby improving thermal conduction and convective heat transfer [24,25]. Moreover, these fins helped control the flow velocity and load distribution of the cement powder flow within the product channel. A smaller fin spacing increases the heat transfer area and the number of sub-channels, promoting more uniform heat transfer and superior performance compared to larger spacing. However, reducing the spacing also significantly increases the risk of particle agglomeration and blockage within the channels. Therefore, vibration devices are required to prevent material accumulation and clogging.

Figure 12a–d display the temperature distribution across the central cross-section of the cement powder flow, measured within 0.5 m from the outlet and at a cooling unit group height of 10 m, across different fin configurations. The presence of fins significantly reduced the area of high-temperature regions, with the reduction becoming more pronounced as fin spacing decreased. Figure 12e–g display the temperature distribution on the fin surfaces under the same cooling unit group height for different fin configurations. Smaller fin spacing promoted a wider distribution of high-temperature regions on the fin surfaces, indicating a higher degree of participation in heat transfer.

Table 6. Average outlet temperatures of the cement powder flow across different fin configurations and cooling unit group heights.

High (m)	Average Outlet Temperature (°C)
	F-3	F-2	F-1	None
1	119.528	119.259	118.637	119.816
4	102.725	102.149	100.714	104.134
7	90.477	89.771	88.022	92.741
10	80.730	79.983	78.430	83.218

presents the average outlet temperatures of the cement powder flow across different cooling unit group heights and fin configurations. At a cooling unit group height of 10 m, the use of fins with the spacings of F-3, F-2, and F-1 resulted in average outlet temperature reductions of 2.488, 3.235, and 4.788 °C, respectively, when compared to the reference condition without fins. Correspondingly, the cooling efficiency improved to 37.90%, 38.48%, and 39.67%, respectively. Increasing the fin length enlarges the heat transfer area; however, excessively long fins can reduce the temperature difference at the tip, thereby decreasing the heat transfer efficiency. Moderately increasing the fin thickness can lower thermal conduction resistance, but overly thick fins reduce the flow cross-sectional area and increase pressure drop. Therefore, by appropriately optimizing the fin length, thickness, and spacing, a balance between enhanced heat transfer and controlled flow resistance can be achieved, effectively improving the overall heat transfer performance.

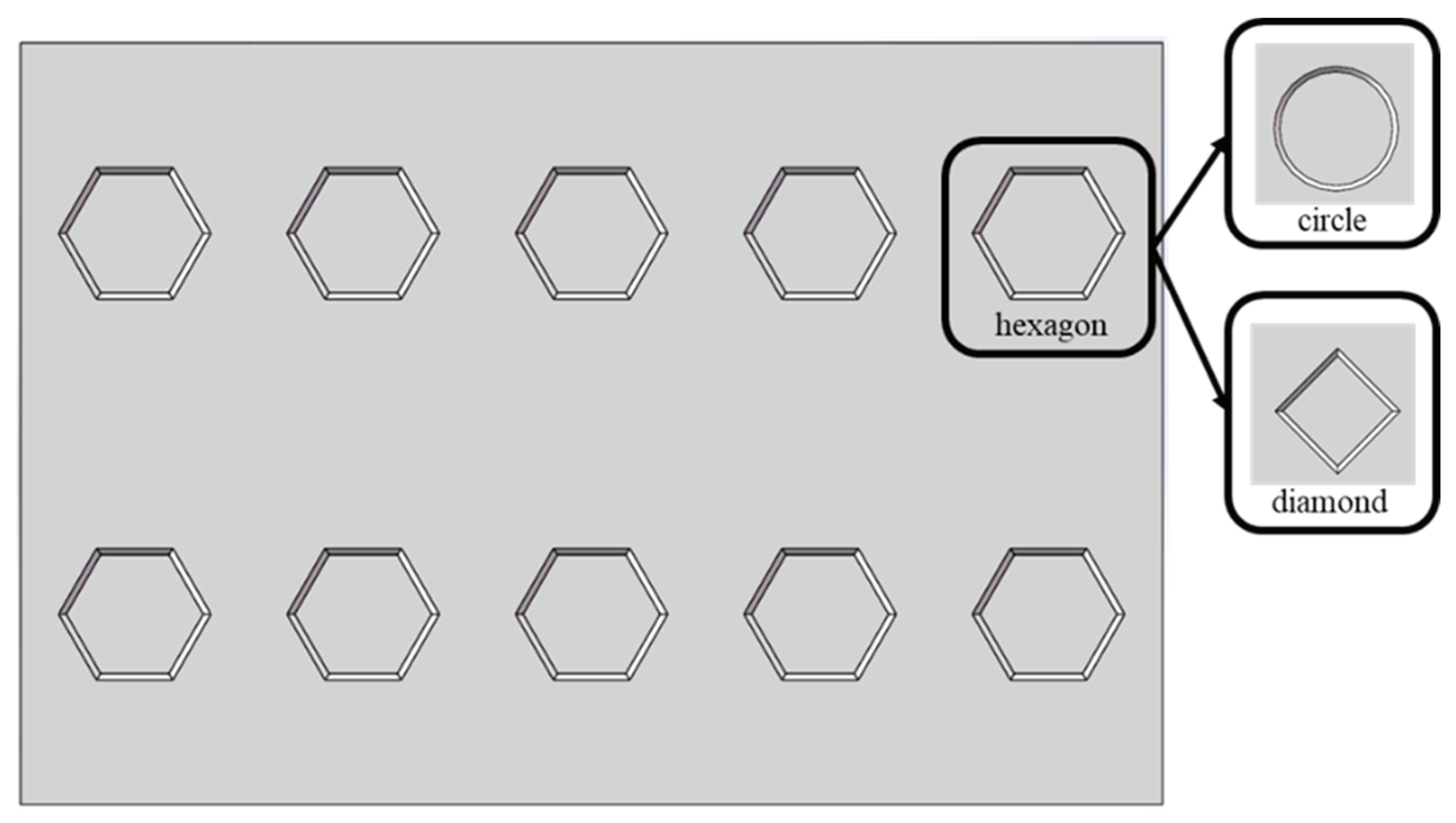
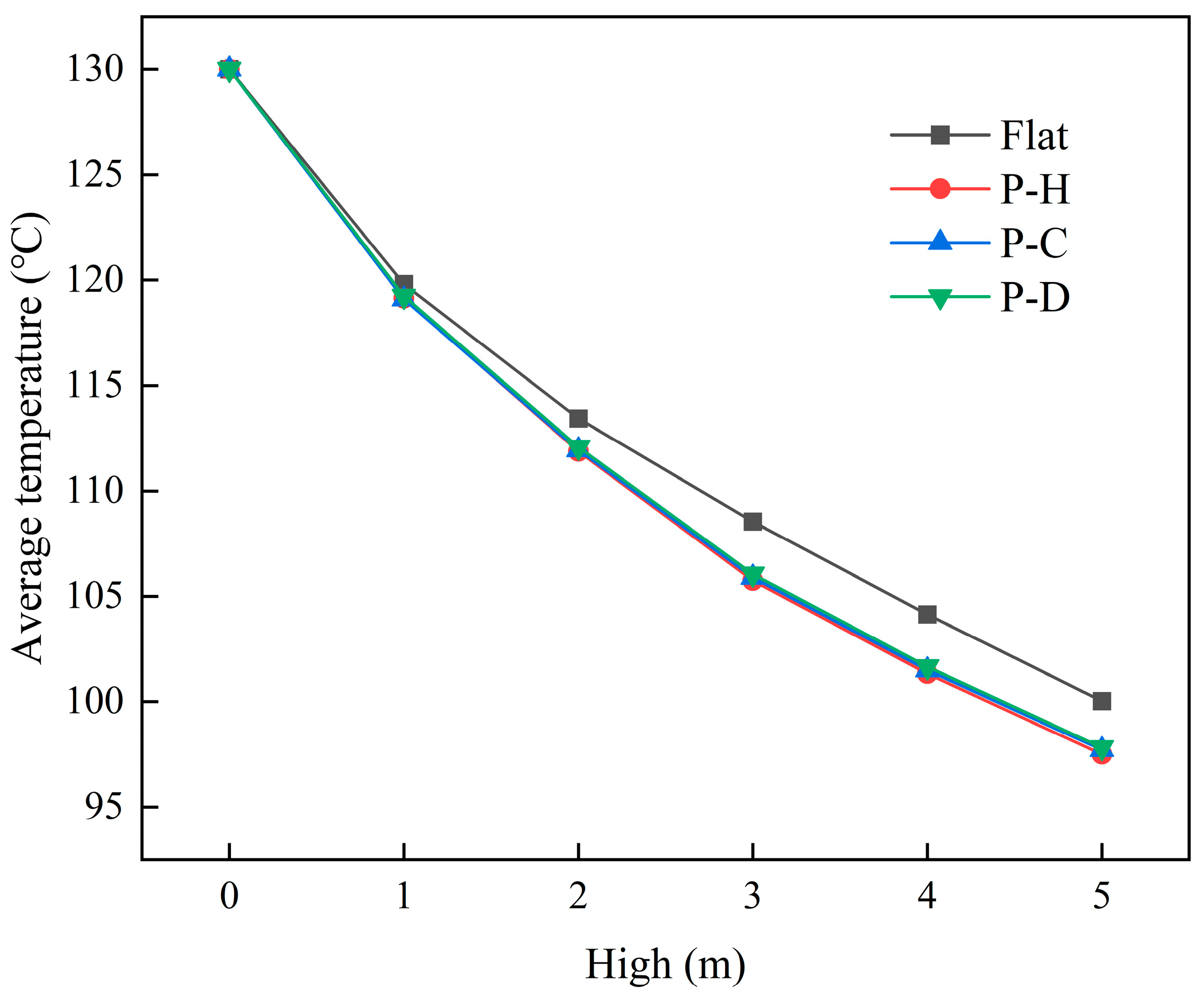
3.1.4. Influence of the Surface Shape of Cooling Plates on Cooling Efficiency

The morphology of cooling plates with three distinct surface shapes, which were installed in the cooling unit group with a height of 1 m, is illustrated in Figure 13. The primary distinction among the three cooling plate surface shapes was their groove shape, which was hexagonal, circular, or diamond-shaped, denoted as P-H, P-C, or P-D, respectively. Figure 14 presents the numerical simulation results for the average outlet temperatures of the cement powder flow across three different cooling plate surface shapes and five different cooling unit group heights. Compared to cooling plates with flat surfaces, those with grooves exhibited superior heat exchange capabilities. However, the difference in cooling efficiency among different groove shapes was minimal. The grooved surfaces not only increased the heat transfer area of the cooling unit group but also enhanced the complexity of the flow channel, thereby increasing cooling efficiency [26].

Figure 15a–f illustrate the temperature distribution across the central cross-section of the cement powder flow, measured within 0.5 m of the outlet and at different cooling unit group heights, for P-H and flat cooling plate surface shapes, respectively. The temperature distribution analysis revealed that the area of the high-temperature regions gradually decreased as the cooling unit group height increased. Furthermore, at the same cooling unit group height, the high-temperature region on the P-H cooling plate was significantly smaller than that on the flat-surface cooling plate.

Table 7. Average outlet temperatures of the cement powder flow across different cooling plate surface shapes and cooling unit group heights.

High (m)	Average Outlet Temperature (°C)
	Flat	P-H	P-C	P-D
1	119.816	119.143	119.101	119.247
2	113.444	111.876	111.943	112.085
3	108.552	105.738	105.895	106.052
4	104.134	101.326	101.497	101.660
5	100.025	97.502	97.720	97.825

presents the simulation results for the average outlet temperature of the cement powder flow across different cooling plate surface shapes and cooling unit group heights. At a cooling unit group height of 5 m, cooling plates with grooves exhibited a 37.9% higher cooling efficiency compared to flat-surface cooling plates.

3.2. Influence of the Operational Parameters of the Cooling Unit Group on Cooling Efficiency

The effects of the two main operational parameters of the cooling unit group, the cement powder treatment capacity and cooling water flow rate, on cooling efficiency were investigated. In these simulations, the cooling plates were constructed from 316L stainless steel, and the product channel width (d) was set to 100 mm.

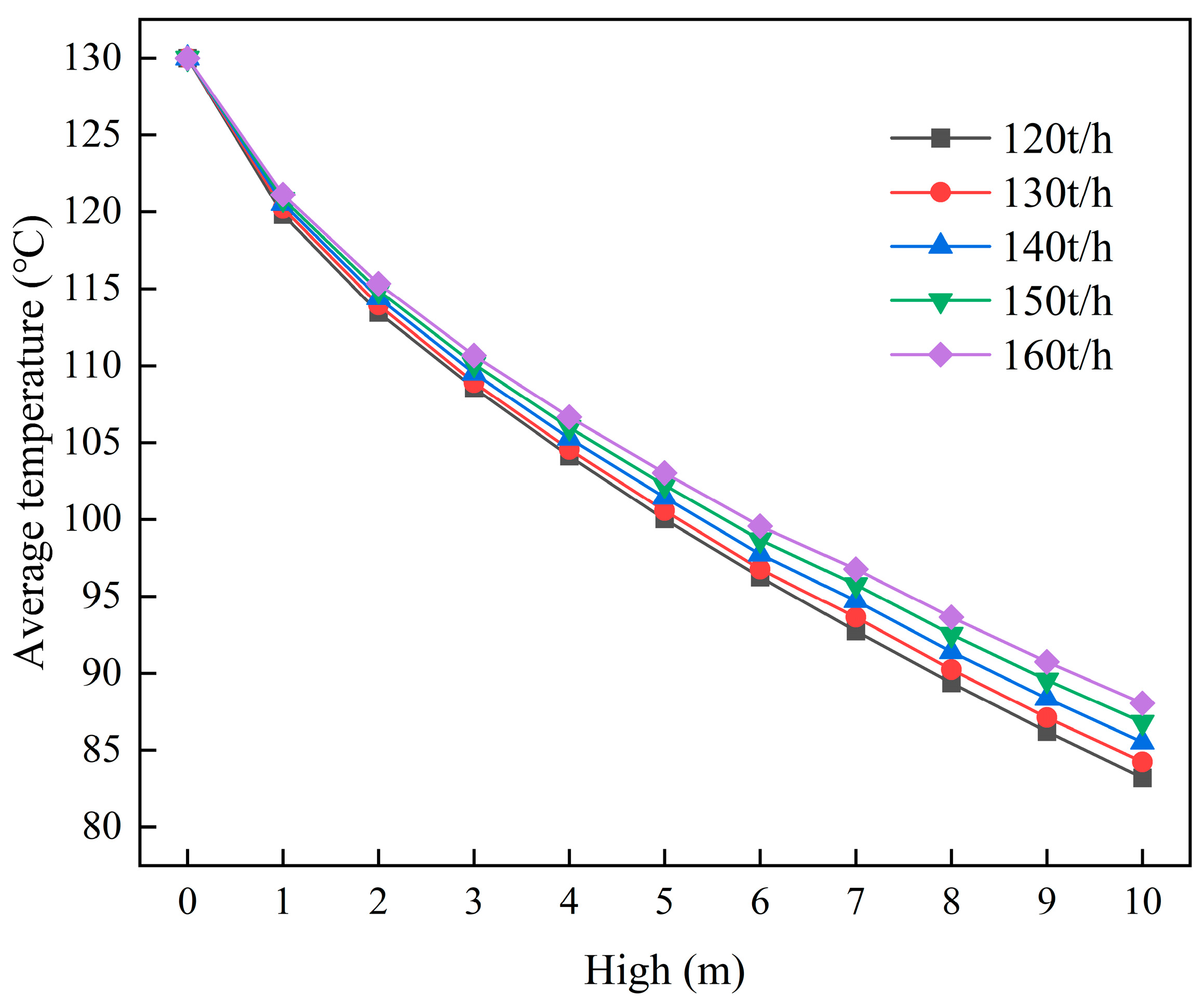
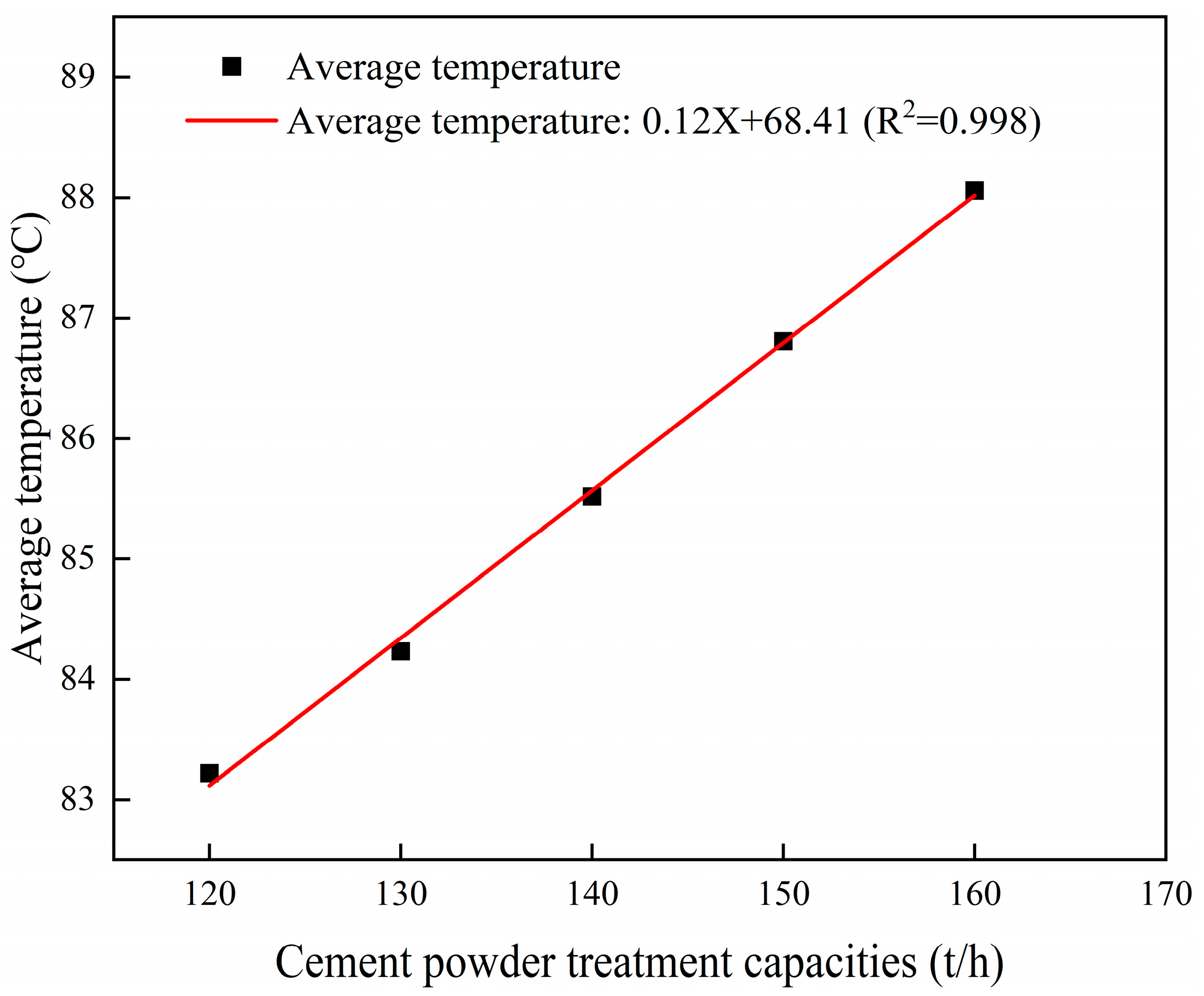
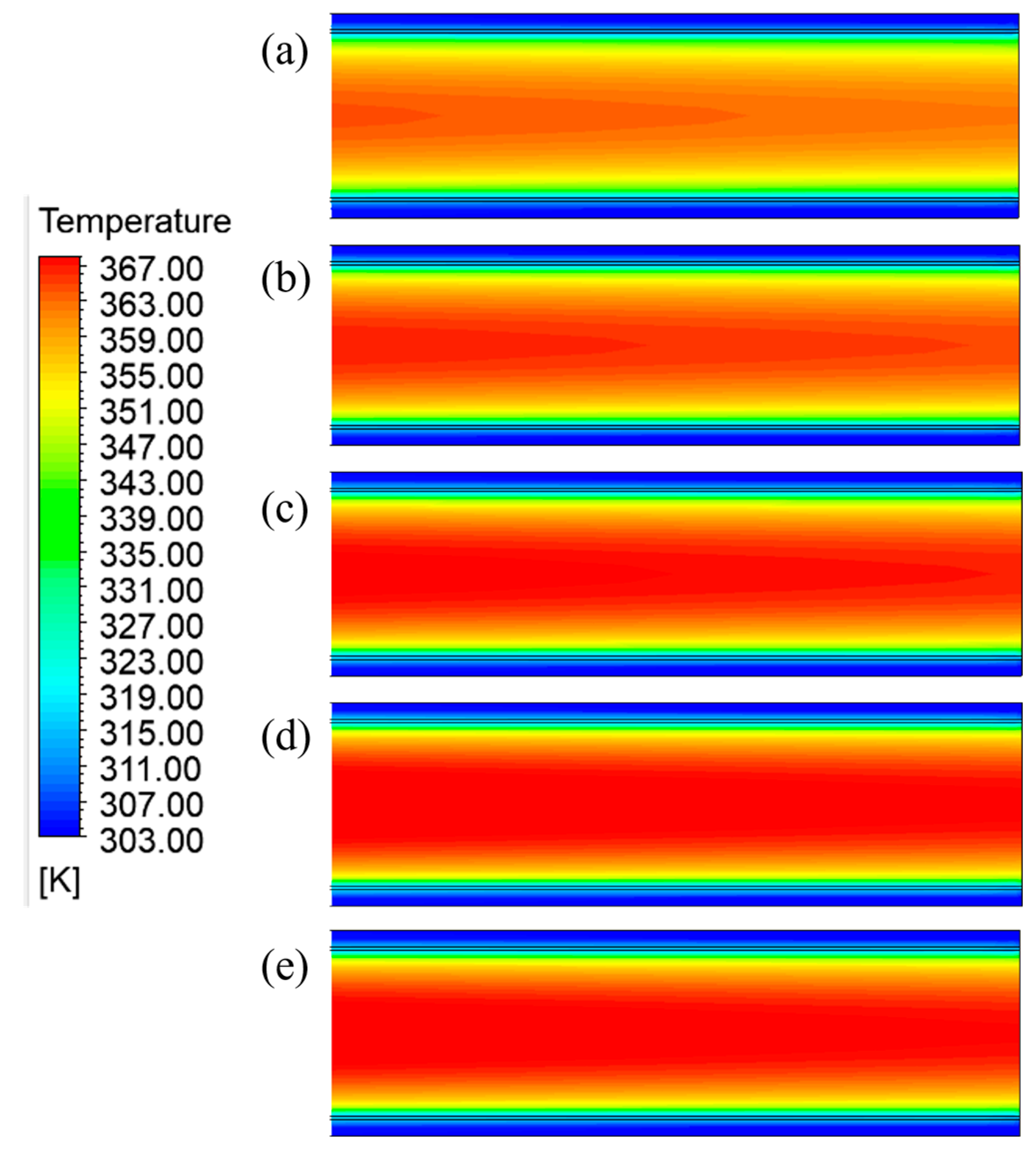
3.2.1. Influence of Cement Powder Treatment Capacity on Cooling Efficiency

Figure 16 displays the simulation results for the average outlet temperatures of the cement powder flow across different cement powder treatment capacities and cooling unit group heights. At the same cooling unit group height, cement powder treatment capacity was negatively correlated with cooling efficiency: as the treatment capacity increased, cooling efficiency decreased. Figure 17 presents the fitted relationship between the average outlet temperature of cement and the processing rate at a heat exchanger height of 10 m. The results indicate that, under otherwise constant conditions, an increase in cement powder treatment capacity elevated the inlet velocity of the cement powder flow, thereby reducing the residence time of the powder within the product channel, resulting in higher average outlet temperatures. Figure 18 depicts the temperature distribution across the central cross-section of the cement powder flow, measured within 0.5 m of the outlet and at a cooling unit group height of 10 m, across different cement powder treatment capacities. As the cement powder treatment capacity of the cooling unit group increased, the high-temperature regions on the cement powder cross-section expanded.

Table 8. Average outlet temperatures of the cement powder flow across different cement powder treatment capacities and cooling unit group heights.

High (m)	Average Outlet Temperature (°C)
	120 t/h	130 t/h	140 t/h	150 t/h	160 t/h
1	119.816	120.217	120.531	120.831	121.130
4	104.134	104.559	105.279	105.984	106.667
7	92.741	93.632	94.707	95.748	96.765
10	83.218	84.232	85.519	86.807	88.059

presents the simulation results for the average outlet temperatures of the cement powder flow across different cement powder treatment capacities and cooling unit group heights. At a cooling unit group height of 10 m, the cooling efficiency decreased from 35.99% at 120 t/h to 35.21%, 34.22%, 33.23%, and 32.27% at 130, 140, 150, and 160 t/h, respectively.

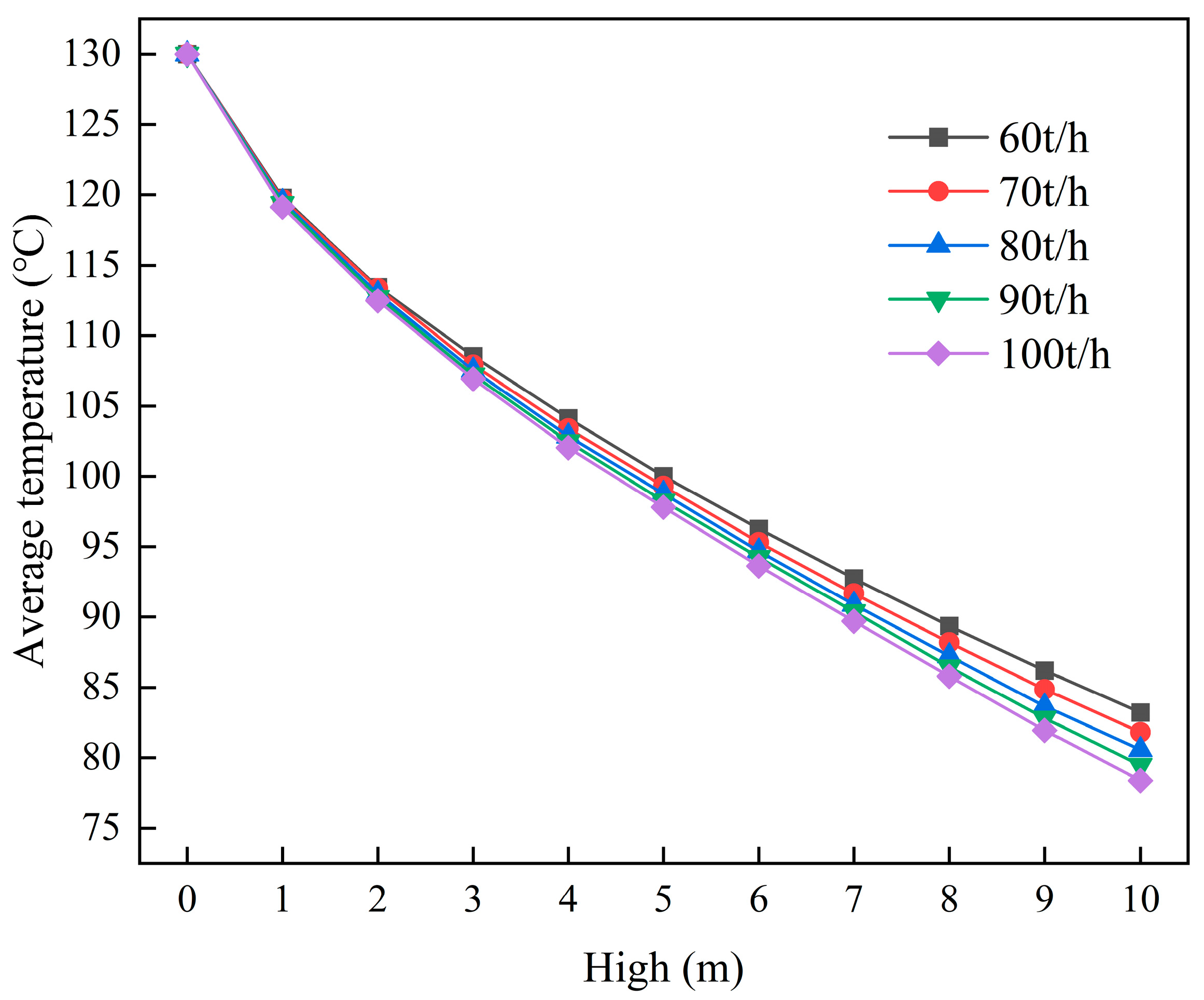
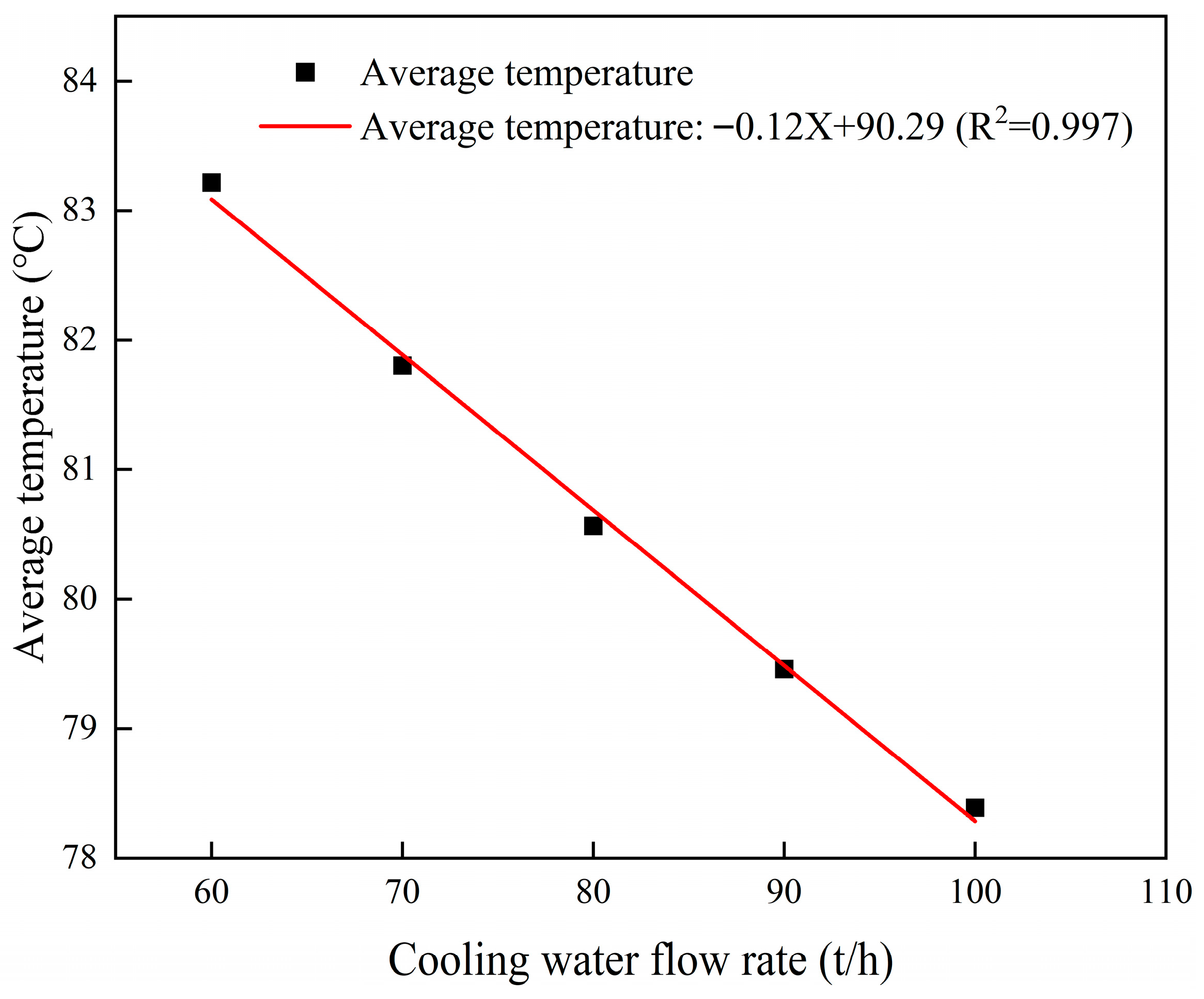
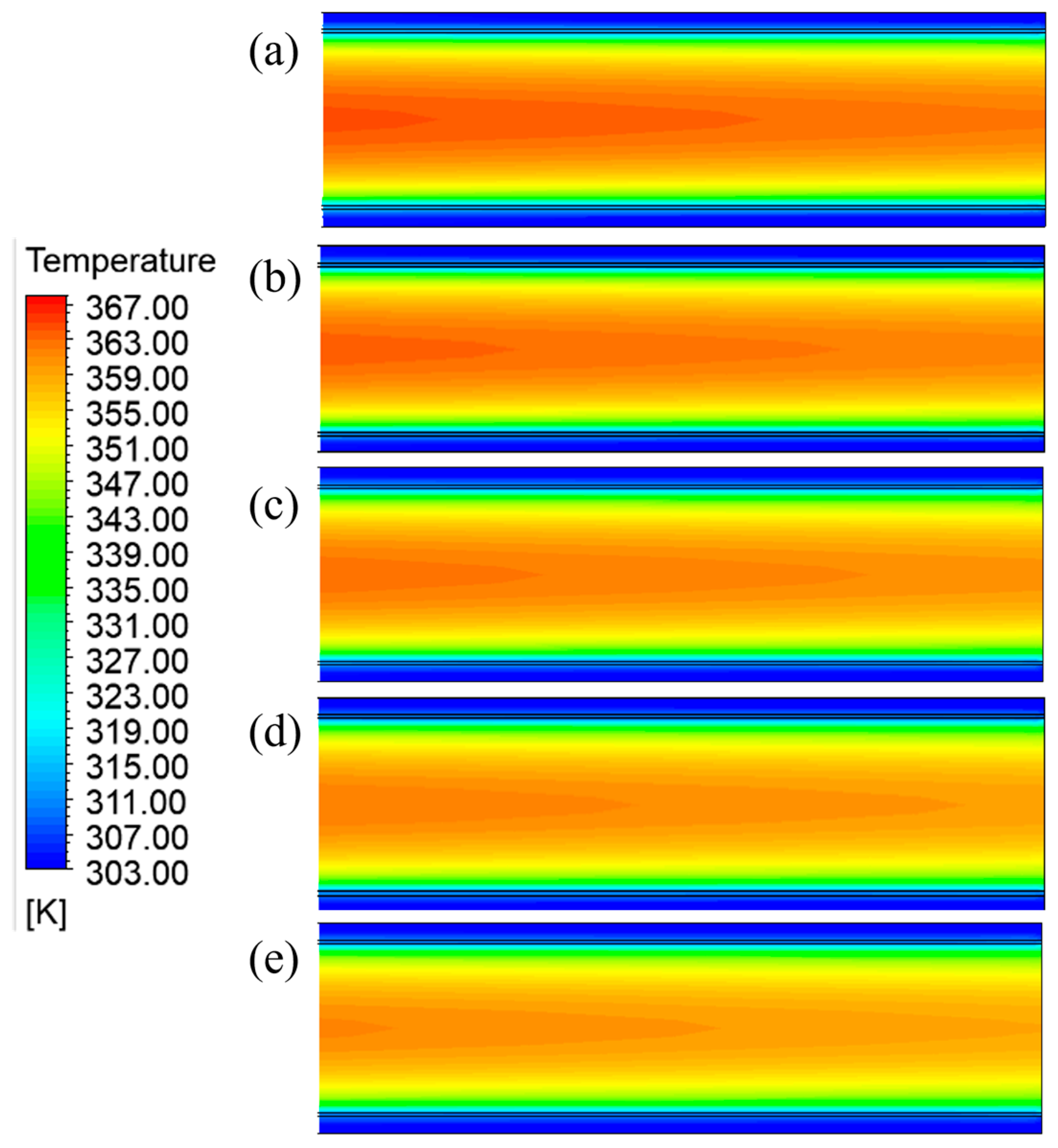
3.2.2. Influence of Cooling Water Consumption on Cooling Efficiency

Figure 19 presents the simulation results for the average outlet temperatures of the cement powder flow across different cooling water flow rates and cooling unit group heights. At the same cooling unit group height, the cooling water flow rate was positively correlated with cooling efficiency: as the flow rate of the cooling water decreased, the average outlet temperature of the cement powder increased. With the inlet area of the cooling unit group remaining constant, increasing the flow rate of the cooling water enhanced its velocity, thereby intensifying turbulence and convective heat transfer. Figure 20 presents the fitted relationship between the outlet temperature of cement and the cooling water flow rate at a heat exchanger height of 10 m. The results show that the outlet temperature continuously decreases as the cooling water flow increases. Once the heat exchanger reaches its heat transfer saturation, further increasing the water flow will no longer improve efficiency.

Figure 21 illustrates the temperature distribution across the central cross-section of the cement powder flow, measured within 0.5 m of the outlet and at a cooling unit group height of 10 m, across different cooling water flow rates. As the cooling water flow rate increased, the area of high-temperature regions decreased.

Table 9. Average outlet temperatures of the cement powder flow across different cooling water flow rates and cooling unit group heights.

High (m)	Average Outlet Temperature (°C)
	60 t/h	70 t/h	80 t/h	90 t/h	100 t/h
1	119.816	119.680	119.534	119.371	119.116
4	104.134	103.404	102.851	102.468	102.035
7	92.741	91.668	90.895	90.378	89.698
10	83.218	81.803	80.566	79.460	78.388

summarizes the simulation results for the average outlet temperatures of the cement powder flow across different cooling water flow rates and cooling unit group heights. At a cooling unit group height of 10 m, increasing the cooling water consumption from 60 t/h to 70, 80, 90, and 100 t/h enhanced the cooling efficiency from 35.99% to 37.08%, 38.03%, 38.88%, and 39.71%, respectively. The cement powder primarily flows under gravity, and the pressure drop is mainly concentrated on the cooling water side. Increasing the cooling water flow inevitably raises the required motor power. For instance, when the cooling water flow increases from 60 t/h to 100 t/h, the installed motor power must be increased from 7.5 kW to 11 kW.

3.3. Summary of Experimental Results

Figure 22, plotted based on the study data, illustrates the outlet temperature distribution under a cooling unit group height of 10 m as material channel width, fin spacing (F-3/F-2/F-1), cement powder processing rate, and cooling water flow rate. The results show that increasing the cooling water flow and reducing the fin spacing significantly lowers the outlet temperature, whereas increasing the channel width or cement processing rate leads to higher outlet temperatures. These findings confirm the synergistic enhancement of heat transfer performance achieved by the fin structure and cooling water flow.

Furthermore, the Layered-Plate Heat Exchangers features a compact stacked configuration, requiring a smaller footprint per unit processing capacity compared with rotary coolers and fluidized bed coolers, making it particularly suitable for plants with limited space. Unlike conventional equipment, this heat exchanger has no rotating mechanical components, resulting in lower energy consumption, fewer moving parts and maintenance points, and easier removal of cooling plates and replacement of local components. Consequently, it demonstrates high operational reliability and maintenance friendliness.

4. Verification of Simulation Results

In this study, heat exchanger verification was conducted under the operating conditions of a cement powder flow rate of 120 t/h, cooling water flow rate of 60 t/h, cooling height of 10 m, channel width of 100 mm, and cooling plate material of 316L steel, following Equations (9)–(13). Based on the material properties, the corresponding dimensionless numbers and heat transfer coefficients were calculated (

Table 10. Heat transfer parameters of different fluid domains.

Material	Characteristic Length (m)	Re	Pr	Nu	h (W/(m2·°C))
Cement	0.039	202,959.83	0.048	108.88	179.65
Water	0.181	1469.26	5.418	44.7	701.06

), and the composite heat transfer coefficient k was obtained considering the heat transfer surface arrangement. An initial assumption of either the cement or cooling water outlet temperature was made, from which the outlet temperature of the other fluid was calculated using the energy balance equation, followed by the determination of the logarithmic mean temperature difference (Δt_m). Using the known kA and Δt_m, Φ₁ was calculated, while Φ₂ was obtained from the four inlet and outlet temperatures. Typically, Φ₁ and Φ₂ are unequal, indicating that the initial outlet temperature assumption is inconsistent. Through iterative recalculation with revised outlet temperature assumptions, convergence was achieved when the discrepancy between Φ₁ and Φ₂ was within 2–5%, at which point the actual outlet temperature was determined.

The results show that the average outlet temperature of the cement powder was approximately 78 °C, with a deviation of 6.27% from the numerical simulation results, thereby confirming the reliability of the simulation. Moreover, the convective thermal resistances per unit area were 5.6 × 10⁻³ (m²·°C)/W on the cement side and 1.4 × 10⁻³ (m²·°C)/W on the cooling water side, while the conduction thermal resistance across the cooling plate thickness was only 4 × 10⁻⁶ (m²·°C)/W. This indicates that heat transfer within the exchanger is dominated by convection.

$${\mathsf{\Phi }}_1=kA∆t_m,$$

(9)

$${\mathsf{\Phi }}_2=q_{mc}{c}_c\left(t_c^{`}-t_c^{``}\right),$$

(10)

$${\mathsf{\Phi }}_3=q_{mc}{c}_c\left(t_c^{`}-t_c^{``}\right)=q_{mw}{c}_w\left(t_w^{``}-t_w^{`}\right),$$

(11)

$$k={\displaystyle \frac{1}{\frac{1}{h_c}+\frac{\delta }{\lambda }+\frac{1}{h_w}}},$$

(12)

$$∆t_m={\displaystyle \frac{∆t_{max}-∆t_{min}}{\ln \frac{∆t_{max}}{∆t_{min}}}}.$$

(13)

where k is the composite surface heat transfer coefficient (W/(kg·°C)); Δt_m is the logarithmic mean temperature difference (°C); A is the heat transfer area (m²); q_mc and q_mw are the mass flow rates of cement and cooling water (kg/s); c_c and c_w are the specific heat capacities of cement and cooling water (J/(kg·°C)); $t_c^{`}$ and $t_c^{``}$ are the inlet and outlet temperatures of cement (°C); $t_w^{`}$ and $t_w^{``}$ are the inlet and outlet temperatures of cooling water (°C); δ is the thickness of the cooling plate (m, 0.002 m); λ is the thermal conductivity of the cooling plate (W/(m·°C)); and Δt<sub>max</sub> and Δt<sub>min</sub> are the greater and lesser of $∆t^{`}$ and $∆t^{``}$, respectively (°C).

5. Conclusions and Prospects

This study introduced a novel layered-plate heat exchanger designed for cooling newly milled cement powder. The structural and operational parameters of the cooling unit group within the heat exchanger were thoroughly analyzed using Fluent 2024 R1 software. The key findings of this study are as follows:

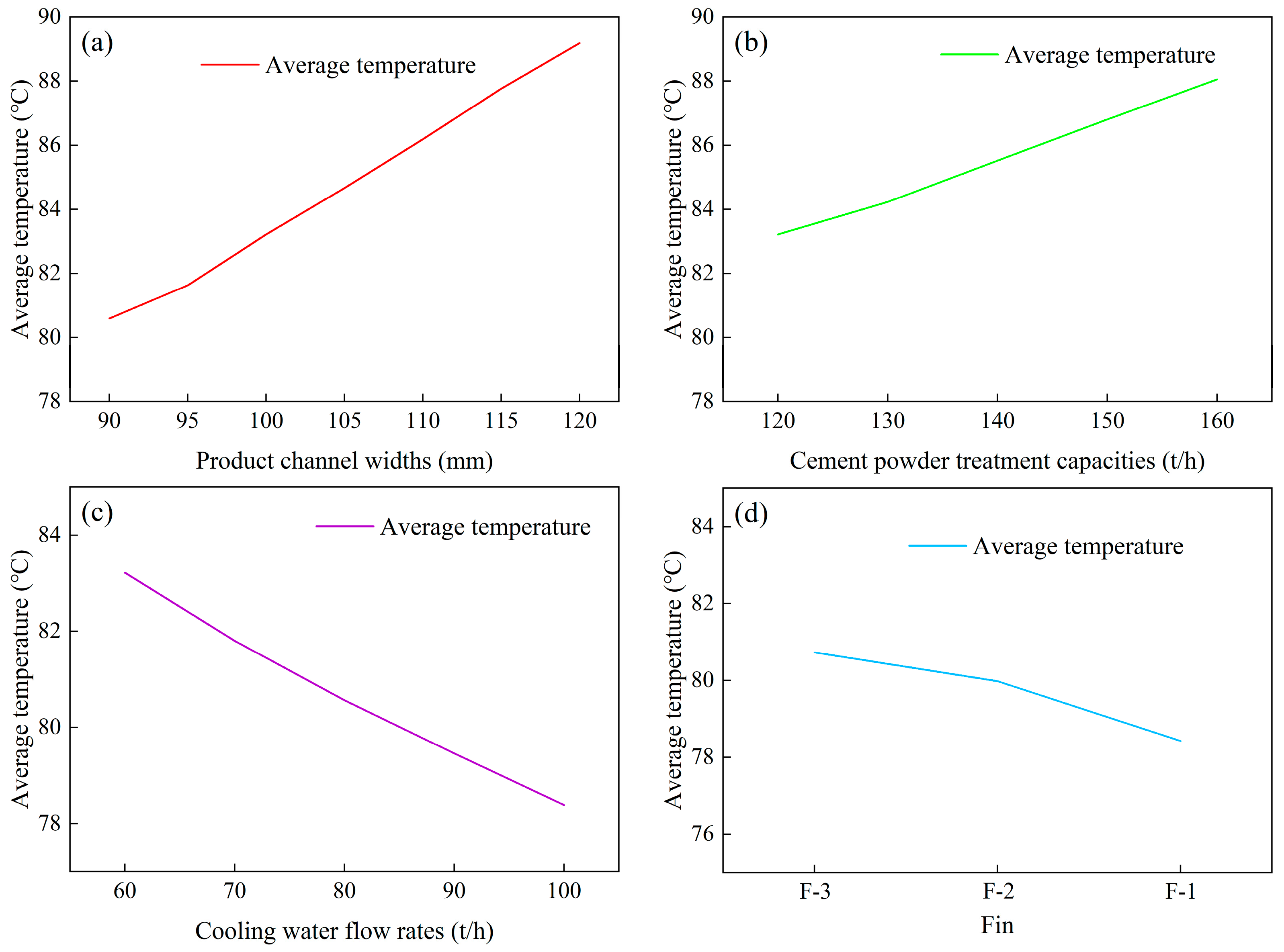
• The height of the heat exchanger has the most significant impact on cooling efficiency. When the height increases from 1 m to 4 m, 7 m, and 10 m, the cooling efficiency rises from 7.83% to 19.90%, 28.66%, and 35.99%, respectively. In contrast, variations in the cooling plate material have a negligible effect on the cooling performance. Moreover, increasing the width of the product channel leads to thickening of the thermal boundary layer and higher thermal resistance. Under a heat exchanger height of 10 m, increasing the channel width from 90 mm to 120 mm results in a decrease in cooling efficiency from 38.00% to 31.39%.
• Incorporating fins in the product channel and reducing fin spacing significantly improved cooling efficiency. These fins increased the heat exchange surface area and disrupted the boundary layer, thereby enhancing heat exchange. At a cooling unit group height of 10 m, adopting the F-1, F-2, and F-3 fin spacings increased the cooling efficiency to 39.67%, 38.47%, and 37.90%, respectively, with the corresponding average outlet temperatures decreasing to 78.430 °C, 79.983 °C, and 80.730 °C, respectively. Modifying the surface shape of the cooling plate also enabled a significant improvement in cooling efficiency. At a cooling unit group height of 5 m, cooling plates with grooves exhibited a 2.5 °C decrease in average outlet temperature and a 1.94% increase in cooling efficiency compared to flat-surface cooling plates.
• At a cooling unit group height of 10 m, increasing the treatment capacity for high-temperature cement powder from 120 t/h to 130 t/h, 140 t/h, 150 t/h, and 160 t/h resulted in a cooling efficiency reduction from 35.99% to 35.21%, 34.22%, 33.23%, and 32.27%, respectively. Conversely, increasing the cooling water flow rate from 60 t/h to 70 t/h, 80 t/h, 90 t/h, and 100 t/h significantly enhanced cooling efficiency from 35.99% to 37.08%, 38.03%, 38.88%, and 39.71%, respectively.

In this study, the inlet cement temperature was set at 130 °C, consistent with the outlet temperature of most cement mills in China; however, the proposed cooler is also applicable to a wider temperature range of 90–200 °C. For higher inlet temperatures, further reduction in the outlet temperature can be achieved by increasing the cooler height, incorporating fins or other enhanced heat transfer elements, and increasing the cooling water flow rate, thereby demonstrating broad temperature adaptability and optimized performance. Energy consumption analysis indicates that the power demand of the proposed exchanger is primarily concentrated on the cooling water pump, whereas conventional multi-tube spiral coolers also require additional energy for material transportation. The average energy consumption of the multi-tube spiral cooler is approximately 0.5–0.6 kWh/t [27], while the estimated consumption of the proposed exchanger is only 0.3–0.45 kWh/t, highlighting its significant potential for energy savings. Moreover, the recovered waste heat from the cooling water could be reused for drying other materials; however, this would require additional heat recovery devices and enlarged water storage facilities, leading to high capital costs and limited overall economic benefits. From an economic perspective, for a cement plant with an annual production capacity of 120 t/h in China, the expected investment payback period of the proposed exchanger is estimated to be 3–5 years. When scaled up for industrial application, the cooler faces several challenges, including maintaining flow uniformity under high throughput, ensuring structural strength and wear resistance, controlling pressure drop and energy consumption, and enabling feasible maintenance and cleaning. These challenges may be addressed by optimizing the feed distribution system and incorporating vibration devices to ensure uniform feeding and smooth material flow; selecting high-strength, wear-resistant, and corrosion-resistant materials (e.g., 316L stainless steel) to enhance structural reliability; and conducting pilot-scale experiments (e.g., at 10 t/h processing capacity) to evaluate operational characteristics prior to full-scale industrial deployment.

The proposed heat exchanger is not only applicable to cement powders but can also be extended to other high-temperature particulate systems. Furthermore, this study highlights the potential integration of artificial intelligence technologies, such as intelligent computational models based on convolutional neural networks (CNNs) or artificial neural networks (ANNs), combined with modules embedding human expertise. Such a hybrid approach, integrating empirical knowledge with AI-driven predictions, can enhance operational safety in industrial applications. This research pathway holds considerable potential for real-time optimization and process control, and future work will further explore its feasibility and integration with the proposed design.