Strut-and-Tie Modeling of Intraply Hybrid Composite-Strengthened Deep RC Beams

Abstract

This study presents a strut-and-tie modeling (STM) framework for reinforced concrete (RC) deep beams strengthened with intraply hybrid composites (IRCs), integrating comprehensive experimental data from beams with three different span lengths (1.0 m, 1.5 m, and 2.0 m). Although the use of fiber-reinforced polymers (FRPs) for shear strengthening of RC members is well established, limited attention has been given to the development of STM formulations specifically adapted for hybrid composite systems. In this research, three distinct IRC configurations—Aramid–Carbon (AC), Glass–Aramid (GA), and Carbon–Glass (CG)—were applied as U-shaped jackets to RC beams without internal transverse reinforcement and tested under four-point bending. All experimental data were derived from the authors’ previous studies, ensuring methodological consistency and providing a robust empirical basis for model calibration. The proposed modified STM incorporates both the axial stiffness and effective strain capacity of IRCs into the tension tie formulation, while also accounting for the enhanced diagonal strut performance arising from composite confinement effects. Parametric evaluations were conducted to investigate the influence of the span-to-depth ratio (a/d), composite configuration, and failure mode on the internal force distribution and STM topology. Comparisons between the STM-predicted shear capacities and experimental results revealed excellent correlation, particularly for deep beams (a/d = 1.0), where IRCs substantially contributed to the shear transfer mechanism through active tensile engagement and confinement. To the best of the authors’ knowledge, this is the first study to formulate and validate a comprehensive STM specifically designed for RC deep beams strengthened with IRCs. The proposed approach provides a unified analytical framework for predicting shear strength and optimizing the design of composite-strengthened RC structures.

1. Introduction

Reinforced concrete (RC) beams are essential structural elements subjected to combined flexural and shear actions in a wide range of civil engineering applications, including bridges, buildings, and industrial infrastructure. Due to the brittle nature of concrete in tension and the limited shear resistance in beams without adequate transverse reinforcement, structural strengthening techniques are often required to restore or enhance performance under service and ultimate loads [1,2]. While traditional methods such as steel plate bonding or external post-tensioning are well established, their application can be limited by issues such as corrosion susceptibility, increased weight, and labor-intensive installation procedures [3,4,5]. In many existing RC structures, particularly those constructed before the enforcement of modern seismic design codes, beams without transverse reinforcement are common due to insufficient stirrup detailing, corrosion of existing steel, or construction practices that neglected shear reinforcement altogether. Such members represent critical retrofit targets, as their shear resistance is inherently limited and their failure mode is typically brittle.

In recent decades, fiber-reinforced polymers (FRPs) have become a prominent solution for retrofitting deficient RC elements, offering advantages such as high strength-to-weight ratio, corrosion resistance, and ease of application [6,7]. Among these, intraply hybrid composites (IRCs) have emerged as a promising subcategory, wherein different fiber types, such as carbon, glass, and aramid, are integrated within a single matrix in varying orientations [8,9,10,11]. This arrangement provides a synergistic improvement in strength, ductility, and energy absorption compared to single-fiber systems [12,13]. Experimental studies have demonstrated the effectiveness of IRCs in enhancing the shear capacity and failure resistance of RC beams lacking stirrups. In particular, prior investigations by [14,15,16] have systematically evaluated the strengthening effects of Aramid-Carbon (AC), Glass-Aramid (GA), and Carbon-Glass (CG) composites on RC beams of varying lengths—2.0 m, 1.5 m, and 1.0 m, respectively—under four-point bending configurations. These studies reported that IRCs could increase shear capacity by up to 36%, depending on the span-to-depth ratio and composite orientation [14,15,16].

Despite growing experimental evidence supporting the efficiency of IRC systems, the development of a mechanics-based analytical model such as the Strut-and-Tie Model (STM) that incorporates the hybrid action of composites remains an unresolved challenge [17]. STM is a widely accepted framework for analyzing discontinuity regions (D-regions) in RC structures, especially deep beams and regions of high shear, by simplifying stress trajectories into discrete struts (compression) and ties (tension) [18]. However, traditional STM approaches typically neglect the contribution of external composite strengthening in the tie zones, or consider it in a simplified manner, without accounting for the composites. In the existing literature, studies that explicitly incorporate the effect of composites into STM formulations remain rather limited, with only a few attempts addressing FRP systems in the tie mechanism [19,20,21,22,23,24]. Moreover, it is important to note that the contribution of externally bonded fiber-reinforced composites, such as intraply hybrid U-jackets, is not explicitly included in the current design provisions of major codes. The authors of [3,4,5] all adopt the STM primarily on the basis of conventional steel reinforcement, limiting tie elements to internal reinforcement bars. While [23] provides guidance for externally bonded FRP systems, this document is supplementary and not integrated into the main STM provisions of [3]. Similarly, refs. [4,5] do not explicitly consider external composite ties in their STM formulations. Therefore, the incorporation of composite tensile contributions into tie capacity, as proposed in this study, extends beyond the direct scope of these codes and represents an analytical advancement rather than a codified design requirement.

To address this critical gap, the present study proposes a modified STM framework for IRC-strengthened RC beams. The STM has been widely adopted for analyzing deep beams and D-regions, typically with shear span-to-depth ratios (a/d) less than 1.0. However, in real structural systems, many members lie in a transition regime where a/d ranges between 1.0 and 3.0. In this range, the internal force transfer gradually shifts from arching action to truss action, yet STM remains a rational mechanics-based framework to describe this behavior. While conventional sectional design methods are limited in capturing D-region behavior, STM provides an explicit load path representation and is well-suited to incorporate the effects of external composite strengthening. Previous studies have shown that such approaches can yield more accurate predictions of ultimate shear capacity for strengthened members, especially when external reinforcement acts as the primary shear-carrying mechanism. The model integrates experimental tensile behavior of IRCs into the formulation of tie forces and adjusts the effective strut strength to account for enhanced confinement provided by composite jackets. Using data from three beam lengths with distinct a/d ratios (3.0, 2.0, and 1.0), the influence of IRC type and beam geometry on STM topology is examined.

The proposed method is validated by comparing predicted and observed load-carrying capacities, crack paths, and failure modes. This study focuses on these deficient members to evaluate and isolate the direct contribution of external intraply hybrid composite strengthening without interference from internal stirrups. By doing so, the effectiveness of the strengthening system can be more clearly quantified and mechanistically understood. This experimental condition reflects practical retrofitting scenarios in many existing buildings, particularly in regions with aging RC stock.

This work contributes to the broader body of knowledge by offering a unified design-oriented modeling approach that links physical composite performance with a rational load transfer mechanism. It is intended to serve both researchers and practitioners in optimizing the design and assessment of RC structures strengthened with advanced hybrid composite systems. To the best of the authors’ knowledge, this work represents the first attempt to propose and validate a strut-and-tie model specifically tailored for RC deep beams strengthened with intraply hybrid composites.

2. Materials and Methods

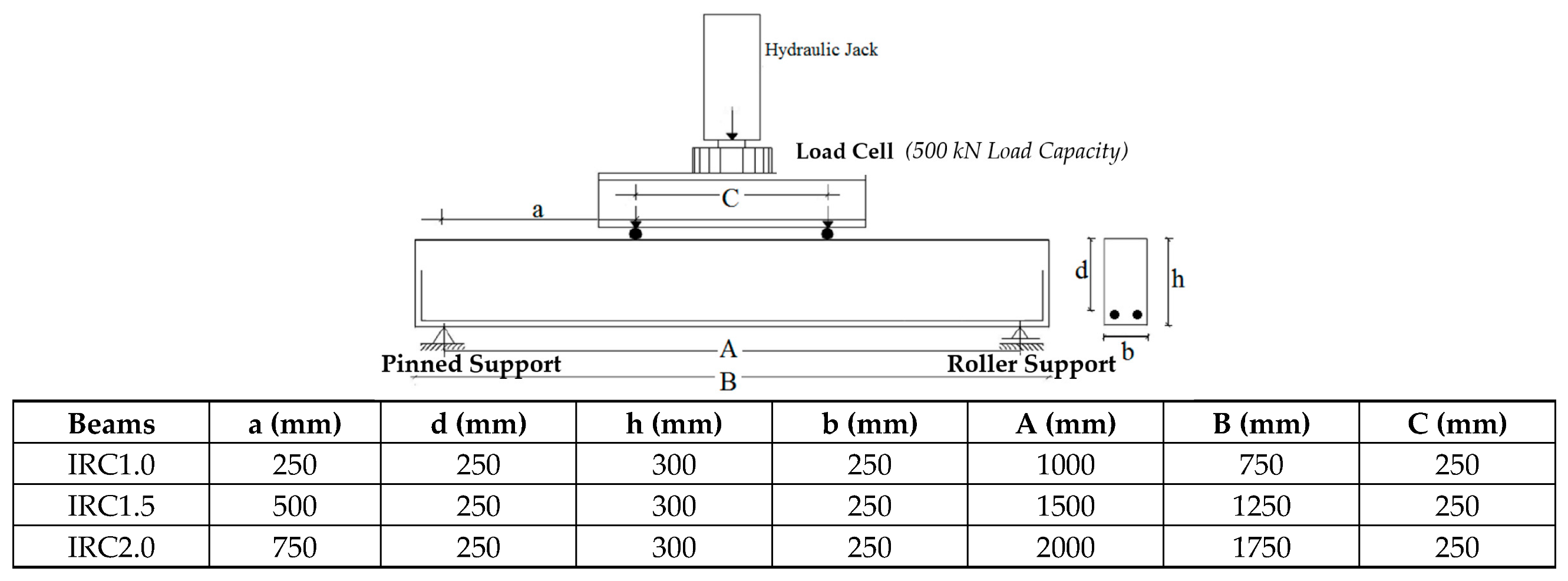
This study integrates experimental data obtained from three previously tested series of RC beams, each strengthened with distinct intraply hybrid composites (IRCs), to develop and validate a STM framework. The three beam series, 1.0 m (IRC1.0), 1.5 m (IRC1.5), and 2.0 m (IRC2.0) in length, were selected to represent varying shear span-to-depth (a/d) ratios of 1.0, 2.0, and 3.0, respectively. All beams lacked transverse shear reinforcement, creating a suitable basis for analyzing deep and shear-critical regions via STM (Figure 1).

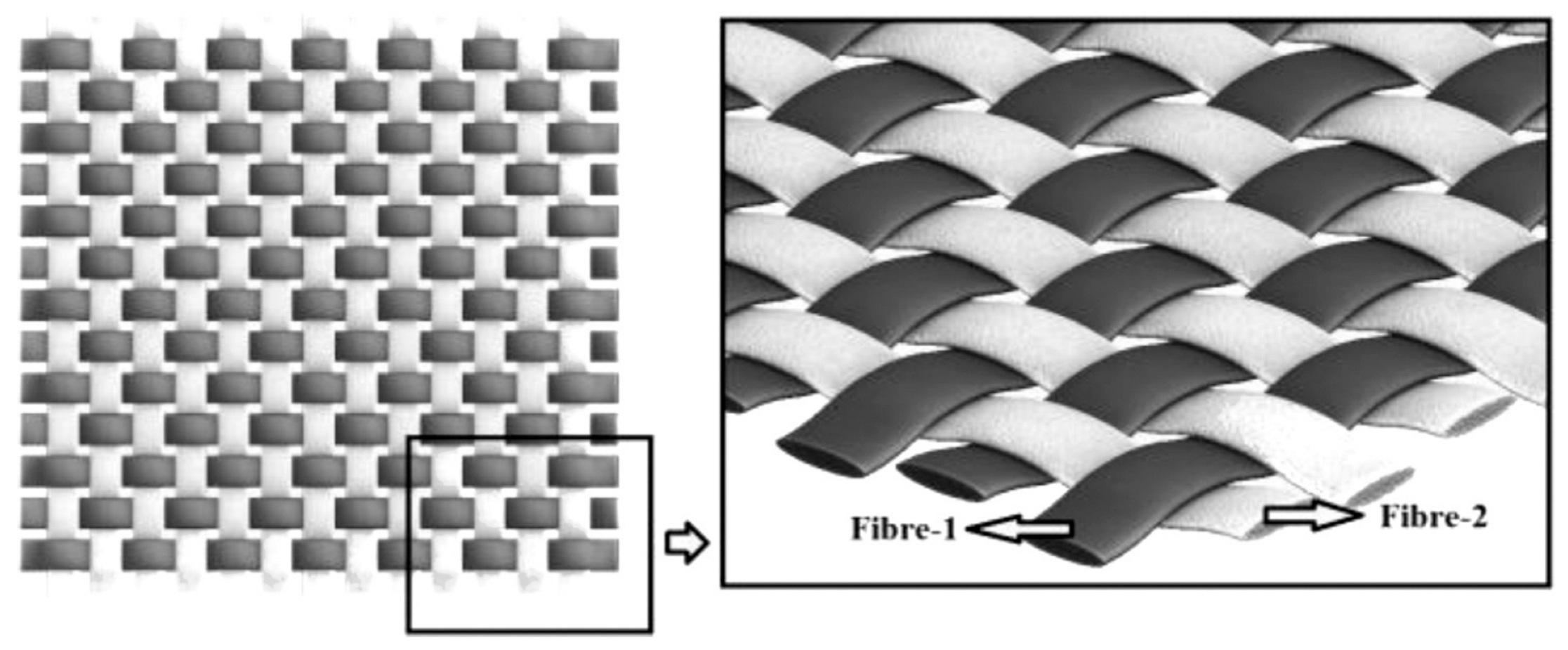
The study utilized three RC beam series without transverse reinforcement, strengthened with U-jacketed IRCs: AC, GA, and CG (Figure 2). All beams had cross-sections of 250 mm × 300 mm and used C40 concrete ($f_c^{\prime }=41.6 \mathrm{MPa})$ with Ø16 mm rebars $(f_y$ = $502 \mathrm{M}\mathrm{P}\mathrm{a}, fsu= 641 \mathrm{M}\mathrm{P}\mathrm{a}$). Each composite had a nominal thickness of 0.2 mm. Tensile tests provided longitudinal Young’s modulus: AC: 88.7 GPa, GA: 72.4 GPa, CG: 44.7 GPa. To remove the negative effects of corners, the rough surfaces of the RC beams were sanded and beveled before the IR fabrics were applied. Each composite fabric had a nominal thickness of 0.2 mm and was applied in U-jacket configuration on three sides of the beam, following surface sanding and resin application using the Duratek AV 21 epoxy system obtained from DURATEK, Kocaeli, Türkiye. Four-point bending tests were conducted, and failure modes, load-deflection responses, and cracking patterns were recorded. The STM was developed for each beam using observed failure angles and load data as boundary conditions. Diagonal struts, horizontal ties (steel + composite), and node zones were modeled accordingly.

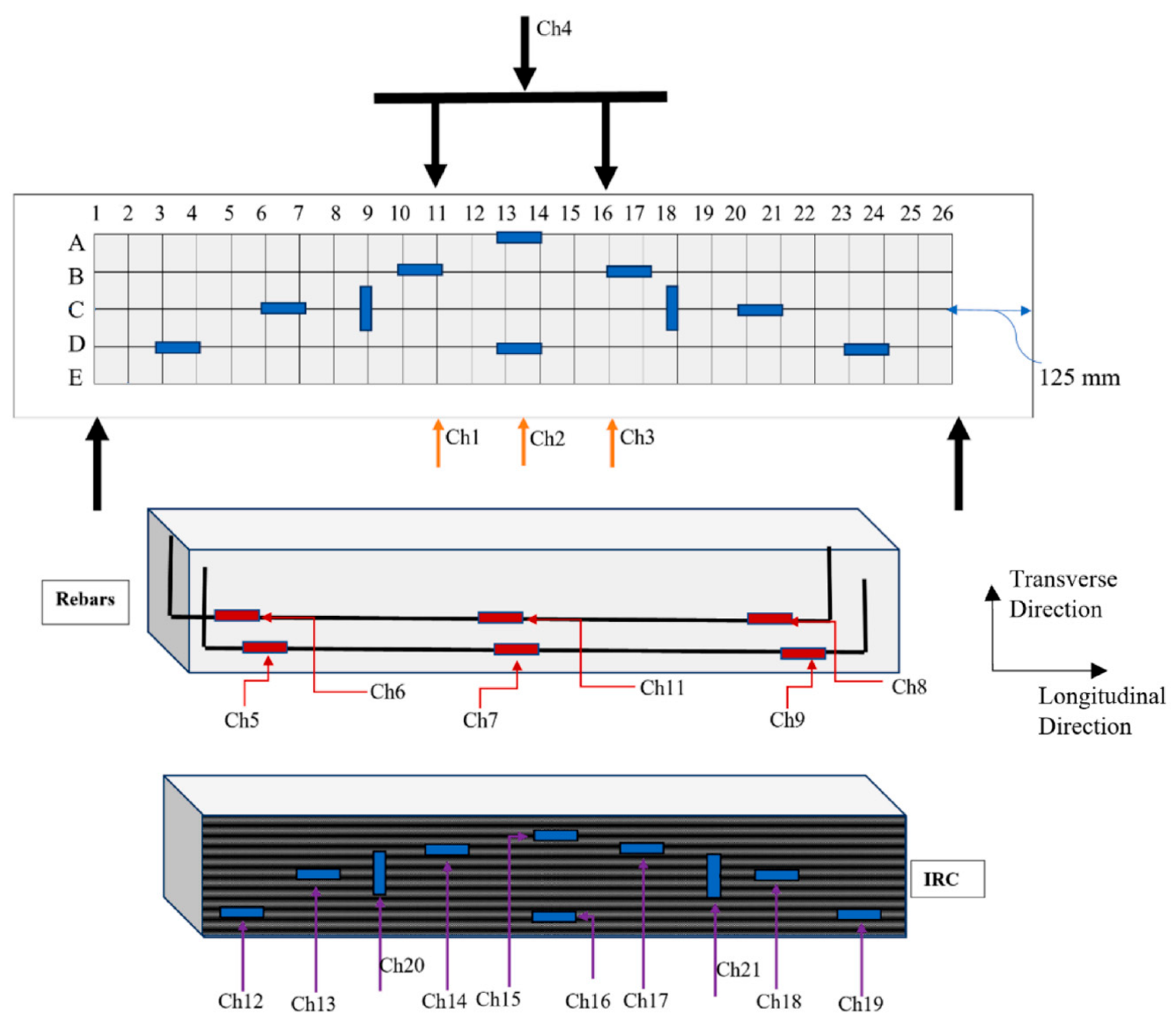
Experimental Testing Procedure

All beams were tested under four-point bending, with loading and support conditions designed to establish a pure shear zone in the region between the two loading points. Linear Variable Differential Transducers (LVDTs) and strain gauges were installed at mid-span and critical shear zones to measure vertical deflection, strain distributions, and failure progression (Figure 3, Figure 4 and Figure 5).

3. Strut-and-Tie Model

3.1. General Concept

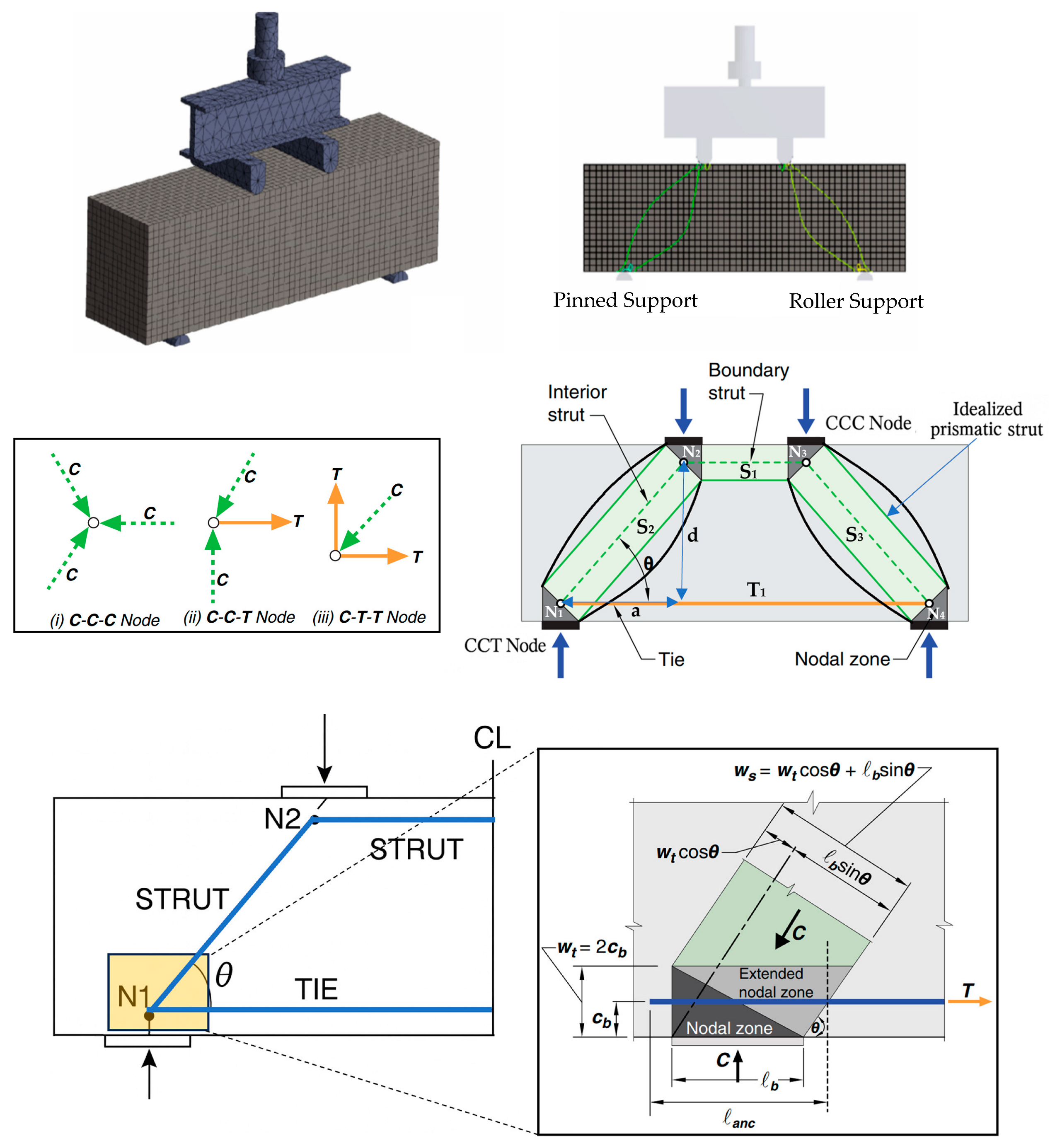
The Strut-and-Tie Model (STM) represents a rational design framework for estimating the shear capacity of deep beams by idealizing the internal force transfer mechanism as a truss system composed of compressive struts, tensile ties, and nodal zones. In the present study, the deep beam was idealized as a symmetrical STM with one main horizontal tie (T₁), one upper boundary strut (S₁), and two inclined compressive struts (S₂, S₃), as illustrated in Figure 6.

3.2. Geometry of Struts and Nodal Zones

The applied shear load (Vu) is equilibrated by the tensile force in the tie and the compressive forces in the diagonal struts. The internal angle of the strut inclination is denoted by θ, corresponding to the shear span-to-depth ratio (a/d).

$$\mathit{tan}\left(\theta \right)={\displaystyle \frac{d}{a}}\Rightarrow \theta ={\mathit{tan}}^{-1}\left({\displaystyle \frac{d}{a}}\right)$$

(1)

where d is the effective depth of the beam, a is the shear span and θ is the inclination angle of the strut.

Tie (tension zone) thickness:

$$w_t=2c_b$$

(2)

Diagonal strut width:

$$w_s=w_t\cos \mathrm{\theta }+l_b\sin \mathrm{\theta }$$

(3)

Strut thickness perpendicular to the strut:

$$t_w={\displaystyle \frac{w_s}{\sin \theta }}={\displaystyle \frac{2c_b\cos \mathrm{\theta }+l_b\sin \theta }{\sin \mathrm{\theta }}}=l_b+2c_b\cot \mathrm{\theta }$$

(4)

Strut area (for each strut):

$$A_{c,i}=b_w t_{w,i}$$

(5)

At each half beam, diagonal compression C (same as S₂ or S₃ on that side) and horizontal tension T meet at the node. Node equilibrium (one side):

$$T=C\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{\theta }$$

(6)

$${\displaystyle \frac{V}{2}}=Csin\theta$$

(7)

Shear from tie view (using T):

$$V_n^{\left(T\right)}=2T\tan \mathrm{\theta }$$

(8)

Shear from strut view (using S₂, S₃):

$$V_n^{\left(S\right)}=\left(S_2+S_3\right)\sin \mathrm{\theta }$$

(9)

3.3. Tie Capacity (T₁)

The total available tie capacity is the sum of the contributions from the longitudinal steel and the externally applied composite:

$$T_{\mathrm{tie}}={T_{concrete}+T}_{\mathrm{steel}}+T_{\mathrm{IRC}}$$

(10)

$${ T}_{concrete}={\psi }_c{A}_c{f}_{c,\mathrm{e}\mathrm{f}\mathrm{f}} (0 \le {\mathrm{\psi }}_{\mathrm{c}} \le 1), \mathrm{in} \mathrm{cracked} \mathrm{regions}, {\psi }_c \approx 0 \mathrm{for} \mathrm{safety}$$

(11)

$$T_{\mathrm{steel}}=A_s{f}_y$$

(12)

$$T_{\mathrm{IRC}}={{\alpha }_{c}A}_f{\mathrm{f}}_{f,\mathrm{e}\mathrm{f}\mathrm{f}} {=\alpha }_c\left(N_{w}n{b}_f{t}_f\right)\left(E_f{\epsilon }_{fe}\right)$$

(13)

$$A_f=N_{w}n{b}_f{t}_f$$

(14)

$${\mathrm{f}}_{f,\mathrm{e}\mathrm{f}\mathrm{f}}=E_f{\epsilon }_{fe}$$

(15)

$${\epsilon }_{fe}=\left\{\begin{array}{cc}min(0.004, 0.75{\epsilon }_{fu})& full wrap\\ {\kappa }_v{\epsilon }_{fu}\le 0.004& U\text{-}wrap/side wrap\end{array}\right.$$

(16)

$$T_{\mathrm{IRC}}={\alpha }_c\left(N_{w}n{b}_f{t}_f\right)\left(E_f{\epsilon }_{fe}\right)$$

(17)

For U-wrap configurations, where ${\kappa }_v$ is a reduction coefficient (0.5–0.8). Practical tie capacity (with T_concrete ≈ 0):

$$T_{\mathrm{tie}}\simeq A_s{f}_y+{\mathrm{\alpha }}_c\left(N_{w}n{b}_f{t}_f\right)\left(E_f{\mathrm{\epsilon }}_{fe}\right)$$

(18)

where $A_f$ is the cross-sectional area of the composite (in mm²), $f_{f,\mathrm{e}\mathrm{f}\mathrm{f}}$ is effective tensile stress in the composite (in MPa), $b_f$ = effective width of the composite jacket, $t_f$ = thickness of the composite layer (in mm), ${\epsilon }_{f,\mathrm{e}\mathrm{f}\mathrm{f}}$ = effective strain (obtained from DIC or strain gauges), $E_f$ = modulus of elasticity of the composite fiber (in MPa).

This equation quantifies the composite’s contribution to the tie force, accounting for its material properties and strain development under load. High-strain capacity composites (e.g., Aramid) provide better ductility and post-cracking performance.

3.4. Strut Capacity (S₁, S₂, S₃)

Each compressive strut S_i (i = 1, 2, 3) consists of the combined action of concrete, confined by both steel and IRC layers, and any reinforcement aligned along the strut axis:

$$S_{\left(i\right)}=S_{\left(i\right)concrete}+S_{\left(i\right)steel}+S_{\left(i\right)IRC}$$

(19)

$$S_{\left(i\right)concrete}=f_{c,\mathrm{e}\mathrm{f}\mathrm{f},i}{A}_{c,i}=f_{c,\mathrm{e}\mathrm{f}\mathrm{f},i}\left(b_w{t}_{w,i}\right)$$

(20)

Instead of directly carrying compressive stress, the composite wrap enhances the lateral confinement of concrete, increasing its effective compressive strength. This is represented by a confinement coefficient, $k_{conf,i}$:

$$f_{c,\mathrm{e}\mathrm{f}\mathrm{f},i}=k_{conf,i}{f}_{c,0}$$

(21)

$$S_{\left(i\right)concrete}=k_{conf,i}{f}_{c,0}\left(b_w{t}_{w,i}\right)$$

(22)

$$k_{\mathrm{conf},i}=k_{\mathrm{concrete}}+k_{\mathrm{steel}}+k_{\mathrm{IRC}}$$

(23)

For plain or unconfined concrete, the confinement factor is unity, meaning it represents the baseline capacity before enhancement:

$$k_{\mathrm{concrete}}=1$$

For internal steel reinforcement (stirrups), the confinement factor is:

$$k_{\mathrm{steel}}={\mathrm{\eta }}_s{\mathrm{\rho }}_{s,\perp ,i}{\displaystyle \frac{f_y}{f_c^{\prime }}}$$

(24)

For external IRC reinforcement, the confinement factor is:

$$k_{\mathrm{IRC}}={\mathrm{\eta }}_f{\mathrm{\rho }}_{f,\perp ,i}{\displaystyle \frac{E_f{\mathrm{\epsilon }}_{fe}}{f_c^{\prime }}}$$

(25)

Substituting the steel and IRC terms, the full confinement model becomes:

$$k_{\mathrm{conf},i}=1+{\mathrm{\eta }}_s{\mathrm{\rho }}_{s,\perp ,i}{\displaystyle \frac{f_y}{f_c^{\prime }}}+{\mathrm{\eta }}_f{\mathrm{\rho }}_{f,\perp ,i}{\displaystyle \frac{E_f{\mathrm{\epsilon }}_{fe}}{f_c^{\prime }}}$$

(26)

Here:

• ${\mathrm{\eta }}_s$: Effectiveness coefficient of steel confinement.
• ${\mathrm{\rho }}_{s,\perp ,i}$: Transverse steel reinforcement ratio.
• ${\displaystyle \frac{f_y}{f_c^{\prime }}}$: Normalized steel-to-concrete strength ratio.
• ${\mathrm{\eta }}_f$: Effectiveness coefficient of IRC confinement.
• ${\mathrm{\rho }}_{f,\perp ,i}$: Transverse IRC reinforcement ratio.
• ${\displaystyle \frac{E_f{\mathrm{\epsilon }}_{fe}}{f_c^{\prime }}}$: Normalized fiber confinement pressure term.

$$S_{\left(i\right)steel}=A_{s,\parallel ,i}{f}_{s,\mathrm{comp}}$$

(27)

$$S_{\left(i\right)IRC}=A_{f,i}{E}_f{\epsilon }_{ef}$$

(28)

where

• N_w = number of sides wrapped (e.g., 2 for U-wrap, 3 for three-side wrap).
• n = number of fiber layers.
• bf,i = effective width of fiber engaged in the ith strut.
• t_f = thickness per fiber layer.

Hence, combined strut capacity:

$$S_{\left(i\right)}=k_{conf,i}{f}_{c,0}\left(b_w{t}_{w,i}\right)+A_{s,\parallel ,i}{f}_{s,\mathrm{comp}}+A_{f,i}{E}_f{\epsilon }_{ef}$$

(29)

3.5. Shear Capacity

The total shear capacity of a deep beam strengthened with IRC materials can be expressed as the sum of contributions from the tie (tensile) and strut (compressive) mechanisms within the STM.

The general expression is:

$$V_n=V_n^{\left(T\right)}+V_n^{\left(S\right)}+V_c$$

(30)

where

• $V_n^{\left(T\right)}$: contribution of the tie (tension member),
• $V_n^{\left(S\right)}$: contribution of the struts (compression members),
• $V_c$: contribution of the uncracked concrete (usually neglected for deep beams).

The tie element resists the horizontal tension developed at the bottom chord of the beam. Its vertical component contributes to the shear resistance:

$$V_n^{\left(T\right)}=2T_{tie}tan\theta$$

(31)

where θ is the inclination angle of the strut, and T_tie is the total tensile force acting along the tie.

The struts (compressive members) transfer the load from the applied force to the supports through diagonal compression fields.

The vertical component of these compressive forces contributes to shear resistance and can be expressed as:

$$V_n^{\left(S\right)}=(S_2+S_3)sin\theta$$

(32)

Total Shear Capacity: Combining all tie and strut contributions, the overall nominal shear strength of the IRC-strengthened beam is:

$$V_n=2\left(A_s{f}_y{\mathrm{\alpha }}_c{N}_{w}n{b}_f{t}_f{E}_f{\mathrm{\epsilon }}_{fe}\right)\tan \mathrm{\theta }+\sum _i\left[k_{conf,i}{f}_c^{\prime }\left(b_w{t}_{w,i}\right)\sin \mathrm{\theta }\right]$$

(33)

4. Results and Discussion

This section presents an in-depth evaluation of the structural behavior of RC beams strengthened with IRCs, emphasizing the accuracy and applicability of the proposed STM. The experimental program consisted of nine RC beam specimens categorized by their span-to-depth ratios (a/d = 1.0, 1.5, and 2.0), each strengthened with one of three composite configurations: AC, GA, and CG. The analysis covers ultimate load capacity, cracking behavior, failure mode, and deformation response. Experimental findings were systematically compared with STM predictions to evaluate the predictive performance of the proposed analytical framework.

4.1. Comparison of Experimental and STM Predictions

The experimental and analytical results demonstrate a high degree of consistency across all beam configurations (

Table 1. Comparison of Experimental Loads and STM Prediction.

Beam Group	Composite Type	Experimental Load (kN)	STM Prediction (kN)	Experimental/STM Prediction
RC-2.0	AC	108.3	130.63	083
RC-2.0	GA	119.6	122.20	0.98
RC-2.0	CG	114.8	126.63	0.91
RC-1.5	AC	132.5	130.63	1.01
RC-1.5	GA	123.0	122.19	1.01
RC-1.5	CG	114.5	126.62	0.90
RC-1.0	AC	229.9	195.95	1.17
RC-1.0	GA	208.3	183.29	1.14
RC-1.0	CG	209.2	189.94	1.10

and Appendix A). The ratio of experimental to STM-predicted shear capacity ranged between 0.83 and 1.17, indicating that the enhanced STM provides a realistic estimation of the ultimate load.

For deep beams (RC-1.0), the experimental-to-predicted ratios were highest, ranging from 1.10 to 1.17, which implies that the STM provides slightly conservative predictions for short-span configurations dominated by arching action. The superior agreement for these specimens highlights the model’s capability to accurately capture D-region behavior, where strut-and-tie mechanisms govern shear transfer.

For intermediate beams (RC-1.5), the experimental-to-predicted ratios were between 0.90 and 1.01, signifying excellent agreement between analytical and experimental outcomes. The AC and GA specimens exhibited nearly identical ratios (≈1.01), confirming the balanced contribution of tensile and compressive actions in the truss mechanism. The CG specimen displayed a slightly lower ratio (0.90), attributed to localized premature debonding and reduced longitudinal stiffness of the hybrid interface.

In the case of slender beams (RC-2.0), the ratios were 0.83–0.98, revealing that STM predictions tended to slightly overestimate the shear capacity. This behavior can be linked to the increasing dominance of flexural deformations and reduced confinement efficiency as the shear span increases. Nevertheless, even in these configurations, deviations remained within ±15%, demonstrating the robustness of the analytical approach.

4.2. Influence of Composite Type

Across all span-to-depth ratios, the AC (Aramid–Carbon) configuration consistently achieved the highest experimental loads, confirming its superior stiffness and stress transfer efficiency. The GA system displayed balanced performance, providing good ductility while maintaining adequate stiffness, resulting in experimental/STM ratios very close to unity. The CG composite, while effective in controlling early crack propagation, generally showed lower shear enhancement efficiency due to its lower modulus and higher susceptibility to interface debonding.

These findings correlate well with earlier reports by [6,9], who emphasized that composite stiffness and bond quality are decisive parameters in determining the effectiveness of external reinforcement systems.

4.3. Crack Pattern and Failure Mode Analysis

Crack development observations supported the analytical trends. Control beams without strengthening exhibited wide diagonal cracks forming abruptly at mid-shear span, leading to brittle failure. In contrast, IRC-strengthened beams showed delayed crack initiation, narrower crack widths, and multiple fine cracks, indicating improved stress redistribution and enhanced ductility. Visual inspection confirmed that the inclination of diagonal cracks corresponded well with the strut angle (θ) predicted by the STM, reinforcing the reliability of the truss analogy.

4.4. Effect of Span-to-Depth Ratio

The span-to-depth ratio played a significant role in governing the shear transfer mechanism. In deep beams (a/d = 1.0), diagonal compression struts dominated, and the full tensile capacity of the IRC ties was effectively mobilized due to short anchorage lengths and direct load paths. In intermediate beams (a/d = 1.5), both flexural and shear actions were present, requiring a balanced representation of strut and tie contributions in the STM formulation. In slender beams (a/d = 2.0), the composite contribution was partially limited by longer load paths and bond-dependent stress transfer, which slightly reduced the accuracy of the STM predictions.

4.5. Parametric Sensitivity and Model Validation

A parametric sensitivity study revealed that ±10% variations in key material parameters—elastic modulus (Ef), effective strain (εfe), and strut effectiveness factor (βs)—resulted in ±6–8% changes in the predicted shear capacity. The AC configuration exhibited higher sensitivity due to its greater stiffness and load transfer efficiency. Parameters such as bond stress (τb) and confinement factor (kconf) had comparatively smaller influence (±3–4%). These findings confirm that the STM’s accuracy is most sensitive to composite tensile properties, underlining the importance of precise material characterization in hybrid composite design.

4.6. Overall Assessment

When compared to conventional STM formulations neglecting composite effects, the proposed enhanced STM produced superior correlation with experimental results across all beam geometries. Incorporating the axial stiffness and effective strain of IRCs into the tie formulation significantly improved prediction accuracy, while the refined representation of nodal confinement provided a more realistic depiction of stress flow within strengthened beams. The narrow deviation range (±17%) validates the STM’s reliability for design applications, especially in deep and intermediate beams, where shear action predominates.

In summary, the proposed STM demonstrates strong predictive performance for IRC-strengthened RC beams of varying geometries. The experimental-to-predicted ratios clustered close to unity (average ≈ 1.00), indicating that the model provides both accurate and conservative estimates of ultimate shear capacity. The integration of IRC tie action and confinement effects into the STM framework represents a significant step toward developing a unified analytical approach for externally strengthened RC structures. Future work involving cyclic and environmental exposure testing is recommended to further assess durability and service life implications.

5. Conclusions

This study developed a mechanics-based STM specifically tailored for RC beams strengthened with IRCs. The model integrates the experimentally derived tensile characteristics of three IRC configurations—AC, GA, and CG—into the tie components of the STM. By examining three beam groups with different shear span-to-depth ratios (a/d = 1.0, 2.0, and 3.0), the analytical framework successfully captured the interaction between geometry, composite type, and load transfer mechanisms in both shear- and flexure-dominated regions. Key findings and implications are summarized below:

Accuracy of the Proposed STM: The proposed model accurately predicted the ultimate shear capacities of composite-strengthened beams, with deviations typically within ±5–10% of the experimental values. The best agreement was obtained for deep beams (a/d = 1.0), where the U-shaped IRC jackets effectively functioned as primary tension ties and ensured efficient load transfer between the strut and tie zones.

Influence of Composite Type: Among the three composite systems, AC composites exhibited the most effective enhancement due to their superior stiffness and tensile strength, enabling higher tie force mobilization. GA composites demonstrated a balanced behavior between ductility and stiffness, performing consistently across deep and intermediate beams. CG composites, although successful in delaying crack initiation, exhibited reduced tensile utilization because of their relatively lower longitudinal stiffness and early debonding tendency.

Strut Geometry and Node Behavior: The modified STM effectively accounted for the inclination of struts, confinement effects, and nodal zone behavior. Observed failure mechanisms, such as node crushing, concrete splitting, and composite rupture, closely matched the stress trajectories predicted by the model. This confirms the ability of the STM to simulate realistic stress transfer paths in D-regions of strengthened members.

Design and Practical Implications: When calibrated using the mechanical parameters of hybrid composites, the STM serves as a rational, conservative, and experimentally validated design tool for RC members externally strengthened with IRC jackets. The framework allows engineers to explicitly incorporate composite tensile contributions and confinement effects in design, in accordance with performance-based seismic and structural design principles.

Applicability Range: The validity of the proposed STM has been verified within the interval 1.0 ≤ a/d ≤ 3.0, which encompasses both deep and moderately slender beam configurations. The highest predictive accuracy is achieved for a/d ≈ 1.0, where short development lengths and steep strut inclinations enhance tie engagement. As a/d increases toward 3.0, a moderate decrease in accuracy is observed, mainly due to the reduced anchorage efficiency and bond limitations of the composite ties. Nonetheless, the model remains conservative and reliable within this range.

Limitations and Future Work: The current STM formulation was developed for monolayer U-jacket configurations under quasi-static loading conditions. Future research should focus on:

• Multi-layer and triple intraply hybrid systems (e.g., Aramid–Glass–Carbon),
• Anchorage and debonding behavior,
• Cyclic and fatigue loading performance,
• Long-term durability and environmental effects,
• The interaction between external IRCs and internal steel reinforcement (stirrups),
• The extension of this formulation into 3D STM models may further improve the accuracy for torsional and asymmetric load cases.

In conclusion, the proposed STM framework successfully bridges the gap between experimental observations and analytical modeling for RC beams strengthened with IRCs. It provides a physically consistent, experimentally validated, and design-oriented approach for predicting shear behavior in hybrid composite systems. This model establishes a foundation for the future integration of advanced composite materials into structural design codes and performance-based assessment methodologies.