Vertical Deformation Calculation Method and In Situ Protection Design for Large-Span Suspended Box Culverts
Abstract
1. Introduction
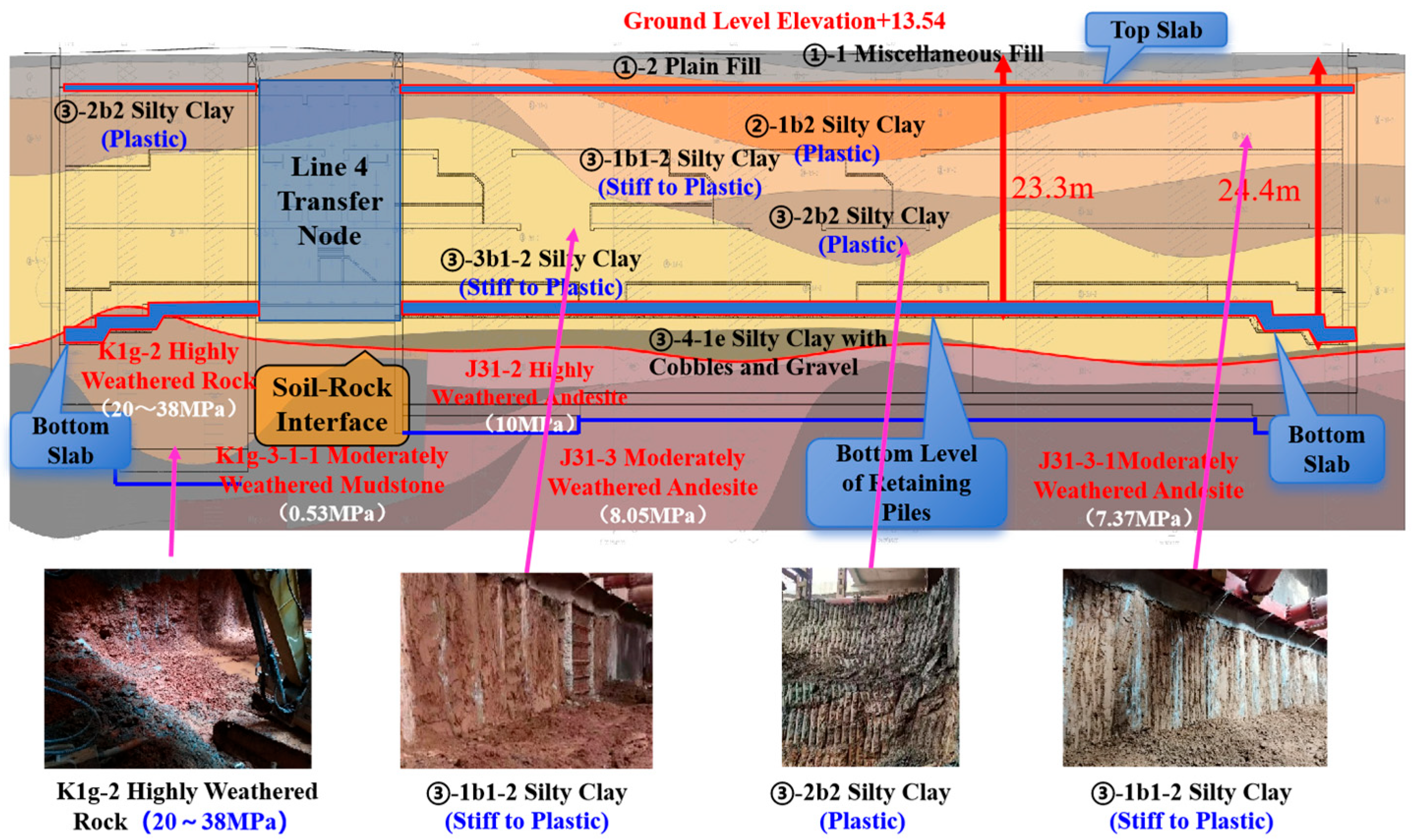
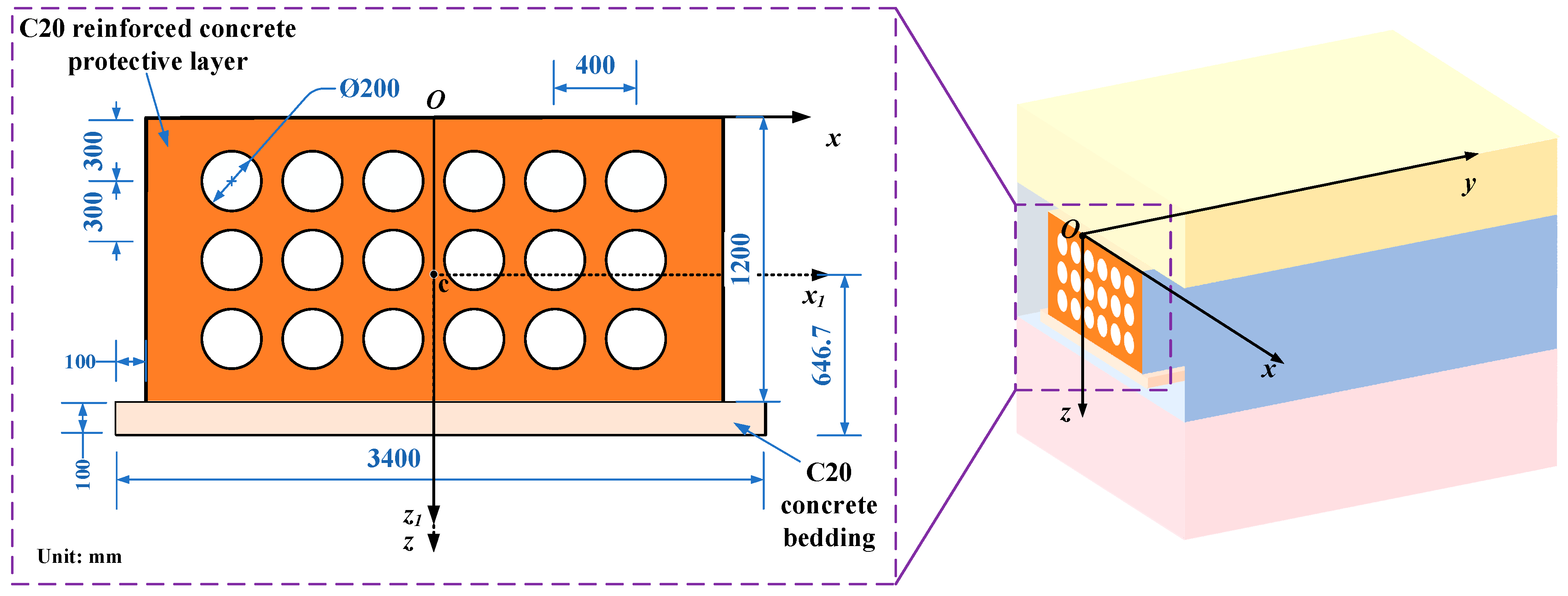
2. Engineering Background
3. Materials and Methods
3.1. Vertical Deformation of the Box Culverts Without Protection
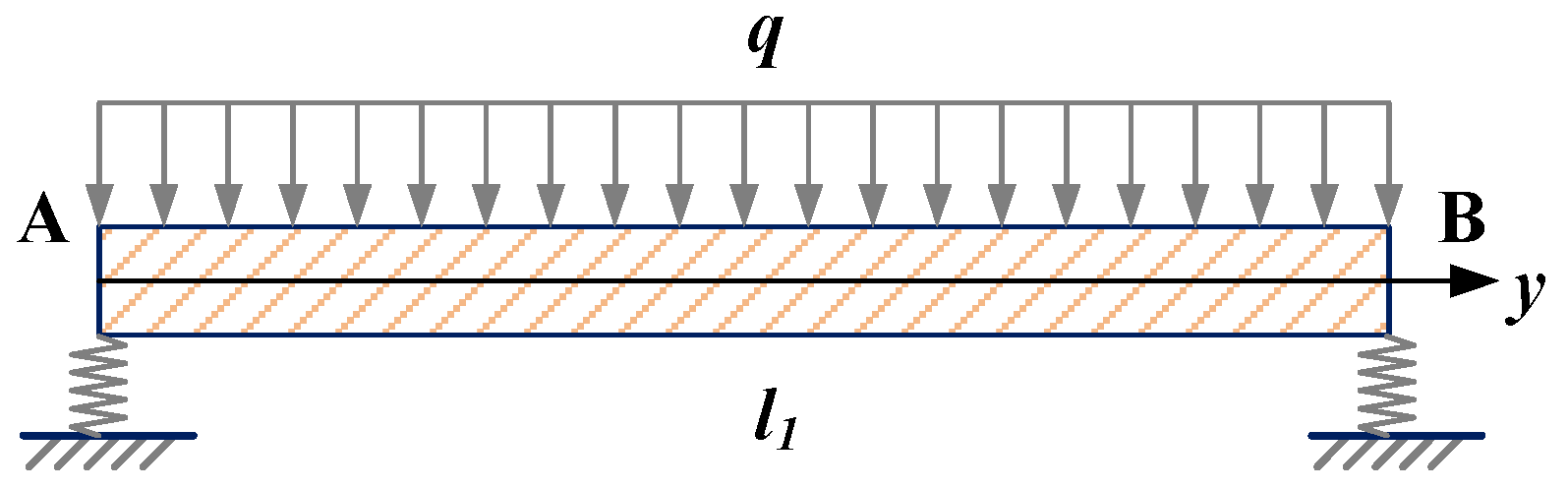
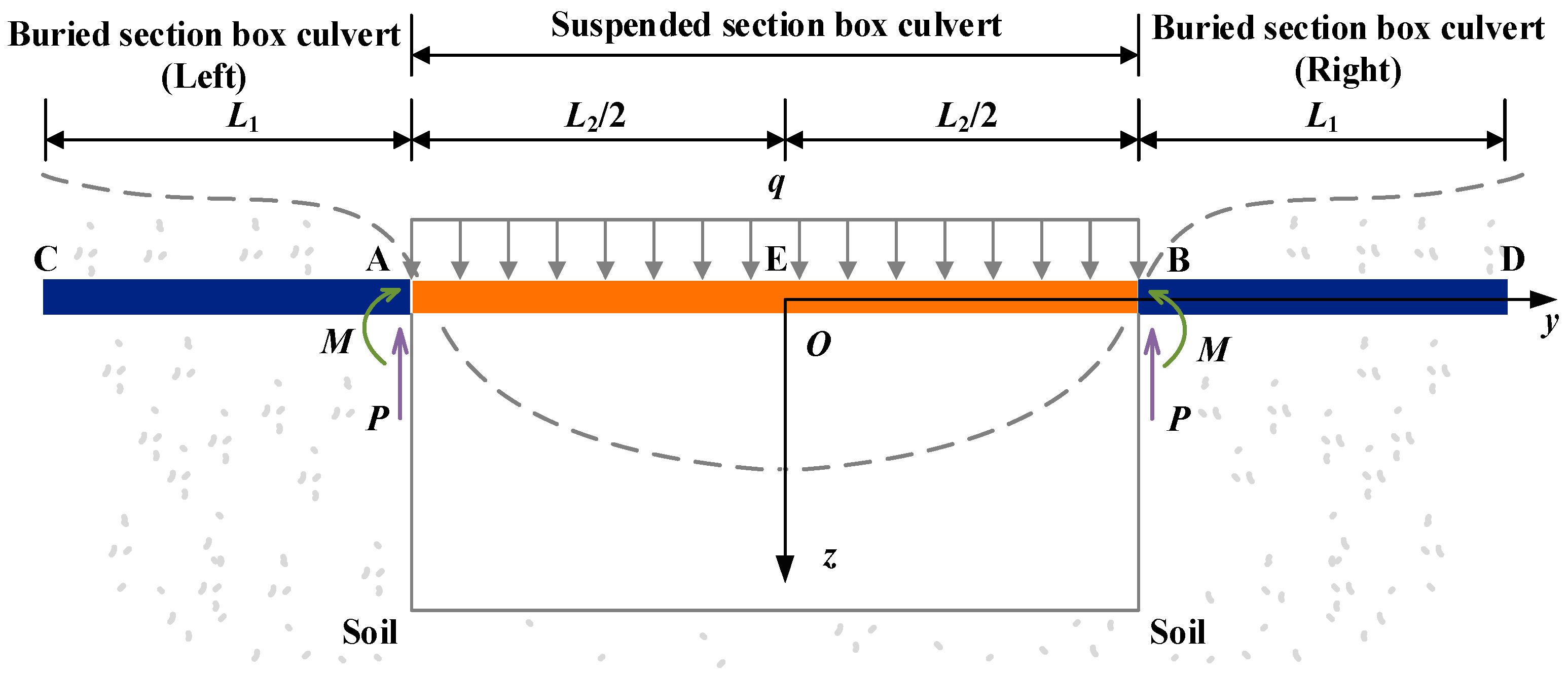
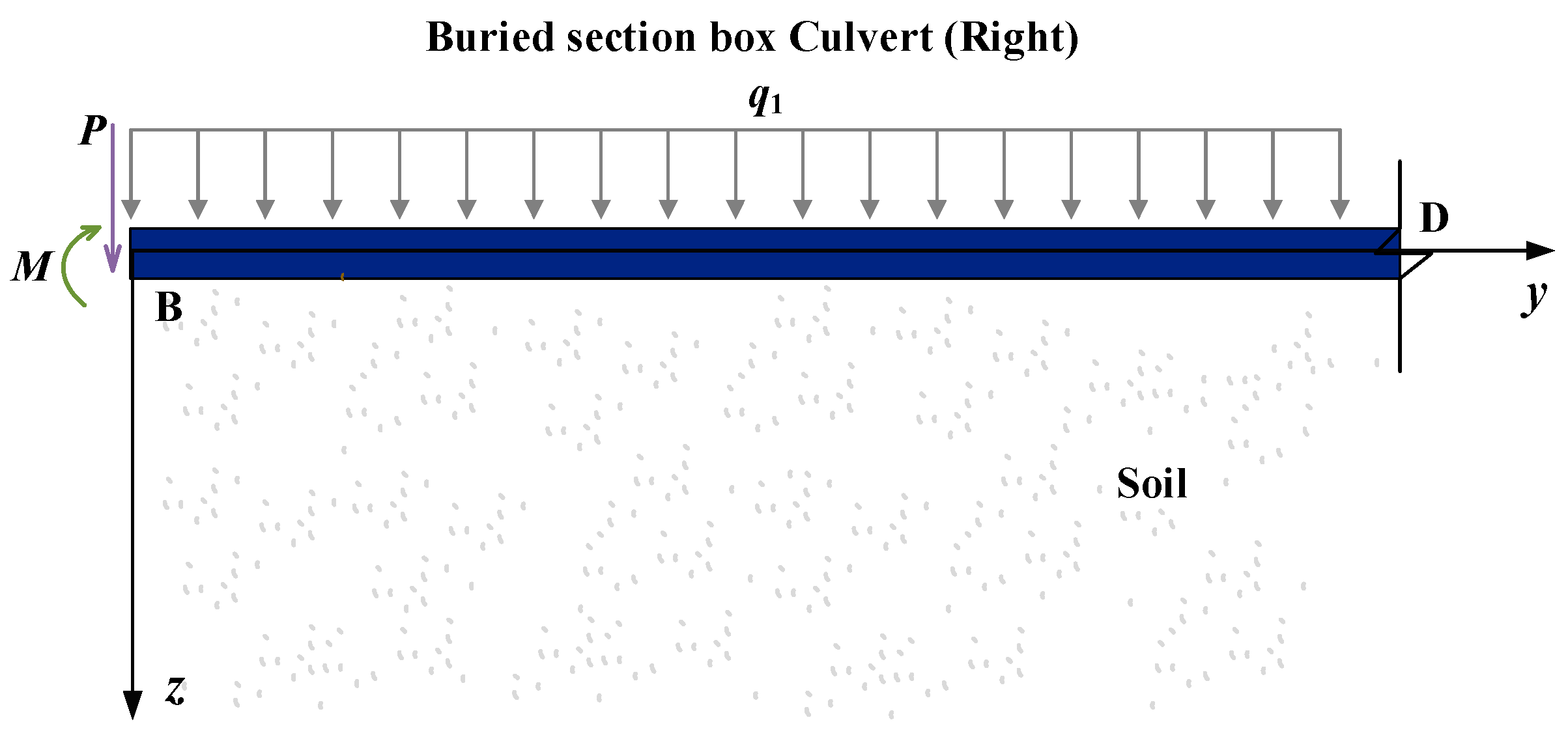
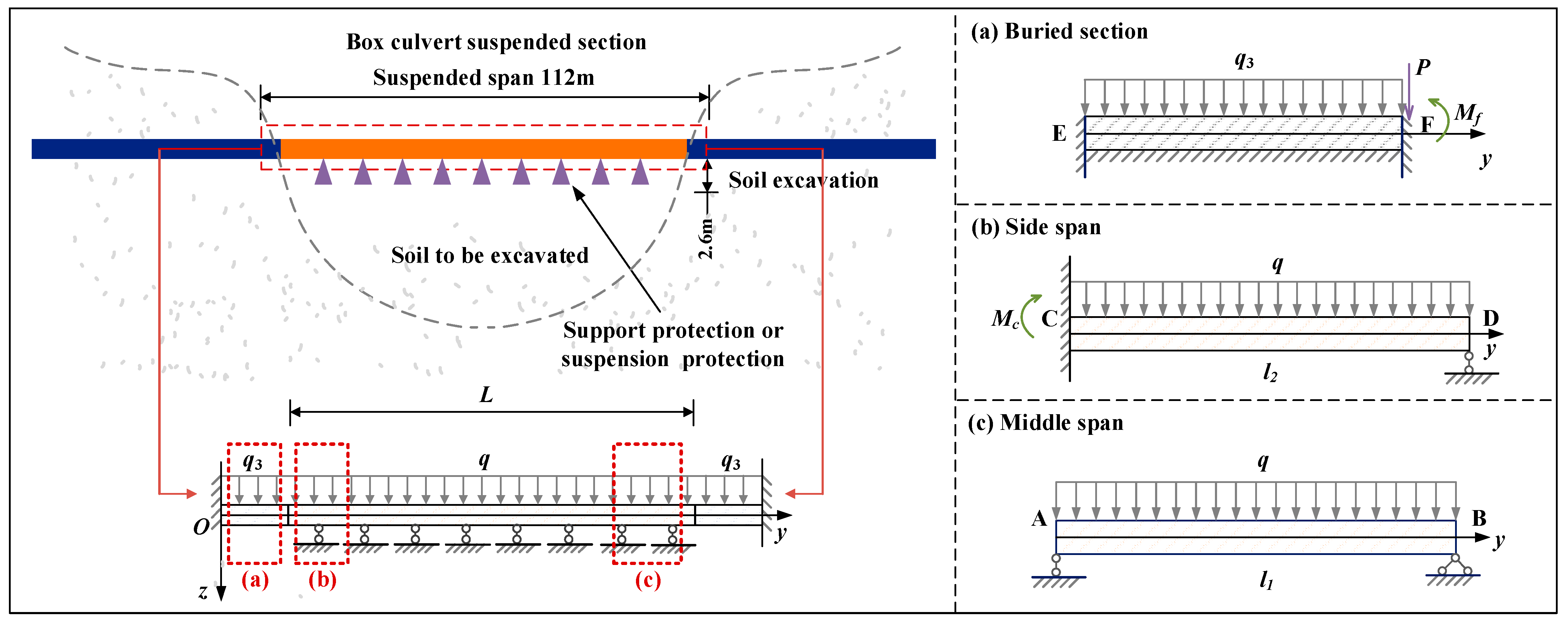
3.1.1. Vertical Deformation Calculation Formula
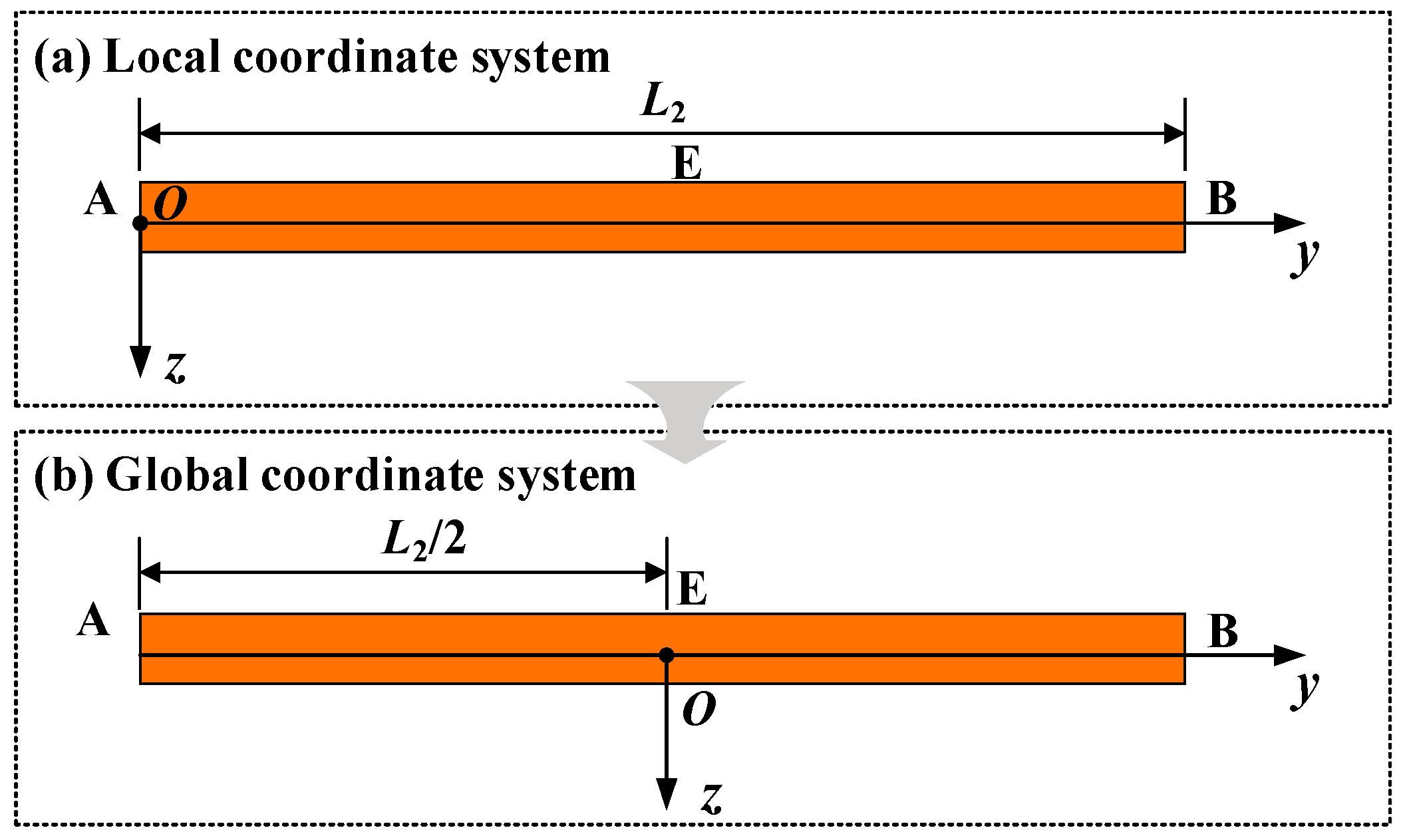
- Point O as the midpoint and coordinate origin of the suspended section;
- Segments AC and BD represent left and right buried sections with length L1;
- Segment AB is the suspended span with length L2.
- (1)
- Vertical deformation of the buried section
- (2)
- Vertical deformation of the suspended section
- (3)
- Vertical deformation formulas for the full-span
3.1.2. Case Study
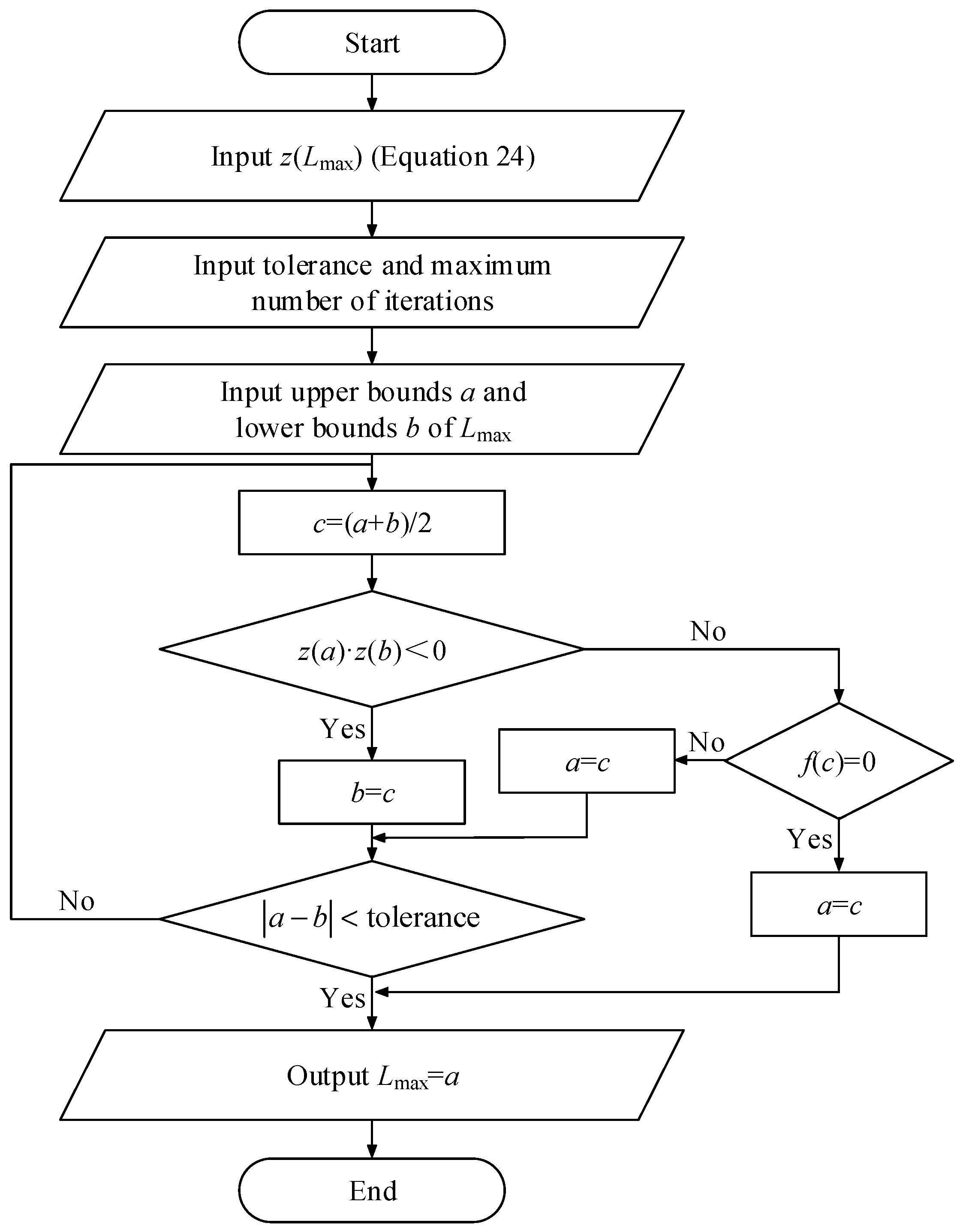
3.2. Vertical Deformation of the Box Culverts Under Protection
3.3. Support Protection and Suspension Protection for Box Culverts and Scheme Comparison
3.3.1. Support Protection for the Box Culverts
3.3.2. Suspension Protection for the Box Culverts
3.3.3. Optimal Protection Scheme for the Box Culverts
4. Results
5. Discussion
6. Conclusions
- A full-span mechanical model was established by dividing the box culvert into buried, side-span, and mid-span sections. Analytical solutions for vertical deformation under both unprotected and protected conditions were derived, enabling the determination of critical engineering parameters such as the maximum allowable unsupported span and the optimal support spacing.
- Taking the 112 m overhanging power box culvert at Yunnan Road Station as a case study, the results indicate that the culvert cannot remain stable under unsupported conditions, requiring in situ protection. The analytically derived support scheme—specifying optimized spacings of 8.5 m (side-span) and 9.0 m (mid-span) with twelve support points—validates the model’s practical utility while maintaining an inherent safety margin.
- Comprehensive validation through three-dimensional ABAQUSs confirms both the accuracy and engineering applicability of the proposed analytical method. The close agreement among theoretical predictions, numerical results, and field measurements establishes the method’s reliability for practical design applications.
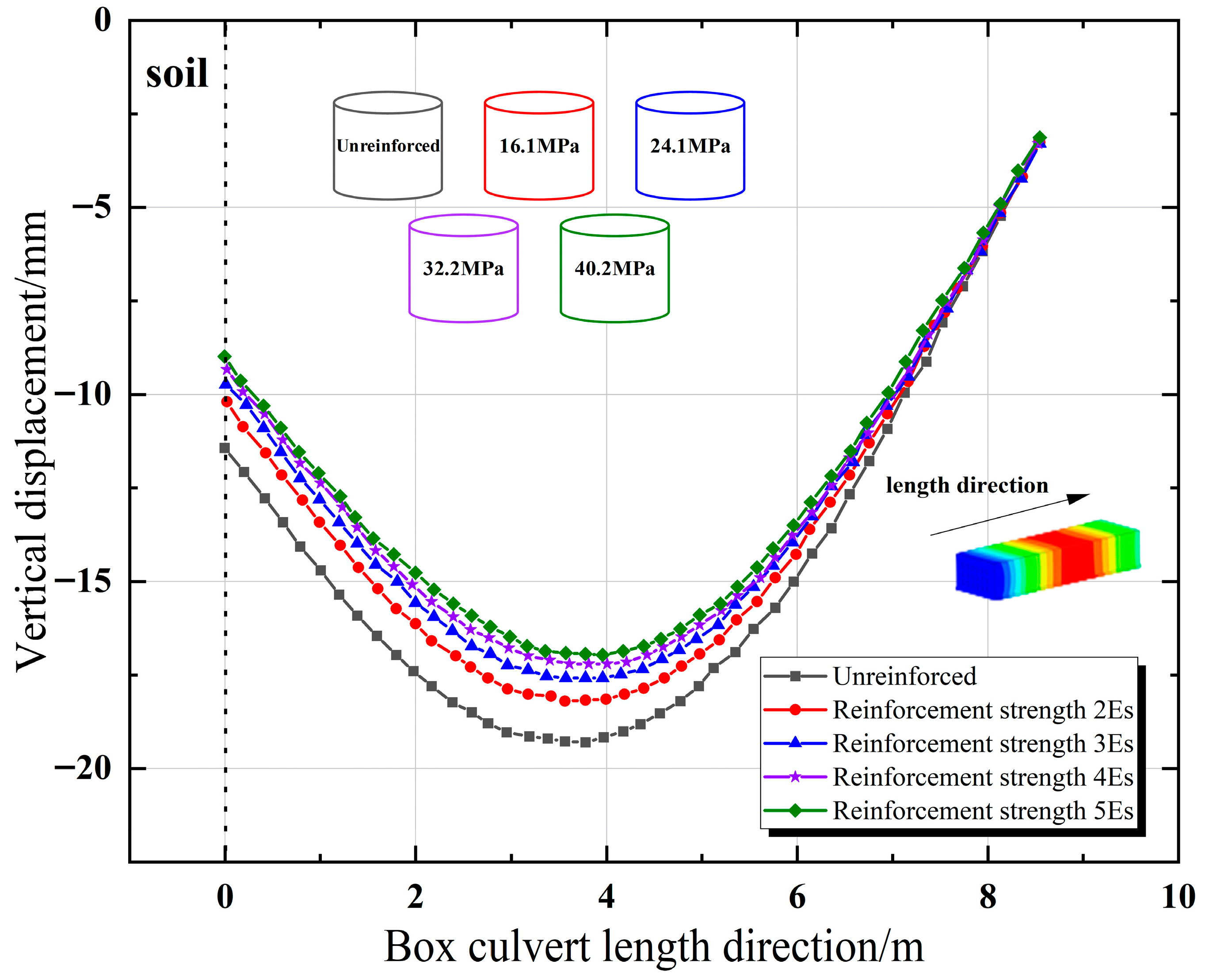
- Parametric analysis reveals that soil reinforcement effectively controls deformation, with a particularly significant finding being the identification of economic thresholds at approximately three times the culvert’s height (3h) and width (3b). This crucial insight enables optimized design by defining the point of diminishing returns for reinforcement investment.
- Comparative analysis between support protection and suspension protection demonstrated that the support protection, despite higher initial costs, offers greater reliability and minimal deformation control for large-span culverts with strict safety requirements, making it more suitable for applications in complex urban environments such as the Yunnan Road Station project.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Temperature Change (°C) | Axial Force Condition (kN) | Maximum Vertical Deformation (mm) | Relative Change (%) |
|---|---|---|---|
| −20 | 836 | 20.69 | 3.45 |
| −10 | 418 | 20.32 | 1.60 |
| 0 | 0 | 20.00 | 0 |
| +10 | −418 | 20.22 | 1.12 |
| +20 | −836 | 20.75 | 3.77 |
Appendix B
References
- Liu, W.; Xue, D.; Yuan, J. Analysis of Influences Caused by Cantilever Pile-Supported Pit Excavation towards Adjacent Buried Pipe Lines. IOP Conf. Ser. Earth Environ. Sci. 2018, 153, 052028. [Google Scholar] [CrossRef]
- Jiang, N.; Gao, T.; Zhou, C.; Luo, X. Effect of Excavation Blasting Vibration on Adjacent Buried Gas Pipeline in a Metro Tunnel. Tunn. Undergr. Space Technol. 2018, 81, 590–601. [Google Scholar] [CrossRef]
- Sun, S.; Rong, C.; Wang, H.; Cui, L.; Shi, X. The Ground Settlement and the Existing Pipeline ResponseInduced by the Nonsynchronous Construction of a Twin-Tunnel. Adv. Civ. Eng. 2021, 2021, 8815304. [Google Scholar] [CrossRef]
- Avgerinos, V.; Potts, D.M.; Standing, J.R. Numerical Investigation of the Effects of Tunnelling on Existing Tunnels. Géotechnique 2017, 67, 808–822. [Google Scholar] [CrossRef]
- Meng, F.; Chen, R.; Xu, Y.; Wu, K.; Wu, H.; Liu, Y. Contributions to Responses of Existing Tunnel Subjected to Nearby Excavation: A Review. Tunn. Undergr. Space Technol. 2022, 119, 104195. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, G.; Ding, X. Special Issue on Tunnel Construction and Underground Space Technology. Buildings 2023, 13, 2988. [Google Scholar] [CrossRef]
- Fu, D.; Deng, B.; Yang, M.; Zhen, B. Analytical Solution of Overlying Pipe Deformation Caused by Tunnel Excavation Based on Pasternak Foundation Model. Sci. Rep. 2023, 13, 921. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, J.; Huang, M.; Yu, J. Winkler Load-Transfer Analysis for Pipelines Subjected to Surface Load. Comput. Geotech. 2019, 111, 147–156. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, M.; Zhao, Q.; Fang, L.; Ding, Z.; Shi, M. Interaction Analyses between Existing Pipeline and Quasi-Rectangular Tunneling in Clays. KSCE J. Civ. Eng. 2021, 25, 326–344. [Google Scholar] [CrossRef]
- Banushi, G.; Wham, B.P. Deformation Capacity of Buried Hybrid-Segmented Pipelines under Longitudinal Permanent Ground Deformation. Can. Geotech. J. 2021, 58, 1095–1117. [Google Scholar] [CrossRef]
- Jiang, T.; Xie, Z.; Wang, J.; Li, D.; Qu, C. A Novel Strain-Based Deformation Monitoring Method for Subsea Free-Spanning Pipelines. Eng. Struct. 2025, 343, 120998. [Google Scholar] [CrossRef]
- Wang, H.; Lei, Z.; Wang, Z.; Guo, Z. Analytical Models of High-Temperature Pipeline Deformation under Submarine Landslides. Thin-Walled Struct. 2025, 210, 112990. [Google Scholar] [CrossRef]
- Nie, H.; Ma, W.; He, X.; Huo, X.; Wang, Y.; Ren, J.; Dang, W.; Wang, K.; Cao, J.; Yao, T.; et al. Study on Buckling Deformation Mechanism of Pipeline Crossing Road. Eng. Fail. Anal. 2022, 139, 106412. [Google Scholar] [CrossRef]
- Wang, C.; Li, C.; Liu, W.; Wang, J.; Wu, J. Pipeline–Soil Separation Model for Natural Gas Pipelines Subjected to Parabolic Driving Force. J. Pipeline Syst. Eng. Pract. 2019, 10, 04018028. [Google Scholar] [CrossRef]
- Wang, X.; Yao, A. Deflection and Internal Force Analysis of Buried Steel Pipelines in Partial Hanging. Eng. Mech. 2008, 25, 218–222. [Google Scholar]
- Liang, L.; Xu, C.; Zhu, B.; Deng, J. Theoretical Method for an Elastic Infinite Beam Resting on a Deformable Foundation with a Local Subsidence. Comput. Geotech. 2020, 127, 103740. [Google Scholar] [CrossRef]
- Li, B.; Fang, H.; Zhai, K.; Yang, K.; Zhang, X.; Wang, Y. Mechanical Behavior of Concrete Pipes with Erosion Voids and the Effectiveness Evaluation of the Polyurethane Grouting. Tunn. Undergr. Space Technol. 2022, 129, 104672. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, A.; Fang, Q.; Wan, Y.; Li, J.; Guo, X. Spatiotemporal Deformation of Existing Pipeline Due to New Shield Tunnelling Parallel Beneath Considering Construction Process. Appl. Sci. 2022, 12, 500. [Google Scholar] [CrossRef]
- Zhao, S.-W.; Li, X.-L.; Li, X.; Chen, L.-G.; Li, T.; Li, S.-H.; Bai, Y. Analysis of Pipeline Deformation Caused by Shield Tunnel Excavation That Obliquely Crosses Existing Pipelines. Arab. J. Geosci. 2022, 15, 227. [Google Scholar] [CrossRef]
- Wang, D.; Dong, J.; Chen, X.; Du, J.; Shu, D.; Krassowska, J. Influence of Gas Explosions in Utility Tunnels on the Structural Safety of Overhead Pipelines. Buildings 2025, 15, 3391. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, W.; Chen, C.; Lu, J.; Tang, P. Study on Settlement Influence of Newly Excavated Tunnel Undercrossing Large Diameter Pipeline. Adv. Civ. Eng. 2022, 2022, 5700377. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, Q.; Jiang, B.; Chen, H. An Underground Pipeline Mapping Method Based on Fusion of Multisource Data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4511711. [Google Scholar] [CrossRef]
- Farh, H.M.H.; Ben Seghier, M.E.A.; Zayed, T. A Comprehensive Review of Corrosion Protection and Control Techniques for Metallic Pipelines. Eng. Fail. Anal. 2023, 143, 106885. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, M. Application of Suspension Protection Technology in Underground Pipe Gallery. Chin. J. Undergr. Space Eng. 2018, 14, 285–290. Available online: https://kns.cnki.net/kcms2/article/abstract?v=vfP_nAZksBLeiSBEI5K00j6RxdC5Yo5NHJVEH4zE-VCQr17rDVx_yoWgMY0C-EeJEKnDju2MUId6dRm2RHVdZIyQhXwofpIMStwZt2DSLHvwELUJMaGU6IWOe5GgSWkr-os0F7s4fU4NI-GrVIKX_6hwgBF3O-0Y9Owzl5Mlgz4=&uniplatform=NZKPT (accessed on 17 September 2025). (In Chinese).
- Meng, Z.; Wei, W.; Han, G.; Yu, Z.; Lu, J.; Wu, M.; Zhang, J.; Yu, J.; Jin, D. Research on Design and Construction Technology of Large Span T-Truss Suspension Beam. IOP Conf. Ser. Earth Environ. Sci. 2021, 804, 022092. [Google Scholar] [CrossRef]
- Yu, H.; Xu, F.; Ma, C.; Zhou, A.; Zhang, M. Experimental Research on the Aerodynamic Responses of a Long-Span Pipeline Suspension Bridge. Eng. Struct. 2021, 245, 112856. [Google Scholar] [CrossRef]
- Zeng, X.; Dong, F.; Xie, X.; Du, G. A New Analytical Method of Strain and Deformation of Pipeline under Fault Movement. Int. J. Press. Vessel. Pip. 2019, 172, 199–211. [Google Scholar] [CrossRef]
- Simão, M.; Mora-Rodriguez, J.; Ramos, H. Design Criteria for Suspended Pipelines Based on Structural Analysis. Water 2016, 8, 256. [Google Scholar] [CrossRef]
- Tschemmernegg, F.; Brändstatter, H. Austria’s Longest Pedestrian Suspension Bridge. Struct. Eng. Int. 1997, 7, 17–18. [Google Scholar] [CrossRef]
- Guo, P.; Sun, T.; Li, H.; Wang, Y. Performance of Pipeline Suspension System for In-Situ Protecting Large-Diameter Pressurized Pipelines Straddling Deep Braced Excavation in Clays. Tunn. Undergr. Space Technol. 2025, 163, 106752. [Google Scholar] [CrossRef]
- Guo, P.; Gong, X.; Wang, Y.; Lin, H.; Zhao, Y. Analysis of Observed Performance of a Deep Excavation Straddled by Shallowly Buried Pressurized Pipelines and underneath Traversed by Planned Tunnels. Tunn. Undergr. Space Technol. 2023, 132, 104946. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, R.; Zhang, H. Mechanical Response Analysis of the Buried Pipeline Due to Adjacent Foundation Pit Excavation. Tunn. Undergr. Space Technol. 2018, 78, 135–145. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, H.; Wu, K.; Xia, M.; Zheng, Q.; Ndubuaku, O.; Adeeb, S. Research Progress of Strain Analysis Methods for Buried Pipelines under Faulting Process. Oil Gas Storage Transp. 2016, 8, 799–807. [Google Scholar] [CrossRef]
- Tan, Y.; Lu, Y. Responses of Shallowly Buried Pipelines to Adjacent Deep Excavations in Shanghai Soft Ground. J. Pipeline Syst. Eng. Pract. 2018, 9, 05018002. [Google Scholar] [CrossRef]
- Wu, B.; Ge, C.; Li, P.; Yang, M.; Li, L. Influence of Deep Foundation Pit Excavation on Adjacent Pipelines: A Case Study in Nanjing, China. Appl. Sci. 2024, 14, 572. [Google Scholar] [CrossRef]
- Jiao, W.; Xu, J.; Tian, J.; Xie, X.; Du, G. Seismic Response Analysis of Buried Pipelines with the High Drop. Int. J. Press. Vessel. Pip. 2021, 191, 104379. [Google Scholar] [CrossRef]
- China Electric Power Press. Technical Specification for Thermal Power Erection and Construction—Part 5: Piping and System; DL 5190.5-2019; China Electric Power Press: Beijing, China, 2019. [Google Scholar]
- Liu, G.; Bai, Y.; Yao, L.; Cheng, Y.; Li, W.; Chang, L. Protection Construction Technique for Overhead 110 kVA Super-Long Power Lines. Archit. Technol. 2021, 52, 1292–1294. Available online: https://kns.cnki.net/kcms2/article/abstract?v=vfP_nAZksBI7M-j7pJhziGySk_DbhXjhLyhs4NCtsMC066bJMPZPkOSGRYD9_GkNWLifjtT-tzosMqb5EQjszhsaHxlLuYp365Q0sBk-L4ecvRB9-csBjBG94psygV1O37Q58XJiVgBFXT-dJeEVbNV-lgOcAKQLpM_gCPnShnA=&uniplatform=NZKPT (accessed on 17 September 2025). (In Chinese).
- Lin, Y.; Lv, Y.; Liu, X.; Chen, F. Analysis of Longitudinal Mechanical Properties of Buried Suspended Pipeline Resisting Collapse. Adv. Civ. Eng. 2019, 2019, 3954390. [Google Scholar] [CrossRef]
- Wang, H.; Xu, M.; Wu, Y.; Cui, M.; Tian, J. Study on the Calculation Method of Vertical Displacement of Pipeline Induced by Tunnel Undercrossing Multiple Pipelines. Indian Geotech. J. 2023, 53, 1165–1174. [Google Scholar] [CrossRef]
- Yang, M.; Yang, T.; Deng, B. Simplified Calculation Method for Overlying Pipeline Deformation Induced by Tunnel Construction in Soil Based on the Energy Principle. Adv. Civ. Eng. 2022, 2022, 2473721. [Google Scholar] [CrossRef]
- Jia, X.; Ni, K.; Li, Y.; Jia, L. Calculation and Prediction of Suspended Span Caused by Erosion of Deep Water Submarine Pipelines. IOP Conf. Ser. Mater. Sci. Eng. 2023, 1294, 012012. [Google Scholar] [CrossRef]
- Xu, L.; Zhao, M.; Huang, J.; Li, H.; Du, X.; Zhao, X.; Cao, S. An Improved Winkler Foundation Modulus for a Beam in a Full Space. Appl. Sci. 2024, 14, 2277. [Google Scholar] [CrossRef]
- Jiangsu Phoenix Science and Technology Publishing House. Technical Specification for Monitoring Measurement of Urban Rail Transit Engineering in Jiangsu Province; DGJ32/J 195-2015; Jiangsu Phoenix Science and Technology Publishing House: Nanjing, China, 2016. [Google Scholar]
- STRESS AND STRAIN. In Mechanics of Materials; John Wiley & Sons: Hoboken, NJ, USA, 2020; pp. 89–90.
- Mei, Y.; Zhou, D.; Wang, X.; Zhao, L.; Shen, J.; Zhang, S.; Liu, Y. Deformation Law of the Diaphragm Wall during Deep Foundation Pit Construction on Lake and Sea Soft Soil in the Yangtze River Delta. Adv. Civ. Eng. 2021, 2021, 6682921. [Google Scholar] [CrossRef]
- Fan, L.; Xun, Z.; Peng, S. A Comparative Case Study on Drainage Consolidation Improvement of Soft Soil under Vacuum Preloading and Surcharge Preloading. Appl. Sci. 2023, 13, 5782. [Google Scholar] [CrossRef]
- Jahed Armaghani, D.; Faizi, K.; Hajihassani, M.; Tonnizam Mohamad, E.; Nazir, R. Effects of Soil Reinforcement on Uplift Resistance of Buried Pipeline. Measurement 2015, 64, 57–63. [Google Scholar] [CrossRef]




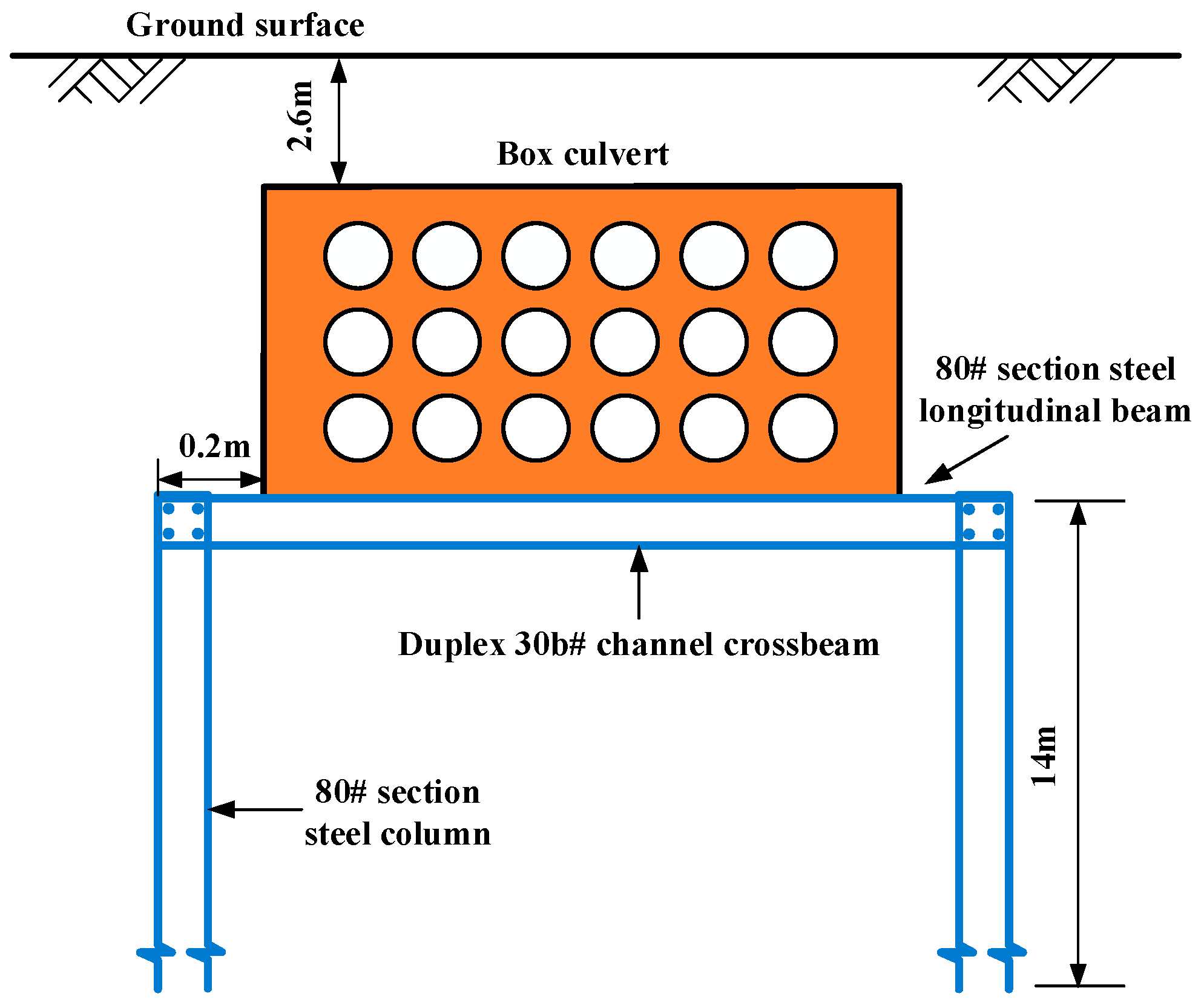
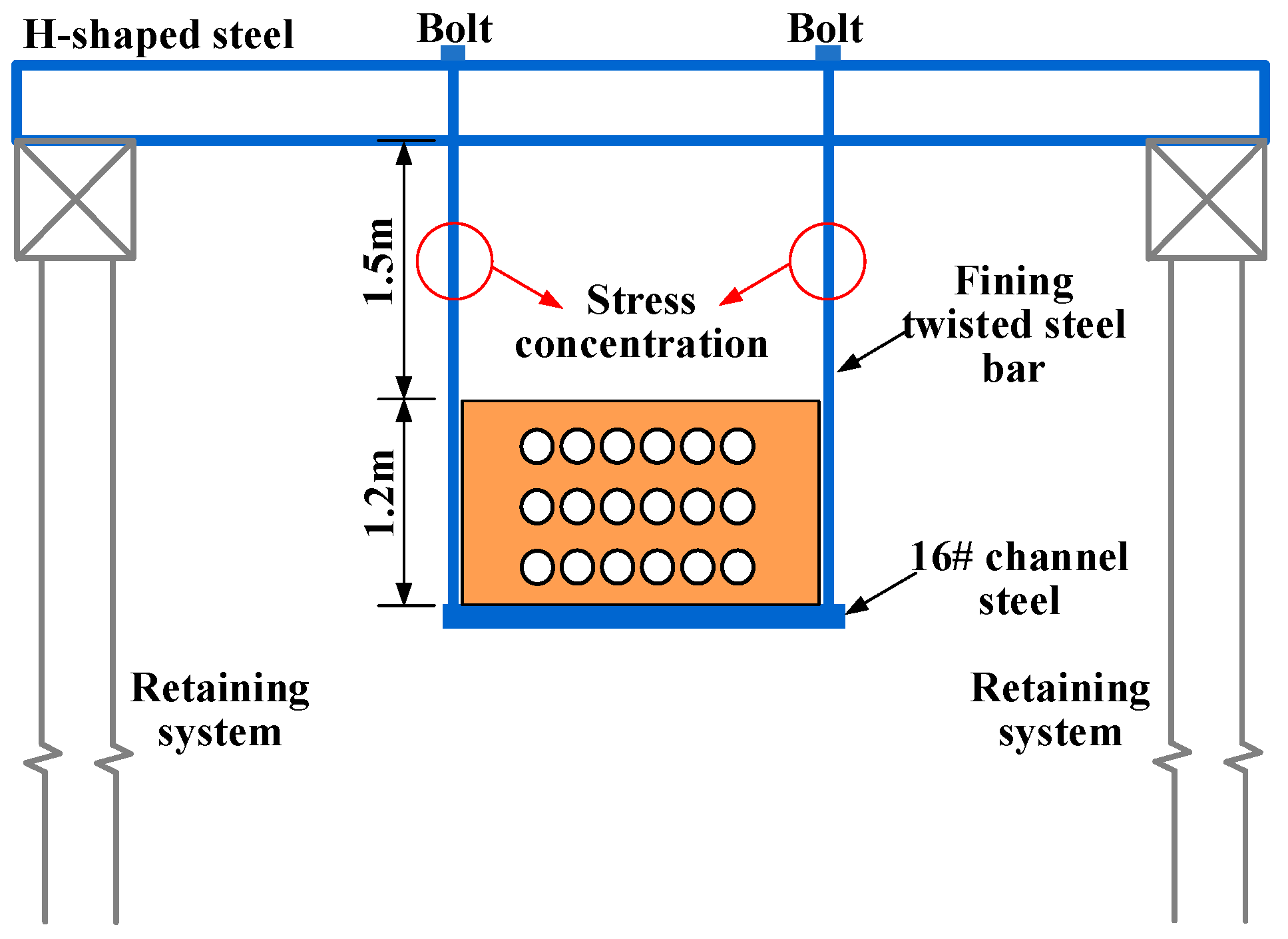

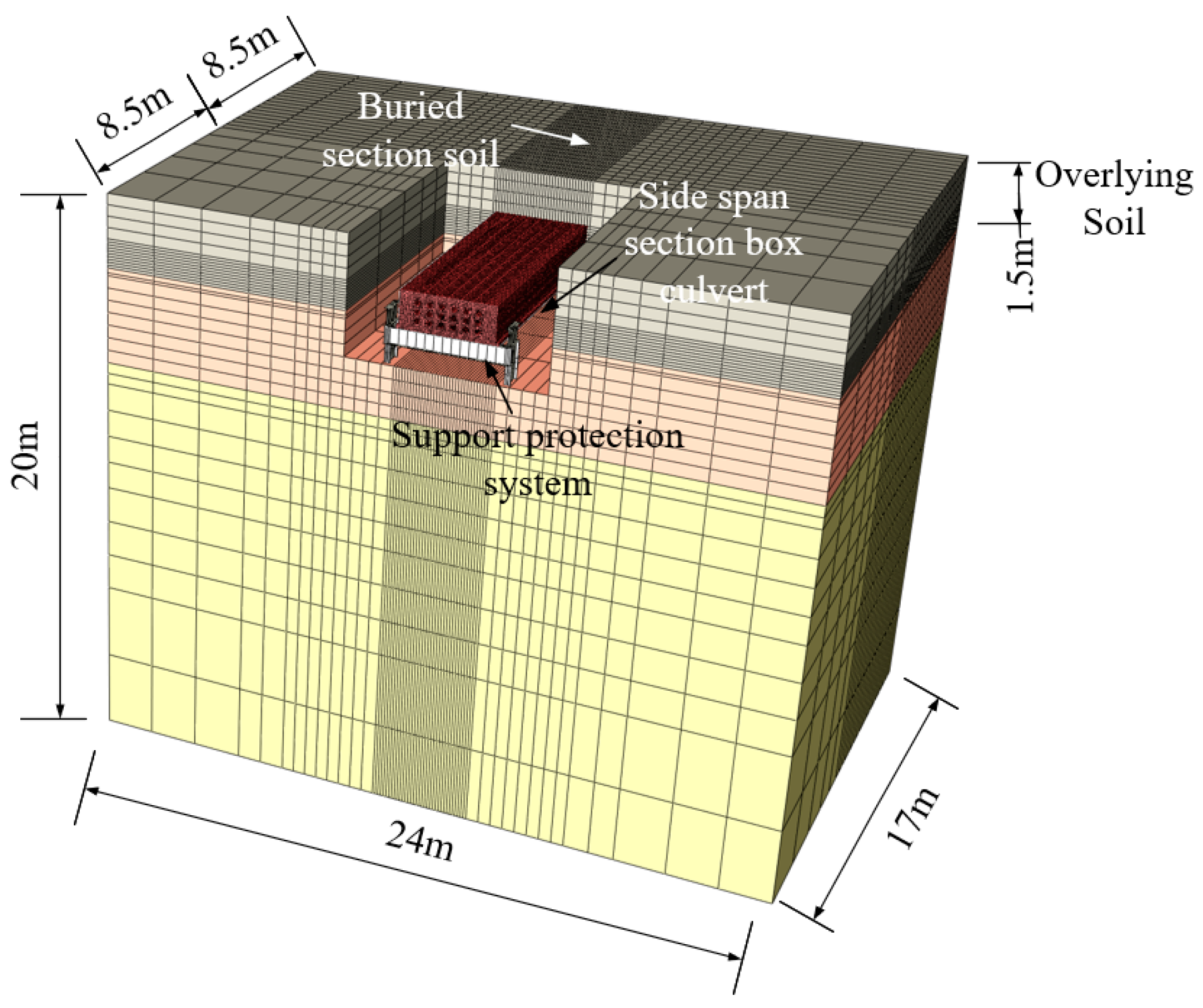

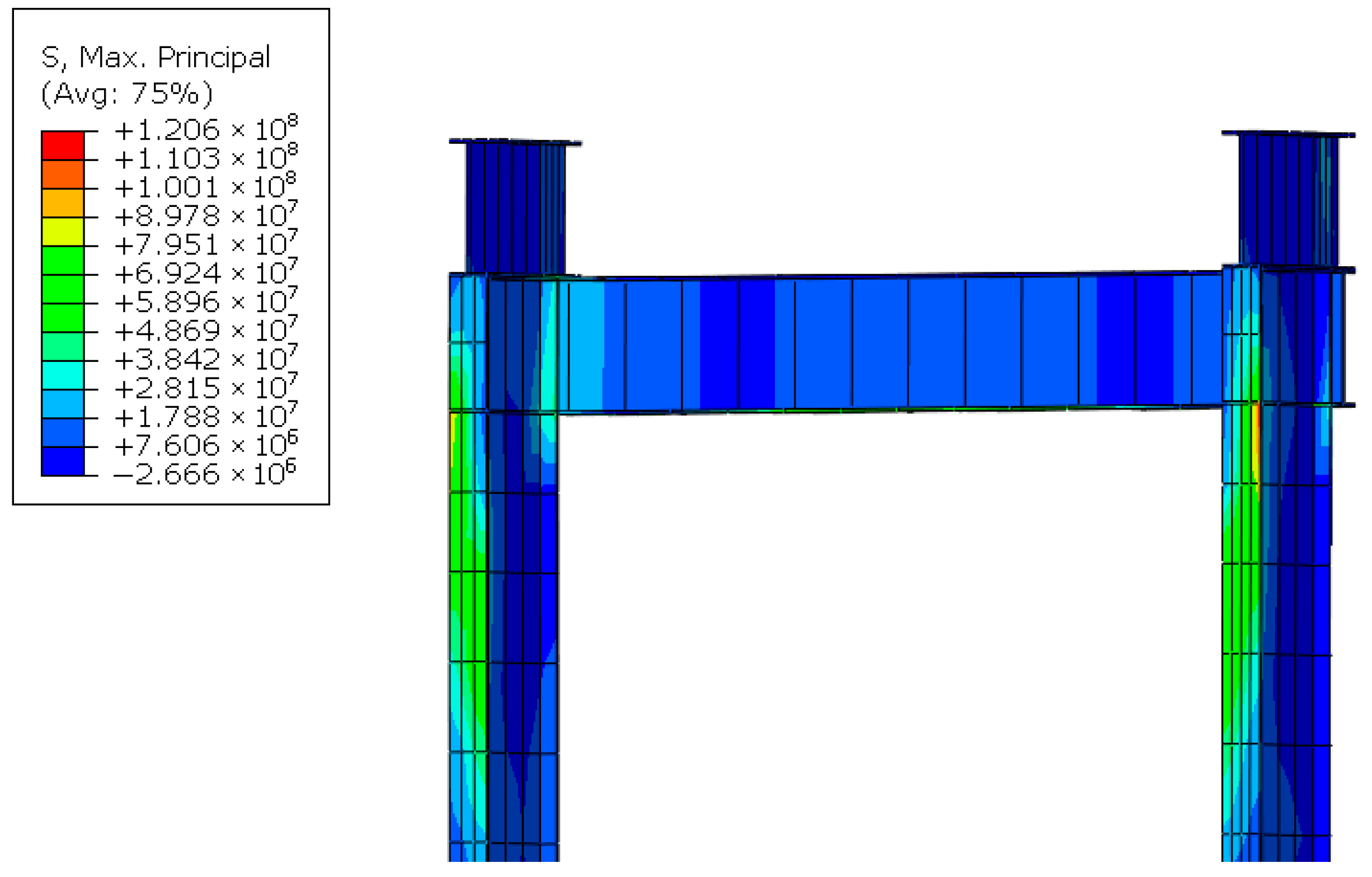
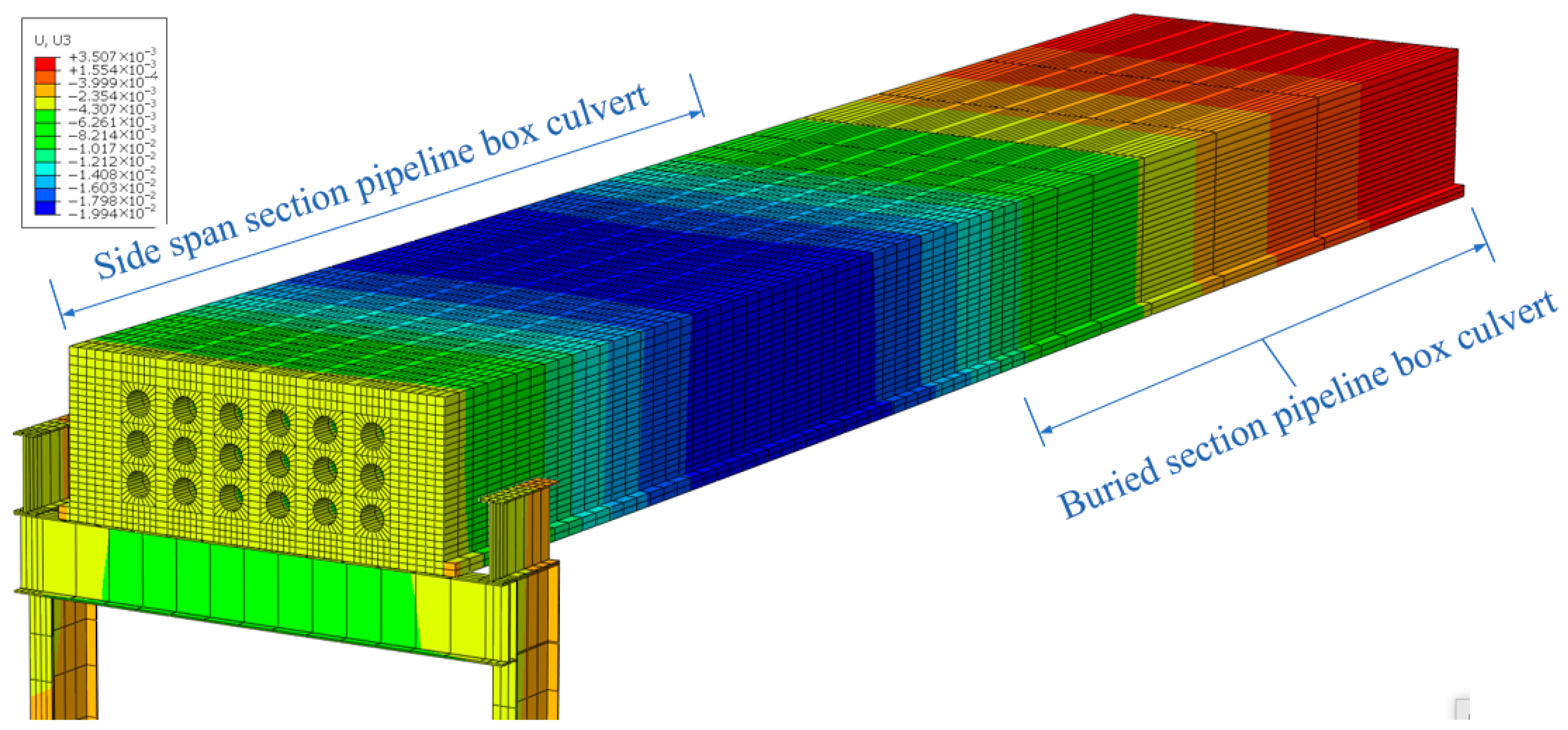

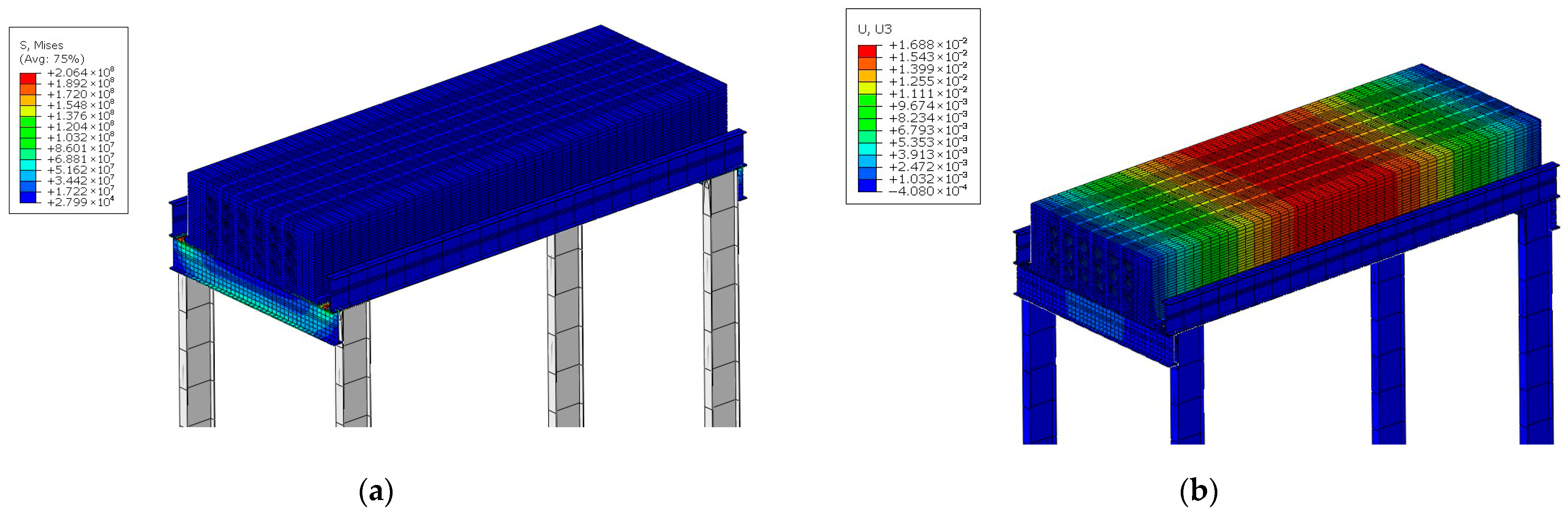


| Types | Protection Methods | Specific Measures | Applicable Engineering Context |
|---|---|---|---|
| Fully buried pipeline | Soil reinforcement [20,21] | Prefabricated vertical Drain (PVD) method, Sand Drain method, Grouting reinforcement, Soil replacement method | Relocatable pipelines, shallow excavation depth, and soft soil conditions. |
| Pipeline relocation [22] | Pipeline realignment, Joint replacement | Easily relocatable pipelines with moderate scope of work and available alternative routes. | |
| Partially suspended pipeline | Support protection [23] | Set support protection | Pipeline requires in situ protection with sections exhibiting a partially suspended state. |
| Suspension protection [24] | Set suspension protection |
| W (m3) | I (m4) | q (kN/m) | E (GPa) | zmax (m) | k0 (N/m) |
|---|---|---|---|---|---|
| 0.65 | 0.56 | 129.6 | 1 | 0.02 | 1.6 × 104 |
| Protection Measures | Number of Protection Points | Spacing Between Points/m | Costs | Required Construction Space |
|---|---|---|---|---|
| Suspension protection | 285 | 0.39 | Low | Relative large |
| Support protection | 12 | 8.73 | High | Relative small |
| Part Name | Thickness /(m) | Density /(kg·m−3) | Elastic Modulus/(N·m−2) | Poisson Ratio | Cohesion /kPa | Angle of Friction/(°) |
|---|---|---|---|---|---|---|
| Miscellaneous fill | 1.5 | 1900 | 5.1 × 106 | 0.16 | 10.0 | 10.0 |
| Plain fill | 2.5 | 1910 | 10.0 × 106 | 0.30 | 34.5 | 12.9 |
| Silty clay | 16.0 | 1970 | 15.1 × 106 | 0.28 | 50.4 | 30.4 |
| Box culvert | 3200 | 1.0 × 109 | 0.28 | |||
| 30#b Channel steel | 5327 | 2.0 × 1011 | 0.17 | |||
| 80# Shaped steel | 7850 | 2.1 × 1011 | 0.17 |
| Comparison Schemes | Modulus of Reinforced Soil/MPa | Reinforced Length/m | Reinforced Widths/m | Reinforced Depths/m |
|---|---|---|---|---|
| 1 | 16.1 | 8.5 | 3.4 | 1.3, 3.9, 7.8, 11.7 |
| 2 | 16.1 | 8.5 | 3.4, 6.8, 10.2, 13.6 | 1.3 |
| 3 | 16.1, 24.1, 32.2, 40.2 | 8.5 | 3.4 | 1.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Yan, X.; Xu, M.; Hu, D.; Wang, Z.; Guo, L.; Xi, P. Vertical Deformation Calculation Method and In Situ Protection Design for Large-Span Suspended Box Culverts. Buildings 2025, 15, 3804. https://doi.org/10.3390/buildings15203804
Liu H, Yan X, Xu M, Hu D, Wang Z, Guo L, Xi P. Vertical Deformation Calculation Method and In Situ Protection Design for Large-Span Suspended Box Culverts. Buildings. 2025; 15(20):3804. https://doi.org/10.3390/buildings15203804
Chicago/Turabian StyleLiu, Heng, Xihao Yan, Mingjie Xu, Dong Hu, Zhengwei Wang, Lei Guo, and Peng Xi. 2025. "Vertical Deformation Calculation Method and In Situ Protection Design for Large-Span Suspended Box Culverts" Buildings 15, no. 20: 3804. https://doi.org/10.3390/buildings15203804
APA StyleLiu, H., Yan, X., Xu, M., Hu, D., Wang, Z., Guo, L., & Xi, P. (2025). Vertical Deformation Calculation Method and In Situ Protection Design for Large-Span Suspended Box Culverts. Buildings, 15(20), 3804. https://doi.org/10.3390/buildings15203804





