Study on the Dynamic Responses of a Concrete-Block-Panel-Wrapped Reinforced Soil Retaining Wall: A Model Test
Abstract
1. Introduction
2. Experimental Program
2.1. Materials
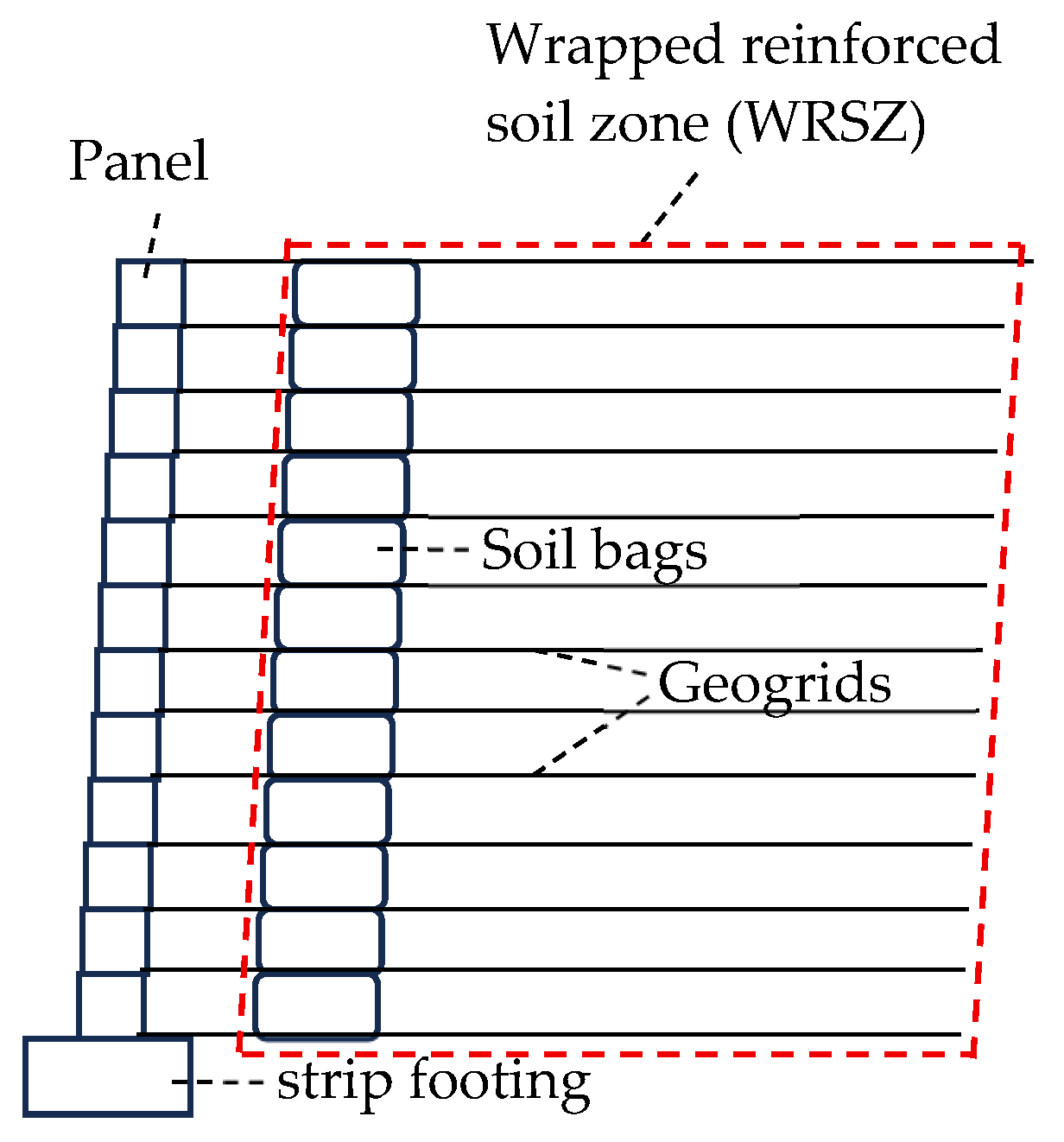
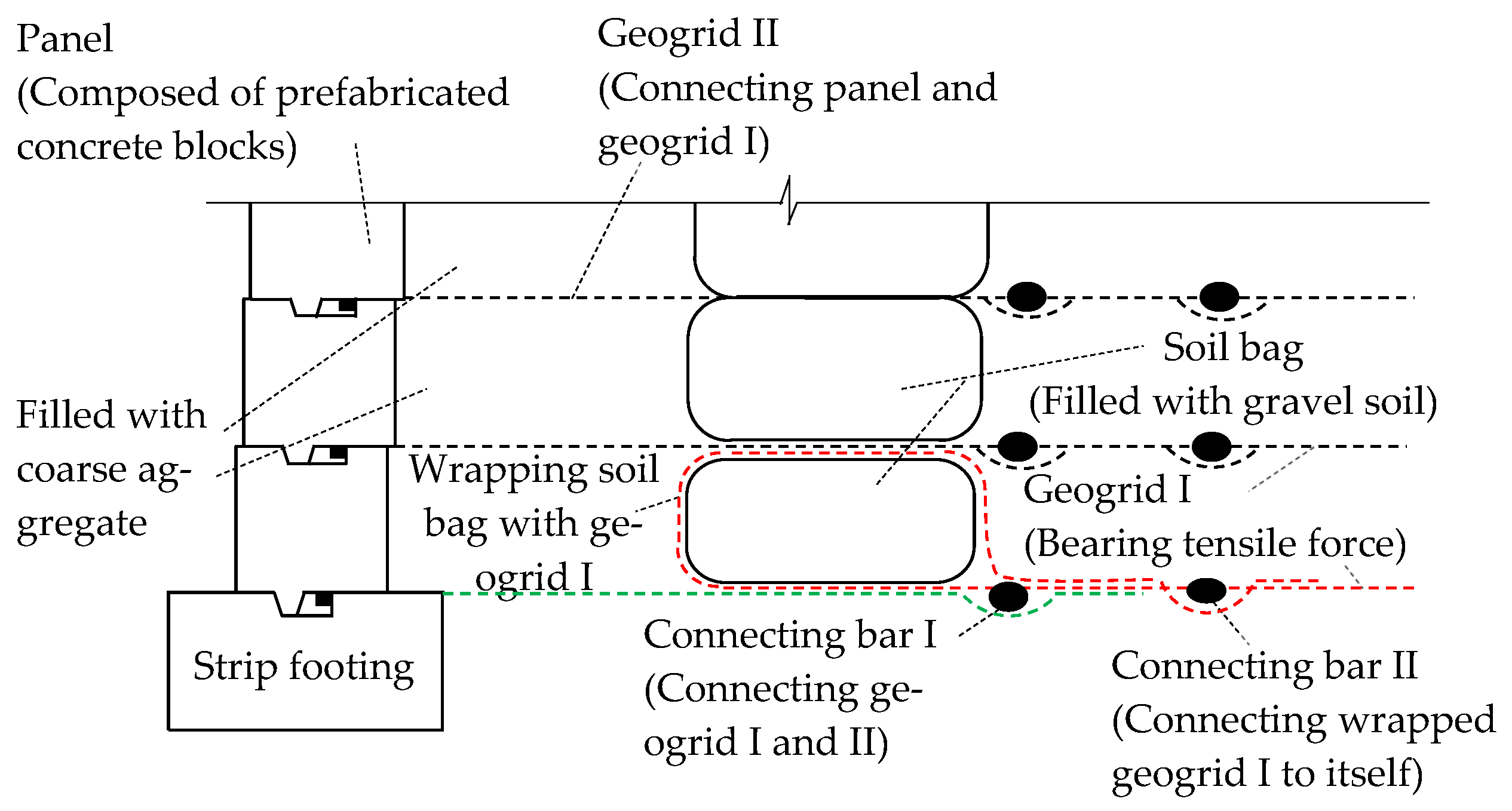
2.2. Model Setup
2.3. Monitoring Scheme
- Portable Signal Conditioner with Superior Anti-Electromagnetic Interference Capability: This device integrates key functions such as signal amplification, low-pass filtering, and pre-balancing, specifically designed to acquire high-quality weak strain/stress signals in complex electromagnetic environments.
- 24-bit Network Dynamic Strain Acquisition System: Used for high-resolution data acquisition.
3. Results
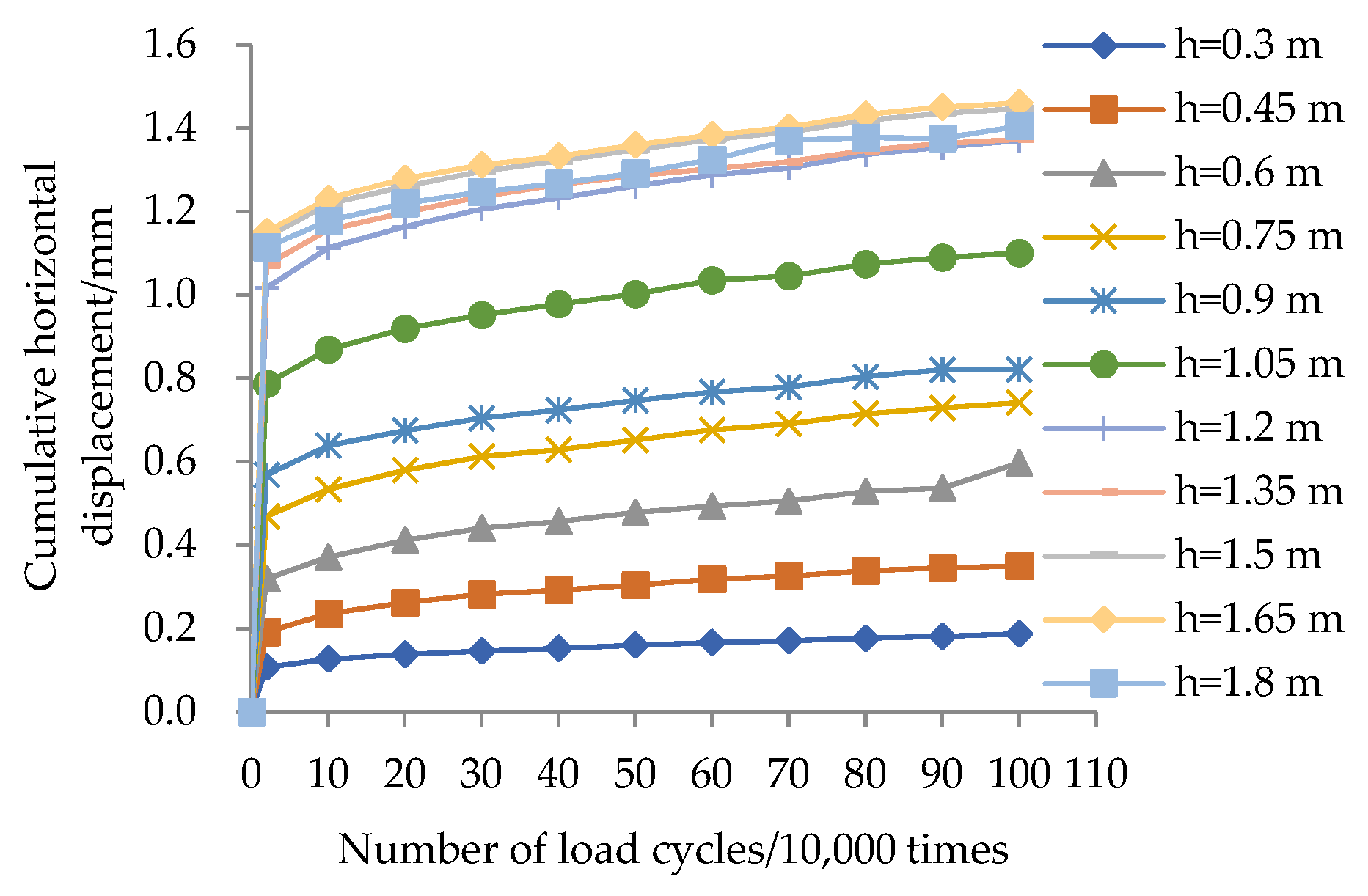
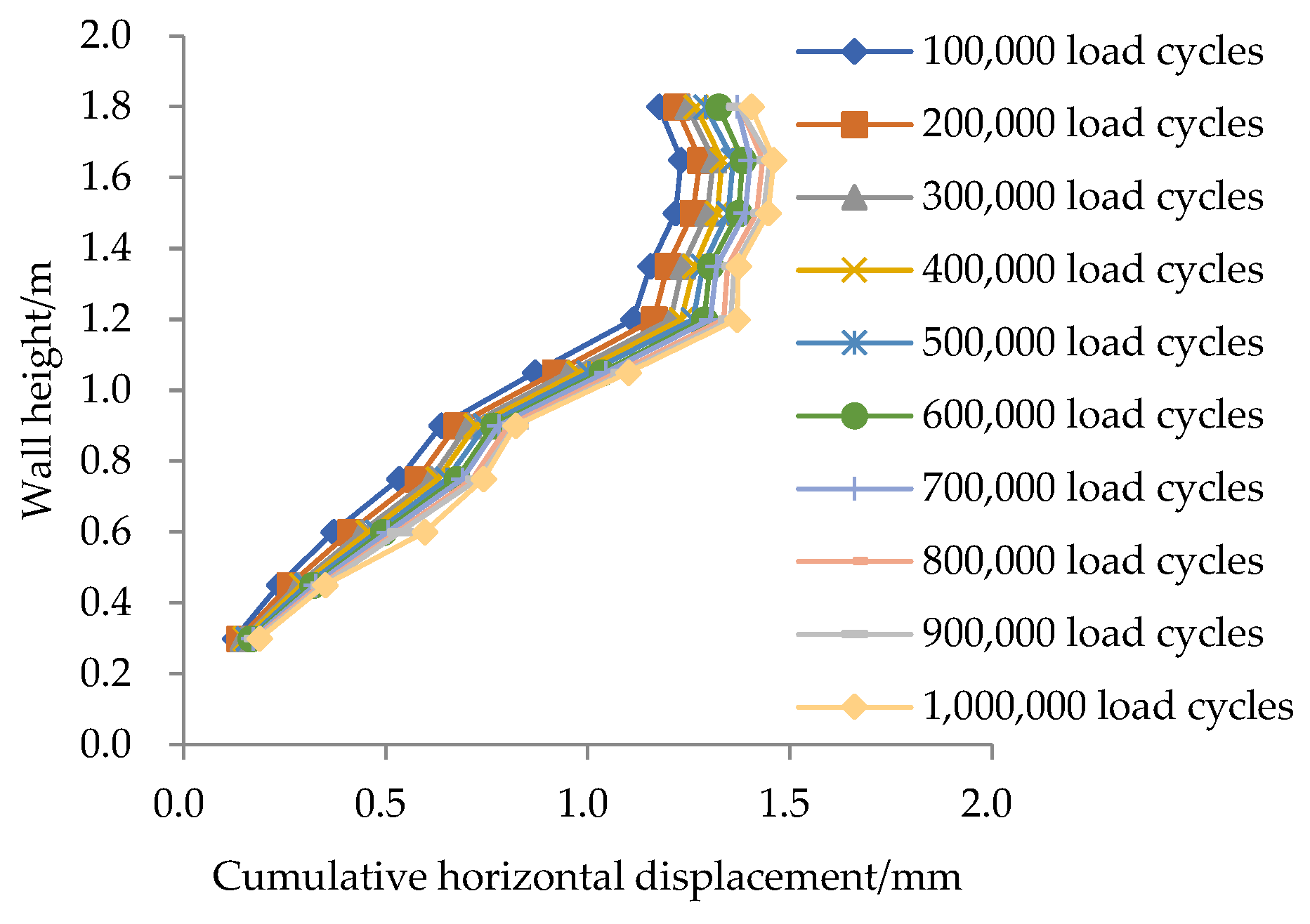
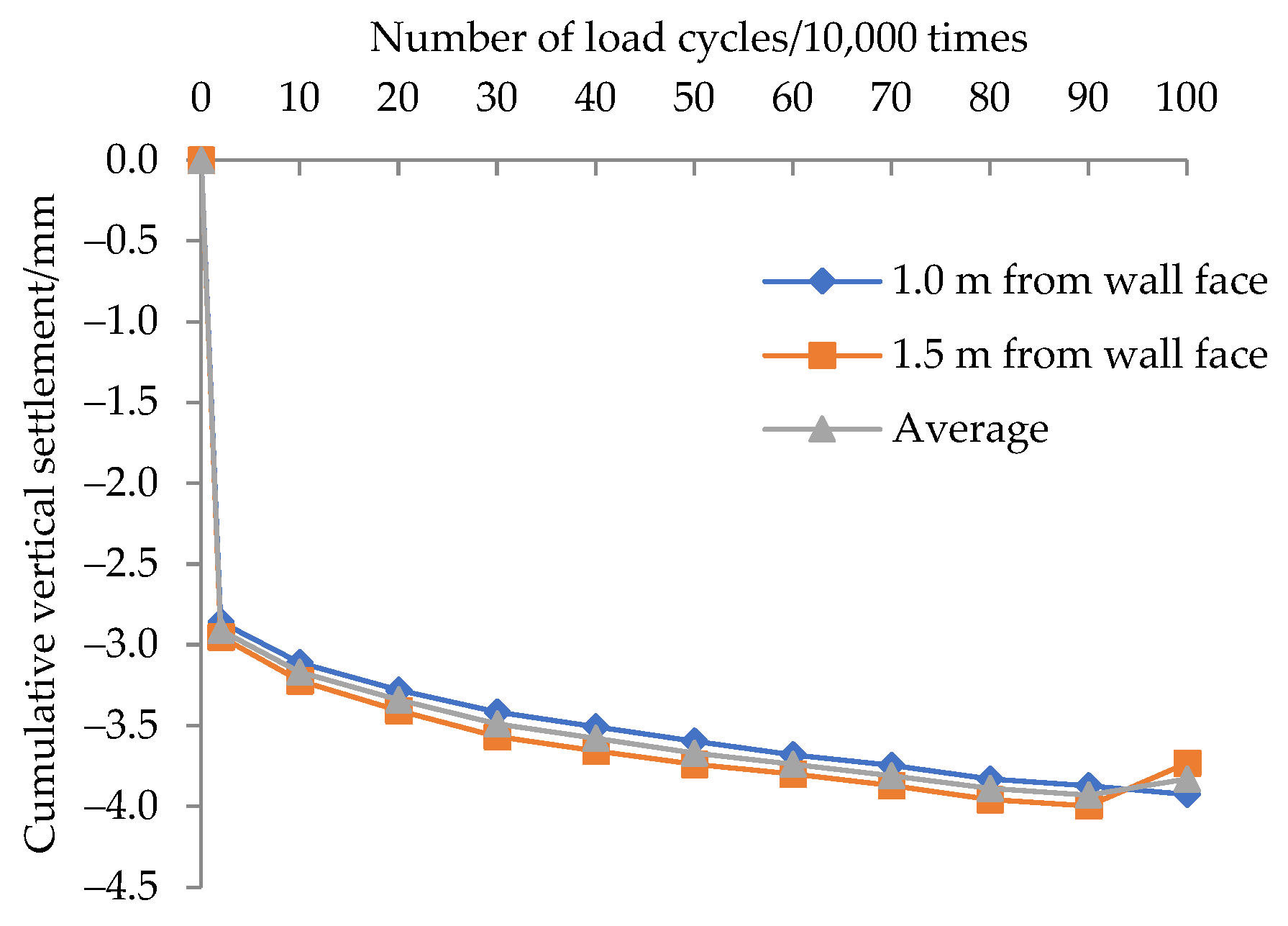
3.1. Deformation
- Settlement induced by one dimensional compression of the reinforced soil;
- Settlement induced by horizontal displacement of the wall.
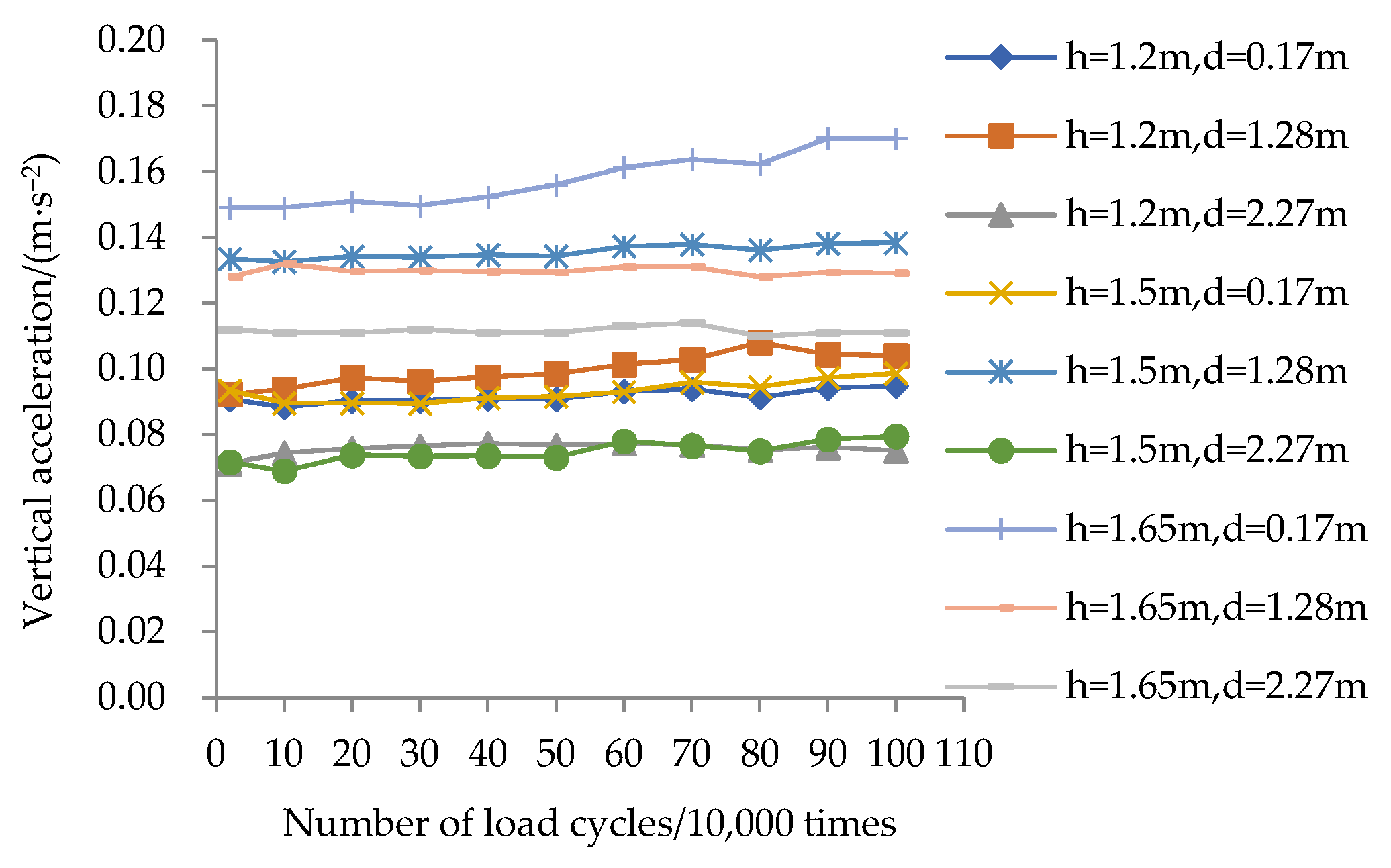
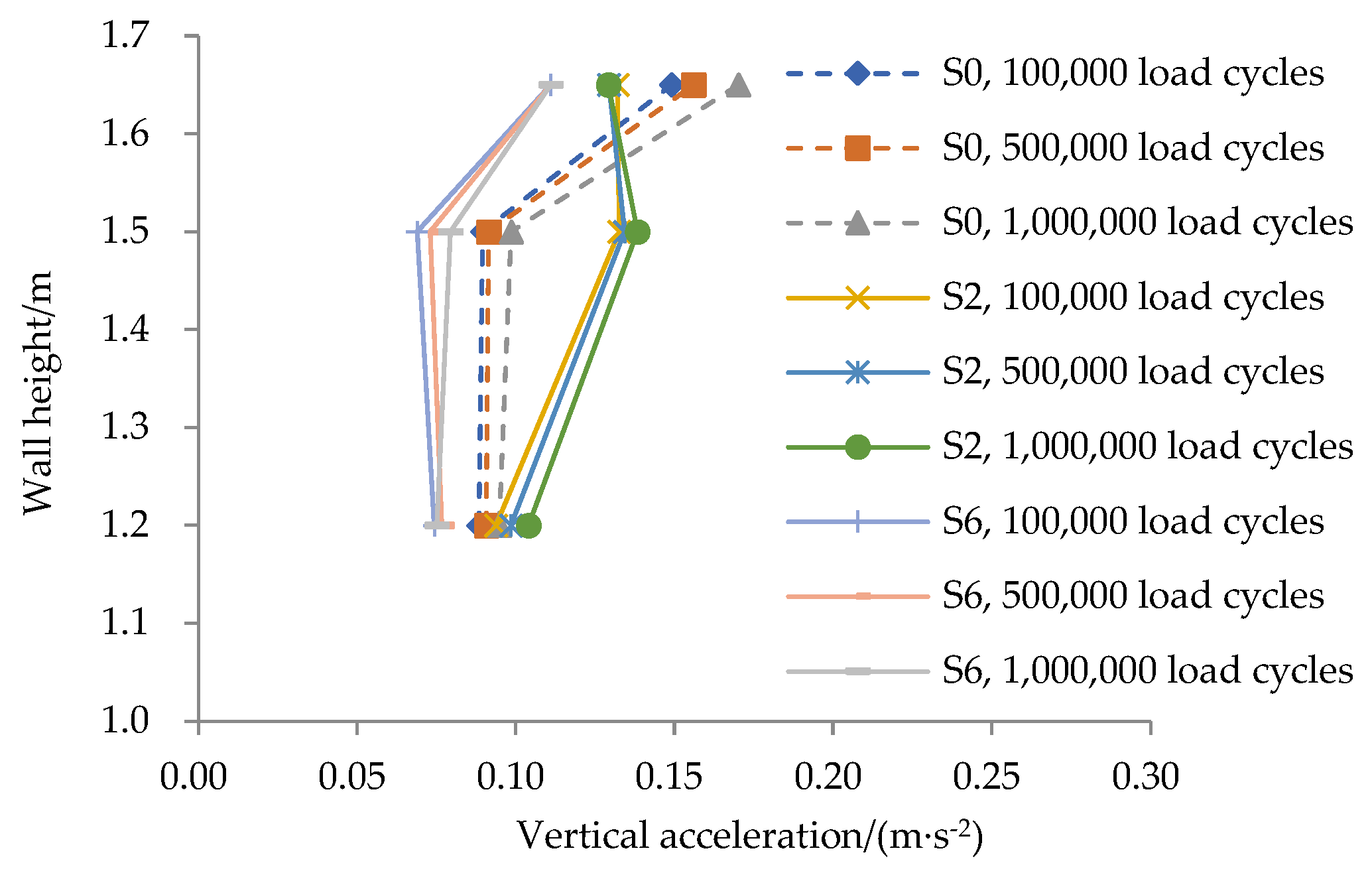
3.2. Vertical Acceleration
- Attenuation is slower at the load center section (S2).
- Attenuation is more rapid in regions located farther from the load center, particularly near the back of the panel (S0) and the rear of the WRSZ (S6).
- Accelerations within the WRSZ (S0 and S2) converge to 0.09–0.10 m/s2.
- Accelerations in the non-WRSZ (S6) are lower, ranging from 0.074 to 0.077 m/s2, thereby confirming the enhanced stiffness provided by the reinforced soil.
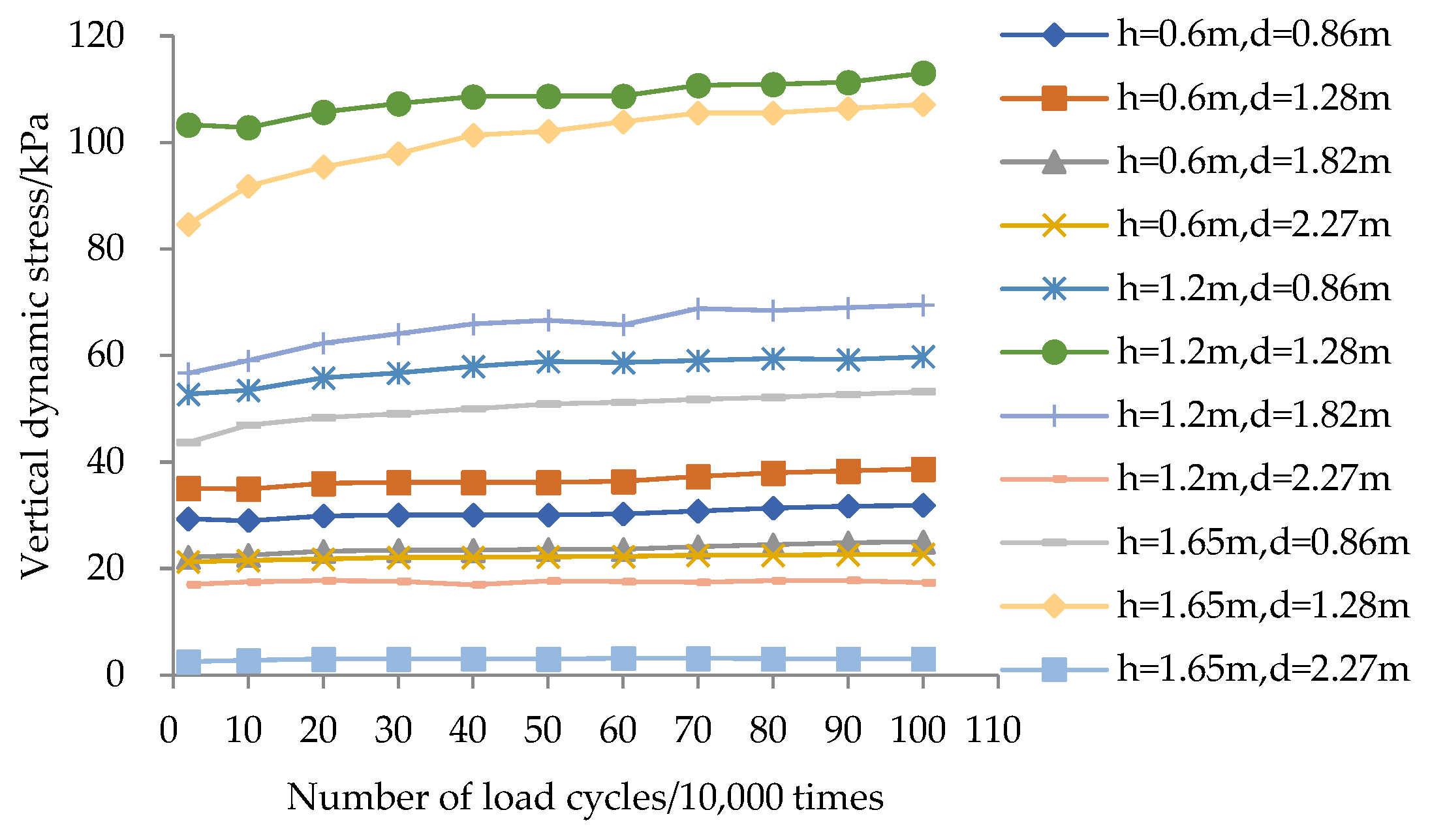
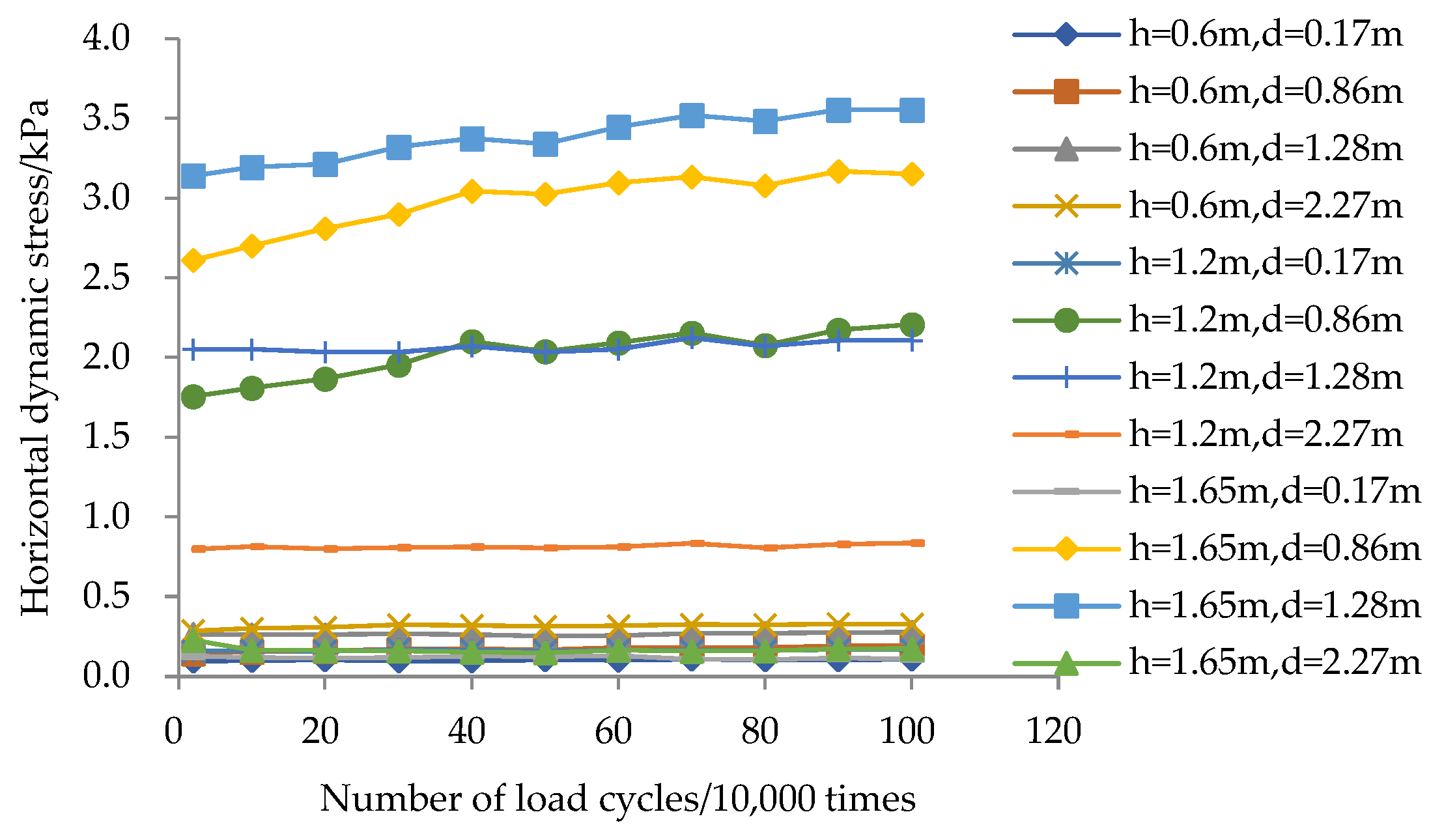
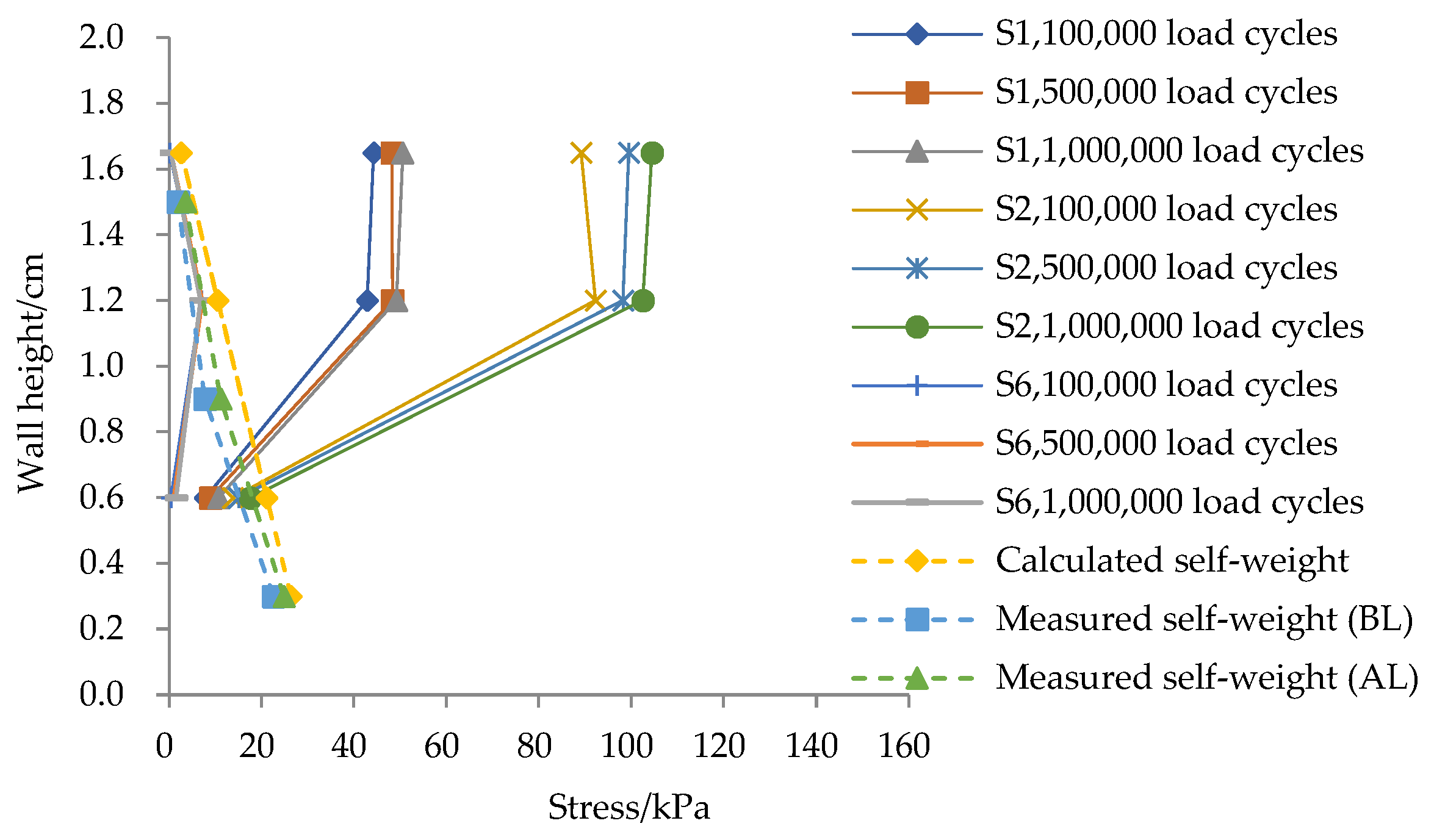
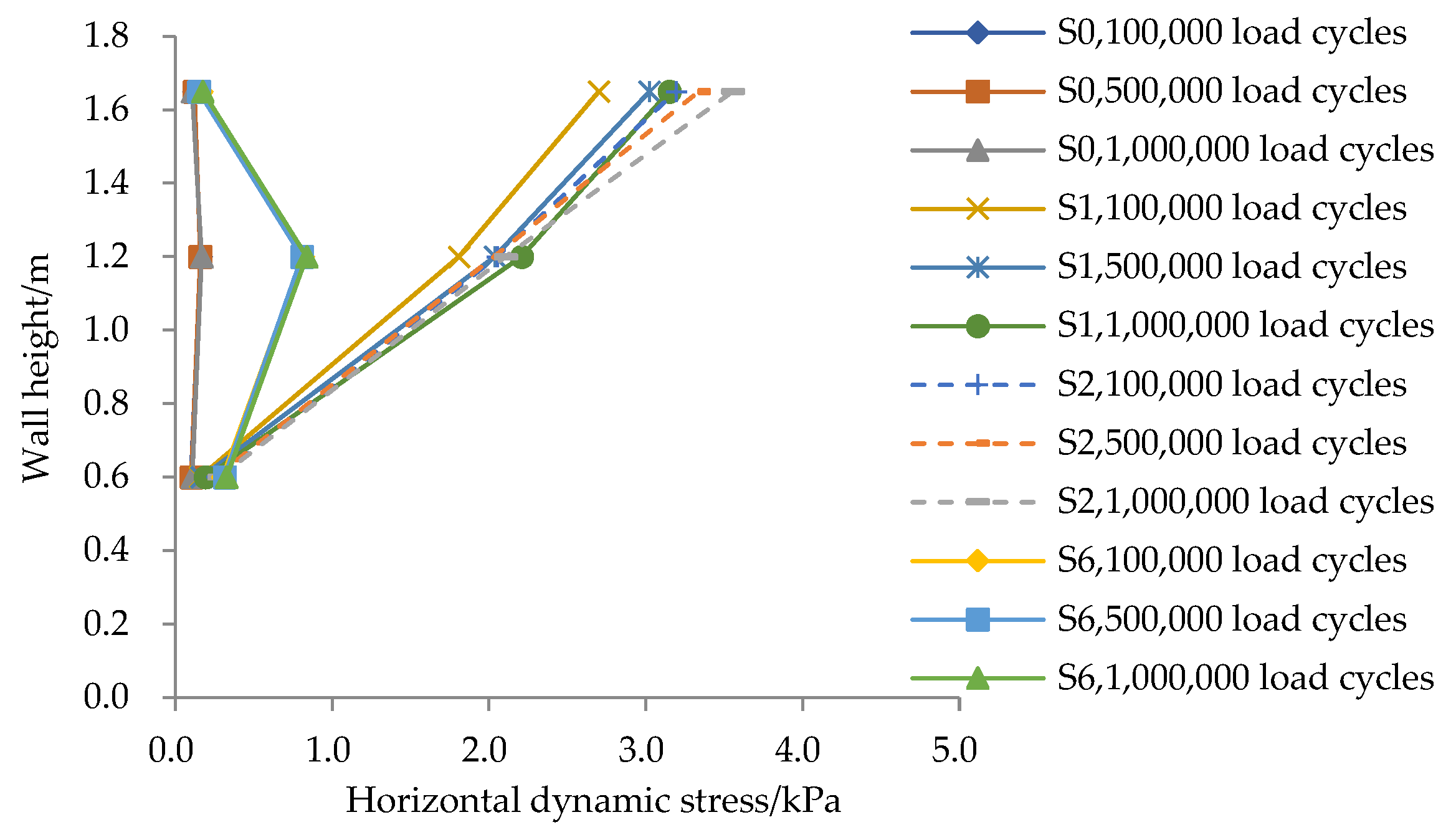
3.3. Soil Stress
- At sections near the loading position (S1 and S2), the vertical dynamic stress remains nearly constant in the upper wall (higher elevation) and gradually attenuates with depth in the mid-lower wall (lower elevation).
- At the section located farther from the loading position (S6), the vertical dynamic stress follows a non-monotonic trend, initially increasing and subsequently decreasing with depth.
- Near the loading position (S1 and S2), horizontal dynamic stress decreases progressively from higher to lower elevations due to stress diffusion.
- At locations farther from the load (S0 and S6), horizontal dynamic stress initially increases and then decreases along the height of the wall.
- At the back of the panel (S0), horizontal dynamic stress remains minimal and is uniformly distributed across the wall height.
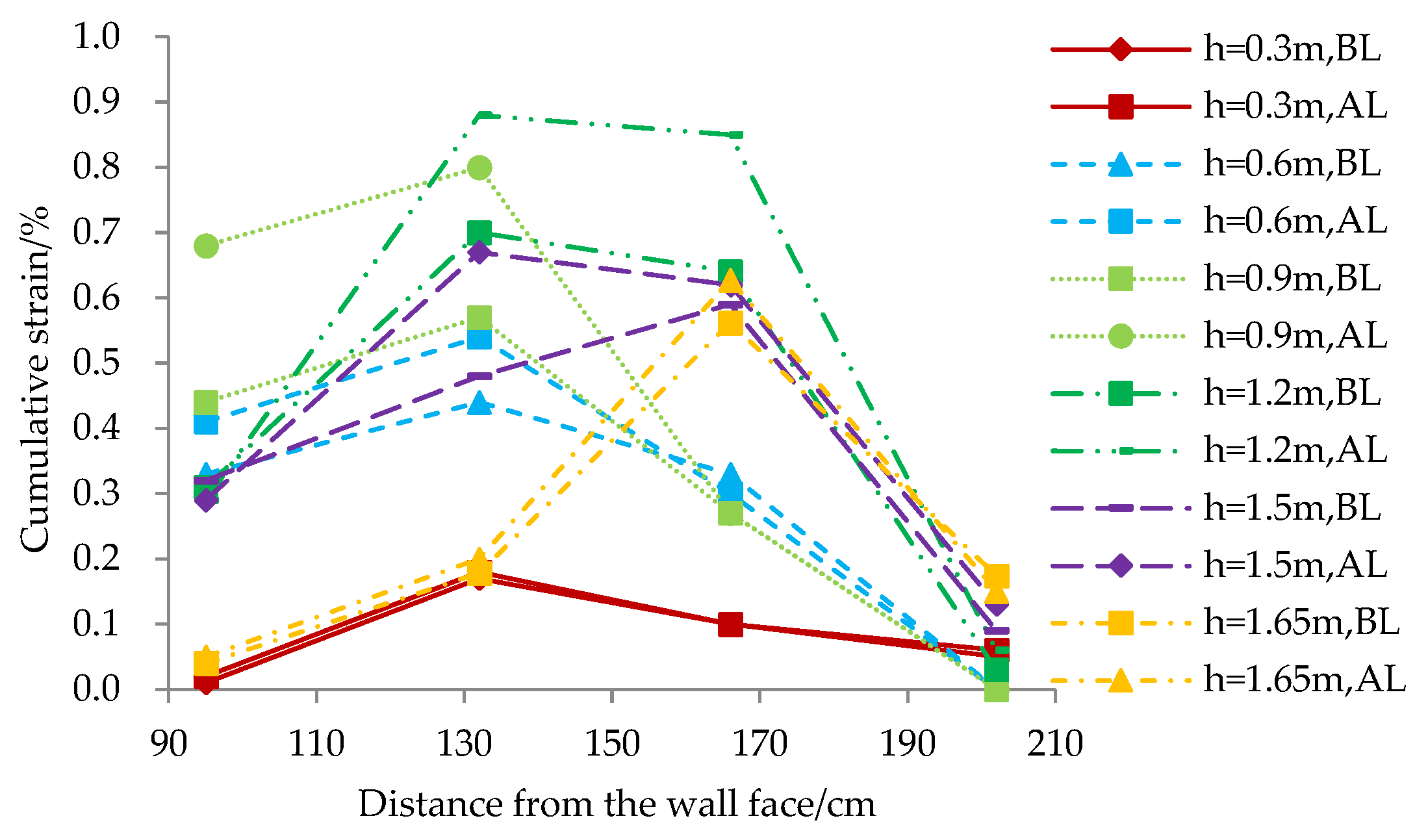
3.4. Geogrid Strain
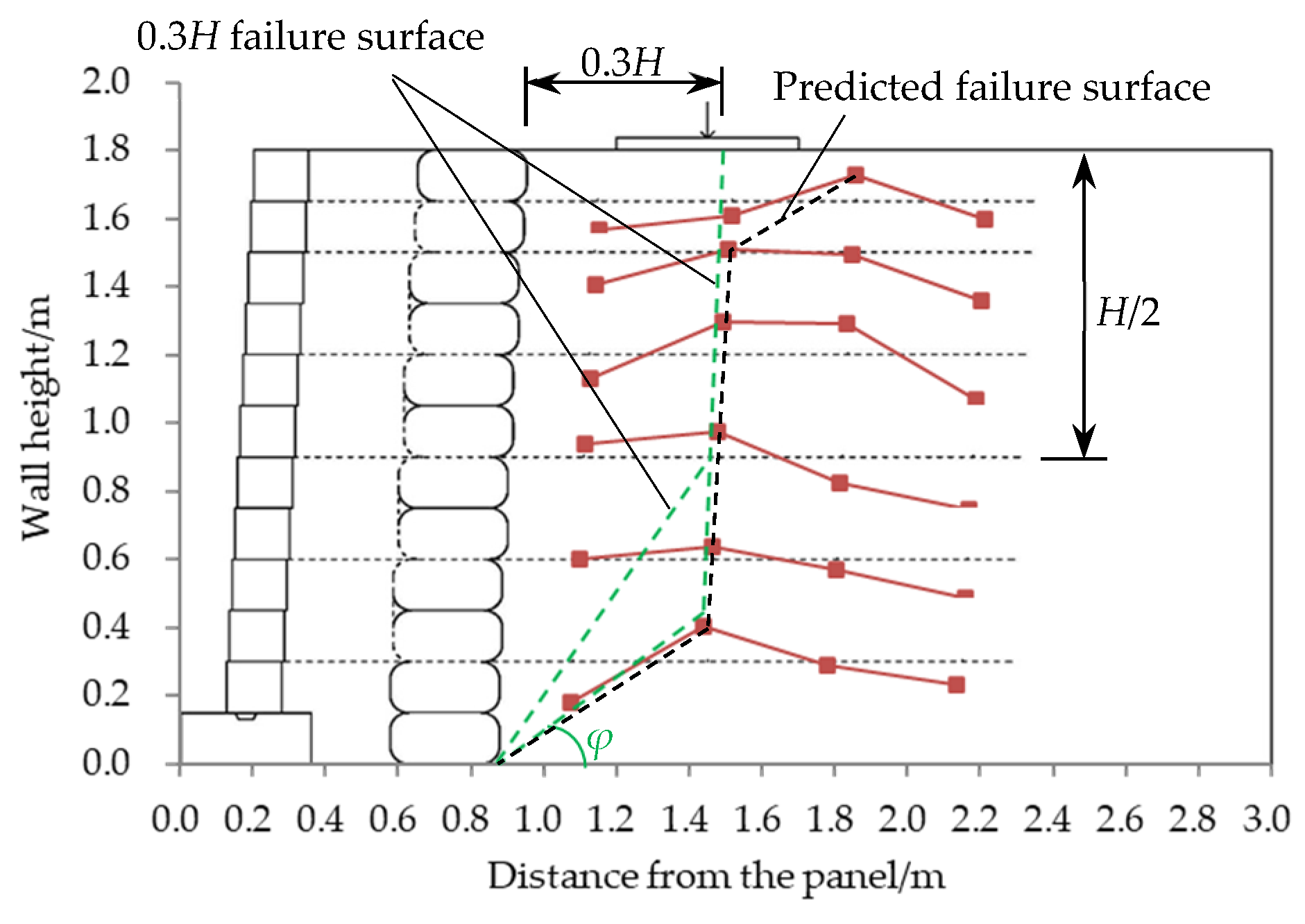
- There is a line parallel to the panel, situated at a distance of 0.3H from the back of the soil bags.
- A second line inclined at an angle equal to the internal friction angle (φ) of the soil relative to the horizontal plane.
- Stress and deformation control: The wrapped structure effectively blocks and homogenizes stress transmission, thereby mitigating strain localization.
- Anti-sliding stability: By intercepting the potential sliding surface passing through the base of the wall, the wrapped system enhances resistance against sliding.
4. Discussion
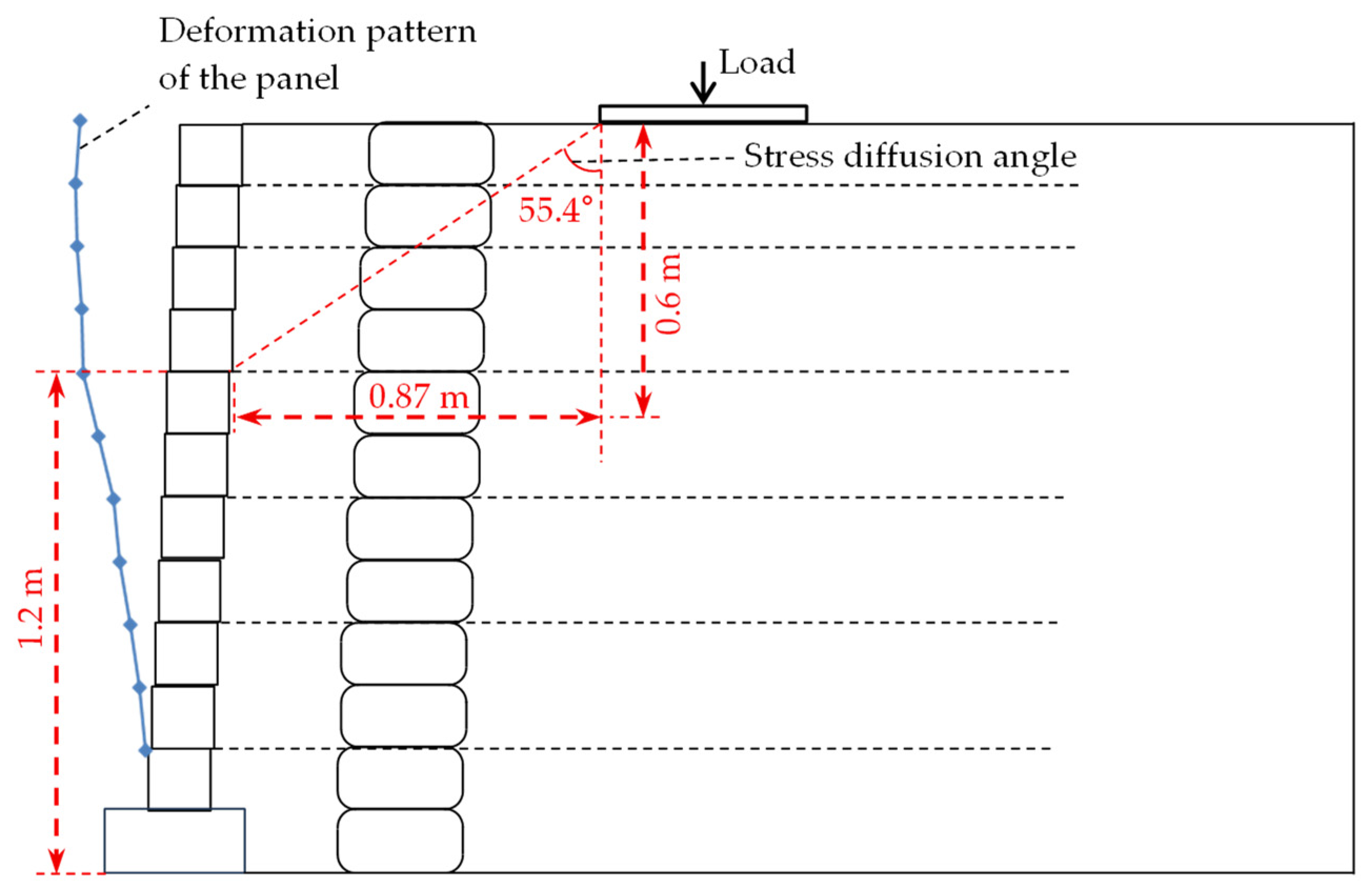
- Reveal the influence of key parameters on concrete-block-panel-wrapped RSW.
- Quantify the stress diffusion angle from computed stress contours precisely.
5. Conclusions
- The horizontal deformation of the panel increases with an increasing number of load cycles and eventually stabilizes, reaching a maximum value of 0.08%H. The deformation progressively increases from the base of the panel to its top. After 20,000 load cycles, deformation growth becomes minimal and relatively uniform along the height of the wall, indicating a stress diffusion angle of 55.4°.
- The maximum average settlement stabilizes at 0.21%H. A significant portion of the total settlement occurs within the first 20,000 load cycles. Beyond this point, settlement increments become negligible, accounting for only 24.02% of the total settlement.
- The vertical acceleration increases marginally with an increasing number of load cycles, with a maximum increment of 0.02 m/s2. The attenuation of the vertical acceleration is slower at the section corresponding to the load center, while it proceeds more rapidly at the sections located behind both the panel and the WRSZ. Through these differing attenuation processes, accelerations within the reinforced zone converge and remain lower than those in the non-reinforced zone.
- Both vertical and horizontal dynamic stresses increase and subsequently stabilize with continued cyclic loading. The decay pattern of vertical dynamic stress aligns with Boussinesq analytical solutions for foundation soils, confirming elastic behavior. The vertical and horizontal dynamic stresses gradually decrease on the vertical sections within the range of load application, and they show a trend of first increasing and then decreasing on the vertical sections outside the range of load application. The horizontal dynamic stress acting on the back of the panel remains low and uniformly distributed. Measured self-weight stress increases during loading but remains below analytically calculated values.
- The cumulative strain of the geogrid exhibits a single-peak distribution along the reinforcement length, with a maximum value of 0.88%, corresponding to maximum tensile stress reaching 20.33% of the geogrid’s ultimate tensile strength. The predicted failure surface approximates a bilinear configuration, comprising a line parallel to the wall face located 0.3H behind the soil bags and a second line inclined at an angle equal to the soil’s internal friction angle (φ) relative to the horizontal plane.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RSW | Reinforced soil retaining wall |
| WRSZ | Wrapped reinforced soil zone |
| HDPE | High-density polyethylene |
| BL | Before loading |
| AL | After loading |
References
- Aalami, M.R.; Anari, A.; Shafighfard, T.; Talatahari, S. A robust finite element analysis of the rail-wheel rolling contact. Adv. Mech. Eng. 2013, 5, 272350. [Google Scholar] [CrossRef]
- Augusto, M.; Felipe, L.; Federico, F. Mechanically Stabilized Earth (MSE) retaining wall at hotel in Bariloche City. E3S Web Conf. 2024, 569, 23004. [Google Scholar] [CrossRef]
- Cai, F. Finite element modeling of mechanical behavior of geogrid reinforced soil retaining walls. Proc. Indian Natl. Sci. Acad. 2025, 91, 484–497. [Google Scholar] [CrossRef]
- Kilic, I.E.; Cengiz, C.; Edincliler, A.; Guler, E. Seismic behavior of geosynthetic-reinforced retaining walls backfilled with cohesive soil. Geotext. Geomembr. 2021, 49, 1256–1269. [Google Scholar] [CrossRef]
- Li, S.H.; Cai, X.G.; Xu, H.L.; Jing, L.P.; Huang, X.; Zhu, C. Dynamic behaviour of reinforced soil retaining wall under horizontal seismic loading. IOP Conf. Ser. Earth Environ. Sci. 2020, 569, 012001. [Google Scholar] [CrossRef]
- Xu, P.; Hatami, K.; Jiang, G.L. Shaking table performance of reinforced soil retaining walls with different facing configurations. Geotext. Geomembr. 2021, 49, 516–527. [Google Scholar] [CrossRef]
- Hossain, M.Z.; Hore, R.; Ansary, M.A. Model tests of reinforced soil retaining sand walls by shaking table test. Arab. J. Geosci. 2024, 17, 166. [Google Scholar] [CrossRef]
- Cai, B.Y.; Cai, X.G.; Li, S.H.; Huang, X.; Zhang, Y.; Xiao, C.Z. Experimental study of shaking table for reinforced soil retaining walls: Analysis of tiered configuration effects. Soil Dyn. Earthq. Eng. 2025, 188 Pt B, 109076. [Google Scholar] [CrossRef]
- Xu, L.; Ling, H.I. Centrifuge modeling and numerical analysis of reinforced soil retaining walls with concrete block facing. Transp. Infrastruct. Geotechnol. 2020, 7, 405–425. [Google Scholar] [CrossRef]
- Mirmoradi, S.H.; Ehrlich, M. Effect of facing stiffness on reinforced soil walls under surcharge loading-unloading. Int. J. Phys. Model. Geotech. 2025, 25, 2–16. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, J.F. Numerical modeling of geosynthetic reinforced soil retaining walls with different toe restraint conditions. Geotext. Geomembr. 2023, 51, 16–29. [Google Scholar] [CrossRef]
- Kim, Y.J.; Jung, H.S.; Lee, Y.J.; Oh, D.W.; Son, M.; Yoon, H.H. Behaviour analysis of reinforced soil retaining wall according to laboratory scale test. Appl. Sci. 2020, 10, 901. [Google Scholar] [CrossRef]
- Zhu, Y.L.; Zhan, Z.J.; Hong, Y.; Guo, P.P.; He, M.; Chen, R.Y. Experimental study on mechanical and deformation characteristics of geogrid-reinforced soil retaining walls. Int. J. Geosynth. Ground Eng. 2024, 10, 74. [Google Scholar] [CrossRef]
- Bhattacharjee, A.; Amin, M.U. Behaviour of Two-Tiered Geosynthetic-Reinforced Soil Walls. INAE Lett. 2019, 4, 91–100. [Google Scholar] [CrossRef]
- Gao, S.; Xiao, C.Z.; Han, J.; Wang, Z.H. Lateral displacements of geosynthetic-reinforced soil walls in a tiered configuration. J. Geotech. Geoenviron. Eng. 2022, 148, 04022066. [Google Scholar] [CrossRef]
- Hulagabali, A.M.; Solanki, C.H.; Dodagoudar, G.R.; Anitha, N. Finite Element Analysis of Segmental Precast Concrete Panel Reinforced Earth Retaining Wall. Jordan J. Civ. Eng. 2023, 17, 582–597. [Google Scholar] [CrossRef]
- Hulagabali, A.M.; Solanki, C.H.; Dodagoudar, G.R.; Anitha, N. Seismic Internal Stability Analysis of Modular Block Reinforced Earth Retaining Wall. Int. J. Geosynth. Ground Eng. 2023, 9, 31. [Google Scholar] [CrossRef]
- Liu, H.B.; Wang, C.H.; Wang, L. Analyzing operational reinforcement loads of geosynthetic-reinforced soil retaining walls based on plasticity theory. Zhongguo Kexue Jishu Kexue/Sci. Sin. Technol. 2022, 52, 1083–1095. [Google Scholar] [CrossRef]
- Lu, L.; Chen, B.; Liu, P.; Wang, Z.J.; Arai, K. Seismic time-history analysis of block-faced reinforced-soil retaining wall based on pseudo-dynamic method. Geotext. Geomembr. 2024, 52, 494–510. [Google Scholar] [CrossRef]
- Ren, F.F.; Huang, Q.Q.; Zhang, F.; Wang, G. Numerical study on seismic performance of tiered reinforced soil retaining walls. Soil Dyn. Earthq. Eng. 2024, 181, 108672. [Google Scholar] [CrossRef]
- Hore, R.; Chakraborty, S.; Shuvon, A.M.; Bari, M.F.; Ansary, M.A. Dynamic response of reinforced soil retaining wall resting on soft clay. Transp. Infrastruct. Geotechnol. 2021, 8, 607–628. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| Internal friction angle/(°) | 36.6 |
| Maximum dry density/(g·cm−3) | 1.76 |
| Water Content/% | 0 |
| Parameter | Value |
|---|---|
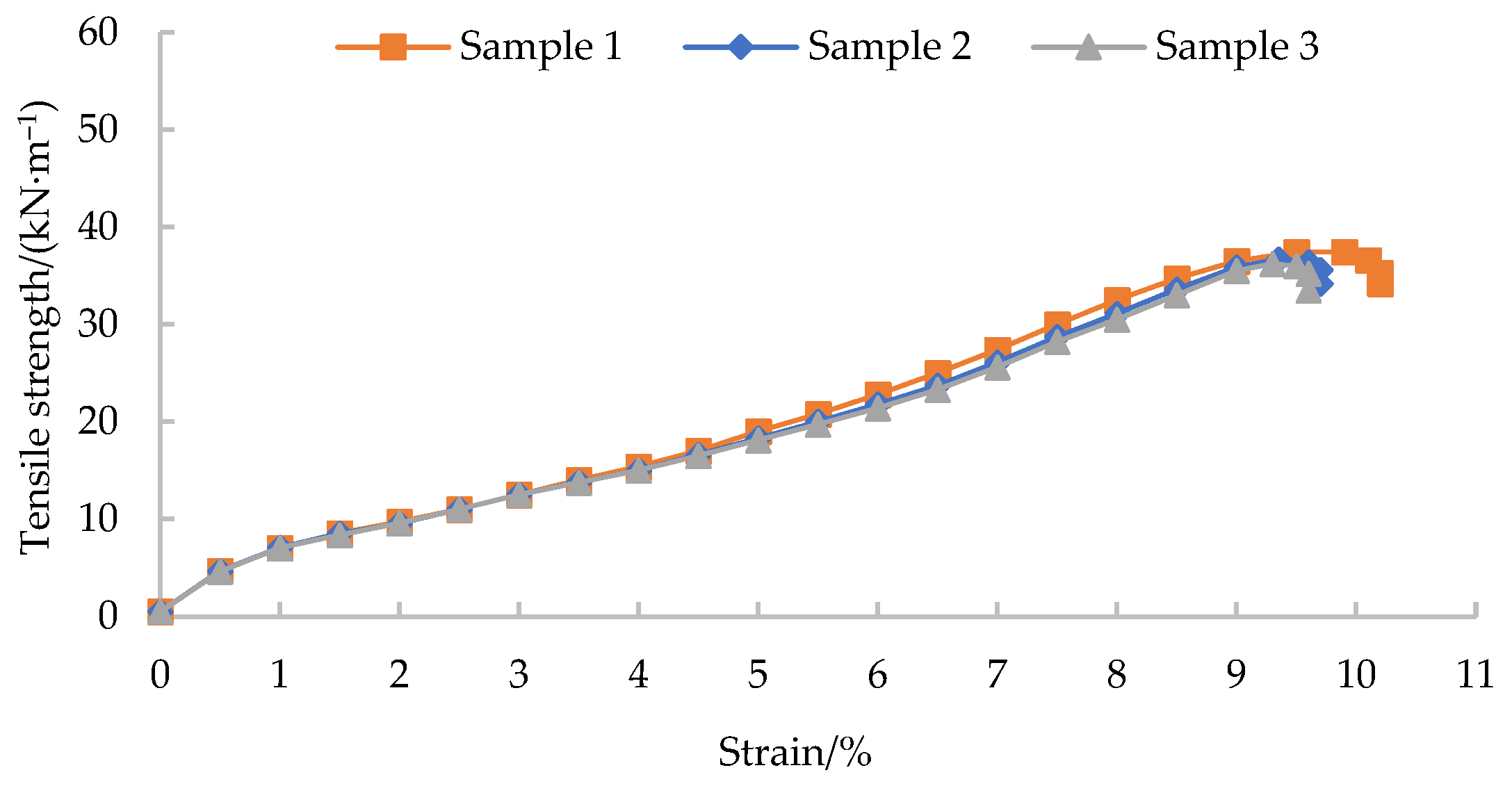
| Tensile strength/(kN·m−1) | 36.79 |
| Tensile strength at 2% strain/(kN·m−1) | 9.45 |
| Tensile strength at 5% strain/(kN·m−1) | 17.74 |
| Maximum strain/% | 9.8 |
| Sensor | Range | Accuracy |
|---|---|---|
| Dynamic soil pressure cell | 0.3 MPa | 1‰ FS (Full Scale) |
| Displacement meter | 50 mm | 0.01 mm |
| Static soil pressure cell | 0.3 MPa | 0.1% FS |
| Accelerometer | ±2 g | 0.1% FS |
| Strain gauge | 50 mm | 0.5% FS |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Zhou, X.; Song, Z.; Wang, H. Study on the Dynamic Responses of a Concrete-Block-Panel-Wrapped Reinforced Soil Retaining Wall: A Model Test. Buildings 2025, 15, 3797. https://doi.org/10.3390/buildings15203797
Xu J, Zhou X, Song Z, Wang H. Study on the Dynamic Responses of a Concrete-Block-Panel-Wrapped Reinforced Soil Retaining Wall: A Model Test. Buildings. 2025; 15(20):3797. https://doi.org/10.3390/buildings15203797
Chicago/Turabian StyleXu, Jiannan, Xiancai Zhou, Zhiwen Song, and He Wang. 2025. "Study on the Dynamic Responses of a Concrete-Block-Panel-Wrapped Reinforced Soil Retaining Wall: A Model Test" Buildings 15, no. 20: 3797. https://doi.org/10.3390/buildings15203797
APA StyleXu, J., Zhou, X., Song, Z., & Wang, H. (2025). Study on the Dynamic Responses of a Concrete-Block-Panel-Wrapped Reinforced Soil Retaining Wall: A Model Test. Buildings, 15(20), 3797. https://doi.org/10.3390/buildings15203797






