Machine Learning-Based Rapid Assessment of Story-Level Seismic Damage in Steel Bundled-Tube Structures
Abstract
1. Introduction
2. Steel Bundled-Tube Story-Level Damage Dataset
2.1. Establishment of the Steel Bundled-Tube Model
2.2. Verification of Model Accuracy
2.3. Assessment of Story-Level Damage States
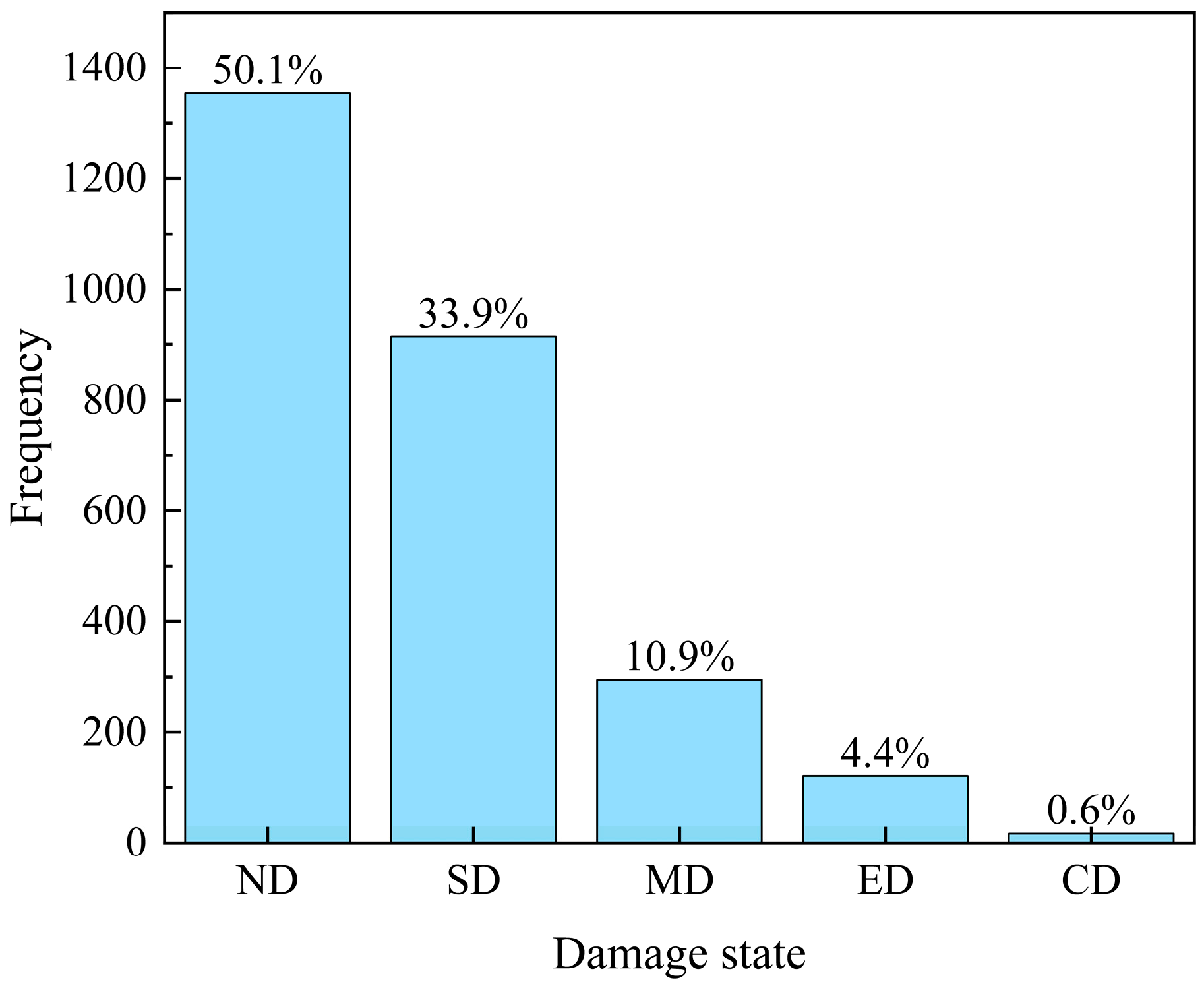
2.4. Construction of the Dataset
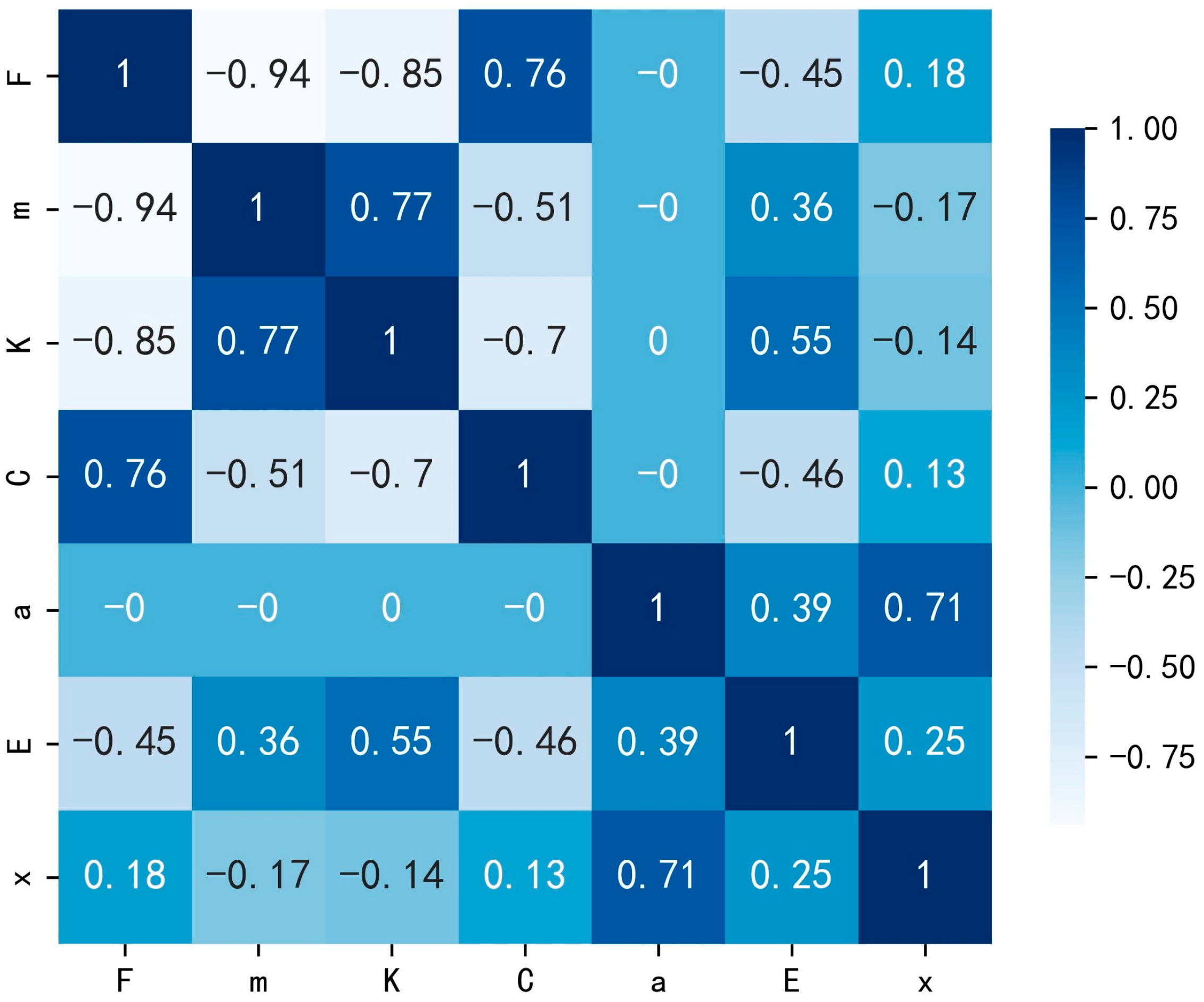
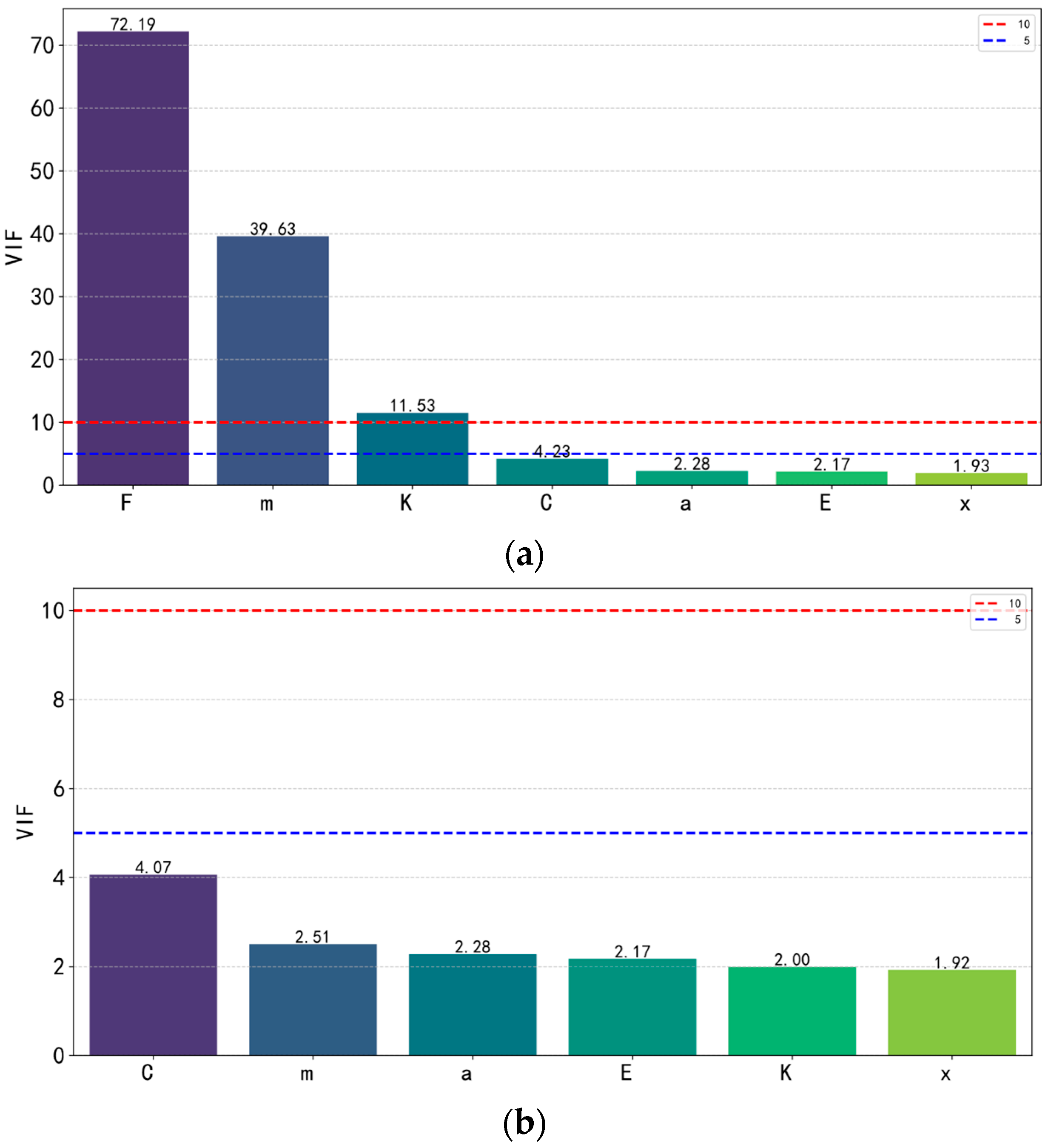
2.5. Optimization of the Dataset
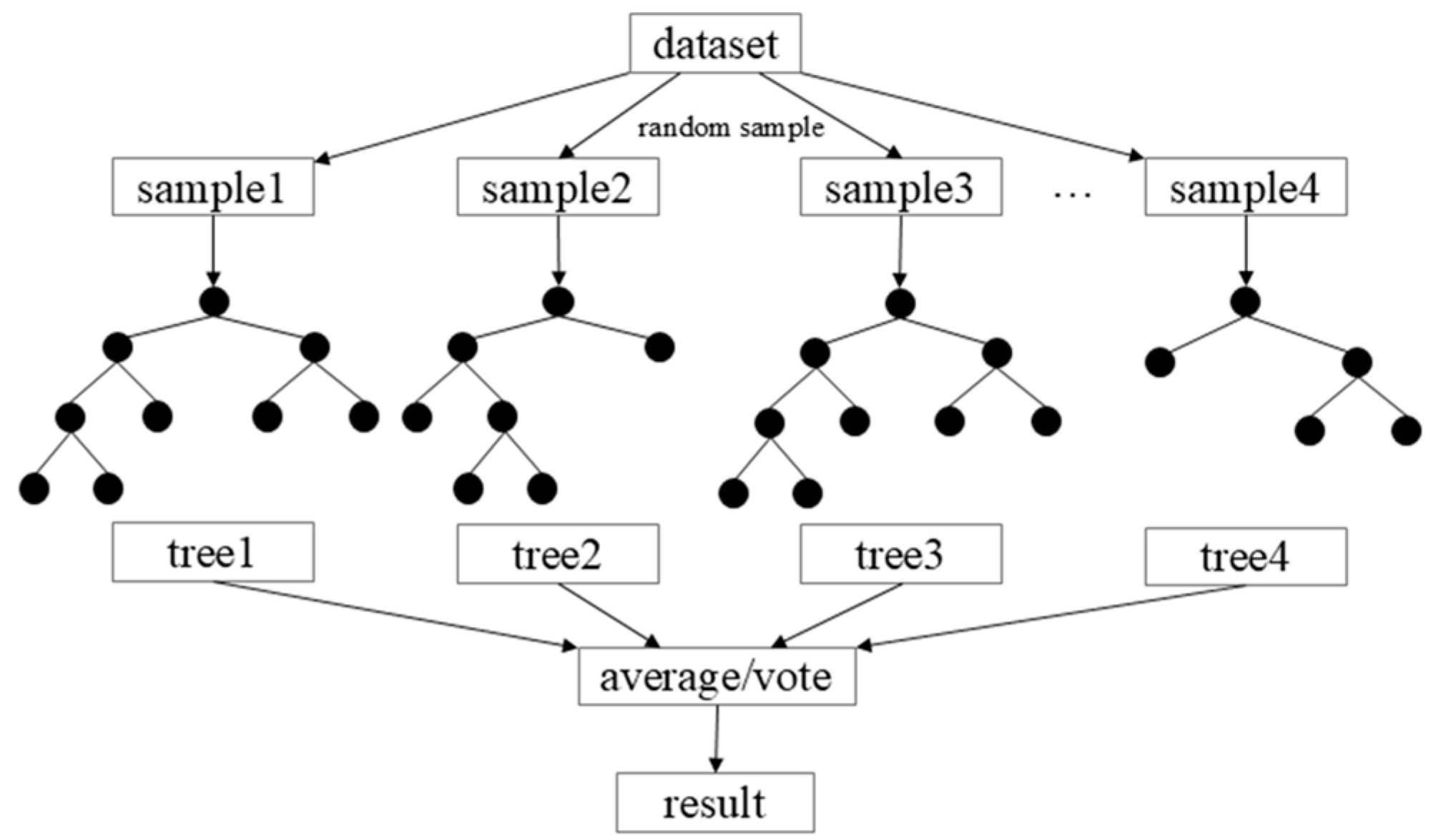
3. Machine Learning Algorithms
3.1. Principles of Machine Learning
3.2. Machine Learning Model Training
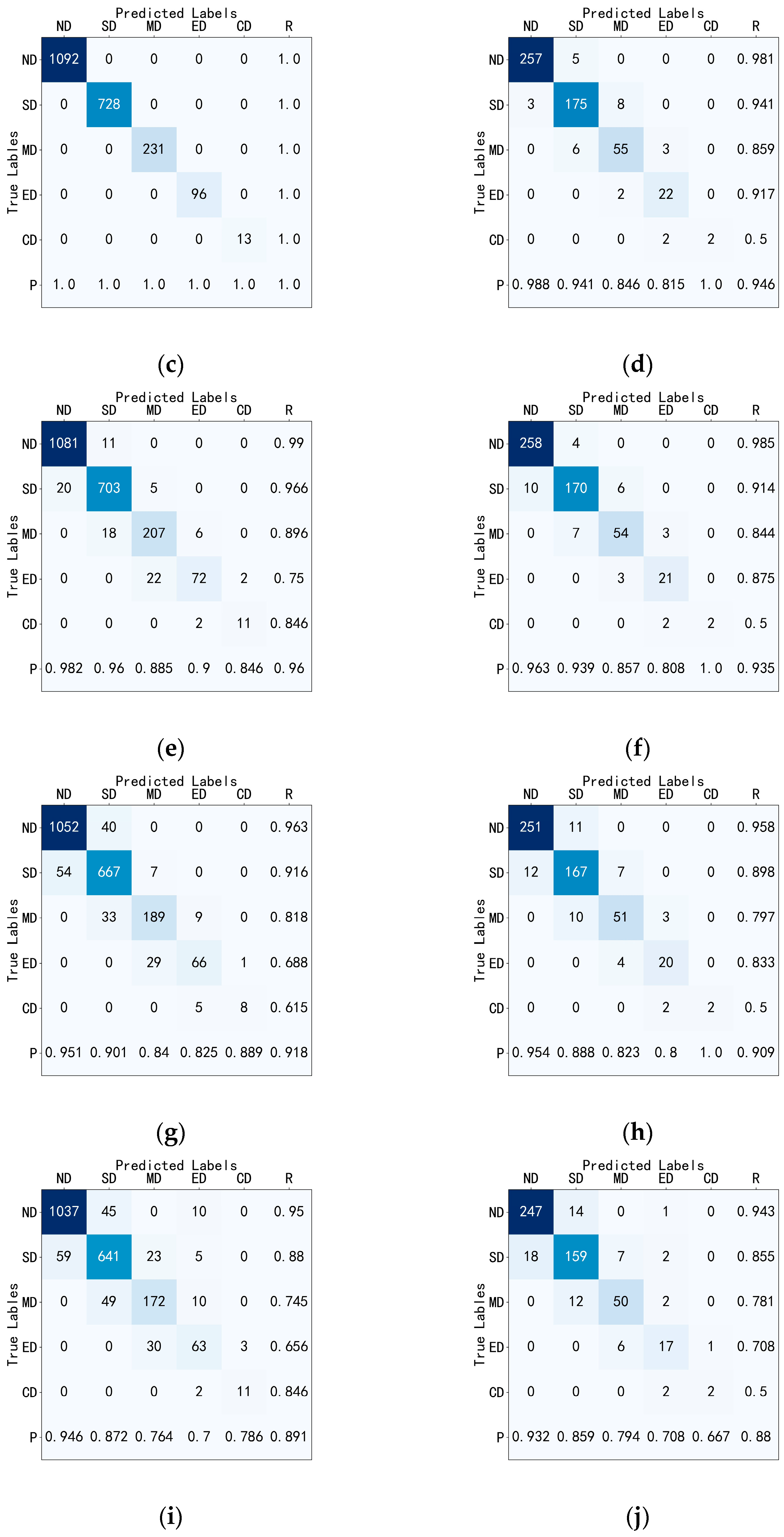
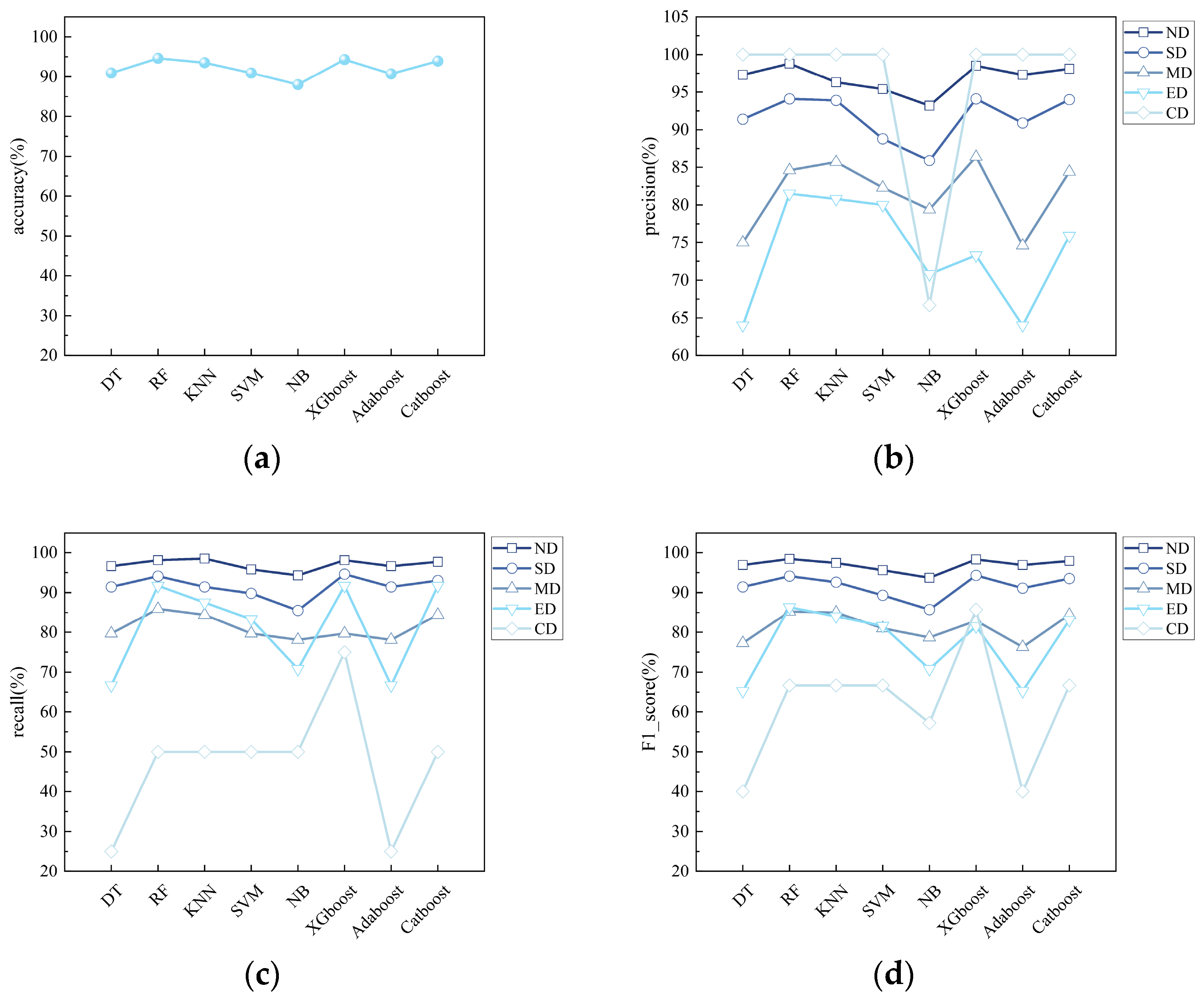
4. Machine Learning Performance Comparison
4.1. Machine Learning Evaluation Metrics
4.2. Analysis of Prediction Results
5. Hyperparameter Optimization
5.1. Fundamentals of Bayesian Optimization
5.2. Model Optimization Process
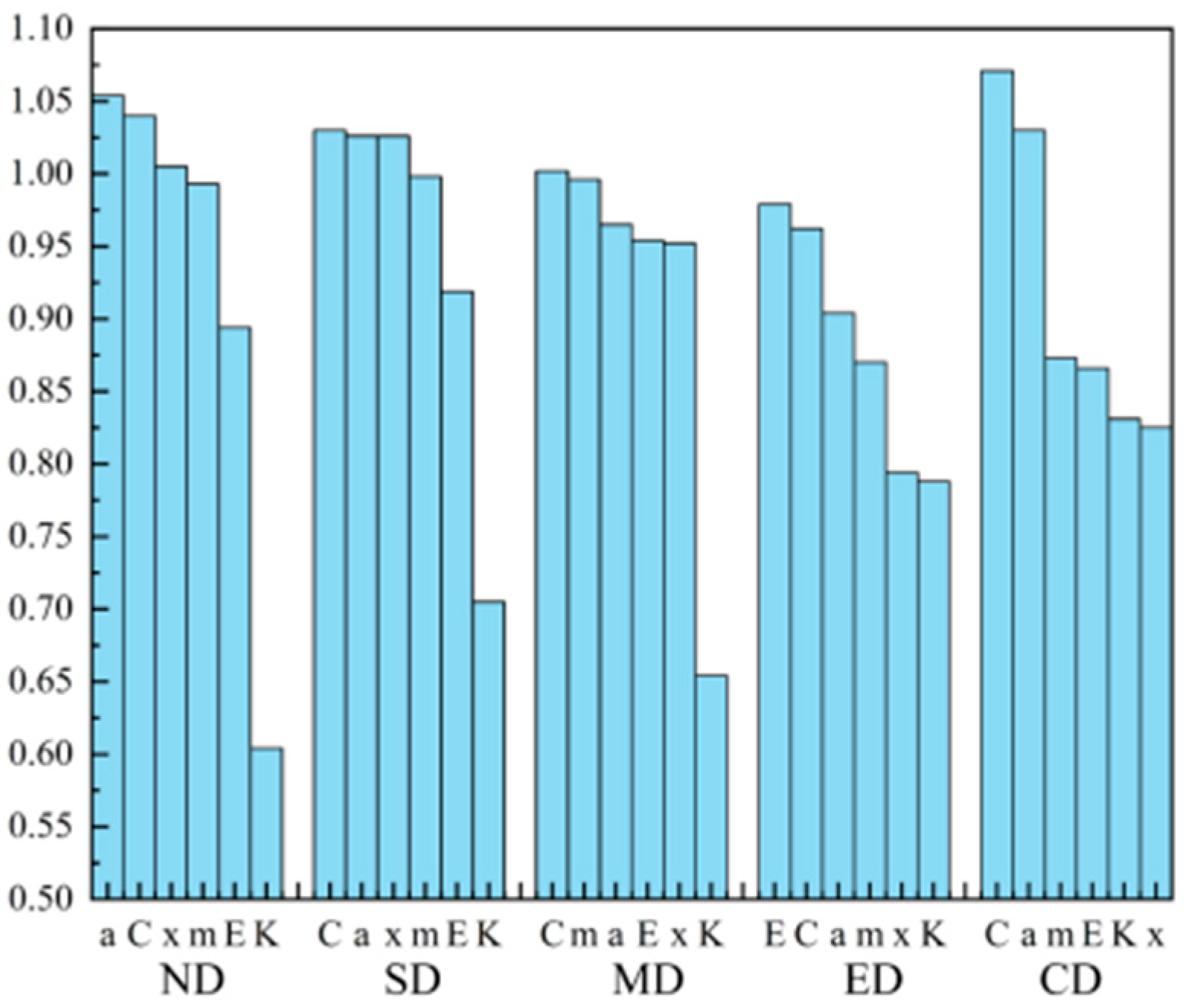
6. Feature Importance Analysis
6.1. Analysis of Feature Importance Using SHAP
- (1)
- Peak acceleration and story load-bearing capacity have larger coefficients of characteristic importance in all damage states, indicating that their contributions to the damage state assessment are always larger, and they are the core variables affecting the damage state assessment. The reason is twofold: peak acceleration directly reflects seismic intensity and destructive force, while story load-bearing capacity is a critical index for ensuring structural safety.
- (2)
- The relatively low coefficient of importance of the story stiffness feature for all damage states indicates that its contribution to the damage state assessment is small, which is attributed to the fact that there is not much difference in the stiffness of the stories, and the overall distribution of the stiffness is more homogeneous.
- (3)
- In assessing the ND and SD states, the maximum story displacement is more important than the story energy consumption. However, in assessing the MD, ED, and CD damage states, the story energy consumption is more important than the maximum story displacement. It is shown that displacement has a more significant effect when assessing low damage states, but not as significant as energy consumption when assessing high damage states. This is because the destruction of a structure is due to the accumulation of energy in excess of its capacity to carry and dissipate energy. Displacement is merely an indirect means and cannot fully and accurately reflect the real causes and processes of structural failure, which provides a theoretical basis for energy-based seismic design.
6.2. Engineering Implications and Design Takeaways
7. Conclusions
- (1)
- When the machine learning models use the original parameters, the accuracies of RF and XGBoost rank among the top two, reaching 94.6% and 94.3%, respectively. Moreover, when evaluating the five damage states, their precision, recall, and F1_score are also ranked relatively high. After optimization, the XGBoost model improved by 2.2% and outperformed the optimized RF model, achieving an accuracy of 96.5%. Therefore, it is recommended to use the XGBoost model optimized by Bayesian optimization as the final prediction model.
- (2)
- Since the steel bundled-tube structure is an efficient lateral force-resistant structure, there is limited data available for high-damage states. In subsequent studies, data on high-damage states can be specifically supplemented, or the synthetic minority over-sampling technique (SMOTE) can be used to expand the dataset to improve the accuracy of the evaluation model in assessing high-damage states.
- (3)
- When evaluating the damage state of stories, attention should be focused on the core variables (peak acceleration and story load-bearing capacity). If the calculation volume is too large and the structural stiffness is uniformly distributed, the story stiffness may not be considered.
- (4)
- Displacement significantly impacts low-damage states (ND, SD), whereas energy consumption becomes dominant in high-damage states (MD, ED, CD). This indicates that there are drawbacks in the traditional seismic design that only focuses on displacement limitations. This conclusion provides theoretical basis and reference value for the energy-based seismic design, and extensive in-depth research on the energy-based seismic design should be carried out.
- (5)
- In engineering applications, this assessment method can be used to quickly locate the weak stories. Then, based on the SHAP analysis results, special reinforcement schemes can be formulated for the weak stories. Ultimately, the systematic optimization of the seismic performance of the steel bundled-tube structure can be achieved.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SHAP | Shapley Additive Explanations |
| RF | Random Forest |
| XGBoost | Extreme Gradient Boosting |
| PCC | Pearson Correlation Coefficient |
| CNN | Convolutional Neural Network |
| ANN | Artificial Neural Network |
| SVR | Support Vector Regression |
| DT | Decision Tree |
| KNN | K-Nearest Neighbors |
| SVM | Support Vector Machine |
| NB | Naive Bayes |
| Adaboost | Adaptive Boosting |
| CatBoost | Categorical Boosting |
| ND | No Damage |
| SD | Slight Damage |
| MD | Moderate Damage |
| ED | Extensive Damage |
| CD | Complete Collapse |
| F | Floor Number |
| m | Story Mass |
| K | Story Stiffness |
| C | Story Load-Bearing Capacity |
| a | Peak Acceleration |
| E | Story Energy Consumption |
| x | Maximum Story Displacement |
| VIF | Variance Inflation Factor |
| SMOTE | Synthetic Minority Over-sampling Technique |
References
- Cheng, S.T.; Han, J.P.; Shang, J.Y. Optimal repair decision and seismic resilience analysis of seismic-damaged RC structures considering rebar corrosion. J. Build. Eng. 2025, 112, 113749. [Google Scholar] [CrossRef]
- Hu, B.B.; Li, S.; Hou, Z.X.; Zhai, C.H. A practical method for functional recovery analysis based on seismic resilience assessment of city building portfolios. J. Build. Eng. 2024, 95, 110304. [Google Scholar] [CrossRef]
- Ali, S.R.; Morteza, R.D.; Mahdi, E.; Delbaz, S. Seismic resilience evaluation of confined masonry school buildings retrofitted by shotcrete method. Soil Dyn. Earthq. Eng. 2024, 187, 108980. [Google Scholar] [CrossRef]
- Lu, J.F.; Li, Z.H.; Teng, J. Seismic resilience assessment for reinforced concrete frame structural systems based on complex network considering repair paths. Structures 2025, 77, 109072. [Google Scholar] [CrossRef]
- Tsuchimoto, K.; Narazaki, Y.; Spencer, B.F. Development and Validation of a Post-Earthquake Safety Assessment System for High-Rise Buildings Using Acceleration Measurements. Mathematics 2021, 9, 1758. [Google Scholar] [CrossRef]
- Ogunjinmi, P.D.; Park, S.S.; Kim, B.; Lee, D. Rapid Post-Earthquake Structural Damage Assessment Using Convolutional Neural Networks and Transfer Learning. Sensors 2022, 22, 3471. [Google Scholar] [CrossRef]
- Feng, D.C.; Yi, X.; Deger, Z.T.; Liu, H.; Chen, S.; Wu, G. Rapid Post-Earthquake Damage Assessment of Building Portfolios Through Deep Learning-Based Component-Level Image Recognition. J. Build. Eng. 2024, 98, 111380. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, Y.; Zhang, R.; Nie, G.; Wang, W. Detection and Assessment of Post-Earthquake Functional Building Ceiling Damage Based on Improved YOLOv8. J. Build. Eng. 2024, 98, 111315. (In Chinese) [Google Scholar] [CrossRef]
- Yu, Q.M.; Yuan, X.; Xu, L.Y. Cross-Material Damage Detection and Analysis for Architectural Heritage Images. Buildings 2025, 15, 3100. [Google Scholar] [CrossRef]
- Zhou, K.; Shi, J.L.; Fu, J.Y.; Zhang, S.X.; Liao, T.; Yang, C.Q.; Wu, J.R.; He, Y.C. An improved YOLOv10 algorithm for automated damage detection of glass curtain-walls in high-rise buildings. J. Build. Eng. 2024, 101, 111812. [Google Scholar] [CrossRef]
- Ling, L.M.; Ma, G.; Hwang, H.J.; Tan, X.J. Post-earthquake detection of surface spalling and cracks in masonry buildings based on computer vision. Structures 2025, 78, 109226. [Google Scholar] [CrossRef]
- Xu, S.D.; Chen, H.N. Deep learning and digital twin integration for structural damage detection in ancient pagodas. Sci. Rep. 2025, 15, 28408. [Google Scholar] [CrossRef]
- Musella, C.; Serra, M.; Menna, C.; Asprone, D. Building Information Modeling and Artificial Intelligence: Advanced Technologies for the Digitalisation of Seismic Damage in Existing Buildings. Struct. Concr. 2021, 22, 2761–2774. [Google Scholar] [CrossRef]
- Gharehbaghi, S.; Gandomi, M.; Plevris, V.; Gandomi, A.R. Prediction of Seismic Damage Spectra Using Computational Intelligence Methods. Comput. Struct. 2021, 253, 106584. [Google Scholar] [CrossRef]
- Morfidis, K.; Stefanidou, S.; Markogiannaki, O. A Rapid Seismic Damage Assessment (RASDA) Tool for RC Buildings Based on an Artificial Intelligence Algorithm. Appl. Sci. 2023, 13, 5100. [Google Scholar] [CrossRef]
- Zhang, W.; Wen, J.; Dong, H.; Han, Q.; Du, X. Post-Earthquake Functionality and Resilience Prediction of Bridge Networks Based on Data-Driven Machine Learning Method. Soil Dyn. Earthq. Eng. 2024, 190, 109127. [Google Scholar] [CrossRef]
- Oh, B.K.; Jung, W.C.; Park, H.S. Artificial Intelligence-Based Damage Localization Method for Building Structures Using Correlation of Measured Structural Responses. Eng. Appl. Artif. Intell. 2023, 121, 106019. [Google Scholar] [CrossRef]
- Bhatta, S.; Dang, J. Machine Learning-Based Classification for Rapid Seismic Damage Assessment of Buildings at a Regional Scale. J. Earthq. Eng. 2024, 28, 1861–1891. [Google Scholar] [CrossRef]
- Chen, Q.; Yu, Z.; Li, B. Image-Based Assessment of Seismic Damage in RC Exterior Beam-Column Joints. J. Build. Eng. 2024, 97, 110971. [Google Scholar] [CrossRef]
- Zhang, B.; Lu, G.; Yang, C.; Yang, C.; Xu, M.; Wang, K. Seismic Damage Assessment of Bonded versus Unbonded Laminated Rubber Bearings: A Deep Learning Perspective. Eng. Struct. 2024, 321, 118996. [Google Scholar] [CrossRef]
- Su, A.; Cheng, J.; Wang, Y.; Pan, Y. Machine Learning-Based Processes with Active Learning Strategies for the Automatic Rapid Assessment of Seismic Resistance of Steel Frames. Structures 2025, 72, 108227. [Google Scholar] [CrossRef]
- He, Y.; Huang, Z.; Liu, D.; Zhang, L.; Liu, Y. A Novel Structural Damage Identification Method Using a Hybrid Deep Learning Framework. Buildings 2022, 12, 2130. [Google Scholar] [CrossRef]
- Bhatta, S.; Dang, J. Seismic Damage Prediction of RC Buildings Using Machine Learning. Earthq. Eng. Struct. Dyn. 2023, 52, 3504–3527. [Google Scholar] [CrossRef]
- Nguyen, H.D.; LaFave, J.M.; Lee, Y.J.; Shin, M. Rapid Seismic Damage-State Assessment of Steel Moment Frames Using Machine Learning. Eng. Struct. 2022, 252, 113737. [Google Scholar] [CrossRef]
- Wang, L.J.; Huang, C.Y.; Shan, J.Z.; Yu, H.; Su, J.R. Machine Learning Prediction Method for Seismic Damage of Existing Buildings Driven by Multiple Features. J. Build. Struct. 2024, 45, 1–12. [Google Scholar]
- Ni, X.; Duan, K. Machine Learning-Based Models for Shear Strength Prediction of UHPFRC Beams. Mathematics 2022, 10, 2918. [Google Scholar] [CrossRef]
- Zhao, C.; Zhu, Y.; Zhou, Z. Machine Learning-Based Approaches for Predicting the Dynamic Response of RC Slabs under Blast Loads. Eng. Struct. 2022, 273, 115104. [Google Scholar] [CrossRef]
- Naderpour, H.; Mirrashid, M.; Parsa, P. Failure Mode Prediction of Reinforced Concrete Columns Using Machine Learning Methods. Eng. Struct. 2021, 248, 113263. [Google Scholar] [CrossRef]
- Mangalathu, S.; Jang, H.; Hwang, S.H.; Jeon, J. Data-Driven Machine-Learning-Based Seismic Failure Mode Identification of Reinforced Concrete Shear Walls. Eng. Struct. 2020, 208, 110331. [Google Scholar] [CrossRef]
- Amir, A.S.; Abouzar, J.; Habib, A.B.; Zhou, Y.; Ertugrul, T. A scaling-based generalizable integrated ML-mechanics model for lateral response of self-centering walls. Eng. Struct. 2025, 336, 120326. [Google Scholar]
- GB 50011-2010; Code for Seismic Design of Buildings. Standardization Administration of China: Beijing, China, 2010. (In Chinese)
- Hao, Y.; Chen, F.; Du, C.H.; Ding, Q.Y.; Lei, H.; Hu, P.C. Seismic Damage Assessment of Floors in Vertically Stepped Steel Bundled-Tube Structures. Build. Sci. 2024, 40, 154–163. (In Chinese) [Google Scholar]
- Raschka, S. Model Evaluation, Model Selection, and Algorithm Selection in Machine Learning. arXiv 2018, arXiv:1811.12808. [Google Scholar]
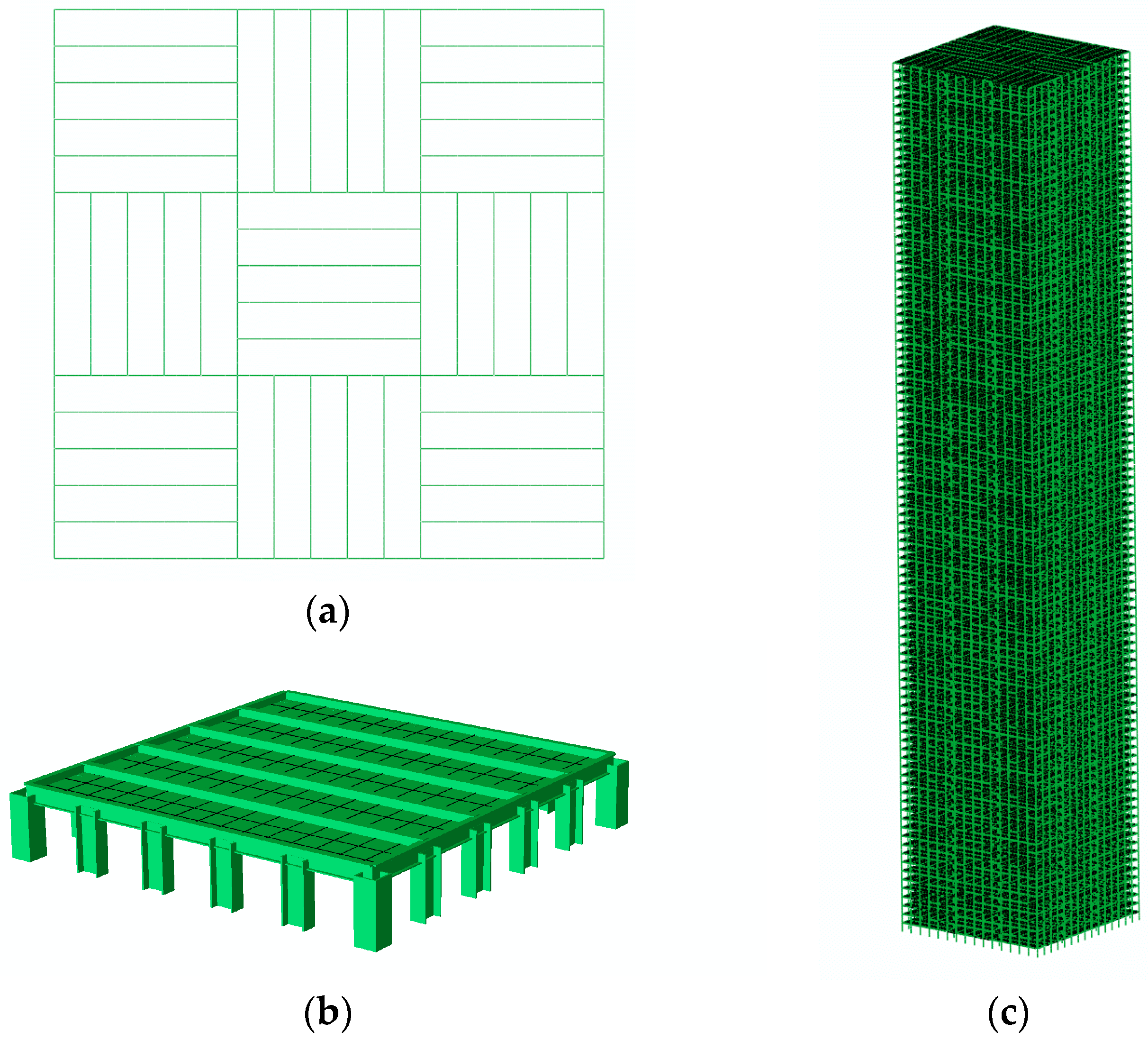




| Name of Member | Section Form | Size of Member (mm × mm × mm × mm) | Section Form |
|---|---|---|---|
| Corner column | Box section | 1300 × 1300 × 100 × 100 | 1–100 |
| Side column | H-section | 1400 × 900 × 90 × 100 | 1–30 |
| 1400 × 900 × 60 × 80 | 31–60 | ||
| 1400 × 900 × 40 × 60 | 61–100 | ||
| Skirt beam | 1000 × 400 × 50 × 70 | 1–60 | |
| 1000 × 400 × 35 × 50 | 61–100 | ||
| Main beam | 1100 × 500 × 30 × 50 | 1–100 |
| PKPM | ABAQUS | PKPM/ABAQUS | |
|---|---|---|---|
| T1/s | 7.38 | 7.42 | 99.5% |
| T2/s | 7.38 | 7.42 | 99.5% |
| T3/s | 4.91 | 4.91 | 100% |
| M/105t | 4.93 | 4.83 | 100% |
| Component Type | Percentage | Slight | Obvious I | Obvious II | Obvious II | Severe |
|---|---|---|---|---|---|---|
| Steel column (plastic strain) | 0~5% | 0.016 | 0.018 | 0.02 | 0.025 | 0.035 |
| 5%~20% | 0.065 | 0.07 | 0.08 | 0.1 | 0.14 | |
| 20%~40% | 0.165 | 0.17 | 0.18 | 0.2 | 0.24 | |
| 40%~60% | 0.265 | 0.27 | 0.28 | 0.3 | 0.34 | |
| 60%~80% | 0.365 | 0.37 | 0.38 | 0.4 | 0.44 | |
| >80% | 0.465 | 0.47 | 0.48 | 0.5 | 0.54 | |
| Steel skirt beam (plastic strain) | 0~5% | 0.005 | 0.01 | 0.015 | 0.02 | 0.025 |
| 5%~20% | 0.02 | 0.04 | 0.06 | 0.08 | 0.1 | |
| 20%~40% | 0.04 | 0.06 | 0.08 | 0.1 | 0.12 | |
| 40%~60% | 0.06 | 0.08 | 0.1 | 0.12 | 0.14 | |
| 60%~80% | 0.08 | 0.1 | 0.12 | 0.14 | 0.16 | |
| >80% | 0.1 | 0.12 | 0.14 | 0.16 | 0.18 | |
| Floor slabs (characterized by plastic strain in floor reinforcement) | 0~5% | 0.002 | 0.004 | 0.006 | 0.008 | 0.01 |
| 5%~20% | 0.02 | 0.025 | 0.03 | 0.035 | 0.04 | |
| 20%~40% | 0.025 | 0.03 | 0.035 | 0.04 | 0.045 | |
| 40%~60% | 0.03 | 0.035 | 0.04 | 0.045 | 0.05 | |
| 60%~80% | 0.035 | 0.04 | 0.045 | 0.05 | 0.055 | |
| >80% | 0.04 | 0.045 | 0.05 | 0.055 | 0.06 |
| Damage Degree | Plastic Strain of Elements |
|---|---|
| Intact | Non-plastic strain |
| Slight | Plastic strain ≤ 0.2% |
| obvious | 0.2% < Plastic strain ≤ 6% |
| Severe | Plastic strain > 6% |
| Damage States | No Damage | Slight Damage | Moderate Damage | Extensive Damage | Complete Damage |
|---|---|---|---|---|---|
| Damage factors | 0~0.2 | 0.2~0.4 | 0.4~0.6 | 0.6~0.9 | ≥0.9 |
| Input Variables | F (Floor) | M (t) | K (kN/m) | C (kN) | A (Gal) | E (J) | X (m) |
|---|---|---|---|---|---|---|---|
| minimum value | 1 | 4622.3 | 974,000 | 1,330,000 | 220 | 4803 | 0.000997 |
| maximum value | 100 | 5088.4 | 58,700,000 | 2,080,000 | 4000 | 4,202,560,000 | 12.805 |
| average value | 50.5 | 4845.3 | 12,594,540 | 1,792,900 | 2008 | 138,495,711 | 4.023 |
| Category | Variable | Retained/Removed | Engineering Rationale |
|---|---|---|---|
| Building information | F | Removed | High multicollinearity (VIF > 70). Redundant when mass, stiffness are known. |
| m | Retained | Fundamental property determining inertial forces. | |
| K | Retained | Governs stress distribution and dynamic response. | |
| C | Retained | Directly related to structural safety margin. | |
| Earthquake information | a | Retained | Primary indicator of ground motion intensity. |
| Response Response | E | Retained | Critical indicator of cumulative damage. |
| x | Retained | Key serviceability and safety limit state parameter. |
| Number | Algorithm Name | Classification of Machine Learning Algorithms |
|---|---|---|
| 1 | DT | Single learning |
| 2 | RF | Ensemble learning |
| 3 | KNN | Single learning |
| 4 | SVM | Single learning |
| 5 | NB | Single learning |
| 6 | XGBoost | Ensemble learning |
| 7 | Adaboost | Ensemble learning |
| 8 | CatBoost | Ensemble learning |
| Hyperparameters | Function |
|---|---|
| n_estimators | Represents the number of decision trees in the forest. |
| max_depth | Limit the maximum depth of each decision tree to prevent overfitting. |
| max_features | Avoid training all decision trees based on the same features, thereby enhancing the generalization ability of the model. |
| learning_rate | Balance the convergence speed and accuracy of the model |
| subsample | Introduce randomness to reduce overfitting. |
| colsample_bytree | Further increase the diversity among decision trees to prevent all decision trees from being trained based on the same features. |
| gamma | The minimum loss reduction used to control node splitting prevents the decision tree from over—splitting and avoids overfitting. |
| reg_alpha | L1 regularization penalties are respectively imposed on the weights of the model to make the weights of the model sparser. |
| reg_lambda | L2 regularization penalties are respectively imposed on the weights of the model to make the weights of the model smaller. |
| Hyperparameters | Optimized Values |
|---|---|
| n_estimators | 96 |
| max_depth | 12 |
| max_features | 2 |
| bootstrap | False |
| class_weight | balanced |
| criterion | gini |
| Hyperparameters | Optimized Values |
|---|---|
| n_estimators | 119 |
| max_depth | 30 |
| learning_rate | 0.6274635497594659 |
| subsample | 0.30713949719439915 |
| colsample_bytree | 0.8246860247165366 |
| gamma | 0.0403280338923106 |
| reg_alpha | 0.5536200711976728 |
| reg_lambda | 0.4993919951300849 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Qin, X.; Hao, Y.; Liu, J.; Hou, R.; Li, P. Machine Learning-Based Rapid Assessment of Story-Level Seismic Damage in Steel Bundled-Tube Structures. Buildings 2025, 15, 3758. https://doi.org/10.3390/buildings15203758
Zhou J, Qin X, Hao Y, Liu J, Hou R, Li P. Machine Learning-Based Rapid Assessment of Story-Level Seismic Damage in Steel Bundled-Tube Structures. Buildings. 2025; 15(20):3758. https://doi.org/10.3390/buildings15203758
Chicago/Turabian StyleZhou, Jinhao, Xiaohui Qin, Yong Hao, Jianchao Liu, Ruifang Hou, and Pucan Li. 2025. "Machine Learning-Based Rapid Assessment of Story-Level Seismic Damage in Steel Bundled-Tube Structures" Buildings 15, no. 20: 3758. https://doi.org/10.3390/buildings15203758
APA StyleZhou, J., Qin, X., Hao, Y., Liu, J., Hou, R., & Li, P. (2025). Machine Learning-Based Rapid Assessment of Story-Level Seismic Damage in Steel Bundled-Tube Structures. Buildings, 15(20), 3758. https://doi.org/10.3390/buildings15203758






