Field Dynamic Testing and Adaptive Dynamic Characteristic Identification of Steel Tower Structures in High-Speed Railway Stations Under Limited Sensor Configurations
Abstract
1. Introduction
2. Structural Overview
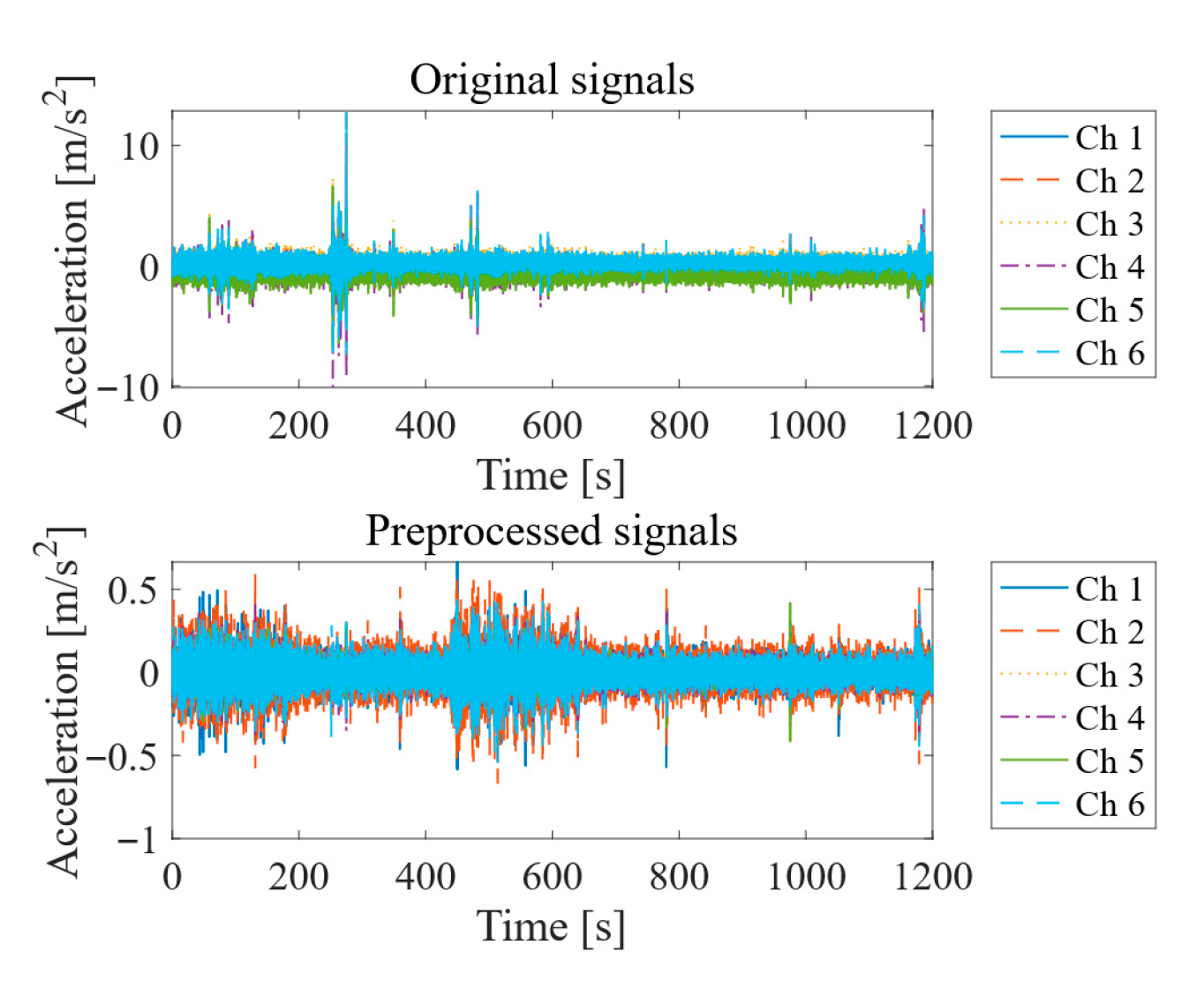
3. In Situ Ambient Excitation Test
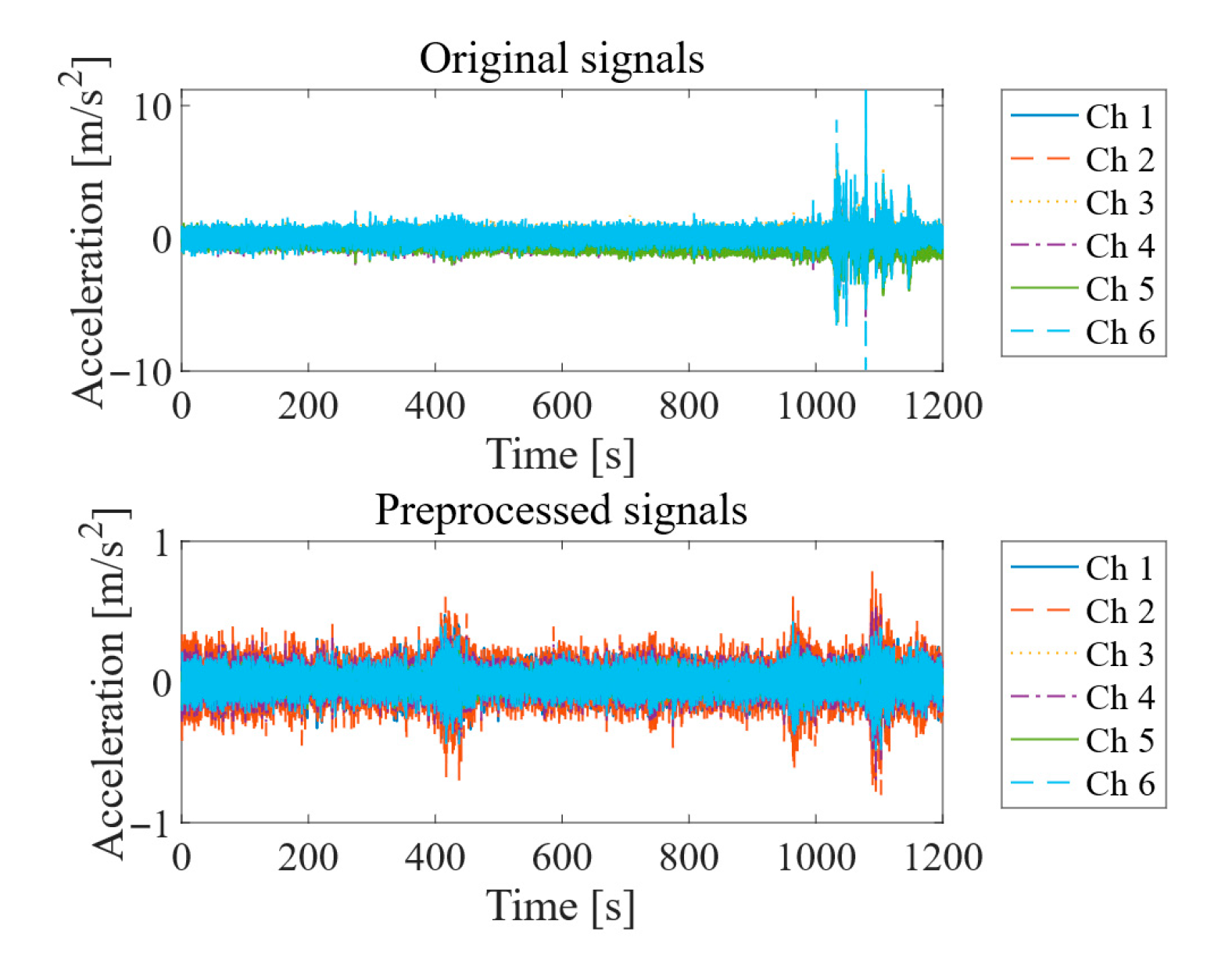
3.1. Test Equipment and Parameter Setup
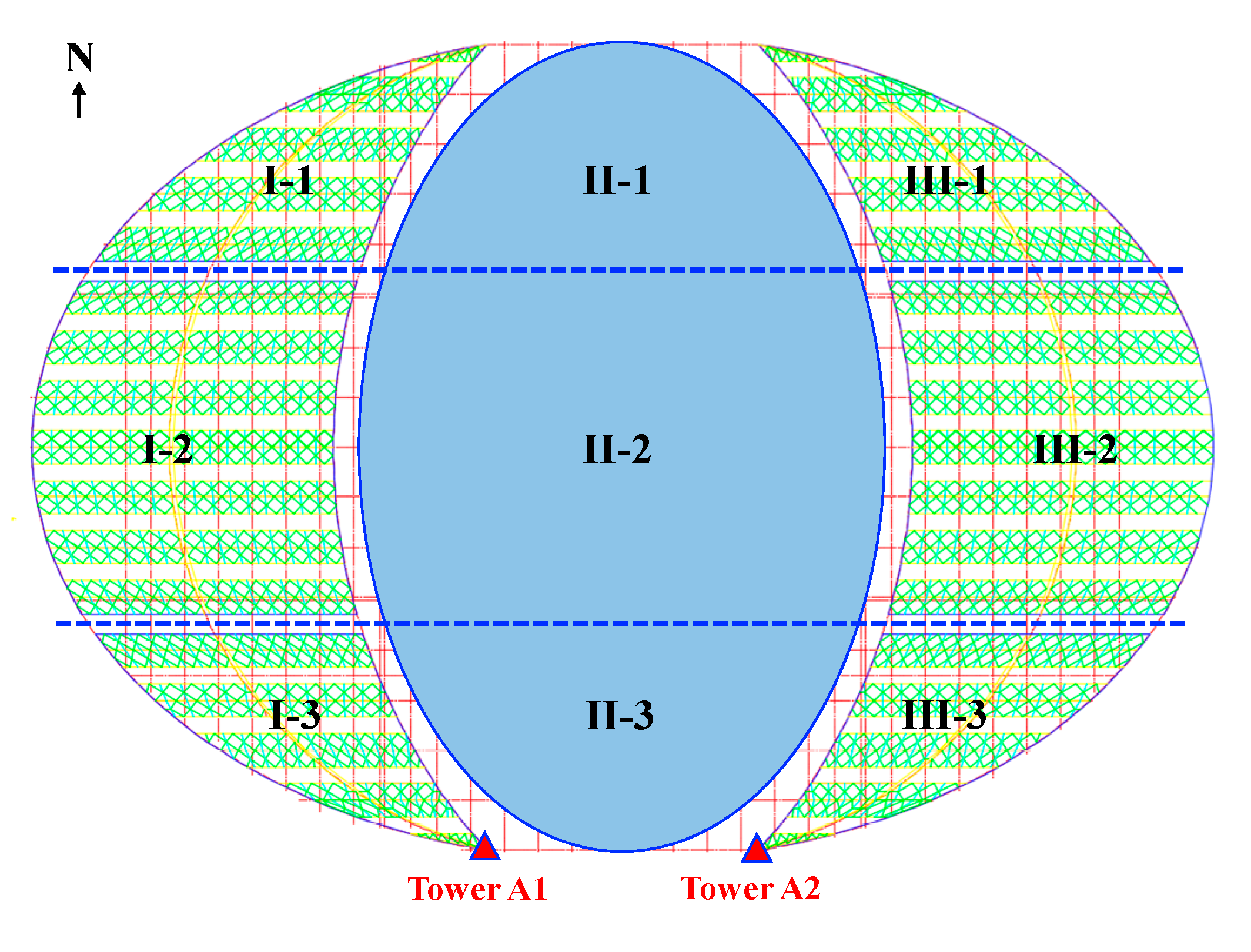
3.2. Sensor Layout Plan
- (i)
- field measurements were carried out under ambient excitation without artificial external input;
- (ii)
- because of the structural form, operational requirements, and sensor layout constraints, sensors could be installed only at the beam and top sections. Higher-order modes with more than two inflection points along the tower height cannot be effectively captured under the current measurement configuration.
4. Automatic Identification Method for Dynamic Characteristics
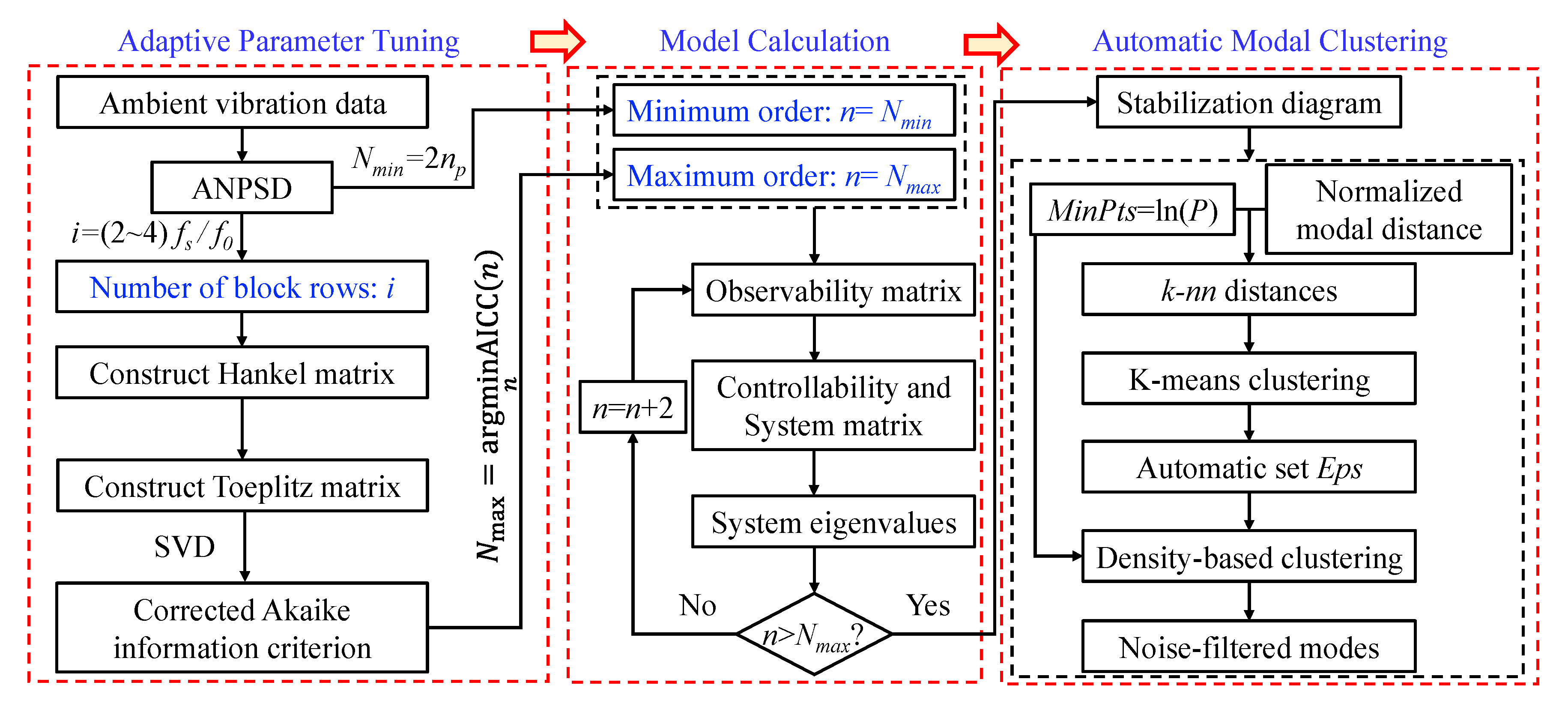
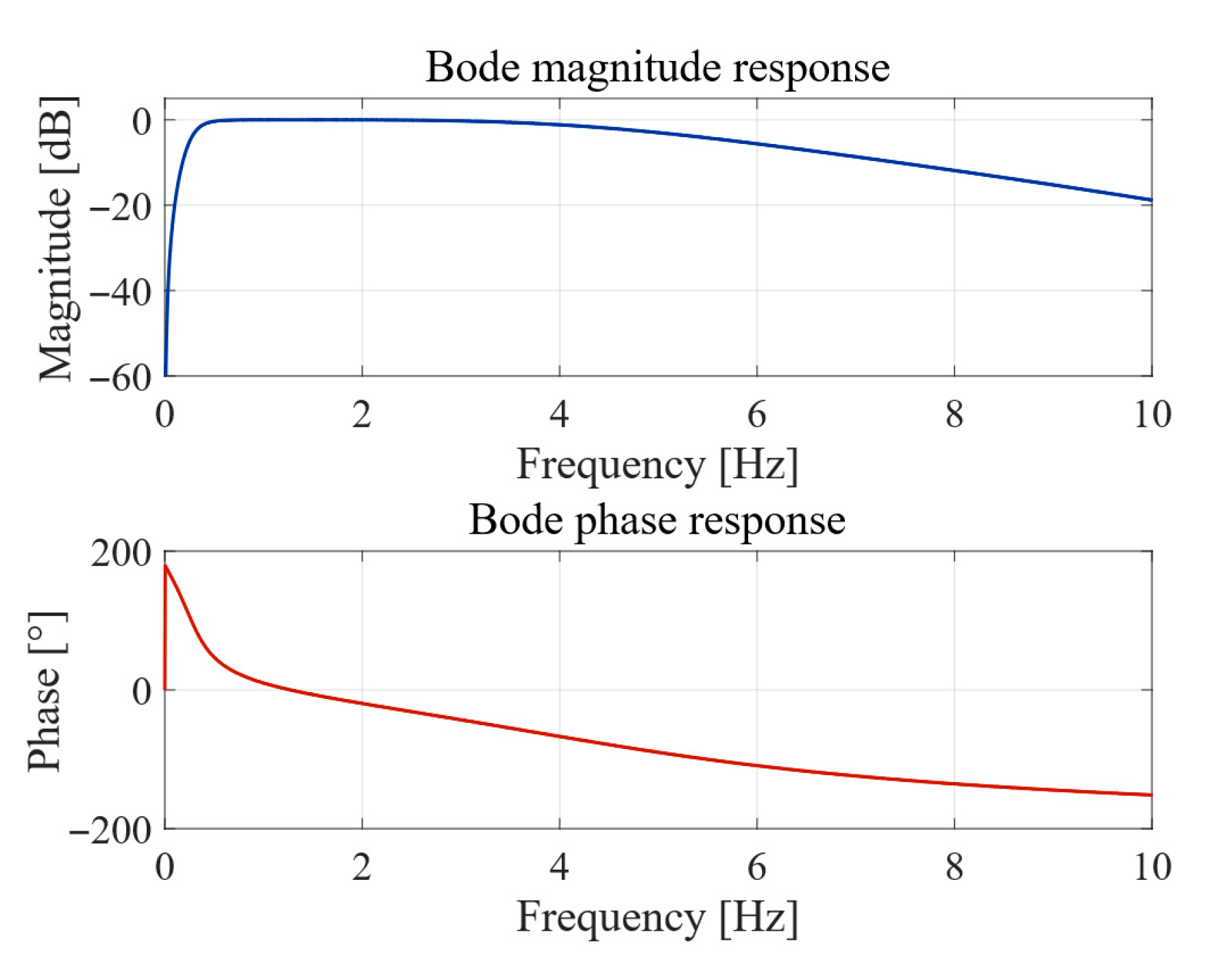
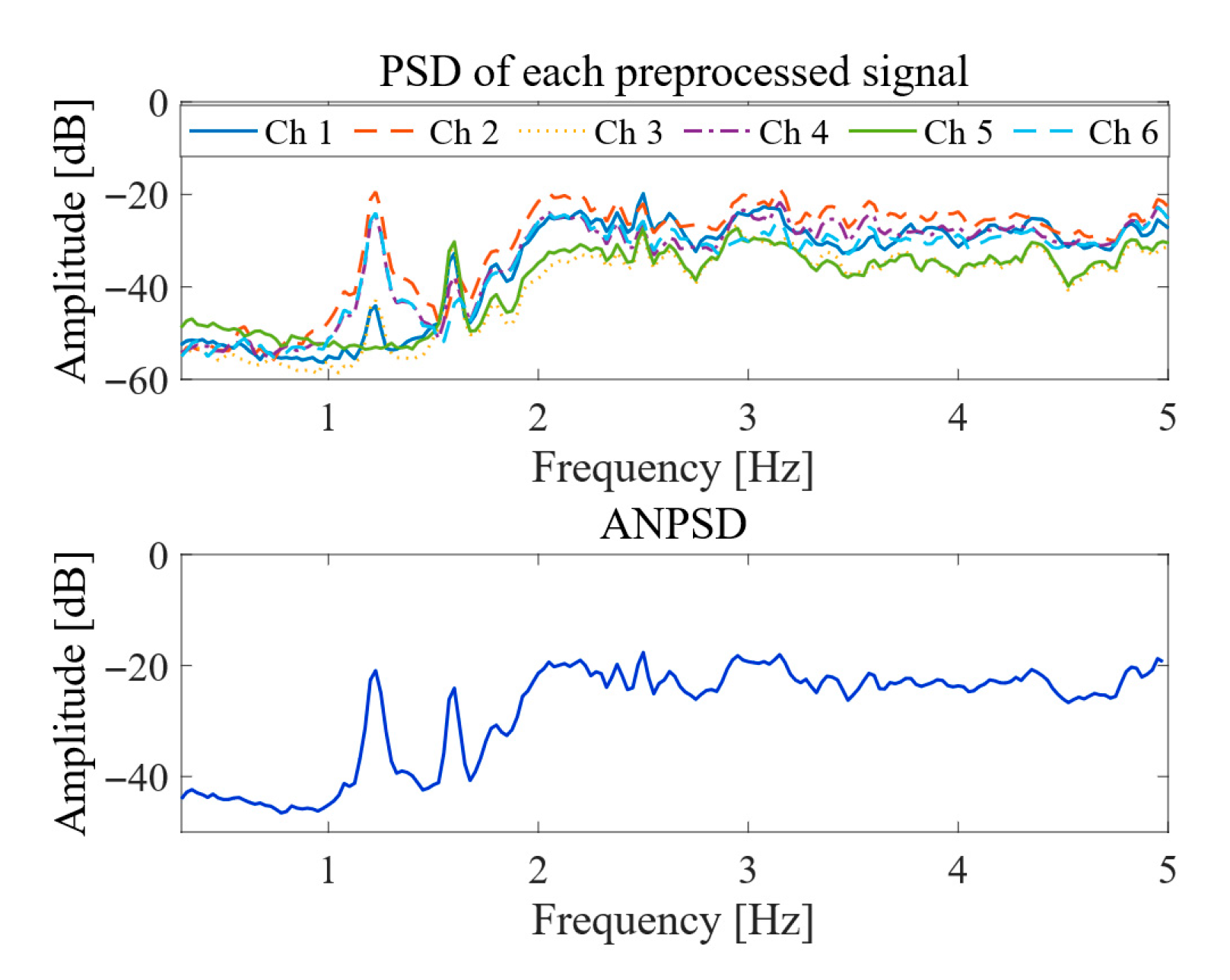
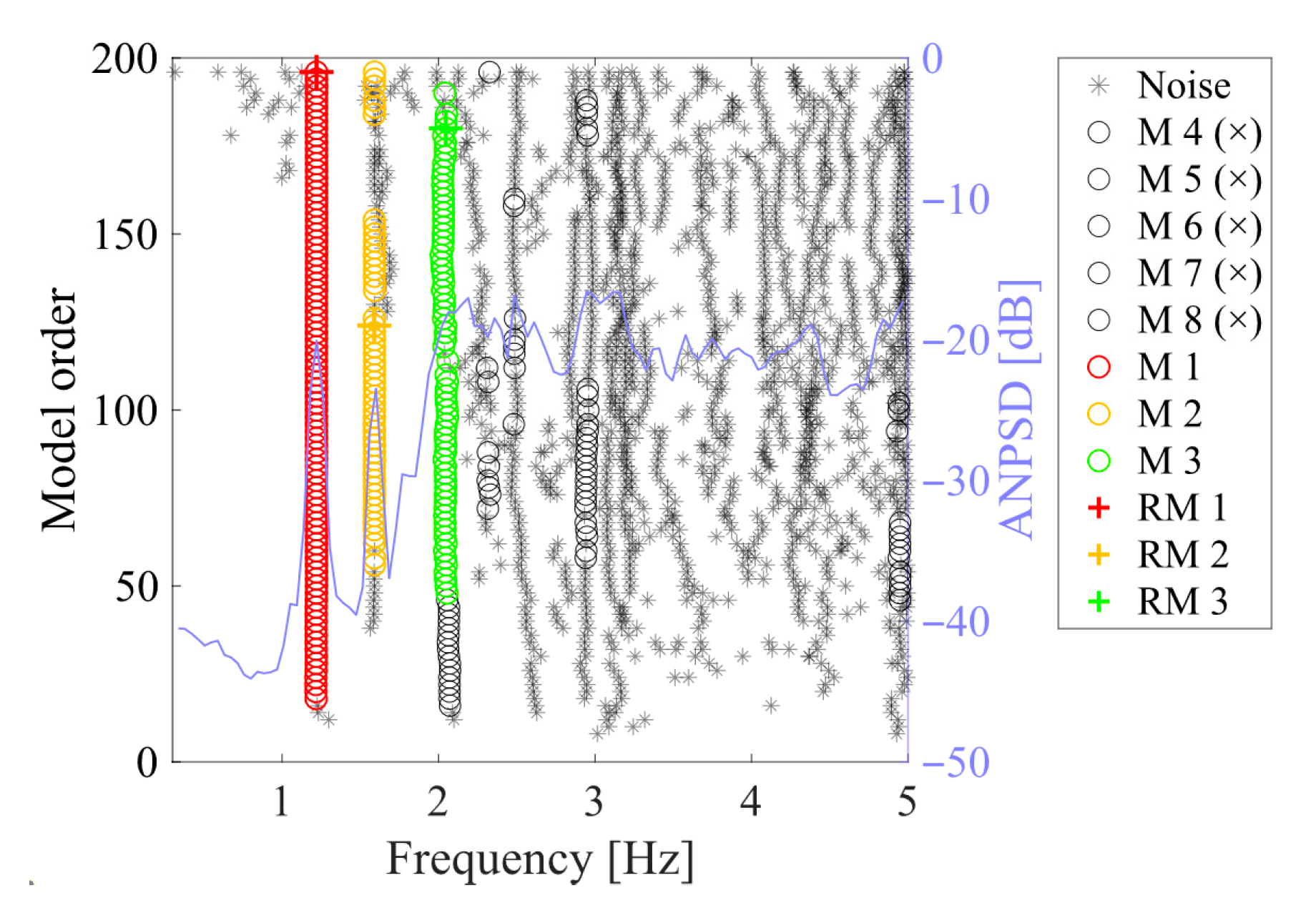
4.1. Frequency Domain Spectrum Analysis Based on ANPSD
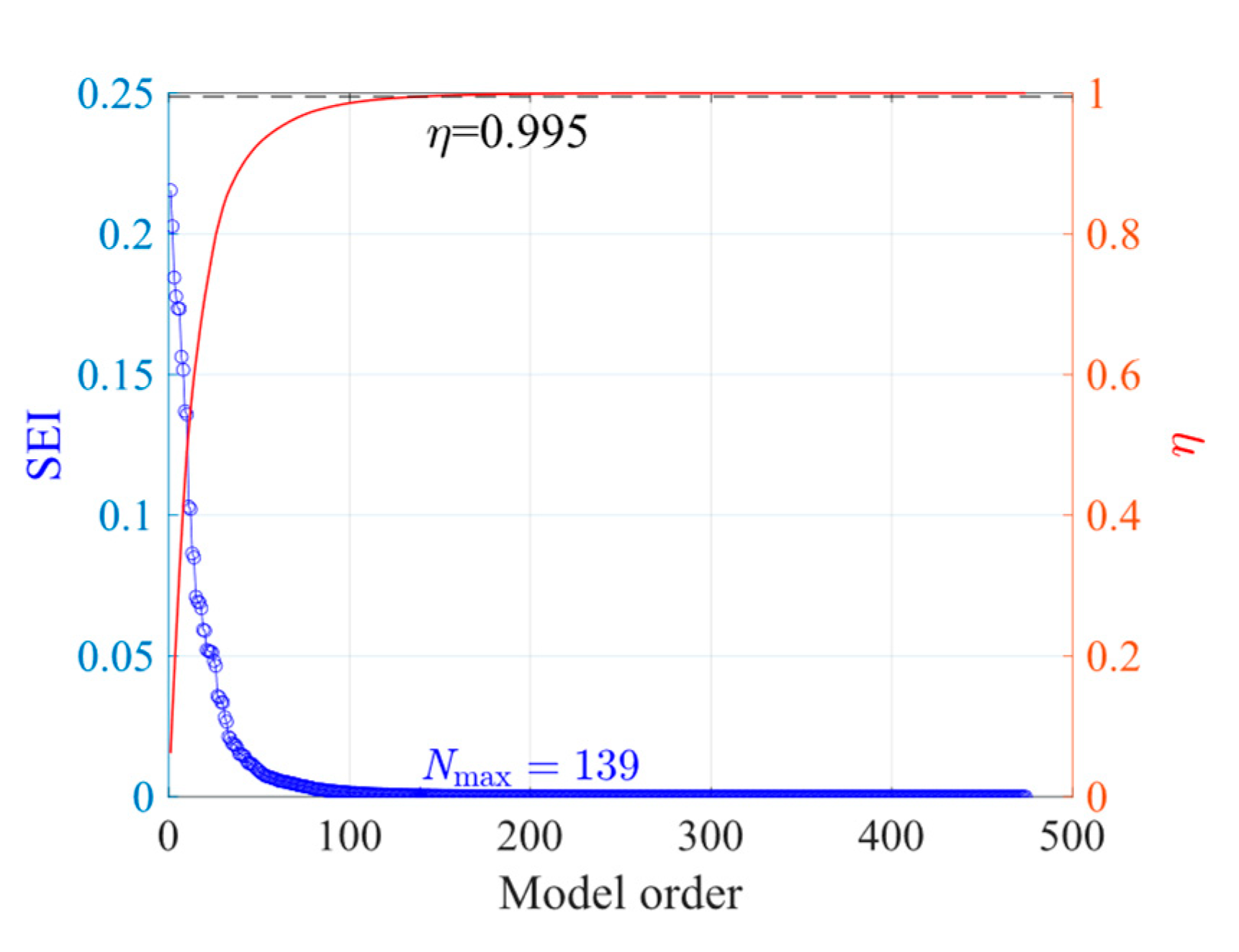
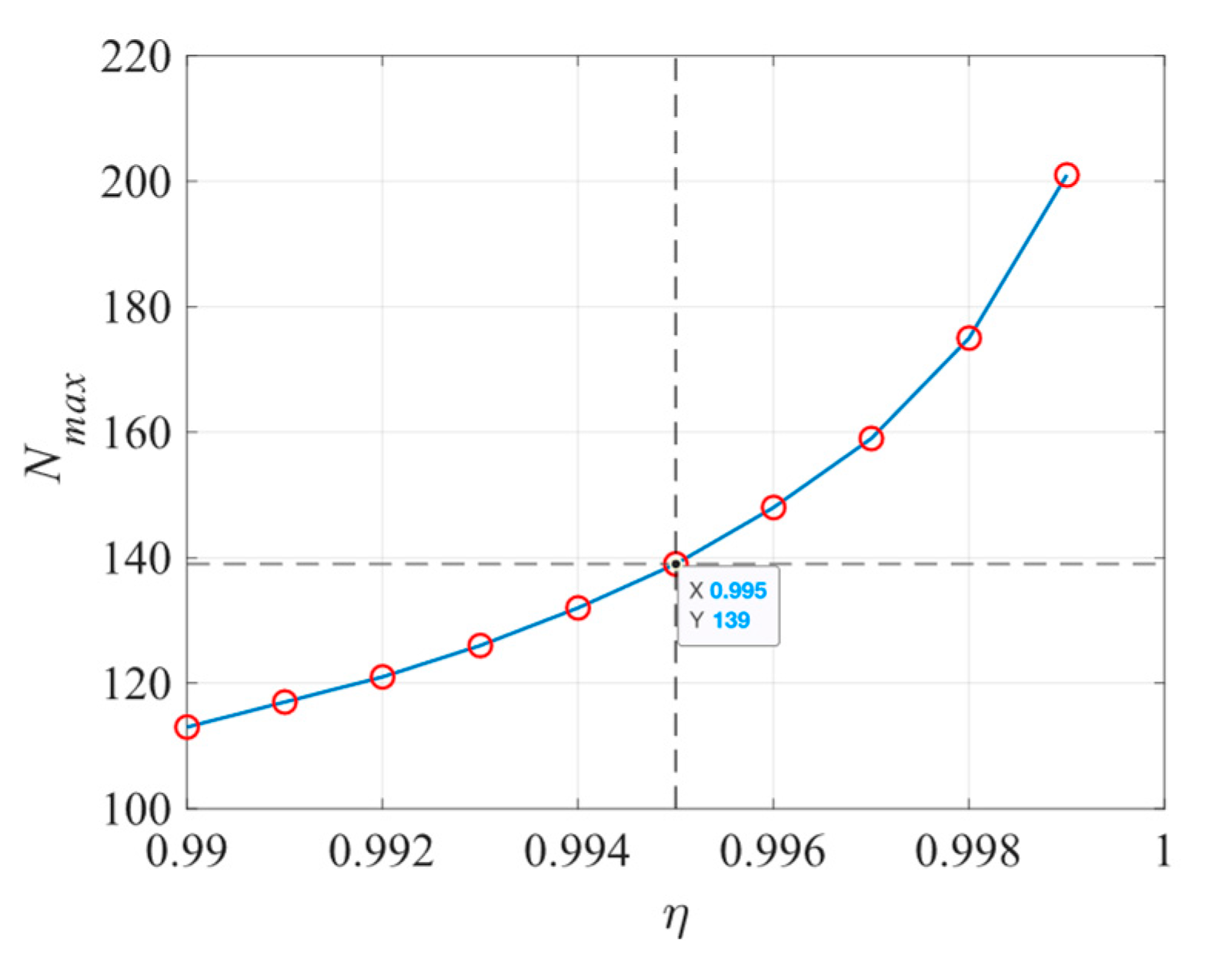
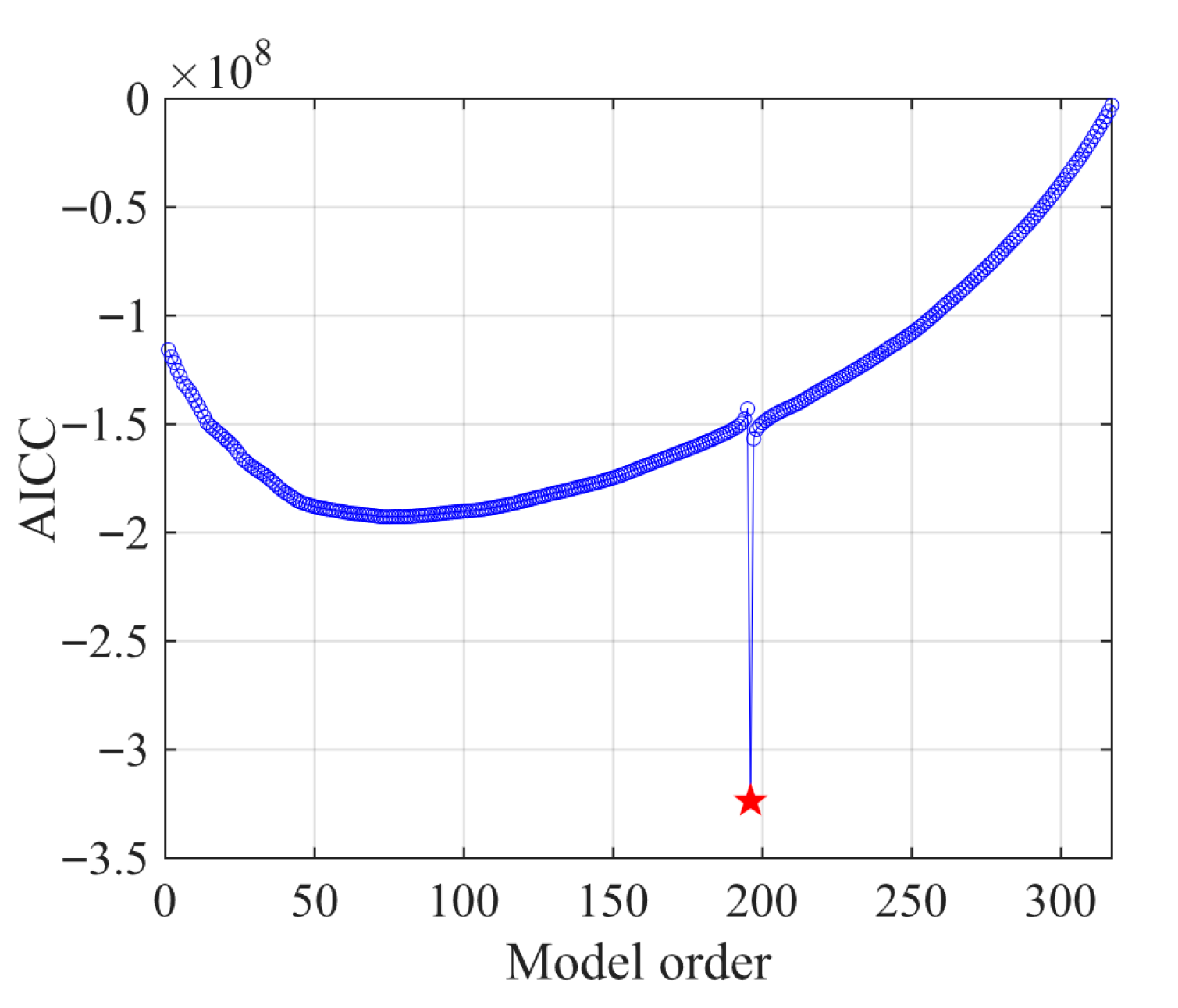
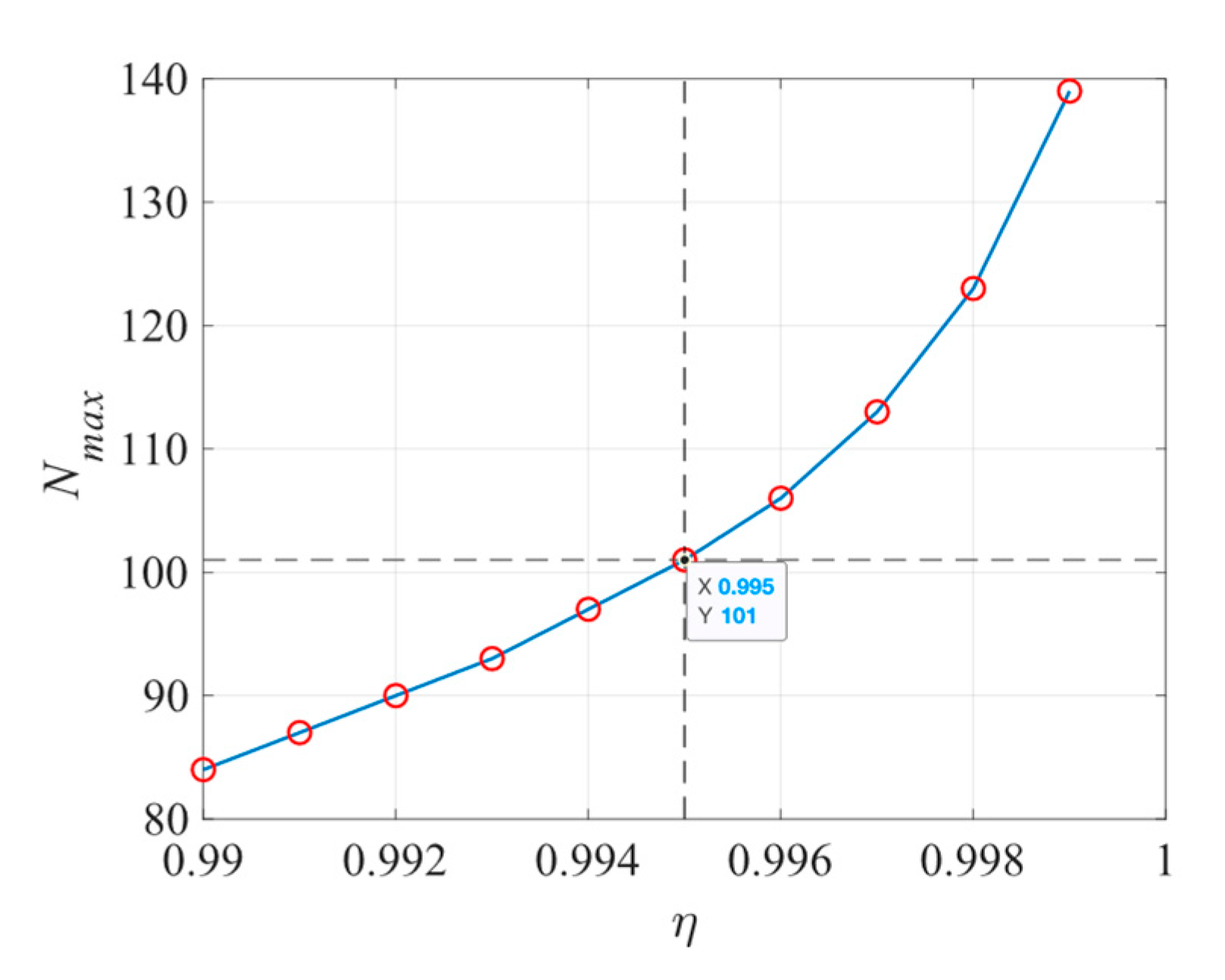
4.2. Automatic Order Determination in Modal Identification Based on State-Space Models
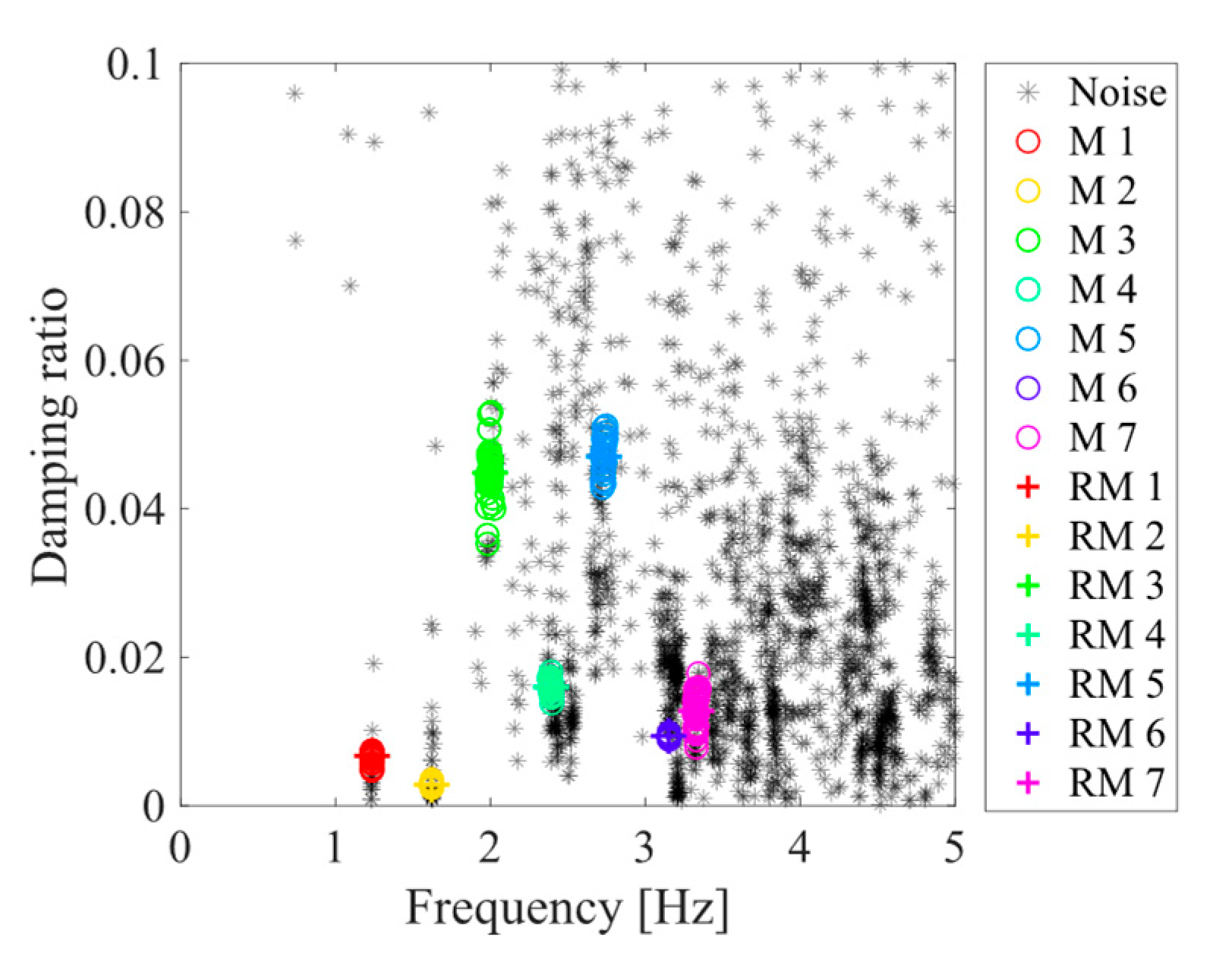
4.3. Automatic Modal Clustering
5. Modal Identification Results
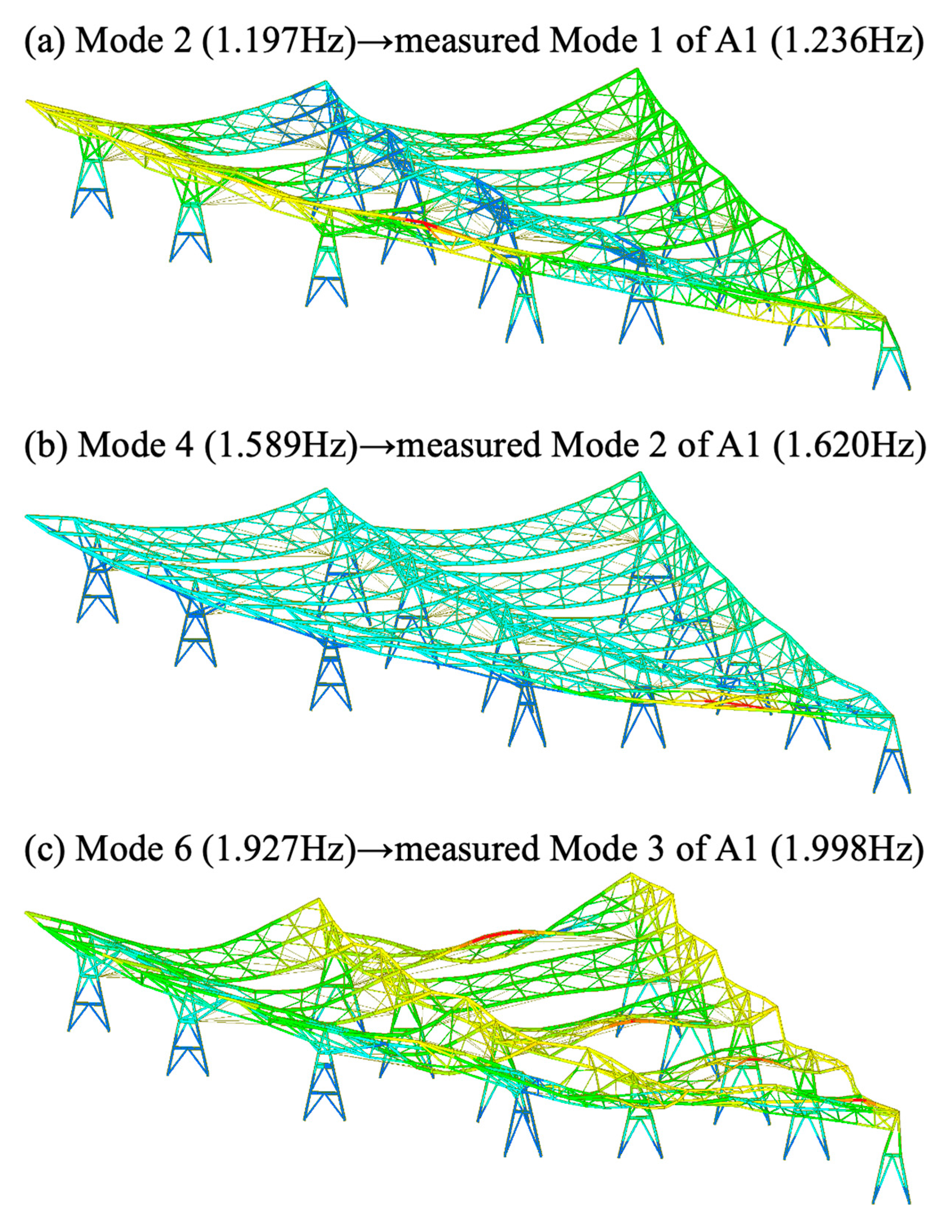
5.1. Tower A1
5.2. Tower A2
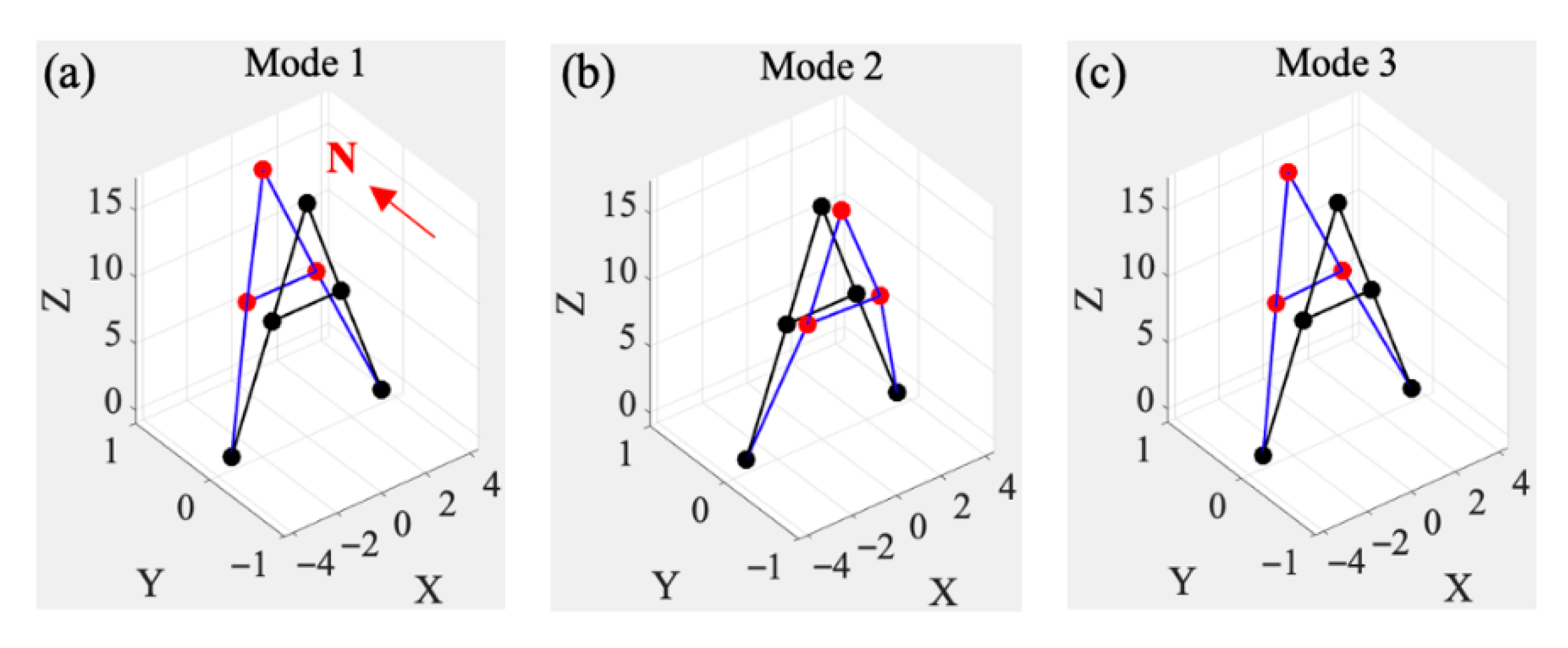
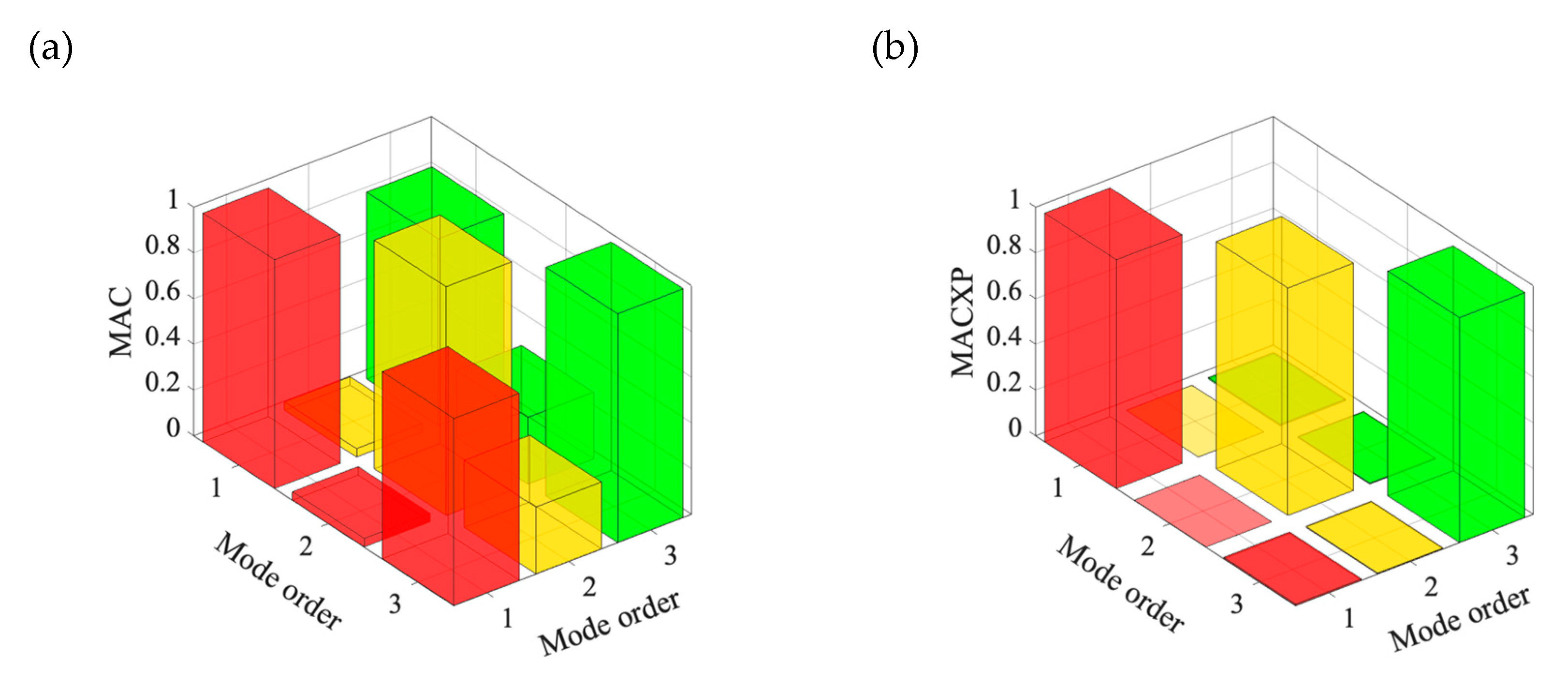
5.3. Discussion of the Results
- (i)
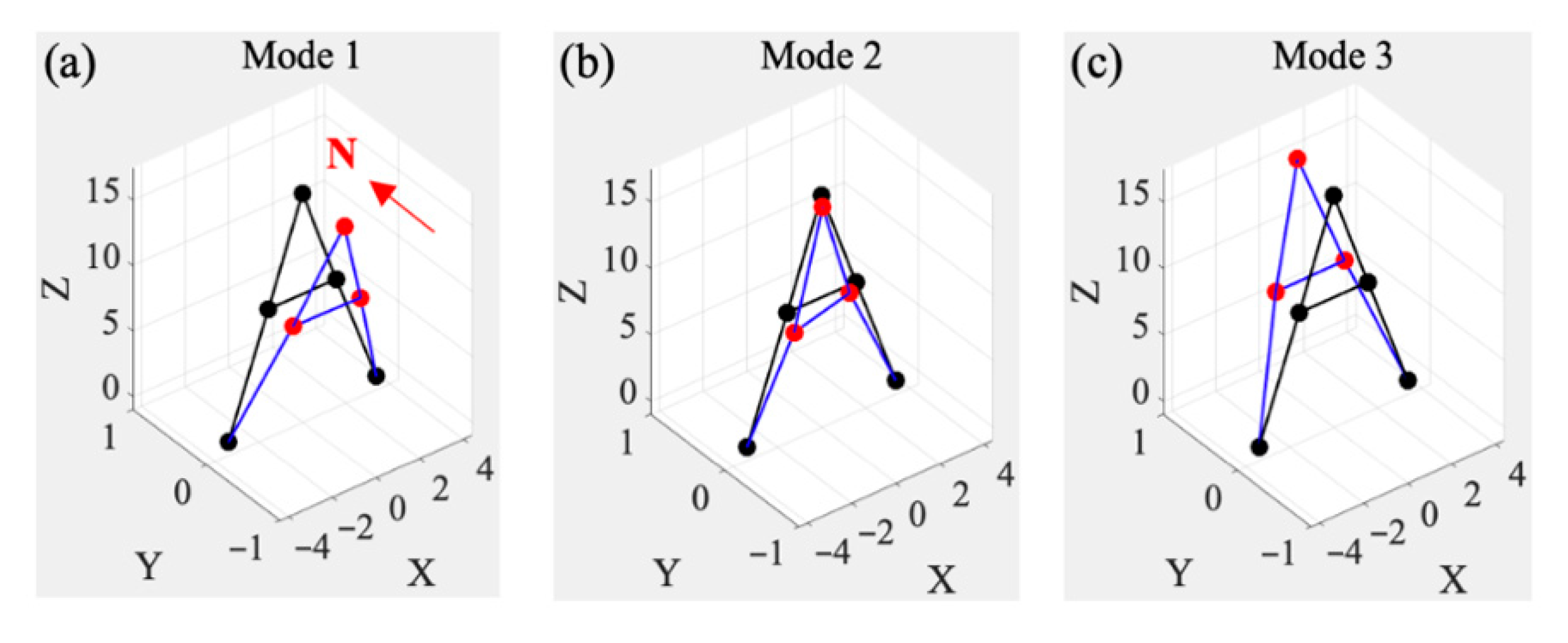
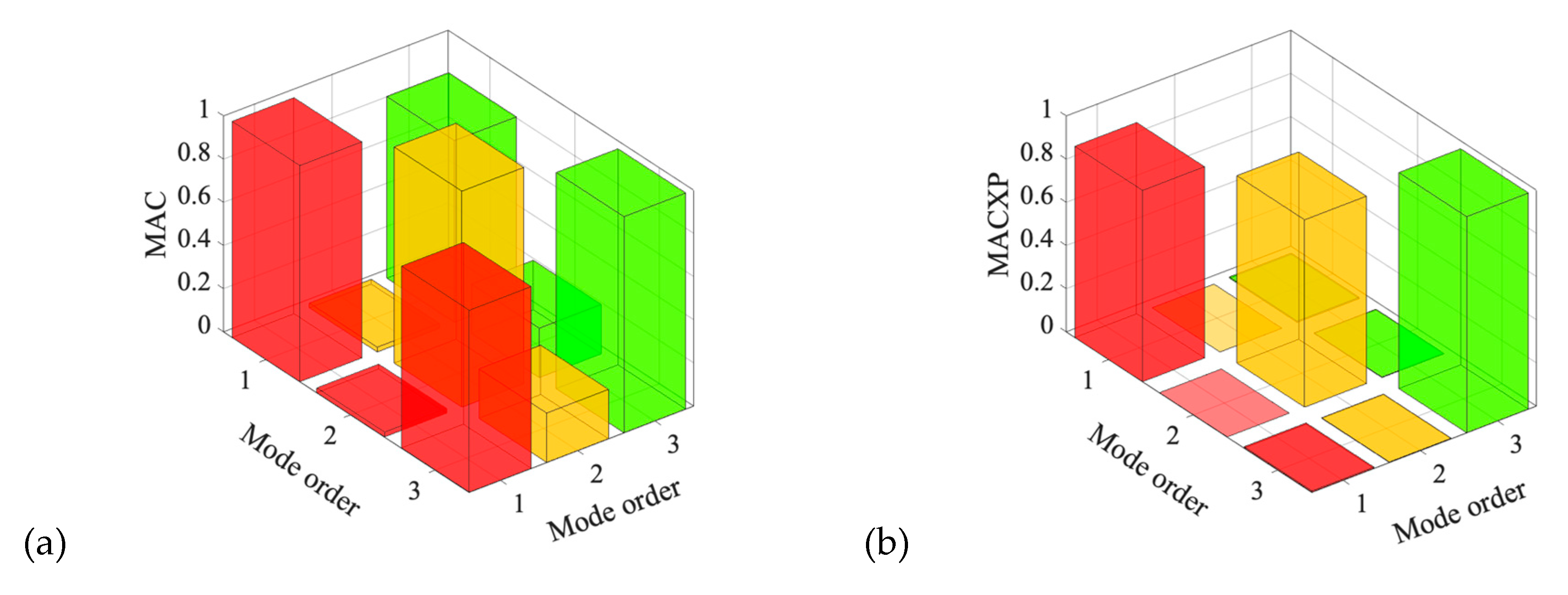
- As summarized in Table 6, the differences in the first three natural frequencies are small, ranging from 1.29% to 2.39%, while the damping ratios differ by 0.56–7.34%. The cross–orthogonality of the mode shapes (COMAC) for the first three modes is 1.00, 0.82, and 0.45, respectively. These results indicate that the two towers exhibit high consistency in their low-order modes, whereas discrepancies increase progressively in higher-order modes. Such a trend suggests that lower modes primarily reflect the overall structural uniformity, while higher modes are more sensitive to local differences, which is important for structural health monitoring and comparative analysis. It is noted that the third-order mode of Tower A1 is primarily oriented along the southwest–northeast (SW–NE) direction, whereas that of Tower A2 is oriented along the southeast–northwest (SE–NW) direction. These nearly orthogonal modal orientations account for the lower COMAC value (0.45) reported in Table 6.
- (ii)
- The comparison of the first three mode shapes for Towers A1 and A2 is summarized in Table 7. Although the overall mode shapes are broadly similar, a notable difference appears in the second mode, which is dominated by in-plane motion. In the reinforced Tower A1, the largest amplitude occurs at the crossbeam, and the out-of-plane components on both sides (#4 and #6 in Table 3) remain essentially consistent, indicating no relative torsion. In contrast, in the unreinforced Tower A2, the second mode shows its maximum amplitude on the west side of the crossbeam, while the out-of-plane components on the two sides (#4 and #6 in Table 5) differ significantly, producing a clear relative torsional response.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pan, Y.; Liu, Y.; Huang, C.; Guo, R.; Bao, H.; Shen, L. A review of structural health monitoring of large railway stations. J. Civ. Environ. Eng. 2020, 42, 70–80. [Google Scholar]
- Du, Y.; Zhang, H.; Liu, B. Consideration on the Current Situation and Development of Structural Health Monitoring of Large Railway Passenger Stations. Railw. Stand. Des. 2023, 67, 1–9. [Google Scholar]
- Yang, N.; Liu, W.; Bai, F.; Qin, S.; Yu, Y. Durability evaluation of steel structure of platform canopy under corrosion. J. Railw. Sci. Eng. 2020, 17, 181–188. [Google Scholar]
- Rainieri, C.; Fabbrocino, G. Operational Modal Analysis of Civil Engineering Structures: An Introduction and Guide for Applications; Springer New York: New York, NY, USA, 2014; ISBN 978-1-4939-0766-3. [Google Scholar]
- Ubertini, F.; Gentile, C.; Materazzi, A.L. Automated Modal Identification in Operational Conditions and Its Application to Bridges. Eng. Struct. 2013, 46, 264–278. [Google Scholar] [CrossRef]
- Zhou, K.; Li, Q.-S.; Han, X.-L. Modal Identification of Civil Structures via Stochastic Subspace Algorithm with Monte Carlo–Based Stabilization Diagram. J. Struct. Eng. 2022, 148, 04022066. [Google Scholar] [CrossRef]
- Li, J.; Bao, T.; Ventura, C.E. An Automated Operational Modal Analysis Algorithm and Its Application to Concrete Dams. Mech. Syst. Signal Process. 2022, 168, 108707. [Google Scholar] [CrossRef]
- Liu, W.; Yang, N.; Bai, F.; Law, S.; Abruzzese, D. An Improved Automated Framework for Operational Modal Analysis with Multi-Stage Clustering and Modal Quality Evaluation. Mech. Syst. Signal Process. 2024, 212, 111235. [Google Scholar] [CrossRef]
- Van Overschee, P.; De Moor, B.L. Subspace Identification for Linear Systems: Theory—Implementation—Applications; Springer Science & Business Media: Dordrecht, The Netherlands, 2012; ISBN 978-1-4613-0465-4. [Google Scholar]
- Mostafaei, H.; Ghamami, M. State of the Art in Automated Operational Modal Identification: Algorithms, Applications, and Future Perspectives. Machines 2025, 13, 39. [Google Scholar] [CrossRef]
- Reynders, E.; Houbrechts, J.; De Roeck, G. Fully Automated (Operational) Modal Analysis. Mech. Syst. Signal Process. 2012, 29, 228–250. [Google Scholar] [CrossRef]
- Qin, S.; Kang, J.; Wang, Q. Operational Modal Analysis Based on Subspace Algorithm with an Improved Stabilization Diagram Method. Shock Vib. 2016, 2016, 7598965. [Google Scholar] [CrossRef]
- Zini, G.; Betti, M.; Bartoli, G. A Quality-Based Automated Procedure for Operational Modal Analysis. Mech. Syst. Signal Process. 2022, 164, 108173. [Google Scholar] [CrossRef]
- Liu, W.; Yang, N.; Liu, B.; Feng, H.; Wang, B.; Du, K.; Abruzzese, D. Sensitivity Analysis and Optimization of User-Defined Parameters in Covariance-Driven Stochastic Subspace Identification. Int. J. Struct. Stab. Dyn. 2025, 2650202. [Google Scholar] [CrossRef]
- Teng, J.; Tang, D.-H.; Zhang, X.; Hu, W.-H.; Said, S.; Rohrmann, R. Automated Modal Analysis for Tracking Structural Change during Construction and Operation Phases. Sensors 2019, 19, 927. [Google Scholar] [CrossRef]
- Pourgholi, M.; Mohammadzadeh Gilarlue, M.; Vahdaini, T.; Azarbonyad, M. Influence of Hankel Matrix Dimension on System Identification of Structures Using Stochastic Subspace Algorithms. Mech. Syst. Signal Process. 2023, 186, 109893. [Google Scholar] [CrossRef]
- Zhang, X.; Li, D.; Song, G. Structure Damage Identification Based on Regularized ARMA Time Series Model under Environmental Excitation. Vibration 2018, 1, 138–156. [Google Scholar] [CrossRef]
- Yaghoubi, V.; Vakilzadeh, M.K.; Abrahamsson, T.J.S. Automated Modal Parameter Estimation Using Correlation Analysis and Bootstrap Sampling. Mech. Syst. Signal Process. 2018, 100, 289–310. [Google Scholar] [CrossRef]
- He, M.; Liang, P.; Zhang, Y.; Yang, F.; Liu, J. Unified Method for Fully Automated Modal Identification and Tracking with Consideration of Sensor Deployment. Eng. Struct. 2022, 260, 114223. [Google Scholar] [CrossRef]
- Vacher, P.; Jacquier, B.; Bucharles, A. Extensions of the MAC Criterion to Complex Modes. In Proceedings of the International Conference on Noise and Vibration Engineering, Leuven, Belgium, 20–22 September 2010; pp. 2713–2726. [Google Scholar]
- Bhusal, U.; Tezcan, J. Automatic Density-Based Clustering for Operational Modal Analysis. Nat. Hazards Rev. 2025, 26, 04025004. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the KDD, Portland, OR, USA, 2–4 August 1996; Volume 96, pp. 226–231. [Google Scholar]
- Ye, C.; Zhao, X. Automated Operational Modal Analysis Based on DBSCAN Clustering. In Proceedings of the 2020 International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS), Vientiane, Laos, 11–12 January 2020; pp. 864–869. [Google Scholar]
- Boroschek, R.L.; Bilbao, J.A. Interpretation of Stabilization Diagrams Using Density-Based Clustering Algorithm. Eng. Struct. 2019, 178, 245–257. [Google Scholar] [CrossRef]
- Civera, M.; Sibille, L.; Zanotti Fragonara, L.; Ceravolo, R. A DBSCAN-Based Automated Operational Modal Analysis Algorithm for Bridge Monitoring. Measurement 2023, 208, 112451. [Google Scholar] [CrossRef]
- Bendat, J.S.; Piersol, A.G. Random Data: Analysis and Measurement Procedures; John Wiley & Sons: Hoboken, NJ, USA, 2011; ISBN 978-1-118-21082-6. [Google Scholar]
- Xia, X. The Comparison of Modal Analysis Methods Under Ambient Vibration. Master’s Thesis, Central South University, Changsha, China, 2013. [Google Scholar]
- Liu, W.; Yang, N.; Bai, F.; Chang, P. Parameter Optimization of Covariance-driven Stochastic Subspace Identification Method Based on Sensitivity Analysis. Eng. Mech. 2021, 38, 157–167. [Google Scholar]
- Zeng, J.; Hu, Z. Automated Operational Modal Analysis Using Variational Gaussian Mixture Model. Eng. Struct. 2022, 273, 115139. [Google Scholar] [CrossRef]
- Liu, W.; Yang, N.; Law, S.S.; Abruzzese, D.; Bai, F.; Cao, X. Automated Operational Modal Analysis with Adaptive DBSCAN-based Algorithm and Its Engineering Application. J. Civ. Struct. Health Monit. 2025. accepted. [Google Scholar] [CrossRef]
- Magalhães, F.; Cunha, Á.; Caetano, E. Online Automatic Identification of the Modal Parameters of a Long Span Arch Bridge. Mech. Syst. Signal Process. 2009, 23, 316–329. [Google Scholar] [CrossRef]
- Tronci, E.M.; De Angelis, M.; Betti, R.; Altomare, V. Multi-Stage Semi-Automated Methodology for Modal Parameters Estimation Adopting Parametric System Identification Algorithms. Mech. Syst. Signal Process. 2022, 165, 108317. [Google Scholar] [CrossRef]



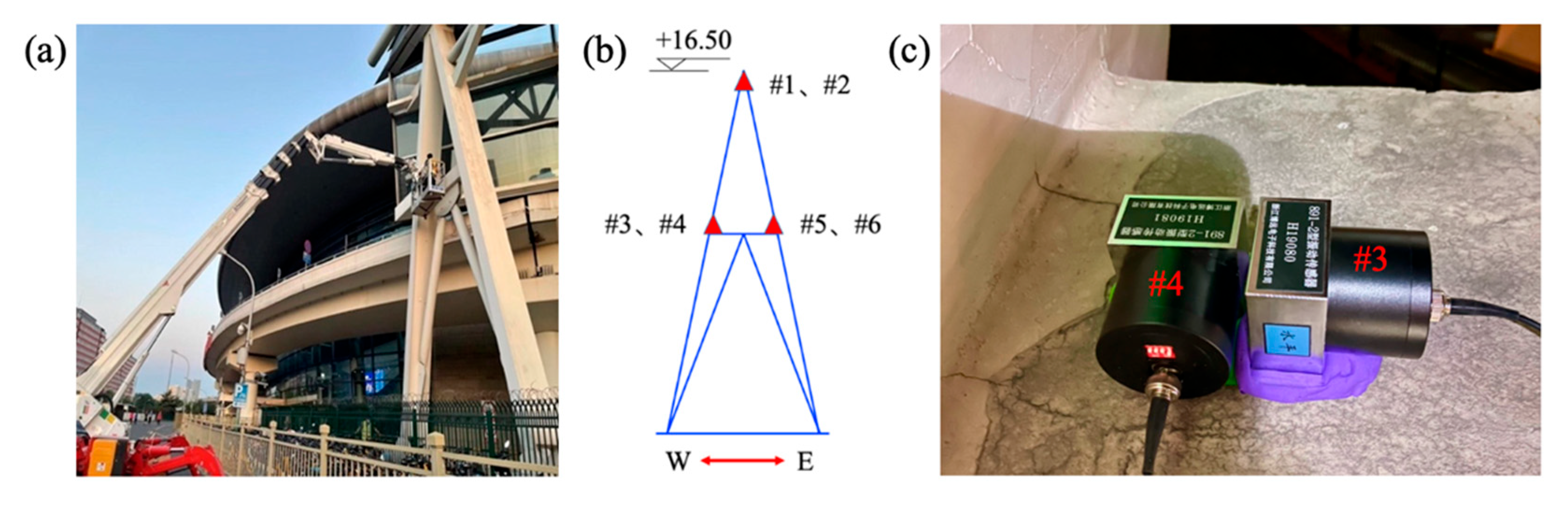







| No. | Position | Direction |
|---|---|---|
| #1 | Tower top | Longitudinal horizontal (in-plane) |
| #2 | Tower top | Lateral horizontal (out-of-plane) |
| #3 | West side of the tower beam | Longitudinal horizontal (in-plane) |
| #4 | West side of the tower beam | Lateral horizontal (out-of-plane) |
| #5 | East side of the tower beam | Longitudinal horizontal (in-plane) |
| #6 | East side of the tower beam | Lateral horizontal (out-of-plane) |
| Mode Order | Frequency (Hz) | Damping Ratio (%) |
|---|---|---|
| 1 | 1.236 | 0.69 |
| 2 | 1.620 | 0.28 |
| 3 | 1.998 | 4.48 |
| Test Point | 1st | 2nd | 3rd |
|---|---|---|---|
| #1 (in-plane) | 0.030 | 0.748 | −0.474 |
| #2 (out-of-plane) | 1.000 | −0.218 | 1.000 |
| #3 (in-plane) | 0.013 | 0.980 | −0.217 |
| #4 (out-of-plane) | 0.576 | −0.177 | 0.558 |
| #5 (in-plane) | 0.017 | 1.000 | −0.214 |
| #6 (out-of-plane) | 0.566 | −0.240 | 0.589 |
| Mode Order | Frequency (Hz) | Damping Ratio (%) |
|---|---|---|
| 1 | 1.220 | 0.69 |
| 2 | 1.589 | 0.27 |
| 3 | 2.046 | 4.81 |
| Test Point | 1st | 2nd | 3rd |
|---|---|---|---|
| #1 (in-plane) | 0.053 | 0.686 | 0.532 |
| #2 (out-of-plane) | 1.000 | 0.082 | 1.000 |
| #3 (in-plane) | −0.064 | 0.939 | 0.168 |
| #4 (out-of-plane) | 0.562 | 0.356 | 0.613 |
| #5 (in-plane) | 0.004 | 1.000 | 0.234 |
| #6 (out-of-plane) | 0.587 | 0.069 | 0.617 |
| No. | Tower A1 | Tower A2 | Differences in Freq. (%) | Differences in Damp. (%) | COMAC | ||
|---|---|---|---|---|---|---|---|
| Freq./ Hz | Damp./(%) | Freq./ Hz | Damp./(%) | ||||
| 1 | 1.236 | 0.69 | 1.220 | 0.69 | 1.29 | 0.56 | 1.00 |
| 2 | 1.620 | 0.28 | 1.589 | 0.27 | 1.91 | 3.18 | 0.82 |
| 3 | 1.998 | 4.48 | 2.046 | 4.81 | 2.39 | 7.34 | 0.45 |
| No. | Tower A1 | Tower A2 | ||||
|---|---|---|---|---|---|---|
| Motion | Dominant Direction | Maximum Amplitude | Motion | Dominant Direction | Maximum Amplitude | |
| 1 | Translation | Out-of-plane (S-N) | Tower top | Translation | Out-of-plane (S-N) | Tower top |
| 2 | Quasi-translation | In-plane (NE-SW) | Beam | Quasi-translation | In-plane (SE-NW) | West side of the tower beam |
| 3 | Quasi-translation | Out-of-plane (NE-SW) | Tower top | Quasi-translation | Out-of-plane (SE-NW) | Tower top |
| Mode | 1 | 2 | 3 | 4 | 5 |
| Freq./Hz | 0.997 | 1.197 | 1.393 | 1.589 | 1.849 |
| Mode | 6 | 7 | 8 | 9 | 10 |
| Freq./Hz | 1.927 | 2.012 | 2.064 | 2.205 | 2.347 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Liu, B.; Feng, H.; Wang, B.; Yang, N.; Gao, Y. Field Dynamic Testing and Adaptive Dynamic Characteristic Identification of Steel Tower Structures in High-Speed Railway Stations Under Limited Sensor Configurations. Buildings 2025, 15, 3754. https://doi.org/10.3390/buildings15203754
Liu W, Liu B, Feng H, Wang B, Yang N, Gao Y. Field Dynamic Testing and Adaptive Dynamic Characteristic Identification of Steel Tower Structures in High-Speed Railway Stations Under Limited Sensor Configurations. Buildings. 2025; 15(20):3754. https://doi.org/10.3390/buildings15203754
Chicago/Turabian StyleLiu, Wei, Boqi Liu, Hailong Feng, Bo Wang, Na Yang, and Yuan Gao. 2025. "Field Dynamic Testing and Adaptive Dynamic Characteristic Identification of Steel Tower Structures in High-Speed Railway Stations Under Limited Sensor Configurations" Buildings 15, no. 20: 3754. https://doi.org/10.3390/buildings15203754
APA StyleLiu, W., Liu, B., Feng, H., Wang, B., Yang, N., & Gao, Y. (2025). Field Dynamic Testing and Adaptive Dynamic Characteristic Identification of Steel Tower Structures in High-Speed Railway Stations Under Limited Sensor Configurations. Buildings, 15(20), 3754. https://doi.org/10.3390/buildings15203754






