Shear Behavior of Dowel–Stud Hybrid Connectors for HSS-HPC Composite Structures: Geometry Optimization and Material Synergistic Effects
Abstract
1. Introduction
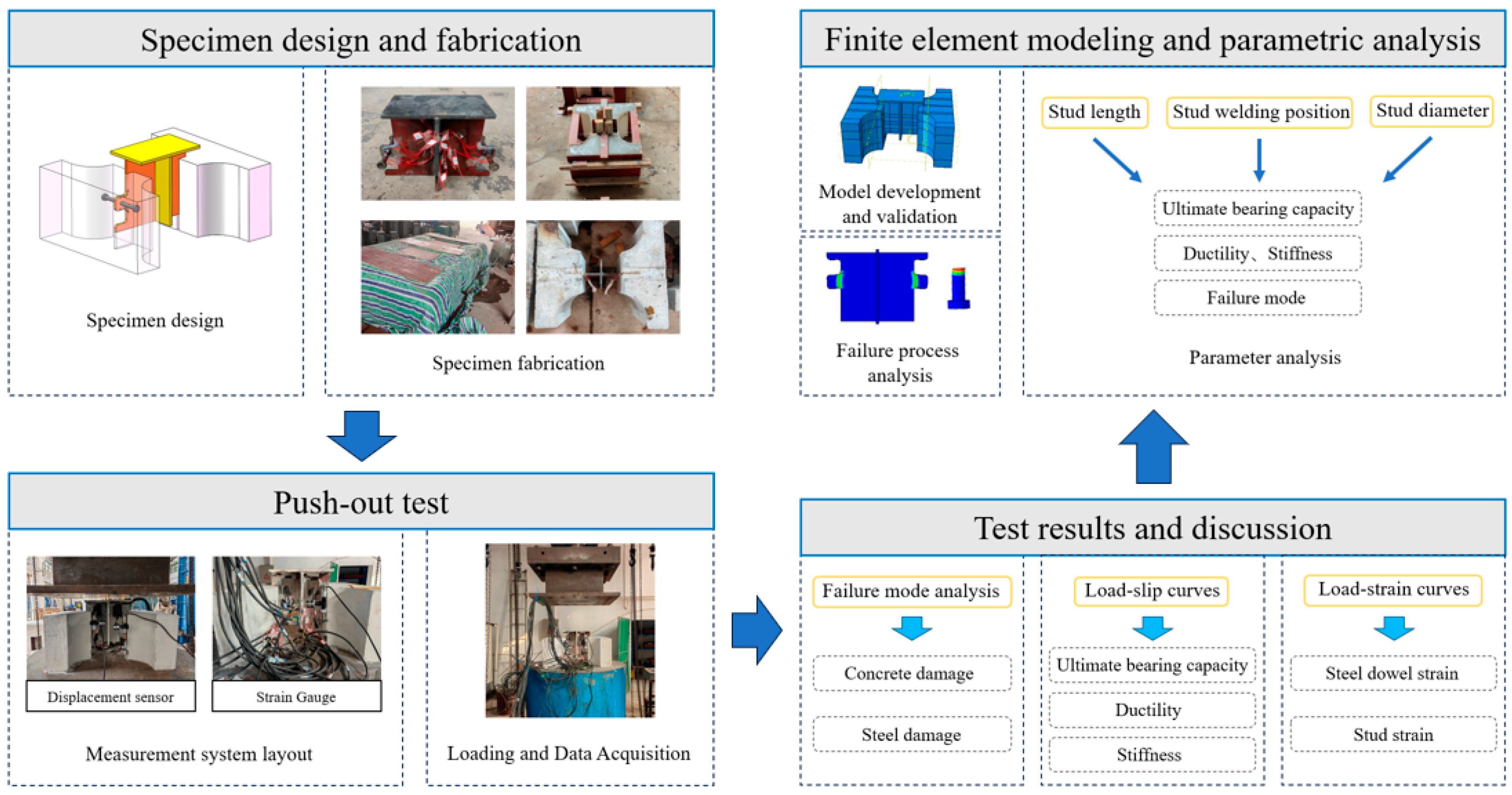
2. Experimental Program
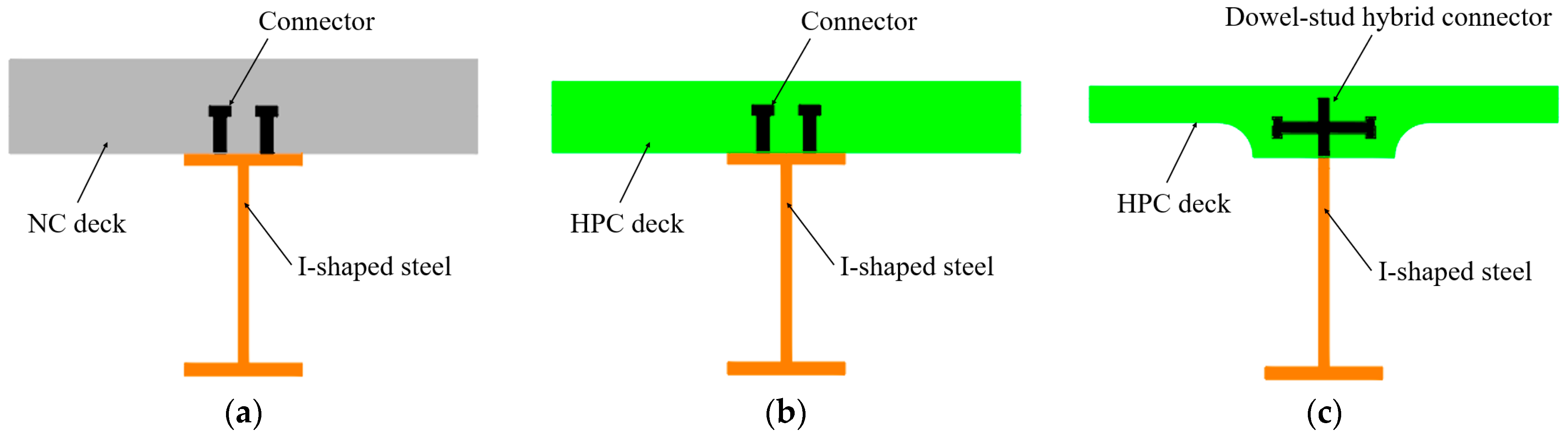
2.1. Specimen Design and Fabrication
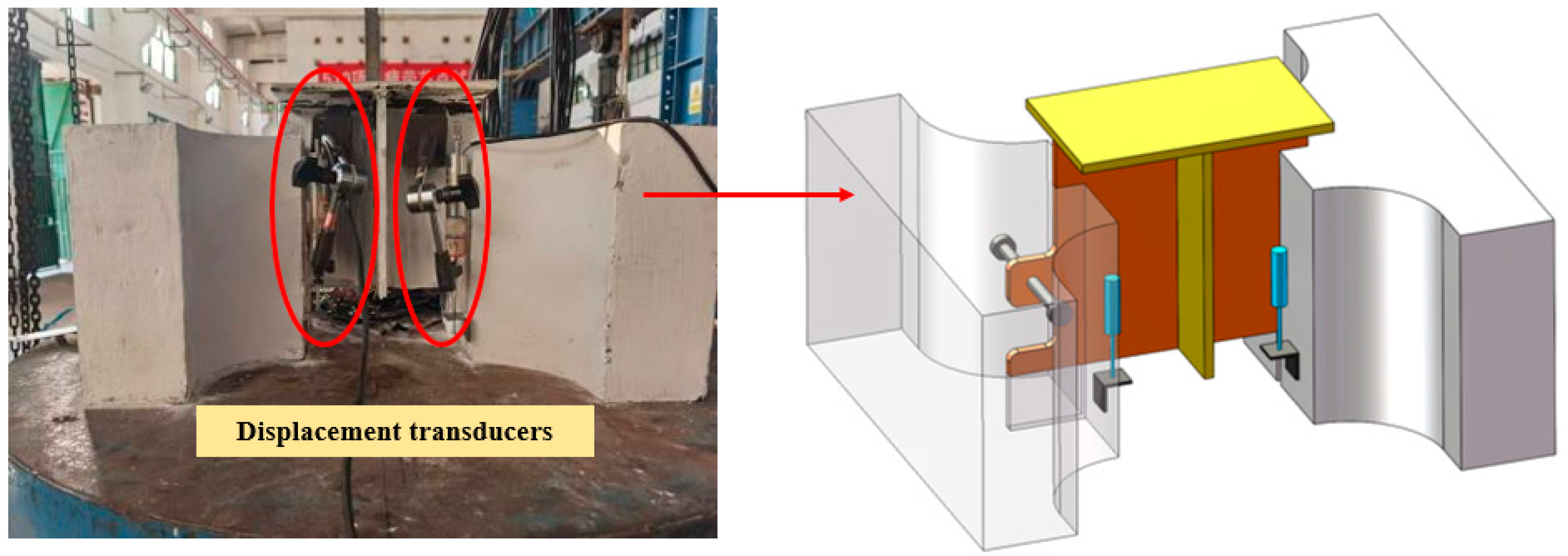
2.2. Layout of Measurement Points
2.3. Test Device and Loading Procedure
3. Test Results and Discussion
3.1. Test Phenomena and Failure Mode
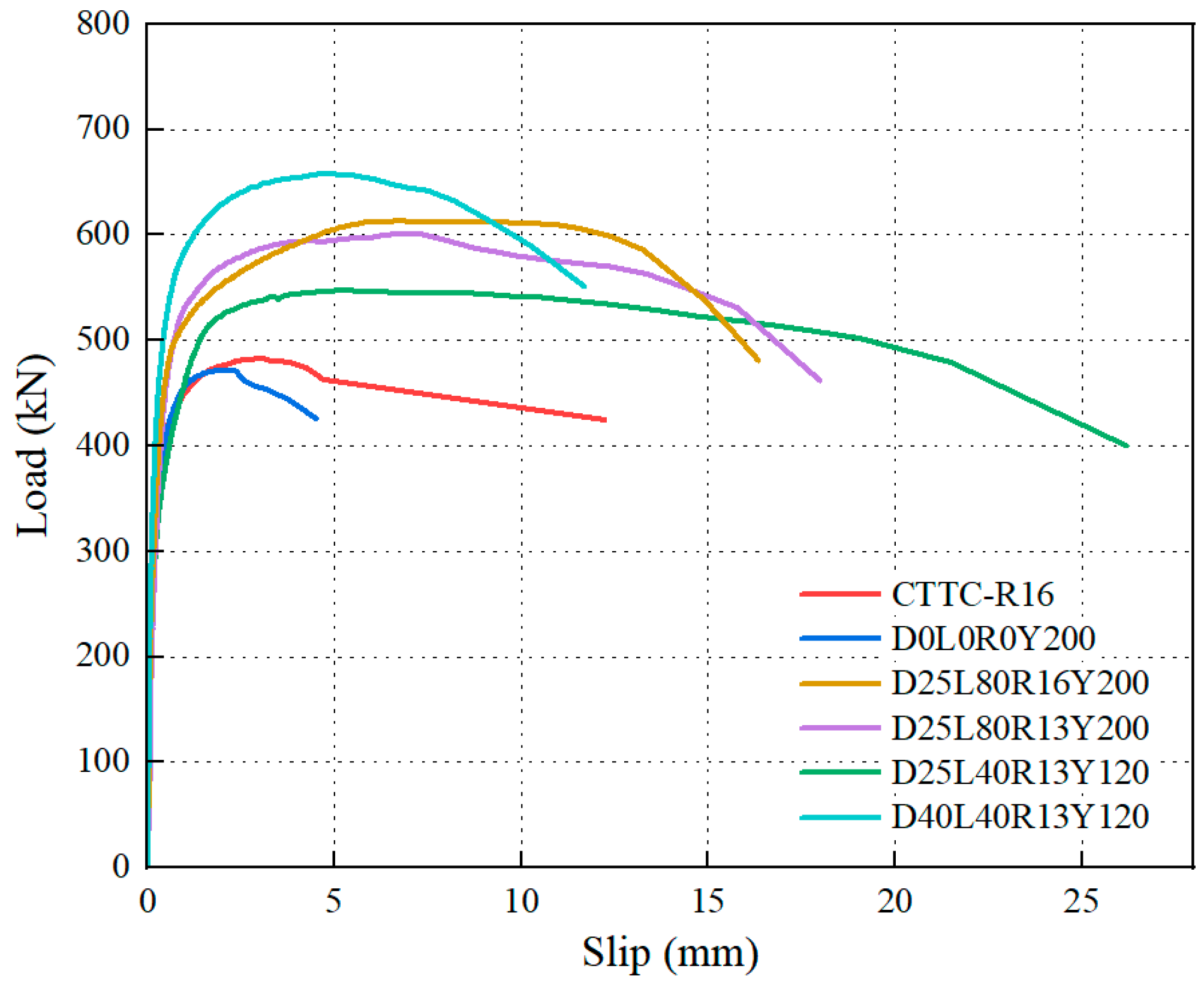
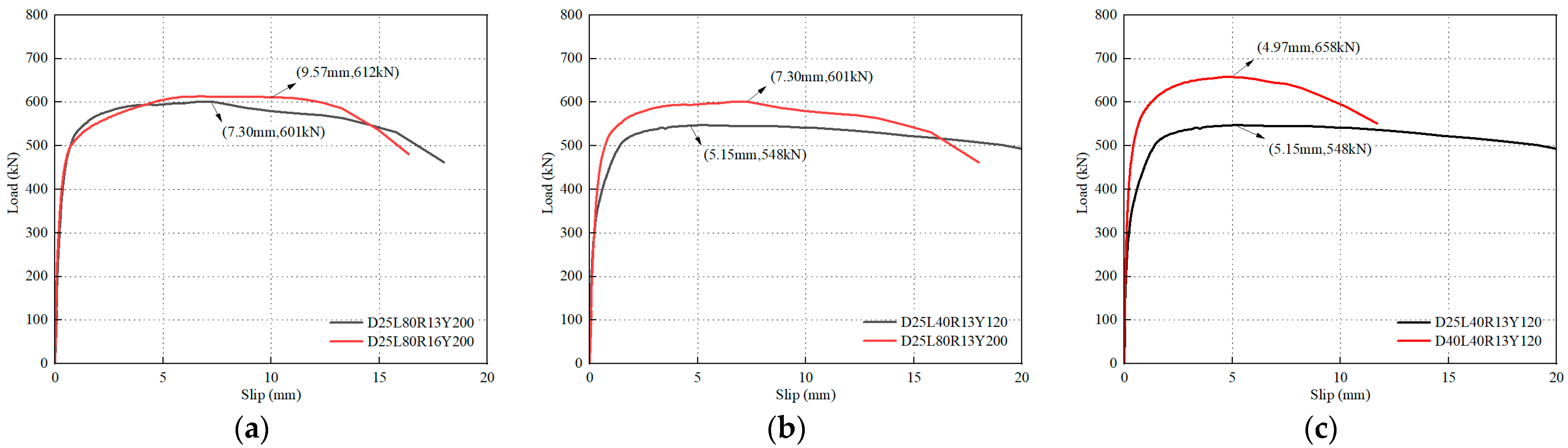
3.2. Load-Slip Curves
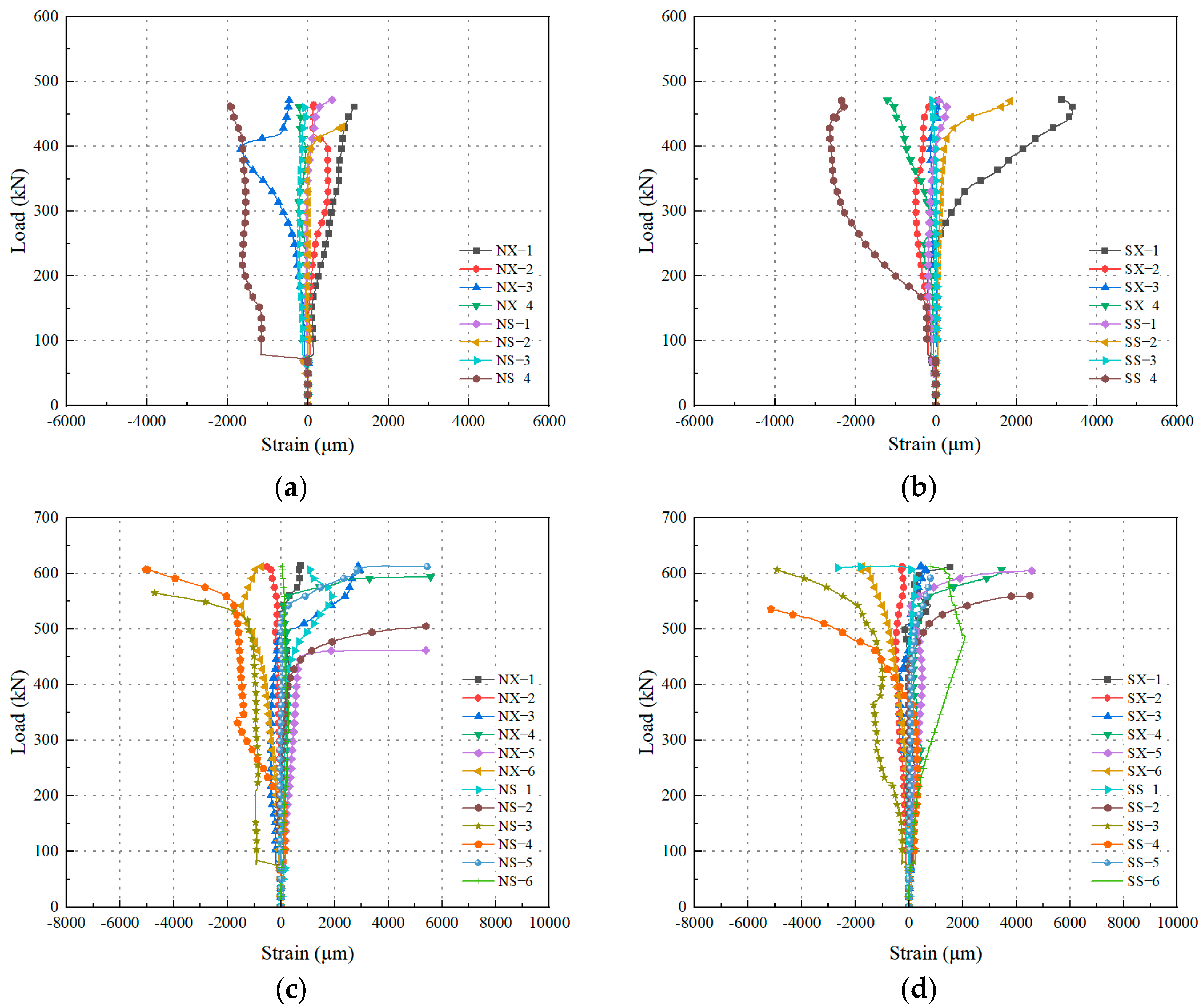
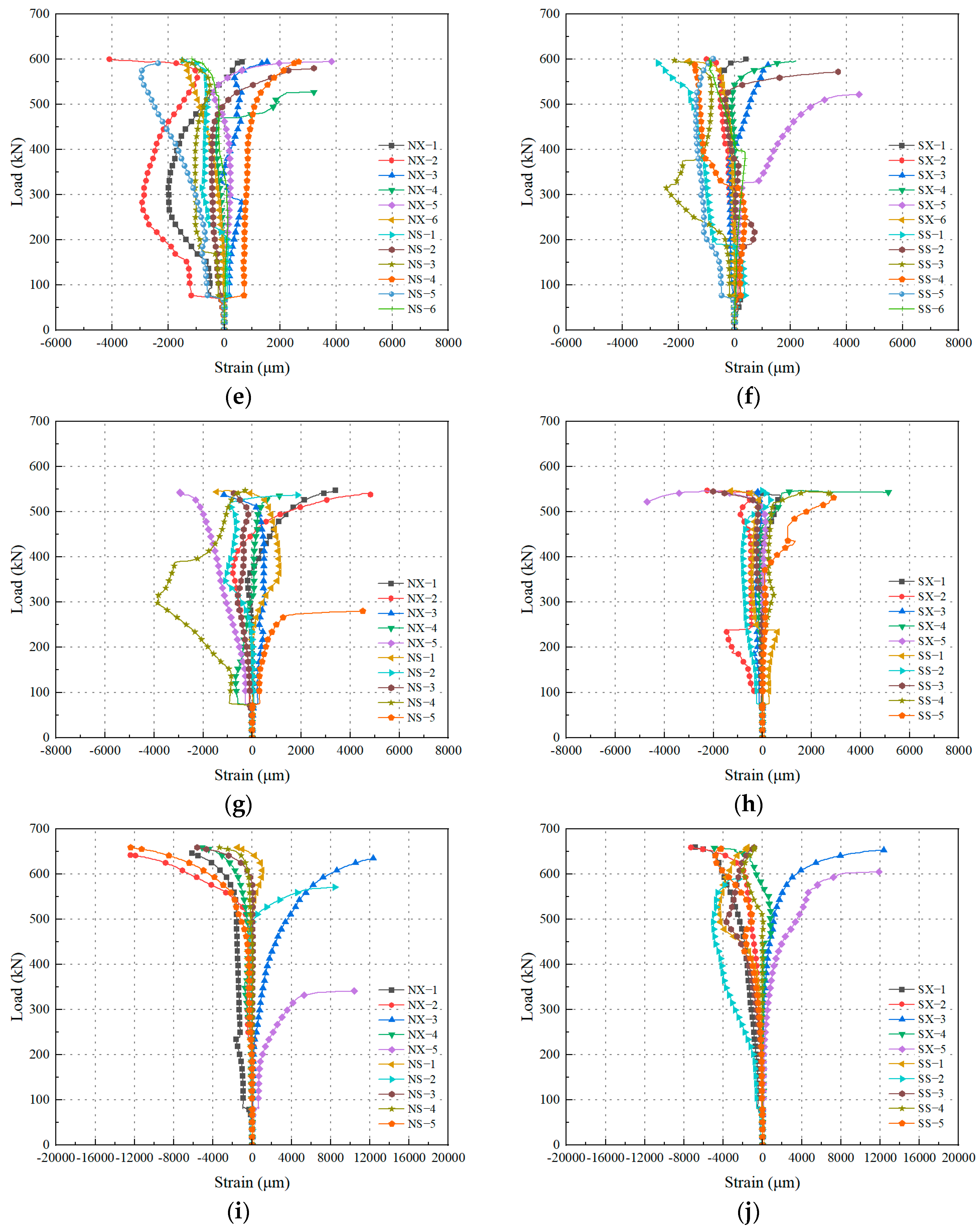
3.3. Load–Strain Curves
3.4. Static Mechanical Properties of Specimens
4. Finite Element Analysis and Validation
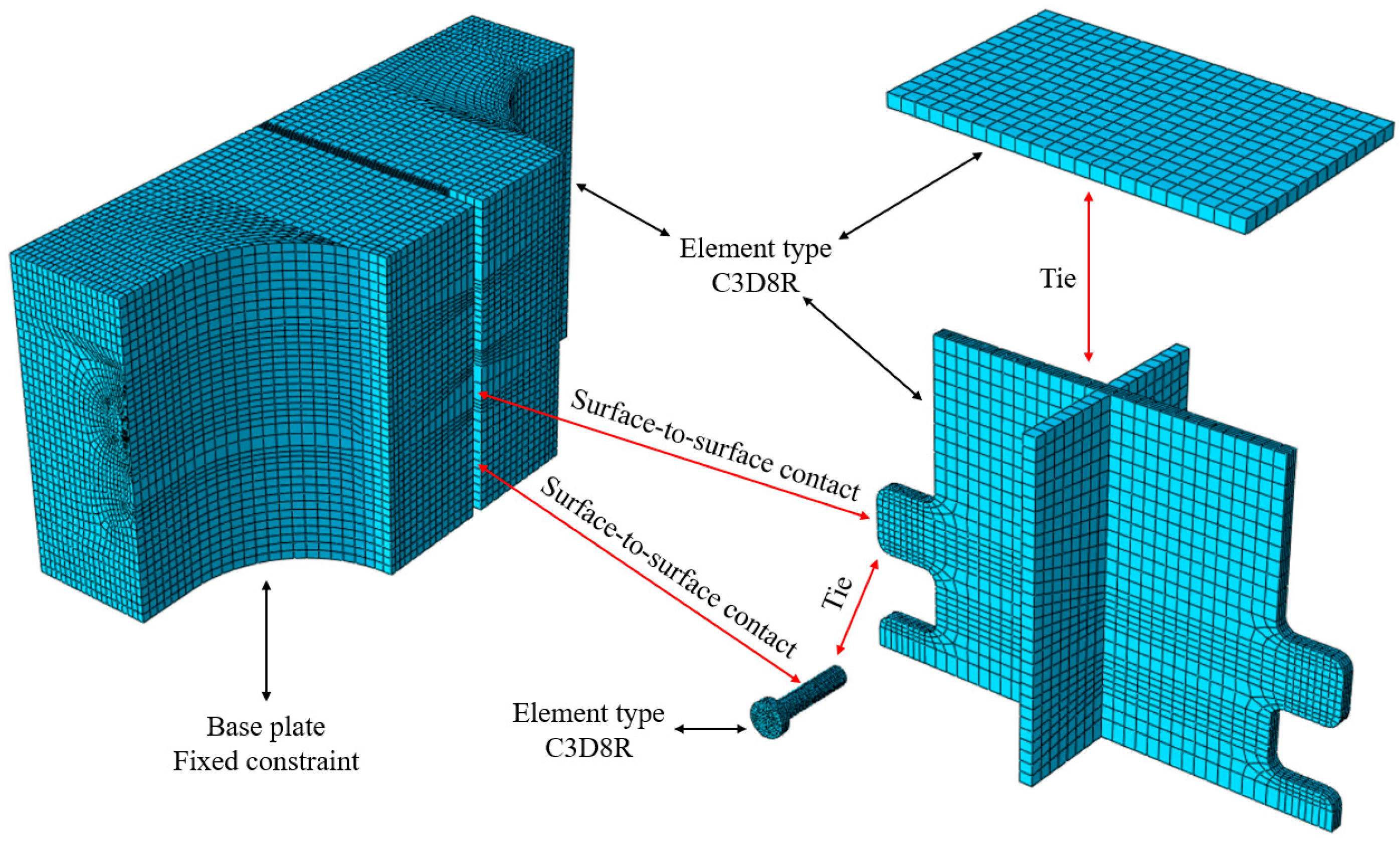
4.1. Finite Element Analysis Model
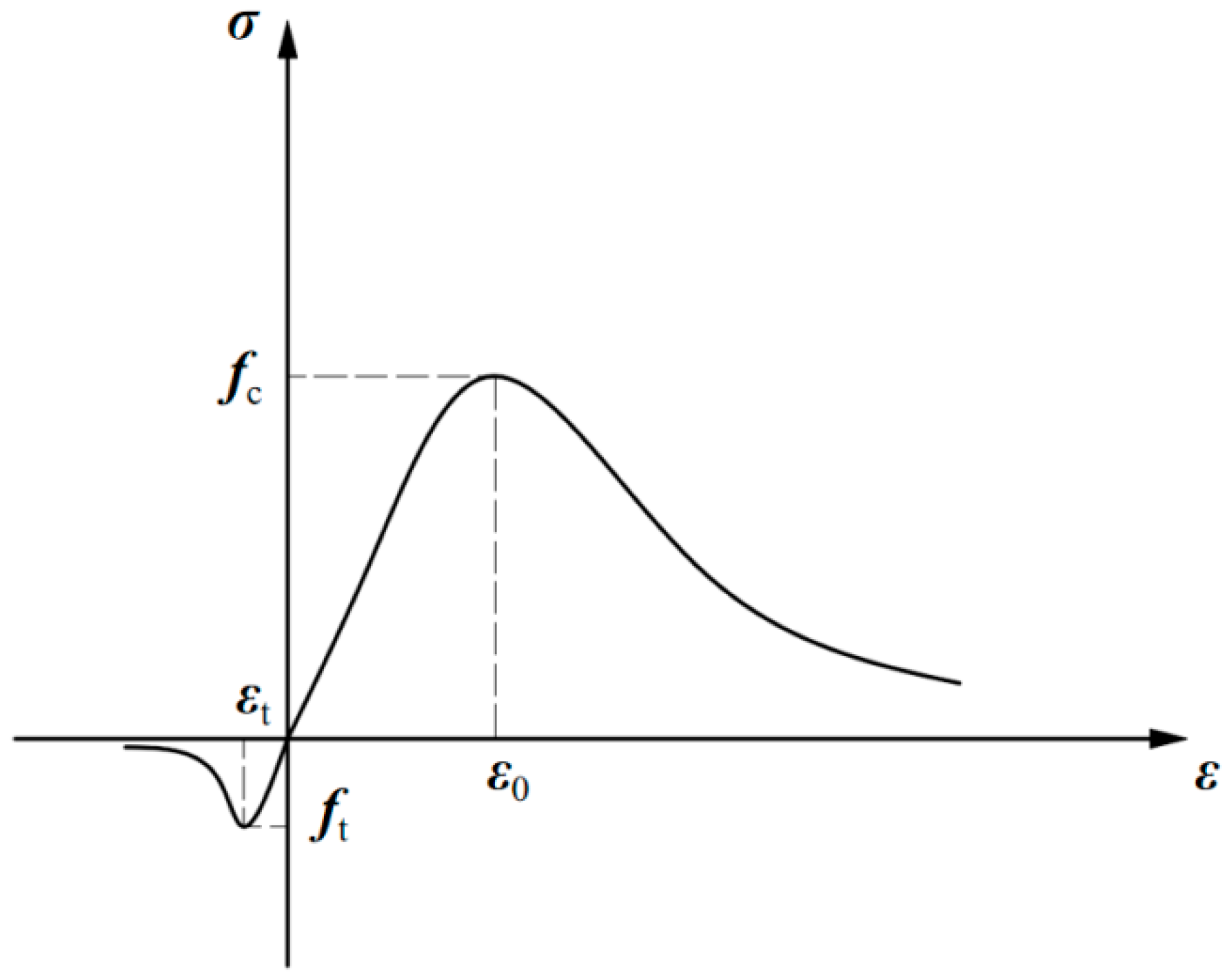
4.2. Constitutive Relationship of Materials
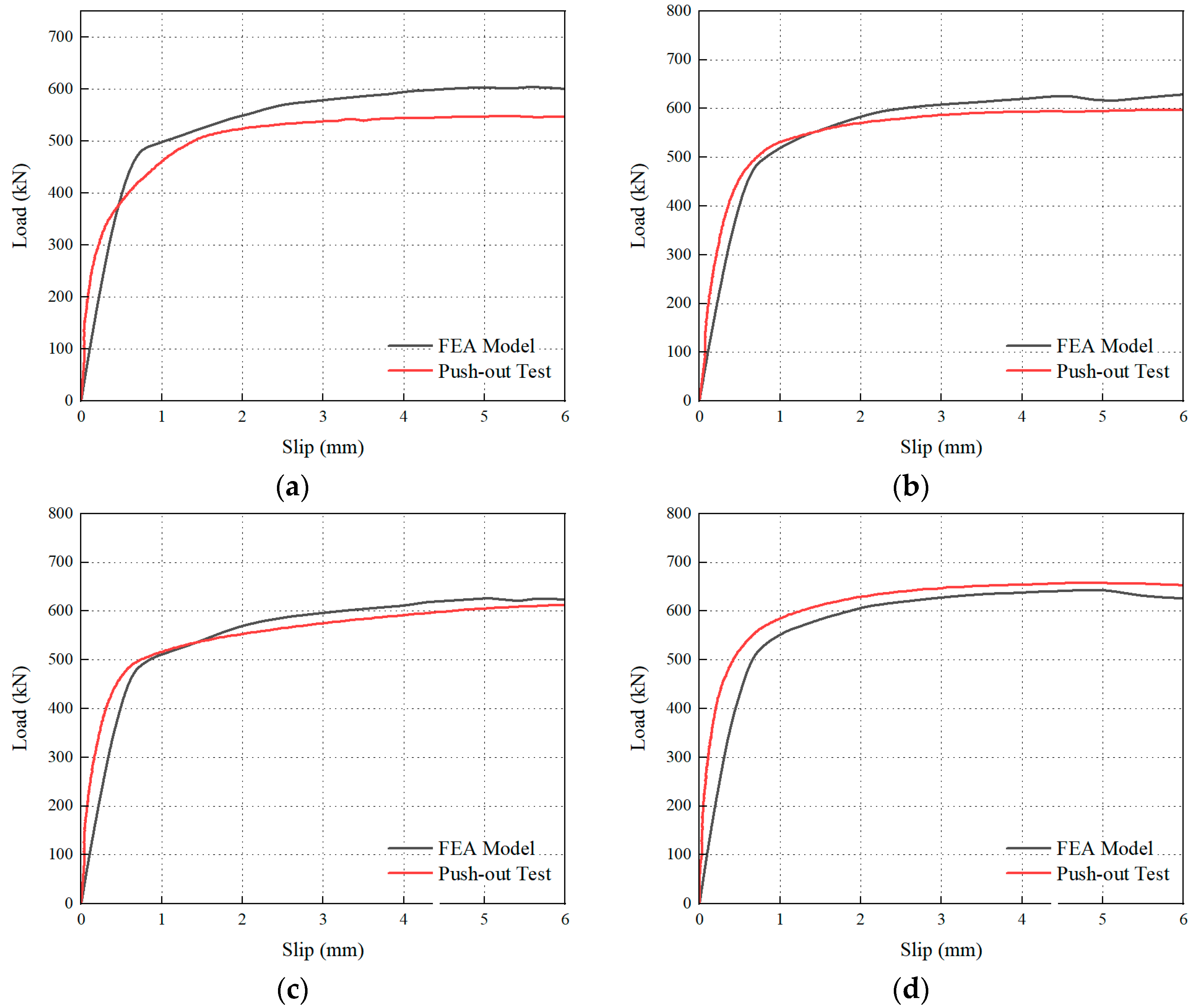
4.3. Model Validation
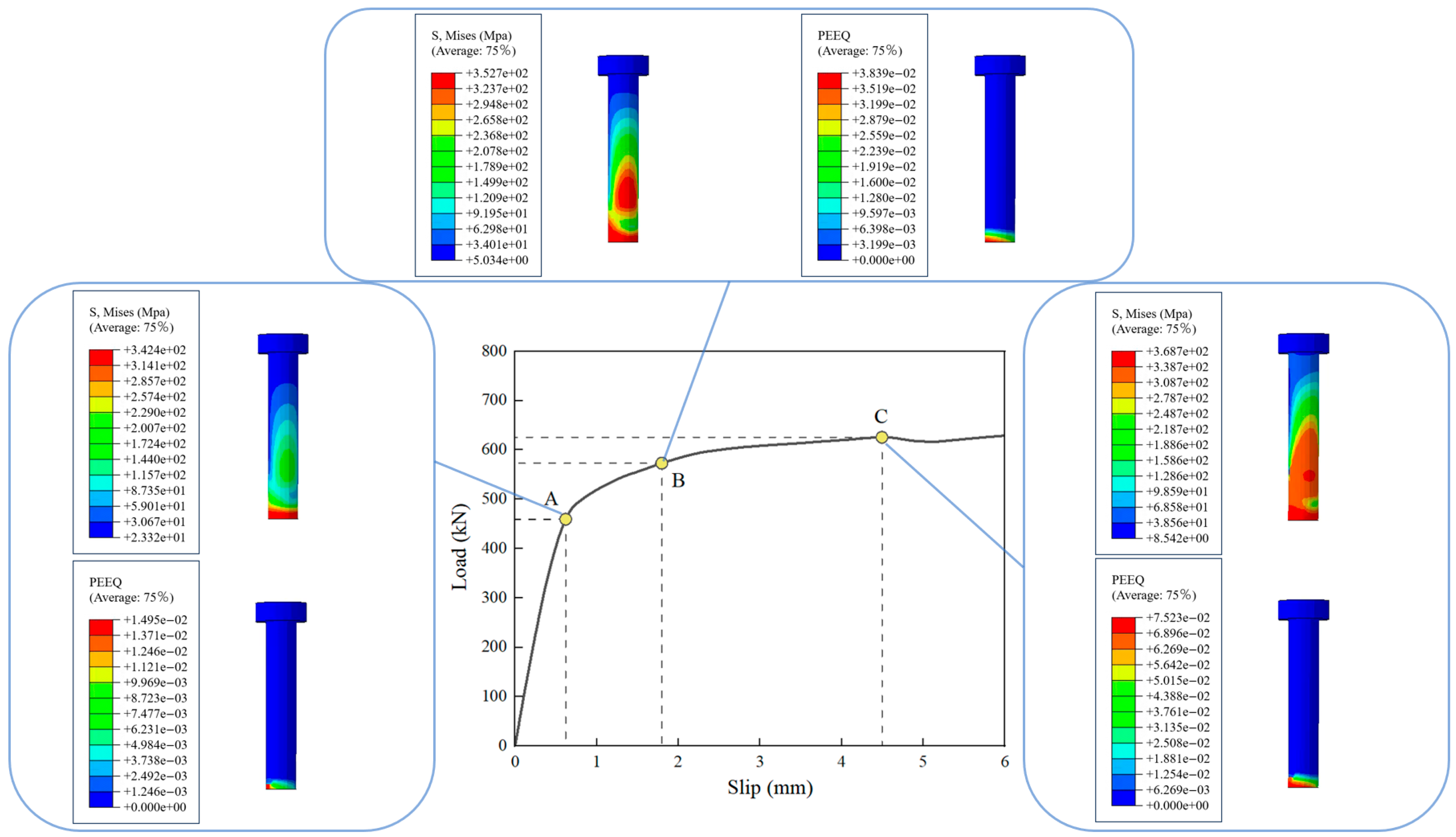
5. Failure Process Analysis
6. Parametric Analysis
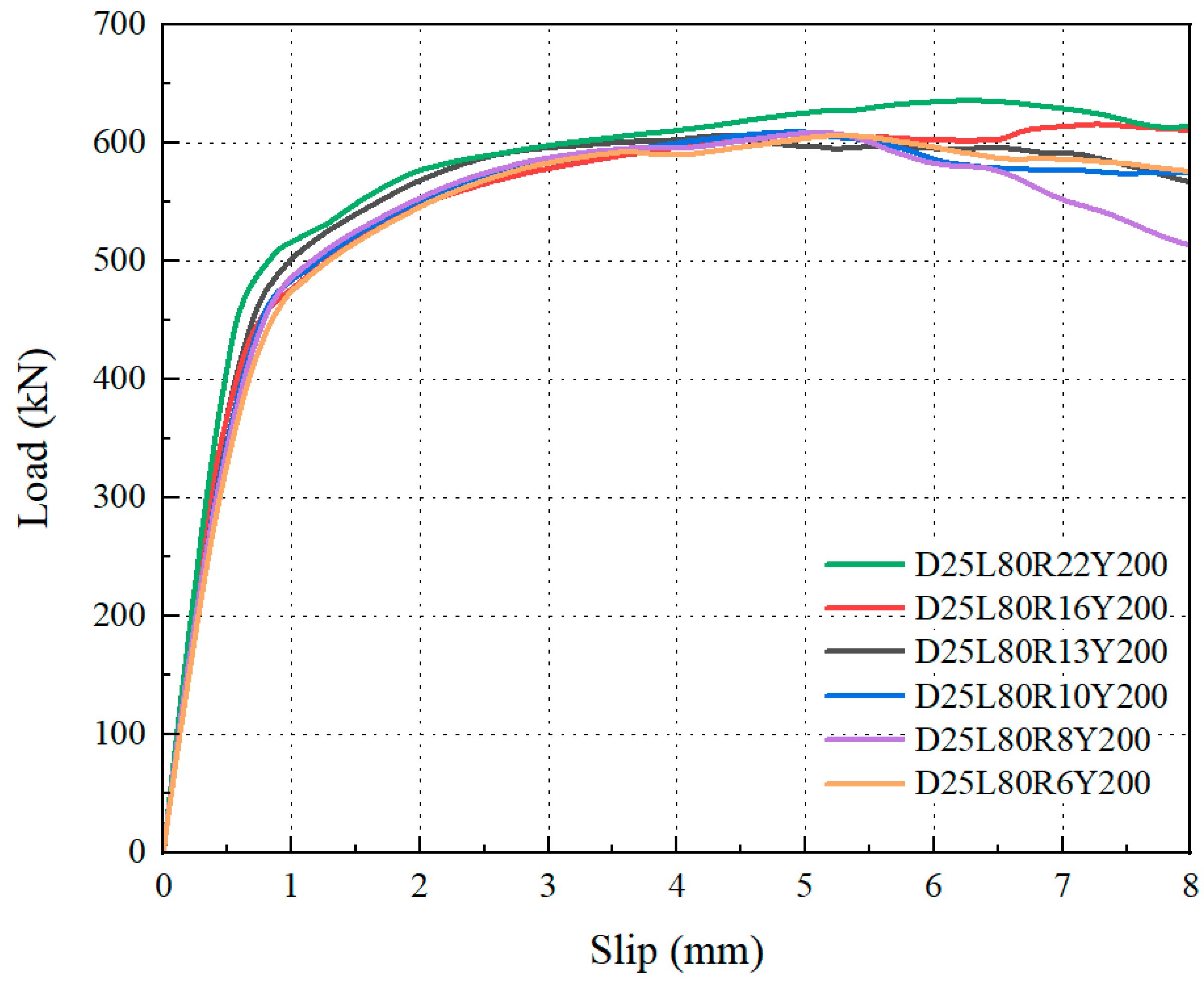
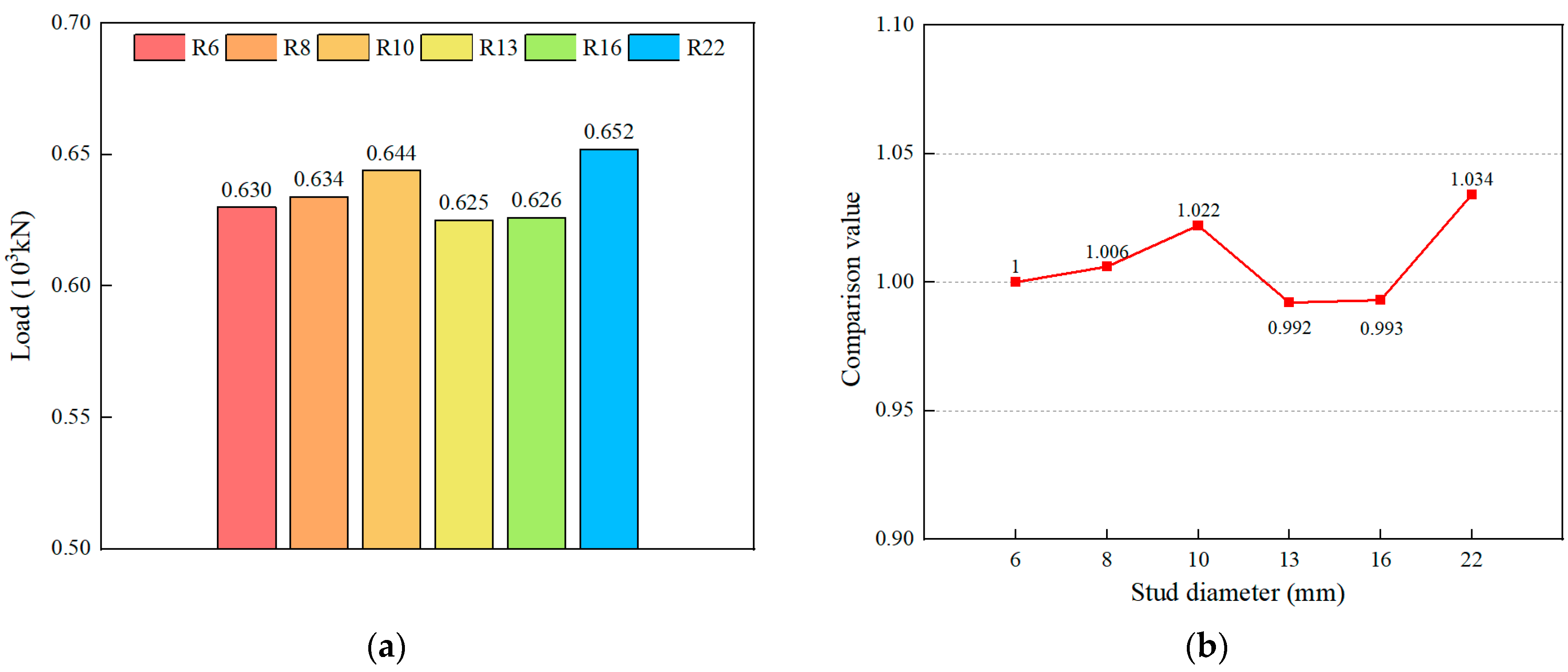
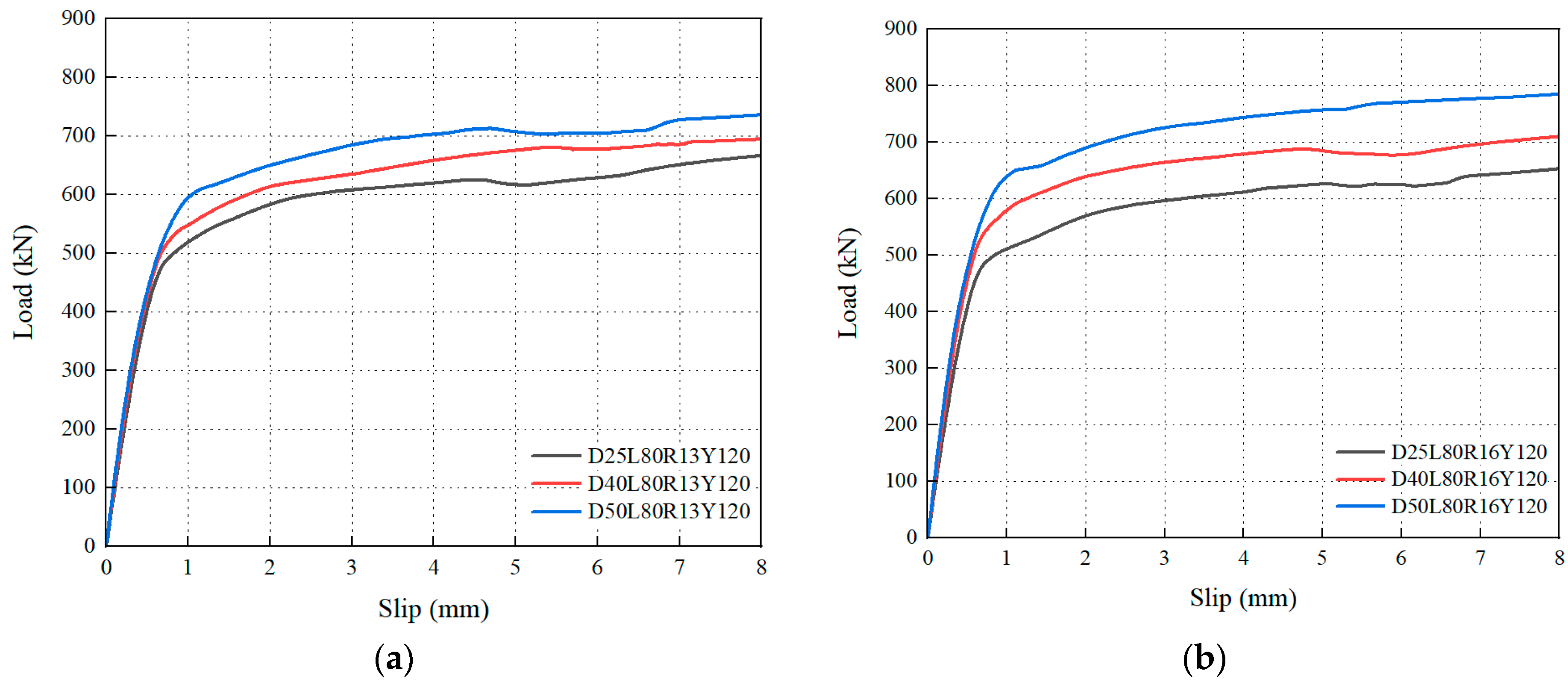
6.1. Effect of the Stud Diameter
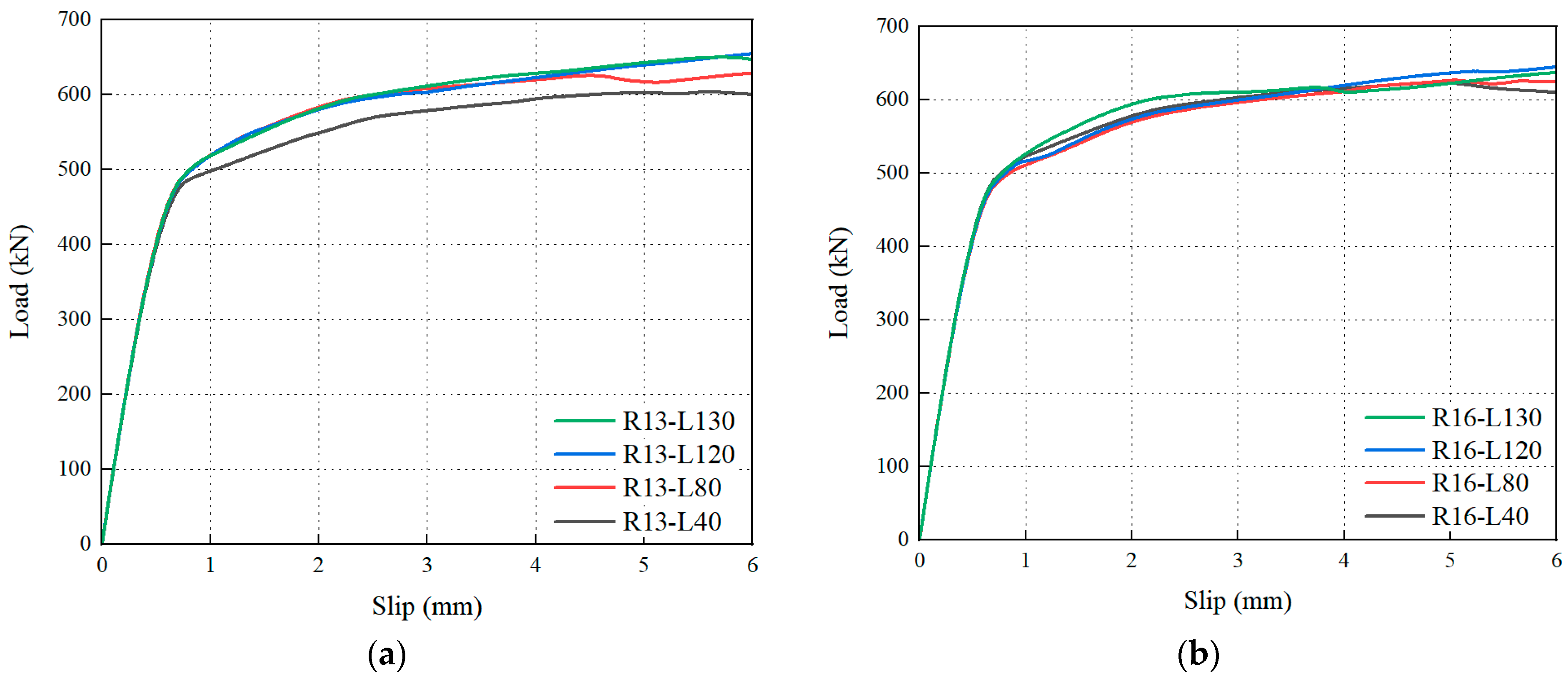
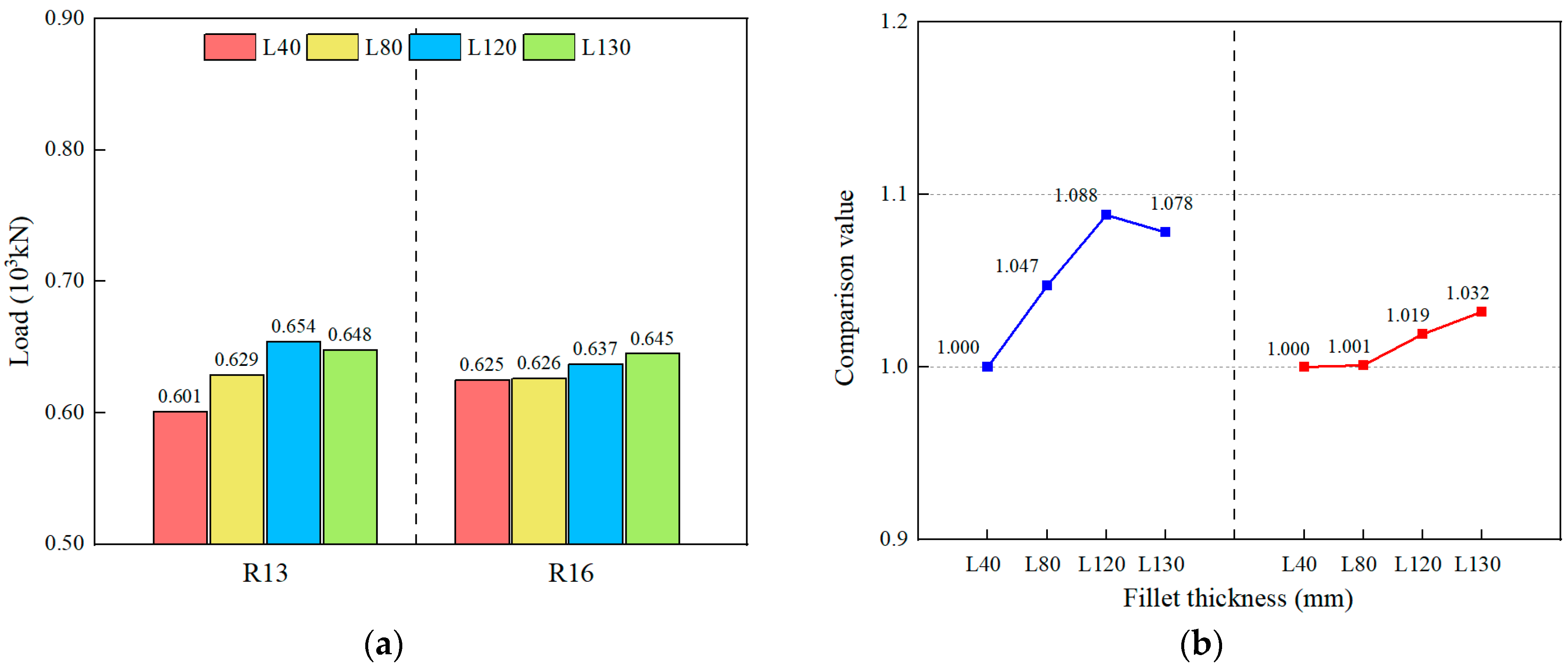
6.2. Effect of the Stud Length
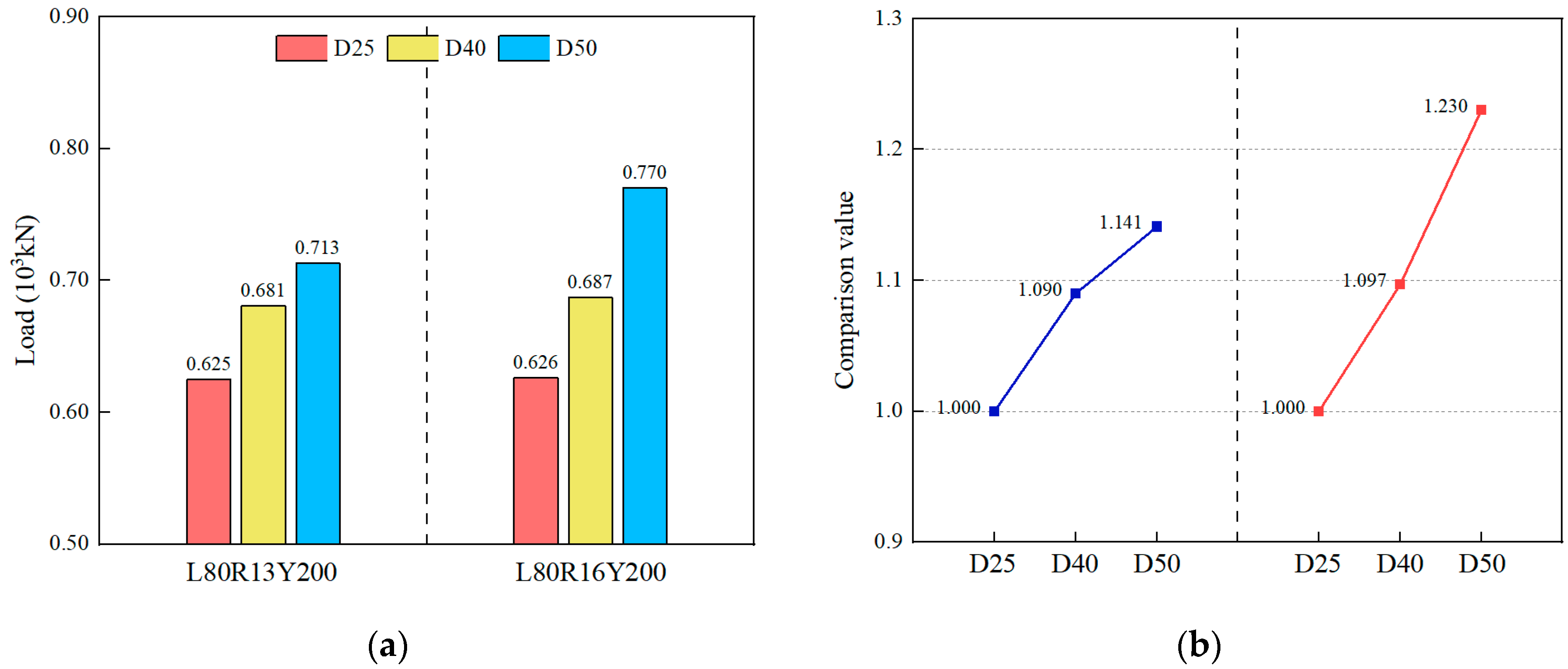
6.3. Effect of the Stud Welding Location
7. Conclusions
- (1)
- Compared to conventional stud connectors and steel dowel connectors, the dowel–stud hybrid connector possessed a higher shear capacity and ductility. The primary failure modes consisted of plastic failure at the roots of both the steel dowel and stud, accompanied by localized crushing of concrete in the lower region.
- (2)
- When the stud diameter increased from 6 mm to 22 mm, the variation in the shear capacity remained within 4%, indicating negligible effects on both the shear capacity and stiffness of the hybrid connectors. However, due to differences in the weld area at the stud root, caused by varying diameters, push-out tests revealed that shear failure occurred at the stud root with a diameter of 13 mm, while the failure mode transitioned to shear fracture at the steel dowel root with a diameter of 16 mm. It is recommended that the optimal value for the stud diameter be 16 mm.
- (3)
- For 13 mm studs, the ultimate load-bearing capacity increased with increasing stud length, reaching a maximum 8.8% enhancement at a 120 mm length. Under 16 mm diameter conditions, increased stud length exerted negligible influence on the ultimate capacity. Elongated studs intensified stress concentration in the concrete beneath studs, delaying the onset of localized concrete failure. It is recommended that the optimal value for the stud length be 80 mm.
- (4)
- The welding location significantly affected the shear capacity, with the shear capacity increasing by up to 23% when welding shifted from the dowel center (D25) to the root underside (D50). Relocating welds toward the web direction shortened load-transfer paths, concentrating uplift resistance on the steel dowel and enabling full mobilization of the stud’s shear capacity, thereby enhancing the overall connector performance. It is recommended that the optimal welding position for the studs be 50 mm below the top of the dowel.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Classen, M.; Herbrand, M.; Kueres, D.; Hegger, J. Derivation of design rules for innovative shear connectors in steel-concrete composites through the systematic use of non-linear finite element analysis (FEA). Struct. Concr. 2016, 17, 646–655. [Google Scholar] [CrossRef]
- El-Zohairy, A.; Salim, H.; Shaaban, H. Experimental investigation on fatigue behavior of composite beams with different studs arrangements. Structures 2022, 35, 146–159. [Google Scholar] [CrossRef]
- Lorenc, W.; Kurz, W.; Seidl, G. Hybrid steel–concrete sections for bridges: Definition and basis for design. Eng. Struct. 2022, 270, 114902. [Google Scholar] [CrossRef]
- Venkateshwaran, A.; Binglin, L.; Liew, J.Y.R. Design of Steel Fiber-Reinforced High-Strength Concrete-Encased Steel Short Columns and Beams. ACI Struct. J. 2021, 118, 45–59. [Google Scholar] [CrossRef]
- Lai, B.; Liew, J.Y.R. Design and testing of concrete encased steel composite beam-columns with C90 concrete and S690 steel section. Eng. Struct. 2020, 220, 110995. [Google Scholar] [CrossRef]
- Ban, H.; Bradford, M.A. Flexural behaviour of composite beams with high strength steel. Eng. Struct. 2013, 56, 1130–1141. [Google Scholar] [CrossRef]
- Shamass, R.; Cashell, K. Behaviour of composite beams made using high strength steel. Structures 2017, 12, 88–101. [Google Scholar] [CrossRef]
- Zhang, Y.; Cai, S.; Zhu, Y.; Fan, L.; Shao, X. Flexural responses of steel-UHPC composite beams under hogging moment. Eng. Struct. 2020, 206, 110134. [Google Scholar] [CrossRef]
- Tong, L.; Chen, L.; Wang, X.; Zhu, J.; Shao, X.; Zhao, Z. Experiment and finite element analysis of bending behavior of high strength steel-UHPC composite beams. Eng. Struct. 2022, 266, 114594. [Google Scholar] [CrossRef]
- Zou, Y.; Di, J.; Zhou, J.; Zhang, Z.; Li, X.; Zhang, H.; Qin, F. Shear behavior of perfobond connectors in the steel-concrete joints of hybrid bridges. J. Constr. Steel Res. 2020, 172, 106217. [Google Scholar] [CrossRef]
- Johnson, R.P. Composite Structures of Steel and Concrete: Beams, Slabs, Columns and Frames for Buildings; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Girhammar, U.A.; Gopu, V.K.A. Composite beam-columns with interlayer slip—Exact analysis. J. Struct. Eng. 1993, 119, 1265–1282. [Google Scholar] [CrossRef]
- Lorenc, W.; Kożuch, M.; Rowiński, S. The behaviour of puzzle-shaped composite dowels—Part I: Experimental study. J. Constr. Steel Res. 2014, 101, 482–499. [Google Scholar] [CrossRef]
- Suzuki, A.; Suzuki, K.; Kimura, Y. Ultimate shear strength of perfobond shear connectors subjected to fully reversed cyclic loading. Eng. Struct. 2021, 248, 113240. [Google Scholar] [CrossRef]
- Wang, B.; Huang, Q.; Liu, X. Comparison of static and fatigue behaviors between stud and perfobond shear connectors. KSCE J. Civ. Eng. 2019, 23, 217–227. [Google Scholar] [CrossRef]
- Zhan, Y.; Yin, C.; Liu, F.; Song, R.; Deng, K.; Sun, J. Pushout tests on headed studs and PBL shear connectors considering external pressure. J. Bridg. Eng. 2020, 25, 04019125. [Google Scholar] [CrossRef]
- Chen, Y.; Ning, J.; Ren, C.; Yang, Y. A strength degradation model of PBL shear connectors under fatigue load. Structures 2023, 48, 1684–1692. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, L.; Wei, X.; Liao, X.; Wang, S. Investigation on fatigue performance and life prediction of PBL connectors in steel-UHPC composite structure. Eng. Struct. 2025, 329, 119762. [Google Scholar] [CrossRef]
- Lin, T. Research on Structural Performance of New Composite Beams with Toothed Shear Connectors. Master’s Thesis, Tongji University, Shanghai, China, 2020. [Google Scholar]
- Lorenc, W.; Seidl, G.; Berthellemy, J. The evolution of the shape of composite dowels. Stud. Geotech. Mech. 2022, 44, 296–316. [Google Scholar] [CrossRef]
- Huang, P.; He, J.; Kong, F.; Mei, K.; Li, X. Experimental study on the bearing capacity of PZ shape composite dowel shear connectors with elliptical holes. Sci. Rep. 2022, 12, 2457. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhang, Q.; Bao, Y.; Deng, P.; Wei, C.; Li, M. Flexural behavior of corrugated steel-UHPC composite bridge decks. Eng. Struct. 2021, 246, 113066. [Google Scholar] [CrossRef]
- Harsanyi, P.; Randl, N.; Tue, N.V. DIC-based failure analysis of high-strength continuous steel shear dowels for composite UHPFRC steel construction. Eng. Struct. 2021, 247, 113093. [Google Scholar] [CrossRef]
- Altoé, J.V.F.; Faria, C.S.d.; Petrauski, M.C.; Pereira, C.L.; Paes, J.L.R.; Veríssimo, G.d.S. Composite dowels shear connectors for steel-concrete composite beams: A review. Rev. IBRACON Estrut. Mater. 2025, 18, e18204. [Google Scholar] [CrossRef]
- Silveira, E.G.d.; Caldas, R.B.; Santos, L.R. Steel failure mode of composite dowel shear connector with rectangular regular cutoff. Rev. IBRACON Estrut. Mater. 2023, 17, e17310. [Google Scholar] [CrossRef]
- Suzuki, A.; Hiraga, K.; Kimura, Y. Mechanical performance of puzzle-shaped shear connectors subjected to fully reversed cyclic stress. J. Struct. Eng. 2023, 149, 04023087. [Google Scholar] [CrossRef]
- Classen, M.; Hegger, J. Shear-slip behaviour and ductility of composite dowel connectors with pry-out failure. Eng. Struct. 2017, 150, 428–437. [Google Scholar] [CrossRef]
- Almeida, R.L.J.d.; Veríssimo, G.d.S.; Ribeiro, J.C.L.; Paes, J.L.R.; Caldas, R.B.; Cardoso, H.d.S.; Fakury, R.H. Assessing the bearing capacity of Crestbond shear connectors to concrete pry-out. Rev. IBRACON Estrut. Mater. 2023, 16, e16107. [Google Scholar] [CrossRef]
- Christou, G.; Wolters, K.; Ungermann, J.; Classen, M.; Hegger, J. Combined shear-tension loading of composite dowels in cracked concrete—Experimental investigations and design. Appl. Sci. 2022, 12, 1449. [Google Scholar] [CrossRef]
- Kopp, M.; Wolters, K.; Claßen, M.; Hegger, J.; Gündel, M.; Gallwoszus, J.; Heinemeyer, S.; Feldmann, M. Composite dowels as shear connectors for composite beams–Background to the design concept for static loading. J. Constr. Steel Res. 2018, 147, 488–503. [Google Scholar] [CrossRef]
- GB/T 228.1-2021; Metallic materials—Tensile Testing—Part 1: Method of Test at Room Temperature. China Standard Press: Beijing, China, 2021.
- GB/T 50152-2012; Test Methods of Concrete Structures. China Standard Press: Beijing, China, 2012.
- GB/T 50107-2010; Evaluation of Concrete Compressive Strength. China Standard Press: Beijing, China, 2010.
- GB/T 1591-2018; High strength low alloy structural steels. China Standard Press: Beijing, China, 2018.
- Yang, J.; Fang, Z. Research on stress-strain relation of ultra high performance concrete. Concrete 2008, 7, 11–15. [Google Scholar]
- Du, R. Study on the Ultimate Bearing Capacity of Reactive Powder Concrete Beams and Arches. Master’s Thesis, Fuzhou University, Fuzhou, China, 2014. [Google Scholar]
- Ma, Y.; Zhang, B.; Peng, A.; Wang, L. Experimental and analytical investigation on shear mechanism of steel-UHPC composite T-Perfobond shear connectors. Eng. Struct. 2023, 286, 116061. [Google Scholar] [CrossRef]

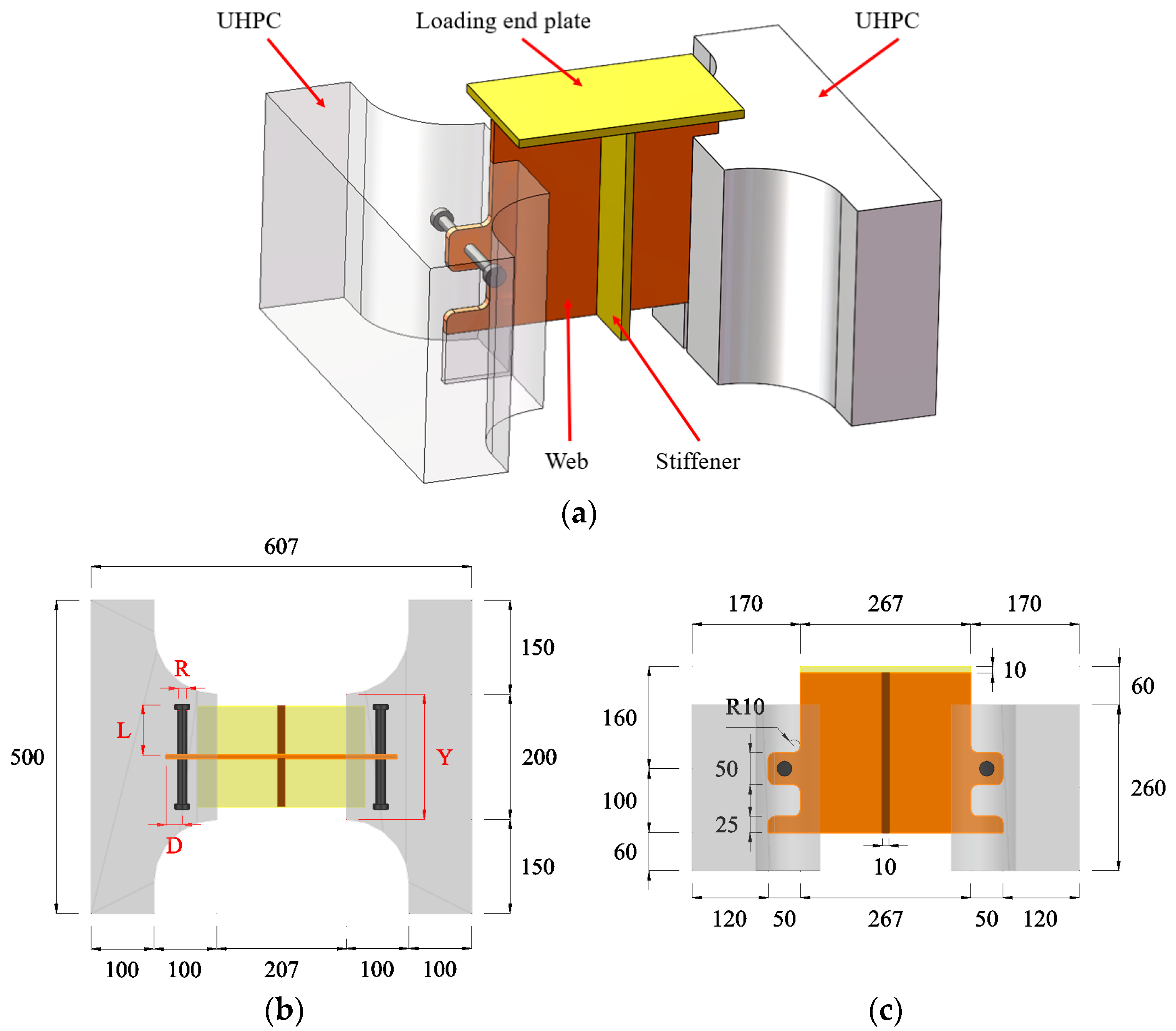













| Specimen Number | D (mm) | L (mm) | R (mm) | Y (mm) |
|---|---|---|---|---|
| CTTC-R16 | — | — | 16 | — |
| D0L0R0Y200 | — | — | — | 200 |
| D25L80R16Y200 | 25 | 80 | 16 | 200 |
| D25L80R13Y200 | 25 | 80 | 13 | 200 |
| D25L40R13Y120 | 25 | 40 | 13 | 120 |
| D40L40R13Y120 | 40 | 40 | 13 | 120 |
| Specimen Number | Ultimate Load (kN) | fcu,o (MPa) | fcu,k (MPa) |
|---|---|---|---|
| 1 | 947 | 95 | 90 |
| 2 | 998 | 100 | 95 |
| 3 | 976 | 98 | 93 |
| Average | 973 | 97 | 92 |
| Steel Grade | Steel Thickness (mm) | Yield Strength, fy (MPa) | Tensile Strength, ft (MPa) | ft/fy | Elongation (%) |
|---|---|---|---|---|---|
| Q345 | 10 | 421.7 | 555.3 | 1.32 | 28.5 |
| Q620 | 10 | 668.6 | 799.2 | 1.20 | 23.5 |
| Q620 | 6 | 638.1 | 805.3 | 1.26 | 21.5 |
| Specimen Number | Pu (kN) | Du (mm) | Fy (kN) | Dy (mm) | K0 (kN/mm) | η |
|---|---|---|---|---|---|---|
| CTTC-R16 | 483 | 3.08 | 418 | 0.53 | 1565 | 5.81 |
| D0L0R0Y200 | 472 | 2.00 | 418 | 0.55 | 1530 | 3.64 |
| D25L80R16Y200 | 614 | 6.73 | 487 | 0.61 | 1601 | 11.03 |
| D25L80R13Y200 | 601 | 7.30 | 497 | 0.69 | 1443 | 10.58 |
| D25L40R13Y120 | 548 | 5.15 | 391 | 0.54 | 1455 | 9.54 |
| D40L40R13Y120 | 658 | 4.97 | 529 | 0.54 | 1980 | 9.20 |
| Specimen Number | Test Results (kN) | FEA Model Results (kN) | Ratio of Tested Value to Predicted Value |
|---|---|---|---|
| D25L40R13Y120 | 548 | 603 | 1.10 |
| D25L80R13Y200 | 601 | 625 | 1.04 |
| D25L80R16Y200 | 614 | 626 | 1.02 |
| D40L40R13Y120 | 658 | 643 | 0.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Chen, J.; Gao, Y.; Zhang, M.; Li, Z. Shear Behavior of Dowel–Stud Hybrid Connectors for HSS-HPC Composite Structures: Geometry Optimization and Material Synergistic Effects. Buildings 2025, 15, 3748. https://doi.org/10.3390/buildings15203748
Chen B, Chen J, Gao Y, Zhang M, Li Z. Shear Behavior of Dowel–Stud Hybrid Connectors for HSS-HPC Composite Structures: Geometry Optimization and Material Synergistic Effects. Buildings. 2025; 15(20):3748. https://doi.org/10.3390/buildings15203748
Chicago/Turabian StyleChen, Bozhao, Jun Chen, Yansong Gao, Miao Zhang, and Zhang Li. 2025. "Shear Behavior of Dowel–Stud Hybrid Connectors for HSS-HPC Composite Structures: Geometry Optimization and Material Synergistic Effects" Buildings 15, no. 20: 3748. https://doi.org/10.3390/buildings15203748
APA StyleChen, B., Chen, J., Gao, Y., Zhang, M., & Li, Z. (2025). Shear Behavior of Dowel–Stud Hybrid Connectors for HSS-HPC Composite Structures: Geometry Optimization and Material Synergistic Effects. Buildings, 15(20), 3748. https://doi.org/10.3390/buildings15203748




