Bayesian-Optimized Ensemble Models for Geopolymer Concrete Compressive Strength Prediction with Interpretability Analysis
Abstract
1. Introduction
- To systematically assess the effectiveness of ensemble machine learning models in predicting the compressive strength of geopolymer concretes.
- To investigate the impact of hyperparameter tuning through BO, providing insights into how model calibration affects prediction accuracy.
- To enhance model interpretability by applying SHAP, an explainable artificial intelligence (XAI) technique, for identifying the most influential variables affecting concrete strength.
- To develop reliable, accurate, fast, and interpretable predictive models supported by a user-friendly GUI, facilitating the practical implementation of AI-driven solutions in designing sustainable and eco-friendly construction materials.
2. Related Studies
3. Predictive Modeling and Explainable AI
3.1. Predictive Models
3.1.1. Extreme Gradient Boosting (XGB)
3.1.2. Random Forest (RF)
3.1.3. Light Gradient Boosting Machine (LightGBM)
3.1.4. Support Vector Regression (SVR)
3.1.5. Artificial Neural Network (ANN)
3.2. Bayesian Hyperparameter Optimization
3.3. Model Performance Evaluation
3.4. Explainable Artificial Intelligence (XAI)
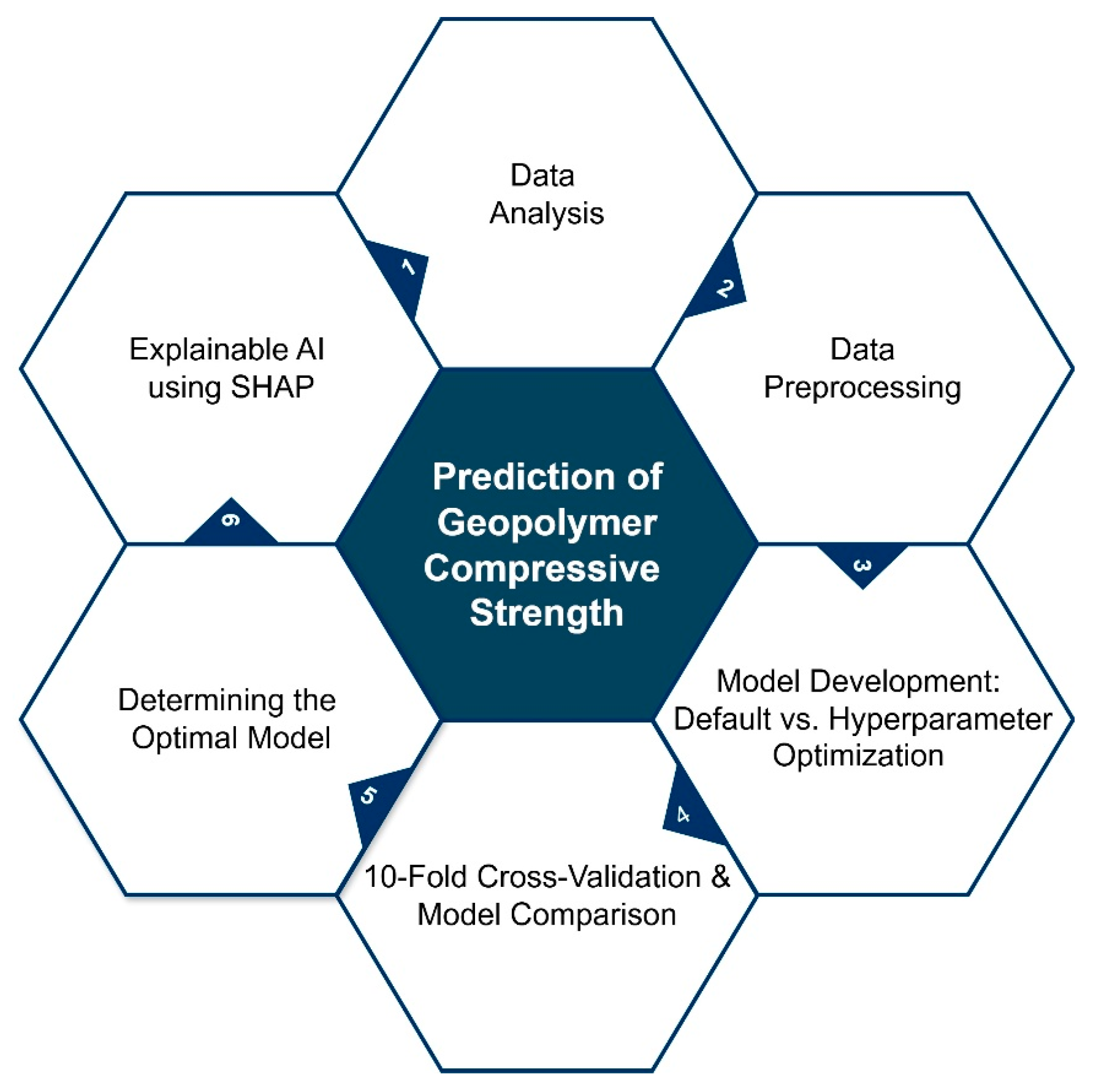
4. Methods
5. Results and Discussion
6. Conclusions
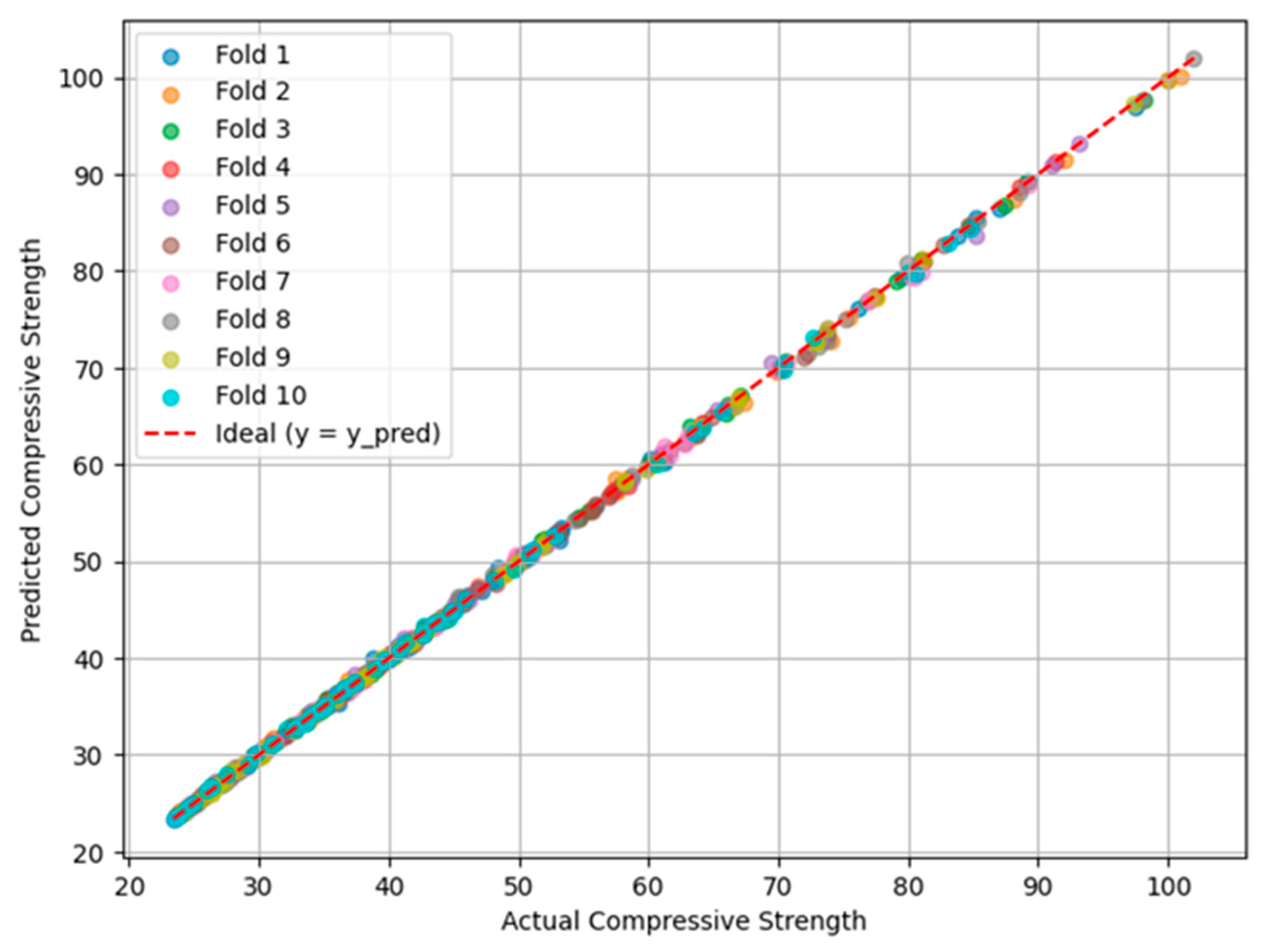
- The XGB-BO model outperformed other ensemble machine learning models in terms of predictive accuracy, as demonstrated by its higher R2 and lower RMSE, MAE, and MAPE values. This model effectively captured the complex, nonlinear relationships among mixture design parameters influencing the compressive strength of geopolymer concretes, providing a robust, reliable, and explainable prediction framework.
- The integration of the XGB model with Bayesian Optimization (BO) has significantly enhanced the model’s predictive performance. The BO approach enabled a more efficient search for optimal hyperparameters, reducing the risk of overfitting and maintaining high prediction accuracy. This optimization strategy provided a notable reduction in error rates and played a key role in improving the model’s robustness and generalization capability.
- Model interpretability analysis using SHAP contribution values revealed that the most influential parameters affecting the compressive strength of geopolymer concretes are coarse aggregate, curing time, and NaOH molar concentration, with corresponding mean SHAP values of 9.109, 7.743, and 2.584, respectively. The SHAP feature importance plot provides an explicit quantification of how each variable contributes to the model’s predictions, highlighting their relative impact. In this way, ensemble learning models, which are often considered black-box approaches, were made explainable, and the model’s decision-making process was rendered more transparent.
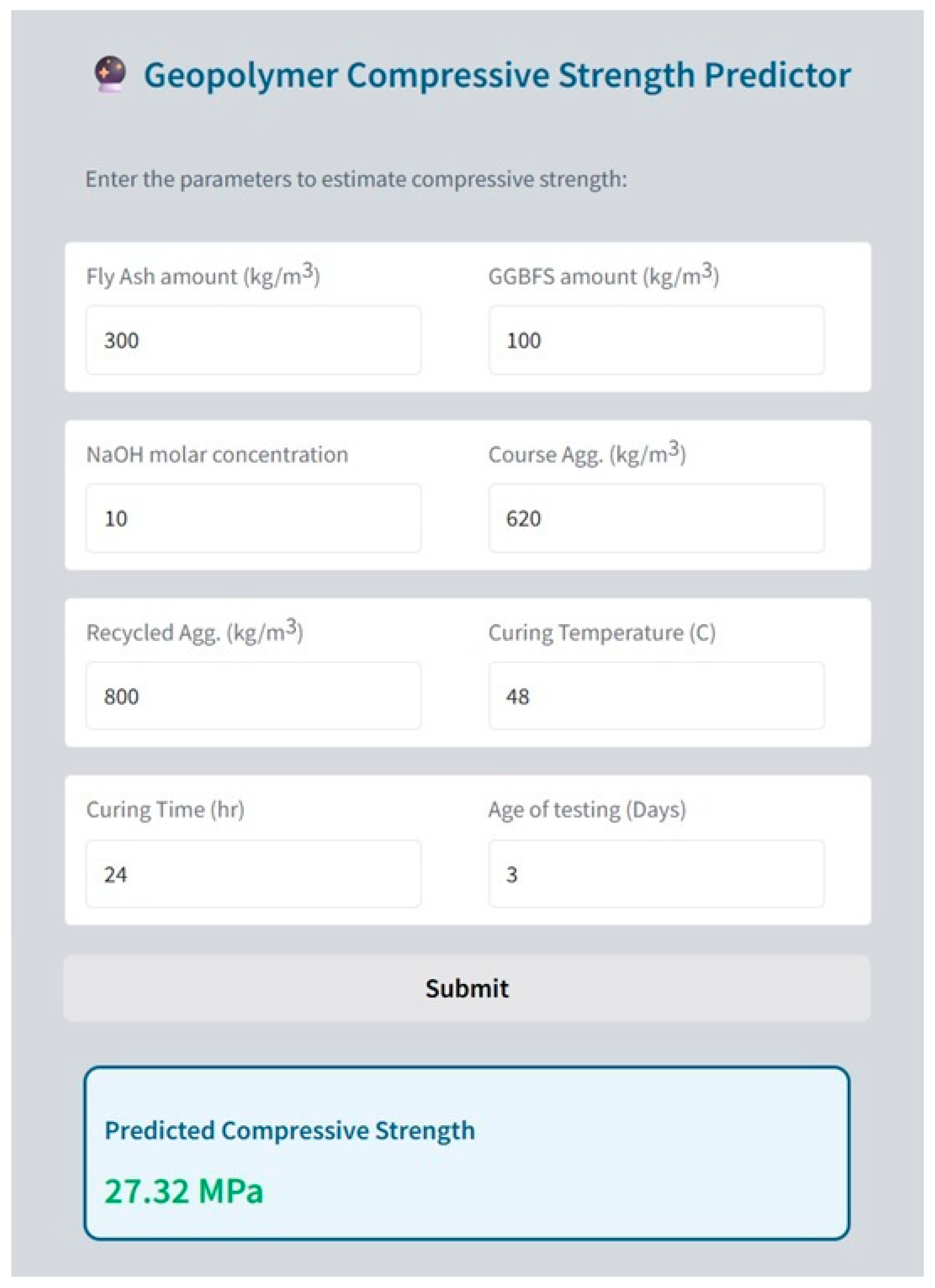
- A user-friendly GUI was developed to enable fast and accessible prediction of the compressive strength of geopolymer concretes based on mixture design parameters. This tool facilitates the practical implementation of the proposed AI-based framework and supports its adoption in real-world engineering applications.
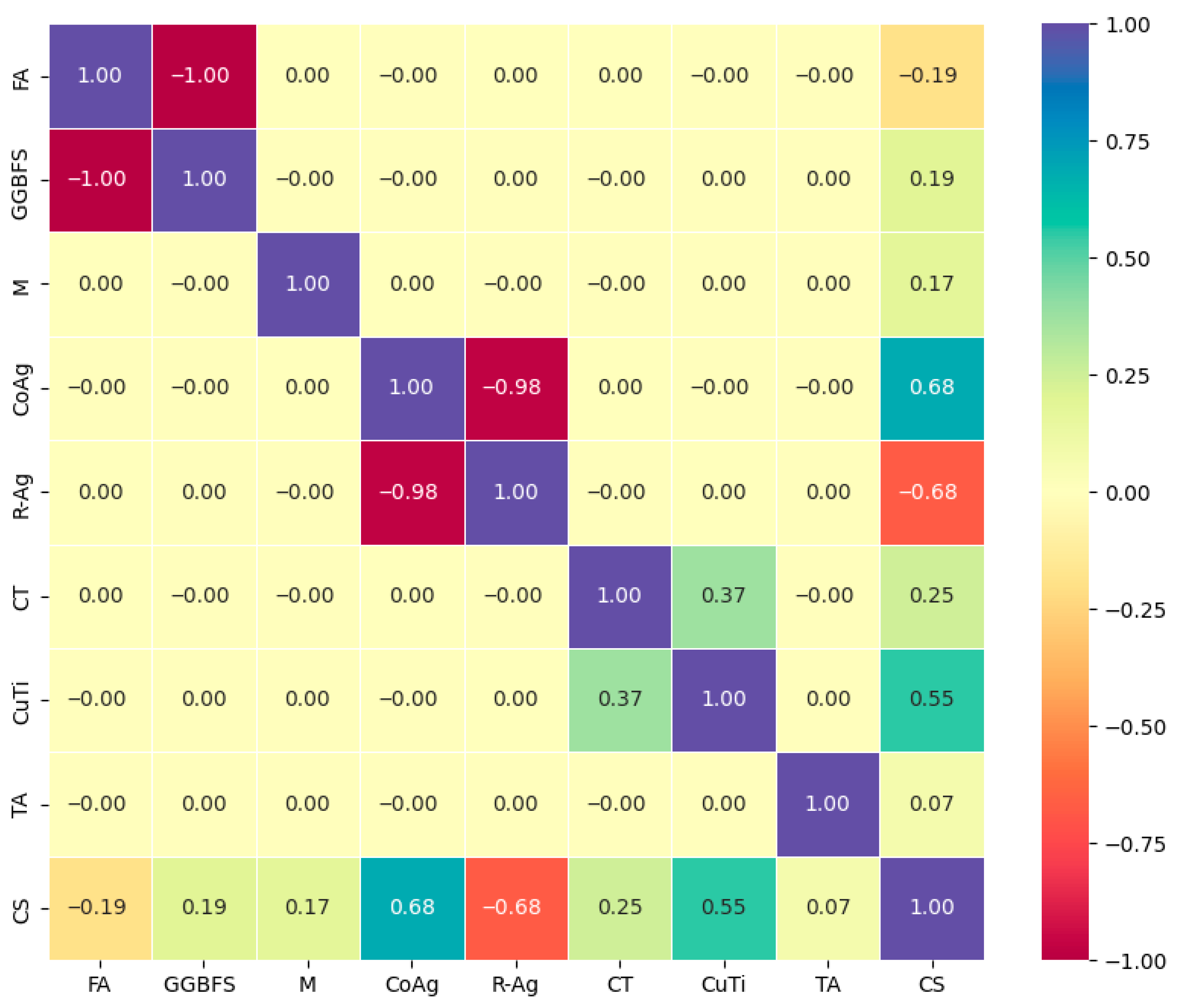
- In this study, R-Ag showed the highest linear correlation with compressive strength (CS); however, CoAg was the most influential feature in the SHAP importance ranking. This indicates that despite its strong linear correlation, the prediction model for R-Ag has a limited impact on actual decision-making. Therefore, using not only correlation coefficients but also model-based explainability methods when selecting parameters for experimental designs offers a more comprehensive and reliable basis for parameter choice and process optimization in complex concrete systems.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ABR | Adaptive boosting regressor |
| AD | Alkali dosage |
| ADA | ADAboost |
| AF | Alccofine |
| Ag | Aggregate |
| ANFIS | Adaptive neuro-fuzzy inference system |
| ANN | Artificial neural networks |
| AS | Alkaline solution |
| ASC | Alkaline solution concentration |
| ASM | Aluminosilicate material |
| B | Binder |
| BC | Basicity coefficient |
| BDT | Boosted decision tree |
| BNN | Bayesian neural network |
| BO | Bayesian Optimization |
| BPNN | Back-propagation neural network |
| BR | Bagging regresor |
| CatBoost | Categorical boosting regressor |
| CCA | Corncob ash |
| CD | Curing duration |
| CFV | Compaction factor value |
| CG | Coal gangue |
| CN2 | CN2 Rule induction |
| CNN | 1 D Convolution neural network |
| CoAg | Coarse aggregate |
| CoS | Copper slag |
| CS | Compressive strength |
| CSG | Concrete strength grade |
| CSO | Cat swarm optimization |
| CT | Curing temperature |
| CuMe | Curing method |
| CuTi | Curing time |
| Dmax | Maximum size of coarse aggregate |
| DNN | Deep neural network |
| DT | Decision tree |
| ECSO | Enhanced cat swarm optimization |
| EL | Ensemble learning |
| ELM | Extreme learning machine |
| EN | Elastic net |
| ESA | Eggshell ash |
| ET | Elevated temperature |
| ETR | Extra trees regressor |
| EW | Extra water |
| FA | Fly ash |
| FAR | Fibre aspect ratio |
| FD | Fibre diameter |
| FE | Elastic modulus of fibre |
| FiAg | Fine aggregate |
| FL | Fibre length |
| Fs | Fineness modulus of fine aggregate |
| FTS | Fibre tensile strength |
| FV | Fibre volume |
| GA | Genetic algorithm |
| GB | Gradient boosting |
| GEP | Gene expression programming |
| GGBFS | Ground granulated blast furnace slag |
| GMDH | Group method of data handling |
| GP | Glass powder |
| GPR | Gaussian process regression |
| GUI | Graphical user interface |
| H | Humidity |
| HCD | High-temperature curing duration |
| HD | Heating duration |
| HM | Hydration modulus |
| HO | Hyperparameter optimization |
| HR | Heating rate |
| HT | Heating temperature |
| HTT | Heat treatment time |
| KNN | K-nearest neighbour |
| L | Liquid |
| LightGBM | Light gradient boosting machine |
| LI | Loss on ignition |
| LoR | Logistic regression |
| LR | Linear regression |
| LSTM | Long short-term memory |
| M | NaOH molar concentration |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MARS | Multivariate adaptive regression splines |
| MEP | Multi-expression programming |
| MK | Metakaolin |
| ML | Machine learning |
| MLP | Multilayer perceptron regressor |
| MLR | Multiple linear regression |
| MP | Mixing procedure |
| MR | Mole ratio |
| Ms | Silica module (SiO2/Na2O) |
| NB | Naive bayes |
| NH | NaOH |
| NS | Na2SiO3 |
| PM | Pozzolanic material |
| PSO | Particle swarm optimization |
| PT | Pretreatment temperature |
| R | Recycled |
| R2 | Coefficient of determination |
| RA | Rubber aggregate |
| RAWA | Recycled aggregate water absorption |
| ResNet | Deep residual network |
| RF | Random forest |
| RHA | Rice husk ash |
| RM | Red Mud |
| RMSE | Root Mean Square Error |
| Rub | Rubber |
| S | Solid |
| SC | Slag cement |
| SF | Silica fume |
| SGD | Stochastic gradient descent |
| SHAP | SHapley Additive exPlanations |
| SHO | Spotted hyena optimization |
| SP | Superplasticizer |
| SS | Silica sand |
| SSA | Specific surface area |
| StF | Steel fiber |
| SVM | Support vector machine |
| TA | Test age |
| UPV | Ultrasonic pulse velocity |
| W | Water |
| WR | Water reducer |
| XAI | Explainable artificial intelligence |
| XGB | Extreme gradient boosting |
References
- Abdellatief, M.; Abd Elrahman, M.; Abadel, A.A.; Wasim, M.; Tahwia, A. Ultra-high performance concrete versus ultra-high performance geopolymer concrete: Mechanical performance, microstructure, and ecological assessment. J. Build. Eng. 2023, 79, 107835. [Google Scholar] [CrossRef]
- Pacheco-Torgal, F. Introduction to handbook of alkali-activated cements, mortars and concretes. In Handbook of Alkali-Activated Cements, Mortars and Concretes; Elsevier: Amsterdam, The Netherlands, 2015; pp. 1–16. [Google Scholar]
- Azimi-Pour, M.; Eskandari-Naddaf, H.; Pakzad, A. Linear and non-linear SVM prediction for fresh properties and compressive strength of high volume fly ash self-compacting concrete. Constr. Build. Mater. 2020, 230, 117021. [Google Scholar] [CrossRef]
- Nguyen, H.; Vu, T.; Vo, T.P.; Thai, H.-T. Efficient machine learning models for prediction of concrete strengths. Constr. Build. Mater. 2021, 266, 120950. [Google Scholar] [CrossRef]
- Rathnayaka, M.; Karunasinghe, D.; Gunasekara, C.; Wijesundara, K.; Lokuge, W.; Law, D.W. Machine learning approaches to predict compressive strength of fly ash-based geopolymer concrete: A comprehensive review. Constr. Build. Mater. 2024, 419, 135519. [Google Scholar] [CrossRef]
- Cihan, M.T. Comparison of artificial intelligence methods for predicting compressive strength of concrete. Građevinar 2021, 73, 617–632. [Google Scholar]
- Cihan, M.T. Prediction of concrete compressive strength and slump by machine learning methods. Adv. Civ. Eng. 2019, 2019, 3069046. [Google Scholar] [CrossRef]
- Shahrokhishahraki, M.; Malekpour, M.; Mirvalad, S.; Faraone, G. Machine learning predictions for optimal cement content in sustainable concrete constructions. J. Build. Eng. 2024, 82, 108160. [Google Scholar] [CrossRef]
- Chen, B.; Wang, L.; Feng, Z.; Liu, Y.; Wu, X.; Qin, Y.; Xia, L. Optimization of high-performance concrete mix ratio design using machine learning. Eng. Appl. Artif. Intell. 2023, 122, 106047. [Google Scholar] [CrossRef]
- Kumar, P.; Pratap, B. Feature engineering for predicting compressive strength of high-strength concrete with machine learning models. Asian J. Civ. Eng. 2024, 25, 723–736. [Google Scholar] [CrossRef]
- Zhao, N.; Zhang, H.; Xie, P.; Chen, X.; Wang, X. Prediction of compressive strength of multiple types of fiber-reinforced concrete based on optimized machine learning models. Eng. Appl. Artif. Intell. 2025, 152, 110714. [Google Scholar] [CrossRef]
- Dong, Y.; Tang, J.; Xu, X.; Li, W.; Feng, X.; Lu, C.; Hu, Z.; Liu, J. A new method to evaluate features importance in machine-learning based prediction of concrete compressive strength. J. Build. Eng. 2025, 102, 111874. [Google Scholar] [CrossRef]
- Ghosh, A.; Ransinchung, G. Application of machine learning algorithm to assess the efficacy of varying industrial wastes and curing methods on strength development of geopolymer concrete. Constr. Build. Mater. 2022, 341, 127828. [Google Scholar] [CrossRef]
- Wang, Y.; Iqtidar, A.; Amin, M.N.; Nazar, S.; Hassan, A.M.; Ali, M. Predictive modelling of compressive strength of fly ash and ground granulated blast furnace slag based geopolymer concrete using machine learning techniques. Case Stud. Constr. Mater. 2024, 20, e03130. [Google Scholar] [CrossRef]
- Revathi, B.; Gobinath, R.; Bala, G.S.; Nagaraju, T.V.; Bonthu, S. Harnessing explainable Artificial Intelligence (XAI) for enhanced geopolymer concrete mix optimization. Results Eng. 2024, 24, 103036. [Google Scholar] [CrossRef]
- Nguyen, K.T.; Nguyen, Q.D.; Le, T.A.; Shin, J.; Lee, K. Analyzing the compressive strength of green fly ash based geopolymer concrete using experiment and machine learning approaches. Constr. Build. Mater. 2020, 247, 118581. [Google Scholar] [CrossRef]
- Peng, Y.; Unluer, C. Analyzing the mechanical performance of fly ash-based geopolymer concrete with different machine learning techniques. Constr. Build. Mater. 2022, 316, 125785. [Google Scholar] [CrossRef]
- Shen, J.; Li, Y.; Lin, H.; Li, H.; Lv, J.; Feng, S.; Ci, J. Prediction of compressive strength of alkali-activated construction demolition waste geopolymers using ensemble machine learning. Constr. Build. Mater. 2022, 360, 129600. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, C.; Zhang, J.; Wang, L.; Wang, F. Effect of composition and curing on alkali activated fly ash-slag binders: Machine learning prediction with a random forest-genetic algorithm hybrid model. Constr. Build. Mater. 2023, 366, 129940. [Google Scholar] [CrossRef]
- Dash, P.K.; Parhi, S.K.; Patro, S.K.; Panigrahi, R. Efficient machine learning algorithm with enhanced cat swarm optimization for prediction of compressive strength of GGBS-based geopolymer concrete at elevated temperature. Constr. Build. Mater. 2023, 400, 132814. [Google Scholar] [CrossRef]
- Gad, M.A.; Nikbakht, E.; Ragab, M.G. Predicting the compressive strength of engineered geopolymer composites using automated machine learning. Constr. Build. Mater. 2024, 442, 137509. [Google Scholar] [CrossRef]
- Gomaa, E.; Han, T.; ElGawady, M.; Huang, J.; Kumar, A. Machine learning to predict properties of fresh and hardened alkali-activated concrete. Cem. Concr. Compos. 2021, 115, 103863. [Google Scholar] [CrossRef]
- Afzali, S.A.E.; Shayanfar, M.A.; Ghanooni-Bagha, M.; Golafshani, E.; Ngo, T. The use of machine learning techniques to investigate the properties of metakaolin-based geopolymer concrete. J. Clean. Prod. 2024, 446, 141305. [Google Scholar] [CrossRef]
- Golafshani, E.; Khodadadi, N.; Ngo, T.; Nanni, A.; Behnood, A. Modelling the compressive strength of geopolymer recycled aggregate concrete using ensemble machine learning. Adv. Eng. Softw. 2024, 191, 103611. [Google Scholar] [CrossRef]
- Liu, L.; Du, Y.T.; Amin, M.N.; Nazar, S.; Khan, K.; Qadir, M.T. Explicable AI-based modeling for the compressive strength of metakaolin-derived geopolymers. Case Stud. Constr. Mater. 2024, 21, e03849. [Google Scholar] [CrossRef]
- Zeng, Y.; Chen, Y.; Liu, Y.; Wu, T.; Zhao, Y.; Jin, D.; Xu, F. Prediction of compressive and flexural strength of coal gangue-based geopolymer using machine learning method. Mater. Today Commun. 2025, 44, 112076. [Google Scholar] [CrossRef]
- Parhi, S.K.; Dwibedy, S.; Panigrahi, S.K. AI-driven critical parameter optimization of sustainable self-compacting geopolymer concrete. J. Build. Eng. 2024, 86, 108923. [Google Scholar] [CrossRef]
- Ji, H.; Lyu, Y.; Ying, W.; Liu, J.-C.; Ye, H. Machine learning guided iterative mix design of geopolymer concrete. J. Build. Eng. 2024, 91, 109710. [Google Scholar] [CrossRef]
- Ranasinghe, R.; Kulasooriya, W.; Perera, U.S.; Ekanayake, I.; Meddage, D.; Mohotti, D.; Rathanayake, U. Eco-friendly mix design of slag-ash-based geopolymer concrete using explainable deep learning. Results Eng. 2024, 23, 102503. [Google Scholar] [CrossRef]
- Bypour, M.; Yekrangnia, M.; Kioumarsi, M. Machine Learning-Driven Optimization for Predicting Compressive Strength in Fly Ash Geopolymer Concrete. Clean. Eng. Technol. 2025, 25, 100899. [Google Scholar] [CrossRef]
- Sathiparan, N.; Jeyananthan, P. Predicting compressive strength of quarry waste-based geopolymer mortar using machine learning algorithms incorporating mix design and ultrasonic pulse velocity. Nondestruct. Test. Eval. 2024, 39, 2486–2509. [Google Scholar] [CrossRef]
- Le, Q.-H.; Nguyen, D.-H.; Sang-To, T.; Khatir, S.; Le-Minh, H.; Gandomi, A.H.; Cuong-Le, T. Machine learning based models for predicting compressive strength of geopolymer concrete. Front. Struct. Civ. Eng. 2024, 18, 1028–1049. [Google Scholar] [CrossRef]
- Khan, A.Q.; Naveed, M.H.; Rasheed, M.D.; Miao, P. Prediction of compressive strength of fly ash-based geopolymer concrete using supervised machine learning methods. Arab. J. Sci. Eng. 2024, 49, 4889–4904. [Google Scholar] [CrossRef]
- Yeluri, S.C.; Singh, K.; Kumar, A.; Aggarwal, Y.; Sihag, P. Estimation of compressive strength of rubberised slag based geopolymer concrete using various machine learning techniques based models. Iran. J. Sci. Technol. Trans. Civ. Eng. 2025, 49, 1157–1172. [Google Scholar]
- Philip, S.; Nakkeeran, G. Soft computing techniques for predicting the compressive strength properties of fly ash geopolymer concrete using regression-based machine learning approaches. J. Build. Pathol. Rehabil. 2024, 9, 108. [Google Scholar] [CrossRef]
- Onyelowe, K.C.; Ebid, A.M.; Awoyera, P.; Kamchoom, V.; Rosero, E.; Albuja, M.; Mancheno, C. Prediction and validation of mechanical properties of self-compacting geopolymer concrete using combined machine learning methods a comparative and suitability assessment of the best analysis. Sci. Rep. 2025, 15, 6361. [Google Scholar] [CrossRef] [PubMed]
- Philip, S.; Nidhi, M.; Ahmed, H.U. A comparative analysis of tree-based machine learning algorithms for predicting the mechanical properties of fibre-reinforced GGBS geopolymer concrete. Multiscale Multidiscip. Model. Exp. Des. 2024, 7, 2555–2583. [Google Scholar]
- Yang, H.; Li, H.; Jiang, J. Predictive modeling of compressive strength of geopolymer concrete before and after high temperature applying machine learning algorithms. Struct. Concr. 2025, 26, 1699–1732. [Google Scholar]
- Diksha; Dev, N.; Goyal, P.K. Utilizing an enhanced machine learning approach for geopolymer concrete analysis. Nondestruct. Test. Eval. 2025, 40, 904–931. [Google Scholar] [CrossRef]
- Mustapha, I.B.; Abdulkareem, Z.; Abdulkareem, M.; Ganiyu, A. Predictive modeling of physical and mechanical properties of pervious concrete using XGBoost. Neural Comput. Appl. 2024, 36, 9245–9261. [Google Scholar] [CrossRef]
- Cutler, A.; Cutler, D.R.; Stevens, J.R. Random forests. In Ensemble Machine Learning: Methods and Applications; Springer: New York, NY, USA, 2012; pp. 157–175. [Google Scholar]
- Akbarzadeh, M.R.; Jahangiri, V.; Naeim, B.; Asgari, A. Advanced computational framework for fragility analysis of elevated steel tanks using hybrid and ensemble machine learning techniques. Structures 2025, 81, 110205. [Google Scholar] [CrossRef]
- Jahangiri, V.; Akbarzadeh, M.R.; Shahamat, S.A.; Asgari, A.; Naeim, B.; Ranjbar, F. Machine learning-based prediction of seismic response of steel diagrid systems. Structures 2025, 80, 109791. [Google Scholar] [CrossRef]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K.; Mitchell, R.; Cano, I.; Zhou, T. Xgboost: Extreme Gradient Boosting. R Package Version 0.4-2. 2015, Volume 1, pp. 1–4. Available online: https://cran.ms.unimelb.edu.au/web/packages/xgboost/vignettes/xgboost.pdf (accessed on 10 May 2025).
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3149. [Google Scholar]
- Cihan, P.; Ozel, H.; Ozcan, H.K. Modeling of atmospheric particulate matters via artificial intelligence methods. Environ. Monit. Assess. 2021, 193, 287. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Zou, J.; Han, Y.; So, S.-S. Artificial Neural Networks: Methods and Applications; Livingstone, D.J., Ed.; Humana Press: Totowa, NJ, USA, 2008; pp. 14–22. [Google Scholar]
- Cihan, P. Bayesian Hyperparameter Optimization of Machine Learning Models for Predicting Biomass Gasification Gases. Appl. Sci. 2025, 15, 1018. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhou, J.; Khandelwal, M.; Yang, H.; Yang, P.; Li, C. Performance evaluation of hybrid WOA-XGBoost, GWO-XGBoost and BO-XGBoost models to predict blast-induced ground vibration. Eng. Comput. 2022, 38, 4145–4162. [Google Scholar] [CrossRef]
- Jones, D.R. A taxonomy of global optimization methods based on response surfaces. J. Glob. Optim. 2001, 21, 345–383. [Google Scholar] [CrossRef]
- Cihan, M.T.; Aral, I.F. Application of AI models for predicting properties of mortars incorporating waste powders under Freeze-Thaw condition. Comput. Concr. 2022, 29, 187–199. [Google Scholar]
- Cihan, P. Comparative performance analysis of deep learning, classical, and hybrid time series models in ecological footprint forecasting. Appl. Sci. 2024, 14, 1479. [Google Scholar] [CrossRef]
- Cihan, P.; Özcan, H.K.; Öngen, A. Prediction of tropospheric ozone concentration with Bagging-MLP method. Gazi Mühendislik Bilim. Derg. 2023, 9, 557–573. [Google Scholar]
- Teodorescu, V.; Obreja Brașoveanu, L. Assessing the Validity of k-Fold Cross-Validation for Model Selection: Evidence from Bankruptcy Prediction Using Random Forest and XGBoost. Comput. 2025, 13, 127. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. Peerj Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Ekanayake, I.; Meddage, D.; Rathnayake, U. A novel approach to explain the black-box nature of machine learning in compressive strength predictions of concrete using Shapley additive explanations (SHAP). Case Stud. Constr. Mater. 2022, 16, e01059. [Google Scholar] [CrossRef]
- Hassanat, A.B.; Ali, H.N.; Tarawneh, A.S.; Alrashidi, M.; Alghamdi, M.; Altarawneh, G.A.; Abbadi, M.A. Magnetic force classifier: A novel method for big data classification. IEEE Access 2022, 10, 12592–12606. [Google Scholar] [CrossRef]
- Rahmati, S.; Mahdikhani, M. Geopolymer Concrete Compressive Strength Data Set for ML. In Mendeley Data; Elsevier, Inc.: Philadelphia, PA, USA, 2023. [Google Scholar]
- Fu, K.; Xue, Y.; Qiu, D.; Wang, P.; Lu, H. Multi-channel fusion prediction of TBM tunneling thrust based on multimodal decomposition and reconstruction. Tunn. Undergr. Space Technol. 2026, 167, 107061. [Google Scholar] [CrossRef]
- Yao, S.; Chen, F.; Wang, Y.; Zhou, H.; Liu, K. Manufacturing defect-induced multiscale weakening mechanisms in carbon fiber reinforced polymers captured by 3D CT-based machine learning and high-fidelity modeling. Compos. Part A Appl. Sci. Manuf. 2025, 197, 109052. [Google Scholar] [CrossRef]
- Niu, Y.; Wang, W.; Su, Y.; Jia, F.; Long, X. Plastic damage prediction of concrete under compression based on deep learning. Acta Mech. 2024, 235, 255–266. [Google Scholar] [CrossRef]
- Gautam, R.; Jaiswal, R.; Yadav, U.S. AI-Enhanced Data-Driven Approach to Model the Mechanical Behavior of Sustainable Geopolymer Concrete. Research Square. 2024. Available online: https://www.researchsquare.com/article/rs-5307352/v1 (accessed on 25 May 2025).
- Luo, B.; Su, Y.; Ding, X.; Chen, Y.; Liu, C. Modulation of initial CaO/Al2O3 and SiO2/Al2O3 ratios on the properties of slag/fly ash-based geopolymer stabilized clay: Synergistic effects and stabilization mechanism. Mater. Today Commun. 2025, 47, 113295. [Google Scholar] [CrossRef]


| References | Sample Size | Inputs | ML Method | HO | Best Model | R/R2 | XAI |
|---|---|---|---|---|---|---|---|
| Ghosh, A. et al. [13] | - | FA, CuTi, CuMe | LR, DT, RF, SVM | × | DT, RF | -/0.9879 | × |
| Wang, Y. et al. [14] | 156 | FA, GGBFS, FiAg, CoAg, NH, NS, SP, CT | ANN, ANFIS, GEP | × | GEP | 0.99/- | × |
| Revathi, B. et al. [15] | 37 | FA, GGBFS, AF, CoAg, FiAg, NH, NS, W | RF | √ | RF | -/0.79 | √ |
| 24 | PM, FA, M, Na/Si, Si/Al, H2O/Na2O, Na/Al | -/0.81 | |||||
| 28 | NH, NS, NS/NH, M, CT, ET | -/0.88 | |||||
| Nguyen, K. T. et al. [16] | 335 | FA, NH, NS, CaAg, FiAg, W, Molarity, CuTi, CT | DNN, ResNet | × | ResNet | 0.9927/- | × |
| Peng, Y. et al. [17] | 110 | FA, SiO2, Al2O3, CoAg, FiAg, NH, Molarity, NS, NS/NH, AA/FA, W, SP | BPNN, SVM, ELM | × | BPNN | -/0.8221 | × |
| Shen, J. et al. [18] | 328 | Ms, Na2O, SiO2/Al2O3, Na2O/SiO2, L/S, PT, HTT, TA | RF, GB, XGB | √ | XGB | -/0.939 | √ |
| Zhang, M. et al. [19] | 616 | Si/Al, Na/Al, Ca/Si, CT, CuTi, H, W | BPNN, LoR, MLR, SVM, RF | √ | RF | 0.9322/- | × |
| Dash, P. K. et al. [20] | 192 | GGBFS, CoAg, FiAg, AS/GGBFS, NH, NS, NS/NH, CuTi, CT | ELM, ELM-CSO, ELM-ECSO | √ | ELM-ECSO | -/0.957 | × |
| Gad, M. A. et al. [21] | 132 | FA, GGBFS, SF, NH, NS, SS, EW, WR, CuMe | CatBoost, XGB, ETR, DT, RF, GB | √ | GB | -/0.9651 | √ |
| Gomaa, E. et al. [22] | 180 | CoAg, FiAg, SiO2, Al2O3, Fe2O3, CaO, MgO, Na2O, K2O, TiO2, P2O5, MnO, LI, W, SSA-FA, MP, CuMe, CT, CuTi, TA | RF | √ | RF | 0.972/0.944 | × |
| Afzali, S. A. E. et al. [23] | 235 | MK, NH, Molarity, NS, EW, W/S, SiO2/Al2O3, H2O/Na2O, Na2O/ Al2O3, CoAg/FiAg, SP, TA, CT | GB, RF, DT, ANN, SVM | √ | GB | -/0.983 | √ |
| Golafshani, E. et al. [24] | 314 | FA, SC, CoAg, R-CoAg, FiAg, NH, NS, SP, RAWA, M, CT, HCD, TA | RF, BR, ETR, ABR, GB, XGB, CatBoost, LightGBM | √ | XGB | -/0.955 | √ |
| Liu, L. et al. [25] | 235 | SiO2/Al2O3, Na2O/Al2O3, H2O/Na2O, CoAg/FiAg, SP, W/S, EW, NH, NS, Molarity, MK, TA, CT | GEP, MEP | √ | MEP | 0.98/0.96 | √ |
| Zeng, Y. et al. [26] | 206 | AD, SiO2/Na2O, W/B, SiO2/Al2O3, CaO/SiO2, Al2O3/Na2O, CaO/Al2O3, CaO/(SiO2+Al2O3), CG | RF, XGB, MLP, DT | √ | XGB | -/0.882 | × |
| Parhi, S. K. et al. [27] | 240 | FA, GGBFS, SiO2, Al2O3, Fe2O3, CaO, CoAg, FiAg, NH, Molarity, NS, NS/NH, AS/B, EW, SP, CuTi, CT | ABR, RF, XGB, Hybrid | √ | Hybrid | -/0.97 | × |
| Ji, H. et al. [28] | 795 | FA, Na2O, Ms, W/FA, CoAg/FA, FiAg/FA, Fs, Dmax, BC, HM, CT, CuTi, TA | XGB | √ | XGB | -/0.95 | × |
| Ranasinghe, R. S. S. et al. [29] | 260 | GGBFS, CCA, FiAg, CoAg, W, NH, NS, CuTi, Molarity, CSG | ANN, DNN, CNN | × | DNN | -/0.972 | √ |
| Bypour, M. et al. [30] | 161 | SiO2, Al2O3, Fe2O3, CaO, P2O5, SO3, K2O, TiO2, MgO, Molarity, Na2O, MnO, CoAg, FiAg, StF, Rub | DT, ETR, RF, GB, XGB, ADA | √ | ADA | -/0.86 | √ |
| Sathiparan, N. et al. [31] | 189 | ESA, RHA, NH, UPV | LR, ANN, BDT, RF, KNN, SVM, XGB | × | KNN | -/0.958 | √ |
| Le, Q. H. et al. [32] | 375 | CoAg, FiAg, NH, NS, ASM, CT, CuTi, TA | DNN, KNN, SVM | √ | DNN | 0.8903/- | × |
| Khan, A. Q. et al. [33] | 149 | FA, SiO2, Al2O3, CoAg, FiAg, NH, Molarity, NS, NS/NH, (NH+NS)/FA, W, CT, CuTi | BPNN, RF, KNN | × | BPNN | -/0.948 | × |
| Yeluri, S. C. et al. [34] | 186 | FA, Molarity, NH, NS, FiAg, CoS, CoAg, RA, CuTi | MARS, GMDH, M5P, LR | × | MARS | 0.9634/- | √ |
| Philip, S. et al. [35] | 309 | FA, CoAg, FiAg, NH, NS, Molarity, NS/NH, (NH+NS)/FA, TA, CT, EW, SP | LR, ADA, RF, SVM, ANN | × | RF | -/0.96 | × |
| Onyelowe, K. C. et al. [36] | 132 | GGBFS, FA, NH, NS, TA | GB, CN2, NB, SVM, SGD, KNN, DT, RF | × | KNN | -/0.99 | × |
| Philip, S. et al. [37] | 110 | GGBFS, CoAg, FiAg, NH, Molarity, NS, NS/NH, (NH+NS)/GGBFS, TA, CT, FV, FL, FD, FAR, FTS | LR, DT, RF, XGB, GB, ADA | × | XGB | -/0.938 | × |
| Yang, H. et al. [38] | 206 | Size, W, NS, Molarity, NH, GGBFS, FA, FiAg, CoAg, CT, HR, HD, HT, CuTi | SVM, EN, GB, XGB, GA-RF, PSO-DNN, BNN, ELM | √ | GA-RF | -/0.937 | √ |
| Diksha, Dev, N. and Goyal, P. K. [39] | 144 | AF/FA, Molarity, L/B, Ag/B, L/Ag, EW, EW/L, CFV, CT, TA | LR, GPR, EL, SVM, ANN | √ | GPR | 0.9951/- | × |
| Metric | Formula | Description |
|---|---|---|
| R2 | It is a measure of how well the model explains the variance of the dependent variable(s), typically ranging between 0 and 1. A value of 1 indicates that the model fits the data perfectly; a value of 0 indicates that the model has no success in explaining the data. The model may take negative values when it predicts worse than the mean value of the target variable [54]. | |
| RMSE | RMSE measures the square root of the mean square differences between the model-predicted values and the actual values. This metric evaluates the overall accuracy of the model by penalizing large errors more. Lower RMSE values indicate better model performance [6,58]. | |
| MAE | It measures the average of the absolute differences between actual and predicted values. Lower MAE values indicate that the model makes more accurate predictions. Unlike squared error metrics, MAE does not disproportionately penalize large errors, making it less sensitive to outliers [58]. | |
| MAPE | It is an error metric that measures the average of the absolute percentage differences between the predicted values and the actual values. MAPE provides a percentage-based measure of how accurately the model makes predictions. MAPE is especially useful for understanding model performance when the dataset contains very large or values close to zero. Low MAPE values indicate that the model makes more accurate predictions [58]. |
| Model | Parameter | Parameter Intervals | Best Value |
|---|---|---|---|
| XGB | learning_rate | 0.01–0.3 | 0.1495 |
| max_depth | 3–10 | 7 | |
| Subsample | 0.5–1.0 | 0.9591 | |
| colsample_bytree | 0.5–1.0 | 0.7033 | |
| n_estimators | 50–500 | 319 | |
| RF | max_depth | 3–20 | 10 |
| min_samples_split | 2–20 | 2 | |
| min_samples_leaf | 1–20 | 1 | |
| n_estimators | 50–500 | 479 | |
| max_features | 0.1–1.0 | 0.8485 | |
| LightGBM | learning_rate | 0.01–0.2 | 0.1926 |
| max_depth | 3–20 | 8 | |
| num_leaves | 20–100 | 54 | |
| n_estimators | 50–500 | 485 | |
| min_child_samples | 5–50 | 13 | |
| Subsample | 0.6–1.0 | 0.6604 | |
| colsample_bytree | 0.6–1.0 | 0.8689 | |
| SVR | C | 1–500 | 299 |
| epsilon | 0.001–0.5 | 0.0789 | |
| gamma | 0.0001–1 | 0.1561 | |
| ANN | hidden1 (neurons) | 16–128 | 109 |
| hidden2 (neurons) | 8–64 | 19 | |
| alpha (L2 penalty) | 1 × 10−6–1 × 10−4 | 0.0018 | |
| learning_rate_init | 1 × 10−4–1 × 10−2 | 0.0019 |
| Parameter | Abbr. | Unit | Mean | Std | Min | 25% | 50% | 75% | Max |
|---|---|---|---|---|---|---|---|---|---|
| Fly ash | FA | kg/m3 | 350 | 50 | 300 | 300 | 350 | 400 | 400 |
| Ground granulated blast furnace slag | GGBFS | kg/m3 | 50 | 50 | 0 | 0 | 50 | 100 | 100 |
| NaOH molar concentration | M | - | 11 | 2.2 | 8 | 9.5 | 11 | 12.5 | 14 |
| NaOH | NH | kg/m3 | 70 | 0 | 70 | 70 | 70 | 70 | 70 |
| Na2SiO3 | NS | kg/m3 | 120 | 0 | 120 | 120 | 120 | 120 | 120 |
| Extra water | EW | kg/m3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Coarse aggregate | CoAg | kg/m3 | 873.3 | 217.2 | 620 | 620 | 850 | 1150 | 1150 |
| Fine aggregate | FiAg | kg/m3 | 650 | 0 | 650 | 650 | 650 | 650 | 650 |
| Recycled aggregate | R-Ag | kg/m3 | 366.7 | 330.2 | 0 | 0 | 300 | 800 | 800 |
| Curing temperature | CT | °C | 49.7 | 11.9 | 24 | 48 | 48 | 60 | 60 |
| Curing time | CuTi | hrs | 44.6 | 20 | 24 | 24 | 48 | 72 | 72 |
| Testing age | TA | Days | 13 | 9.5 | 3 | 6 | 10.5 | 17.5 | 28 |
| Compressive Strength | CS | MPa | 44.7 | 17.2 | 23.4 | 32.7 | 39.9 | 52.1 | 102 |
| Model | R2 | RMSE (MPa) | MAE (MPa) | MAPE (%) |
|---|---|---|---|---|
| XGB-Default | 0.9990 ± 0.0006 | 0.4956 ± 0.1477 | 0.2845 ± 0.0601 | 0.64 |
| XGB-BO | 0.9997 ± 0.0001 | 0.3100 ± 0.0616 | 0.2191 ± 0.0368 | 0.50 |
| RF-Default | 0.9965 ± 0.0020 | 0.9523 ± 0.2365 | 0.6113 ± 0.1314 | 1.39 |
| RF-BO | 0.9966 ± 0.0020 | 0.9462 ± 0.2449 | 0.6222 ± 0.1522 | 1.39 |
| LightGBM-Default | 0.9977 ± 0.0009 | 0.7959 ± 0.1305 | 0.5287 ± 0.0561 | 1.15 |
| LightGBM-BO | 0.9996 ± 0.0001 | 0.3567 ± 0.0599 | 0.2480 ± 0.0426 | 0.57 |
| SVR-Default | 0.9993 ± 0.0003 | 0.4367 ± 0.1075 | 0.2746 ± 0.0468 | 0.59 |
| SVR-BO | 0.9995 ± 0.0002 | 0.3705 ± 0.0863 | 0.2274 ± 0.0287 | 0.51 |
| ANN-Default | 0.9824 ± 0.0073 | 2.1965 ± 0.3982 | 1.6265 ± 0.3104 | 3.66 |
| ANN-BO | 0.9961 ± 0.0012 | 1.0493 ± 0.1222 | 0.8054 ± 0.0908 | 1.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cihan, M.T.; Cihan, P. Bayesian-Optimized Ensemble Models for Geopolymer Concrete Compressive Strength Prediction with Interpretability Analysis. Buildings 2025, 15, 3667. https://doi.org/10.3390/buildings15203667
Cihan MT, Cihan P. Bayesian-Optimized Ensemble Models for Geopolymer Concrete Compressive Strength Prediction with Interpretability Analysis. Buildings. 2025; 15(20):3667. https://doi.org/10.3390/buildings15203667
Chicago/Turabian StyleCihan, Mehmet Timur, and Pınar Cihan. 2025. "Bayesian-Optimized Ensemble Models for Geopolymer Concrete Compressive Strength Prediction with Interpretability Analysis" Buildings 15, no. 20: 3667. https://doi.org/10.3390/buildings15203667
APA StyleCihan, M. T., & Cihan, P. (2025). Bayesian-Optimized Ensemble Models for Geopolymer Concrete Compressive Strength Prediction with Interpretability Analysis. Buildings, 15(20), 3667. https://doi.org/10.3390/buildings15203667





