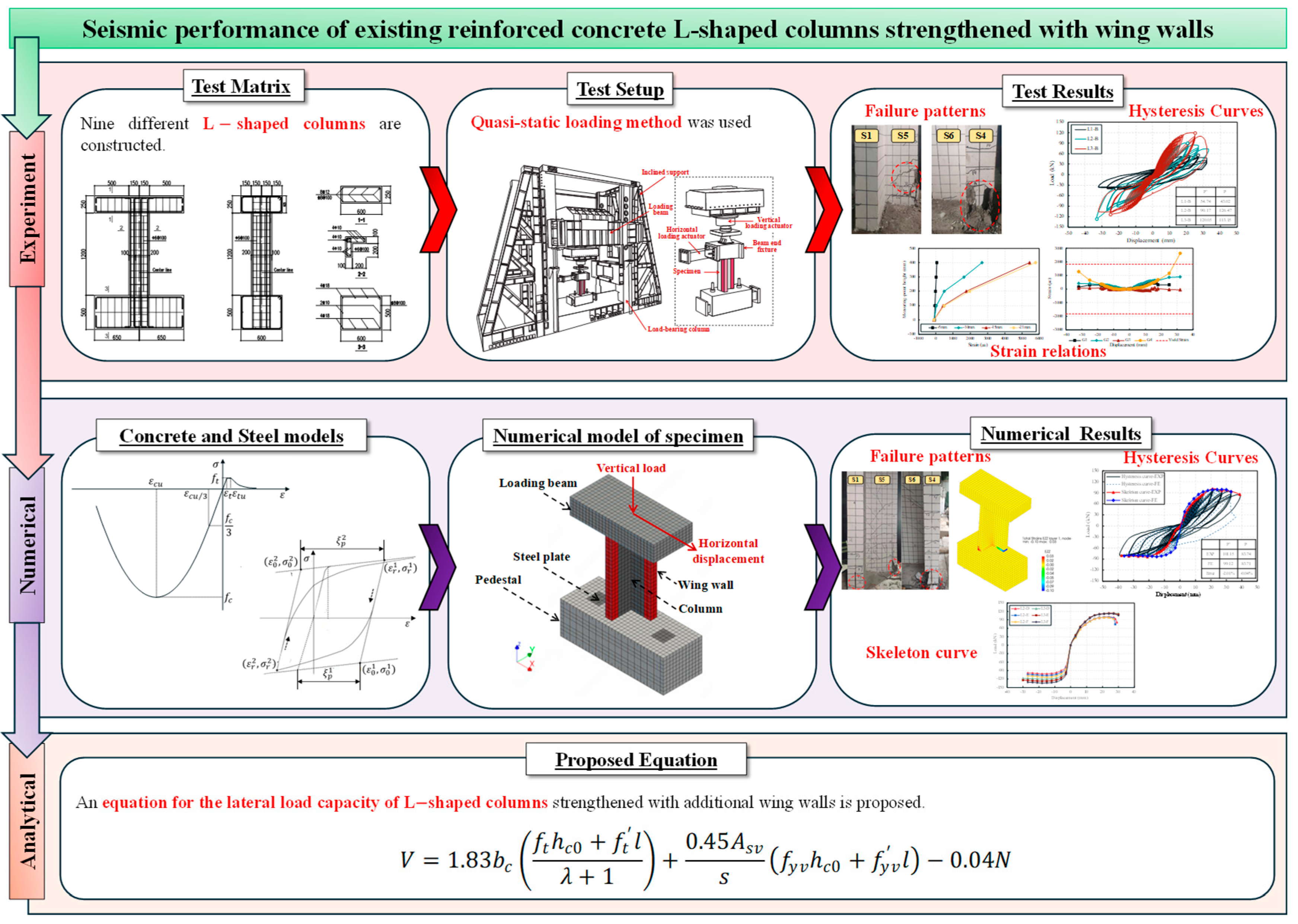
Seismic Performance of Existing Reinforced Concrete L-Shaped Columns Strengthened with Wing Walls
Abstract
1. Introduction
2. Framework
3. Experiment Program
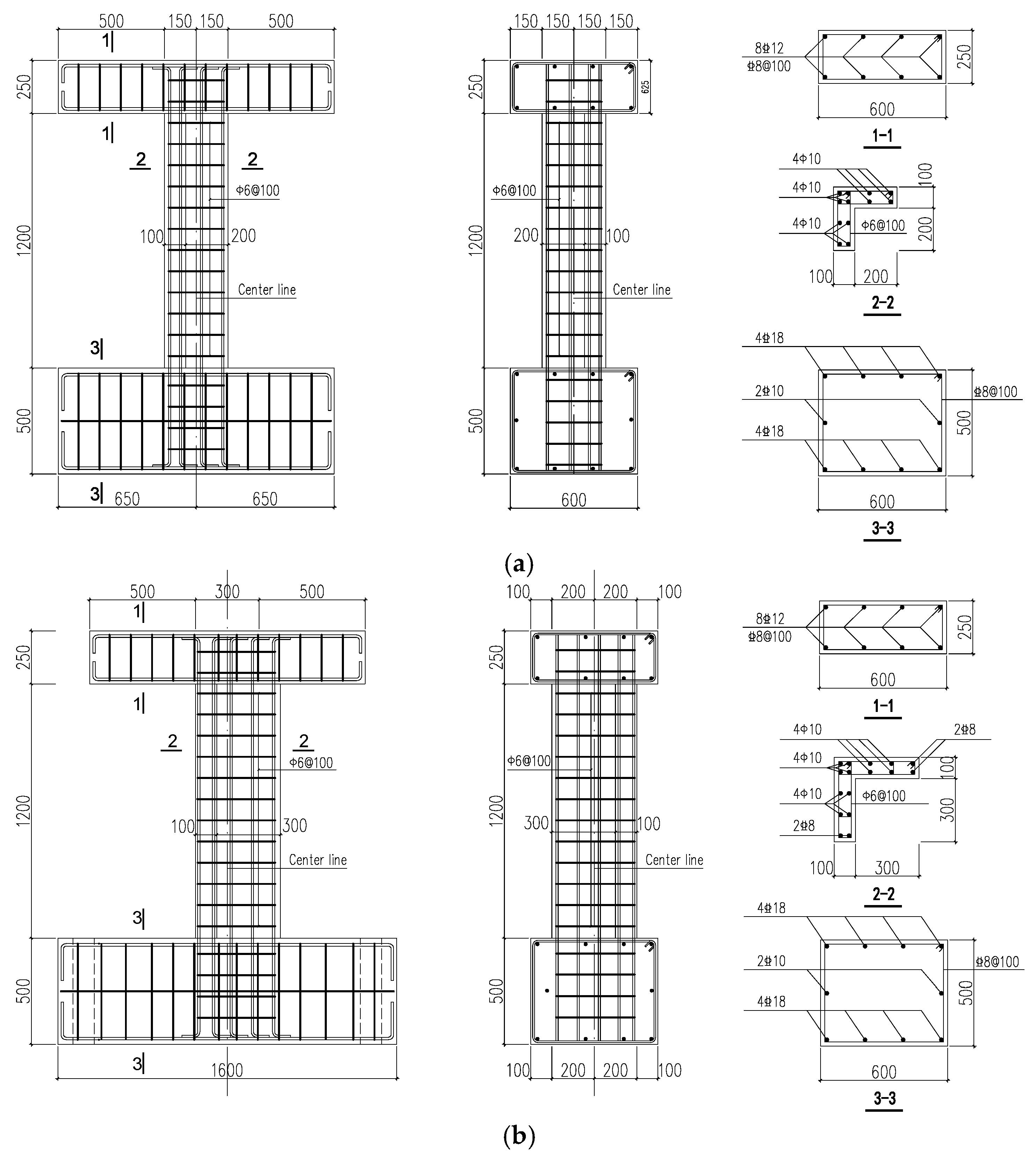
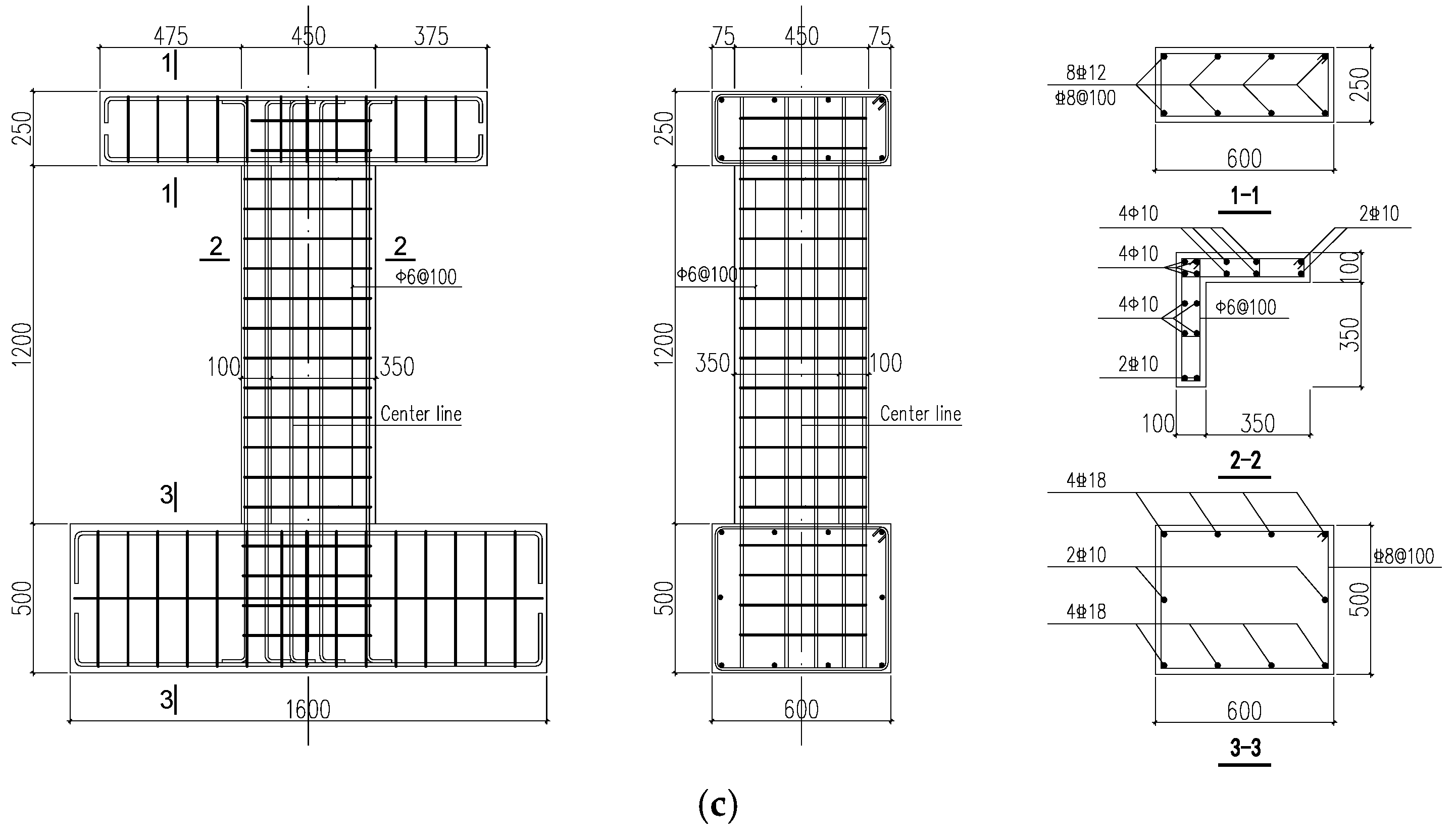
3.1. Specimen Design and Fabrication
- (a)
- The concrete cover at the ends of the column limbs was chipped away to expose the longitudinal reinforcement and stirrups of the original column, as shown in Figure 3a.
- (b)
- Holes corresponding to the diameters of the wing wall reinforcement bars were drilled into the base and the loading beam. Bonding adhesive was injected, and longitudinal bars for the wing walls were embedded to a depth 15 times the bar diameter, followed by curing.
- (c)
- New stirrups for the wing walls were tied to the exposed longitudinal bars of the original columns using closed-loop connections and by maintaining the original stirrup spacing to ensure consistent confinement, as shown in Figure 3b.
- (d)
3.2. Material Properties
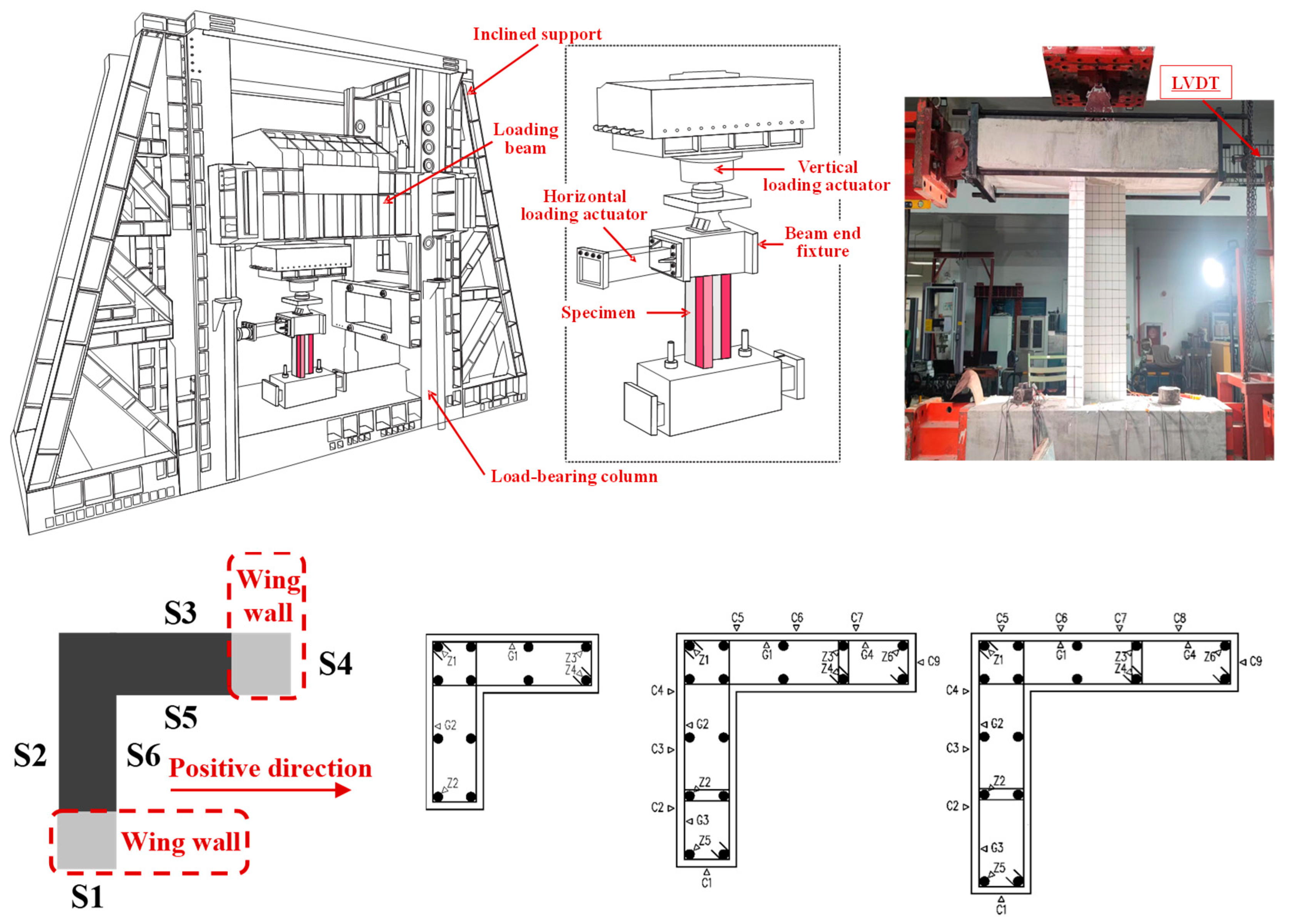
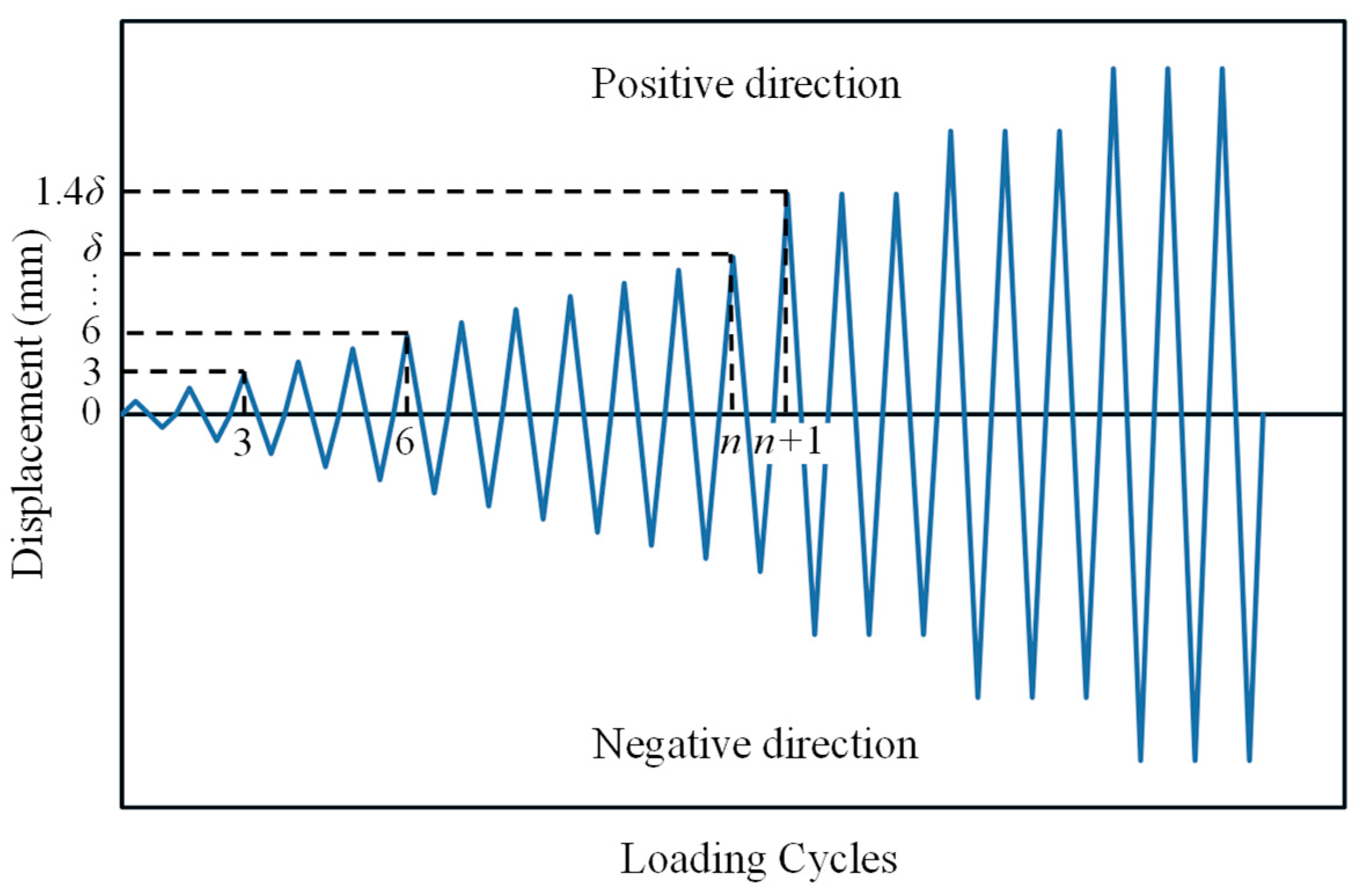
3.3. Test Setup and Loading Protocol
3.4. Measurement
4. Experimental Results and Discussion
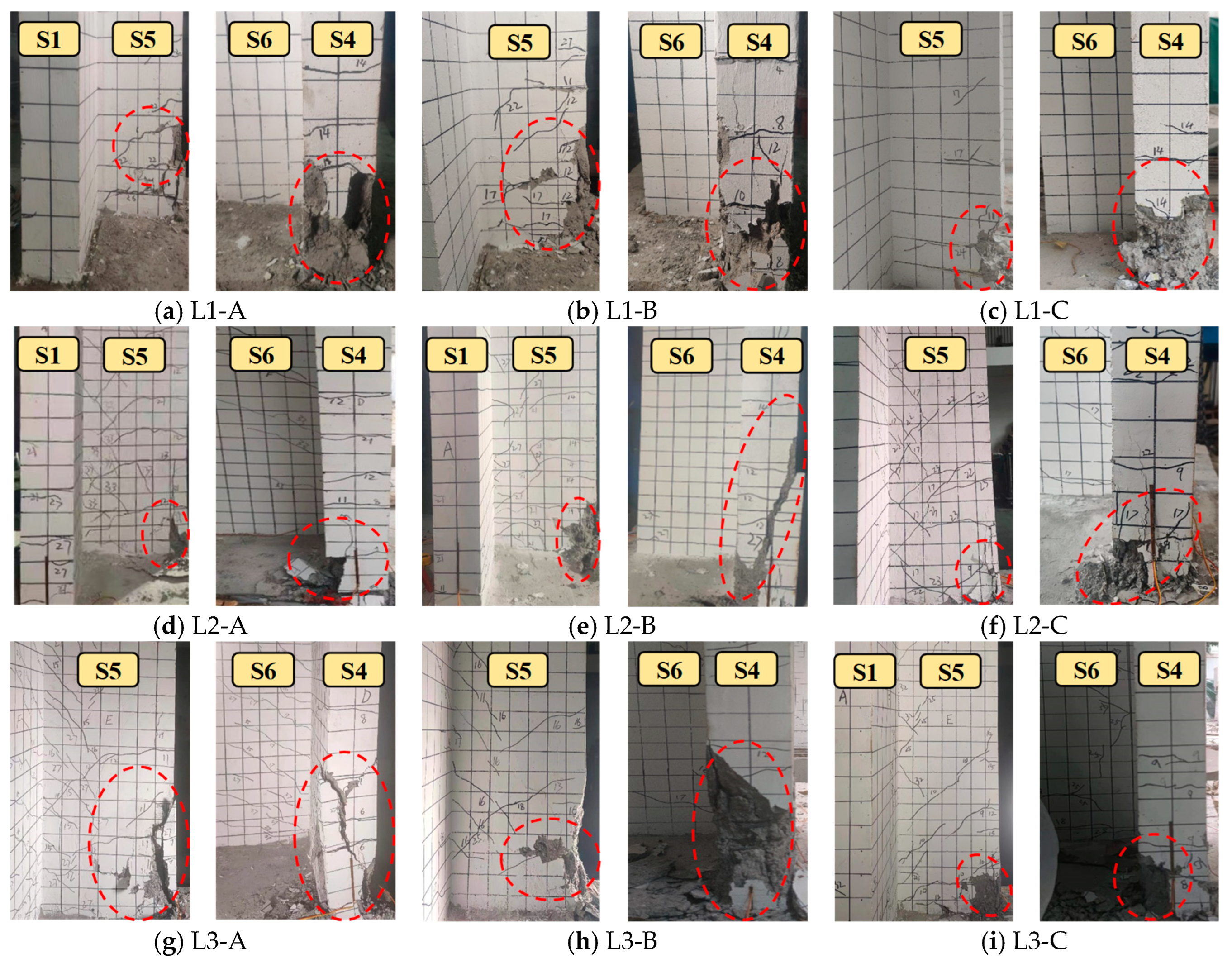
4.1. Experimental Phenomena
4.1.1. Test Observation of Group L1 Specimens (Un-Strengthened Specimens)
4.1.2. Test Observation of Group L2 Specimens (Strengthened with 100 mm Wing Walls)
4.1.3. Test Observation of Group L3 Specimens (Strengthened with 150 mm Wing Walls)
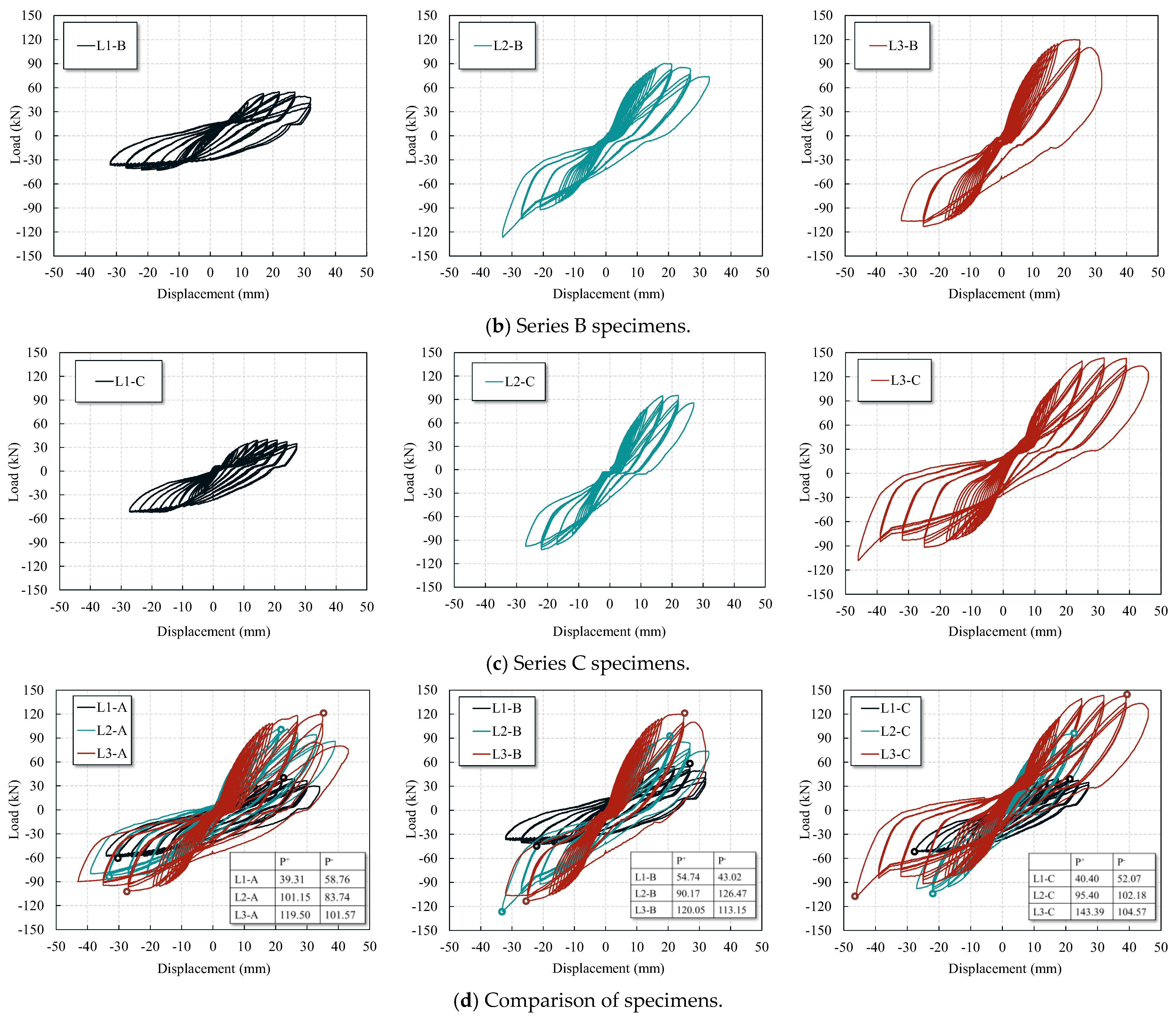
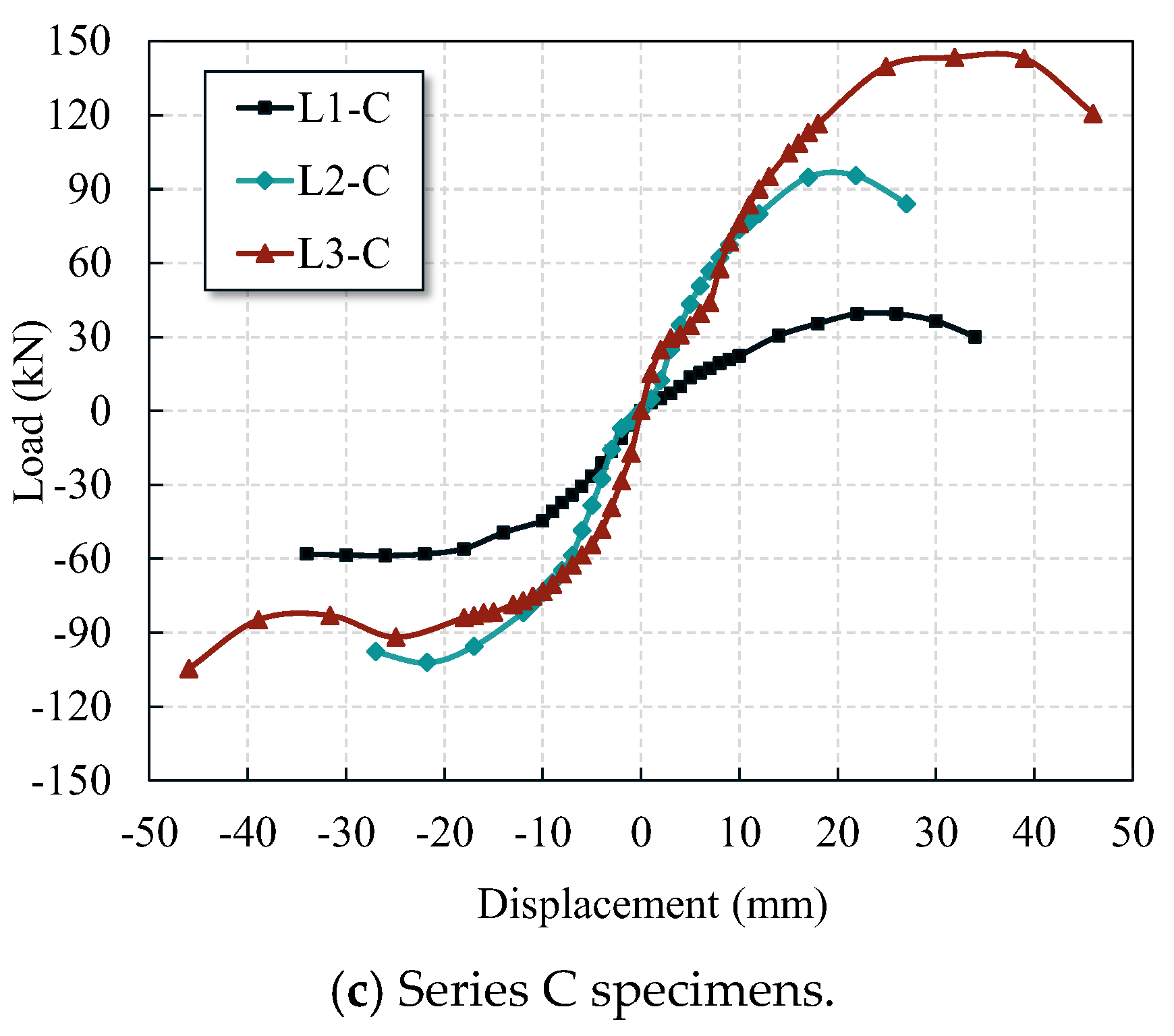
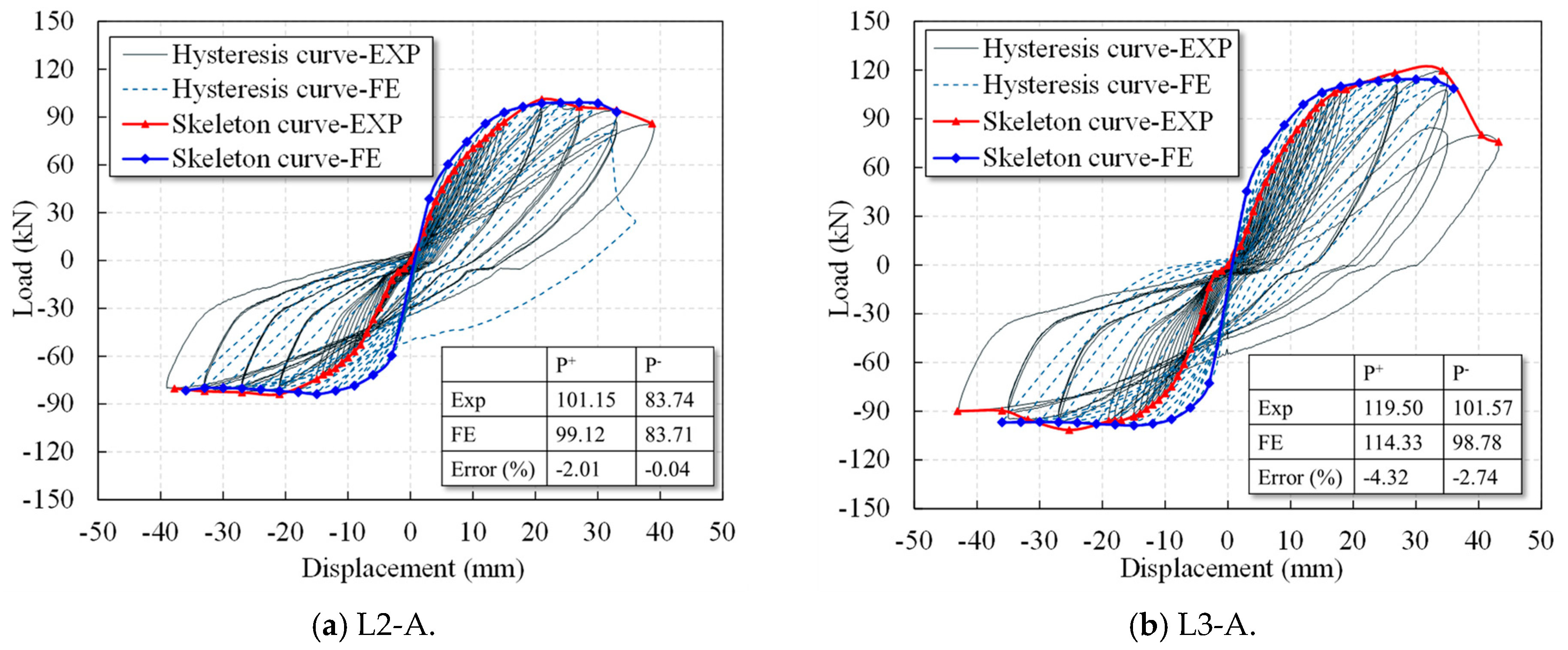
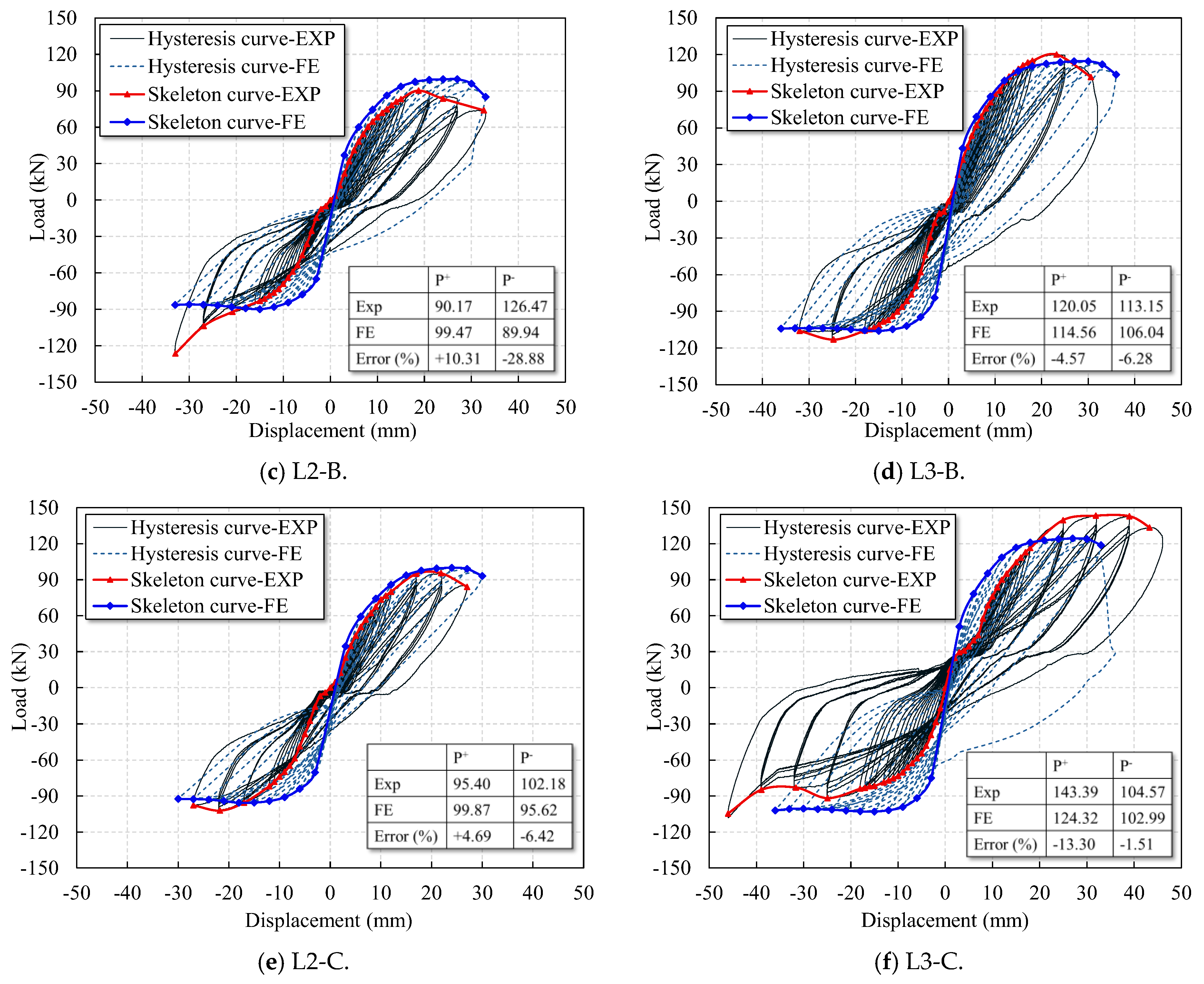
4.2. Hysteretic Curve
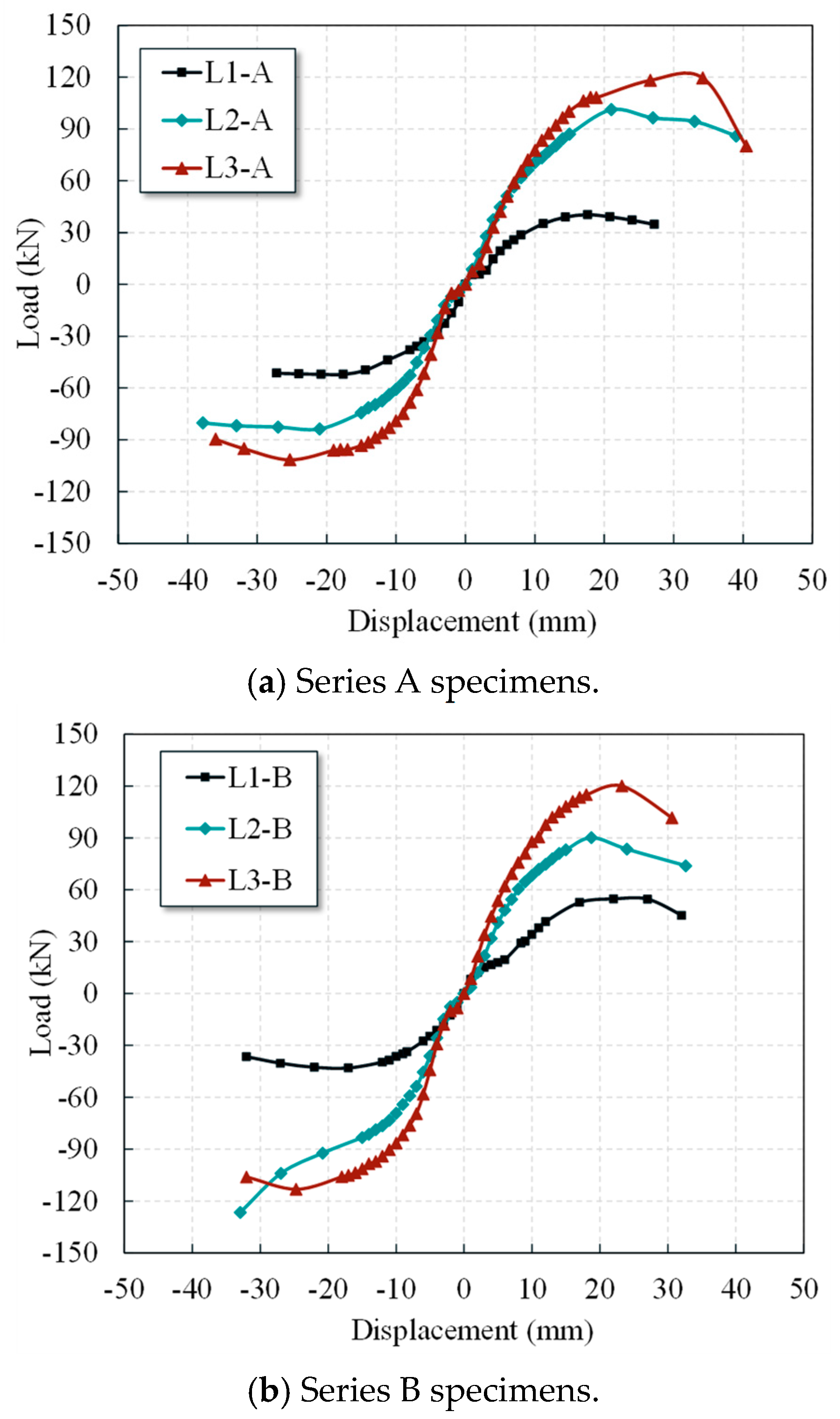
4.3. Skeleton Curve and Load Bearing Capacity
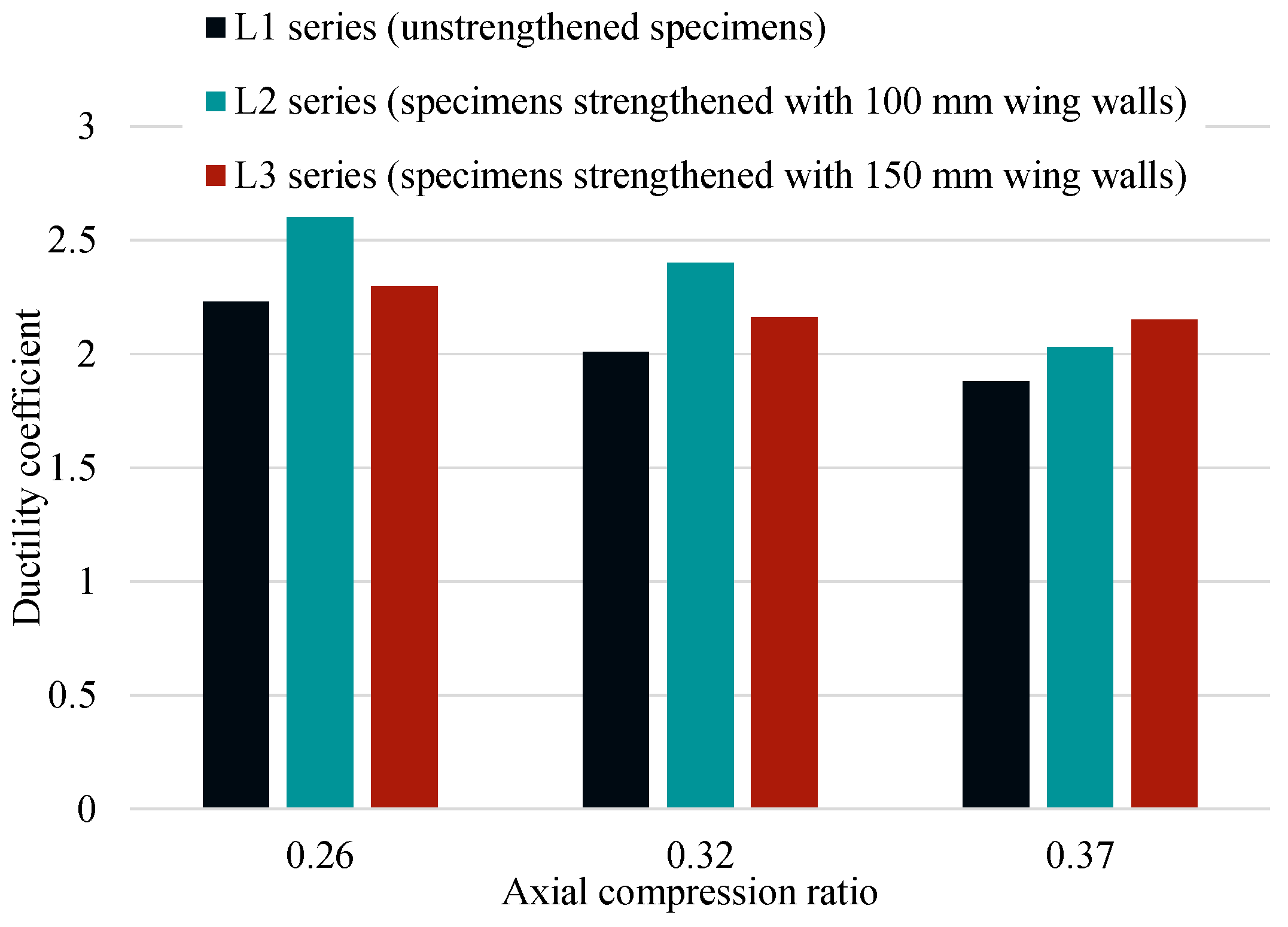
4.4. Ductility Analysis
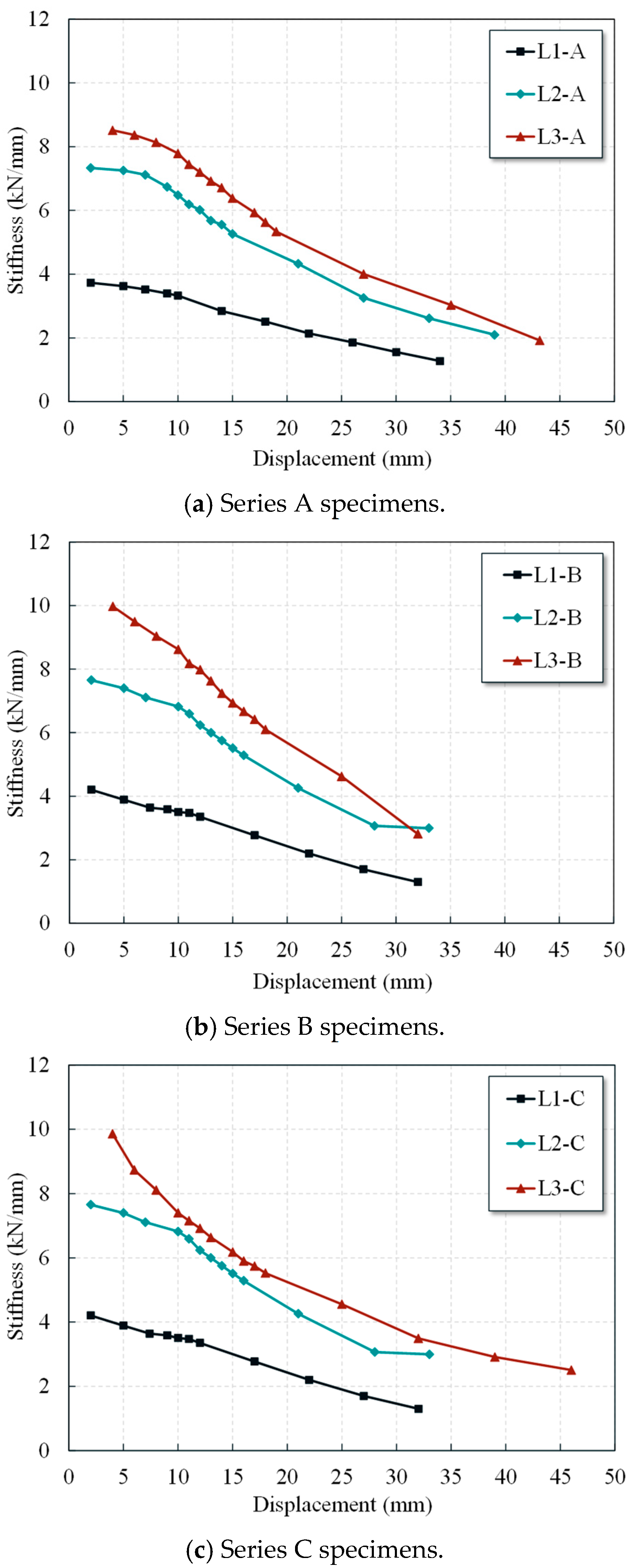
4.5. Stiffness Degradation
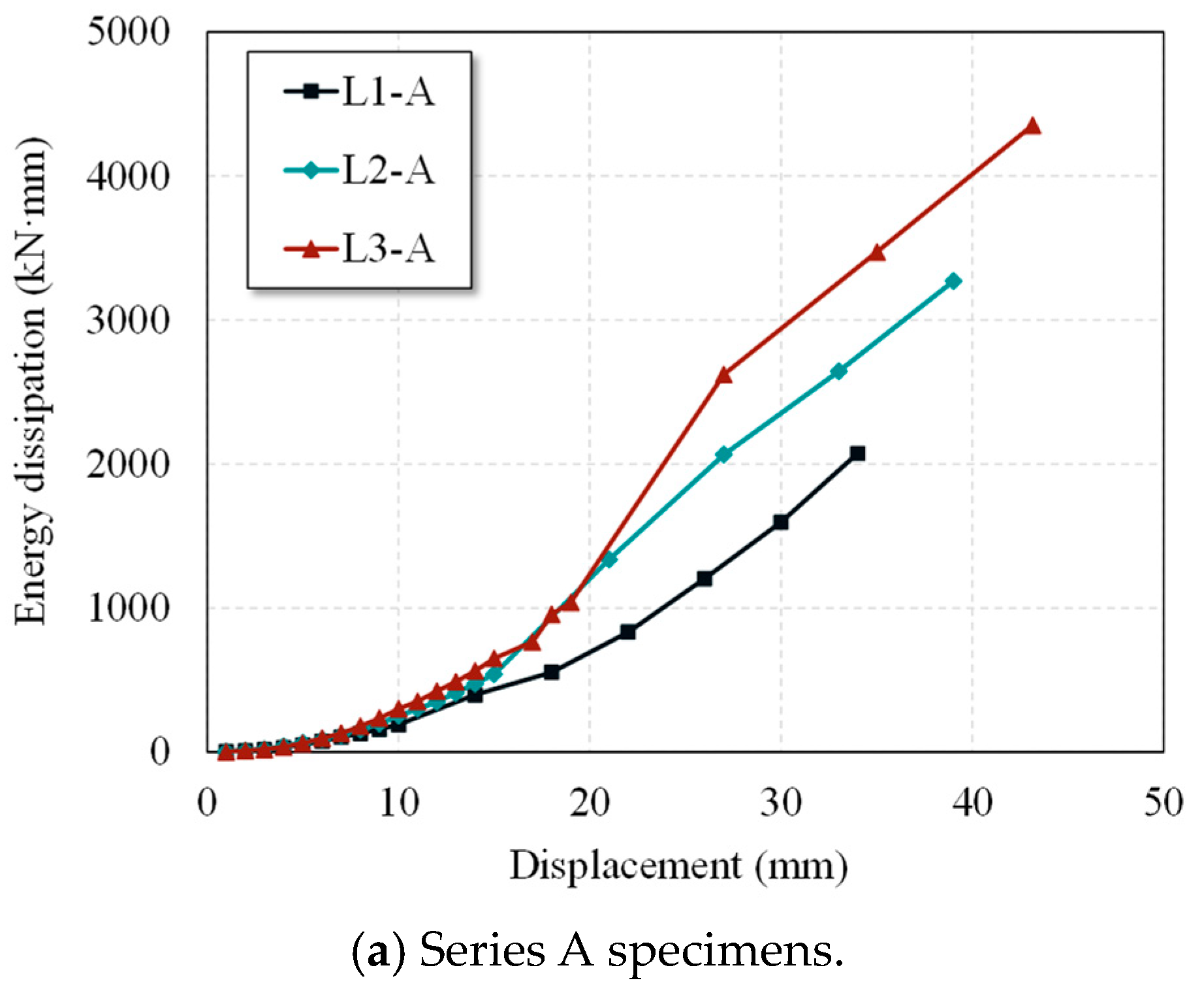
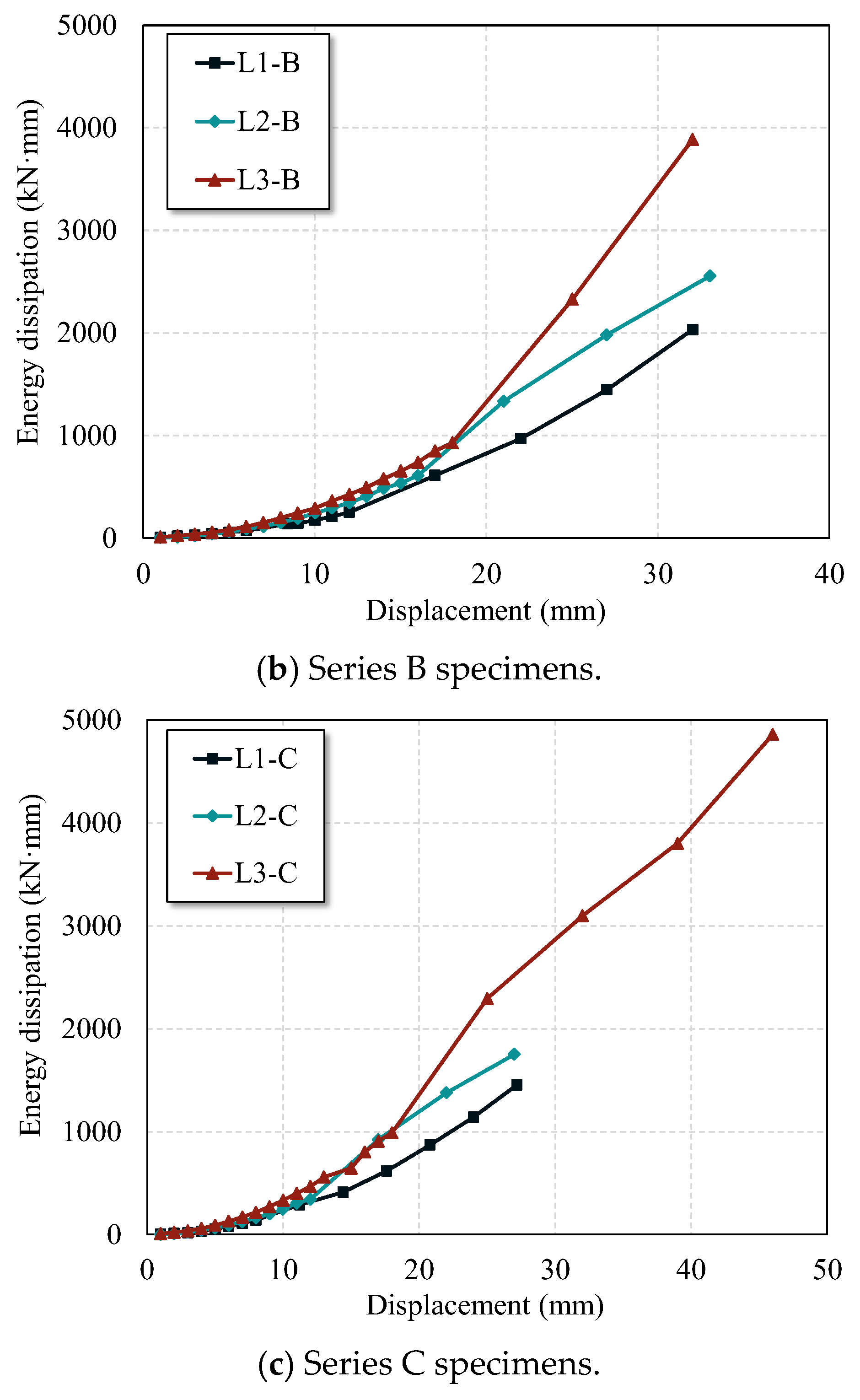
4.6. Energy Dissipation Capacity
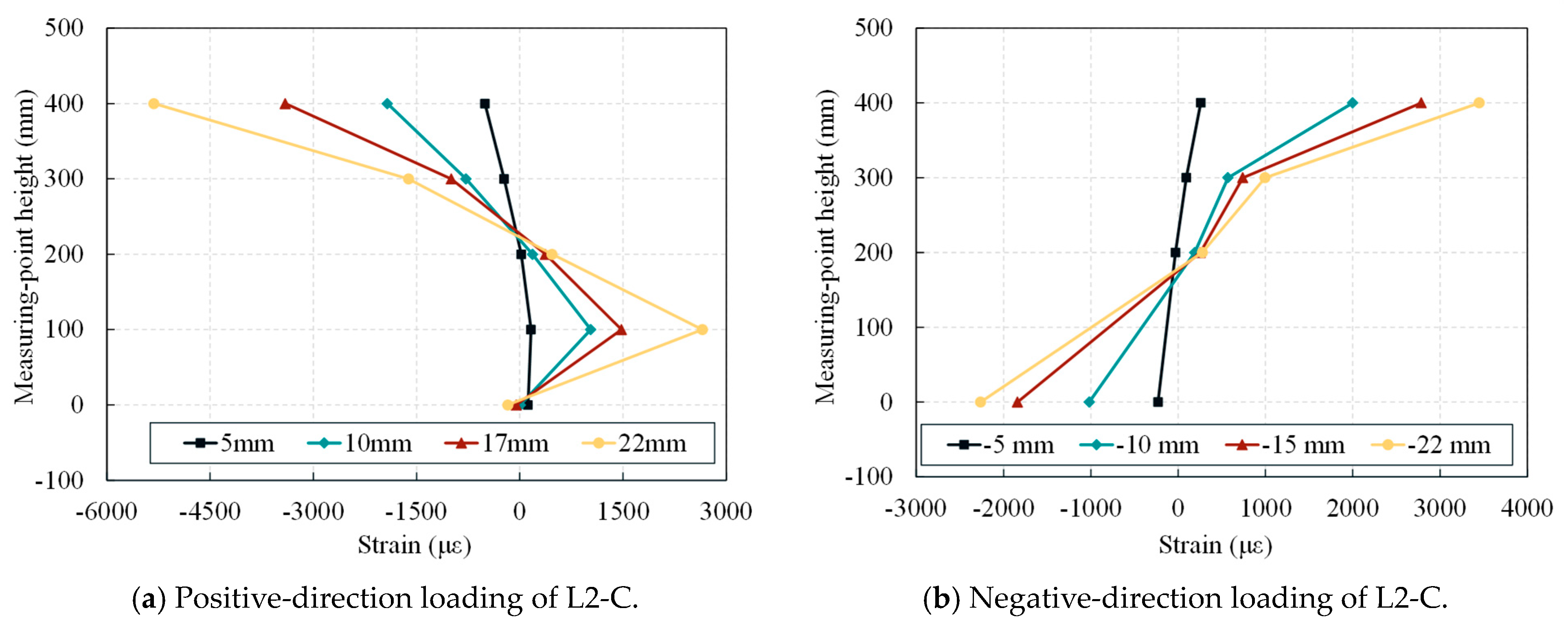
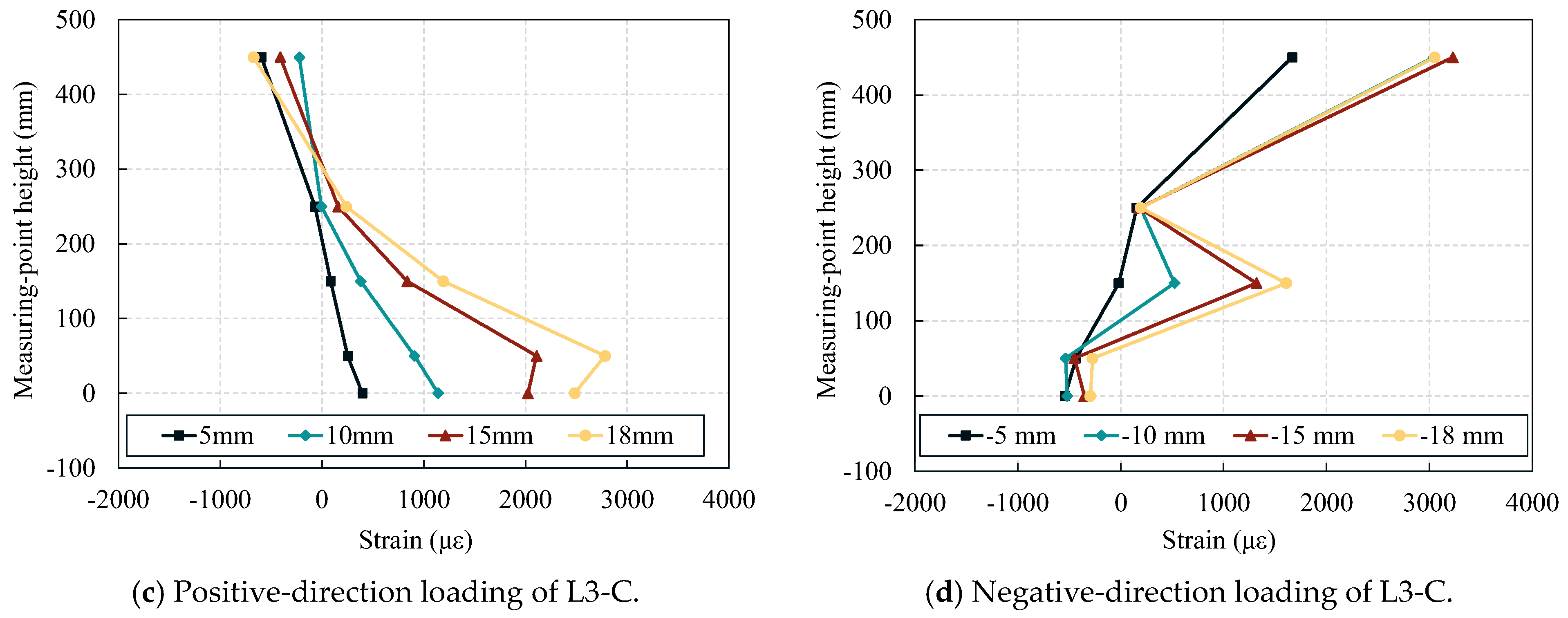
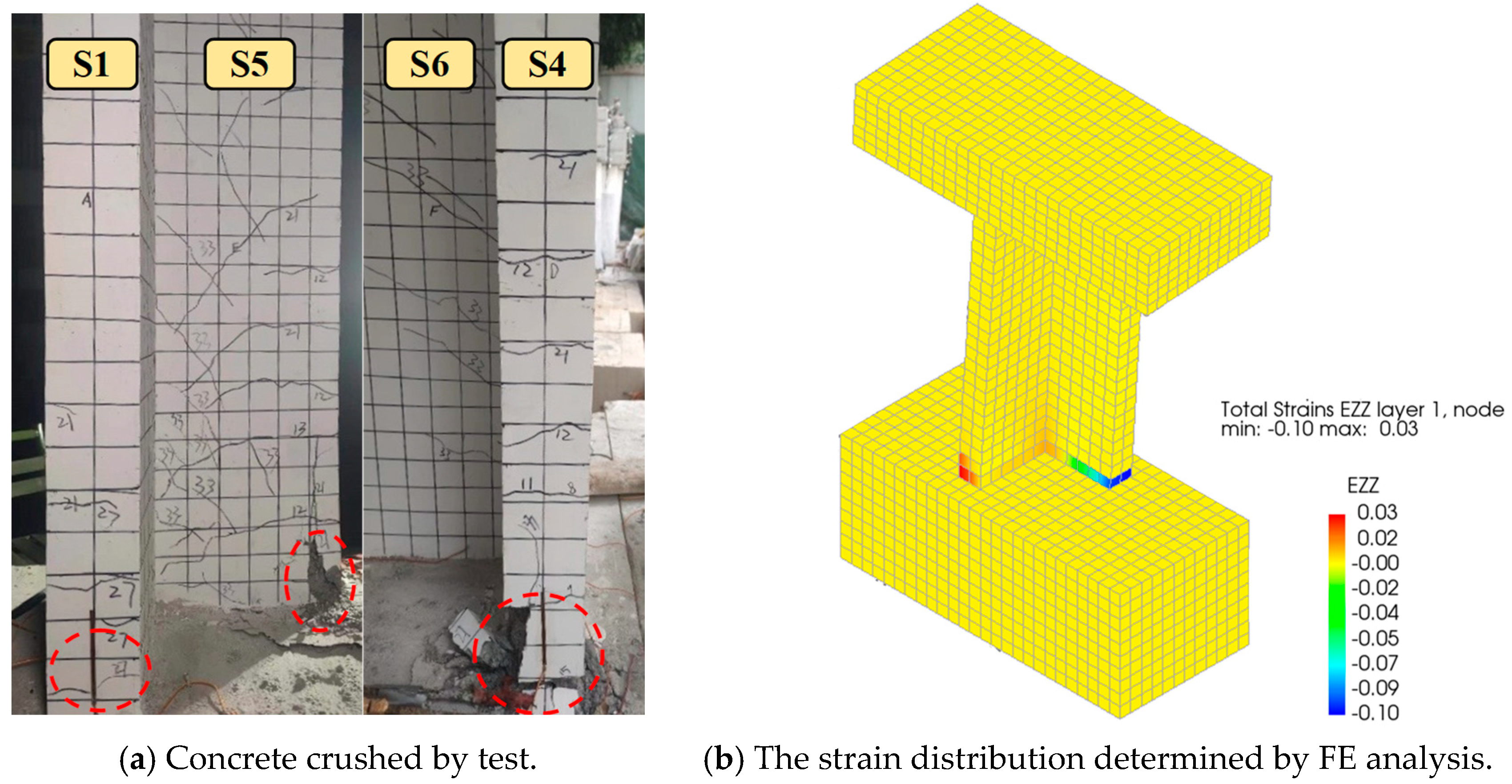
4.7. Strain Analysis
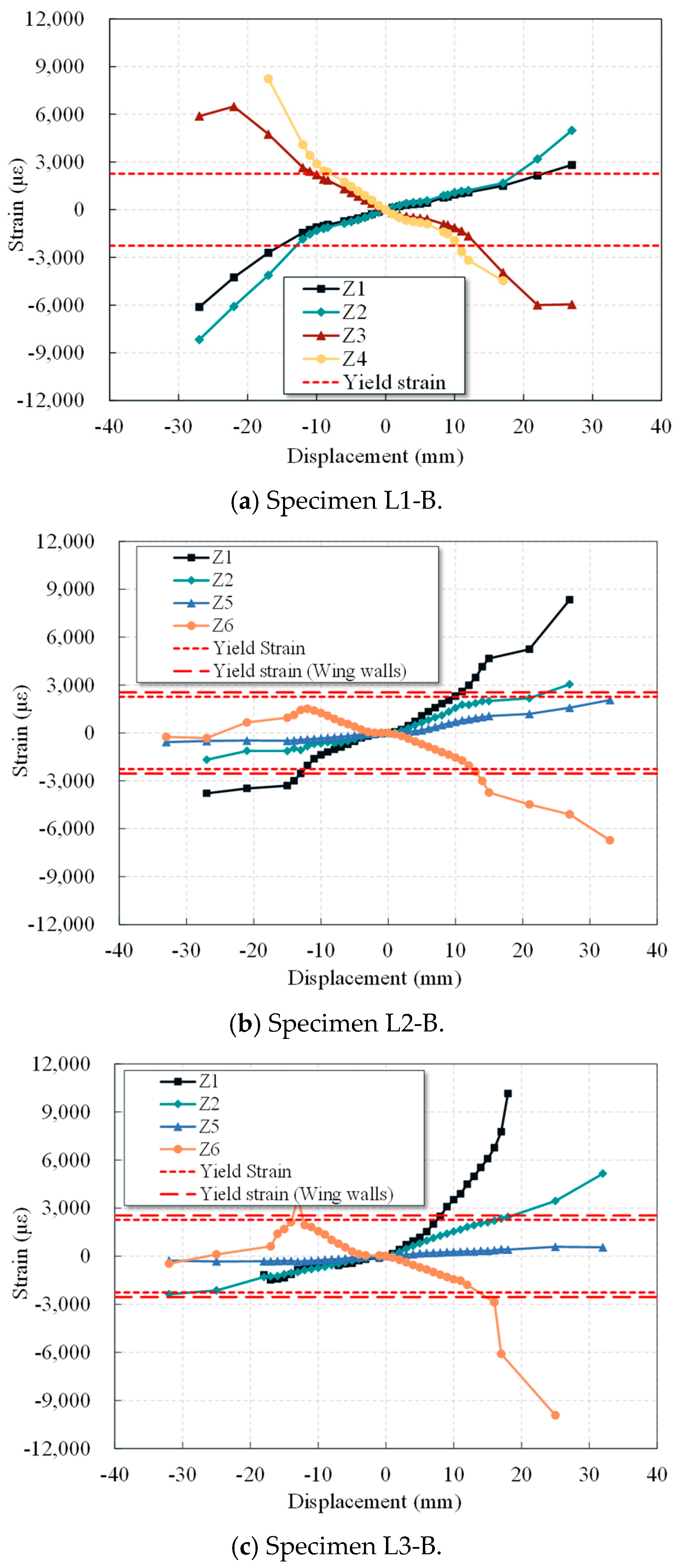
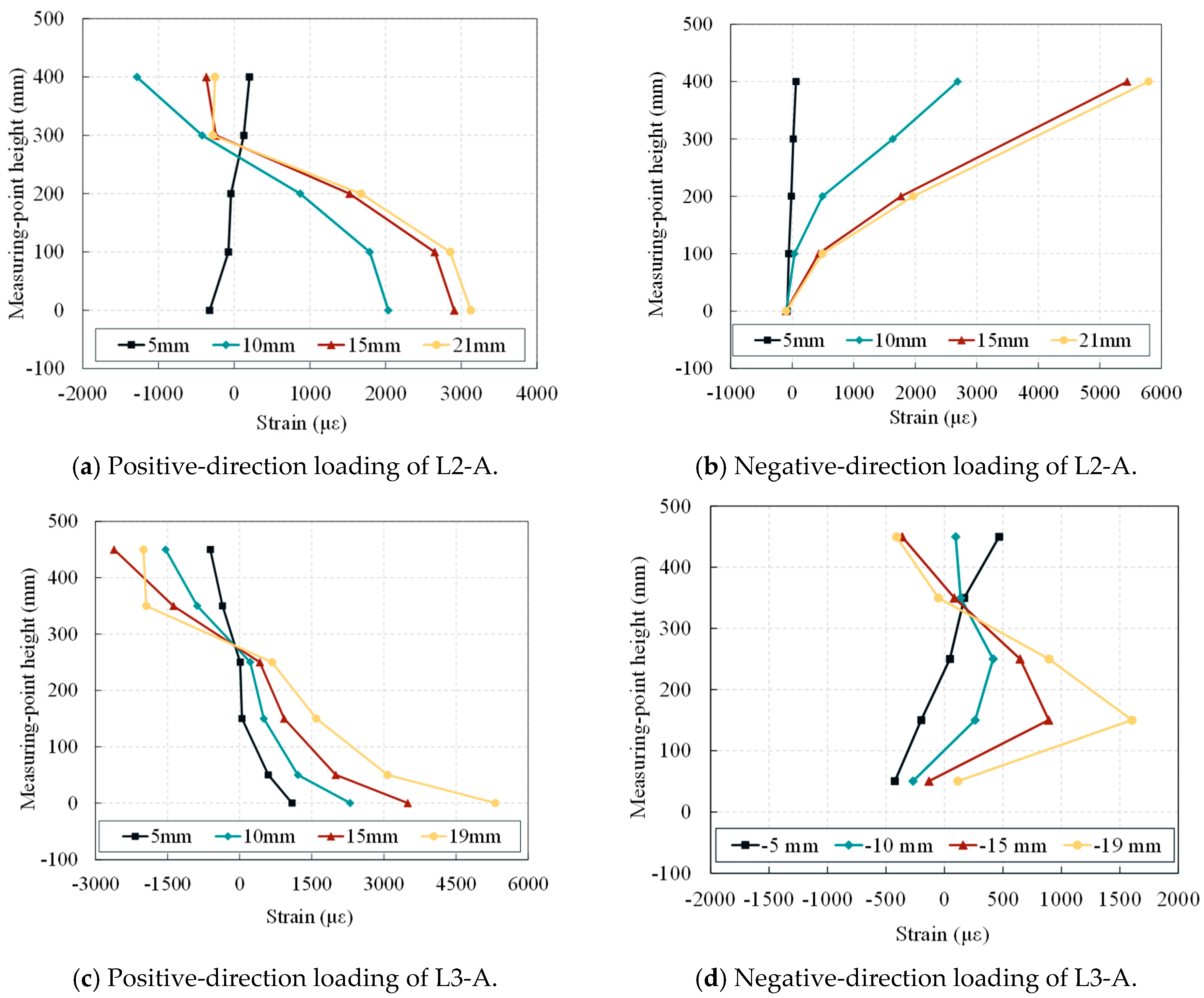
4.7.1. Steel Strain
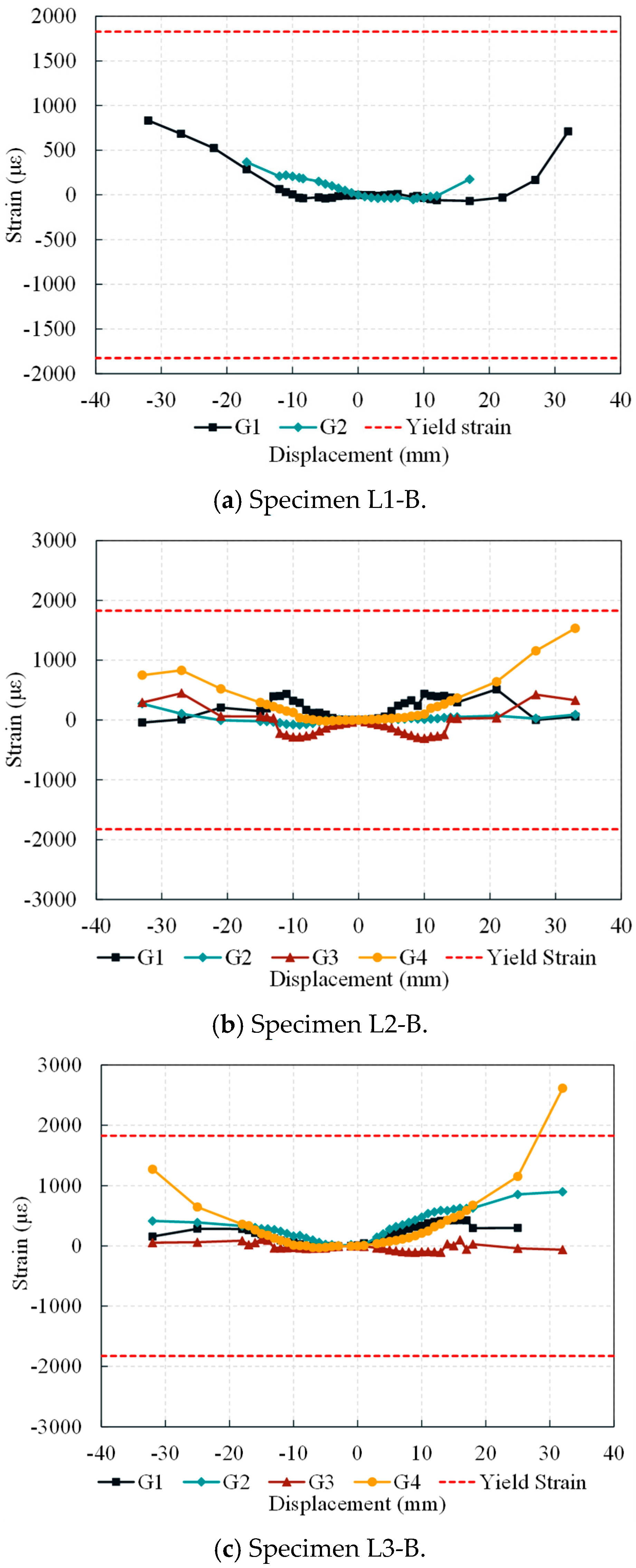
4.7.2. Concrete Strain
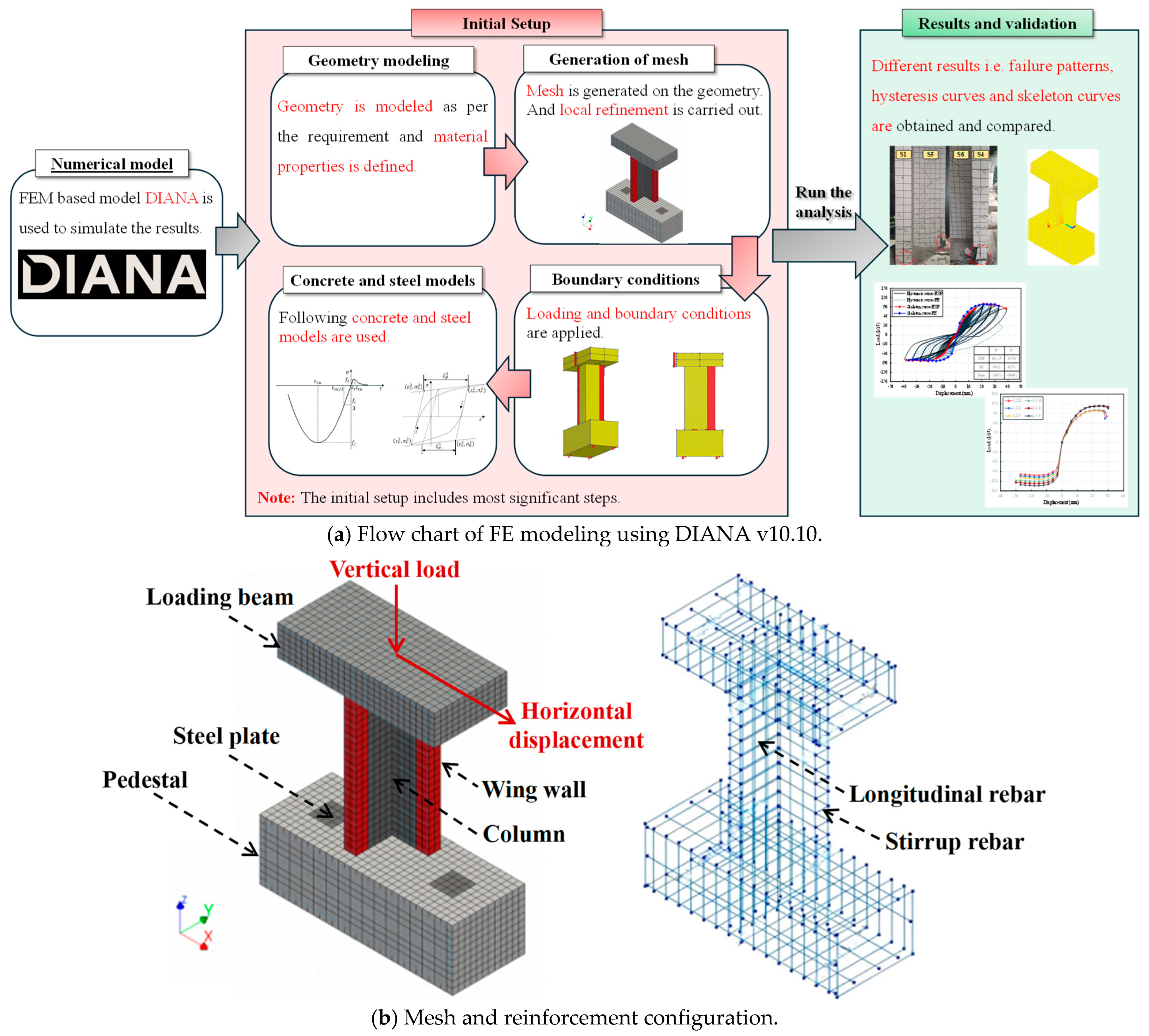
5. Finite Element Analysis
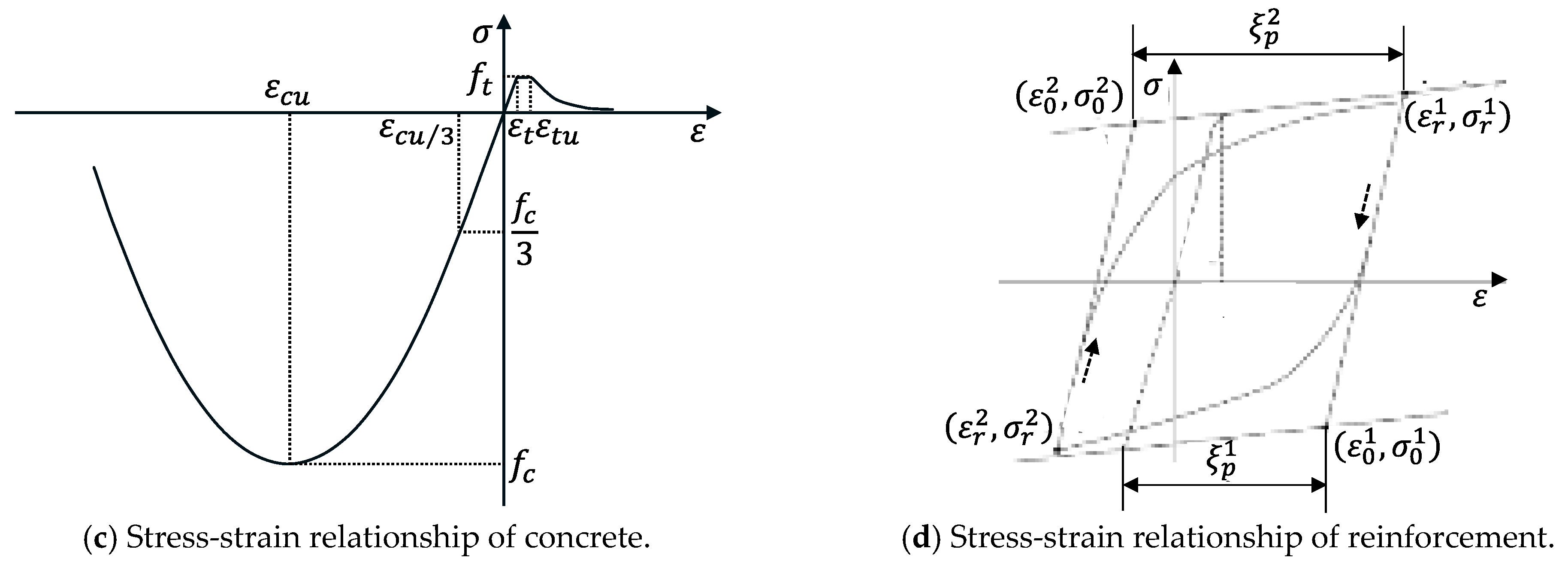
5.1. Finite Element Model
5.2. Validation of Numerical FE Model
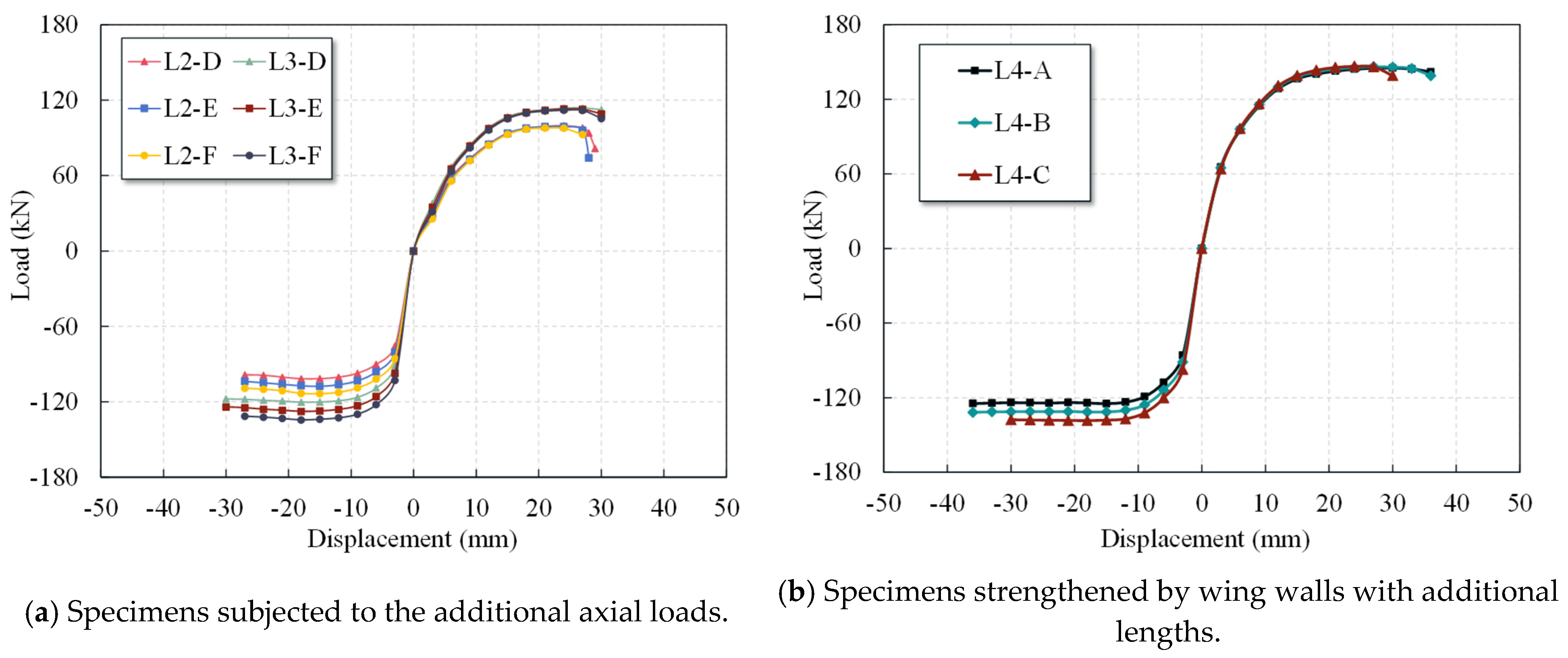
5.3. Parametric Investigation
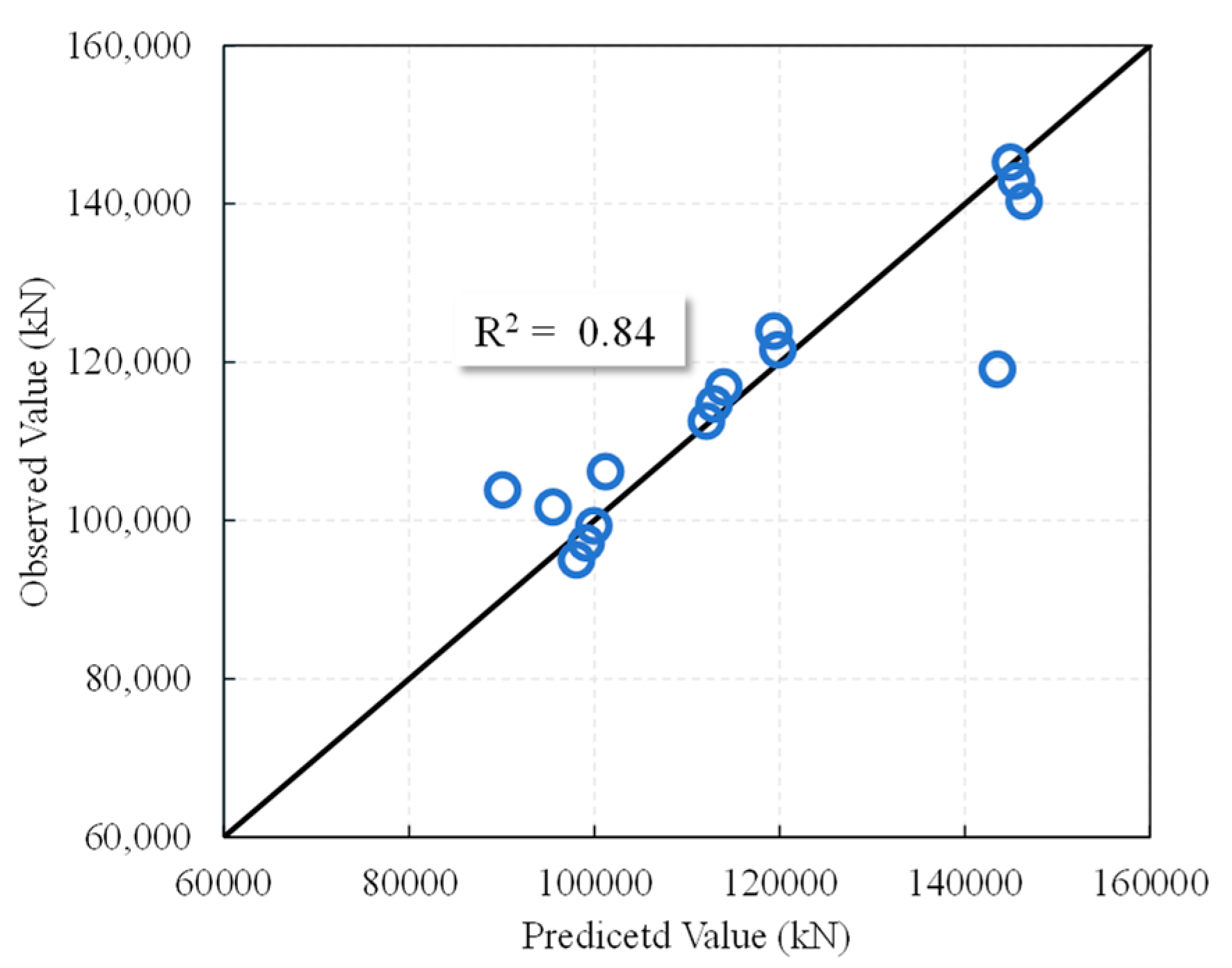
5.4. Regression Analysis of Lateral Load Bearing Capacity Calculation
6. Conclusions
- The failure process of both the un-strengthened and wing wall-strengthened L-shaped columns was similar, characterized by bending–shear failure, with damage typically occurring at the base of the limb on the side without flange. However, when the length of the added wing wall was increased to 150 mm, the failure mode gradually changed from the conventional column failure mode to a shear wall-type failure, accompanied by more brittle behavior. Therefore, when strengthening the wing wall, the length of the added wing wall must be selected appropriately based on the height-to-thickness ratio of the limb in the L-shaped column.
- Wing wall strengthening significantly improves the lateral load-bearing capacity of the L-shaped columns, with the enhancement becoming more pronounced under higher axial compression ratios. The addition of wing walls with lengths of 100 mm and 150 mm increased the lateral load bearing capacity by approximately 43–194% and 73–254%, respectively. Specifically, under the strengthening condition with 100 mm wing walls, the positive load bearing capacity was increased by up to 157% at the original column axial compression ratio of 0.26, and the negative load bearing capacity was increased by up to 194% at the original column axial compression ratio of 0.32. Additionally, under the strengthening condition with 150 mm wing walls, the positive and negative load bearing capacities were increased by up to 254% and 169%, respectively, at the original column axial compression ratios of 0.37 and 0.32. Furthermore, this strengthening significantly increased the initial stiffness of the columns and the energy dissipation capacity. Consequently, the strengthened specimens exhibited slower stiffness degradation in the later loading stages, reflecting improved seismic performance.
- The addition of a wing wall also significantly affected the positive ductility of the specimens. This effect varied with the change in wing wall length and the axial compression ratio level. Under high axial compression ratios, the ductility coefficient continued to increase with increasing wing wall length. Conversely, under low axial compression ratios, the increasing leg height-to-thickness ratio with increasing wing wall lengths resulted in a gradual shift toward the brittle failure mode of the L-shaped column, similarly to that of a shear wall. Consequently, an increasing trend in the ductility coefficient was found, with a decrease in later stages, as the wing wall length was increased. This observation is consistent with the characteristics of the component failure modes.
- The FE model concurred well with the experimental results in terms of the hysteresis behavior, skeleton curves, and load bearing capacity. Furthermore, a lateral load bearing capacity prediction formula for the L-shaped columns that were strengthened with wing walls was established through regression analysis. This formula provides theoretical support and serves as a practical reference for the seismic strengthening design of L-shaped columns with wing walls.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ahmed, A.A.; Ozturk, H.; Aslan, T.A. Comparative Analysis of Buildings with Different Story Heights According to TBDY 2018 and Eurocode 8. J. Çukurova Univ. Fac. Eng. 2025, 40, 265–272. [Google Scholar] [CrossRef]
- Unsal, I.; Balca, N.; Sahan, M.F. Comparison of structural system types given in the TBDY 2018 regulation for medium-rise buildings using linear analysis method. Adıyaman Univ. J. Eng. Sci. 2022, 9, 431–446. [Google Scholar] [CrossRef]
- Jafari, A.; Shahmansouri, A.A.; Bengar, H.A.; Zhou, Y. Flexural rigidity of SFRC columns at the onset of buckling failure: Analytical and numerical study. Steel Compos. Struct. 2025, 55, 533–552. [Google Scholar] [CrossRef]
- Marin, J. Design aids for L-shaped reinforced concrete columns. J. Am. Concr. Inst. 1979, 76, 1197–1216. [Google Scholar]
- Li, Q.; Wang, K.; Xue, Y.; Tian, Q.; Tao, Y. Dynamic fracture process of T-shaped beam-column specimens with prefabricated cracks under offset impact. Theor. Appl. Fract. Mech. 2022, 121, 103518. [Google Scholar] [CrossRef]
- Chen, Z.; Ning, F.; Chen, J.; Liu, X.; Xu, D. Test on mechanical behavior of SRC L-shaped columns under combined torsion and bending moment. Earthq. Eng. Eng. Vib. 2021, 20, 161–177. [Google Scholar] [CrossRef]
- Zhou, T.; Jia, Y.; Xu, M.; Wang, X.; Chen, Z. Experimental study on the seismic performance of L-shaped column composed of concrete-filled steel tubes frame structures. J. Constr. Steel Res. 2015, 114, 77–88. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Y.; Fu, F.; Liu, J. Static behavior of T-shaped concrete-filled steel tubular columns subjected to concentric and eccentric compressive loads. Thin Wall Struct. 2015, 95, 374–388. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, C.; Shang, F.; Wang, L.; Wang, L.; Chen, J.; Zhang, L.; Nehdi, M.L. Seismic behavior of full-scale precast assembly frame joints of special-shaped columns. Structures 2025, 75, 108781. [Google Scholar] [CrossRef]
- Zhang, Z.; Shi, G.; Wang, S.; Zhou, L. Investigation on buckling behavior of T-shaped box-T section columns under axial load. Eng. Struct. 2022, 254, 113904. [Google Scholar] [CrossRef]
- Chen, H.; Wang, L.; Chen, H.; Cui, W. Experimental study on the seismic behavior of prefabricated L-shaped concrete-filled steel tube with rectangular multi-cell columns under different lateral loading directions. J. Constr. Steel Res. 2021, 177, 106480. [Google Scholar] [CrossRef]
- Li, W.; Ye, H.; Sun, L. Experimental study on seismic behavior of T-shaped steel fiber reinforced concrete columns. Struct. Concr. 2023, 24, 612–633. [Google Scholar] [CrossRef]
- Li, Y.; Cao, X.-Y.; Feng, D.-C. A numerical model database for seismic retrofitting of existing RC structures towards urban renewal. Bull. Earthq. Eng. 2025, 23, 3295–3325. [Google Scholar] [CrossRef]
- Zhong, S.; Hu, X.; Peng, G.; Hou, J. The effect of section enlargement with cementitious grout on the eccentric compression behavior of RC columns. KSCE J. Civ. Eng. 2024, 28, 3378–3393. [Google Scholar] [CrossRef]
- Ramírez, J.L. Ten concrete column repair methods. Constr. Build. Mater. 1996, 10, 195–202. [Google Scholar] [CrossRef]
- Mahmoud, K.M.; Sallam, E.A.; Ibrahim, H.M.H. Behavior of partially strengthened reinforced concrete columns from two or three sides of the perimeter. Case Stud. Constr. Mater. 2022, 17, e01180. [Google Scholar] [CrossRef]
- Nematzadeh, M.; Mousavimehr, M.; Shayanfar, J.; Omidalizadeh, M. Eccentric compressive behavior of steel fiber-reinforced RC columns strengthened with CFRP wraps: Experimental investigation and analytical modeling. Eng. Struct. 2021, 226, 111389. [Google Scholar] [CrossRef]
- Khorramian, K.; Sadeghian, P. Hybrid system of longitudinal CFRP laminates and GFRP wraps for strengthening of existing circular concrete columns. Eng. Struct. 2021, 235, 112028. [Google Scholar] [CrossRef]
- Samy, K.; Fouda, M.A.; Fawzy, A.; Elsayed, T. Enhancing the effectiveness of strengthening RC columns with CFRP sheets. Case Stud. Constr. Mater. 2022, 17, e01588. [Google Scholar] [CrossRef]
- Ciampa, E.; Ceroni, F.; De Angelis, A.; Pecce, M.R. Bond tests on concrete elements externally bonded with steel plates and assessment of bond strength models. Eng. Struct. 2023, 296, 116835. [Google Scholar] [CrossRef]
- Hamoda, A.; Shahin, R.I.; Ahmed, M.; Abadel, A.A.; Baktheer, A.; Yehia, S.A. Strengthening of reinforced concrete columns incorporating different configurations of stainless-steel plates. Structures 2024, 64, 106577. [Google Scholar] [CrossRef]
- Huang, H.; Guo, M.; Zhang, W.; Huang, M. Seismic behavior of strengthened RC columns under combined loadings. J. Bridge Eng. 2022, 27, 05022005. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Q.; Zhao, K.; Hao, J.; Hu, Y. Experimental study on seismic performance of shear wall with insufficient concrete strength strengthened by partial concrete replacement. Structures 2024, 69, 107537. [Google Scholar] [CrossRef]
- Wardi, S.; Sanada, Y.; Saha, N.; Takahashi, S. Improving integrity of RC beam-column joints with deficient beam rebar anchorage. Earthq. Eng. Struct. Dyn. 2020, 49, 234–260. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, X.; Skalomenos, K.A.; Lin, X.; Zhu, B. Investigation on the seismic performance of single-span RC frame school buildings retrofitted with wing walls under different seismic design intensities. Structures 2022, 44, 1945–1961. [Google Scholar] [CrossRef]
- Li, Y.; Wang, H.; Xing, S.; Shan, L.; Wang, X. Influence of the vertical load bearing status on the seismic performance of weak-joint-type RC frames strengthened by the wing wall installation method. J. Earthq. Tsunami 2024, 18, 2450017. [Google Scholar] [CrossRef]
- Liu, K.-C.; Liu, Y.-W.; Huang, W.-C.; Chen, C.-Y. The structure behavior of reinforced concrete wing–wall under earthquake. Int. J. Phys. Sci. 2010, 5, 1164–1174. Available online: http://www.academicjournals.org/IJPS (accessed on 4 August 2025).
- Kaltakci, M.Y.; Yavuz, G. An experimental study on strengthening of vulnerable RC frames with RC wing walls. Struct. Eng. Mech. 2012, 41, 691–710. [Google Scholar] [CrossRef]
- Bai, Y.; Bai, G. Pseudo-dynamic and quasi-static testing of an irregular steel concrete composite frame with wing walls. Int. J. Struct. Stab. Dyn. 2016, 16, 1450095. [Google Scholar] [CrossRef]
- Yang, W.; Guo, X.; Xu, W.; Yuan, X. Wing walls for enhancing the seismic performance of reinforced concrete frame structures. Earthq. Eng. Eng. Vib. 2016, 15, 411–423. [Google Scholar] [CrossRef]
- Li, Y.; Sanada, Y. Seismic strengthening of existing RC beam-column joints by wing walls. Earthq. Eng. Struct. Dyn. 2017, 46, 1987–2008. [Google Scholar] [CrossRef]
- Li, Y.; Sanada, Y.; Maekawa, K.; Katayama, H.; Choi, H.; Matsukawa, K.; Takahashi, S. Seismic strengthening and rehabilitation of RC frame structures with weak beam-column joints by installing wing walls. Bull. Earthq. Eng. 2019, 17, 2533–2567. [Google Scholar] [CrossRef]
- Wang, B.; Guan, S.; Zhang, Y.; Bai, Y. Experimental behavior and failure modes of hybrid beam-to-column connections with RC wing-walls in industrial construction. Constr. Build. Mater. 2019, 218, 628–643. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, C.; Chen, Y. Comparing seismic performances of single-span RC frames with and without wing wall retrofitting by shaking table tests. J. Build. Eng. 2024, 88, 109158. [Google Scholar] [CrossRef]
- JGJ 149-2017; Technical Specification for Concrete Structures with Specially Shaped Columns. China Construction Industry Press: Beijing, China, 2017.
- GB/T 50081-2019; Standard for Test Methods of Concrete Physical and Mechanical Properties. China Construction Industry Press: Beijing, China, 2019.
- GB/T 228.1-2021; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. China Construction Industry Press: Beijing, China, 2021.
- JGJ 116-2009; Technical Specification for Seismic Strengthening of Buildings. China Construction Industry Press: Beijing, China, 2009.
- Oh, Y.; Han, S.W.; Lee, L. Effect of boundary element details on the seismic deformation capacity of structural walls. Earthq. Eng. Struct. Dyn. 2002, 31, 1583–1602. [Google Scholar] [CrossRef]
- Su, R.K.L.; Wong, S.M. Seismic behaviour of slender reinforced concrete shear walls under high axial load ratio. Eng. Struct. 2007, 29, 1957–1965. [Google Scholar] [CrossRef]
- Lestuzzi, P.; Bachmann, H. Displacement ductility and energy assessment from shaking table tests on RC structural walls. Eng. Struct. 2007, 29, 1708–1721. [Google Scholar] [CrossRef]
- Wang, T.C.; Chen, X.S. Experimental study on shear capacity of broad-limb special-shaped columns. Adv. Mater. Res. 2011, 250–253, 2412–2417. [Google Scholar] [CrossRef]
- Nguyen, T.K.; Nguyen, N.T. Finite element investigation of the shear performance of corroded RC deep beams without shear reinforcement. Case Stud. Constr. Mater. 2021, 15, e00757. [Google Scholar] [CrossRef]
- Abdullah, M.; Nakamura, H.; Miura, T. A numerical evaluation on the effect of vertical stirrup legs to shear failure behavior in RC beams based on 3D RBSM. Eng. Struct. 2025, 343, 121268. [Google Scholar] [CrossRef]
- Abdullah, M.; Nakamura, H.; Miura, T. Numerical Investigation on Influence of Vertical Shear Leg Stirrups to Shear Failure Behavior in Wide Beams Using 3D-RBSM. Build. Future Durable Sustain. Resilient 2023, 349, 1567–1577. [Google Scholar] [CrossRef]
- Nakamura, H.; Higai, T. Compressive fracture energy and fracture zone length of concrete. In Modeling of Inelastic Behavior of RC Structures under Seismic Loads; Shing, B., Tanabe, T., Eds.; ASCE: Reston, VA, USA, 2001; pp. 471–487. [Google Scholar]
- Japan Society of Civil Engineers. JSCE Guidelines for Concrete: Standard Specifications for Concrete Structures—2007 "Design"; Japan Society of Civil Engineers: Tokyo, Japan, 2010. [Google Scholar]




| Specimen | Length of Wing Walls (mm) | Original Columns Axial Compression Ratio | Actual Axial Compression Ratio | Axial Load (kN) |
|---|---|---|---|---|
| L1-A | 0 | 0.26 | 0.26 | 287 |
| L1-B | 0 | 0.32 | 0.32 | 344 |
| L1-C | 0 | 0.37 | 0.37 | 401 |
| L2-A | 100 | 0.26 | 0.19 | 287 |
| L2-B | 100 | 0.32 | 0.23 | 344 |
| L2-C | 100 | 0.37 | 0.26 | 401 |
| L3-A | 150 | 0.26 | 0.16 | 287 |
| L3-B | 150 | 0.32 | 0.20 | 344 |
| L3-C | 150 | 0.37 | 0.23 | 401 |
| Reinforcement | Concrete | |||||
|---|---|---|---|---|---|---|
| Rebar Types | d (mm) | fy (MPa) | fu (MPa) | E (105 N/mm2) | Part of Columns | fc’ (MPa) |
| HPB300 | 6 | 422 | 518 | 2.31 | Original column | 34.3 |
| 10 | 412 | 531 | 1.82 | Wing wall | 35.8 | |
| HRB400 | 8 | 524 | 618 | 2.06 | ||
| 10 | 449 | 562 | 1.73 | |||
| 12 | 429 | 533 | 1.91 | |||
| 18 | 446 | 561 | 2.01 | |||
| Specimen | Length of Wing Walls (mm) | Axial Load ((kN) | Peak Load of Positive Direction (kN) | Peak Load of Negative Direction (kN) | Initial Stiffness ((kN/mm) |
|---|---|---|---|---|---|
| L2-D | 100 | 458 | 99.73 | 101.66 | 17.89 |
| L3-D | 150 | 458 | 113.81 | 120.26 | 21.55 |
| L2-E | 100 | 515 | 98.97 | 107.60 | 18.24 |
| L3-E | 150 | 515 | 113.08 | 127.65 | 22.01 |
| L2-F | 100 | 572 | 97.86 | 113.57 | 18.57 |
| L3-F | 150 | 572 | 112.04 | 134.40 | 22.38 |
| L4-A | 200 | 287 | 145.07 | 124.77 | 25.26 |
| L4-B | 200 | 344 | 146.06 | 131.79 | 26.04 |
| L4-C | 200 | 401 | 146.50 | 138.45 | 26.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Liao, J.; Li, Z.; Xie, M.; Fang, C.; Abdullah, M.; Zhang, M. Seismic Performance of Existing Reinforced Concrete L-Shaped Columns Strengthened with Wing Walls. Buildings 2025, 15, 3645. https://doi.org/10.3390/buildings15203645
Wang W, Liao J, Li Z, Xie M, Fang C, Abdullah M, Zhang M. Seismic Performance of Existing Reinforced Concrete L-Shaped Columns Strengthened with Wing Walls. Buildings. 2025; 15(20):3645. https://doi.org/10.3390/buildings15203645
Chicago/Turabian StyleWang, Weilun, Jiaqi Liao, Zixuan Li, Mingyuan Xie, Changle Fang, Muhammad Abdullah, and Mingyang Zhang. 2025. "Seismic Performance of Existing Reinforced Concrete L-Shaped Columns Strengthened with Wing Walls" Buildings 15, no. 20: 3645. https://doi.org/10.3390/buildings15203645
APA StyleWang, W., Liao, J., Li, Z., Xie, M., Fang, C., Abdullah, M., & Zhang, M. (2025). Seismic Performance of Existing Reinforced Concrete L-Shaped Columns Strengthened with Wing Walls. Buildings, 15(20), 3645. https://doi.org/10.3390/buildings15203645








