Mathematical Development for the Minimum Cost of Elliptical Combined Footings

Abstract

This work shows the mathematical development for the minimum cost of ECF (elliptical combined footings) subjected to biaxial bending due to the two columns, assuming that the distribution of soil pressure below the footing is linear and that the footing rests on elastic soil. There are no similar contributions on the subject of this article, as it is an innovative contribution in terms of its form. This work is developed in two parts: first, determine the minimum area in contact with the soil below the footing, and then the minimum cost is obtained. The formulation of the development by integration is shown to determine the moments, unidirectional shears, and punching shears acting on the critical sections, according to the ACI (American Concrete Institute) design code, and then the flowchart algorithm is applied to determine the solution using Maple Software, which is the main contribution of this article. Some authors show studies on the combined footings of various shapes such as rectangular, trapezoidal, strap, corner or L, and T, but there are none for ECF. Two numerical studies are shown with different length: the first with free ends in the longitudinal direction and the second with ends limited in the longitudinal direction to estimate the minimum cost of ECF under biaxial bending. A third numerical study is shown, with different allowable bearing capacities of the ground and with free ends in the longitudinal direction. Also, a comparison is developed between ECF and RCF (rectangular combined footings). The model for the design of ECF shows a savings of 7.17% with limited ends and a savings of 1.67% with free ends for the minimum area, and for the minimum cost, it shows a savings of 23.95% with limited ends and a savings of 9.14% with free ends rather than RCF. Therefore, the proposed development will be of great help to structural engineers specializing in foundations, as it represents significant savings.

1. Introduction

The main function of a foundation is to transfer the loads from the superstructure to the ground that supports the entire construction.

The types of foundations usually depend on the depth and are called shallow and deep. Shallow foundations can be (1) masonry foundations, also known as stone foundations or cyclopean foundations, which are a type of shallow foundation used to build load-bearing walls; (2) isolated footings are usually square, rectangular, circular, and recently elliptical, and are used to support point loads, such as those from columns or pillars, distributing the weight of the structure over the ground; (3) combined footings can be of various types such as rectangular, trapezoidal, strap, corner or L-shaped, and T-shaped and are used to distribute the load of two or more adjacent columns over a larger area of land, and they are also are used when columns are close together or when a column is close to a property line, avoiding the overlapping of individual footings; (4) strip footings, also known as continuous footings, are used to distribute the weight of load-bearing walls or a series of columns across a continuous strip of reinforced concrete; and (5) foundation slabs are reinforced concrete slabs that extend across the entire area of a building and distribute the weight of the structure over the ground.

The ground pressure below the foundation depends on the type and relative stiffness of the ground, as well as the stiffness and depth of the foundation.

Figure 1 shows the distribution of pressure below the footing as a function of the ground type and the stiffness of the foundation. Figure 1a presents a rigid base on sandy ground. Figure 1b shows a rigid base on clay ground. Figure 1c presents a flexible base on sandy ground. Figure 1d shows a flexible base on clay ground. Figure 1e presents the uniform distribution commonly used in design for all types of soil, assuming that the load is located at the center of gravity of the footing [1].

This mathematical development assumes that the distribution of pressure of the ground below the footing is linear because it is subjected to biaxial bending in each column, i.e., the resultant force is not located at the center of gravity of the footing.

Mathematical developments have been investigated to determine the smallest contact area with the soil for isolated footings with square, rectangular, and circular shapes under biaxial bending [2,3,4,5,6,7,8,9,10,11,12,13]. Complete models for the design of reinforced concrete isolated footings of square, rectangular, circular, and elliptical shapes subjected to biaxial bending have been studied [14,15,16,17,18,19,20,21,22,23,24].

Mathematical developments have been studied to estimate the smallest contact area with the soil for combined footings with rectangular, trapezoidal, strap, L (corner), and T shapes under biaxial bending due to each column [25,26,27]. Complete models for the design of reinforced concrete combined footings of rectangular, trapezoidal, strap, L (corner), and T shapes subjected to biaxial bending due to each column have been presented [28,29,30,31,32,33,34,35,36,37].

The most recent studies on the topic of cost optimization in footing design using computational approaches are by Waheed et al. [38], who introduced a parametric investigation based on cost optimization for foundation design by applying the Metaheuristic Practical Tool; Nawaz et al. [39] developed a cost optimization for the design of isolated footings resting cohesively by introducing ultimate and serviceability limit states; Khajehzadeh et al. [40] conducted research to predict the maximum load capacity of footings using artificial neural networks and a modified rat swarm optimizer by introducing the optimal design. All these works have been developed for rectangular isolated footings.

Listed below are the articles most related to the topic of elliptical footings: Diaz-Gurrola et al. [22] presented an investigation to obtain the minimum cost for elliptical isolated footings; Elhanash et al. [21] presented a method to determine the minimum cost of circular and elliptical isolated footings using Lagrange multipliers, but the numerical studies are developed only for circular isolated footings and not for elliptical isolated footings. All these works have been developed for elliptical isolated footings.

After the bibliographic review, it is observed that there is no article on the minimum cost of ECF, so this study is innovative research.

This article presents a new model for the minimum cost of ECF subjected to biaxial bending due to the two columns, assuming that the ground pressure distribution below the footing is linear and that the footing rests on elastic soil (innovative contribution in terms of its form). This study is presented in two parts: first, find the minimum area in contact with the ground under the footing, and then the minimum cost is determined. Some authors present studies on the combined footings of various shapes such as rectangular, trapezoidal, strap, L (corner), and T, but there are none for ECF. Two numerical examples are shown with different lengths: the first with free ends in the longitudinal direction and the second with ends limited in the longitudinal direction to obtain the minimum cost for ECF subjected to biaxial bending. A third numerical study is shown, with different allowable bearing capacities of the ground and with free ends in the longitudinal direction. Since there are no articles that refer to this topic, a comparison is made between elliptical and rectangular combined footings for RCF limited at its ends in the longitudinal direction [41] and for RCF free at its ends in the longitudinal direction [42]. Therefore, the proposed development will be of great help to structural engineers specializing in foundations, as it represents significant savings.

2. Methodology

The loads and moments that the footings must support are transferred from the columns that support the entire structure. The minimum contact surface with the ground is developed from the loads and moments without applying the factors “P, M_x, and M_y”. The minimum cost is estimated from the factored loads and moments “P_u, M_xu and M_yu”.

This paper is based on the following assumption: the foundation is completely rigid and rests on elastic and homogeneous soils; that is, the ground pressure under the foundation behaves linearly according to Bowles [1], Das et al. [43], and McCormac and Brown [44].

The soil pressure on any type of foundation due to biaxial bending can be expressed as follows (the contact surface with the ground is fully compressed):

$$p_s={\displaystyle \frac{P}{A}}+{\displaystyle \frac{M_{x}y}{I_x}}+{\displaystyle \frac{M_{y}x}{I_y}}.$$

(1)

The resultant force and resultant moments about each axis can be seen as follows:

$$R=P_1+P_2,$$

(2)

$$M_{xT}=M_{x1}+M_{x2}+R{e}_y-P_{2}L,$$

(3)

$$M_{yT}=M_{y1}+M_{y2}.$$

(4)

The geometric properties of an ellipse are shown below:

$$A=\pi ab,$$

(5)

$$I_x={\displaystyle \frac{\pi a{b}^3}{4}},$$

(6)

$$I_y={\displaystyle \frac{\pi a^{3}b}{4}}.$$

(7)

Figure 2 shows an ECF subjected to biaxial bending due to the two columns that rest on the footing.

The general equation with the center of the footing at the origin is shown below:

$${\displaystyle \frac{x^2}{a^2}}+{\displaystyle \frac{y^2}{b^2}}=1\to x={\displaystyle \frac{a\sqrt{b^2-y^2}}{b}}.$$

(8)

Substituting Equations (5)–(8) into Equation (1) (assuming P = R, M_x = M_xT, and M_y = M_yT), the soil pressure at any part located below the footing is determined:

$$p_s={\displaystyle \frac{R}{\pi ab}}+{\displaystyle \frac{4M_{xT}y}{\pi a{b}^3}}+{\displaystyle \frac{4M_{yT}\sqrt{b^2-y^2}}{\pi a^2{b}^2}}.$$

(9)

Deriving Equation (9) with respect to y to determine the location of maximum pressure and minimum pressure, these points are shown below:

$$y_{max}={\displaystyle \frac{ab{M}_{xT}}{\sqrt{a^2{M_{xT}}^2+b^2{M_{yT}}^2}}};y_{min}=-{\displaystyle \frac{ab{M}_{xT}}{\sqrt{a^2{M_{xT}}^2+b^2{M_{yT}}^2}}}.$$

(10)

Now, substitute Equation (10) into Equation (8) to obtain x_max and x_min:

$$x_{max}={\displaystyle \frac{ab{M}_{yT}}{\sqrt{a^2{M_{xT}}^2+b^2{M_{yT}}^2}}};x_{min}=-{\displaystyle \frac{ab{M}_{yT}}{\sqrt{a^2{M_{xT}}^2+b^2{M_{yT}}^2}}}.$$

(11)

The coordinates of the maximum pressure “c_max” are shown as follows:

$$c_{max}=\left(x_{max},y_{max}\right)=\left({\displaystyle \frac{ab{M}_{yT}}{\sqrt{a^2{M_{xT}}^2+b^2{M_{yT}}^2}}},{\displaystyle \frac{ab{M}_{xT}}{\sqrt{a^2{M_{xT}}^2+b^2{M_{yT}}^2}}}\right).$$

(12)

The coordinates of the minimum pressure “c_min” are shown as follows:

$$c_{min}=\left(x_{min},y_{min}\right)=\left(-{\displaystyle \frac{ab{M}_{yT}}{\sqrt{a^2{M_{xT}}^2+b^2{M_{yT}}^2}}},-{\displaystyle \frac{ab{M}_{xT}}{\sqrt{a^2{M_{xT}}^2+b^2{M_{yT}}^2}}}\right).$$

(13)

Now, by substituting Equation (12) into Equation (9), the maximum pressure is determined:

$$p_{max}={\displaystyle \frac{R}{\pi ab}}+{\displaystyle \frac{4\sqrt{a^2{M_{xT}}^2+b^2{M_{yT}}^2}}{\pi a^2{b}^2}}.$$

(14)

Now, by substituting Equation (13) into Equation (9), the minimum pressure is determined:

$$p_{min}={\displaystyle \frac{R}{\pi ab}}-{\displaystyle \frac{4\sqrt{a^2{M_{xT}}^2+b^2{M_{yT}}^2}}{\pi a^2{b}^2}}.$$

(15)

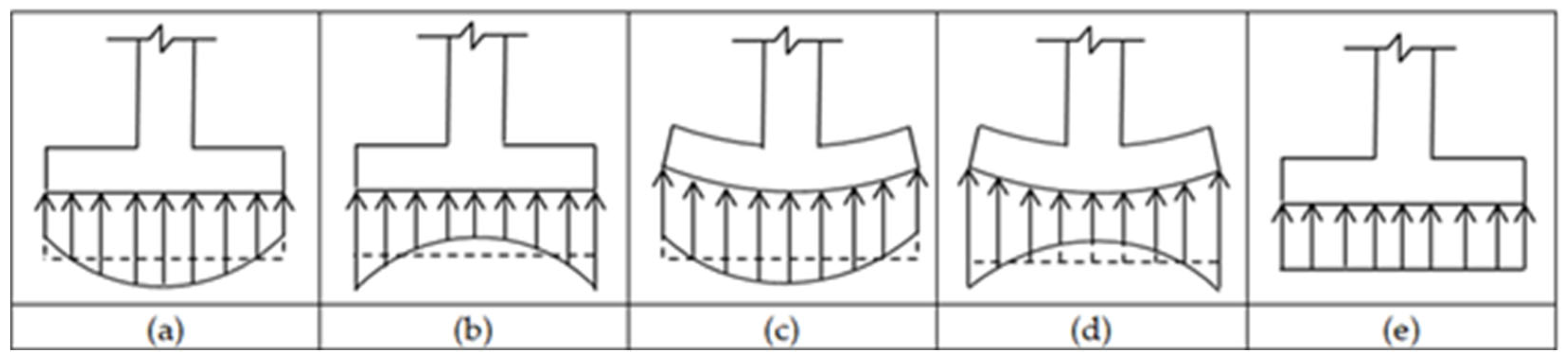
2.1. Minimum Surface of Elliptical Combined Footings

A_min (objective function) can be determined as follows:

$$A_{min}=\pi ab.$$

(16)

The constraints are shown in Equations (14) and (15), where 0 ≤ p_max and p_min ≤ p_aabcs. p_aabcs is equal to the p_abcs less γ_cd and less γ_sd.

2.2. Minimum Cost of Elliptical Combined Footings

p_u by Equation (1) with factored loads and factored moments (X and Y axes) is determined as follows:

$$p_u\left(x, y\right)={\displaystyle \frac{R_u}{\pi ab}}+{\displaystyle \frac{4M_{uxT}y}{\pi a{b}^3}}+{\displaystyle \frac{4M_{uyT}x}{\pi a^{3}b}},$$

(17)

where the factored loads and factored moments can be determined as follows: 1.2D + 1.6L, where D represents the dead load or moment due to dead load, and L represents the live load or moment due to live load, according to ACI [45].

p_u1 by Equation (1) with P_u1, M_ux1, and M_uy1 is determined as follows:

$$p_{u1}\left(x, y\right)={\displaystyle \frac{P_{u1}}{2h_1{w}_1}}+{\displaystyle \frac{6M_{ux1}{y}_1}{h_1{w_1}^3}}+{\displaystyle \frac{3M_{uy1}{x}_1}{2{h_1}^3{w}_1}}.$$

(18)

p_u2 by Equation (1) with P_u2, M_ux2, and M_uy2 is determined as follows:

$$p_{u2}\left(x, y\right)={\displaystyle \frac{P_{u2}}{2h_2{w}_2}}+{\displaystyle \frac{6M_{ux2}{y}_2}{h_2{w_2}^3}}+{\displaystyle \frac{3M_{uy2}{x}_2}{2{h_2}^3{w}_2}}.$$

(19)

The thickness of all reinforced concrete foundations must satisfy the effects of moments, unidirectional shears, and punching shears, according to ACI [45].

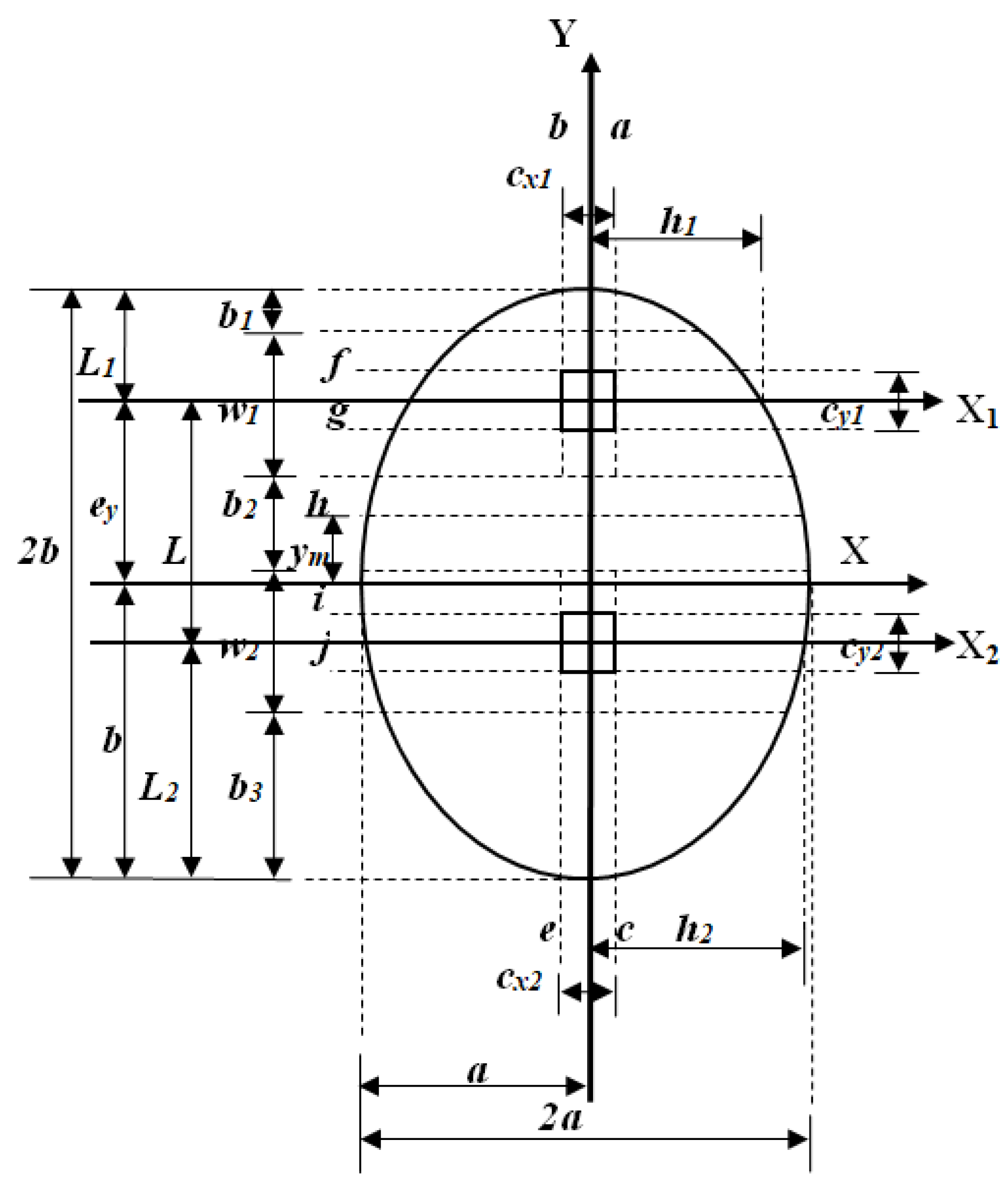
2.2.1. Moments

Figure 3 indicates the sections where the moments must be considered for an ECF subjected to biaxial bending due to each column; these sections occur at the faces of the column, according to ACI [45].

Factored moments about axes parallel to the Y axis (axes a, b, c, and e) are determined below:

$$M_{ua}=-{\int }_{{\displaystyle \frac{c_{x1}}{2}}}^{h_1}{\int }_{-{\displaystyle \frac{w_1}{2}}}^{{\displaystyle \frac{w_1}{2}}}{p}_{u1}\left(x_1, y_1\right)\left(x-{\displaystyle \frac{c_{x1}}{2}}\right)dydx,$$

(20)

$$M_{ub}={\displaystyle \frac{P_{u1}{c}_{x1}}{2}}+M_{uy1}-{\int }_{-{\displaystyle \frac{c_{x1}}{2}}}^{h_1}{\int }_{-{\displaystyle \frac{w_1}{2}}}^{{\displaystyle \frac{w_1}{2}}}{p}_{u1}\left(x_1, y_1\right)\left(x+{\displaystyle \frac{c_{x1}}{2}}\right)dydx,$$

(21)

$$M_{uc}=-{\int }_{{\displaystyle \frac{c_{x2}}{2}}}^{h_2}{\int }_{-{\displaystyle \frac{w_2}{2}}}^{{\displaystyle \frac{w_2}{2}}}{p}_{u2}\left(x_2, y_2\right)\left(x-{\displaystyle \frac{c_{x2}}{2}}\right)dydx,$$

(22)

$$M_{ue}={\displaystyle \frac{P_{u2}{c}_{x2}}{2}}+M_{uy2}-{\int }_{-{\displaystyle \frac{c_{x2}}{2}}}^{h_2}{\int }_{-{\displaystyle \frac{w_2}{2}}}^{{\displaystyle \frac{w_2}{2}}}{p}_{u2}\left(x_2, y_2\right)\left(x+{\displaystyle \frac{c_{x2}}{2}}\right)dydx.$$

(23)

Factored moments about axes parallel to the X axis (axes f, g, h, i, and j) are obtained below:

$$M_{uf}=-{\int }_{e_y+{\displaystyle \frac{c_{y1}}{2}}}^b{\int }_{-{\displaystyle \frac{a\sqrt{b^2-y^2}}{b}}}^{{\displaystyle \frac{a\sqrt{b^2-y^2}}{b}}}{p}_u\left(x, y\right)\left(y-e_y-{\displaystyle \frac{c_{y1}}{2}}\right)dxdy,$$

(24)

$$M_{ug}={\displaystyle \frac{P_{u1}{c}_{y1}}{2}}+M_{ux1}-{\int }_{e_y-{\displaystyle \frac{c_{y1}}{2}}}^b{\int }_{-{\displaystyle \frac{a\sqrt{b^2-y^2}}{b}}}^{{\displaystyle \frac{a\sqrt{b^2-y^2}}{b}}}{p}_u\left(x, y\right)\left(y-e_y+{\displaystyle \frac{c_{y1}}{2}}\right)dxdy,$$

(25)

$$M_{uh}=P_{u1}\left(e_y-y_m\right)+M_{ux1}-{\int }_{y_m}^b{\int }_{-{\displaystyle \frac{a\sqrt{b^2-y^2}}{b}}}^{{\displaystyle \frac{a\sqrt{b^2-y^2}}{b}}}{p}_u\left(x, y\right)\left(y-y_m\right)dxdy,$$

(26)

$$M_{ui}=P_{u1}\left(L-{\displaystyle \frac{c_{y2}}{2}}\right)+M_{ux1}-{\int }_{e_y-L+{\displaystyle \frac{c_{y2}}{2}}}^b{\int }_{-{\displaystyle \frac{a\sqrt{b^2-y^2}}{b}}}^{{\displaystyle \frac{a\sqrt{b^2-y^2}}{b}}}{p}_u\left(x, y\right)\left(y-e_y+L-{\displaystyle \frac{c_{y2}}{2}}\right)dxdy,$$

(27)

$$M_{uj}=P_{u1}\left(L+{\displaystyle \frac{c_{y2}}{2}}\right)+{\displaystyle \frac{P_{u2}{c}_{y2}}{2}}+M_{ux1}+M_{ux2}-{\int }_{e_y-L-{\displaystyle \frac{c_{y2}}{2}}}^b{\int }_{-{\displaystyle \frac{a\sqrt{b^2-y^2}}{b}}}^{{\displaystyle \frac{a\sqrt{b^2-y^2}}{b}}}{p}_u\left(x, y\right)\left(y-e_y+L+{\displaystyle \frac{c_{y2}}{2}}\right)dxdy,$$

(28)

Note: M_uh is obtained by developing the integral of Equation (26), then it is derived with respect to y_m, and then y_m is substituted into Equation (26) to determine the M_uh.

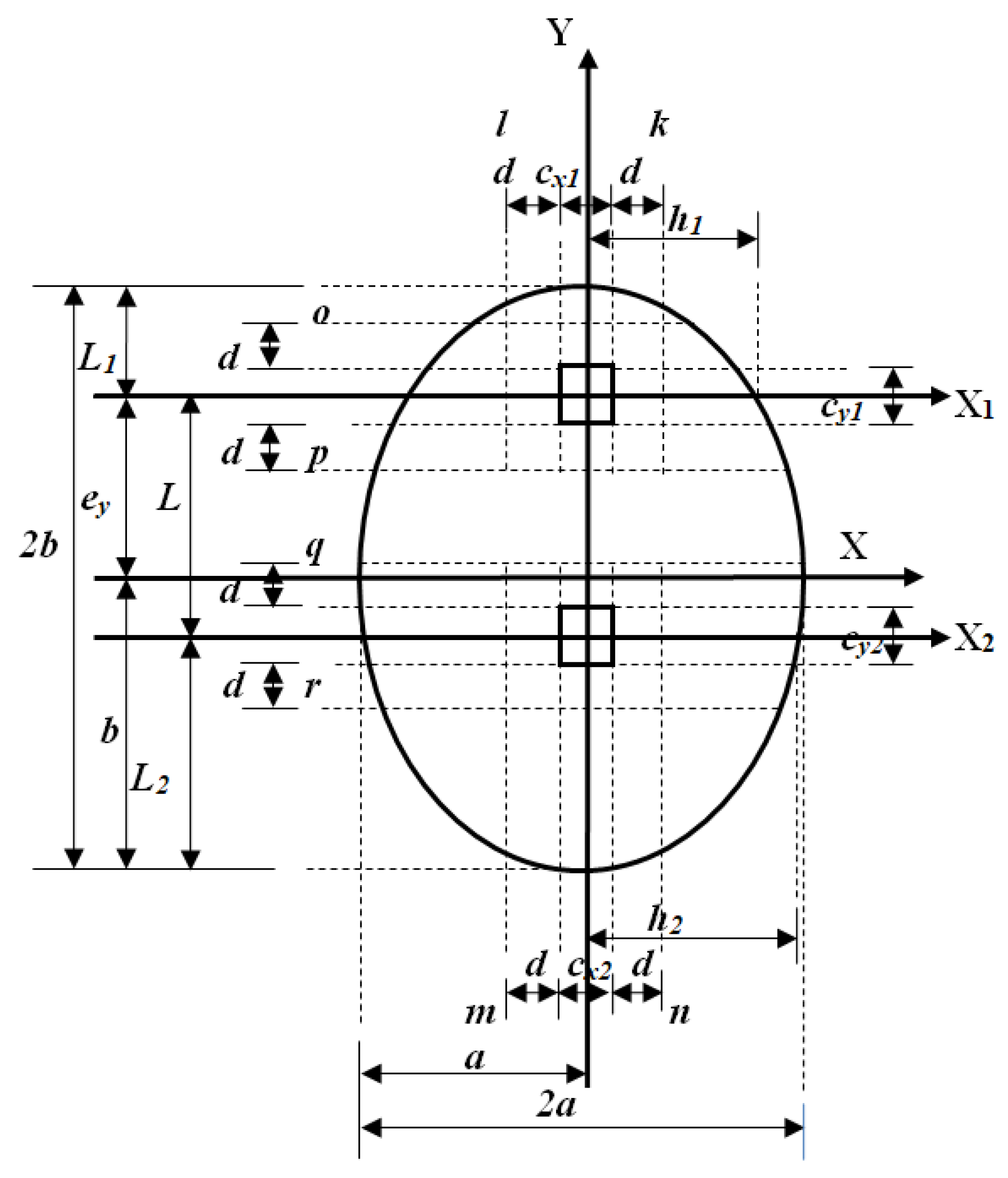
2.2.2. Unidirectional Shears

Figure 4 indicates the sections where the unidirectional shears must be considered for an ECF subjected to biaxial bending, these sections occur at a distance d from the column faces, according to ACI [45].

Factored unidirectional shears in the axes parallel to the Y axis are determined below:

$$V_{uk}=-{\int }_{{\displaystyle \frac{c_{x1}}{2}}+d}^{h_1}{\int }_{-{\displaystyle \frac{w_1}{2}}}^{{\displaystyle \frac{w_1}{2}}}{p}_{u1}\left(x_1, y_1\right)dydx,$$

(29)

$$V_{ul}=P_{u1}-{\int }_{-{\displaystyle \frac{c_{x1}}{2}}-d}^{h_1}{\int }_{-{\displaystyle \frac{w_1}{2}}}^{{\displaystyle \frac{w_1}{2}}}{p}_{u1}\left(x_1, y_1\right)dydx,$$

(30)

$$V_{um}=-{\int }_{{\displaystyle \frac{c_{x2}}{2}}+d}^{h_2}{\int }_{-{\displaystyle \frac{w_2}{2}}}^{{\displaystyle \frac{w_2}{2}}}{p}_{u2}\left(x_2, y_2\right)dydx,$$

(31)

$$V_{un}=P_{u2}-{\int }_{-{\displaystyle \frac{c_{x2}}{2}}-d}^{h_2}{\int }_{-{\displaystyle \frac{w_2}{2}}}^{{\displaystyle \frac{w_2}{2}}}{p}_{u2}\left(x_2, y_2\right)dydx.$$

(32)

Factored unidirectional shears in the axes parallel to the X axis are determined below:

$$V_{uo}=-{\int }_{e_y+{\displaystyle \frac{c_{y1}}{2}}+d}^b{\int }_{-{\displaystyle \frac{a\sqrt{b^2-y^2}}{b}}}^{{\displaystyle \frac{a\sqrt{b^2-y^2}}{b}}}{p}_u\left(x, y\right)dxdy,$$

(33)

$$V_{up}=P_{u1}-{\int }_{e_y-{\displaystyle \frac{c_{y1}}{2}}-d}^b{\int }_{-{\displaystyle \frac{a\sqrt{b^2-y^2}}{b}}}^{{\displaystyle \frac{a\sqrt{b^2-y^2}}{b}}}{p}_u\left(x, y\right)dxdy,$$

(34)

$$V_{uq}=P_{u1}-{\int }_{e_y-L+{\displaystyle \frac{c_{y2}}{2}}+d}^b{\int }_{-{\displaystyle \frac{a\sqrt{b^2-y^2}}{b}}}^{{\displaystyle \frac{a\sqrt{b^2-y^2}}{b}}}{p}_u\left(x, y\right)dxdy,$$

(35)

$$V_{ur}=P_{u1}+P_{u2}-{\int }_{e_y-L-{\displaystyle \frac{c_{y2}}{2}}-d}^b{\int }_{-{\displaystyle \frac{a\sqrt{b^2-y^2}}{b}}}^{{\displaystyle \frac{a\sqrt{b^2-y^2}}{b}}}{p}_u\left(x, y\right)dxdy.$$

(36)

Note: When column 1 is located at the end of the footing in the positive Y-axis direction, V_uo = 0. When column 2 is located at the end of the footing in the negative Y-axis direction, V_ur = 0 (because the columns are located on the property boundary).

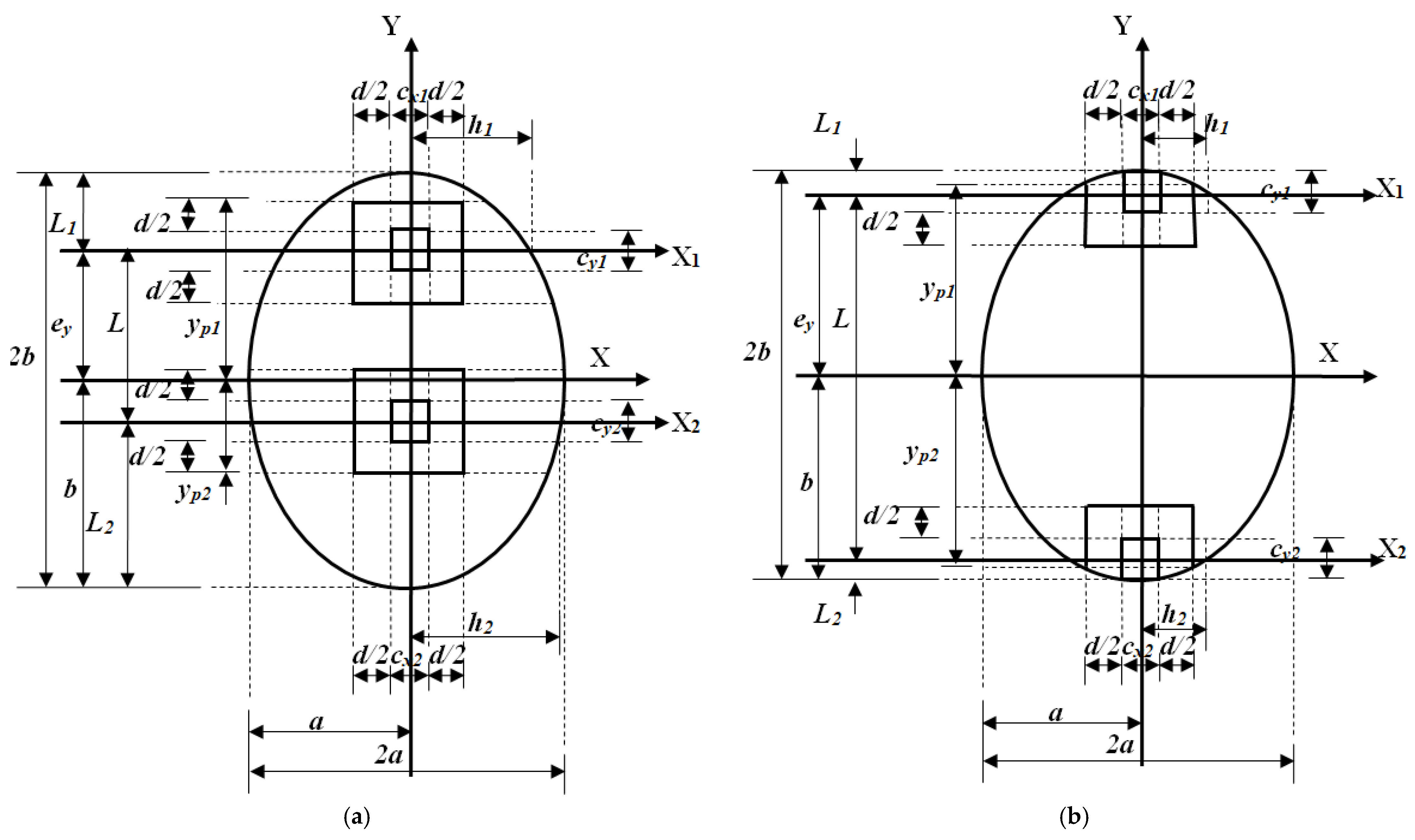
2.2.3. Punching Shears

Figure 5 indicates two cases for the sections where the punching shears must be considered for an ECF subjected to biaxial bending; these sections occur at a distance “d/2” from the column faces in both directions, according to ACI [45].

Factored punching shears at the critical sections are determined as follows:

$$V_{up1}=P_{u1}-{\int }_{e_y-{\displaystyle \frac{c_{y1}}{2}}-{\displaystyle \frac{d}{2}}}^{y_{p1}}{\int }_{-{\displaystyle \frac{c_{x1}}{2}}-{\displaystyle \frac{d}{2}}}^{{\displaystyle \frac{c_{x1}}{2}}+{\displaystyle \frac{d}{2}}}{p}_u\left(x, y\right)dxdy,$$

(37)

$$V_{up2}=P_{u2}-{\int }_{y_{p2}}^{e_y-L+{\displaystyle \frac{c_{y2}}{2}}+{\displaystyle \frac{d}{2}}}{\int }_{-{\displaystyle \frac{c_{x2}}{2}}-{\displaystyle \frac{d}{2}}}^{{\displaystyle \frac{c_{x2}}{2}}+{\displaystyle \frac{d}{2}}}{p}_u\left(x, y\right)dxdy.$$

(38)

where y_p1 = e_y + c_y1/2 + d/2 and y_p2 = e_y − L − c_y1/2 − d/2 (critical perimeter not limited), and $y_{p1}=b\sqrt{{\displaystyle \frac{4a^2-{\left(c_{x1}+d\right)}^2}{4a^2}}}$ and $y_{p2}=-b\sqrt{{\displaystyle \frac{4a^2-{\left(c_{x2}+d\right)}^2}{4a^2}}}$ (critical perimeter limited in the Y-axis direction).

2.2.4. Objective Function

The minimum total cost is determined as follows:

$$C_{min}=V_c{C}_c+{V_s\gamma }_s{C}_s.$$

(39)

The reinforcing steel in the X and Y directions is determined as follows:

$$\begin{array}{ll}{A}_{sxtB1}& =0.0018b_{1}d;A_{sxtB2}=0.0018b_{2}d;A_{sxtB3}=0.0018b_{3}d;A_{sxBp1}={\rho }_1{w}_{1}d;A_{sxBp2}\\ & ={\rho }_2{w}_{2}d;A_{sxtT}=0.0036bd;A_{syf}=2{\rho }_{yB}{b}_{xf}d;A_{syg}=2{\rho }_{yB}{b}_{xg}d;A_{syi}\\ & =2{\rho }_{yB}{b}_{xi}d;A_{syj}=2{\rho }_{yB}{b}_{xj}d;A_{sylB}\ge A_{syf},A_{syg},A_{syi},A_{syj};A_{sylT}\\ & =2{\rho }_{yT}{b}_{xh}d,\end{array}$$

(40)

where A_sxBp1 indicates the largest reinforcing steel of A_sxa and A_sxb in the X direction at the bottom of column 1; A_sxBp2 indicates the largest reinforcing steel of A_sxc and A_sxe in the X direction at the bottom of column 2; A_sylB indicates the largest reinforcing steel of A_syf, A_syg, A_syi, and A_syj at the bottom in the Y direction (negative maximum moment).

Note: In widths b₁, b₂, and b₃, no bending occurs; therefore, the steel reinforcement must be by temperature according to ACI [45] and this equation is given by

$$A_{st}=0.0018b_{w}d.$$

(41)

The widths of each section can be determined as follows:

$$\begin{gathered} b_1=L_1-{\displaystyle \frac{w_1}{2}};b_2=L-{\displaystyle \frac{w_1}{2}}-{\displaystyle \frac{w_2}{2}};b_3=L_2-{\displaystyle \frac{w_2}{2}};b_{xf}={\displaystyle \frac{2a}{b}}\sqrt{b^2-{\left(e_y+{\displaystyle \frac{c_{y1}}{2}}\right)}^2};b_{xg}={\displaystyle \frac{2a}{b}}\sqrt{b^2-{\left(e_y-{\displaystyle \frac{c_{y1}}{2}}\right)}^2};b_{xi} \\ ={\displaystyle \frac{2a}{b}}\sqrt{b^2-{\left(e_y-L+{\displaystyle \frac{c_{y2}}{2}}\right)}^2};b_{xj}={\displaystyle \frac{2a}{b}}\sqrt{b^2-{\left(e_y-L-{\displaystyle \frac{c_{y2}}{2}}\right)}^2};b_{xh}={\displaystyle \frac{2a\sqrt{b^2-{y_m}^2}}{b}}. \end{gathered}$$

(42)

The number of rods parallel to the X and Y axes can be determined as follows:

$$\begin{gathered} n_{xtB1}={\displaystyle \frac{A_{sxtB1}}{a_{st}}};n_{xtB2}={\displaystyle \frac{A_{sxtB2}}{a_{st}}};n_{xtB3}={\displaystyle \frac{A_{sxtB3}}{a_{st}}};n_{xBp1}={\displaystyle \frac{A_{sxBp1}}{a_{sp1}}};n_{xBp2}={\displaystyle \frac{A_{sxBp2}}{a_{sp2}}};n_{xtT} \\ ={\displaystyle \frac{A_{sxtT}}{a_{st}}};n_{ylB}={\displaystyle \frac{A_{sylB}}{a_{slB}}};n_{ylT}={\displaystyle \frac{A_{sylT}}{a_{slT}}}. \end{gathered}$$

(43)

The separation of the rods for each zone can be obtained as follows:

$$\begin{gathered} s_{xtB1}={\displaystyle \frac{b_1{a}_{st}}{A_{sxtB1}}};s_{xtB2}={\displaystyle \frac{b_2{a}_{st}}{A_{sxtB2}}};s_{xtB3}={\displaystyle \frac{b_3{a}_{st}}{A_{sxtB3}}};s_{xBp1}={\displaystyle \frac{w_1{a}_{sp1}}{A_{sxBp1}}};s_{xBp2}={\displaystyle \frac{w_2{a}_{sp2}}{A_{sxBp2}}};s_{xtT} \\ ={\displaystyle \frac{2b{a}_{st}}{A_{sxtT}}};s_{ylB}={\displaystyle \frac{2a{a}_{slB}}{A_{sylB}}};s_{ylT}={\displaystyle \frac{2a{a}_{slT}}{A_{sylT}}}. \end{gathered}$$

(44)

The total lengths of the rods in the X and Y directions are determined as follows:

$$L_{xBp1}=2a\sum _{i=0}^{n_{xBp1}}{\displaystyle \frac{\sqrt{b^2-{\left(b-L_1+0.5c_{y1}+0.5d-i{s}_{xBp1}\right)}^2}}{b}},$$

(45)

$$L_{xBp2}=2a\sum _{j=0}^{n_{xBp2}}{\displaystyle \frac{\sqrt{b^2-{\left(b-L-L_1+0.5c_{y2}+0.5d-j{s}_{xBp2}\right)}^2}}{b}},$$

(46)

$$L_{xtB1}=2a\sum _{h=0}^{n_{xtB1}}{\displaystyle \frac{\sqrt{b^2-{\left(h{s}_{xtB1}\right)}^2}}{b}},$$

(47)

$$L_{xtB2}=2a\sum _{m=0}^{n_{xtB2}}{\displaystyle \frac{\sqrt{b^2-{\left(b-L_1-0.5c_{y1}-0.5d-m{s}_{xtB2}\right)}^2}}{b}},$$

(48)

$$L_{xtB3}=2a\sum _{l=0}^{n_{xtB3}}{\displaystyle \frac{\sqrt{b^2-{\left(b-L_2+0.5c_{y2}+0.5d-l{s}_{xtB3}\right)}^2}}{b}},$$

(49)

$$L_{xtT}=4a\sum _{o=0}^{n_{xtT}/2}{\displaystyle \frac{\sqrt{b^2-{\left(o{s}_{xtT}\right)}^2}}{b}}-2a,$$

(50)

$$L_{ylB}=4b\sum _{r=0}^{n_{ylB}/2}{\displaystyle \frac{\sqrt{a^2-{\left(r{s}_{ylB}\right)}^2}}{a}}-2b,$$

(51)

$$L_{ylT}=4b\sum _{q=0}^{n_{ylT}/2}{\displaystyle \frac{\sqrt{a^2-{\left(q{s}_{ylT}\right)}^2}}{a}}-2b.$$

(52)

V_s is determined as follows:

$$V_s=a_{st}\left(L_{xtB1}+L_{xtB2}+L_{xtB3}+L_{xtT}\right)+a_{sp1}{L}_{xBp1}+a_{sp2}{L}_{xBp2}+a_{sylB}{L}_{ylB}+a_{sylT}{L}_{ylT}.$$

(53)

V_c is determined as follows:

$$V_c=\pi ab\left(d+r\right)-V_s.$$

(54)

Substituting Equation (54) into Equation (39) determines

$$C_{min}=\left[\pi ab\left(d+r\right)-V_s\right]C_c+V_s{\gamma }_s{C}_s.$$

(55)

Substituting α = γ_sC_s/C_c → γ_sC_s = αC_c into Equation (55) determines

$$C_{min}=\left[\pi ab\left(d+r\right)+\left(\alpha -1\right)V_s\right]C_c.$$

(56)

Now, by substituting Equation (53) and all the values of the lengths of the rods into Equation (56), the general equation for the minimum cost of ECF is determined:

$$\begin{gathered} C_{min}=\left\{\left(\alpha -1\right)\left[2a_{st}a\left(\sum _{h=0}^{n_{xtB1}}{\displaystyle \frac{\sqrt{b^2-{\left(h{s}_{xtB1}\right)}^2}}{b}}+\sum _{m=0}^{n_{xtB2}}{\displaystyle \frac{\sqrt{b^2-{\left(b-L_1-0.5c_{y1}-0.5d-m{s}_{xtB2}\right)}^2}}{b}} \\ +\sum _{l=0}^{n_{xtB3}}{\displaystyle \frac{\sqrt{b^2-{\left(b-L_2+0.5c_{y2}+0.5d-l{s}_{xtB3}\right)}^2}}{b}}+2\sum _{o=0}^{{\displaystyle \frac{n_{xtT}}{2}}}{\displaystyle \frac{\sqrt{b^2-{\left(o{s}_{xtT}\right)}^2}}{b}}-1\right)-2\left(a_{sylB}+a_{sylT}\right)b \\ +2a_{sp1}a\sum _{i=0}^{n_{xBp1}}{\displaystyle \frac{\sqrt{b^2-{\left(b-L_1+0.5c_{y1}+0.5d-i{s}_{xBp1}\right)}^2}}{b}}+4a_{sylT}b\sum _{q=0}^{{\displaystyle \frac{n_{ylT}}{2}}}{\displaystyle \frac{\sqrt{a^2-{\left(q{s}_{ylT}\right)}^2}}{a}} \\ +2a_{sp2}a\sum _{j=0}^{n_{xBp2}}{\displaystyle \frac{\sqrt{b^2-{\left(b-L-L_1+0.5c_{y2}+0.5d-j{s}_{xBp2}\right)}^2}}{b}}+4a_{sylB}b\sum _{r=0}^{{\displaystyle \frac{n_{ylB}}{2}}}{\displaystyle \frac{\sqrt{a^2-{\left(r{s}_{ylB}\right)}^2}}{a}} \\ -2a_{sylB}b\right]+\pi ab\left(d+r\right)\right\}{C}_c. \end{gathered}$$

(57)

2.2.5. Constraints

The ACI code equations are shown [45].

The moments can be expressed as follows [45]:

$$\left|M_{ua}\right|,\left|M_{ub}\right|\le {Ø}_f{f}_{y}d{A}_{sxBp1}\left(1 - {\displaystyle \frac{A_{sxBp1}{f}_y}{1.7w_{1}d{f^{\prime }}_c}}\right),$$

(58)

$$\left|M_{uc}\right|,\left|M_{ue}\right|\le {Ø}_f{f}_{y}d{A}_{sxBp2}\left(1-{\displaystyle \frac{A_{sxBp2}{f}_y}{1.7w_{2}d{f^{\prime }}_c}}\right),$$

(59)

$$\left|M_{uf}\right|\le {Ø}_f{f}_{y}d{A}_{syf}\left(1-{\displaystyle \frac{A_{syf}{f}_y}{1.7b_{xf}d{f^{\prime }}_c}}\right),$$

(60)

$$\left|M_{ug}\right|\le {Ø}_f{f}_{y}d{A}_{syg}\left(1-{\displaystyle \frac{A_{syg}{f}_y}{1.7b_{xg}d{f^{\prime }}_c}}\right),$$

(61)

$$\left|M_{uh}\right|\le {Ø}_f{f}_{y}d{A}_{syT}\left(1-{\displaystyle \frac{A_{syT}{f}_y}{1.7b_{xh}d{f^{\prime }}_c}}\right),$$

(62)

$$\left|M_{ui}\right|\le {Ø}_f{f}_{y}d{A}_{syi}\left(1-{\displaystyle \frac{A_{syi}{f}_y}{1.7b_{xi}d{f^{\prime }}_c}}\right),$$

(63)

$$\left|M_{uj}\right|\le {Ø}_f{f}_{y}d{A}_{syj}\left(1-{\displaystyle \frac{A_{syj}{f}_y}{1.7b_{xj}d{f^{\prime }}_c}}\right),$$

(64)

where Ø_f = 0.90.

The unidirectional shears can be expressed as follows [45]:

$$\left|V_{uk}\right|,\left|V_{ul}\right|\le 0.17{Ø}_v\sqrt{{f^{\prime }}_c}{w}_{1}d,$$

(65)

$$\left|V_{um}\right|,\left|V_{un}\right|\le 0.17{Ø}_v\sqrt{{f^{\prime }}_c}{w}_{1}d,$$

(66)

$$\left|V_{uo}\right|\le 0.17{Ø}_v\sqrt{{f^{\prime }}_c}{b}_{wsxo}d,$$

(67)

$$\left|V_{up}\right|\le 0.17{Ø}_v\sqrt{{f^{\prime }}_c}{b}_{wsxp}d,$$

(68)

$$\left|V_{uq}\right|\le 0.17{Ø}_v\sqrt{{f^{\prime }}_c}{b}_{wsxq}d,$$

(69)

$$\left|V_{ur}\right|\le 0.17{Ø}_v\sqrt{{f^{\prime }}_c}{b}_{wsxr}d,$$

(70)

where Ø_v = 0.85.

Note: b_wsxo, b_wsxp, b_wsxq, and b_wsxr are expressed as follows:

$$\begin{gathered} b_{wsxo}={\displaystyle \frac{2a}{b}}\sqrt{b^2-{\left(e_y+{\displaystyle \frac{c_{y1}}{2}}+d\right)}^2};b_{wsxp}={\displaystyle \frac{2a}{b}}\sqrt{b^2-{\left(e_y-{\displaystyle \frac{c_{y1}}{2}}-d\right)}^2};b_{wsxq} \\ ={\displaystyle \frac{2a}{b}}\sqrt{b^2-{\left(e_y-L+{\displaystyle \frac{c_{y2}}{2}}+d\right)}^2};b_{wsxr}={\displaystyle \frac{2a}{b}}\sqrt{b^2-{\left(e_y-L-{\displaystyle \frac{c_{y2}}{2}}-d\right)}^2}. \end{gathered}$$

(71)

The punching shears can be expressed as follows [39]:

$$\left|V_{up1}\right|,\left|V_{up2}\right|\le \left\{\begin{array}{c}0.17{Ø}_v\left(1+{\displaystyle \frac{2}{{\beta }_c}}\right)\sqrt{{f\prime }_c}{b}_{0}d\\ 0.083{Ø}_v\left({\displaystyle \frac{{\alpha }_{s}d}{b_0}}+2\right)\sqrt{{f\prime }_c}{b}_{0}d\\ 0.33{Ø}_v\sqrt{{f\prime }_c}{b}_{0}d\end{array}\right.,$$

(72)

where b₀ = 2(c_x + c_y) + 4d (critical perimeter not limited), b₀ = c_x + 2c_y + 2d (critical perimeter limited in the Y-axis direction), b₀ = 2c_x + c_y + 2d (critical perimeter limited in the X-axis direction), b₀ = c_x + c_y + d (critical perimeter limited in the X and Y axes directions); α_s = 20 for the corner column; α_s = 30 for the edge column; and α_s = 40 for the interior column [45]. For an ECF b₀ = 2(c_x + c_y) + 4d (unconstrained critical perimeter), b₀ = c_x + c_y + 2d + 2y_p − 2e_y (constrained critical perimeter in the Y-axis direction); for the other two cases, it is not possible due to space problems.

The percentages of steel can be expressed as follows [45]:

$${\rho }_1,{\rho }_2,{\rho }_{yB},{\rho }_{yT}\le 0.75\left[{\displaystyle \frac{0.85{\beta }_1{f\prime }_c}{f_y}}\left({\displaystyle \frac{600}{600+f_y}}\right)\right],$$

(73)

$${\rho }_1,{\rho }_2,{\rho }_{yB},{\rho }_{yT}\ge \left\{\begin{array}{c}{\displaystyle \frac{0.25\sqrt{{f^{\prime }}_c}}{f_y}}\\ {\displaystyle \frac{1.4}{f_y}}\end{array}\right.,$$

(74)

$$0.65\le {\beta }_1=\left(1.05-{\displaystyle \frac{{f^{\prime }}_c}{140}}\right)\le 0.85.$$

(75)

The steel area of each section is presented in Equation (40).

The number of rods in each section is shown in Equation (43).

The separation of rods in each section is presented in Equation (44).

The proposed model is presented in two stages: the first step consists of determining the minimum area, and the second consists of obtaining the minimum cost. For the minimum area, the independent or known parameters are p_aabcs, L, c_x1, c_x2, c_y1, c_y2, P₁, M_x1, M_y1, P₂, M_x2, and M_y2, and the design or unknown variables are A_min, a, b, L₁, L₂, e_y, p_max, and p_min. For the minimum cost: the independent or known parameters are a, b, P_u1, M_ux1, M_uy1, P_u2, M_ux2, M_uy2, a_st, a_slB, a_slT, a_sp1, and a_sp2, and the design or unknown variables are C_min, d, A_sxtB1, A_sxtB2, A_sxtB3, A_sxBp1, A_sxBp2, A_sxtT, A_sylB, A_sylT, ρ₁, ρ₂, ρ_yB, ρ_yT, s_xtB1, s_xtB2, s_xtB3, s_xBp1, s_xBp2, s_xtT, s_ylB, s_ylT, n_xtB1, n_xtB2, n_xtB3, n_xBp1, n_xBp2, n_xtT, n_ylB, and n_ylT.

The minimum cost procedure of an ECF is shown in the flowchart algorithm (see Figure 6).

The procedure is detailed for the design in the following steps below:

• The parameters known as L, c_x1, c_x2, c_y1, c_y2, P₁, P₂, M_x1, M_x2, M_y1, M_y2, and p_aabcs must be well defined, where p_aabcs = p_abcs − γ_cdH − γ_sd(H − t).
• Show the objective function and evaluate the constraints for minimum area.
• Use MAPLE software to determine the minimum area, assuming all variables are non-negative except M_xT, which can be negative.
• If the optimal solution is not obtained, narrow the decision variables and then determine the optimal solution again. Once the solution is reached, these variables are adjusted.
• Determine the factored moments, the factored bending shears, and the factored punching shears (the latter two are presented as a function of “d”).
• Show the objective function and evaluate the constraints for minimum cost.
• Use MAPLE software to determine the minimum cost, assuming all variables are non-negative.
• Step 4 is the same but for the minimum cost.

Using the Maple software (v.15) to determine the minimum cost of an ECF is presented in the flowchart (see Figure 7).

3. Numerical Studies

Two numerical studies are shown with different lengths: the first with free ends in the longitudinal direction and the second with ends limited in the longitudinal direction to estimate the minimum cost of ECF subjected to biaxial bending. The data provided for the two studies are c_x1 = c_y1 = c_x2 = c_y2 = 40 cm, H = 2.00 m, r = 7.5 cm, P_D1 = 1000 kN, P_L1 = 1100 kN, P_D2 = 700 kN, P_L2 = 900 kN, M_Dx1 = 70 kN-m, M_Lx1 = 80 kN-m, M_Dx2 = 100 kN-m, M_Lx2 = 150 kN-m, M_Dy1 = 200 kN-m, M_Ly1 = 300 kN-m, M_Dy2 = 90 kN-m, M_Ly2 = 110 kN-m, a_st = 2.85 cm² (Ø 3/4″), a_slB = a_slT = a_sp1 = a_sp2 = 7.92 cm² (Ø 1–1/4″), p_abcs = 260 kN/m², γ_cd = 24 kN/m³, γ_sd = 15 kN/m³, f’_c = 21 MPa, f_y = 420 MPa, and α = 90.

The proposed thickness of the footing after several iterations is 1.04 m and p_aabcs = p_abcs − γ_cdH − γ_sd(H − t) = 260 − 24(1.04) − 15(2.00 − 1.04) = 220.64 kN/m².

Now, the unfactored loads and moments acting on the soil are P₁ = 2100 kN, M_x1 = 150 kN-m, M_y1 = 500 kN-m, P₂ = 1600 kN, M_x2 = 250 kN-m, and M_y2 = 200 kN-m.

Table 1. Optimal area for elliptical combined footings with L₁ ≥ c_y1/2 and L₂ ≥ c_y2/2 (study 1).

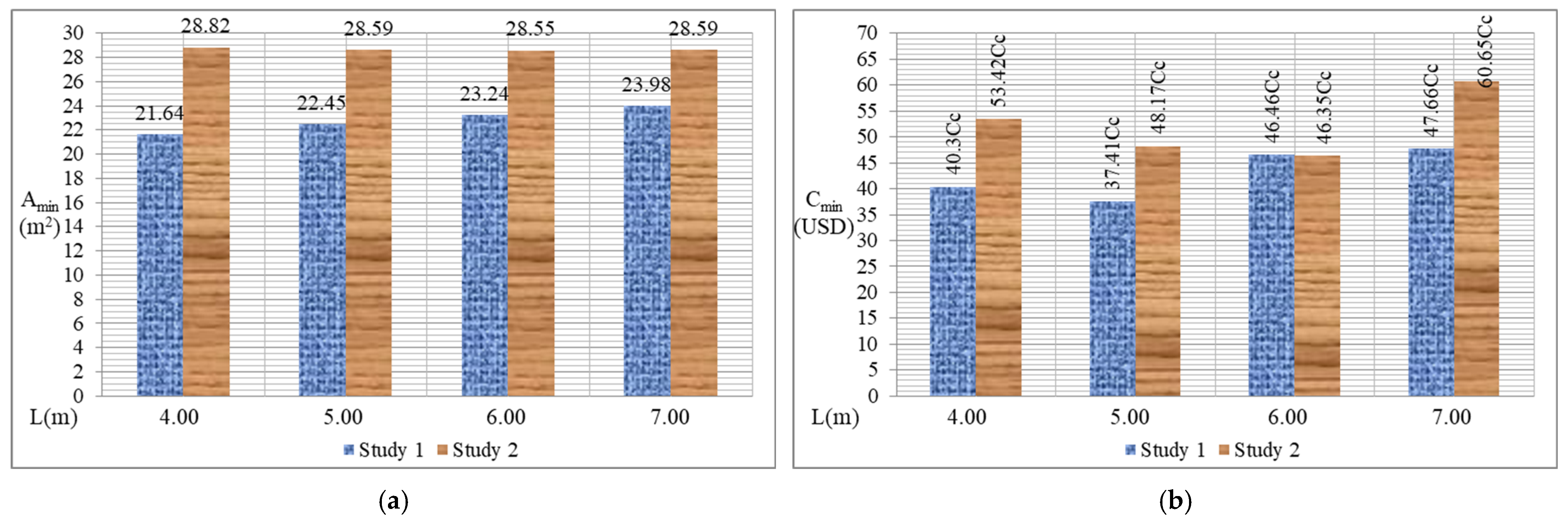
Example	a (m)	b (m)	ey (m)	L (m)	L1 (m)	L2 (m)	h1 (m)	h2 (m)	R (kN)	MxT (kN-m)	MyT (kN-m)	pmax (kN/m2)	pmin (kN/m2)	Amin (m2)
1.1	2.68	2.57	1.63	4.00	0.94	0.20	2.07	1.04	3700	47.15	700	219.33	122.66	21.64
1.2	2.29	3.12	2.08	5.00	1.04	0.20	1.71	0.81	3700	78.85	700	219.50	110.18	22.45
1.3	2.01	3.68	2.52	6.00	1.16	0.20	1.46	0.65	3700	120.15	700	219.43	99.01	23.24
1.4	1.80	4.24	2.97	7.00	1.28	0.20	1.28	0.56	3700	171.44	700	219.54	89.09	23.98

shows the minimum area with free ends in the longitudinal direction for L = 4.00, 5.00, 6.00, and 7.00 m (study 1).

Now, the factored loads and moments acting on the soil are P_u1 = 2960 kN, M_ux1 = 212 kN-m, M_uy1 = 720 kN-m, P_u2 = 2280 kN, M_ux2 = 360 kN-m, and M_uy2 = 284 kN-m.

Table 2. Optimal design for elliptical combined footings with L₁ ≥ c_y1/2 and L₂ ≥ c_y2/2 (study 1).

Example	MuxT (kN-m)	MuyT (kN-m)	Ru (kN)	AsxBp1 (cm2)	AsxBp2 (cm2)	AsxtB1 (cm2)	AsxtB2 (cm2)	AsxtT (cm2)	AsylB (cm2)	AsylT (cm2)	d (m)	ρ1	ρ2	ρyT	ρyB	Cmin (USD)
1.1	−6.80	1004	5240	61.34	41.28	4.78	39.09	70.90	173.28	219.32	0.77	0.00686	0.00688	0.00601	0.00601	40.30Cc
1.2	71.20	1004	5240	74.55	60.53	6.47	50.77	81.84	120.96	120.96	0.73	0.00906	0.01087	0.00413	0.00531	37.41Cc
1.3	96.80	1004	5240	50.51	32.84	8.19	72.68	112.62	144.74	187.38	0.85	0.00475	0.00468	0.00629	0.00629	46.46Cc
1.4	174.80	1004	5240	99.47	70.55	10.23	99.26	149.81	95.05	110.90	0.98	0.00734	0.00807	0.00362	0.00405	47.66Cc

C_min is represented as a function of C_c.

indicates the minimum cost with free ends in the longitudinal direction for L = 4.00, 5.00, 6.00, and 7.00 m (study 1).

Table 3. Optimal area for elliptical combined footings with L₁ = c_y1/2 and L₂ = c_y2/2 (study 2).

Example	a (m)	b (m)	ey (m)	L (m)	L1 (m)	L2 (m)	h1 (m)	h2 (m)	R (kN)	MxT (kN-m)	MyT (kN-m)	pmax (kN/m2)	pmin (kN/m2)	Amin (m2)
2.1	4.17	2.20	2.00	4.00	0.20	0.20	1.74	1.74	3700	1400	700	219.72	37.04	28.82
2.2	3.37	2.70	2.50	5.00	0.20	0.20	1.27	1.27	3700	1650	700	219.76	39.12	28.59
2.3	2.84	3.20	3.00	6.00	0.20	0.20	0.99	0.99	3700	1900	700	219.67	39.52	28.55
2.4	2.46	3.70	3.50	7.00	0.20	0.20	0.80	0.80	3700	2150	700	219.90	38.89	28.59

indicates the minimum area with ends limited in the longitudinal direction for L = 4.00, 5.00, 6.00, and 7.00 m (study 2).

Table 4. Optimal design for elliptical combined footings with L₁ = c_y1/2 and L₂ = c_y2/2 (study 2).

Example	MuxT (kN-m)	MuyT (kN-m)	Ru (kN)	AsxBp1 (cm2)	AsxBp2 (cm2)	AsxtB2 (cm2)	AsxtT (cm2)	AsylB (cm2)	AsylT (cm2)	d (m)	ρ1	ρ2	ρyT	ρyB	Cmin (USD)
2.1	1932	1004	5240	41.51	27.83	43.48	70.65	220.18	220.36	0.89	0.00550	0.00368	0.00359	0.00515	53.42Cc
2.2	2272	1004	5240	33.51	21.63	54.39	77.17	177.94	177.94	0.79	0.00530	0.00342	0.00408	0.00635	48.17Cc
2.3	2612	1004	5240	26.73	20.75	66.88	88.61	149.95	149.95	0.77	0.00443	0.00344	0.00424	0.00709	46.35Cc
2.4	2952	1004	5240	57.69	112.50	88.29	113.70	189.91	233.56	0.85	0.00817	0.01594	0.00692	0.01000	60.65Cc

indicates the minimum cost with ends limited in the longitudinal direction for L = 4.00, 5.00, 6.00, and 7.00 m (study 2).

A third numerical study is shown with different allowable bearing capacities of the ground and with free ends in the longitudinal direction to determine the minimum cost of an ECF subjected to biaxial bending. The data provided for this study are c_x1 = c_y1 = c_x2 = c_y2 = 40 cm, H = 2.00 m, r = 7.5 cm, P_D1 = 700 kN, P_L1 = 500 kN, P_D2 = 400 kN, P_L2 = 300 kN, M_Dx1 = 600 kN-m, M_Lx1 = 400 kN-m, M_Dx2 = 300 kN-m, M_Lx2 = 200 kN-m, M_Dy1 = 300 kN-m, M_Ly1 = 200 kN-m, M_Dy2 = 150 kN-m, M_Ly2 = 100 kN-m, a_st = 2.85 cm² (Ø 3/4″), a_slB = a_slT = a_sp1 = a_sp2 = 7.92 cm² (Ø 1–1/4″), L = 5.00 m, γ_cd = 24 kN/m³, γ_sd = 13 kN/m³, f’_c = 21 MPa, f_y = 420 MPa, and α = 90.

Now, the unfactored loads and moments acting on the soil are P₁ = 1200 kN, M_x1 = 1000 kN-m, M_y1 = 500 kN-m, P₂ = 700 kN, M_x2 = 500 kN-m, and M_y2 = 250 kN-m.

Table 5. Optimal area for elliptical combined footings with L₁ ≥ c_y1/2 and L₂ ≥ c_y2/2 (study 3).

Example	paabcs (kN/m2)	a (m)	b (m)	ey (m)	L1 (m)	L2 (m)	h1 (m)	h2 (m)	R (kN)	MxT (kN-m)	MyT (kN-m)	pmax (kN/m2)	pmin (kN/m2)	Amin (m2)
3.1	120.25	2.18	4.02	1.18	2.84	0.20	2.08	0.70	1900	243.28	750	119.76	18.26	27.53
3.2	170.25	1.74	3.95	1.25	2.71	0.20	1.65	0.55	1900	369.64	750	169.71	6.28	21.59
3.3	220.25	1.63	3.93	1.27	2.65	0.20	1.54	0.51	1900	419.19	750	188.29	0.53	20.12
3.4	270.25	1.63	3.93	1.27	2.65	0.20	1.54	0.51	1900	419.19	750	188.29	0.53	20.12

shows the minimum area for different allowable bearing capacities of the ground, p_abcs = 160, 210, 260, and 310 kN/m² (study 3).

The proposed thickness of the footing after several iterations is 1.25 m, and p_aabcs for each example is obtained as follows: p_aabcs = p_abcs − γ_cdH − γ_sd(H − t).

Now, the factored loads and moments acting on the soil are P_u1 = 1640 kN, M_ux1 = 1360 kN-m, M_uy1 = 680 kN-m, P_u2 = 960 kN, M_ux2 = 680 kN-m, and M_uy2 = 340 kN-m.

Table 6. Optimal design for elliptical combined footings with L₁ ≥ c_y1/2 and L₂ ≥ c_y2/2 (study 3).

Example	MuxT (kN-m)	MuyT (kN-m)	Ru (kN)	AsxBp1 (cm2)	AsxBp2 (cm2)	AsxtB1 (cm2)	AsxtB2 (cm2)	AsxtT (cm2)	AsylB (cm2)	AsylT (cm2)	d (m)	ρ1	ρ2	ρyT	ρyB	Cmin (USD)
3.1	308.00	1020	2600	117.81	71.50	43.78	73.01	172.11	257.78	265.68	1.19	0.00623	0.00604	0.00529	0.00529	79.50Cc
3.2	490.00	1020	2600	65.47	41.00	37.51	67.09	149.28	133.19	138.35	1.05	0.00430	0.00422	0.00392	0.00392	45.60Cc
3.3	542.00	1020	2600	48.35	31.04	35.22	65.02	142.15	102.81	107.05	1.01	0.00343	0.00342	0.00338	0.00338	41.23Cc
3.4	542.00	1020	2600	48.35	31.04	35.22	65.02	142.15	102.81	107.05	1.01	0.00343	0.00342	0.00338	0.00338	41.23Cc

indicates the minimum cost for different allowable bearing capacities of the ground p_abcs = 160, 210, 260, and 310 kN/m² (study 3).

4. Results

The new development can be verified by the equilibrium and continuity as follows.

For moments

• If the integral of Equation (20) is developed with limits from “h₁” to “h₁”, the moment at the free end at “h₁” gives M_ua = 0.
• If the integral of Equation (20) is developed with limits from “−h₁” to “h₁”, the moment at the free end at “−h₁” gives M_ua = − M_uy1 − P_u1h₁. This moment is equal to the moment acting on the footing but of opposite signs.
• If the integral of Equation (20) is developed with limits from “0” to “h₁”, the moment at “0” gives M_ua = − M_uy1/2 − P_u1h₁/4; now, if the integral of Equation (21) is developed with limits from “−h₁” to “0”, the moment at “0” gives M_ub = M_uy1/2 + P_u1h₁/4. Therefore, M_ua and M_ub are the same, but in the opposite signs. In this way, continuity is verified.
• If the integral of Equation (22) is developed with limits from “h₂” to “h₂”, the moment at the free end at “h₂” gives M_uc = 0.
• If the integral of Equation (22) is developed with limits from “−h₂” to “h₂”, the moment at the free end at “−h₂” gives M_uc = −M_uy2 − P_u2h₂. This moment is equal to the moment acting on the footing but of opposite signs.
• If the integral of Equation (22) is developed with limits from “0” to “h₂”, the moment at “0” gives M_uc = −M_uy2/2 − P_u2h₂/4; now, if the integral of Equation (23) is developed with limits from “−h₂” to “0”, the moment at “0” gives M_ue = M_uy2/2 + P_u2h₂/4. Therefore, M_uc and M_ue are the same but in the opposite signs. In this way, continuity is verified.
• If the integral of Equation (24) is developed with limits from “b” to “b”, the moment at the free end at “b” gives M_uf = 0.
• If the integral of Equation (24) is developed with limits from “b − L₁” to “b”, the moment at “b − L₁”gives M_uf; now, if the integral of Equation (25) is developed with limits from “b − L₁” to “b”, the moment at “b − L₁”gives M_ug, and if M_uf = M_ug is performed, the following is given: M_ux1.
• If the integral of Equation (27) is developed with limits from “b − L₁ − L” to “b”, the moment at “b − L₁ − L” gives M_ui; now, if the integral of Equation (28) is developed with limits from “b − L₁ − L” to “b”, the moment at “b − L₁ − L” gives M_uj, and if M_ui = M_uj is performed, the following is given: M_ux2.
• If the integral of Equation (28) is developed with limits from “−b” to “b”, the moment at the free end at “−b” gives M_uj = 0.

For unidirectional shears

• If the integral of Equation (29) is developed with limits from “h₁” to “h₁”, the unidirectional shear at the free end at “h₁” gives V_uk = 0.
• If the integral of Equation (29) is developed with limits from “−h₁” to “h₁”, the unidirectional shear at the free end at “−h₁” gives V_uk = − P_u1. This unidirectional shear is equal to the unidirectional shear acting on the footing but of opposite signs.
• If the integral of Equation (29) is developed with limits from “0” to “h₁”, the unidirectional shear at “0” gives V_uk = −3M_uy1/4h₁ − P_u1/2; now, if the integral of Equation (30) is developed with limits from “−h₁” to “0”, the unidirectional shear at “0” gives V_ul = 3M_uy1/4h₁ + P_u1/2. Therefore, V_uk and V_ul are the same but in the opposite signs. In this way, continuity is verified.
• If the integral of Equation (31) is developed with limits from “h₂” to “h₂”, the unidirectional shear at the free end at “h₂” gives V_um = 0.
• If the integral of Equation (31) is developed with limits from “−h₂” to “h₂”, the unidirectional shear at the free end at “−h₂” gives V_um = −P_u2. This unidirectional shear is equal to the unidirectional shear acting on the footing but of opposite signs.
• If the integral of Equation (31) is developed with limits from “0” to “h₂”, the unidirectional shear at “0” gives V_um = −3M_uy2/4h₂ − P_u2/2; now, if the integral of Equation (32) is developed with limits from “−h₂” to “0”, the unidirectional shear at “0” gives V_un = 3M_uy2/4h₂ + P_u2/2. Therefore, V_um and V_un are the same but in the opposite signs. In this way continuity is verified.
• If the integral of Equation (33) is developed with limits from “b” to “b”, the unidirectional shear at the free end at “b” gives V_uo = 0.
• If the integral of Equation (33) is developed with limits from “b − L₁” to “b”, the unidirectional shear at “b − L₁” gives V_uo; now, if the integral of Equation (34) is developed with limits from “b − L₁” to “b”, the unidirectional shear at “b − L₁”gives V_up, and if V_uo = V_up is performed, the following is given: P_u1.
• If the integral of Equation (35) is developed with limits from “b − L₁ − L” to “b”, the unidirectional shear at “b − L₁ − L” gives V_uq, now, if the integral of Equation (36) is developed with limits from “b − L₁ − L” to “b”, the unidirectional shear at “b − L₁ − L” gives V_ur, and if V_uq = V_ur is performed, the following is given: P_u2.
• If the integral of Equation (36) is developed with limits from “−b” to “b”, the unidirectional shear at the free end at “−b” gives V_ur = 0.

Table 1 shows the results for the optimal area with the free ends (L₁ ≥ c_y1/2 and L₂ ≥ c_y2/2) of study 1: As L increases, a, h₁, h₂, and p_min decrease; A_min, b, e_y, L₁, and M_xT increase; and L₂, R, and M_yT remain constant.

Table 2 presents the results for the optimal cost with the free ends (L₁ ≥ c_y1/2 and L₂ ≥ c_y2/2) of study 1: As L increases, A_sxtB1, A_sxtB2, A_sxtT, and M_uxT increase; A_sxBp1, A_sxBp2, ρ₁, and ρ₂ increase up to L = 5.00 m, then decrease to L = 6.00 m, and then increase; A_sylB, A_sylT, ρ_yB, and ρ_yT decrease to L = 5.00 m, then increase up to L = 6.00 m, and then decrease; C_min and d decrease to L = 5.00 m and then increase; and R_u and M_uyT remain constant. The d is governed by unidirectional shears: The unidirectional critical shear appears in section “k” for L = 4.00 m, and the unidirectional critical shear appears in section “p” for L = 500, 6.00, and 7.00 m. This is because in section “k” the value of h₁ tends to decrease, and then section “p” becomes critical.

Table 3 shows the results for the optimal area with ends limited in the longitudinal direction (L₁ = c_y1/2 and L₂ = c_y2/2) of study 2: As L increases, a, h₁, and h₂ decrease; b, e_y, and M_xT increase; p_min increases up to L = 6.00 m and then decreases; L₁, L₂, R, and M_yT remain constant; and A_min decreases to L = 6.00 m and then increases.

Table 4 presents the results for the optimal cost with ends limited in the longitudinal direction (L₁ = c_y1/2 and L₂ = c_y2/2) of study 2: As L increases, A_sxtB2, A_sxtT, ρ_yB, ρ_yT, and M_uxT increase; A_sxBp1, A_sxBp2, ρ₁, and ρ₂ decrease to L = 6.00 m and then increase; C_min, A_sylB, A_sylT, and d decrease up to L = 6.00 m and then increase; and R_u and M_uyT remain constant. The d is governed by unidirectional shears: The unidirectional critical shear appears in section “k” for L = 4.00 and 5.00 m, and the unidirectional critical shear appears in section “p” for L = 6.00 and 7.00 m. This is because in section “k” the value of h₁ tends to decrease, and then section “p” becomes critical.

Figure 8 shows the two studies for the elliptical combined footings varying the lengths between the columns, for which L = 4, 5, 6, and 7 m.

Figure 8a shows the optimal or minimum area for two studies: Study 1 (L₁ ≥ c_y1/2 and L₂ ≥ c_y2/2) shows that increasing the length of the column spacing results in a larger area, and study 2 (L₁ = c_y1/2 and L₂ = c_y2/2) shows a decrease to L = 6.00 m, and then it increases.

Figure 8b shows the optimal or minimum cost for two studies: Study 1 (L₁ ≥ c_y1/2 and L₂ ≥ c_y2/2) shows a decrease to L = 5.00 m, and then it increases, and study 2 (L₁ = c_y1/2 and L₂ = c_y2/2) shows a decrease to L = 6.00 m, and then it increases.

Table 5 shows the results for the optimal area for different allowable bearing capacities of the ground and with the free ends (L₁ ≥ c_y1/2 and L₂ ≥ c_y2/2) of study 3: As p_aabcs increases, a, b, L₁, h₁, and h₂ decrease; e_y and M_xT increase; p_min decreases; L₂, R, and M_yT remain constant; and A_min decreases. Examples 3.3 and 3.4 are the same because they are governed by p_min, which is zero.

Table 6 presents the results for the optimal cost for different allowable bearing capacities of the ground and with the free ends (L₁ ≥ c_y1/2 and L₂ ≥ c_y2/2) of study 3: As p_aabcs increases, M_uxT increases; C_min, A_sxBp1, A_sxBp2, A_sxtB2, A_sxtT, A_sylB, A_sylT, ρ₁, ρ₂, ρ_yB, ρ_yT, and d decrease; and R_u and M_uyT remain constant. Examples 3.3 and 3.4 are the same because they are governed by p_min, which is zero.

Figure 9 shows the third study for the elliptical combined footings with L = 5 m and free ends and different allowable ground bearing capacities p_aabcs for p_aabcs = 120.25, 170.25, 220.75, and 270.25 kN/m².

Figure 9a shows the optimal or minimum area for third study (L₁ ≥ c_y1/2 and L₂ ≥ c_y2/2), which shows a decrease to p_aabcs 220.75 kN/m², and then it remains constant.

Figure 9b shows the optimal or minimum cost for the third study; this study shows the same behavior as the optimal area.

A sensitivity analysis is presented for study 1 of example 1.1 for parameter “a” to show the validity of this model.

Table 7. Optimal area for study 1 of example 1.1.

Example	a (m)	b (m)	ey (m)	L (m)	L1 (m)	L2 (m)	h1 (m)	h2 (m)	R (kN)	MxT (kN-m)	MyT (kN-m)	pmax (kN/m2)	pmin (kN/m2)	Amin (m2)
1.1	2.00	3.70	1.62	4.00	2.08	1.32	1.80	1.53	3700	0.98	700	219.40	98.93	23.25
	2.20	3.28	1.62	4.00	1.66	0.90	1.91	1.51	3700	0.99	700	219.36	107.07	22.67
	2.40	2.94	1.62	4.00	1.32	0.56	2.00	1.41	3700	0.99	700	219.54	114.28	22.17
	2.60	2.66	1.62	4.00	1.04	0.28	2.06	1.16	3700	0.99	700	219.86	120.73	21.73
	2.68	2.57	1.63	4.00	0.94	0.20	2.07	1.04	3700	47.15	700	219.33	122.66	21.64
	2.80	2.50	1.70	4.00	0.80	0.20	2.05	1.10	3700	290.00	700	218.38	118.12	21.99
	3.00	2.43	1.77	4.00	0.66	0.20	2.06	1.19	3700	549.00	700	218.28	104.83	22.90
	3.20	2.38	1.82	4.00	0.56	0.20	2.06	1.28	3700	734.00	700	217.85	91.43	23.93
	3.40	2.34	1.86	4.00	0.48	0.20	2.06	1.38	3700	882.00	700	216.77	79.30	24.99

shows the optimal area and

Table 8. Optimal cost design for study 1 of example 1.1.

Example	MuxT (kN-m)	MuyT (kN-m)	Ru (kN)	AsxBp1 (cm2)	AsxBp2 (cm2)	AsxtB1 (cm2)	AsxtB2 (cm2)	AsxtB3 (cm2)	AsxtT (cm2)	AsylB (cm2)	AsylT (cm2)	d (m)	ρ1	ρ2	ρyT	ρyB	Cmin (USD)
1.1	−59.20	1004	5240	70.27	70.27	22.94	43.62	10.68	119.41	207.79	225.48	0.90	0.00605	0.00605	0.00666	0.00666	55.30Cc
	−59.20	1004	5240	86.67	72.69	16.53	44.30	3.98	108.32	226.91	234.58	0.92	0.00717	0.00602	0.00676	0.00676	54.42Cc
	−59.20	1004	5240	83.69	71.27	10.98	44.84	0	98.92	209.63	244.06	0.93	0.00671	0.00571	0.00595	0.00595	51.51Cc
	−59.20	1004	5240	45.81	44.80	6.25	45.12	0	90.37	137.28	146.50	0.94	0.00361	0.00333	0.00333	0.00384	41.31Cc
	−6.80	1004	5240	61.34	41.28	4.78	39.09	0	70.90	173.28	219.32	0.77	0.00686	0.00688	0.00601	0.00601	40.30Cc
	360.00	1004	5240	73.29	46.02	2.15	45.23	0	85.26	170.31	230.55	0.95	0.00574	0.00556	0.00494	0.00494	46.14Cc
	726.80	1004	5240	64.51	40.58	0	51.95	0	105.44	158.40	212.12	1.21	0.00333	0.00336	0.00337	0.00374	53.95Cc
	988.80	1004	5240	170.72	131.56	0	46.21	0	83.94	291.50	475.23	0.98	0.01263	0.01509	0.00880	0.00879	70.68Cc
	1198.40	1004	5240	170.63	131.56	0	46.21	0	82.54	277.89	501.04	0.98	0.01262	0.01509	0.00880	0.00879	73.00Cc

shows the optimal cost design for an elliptical combined footing for different values of a = 2.00, 2.20, 2.40, 2.60, 2.68, 2.80, 3.00, 3.20, and 3.40 m and with free ends (L₁ ≥ c_y1/2 and L₂ ≥ c_y2/2) (study 1 of example 1.1).

Table 7 shows the results for the optimal area with the free ends (L₁ ≥ c_y1/2 and L₂ ≥ c_y2/2) of study 1 of example 1.1: As “a” increases, b and L₁ decrease; L₂ decreases to a = 2.60 and then remains constant; e_y remains constant until a = 2.60 and then increases; h₁ increases up to a = 2.68 and then more or less remains constant; h₂ decreases to a = 2.68 and then increases; M_xT tends to be constant with a value very close to 1 until a = 2.60 and then increases; and A_min decreases to a = 2.68 and then increases. Therefore, the optimal or minimum area is verified for a = 2.68 m of A_min = 21.64 m², as shown in Table 1.

Table 8 shows the results for the optimal cost design with the free ends (L₁ ≥ c_y1/2 and L₂ ≥ c_y2/2) of study 1 of example 1.1: As “a” increases, d increases up to a = 2.60, then decreases to a = 2.68, then increases up to a = 3.00, and then remains constant; M_uxT tends to be constant with a value of −59.20 until a = 2.60, and then it increases; and C_min decreases to a = 2.68 and then increases. Therefore, the optimal or minimum cost design is verified for a = 2.68 m of C_min = 40.30C_c, as shown in Table 2.

Also, two comparisons are made to demonstrate the superiority of the proposed model for ECF (elliptical combined footings) over other authors for RCF (rectangular combined footings).

The first comparison is the model developed by Luévanos-Rojas [41] for an RCF versus the model proposed for an ECF; both are limited in the longitudinal direction (Y direction). The data provided for the two examples are c_x1 = c_y1 = c_x2 = c_y2 = 40 cm, H = 2.00 m, r = 8 cm, L = 5.60 m, P_D1 = 600 kN, P_L1 = 400 kN, P_D2 = 500 kN, P_L2 = 300 kN, M_Dx1 = 140 kN-m, M_Lx1 = 100 kN-m, M_Dx2 = 120 kN-m, M_Lx2 = 100 kN-m, M_Dy1 = 120 kN-m, M_Ly1 = 80 kN-m, M_Dy2 = 110 kN-m, M_Ly2 = 90 kN-m, a_st = 2.85 cm² (Ø 3/4″), a_slB = a_slT = a_sp1 = a_sp2 = 7.92 cm² (Ø 1–1/4″), p_abcs = 220 kN/m², γ_cd = 24 kN/m³, γ_sd = 15 kN/m³, f’_c = 21 MPa, f_y = 420 MPa, and α = 90.

The proposed thickness of the ECF after several iterations is 0.62 m and p_aabcs = 184.42 kN/m².

The unfactored loads and moments acting on the soil are P₁ = 1000 kN, M_x1 = 240 kN-m, M_y1 = 200 kN-m, P₂ = 800 kN, M_x2 = 220 kN-m, and M_y2 = 200 kN-m.

Now, the factored loads and moments acting on the soil are P_u1 = 1360 kN, M_ux1 = 328 kN-m, M_uy1 = 272 kN-m, P_u2 = 1080 kN, M_ux2 = 304 kN-m, and M_uy2 = 276 kN-m.

Table 9. Optimal design for an ECF using the proposed model and for an RCF using the model developed by Luévanos-Rojas [41].

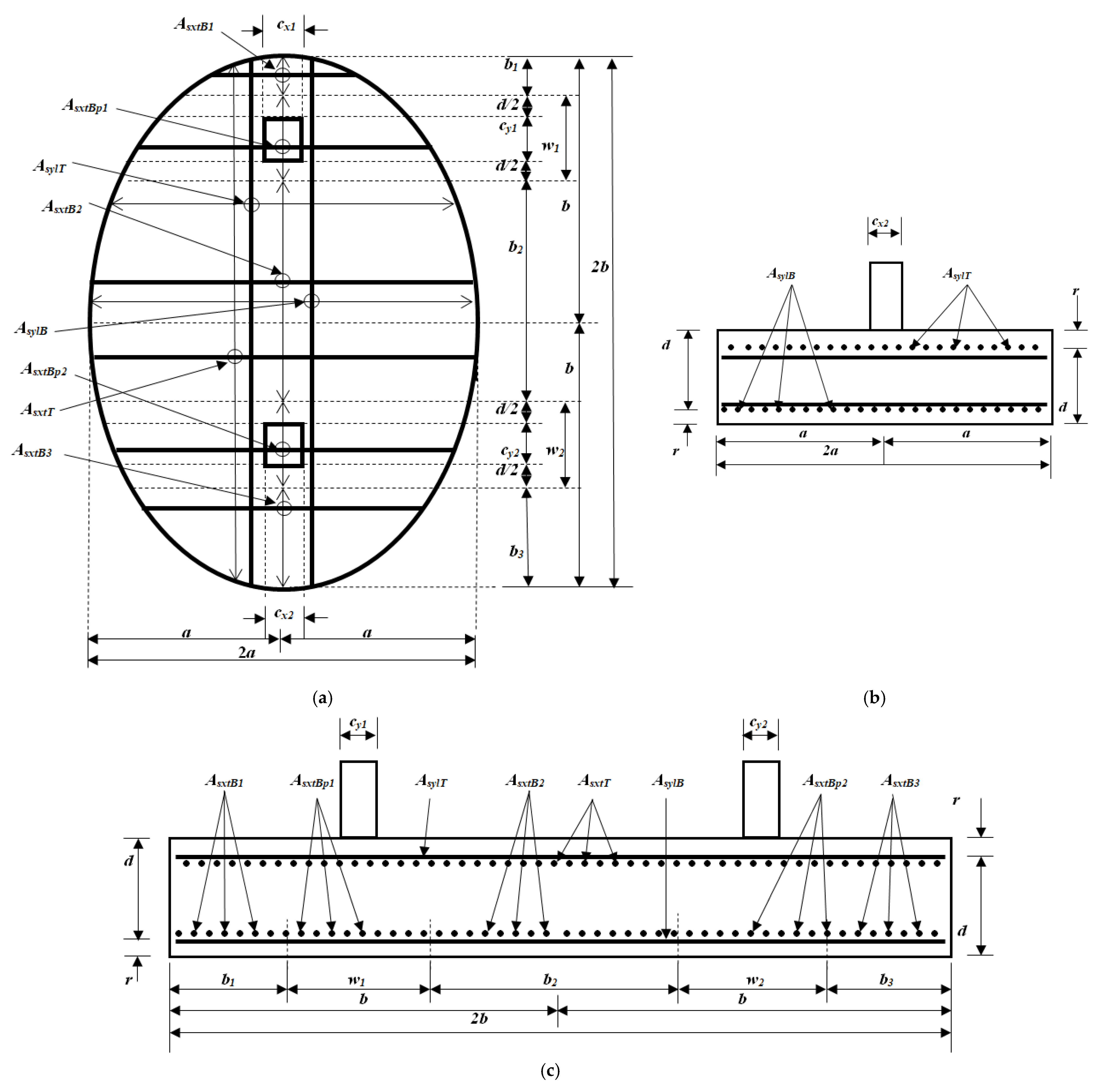
Footing	a (m)	b (m)	d (m)	L (m)	L1 (m)	L2 (m)	AsxBp1 (cm2)	AsxBp2 (cm2)	AsxtB2 (cm2)	AsxtT (cm2)	AsylB (cm2)	AsylT (cm2)	ρp1	ρp2	ρyB	ρyT	Amin (m2)	Cmin (USD)
ECF	1.95	3.00	0.53	5.60	0.20	0.20	27.73	27.73	44.58	57.29	102.96	102.96	0.00786	0.00786	0.00998	0.00604	18.38	24.45Cc
RCF	6.00	3.30	0.77	5.60	0.20	0.20	22.80	22.80	68.41	94.06	86.19	86.19	0.00333	0.00333	0.00333	0.00333	19.80	32.15Cc

Where a describes the side of the base in the Y direction for RCF, b indicates the side of the base in the X direction for RCF, a describes the X semi-axis of the base for ECF, and b indicates the Y semi-axis of the base for ECF.

presents the minimum cost with ends limited in the longitudinal direction of the model developed by Luévanos-Rojas (2016) [41] for RCF and the new model for ECF.

The second comparison is the model developed by Velázquez-Santillán et al. [42] for an RCF versus the model proposed for an ECF, both with free ends in the longitudinal direction (Y direction). The data provided for the two examples are c_x1 = c_y1 = c_x2 = c_y2 = 40 cm, H = 1.50 m, r = 8 cm, L = 6.00 m, P_D1 = 700 kN, P_L1 = 500 kN, P_D2 = 1400 kN, P_L2 = 1000 kN, M_Dx1 = 140 kN-m, M_Lx1 = 100 kN-m, M_Dx2 = 280 kN-m, M_Lx2 = 200 kN-m, M_Dy1 = 120 kN-m, M_Ly1 = 80 kN-m, M_Dy2 = 240 kN-m, M_Ly2 = 160 kN-m, a_st = 2.85 cm² (Ø 3/4″), a_slB = a_slT = a_sp1 = a_sp2 = 7.92 cm² (Ø 1–1/4″), p_abcs = 220 kN/m², γ_cd = 24 kN/m³, γ_sd = 15 kN/m³, f’_c = 21 MPa, f_y = 420 MPa, and α = 90.

The proposed thickness of the ECF after several iterations is 0.80 m and p_aabcs = 190.30 kN/m².

The unfactored loads and moments acting on the soil are P₁ = 1200 kN, M_x1 = 240 kN-m, M_y1 = 200 kN-m, P₂ = 2400 kN, M_x2 = 480 kN-m, and M_y2 = 400 kN-m.

Now, the factored loads and moments acting on the soil are P_u1 = 1640 kN, M_ux1 = 328 kN-m, M_uy1 = 272 kN-m, P_u2 = 3280 kN, M_ux2 = 656 kN-m, and M_uy2 = 544 kN-m.

Table 10. Optimal design for an ECF using the proposed model and for an RCF using the model developed by Velázquez-Santillán et al. [42].

Footing	a (m)	b (m)	d (m)	L (m)	L1 (m)	L2 (m)	AsxBp1 (cm2)	AsxBp2 (cm2)	AsxtB2 (cm2)	AsxtB3 (cm2)	AsxtT (cm2)	AsylB (cm2)	AsylT (cm2)	ρp1	ρp2	ρyB	ρyT	Amin (m2)	Cmin (USD)
ECF	2.01	4.00	0.71	6.00	0.20	1.80	18.10	58.03	63.01	16.02	103.22	83.10	98.75	0.00333	0.00725	0.00333	0.00409	25.26	37.97Cc
RCF	9.11	2.82	0.80	6.00	0.20	2.91	21.14	31.68	68.76	33.09	130.33	74.84	74.84	0.00333	0.00333	0.00333	0.00333	25.69	41.79Cc

Where a describes the side of the base in the Y direction for RCF, b indicates the side of the base in the X direction for RCF, a describes the X semi-axis of the base for ECF, and b indicates the Y semi-axis of the base for ECF.

shows the minimum cost with free ends in the longitudinal direction of the model developed by Velázquez-Santillán et al. (2018) [42] for RCF and the new model for ECF.

Table 9 presents the comparison of the minimum area and the minimum cost with ends limited in the longitudinal direction of the model developed by Luévanos-Rojas (2016) [41] for RCF and the new model for ECF:

• The minimum area “A_min” is smaller for ECF compared to RCF, presenting a savings of 7.17% using the ECF.
• The minimum cost “C_min” is lower for ECF compared to RCF, showing a savings of 23.95% using the ECF.
• The ECF and RCF are governed by unidirectional shears: For the unidirectional critical shear for RCF, it appears in section “k”, and for ECF, it appears in section “p”. This is because in section “k” for ECF h₁ = 0.70 m, the critical section must appear at a distance “d” from the face of the column, and this distance is outside the footing. For this reason, “d” is smaller for ECF, and therefore, ECF is more economical than RCF.

Table 10 presents the comparison of the minimum area and the minimum cost with free ends in the longitudinal direction of the model developed by Velázquez-Santillán et al. (2018) [42] for RCF and the new model for ECF:

• The minimum area “A_min” is smaller for ECF compared to RCF, presenting a savings of 1.67% using the ECF.
• The minimum cost “C_min” is lower for ECF compared to RCF, showing a savings of 9.14% using the ECF.
• ECF and RCF are governed by unidirectional shears: For the unidirectional critical shear for RCF, it appears in section “k”, and for ECF, it appears in section “p”. This is because in section “k” for ECF h₁ = 0.63 m, the critical section must appear at a distance “d” from the face of the column, and this distance is outside the footing. For this reason, “d” is smaller for ECF, and therefore, ECF is more economical than RCF.

Figure 10 indicates, in detail, the assembly of the steel reinforcement of an ECF. Figure 10a represents the plan view. Figure 10b indicates the elevation view of the cross section. Figure 10c represents the elevation view of the longitudinal section.

5. Conclusions

This research presents a mathematical model to determine the minimum cost of design of an ECF under biaxial bending in the two columns, assuming that the base is rigid and rests on elastic soils, and the soil pressure acts linearly (innovative contribution in terms of its form). This model can be used for an ECF with free ends in the Y direction and ends limited in the Y direction.

The proposed model for ECF is developed in two steps: first, determining the minimum area and second, obtaining the minimum cost. For the minimum area, the known values (independent parameters) are p_aabcs, L, c_x1, c_x2, c_y1, c_y2, P₁, M_x1, M_y1, P₂, M_x2, and M_y2, and the unknown values (design variables) are A_min, a, b, L₁, L₂, e_y, p_max, and p_min. For the minimum cost, the known values (independent parameters) are a, b, P_u1, M_ux1, M_uy1, P_u2, M_ux2, M_uy2, a_st, a_slB, a_slT, a_sp1, and a_sp2, and the unknown values (design variables) are C_min, d, A_sxtB1, A_sxtB2, A_sxtB3, A_sxBp1, A_sxBp2, A_sxtT, A_sylB, A_sylT, ρ₁, ρ₂, ρ_yB, ρ_yT, s_xtB1, s_xtB2, s_xtB3, s_xBp1, s_xBp2, s_xtT, s_ylB, s_ylT, n_xtB1, n_xtB2, n_xtB3, n_xBp1, n_xBp2, n_xtT, n_ylB, and n_ylT.

The main conclusions are shown below:

(1)

There are no similar contributions on the subject of this article, as it is an innovative contribution in terms of its form.

(2)

The moments and unidirectional shears are verified by continuity and equilibrium (see results section).

(3)

This model for an ECF can be used for other construction codes since the moments, unidirectional shears, and punching shears acting on the foundation do not vary; the values that vary are the resistant effects.

(4)

When the spacing “L” between columns increases with free ends in the Y direction for these examples, the minimum area “A_min” increases (see Table 1).

(5)

When the spacing “L” between columns increases with free ends in the Y direction for these examples, the minimum cost “C_min” tends to decrease to L = 5.00 m and then increases (see Table 2).

(6)

When the spacing “L” between columns increases with ends limited in the Y direction for these examples, the minimum area “A_min” tends to decrease to L = 6.00 m and then increases (see Table 3).

(7)

When the spacing “L” between columns increases with ends limited in the Y direction for these examples, the minimum cost “C_min” tends to decrease to L = 6.00 m and then increases (see Table 4).

(8)

When the allowable bearing capacity of the ground “p_abcs” increases with free ends in the Y direction for these examples, the minimum area “A_min” decreases (see Table 5).

(9)

When the allowable bearing capacity of the ground “p_abcs” increases with free ends in the Y direction for these examples, the minimum cost “C_min” decreases (see Table 6).

(10)

ECFs are cheaper than RCFs in the minimum area, with a savings of 7.17% with limited ends and a savings of 1.67% with free ends, and the minimum cost, with a savings of 23.95% with limited ends and a savings of 9.14% with free ends (see Table 9 and Table 10).

One of the limitations of this type of footing is that it cannot be used on property or edge boundaries in the X direction.

Suggestions for future studies are a model for the minimum area and minimum cost of an ECF, assuming that the surface in contact with the ground operates partially under compression.