Research on the Mechanical Properties of Mechanically Connected Splices of Prestressing Screw Bars Under Monotonic and Cyclic Loads
Abstract
1. Introduction
2. Three-Dimensional Refined Numerical Modeling
2.1. Splices’ Geometric Parameters
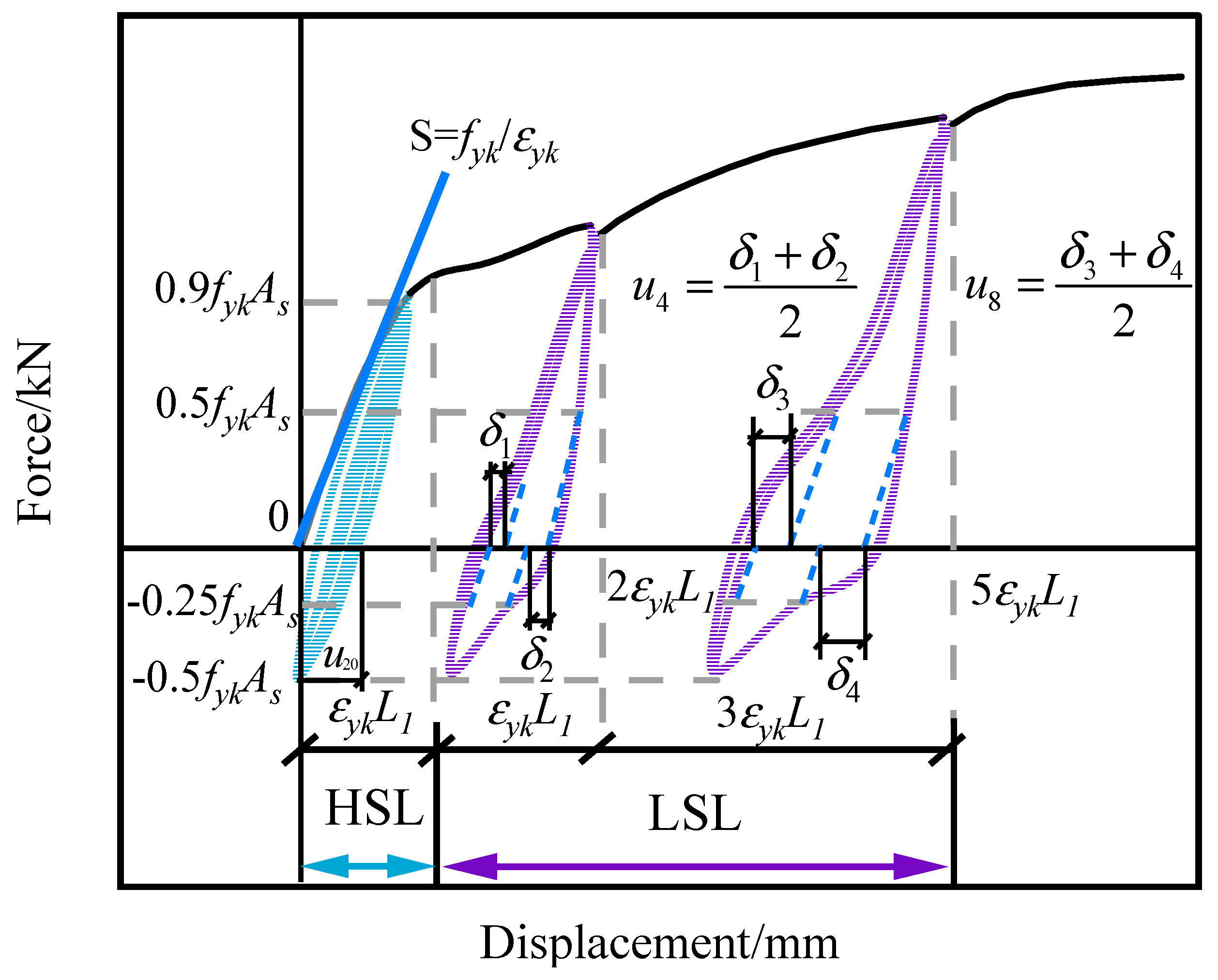
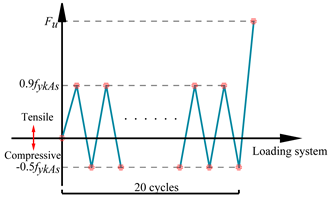
2.2. Testing Procedure for Loads and Loading Schedule
2.3. Element Selection and Grid Division
2.4. Constitutive Model of Splices
2.4.1. Constitutive Model of PSB
2.4.2. Constitutive Model of Coupler
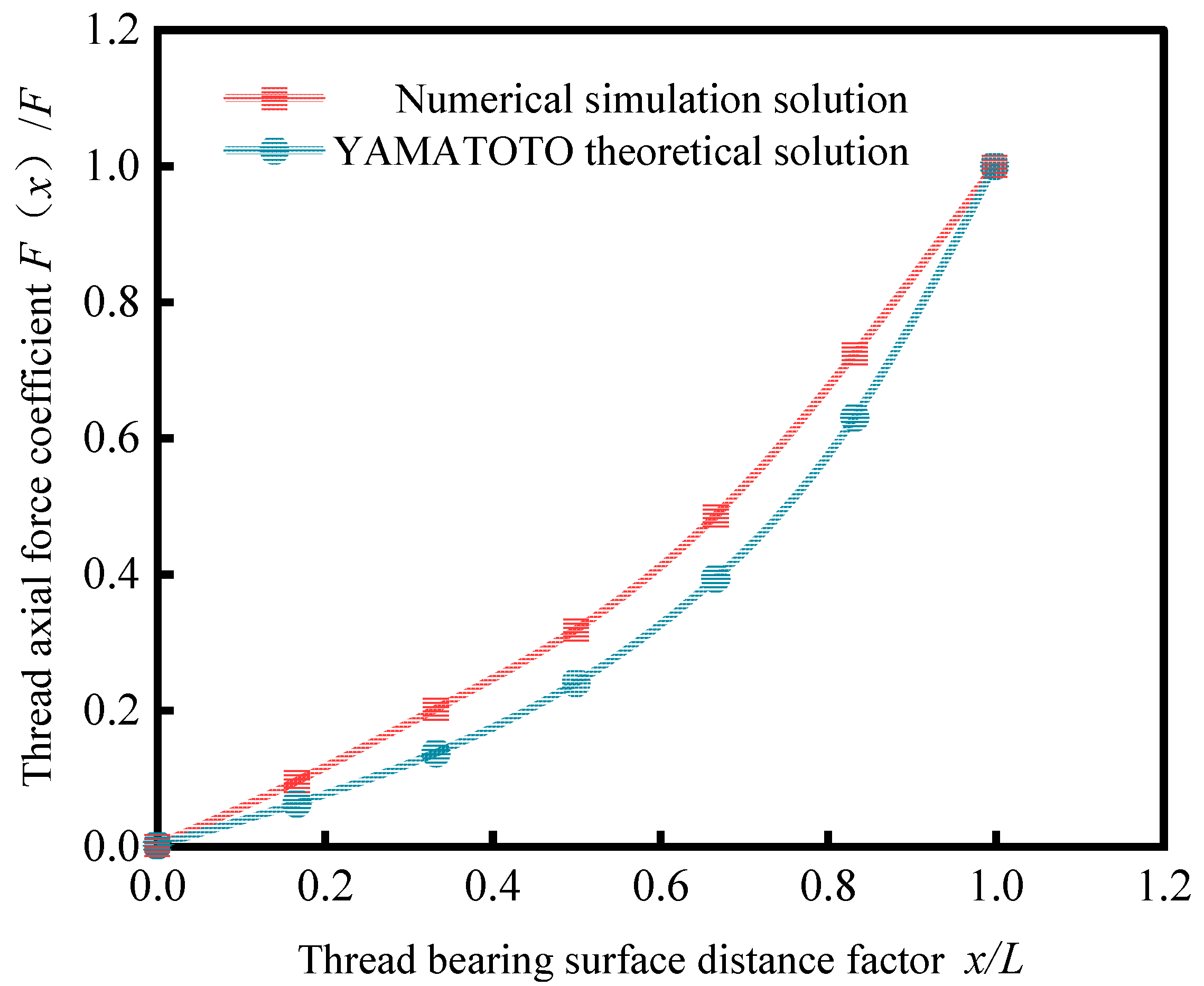
2.5. Verification of the Validity of the Refinement Model
3. Splice Connection Performance Analysis
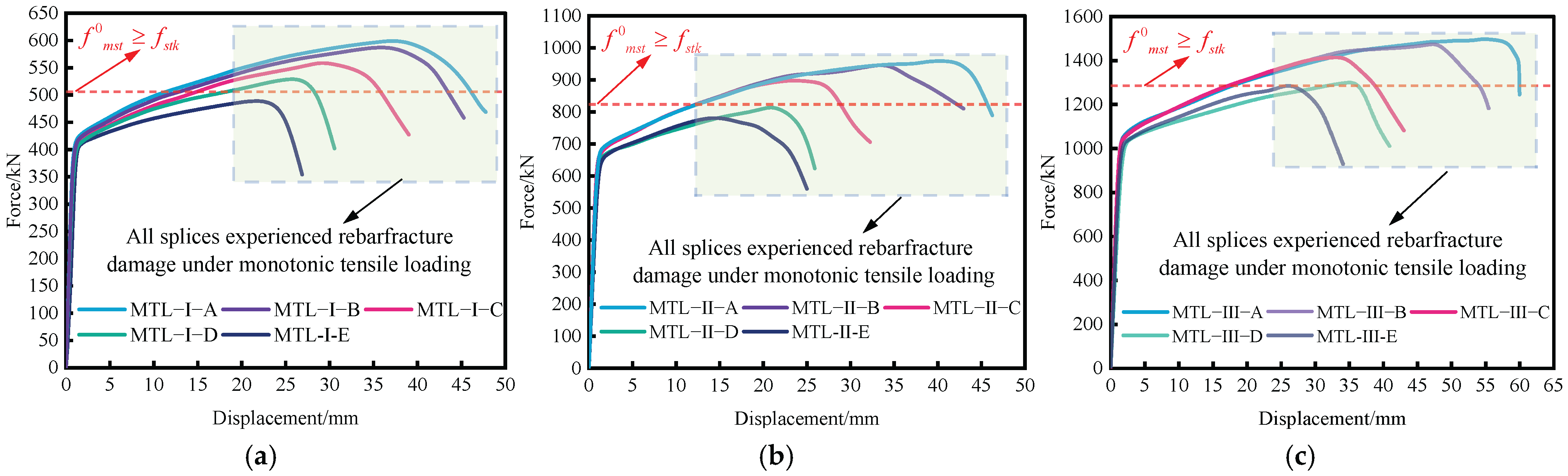
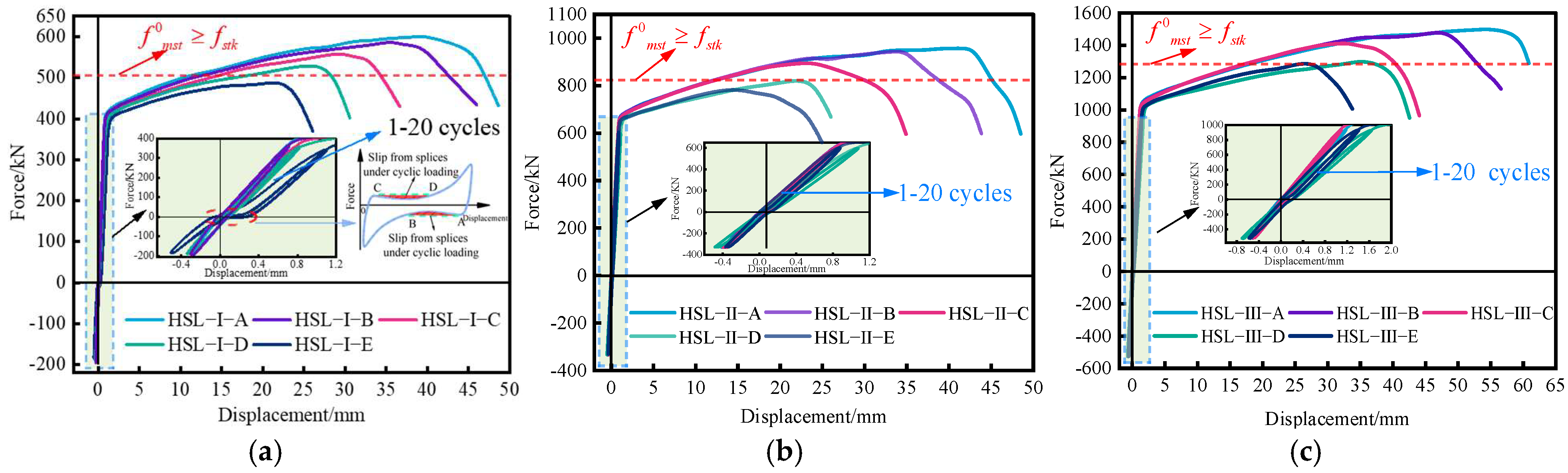
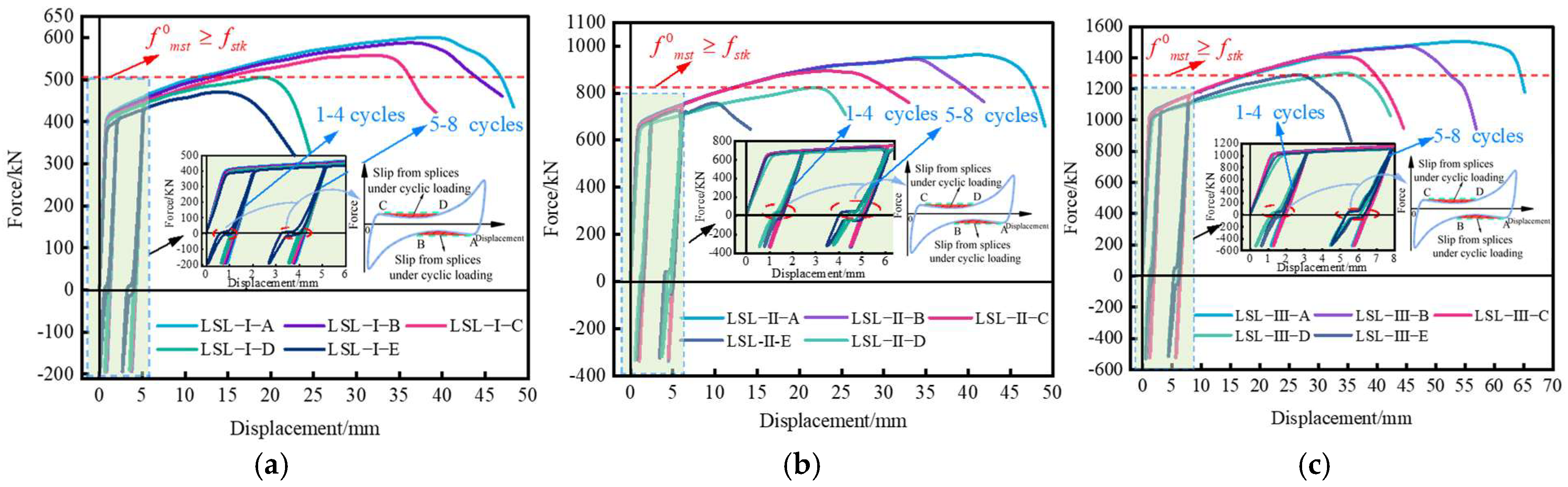
3.1. Load–Displacement Curves of Splices
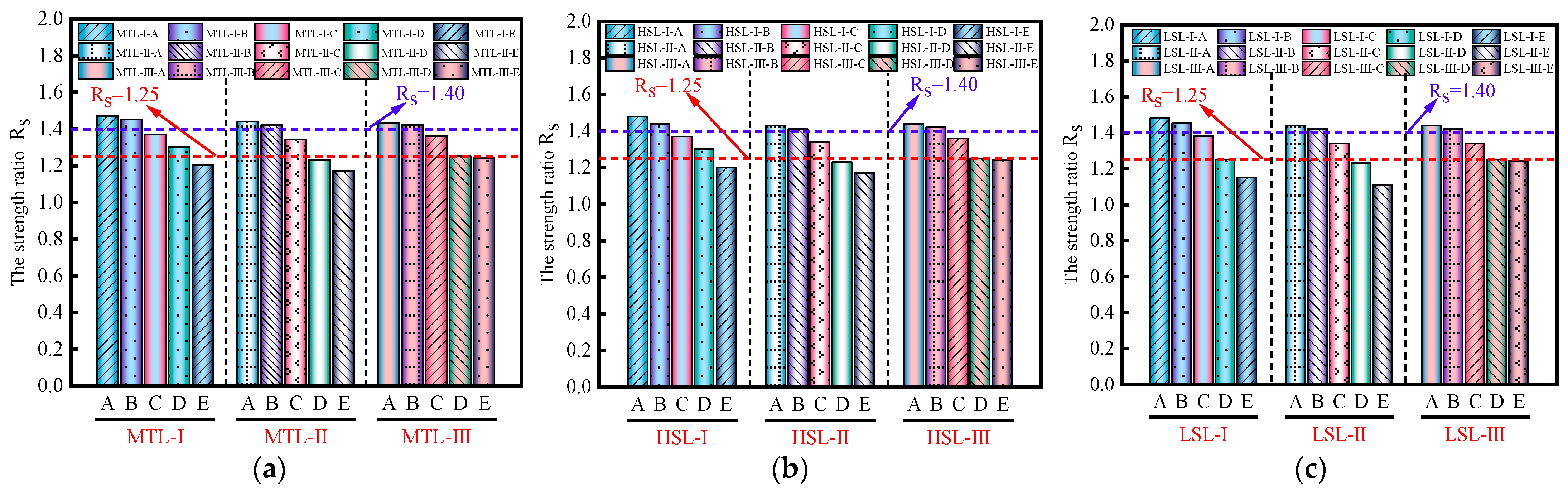
3.2. The Strength Ratio
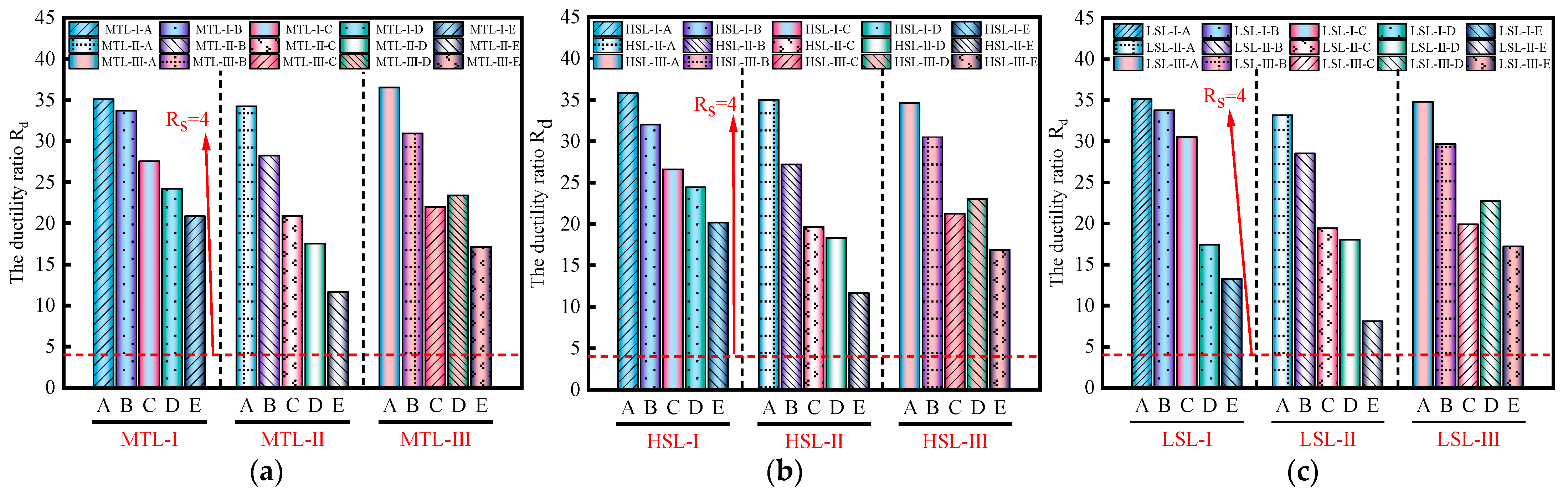
3.3. The Ductility Ratio
3.4. Residual Deformation
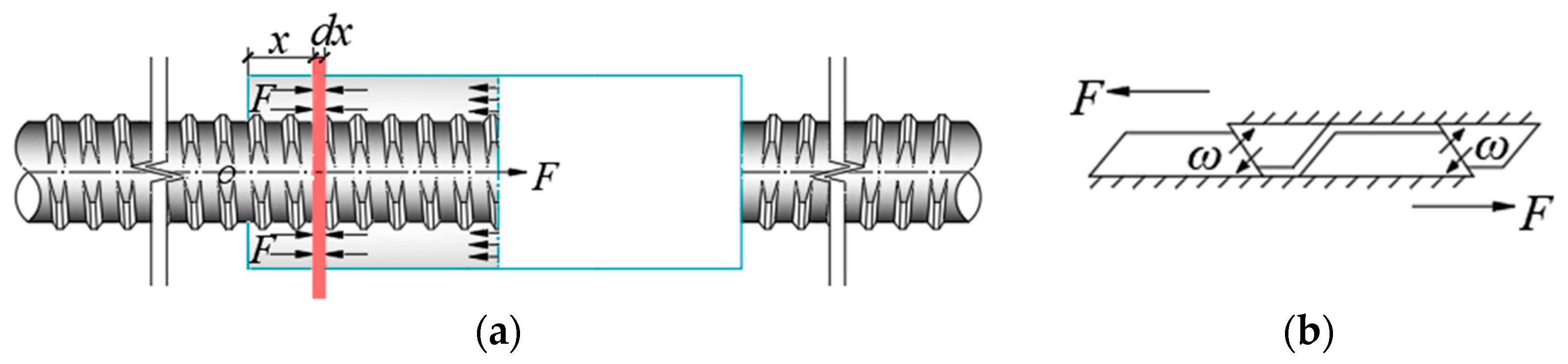
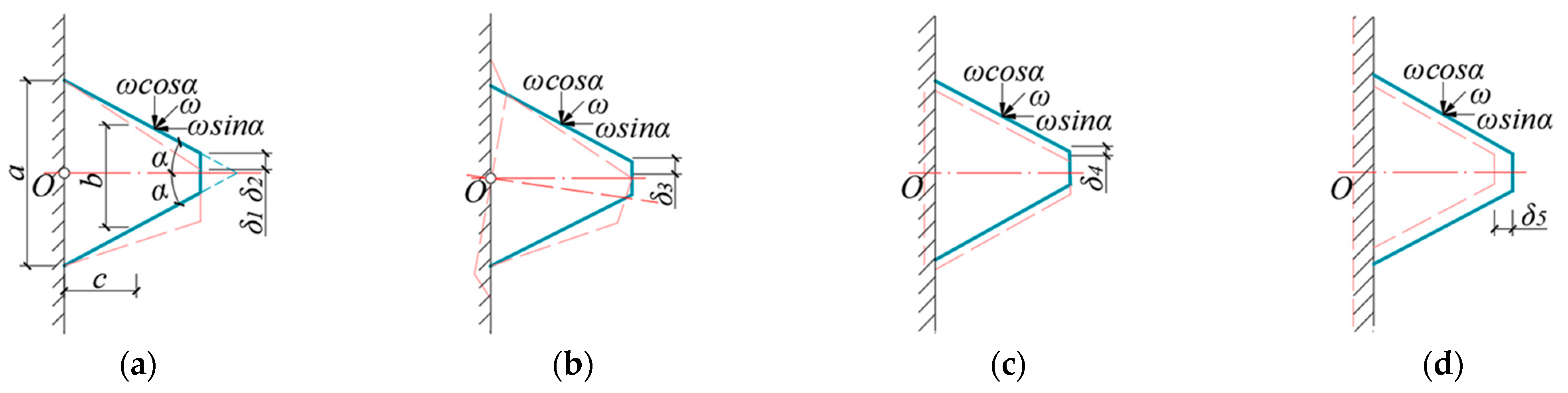
4. Load-Bearing Mechanism of Threaded Ribs of Splices
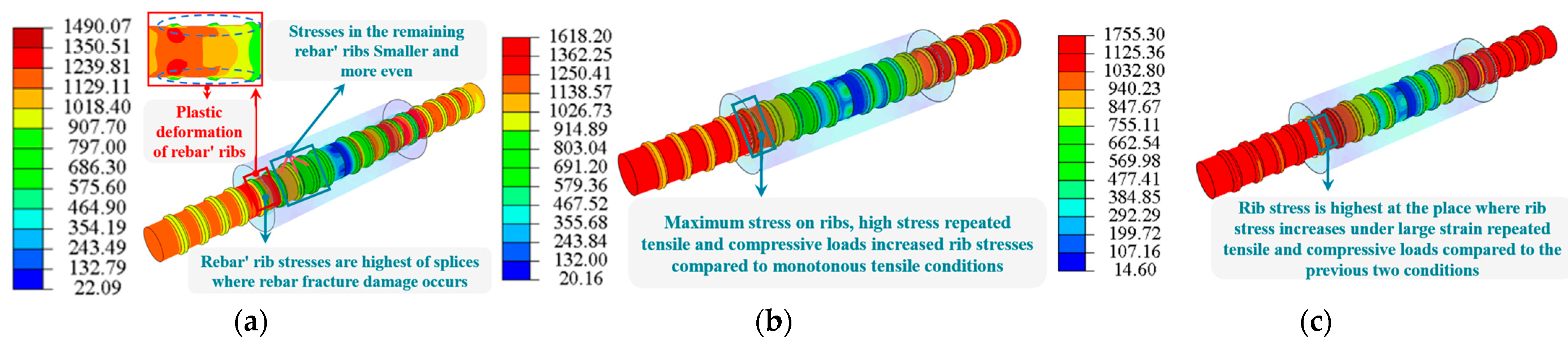
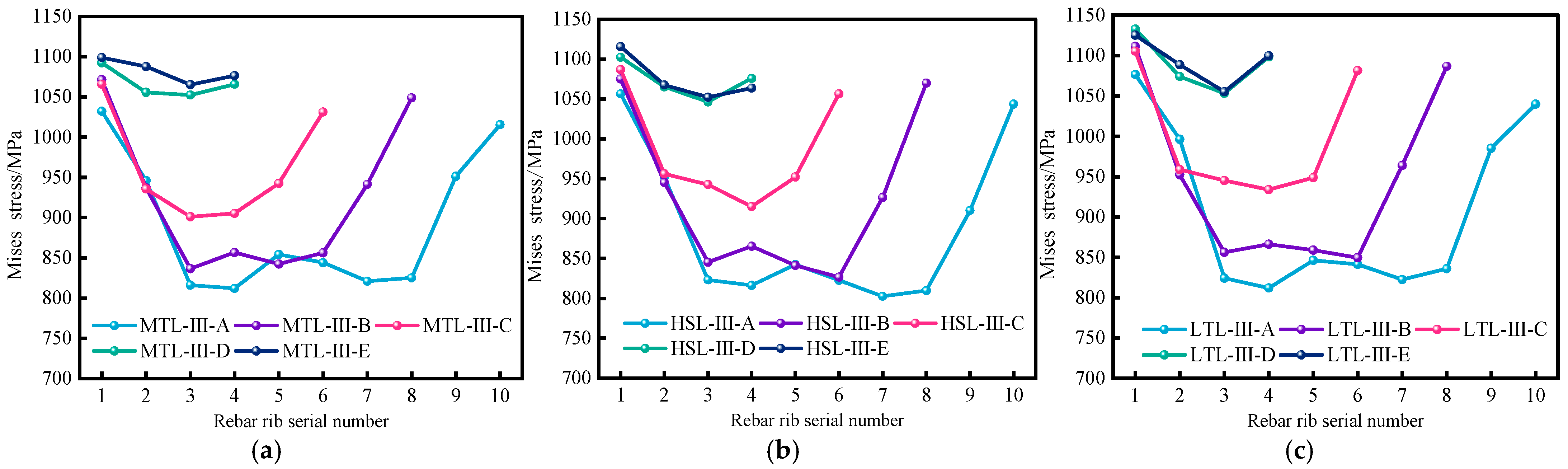
4.1. Stress Distribution in Threaded Ribs of Splices
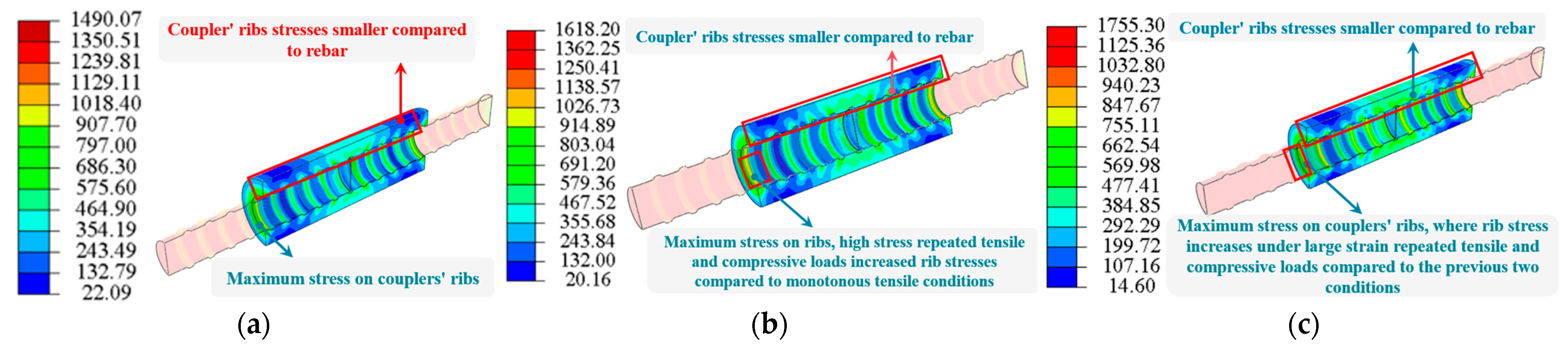
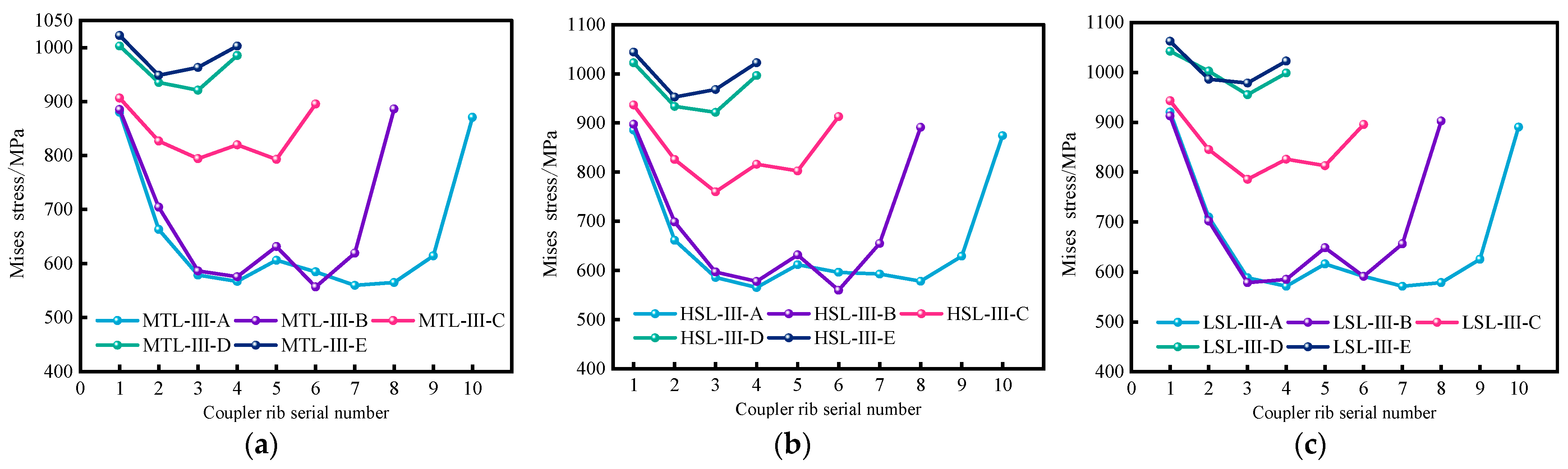
4.2. Stress Distribution in Couplers’ Ribs
5. Conclusions
- According to “Screw-threaded steel bars for the prestressing of concrete” (GB/T 20065-2016), class I splices can satisfy the requirements of “Technical specification for mechanical splicing of steel reinforcing bars” (JGJ 107-2016) if the thread rib spacing of the steel bars is 0.6~0.8 times the nominal diameter of the steel bars under the action of monotonic and cyclic loads. When it comes to PSB thread rib spacing, the specification is conservative. Splices fail to meet code requirements for load bearing when the threaded rib spacing exceeds 1.0 times the nominal diameter of the rebar. The PSB830 splices’ bearing capacity and plastic deformation capacity can be guaranteed by increasing the specification of threaded intercostal ribs to 0.6~0.8 times the nominal diameter of rebar. This will also effectively reduce the actual project’s PSB steel consumption.
- Under various operating situations, the load-carrying capacity of PSB splices is mostly influenced by the 1–2 turns of threaded ribs near the couplers’ ends, and its load-carrying ratio is approximately 50%. Cyclic loading, in contrast to monotonic loading, caused an increase in rib stresses close to the coupler ends. When the spacing between the threaded ribs was between 0.6 and 0.8 times the rebar’s nominal diameter, the stresses were low and average. The number of threaded ribs reduced as the space between them grew to 1.0 to 1.2 times the nominal diameter of the rebar. As a result, the threaded rib stresses increased from monotonic tension splices by 5.49% to 27.76%. Disadvantageously compared to normative rib spacing splices, those with threaded rib spacing have an enhanced ultimate load-carrying capacity of 1.0 to 1.2 times the nominal diameter of the rebar, a loss of 11.95% to 22.73%.
- Under monotonic tensile load, high-stress repeated tensile and compressive loads, and large-strain repeated tensile and compressive loads, PSB830 mechanical connection splices can experience two types of damage: rebar fracture and rebar pullout from the couplers. Under high-stress and large-strain repeated tensile and compressive loads, the couplings’ load–displacement curve and the couplings’ damage form are essentially the same as those under monotonic tensile load. Cyclic loading does not affect the couplers’ ductility or overload limits. Neither the ultimate load capacity nor the splice ductility was significantly reduced by cyclic loading.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhong, X.G.; Zhang, T.Y.; Zhao, C.; Shu, X.J.; Shen, M.Y.; Chen, Y.F. New non-destructive dynamic tensile testing of prestressing fine-rolled screw-threaded steel bars. Eng. Struct. 2019, 182, 153–163. [Google Scholar] [CrossRef]
- Liu, B.Q.; Huang, J.; Xing, G.H. Crack behavior of concrete beam in flexure strengthened with NSM prestressing screw-thread steel bars. Mater. Struct. 2020, 53, 80. [Google Scholar] [CrossRef]
- Ren, D.X.; Peng, T.; Yang, Z.Y.; Xue, P.; Fu, W.X.; Zhao, X.Y.; Li, J.L.; Peng, J.C. Application on underreamed anti-floating anchors of prestressing screw-thread steel bars in pebble stratum of Chengdu. Build. Struct. 2025, 55, 1–10. [Google Scholar] [CrossRef]
- Bompa, D.; Elghazouli, A. Monotonic and cyclic performance of threaded reinforcement splices. Structures 2018, 16, 358–372. [Google Scholar] [CrossRef]
- Rowell, S.P.; Haer, K.P. Investigation of the dynamic performance of large reinforcement bar mechanical couplers In Proceedings of the 2010 Structures Congress—ASCE. Orlando, FL, USA, 12–15 May 2010; pp. 2059–2075. [Google Scholar]
- Ruangrassamee, A.; Mounnarath, P. Monotonic and cyclic behaviors of energy-dissipating threaded mechanical splices. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008; Seismological Press: Beijing, China, 2008. [Google Scholar]
- Li, C.; Zhu, H.; Liu, X.Y.; Xia, C.X.; Wang, P.J.; Liu, F.Z.; Fang, Z.Z.; Wei, D. Mechanical properties of plate type steel bar connectors for prefabricated concrete structures. Adv. Struct. Eng. 2022, 25, 1027–1041. [Google Scholar] [CrossRef]
- Jeong, J.H.; Kim, I.T.; Kim, T.J.; Lee, M.J.; Ahn, J.H. Mechanical performance evaluation of rolling thread steel rebar connection with taper type coupler. J. Korea Inst. Struct. Maint. Insp. 2015, 19, 40–51. [Google Scholar] [CrossRef]
- Li, N.B.; Qian, J.R.; Ye, L.P.; Liu, S.W. Tests on seismic behavior of precast RC shear walls with vertical rebar splicing by pressed sleeve. J. Build. Struct. 2016, 37, 31–40. [Google Scholar]
- Zhang, W.J.; Guo, Y.Y.; Liu, S.W. Experimental research on seismic behavior of precast RC columns with steel bars spliced by compressive sleeves. Eng. Mech. 2016, 33, 119–127. [Google Scholar]
- Bompa, D.; Elghazouli, A. Inelastic cyclic behaviour of RC members incorporating threaded reinforcement couplers. Eng. Struct. 2019, 180, 468–483. [Google Scholar] [CrossRef]
- Liu, Q.Z.; Lin, Y.H.; Li, J.Z.; Yang, C.J.; Chen, J.Y.; Zhang, M.; Liu, B. Bond strength prediction model of defective grout materials in half-grouted sleeve connections under uniaxial and cyclic loadings. Constr. Build. Mater. 2022, 352, 128981. [Google Scholar] [CrossRef]
- Bao, J.W.; Gao, Q.; Tang, L.; Zhao, W.J. Refined finite element analysis of tensile property of grout sleeve splicing of rebars. J. Zhejiang Univ. (Eng. Sci.) 2023, 57, 814–823. [Google Scholar]
- Fukuoka, T.; Nomura, M. Proposition of helical thread modeling with accurate geometry and finite element analysis. J. Press. Vessel. Technol. 2008, 130, 011204. [Google Scholar] [CrossRef]
- Chen, J.J.; Shih, Y.S. A study of the helical effect on the thread connection by three dimensional finite element analysis. Nucl. Eng. Des. 1999, 191, 109–116. [Google Scholar] [CrossRef]
- GB/T 20065-2016; Screw-Thread Steel Bars for the Prestressing of Concrete. Standards Press of China: Beijing, China, 2016.
- ISO 6934-5; Steel for the Prestressing of Concrete Part 5: Hot-Rolled Steel Bars with or Without Subsequent Processing. International Organization for Standardization: Geneva, Switzerland, 2024.
- Bao, J.W.; Zhao, W.J.; Gao, Q.; Tao, Y.C. Refined finite element analysis of grouted-sleeve connection on the bond-slip relationship. J. Harbin Inst. Technol. 2024, 56, 68–76. [Google Scholar]
- GB 1499.2−2024; Steel for Reinforcement of Concrete: Part 2: Hot Rolled Ribbed Bars. Standards Press of China: Beijing, China, 2024.
- BS EN 10080; Steel for the Reinforcement of Concrete—Weldable Reinforcing Steel-General. The European Standard: London, UK, 2005.
- ISO 15835-2; Steels for the Reinforcement of Concrete—Reinforcement Couplers for Mechanical Splices of Bars Part 2: Test Methods. International Organization for Standardization: Geneva, Switzerland, 2009.
- JGJ 107-2016; Technical Specification for Mechanical Splicing of Steel Reinforcing Bars. China Architecture Building Press: Beijing, China, 2016.
- Housari, B.A.; Nassar, S.A. Effect of thread and bearing friction coefficients on the vibration-induced loosening of threaded fasteners. J. Vib. Acoust. 2007, 129, 484–494. [Google Scholar] [CrossRef]
- He, L.G.; Zhang, B.; Zheng, J.J.; Zhou, L.; Su, J.Q.; Shi, W.J. Axial Load Distribution Law of High Temperature Thread Pair Considering Material Creep. J. Southwest Jiaotong Univ. 2022, 57, 1024–1031. [Google Scholar]
- Lei, Y.Y.; Xie, X. Improved method of Giuffre-Menegotto-Pinto hysteretic constitutive model. J. Zhejiang Univ. (Eng. Sci.) 2018, 52, 1926–1934. [Google Scholar]
- Nguyen, V.T.; Nguyen, X.D. Optimal procedure for determining constitutive parameters of Giuffre-Menegotto-Pinto model for steel based on experimental results. Int. J. Steel Struct. 2022, 22, 851–863. [Google Scholar] [CrossRef]
- Zhang, X.C.; Zhao, J.B.; Wang, Z.D.; Liu, Z.Y.; Zhao, J. Theoretical and Numerical Simulation of Seismic Behavior of Concrete Columns Reinforced with Prestressing-screw Bars. Sci. Technol. Eng. 2023, 23, 12638–12647. [Google Scholar]
- Fukuhara, T.; Sun, Y.P. Evaluation method of seismic performanceof high-strength RC members and frames. In Proceedings of the AlJ Annual Conventional, Tokyo, Japan, 14 November 2005; Architectural Institute of Japan: Tokyo, Japan, 2005; pp. 193–198. [Google Scholar]
- GB/T 3077-2015; Alloy Structures Steels. Standards Press of China: Beijing, China, 2015.
- Wang, J.Y. Research on Lean Prefabricated Structure System and the Connecting of Bar. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2018. [Google Scholar]
- Yamatoto, A. The Theory and Computation of Threads Connection; Yokendo: Tokyo, Japan, 1980; pp. 58–61. [Google Scholar]
- Huang, H.; Wang, Y.H.; Wei, T.; Xue, W.H.; Yao, J.J. Sensitivity Analysis of Friction and Room Temperature Creep on Preload Relaxation of Wind Turbine Bolt. Acta Energiae Solaris Sin. 2023, 44, 289–296. [Google Scholar]
- Ling, J.H.; Rahman, A.B.A.; Ibrahim, I.S.; Hamid, Z.A. Behaviour of grouted pipe splice under incremental tensile load. Constr. Build. Mater. 2012, 33, 90–98. [Google Scholar] [CrossRef]
- BS 8110-1:1997; Structural Use of Concrete—Part 1: Code of Practice for Design and Construction. The British Standard: London, UK, 1997.
- ACI 318-11; Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2011.
- Soudki, K.A.; Rizkalla, S.H.; Leblanc, B. Horizontal connections for precast concrete shear walls subjected to cyclic deformations part 1: Mild steel con-nections. PCI J. 1995, 40, 78–96. [Google Scholar] [CrossRef]
- Duan, L.S.; Zhang, H.B.; Ding, T.T.; Zhou, Y.L.; Wu, N.; Pan, H.; Xia, M.G.; Li, H. Experimental study on rebar mechanical connection performance of steel plate composite blind bolts under high stress repeated tension compression load. J. Archit. Civ. Eng. 2023, 40, 108–118. [Google Scholar]
- Liu, Q.Z.; Li, J.Z.; Li, M.F.; Wu, X.K.; Li, Y.C.; Zhang, L. Bond performance prediction model of defective grout in post-fire sleeve connections under cyclic loading. Constr. Build. Mater. 2023, 400, 132442. [Google Scholar] [CrossRef]
- GB/T 14370-2015; Anchorage, Grip and Coupler for Prestressing Tendons. Standards Press of China: Beijing, China, 2015.


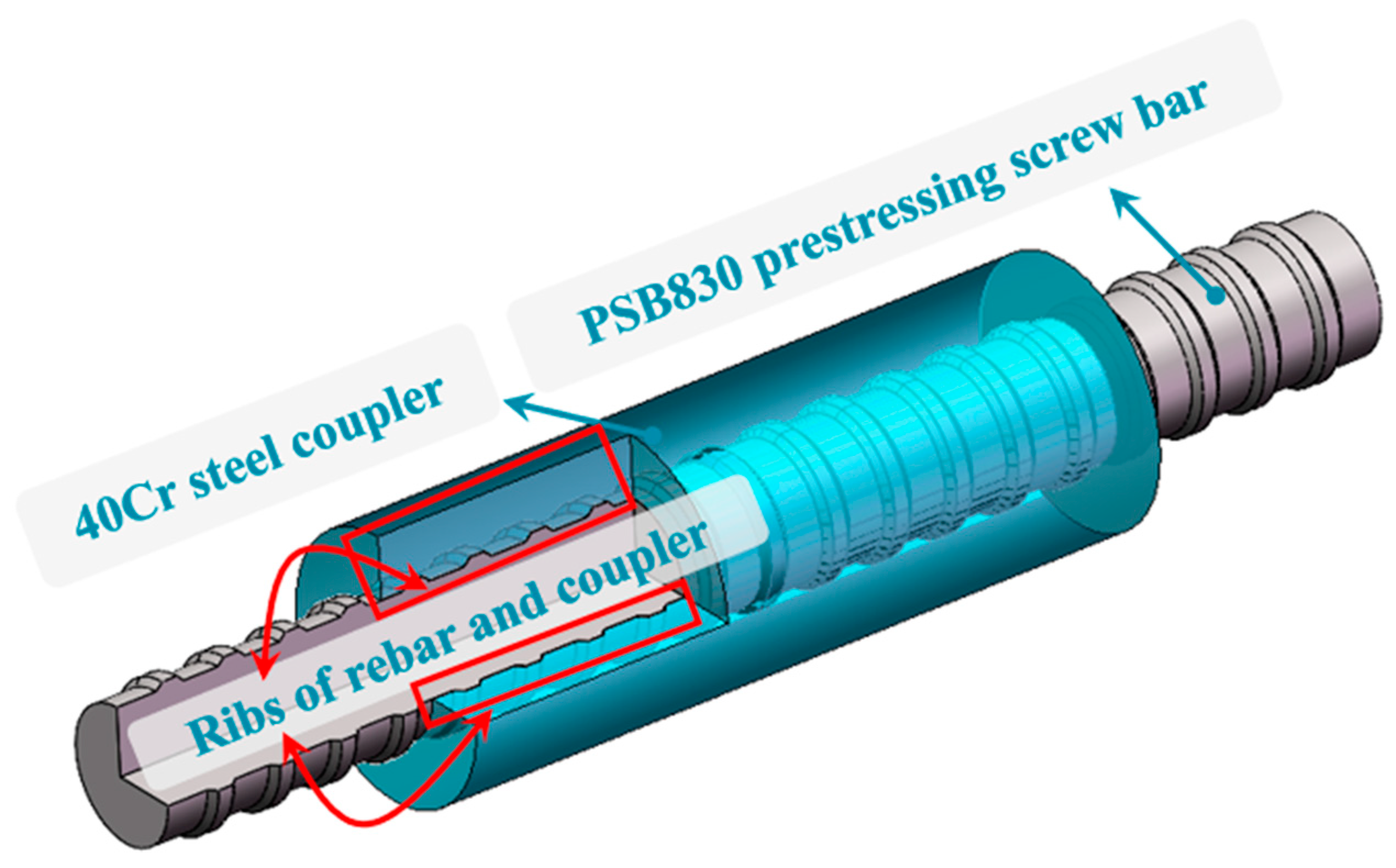
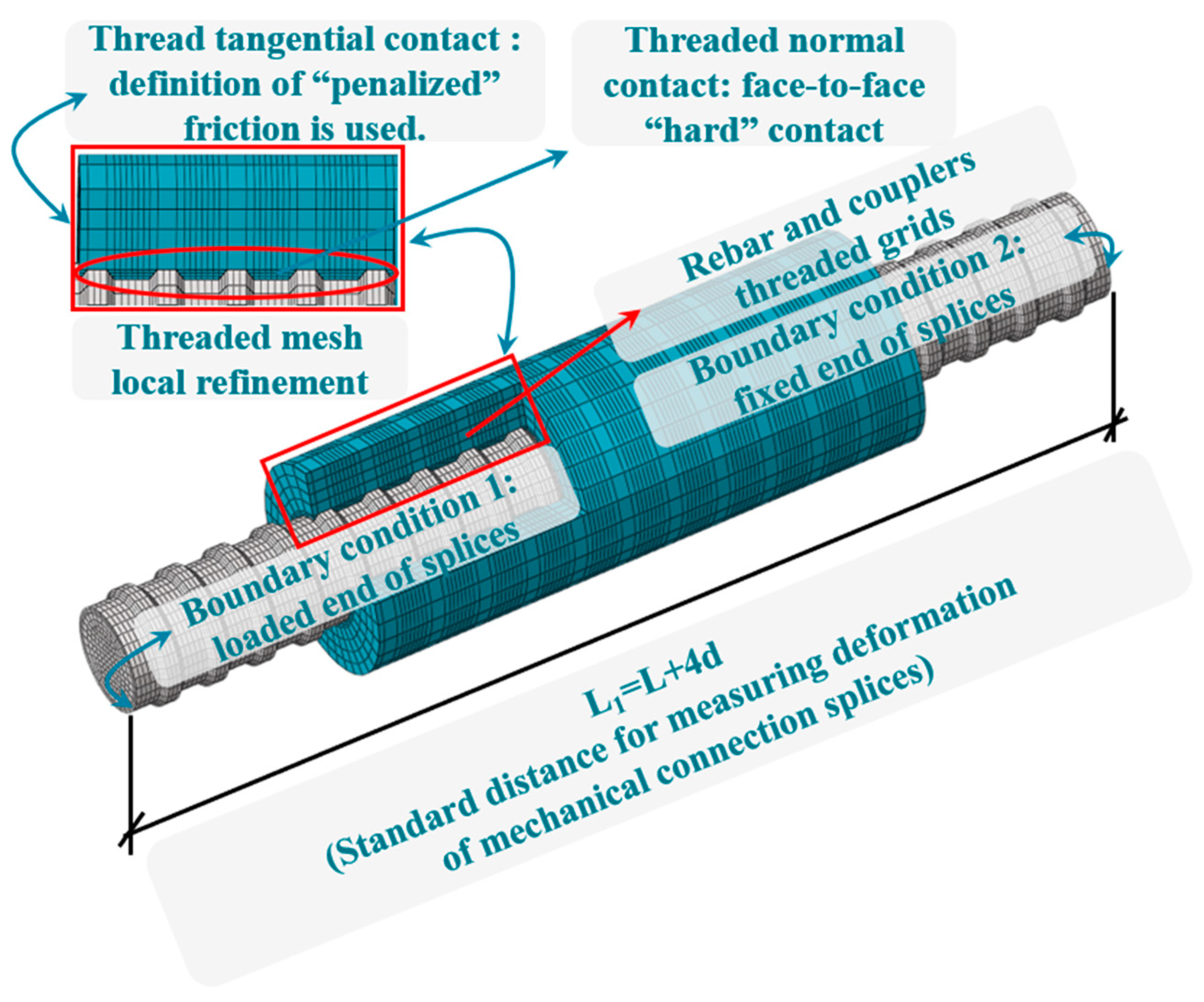

| Splice Varieties | Specimens Under Monotonic Loading | Various Specimens Under High Stress in Both Tensile and Compressive Modes | Various Specimens Under Large Strain in Both Tensile and Compressive Modes |
|---|---|---|---|
| I | MTL-I-A/B/C/D/E | HSL-I-A/B/C/D/E | LSL-I-A/B/C/D/E |
| II | MTL-II-A/B/C/D/E | HSL-II-A/B/C/D/E | LSL-II-A/B/C/D/E |
| III | MTL-III-A/B/C/D/E | HSL-III-A/B/C/D/E | LSL-III-A/B/C/D/E |
| Splices Designator | Nominal Diameters | Heights of Ribs | Top Widths of Ribs | Bottom Widths of Ribs | Pitches of Ribs | Outer Diameters of Couplers | Lengths of Couplers | Lengths of Splices |
|---|---|---|---|---|---|---|---|---|
| d/mm | h/mm | a/mm | b/mm | l/mm | dt/mm | L/mm | L1/mm | |
| MTL-I-A | 25 | 1.37 | 3.26 | 6 | 12 | 50 | 132 | 232 |
| MTL-I-B | 25 | 1.37 | 3.26 | 6 | 15 | 50 | 132 | 232 |
| MTL-I-C | 25 | 1.37 | 3.26 | 6 | 20 | 50 | 132 | 232 |
| MTL-I-D | 25 | 1.37 | 3.26 | 6 | 25 | 50 | 132 | 232 |
| MTL-I-E | 25 | 1.37 | 3.26 | 6 | 30 | 50 | 132 | 232 |
| MTL-II-A | 32 | 1.71 | 3.58 | 7 | 16 | 60 | 168 | 296 |
| MTL-II-B | 32 | 1.71 | 3.58 | 7 | 19.2 | 60 | 168 | 296 |
| MTL-II-C | 32 | 1.71 | 3.58 | 7 | 25.6 | 60 | 168 | 296 |
| MTL-II-D | 32 | 1.71 | 3.58 | 7 | 32 | 60 | 168 | 296 |
| MTL-II-E | 32 | 1.71 | 3.58 | 7 | 38.4 | 60 | 168 | 296 |
| MTL-III-A | 40 | 2.14 | 3.72 | 8 | 20 | 75 | 220 | 380 |
| MTL-III-B | 40 | 2.14 | 3.72 | 8 | 24 | 75 | 220 | 380 |
| MTL-III-C | 40 | 2.14 | 3.72 | 8 | 32 | 75 | 220 | 380 |
| MTL-III-D | 40 | 2.14 | 3.72 | 8 | 40 | 75 | 220 | 380 |
| MTL-III-E | 40 | 2.14 | 3.72 | 8 | 48 | 75 | 220 | 380 |
| HSL-I-A | 25 | 1.37 | 3.26 | 6 | 12 | 50 | 132 | 232 |
| HSL-I-B | 25 | 1.37 | 3.26 | 6 | 15 | 50 | 132 | 232 |
| HSL-I-C | 25 | 1.37 | 3.26 | 6 | 20 | 50 | 132 | 232 |
| HSL-I-D | 25 | 1.37 | 3.26 | 6 | 25 | 50 | 132 | 232 |
| HSL-I-E | 25 | 1.37 | 3.26 | 6 | 30 | 50 | 132 | 232 |
| HSL-II-A | 32 | 1.71 | 3.58 | 7 | 16 | 60 | 168 | 296 |
| HSL-II-B | 32 | 1.71 | 3.58 | 7 | 19.2 | 60 | 168 | 296 |
| HSL-II-C | 32 | 1.71 | 3.58 | 7 | 25.6 | 60 | 168 | 296 |
| HSL-II-D | 32 | 1.71 | 3.58 | 7 | 32 | 60 | 168 | 296 |
| HSL-II-E | 32 | 1.71 | 3.58 | 7 | 38.4 | 60 | 168 | 296 |
| HSL-III-A | 40 | 2.14 | 3.72 | 8 | 20 | 75 | 220 | 380 |
| HSL-III-B | 40 | 2.14 | 3.72 | 8 | 24 | 75 | 220 | 380 |
| HSL-III-C | 40 | 2.14 | 3.72 | 8 | 32 | 75 | 220 | 380 |
| HSL-III-D | 40 | 2.14 | 3.72 | 8 | 40 | 75 | 220 | 380 |
| HSL-III-E | 40 | 2.14 | 3.72 | 8 | 48 | 75 | 220 | 380 |
| LSL-I-A | 25 | 1.37 | 3.26 | 6 | 12 | 50 | 132 | 232 |
| LSL-I-B | 25 | 1.37 | 3.26 | 6 | 15 | 50 | 132 | 232 |
| LSL-I-C | 25 | 1.37 | 3.26 | 6 | 20 | 50 | 132 | 232 |
| LSL-I-D | 25 | 1.37 | 3.26 | 6 | 25 | 50 | 132 | 232 |
| LSL-I-E | 25 | 1.37 | 3.26 | 6 | 30 | 50 | 132 | 232 |
| LSL-II-A | 32 | 1.71 | 3.58 | 7 | 16 | 60 | 168 | 296 |
| LSL-II-B | 32 | 1.71 | 3.58 | 7 | 19.2 | 60 | 168 | 296 |
| LSL-II-C | 32 | 1.71 | 3.58 | 7 | 25.6 | 60 | 168 | 296 |
| LSL-II-D | 32 | 1.71 | 3.58 | 7 | 32 | 60 | 168 | 296 |
| LSL-II-E | 32 | 1.71 | 3.58 | 7 | 38.4 | 60 | 168 | 296 |
| LSL-III-A | 40 | 2.14 | 3.72 | 8 | 20 | 75 | 220 | 380 |
| LSL-III-B | 40 | 2.14 | 3.72 | 8 | 24 | 75 | 220 | 380 |
| LSL-III-C | 40 | 2.14 | 3.72 | 8 | 32 | 75 | 220 | 380 |
| LSL-III-D | 40 | 2.14 | 3.72 | 8 | 40 | 75 | 220 | 380 |
| LSL-III-E | 40 | 2.14 | 3.72 | 8 | 48 | 75 | 220 | 380 |
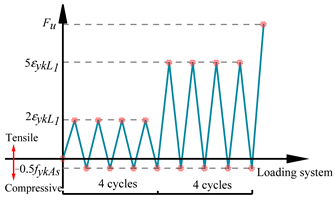
| Cyclic Loading Systems for Splices | |
|---|---|
| High- stress repeated tensile and compressive cycle loading (HSL) | 0→(0.9fykAs→−0.5fykAs)…(0.9fykAs→−0.5fykAs)→Ultimate load capacity of splices (Fu) |
 | |
| Large- strain repeated tensile and compressive cycle loading (LSL) | 0→(2εykL1→−0.5fykAs)…(5εyk L1→−0.5fykAs)→Ultimate load capacity of splices (Fu) |
 | |
| Material Name | ρ/(kg/m3) | ν | E/MPa | /MPa | /MPa | ||
|---|---|---|---|---|---|---|---|
| PSB830 [16] | 7850 | 0.3 | 201,000 | 830 | 0.0041 | 1030 | 0.07 |
| 40Cr [29] | 7850 | 0.3 | 210,000 | 785 | 0.0037 | 980 | 0.09 |
| Names of Splices | Rs | Rd | Modes of Damage | |
|---|---|---|---|---|
| MTL-I | A | 1.47 | 35.11 | Rebar fracture |
| B | 1.45 | 33.71 | Rebar fracture | |
| C | 1.37 | 27.54 | Rebar fracture | |
| D | 1.30 | 24.20 | Rebar fracture | |
| E | 1.20 | 20.83 | Rebar fracture | |
| MTL-II | A | 1.44 | 34.22 | Rebar fracture |
| B | 1.42 | 28.21 | Rebar fracture | |
| C | 1.34 | 20.87 | Rebar fracture | |
| D | 1.23 | 17.51 | Rebar fracture | |
| E | 1.17 | 11.59 | Rebar fracture | |
| MTL-III | A | 1.43 | 36.52 | Rebar fracture |
| B | 1.42 | 30.92 | Rebar fracture | |
| C | 1.36 | 21.96 | Rebar fracture | |
| D | 1.25 | 23.66 | Rebar fracture | |
| E | 1.24 | 17.11 | Rebar fracture | |
| Names of Splices | Rs | Rd | Modes of Damage | ||
|---|---|---|---|---|---|
| HSL-I | A | 1.48 | 35.77 | 0.090 | Rebar fracture |
| B | 1.44 | 32.00 | 0.098 | Rebar fracture | |
| C | 1.37 | 26.58 | 0.114 | Rebar fracture | |
| D | 1.30 | 24.40 | 0.130 | Rebar fracture | |
| E | 1.20 | 20.13 | 0.177 | Rebar fracture | |
| HSL-II | A | 1.43 | 34.96 | 0.068 | Rebar fracture |
| B | 1.41 | 27.16 | 0.069 | Rebar fracture | |
| C | 1.34 | 19.61 | 0.072 | Rebar fracture | |
| D | 1.23 | 18.29 | 0.105 | Rebar fracture | |
| E | 1.17 | 11.60 | 0.118 | Rebar fracture | |
| HSL-III | A | 1.44 | 34.60 | 0.090 | Rebar fracture |
| B | 1.42 | 30.50 | 0.094 | Rebar fracture | |
| C | 1.36 | 21.23 | 0.096 | Rebar fracture | |
| D | 1.25 | 23.01 | 0.188 | Rebar fracture | |
| E | 1.24 | 16.83 | 0.195 | Rebar fracture | |
| Names of Splices | Rs | Rd | Modes of Damage | |||
|---|---|---|---|---|---|---|
| LSL-I | A | 1.48 | 35.14 | 0.070 | 0.101 | Rebar fracture |
| B | 1.45 | 33.78 | 0.092 | 0.121 | Rebar fracture | |
| C | 1.38 | 30.50 | 0.096 | 0.137 | Rebar fracture | |
| D | 1.25 | 17.39 | 0.105 | 0.180 | Rebar fracture | |
| E | 1.15 | 13.20 | 0.212 | 0.306 | Rebar fracture | |
| LSL-II | A | 1.44 | 33.14 | 0.127 | 0.150 | Rebar fracture |
| B | 1.42 | 28.49 | 0.132 | 0.156 | Rebar fracture | |
| C | 1.34 | 19.40 | 0.137 | 0.163 | Rebar fracture | |
| D | 1.23 | 18.01 | 0.154 | 0.241 | Rebar fracture | |
| E | 1.11 | 8.04 | 0.187 | 0.299 | Rebar pullout | |
| LSL-III | A | 1.44 | 34.80 | 0.033 | 0.096 | Rebar fracture |
| B | 1.42 | 29.65 | 0.081 | 0.106 | Rebar fracture | |
| C | 1.34 | 19.86 | 0.112 | 0.124 | Rebar fracture | |
| D | 1.25 | 22.68 | 0.157 | 0.248 | Rebar fracture | |
| E | 1.24 | 17.14 | 0.185 | 0.365 | Rebar fracture | |
 : The connection performs as expected, and the damage type is rebar fracture damage.
: The connection performs as expected, and the damage type is rebar fracture damage.  : The connection performance falls short of the specified standards, and the damage mode is rebar fracture damage.
: The connection performance falls short of the specified standards, and the damage mode is rebar fracture damage.  : The splice connection performance falls short of the specifications, and the damage mode is rebar pullout.
: The splice connection performance falls short of the specifications, and the damage mode is rebar pullout.  : The connecting performance of the splices does not match the requirements of the specification.
: The connecting performance of the splices does not match the requirements of the specification.Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, L.; Ma, Y.; Xie, B.; Bai, J.; Hu, M.; Guo, Z. Research on the Mechanical Properties of Mechanically Connected Splices of Prestressing Screw Bars Under Monotonic and Cyclic Loads. Buildings 2025, 15, 3614. https://doi.org/10.3390/buildings15193614
Lei L, Ma Y, Xie B, Bai J, Hu M, Guo Z. Research on the Mechanical Properties of Mechanically Connected Splices of Prestressing Screw Bars Under Monotonic and Cyclic Loads. Buildings. 2025; 15(19):3614. https://doi.org/10.3390/buildings15193614
Chicago/Turabian StyleLei, Liangyu, Yue Ma, Bo Xie, Jing Bai, Mei Hu, and Zhezhuo Guo. 2025. "Research on the Mechanical Properties of Mechanically Connected Splices of Prestressing Screw Bars Under Monotonic and Cyclic Loads" Buildings 15, no. 19: 3614. https://doi.org/10.3390/buildings15193614
APA StyleLei, L., Ma, Y., Xie, B., Bai, J., Hu, M., & Guo, Z. (2025). Research on the Mechanical Properties of Mechanically Connected Splices of Prestressing Screw Bars Under Monotonic and Cyclic Loads. Buildings, 15(19), 3614. https://doi.org/10.3390/buildings15193614






