Minimally Invasive Design and Energy Efficiency Evaluation of Photovoltaic–Energy Storage–Direct Current–Flexible Systems in Low-Carbon Retrofitting of Existing Buildings
Abstract
1. Introduction
- ◉
- A co-optimization framework integrating spatial layout and operational strategy to address physical and operational constraints simultaneously.
- ◉
- A solution to the PV-ESS layout combinatorial optimization problem by incorporating equipment and pathway placement codes and constraints, defining optimization objectives, and designing an efficient algorithm to identify Pareto-optimal solutions under minimally invasive conditions.
- ◉
- The application of advanced deep reinforcement learning (DRL) to flexible operation control, training an adaptive energy management agent via a tailored reward function to maximize comprehensive benefits under varying conditions.
- ◉
- A quantitative multi-dimensional benefit evaluation via case simulation assessing energy, economic, and grid-interaction performance, demonstrating the effectiveness and superiority of the proposed approach.
2. Analysis of Key Issues in Minimally Invasive Retrofitting of PEDF Systems for Existing Buildings
- ◉
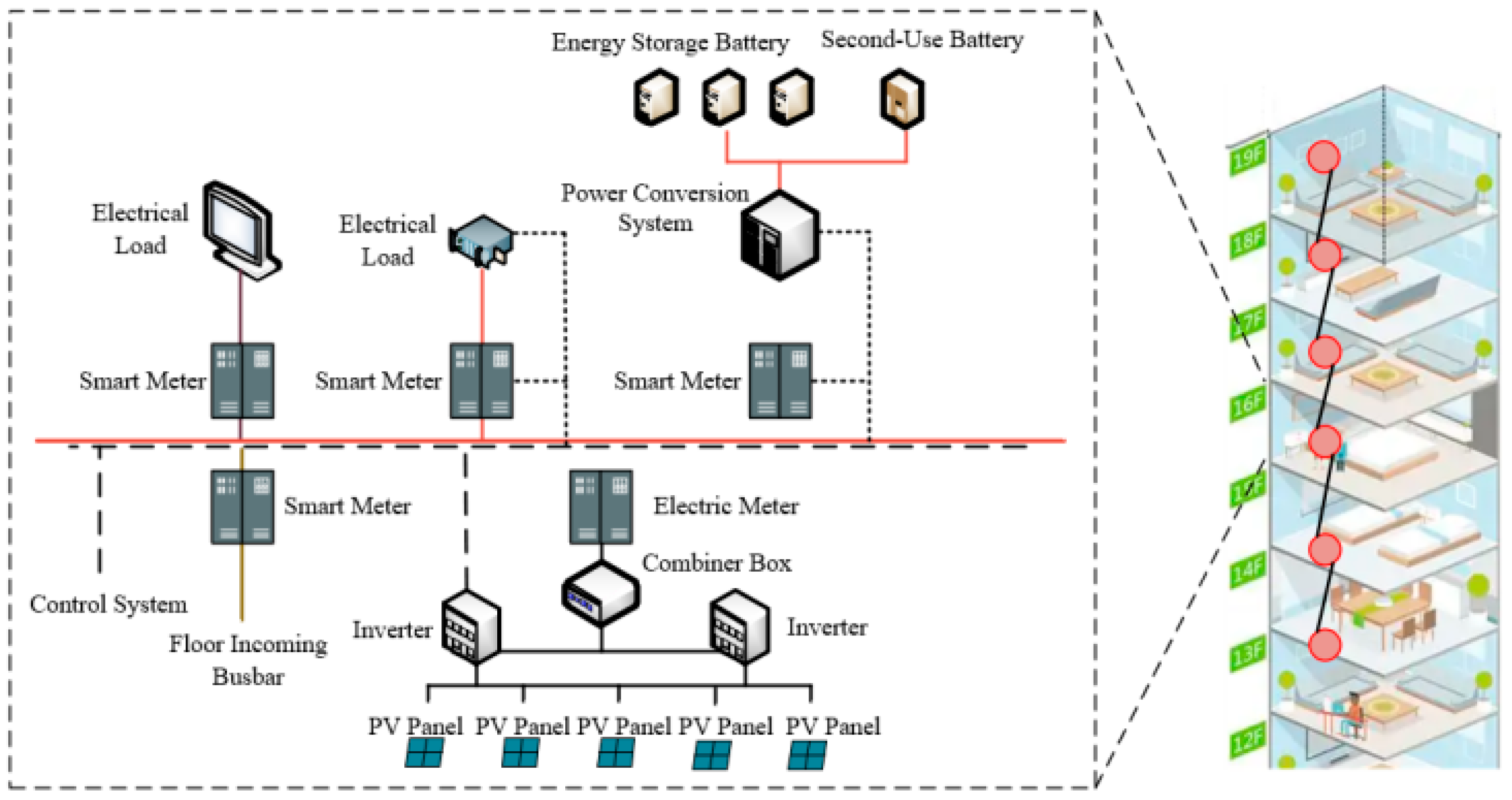
- Spatial and Structural Level: The deployment of PV modules is constrained by available roof area, load-bearing capacity, and shading from existing pipes and facilities, often preventing optimal orientation and tilt angles. Energy storage systems face dual pressures of weight, volume, and stringent safety codes, requiring their siting to precisely match the building’s limited spaces with adequate load-bearing capacity and safety conditions.
- ◉
- Electrical Engineering Level: The foremost challenge lies in the installation of the DC distribution network. It must maximize the use of spare capacity in existing cable trays and conduit shafts or utilize co-installation with the original AC system, strenuously avoiding large-scale chasing of walls and cutting holes in floors. This concerns not only cost but also the building’s structural safety and aesthetics.
- ◉
- Furthermore, the retrofit process must ensure the continuity and safety of the building’s original functions, requiring the new system to possess seamless compatibility and smooth integration capabilities with the aging electrical system [23].
- (1)
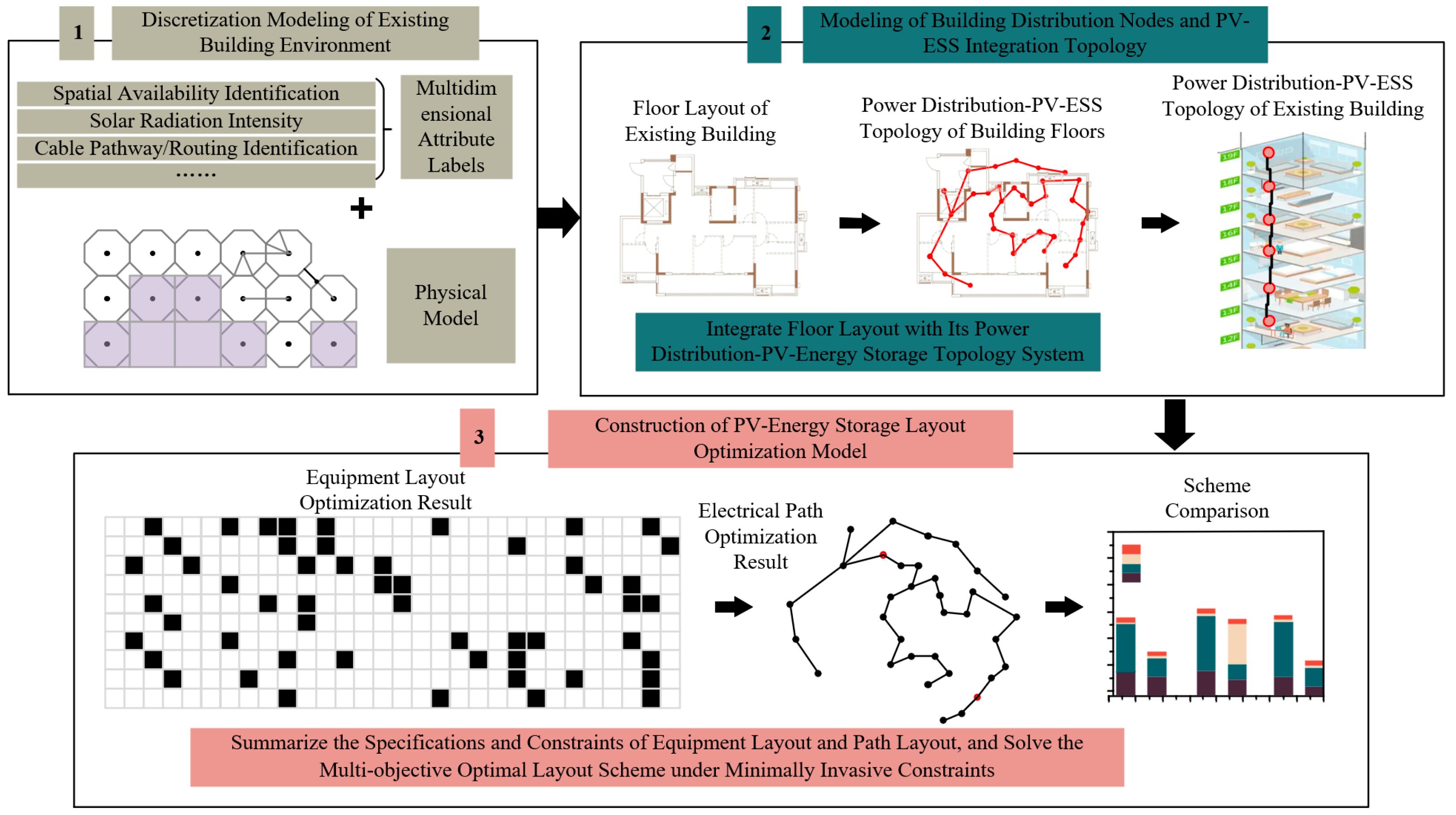
- The “PV-ESS Layout Optimization” Problem falls under static hardware decision-making. It aims to make co-optimization decisions regarding the installation location and string configuration of PV arrays, the capacity and location of the energy storage system, and the routing of critical DC pathways, all while satisfying the aforementioned minimally invasive constraints. The objectives are multidimensional: minimizing initial investment and construction costs, maximizing expected PV power generation revenue, and minimizing line losses caused by non-ideal layouts. The solution to this problem outputs a feasible physical system design, setting the theoretical upper limit for its operational performance.
- (2)
- The “Flexible Energy Management Strategy Optimization” Problem falls under dynamic software decision-making. This problem involves determining the optimal year-round hourly charging/discharging strategy for the energy storage system and the interactive power exchange with the grid, within the physical boundaries defined by a given hardware layout. The objectives are to minimize whole-life-cycle operating costs, enhance the PV self-consumption rate, and achieve peak shaving and valley filling through smoothed control of the grid interface power.
3. Formulation of the Co-Optimization Methodology for Minimally Invasive Retrofitting
3.1. PV-ESS Layout Optimization Model
- (1)
- Minimization of Total System Investment Cost: This is the most critical economic indicator, integrating initial investment and construction costs. Its function is expressed as:Min f1 = Ccap = (Cpv × Npv) + (Cess × Pess_rated) + (Cinv × Ninv) + (Ccable × Cinstall)
- (2)
- Maximization of Expected Power Generation Revenue from the PV System: This objective is directly related to the system’s long-term revenue generation capability. Under minimally invasive constraints, PV installation sites often cannot achieve optimal orientation and tilt angles; thus, energy capture must be maximized at the given locations. The function is expressed as:Max f2 = Rpv = ∑(OUTpv-i × EP)
- (3)
- Minimization of Total Equivalent Line Losses on the DC Side: This objective aims to improve overall system energy efficiency. Non-ideal layouts can lead to longer cables and the use of thinner gauges, thereby increasing losses. The function is expressed as:Min f3 = Ploss = ∑(I2 × R × t)
- (4)
- Maximization of Load Distribution Uniformity of Equipment Group: This objective is a rigid constraint to ensure structural safety. The function is expressed as:Max f4 = Pload = |CGx − COx|/Lx + |CGy − COy|/Ly
- (5)
- Maximization of Maintenance Accessibility Index: This objective concerns the convenience and safety of long-term system operation. The function is expressed as:Max f5 = Aops = ∑(Wk × Score(ABk))
- (6)
- Maximization of Minimally Invasive Construction Index: This objective is the concentrated embodiment of the “minimally invasive” concept and is a comprehensive indicator. The function is expressed as:Max f6 = Icons = − [α × NCL + β × NNP + γ × NB]
- (1)
- Minimization of Total Equivalent Pathway Cost: This objective is the core economic consideration, extending beyond mere cable length minimization. Its function is expressed as:Min d1 = Cpath = ∑(Ccabletype × Lseg) + ∑(Cpen × Npen) + ∑(Cbend × Nbend) + (Clabour × Tinstall)
- (2)
- Maximization of Pathway Orthogonality and Utilization of Existing Channels: This objective is a key technical indicator for achieving “minimally invasive” construction. The function is expressed as:Max d2 = Uexi = ∑(Lseg_in/Lseg_total) × Wchannel − ∑(|sin(ρseg)| × Lseg_new)
- (3)
- Minimization of System Voltage Drop and Line Losses: This objective concerns the final operational energy efficiency level of the system. Assuming ΔVpath-i is the steady-state voltage drop for the i-th critical electrical circuit, the function is expressed as:Min d3 = ΔVmax = max(ΔVpath-i) for each critical path
- (4)
- Maximization of Isolation of High-Power-Density Pathways: This objective originates from the “energy zoning function” and focuses on safety and electromagnetic compatibility (EMC). The function is expressed as:Max d4 = SHP = ∑(min(DIS))
- (5)
- Minimization of Comprehensive Minimally Invasive Penalty Function: This function is a mathematical expression integrating all rigid minimally invasive constraints. A value of 0 indicates full compliance with all constraints, while a positive value represents the degree of constraint violation:Min d5 = Ptotal = Pstr + Psafety + Pcode
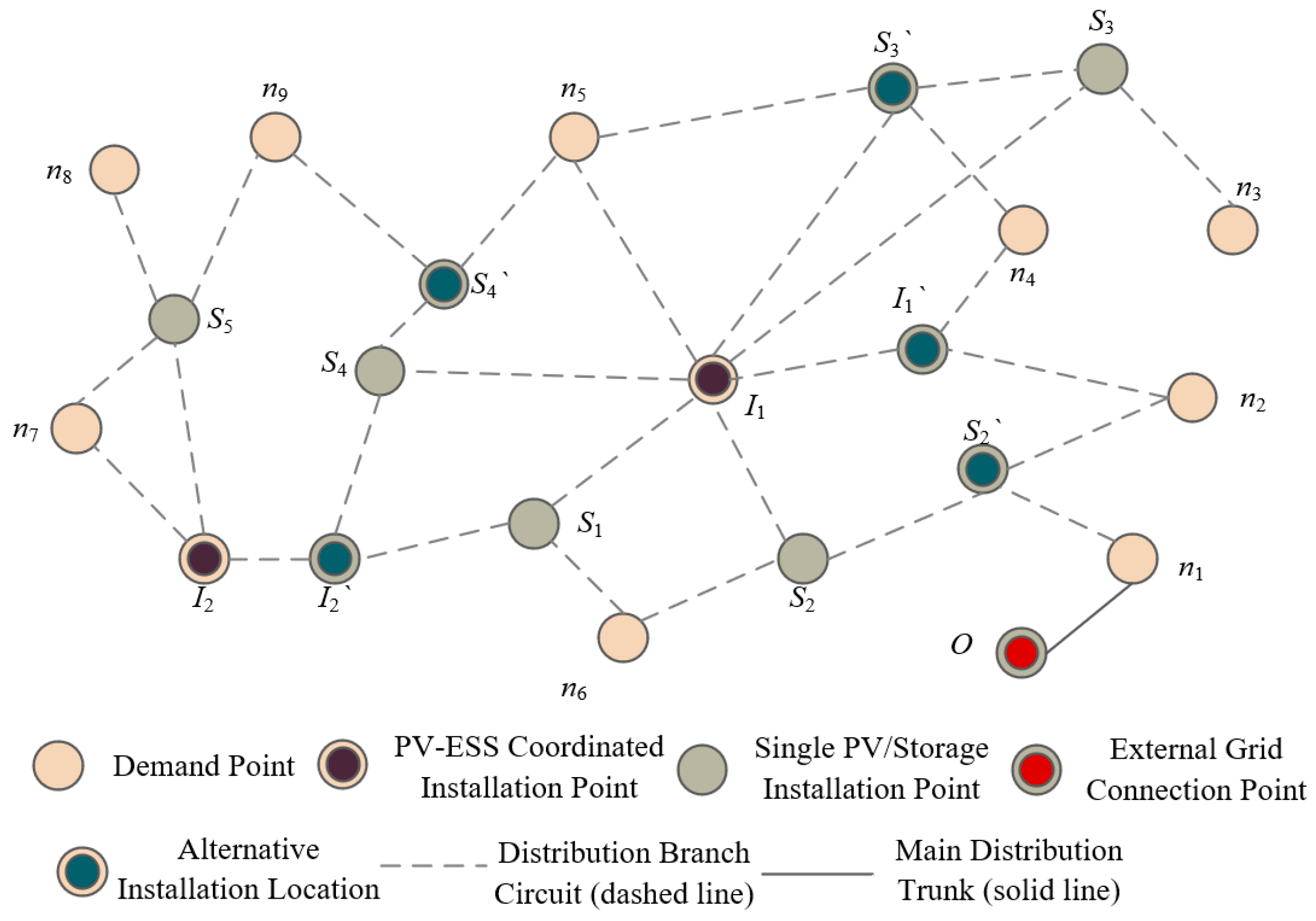
- ◉
- Spatial Constraints: No equipment can be placed on “unavailable” grid cells; minimum safe clearances must be maintained between equipment and between equipment and walls [26].
- ◉
- Structural Constraints: The total weight of equipment must not exceed the allowable load capacity of the floor slab in that area; heavy equipment like energy storage systems must be placed in structurally designated load-bearing zones [27].
- ◉
- Electrical Code Constraints: The installation of all electrical pathways must comply with safety regulations [28]; DC voltage drop must remain within permissible limits.
- ◉
- Geometric Constraints: PV strings must be installed within contiguous and integral available areas; equipment shape must match the installation space profile.
- ◉
- Structural Integrity Constraints: Pathways are strictly prohibited from penetrating the building’s core load-bearing structures unless utilizing pre-existing or pre-designed penetrations.
- ◉
- Safety Clearance Constraints: Pathways must maintain absolute minimum safe distances from combustibles, gas pipes, water pipes, etc., as explicitly defined by national electrical codes [29].
- ◉
- Voltage Drop Constraint: The voltage drop in any critical circuit must not exceed the system’s allowable maximum. This is a mandatory electrical performance constraint [30].
- ◉
- Capacity Constraint: Within any single conduit shaft or cable tray, the total cross-sectional area of all cables must not exceed the legally mandated fill ratio of its internal cross-sectional area.
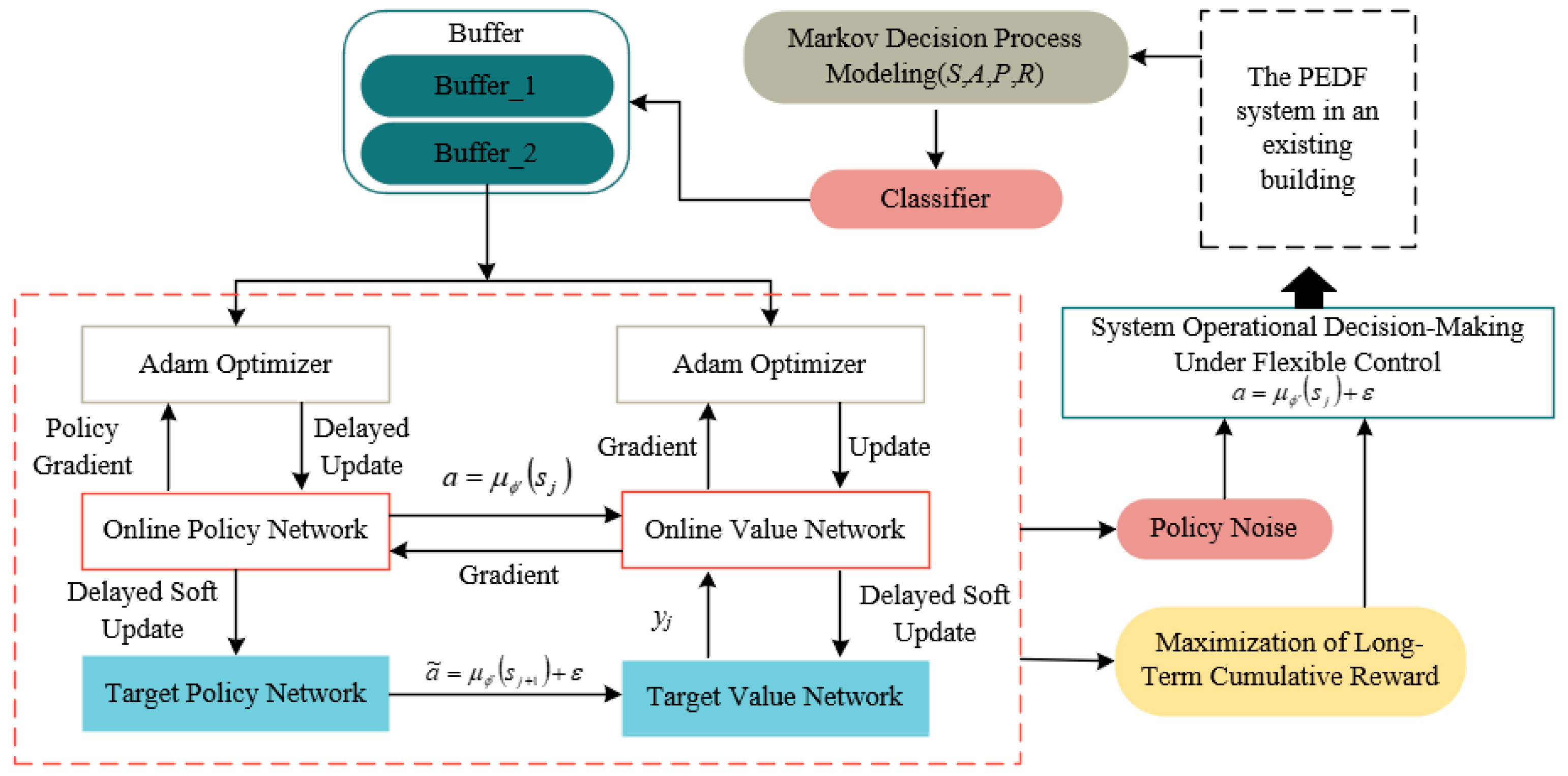
3.2. Optimization Model for Flexible Energy Management Strategy
- (1)
- State Space (S)
- ◉
- t (Time): The current time of day, used to implicitly encode the periodicity of solar irradiance, load patterns, and Time-of-Use (ToU) electricity price cycles. It is a crucial temporal feature for predicting future PV output and load demand.
- ◉
- Ppv(t) (PV Generation Power): The real-time net output power of the PV array. This is the theoretical maximum generation capacity minus losses due to non-ideal factors caused by the minimally invasive layout, such as non-optimal orientation/tilt, partial shading, and line losses from extended pathways. It is the direct input for the agent to perceive current renewable energy availability.
- ◉
- Pload(t) (Load Demand Power): The real-time power demand of the total load on the building’s DC bus. It reflects the aggregated energy consumption of all electrical devices in the building, and its variability is a major source of uncertainty for the system.
- ◉
- SOC(t) (State of Charge): The current state of charge of the battery energy storage system. Its value directly constrains the range of energy the agent can dispatch and is a core state for ensuring the safe operation of the storage unit.
- ◉
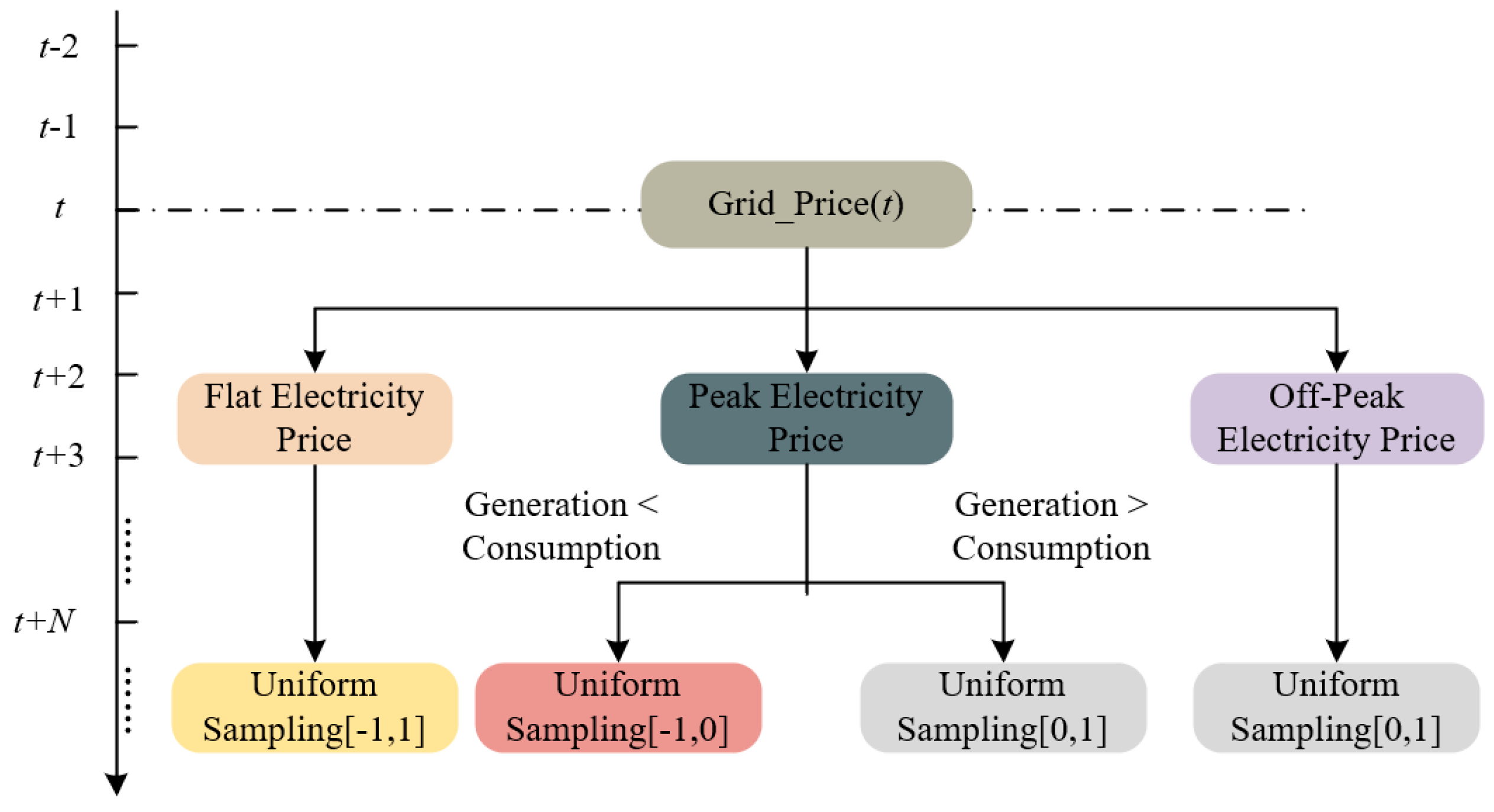
- Grid_Price(t) (Electricity Price Signal): The current ToU electricity price signal at the grid connection point. This provides the direct external economic incentive for the agent to perform economic dispatch, enabling arbitrage or cost minimization.
- ◉
- Pgrid_his(t-k:t) (Historical Grid Power): A historical sequence of the power at the grid connection point over recent timesteps (t-k to t). This allows the agent to perceive the current power interaction trend, which is crucial for smoothing power fluctuations, avoiding abrupt power changes, and is a key state reflecting “flexibility” and grid-friendliness.
- (2)
- Action Space (A)
- (3)
- State Transition Probability (P)
- ◉
- The stochasticity of PV output (Ppv fluctuations) caused by short-term cloud movement and instantaneous changes in irradiance.
- ◉
- The stochasticity of load demand (Pload fluctuations) arising from the unpredictability of human activity within the building and the random switching of equipment.
- (4)
- Reward Function (R)
ϕ′ ← τϕ + (1 − τ)ϕ′
4. Case Study and Simulation Analysis
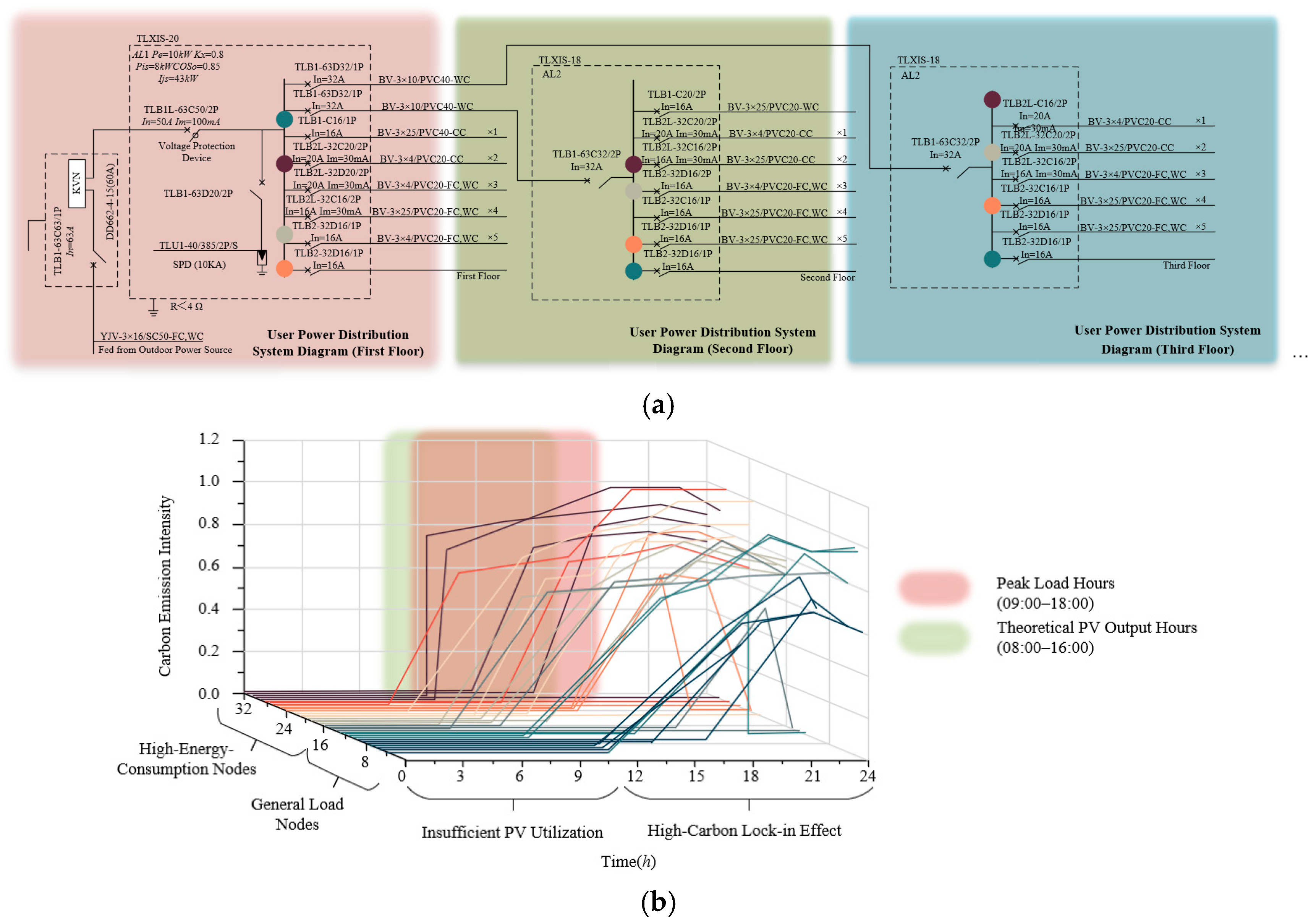
4.1. Simulation Experimental Environment and Baseline Characteristic Analysis
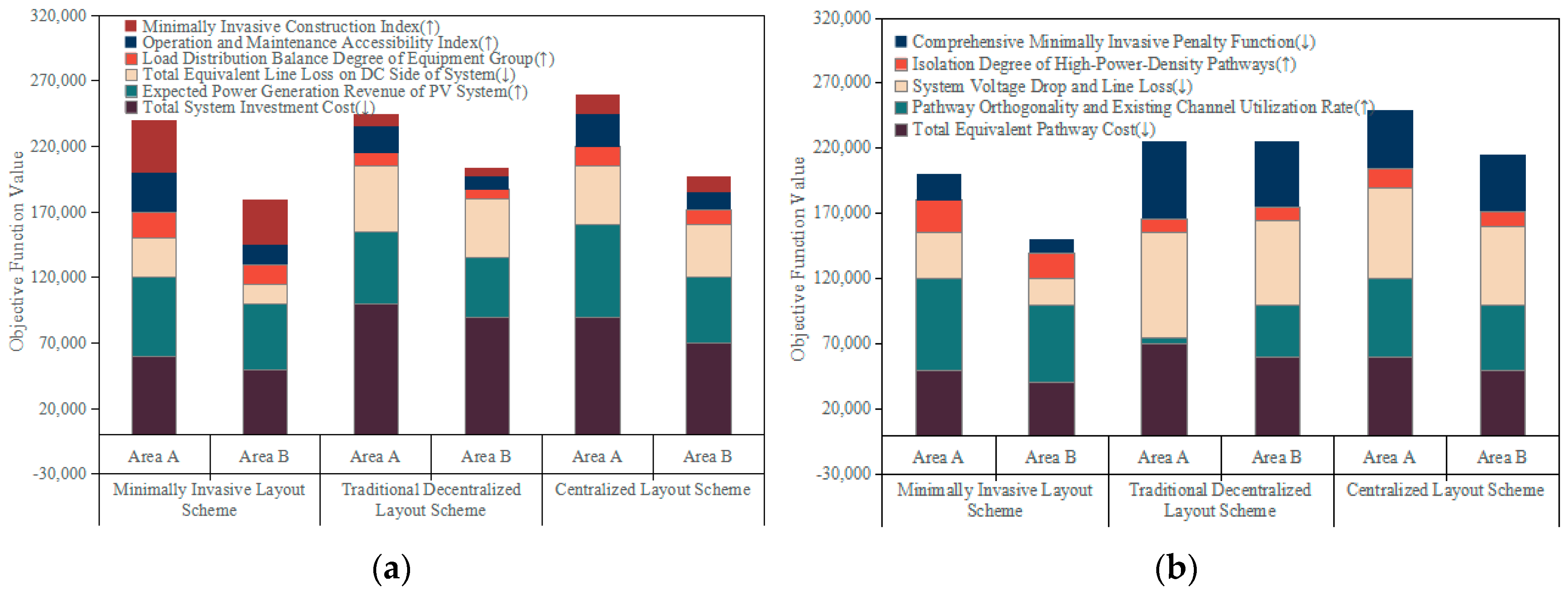
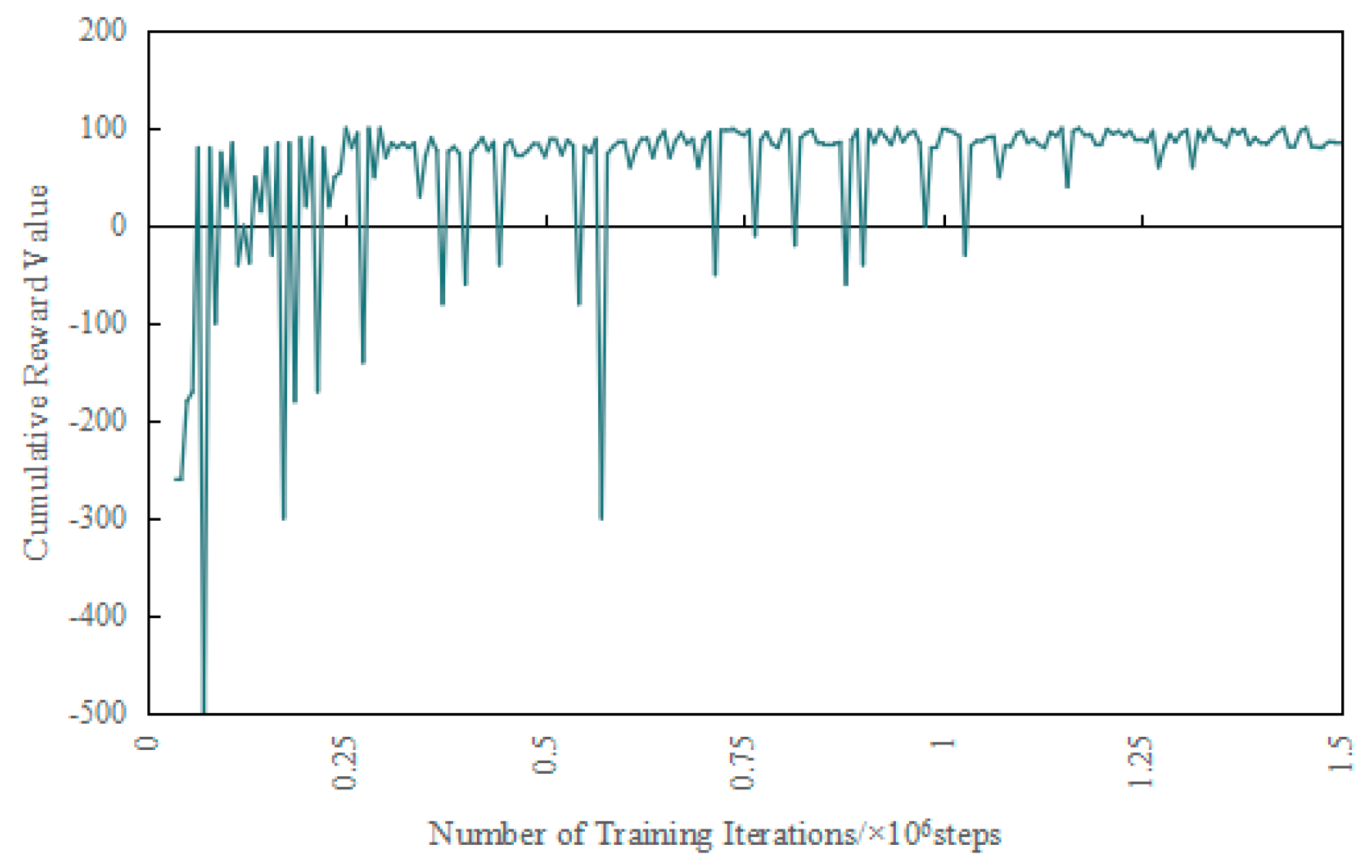
4.2. PEDF Systems Design Optimization and Algorithm Verification
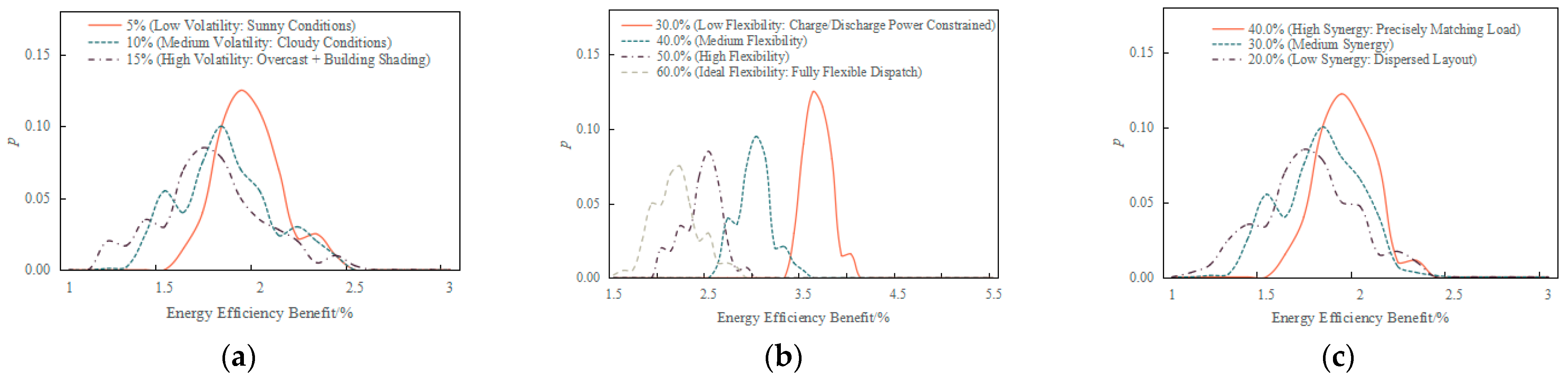
4.3. Analysis of the Impact Mechanism of Key Characteristics on Energy Efficiency Benefits
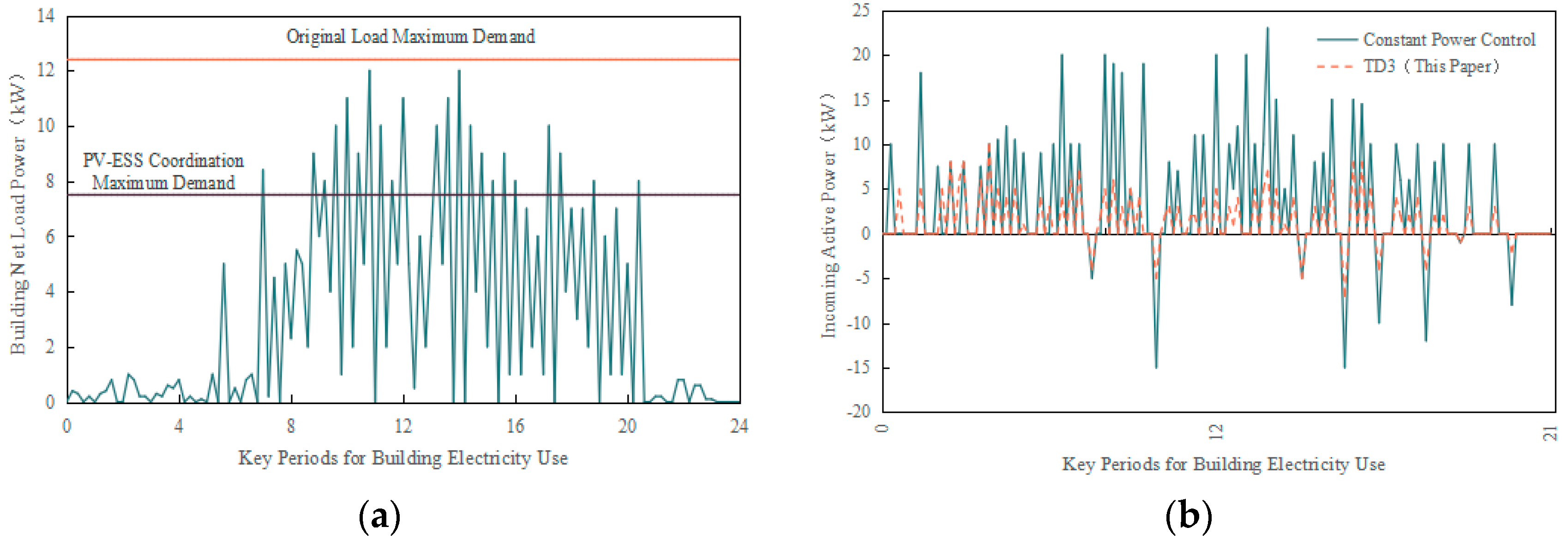
4.4. Comprehensive Performance Verification and Benefit Evaluation of the PEDF Systems
5. Discussion
6. Conclusions
- ◉
- Sensing and State Estimation Requirements: The proposed flexible energy management strategy relies heavily on accurate, high-frequency perception of the global system state. In practice, this necessitates the deployment of a dense and highly reliable sensor network and data acquisition system. The initial investment, communication latency, and maintenance costs present practical barriers to achieving plug-and-play applicability.
- ◉
- Computational Load for Real-Time Control: Although the trained DRL agent requires minimal inference time during execution—meeting real-time control demands—its offline training process is computationally intensive and must be performed on high-performance servers. Future research should explore lightweight model design, transfer learning, and edge computing deployment to reduce reliance on centralized computational resources.
- ◉
- Integration Challenges with Conventional Electrical Systems: Existing buildings often feature traditional electrical distribution systems not designed for plug-and-play DC microgrid integration. Therefore, achieving safe and seamless switching between old and new systems, re-coordinating relay protection settings, and ensuring protocol and data interoperability with existing building automation or energy management platforms constitute unavoidable complexities in practice, requiring interdisciplinary collaborative design.
- ◉
- Cost of Generalizability Across Building Types: Although the framework is generalizable, applying it to new contexts such as residential or commercial buildings requires additional data collection and model fine-tuning tailored to their specific load profiles and operational patterns. This process still demands significant manual intervention and domain expertise. Developing an automated and adaptive cross-domain deployment framework is essential for large-scale implementation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shi, Y.; Chen, P.F. Energy retrofitting of hospital buildings considering climate change: An approach integrating automated machine learning with NSGA-III for multi-objective optimization. Energy Build. 2024, 319, 114571. [Google Scholar] [CrossRef]
- Liu, X.; Liu, X.; Jiang, Y.; Zhang, T.; Hao, B. Photovoltaics and Energy Storage Integrated Flexible Direct Current Distribution Systems of Buildings: Definition, Technology Review, and Application. CSEE J. Power Energy Syst. 2023, 9, 829–845. [Google Scholar] [CrossRef]
- Li, T.; Ye, P.; Wang, H.; Liu, W.; Huang, X.; Ke, J. Optimization and Evaluation of the PEDF System Configuration Based on Planning and Operating Dual-Layer Model. Appl. Sci. 2025, 15, 7776. [Google Scholar] [CrossRef]
- Amoruso, F.M.; Schuetze, T. Hybrid timber-based systems for low-carbon, deep renovation of aged buildings: Three exemplary buildings in the Republic of Korea. Build. Environ. 2022, 214, 108889. [Google Scholar] [CrossRef]
- Lin, Y.; Cui, C.; Liu, X.; Mao, G.; Xiong, J.; Zhang, Y. Green Renovation and Retrofitting of Old Buildings: A Case Study of a Concrete Brick Apartment in Chengdu. Sustainability 2023, 15, 12409. [Google Scholar] [CrossRef]
- Kertsmik, K.A.; Arumägi, E.; Hallik, J.; Kalamees, T. Low carbon emission renovation of historical residential buildings. Energy Rep. 2024, 11, 3836–3847. [Google Scholar] [CrossRef]
- Zhang, A.; Wang, F.; Li, H.; Pang, B.; Nie, K.; Ma, X.; Zhuang, C.; Pan, Z.; Jiang, Y.; Yang, J. A framework of carbon-negative rural housing renovation with novel heating methods and digital twin-based carbon emission monitoring. Build. Environ. 2025, 282, 113158. [Google Scholar] [CrossRef]
- Ahmed, A.; Mateo-Garcia, M.; Arewa, A.; Caratella, K. Integrated Performance Optimization of Higher Education Buildings Using Low-Energy Renovation Process and User Engagement. Energies 2021, 14, 1475. [Google Scholar] [CrossRef]
- Kertsmik, K.A.; Kuusk, K.; Lylykangas, K.; Kalamees, T. Evaluation of renovation strategies: Cost-optimal, CO2e optimal, or total energy optimal? Energy Build. 2023, 287, 112995. [Google Scholar] [CrossRef]
- Liu, Y.; Xue, S.; Guo, X.; Zhang, B.; Sun, X.; Zhang, Q.; Wang, Y.; Dong, Y. Towards the goal of zero-carbon building retrofitting with variant application degrees of low-carbon technologies: Mitigation potential and cost-benefit analysis for a kindergarten in Beijing. J. Clean. Prod. 2023, 393, 136316. [Google Scholar] [CrossRef]
- Chiradeja, P.; Thongsuk, S.; Ananwattanaporn, S.; Ngaopitakkul, A. Renovation of an Academic Building’s Envelope, Lighting, and Air Conditioning System According to Thailand Building Energy Code for Energy Consumption Reduction. Sustainability 2023, 15, 15298. [Google Scholar] [CrossRef]
- Prieto, A.; Armijos-Moya, T.; Konstantinou, T. Renovation process challenges and barriers: Addressing the communication and coordination bottlenecks in the zero-energy building renovation workflow in European residential buildings. Archit. Sci. Rev. 2024, 67, 205–217. [Google Scholar] [CrossRef]
- Fahlstedt, O.; Ramesh, R.; Hamdy, M.; Temeljotov-Salaj, A.; Rasmussen, F.N.; Bohne, R.A. Building renovation plan- introducing energy and cost into the managerial perspectives: A case study. Energy Build. 2024, 310, 114080. [Google Scholar] [CrossRef]
- Mpouzianas, N.; Koltsios, S.; Pastaltzidis, I.; Katsaros, N.; Giannopoulos, G.; Klonis, P.; Chatzipanagiotidou, P.; Ioannidis, D.; Tzovaras, D. Building renovation Roadmapping: An automated methodology framework for energy efficiency improvement and sustainable renovation planning. Int. J. Sustain. Energy 2024, 43, 2344508. [Google Scholar] [CrossRef]
- Van de Moortel, E.; Allacker, K.; De Troyer, F.; Schoofs, E.; Stijnen, L. Dynamic Versus Static Life Cycle Assessment of Energy Renovation for Residential Buildings. Sustainability 2022, 14, 6838. [Google Scholar] [CrossRef]
- Eksi, M.; Akarsu, R.T.; Ozcan, M. Net-zero energy building transformation: Techno-economic and environmental evaluation in the Mediterranean Region. Environ. Dev. Sustain. 2025. [Google Scholar] [CrossRef]
- Chen, J.L.; Stouffs, R. SE-VGAE: Unsupervised disentangled representation learning for interpretable architectural layout design graph generation. Build. Environ. 2025, 284, 113450. [Google Scholar] [CrossRef]
- Sharma, S.; Verma, A.; Xu, Y.; Panigrahi, B.K. Robustly Coordinated Bi-Level Energy Management of a Multi-Energy Building Under Multiple Uncertainties. IEEE Trans. Sustain. Energy 2021, 12, 3–13. [Google Scholar] [CrossRef]
- Chen, J.; Jing, Y.; Yang, X.; Hao, B. Research on the design optimization of energy storage system in Photovoltaic Energy storage Direct current and Flexibility (PEDF) system in buildings. In Building Simulation; Tsinghua University Press: Beijing, China, 2025. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, T.; Liu, X.; Huang, Z.; Li, Q. Multi-Port Collaborative Control Strategy With Smooth Operational Transitions for Photovoltaics, Energy Storage, Direct Current, and Flexibility System. IEEE Trans. Power Electron. 2025, 40, 11715–11724. [Google Scholar] [CrossRef]
- Passoni, C.; Caruso, M.; Marini, A.; Pinho, R.; Landolfo, R. The role of life cycle structural engineering in the transition towards a sustainable building renovation: Available tools and research needs. Buildings 2022, 12, 1107. [Google Scholar] [CrossRef]
- Hernandez-Cruz, P.; Flores-Abascal, I.; Hidalgo-Betanzos, J.M.; Almeida, M.; Erkoreka-Gonzalez, A. Environmental and energy analysis of the renovation of social housing buildings under various climate change scenarios and user profiles. J. Build. Eng. 2024, 98, 111164. [Google Scholar] [CrossRef]
- Zhang, X.; Gu, Y.; Pei, W.; Jiang, Y. AC transmission network expansion planning considering cascading failures and uncertainty of wind and photovoltaic energy. Electr. Power Syst. Res. 2025, 248, 111633. [Google Scholar] [CrossRef]
- Sahbaz, K.; Basaraner, M. A zonal displacement approach via grid point weighting in building generalization. ISPRS Int. J. Geo-Inf. 2021, 10, 105. [Google Scholar] [CrossRef]
- Ospina, A.M.; Chen, Y.; Bernstein, A.; Dall’Anese, E. Learning-based demand response in grid-interactive buildings via Gaussian Processes. Electr. Power Syst. Res. 2022, 211, 108406. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, S.; Zhao, Q.; Zhang, W. Modelling and calculation method of minimum safety distance for photovoltaic fire extinguishing under energized conditions. Sol. Energy 2025, 288, 113300. [Google Scholar] [CrossRef]
- Möller, M.C.; Krauter, S. Investigation of different load characteristics, component dimensioning, and system scaling for the optimized design of a hybrid hydrogen-based PV energy system. Hydrogen 2023, 4, 408–433. [Google Scholar] [CrossRef]
- Yang, R.; Zang, Y.; Yang, J.; Wakefield, R.; Nguyen, K.; Shi, L. Fire safety requirements for building integrated photovoltaics (BIPV): A cross-country comparison. Renew. Sustain. Energy Rev. 2023, 173, 113112. [Google Scholar] [CrossRef]
- Wang, X.; Wang, P.; Huang, R.; Zhu, X.; Arroyo, J.; Li, N. Safe deep reinforcement learning for building energy management. Appl. Energy 2025, 377, 124328. [Google Scholar] [CrossRef]
- Zhang, X.; Guo, C.; Zhou, Y.; Xu, X.; Liao, J.; Zhou, N.; Wang, Q. Unbalanced voltage suppression of bipolar DC microgrids with integration of DC zero-carbon buildings. J. Mod. Power Syst. Clean Energy 2024, 12, 1942–1956. [Google Scholar] [CrossRef]
- Futakuchi, M.; Takayama, S.; Ishigame, A. Scheduled operation of wind farm with battery system using deep reinforcement learning. IEEJ Trans. Electr. Electron. Eng. 2021, 16, 696–703. [Google Scholar] [CrossRef]
- Baccari, S.; Mostacciuolo, E.; Tipaldi, M.; Mariani, V. A deep reinforcement learning approach for energy management in low earth orbit satellite electrical power systems. Electronics 2025, 14, 3110. [Google Scholar] [CrossRef]
- Fan, P.; Ke, S.; Yang, J.; Li, R.; Li, Y.; Yang, S.; Liang, J.; Fan, H.; Li, T. A load frequency coordinated control strategy for multimicrogrids with V2G based on improved MA-DDPG. Int. J. Electr. Power Energy Syst. 2023, 146, 108765. [Google Scholar] [CrossRef]
- Wang, D.; Hu, M.Q. Deep deterministic policy gradient with compatible critic network. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 4332–4344. [Google Scholar] [CrossRef]
- Chakraborty, T.; Kopp, C.; Toosi, A.N. Optimizing renewable energy utilization in cloud data centers through dynamic overbooking: An MDP-based approach. IEEE Trans. Cloud Comput. 2025, 13, 1–17. [Google Scholar] [CrossRef]
- Aatabe, M.; Latif, R.; Mosaad, M.I.; Hussien, S.A. Stochastic energy management of DC photovoltaic microgrids using Markov decision process. Results Eng. 2025, 27, 105835. [Google Scholar] [CrossRef]
- Kim, K.H.; Kim, C. Post-processing of iterative estimation and cancellation scheme for clipping noise in OFDM systems. IEICE Trans. Commun. 2023, E106-B, 352–358. [Google Scholar]
- Frömming, A.; Häring, L.; Czylwik, A. Spectral properties of clipping noise. Mathematics 2021, 9, 2592. [Google Scholar] [CrossRef]
- Xu, X.; Ling, G.; Wang, F.; Cheng, L.; Ge, M.F. Grey dispersion entropy based on truncated Gaussian whitenization function: A novel time series complexity measure. Nonlinear Dyn. 2025, 113, 8305–8327. [Google Scholar] [CrossRef]

| Category | Component | Specification |
|---|---|---|
| Hardware Environment | Processor (CPU) | AMD Ryzen 9 5900X |
| Graphics Card (GPU) | NVIDIA GeForce RTX 3080Ti 12G | |
| Memory (RAM) | 32GB DDR4-3600 | |
| Storage | 1TB NVMe SSD | |
| Software Environment | Operating System | Ubuntu 20.04 LTS |
| Traditional Optimization Platform | Matlab R2023b | |
| Building Energy Simulation Tool | EnergyPlus v9.5 | |
| Distribution System Simulator | OpenDSS v9.0 | |
| Reinforcement Learning Framework | TensorFlow 2.6.2 + Custom Gym Environment (Building-PV-ESS) | |
| Programming Language | Python 3.9.7 | |
| Datasets |
|
| Algorithm | Hypervolume (HV) ↑ (×103) | Inverted Generational Distance (IGD) ↓ (×10−2) | Spacing (SP) ↓ (×10−2) | Spread ↓ | Average Computation Time (s) |
|---|---|---|---|---|---|
| NSGA-II | 7.15 ± 0.24 | 4.86 ± 0.31 | 10.52 ± 1.15 | 0.783 ± 0.045 | 152 |
| MOEA/D | 7.38 ± 0.19 | 4.25 ± 0.28 | 9.14 ± 0.98 | 0.721 ± 0.038 | 175 |
| MOSPO | 7.29 ± 0.26 | 4.63 ± 0.35 | 9.87 ± 1.07 | 0.754 ± 0.042 | 138 |
| SPEA2 | 7.42 ± 0.17 | 4.12 ± 0.26 | 8.95 ± 0.92 | 0.698 ± 0.036 | 189 |
| I-ABC-GA (Proposed) | 7.84 ± 0.11 | 3.58 ± 0.19 | 7.23 ± 0.76 | 0.705 ± 0.032 | 163 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Iterations | 1.5 × 106 steps | Discount Factor | 0.93 |
| Replay Buffer Size | 1 × 106 transitions | Exploration Noise Variance | 0.5 |
| Network Learning Rate | 0.0003 (Actor) 0.001 (Critic) | Target Policy Smoothing Noise Variance | 1 |
| Batch Size | 128 | Policy Update Delay | Every 4 steps |
| Gradient Steps per Iteration | 2 updates per step | Soft Update Rate | 0.005 |
| Noise Type | Ornstein–Uhlenbeck | Reward Function Weights | 1. Economic (0.4) 2. Lifespan (0.2) 3. Grid-Friendliness (0.2) 4. Operational-Safety (0.2) |
| Variable Condition | Scenario Description | Daily Operational Cost (CNY) | Payback Period (years) | Peak-to-Valley Reduction Rate (%) |
|---|---|---|---|---|
| Base Scenario | Office Bldg + TOU | 315.7 | 5.8 | 29.5 |
| Electricity Price Change | Office Bldg + Real-Time Pricing (RTP) | 267.9 (−15.2%) | 5.1 | 31.8 |
| Load Profile Change | Residential Bldg + TOU | 289.5 (−8.3%) | 5.9 | 28.1 |
| Commercial Bldg + TOU | 352.1 ( + 11.5%) | 6.3 | 30.6 |
| Category | Performance Indicator | Value | Unit | Note/Benchmark |
|---|---|---|---|---|
| Economic | Annual Comprehensive Electricity Cost | 102,357 | CNY | — |
| Cost Saving vs. Rule-Based Control | 18.7% | — | Benchmark: TOU-based strategy | |
| Energy Efficiency | Annual PV Self-Consumption Rate | 86.5% | — | — |
| Overall Energy Efficiency Improvement | 12.3% | — | Compared to pre-retrofit system | |
| Grid Interaction | Avg. Peak-Valley Reduction Rate | 31.2% | — | — |
| Std. Dev. of Grid Injection Power | 4.8 | kW | Lower value indicates smoother grid interaction | |
| Equipment & Environment | Avg. Daily Battery Cycles | 0.82 | cycles/day | Shallow cycling helps extend battery life |
| Annual CO2 Emission Reduction | 16.9 | tCO2 | — |
| Area | Control Strategy | Energy Saving Rate(%) | Operational Cost (¥/day) | Peak-Valley Difference Reduction Rate (%) | Carbon Reduction (kgCO2/day) | Strategy Delay (ms) | Training Time (s/epoch) |
|---|---|---|---|---|---|---|---|
| Office Area | Traditional Constant Power Control | 8.2 | 125.6 | 15.3 | 18.5 | 500 | - (No Training) |
| Time-of-Use Price Response | 12.1 | 112.4 | 22.5 | 25.3 | 300 | - | |
| DQN | 15.7 | 98.3 | 28.6 | 32.1 | 80 | 1200 | |
| DDPG | 17.2 | 92.5 | 31.4 | 35.6 | 60 | 1500 | |
| Standard TD3 | 18.5 | 89.2 | 33.7 | 37.9 | 50 | 1600 | |
| TD3 (This Paper) | 21.3 | 82.6 | 38.2 | 42.5 | 45 | 1400 | |
| Commercial Area | Traditional Constant Power Control | 6.5 | 210.3 | 12.7 | 12.8 | 550 | - |
| Time-of-Use Price Response | 10.2 | 185.6 | 18.9 | 19.4 | 350 | - | |
| DQN | 14.5 | 152.4 | 25.3 | 26.7 | 90 | 1300 | |
| DDPG | 16.3 | 145.2 | 28.1 | 29.4 | 70 | 1600 | |
| Standard TD3 | 17.8 | 138.5 | 30.5 | 31.7 | 60 | 1700 | |
| TD3 (This Paper) | 20.1 | 125.8 | 34.6 | 35.2 | 50 | 1500 | |
| Public Area | Traditional Constant Power Control | 7.3 | 98.5 | 14.2 | 16.4 | 450 | - |
| Time-of-Use Price Response | 11.5 | 82.3 | 20.1 | 22.7 | 280 | - | |
| DQN | 15.2 | 68.5 | 26.5 | 29.3 | 75 | 1100 | |
| DDPG | 16.8 | 63.2 | 29.4 | 31.8 | 65 | 1400 | |
| Standard TD3 | 18.1 | 59.7 | 32.1 | 34.2 | 55 | 1500 | |
| TD3 (This Paper) | 20.5 | 52.4 | 36.7 | 37.9 | 48 | 1350 |
| Dimension | Indicator | Scheme A: Conventional Full Retrofit | Scheme B: Hybrid Conservative System | Scheme C: Proposed Minimally Invasive PEDF Scheme | Unit |
|---|---|---|---|---|---|
| Economic | Total Initial Investment | 156.8 | 118.3 | 99.5 | ×104 CNY |
| Unit Area Retrofit Cost | 1570 | 1185 | 995 | CNY/m2 | |
| Static Payback Period | 9.8 | 7.5 | 5.8 | years | |
| Engineering | Estimated Installation Time | 28 | 20 | 14 | days |
| Main Cable Replacement | ~95% | ~60% | < 30% | — | |
| Energy Saving | Annual Energy Savings | 19.5 | 20.8 | 23.6 | MWh |
| Annual CO2 Reduction | 15.6 | 16.6 | 18.9 | tCO2 | |
| Grid Interaction | Net Electricity Purchase During Peak Hours | 35.2 | 32.5 | 28.1 | MWh |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, C.; Yang, L.; Jin, W.; Zhao, J.; Zhang, C.; Li, Y. Minimally Invasive Design and Energy Efficiency Evaluation of Photovoltaic–Energy Storage–Direct Current–Flexible Systems in Low-Carbon Retrofitting of Existing Buildings. Buildings 2025, 15, 3599. https://doi.org/10.3390/buildings15193599
Jia C, Yang L, Jin W, Zhao J, Zhang C, Li Y. Minimally Invasive Design and Energy Efficiency Evaluation of Photovoltaic–Energy Storage–Direct Current–Flexible Systems in Low-Carbon Retrofitting of Existing Buildings. Buildings. 2025; 15(19):3599. https://doi.org/10.3390/buildings15193599
Chicago/Turabian StyleJia, Chenxi, Longyue Yang, Wei Jin, Jifeng Zhao, Chuanjin Zhang, and Yutan Li. 2025. "Minimally Invasive Design and Energy Efficiency Evaluation of Photovoltaic–Energy Storage–Direct Current–Flexible Systems in Low-Carbon Retrofitting of Existing Buildings" Buildings 15, no. 19: 3599. https://doi.org/10.3390/buildings15193599
APA StyleJia, C., Yang, L., Jin, W., Zhao, J., Zhang, C., & Li, Y. (2025). Minimally Invasive Design and Energy Efficiency Evaluation of Photovoltaic–Energy Storage–Direct Current–Flexible Systems in Low-Carbon Retrofitting of Existing Buildings. Buildings, 15(19), 3599. https://doi.org/10.3390/buildings15193599






