Study on Chloride Diffusion Performance and Structural Durability Design of UHPC Under Chloride Salt Erosion
Abstract
1. Introduction
2. Experimental Program
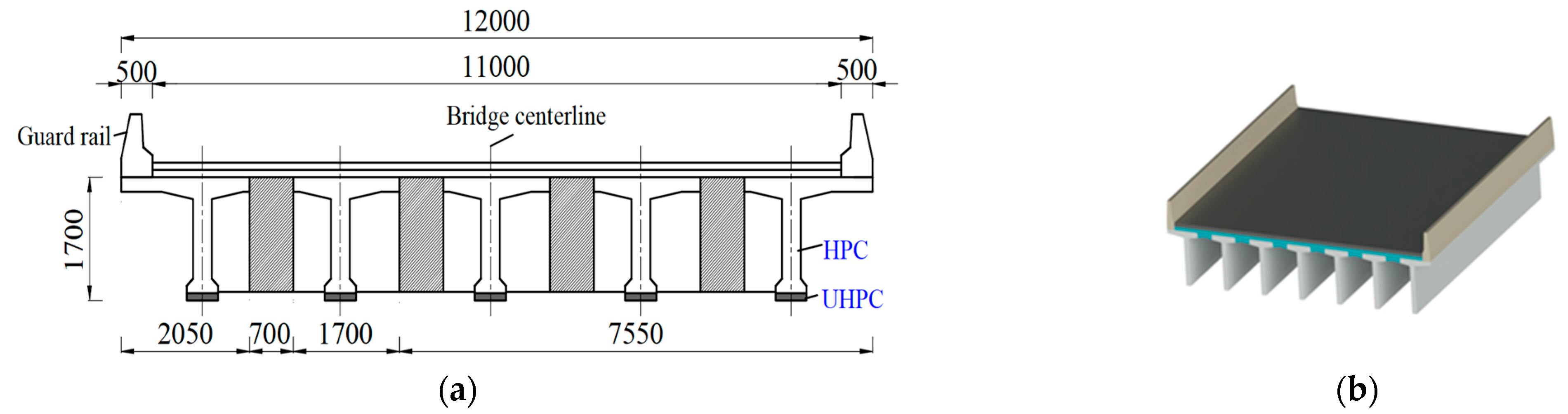
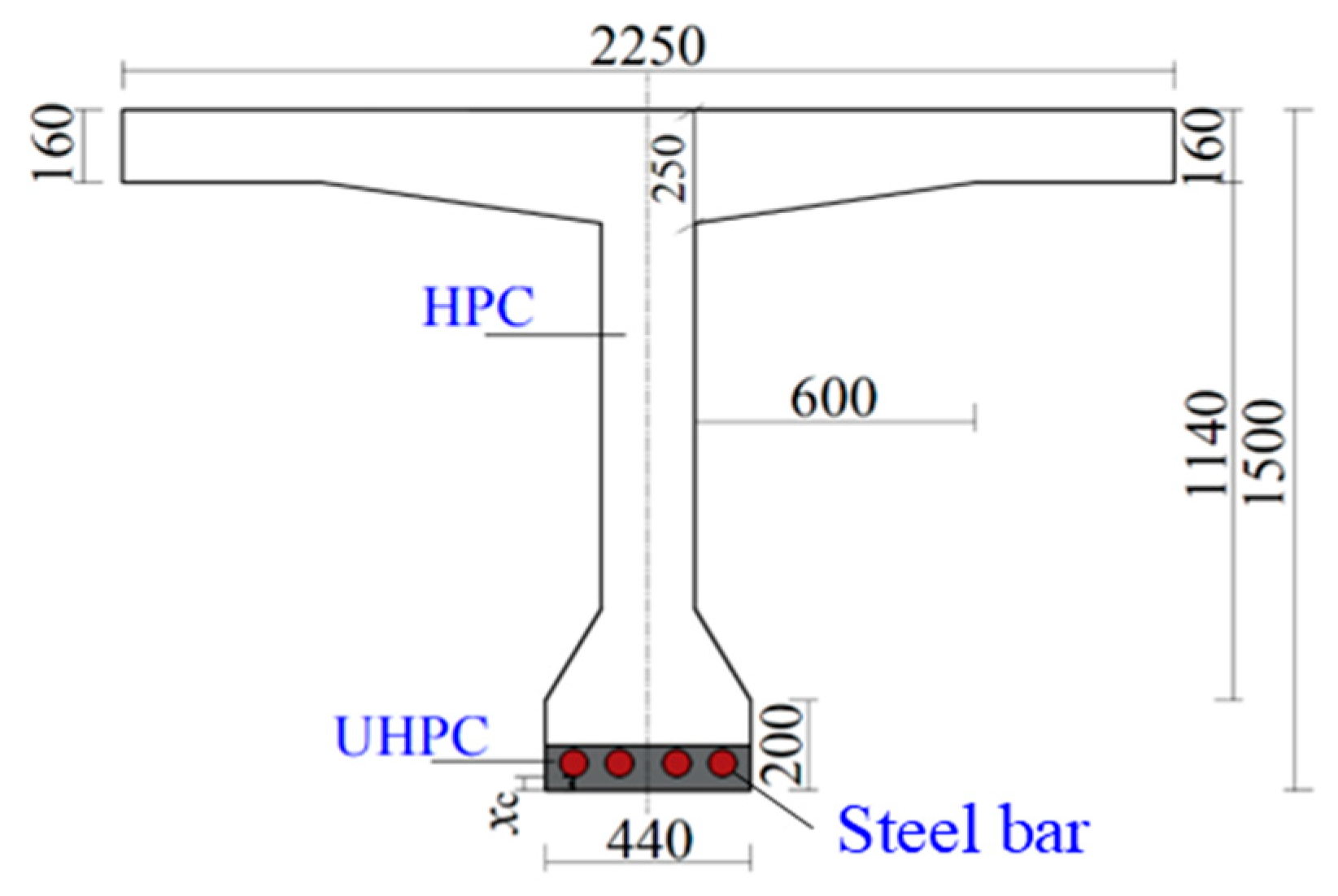
2.1. Overview of the Specimens
2.2. Test Parameters
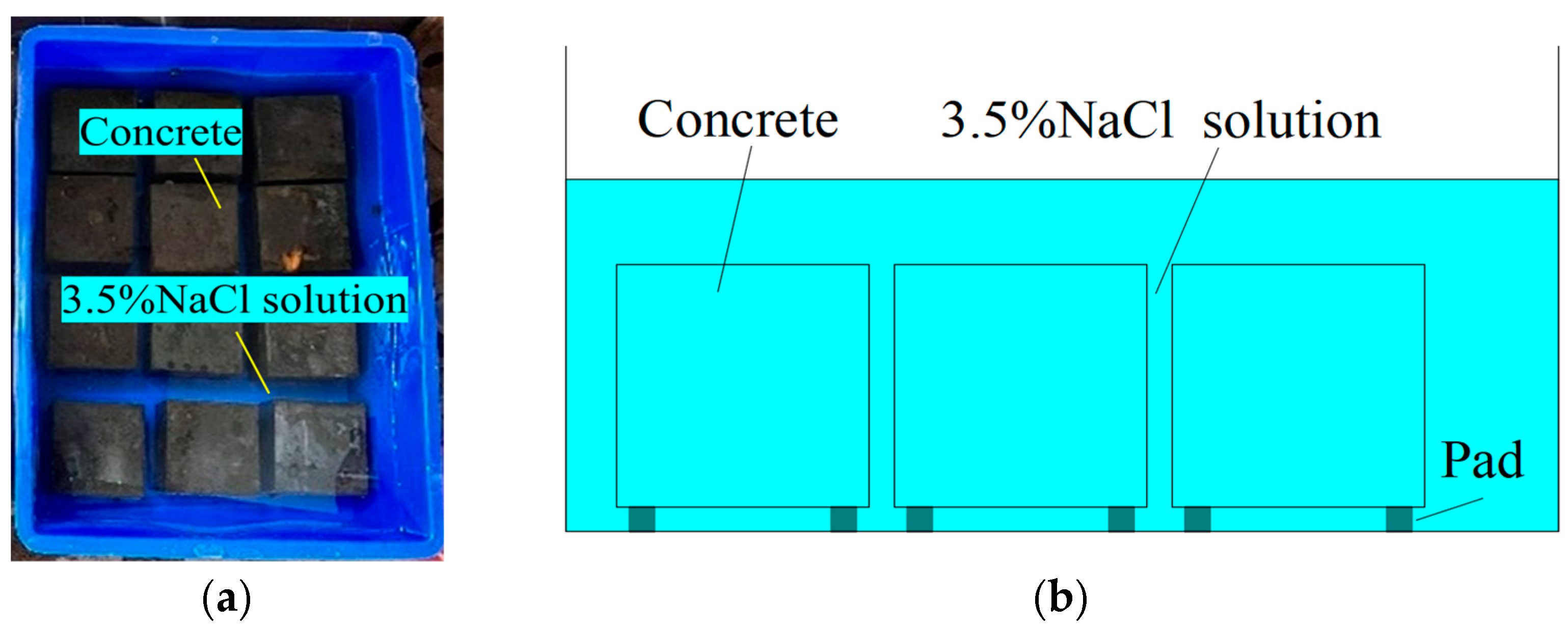
2.3. Test Procedure
- (1)
- LTI
- (2)
- RCM experiment
2.4. Chloride Content Test Method
- (1)
- RCM
- (2)
- Chloride content determination
3. Test Results
3.1. LTI Diffusion Model
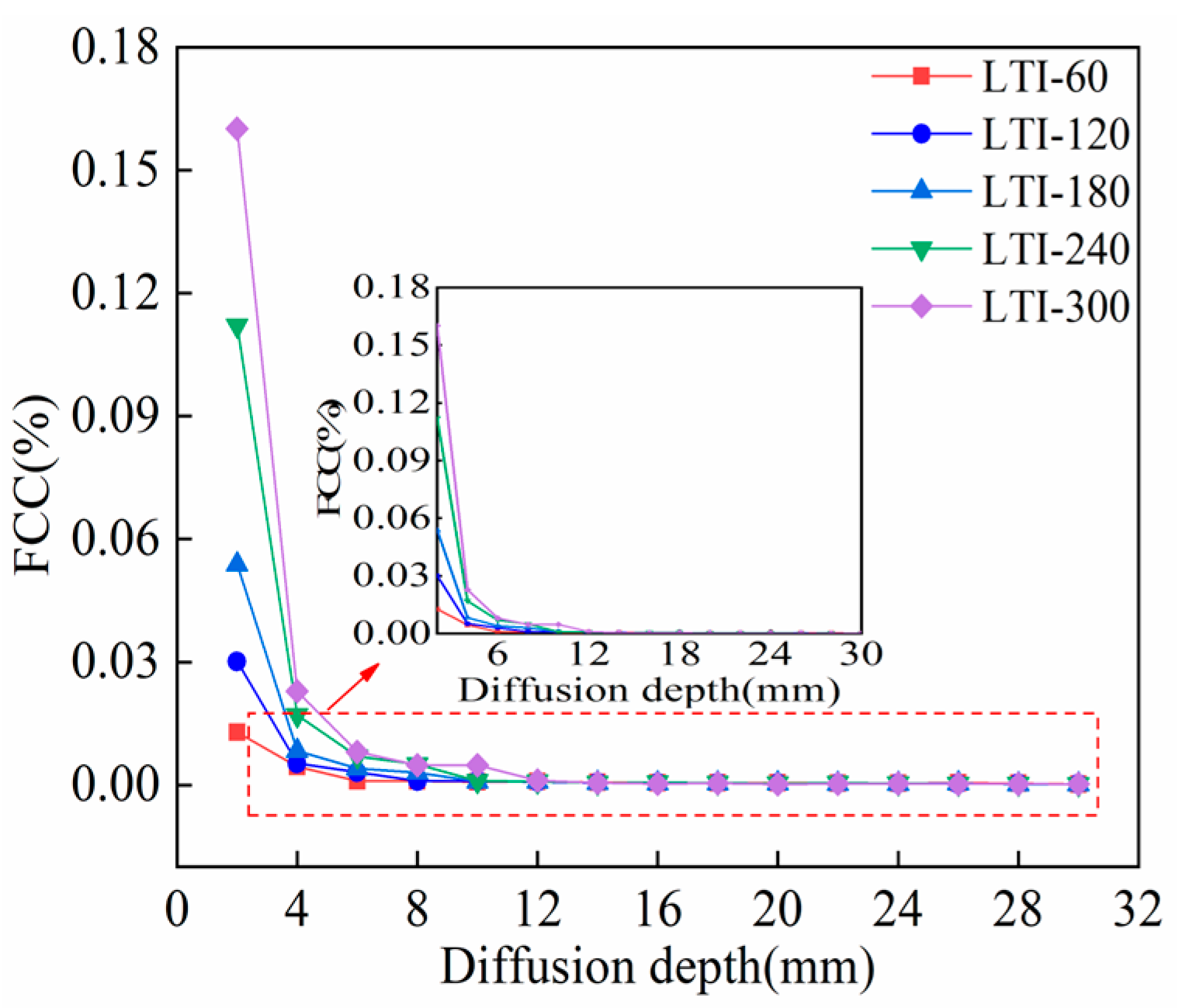
3.2. FCC
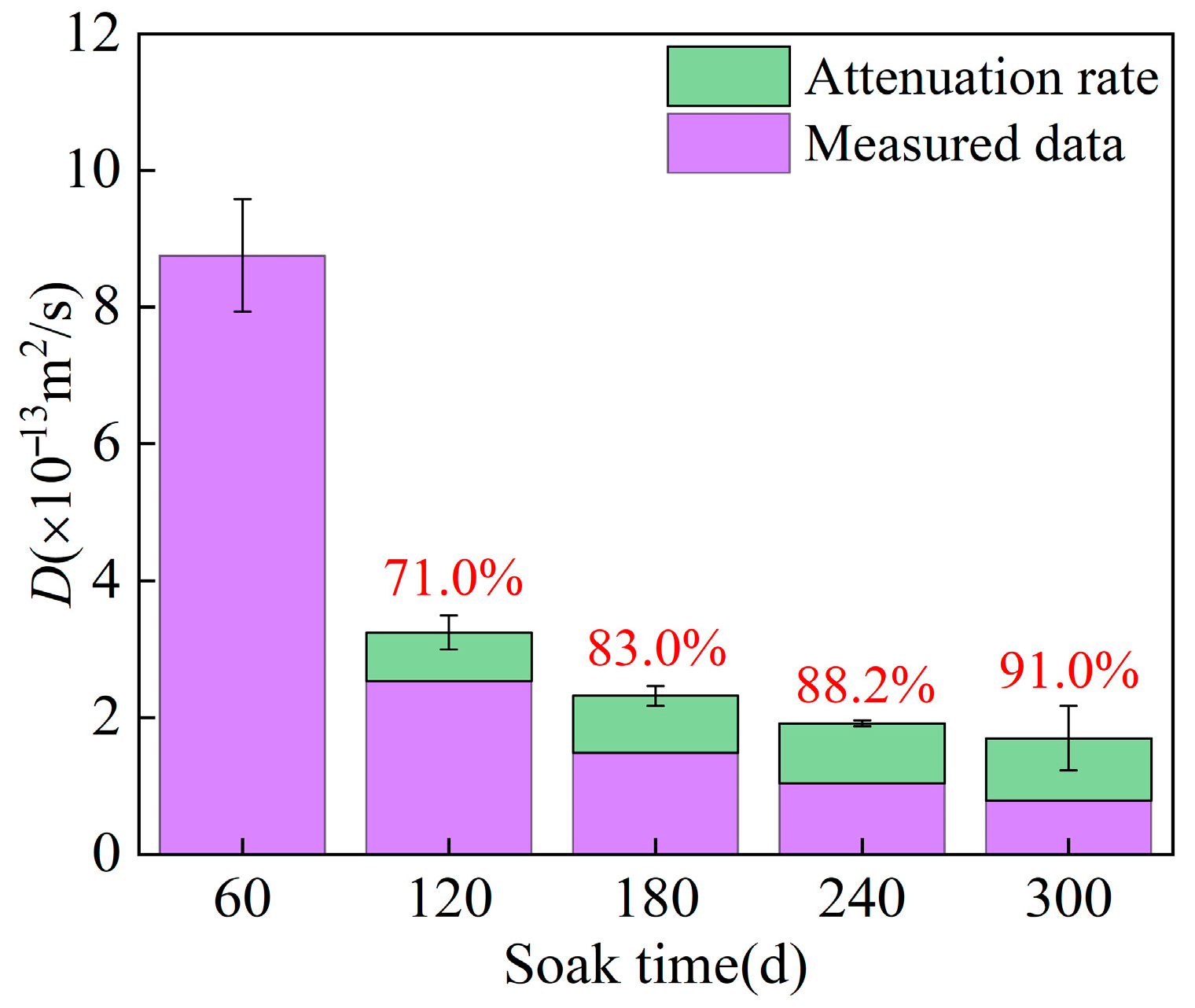
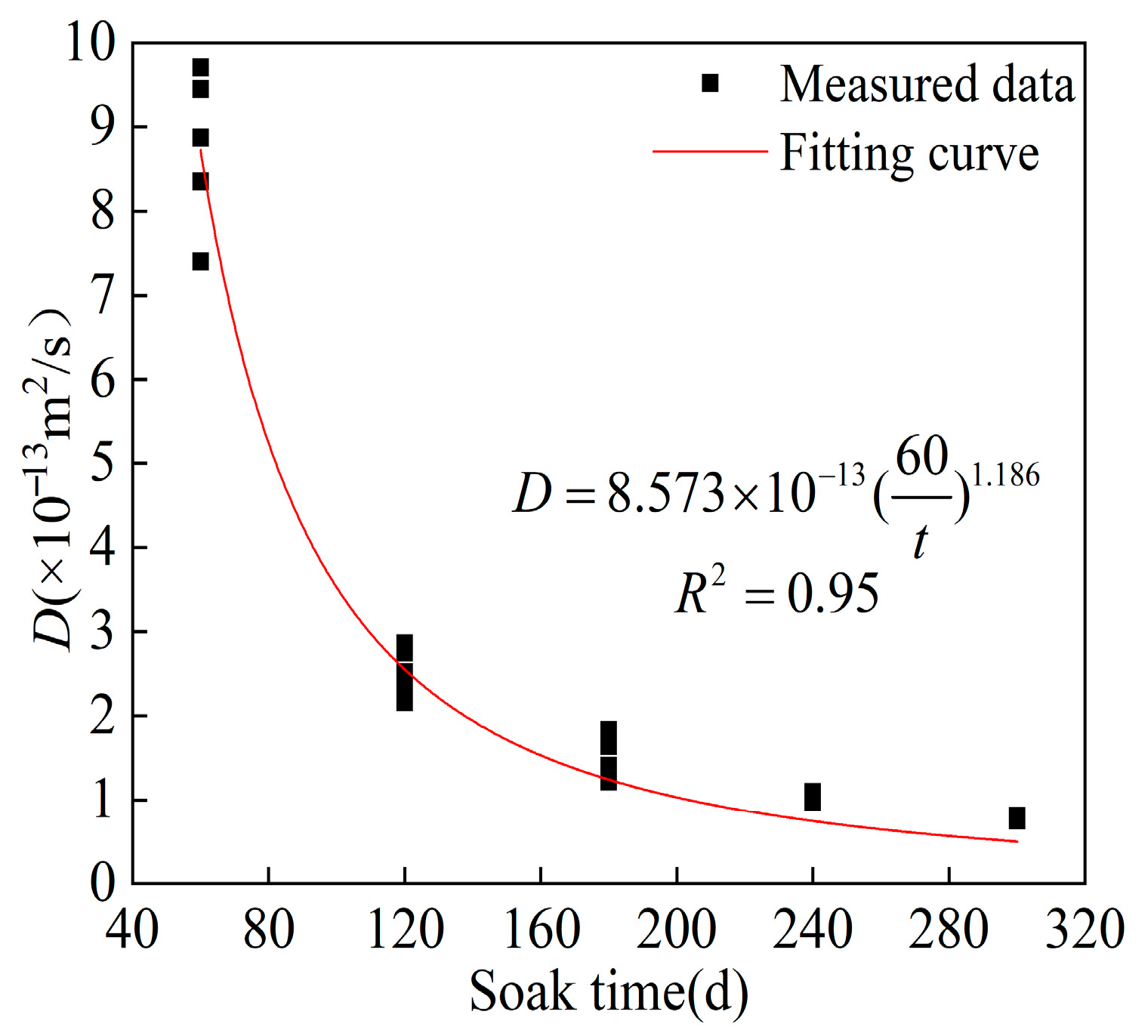
3.3. D
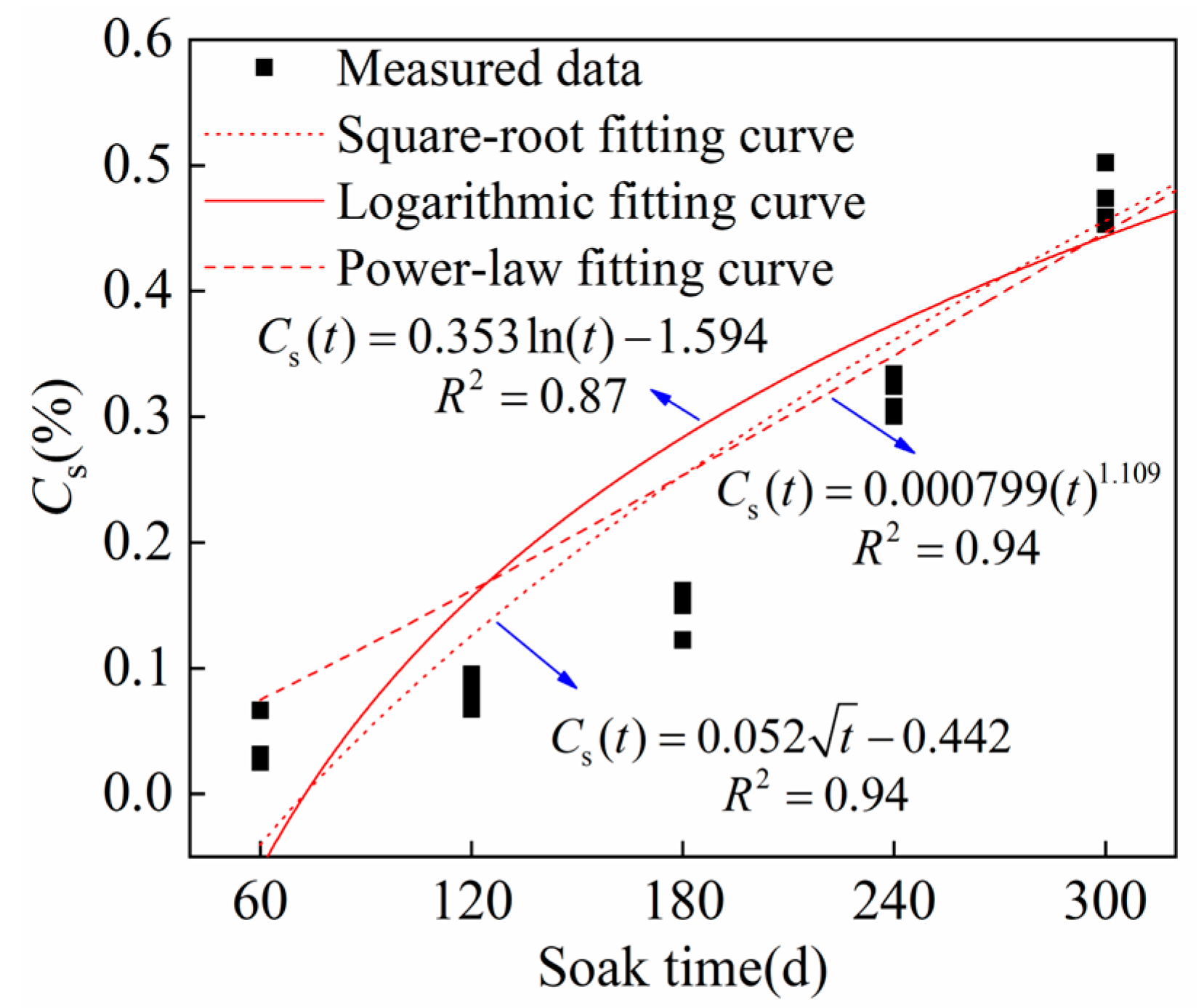
3.4. Cs
3.5. Time-Dependent Model of D
3.6. Time-Dependent Model of Cs
4. Finite-Element Simulation of Chloride Diffusion
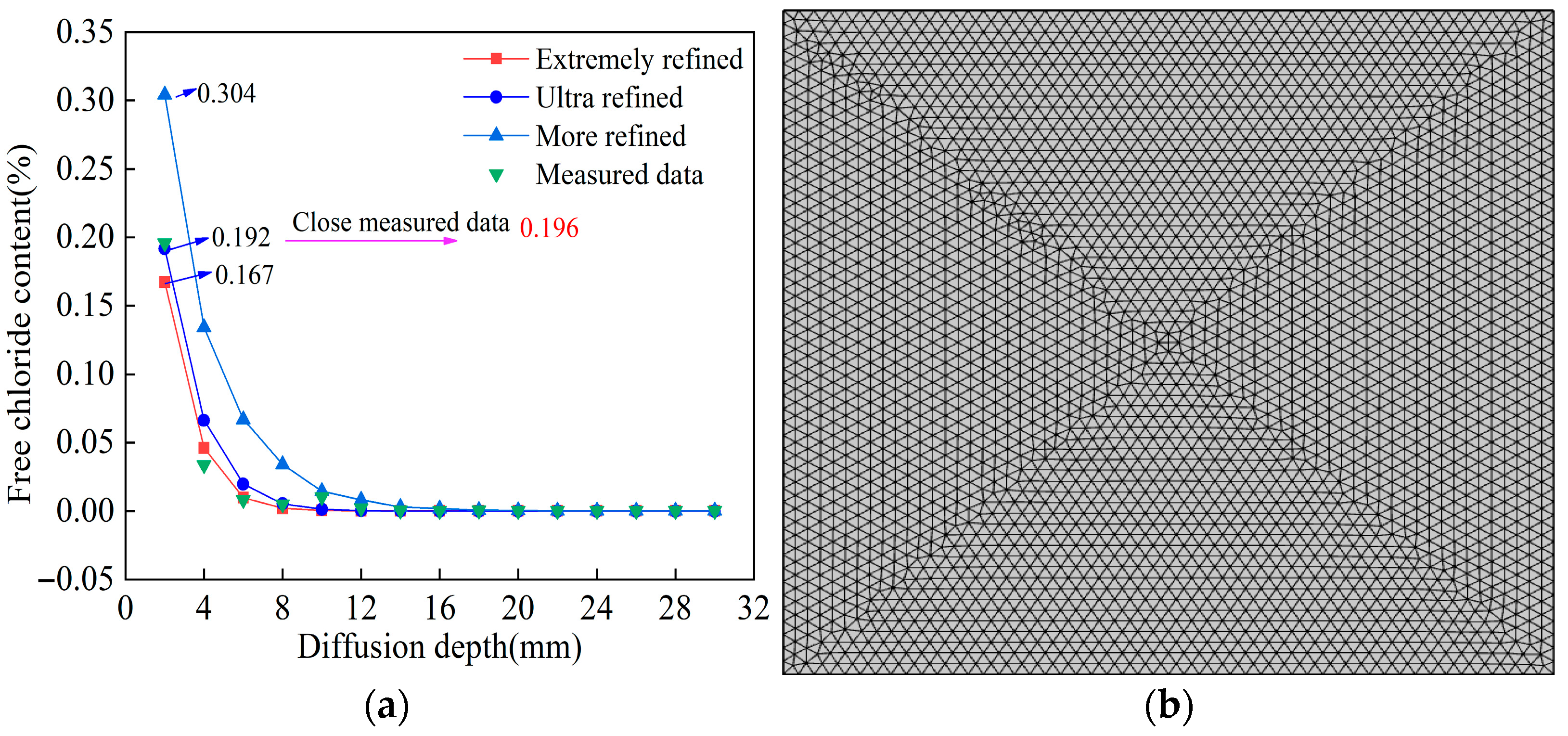
4.1. Finite-Element Model Building
- (1)
- Boundary set
- (2)
- Mesh subdivision
- (3)
- Model solution calculation
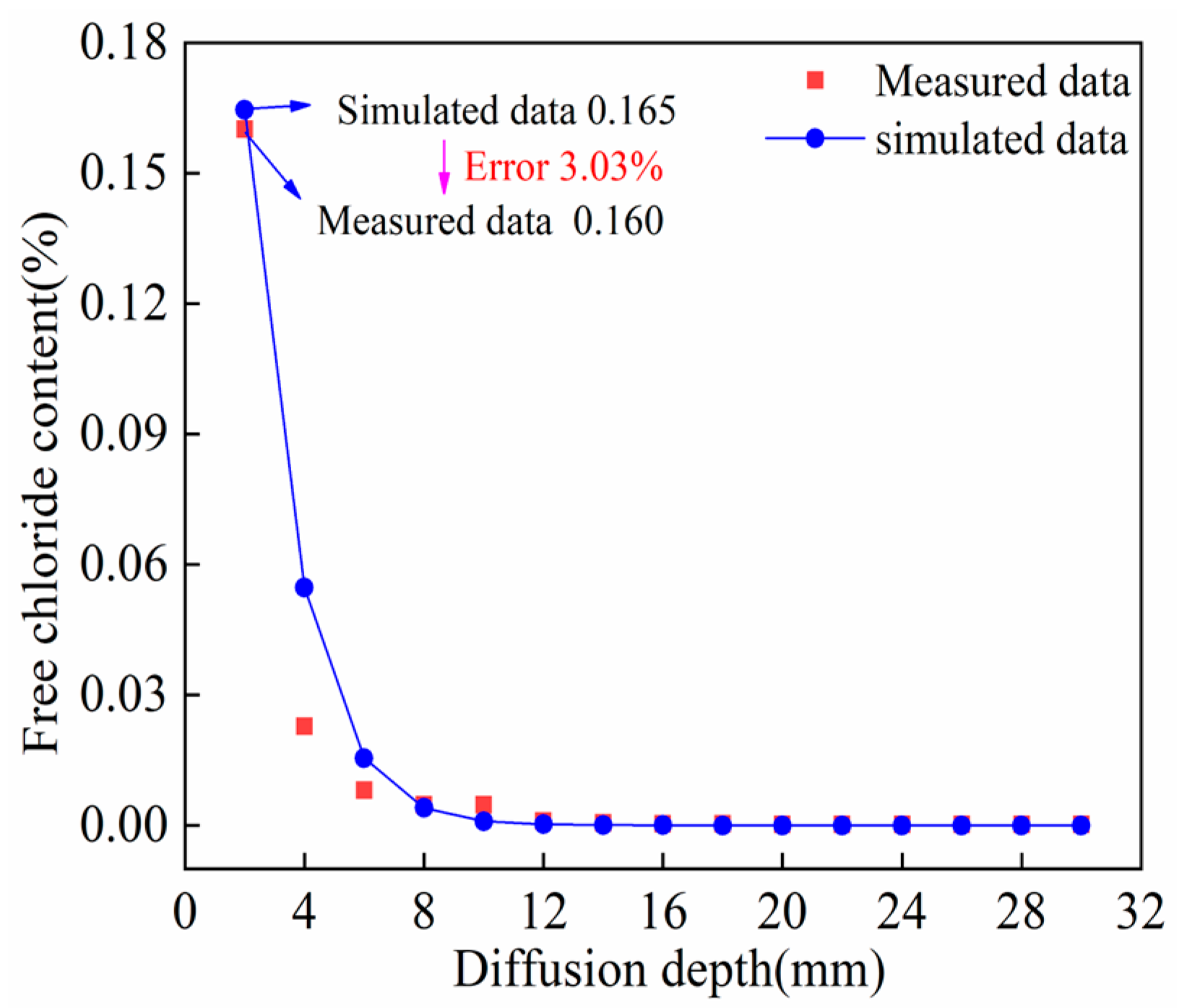
4.2. Comparative Analysis of Experimental and Numerical Results
4.3. Parametric Analysis
- (1)
- Temperature
- (2)
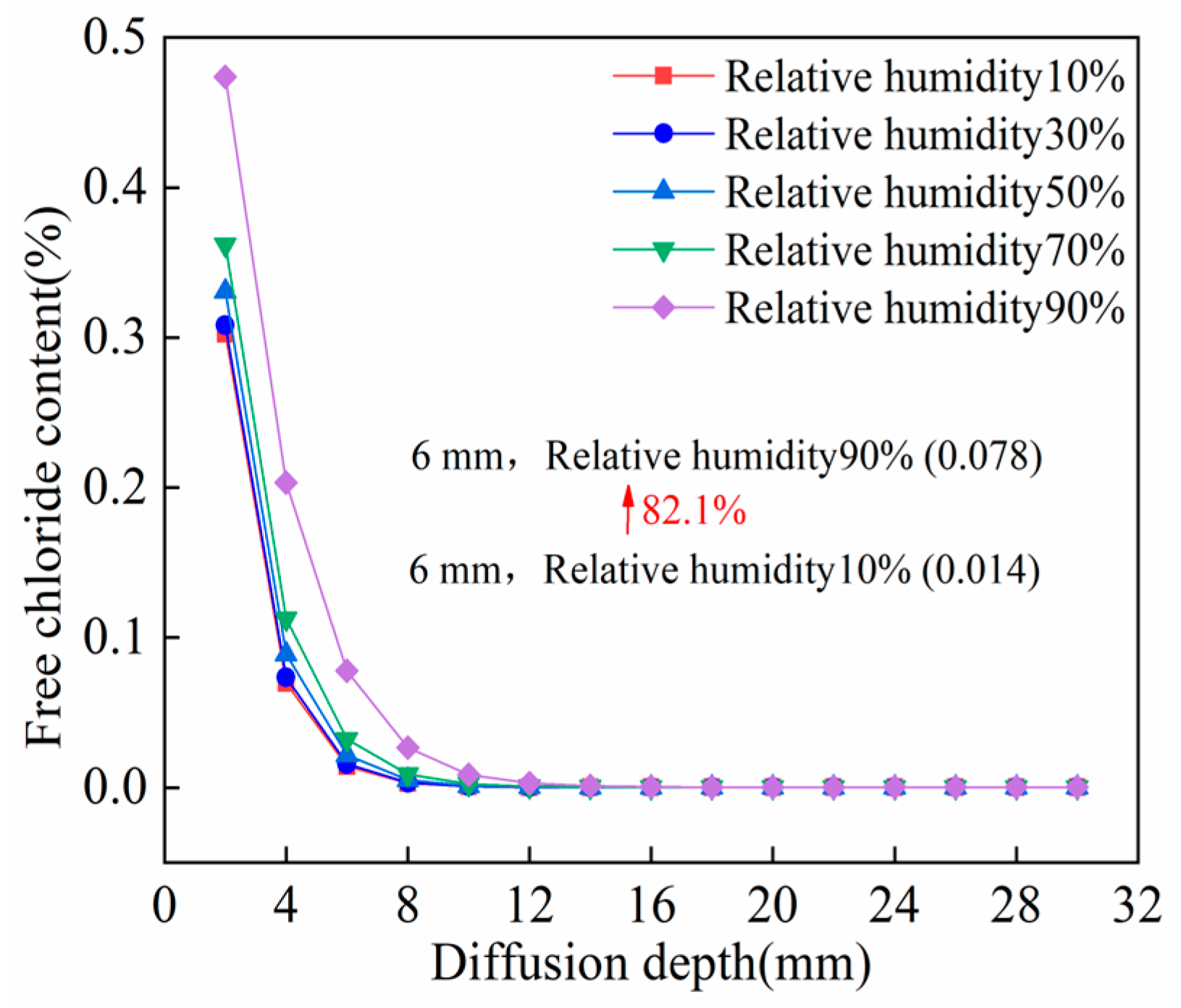
- Relative humidity
- (3)
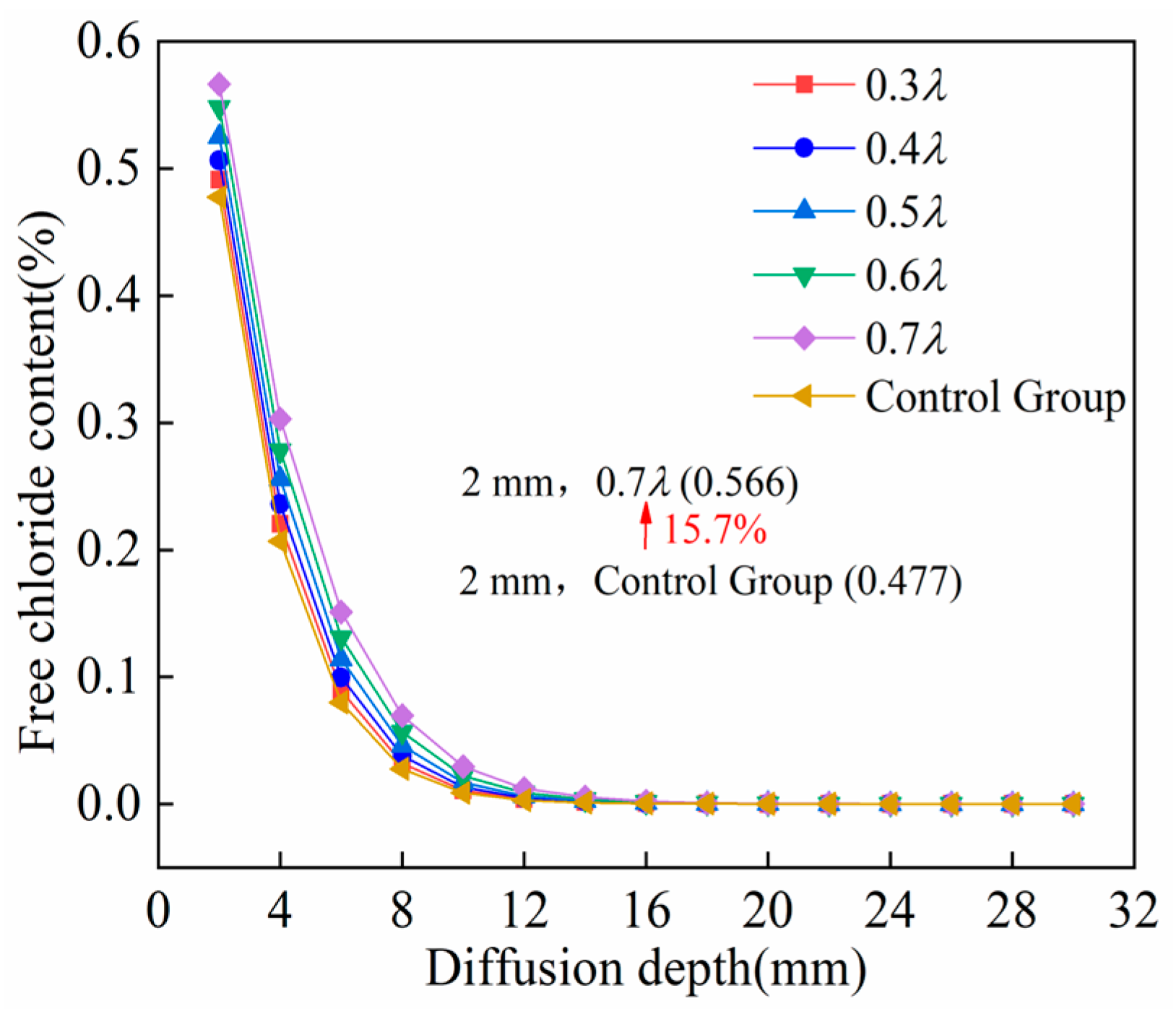
- Tensile stress ratio
5. Durability Design of UHPC-HPC Composite Beams
5.1. Durability Limit State
5.2. Example Verification of UHPC-HPC Composite Beam
- (1)
- Parameter setting
- 1)
- Partial safety factor
- 2)
- 3)
- 4)
5.3. Design of UHPC-HPC Composite Beam
6. Conclusions
- (1)
- The of UHPC with steel fibers was 37.9% lower than that of UHPC without steel fibers, indicating that steel fibers effectively mitigate chloride-induced corrosion. Under LTI, the FCC in UHPC exhibits a negative correlation with diffusion depth, while it shows a positive correlation with erosion time.
- (2)
- Under LTI, the of UHPC decreased, and increased with prolonged corrosion time, with a maximum reduction in D of 91.0% and a maximum increase in FCC of 92.5%, respectively. The time-dependent models for and follow power-law and logarithmic functions, respectively.
- (3)
- The chloride erosion resistance of UHPC decreases significantly (with marked FCC increase) under elevated surface temperatures, internal relative humidity levels exceeding 50%, and tensile stress ratios exceeding 0.4.
- (4)
- The calculated protective layer thickness for UHPC structures with a 100-year design service life is 30 mm, which falls within the 25–35 mm range specified in the UHPC structure draft technical specifications for the same service life; this result provides a reference for durability design of UHPC structures with different service life requirements.
- (5)
- Further research is required on the durability of UHPC and UHPC composite beams under multi-factor coupling conditions. This research on durability is crucial for consolidating and advancing the theoretical system of UHPC durability, specifically in chloride erosion environments.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lu, Z.; Li, J.; Xie, J.; Huang, P.; Xue, L. Durability of Flexurally Strengthened RC Beams with Prestressed CFRP Sheet under Wet–Dry Cycling in a Chloride-Containing Environment. Compos. Struct. 2021, 255, 112869. [Google Scholar] [CrossRef]
- Zhao, Y.; Yu, J.; Jin, W. Damage Analysis and Cracking Model of Reinforced Concrete Structures with Rebar Corrosion. Corros. Sci. 2011, 53, 3388–3397. [Google Scholar] [CrossRef]
- Mohammed, H.; Giuntini, F.; Sadique, M.; Shaw, A.; Bras, A. Polymer Modified Concrete Impact on the Durability of Infrastructure Exposed to Chloride Environments. Constr. Build. Mater. 2022, 317, 125771. [Google Scholar] [CrossRef]
- Wu, L.; Ju, X.; Liu, M.; Guan, L.; Ma, Y.; Li, M. Influences of Multiple Factors on the Chloride Diffusivity of the Interfacial Transition Zone in Concrete Composites. Compos. Part B Eng. 2020, 199, 108236. [Google Scholar] [CrossRef]
- Šavija, B.; Pacheco, J.; Schlangen, E. Lattice Modeling of Chloride Diffusion in Sound and Cracked Concrete. Cem. Concr. Compos. 2013, 42, 30–40. [Google Scholar] [CrossRef]
- Fares, M.; Villain, G.; Bonnet, S.; Palma Lopes, S.; Thauvin, B.; Thiery, M. Determining Chloride Content Profiles in Concrete Using an Electrical Resistivity Tomography Device. Cem. Concr. Compos. 2018, 94, 315–326. [Google Scholar] [CrossRef]
- Wang, Y.; Miao, Y.; Liu, Z.; Wang, F.; Wang, L.; Gao, S.; Jiang, J. Convection-Diffusion-Electromigration Coupled Numerical Simulation of Water and Chloride in Cement-Based Materials. Constr. Build. Mater. 2024, 426, 136149. [Google Scholar] [CrossRef]
- Noushini, A.; Castel, A.; Aldred, J.; Rawal, A. Chloride Diffusion Resistance and Chloride Binding Capacity of Fly Ash-Based Geopolymer Concrete. Cem. Concr. Compos. 2020, 105, 103290. [Google Scholar] [CrossRef]
- Ying, J.; Chen, W.; Chen, S.; Chen, B. Chloride Ion Diffusion in Recycled Concrete Containing Slag under Biaxial Compression. Constr. Build. Mater. 2024, 454, 139136. [Google Scholar] [CrossRef]
- Li, P.; Li, C.; Jia, C.; Li, D. A Comparative Study on Chloride Diffusion in Concrete Exposed to Different Marine Environment Conditions. J. Build. Eng. 2024, 94, 109845. [Google Scholar] [CrossRef]
- Yiğiter, H.; Yazıcı, H.; Aydın, S. Effects of Cement Type, Water/Cement Ratio and Cement Content on Sea Water Resistance of Concrete. Build. Environ. 2007, 42, 1770–1776. [Google Scholar] [CrossRef]
- Han, S.-H. Influence of Diffusion Coefficient on Chloride Ion Penetration of Concrete Structure. Constr. Build. Mater. 2007, 21, 370–378. [Google Scholar] [CrossRef]
- Zhou, Q.; Lu, C.; Wang, W.; Wei, S.; Lu, C.; Hao, M. Effect of Fly Ash and Sustained Uniaxial Compressive Loading on Chloride Diffusion in Concrete. J. Build. Eng. 2020, 31, 101394. [Google Scholar] [CrossRef]
- Shafikhani, M.; Chidiac, S.E. A Holistic Model for Cement Paste and Concrete Chloride Diffusion Coefficient. Cem. Concr. Res. 2020, 133, 106049. [Google Scholar] [CrossRef]
- Song, H.-W.; Lee, C.-H.; Ann, K.Y. Factors Influencing Chloride Transport in Concrete Structures Exposed to Marine Environments. Cem. Concr. Compos. 2008, 30, 113–121. [Google Scholar] [CrossRef]
- Petcherdchoo, A. Time Dependent Models of Apparent Diffusion Coefficient and Surface Chloride for Chloride Transport in Fly Ash Concrete. Constr. Build. Mater. 2013, 38, 497–507. [Google Scholar] [CrossRef]
- Bao, J.; Wei, J.; Zhang, P.; Zhuang, Z.; Zhao, T. Experimental and Theoretical Investigation of Chloride Ingress into Concrete Exposed to Real Marine Environment. Cem. Concr. Compos. 2022, 130, 104511. [Google Scholar] [CrossRef]
- Liu, Q.; Hu, Z.; Lu, X.; Yang, J.; Azim, I.; Sun, W. Prediction of Chloride Distribution for Offshore Concrete Based on Statistical Analysis. Materials 2020, 13, 174. [Google Scholar] [CrossRef]
- Liao, C.; Jin, H.; Liu, W.; Liu, J.; Zhong, S.; Xing, F.; Tang, L. Numerical and Experimental Analysis of Chloride and Iodide Transports in Concrete under Natural Diffusion. Constr. Build. Mater. 2023, 392, 131902. [Google Scholar] [CrossRef]
- Wang, J.; Yang, L.; Huang, J.; Yu, B. Service Life Prediction Model for Marine Concrete Structures Considering Structural Shape and Time-Dependent Behaviour. Ocean Eng. 2023, 285, 115276. [Google Scholar] [CrossRef]
- Yuan, S.; Liu, Z.; Tong, T.; Liu, J. Experimental, Analytical, and Numerical Investigation on Flexural Behavior of Hybrid Beams Consisting of Ultra-High Performance and Normal-Strength Concrete. Eng. Struct. 2022, 268, 114725. [Google Scholar] [CrossRef]
- Provete Vincler, J.; Sanchez, T.; Turgeon, V.; Conciatori, D.; Sorelli, L. A Modified Accelerated Chloride Migration Tests for UHPC and UHPFRC with PVA and Steel Fibers. Cem. Concr. Res. 2019, 117, 38–44. [Google Scholar] [CrossRef]
- Chuang, M.L.; Huang, W.H. Durability Analysis Testing on Reactive Powder Concrete. Adv. Mater. Res. 2013, 811, 244–248. [Google Scholar] [CrossRef]
- Roux, N.; Andrade, C.; Sanjuan, M.A. Experimental Study of Durability of Reactive Powder Concretes. J. Mater. Civ. Eng. 1996, 8, 1–6. [Google Scholar] [CrossRef]
- Dobiáš, D.; Pernicová, R.; Mandlík, T. Water Transport Properties and Depth of Chloride Penetration in Ultra High Performance Concrete. Key Eng. Mater. 2016, 711, 137–142. [Google Scholar] [CrossRef]
- Voo, Y.; Foster, S. Characteristics of Ultra-High Performance ‘Ductile’ Concrete and Its Impact on Sustainable Construction. IES J. Part A Civ. Struct. Eng. 2010, 3, 168–187. [Google Scholar] [CrossRef]
- Yang, J.; Chen, B.; Su, J.; Xu, G.; Zhang, D.; Zhou, J. Effects of Fibers on the Mechanical Properties of UHPC: A Review. J. Traffic Transp. Eng. (Engl. Ed.) 2022, 9, 363–387. [Google Scholar] [CrossRef]
- Park, S.; Wu, S.; Liu, Z.; Pyo, S. The Role of Supplementary Cementitious Materials (SCMs) in Ultra High Performance Concrete (UHPC): A Review. Materials 2021, 14, 1472. [Google Scholar] [CrossRef]
- Abbas, S.; Soliman, A.M.; Nehdi, M.L. Exploring Mechanical and Durability Properties of Ultra-High Performance Concrete Incorporating Various Steel Fiber Lengths and Dosages. Constr. Build. Mater. 2015, 75, 429–441. [Google Scholar] [CrossRef]
- Algaifi, H.A.; Bakar, S.A.; Sam, A.R.M.; Abidin, A.R.Z.; Shahir, S.; AL-Towayti, W.A.H. Numerical Modeling for Crack Self-Healing Concrete by Microbial Calcium Carbonate. Constr. Build. Mater. 2018, 189, 816–824. [Google Scholar] [CrossRef]
- Pourjahanshahi, A.; Madani, H. Chloride Diffusivity and Mechanical Performance of UHPC with Hybrid Fibers under Heat Treatment Regime. Mater. Today Commun. 2021, 26, 102146. [Google Scholar] [CrossRef]
- Chen, M.-Y.; Chen, R.-P.; Chen, Y.-Q.; Ma, X.-Y.; Kang, X. Stray Current Induced Chloride Ion Transport and Corrosion Characteristics of Cracked Ultra-High Performance Concrete. Constr. Build. Mater. 2023, 398, 132536. [Google Scholar] [CrossRef]
- Pyo, S.; Koh, T.; Tafesse, M.; Kim, H.-K. Chloride-Induced Corrosion of Steel Fiber near the Surface of Ultra-High Performance Concrete and Its Effect on Flexural Behavior with Various Thickness. Constr. Build. Mater. 2019, 224, 206–213. [Google Scholar] [CrossRef]
- Li, T.; Yan, Y.; Xu, C.; Han, X.; Liu, Y.; Qi, H.; Ming, Y. Effect of Hollow 304 Stainless Steel Fiber on Corrosion Resistance and Mechanical Properties of Ultra-High Performance Concrete (UHPC). Materials 2023, 16, 3612. [Google Scholar] [CrossRef]
- Lü, C.; Liu, D.; Ding, Y.; Lü, X.; Zhou, Z.; Mu, S.; Sun, Y. Effect of Early Dry-Wet Cycles on the Mechanical Performance and Microstructure Characteristics of Ultra-High Performance Concrete (UHPC) with Varying Metakaolin (MK) Contents. Constr. Build. Mater. 2025, 490, 142471. [Google Scholar] [CrossRef]
- Niu, L.; Zhang, S. Performance of Cracked Ultra-high-performance Fiber-reinforced Concrete Exposed to Dry-wet Cycles of Chlorides. Adv. Mater. Sci. Eng. 2021, 2021, 4625972. [Google Scholar] [CrossRef]
- Sohail, M.G.; Kahraman, R.; Al Nuaimi, N.; Gencturk, B.; Alnahhal, W. Durability Characteristics of High and Ultra-High Performance Concretes. J. Build. Eng. 2021, 33, 101669. [Google Scholar] [CrossRef]
- Zhou, Q.; Mei, K.; Wang, F.; Li, B.; Xu, S.; Sun, S. Complex Salt Frost Resistance of Pre-Damaged Reinforced HPC Columns Wrapped with BFRP Sheets. Arch. Civ. Mech. Eng. 2024, 25, 34. [Google Scholar] [CrossRef]
- Wang, Y.; Fu, K. Comparisons of Instantaneous Chloride Diffusion Coefficients Determined by RCM Method and Chloride Natural Diffusion Test. Constr. Build. Mater. 2019, 223, 595–604. [Google Scholar] [CrossRef]
- GB/T 50082-2024; Standard for Test Methods of Long-Term Performance and Durability of Concrete. China Architecture & Building Press: Beijing, China, 2024.
- CEN-EN 12390-11; Testing Hardened Concrete—Part 11: Determination of the Chloride Resistance of Concrete, Unidirectional Diffusion. BSI Standards Limited: Chiswick, UK, 2015.
- C1202; Standard Test Method for Electrical Indication of Concrete’s Ability to Resist Chloride Ion Penetration. American Society for Testing and Materials: Conshohocken, PA, USA, 2022.
- Yu, H.; Li, L.; Ma, H.; Lu, Y.; Hu, D. Study on Time Range of Definite Integral in Derivation Process of Chloride Ion Diffusion Theoretical Model of Concrete. Constr. Build. Mater. 2024, 428, 135876. [Google Scholar] [CrossRef]
- Liu, J.; Jia, Y.; Wang, J. Calculation of Chloride Ion Diffusion in Glass and Polypropylene Fiber-Reinforced Concrete. Constr. Build. Mater. 2019, 215, 875–885. [Google Scholar] [CrossRef]
- Wang, J.; Kim, Y.J. Evolutionary Characteristics of Microstructural Hydration and Chloride Diffusion in UHPC. Mater. Des. 2023, 225, 111528. [Google Scholar] [CrossRef]
- Dong, L.; Yang, Y.; Liu, Z.; Yang, T.; Xue, C.; Shao, R.; Wu, C. Effect of Chloride Ion Migration Behaviour on the Microstructure and Mechanical Properties of Ultra-High Performance Concrete: A Review. J. Build. Eng. 2024, 82, 108233. [Google Scholar] [CrossRef]
- Ou, Y.; Xu, M.; Chen, D.; Jiang, M.; Xiao, L.; Mei, G. Effect of Reverse Water Pressure on Chloride Penetration within Finite Concrete during Drying-Wetting Cycles. Ocean Eng. 2022, 257, 111606. [Google Scholar] [CrossRef]
- Wu, L.; Wang, Y.; Wang, Y.; Ju, X.; Li, Q. Modelling of Two-Dimensional Chloride Diffusion Concentrations Considering the Heterogeneity of Concrete Materials. Constr. Build. Mater. 2020, 243, 118213. [Google Scholar] [CrossRef]
- Konečný, P.; Lehner, P.; Ghosh, P.; Morávková, Z.; Tran, Q. Comparison of Procedures for the Evaluation of Time Dependent Concrete Diffusion Coefficient Model. Constr. Build. Mater. 2020, 258, 119535. [Google Scholar] [CrossRef]
- Zhou, S. Analytical Model for Square Root Increase of Surface Chloride Concentration and Decrease of Chloride Diffusivity. J. Mater. Civ. Eng. 2016, 28, 4015181. [Google Scholar] [CrossRef]
- Pack, S.-W.; Jung, M.-S.; Song, H.-W.; Kim, S.-H.; Ann, K.Y. Prediction of Time Dependent Chloride Transport in Concrete Structures Exposed to a Marine Environment. Cem. Concr. Res. 2010, 40, 302–312. [Google Scholar] [CrossRef]
- Guo, R.; Wang, J.; Yuan, Y.; Li, D.; Jin, Y.; Shan, H. Interpretation of Dual Time-Dependent Chloride Diffusion in Concrete Based on Physical Information Neural Networks. Case Stud. Constr. Mater. 2024, 21, e03769. [Google Scholar] [CrossRef]
- Yang, L.; Wang, L.; Yu, B. Time-Varying Behavior and Its Coupling Effects with Environmental Conditions and Cementitious Material Types on Surface Chloride Concentration of Marine Concrete. Constr. Build. Mater. 2021, 303, 124578. [Google Scholar] [CrossRef]
- Page, C.L.; Short, N.R.; El Tarras, A. Diffusion of Chloride Ions in Hardened Cement Pastes. Cem. Concr. Res. 1981, 11, 395–406. [Google Scholar] [CrossRef]
- Lyu, W.; Poh, L.H. Temperature Effect on Chloride Transport in Cement-Based Materials. J. Build. Eng. 2025, 111, 113311. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Najjar, L.J. Nonlinear Water Diffusion in Nonsaturated Concrete. Matér. Constr. 1972, 5, 3–20. [Google Scholar] [CrossRef]
- Jin, H.; Fan, X.; Li, Z.; Zhang, W.; Liu, J.; Zhong, D.; Tang, L. An Experimental Study on the Influence of Continuous Ambient Humidity Conditions on Relative Humidity Changes, Chloride Diffusion and Microstructure in Concrete. J. Build. Eng. 2022, 59, 105112. [Google Scholar] [CrossRef]
- Li, W. Simulation of Chloride Ions Erosion in Concrete Under Loadings and Environmental Factors. Ph.D. Thesis, Southeast University, Nanjing, China, 2019. [Google Scholar] [CrossRef]
- Zhong, R.; Ai, X.; Pan, M.; Yao, Y.; Cheng, Z.; Peng, X.; Wang, J.; Zhou, W. Durability of Micro-Cracked UHPC Subjected to Coupled Freeze-Thaw and Chloride Salt Attacks. Cem. Concr. Compos. 2024, 148, 105471. [Google Scholar] [CrossRef]
- Su, Y.; Li, J.; Wu, C.; Wu, P.; Li, Z.-X. Effects of Steel Fibres on Dynamic Strength of UHPC. Constr. Build. Mater. 2016, 114, 708–718. [Google Scholar] [CrossRef]
- JTS 153-2015; Standard for Durability Design of Port and Waterway Engineering Structure. China Communications Press: Beijing, China, 2015.
- Chen, A.; Feng, S.; Ma, R. Study on design method of durability of concrete bridge based on partial safety factor. J. Highw. Transp. Res. Dev. 2014, 31, 64–70. [Google Scholar] [CrossRef]
- Ma, X.; Xue, H.; Qi, J.; Liu, G. Service life prediction of ultra-high performance concrete based on chloride ion permeation mechanism. J. Shenyang Jianzhu. Univ. Nat. Sci. 2018, 34, 22–30. [Google Scholar]
- Huang, W.; Chen, Z.; Chen, R.; Ying, F.; Huang, Q.; Liu, S. Passivation behavior of steel bar in ultra-high performance concrete under coupling effect of different internal chloride salts. J. China. Ceram. Soc. 2023, 51, 1928–1937. [Google Scholar] [CrossRef]
- Wu, L. Chloride Penetration and Durability Assessment of Harbor Concrete Structures. Ph.D. Thesis, Shanghai Jiaotong University, Shanghai, China, 2016. [Google Scholar] [CrossRef]
- Wang, S.; Su, Q.; Fan, Z.; Li, Q.; Zhou, X.; Li, K. Durability design principle and method for concrete structures in Hong Kong-Zhuai-Macau sea link project. China Civ. Eng. J. 2014, 47, 1–8. [Google Scholar] [CrossRef]
- Xu, Y.; Gao, Y.; Yu, H.; Ma, H.; Xu, M.; Xu, Z.; Feng, T. Time Variation Law of Chlorine Diffusion Coefficient of Marine Concrete Structures in Tidal Zone and Its Influence on Service Life. J. Build. Eng. 2023, 76, 107379. [Google Scholar] [CrossRef]
- Wu, Q. Research on Flexural RC Components Exposed to Marine Environments: Durability and Life Prediction. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2010. [Google Scholar] [CrossRef]
- Firodiya, P.K.; Sengupta, A.K.; Pillai, R.G. Evaluation of Corrosion Rates of Reinforcing Bars for Probabilistic Assessment of Existing Road Bridge Girders. J. Perform. Constr. Facil. 2015, 29, 4014067. [Google Scholar] [CrossRef]
- Vu, K.A.T.; Stewart, M.G. Structural Reliability of Concrete Bridges Including Improved Chloride-Induced Corrosion Models. Struct. Saf. 2000, 22, 313–333. [Google Scholar] [CrossRef]
- GB/T 50476-2019; Standard for Design of Concrete Structure Durability. China Architecture & Building Press: Beijing, China, 2019.
- NF P 18-710; National Addition to Eurocode 2-Design of Concrete Structures: Specific Rules for Ultra-High Performance Fibre-Reinforced Concrete (UHPFRC). French Standardization Association: Paris, France, 2016.







| Premix (kg·m−3) | Water Reducer (kg·m−3) | Water (kg·m−3) | Steel Fibers (kg·m−3) |
|---|---|---|---|
| 2232 | 16 | 199 | 195 |
| Experiment | Solution Concentration | Material | Sample Number | Erosion Methods (d) |
|---|---|---|---|---|
| RCM | 10.0% NaCl | UHPCSF0 | 3 | / |
| UHPCSF2 | 3 | / | ||
| Diffusion experiment | 3.5% NaCl | UHPCSF2 | 5 × 5 | LTI 60, 120, 180, 240, 300 |
| Specimen | Mean Value | |||
|---|---|---|---|---|
| UHPCSF0 | 8.6 | 8.4 | 8.3 | 8.43 |
| UHPC | 5.4 | 4.6 | 5.7 | 5.23 |
| Water–Cement Ratio | U/(KJ/mol) |
|---|---|
| 0.4 | 41.8 ± 4.0 |
| 0.5 | 44.6 ± 4.3 |
| 0.6 | 32.0 ± 2.4 |
| Life365 model | 35.0 |
| Variable | Distribution Pattern | Mean Value | Coefficient of Variation | Standard Deviation |
|---|---|---|---|---|
| lognormal distribution | 1.130 × 10−14 m2/s | 0.1 [68] | 0.80 | |
| 1.00%B | 0.5 [69] | 0.50 | ||
| 0.75%B | 0.2 [70] | 0.15 |
| Design Service Life (a) | 100 | 150 | 200 | 100 [72] |
|---|---|---|---|---|
| (mm) | 30 | 37 | 43 | 25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, W.; Mei, K.; Liu, W.; Sun, S. Study on Chloride Diffusion Performance and Structural Durability Design of UHPC Under Chloride Salt Erosion. Buildings 2025, 15, 3569. https://doi.org/10.3390/buildings15193569
Kang W, Mei K, Liu W, Sun S. Study on Chloride Diffusion Performance and Structural Durability Design of UHPC Under Chloride Salt Erosion. Buildings. 2025; 15(19):3569. https://doi.org/10.3390/buildings15193569
Chicago/Turabian StyleKang, Wenbo, Kuihua Mei, Wei Liu, and Shengjiang Sun. 2025. "Study on Chloride Diffusion Performance and Structural Durability Design of UHPC Under Chloride Salt Erosion" Buildings 15, no. 19: 3569. https://doi.org/10.3390/buildings15193569
APA StyleKang, W., Mei, K., Liu, W., & Sun, S. (2025). Study on Chloride Diffusion Performance and Structural Durability Design of UHPC Under Chloride Salt Erosion. Buildings, 15(19), 3569. https://doi.org/10.3390/buildings15193569




