Deformation and Energy-Based Comparison of Outrigger Locations in RC and BRB-Core Tall Buildings Under Repetitive Earthquakes
Abstract
1. Introduction
2. Numerical Validation of BRB
3. Numerical Models
3.1. Studied Archetypes
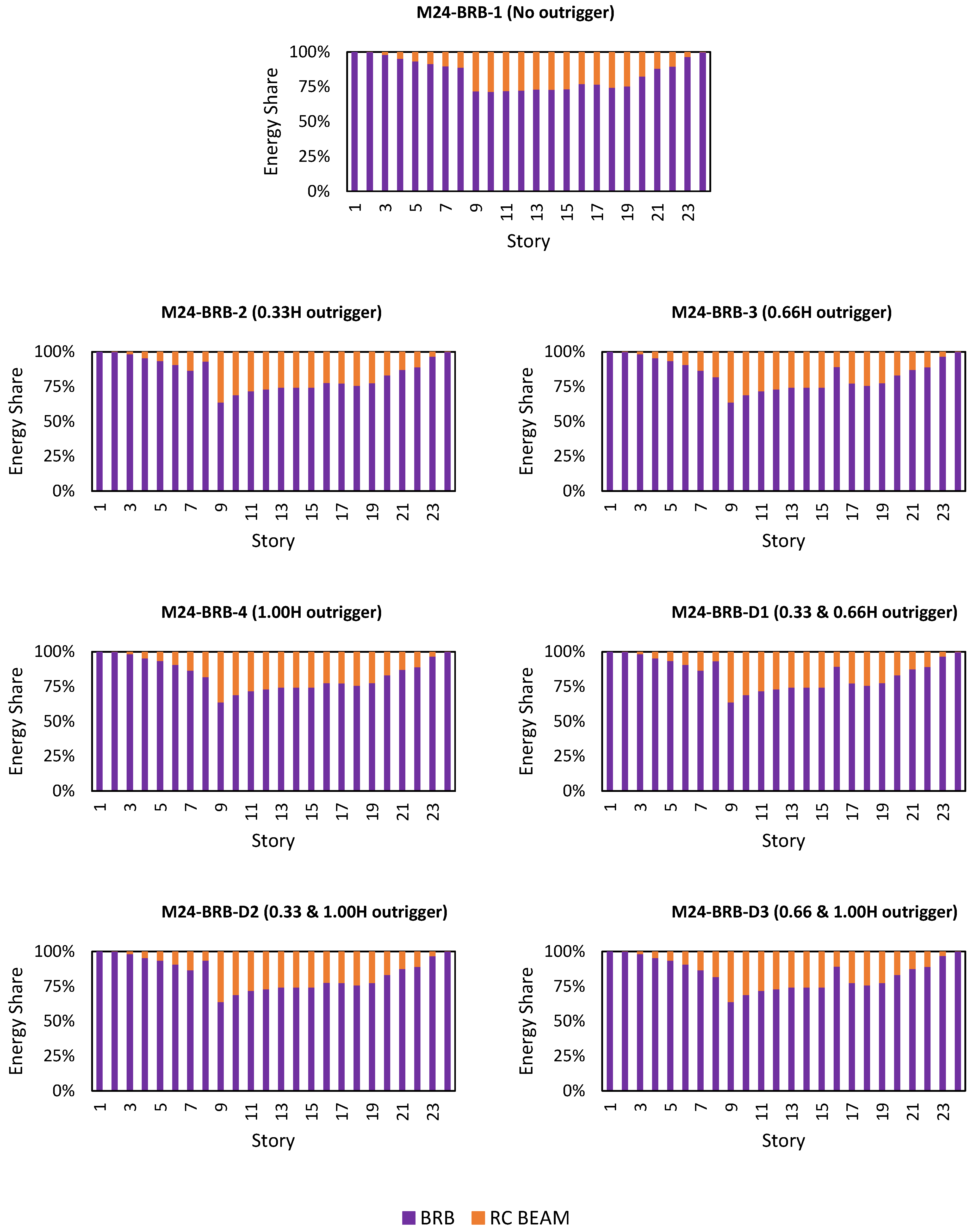
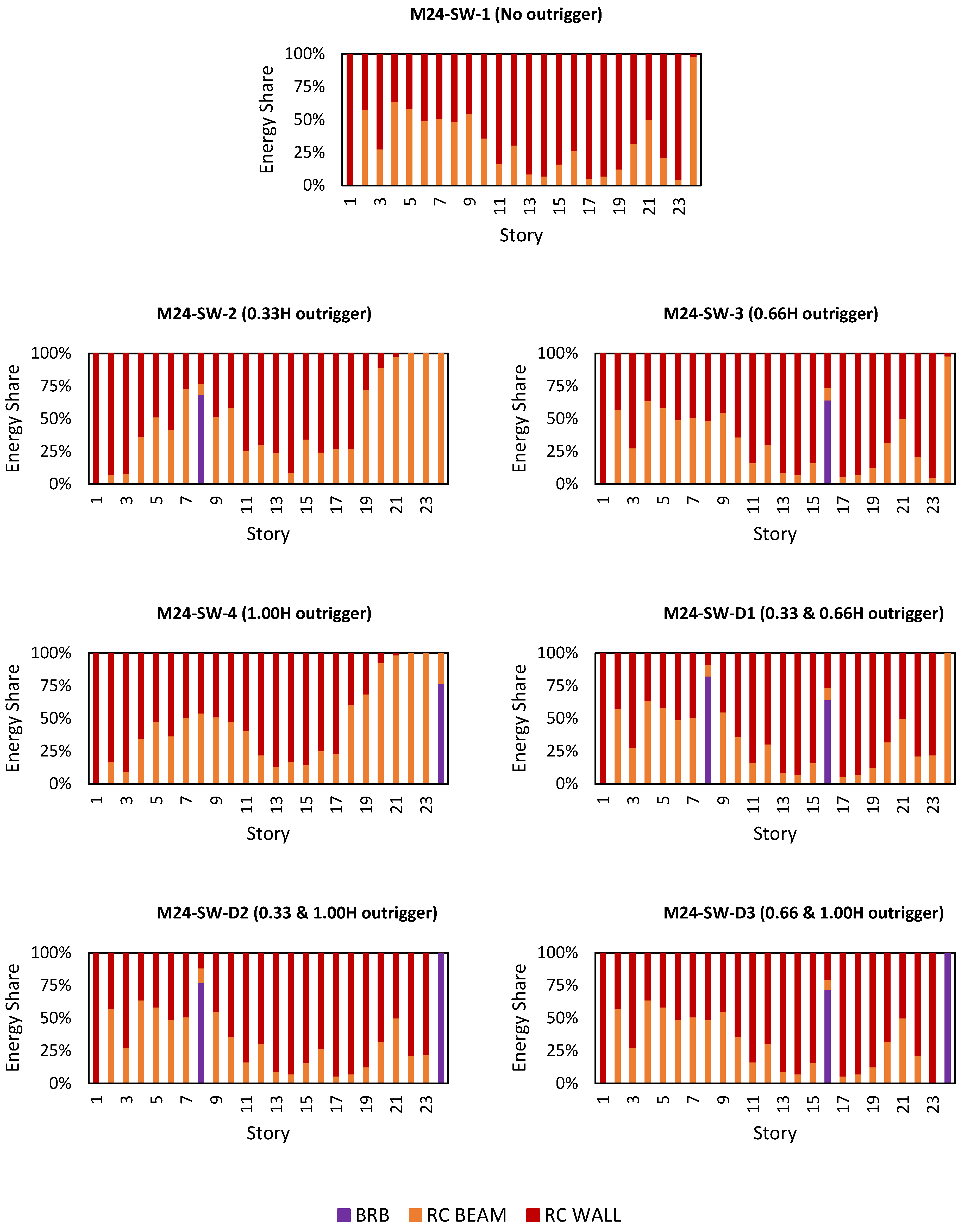
3.2. Numerical Modeling of BRBs
4. Nonlinear Time History Analyses
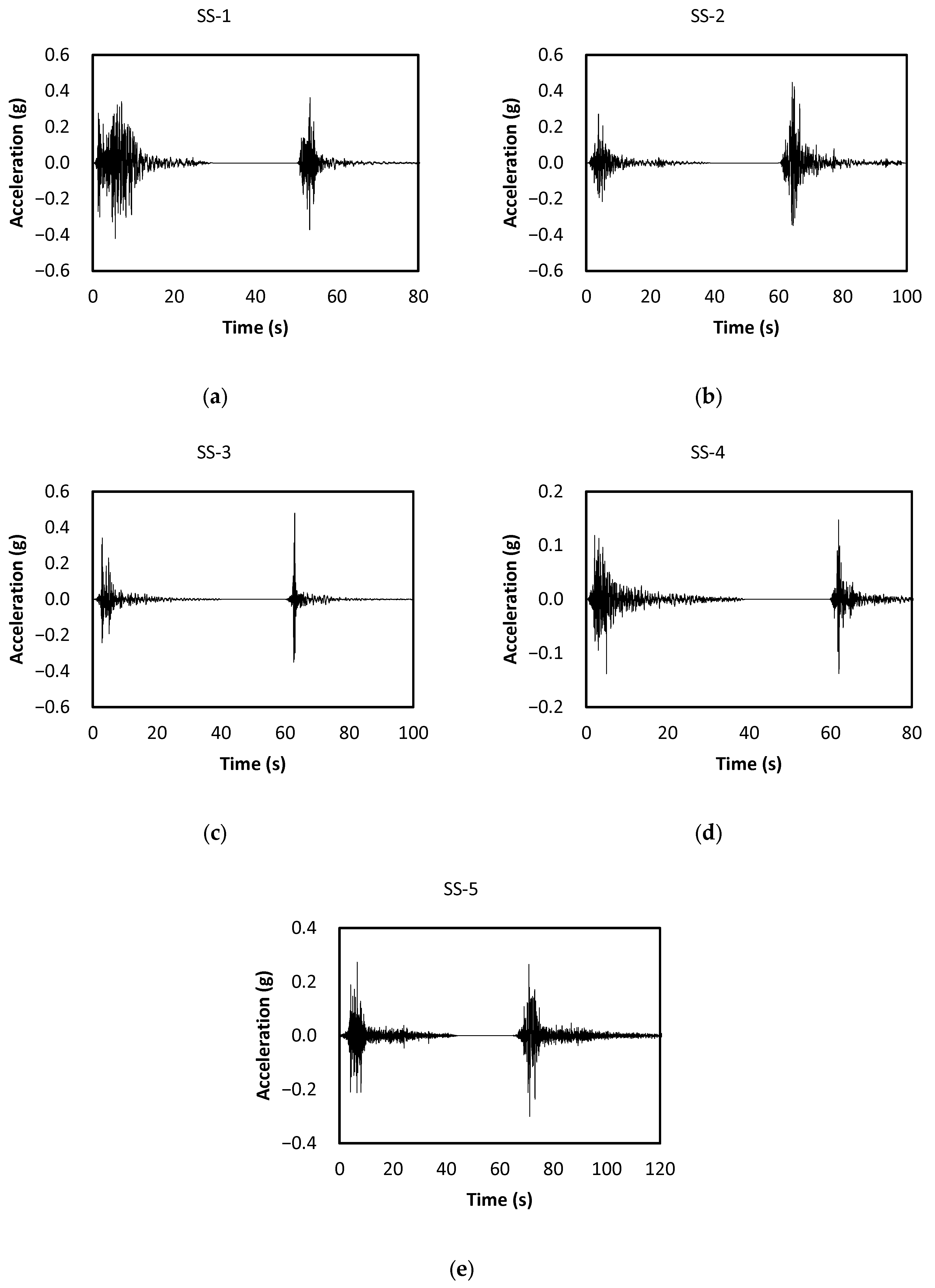
4.1. Mainshock-Aftershock Seismic Sequences
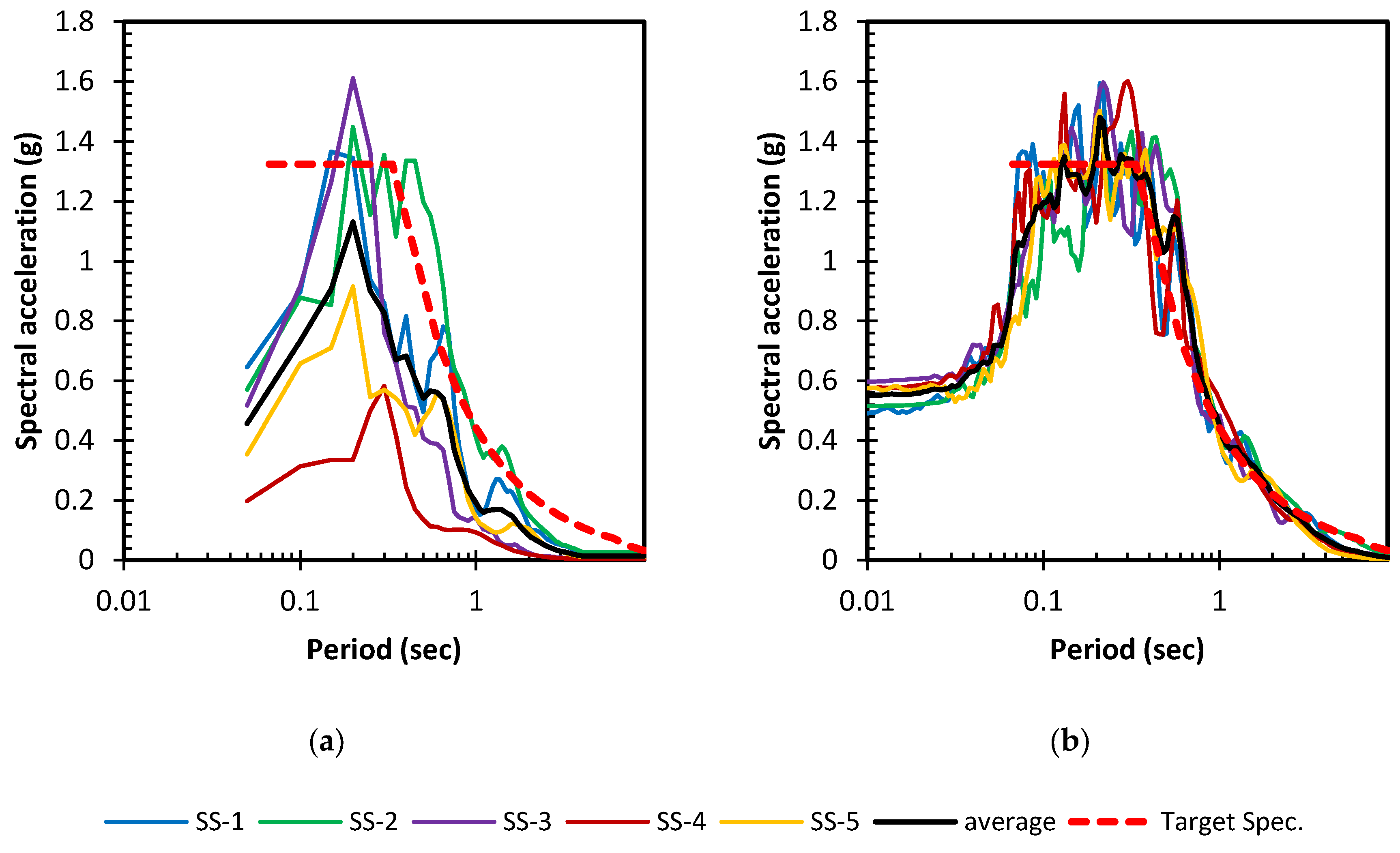
4.2. Matching the Accelerograms
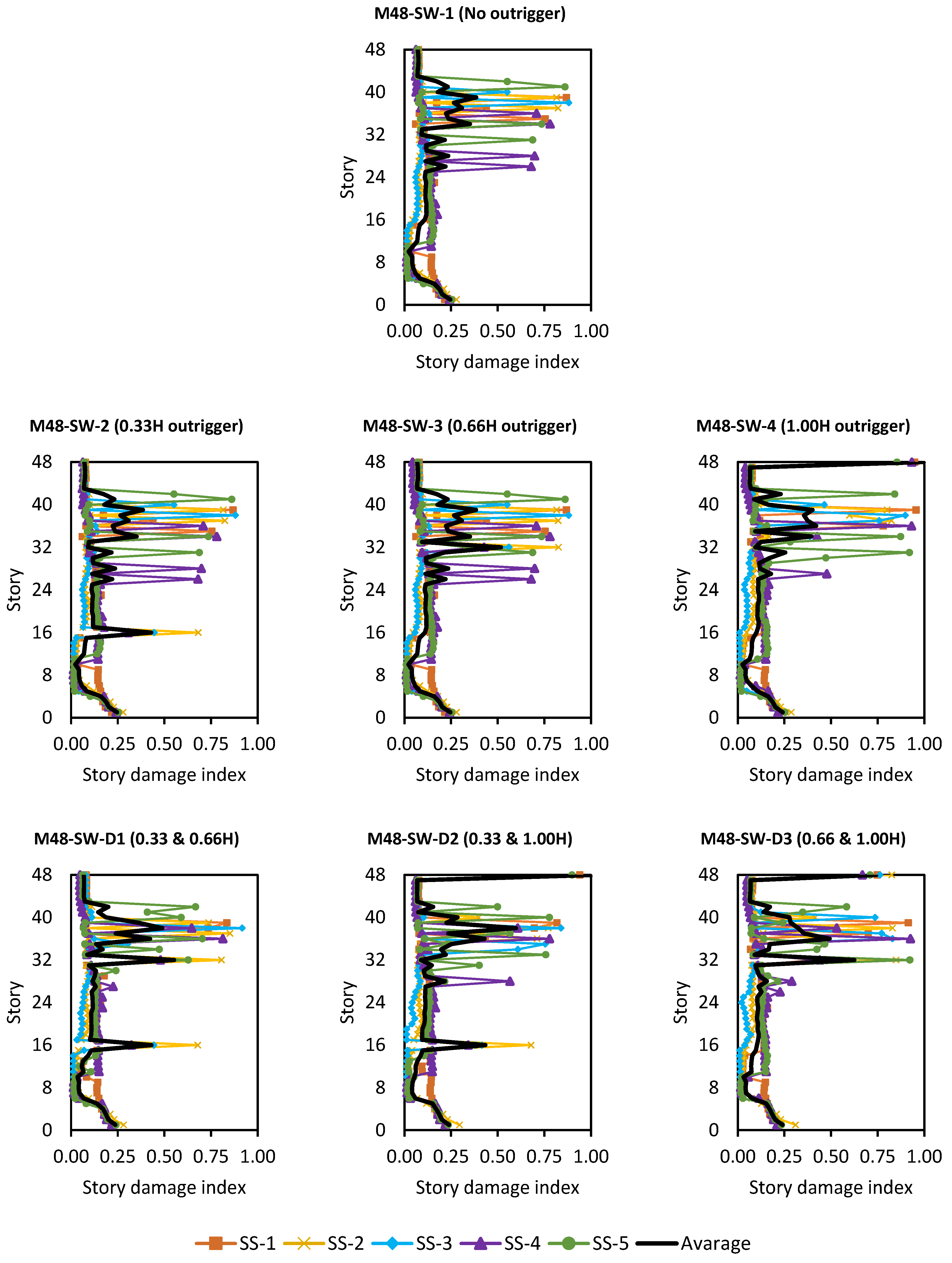
5. Effect of Outrigger Level on Structural Response
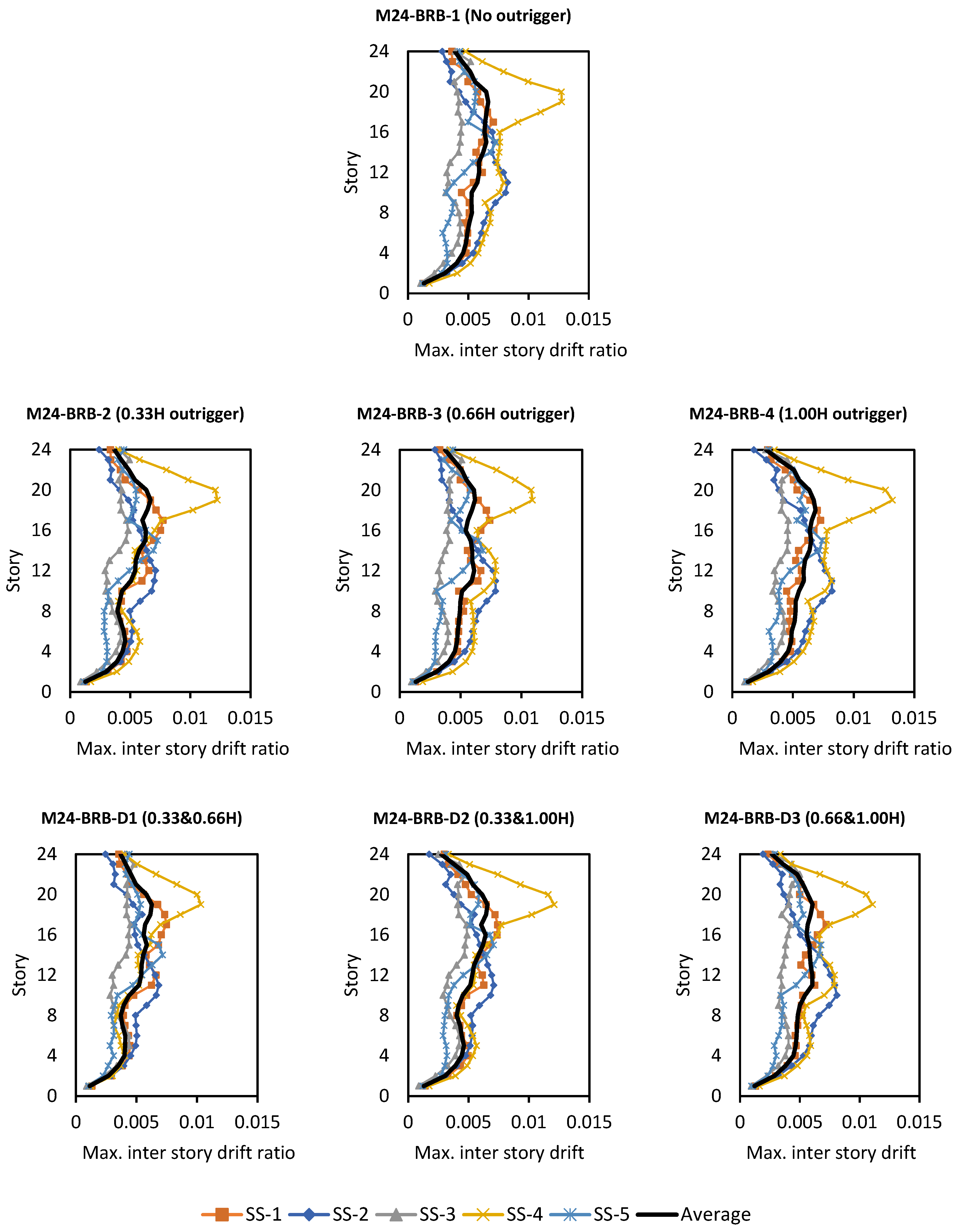
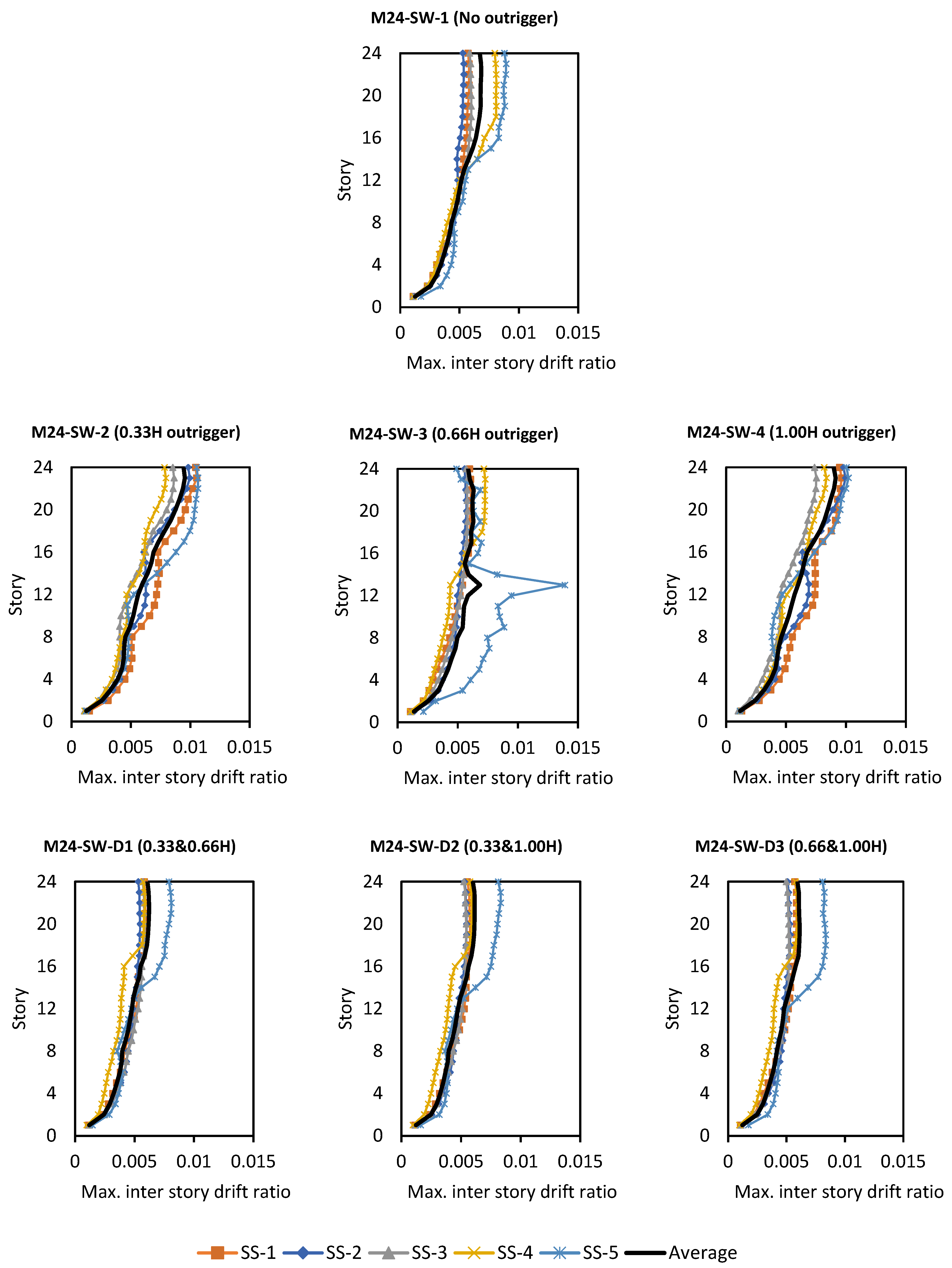
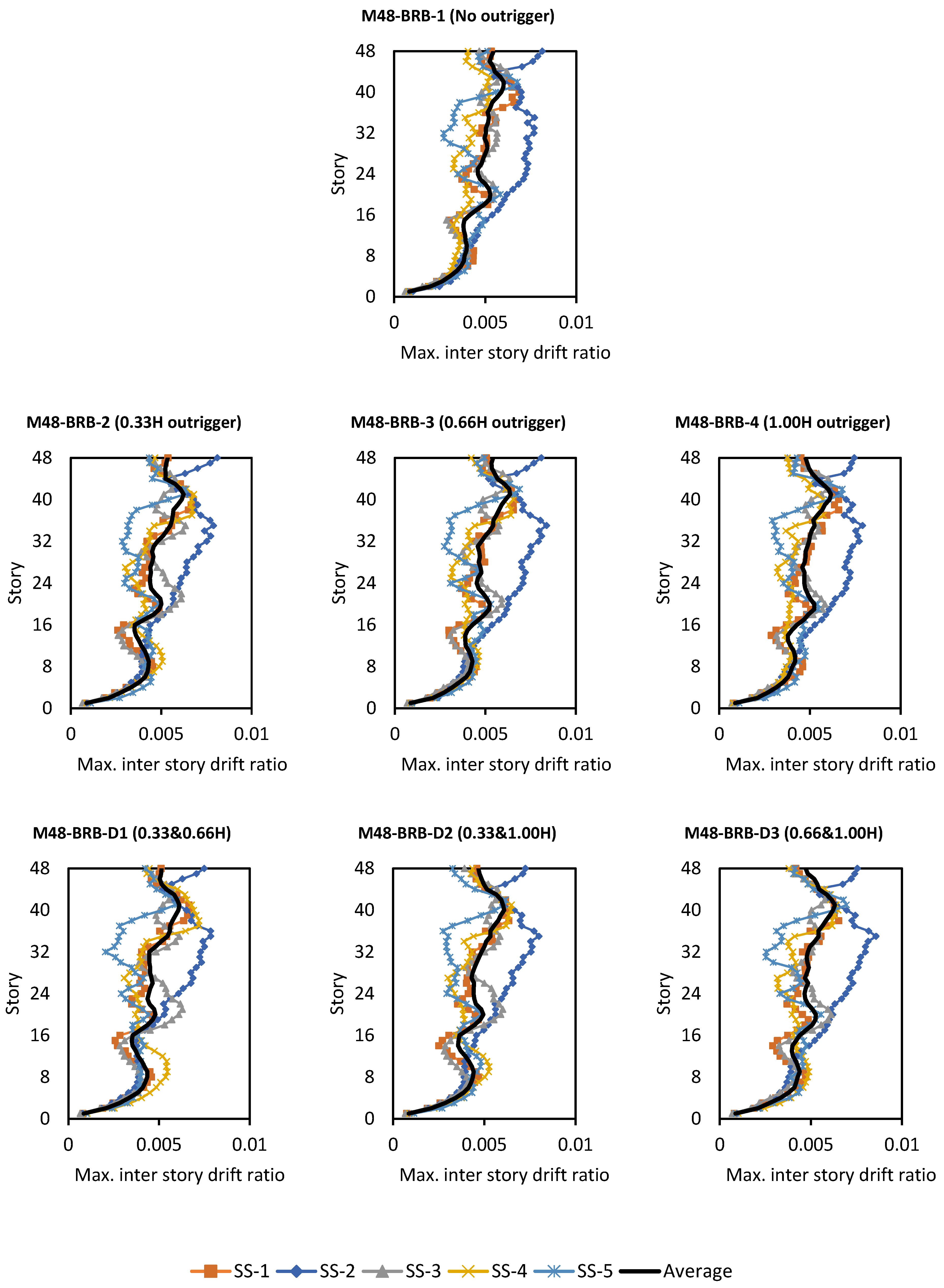
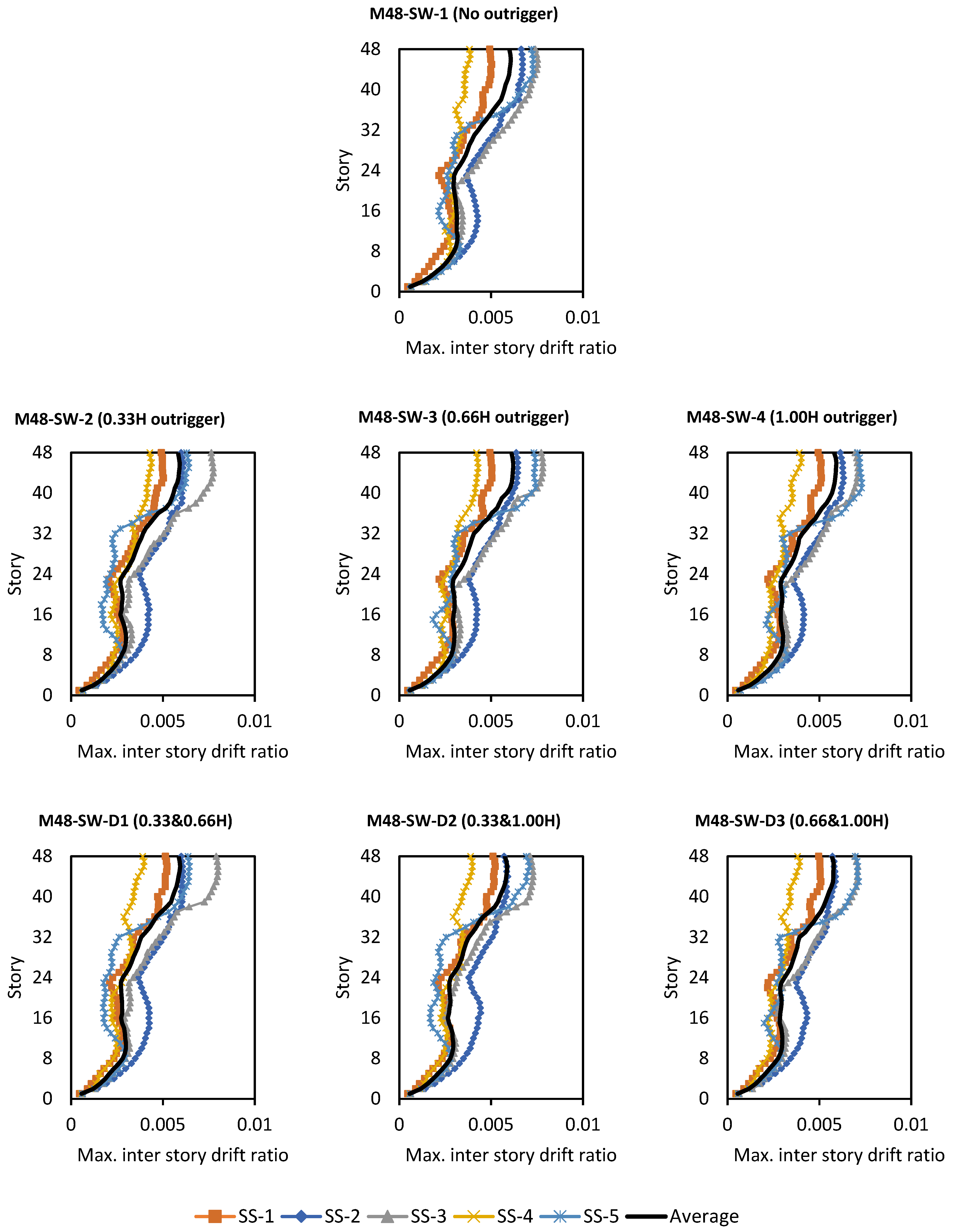
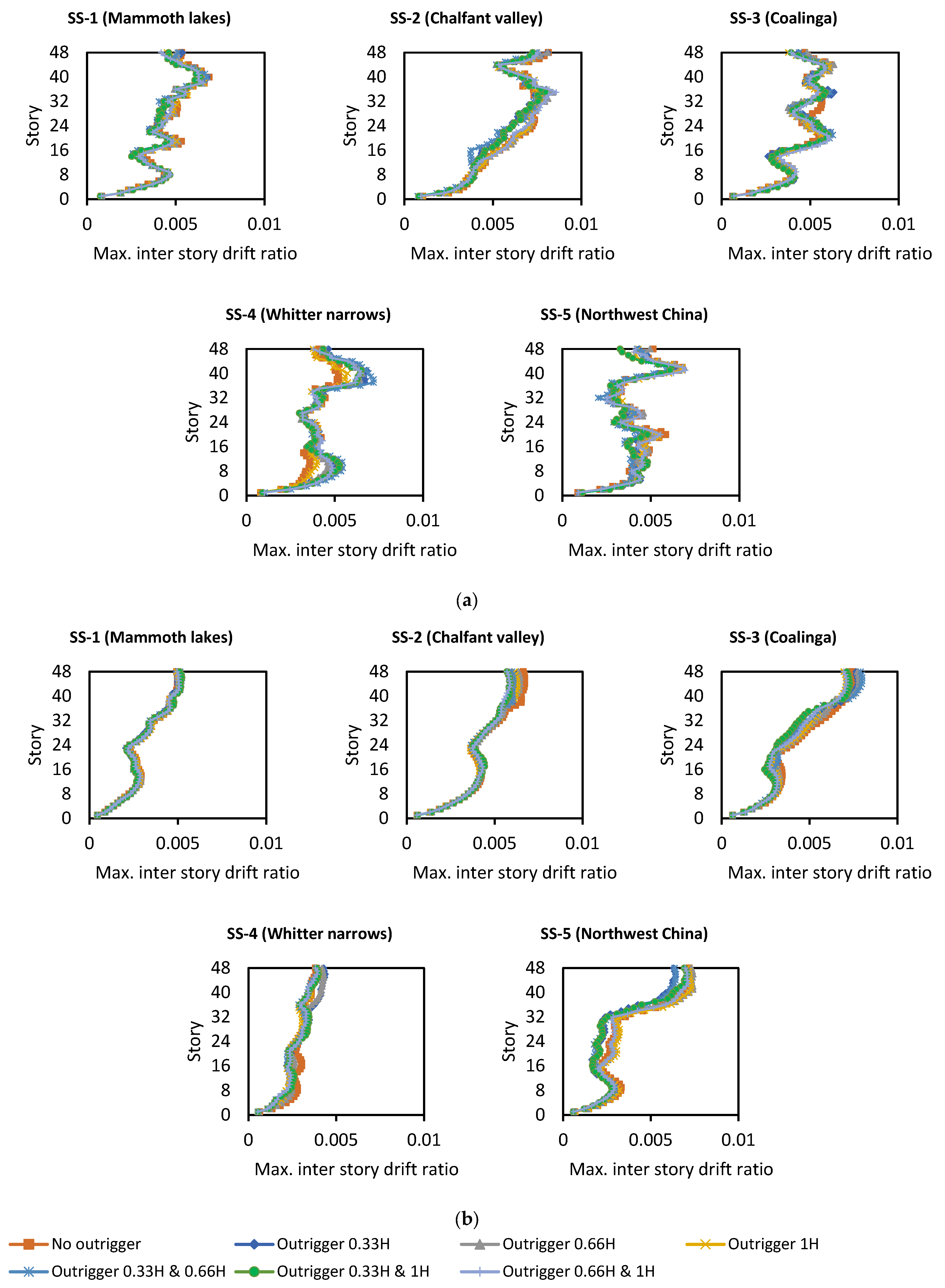
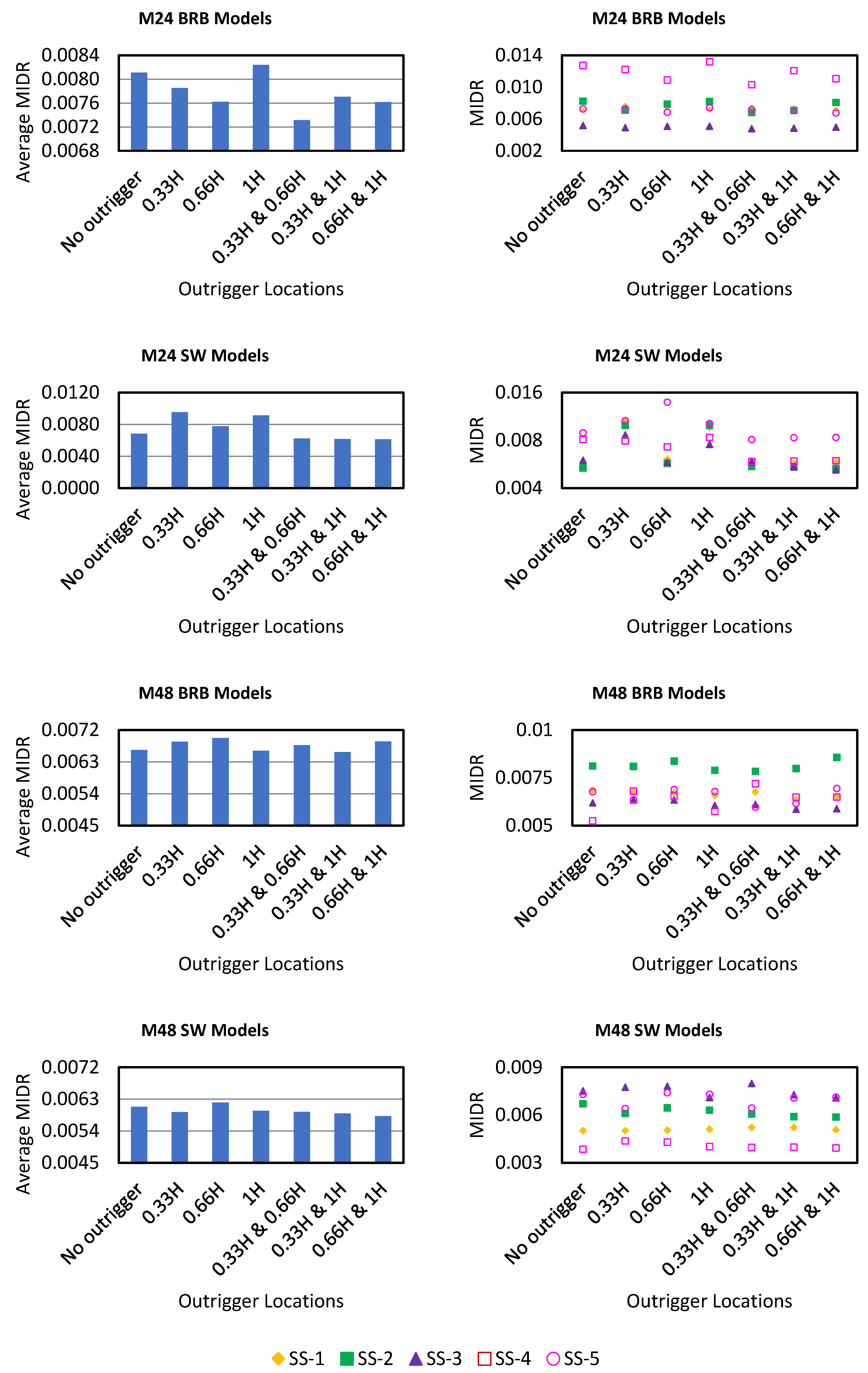
5.1. Maximum Inter-Story Drift Ratio
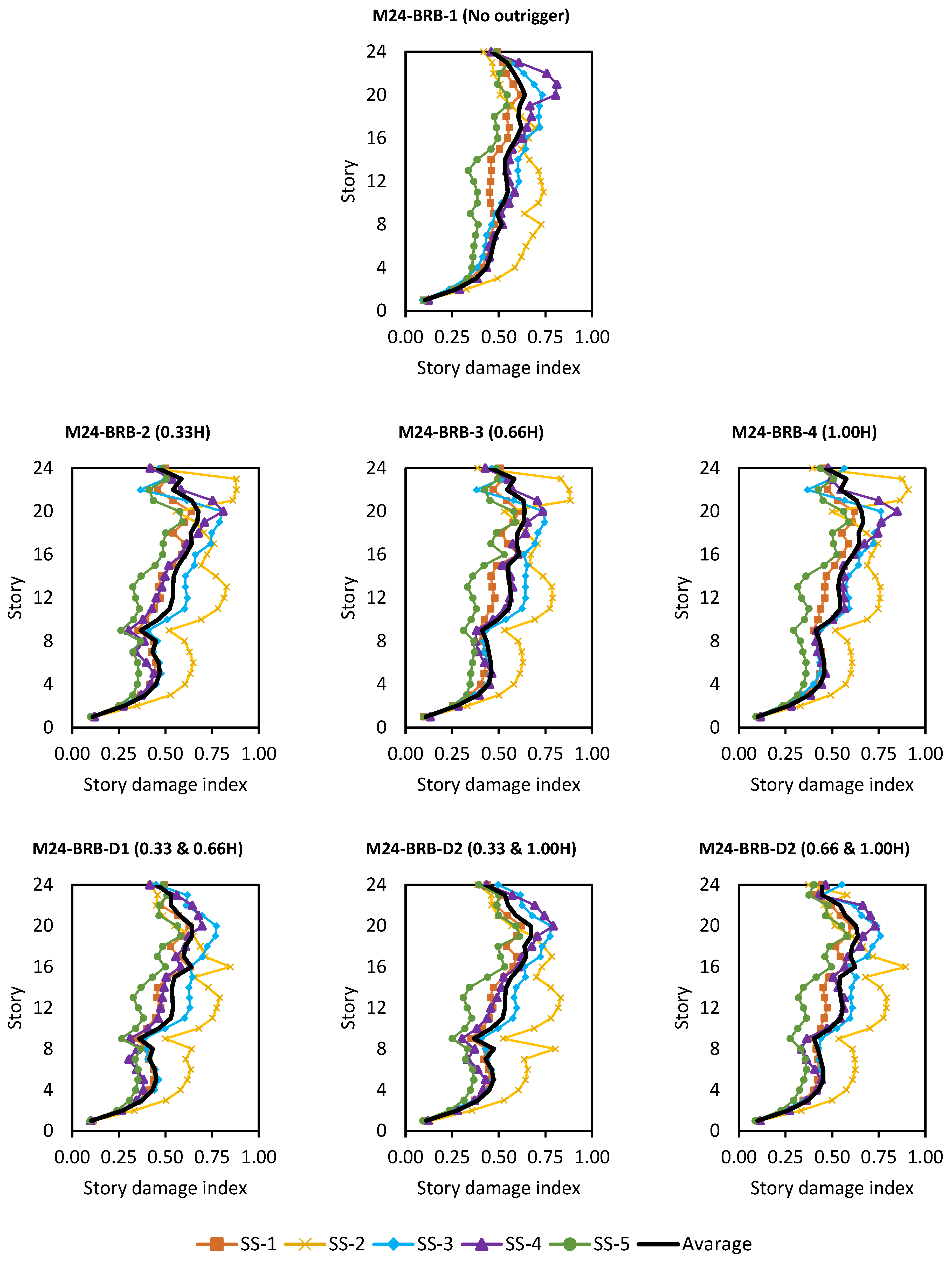
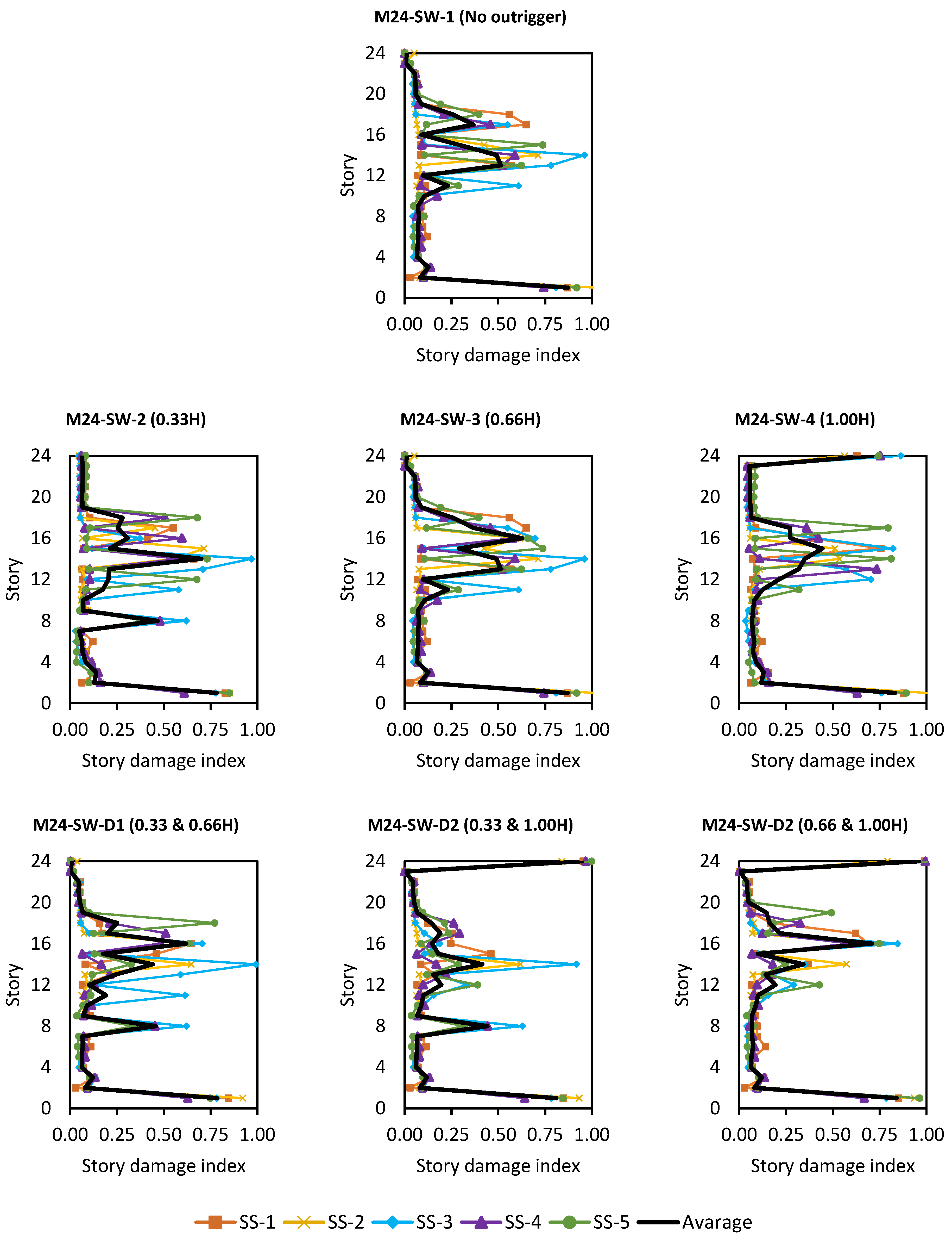
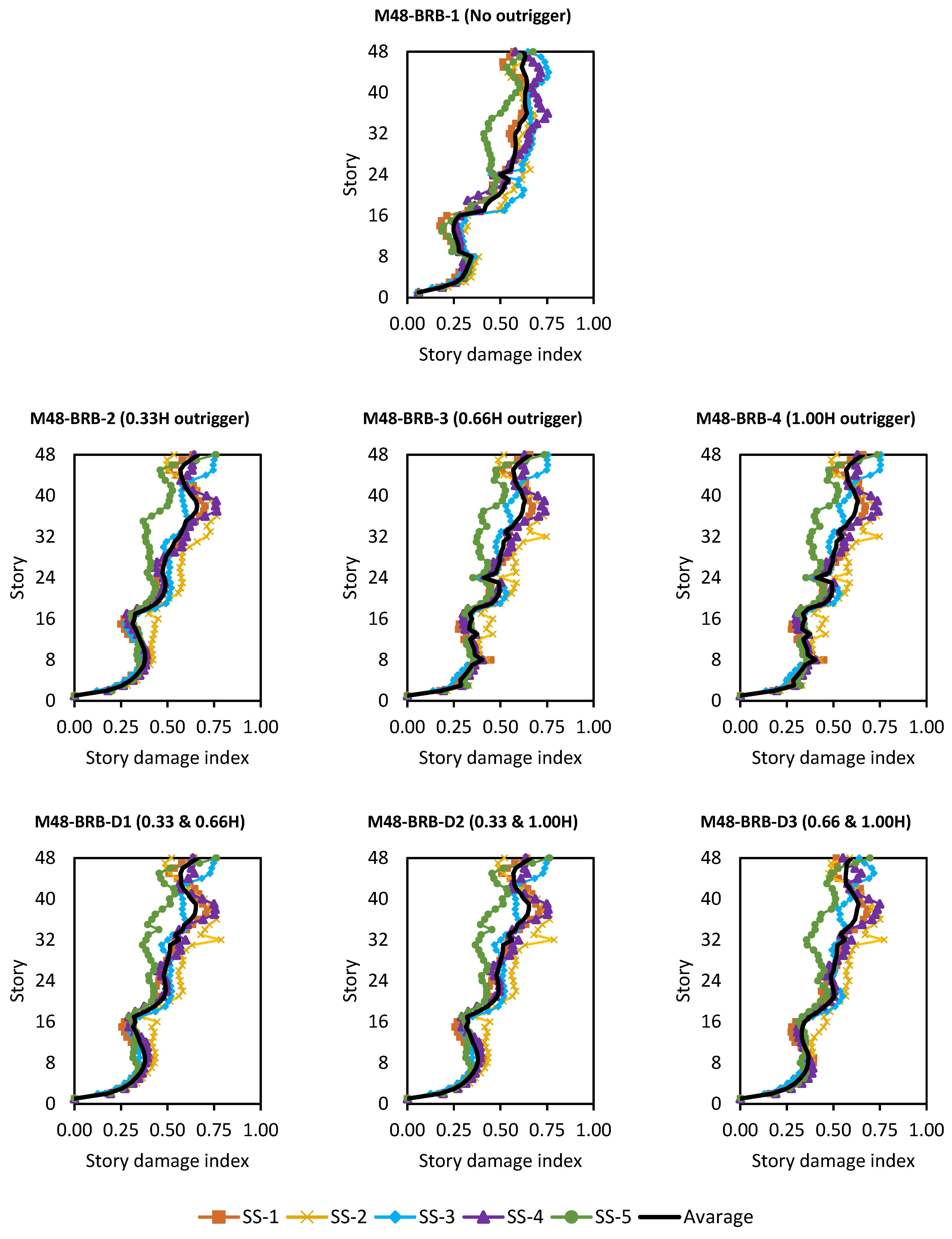
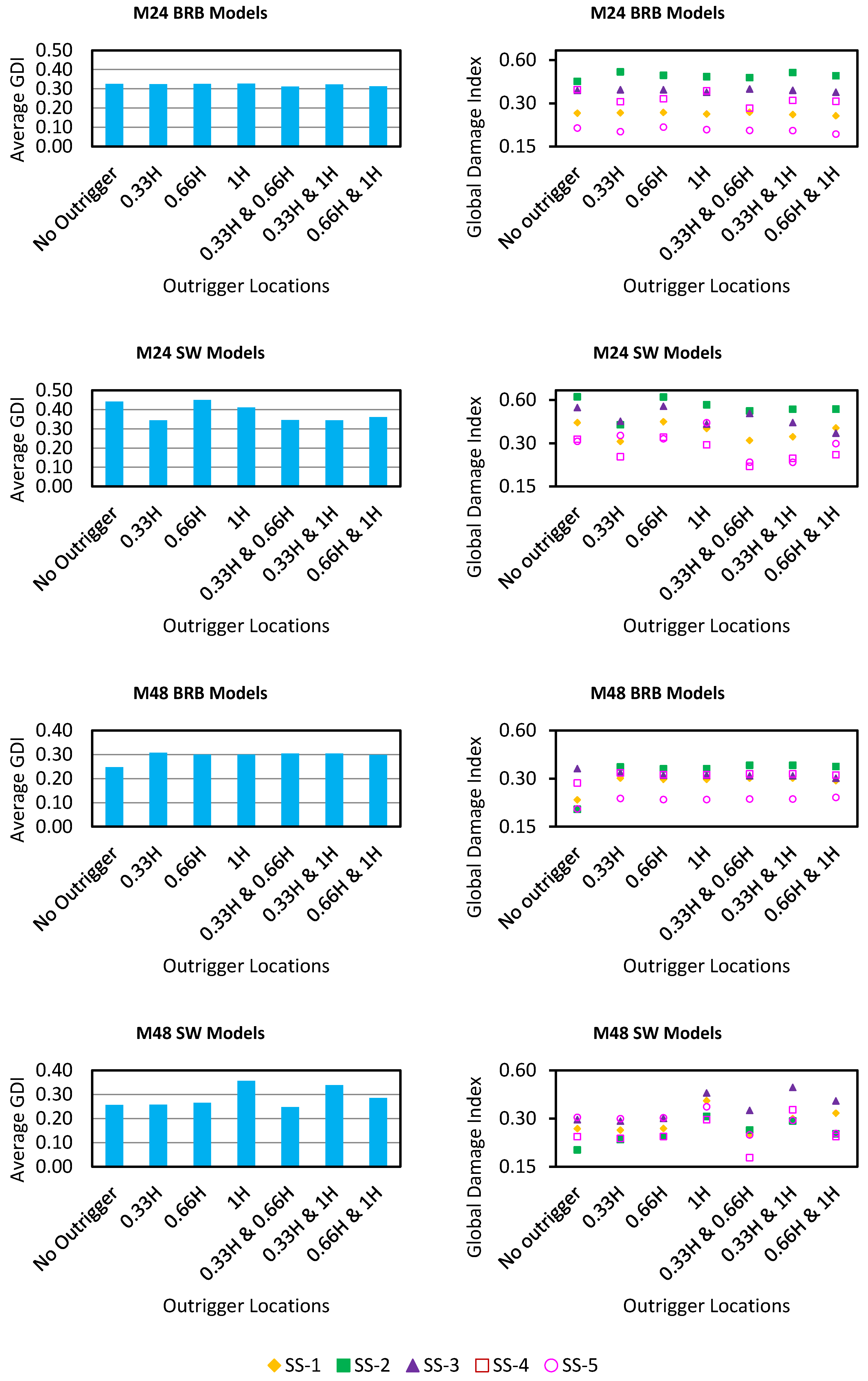
5.2. Cumulative Damage Indices
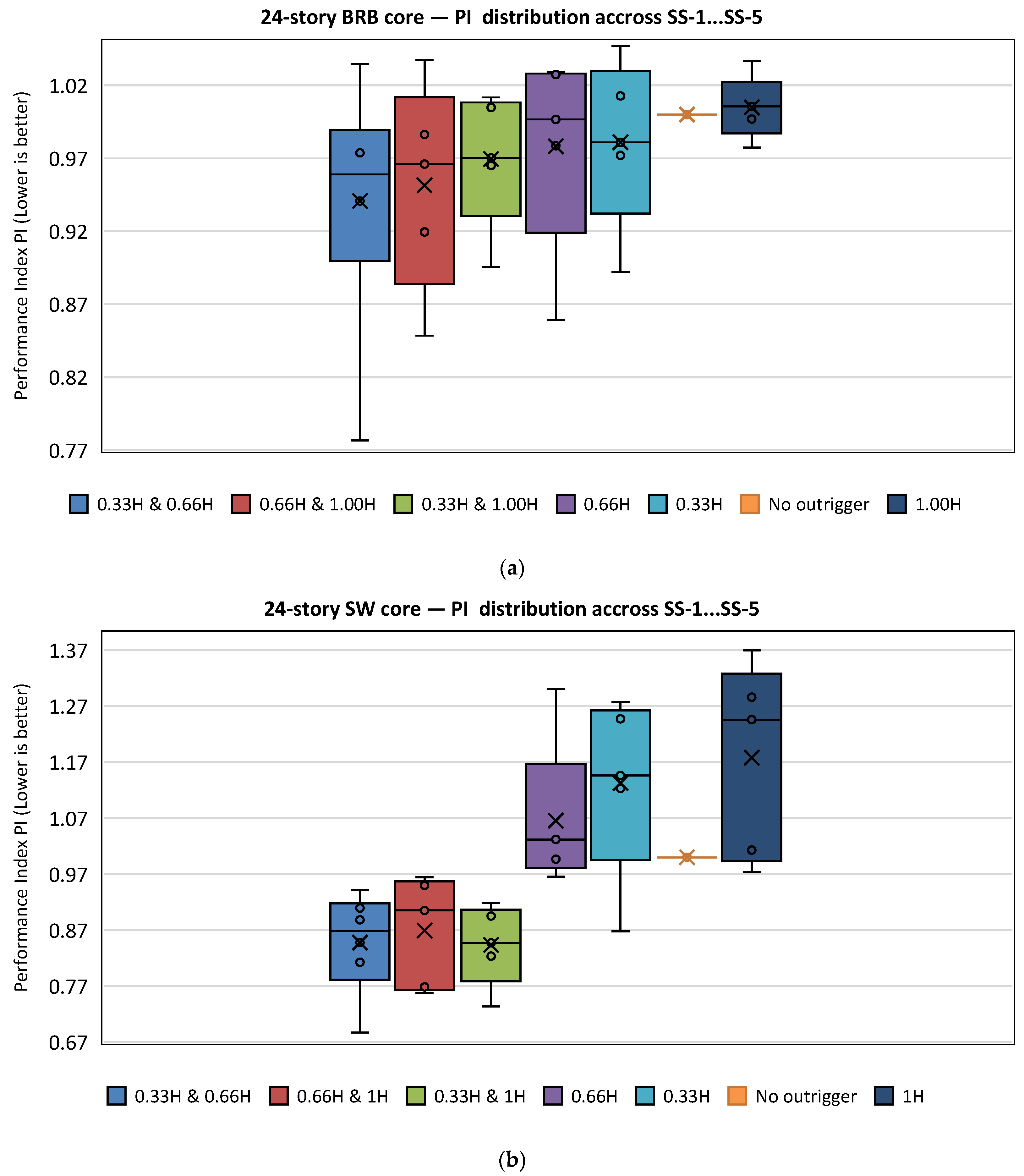
5.3. Integrated Performance Index (PI) and Ranking
6. Conclusions
6.1. Desing Orientation and Interpretation
6.2. Summary of Observed Results
- GDI indicates overall energy loss and structural degeneration. Even if the drift ratio remains within permissible limits, the GDI may nevertheless indicate a considerable danger of damage, especially in the case of consecutive seismic events.
- For single outrigger systems, it has been shown that the optimal approach to minimizing relative inter-story drift ratio is obtained when the outrigger is located at approximately 0.33H (one-third of the building height).
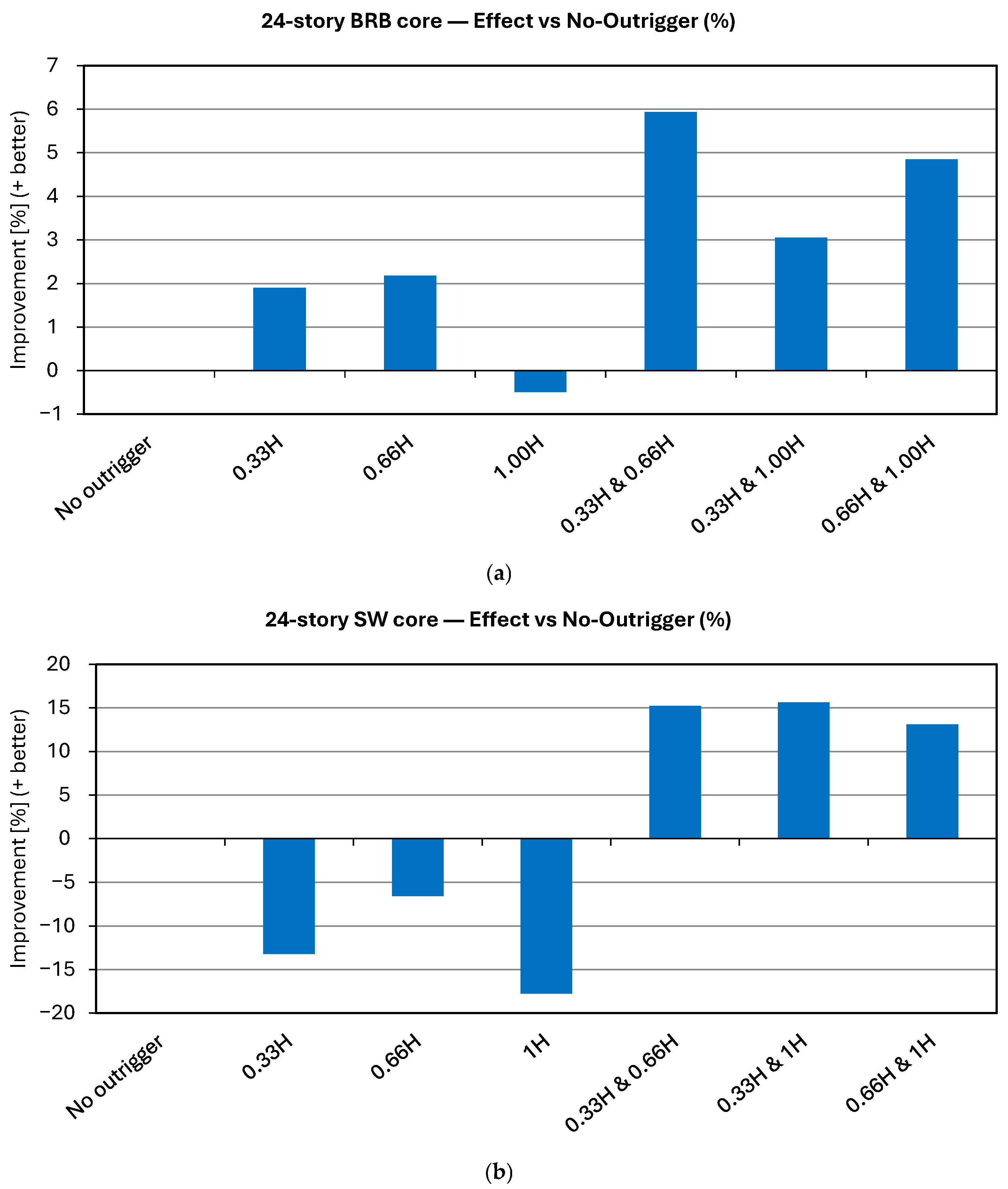
- Dual locations of outriggers (0.33H and 0.66H or 0.33H and 1.0H) provide more consistent inter-story drift ratio reductions throughout the building height compared to single-outrigger configurations. For tall buildings with flexible core systems such as BRB cores that provide both base and top floor control, 0.33H and 1.0H have been found to be a suitable choice between these configurations.
- RC wall cores maintain lower drift profiles even without outriggers but still show notable improvements with optimal placement, especially in 48-story cases.
- Drift ratio requirement is greatly impacted by seismic sequence features, with SS-4 and SS-5 sequences being the most crucial for all building model types.
- RC wall core systems respond more consistently to various seismic sequence inputs and provide superior inter-story drift ratio control.
- In all seismic sequence conditions, dual outriggers provide the best drift ratio reduction, particularly at 0.33H and 1.0H. While the dual-outrigger placement shows optimal performance, its implementation in real buildings may be limited by architectural and construction constraints. Future studies may consider multi-disciplinary optimization for practical integration.
- Outrigger placements are quite beneficial in reducing local DI and GDI, especially in BRB cored models and taller building models. This is especially true at 0.33H and 1.00H of the double outrigger configurations.
- Based on average GDI relative to the no-outrigger baseline across SS-1–SS-5, dual 0.33H and 0.66H (~4.0%) or dual 0.66H and 1.0H (~3.9%) in 24-story BRB cores may be considered, single 0.33H (~22.1%) or dual 0.33H and 1.0H (~21.9%) in 24-story RC shear-wall cores may be considered, outriggers in 48-story BRB cores may not provide average GDI reductions (e.g., dual 0.66H and 1.0H ≈ −20.9%) and thus may not be relied upon for GDI control, and dual 0.33H and 0.66H in 48-story RC shear-wall cores offers a modest average reduction (~3.3%) while single 1.0H appears detrimental (~−39.0%), with all values reflecting averages across sequences and sequence-to-sequence scatter that should be considered in performance-based design.
- Although outrigger optimization is still advantageous, RC shear wall cores naturally perform better under seismic conditions.
- While MISD may indicate acceptable deformation levels, the GDI can reveal hidden vulnerabilities related to material degradation and low-cycle fatigue, especially in BRB-core systems.
- These findings provide practical design guidance by indicating that dual outrigger placements at 0.33H and 1.0H offer a favorable balance between stiffness enhancement and energy dissipation, especially in BRB-core tall buildings.
- The strategic use of outriggers in RC wall core systems, even if these cores already offer high stiffness, helps further reduce drift demands in critical stories and supports serviceability requirements.
- It is important to consider seismic sequences rather than individual events when assessing damage accumulation. Outrigger systems are effective in reducing permanent damage caused by multiple events.
- Design codes and performance-based frameworks can benefit from explicit recommendations for outrigger positions and configurations that account for both deformation-based and energy-based damage measurements under sequential ground motions.
6.3. Limitations and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Archetype | Outrigger Configuration | Mode | T_i [s] | Mass Participation Mx [%] | Cumulative ΣMx [%] |
|---|---|---|---|---|---|
| 24F–BRB | No outrigger | 1 | 4.175 | 70.88% | 70.88% |
| 2 | 1.437 | 12.66% | 83.54% | ||
| 3 | 0.837 | 4.95% | 88.49% | ||
| 4 | 0.558 | 2.52% | 91.01% | ||
| 5 | 0.405 | 1.69% | 92.70% | ||
| 0.33H | 1 | 4.032 | 70.33% | 70.33% | |
| 2 | 1.422 | 13.92% | 84.25% | ||
| 3 | 0.836 | 4.66% | 88.91% | ||
| 4 | 0.55 | 2.04% | 90.95% | ||
| 5 | 0.397 | 1.62% | 92.57% | ||
| 0.66H | 1 | 4.122 | 71.57% | 71.57% | |
| 2 | 1.41 | 11.97% | 83.54% | ||
| 3 | 0.836 | 5.08% | 88.62% | ||
| 4 | 0.547 | 2.45% | 91.07% | ||
| 5 | 0.405 | 1.66% | 92.73% | ||
| 1.0H | 1 | 4.173 | 70.92% | 70.92% | |
| 2 | 1.434 | 12.68% | 83.60% | ||
| 3 | 0.832 | 4.96% | 88.56% | ||
| 4 | 0.553 | 2.53% | 91.09% | ||
| 5 | 0.4 | 1.71% | 92.80% | ||
| 0.33H and 0.66H | 1 | 3.978 | 71.09% | 71.09% | |
| 2 | 1.396 | 13.16% | 84.25% | ||
| 3 | 0.835 | 4.79% | 89.04% | ||
| 4 | 0.538 | 1.96% | 91.00% | ||
| 5 | 0.397 | 1.63% | 92.63% | ||
| 0.33H and 1.0H | 1 | 4.03 | 70.37% | 70.37% | |
| 2 | 1.419 | 13.93% | 84.30% | ||
| 3 | 0.831 | 4.66% | 88.96% | ||
| 4 | 0.544 | 2.06% | 91.02% | ||
| 5 | 0.391 | 1.66% | 92.68% | ||
| 0.66H and 1.0H | 1 | 4.12 | 71.60% | 71.60% | |
| 2 | 1.407 | 11.99% | 83.59% | ||
| 3 | 0.832 | 5.08% | 88.67% | ||
| 4 | 0.541 | 2.49% | 91.16% | ||
| 5 | 0.4 | 1.66% | 92.82% | ||
| 24F–SW | No outrigger | 1 | 2.683 | 63.85% | 63.85% |
| 2 | 0.581 | 18.80% | 82.65% | ||
| 3 | 0.243 | 6.96% | 89.61% | ||
| 4 | 0.142 | 3.33% | 92.94% | ||
| 5 | 0.098 | 1.90% | 94.84% | ||
| 0.33H | 1 | 2.621 | 63.59% | 63.59% | |
| 2 | 0.578 | 19.20% | 82.79% | ||
| 3 | 0.243 | 6.86% | 89.65% | ||
| 4 | 0.141 | 3.27% | 92.92% | ||
| 5 | 0.098 | 1.93% | 94.85% | ||
| 0.66H | 1 | 2.638 | 64.11% | 64.11% | |
| 2 | 0.579 | 18.53% | 82.64% | ||
| 3 | 0.243 | 6.97% | 89.61% | ||
| 4 | 0.142 | 3.32% | 92.93% | ||
| 5 | 0.098 | 1.89% | 94.82% | ||
| 1.0H | 1 | 2.6 | 64.55% | 64.55% | |
| 2 | 0.569 | 18.24% | 82.79% | ||
| 3 | 0.241 | 6.86% | 89.65% | ||
| 4 | 0.141 | 3.30% | 92.95% | ||
| 5 | 0.097 | 1.88% | 94.83% | ||
| 0.33H and 0.66H | 1 | 2.577 | 63.85% | 63.85% | |
| 2 | 0.576 | 18.93% | 82.78% | ||
| 3 | 0.243 | 6.88% | 89.66% | ||
| 4 | 0.141 | 3.26% | 92.92% | ||
| 5 | 0.098 | 1.92% | 94.84% | ||
| 0.33H and 1.0H | 1 | 2.585 | 63.90% | 63.90% | |
| 2 | 0.573 | 18.95% | 82.85% | ||
| 3 | 0.242 | 6.82% | 89.67% | ||
| 4 | 0.141 | 3.26% | 92.93% | ||
| 5 | 0.098 | 1.92% | 94.85% | ||
| 0.66H and 1.0H | 1 | 2.603 | 64.41% | 64.41% | |
| 2 | 0.574 | 18.30% | 82.71% | ||
| 3 | 0.242 | 6.93% | 89.64% | ||
| 4 | 0.141 | 3.31% | 92.95% | ||
| 5 | 0.098 | 1.88% | 94.83% | ||
| 48F–BRB | No outrigger | 1 | 8.861 | 66.07% | 66.07% |
| 2 | 2.966 | 15.05% | 81.12% | ||
| 3 | 1.741 | 6.12% | 87.24% | ||
| 4 | 1.139 | 2.71% | 89.95% | ||
| 5 | 0.801 | 1.76% | 91.71% | ||
| 0.33H | 1 | 8.587 | 65.53% | 65.53% | |
| 2 | 2.936 | 16.28% | 81.81% | ||
| 3 | 1.74 | 5.80% | 87.61% | ||
| 4 | 1.121 | 2.29% | 89.90% | ||
| 5 | 0.786 | 1.77% | 91.67% | ||
| 0.66H | 1 | 8.772 | 66.55% | 66.55% | |
| 2 | 2.934 | 14.59% | 81.14% | ||
| 3 | 1.741 | 6.17% | 87.31% | ||
| 4 | 1.127 | 2.70% | 90.01% | ||
| 5 | 0.8 | 1.71% | 91.72% | ||
| 1.0H | 1 | 8.854 | 66.11% | 66.11% | |
| 2 | 2.961 | 15.05% | 81.16% | ||
| 3 | 1.735 | 6.13% | 87.29% | ||
| 4 | 1.132 | 2.70% | 89.99% | ||
| 5 | 0.795 | 1.77% | 91.76% | ||
| 0.33H and 0.66H | 1 | 8.498 | 66.03% | 66.03% | |
| 2 | 2.905 | 15.79% | 81.82% | ||
| 3 | 1.739 | 5.84% | 87.66% | ||
| 4 | 1.109 | 2.27% | 89.93% | ||
| 5 | 0.786 | 1.73% | 91.66% | ||
| 0.33H and 1.0H | 1 | 8.58 | 65.57% | 65.57% | |
| 2 | 2.93 | 16.29% | 81.86% | ||
| 3 | 1.733 | 5.79% | 87.65% | ||
| 4 | 1.114 | 2.28% | 89.93% | ||
| 5 | 0.78 | 1.79% | 91.72% | ||
| 0.66H and 1.0H | 1 | 8.765 | 66.58% | 66.58% | |
| 2 | 2.928 | 14.60% | 81.18% | ||
| 3 | 1.735 | 6.17% | 87.35% | ||
| 4 | 1.12 | 2.70% | 90.05% | ||
| 5 | 0.794 | 1.72% | 91.77% | ||
| 48F–SW | No outrigger | 1 | 7.653 | 64.71% | 64.71% |
| 2 | 1.832 | 16.35% | 81.06% | ||
| 3 | 0.757 | 6.66% | 87.72% | ||
| 4 | 0.417 | 3.44% | 91.16% | ||
| 5 | 0.27 | 2.11% | 93.27% | ||
| 0.33H | 1 | 7.296 | 64.10% | 64.10% | |
| 2 | 1.813 | 17.27% | 81.37% | ||
| 3 | 0.756 | 6.43% | 87.80% | ||
| 4 | 0.413 | 3.32% | 91.12% | ||
| 5 | 0.269 | 2.17% | 93.29% | ||
| 0.66H | 1 | 7.544 | 65.01% | 65.01% | |
| 2 | 1.822 | 16.04% | 81.05% | ||
| 3 | 0.757 | 6.67% | 87.72% | ||
| 4 | 0.416 | 3.44% | 91.16% | ||
| 5 | 0.27 | 2.10% | 93.26% | ||
| 1.0H | 1 | 7.586 | 64.98% | 64.98% | |
| 2 | 1.813 | 16.16% | 81.14% | ||
| 3 | 0.753 | 6.61% | 87.75% | ||
| 4 | 0.415 | 3.43% | 91.18% | ||
| 5 | 0.269 | 2.11% | 93.29% | ||
| 0.33H and 0.66H | 1 | 7.196 | 64.41% | 64.41% | |
| 2 | 1.803 | 16.96% | 81.37% | ||
| 3 | 0.756 | 6.45% | 87.82% | ||
| 4 | 0.412 | 3.32% | 91.14% | ||
| 5 | 0.269 | 2.16% | 93.30% | ||
| 0.33H and 1.0H | 1 | 7.233 | 64.39% | 64.39% | |
| 2 | 1.795 | 17.07% | 81.46% | ||
| 3 | 0.752 | 6.38% | 87.84% | ||
| 4 | 0.412 | 3.31% | 91.15% | ||
| 5 | 0.268 | 2.17% | 93.32% | ||
| 0.66H and 1.0H | 1 | 7.482 | 65.27% | 65.27% | |
| 2 | 1.803 | 15.86% | 81.13% | ||
| 3 | 0.753 | 6.62% | 87.75% | ||
| 4 | 0.415 | 3.42% | 91.17% | ||
| 5 | 0.269 | 2.10% | 93.27% |
References
- Samadi, M.; Jahan, N. Comparative study on the effect of outrigger on seismic response of tall buildings with braced and RC wall core. I: Optimum level and examining modal response spectrum analysis reliability. Struct. Des. Tall Spec. Build. 2021, 30, e1848. [Google Scholar] [CrossRef]
- Xing, L.; Zhou, Y.; Huang, W. Seismic optimization analysis of high-rise buildings with a buckling-restrained brace outrigger system. Eng. Struct. 2020, 220, 110959. [Google Scholar] [CrossRef]
- Bai, J.; Chen, H.; Jin, S. Investigation on the interaction between BRBs and the RC frame in BRB-RCF systems. Eng. Struct. 2021, 243, 112685. [Google Scholar] [CrossRef]
- Ayash, N.M.; Shaker, F.M.F.; Mahmoud, F.A. Seismic Performance of Tall Buildings having Steel Plate Shear Wall Combined with BRB-Outriggers. Eng. Res. J. 2024, 183, 107–132. [Google Scholar] [CrossRef]
- Sthapit, N.; Shrestha, R.K.; Paudel, S. Seismic Response Analysis of High-Rise Reinforced Concrete Buildings Using Outrigger System. J. Inst. Eng. Ser. A 2023, 104, 943–952. [Google Scholar] [CrossRef]
- Kushwaha, V.; Mishra, N. A Review on Dynamic Analysis of Outrigger Systems in High Rise Building against Lateral Loading. Int. J. Res. Appl. Sci. Eng. Technol. 2022, 10, 564–568. [Google Scholar] [CrossRef]
- Morales-Beltran, M.; Turan, G.; Dursun, O.; Nijsse, R. Energy dissipation and performance assessment of double damped outriggers in tall buildings under strong earthquakes. Struct. Des. Tall Spec. Build. 2019, 28, e1554. [Google Scholar] [CrossRef]
- Hatzivassiliou, M.; Hatzigeorgiou, G.D. Seismic sequence effects on three-dimensional reinforced concrete buildings. Soil. Dyn. Earthq. Eng. 2015, 72, 77–88. [Google Scholar] [CrossRef]
- Hoveidae, N.; Radpour, S. Performance evaluation of buckling-restrained braced frames under repeated earthquakes. Bull. Earthq. Eng. 2021, 19, 241–262. [Google Scholar] [CrossRef]
- Kim, J.; Choi, H.; Chung, L. Energy-based seismic design of structures with buckling-restrained braces. Steel Compos. Struct. 2004, 4, 437–452. [Google Scholar] [CrossRef]
- Choi, H.; Kim, J. Energy-based seismic design of buckling-restrained braced frames using hysteretic energy spectrum. Eng. Struct. 2006, 28, 304–311. [Google Scholar] [CrossRef]
- Gholami, N.; Garivani, S.; Askariani, S.S. State-of-the-Art Review of Energy-Based Seismic Design Methods. Arch. Comput. Methods Eng. 2021, 29, 1965–1996. [Google Scholar] [CrossRef]
- Leelataviwat, S.; Saewon, W.; Goel, S.C. An Energy Based Method for Seismic Evaluation of Structures. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Park, B.Y.-J.; Ang, A.H.-S.; Asce, F. Mechanistic Seismic Damage Model for Reinforced Concrete. J. Struct. Eng. 1985, 111, 722–739. [Google Scholar] [CrossRef]
- Kappos, A.J. Seismic damage indices for RC buildings: Evaluation of concepts and procedures. Prog. Struct. Eng. Mater. 1997, 1, 78–87. [Google Scholar] [CrossRef]
- Cao, V.V.; Ronagh, H.R.; Ashraf, M.; Baji, H. A new damage index for reinforced concrete structures. Earthq. Struct. 2014, 6, 581–609. [Google Scholar] [CrossRef]
- Hait, P.; Sil, A.; Choudhury, S. Prediction of global damage index of reinforced concrete building using artificial neural network. Int. J. Comput. Methods Eng. Sci. Mech. 2021, 22, 386–399. [Google Scholar] [CrossRef]
- Kalateh-Ahani, M.; Amiri, S. A Park-Ang damage index-based framework for post-mainshock structural safety assessment. Structures 2021, 33, 820–829. [Google Scholar] [CrossRef]
- Zhao, P.P.; Wang, Z.Y.; Babaei, M.; Asemi, K. Applying Improved Performance-Based Instructions to Investigate Seismic Performance of a Code-Conforming Steel Trussed-Tube Building. Buildings 2025, 15, 34. [Google Scholar] [CrossRef]
- Merritt, S.; Uang, C.M.; Benzoni, G. Subassemblage Testing of Star Seismic Buckling-Restrained Braces; Report No. TR-2003/04; Department of Structural Engineering, University of California San Diego: La Jolla, CA, USA, 2003. [Google Scholar]
- Newell, J.; Uang, C.-M.; Benzoni, G. Subassemblage Testing of Corebrace Buckling-Restrained Braces (G Series); Report No. TR-06/01; Department of Structural Engineering, University of California San Diego: La Jolla, CA, USA, 2006. [Google Scholar]
- Etabs. Software for Building Analysis and Design, Version 20; Computers and Structures Inc.: Walnut Creek, CA, USA, 2020.
- TBSC-2018; Turkish Building Seismic Code. Disaster and Emergency Management: Ankara, Turkey, 2018.
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical Stress-Strain Model for Confined Concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- PEER. Available online: https://peer.berkeley.edu/home (accessed on 6 January 2025).
- Arias, A. A measure of earthquake intensity. Seismic Design for Nuclear Power Plants. Mass. Inst. Technol. 1970, 60, 124–130. [Google Scholar]
- De Jesus Vega, E.; Montejo, L.A. Influence of ground motion duration on ductility demands of reinforced concrete structures. Int. J. Adv. Struct. Eng. 2019, 11, 503–517. [Google Scholar] [CrossRef]
- Pawirodikromo, W. The effects of earthquake significant duration D595 to the earthquake intensity measures and the inelastic response of SDOF reinforced concrete structure. MATEC Web Conf. 2019, 280, 1005. [Google Scholar] [CrossRef]
- Bertero, R.D.; Bertero, V.V. Performance-based seismic engineering: The need for a reliable conceptual comprehensive approach. Earthq. Eng. Struct. Dyn. 2002, 31, 627–652. [Google Scholar] [CrossRef]
- Park, Y.J.; Ang, A.H.; Wen, Y.K. Damage-Limiting Aseismic Design of Buildings. Earthq. Spectra 1987, 3, 1–26. [Google Scholar] [CrossRef]
- Ang, A.H.-S. Seismic damage assessment and basis for damage-limiting design. Probabilistic Eng. Mech. 1988, 3, 146–150. [Google Scholar] [CrossRef]
- ASCE 7-22; Minimum Design Loads and Associated Criteria for Buildings and Other Structures. ASCE: Reston, VA, USA, 2022.

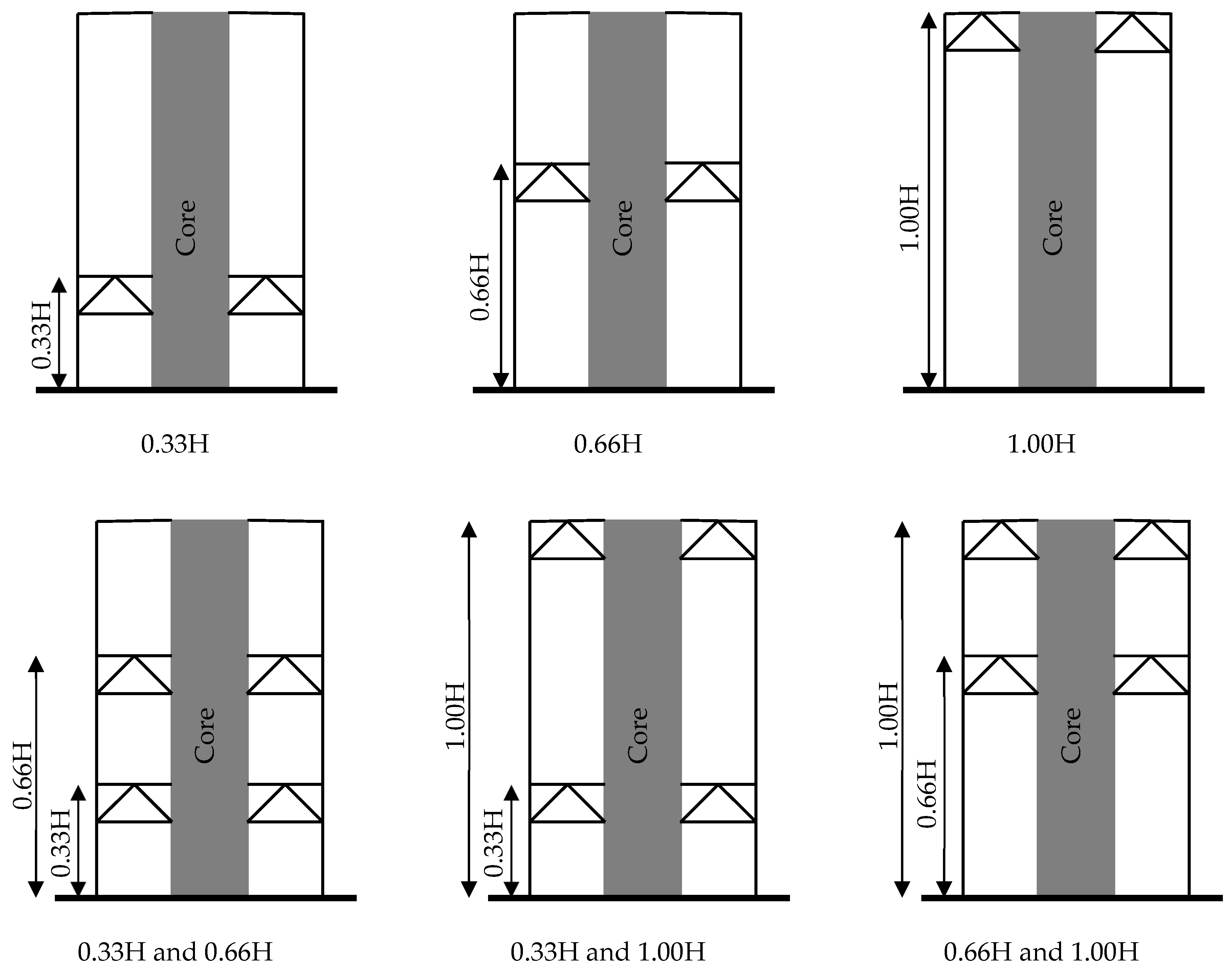




| Structure Type | Stories | Column Dimensions (cm) | Wall Thickness (cm) | Beam Dimension (cm) |
|---|---|---|---|---|
| 24-story | 1–8 | 110 × 110 | 50 | 30 × 70 |
| 9–16 | 90 × 90 | |||
| 17–24 | 70 × 70 | |||
| 48-story | 1–3 | 160 × 160 | 70 | |
| 4–6 | 140 × 140 | |||
| 7–8 | 120 × 120 |
| SINGLE OUTRIGGER LEVEL | DOUBLE OUTRIGGER LEVELS | ||||||
|---|---|---|---|---|---|---|---|
| Model Type | T (s) | ||||||
| No Outrigger | 0.33H | 0.66H | 1H | 0.33H, 0.66H | 0.33H, 1H | 0.66H, 1H | |
| M24-BRB | 4.175 | 4.032 | 4.121 | 4.172 | 3.978 | 4.030 | 4.119 |
| M48-BRB | 8.861 | 8.596 | 8.771 | 8.854 | 8.498 | 8.580 | 8.765 |
| M24-SW | 3.183 | 3.072 | 3.112 | 3.134 | 3.005 | 3.025 | 3.067 |
| M48-SW | 7.653 | 7.295 | 7.544 | 7.585 | 7.196 | 7.232 | 7.481 |
| Building Type | Story Number | KFR Story Stiff. (kN/m) | Sum of BRB Yielding Section Area Asc (mm2) | Input Values | |
|---|---|---|---|---|---|
| k = 1 | Yield Force (kN) | Ultimate Force (kN) | |||
| 24-story | 0–1 | 203,794 | 5188 | 610 | 881 |
| 2–8 | 78,265 | 1992 | 234 | 338 | |
| 9–16 | 32,098 | 817 | 96 | 139 | |
| 17–24 | 30,285 | 771 | 91 | 131 | |
| 48-story | 0–1 | 512,648 | 13,050 | 1533 | 2215 |
| 2–16 | 183,029 | 4659 | 547 | 791 | |
| 17–32 | 39,388 | 1003 | 118 | 170 | |
| 33–48 | 36,966 | 941 | 111 | 160 | |
| Seismic Sequence No. | Event Name | Station | Record Sequential Number | Date | PGA (g) | Magnitude | (s) | (m/s) |
|---|---|---|---|---|---|---|---|---|
| SS-1 | Mammoth Lakes | Convict Creek | 230 | 5/25/1980 (16:34) | 0.44 | 6.1 | 9.18 | 2.245 |
| 240 | 5/25/1980 (20:35) | 0.48 | 5.7 | 3.67 | 0.647 | |||
| SS-2 | Chalfant Valley | Brothers Ranch | 547 | 7/20/1986 (14:29) | 0.27 | 5.8 | 8.48 | 0.525 |
| 558 | 7/21/1986 (14:42) | 0.45 | 6.2 | 6.17 | 1.938 | |||
| SS-3 | Coalinga | 46T04 CHP | 406 | 7/22/1983 (02:39) | 0.52 | 5.8 | 8.51 | 0.543 |
| 418 | 7/25/1983 (22:31) | 0.68 | 5.2 | 2.84 | 0.576 | |||
| SS-4 | Whittier Narrows | San Marino | 691 | 10/1/1987 (14:42) | 0.19 | 6.0 | 11.44 | 0.130 |
| 716 | 10/4/1987 (10:59) | 0.21 | 5.3 | 3.70 | 0.094 | |||
| SS-5 | Northwest China | Jiashi, China | 1748 | 5/4/1997 (23:46) | 0.27 | 6.1 | 14.38 | 0.491 |
| 1752 | 11/4/1997 (5:34) | 0.30 | 5.9 | 13.44 | 0.624 |
| Maximum Inter-Story Drift Ratio (MIDR) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Stories | Core | Outrigger Location | SS-1 | SS-2 | SS-3 | SS-4 | SS-5 | Average |
| 24 | BRB | No outrigger | 0.007088 | 0.008253 | 0.005186 | 0.012745 | 0.007277 | 0.00811 |
| 0.33H | 0.007714 | 0.007107 | 0.004925 | 0.01224 | 0.007282 | 0.00785 | ||
| 0.66H | 0.007396 | 0.007878 | 0.005092 | 0.010911 | 0.006847 | 0.00762 | ||
| 1H | 0.007279 | 0.008212 | 0.0051 | 0.013201 | 0.007416 | 0.00824 | ||
| 0.33H and 0.66H | 0.007479 | 0.006831 | 0.004798 | 0.01032 | 0.007158 | 0.00732 | ||
| 0.33H and 1H | 0.007413 | 0.007081 | 0.004872 | 0.012095 | 0.00707 | 0.00771 | ||
| 0.66H and 1H | 0.00719 | 0.008091 | 0.004974 | 0.011065 | 0.006763 | 0.00762 | ||
| SW | No outrigger | 0.005804 | 0.005367 | 0.005995 | 0.00811 | 0.008936 | 0.00684 | |
| 0.33H | 0.010539 | 0.009958 | 0.008636 | 0.007948 | 0.01064 | 0.00954 | ||
| 0.66H | 0.006092 | 0.005739 | 0.005818 | 0.007288 | 0.013916 | 0.00777 | ||
| 1H | 0.009644 | 0.009974 | 0.007539 | 0.008372 | 0.010215 | 0.00915 | ||
| 0.33H and 0.66H | 0.005943 | 0.005478 | 0.005838 | 0.005887 | 0.008102 | 0.00625 | ||
| 0.33H and 1H | 0.005753 | 0.005463 | 0.005439 | 0.005932 | 0.008323 | 0.00618 | ||
| 0.66H and 1H | 0.005868 | 0.005313 | 0.005224 | 0.005956 | 0.008352 | 0.00614 | ||
| 48 | BRB | No outrigger | 0.006867 | 0.008128 | 0.006187 | 0.005252 | 0.006772 | 0.00664 |
| 0.33H | 0.006773 | 0.008102 | 0.00634 | 0.00681 | 0.006346 | 0.00687 | ||
| 0.66H | 0.00672 | 0.008378 | 0.006339 | 0.006546 | 0.006889 | 0.00697 | ||
| 1H | 0.006586 | 0.007901 | 0.006053 | 0.005745 | 0.006787 | 0.00661 | ||
| 0.33H and 0.66H | 0.006764 | 0.007847 | 0.006109 | 0.007197 | 0.005973 | 0.00678 | ||
| 0.33H and 1H | 0.006381 | 0.007989 | 0.005853 | 0.00649 | 0.006161 | 0.00657 | ||
| 0.66H and 1H | 0.006526 | 0.008574 | 0.005881 | 0.006494 | 0.00695 | 0.00689 | ||
| SW | No outrigger | 0.005021 | 0.006711 | 0.007524 | 0.003863 | 0.007296 | 0.00608 | |
| 0.33H | 0.005024 | 0.006112 | 0.007744 | 0.004378 | 0.006409 | 0.00593 | ||
| 0.66H | 0.005047 | 0.006451 | 0.007814 | 0.004298 | 0.007413 | 0.0062 | ||
| 1H | 0.005108 | 0.006312 | 0.0071 | 0.004019 | 0.00731 | 0.00597 | ||
| 0.33H and 0.66H | 0.005225 | 0.006078 | 0.007992 | 0.003971 | 0.006444 | 0.00594 | ||
| 0.33H and 1H | 0.005219 | 0.005901 | 0.007281 | 0.003984 | 0.007079 | 0.00589 | ||
| 0.66H and 1H | 0.005076 | 0.005877 | 0.007084 | 0.003934 | 0.007136 | 0.00582 | ||
| Reduction (%) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Stories | Core | Outrigger Location | SS-1 | SS-2 | SS-3 | SS-4 | SS-5 | Average |
| 24 | BRB | No outrigger | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 0.33H | −8.83 | 13.89 | 5.03 | 3.96 | −0.07 | 3.16 | ||
| 0.66H | −4.35 | 4.54 | 1.81 | 14.39 | 5.91 | 5.98 | ||
| 1H | −2.69 | 0.50 | 1.66 | −3.58 | −1.91 | −1.63 | ||
| 0.33H and 0.66H | −5.52 | 17.23 | 7.48 | 19.03 | 1.64 | 9.77 | ||
| 0.33H and 1H | −4.59 | 14.20 | 6.05 | 5.10 | 2.84 | 4.98 | ||
| 0.66H and 1H | −1.44 | 1.96 | 4.09 | 13.18 | 7.06 | 6.08 | ||
| SW | No outrigger | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.33H | −81.58 | −85.54 | −44.05 | 2.00 | −19.07 | −39.49 | ||
| 0.66H | −4.96 | −6.93 | 2.95 | 10.14 | −55.73 | −13.57 | ||
| 1H | −66.16 | −85.84 | −25.75 | −3.23 | −14.31 | −33.71 | ||
| 0.33H and 0.66H | −2.39 | −2.07 | 2.62 | 27.41 | 9.33 | 8.66 | ||
| 0.33H and 1H | 0.88 | −1.79 | 9.27 | 26.86 | 6.86 | 9.65 | ||
| 0.66H and 1H | −1.10 | 1.01 | 12.86 | 26.56 | 6.54 | 10.23 | ||
| 48 | BRB | No outrigger | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 0.33H | 1.37 | 0.32 | −2.47 | −29.66 | 6.29 | −3.51 | ||
| 0.66H | 2.14 | −3.08 | −2.46 | −24.64 | −1.73 | −5.02 | ||
| 1H | 4.09 | 2.79 | 2.17 | −9.39 | −0.22 | 0.40 | ||
| 0.33H and 0.66H | 1.50 | 3.46 | 1.26 | −37.03 | 11.80 | −2.06 | ||
| 0.33H and 1H | 7.08 | 1.71 | 5.40 | −23.57 | 9.02 | 1.00 | ||
| 0.66H and 1H | 4.97 | −5.49 | 4.95 | −23.65 | −2.63 | −3.67 | ||
| SW | No outrigger | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.33H | −0.06 | 8.93 | −2.92 | −13.33 | 12.16 | 2.46 | ||
| 0.66H | 26.50 | 3.87 | −3.85 | −11.26 | −1.60 | −2.00 | ||
| 1H | 25.62 | 5.95 | 5.64 | −4.04 | −0.19 | 1.86 | ||
| 0.33H and 0.66H | 23.91 | 9.43 | −6.22 | −2.80 | 11.68 | 2.32 | ||
| 0.33H and 1H | 24.00 | 12.07 | 3.23 | −3.13 | 2.97 | 3.13 | ||
| 0.66H and 1H | 26.08 | 12.43 | 5.85 | −1.84 | 2.19 | 4.30 | ||
| Damage Index | Degree of Damage | Physical Appearance |
|---|---|---|
| <0.10 | Slight | Sporadic occurrence of cracking |
| 0.10–0.25 | Minor | Minor cracks; partial crushing of concrete in columns |
| 0.25–0.40 | Moderate | Extensive large cracks; spalling of concrete in weaker elements |
| 0.40–1.00 | Severe | Extensive crashing of concrete; disclosure of buckled reinforcement |
| >1.00 | Collapse | Partial or total collapse of building |
| Archetype | Outrigger Config. | h [m] | System | Ct | x | Ta = Ct*h^x [s] | T1 [s] | T1/Ta |
|---|---|---|---|---|---|---|---|---|
| 24F–BRB | No outrigger | 96 | Braced/Dual | 0.0731 | 0.75 | 2.242 | 4.175 | 1.86 |
| 0.33H | 96 | Braced/Dual | 0.0731 | 0.75 | 2.242 | 4.032 | 1.80 | |
| 0.66H | 96 | Braced/Dual | 0.0731 | 0.75 | 2.242 | 4.121 | 1.84 | |
| 1.0H | 96 | Braced/Dual | 0.0731 | 0.75 | 2.242 | 4.172 | 1.86 | |
| 0.33H and 0.66H | 96 | Braced/Dual | 0.0731 | 0.75 | 2.242 | 3.978 | 1.77 | |
| 0.33H and 1.0H | 96 | Braced/Dual | 0.0731 | 0.75 | 2.242 | 4.03 | 1.80 | |
| 0.66H and 1.0H | 96 | Braced/Dual | 0.0731 | 0.75 | 2.242 | 4.119 | 1.84 | |
| 24F–SW | No outrigger | 96 | Shear wall | 0.0488 | 0.75 | 1.497 | 3.183 | 2.13 |
| 0.33H | 96 | Shear wall | 0.0488 | 0.75 | 1.497 | 3.072 | 2.05 | |
| 0.66H | 96 | Shear wall | 0.0488 | 0.75 | 1.497 | 3.112 | 2.08 | |
| 1.0H | 96 | Shear wall | 0.0488 | 0.75 | 1.497 | 3.134 | 2.09 | |
| 0.33H and 0.66H | 96 | Shear wall | 0.0488 | 0.75 | 1.497 | 3.005 | 2.01 | |
| 0.33H and 1.0H | 96 | Shear wall | 0.0488 | 0.75 | 1.497 | 3.025 | 2.02 | |
| 0.66H and 1.0H | 96 | Shear wall | 0.0488 | 0.75 | 1.497 | 3.067 | 2.05 | |
| 48F–BRB | No outrigger | 192 | Braced/Dual | 0.0731 | 0.75 | 3.770 | 8.861 | 2.35 |
| 0.33H | 192 | Braced/Dual | 0.0731 | 0.75 | 3.770 | 8.596 | 2.28 | |
| 0.66H | 192 | Braced/Dual | 0.0731 | 0.75 | 3.770 | 8.771 | 2.33 | |
| 1.0H | 192 | Braced/Dual | 0.0731 | 0.75 | 3.770 | 8.854 | 2.35 | |
| 0.33H and 0.66H | 192 | Braced/Dual | 0.0731 | 0.75 | 3.770 | 8.498 | 2.25 | |
| 0.33H and 1.0H | 192 | Braced/Dual | 0.0731 | 0.75 | 3.770 | 8.58 | 2.28 | |
| 0.66H and 1.0H | 192 | Braced/Dual | 0.0731 | 0.75 | 3.770 | 8.765 | 2.32 | |
| 48F–SW | No outrigger | 192 | Shear wall | 0.0488 | 0.75 | 2.517 | 7.653 | 3.04 |
| 0.33H | 192 | Shear wall | 0.0488 | 0.75 | 2.517 | 7.295 | 2.90 | |
| 0.66H | 192 | Shear wall | 0.0488 | 0.75 | 2.517 | 7.544 | 3.00 | |
| 1.0H | 192 | Shear wall | 0.0488 | 0.75 | 2.517 | 7.585 | 3.01 | |
| 0.33H and 0.66H | 192 | Shear wall | 0.0488 | 0.75 | 2.517 | 7.196 | 2.86 | |
| 0.33H and 1.0H | 192 | Shear wall | 0.0488 | 0.75 | 2.517 | 7.232 | 2.87 | |
| 0.66H and 1.0H | 192 | Shear wall | 0.0488 | 0.75 | 2.517 | 7.481 | 2.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
İnam, İ.E.; Dindar, A.A. Deformation and Energy-Based Comparison of Outrigger Locations in RC and BRB-Core Tall Buildings Under Repetitive Earthquakes. Buildings 2025, 15, 3563. https://doi.org/10.3390/buildings15193563
İnam İE, Dindar AA. Deformation and Energy-Based Comparison of Outrigger Locations in RC and BRB-Core Tall Buildings Under Repetitive Earthquakes. Buildings. 2025; 15(19):3563. https://doi.org/10.3390/buildings15193563
Chicago/Turabian Styleİnam, İlhan Emre, and Ahmet Anıl Dindar. 2025. "Deformation and Energy-Based Comparison of Outrigger Locations in RC and BRB-Core Tall Buildings Under Repetitive Earthquakes" Buildings 15, no. 19: 3563. https://doi.org/10.3390/buildings15193563
APA Styleİnam, İ. E., & Dindar, A. A. (2025). Deformation and Energy-Based Comparison of Outrigger Locations in RC and BRB-Core Tall Buildings Under Repetitive Earthquakes. Buildings, 15(19), 3563. https://doi.org/10.3390/buildings15193563






