A Box-Based Method for Regularizing the Prediction of Semantic Segmentation of Building Facades
Abstract
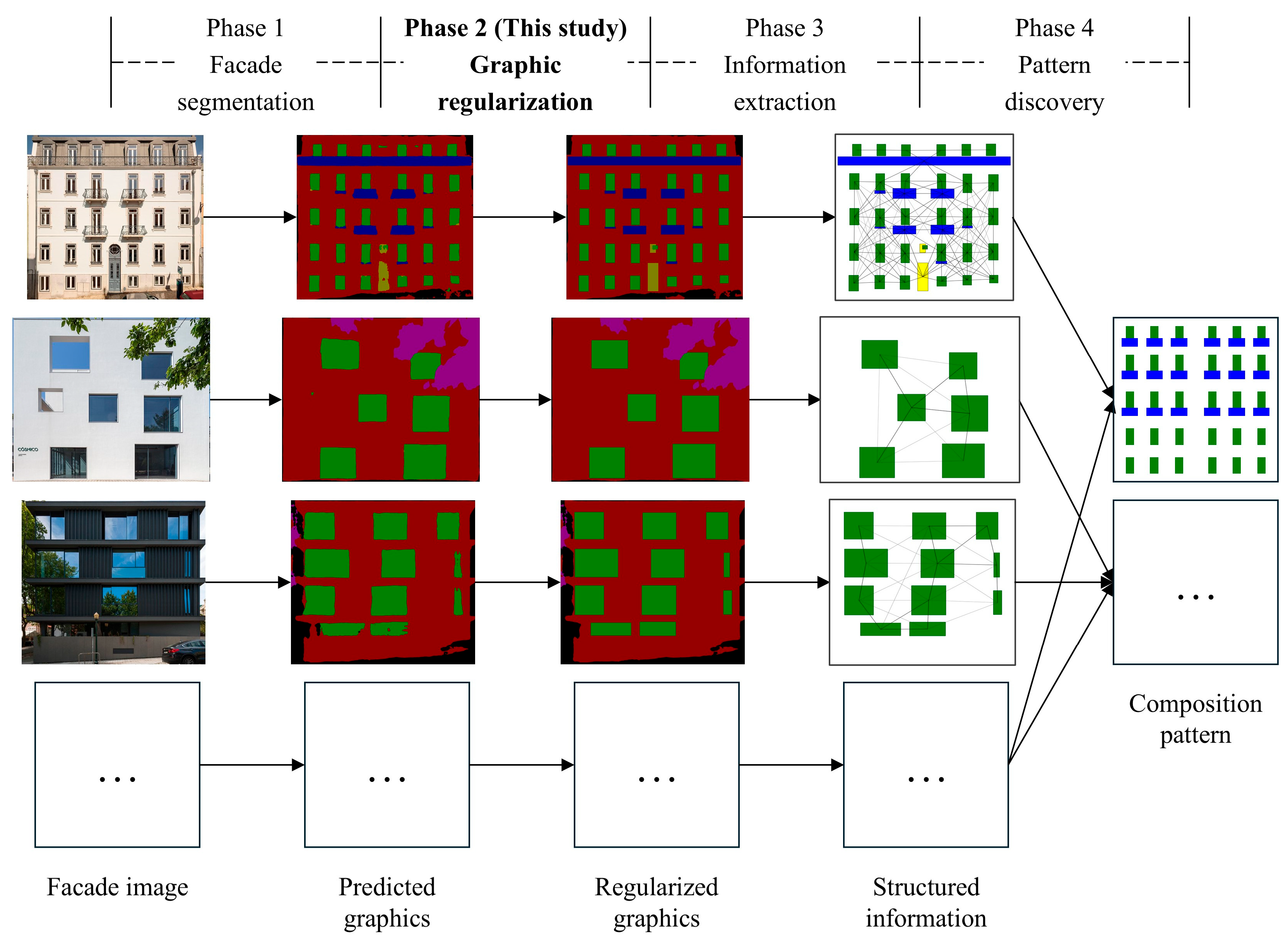
1. Introduction
- The proposed method regularizes the predicted graphics into basic rectilinear polygons that conform to the composition characteristics of building facades. The regularized graphics are useful for many image-based applications of building facades.
- A simple yet effective mechanism of graphic regularization is provided, which can be applied to other similar tasks easily and flexibly.
- This study demonstrates the importance of prior knowledge in regularization tasks, serving as a reference for related research.
2. Related Work
2.1. Polygon-Based Methods
2.1.1. Vertex-Based Approaches
2.1.2. Area-Based Approaches
2.1.3. Axis-Based Approaches
2.2. Conversion-Based Methods
2.3. Snake-Based Methods
2.4. Summary
3. Methodology
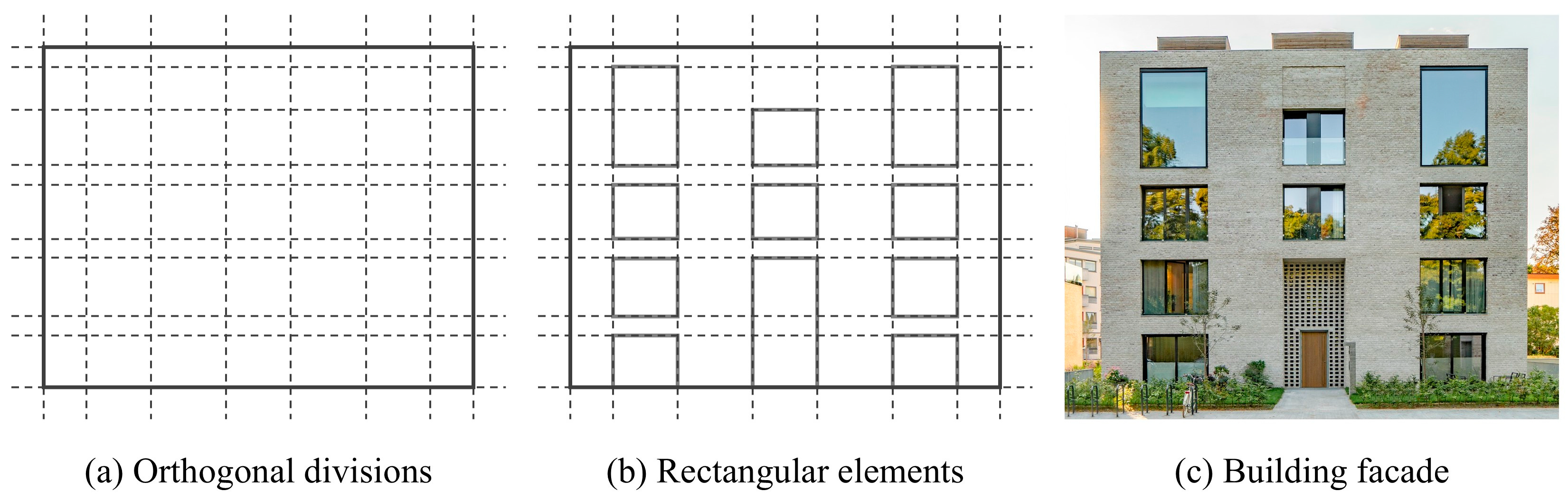
3.1. Principles
3.1.1. Principle 1: A Complex Shape Can Be Regarded as the Uncovered Part of a Partially Covered Rectangle
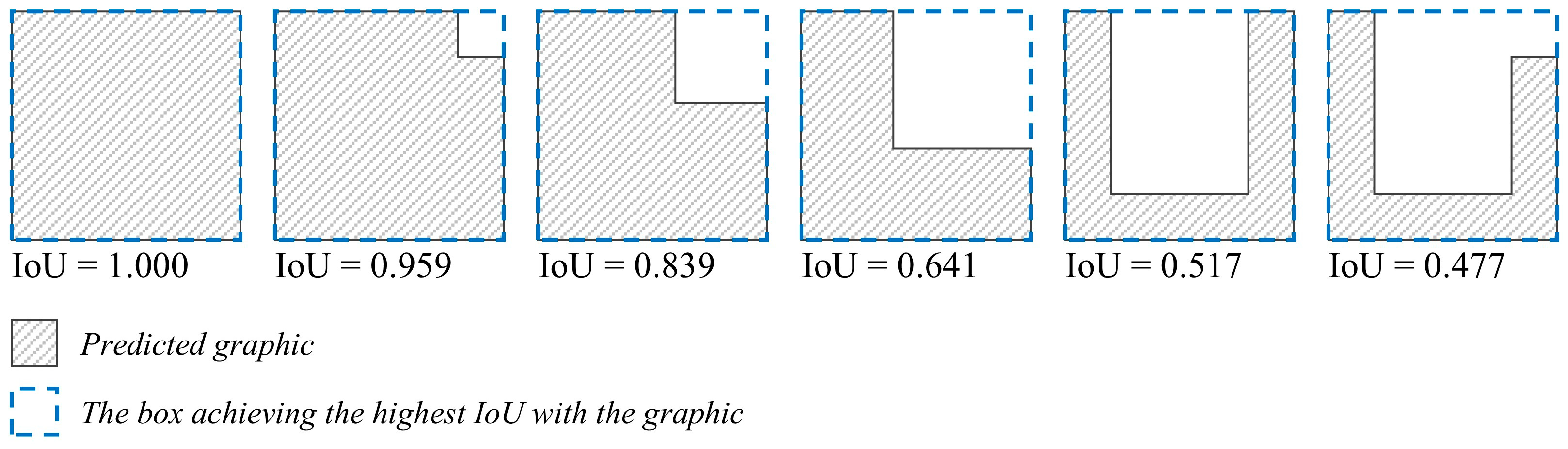
3.1.2. Principle 2: The Higher the Complexity of a Graphic, the Lower Its Highest Achievable IoU with a Rectangle
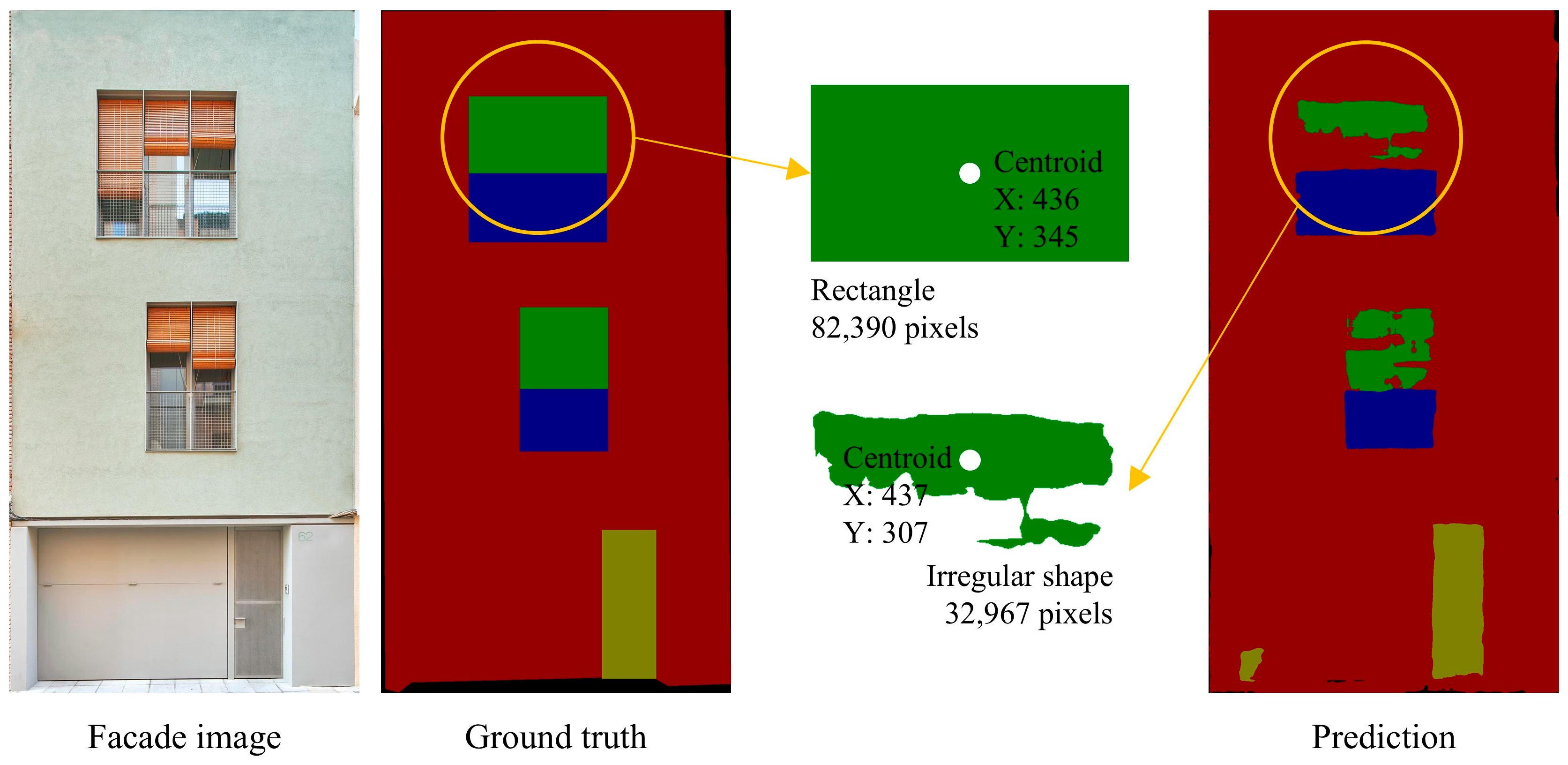
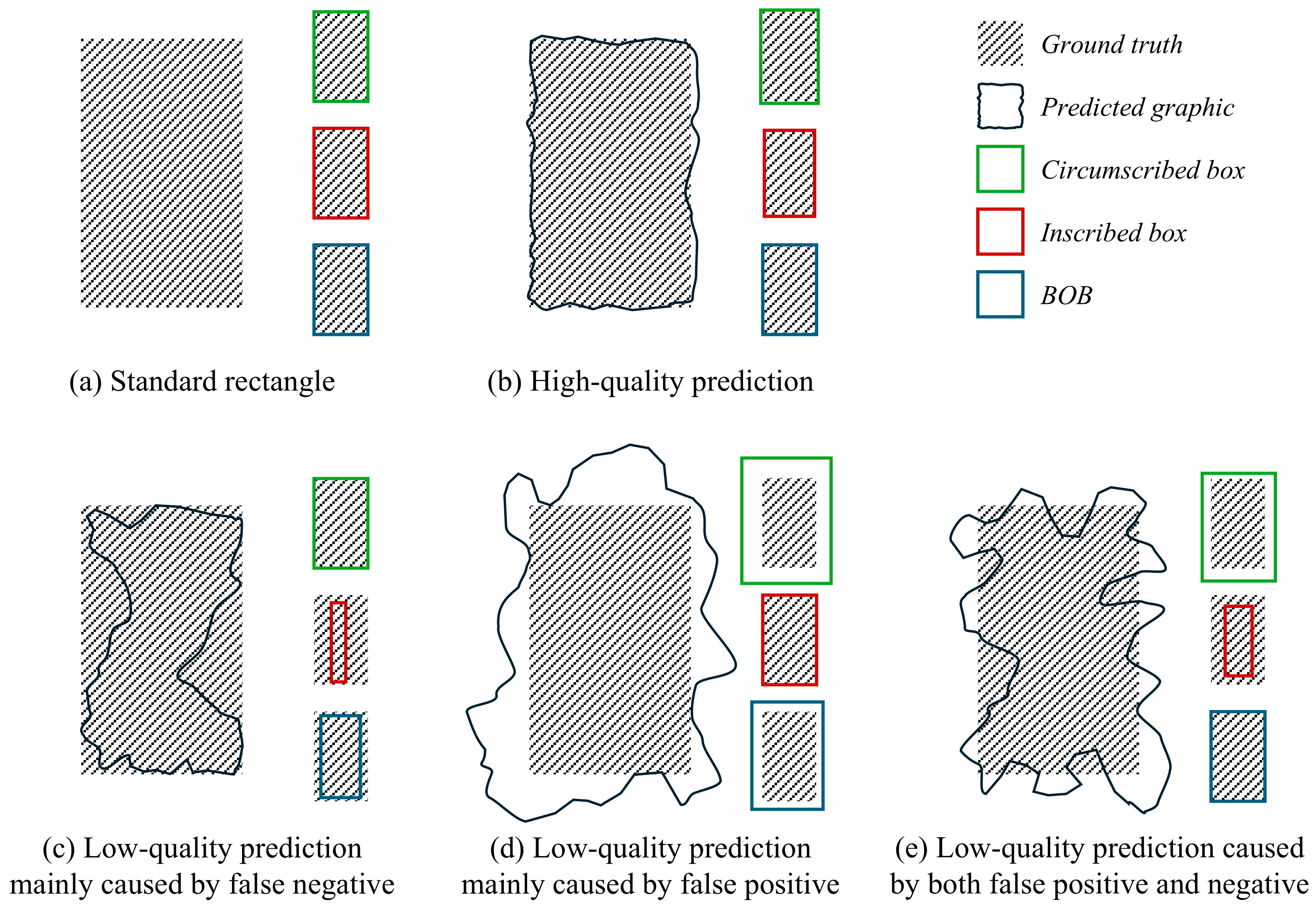
3.2. Definitions
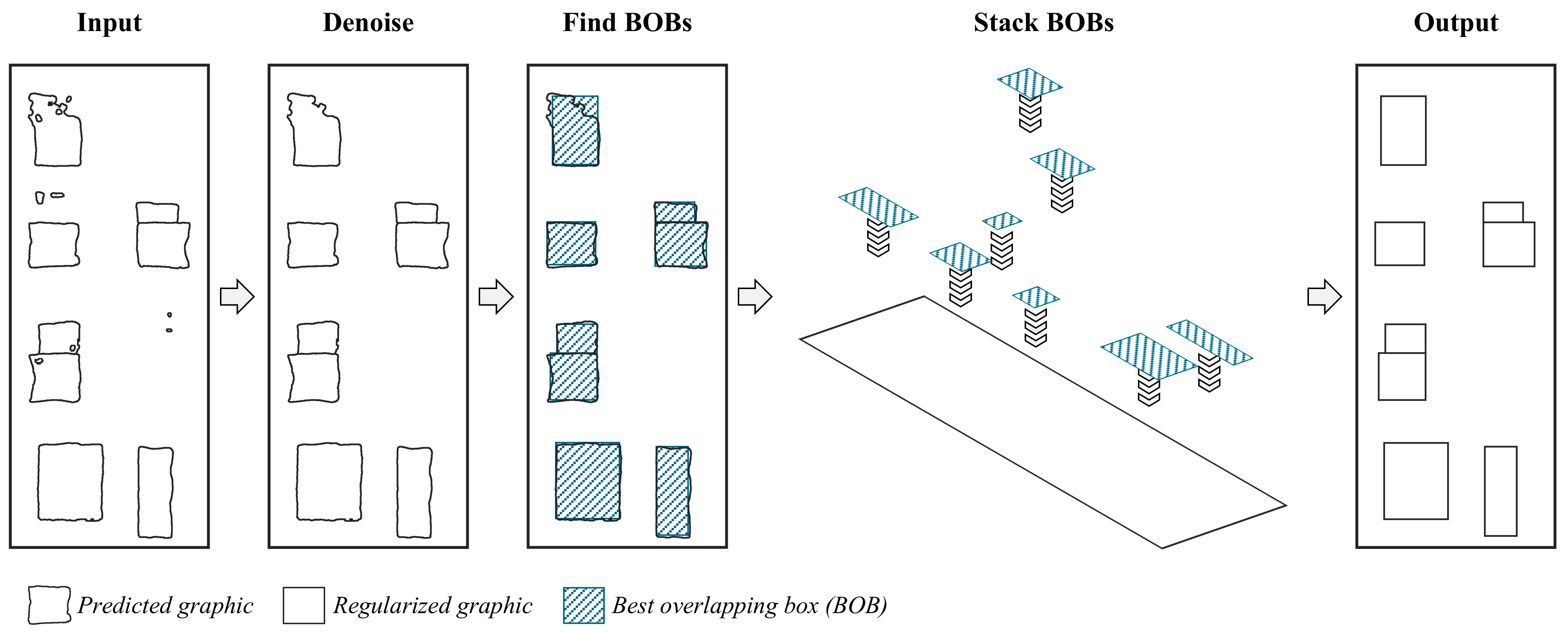
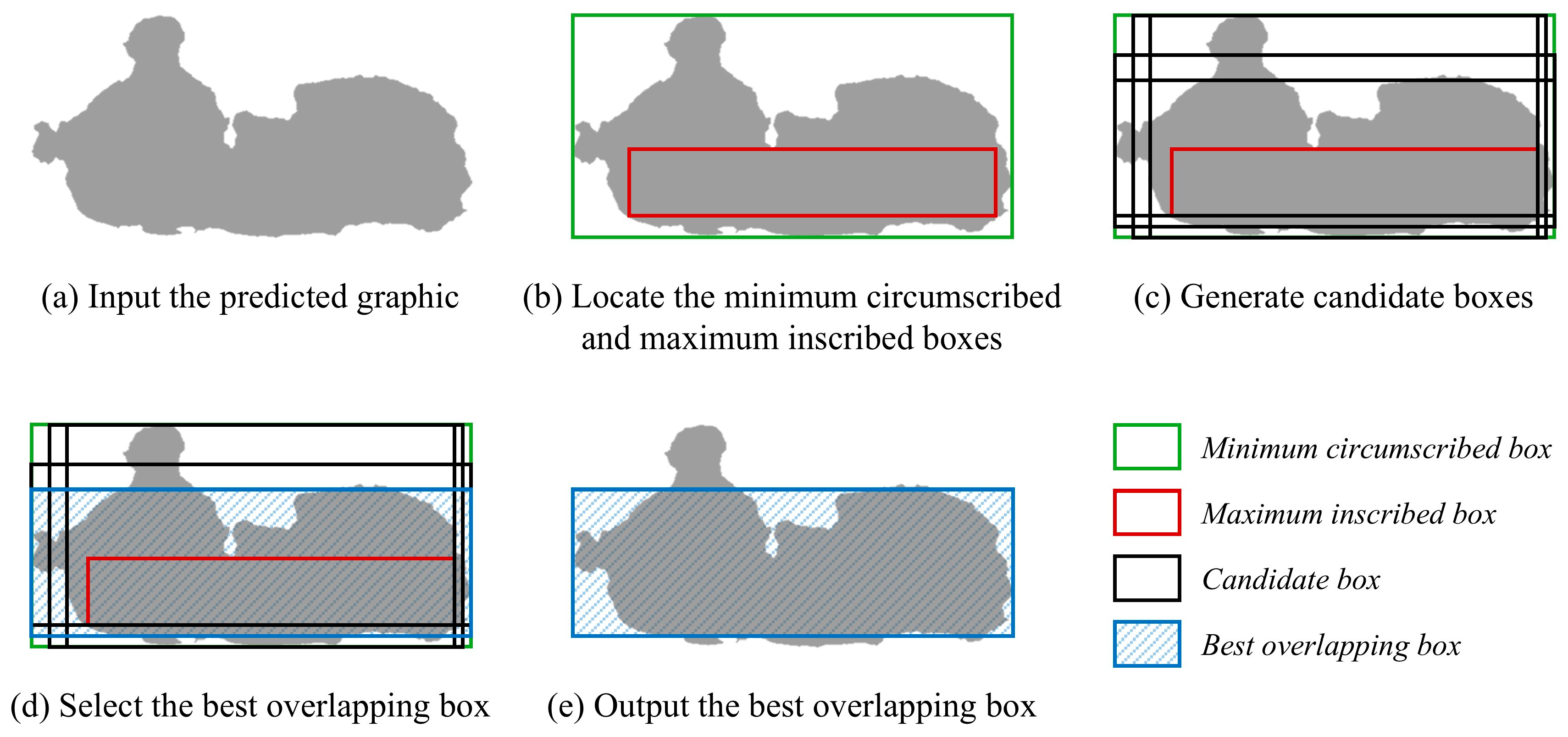
3.3. Process
| Algorithm 1. The box-based graphic regularization for segmented facades. | |
| Input: A set of segmented facades with predicted graphics of facade elements | |
| Output: A set of Segmented facades with regularized graphics of facade elements | |
| 1: | for i in [1, m] (m = the number of input facade images) |
| 2: | Regularize the predicted graphics in the i-th image |
| 3: | # Stage 1: Denoising # |
| 4: | Count the number of pixels of each graphic of facade elements |
| 5: | Remove the graphics whose pixel count is below the threshold |
| 6: | Fill the holes inside the graphics of facade elements |
| 7: | # Stage 2: BOB finding # |
| 8: | for j in [1, n] (n = the number of graphics in the denoised image) |
| 9: | Locate the MCB (LMCB, BMCB, RMCB, TMCB) of the j-th graphic |
| 10: | Locate the MIB (LMIB, BMIB, RMIB, TMIB) of the j-th graphic |
| 11: | # Horizontal sliding # |
| 12: | for LCB in [LMCB, LMIB] |
| 13: | for RCB in [RMIB, RMCB] |
| 14: | Generate a CB [LCB, BCB = BMCB, RCB, TCB = TMCB] |
| 15: | Compute the IoU between the CB and the j-th graphic |
| 16: | # Vertical sliding # |
| 17: | for BCB in [BMCB, BMIB] |
| 18: | for TCB in [TMIB, TMCB] |
| 19: | Generate a CB [LCB = LMCB, BCB, RCB = RMCB, TCB] |
| 20: | Compute the IoU between the CB and the j-th graphic |
| 21: | Select the CB with the highest IoU as the BOB of the j-th graphic |
| 22: | until the BOBs of all graphics are found |
| 23: | # Stege 3: BOB stacking # |
| 24: | Sort the BOBs in ascending order of their IoU |
| 25: | Stack the BOBs onto the same layer according to this order |
| 26: | Replace the pixels in the i-th image with those from this layer |
| 27: | # Return # |
| 28: | return the i-th facade image with regularized graphics |
| 29: | until all input facade images are regularized |
3.3.1. Denoising
3.3.2. BOB Finding
3.3.3. BOB Stacking
3.4. Complexity
4. Experiment
4.1. Data
4.2. Methods
4.3. Metrics
4.4. Results
4.4.1. Effect
4.4.2. Correctness
4.4.3. Time Consumption
4.4.4. Ablation Analysis
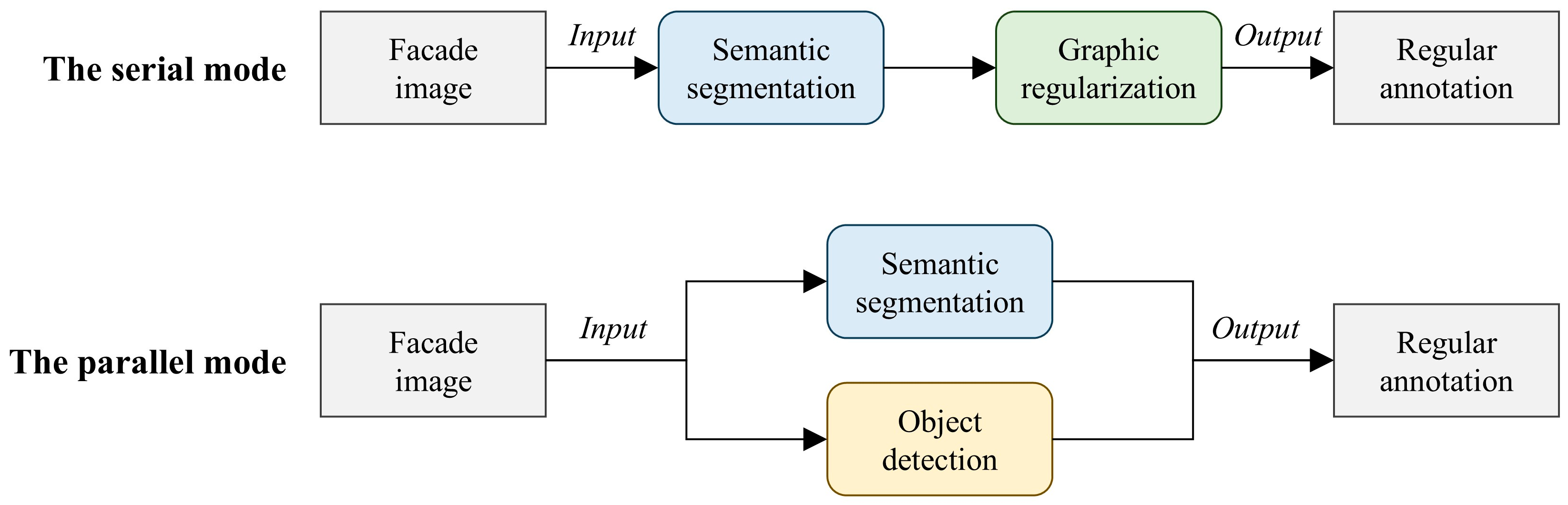
5. Discussion
5.1. Regularizing Predictions with Prior Knowledge
5.2. Comparison with Object Detection
5.3. Future Applications
6. Limitations
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, J.; Wang, L.; Zhou, W.; Zhang, H.; Cui, X.; Guo, Y. Viewpoint assessment and recommendation for photographing architectures. IEEE Trans. Vis. Comput. Graph. 2019, 25, 2636–2649. [Google Scholar] [CrossRef]
- Liu, S.; Zou, G.; Zhang, S. A clustering-based method of typical architectural case mining for architectural innovation. J. Asian Arch. Build. Eng. 2020, 19, 71–89. [Google Scholar] [CrossRef]
- Demir, G.; Çekmiş, A.; Yeşilkaynak, V.B.; Unal, G. Detecting visual design principles in art and architecture through deep convolutional neural networks. Autom. Constr. 2021, 130, 103826. [Google Scholar] [CrossRef]
- Zhang, X.; Aliaga, D. RFCNet: Enhancing urban segmentation using regularization, fusion, and completion. Comput. Vis. Image Underst. 2022, 220, 103435. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, J.; Zhang, R.; Li, Y.; Li, L.; Nakashima, Y. Improving facade parsing with vision transformers and line integration. Adv. Eng. Inform. 2024, 60, 102463. [Google Scholar] [CrossRef]
- Zhang, R.; Jing, M.; Lu, G.; Yi, X.; Shi, S.; Huang, Y.; Liu, L. Building element recognition with MTL-AINet considering view perspectives. Open Geosci. 2023, 15, 20220506. [Google Scholar] [CrossRef]
- Hou, J.; Zhou, J.; He, Y.; Hou, B.; Li, J. Automatic reconstruction of semantic façade model of architectural heritage. Herit. Sci. 2024, 12, 400. [Google Scholar] [CrossRef]
- Liu, Y.; Chua, D.K.; Yeoh, J.K. Automated engineering analysis of crack mechanisms on building façades using UAVs. J. Build. Eng. 2025, 103, 112176. [Google Scholar] [CrossRef]
- Gu, D.; Chen, W.; Lu, X. Automated assessment of wind damage to windows of buildings at a city scale based on oblique photography, deep learning and CFD. J. Build. Eng. 2022, 52, 104355. [Google Scholar] [CrossRef]
- Cao, J.; Metzmacher, H.; O’DOnnell, J.; Frisch, J.; Bazjanac, V.; Kobbelt, L.; van Treeck, C. Facade geometry generation from low-resolution aerial photographs for building energy modeling. Build. Environ. 2017, 123, 601–624. [Google Scholar] [CrossRef]
- Zhang, Y.; Deng, X.; Zhang, Y. Generation of sub-item load profiles for public buildings based on the conditional generative adversarial network and moving average method. Energy Build. 2022, 268, 112185. [Google Scholar] [CrossRef]
- Sewasew, Y.; Tesfamariam, S. Historic building information modeling using image: Example of port city Massawa, Eritrea. J. Build. Eng. 2023, 78, 107662. [Google Scholar] [CrossRef]
- Dai, M.; Ward, W.O.; Meyers, G.; Tingley, D.D.; Mayfield, M. Residential building facade segmentation in the urban environment. Build. Environ. 2021, 199, 107921. [Google Scholar] [CrossRef]
- Hu, Y.; Wei, J.; Zhang, S.; Liu, S. FDIE: A graph-based framework for extracting design information from annotated building facade images. J. Asian Arch. Build. Eng. 2024, 24, 2530–2553. [Google Scholar] [CrossRef]
- Lotte, R.G.; Haala, N.; Karpina, M.; Aragão, L.E.O.e.C.d.; Shimabukuro, Y.E. 3D Façade Labeling over Complex Scenarios: A Case Study Using Convolutional Neural Network and Structure-From-Motion. Remote Sens. 2018, 10, 1435. [Google Scholar] [CrossRef]
- Zhao, K.; Kang, J.; Jung, J.; Sohn, G. Building extraction from satellite images using Mask R-CNN with building boundary regularization. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 242–246. [Google Scholar]
- Kong, L.; Qian, H.; Xie, L.; Huang, Z.; Qiu, Y.; Bian, C. Multilevel regularization method for building outlines extracted from high-resolution remote sensing images. Appl. Sci. 2023, 13, 12599. [Google Scholar] [CrossRef]
- Wei, S.; Ji, S.; Lu, M. Toward automatic building footprint delineation from aerial images using CNN and regularization. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2178–2189. [Google Scholar] [CrossRef]
- Douglas, D.H.; Peucker, T.K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. Cartogr. Int. J. Geogr. Inf. Geovis. 1973, 10, 112–122. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, J.; Xu, F.; Huang, Z.; Li, Y. Adaptive algorithm for automated polygonal approximation of high spatial resolution remote sensing imagery segmentation contours. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1099–1106. [Google Scholar] [CrossRef]
- Mousa, Y.A.; Helmholz, P.; Belton, D.; Bulatov, D. Building detection and regularisation using DSM and imagery information. Photogramm. Rec. 2019, 34, 85–107. [Google Scholar] [CrossRef]
- Wu, J.-S.; Leou, J.-J. New polygonal approximation schemes for object shape representation. Pattern Recognit. 1993, 26, 471–484. [Google Scholar] [CrossRef]
- Wang, S.; Yang, Y.; Chang, J.; Gao, X. Optimization of building contours by classifying high-resolution images. Laser Optoelectron. Prog. 2020, 57, 022801. (In Chinese) [Google Scholar] [CrossRef]
- Du, J.; Chen, D.; Wang, R.; Peethambaran, J.; Mathiopoulos, P.T.; Xie, L.; Yun, T. A novel framework for 2.5-D building contouring from large-scale residential scenes. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4121–4145. [Google Scholar] [CrossRef]
- Pan, M.; Chang, J.; Gao, X.; Yang, Y.; Zhong, K. Building contour optimization method based on main direction. Acta Opt. Sin. 2022, 42, 5892. (In Chinese) [Google Scholar] [CrossRef]
- Li, X.; Qiu, F.; Shi, F.; Tang, Y. A recursive hull and signal-based building footprint generation from airborne LiDAR data. Remote Sens. 2022, 14, 5892. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, L.; Waslander, S.L.; Liu, X. An end-to-end shape modeling framework for vectorized building outline generation from aerial images. ISPRS J. Photogramm. Remote Sens. 2020, 170, 114–126. [Google Scholar] [CrossRef]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2881–2890. [Google Scholar] [CrossRef]
- Kass, M.; Witkin, A.; Terzopoulos, D. Snakes: Active contour models. Int. J. Comput. Vis. 1988, 1, 321–331. [Google Scholar] [CrossRef]
- Menet, S.; Saint-Marc, P.; Medioni, G. Active contour models: Overview, implementation and applications. In Proceedings of the 1990 IEEE International Conference on Systems, Man, and Cybernetics Conference Proceedings, Los Angeles, CA, USA, 4–7 November 1990; pp. 194–199. [Google Scholar] [CrossRef]
- Brigger, P.; Hoeg, J.; Unser, M. B-spline snakes: A flexible tool for parametric contour detection. IEEE Trans. Image Process. 2000, 9, 1484–1496. [Google Scholar] [CrossRef]
- Velut, J.; Benoit-Cattin, H.; Odet, C. Locally regularized smoothing B-snake. EURASIP J. Adv. Signal Process. 2007, 2007, 076241. [Google Scholar] [CrossRef][Green Version]
- Xu, C.; Prince, J.L. Snakes, shapes, and gradient vector flow. IEEE Trans. Image Process. 1998, 7, 359–369. [Google Scholar] [CrossRef]
- Xu, C.; Prince, J.L. Generalized gradient vector flow external forces for active contours. Signal Process. 1998, 71, 131–139. [Google Scholar] [CrossRef]
- Chang, J.; Gao, X.; Yang, Y.; Wang, N. Object-oriented building contour optimization methodology for image classification results via generalized gradient vector flow snake model. Remote Sens. 2021, 13, 2406. [Google Scholar] [CrossRef]
- Wei, J.; Hu, Y.; Zhang, S.; Liu, S. Irregular Facades: A dataset for semantic segmentation of the free facade of modern buildings. Buildings 2024, 14, 2602. [Google Scholar] [CrossRef]
- Tylecek, R. The CMP Facade Database (Version 1.1); Czech Technical University in Prague: Prague, Czech Republic, 2013; Research Report CTU-CMP-2012-24. [Google Scholar]
- Teboul, O.; Simon, L.; Koutsourakis, P.; Paragios, N. Segmentation of building facades using procedural shape priors. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 3105–3112. [Google Scholar]
- Riemenschneider, H.; Krispel, U.; Thaller, W.; Donoser, M.; Havemann, S.; Fellner, D.; Bischof, H. Irregular lattices for complex shape grammar facade parsing. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 1640–1647. [Google Scholar]
- Chen, L.-C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 833–851. [Google Scholar] [CrossRef]
- Jaccard, P. The distribution of the flora in the alpine zone. New Phytol. 1912, 11, 37–50. [Google Scholar] [CrossRef]
- Yu, W.; Shu, J.; Yang, Z.; Ding, H.; Zeng, W.; Bai, Y. Deep learning-based pipe segmentation and geometric reconstruction from poorly scanned point clouds using BIM-driven data alignment. Autom. Constr. 2025, 173, 106071. [Google Scholar] [CrossRef]
- Kwak, E.; Habib, A. Automatic representation and reconstruction of DBM from LiDAR data using Recursive Minimum Bounding Rectangle. ISPRS J. Photogramm. Remote Sens. 2014, 93, 171–191. [Google Scholar] [CrossRef]
- Neuhausen, M.; König, M. Automatic window detection in facade images. Autom. Constr. 2018, 96, 527–539. [Google Scholar] [CrossRef]
- Liu, H.; Xu, Y.; Zhang, J.; Zhu, J.; Li, Y.; Hoi, S.C.H. DeepFacade: A Deep Learning Approach to Facade Parsing With Symmetric Loss. IEEE Trans. Multimedia 2020, 22, 3153–3165. [Google Scholar] [CrossRef]
- Zhang, G.; Pan, Y.; Zhang, L. Deep learning for detecting building façade elements from images considering prior knowledge. Autom. Constr. 2022, 133, 104016. [Google Scholar] [CrossRef]






| Hyperparameter | Description |
|---|---|
| network = “DeepLabv3+” | The network DeepLabv3+ was used to train classifiers. |
| backbone = “MobileNet” | The backbone for DeepLabv3+ was MobileNet. |
| batch_size = 16 | Parameters were updated every time 16 samples were input. |
| epochs = 50 | The training ran for 50 epochs. |
| learning_rate = 0.01 | The update to parameters is 0.01 times the gradient. |
| crop_size = 513 | Input images were resized to 513 × 513 pixels. |
| random_seed = 1 | - |
| IoU | F1 | |||||||
|---|---|---|---|---|---|---|---|---|
| Dataset | Graphic | Mean | SD | 95% CI | Mean | SD | 95% CI | |
| IRFs | Prediction | 0.722 | 0.147 | 0.713–0.731 | 0.828 | 0.125 | 0.821–0.836 | |
| Du et al.’s reg | 0.715 *** | 0.148 | 0.706–0.724 | 0.823 *** | 0.127 | 0.815–0.831 | ||
| Pan et al.’s reg | 0.715 *** | 0.150 | 0.706–0.724 | 0.823 *** | 0.128 | 0.815–0.831 | ||
| Our reg | 0.723 | 0.151 | 0.714–0.732 | 0.828 | 0.129 | 0.820–0.836 | ||
| CMP | Prediction | 0.707 | 0.103 | 0.697–0.717 | 0.824 | 0.075 | 0.816–0.831 | |
| Du et al.’s reg | 0.702 *** | 0.105 | 0.692–0.713 | 0.820 *** | 0.077 | 0.813–0.828 | ||
| Pan et al.’s reg | 0.705 * | 0.106 | 0.694–0.715 | 0.822 * | 0.078 | 0.814–0.830 | ||
| Our reg | 0.718 *** | 0.106 | 0.708–0.729 | 0.831 *** | 0.077 | 0.824–0.839 | ||
| ECP | Prediction | 0.713 | 0.088 | 0.696–0.730 | 0.829 | 0.068 | 0.816–0.842 | |
| Du et al.’s reg | 0.700 *** | 0.090 | 0.683–0.717 | 0.820 *** | 0.070 | 0.806–0.834 | ||
| Pan et al.’s reg | 0.692 *** | 0.094 | 0.674–0.710 | 0.814 *** | 0.076 | 0.799–0.828 | ||
| Our reg | 0.730 *** | 0.085 | 0.713–0.746 | 0.841 *** | 0.065 | 0.828–0.853 | ||
| Graz50 | Prediction | 0.637 | 0.096 | 0.611–0.664 | 0.774 | 0.081 | 0.751–0.796 | |
| Du et al.’s reg | 0.629 *** | 0.092 | 0.604–0.655 | 0.768 ** | 0.078 | 0.747–0.790 | ||
| Pan et al.’s reg | 0.631 * | 0.093 | 0.605–0.657 | 0.769 * | 0.079 | 0.747–0.791 | ||
| Our reg | 0.651 *** | 0.097 | 0.624–0.678 | 0.784 *** | 0.081 | 0.761–0.806 | ||
| Dataset | NN | NT | NN/NT | NF | NN/NF |
|---|---|---|---|---|---|
| IRFs | 1324 | 18,236 | 0.072 | 1057 | 1.253 |
| CMP | 69 | 11,895 | 0.006 | 378 | 0.183 |
| ECP | 0 | 5007 | 0 | 104 | 0 |
| Graz50 | 0 | 1094 | 0 | 50 | 0 |
| Total Time (s) | Time per Image (s) | |||||||
|---|---|---|---|---|---|---|---|---|
| Dataset | Nimage | Du et al. | Pan et al. | Ours | Du et al. | Pan et al. | Ours | |
| IRFs | 1057 | 376 | 304 | 1739 | 0.36 | 0.29 | 1.65 | |
| CMP | 378 | 136 | 92 | 424 | 0.36 | 0.24 | 1.12 | |
| ECP | 104 | 33 | 13 | 56 | 0.32 | 0.13 | 0.54 | |
| Graz50 | 50 | 6 | 2 | 18 | 0.12 | 0.04 | 0.36 | |
| Number of Graphics per Image | Time Consumption per Graphic (ms) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Dataset | Mean | Median | SD | Range | 95% CI | Mean | Median | SD | Range | 95% CI | |
| IRFs | 17.3 | 11.0 | 17.5 | 0–124 | 16.2–18.3 | 90.2 | 19.0 | 1246.0 | 2.5–110,461.1 | 72.2–108.3 | |
| CMP | 31.5 | 29.0 | 17.4 | 5–149 | 29.7–33.2 | 32.5 | 9.9 | 276.9 | 2.7–24,162.0 | 27.6–37.5 | |
| ECP | 48.1 | 46.5 | 10.6 | 27–84 | 46.1–50.2 | 10.0 | 5.2 | 23.1 | 2.1–604.8 | 9.3–10.6 | |
| Graz50 | 21.9 | 22.0 | 5.9 | 10–34 | 20.3–23.5 | 14.8 | 7.7 | 49.8 | 2.1–1321.3 | 11.8–17.7 | |
| DL (Pixel) | DR (Pixel) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Dataset | Mean | Median | SD | Range | 95% CI | Mean | Median | SD | Range | 95% CI | |
| IRFs | 5.4 | 2 | 18.7 | 0–1315 | 5.1–5.7 | 5.5 | 2 | 16.4 | 0–694 | 5.3–5.8 | |
| CMP | 3.3 | 1 | 13.6 | 0–634 | 3.0–3.5 | 3.2 | 1 | 12.5 | 0–748 | 3.0–3.5 | |
| ECP | 1.9 | 1 | 3.4 | 0–82 | 1.8–2.0 | 1.7 | 1 | 3.6 | 0–75 | 1.6–1.8 | |
| Graz50 | 1.6 | 1 | 1.7 | 0–24 | 1.5–1.7 | 1.6 | 1 | 2.5 | 0–41 | 1.5–1.8 | |
| DB (Pixel) | DT (Pixel) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Dataset | Mean | Median | SD | Range | 95% CI | Mean | Median | SD | Range | 95% CI | |
| IRFs | 4.5 | 2 | 10.4 | 0–347 | 4.3–4.6 | 4.2 | 2 | 9.1 | 0–266 | 4.1–4.3 | |
| CMP | 2.7 | 1 | 6.2 | 0–252 | 2.6–2.8 | 2.7 | 1 | 7.4 | 0–246 | 2.6–2.9 | |
| ECP | 1.3 | 1 | 1.8 | 0–30 | 1.2–1.3 | 2.1 | 1 | 3.9 | 0–72 | 2.0–2.2 | |
| Graz50 | 2.0 | 1 | 2.8 | 0–44 | 1.8–2.2 | 2.0 | 2 | 2.1 | 0–28 | 1.8–2.1 | |
| Dataset | Box | IoU | Precision | Recall | F1 |
|---|---|---|---|---|---|
| BOB | 0.723 | 0.847 | 0.818 | 0.828 | |
| IRFs | MCB | 0.711 (−0.012) *** | 0.782 (−0.065) *** | 0.871 (+0.053) *** | 0.820 (−0.008) *** |
| MIB | 0.633 (−0.090) *** | 0.902 (+0.055) *** | 0.671 (−0.147) *** | 0.762 (−0.066) *** | |
| BOB | 0.718 | 0.838 | 0.830 | 0.831 | |
| CMP | MCB | 0.682 (−0.036) *** | 0.745 (−0.093) *** | 0.887 (+0.057) *** | 0.805 (−0.026) *** |
| MIB | 0.665 (−0.053) *** | 0.923 (+0.085) *** | 0.700 (−0.130) *** | 0.792 (−0.039) *** | |
| BOB | 0.730 | 0.827 | 0.857 | 0.841 | |
| ECP | MCB | 0.673 (−0.057) *** | 0.729 (−0.098) *** | 0.892 (+0.035) *** | 0.802 (−0.039) *** |
| MIB | 0.663 (−0.067) *** | 0.904 (+0.077) *** | 0.709 (−0.148) *** | 0.792 (−0.049) *** | |
| BOB | 0.651 | 0.766 | 0.807 | 0.784 | |
| Graz50 | MCB | 0.629 (−0.022) *** | 0.698 (−0.068) *** | 0.859 (+0.052) *** | 0.768 (−0.016) *** |
| MIB | 0.569 (−0.082) *** | 0.862 (+0.096) *** | 0.621 (−0.186) *** | 0.719 (−0.065) *** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Wang, Z.; Hu, Y.; Zhao, X.; Zhang, S. A Box-Based Method for Regularizing the Prediction of Semantic Segmentation of Building Facades. Buildings 2025, 15, 3562. https://doi.org/10.3390/buildings15193562
Liu S, Wang Z, Hu Y, Zhao X, Zhang S. A Box-Based Method for Regularizing the Prediction of Semantic Segmentation of Building Facades. Buildings. 2025; 15(19):3562. https://doi.org/10.3390/buildings15193562
Chicago/Turabian StyleLiu, Shuyu, Zhihui Wang, Yuexia Hu, Xiaoyu Zhao, and Si Zhang. 2025. "A Box-Based Method for Regularizing the Prediction of Semantic Segmentation of Building Facades" Buildings 15, no. 19: 3562. https://doi.org/10.3390/buildings15193562
APA StyleLiu, S., Wang, Z., Hu, Y., Zhao, X., & Zhang, S. (2025). A Box-Based Method for Regularizing the Prediction of Semantic Segmentation of Building Facades. Buildings, 15(19), 3562. https://doi.org/10.3390/buildings15193562






