Experimental Study on Bidirectional Bending Performance of Steel-Ribbed Composite Slabs for Electrical Substations
Abstract
1. Introduction
2. Experimental Overview
2.1. Project Background
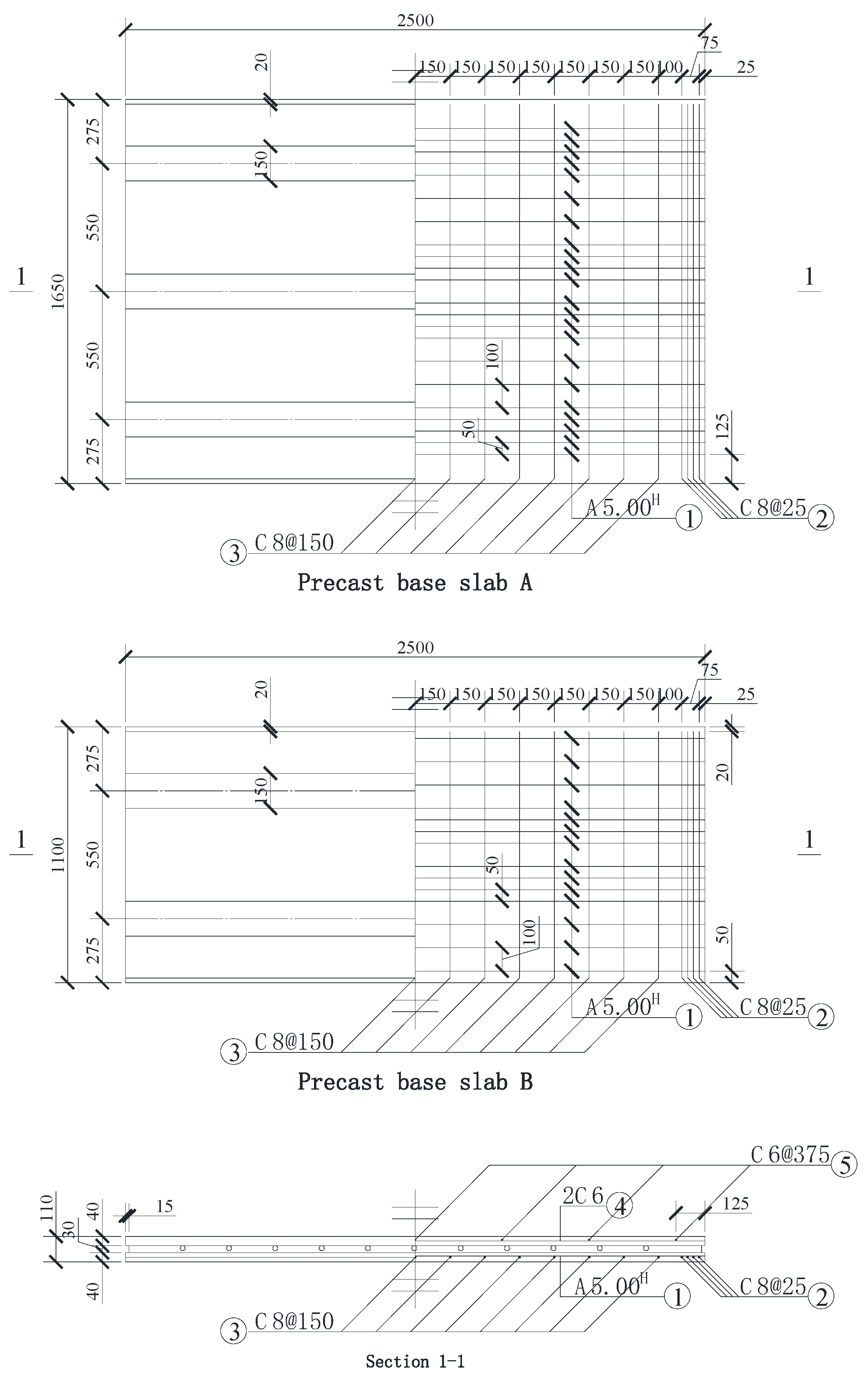
2.2. Specimen Design of Steel-Ribbed Composite Slabs
2.3. Specimen Fabrication
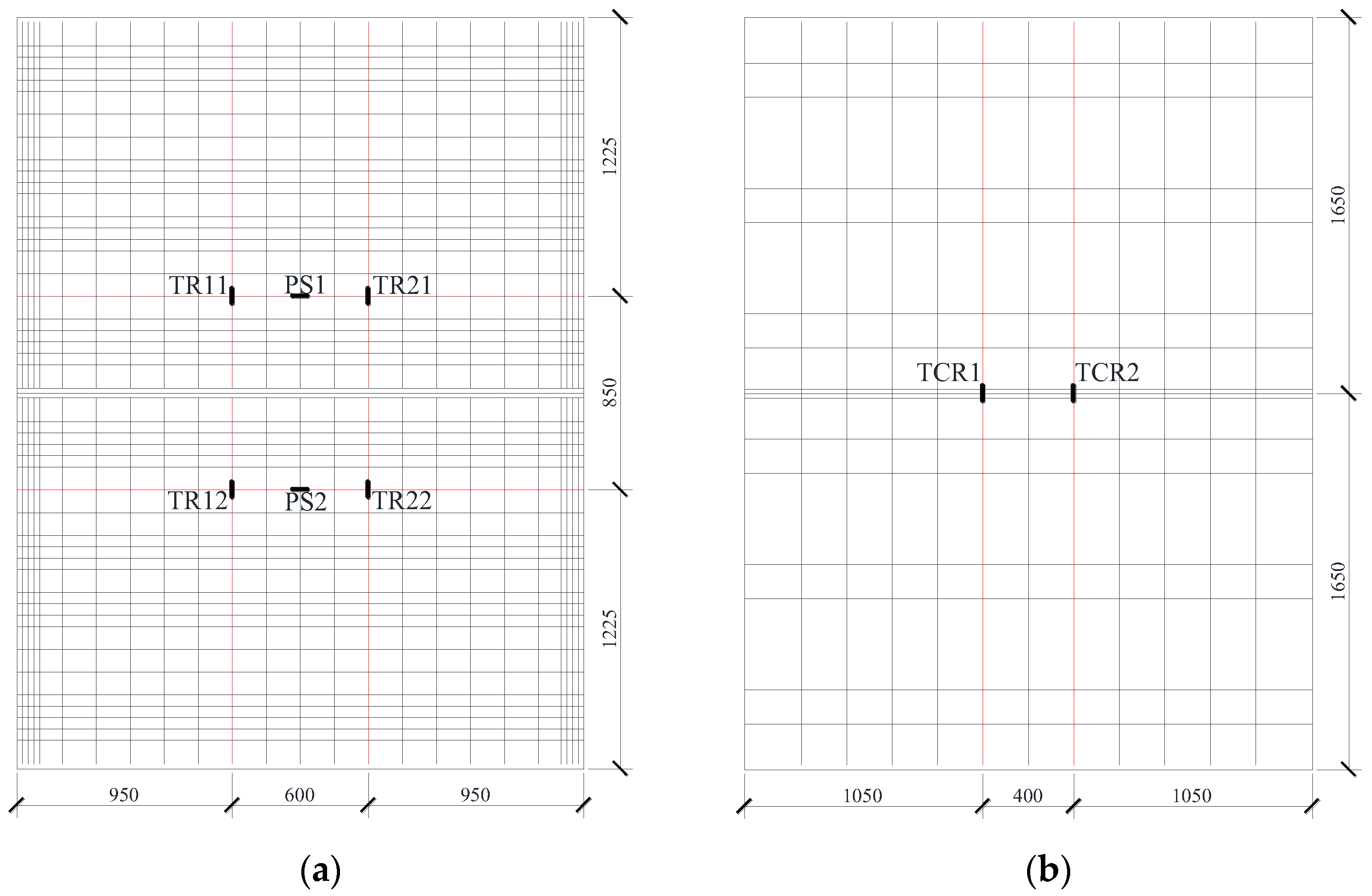
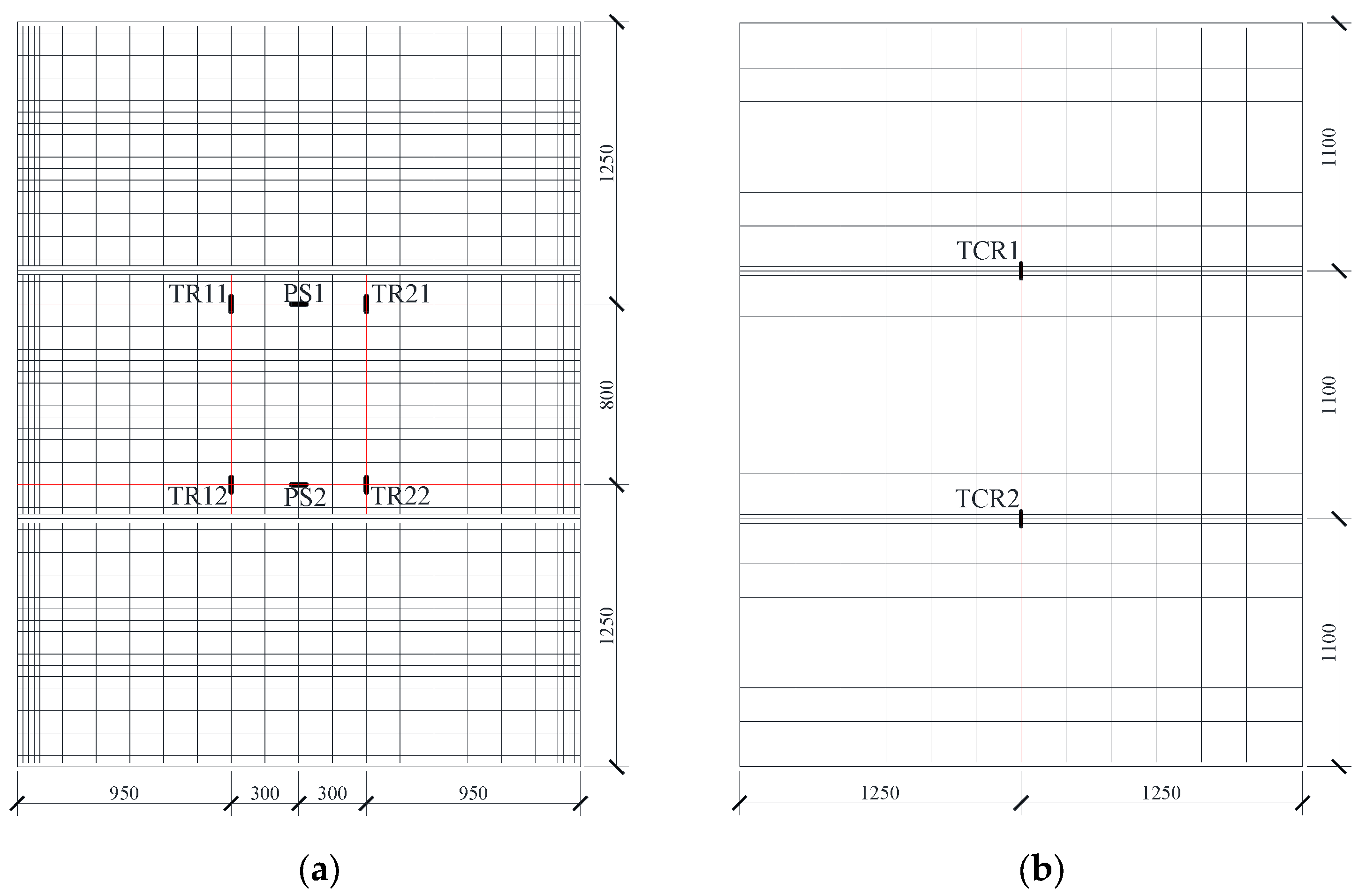
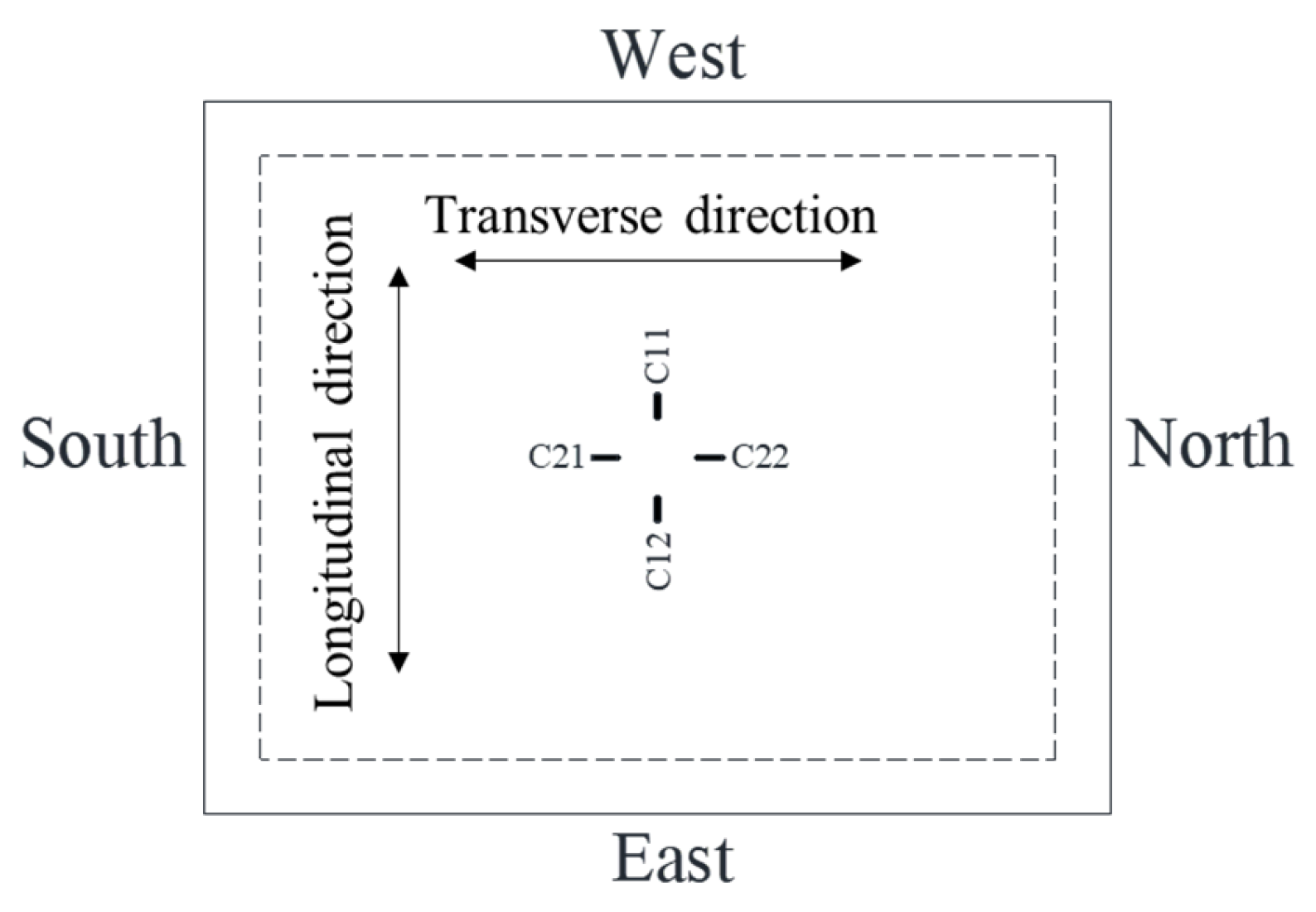
2.4. Loading Apparatus and Instrumentation Layout
3. Experimental Results
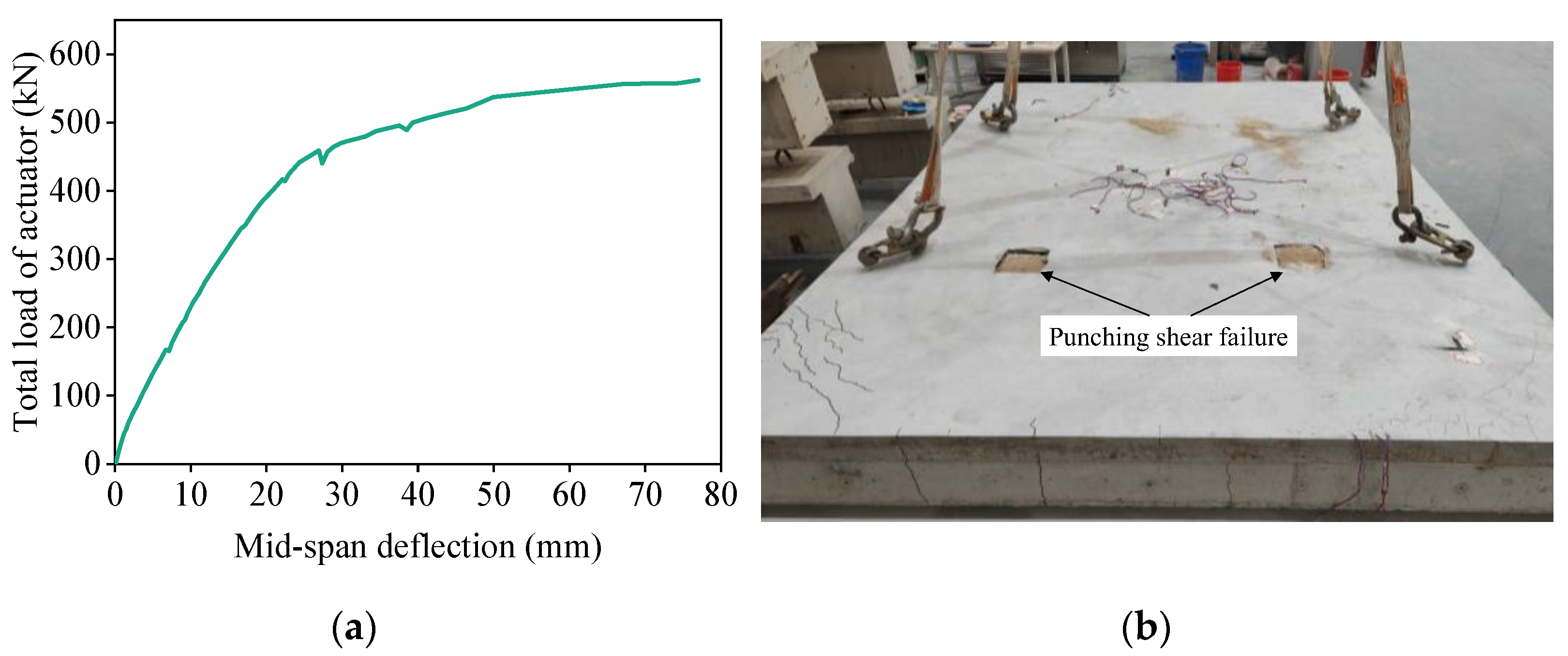
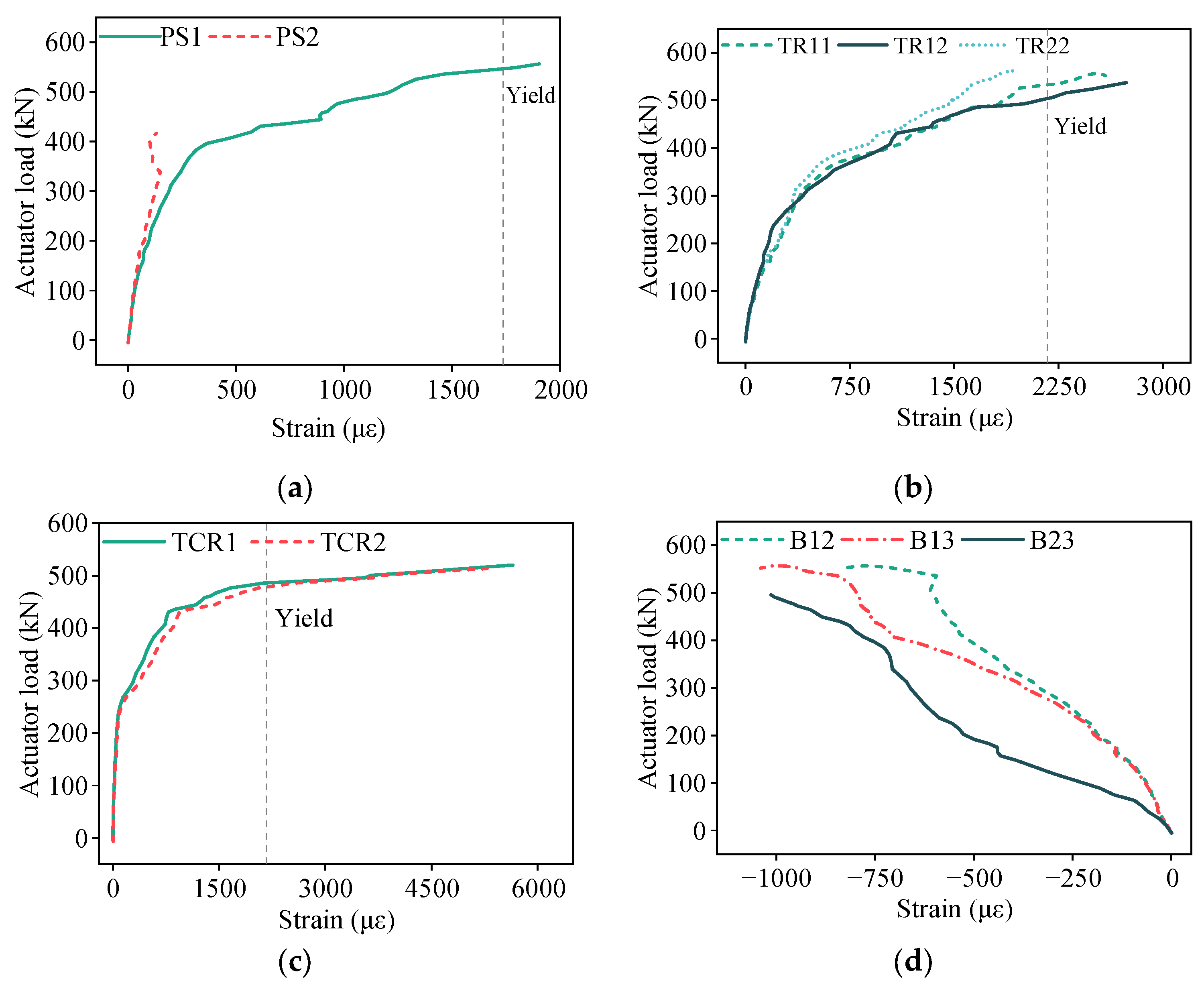
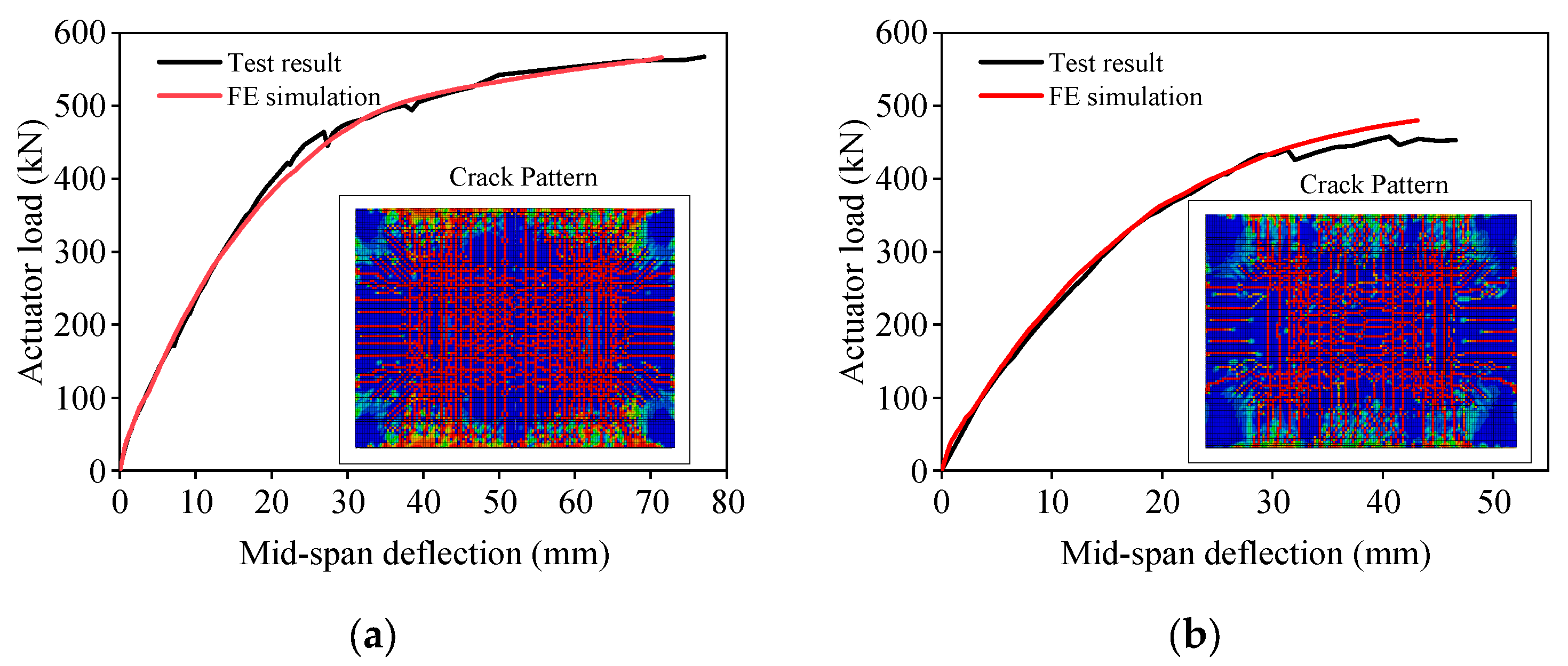
3.1. Double-Spliced Steel-Ribbed Bidirectional Composite Slab
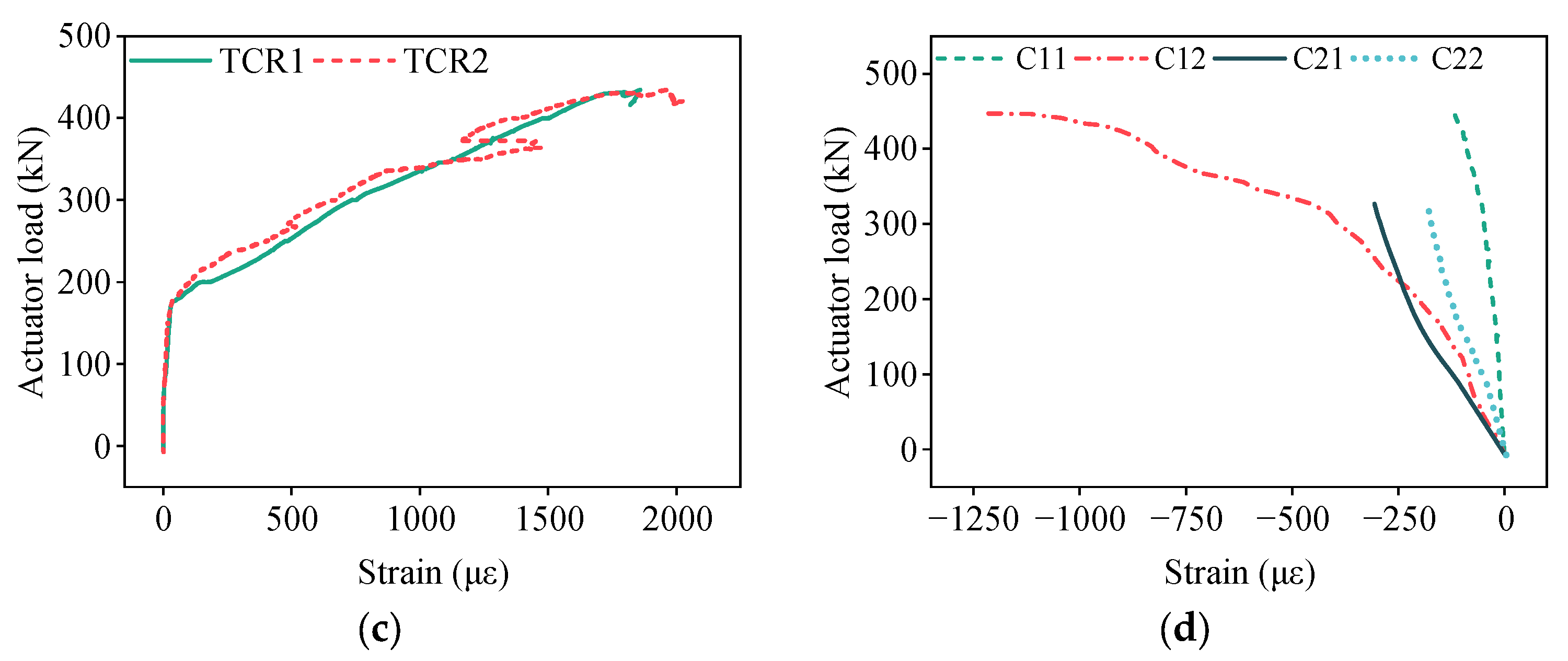
3.2. Triple-Spliced Steel-Ribbed Bidirectional Composite Slab
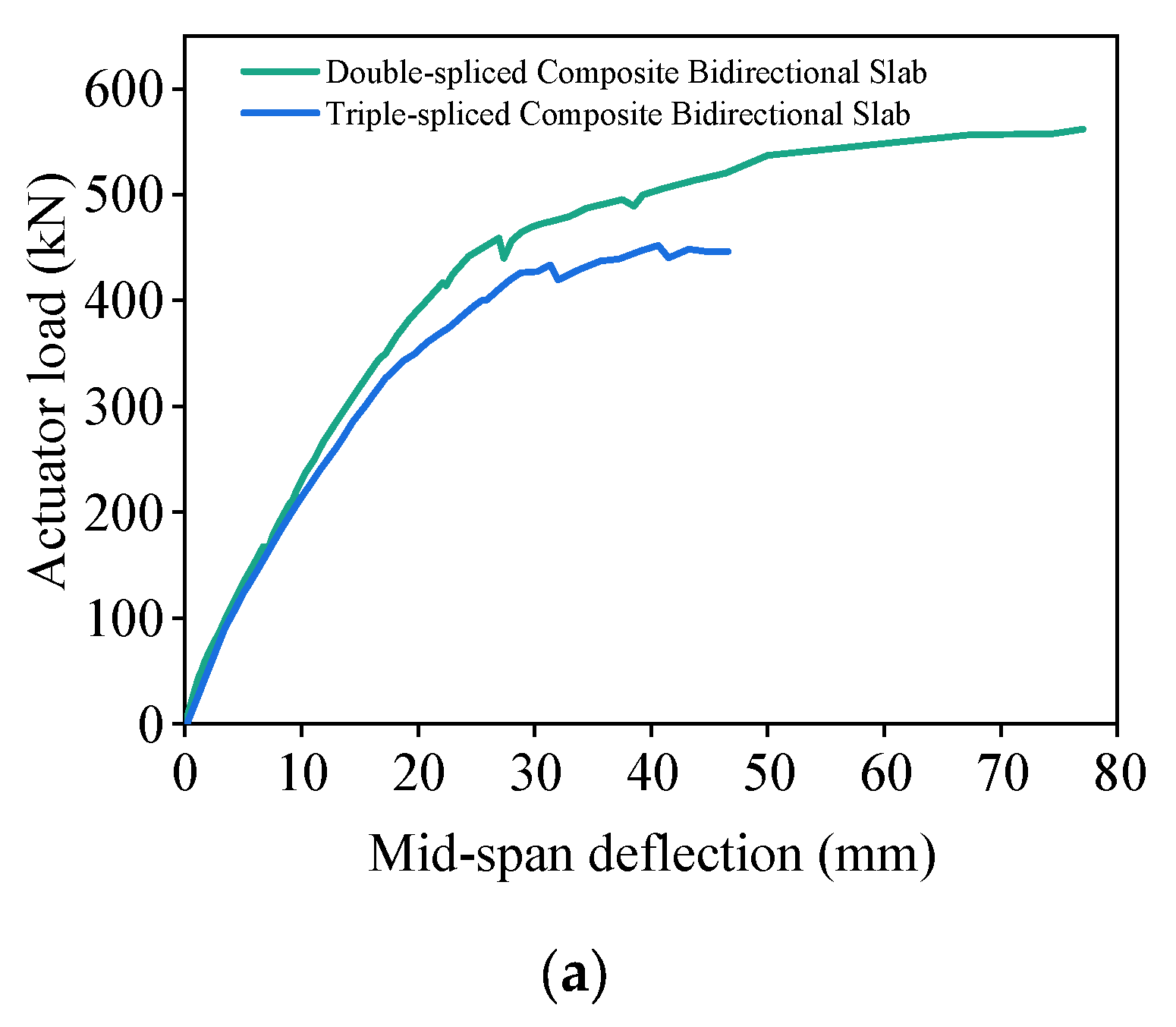
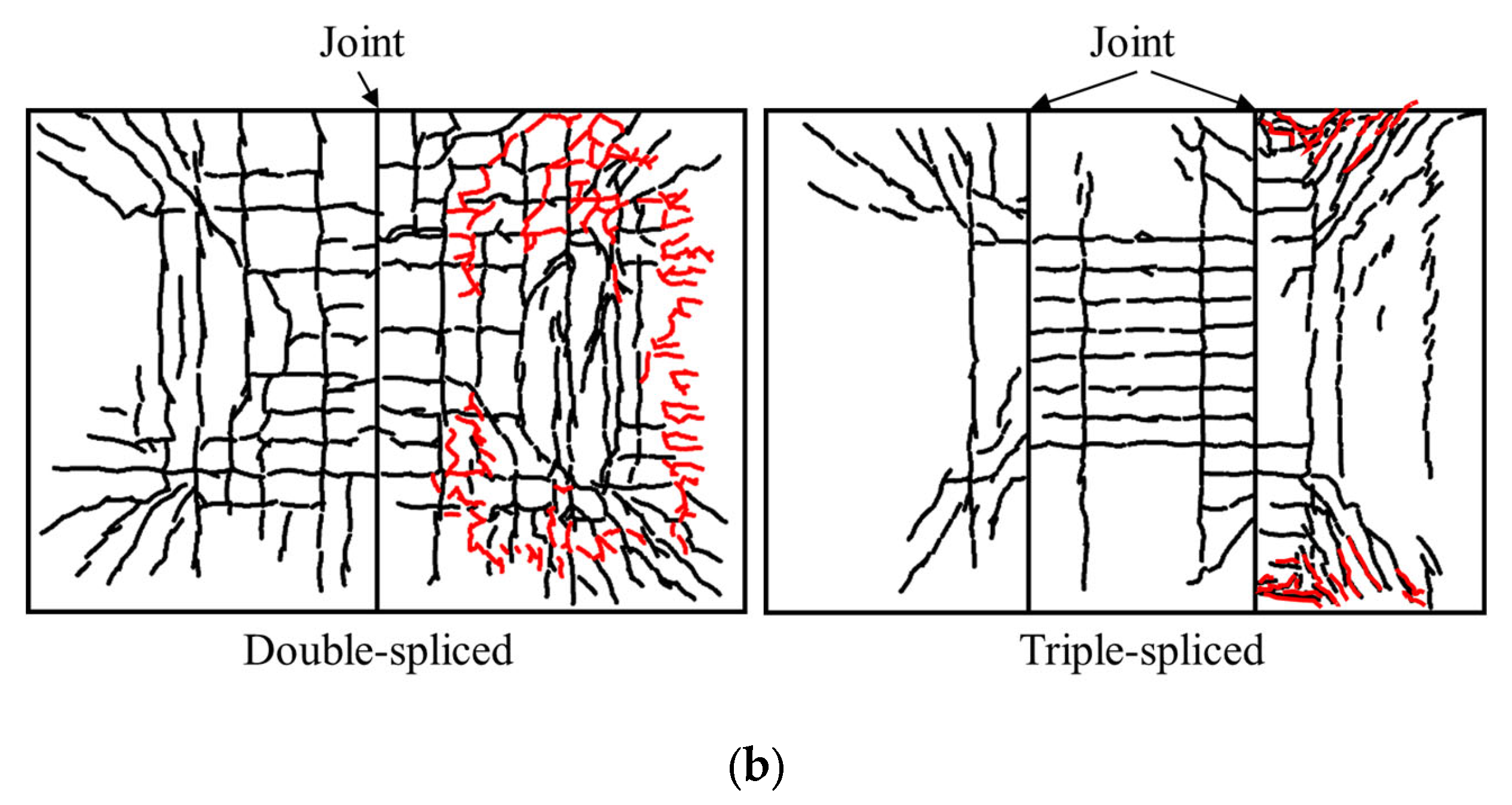
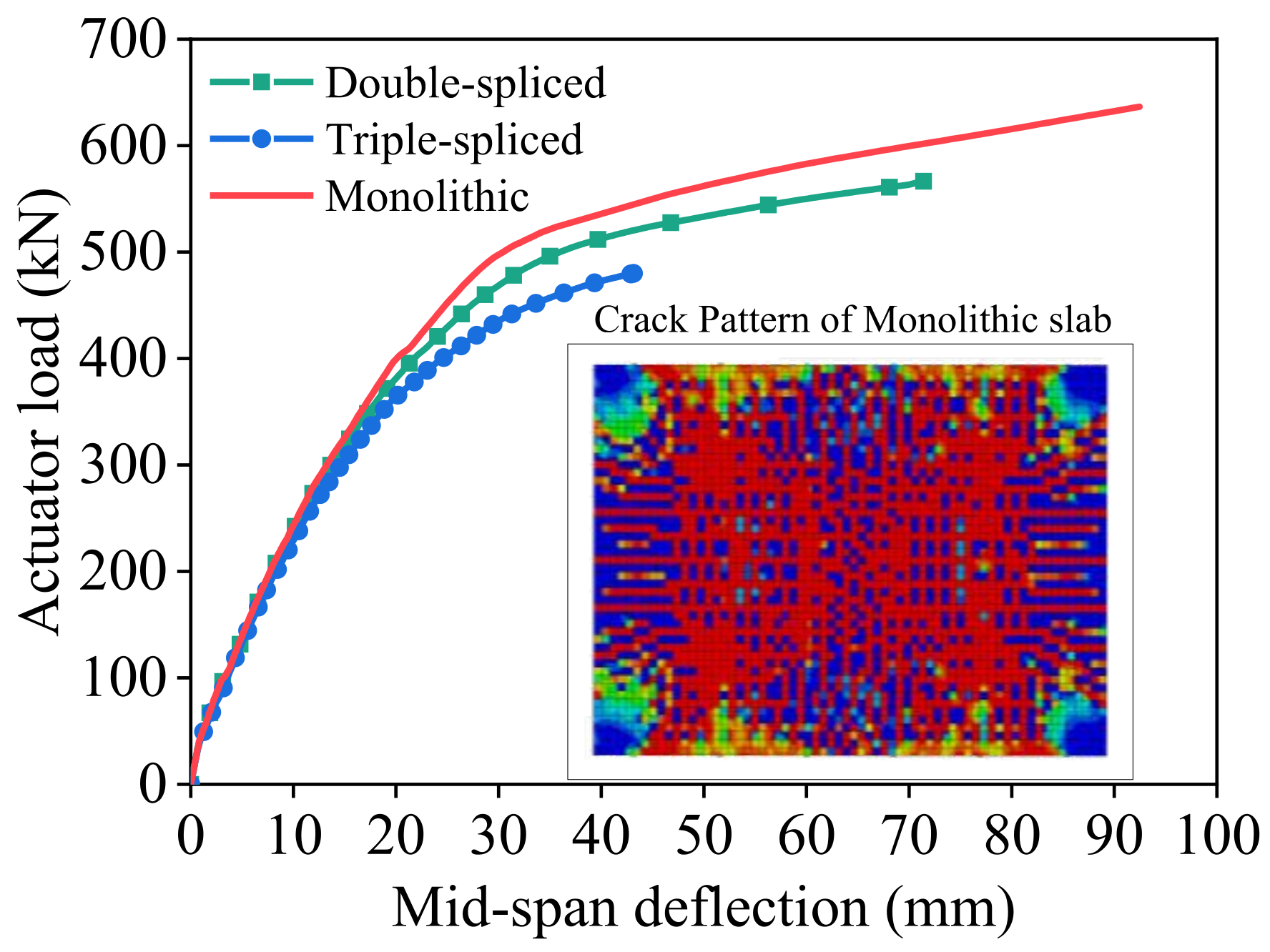
3.3. Discussion of Experimental Results
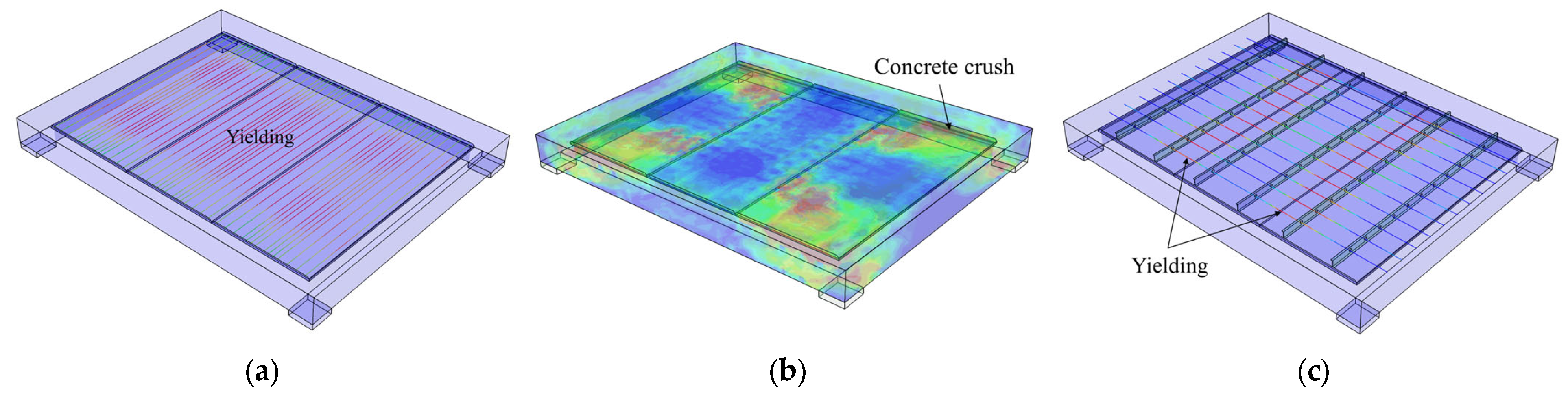
4. Finite Element Modeling and Parametric Analysis
5. Conclusions
- (1)
- Compared to the triple-spliced slabs, double-spliced slabs exhibited a 24.5% increase in ultimate load-bearing capacity and a 65.3% improvement in ductility under given bidirectional bending conditions in this paper. Double-spliced slabs demonstrated typical bidirectional behavior, with well-developed orthogonal crack pattern and yielding of both longitudinal prestressing steel and transverse reinforcement at failure. Triple-spliced slabs showed only partial bidirectional bending response due to poorer transverse integrity. Upon failure, longitudinal prestressing steel approached yielding while transverse reinforcement exhibited low stress levels.
- (2)
- Compared with the monolithic spliced slabs, the spliced slabs exhibited nearly identical stiffness at the onset of cracking, but their stiffness progressively declined during the mid-to-late loading stages, ultimately leading to lower load-bearing capacity and ductility at failure. Joint-crossing reinforcement was confirmed to be the main path for transverse load transfer. The strains in the joint-crossing reinforcement at failure were significantly higher than those in the transverse distribution rebars, with a ratio of about 2.3:1–3.1:1. Increased joint quantity will reduce transverse continuity and load transfer, degrading load capacity and ductility.
- (3)
- Parametric analysis shows that the longitudinal prestress ratio has the greatest influence on the behavior of spliced slabs, followed by the diameter of the joint-crossing reinforcement and the concrete strength, while the effect of the joint-crossing reinforcement strength is comparatively minor. Increasing the prestressing ratio significantly enhances the ultimate bearing capacity and ductility, but the marginal gains diminish at higher ratios as the governing failure mode shifts from prestressing steel yielding to joint-controlled failure. Enlarging reinforcement diameter is more effective than increasing its strength in preventing premature joint failure. Increasing concrete strength offers limited capacity gains and may reduce ductility.
- (4)
- For engineering applications such as 500 kV prefabricated substations, double-spliced slabs are more preferable to enhance bidirectional bending performance, particularly in high-load zones. Triple-spliced slabs require careful attention to preventive measures, including local reinforcement at slab corners and optimized joint detailing. This study mainly focuses on the ultimate capacity and ductility of steel-ribbed composite slabs. Future work will address the serviceability and durability aspects of the floor system, including crack control under service loads, long-term joint slip, and rib corrosion, to ensure reliable life-cycle performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Luo, T.; Xue, X.L.; Wang, Y.N.; Xue, W.R.; Tan, Y.T. A systematic overview of prefabricated construction policies in China. J. Clean Prod. 2021, 280, 124371. [Google Scholar] [CrossRef]
- Bonamente, E.; Cotana, F. Carbon and energy footprints of prefabricated industrial buildings: A systematic life cycle assessment analysis. Energies 2015, 8, 12685–12701. [Google Scholar] [CrossRef]
- He, H.; Zhou, S.; Zhang, L.; Zhao, W.; Xiao, X. Dynamic accounting model and method for carbon emissions on the power grid side. Energies 2023, 16, 5016. [Google Scholar] [CrossRef]
- Bai, S.; Li, M.C.; Song, L.G.; Kong, R. Developing a common library of prefabricated structure components through graphic media mapping to improve design efficiency. J. Constr. Eng. Manag. 2021, 147, 04020156. [Google Scholar] [CrossRef]
- Jiang, Y.; Shu, J.P.; Ye, J.; Zhao, W.J. Virtual trail assembly of prefabricated structures based on point cloud and BIM. Autom. Constr. 2023, 155, 105049. [Google Scholar] [CrossRef]
- Zhao, Y.Y.; Li, R.; Yue, S.Y. Comparative Analysis of Modular Prefabricated Module Substation and Conventional Substation. In Proceedings of the 3rd International Conference on Cognitive Based Information Processing and Applications, Guangzhou, China, 2–3 November 2023. [Google Scholar] [CrossRef]
- Nie, J.G.; Jiang, Y.X.; Nie, X.; Zhuang, L.D. Effect of truss reinforcement on mechanical properties of prefabricated slabs. Build. Struct. 2021, 42, 151–158. [Google Scholar] [CrossRef]
- Zhou, G.Q.; Li, S.R.; Zhang, X.; Yang, X. Experimental study on mechanical behavior of prestressed concrete composite slab with steel-tube truss. Build. Struct. 2025, 55, 26–31. [Google Scholar] [CrossRef]
- Liu, J.P.; Hu, H.F.; Li, J.; Chen, Y.F.; Zhang, L. Flexural behavior of prestressed concrete composite slab with precast inverted T-shaped ribbed panels. Eng. Struct. 2020, 215, 110687. [Google Scholar] [CrossRef]
- Hou, H.T.; Liu, X.; Qu, B.; Ma, T.; Liu, H.; Feng, M.; Zhang, B. Experimental evaluation of flexural behavior of composite beams with cast-in-place concrete slabs on precast prestressed concrete decks. Eng. Struct. 2016, 126, 405–416. [Google Scholar] [CrossRef]
- Chen, X.D.; Ma, Q.Y. Experimental study on the flexural performance of concrete hollow composite slabs with tightly connected panel sides. Sci. Rep. 2024, 14, 20784. [Google Scholar] [CrossRef]
- Karimipanah, A.; Zeynalian, M.; Ataei, A. Structural performance of cold formed steel composite beams with profiled steel sheeting. Int. J. Civ. Eng. 2024, 22, 1099–1116. [Google Scholar] [CrossRef]
- Lu, L.F.; Ding, Y.Z.; Guo, Y.; Hao, H.L.; Ding, S.L. Flexural performance and design method of the prefabricated RAC composite slab. Structures 2022, 38, 572–584. [Google Scholar] [CrossRef]
- Lu, L.F.; Gao, M.; Guo, Y.; Wang, W.; Yan, H.W.; Jiang, T.S. Experiments on flexural behavior of the prefabricated RAC and NWC composite slab. Ain Shams Eng. J. 2022, 13, 101789. [Google Scholar] [CrossRef]
- Lu, L.F.; Wang, W.; Zhang, L.X.; Shao, Y.J. Longitudinal shear strength of recycled aggregate concrete prefabricated superimposed slabs. Eng. Struct. 2023, 281, 115745. [Google Scholar] [CrossRef]
- Stehle, J.; Kanellopoulos, A.; Karihaloo, B.L. Performance of joints in reinforced concrete slabs for two-way spanning action. Proc. Inst. Civil Eng. Struct. Build. 2011, 164, 197–209. [Google Scholar] [CrossRef]
- Cheng, Z.J.; Ma, Z.Z.; Hu, J.; Yu, S.L.; Zhao, Y. Experimental research on heap loading of reinforced concrete composite two-way slab with lattice girders and connected without gap. Build. Struct. 2021, 51, 111–119. [Google Scholar] [CrossRef]
- Wang, G.S.; Liu, J.H.; Zhang, Y.B.; Zhang, Z.Y.; Tao, J.W.; Wu, D.Y. Theoretical and experimental study on the stress state of joints in two-way composite slabs. Buildings 2024, 14, 3374. [Google Scholar] [CrossRef]
- Ciu, S.Q.; Liu, C.Q.; Liu, W.Z.; Shi, L. Research on experiment and calculating methods of flexural stiffness in direction perpendicular to separating-type joints for concrete composite slab. J. Build. Struct. 2018, 39, 75–84. [Google Scholar] [CrossRef]
- Chen, Y.H.; Lu, D.; Zhang, M.; Sun, H.W.; Xie, G.X. Research on connection technique for bidirectional composite floor slabs without gap. Ind. Constr. 2020, 50, 31–35. [Google Scholar] [CrossRef]
- Li, J.; Ni, D.Y.; Liu, X.; Zhang, J.R. Experimental study of mechanical properties of L-shaped joint laminated two-way slabs. Build. Struct. 2020, 50, 67–71+86. [Google Scholar] [CrossRef]
- Shill, S.K.; Garcez, E.O.; Al-Ameri, R.; Subhani, M. Performance of two-way concrete slabs reinforced with basalt and carbon FRP rebars. J. Compos. Sci. 2022, 6, 74. [Google Scholar] [CrossRef]
- Wang, Y.H.; Peng, Y.P. Force transfer mechanism analysis of CFRP-concrete two-way composite slab connected without gap under vertical load. Struct. Eng. 2024, 40, 107–115. [Google Scholar] [CrossRef]
- Lu, J.S.; Wu, J.H.; Zheng, Z.P. Structural design of precast reinforced concrete frame structure of Miaosan 110kV transformer substation. Build. Struct. 2014, 44, 24–28. [Google Scholar] [CrossRef]
- Liu, Y.; Wei, Z.Z.; Zheng, Y.C.; Jiao, J.F. Application exploration and practice of prestressed steel pipetruss floor slab in substation. Shandong Electr. Power 2021, 48, 39–43. [Google Scholar]
- Li, Z.D.; Tan, B.; Cheng, Z.; Xiong, M.Q. Application of prefabricated structure in substation industrialization project. Struct. Constr. 2021, 43, 228–231. [Google Scholar] [CrossRef]
- Lei, X.S.; Ouyang, J.W.; Wang, Y.F.; Wang, X.H.; Zhang, X.F.; Chen, F.; Xia, C.; Liu, Z.; Zhou, C.Y. Thermal–mechanical coupling evaluation of the panel performance of a prefabricated cabin-type substation based on machine learning. Fire 2021, 4, 93. [Google Scholar] [CrossRef]
- Li, L.; Liu, Y.; Wei, Z.Z.; Jiang, Y.N.; Chen, H.M.; Zhang, Y.; Liu, C.; Rong, K.J.; Tian, L. Numerical study on the bending performance of steel-ribbed composite slabs for substations. Appl. Sci. 2025, 15, 2876. [Google Scholar] [CrossRef]
- Abaqus, Computer Software. version 6.14. SIMULIA: Providence, RI, USA, 2014.



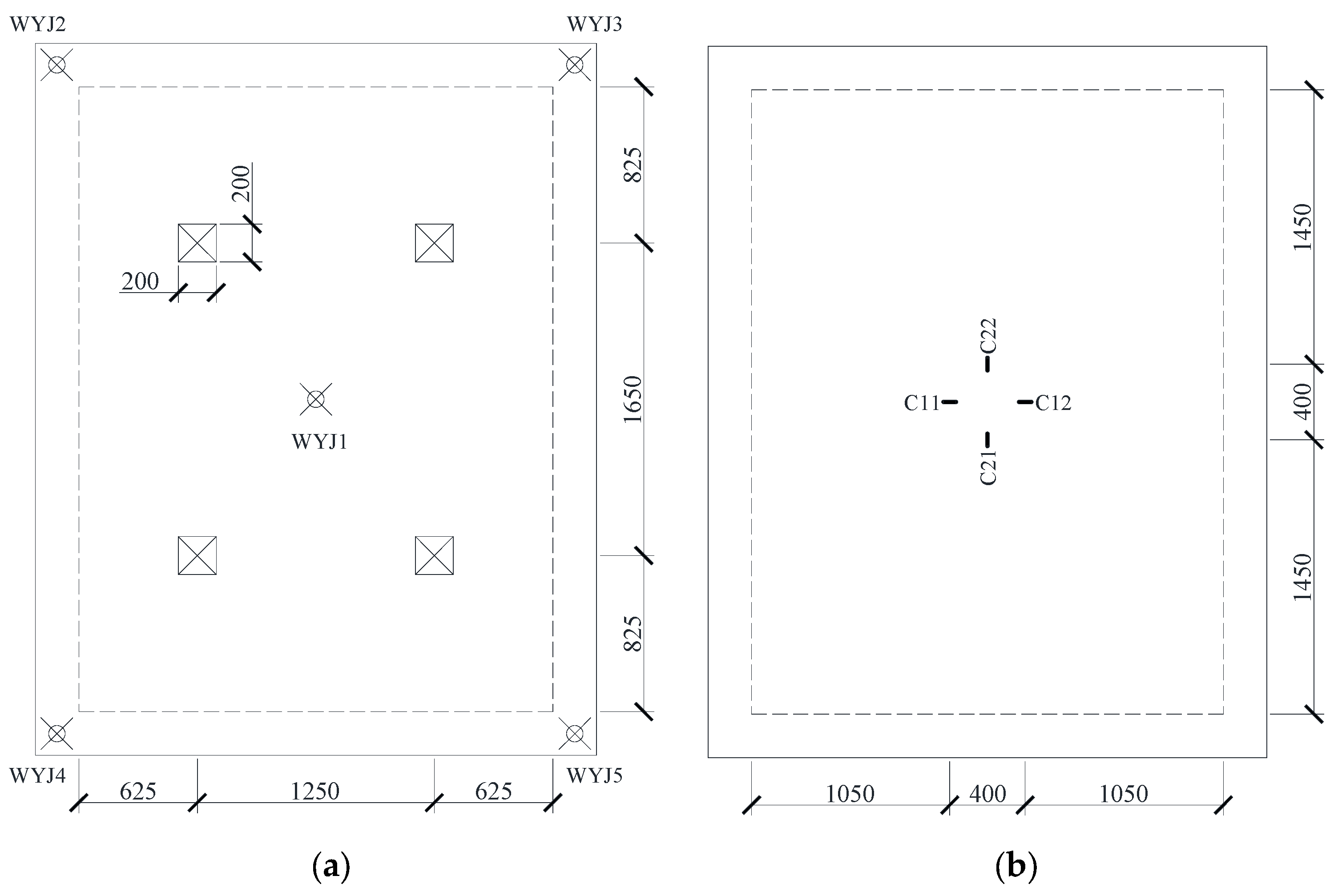





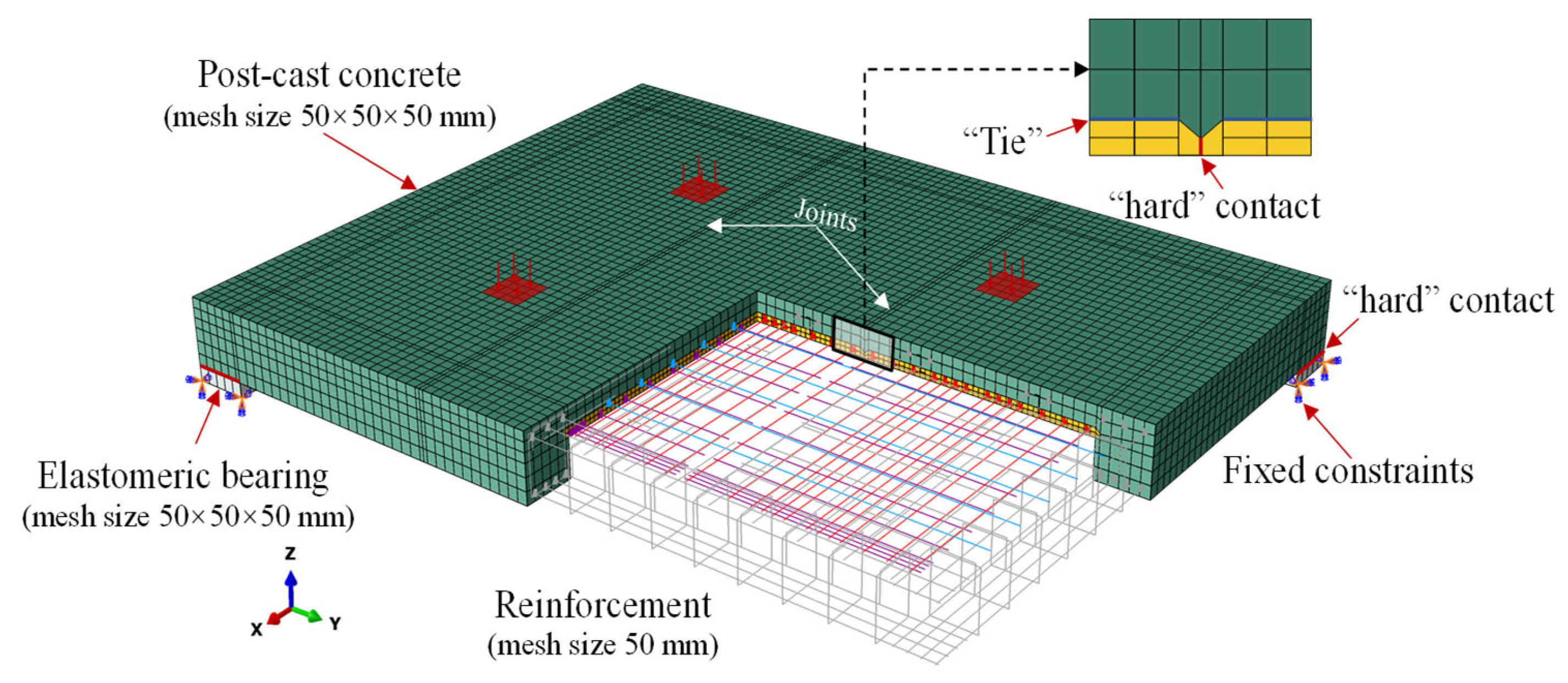
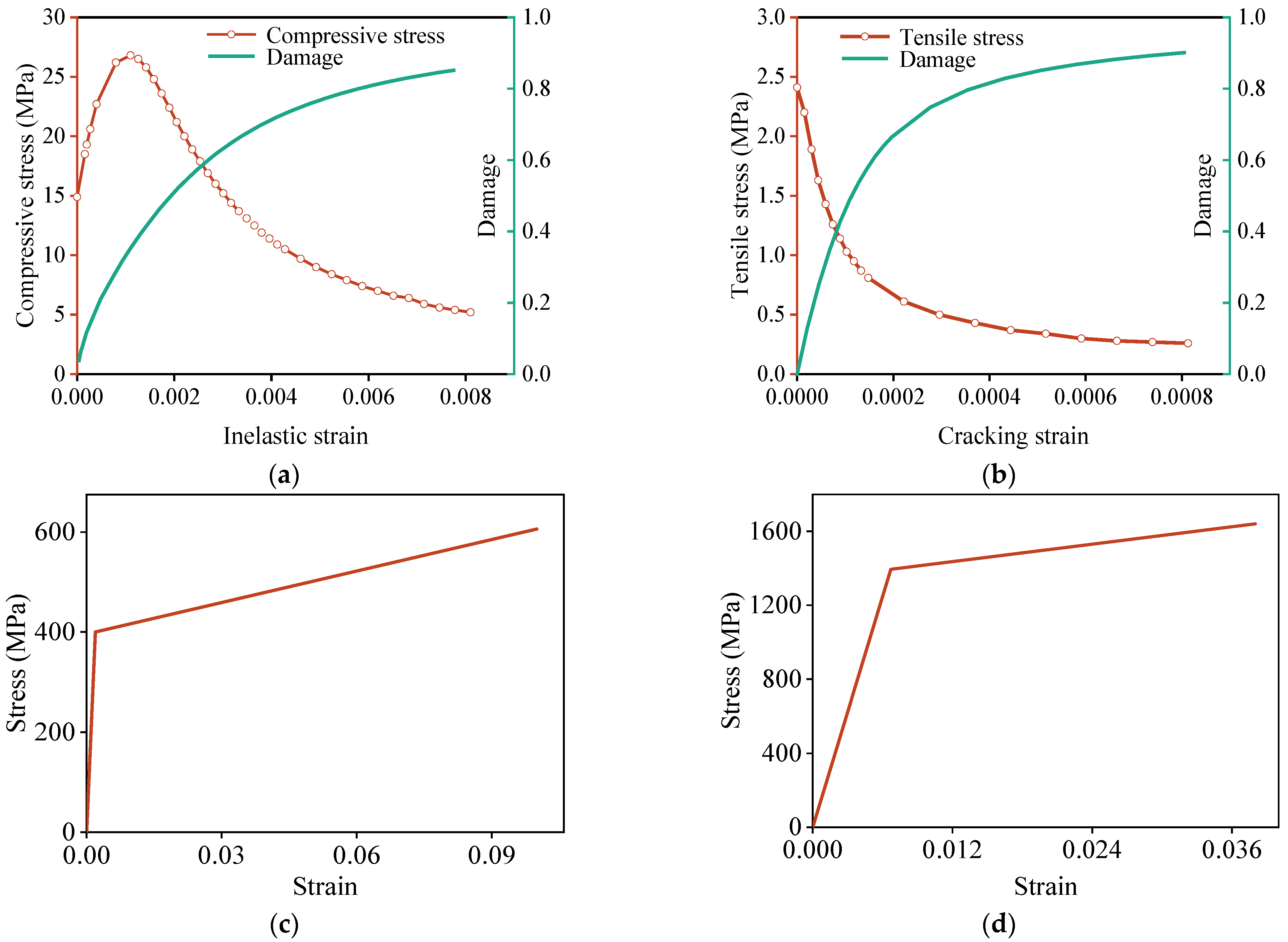


| Component | Young’s Modulus (MPa) | Poisson’s Ratio | Yield Stress (MPa) |
|---|---|---|---|
| Prestressing steel | 196,000 | 0.3 | 1477 |
| Rebar | 188,000 | 0.3 | 408 |
| Steel rib | 206,000 | 0.3 | 235 |
| Concrete | 32,500 | 0.2 | 2.4/26.8 1 |
| Dilation Angle | Eccentricity | fb0/fc0 | K | Viscosity Parameter |
|---|---|---|---|---|
| 30 | 0.1 | 1.16 | 0.6667 | 0.005 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Wei, Z.; Liu, Y.; Jiang, Y.; Chen, H.; Zhang, Y.; Zhang, K.; Rong, K.; Tian, L. Experimental Study on Bidirectional Bending Performance of Steel-Ribbed Composite Slabs for Electrical Substations. Buildings 2025, 15, 3540. https://doi.org/10.3390/buildings15193540
Li L, Wei Z, Liu Y, Jiang Y, Chen H, Zhang Y, Zhang K, Rong K, Tian L. Experimental Study on Bidirectional Bending Performance of Steel-Ribbed Composite Slabs for Electrical Substations. Buildings. 2025; 15(19):3540. https://doi.org/10.3390/buildings15193540
Chicago/Turabian StyleLi, Lin, Zhenzhong Wei, Yong Liu, Yunan Jiang, Haomiao Chen, Yu Zhang, Kaifa Zhang, Kunjie Rong, and Li Tian. 2025. "Experimental Study on Bidirectional Bending Performance of Steel-Ribbed Composite Slabs for Electrical Substations" Buildings 15, no. 19: 3540. https://doi.org/10.3390/buildings15193540
APA StyleLi, L., Wei, Z., Liu, Y., Jiang, Y., Chen, H., Zhang, Y., Zhang, K., Rong, K., & Tian, L. (2025). Experimental Study on Bidirectional Bending Performance of Steel-Ribbed Composite Slabs for Electrical Substations. Buildings, 15(19), 3540. https://doi.org/10.3390/buildings15193540








