Study on Seismic Performance of Asymmetric Rectangular Prefabricated Subway Station Structures in Soft Soil

Abstract

With the continuous improvement of the prefabricated modular technology system, the prefabricated subway station structures are widely used in underground engineering projects. However, prefabricated subway stations in soft soil can suffer significant adverse effects under seismic action. In order to study the seismic performance of a prefabricated subway station, this work is based on an actual project of a subway station in soft soil. And the nonlinear static and dynamic coupling two-dimensional finite element models of cast-in-place structures (CIPs), assembly splicing structures (ASSs), and assembly monolithic structures (AMSs) are established, respectively. The soil-structure interaction is considered, and different peak ground accelerations (PGA) are selected for incremental dynamic analysis. The displacement response, internal force characteristics, and structural damage distribution for three structural forms are compared. The research results show that the inter-story displacement of the AMS is slightly greater than that of the CIP, while the inter-story displacement of the ASS is the largest. The CIP has the highest internal force in the middle column, the ASS has the lowest internal force in the middle column, and the AMS is between the two. The damage to the CIP is concentrated at the bottom of the middle column and sidewall. The AMS compression damage moves upward, but the tensile damage mode is similar to the CIP. The ASS can effectively reduce damage to the middle column and achieve redistribution of internal force. Further analysis shows that the joint splicing interface between cast-in-place and prefabricated components is the key to controlling the overall deformation and seismic performance of the structure. The research results can provide a theoretical basis for the seismic design optimization of subway stations in earthquake-prone areas.

1. Introduction

The rapid expansion of urban rail transit has made subway construction a key driver in advancing urbanization and improving the efficiency of public transportation systems. However, traditional cast-in-place subway stations have revealed limitations in practical applications, such as long construction periods, severe environmental pollution, and difficulties in quality control [1]. Prefabricated and assembled subway stations, leveraging the advantages of high industrialization, standardization, and green construction, have gradually become a research highlight and development direction in underground engineering construction. As the design theory and construction technology of prefabricated concrete structures continue to improve, various forms of prefabricated subway stations, including assembled splicing structures and assembled integral structures, have been successfully applied in multiple urban rail transit projects both domestically and internationally. Among them, the assembled splicing subway station, as an innovative structural system, involves the standardized prefabrication of certain components in factories, followed by high-precision lifting and rapid splicing on-site. Key joint areas are combined with cast-in-place concrete layers to form an integrated structure where prefabrication and cast-in-place forces collaboratively work together. This technology not only enhances construction efficiency and reduces ecological damage but also significantly improves the construction quality of engineering projects, offering a more efficient, environmentally friendly, and sustainable solution for subway station construction [2]. The construction site is illustrated in Figure 1. Nevertheless, as urban underground space development extends to deeper and more complex geological conditions, coupled with increasingly frequent seismic activities globally, subway stations, as key hubs and densely populated areas in urban lifeline projects, are attracting widespread attention regarding structural safety, stability, and integrity under extreme disasters such as strong earthquakes and explosions [3,4]. Especially in unfavorable geological and environmental conditions such as soft soil and high-intensity earthquake zones, the dynamic soil-structure interaction is complex, and the structure is prone to adverse responses such as large deformation, joint opening, and slippage, posing severe challenges to the connection reliability and overall seismic resistance of prefabricated structures [5,6].

The mechanical properties of joints have a decisive impact on the seismic performance of prefabricated underground structures, and different types of joints exhibit varying seismic responses. Yang et al. [7,8,9] systematically investigated the mechanical behavior of grouted mortise-and-tenon joints in prefabricated subway structures through four-point pure shear tests and numerical simulations, revealing the influence of key geometric parameters on bending stiffness and deformation, and proposed an improved shear key method for predicting shear capacity under various loading conditions, which was validated for safety and reliability in the application of Changchun Metro Line 2. Lin et al. [10], based on the full-process monitoring data of prefabricated stations on Changchun Metro Line 2, systematically studied the mechanical behavior and deformation characteristics of double-tenon joints at the crown and single-tenon joints at the foot under high bending moments through on-site monitoring and numerical simulation comparisons. Xiong [11] proposed and verified a new tenon-bolt-type prefabricated column end joint through experiments and numerical simulations, revealing its seismic advantages of high ductility and good energy dissipation under different axial compression ratios. In addition, Liu et al. [12,13] conducted quasi-static loading tests on large-diameter grouted sleeve-connected beam–plate–column, column–plate, and side wall–plate joints, revealing that while these prefabricated joints exhibit comparable bearing and deformation capacities to cast-in-place monolithic joints, they differ significantly in ductility and ultimate failure modes. Qiu et al. [14] systematically investigated the mechanical behavior of prefabricated double-wall integrated underground diaphragm wall assembly joints through full-scale pure bending tests and mechanical modeling, revealing the role of axial force in crack suppression, non-planar deformation mechanisms, and the critical contribution of fasteners, and confirmed that the joint outperforms cast-in-place sections in bearing capacity and stiffness degradation while demonstrating high safety and low-carbon advantages in the Shenzhen Metro Line 8 application. Liu et al. [15,16] experimentally demonstrated that Y-shaped joints with embedded steel plates outperform those with embedded connectors in mechanical stability, strength, stiffness, energy dissipation, and ductility, while wall–beam–column joints connected by welded steel plates exhibit superior energy dissipation and ductility compared to mechanical connector joints, despite similar ultimate bearing capacities.

The influence of soil-structure interaction on the seismic response of underground structures has garnered increasing attention. Particularly, the adverse effects caused by large deformations and weak bearing capacity in soft soil are more pronounced, making it a crucial issue that cannot be overlooked in the performance-based seismic design of underground engineering. Zhu et al. [17,18] conducted centrifuge shaking table tests in Sendai, revealing that the superstructure, through soil-structure interaction, significantly amplifies near-field soil acceleration and excess pore water pressure accumulation, thereby intensifying foundation lateral deformation and dynamic loading on underground structures, leading to joint cracking, internal force redistribution, and overall response deterioration. Yan et al. [19] demonstrated through centrifuge shaking table tests that in soft soil areas, soil-structure interaction significantly influences subway station seismic response, where liquefiable interlayers or fully liquefied sites reduce soil stiffness and seismic energy transmission, producing a natural isolation effect that results in less damage compared to stiffer but less deformation-compatible clay sites. Li et al. [20] investigated the seismic performance of cross-transfer subway stations in soft soil under horizontal seismic action, showing that soil-structure interaction significantly influences their response, with superior cooperative deformation compared to single stations, but increased reinforcement stiffness in the overlapping soil layer alters the dynamic coupling, intensifying the seismic response of both upper and lower stations. Miao et al. [21] developed an automatic modeling system incorporating soft soil nonlinearity through shaking table tests and validated simulations, revealing the mechanism by which surface structure-soil-substructure interaction influences subway station seismic response. Wu et al. [22] combined shaking table tests with calibrated nonlinear finite element simulations to systematically study the seismic performance of a typical two-story, three-span Shanghai subway station in soft soil, revealing the scale effect on deformation and bending moment, identifying the bottom column base as the weakest part, and confirming the recurrence risk of the Daikai station failure mode in soft soil. Hashash [23] pointed out that seismic loads on underground structures are primarily manifested as the restraint from surrounding ground deformation, rather than inertial forces as in surface structures, and reviewed various soil-structure interaction analysis methods, ranging from free-field deformation to dynamic numerical simulations. Wang [24] simulated the seismic response of a double-walled subway station in soft soil using a discrete-finite element method, revealing soil-structure and structure-structure interface contact and collision behaviors, and found that high-pulse ground motions may cause disproportionate amplification of structural deformation and cracking. Wang et al. [25] systematically investigated the dynamic soil-structure-structure interaction between an underground station and adjacent pile foundations under vertical S-waves using frequency-domain numerical analysis with enhanced ANSYS 14.5 software, revealing the influence of structural layout, earthquake direction, spacing, soil parameters, and superstructure characteristics on system response. Zhuang et al. [26,27] found through numerical analysis that large underground structures significantly alter the liquefaction potential of the surrounding soil in liquefiable soil layers and recommended the use of elastic sliding supports to reduce the risk of seismic damage. Tamari et al. [28], Wang et al. [29], and Ma et al. [30] systematically studied the seismic behavior of underground structures and their interaction with soil, revealing the important role of soil-structure interaction in the stress, deformation, and failure mechanisms of structures.

Practical engineering applications have shown that prefabricated construction technology not only effectively addresses complex construction challenges but also exhibits irreplaceable comprehensive advantages in improving project quality, construction efficiency, operational safety, and environmental protection [31,32]. Prefabricated subway stations have been widely studied and promoted for application in multiple cities in China, primarily utilizing two construction modes. One is the “fully prefabricated structure”, where all main structural components are prefabricated in the factory and assembled on-site. The other is the “assembled splicing structure”, where some key components of the station, such as the roof, floor, side walls, columns, or beams, are prefabricated and then assembled to form an overall structural system through stacking or connection. The connection and assembly technology of prefabricated structures is crucial for achieving efficient and safe application. Currently, it mainly includes prestressed tendon connections [33,34,35], bolt connections [36,37], cast-in-place concrete connections [38], and grouted splicing connections. These technologies have been widely applied in various structural forms such as bridges, buildings, and underground engineering. Among them, prestressed tendon connections and bolt connections belong to “dry connections”, which are characterized by the elimination of on-site wet concrete pouring, fast construction speed, minimal environmental impact, and good recoverability and deformation capacity. Their mechanical behavior is mainly controlled by nonlinear mechanisms such as opening, sliding, and retraction of the joint interface during loading. However, dry connections have relatively limited integrity and energy dissipation capacity [39]. In contrast, cast-in-place concrete connections and various grouted splicing connections are classified as “wet connections”, which achieve rigid connections between components through post-cast concrete or high-strength grouting materials. They exhibit higher integrity and stiffness, and their structural performance can approach or even reach the level of cast-in-place monolithic structures. Such connection methods are particularly suitable for key parts with high requirements for bearing capacity, stiffness, and durability, and they facilitate quality control and on-site construction organization.

Given the frequent occurrence of earthquakes worldwide, as an important component of urban rail transit, the seismic performance of subway stations has become a key research area in civil engineering and a crucial topic in engineering practice [40,41,42]. Huo et al. [43] studied the load transfer mechanism of underground structures through dynamic numerical analysis, revealing that the relative stiffness and interfacial friction characteristics of the structure are key factors affecting seismic response. Wang et al. [44] investigated the shock absorption effect of different seismic isolation measures on underground station structures, finding that the lower the stiffness of the flexible seismic isolation layer, the more significant the shock absorption effect. Wu et al. [45] proposed a new partially prefabricated structure with prefabricated arched roof panels, which showed less column damage, more uniform force distribution, and better inter-story deformation capacity compared to monolithic structures. Gao et al. [46] revealed the impact of assembly technology and construction sequence on structures through full-process construction simulation and seismic response analysis. Qin et al. [47] studied the optimal seismic demand parameters for prefabricated subway stations at different burial depths and, based on the optimized intensity measure (IM), developed seismic fragility curves that enhance the accuracy of seismic vulnerability assessment for underground infrastructure. Ding et al. [48] systematically investigated the mechanical response of prefabricated subway stations under horizontal seismic action in a single-ring configuration, demonstrating that the structure exhibits high safety and stability during seismic loading. Chen et al. [49] pointed out that the potential failure modes of prefabricated columns are relatively minor, but both structures exhibited a failure mode of column failure before wall failure, with the most unfavorable seismic location located at the bottom of the lower column. Cheng et al. [50] established a numerical model using OpenSees 2.3.0 and found that the burial depth of the structure significantly affects its seismic performance and failure mechanism. Other studies have shown that the dynamic response characteristics of prefabricated structures under seismic action are significantly different from those of cast-in-place monolithic structures [51,52,53].

Based on the assembly methods of prefabricated components, prefabricated structures can be divided into wet connection (requiring the casting of grout or concrete) and dry connection (using methods such as bolts and welding that do not require wet operations). Traditionally, prefabricated underground structures have predominantly adopted the dry connection method, and related research has mainly focused on the seismic performance of prefabricated monolithic subway stations with dry connections or cast-in-place subway stations. However, this work introduces a novel subway station structure that combines wet and dry connections. Taking the actual subway station project of Shenzhen Metro Line 15 in Guangdong Province as the research object, the nonlinear static-dynamic coupled refined finite element model considering soil-structure interaction was established. Three types of underground structures with the same proportional dimensions (CIP, ASS, and AMS) were comparatively analyzed to systematically evaluate the seismic performance of different types of underground structures. By comparing the displacement response, internal force characteristics, and structural damage distribution of these three types of structural forms under seismic action, the differences in the seismic performance were comprehensively explored. In particular, the impact of the characteristics of splicing interfaces at different locations on the seismic response of the ASS was also investigated. This research provides new ideas and technical support for the safe construction of urban rail transit infrastructure, thereby promoting the development of the construction industry towards a more sustainable direction.

2. Numerical Model

2.1. Geometric Description of the Subway Station

This study is based on the practical engineering project design scheme of a subway station on Shenzhen Metro Line 15 in Guangdong Province, which adopts the novel assembly splicing structural system. The main structure is a two-story and two-span reinforced concrete frame system with the asymmetric plane layout. The total horizontal width of the structure is 21.1 m, with a left span of 11.3 m and a right span of 9.8 m. The overall structural height is 15.1 m. The top slab is covered with 3.5 m of soil. The system integrates both precast and cast-in-place structural components, forming the hybrid connection mode of dry and wet combination. And the middle column adopts prefabricated reinforced concrete components, with pre-embedded grouting sleeves at the upper and lower ends, achieving reliable connection of vertical components through high-strength cement-based grouting materials. The middle slab adopts a prefabricated reinforced concrete slab, while the sidewall adopts a prefabricated component with the bracket to support the middle slab, jointly forming the main prefabricated structural skeleton. The bottom slab is a cast-in-place concrete structure. Both the sidewall and the top slab adopt the splicing method of prefabricated and cast-in-place laminated layers, that is, setting cast-in-place concrete layers on the prefabricated sidewall and prefabricated top slab. At key stress-bearing locations, such as the intersection areas of the middle column and middle slab and the sidewall and top slab, cast-in-place concrete is used for wet connection, forming post-cast strips. The main joints in the horizontal structure of the station are all connected using concrete post-cast strips or grouting sleeves. In addition, the splicing contact surfaces of all prefabricated components are treated with mechanical chiseling or roughening to form a rough interface as specified by standards. Figure 2 shows the typical cross-sectional structural information of the ASS, including geometric dimensions and the steel bar arrangement scheme.

2.2. Establishment of Finite Element Model

In this study, the two-dimensional finite element model of the rectangular subway station considering soil-structure interaction was established using ABAQUS 2024 software for dynamic time-history analysis.

To minimize lateral boundary effects on the structural response and enhance simulation accuracy, the horizontal distance from the structure to the lateral boundaries was established as at least three times the structural width [54,55,56]. The total width of the model was set to 150 m. The upper boundary of the model was set to the ground surface, and the lower boundary extended to the bedrock layer with a depth of 100 m. In the finite element modeling process, each component of the prefabricated and assembly splicing structure was modeled as the independent geometric part to accurately reflect the assembly characteristics and splicing interface behavior. The soil and structures were discretized using four-node plane strain reduced integration elements (CPE4R), which have good shear self-locking performance and are suitable for simulating large deformation and nonlinear material behavior. The steel bars and connecting sleeves were discretized using two-dimensional beam elements (B21), coupled with the surrounding concrete elements through embedded region constraints, thus more accurately reflecting the stress transfer mechanism, local yield behavior, and collaborative performance between steel bars and concrete. In the dynamic response sensitive areas around the structure, the soil elements were divided into fine grids of 1 m × 1 m to accurately capture the soil-structure interaction and local stress–strain relationship. In the peripheral areas far from the structure and with little impact on dynamic response, the element size gradually increased to 2 m × 2 m. The grid size of the subway station is 0.1 m × 0.1 m, and that of the reinforcing steel bars is 0.3 m. To avoid abrupt changes in element size, a graded meshing approach is adopted from the structure’s periphery towards the far-field soil region. Specifically, a high-resolution grid is maintained near the structure-soil contact interface to accurately capture stress concentration and local nonlinear behavior. Subsequently, through multiple transition layers, the grid size is gradually increased by 1.2~1.5 times in each layer, smoothly transitioning to a coarse grid of 2 m × 2 m in the far field. Figure 3 shows the finite element numerical model of the soil-structure system used for dynamic time history analysis and three different types of structures used for comparative analysis.

The determination of mesh size is crucial for the accuracy and computational efficiency of finite element dynamic analysis, especially in time-history analysis involving seismic wave propagation. This study adopts the classical criterion proposed by Kuhlemeyer and Lysmer [57] to determine the maximum mesh size of the finite element model. This criterion is based on the propagation characteristics of seismic waves in the medium, ensuring sufficient element division within the shortest effective wavelength to accurately capture the wave propagation process and suppress numerical dispersion errors. The maximum mesh size h_max can be obtained by the following equation:

$$h_{\max }\le \left({\displaystyle \frac{1}{8}}~{\displaystyle \frac{1}{10}}\right)\times {\displaystyle \frac{v_{\min }}{f_{\max }}}$$

(1)

where f_max is the highest frequency with significant energy of ground motion and ν_min is the minimum shear wave velocity of soil. Based on the propagation characteristics of seismic wave and the requirements for numerical stability, the maximum allowable grid size is calculated to be 2.54 m using the Kuhlemeyer-Lysmer criterion. Therefore, the maximum mesh size adopted in this study can meet the requirement for precise simulation.

2.3. Material Properties

The response and damage mechanism of subway station structures under seismic action not only stem from the dynamic characteristics of the structures but are also primarily controlled by the nonlinear large deformation and local shear yield behaviors of the surrounding soil. Since soil-structure interaction plays a crucial role during earthquakes, reasonable modeling of the dynamic nonlinear characteristics of soil is the premise and key to accurately predicting the seismic response of underground structures and evaluating their safety performance.

In this study, to effectively capture the nonlinear mechanical behavior of soft soil under strong earthquakes, the Mohr–Coulomb elasto-plastic constitutive model was adopted to describe the constitutive model of soil. Based on the shear strength parameters of soil, the model can determine whether the material enters a plastic yield state, simulate the formation and development of shear failure surfaces, and reflect the hardening or softening behavior of soil under different stress paths. It is widely used in static and dynamic analysis of soil in engineering practice [58]. According to detailed geological survey data and the consolidation undrained triaxial shear tests, the soil deposit distribution at the site where the subway station is located is complex, which can be vertically divided into five main soil layers. Each soil layer exhibits significant differences in physical properties, showing obvious heterogeneity. Figure 4 shows the main soil profile and the physical and mechanical parameters. Where γ represents the natural unit weight, V_s is the shear wave velocity, and c and φ represent the cohesiveness and the internal friction angle, respectively.

During dynamic time-history analysis, as the intensity of seismic motion increases, the soil can undergo a transition from elasticity to nonlinearity, exhibiting significant stiffness degradation and damping growth characteristics. Therefore, it is necessary to fully consider the material nonlinearity of the soil layer and describe the strain-dependent behavior through a reasonable constitutive relationship model. This is crucial for accurately simulating soil-structure interaction.

This study employed a nonlinear dynamic parameter model that varies with strain. By defining the functional relationship between the shear modulus ratio G/Gmax, damping ratio, and shear strain, the nonlinear response of soil under different strain levels was characterized. The nonlinear curve was obtained based on dynamic test data from on-site soil samples and was reasonably fitted by combining parameters such as the plasticity index, water content, and shear wave velocity of each soil layer from geological survey results, thereby ensuring that the model can accurately reflect the stiffness softening and damping evolution characteristics of different soil layers during earthquakes. The curves showing the variation in shear modulus ratio (G/Gmax) and damping ratio with shear strain are presented in Figure 5.

To simulate the hysteretic energy dissipation characteristics and nonlinear dynamic behavior of the structure under seismic action, this study employs Rayleigh damping to characterize the damping mechanism [26,48]. The viscous damping matrix can be expressed as

$$\left[C\right]=\alpha \left[M\right]+\beta \left[K\right]$$

(2)

$$\left\{\begin{array}{l}\alpha \\ \beta \end{array}\right\}={\displaystyle \frac{2\zeta }{{\omega }_1+{\omega }_2}}\left\{\begin{array}{c}{\omega }_1{\omega }_2\\ 1\end{array}\right\}$$

(3)

where [K] and [M] are stiffness and mass matrixes. ζ is the damping ratio of the fundamental mode, taken as 5% in this analysis. ω₁ and ω₂ are the first and second natural vibration frequencies of the structure. Through modal analysis, the eigenvalue problem of structural systems can be solved to determine the natural vibration characteristics.

The Concrete Damaged Plasticity (CDP) developed by Lee and Fenves [59] was utilized and appropriately improved based on actual engineering needs to more accurately simulate the nonlinear mechanical behavior of concrete under complex stress states. By introducing damage factors and plastic strain variables, the stiffness degradation and residual deformation behavior of materials under cyclic loading can be well described. In addition, the bilinear stress–strain relationship model was adopted to simulate the mechanical behavior of steel bars and grouted sleeves. All components of the concrete are C50, while the steel bars are HRB400.

The material parameters for C50 are listed in

Table 1. Material properties of C50.

Material	Elastic Modulus Ec (GPa)	Poisson’s Ratio vc	Density ρc (kg/m3)	Dilation Angle ψ (°)	Tensile Yield Stress ft (MPa)	Ultimate Compressive Stress fc (MPa)
C50	34.5	0.2	2450	32.46	1.89	23.1

and

Table 2. Relevant plastic damage parameters of C50.

Compressive Stress (MPa)	15.84	22.43	16.37	12.79	11.37	9.72	8.17	5.96	2.74
Plastic Strain (%)	0	0.078	0.231	0.337	0.403	0.472	0.547	0.734	1.493
dc	0	0.294	0.594	0.642	0.737	0.771	0.783	0.846	0.942
Tensile Stress (MPa)	2.24	1.68	1.36	0.94	0.57	0.28	0.14	0.07	0.01
Plastic Strain (%)	0	0.010	0.018	0.024	0.072	0.167	0.548	1.269	9.528
dt	0	0.382	0.496	0.658	0.843	0.919	0.956	0.973	0.997

, which ensure that the numerical model can accurately reflect the complex mechanical properties of concrete in actual engineering. The elastic modulus E_s for steel bars is 200 GPa, the yield strength f_y is 400 MPa, and the ultimate strain ε_s is 0.17, ensuring the reliability and safety of the structure during the stress process. Figure 6 shows the mechanical behavior model used to reflect the constitutive relationship between concrete and steel bars.

2.4. Boundary and Contact Conditions

To accurately simulate the dynamic response of the soil-structure system under seismic action, this study employed the two-stage numerical analysis method. Through reasonable boundary condition settings and load application methods, the establishment of the static initial state and the solution of the dynamic response were achieved step by step. The first stage involved the static geostress equilibrium analysis. In this stage, normal displacement constraints were applied to the lateral boundaries on both sides of the model. And the bottom boundary was fully fixed. Under static conditions, only the self-weight effects of the soil and structure were considered, and the system was gradually loaded to reach the stable initial stress state. The second stage was the dynamic time-history analysis, which was used to solve the dynamic response of the system under seismic action. At this stage, the boundary conditions were adjusted to more accurately reflect the wave propagation mechanism. The original lateral normal constraint was replaced with a node-to-node multi-point constraint (MPC), set to “Pin” type, which allowed vertical free sliding but maintained horizontal displacement coordination. The MPC technique has been applied and validated in prior research [60,61]. For nodes with the same y coordinate on the left and right boundaries, the horizontal displacements were coupled with the corresponding free-field reference nodes to achieve free-field boundary conditions, effectively reducing non-physical reflections of seismic waves at the lateral boundaries and improving the simulation accuracy of wavefield propagation. Simultaneously, the x-direction degrees of freedom at the bottom boundary were released. The horizontal seismic motion was applied in the form of vertically incident shear waves, through the specified acceleration time-history curve, from the bottom of the model upwards, simulating the process of seismic waves propagating from the bedrock to the surface.

The prefabricated subway station structure is assembled on-site from a large number of factory-fabricated components. The force transfer mechanism of the spliced joints mainly consists of three parts: the dowel action of steel bars, the shear key mechanism of keyways or concave-convex tenons, and the bond adhesion of post-cast cement-based grout or interfacial mortar. The dowel action of steel bars and the mechanical engagement effect of keyways are usually reflected through precise geometric modeling in finite element models. However, the bond strength between interfaces is influenced by various factors and exhibits high nonlinearity and uncertainty.

In order to systematically evaluate the impact of different connection states on the overall performance of the structure, this study defines two typical interfacial mechanical boundary conditions in finite element analysis, representing the upper and lower limits of splicing performance, namely the ideal connection state and the most unfavorable connection state. For the former, it is assumed that the splicing interface works in complete coordination, with no relative slippage or separation. And the interface is defined as “Tie Contact”, where the degrees of freedom of the nodes on both sides are fully coupled, forming a continuous mechanical whole. The model was used to simulate situations where there is good bonding between the post-cast layer and the prefabricated components and reliable anchoring of the steel bar. It corresponds to the AMS. For the latter, the “Surface-to-Surface Contact” method was used to simulate the splicing interface, allowing normal opening and closing as well as tangential slippage. The normal behavior adopts “Hard Contact”, which transfers pressure only when in compression and allows separation when in tension. And the tangential behavior is based on the penalty method combined with the Coulomb friction model, with a friction coefficient taken as 0.6. The model was used to simulate the nonlinear interface response under splicing performance degradation or extreme seismic action, corresponding to the ASS. In contrast, a CIP is considered a completely continuous homogeneous structure in modeling, with no physical joints between components and no contact interfaces set up, thus eliminating the adverse effects of joint weakening and representing the ideal integrity state under traditional construction methods. In addition, to accurately simulate soil-structure interaction, the “face-to-face contact” method was used to model the interaction between the soil and the outer surface of the structure in all three structural types, with the soil as the primary surface and the structure as the secondary surface. The tangential behavior of the contact was also modeled using the Coulomb friction model, with a friction coefficient of 0.4.

2.5. Selection of Ground Motions

To comprehensively evaluate the dynamic response and seismic performance of prefabricated subway station structures under varying seismic characteristics, this study selected three representative ground motion records from the NGA West 2 database of the Pacific Earthquake Engineering Research Center (PEER) [62], namely the Loma Prieta, Imperial Valley, and Chi-Chi earthquake events as input ground motions. The selected seismic records exhibit significant differences in multiple aspects. They effectively reflect the seismic input characteristics under different geological conditions and source mechanisms, thus comprehensively covering the potential seismic environments faced by prefabricated stations.

Table 3. The information of the ground motions.

NO.	Earthquake Event	Station	Year	Magnitude (Mw)	PGA (g)	PGA/PGV (g/(m/s))	Classification
1	Loma Prieta	Treasure Island	1989	6.93	0.37	0.781	Low frequency
2	Imperial Valley	Cerro Prieto	1979	6.53	0.31	0.984	Medium frequency
3	Chi-Chi	TCU045	1999	7.62	0.36	1.674	High frequency

presents detailed information on ground motions.

From a theoretical perspective, the three sets of seismic records selected in this work, namely Loma Prieta, Imperial Valley, and Chi-Chi, can approximately represent near-field bedrock inputs acting on underground structures. The significant velocity pulse characteristics and high-intensity features can effectively stimulate the dynamic interaction between soil and underground structures, making them suitable for studying the seismic response mechanism under complex soil-structure coupling effects. Furthermore, the frequency components of seismic motion are one of the key factors affecting the dynamic response of underground structures. According to the classification criteria proposed in reference [63], seismic motion can be divided based on the ratio of PGA to PGV: high-frequency seismic motion when PGA/PGV > 1.2, medium-frequency seismic motion when 0.8 < PGA/PGV < 1.2, and low-frequency seismic motion when PGA/PGV < 0.8. As shown in Table 3, the seismic records selected in this work cover three frequency types: high, medium, and low, enabling a comprehensive investigation of the impact of different spectral characteristics on structural response. In order to analyze the structural damage and failure process under strong seismic action, the ground motion is scaled horizontally at the base of the model soil foundation with PGA incrementally increased from 0.2 g to 1.0 g in steps of 0.2 g. Figure 7 shows the seismic characteristics of three ground motion records.

3. Seismic Response of Structures

3.1. Inter-Story Drift Ratio

To systematically evaluate the dynamic response differences between prefabricated and cast-in-place subway station structures under seismic action, this study selected two typical prefabricated structural forms, namely ASS and AMS, and compared them with traditional CIP. For three types of subway station models under the same site conditions, nonlinear dynamic time-history analysis was conducted under seismic input of different intensity levels.

To visually compare the deformation capacity differences between prefabricated structures and traditional CIP, the inter-story drift ratio (IDR) can be adopted as the key evaluation indicator. IDR is defined as the ratio of the horizontal relative displacement generated between adjacent floors during the seismic response process to the story height, which can effectively reflect the degree of lateral deformation and the quality of seismic performance of the structure. The IDR can be expressed as follows:

$$IDR={\displaystyle \frac{\left|u_2-u_1\right|}{h_c}}$$

(4)

where u₁ is the displacement of Floor 1 (middle slab to bottom slab), u₂ is the displacement of Floor 2 (top slab to middle slab), and h_c is the floor height.

From Figure 8, it can be observed that a comparison of the IDR of the station structures under different ground motions reveals that the Loma Prieta ground motion induces the largest IDR, while the Chi-Chi ground motion results in the smallest IDR, indicating the significant impact of ground motion spectral characteristics on structural response. Therefore, seismic ground motions with low-frequency characteristics have the most significant adverse effects on structures, followed by those with medium-frequency characteristics, while the effects of high-frequency seismic ground motions are relatively minor. As the PGA increases from 0.2 g to 1.0 g, the overall IDR of the structure shows an upward trend, consistent with the basic law of nonlinear dynamic response. When PGA = 0.2 g, the IDR of all three types of structures is at a relatively low level with insignificant differences, indicating that under low-intensity seismic motion, prefabricated and cast-in-place structures exhibit comparable deformation control capabilities, with good structural integrity and mechanical behavior in the joint area approaching ideal rigid connections. However, as the seismic intensity increases, the discontinuity and nonlinear characteristics of the joint connection area gradually emerge, becoming a key factor affecting overall performance. In this context, although the IDR of the AMS remains relatively low, it is slightly higher than that of the CIP under high PGA conditions, indicating that its splicing interface may experience slight slippage or local damage under strong earthquakes, but it still exhibits good deformation coordination capability. In contrast, the IDR of the ASS is higher than that of both CIP and AMS under all ground motion inputs, and the gap further widens as PGA increases. This phenomenon indicates that the joints of the ASS may possess significant flexibility, making them prone to accumulating inelastic deformation under seismic action, thereby exacerbating IDR. Especially under strong seismic action, the joint area may evolve into the deformation concentration zone, leading to stiffness degradation and internal force redistribution, ultimately weakening the structural integrity and seismic stability. Therefore, optimizing the joint construction details and enhancing connection stiffness and energy dissipation capacity are key to improving the seismic performance of prefabricated subway stations.

In addition, under the same structural conditions, as PGA increases from 0.2 g to 0.4 g, IDR of all three structures shows a significant increasing trend. The IDR of the ASS growth rate is about 55%. However, as PGA continued to increase to 0.8 g, the growth rate of IDR significantly slowed down, only increasing by about 13%. The trend of change is mainly due to the nonlinear dynamic response mechanism in soil structure interaction. The subway station in this work is shallowly buried in soft soil, and the dynamic response characteristics are highly dependent on the physical and mechanical properties of the foundation soil. When the seismic intensity reaches a certain level, the foundation soil begins to exhibit obvious strain-softening characteristics. The nonlinear behavior causes the soil to attenuate seismic energy during the earthquake process, achieving a natural isolation effect and thus suppressing further growth of the IDR for the structure to some degree. When PGA increases from 0.8 g to 1.0 g, the IDR of the three structures increases significantly. The structure and foundation soil have entered a more serious nonlinear deformation stage. Under such extreme conditions, even if there is a certain soil softening effect, it cannot completely inhibit the sharp rise in the IDR of the structure, which reflects the non-negligible destructive force of high-intensity ground motions on the structure.

When designing prefabricated structures, the matching relationship between the seismic spectrum and the natural vibration characteristics of the structure should be fully considered to avoid resonance in the low-frequency dominant region. At the same time, excessive reliance on the passive energy dissipation of soil should be avoided, and active optimization of joint construction should be implemented to enhance connection stiffness and ductility. In particular, technologies such as high-strength grouted sleeves, shear connectors, or prestressed splicing should be adopted on key force transfer paths to enhance the deformation coordination capacity and energy dissipation mechanism of the joints. While ensuring the integrity of the structure, inter-story drift should be reasonably controlled to prevent the formation of weak hinges or instability mechanisms under strong earthquakes.

3.2. Internal Force Response

To evaluate the mechanical performance differences in various structural forms under seismic action, detailed observations and comparative analyses were conducted on the internal force responses of key components such as the sidewalls and middle columns of CIPs, AMSs, and ASSs. Figure 9 shows that multiple monitoring sections are set up at key structural stress-bearing areas, including the middle column (M), the left sidewall (L), and the right sidewall (R), to record in real-time the changes in axial force, shear force, and bending moment of each component during the seismic excitation process. Figure 10 shows the maximum internal forces sustained by the middle columns and sidewalls of each structural form at the monitoring sections when PGA = 1.0 g.

As can be seen from Figure 10, the internal force of the sidewalls of the three structural forms, CIP, AMS, and ASS, are highly consistent overall, and the internal force curves are basically superimposed, indicating similar overall stress patterns. And the trends of internal force changes corresponding to the three types of seismic motions are basically similar. It is worth noting that the internal force values of the left sidewall are generally higher than those of the right sidewall. This phenomenon is mainly attributed to the asymmetric layout design of the structure, which results in the left sidewall bearing greater vertical soil load and structural self-weight and generating the larger internal force response. In addition, due to the eccentricity of the structural center of gravity, the uneven distribution of seismic inertial force further increases the stress on the left sidewall. As can be seen from Figure 10c, the internal force of the middle column in the CIP is the largest, especially at the two key sections of the column top and bottom, where the internal force is significantly higher than that in AMS and ASS. This is consistent with its characteristics of high integrity, large stiffness, and direct internal force transfer paths. In contrast, the internal force of the AMS at the column top is close to that of the CIP, indicating that the upper connection joints have good stiffness and force transfer capabilities. However, in the bottom of the column area, the internal force of the AMS is significantly lower than that of the CIP. This phenomenon may stem from the design of using grouting sleeves for connection at the column base. The prefabricated column is connected to the structure with high-strength connections through embedded sleeves, effectively enhancing the stiffness and ductility of local sections. For the ASS, the internal force of the middle column is significantly lower than that of the CIP and AMS throughout the entire height range, exhibiting the lowest level of internal force. This indicates that the assembly splicing structure has a certain internal force weakening effect under seismic action; that is, due to the existence of the splicing interface, the overall stiffness of the structure is reduced, and the concentrated transmission of seismic force to the central column is partially suppressed, and internal force tends to be dispersed and transmitted through multiple paths. This characteristic can be seen to some extent as the passive “isolation” or “energy dissipation” mechanism, which helps alleviate the stress state of key components but may also be accompanied by greater overall deformation. In addition, Figure 10 also shows that the maximum internal force of both the sidewalls and the middle columns occurs at the bottom section of the lower floor, which is the most unfavorable stress position of the structure and the key control section in seismic design.

In summary, the distribution characteristics of internal force reveal that although the overall stress patterns of CIP, AMS, and ASS structural forms are similar, there are significant differences in the forces acting on key parts, reflecting the profound impact of different connection methods on structural mechanical behavior. The asymmetric layout of the structure leads to uneven stress distribution on the side walls, with the left side wall bearing higher internal forces under seismic action. In seismic design, symmetry should be optimized to reduce the eccentric effect. As the main load-bearing component, the middle column experiences concentrated internal force at the top and bottom areas, with the lowermost part being the most unfavorable section, requiring special attention to enhance its bearing capacity and ductility construction. The CIP, with good integrity and high stiffness, transfers internal forces directly and concentrically. The internal force at the top of the column in the AMS is close to that in the CIP, indicating that the upper connections have good force transfer performance. However, the lower internal force at the column base may be related to the characteristics of the grouted sleeve connections, requiring attention to the stiffness matching and construction quality of the connection area. In contrast, the internal force in the middle column of the ASS is significantly lower, indicating that the introduction of flexibility into the splicing interface reduces the overall stiffness, weakens the concentrated transfer of seismic forces to the core components, and leads to a passive redistribution of forces or energy dissipation mechanism, which can help alleviate stress in key parts but may also be accompanied by a greater deformation response. In seismic design, the mindset should shift from “equivalent to cast-in-place” to performance-based design, making rational use of the flexibility characteristics of prefabricated joints to achieve redistribution of internal forces, balance structural stiffness and energy dissipation capacity, and ensure the safety of key parts while enhancing the seismic robustness and recoverability of the structure.

3.3. Damage Analysis

Figure 11 shows the seismic damage to the station structures (under Loma Prieta motion with PGA = 1.0 g). Figure 12 shows the tension damage contour plots for three types of subway station structures under three types of ground motions when PGA = 1.0 g. The three subway station structures in Figure 11 and Figure 12 are labeled as CIP, AMS, and ASS, respectively. If the tension damage coefficient (DAMAGET) is greater than 0, it indicates that the concrete begins to show slight damage under tension. When the coefficient approaches 1.0, it indicates that the concrete is close to complete tensile failure. If the compression damage coefficient (DAMAGEC) exceeds 0, the concrete begins to show slight compressive damage under compressive stress. As the coefficient approaches 1.0, the concrete approaches complete compressive failure. The default average threshold for stress calculation at element nodes is 75%.

From Figure 11, it can be seen that when PGA = 1.0 g, the compression damage of the three structural forms (CIP, AMS, and ASS) is generally at a low level, indicating that the structure is not in a severe compression damage state. Compression damage is mainly concentrated in key joint areas, with the most significant being the connection between the middle column and the bottom slab. The area is prone to compression damage due to the combined effects of significant axial pressure and bending moment. Secondly, there is also a certain degree of compression damage at the intersection of the top slab and the middle column, as well as at the intersection of the top slab and the sidewalls, which is mainly due to the local stress concentration of the top slab under the combined action of soil cover load and seismic inertial force. However, the extent of the damage in these areas is generally small, and the damage variables are far from reaching a completely destroyed state, indicating that the concrete still maintains good bearing capacity, and the impact of compression damage on the overall structural performance is relatively limited. It is worth noting that compared with the CIP, the compression damage distribution of the AMS shows a significant upward movement of damage; that is, the damage area originally concentrated at the bottom of the column in the CIP is transferred to the upper part of the column in the AMS. The phenomenon may be attributed to the structural measure of the AMS using a grouting sleeve connection at the bottom of the column, which significantly enhances the local stiffness and restraint ability of the column base area, effectively suppressing the crushing and microcrack development of concrete in this area, thereby redistributing some of the stress and damage originally concentrated at the bottom of the column to the unreinforced area above it. The damage transfer mechanism to some extent protects the key column bottom joints and avoids the premature brittle collapse. In contrast, the distribution of compressive damage in ASS is more dispersed, which is related to the coordination of slip and deformation allowed by the splicing interfaces, resulting in a decrease in stress concentration. The findings are consistent with the observations reported by Chen et al. [64], further validating the reliability of the results obtained in this study. To sum up, under strong seismic actions the prefabricated structures can effectively regulate the damage development path through reasonable joint design, effectively utilize the stiffness gradient and deformation capacity of prefabricated joints, and achieve protection of key parts and optimization of damage mechanisms, thereby enhancing the repairability and seismic robustness of the structure while ensuring safety.

From Figure 12, it can be seen that all three types of station structures exhibit extensive tensile damage to the cross-section at the joint connections. It can be inferred that there is severe cracking damage to the concrete at these locations. By further comparing the tensile damage of the structures, it can be observed that the overall tension damage distribution area of AMSs and CIPs is basically equivalent, indicating that under high seismic excitation, although the AMS adopts grouting sleeves, the development degree of tension damage is similar to CIPs, and the two have similar mechanical response characteristics. Tension damage is mainly concentrated in the key stress joints of the structure, such as the boundary between the slab and column and the junction between the sidewall and the slab, which become high-risk areas for concrete tension damage. In contrast, the tension damage of ASSs exhibits significantly different distribution characteristics. The damage area in the joint area is significantly reduced, especially in the complex joint area where the slab and column intersect, with the smaller damage range and lower damage degree. This phenomenon is mainly attributed to the widely used non-rigid splicing joint design in ASSs. The types of nodes allow for a certain degree of relative rotation and slight slippage between components, thereby weakening rigid constraints and reducing the efficiency of direct transmission of internal force. The connection mechanism plays a role in passive energy dissipation and internal force redistribution to a certain extent, reducing the concentration of tensile stress in key components, effectively protecting the core load-bearing system of the structure, and improving the overall seismic resilience. However, due to the fact that the splicing joint itself becomes a key part of deformation coordination, its repeated tension and closure under earthquake action can easily cause local stress concentration in the sidewall joint area, resulting in more obvious tensile damage to the sidewall concrete near the joint. This indicates that although the ASS performs well in reducing damage to the middle column, the seismic performance of the sidewall joints needs to be given special attention in design to prevent premature local failure under strong earthquakes.

To further examine and contrast the damage evolution patterns of the three structures, Figure 13 shows the changing trends of compression and tension damage factors in key areas of each structure under Loma Prieta motion with the increase in PGA.

As shown in Figure 13a, under varying seismic intensities, the compression damage factors (DAMAGEC) of the key parts of the three structures show certain differences. For CIP, the DAMAGEC values at the bottom of the central column and the bottom of the side walls are relatively high and continue to increase with the increase in PGA, indicating that these areas are typical stress concentration sites under seismic action and are prone to concrete compression damage. AMSs and CIPs have similar overall compression damage development patterns, and the trend of the maximum DAMAGEC increasing with PGA is basically consistent with CIPs. In contrast, ASSs exhibit a unique damage distribution pattern. As PGA increases from 0.2 g to 1.0 g, the DAMAGEC value of the ASS at the bottom of the sidewall is significantly higher than that of the CIP and AMS, indicating that the joint interface is prone to non-coordinated deformation in the joint area under high stress conditions, leading to increased damage in that area. However, it is worth noting that the compression damage level of the ASS middle column is significantly lower than that of the CIP and AMS, especially under high PGA conditions, where the advantage is more prominent. This indicates that non-rigid joints effectively regulate the distribution of internal force by allowing a certain degree of relative slip, reducing the concentrated transmission of load to the middle column, and thus improving the compressive performance of the middle column area. According to the development curve of the tension damage factors (DAMAGET) shown in Figure 13b, under low PGA conditions, the tensile damage development at the top and bottom of the upper column in the ASS is gradual, with damage values considerably lower than those observed in the CIP and AMS, reflecting the good integrity and damage control ability under small earthquakes. However, the DAMAGET values at the top and bottom of the sidewalls are significantly higher than the other two structures, reflecting that the joint area is more prone to local peeling under tensile stress, becoming the potential weak link. As PGA further increases to 1.0 g, the rapid development of DAMAGET in all three structures approaches 1.0. Overall, under the action of small earthquakes, the damage of the ASS on key load-bearing components such as middle columns is significantly lower than that of the CIP and AMS, demonstrating superior damage control capabilities. But as the intensity of the earthquake increases, the damage development of the lateral joint interface accelerates, and the damage is concentrated in the joint area of the sidewalls.

In the design of prefabricated structures, by reasonably designing the stiffness, strength, and deformation capacity of joints, damage is actively guided to occur in non-critical areas that are easy to detect and repair and do not affect overall stability, achieving the seismic strategy of “strong columns and weak joints” or “damage isolation”. At the same time, structural measures must be strengthened in the joint area, such as setting up tensile anchors, interfacial shear keys, or elastic sealing materials, to improve the durability and impermeability, ensuring that the structure still has the necessary safety reserves and recoverable functions after strong earthquakes.

3.4. Response of Splicing Interface

To obtain the maximum deformation response of the assembly joint interface, and acknowledging that the left sidewall typically bears a heavier load than the right under seismic action, this study established multiple monitoring sections at critical joints within the ASS under intense earthquake conditions featuring a PGA of 1.0 g. Specifically, the monitoring sections encompass the left sidewall (L) and the middle column (C), as illustrated in Figure 14.

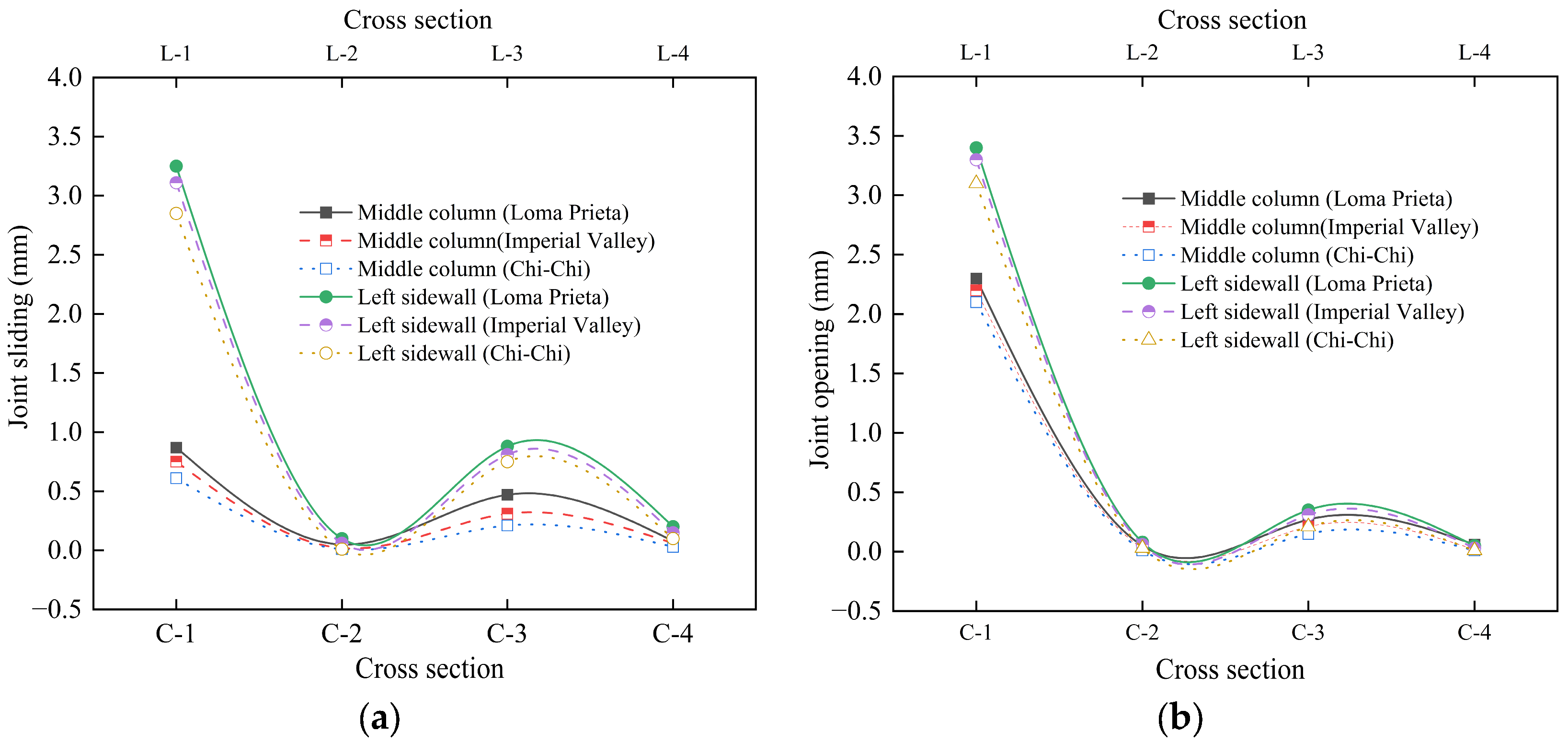
Figure 15 illustrates the maximum deformation response at the splicing interface of the monitoring sections with respect to the distribution characteristics of both horizontal sliding distance and vertical opening width. As depicted in Figure 15a, during intense seismic activity, the horizontal relative displacement at the top monitoring section (L-1) on the left sidewall attains a maximum value of 3.25 mm, markedly exceeding that of other monitored zones, thereby emerging as the most prominent deformation area among joints. This observation suggests that the top of the left sidewall undergoes substantial bending moment and shear force. Given that the area typically resides at the junction of prefabricated wall panels, it experiences weaker boundary constraints and possesses lower connection stiffness compared to CIP, leading to enhanced lateral deformation capacity and susceptibility to cumulative slip, demonstrating typical flexible joint behavior. Furthermore, the horizontal sliding distance of the monitoring section (C-1) at the top of the middle column measures just 0.87 mm, significantly less than that at the top of the sidewall. This indicates that the connection joint between the middle column and the top slab exhibits greater connection stiffness and enhanced lateral displacement resistance. This is primarily attributed to the superior structural integrity and more comprehensive restraint conditions of the middle column, which facilitates the effective transmission of horizontal shear force. The horizontal sliding in the remaining monitoring areas is confined to within 0.45 mm, with some areas approaching zero, which demonstrates the exceptional deformation coordination capabilities, free from any noticeable sliding or detachment. Further analysis reveals that the non-uniform distribution of joint slip underscores the stress redistribution process within the structure during intense earthquakes and also emphasizes the localized areas of structural weakness. As the pivotal lateral load-resisting element, excessive slip at the top of the sidewall could result in deteriorated joint sealing performance and compromised waterproof layers and potentially impact the support conditions of the roof, ultimately jeopardizing the overall structural safety. Consequently, this area serves as the critical control part for seismic performance. Upon examining the distribution of joint opening width depicted in Figure 15b, it becomes evident that the top of the left sidewall exhibits not only pronounced horizontal sliding but also the relatively significant vertical opening width, further confirming the nonlinear response characteristics of the joint under complex loading conditions. Consequently, in seismic design, it is imperative to implement reinforcement measures for such crucial connection sections to enhance the long-term serviceability. Therefore, in the design of prefabricated structures, attention should not only be paid to the overall load-bearing capacity but also to the refined design of the joint. For areas with high deformation requirements, such as the top of the sidewall, joint constructions with good ductility, adaptive deformation capacity, and reliable waterproof performance should be adopted, such as setting shear keys, pre-compressed springs, elastic filler material, or slidable energy dissipation devices to coordinate large displacements, alleviate stress concentration, and maintain sealing function. For key force transmission paths such as the central column, high-rigidity connections should be maintained to ensure efficient force flow transmission.

4. The Impact of Splicing Interface on Seismic Response

The splicing interface, as a key connecting part between prefabricated components, constitutes a critical link in the structural force transmission system, and the mechanical behavior directly determines the seismic performance of the structure. In order to further explore the influence mechanism of the splicing interface under seismic action, this study adopted two contact modeling strategies, namely “Surface to Surface Contact” and “Tie Contact”, to more accurately reflect the sliding, opening, and force transmission characteristics of the interface. The study systematically regulated the contact conditions of key joint interfaces, with a focus on analyzing the effects on the deformation modes and internal force redistribution of underground structures when PGA = 1.0 g. The component splicing interface is shown in Figure 16. Where TW represents the splicing interface at the top of the sidewall, BW represents the splicing interface at the bottom of the sidewall, CP represents the splicing interface in the assembly area between cast-in-place and prefabricated components, and MC represents the splicing interface at the end of the middle column. Six different cases of splicing interface configurations were designed. The results are summarized in

Table 4. The relationship between the splicing interface contact and the layer deformation.

Case	T-Interface	Floor 1		Floor 2		Overall
		IDR (%)	η	IDR (%)	η	IDR (%)	η
T-A	All	0.553	/	0.593	/	0.573	/
S-A	None	0.569	1.029	0.604	1.019	0.587	1.024
T-TW	Interface-TW	0.564	1.020	0.599	1.011	0.578	1.009
T-BW	Interface-BW	0.555	1.004	0.593	1.000	0.573	1.000
T-MC	Interface-MC	0.558	1.009	0.596	1.005	0.575	1.003
T-CP	Interface-CP	0.568	1.027	0.602	1.015	0.584	1.020

. Where “T” represents “Tie Contact”, “S” represents “Surface to Surface Contact”, and “A” represents that all splicing interfaces are uniformly set to the same contact type. In addition, η is defined as the ratio of the IDR under each case to that of the T-A case.

From Table 4, it can be seen that the splicing interface CP between cast-in-place components and prefabricated components exerts the greatest influence on the IDR of the subway station structure and is the dominant factor controlling the overall deformation characteristics. The splicing interface TW between the top of the sidewall and the top slab also exhibits strong sensitivity, and the quality of the connection performance directly affects the deformation response. If the bonding strength between the two key splicing interfaces is insufficient, interface sliding or opening is prone to occur under seismic action, resulting in stiffness degradation in the joint area, thereby reducing the structure’s overall lateral stiffness and even localized deformation concentration, seriously weakening the seismic performance. In contrast, the connection strength of splicing interface MC has a relatively small impact on deformation response and is a non-critical influencing factor. This phenomenon indicates that although the middle column bears the main vertical load, the variation in the joint connection stiffness has limited control over the overall horizontal deformation, and the lateral deformation response depends more on the integrity and collaborative working ability of the sidewalls. However, it is worth noting that when the splicing interface BW between the bottom of the sidewall and the bottom slab connection area is set with “Tie Contact”, the IDR of the structure is significantly reduced. This indicates that a good connection in this area can effectively enhance the lateral constraint capability at the bottom of the structure.

Figure 17 presents a comparison of the maximum internal force response of the middle column and two sidewalls for six distinct joint splicing interface cases under Loma Prieta motion when PGA = 1.0 g. From Figure 17, it can be observed that the T-CP case exhibits the lowest internal force response level, closely matching the internal force values of the T-A case, both of which fall within the lower bound of the overall internal force response range. This suggests that achieving the rigid connection at the CP interface significantly enhances structural integrity and facilitates more efficient load transfer pathways, thereby effectively mitigating stress concentrations in critical components and improving the structural collaborative performance. In contrast, the internal force response curves for the T-TW, T-BW, and T-MC cases nearly overlap with the results from the S-A case, all reaching the upper limit of internal force response. This observation indicates that even when the critical joint splicing interfaces between the prefabricated components are idealized as rigid connections, the contribution to improving overall structural force redistribution remains minimal.

The joint splicing interface CP between cast-in-place and prefabricated components is the core controlling factor that determines the seismic performance of the structure. The area is located at a critical joint for structural stress conversion and plays an important role in coordinating vertical load transmission and horizontal forces. If the splicing interface connection is weak, it is highly likely to form weak hinges, leading to sudden stiffness changes and imbalanced redistribution of internal force, and even causing local failure to evolve into overall instability. In contrast, splicing interfaces such as TW, BW, and MC have less impact on the distribution of internal force in the main structure due to the secondary path or relatively uniform force distribution in the overall force transmission system. In the design and construction of prefabricated subway station structures, emphasis should be placed on ensuring the connection quality of the joint splicing interface CP between the cast-in-place and the prefabricated components, ensuring that it has sufficient rigidity and ductility.

In the design of prefabricated structures, emphasis should be placed on the design of joint stiffness and strength, especially at key joints where stress concentration and high deformation demands occur. The joint constructions with high stiffness, high strength, and good ductility should be adopted to ensure efficient and stable force flow transmission while avoiding problems such as sudden changes in stiffness and uneven distribution of internal forces caused by joint weakening. For non-critical areas, flexible joints can be appropriately used to distribute stress and increase the overall toughness of the structure. However, factors such as joint durability, waterproof performance, and maintenance costs need to be comprehensively considered during design to ensure the safety, reliability, and functional integrity of the structure throughout the life cycle.

5. Conclusions

This study aims to evaluate the seismic performance of asymmetric rectangular prefabricated subway station structures in soft soil environments. Two typical asymmetric rectangular prefabricated structures (AMS and ASS) were selected and compared with the traditional CIP. By constructing the refined nonlinear finite element model considering soil-structure interaction and performing nonlinear incremental dynamic time-history analysis under three typical ground motions, the performance of each structure in terms of seismic response and damage evolution was systematically compared. Furthermore, multiple contact cases were set up for simulation analysis. The main conclusions are as follows:

(1)

The adverse effects of low-frequency ground motion on prefabricated structures are most significant, significantly exacerbating the IDR. During the phase when the PGA increases from 0.2 g to 0.4 g, the IDR of the ASS increases by as much as 55%. However, when the PGA continues to increase to 0.8 g, the growth rate slows down significantly to about 13%. When the PGA further increases to 1.0 g, the IDR rises significantly again. The CIP, due to its high overall stiffness, consistently exhibits the smallest IDR and excellent deformation control capability. The IDR of the AMS is slightly higher than that of the CIP, but the difference is minor at most PGA levels, with only a slight increase under high intensity, demonstrating good joint performance and deformation coordination ability. In contrast, the ASS exhibits the highest IDR under all conditions, which can easily lead to cumulative deformation under strong seismic action.

(2)

Under strong seismic action, the internal force response for three types of structures on sidewalls is relatively consistent, and the overall stress pattern is mainly controlled by geometric shape and external loads. The left sidewall bears a higher bending moment and shear force due to the large left span. The internal force responses of the types of structures in the middle column are significantly different. Because of the high stiffness and strong continuity of the CIP, the internal force concentration of the intermediate column is obvious. The ASS effectively alleviates the concentration and transmission of internal force by virtue of splicing interfaces and significantly reduces the internal force of key parts. The internal force response of the AMS is between the CIP and ASS.

(3)

The damage to the CIP primarily occurs in stress concentration zones, such as the base of the middle column and the bottom of sidewalls. The AMS enhances the integrity of the connection through grouting sleeves, shifting the location of compression damage upward, but the distribution of tensile damage is similar to the CIP. In contrast, the ASS effectively mitigates damage to the middle column through the use of non-rigid splicing, facilitating redistribution of internal force and protection of critical components, thereby demonstrating excellent seismic performance. However, the splicing area of the sidewalls tends to concentrate damage. The damage to key components in prefabricated structures is less severe than that of the CIP, and the damage patterns are significantly influenced by the connection properties.

(4)

The joint at the top of the left sidewall slid horizontally by 3.25 mm under strong earthquakes, accompanied by significant vertical opening, which is much higher than the 0.87 mm at the top of the middle column and the less than 0.45 mm in other areas, highlighting the nonlinear deformation concentration characteristics as a flexible weak zone. The deformation of the joint splicing interface of the ASS is significantly uneven, with the top of the left side wall becoming the concentrated area of maximum horizontal sliding and vertical opening, reflecting the weakness of the flexible joint. In contrast, the small slip at the top of the middle column indicated the high connection stiffness and good overall deformation coordination. Due to the significant sliding and opening of the splicing interface, the top of the sidewall is a key part affecting the seismic performance of the prefabricated structure.

(5)

The joint splicing interface between cast-in-place and prefabricated components has a significant impact on the deformation and internal force distribution and is a key factor in controlling the overall deformation characteristics and seismic performance. The connection characteristic at the top of the sidewall significantly affects the structural deformation response, while the influence of the middle column and other splicing interfaces is relatively small. Optimizing the connection characteristics of the joint interface between cast-in-place components and prefabricated components can significantly improve the overall collaborative performance and lateral stiffness and redistribute the internal force of prefabricated subway station structures.

(6)

For CIPs, the ductility and damage dissipation capacity should be improved by optimizing the reinforcement configuration, introducing local fiber reinforcement, or setting up controllable weak zones to avoid premature yielding of the joints. As for ASSs, while retaining moderate flexibility in non-critical paths to facilitate energy dissipation, shear connectors, pre-compression devices, or elastic sealing systems should be strengthened in high deformation areas such as the top of sidewalls and slab-column connections to enhance the deformation compatibility and durability of the joints. In terms of AMSs, emphasis should be placed on optimizing the stiffness transition and restraint conditions in the joint areas to ensure sufficient connection strength and strengthening quality control and inspection measures on critical load-transmitting paths to fully leverage their performance advantages.

This study reveals the seismic response characteristics of prefabricated subway station structures in soft soil through nonlinear finite element analysis. It clarifies the key influence of joints on seismic performance, providing a useful reference for the design of prefabricated underground structures. However, the study still has certain limitations. The seismic input only includes horizontal components, ignoring the potential impact of vertical ground motions on structural joint opening and components. Moreover, the use of a 2D plane strain model makes it difficult to truly reflect the 3D spatial effects of subway stations. This limits the comprehensive characterization of overall mechanical behavior to some extent. Future work should focus on 3D refined simulation, incorporating vertical and traveling wave seismic inputs and combining tests or field monitoring data for multi-scale verification, and using interface elements or fiber beam models with bond-slip constitutive laws. This will enable a more accurate assessment of the dynamic performance of prefabricated structures under strong earthquakes.