Experimental Study of the Actual Structural Behaviour of CLT and CLT–Concrete Composite Panels with Embedded Moment-Resisting Joint
Abstract
1. Introduction
- High strength in relation to the self-weight of the material.
- Small manufacturing tolerances and good dimensional stability.
- Good load-bearing capacity in fire.
- Good thermal insulation capacity.
- Low self-weight, which means lower transport and assembly costs, as well as lower foundation costs.
- Good capacity to tolerate chemically aggressive environments.
- Flexible production that even allows the manufacture of curved surfaces.
2. Experimental Investigation
2.1. Description of Specimens and Material
- Series A (CLT panel without joints and without a concrete slab);
- Series AC (CLT panel without joints and with a concrete slab);
- Series B (CLT panel with joints and without a concrete slab);
- Series BC (CLT panel with joints and with a concrete slab).
2.2. Test Set-Up and Loading Procedure
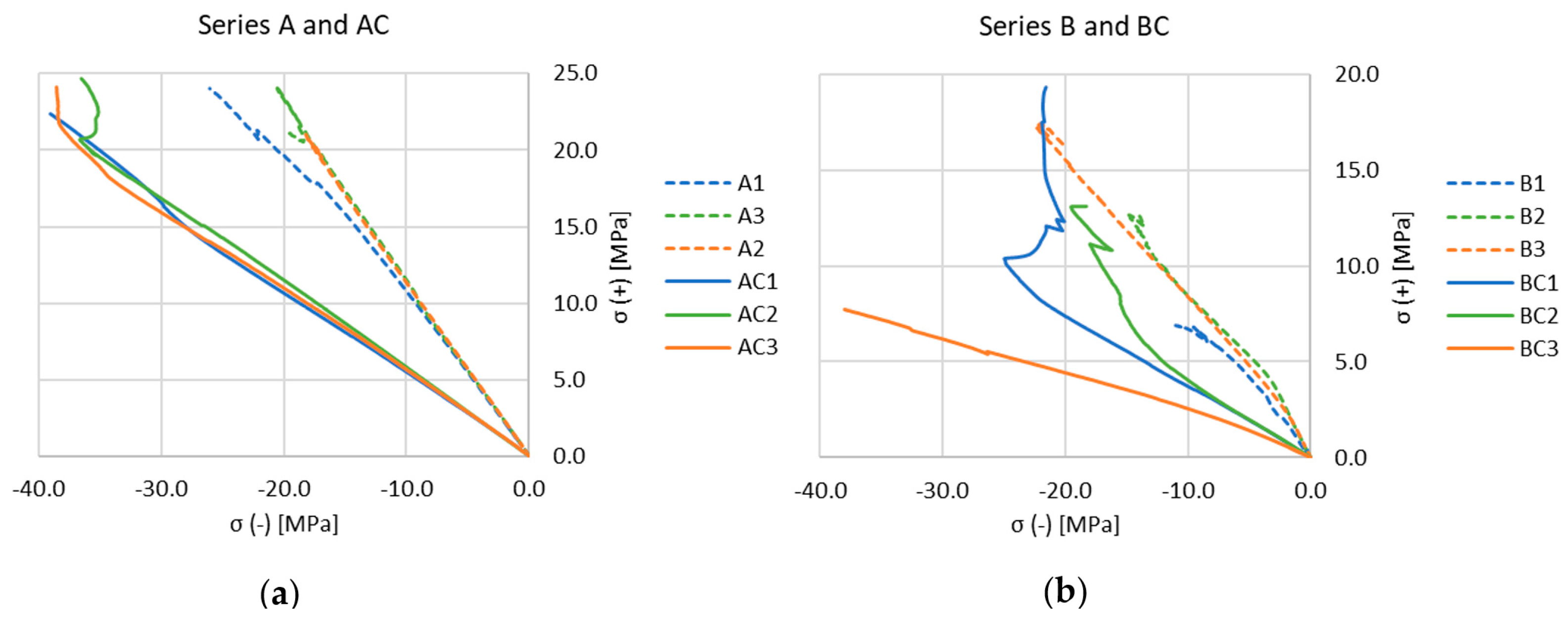
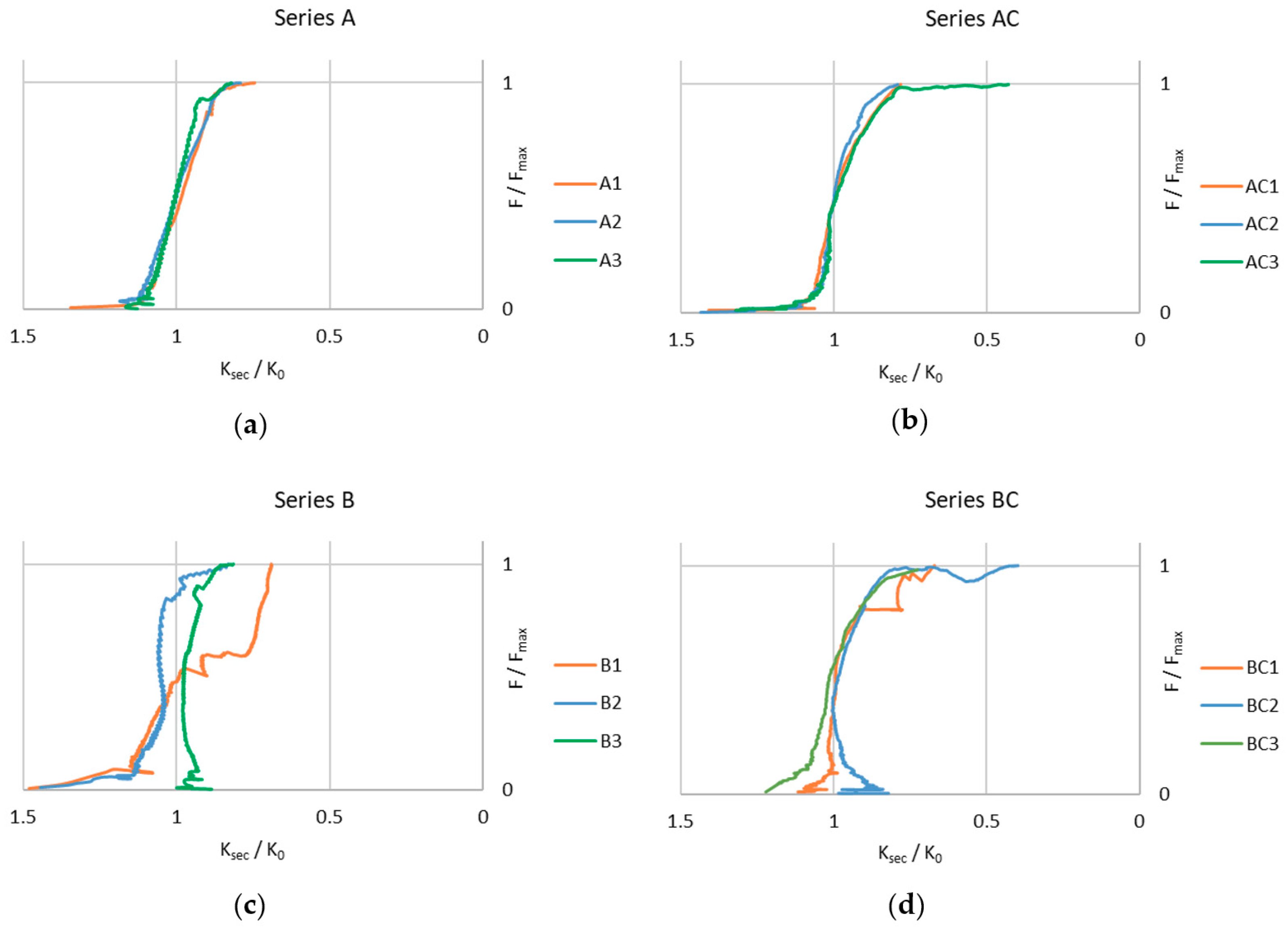
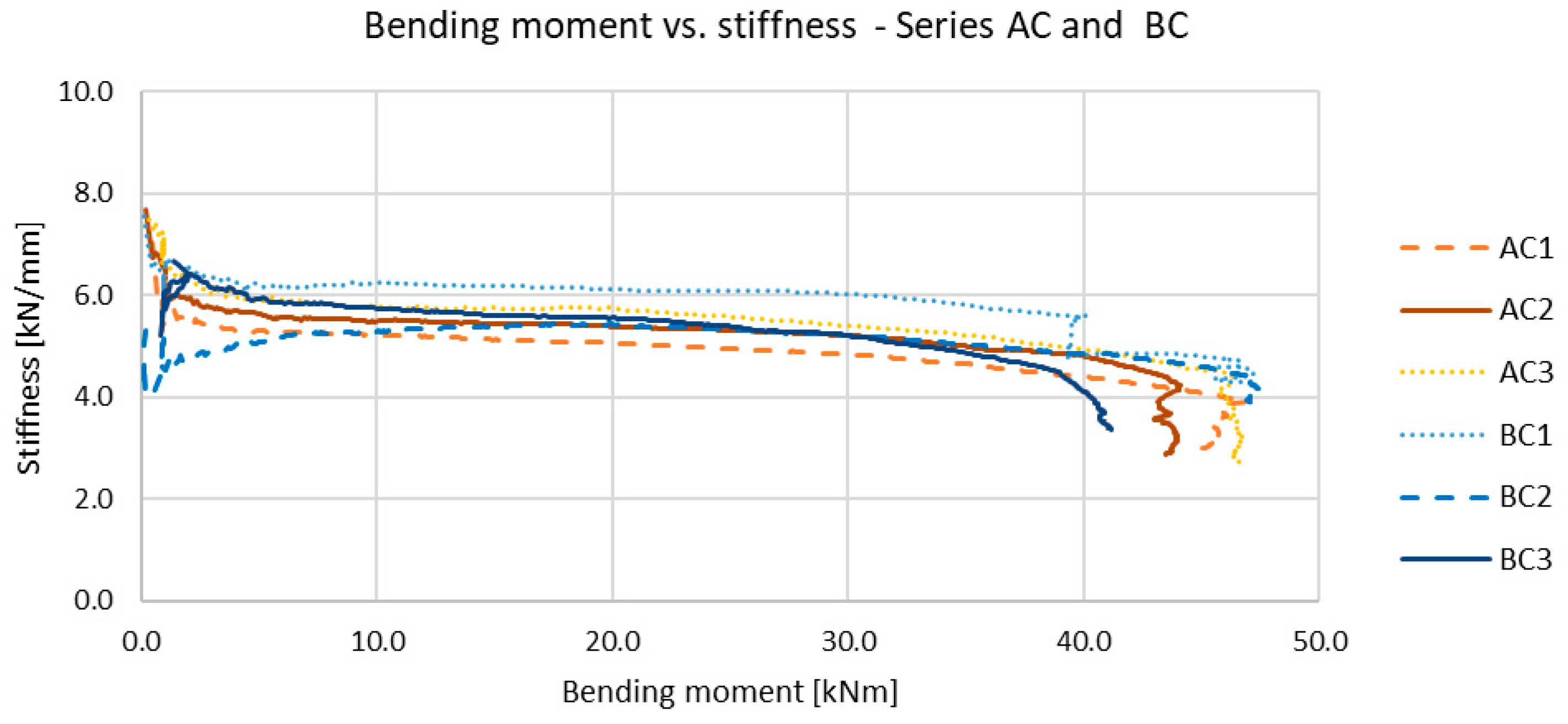
3. Experimental Results
4. Discussion
4.1. Observed Behaviour
4.2. Possible Concept of a Theoretical Model of the Joint
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schickhofer, G. Starrer und Nachgiebiger Verbund bei Geschichteten, Flächenhaften Holzstrukturen; Graz University of Technology: Graz, Austria, 2013; ISBN 978-3-85125-268-2. [Google Scholar]
- 100 Projects UK CLT. Produced by Waugh Thistleton Architects on behalf of the Softwood Lumber Board & Forestry Innovation Investment. Printed in Canada, 2018. Available online: https://waughthistleton.com/100-projects-uk-clt/ (accessed on 28 September 2025).
- Swedish Wood. The CLT Handbook. CLT Structures—Facts and Planning. Stockholm, May 2019. Available online: https://www.swedishwood.com/publications/list_of_swedish_woods_publications/the-clt-handbook/ (accessed on 28 September 2025).
- Karacabeyli, E.; Gagnon, S. Eds. Canadian CLT Handbook. 2019. Available online: https://web.fpinnovations.ca/clt/ (accessed on 28 September 2025).
- Kremer, P.D.; Guiver, J. Mass Timber Construction in Australia and New Zealand–Status, and Economic and Environmental Influences on Adoption. Wood Fiber Sci. 2018, 50, 128–138. [Google Scholar] [CrossRef]
- Abed, J.; Rayburg, S.; Rodwell, J.; Neave, M. A Review of the Performance and Benefits of Mass Timber as an Alternative to Concrete and Steel for Improving the Sustainability of Structures. Sustainability 2022, 14, 5570. [Google Scholar] [CrossRef]
- Structural Timber Association, Technical Bulletin 01—Timber as a Structural Material—An Introduction. Available online: https://www.structuraltimber.co.uk/ (accessed on 31 July 2025).
- Harte, A.M. Mass Timber–the Emergence of a Modern Construction Material. J. Struct. Integr. Maint. 2017, 2, 121–132. [Google Scholar] [CrossRef]
- Ibn-Mohammed, T.; Greenough, R.; Taylor, S.; Ozawa-Meida, L.; Acquaye, A. Operational vs. embodied emissions in buildings—A review of current trends. Energy Build. 2013, 66, 232–245. [Google Scholar] [CrossRef]
- Taylor, A.; Gu, H.; Nepal, P.; Bergman, R. Carbon Credits for Mass Timber Construction. Bioprod. Bus. 2023, 8, 1–12. [Google Scholar] [CrossRef]
- Andersen, J.H.; Rasmussen, N.L.; Ryberg, M.W. Comparative life cycle assessment of cross-laminated timber building and concrete building with special focus on biogenic carbon. Energy Build. 2022, 254, 111604. [Google Scholar] [CrossRef]
- Chen, C.X.; Pierobon, F.; Jones, S.; Maples, I.; Gong, Y.; Ganguly, I. Comparative life cycle assessment of mass timber and concrete residential buildings: A case study in China. Sustainability 2022, 14, 144. [Google Scholar] [CrossRef]
- Pierobon, F.; Huang, M.; Simonen, K.; Ganguly, I. Environmental benefits of using hybrid CLT structure in mid-rise non-residential construction: An LCA-based comparative case study in the U.S. Pacific Northwest. J. Build. Eng. 2019, 26, 100862. [Google Scholar] [CrossRef]
- EN 15804:2012+A2:2019; Sustainability of Construction Works—Environmental Product Declarations—Core Rules for the Product Category of Construction Products. European Committee for Standardization, CEN: Brussels, Belgium, 2019.
- EN 15978:2011; Sustainability of Construction Works—Assessment of Environmental Performance of Buildings—Calculation Method. European Committee for Standardization, CEN: Brussels, Belgium, 2011.
- ASTM E2921–22; Standard Practice for Minimum Criteria for Comparing Whole Building Life Cycle Assessments for Use with Building Codes, Standards, and Rating Systems. ASTM International: West Conshohocken, PA, USA, 2023.
- ISO 14044:2006; Environmental Management—Life Cycle Assessment—Requirements and Guidelines. International Organization for Standardization: Geneva, Switzerland, 2006.
- ISO 21930:2017; Sustainability in Buildings and Civil Engineering Works—Core Rules for Environmental Product Declarations of Construction Products and Services. International Organization for Standardization: Geneva, Switzerland, 2017.
- Wallner-Novak, M.; Koppelhuber, J.; Pock, K. Cross-Laminated Timber Structural Design—Basic Design and Engineering Principles According to Eurocode, 1st ed.; Working group of the Austrian timber industry for promotion of the application of timber; proHolz: Vienna, Austria, 2014; ISBN 978-3-902926-03-6. [Google Scholar]
- Stieb, T.; Maderebner, R.; Dietsch, P. A Timber–Concrete–Composite Edge Connection for Two-Way Spanning Cross-Laminated Timber Slabs—Experimental Investigations and Analytical Approach. Buildings 2023, 13, 3004. [Google Scholar] [CrossRef]
- Hosseini, A.; Shahnewaz, M.; Zhou, J.; Tannert, T. Structural performance of CLT moment connections in the minor strength axis. Eng. Struct. 2025, 328, 119788. [Google Scholar] [CrossRef]
- Ganjali, H.; Pace, A.; Tannert, T. Structural performance of adhesively bonded and hybrid screw-adhesive CLT panel-to-panel floor joints. Constr. Build. Mater. 2025, 475, 141139. [Google Scholar] [CrossRef]
- Lal, R.; Hashemi, A.; Quenneville, P. An innovative connection system for platform-type mass timber buildings. Resilient Cities Struct. 2025, 4, 14–29. [Google Scholar] [CrossRef]
- Piazza, M. Optimization Process in the Use of Wood and Wood-Based Materials in Hybrid and Composite Structures. In WCTE 2016 e-Book: Containing all Full Papers Submitted to the World Conference on Timber Engineering (WCTE 2016), Vienna, Austria, 22–25 August 2016; TU Verlag Wien: Vienna, Austria, 2016. [Google Scholar]
- Bajzecerová, V. Bending Stiffness of CLT-Concrete Composite Members—Comparison of Simplified Calculation Methods. Procedia Eng. 2017, 190, 15–20. [Google Scholar] [CrossRef]
- Bajzecerová, V.; Kanócz, J.; Rovňák, M.; Kováč, M. Prestressed CLT-concrete composite panels with adhesive shear connection. J. Build. Eng. 2022, 56, 104785. [Google Scholar] [CrossRef]
- Pang, S.J.; Ahn, K.S.; Jeong, S.M.; Lee, G.C.; Kim, H.S.; Oh, J.K. Prediction of bending performance for a separable CLT-concrete composite slab connected by notch connectors. J. Build. Eng. 2022, 49, 103900. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, B.; Kilpatrick, T.; Sanderson, I. Numerical Analysis on Global Serviceability Behaviours of Tall CLT Buildings to the Eurocodes and UK National Annexes. Buildings 2021, 11, 124. [Google Scholar] [CrossRef]
- Van de Lindt, J.; Amini, M.O.; Rammer, D.; Line, P.; Pei, S.; Popovski, M. Determination of Seismic Performance Factors for Cross-Laminated Timber Shear Walls Based on FEMA P695 Methodology; General Technical Report FPL-GTR-281; U. S. Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2023; p. 515.
- Perković, N.; Skejić, D.; Rajčić, V. Numerical Analysis of Fire Resistance in Cross-Laminated Timber (CLT) Constructions Using CFD: Implications for Structural Integrity and Fire Protection. Forests 2024, 15, 2046. [Google Scholar] [CrossRef]
- Dúbravská, K.; Tereňová, Ľ.; Štefková, J. CLT Construction Performance Under Thermal Loading. Wood Res. 2020, 65, 605–614. [Google Scholar] [CrossRef]
- Xing, Z.; Zhang, J.; Aslani, F. CLT two-way slabs fire resistance test; numerical simulation analysis. J. Build. Eng. 2025, 105, 112529. [Google Scholar] [CrossRef]
- Di Bella, A.; Mitrovic, M. Acoustic Characteristics of Cross-Laminated Timber Systems. Sustainability 2020, 12, 5612. [Google Scholar] [CrossRef]
- Schenk, M.; Ohm, J.; Winter, S. Eurocode5: From Mandate to Second Generation—Review, Insight and Outlook. In Proceedings of the 14th World Conference on Timber Engineering 2025 (WCTE 2025), Brisbane, Australia, 22–26 June 2025; pp. 36–45. [Google Scholar] [CrossRef]
- Onishi, S.; Karube, Y.; Nasu, H. Study on Control Wooden Joint Rigidity, Strength and Ductility with Combinations of Wooden Fibre Directions. In WCTE 2016 e-Book: Containing all Full Papers Submitted to the World Conference on Timber Engineering (WCTE 2016), Vienna, Austria, 22–25 August 2016; TU Verlag Wien: Vienna, Austria, 2016; Available online: https://repositum.tuwien.at/handle/20.500.12708/172 (accessed on 28 September 2025).
- Joyce, T.; Ballerini, M.; Smith, I. Mechanical behaviour of in-plane shear connections between CLT wall panels. In Proceedings of the CIB Working Commission W18–Timber Structures. 44th Meeting, Alghero, Italy, 29 August–1 September 2011; Available online: https://www.researchgate.net/publication/267244948 (accessed on 28 September 2025).
- Hossain, A.; Danzig, I.; Tannert, T. Cross-laminated timber shear connections with double-angled self-tapping screw assemblies. J. Struct. Eng. 2016, 142, 04016099. [Google Scholar] [CrossRef]
- Subhani, M.; Shill, S.K.; Al-Deen, S.; Anwar-Us-Saadat, M.; Ashraf, M. Flexural Performance of Splice Connections in Cross-Laminated Timber. Buildings 2022, 12, 1124. [Google Scholar] [CrossRef]
- Sadeghi, M.; Ballerini, M.; Smith, I.; Pedrotti, E. Bending properties of connections in cross laminated timber. In Proceedings of the IABSE Conference: Elegance in Structures, Nara, Japan, 13–15 May 2015; pp. 366–367. [Google Scholar] [CrossRef]
- Asselstine, J.; Lam, F.; Zhang, C. New edge connection technology for cross laminated timber (CLT) floor slabs promoting two-way action. Eng. Struct. 2021, 233, 111777. [Google Scholar] [CrossRef]
- Tlustochowicz, G.; Serrano, E.; Steiger, R. State-of-the-art review on timber connections with glued-in steel rods. Mater. Struct. 2011, 44, 997–1020. [Google Scholar] [CrossRef]
- Ayansola, G.S.; Tannert, T.; Vallee, T. Experimental investigations of glued-in rod connections in CLT. Constr. Build. Mater. 2022, 324, 126680. [Google Scholar] [CrossRef]
- Shirmohammadli, Y.; Hashemi, A.; Masoudnia, R.; Quenneville, P. Experimental and numerical investigation of cross-laminated timber joints with multiple glued-in rods. In Proceedings of the World Conference on Timber Engineering (WCTE 2023), Oslo, Norway, 19–22 June 2023; pp. 1389–1396. [Google Scholar] [CrossRef]
- Ayansola, G.S.; Tannert, T.; Vallee, T. Glued-in multiple steel rod connections in cross-laminated timber. J. Adhes. 2021, 98, 810–826. [Google Scholar] [CrossRef]
- Azinović, B.; Danielsson, H.; Serrano, E.; Kramar, M. Glued-in rods in cross laminated timber—Numerical simulations and parametric studies. Constr. Build. Mater. 2019, 212, 431–441. [Google Scholar] [CrossRef]
- EN 1995-1-1:2004+A2:2014; Eurocode 5: Design of Timber Structures—Part 1-1: General—Common Rules and Rules for Buildings. European Committee for Standardization, CEN: Brussels, Belgium, 2014.
- Esmaeildoust, S.; Tomlinson, D.; Chui, Y.H. Performance of Timber-Concrete Composite (TCC) Systems Connected with Inclined Screws: A Literature Review. J. Compos. Sci. 2025, 9, 13. [Google Scholar] [CrossRef]
- Du, H.; Hu, X.; Xie, Z.; Wang, H. Study on shear behavior of inclined cross lag screws for glulam-concrete composite beams. Constr. Build. Mater. 2019, 224, 132–143. [Google Scholar] [CrossRef]
- Li, M. Evaluating rolling shear strength properties of cross-laminated timber by short-span bending tests and modified planar shear tests. J. Wood Sci. 2017, 63, 331–337. [Google Scholar] [CrossRef]
- Li, X.; Ashraf, M.; Subhani, M.; Kremer, P.; Li, H.; Anwar-Us-Saadat, M. Rolling shear properties of cross-laminated timber (CLT) made from Australian Radiata Pine–An experimental study. Structures 2021, 33, 423–432. [Google Scholar] [CrossRef]
- Sandoli, A.; Calderoni, B. The rolling shear influence on the out-of-plane behavior of CLT panels: A comparative analysis. Buildings 2020, 10, 42. [Google Scholar] [CrossRef]
- STN EN 1995-1-1/NA:2019-12; National Annex to EN 1995-1-1:2004+A2:2014 Eurocode 5: Design of Timber Structures—Part 1-1: General—Common Rules and Rules for Buildings. ÚNMS SR: Bratislava, Slovakia, 2019.
- EN 408:2010+A1:2012; Timber Structures—Structural Timber and Glued Laminated Timber—Determination of Some Physical and Mechanical Properties. European Committee for Standardization, CEN: Brussels, Belgium, 2012.
- EN 26891:1991; Timber Structures—Joints Made with Mechanical Fasteners—General Principles for the Determination of Strength and Deformation Characteristics. European Committee for Standardization, CEN: Brussels, Belgium, 1991.
- EN 16351:2021; Timber Structures—Cross Laminated Timber—Requirements. European Committee for Standardization: Brussels, Belgium, 2021.
- Zoetemeijer, P. A Design Method for the Tension Side of Statically Loaded, Bolted Beam-to-Column Connections. Heron 1974, 20, 1–59. Available online: https://resolver.tudelft.nl/uuid:f2dff8e5-dd92-4a3c-89db-c4fa945ea759 (accessed on 28 September 2025).
- Steenhuis, M.; Jaspart, J.-P.; Gomes, F.; Leino, T. Application of the Component Method to Steel Joints. In Proceedings of the Control of the Semi-Rigid Behaviour of Civil Engineering Structural Connections, Liège, Belgium, 17–19 September 1998. [Google Scholar]
- EN 1993-1-8; Eurocode 3—Design of Steel Structures—Part 1-8: Design of Joints. CEN: Brussels, Belgium, 2005.
- Tao, H.; Mao, M.; Yang, H.; Liu, W. Theoretical and experimental behaviour of a hybrid semi-rigid glulam beam-to-column connection with top and seat angles. Adv. Struct. Eng. 2020, 23, 891–904. [Google Scholar] [CrossRef]
- Yang, H.; Liu, W.; Ren, X. A Component Method for Moment-Resistant Glulam Beam–Column Connections with Glued-in Steel Rods. Eng. Struct. 2016, 115, 42–54. [Google Scholar] [CrossRef]
- Buchholz, L.; Kuhlmann, U.; Knobloch, M. Design of Timber Structures in View of Sustainability Based on the Component Method. In Proceedings of the 14th World Conference on Timber Engineering 2025 (WCTE 2025), Brisbane, Australia, 22–26 June 2025. [Google Scholar] [CrossRef]
- Hunger, F.; Stepinac, M.; Rajčić, V.; van de Kuilen, J.-W.G. Pull-Compression Tests on Glued-In Metric Thread Rods Parallel to Grain in Glulam and Laminated Veneer Lumber of Different Timber Species. Eur. J. Wood Wood Prod. 2016, 74, 379–391. [Google Scholar] [CrossRef]
- Oh, J.; Ahn, K.-S.; Lee, G.R.; Kim, M.-J.; You, S.-H.; Pang, S.-J.; Kim, C.-K.; Kim, K.-H.; Oh, J.-K. Theoretical Modeling of Pull-Out Stiffness of Glued-In Single Rod in Timber. Eng. Struct. 2025, 325, 119346. [Google Scholar] [CrossRef]
- Totsuka, M.; Jockwer, R.; Aoki, K.; Inayama, M. Experimental study on partial compression parallel to grain of solid timber. J. Wood Sci. 2021, 67, 39. [Google Scholar] [CrossRef]
- Totsuka, M.; Jockwer, R.; Kawahara, H.; Aoki, K.; Inayama, M. Experimental study of compressive properties parallel to grain of glulam. J. Wood Sci. 2022, 68, 33. [Google Scholar] [CrossRef]
- Flaig, M.; Schmidt, T.; Blas, H.J. Compressive strength and stiffness of end-grain contact joints in glulam and CLT. In Proceedings of the International Network on Timber Engineering Research (INTER), Meeting 52, Tacoma, WA, USA, 26–29 August 2019; pp. 313–325, ISSN 2199-9740. [Google Scholar]
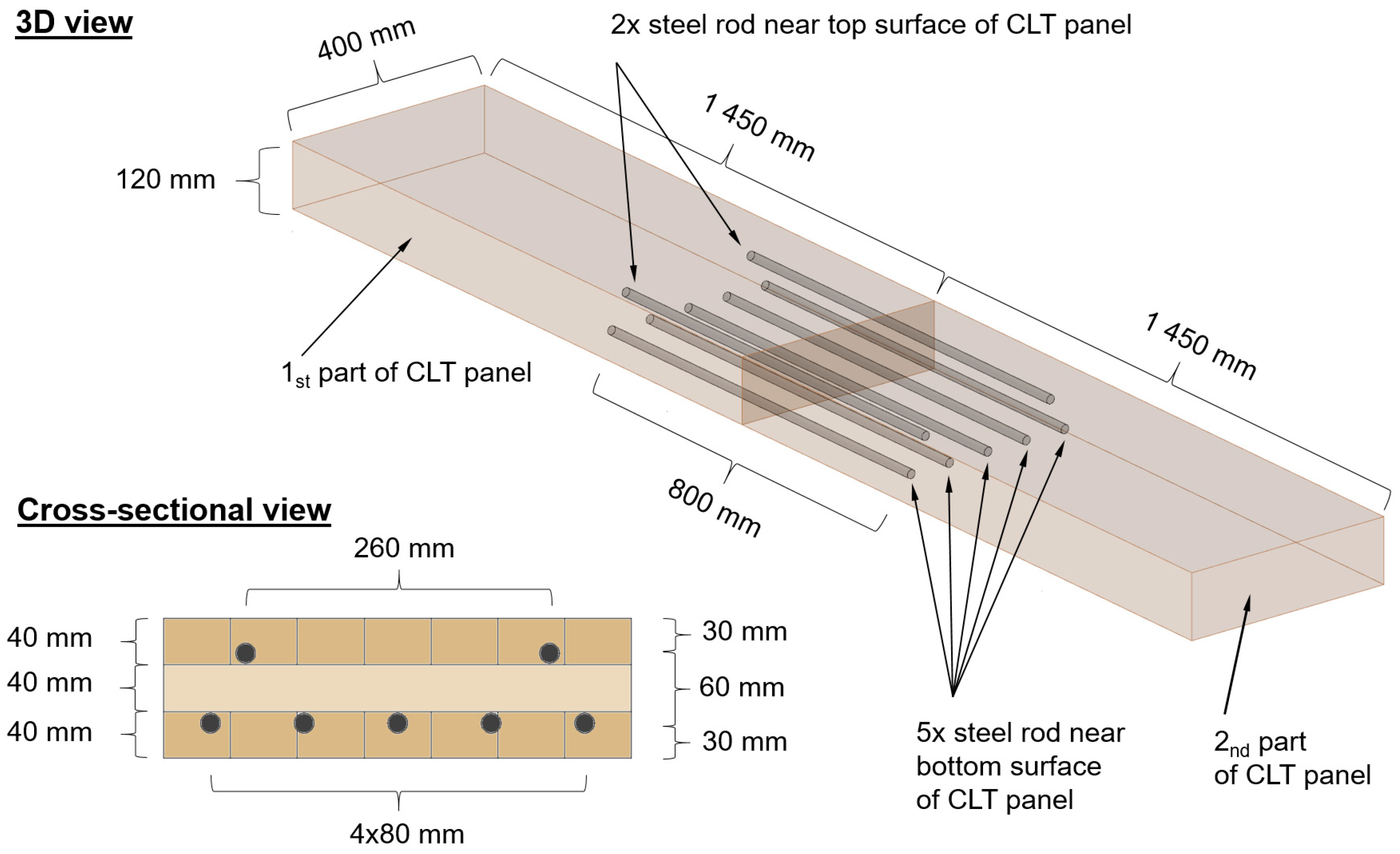

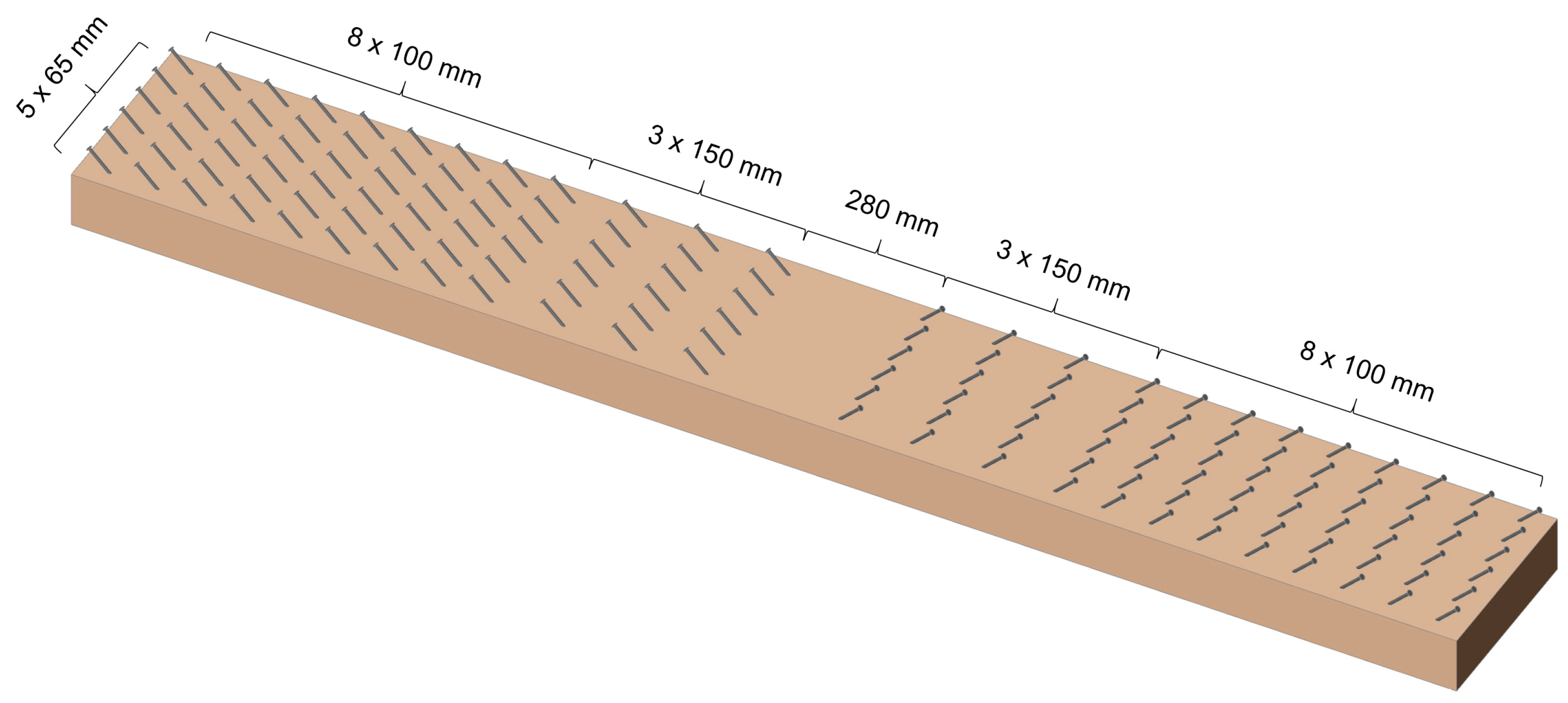

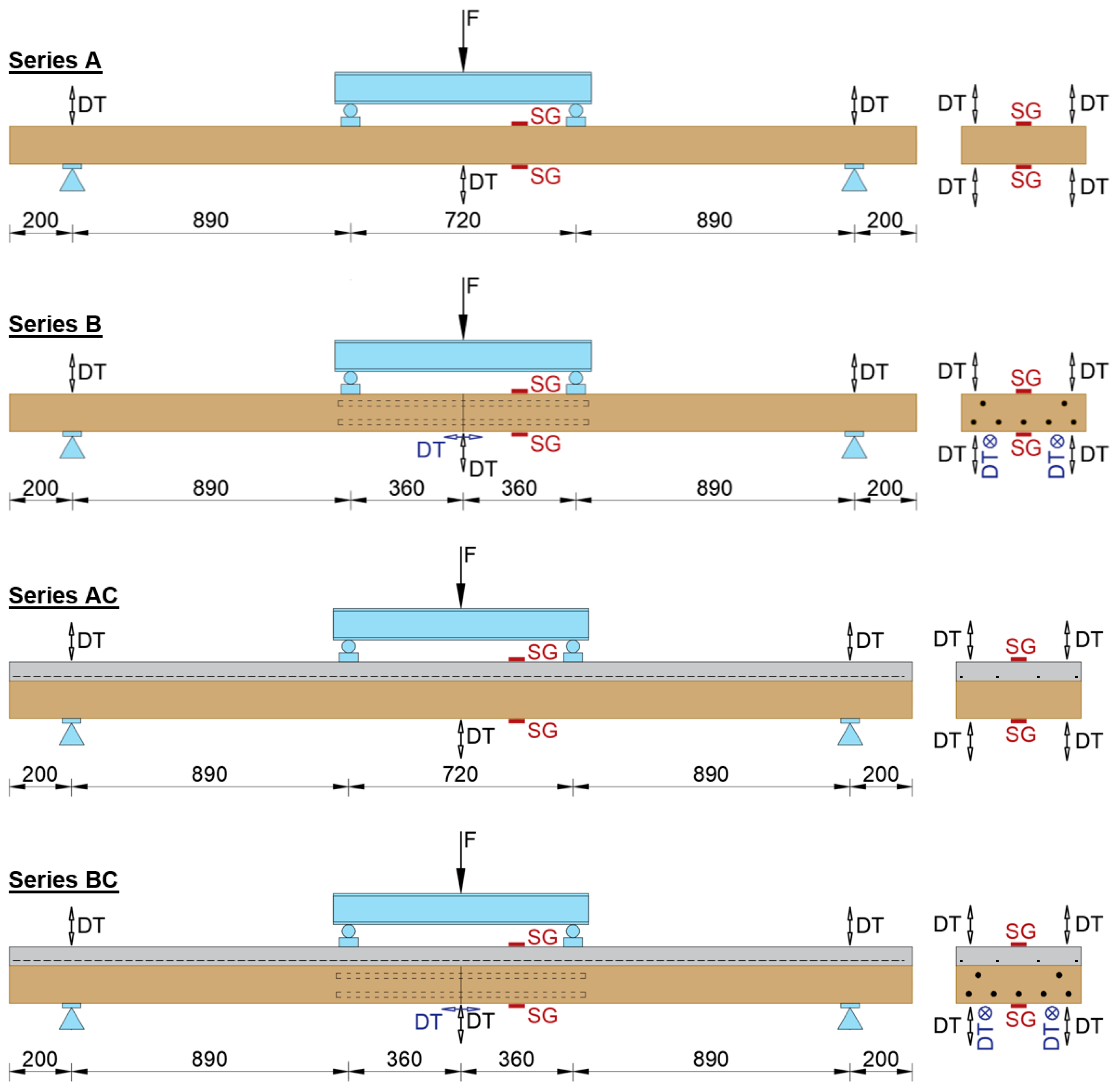
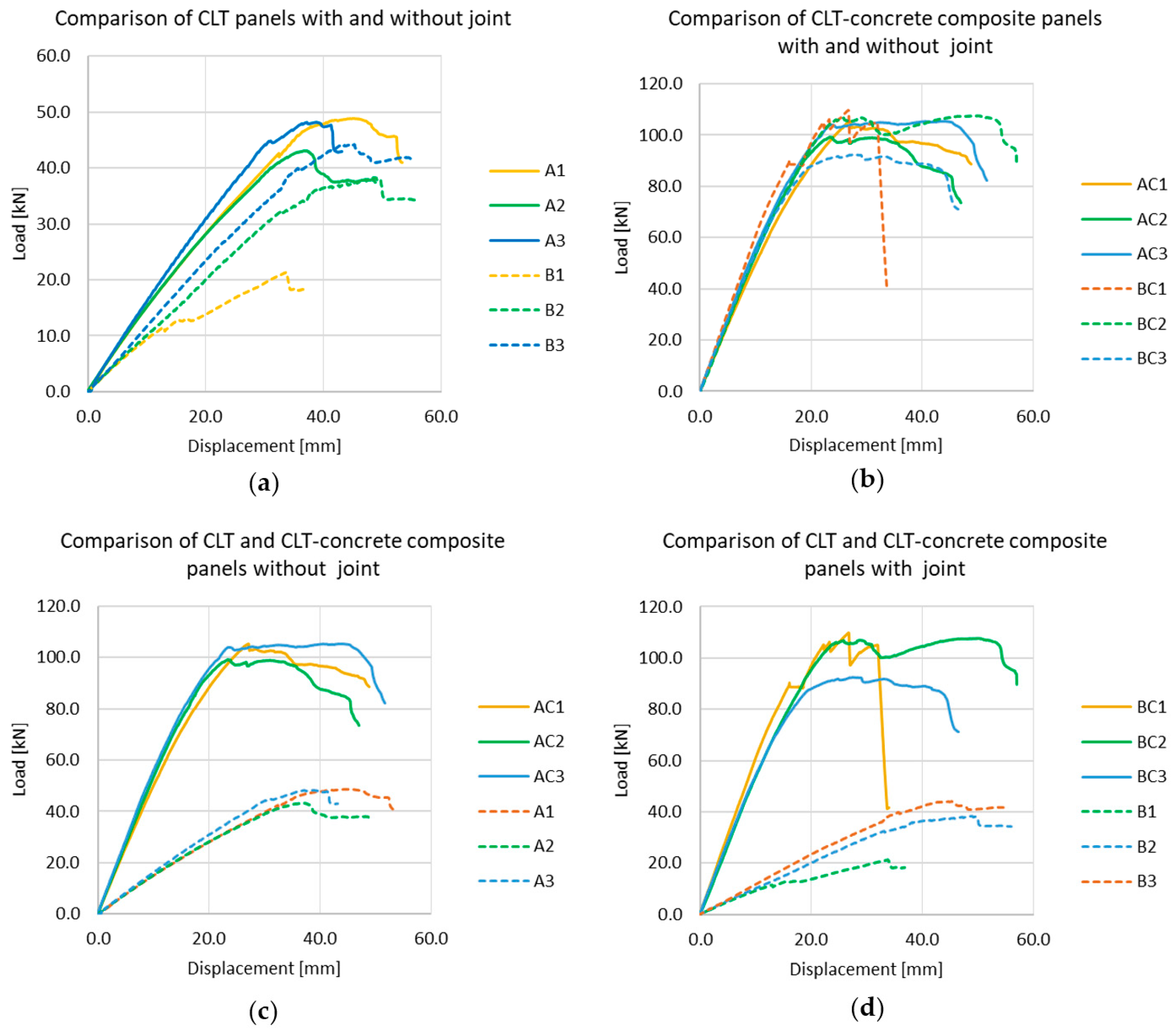



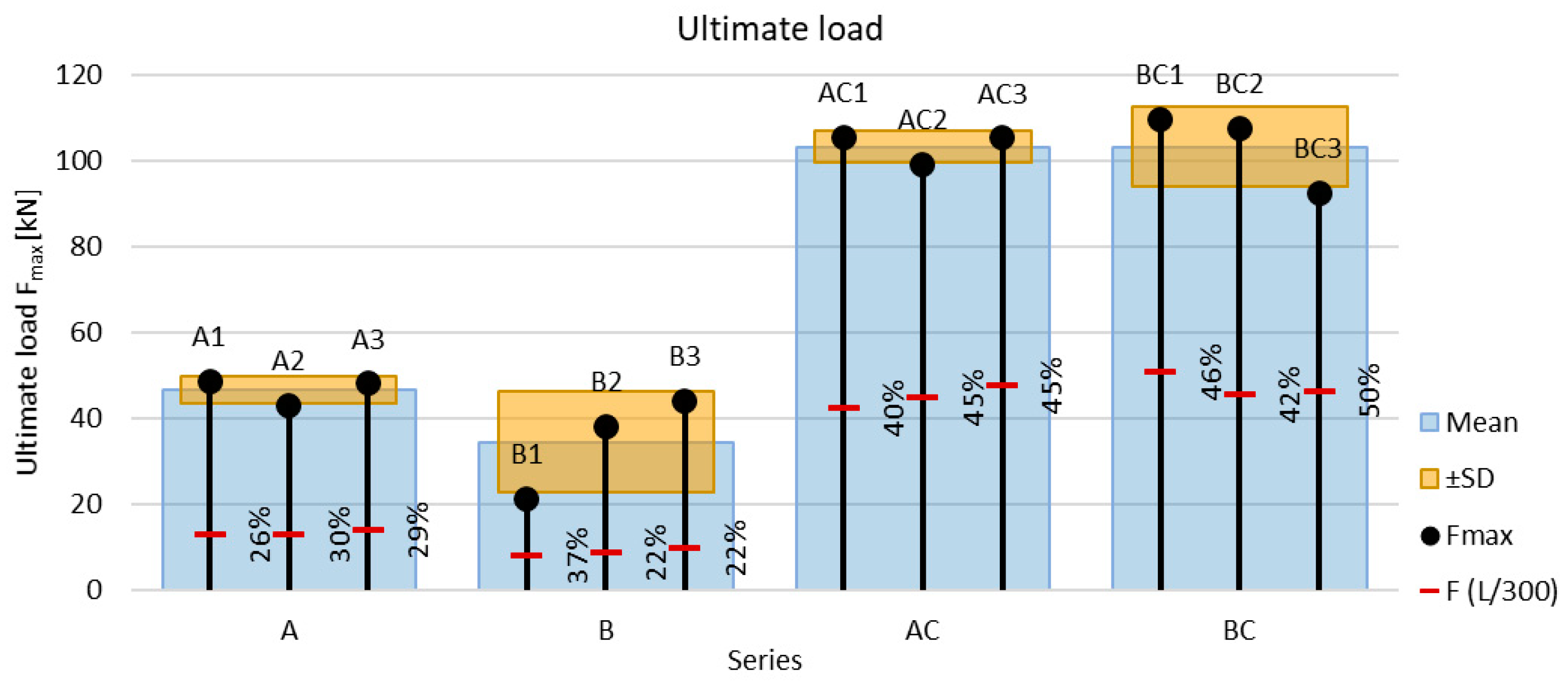



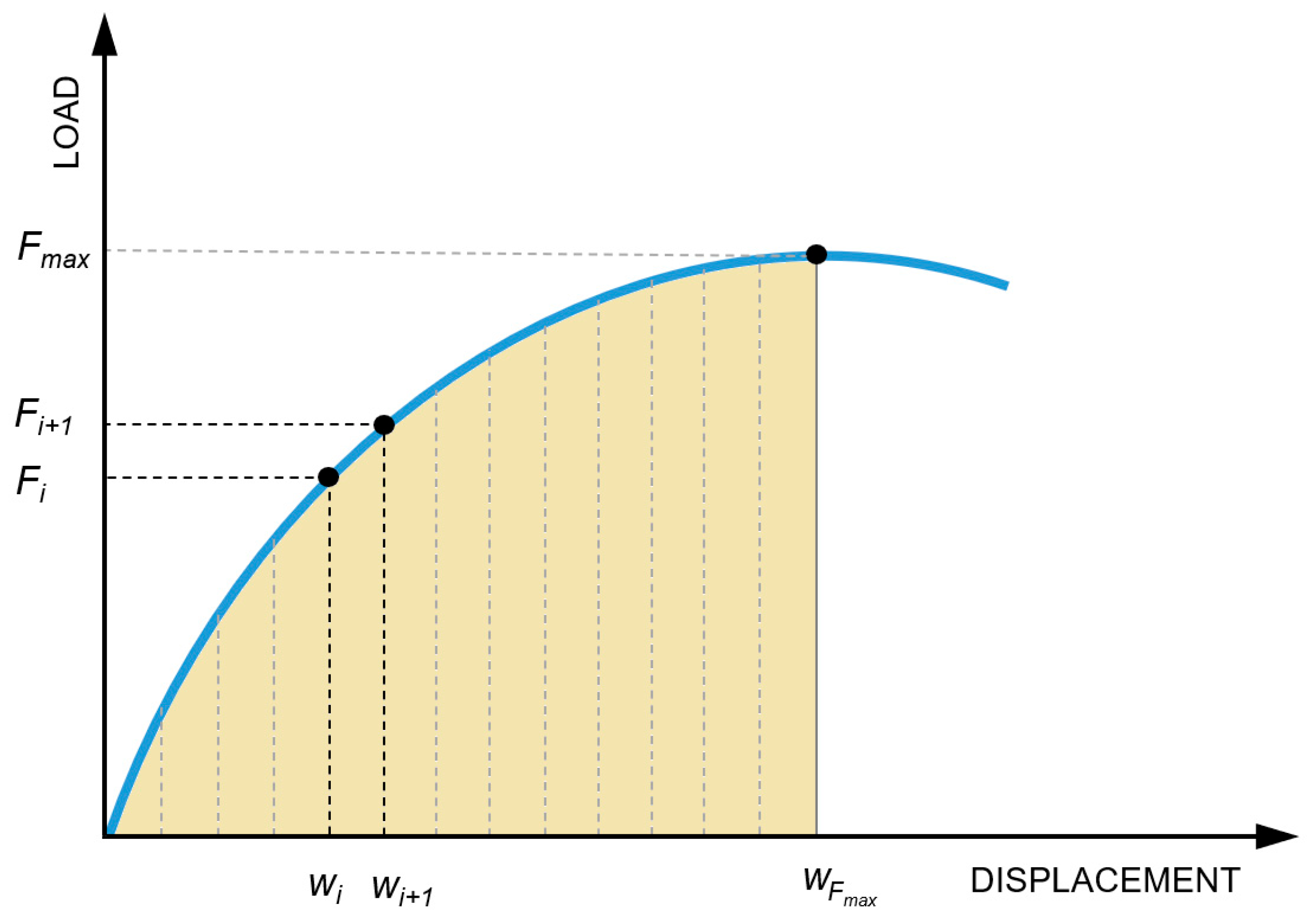
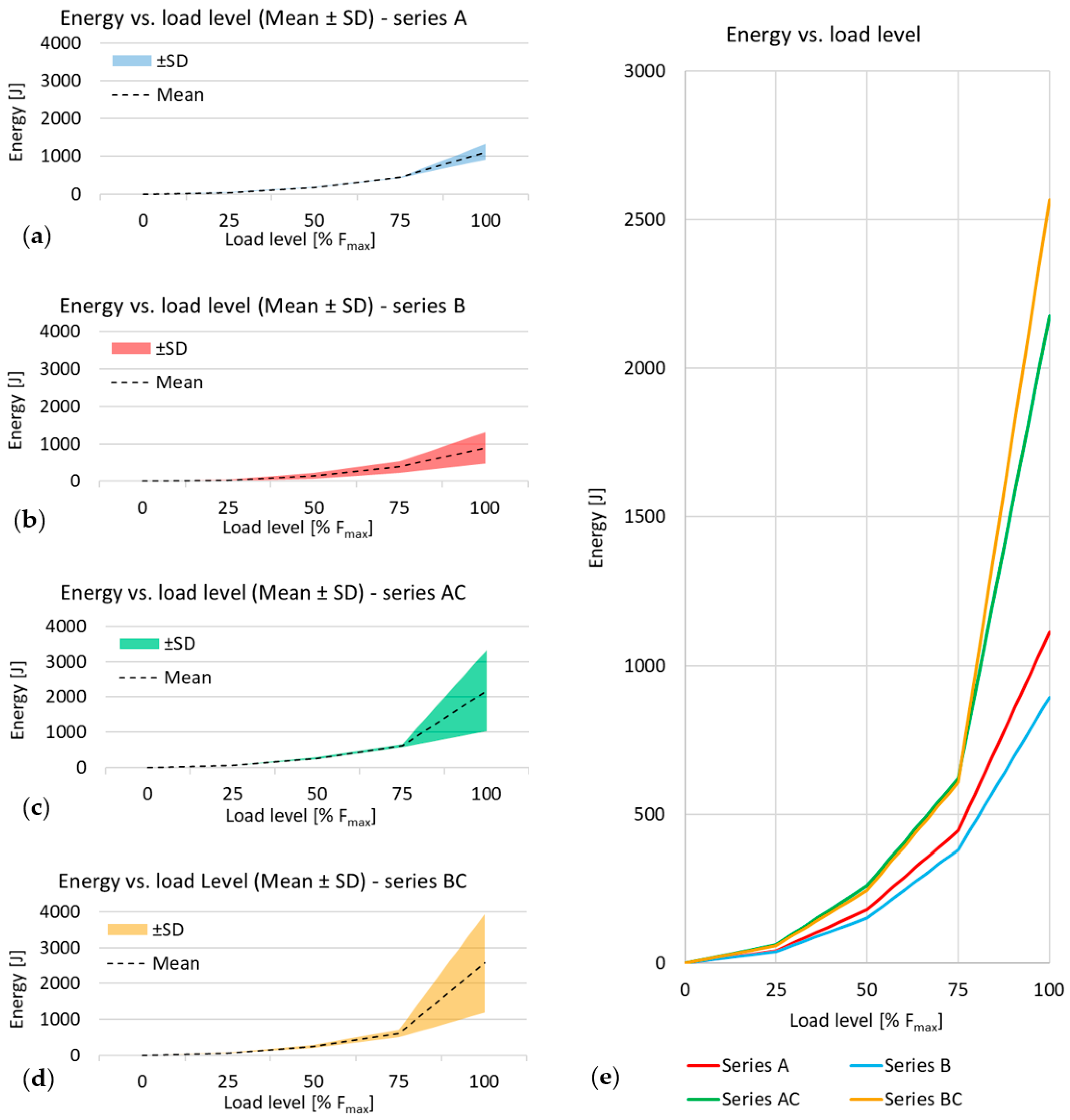


| Specimen | Ultimate Load Fmax | Deflection at Fmax | Failure Mode |
|---|---|---|---|
| - | [kN] | [mm] | - |
| A1 | 48.80 | 45.21 | shear |
| A2 | 43.12 | 37.26 | delamination and shear |
| A3 | 48.24 | 37.16 | partial delamination and shear |
| B1 | 21.31 | 33.71 | joint |
| B2 | 38.29 | 48.97 | shear |
| B3 | 44.14 | 45.26 | partial delamination and shear |
| AC1 | 105.43 | 27.16 | shear |
| AC2 | 99.12 | 23.40 | shear |
| AC3 | 105.40 | 24.14 | partial delamination and shear |
| BC1 | 109.71 | 26.70 | joint and bending |
| BC2 | 107.65 | 28.91 | shear |
| BC3 | 92.49 | 27.44 | delamination and shear |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farbák, M.; Gocál, J.; Koteš, P. Experimental Study of the Actual Structural Behaviour of CLT and CLT–Concrete Composite Panels with Embedded Moment-Resisting Joint. Buildings 2025, 15, 3534. https://doi.org/10.3390/buildings15193534
Farbák M, Gocál J, Koteš P. Experimental Study of the Actual Structural Behaviour of CLT and CLT–Concrete Composite Panels with Embedded Moment-Resisting Joint. Buildings. 2025; 15(19):3534. https://doi.org/10.3390/buildings15193534
Chicago/Turabian StyleFarbák, Matúš, Jozef Gocál, and Peter Koteš. 2025. "Experimental Study of the Actual Structural Behaviour of CLT and CLT–Concrete Composite Panels with Embedded Moment-Resisting Joint" Buildings 15, no. 19: 3534. https://doi.org/10.3390/buildings15193534
APA StyleFarbák, M., Gocál, J., & Koteš, P. (2025). Experimental Study of the Actual Structural Behaviour of CLT and CLT–Concrete Composite Panels with Embedded Moment-Resisting Joint. Buildings, 15(19), 3534. https://doi.org/10.3390/buildings15193534







