Foundation-Specific Hybrid Models for Expansive Soil Deformation Prediction and Early Warning
Abstract
1. Introduction
2. Methodology
2.1. Data Characteristics and Preprocessing
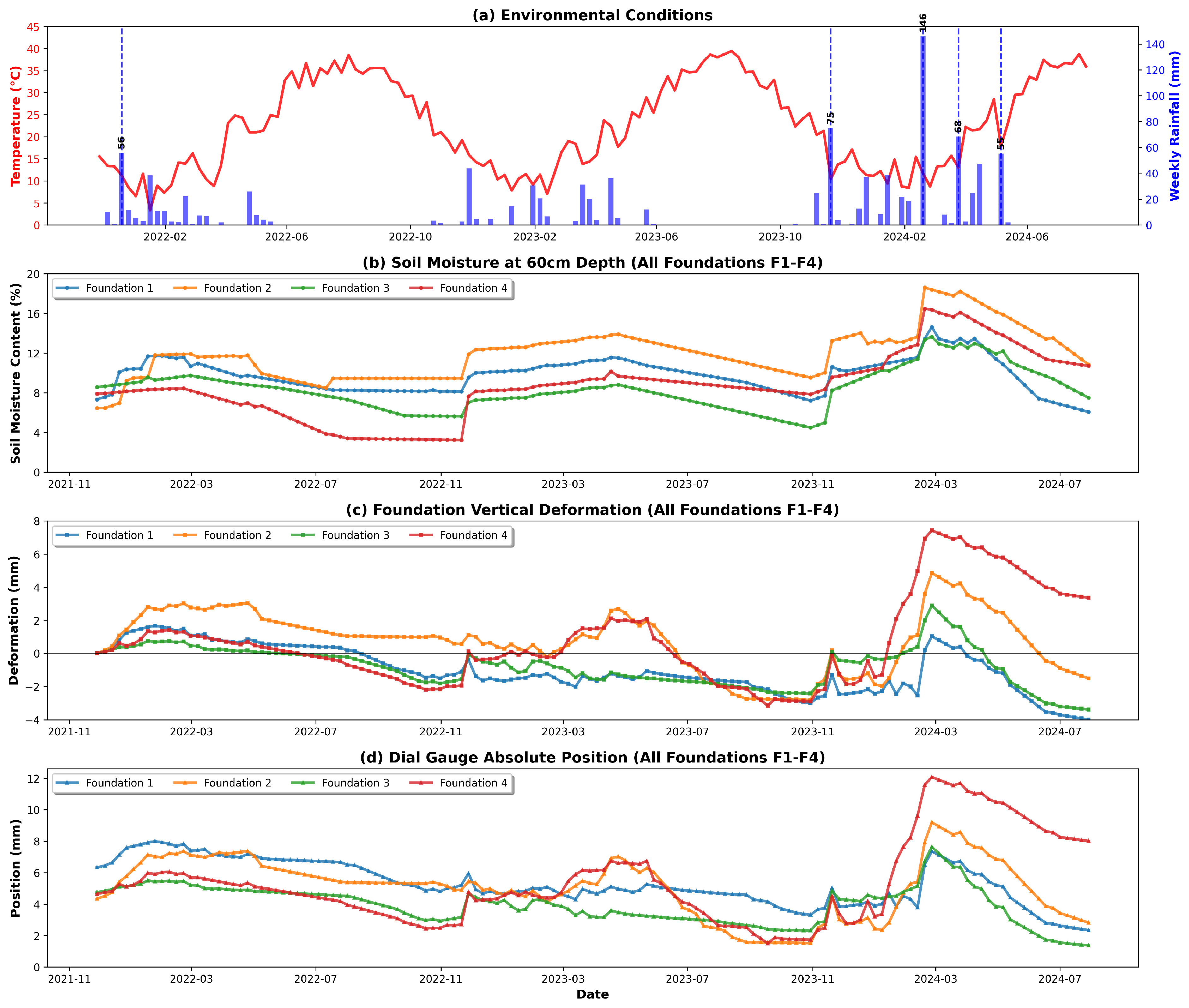
2.1.1. Environmental Conditions and Spatial Variability
2.1.2. Foundation Deformation Patterns and Measurement Validation
2.1.3. Statistical Analysis and Data Quality Assessment
2.1.4. Feature Categorization Framework
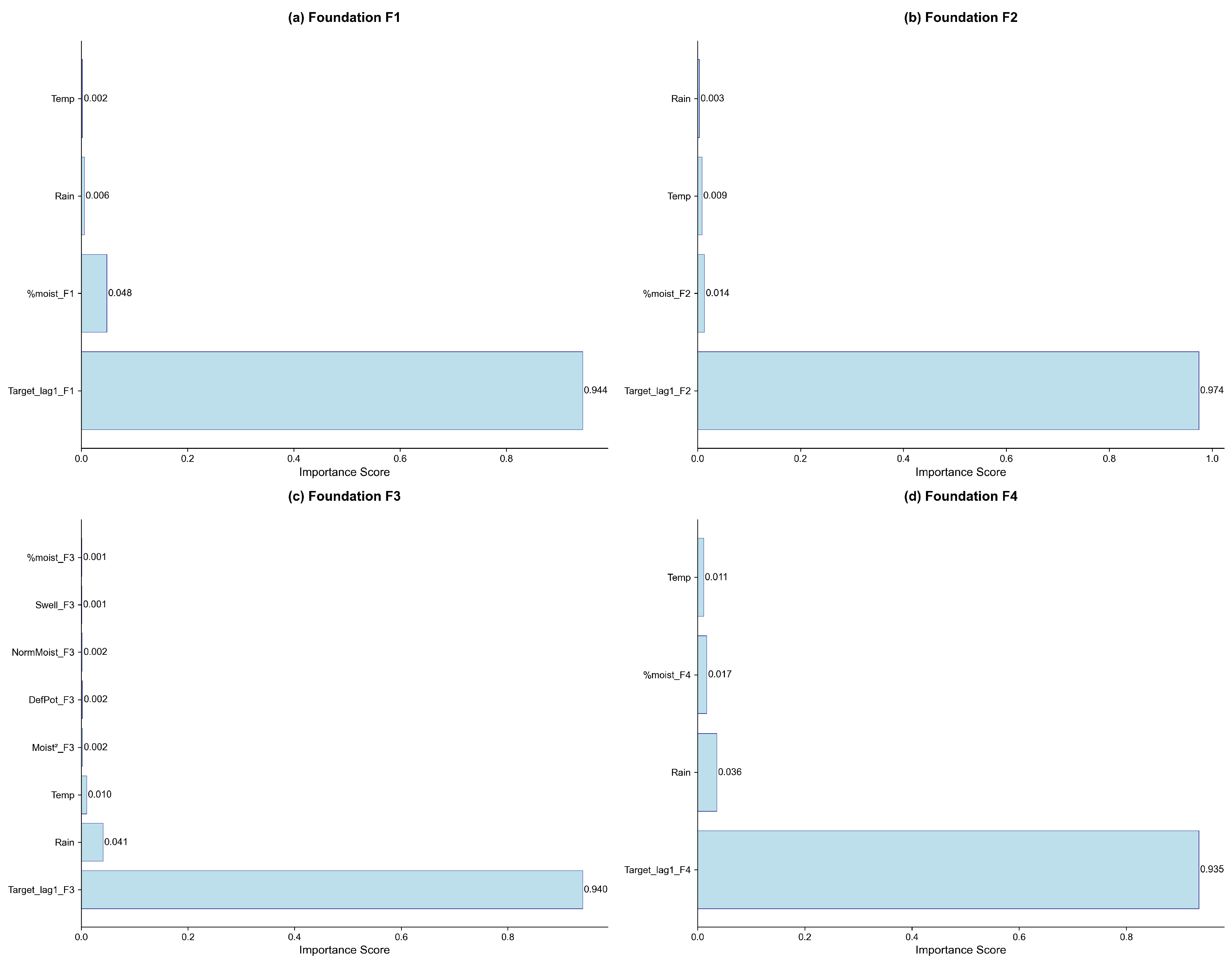
2.1.5. Foundation-Specific Feature Selection Methodology
2.1.6. Correlation Analysis with Statistical Validation and Feature Derivation Effects
- F1 (Figure 2a): Moderate correlations across moisture-derived features (NormMoist_F1, Swell_F1, DefPot_F1, %moist_F1: all r = 0.41, with range r = 0.38–0.41, all p < 0.001), indicating systematic but constrained response mechanisms
- F2 (Figure 2b): Unique seasonal sensitivity (Month_sin: r = 0.65, p < 0.001) with significant temperature-related effects, reflecting annual cycle dependencies
- F3 (Figure 2c): Consistent strong correlations across moisture-related variables (Swell_F3, %moist_F3, NormMoist_F3, DefPot_F3: all r = 0.60, with range r = 0.59–0.60, all p < 0.001) with pronounced negative temperature effects (r = −0.58 to −0.59, p < 0.001)
- F4 (Figure 2d): Highest physics-based correlations with five moisture-derived features (NormMoistLag1_F4, SwellLag1_F4, DefPotLag1_F4, MoistLag1_F4, %moist_F4: all r = 0.78), consistent with pronounced moisture-expansion response characteristics.
2.2. Baseline Model Selection Rationale
2.3. Hybrid Model Development Framework
2.3.1. Residual-Clustering Hybrid
| Algorithm 1: Residual-Clustering Hybrid |
| Input: Training features X_train, targets y_train, test features X_test Output: Predictions y_pred 1: base_model ← HuberRegressor(α = 0.01, ε = 1.35).fit(X_train, y_train) 2: residuals ← y_train − base_model.predict(X_train) 3: clusters ← KMeans(k = 2).fit_predict(residuals.reshape(−1,1)) 4: cluster_models ← [BayesianRidge().fit(X_train[c], residuals[c]) for c in clusters] 5: cluster_predictor ← RandomForestClassifier(50).fit(X_train, clusters) 6: test_clusters ← cluster_predictor.predict(X_test) 7: corrections ← [cluster_models[c].predict(X_test[mask]) for c, mask in test_clusters] 8: y_pred ← base_model.predict(X_test) + corrections 9: return y_pred |
2.3.2. Elastic Net Fusion
| Algorithm 2: Elastic Net Fusion |
| Input: Training features X_train, targets y_train, test features X_test Output: Predictions y_pred 1: base_model ← ElasticNet(α = 0.1, l1 = 0.5).fit(X_train, y_train) 2: physics_features ← extract_physics_features(X_train) 3: residuals ← y_train − base_model.predict(X_train) 4: physics_corrector ← Ridge(α = 1.0).fit(physics_features, residuals) 5: correction ← physics_corrector.predict(X_test_physics) 6: y_pred ← base_model.predict(X_test) + 0.2 × correction 7: return y_pred |
2.3.3. Residual Correction
| Algorithm 3: Residual Correction |
| Input: Training features X_train, targets y_train, test features X_test Output: Predictions y_pred 1: base_model ← LinearRegression().fit(X_train, y_train) 2: residuals ← y_train − base_model.predict(X_train) 3: physics_features ← extract_physics_features(X_train) 4: strength ← optimize([0.05, 0.08, 0.12, 0.15, 0.18], physics_features, residuals) 5: corrector ← Ridge(α = 2.0).fit(physics_features, residuals) 6: y_pred ← base_model.predict(X_test) + strength × corrector.predict(X_test_physics) 7: return y_pred |
2.3.4. Enhanced Robust Huber
| Algorithm 4: Enhanced Robust Huber |
| Input: Training features X_train, targets y_train, test features X_test Output: Predictions y_pred 1: base_model ← HuberRegressor(α = 0.05, ε = 1.2).fit(X_train, y_train) 2: base_pred ← base_model.predict(X_train) 3: enhanced_features ← concatenate([X_train, base_pred.reshape(−1,1)]) 4: residuals ← y_train − base_pred 5: enhancer ← HuberRegressor(α = 0.2, ε = 1.5).fit(enhanced_features, residuals) 6: test_enhanced ← concatenate([X_test, base_model.predict(X_test).reshape(−1,1)]) 7: y_pred ← base_model.predict(X_test) + 0.1 × enhancer.predict(test_enhanced) 8: return y_pred |
2.4. Feature Engineering and Selection Protocol
2.5. Statistical Validation Methods
2.6. Early Warning System Design
2.7. Implementation Details
3. Results
3.1. Optimal Feature Selection Performance
3.2. Comparative Model Performance
3.3. Statistical Significance Testing
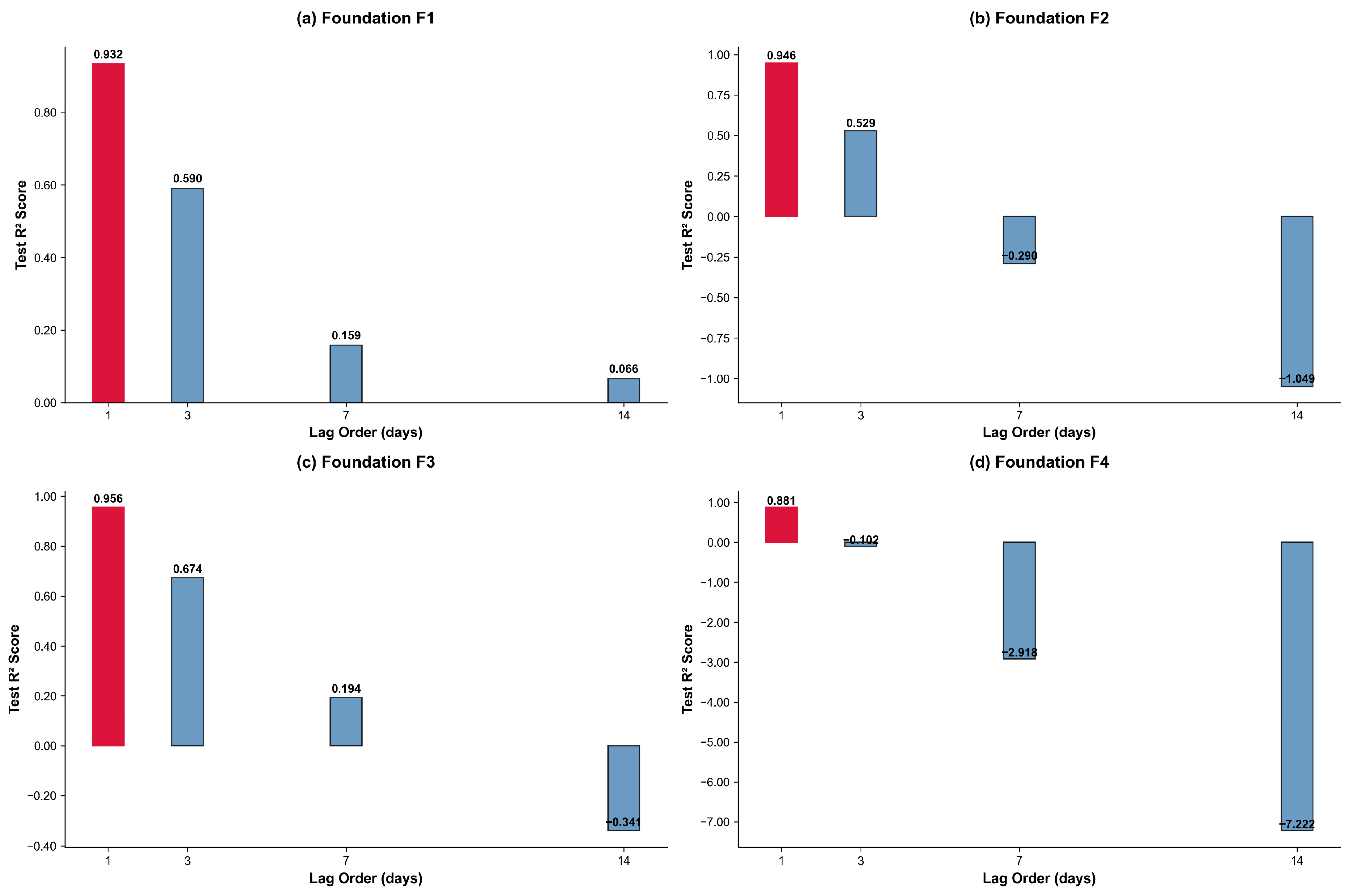
3.4. Time Series Forecasting Accuracy
3.5. Feature Importance and Ablation Analysis
3.6. Early Warning System Performance
4. Discussion
4.1. Temporal Dominance and Feature Hierarchy Implications
4.2. Foundation-Specific Modeling Requirements and Heterogeneity
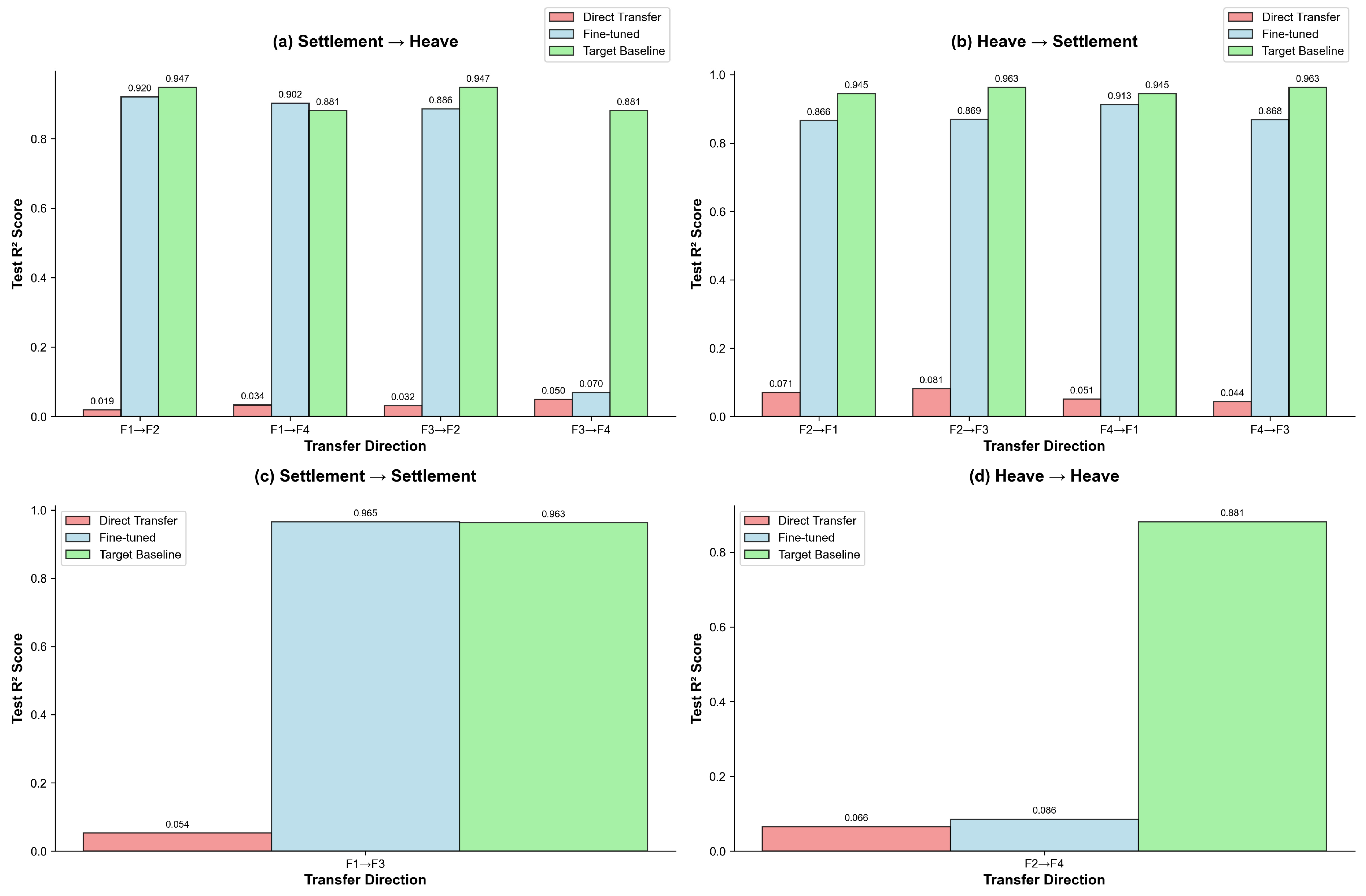
4.3. Advanced Analysis and Model Extensions
4.4. Practical Implementation and Operational Considerations
4.5. Methodological Insights and Statistical Validation
4.6. Limitations and Future Research Directions
5. Conclusions
- Foundation-specific effectiveness: Hybrid models achieved superior performance with varying improvements (ΔR2 = +0.001 to +0.663) across four foundations, with 35.7% achieving statistical significance
- Temporal dominance: Autoregressive features provided overwhelming predictive power (removing temporal features caused catastrophic failure: ΔR2 = −0.855 to −0.947)
- Operational reliability: Early warning systems achieved F1-scores of 0.900–0.982 with quantified uncertainty bounds (±0.654–0.977 mm)
- Foundation-specific optimization: Different complexity requirements (4–8 features) reflect spatial heterogeneity in soil-structure interactions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Feature Name | Feature Abbrev | Mathematical Definition | Physical Interpretation |
|---|---|---|---|
| deform_fi_mm | Target_Fi | Raw deformation measurement | Foundation vertical displacement |
| moisture_fi_percent | %moist_Fi | Raw moisture measurement | Soil moisture at foundation depth |
| temperature_celsius | Temp | Raw temperature measurement | Ambient temperature |
| rainfall_mm | Rain | Raw precipitation measurement | Daily precipitation |
| day | Day | Sequential day number | Cumulative day counter |
| date | Date | Timestamp | Date information (preprocessing only) |
| moisture_fi_normalized | NormMoist_Fi | (moisture_fi_percent − μ_train)/σ_train | Standardized moisture content |
| moisture_fi_squared | Moist2_Fi | (moisture_fi_percent)2 | Nonlinear moisture effect |
| swelling_potential_fi | Swell_Fi | moisture_fi_percent × 0.016 | Empirical swelling potential |
| deform_potential_fi | DefPot_Fi | (moisture_fi_percent − 8.0) × 0.1 | Deformation potential |
| month | Month | date.dt.month | Calendar month (1–12) |
| month_sin | Month_sin | sin(2π × month/12) | Sinusoidal seasonal encoding |
| month_cos | Month_cos | cos(2π × month/12) | Cosinusoidal seasonal encoding |
| day_of_year | Day_yr | date.dt.dayofyear | Annual day position (1–365) |
| target_fi_lag1 | Target_lag1_Fi | deform_fi_mm(t − 1) | Previous day foundation deformation |
| moisture_fi_percent_lag1 | MoistLag1_Fi | moisture_fi_percent(t − 1) | Previous day moisture content |
| moisture_fi_normalized_lag1 | NormMoistLag1_Fi | moisture_fi_normalized(t − 1) | Previous day normalized moisture |
| swelling_potential_fi_lag1 | SwellLag1_Fi | swelling_potential_fi(t − 1) | Previous day swelling potential |
| deform_potential_fi_lag1 | DefPotLag1_Fi | deform_potential_fi(t − 1) | Previous day deformation potential |
| rainfall_mm_lag1 | Rain_lag1 | rainfall_mm(t − 1) | Previous day precipitation |
| temperature_celsius_lag1 | TempLag1 | temperature_celsius(t − 1) | Previous day temperature |
| Baseline Models | Hybrid Models | ||||
|---|---|---|---|---|---|
| Model Name | Key Parameters | Parameter Setting | Model Name | Key Parameters | Parameter Setting |
| Linear Regression | fit_intercept | True | Residual-Clustering Hybrid | n_clusters | 2 |
| Ridge | alpha | 10.0 | cluster_model | BayesianRidge | |
| Lasso | alpha | 0.1 | cluster_predictor_trees | 50 | |
| Elastic Net | alpha | 0.1 | Elastic Net Fusion | alpha | 0.1 |
| l1_ratio | 0.5 | l1_ratio | 0.5 | ||
| Huber Regressor | alpha | 0.1 | physics_weight | 0.2 | |
| epsilon | 1.35 | Residual Correction | base_model | LinearRegression | |
| Bayesian Ridge | alpha_1 | 1 × 10−6 | corrector | Ridge (α = 2.0) | |
| lambda_1 | 1 × 10−6 | correction_strength | 0.05–0.18 (optimized) | ||
| Random Forest | n_estimators | 50 | Enhanced Robust Huber | base_alpha | 0.05 |
| max_depth | 4 | base_epsilon | 1.2 | ||
| min_samples_split | 10 | enhancer_alpha | 0.2 | ||
| enhancer_epsilon | 1.5 | ||||
| enhancement_weight | 0.1 | ||||
| Model | Train_R2 | Train_RMSE | Train_MAE | Train_MAPE | Test_R2 | Test_RMSE | Test_MAE | Test_MAPE | Over Fitting_Gap | BootstrapR2 (95%_CI) | CV_R2_Mean | Uncertainty_95CI | Train_Time | Test_Time | Total_Time |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Foundation F1 | |||||||||||||||
| RCH | 0.987 | 0.144 | 0.081 | 10.14 | 0.945 | 0.381 | 0.308 | 41.93 | 0.042 | (0.914, 0.973) | 0.055 | ±0.6544 | 0.123 | 0.009 | 0.132 |
| LR | 0.976 | 0.198 | 0.129 | 15.2 | 0.926 | 0.44 | 0.349 | 54.07 | 0.049 | (0.885, 0.960) | −0.402 | ±0.7792 | 0.002 | 0.002 | 0.004 |
| BR | 0.976 | 0.198 | 0.129 | 15.21 | 0.926 | 0.44 | 0.35 | 54.05 | 0.049 | (0.885, 0.960) | −1.02 | ±0.7789 | 0.002 | 0.003 | 0.005 |
| Huber | 0.975 | 0.201 | 0.127 | 14.76 | 0.924 | 0.448 | 0.355 | 60.36 | 0.051 | (0.873, 0.958) | −0.097 | ±0.8083 | 0.011 | 0.002 | 0.013 |
| Lasso | 0.957 | 0.261 | 0.2 | 22.65 | 0.897 | 0.52 | 0.456 | 55.71 | 0.060 | (0.836, 0.930) | −5.485 | ±0.8629 | 0.002 | 0.002 | 0.004 |
| EN | 0.945 | 0.296 | 0.234 | 27.82 | 0.884 | 0.552 | 0.496 | 53.09 | 0.061 | (0.823, 0.922) | −6.032 | ±0.8793 | 0.002 | 0.002 | 0.004 |
| Ridge | 0.940 | 0.311 | 0.248 | 31.1 | 0.882 | 0.556 | 0.502 | 51.23 | 0.057 | (0.816, 0.922) | −9.21 | ±0.8474 | 0.002 | 0.002 | 0.004 |
| Foundation F2 | |||||||||||||||
| ENF | 0.964 | 0.327 | 0.25 | 30.34 | 0.947 | 0.468 | 0.356 | 159.39 | 0.017 | (0.897, 0.979) | −3.886 | ±0.9143 | 0.002 | 0.001 | 0.003 |
| Lasso | 0.968 | 0.312 | 0.228 | 30.38 | 0.946 | 0.472 | 0.36 | 163.15 | 0.021 | (0.896, 0.979) | −2.756 | ±0.9238 | 0.002 | 0.005 | 0.008 |
| EN | 0.964 | 0.33 | 0.253 | 30.9 | 0.946 | 0.473 | 0.36 | 160.4 | 0.018 | (0.892, 0.980) | −3.773 | ±0.9277 | 0.002 | 0.002 | 0.004 |
| Huber | 0.974 | 0.279 | 0.176 | 28.32 | 0.944 | 0.484 | 0.324 | 107.98 | 0.030 | (0.888, 0.985) | 0.274 | ±0.9360 | 0.01 | 0.002 | 0.012 |
| BR | 0.974 | 0.276 | 0.18 | 28.33 | 0.943 | 0.487 | 0.322 | 99.27 | 0.032 | (0.890, 0.983) | −0.463 | ±0.9471 | 0.002 | 0.003 | 0.005 |
| LR | 0.974 | 0.276 | 0.18 | 28.35 | 0.943 | 0.487 | 0.322 | 99.33 | 0.032 | (0.890, 0.983) | −0.244 | ±0.9483 | 0.002 | 0.002 | 0.003 |
| Ridge | 0.963 | 0.332 | 0.256 | 30.52 | 0.941 | 0.494 | 0.329 | 99.96 | 0.022 | (0.875, 0.982) | −4.868 | ±0.9190 | 0.002 | 0.002 | 0.004 |
| Foundation F3 | |||||||||||||||
| RC | 0.962 | 0.178 | 0.113 | 61.35 | 0.963 | 0.386 | 0.287 | 57.46 | −0.001 | (0.932, 0.983) | −0.124 | ±0.7409 | 0.008 | 0.001 | 0.008 |
| LR | 0.959 | 0.183 | 0.119 | 64.79 | 0.956 | 0.421 | 0.294 | 57.17 | 0.004 | (0.920, 0.984) | −0.134 | ±0.8048 | 0.003 | 0.003 | 0.006 |
| BR | 0.959 | 0.183 | 0.119 | 65.43 | 0.954 | 0.428 | 0.307 | 56.43 | 0.005 | (0.919, 0.982) | −0.263 | ±0.8045 | 0.002 | 0.002 | 0.004 |
| Huber | 0.95 | 0.203 | 0.107 | 54.93 | 0.951 | 0.444 | 0.354 | 55.08 | −0.001 | (0.924, 0.970) | 0.402 | ±0.7231 | 0.014 | 0.002 | 0.016 |
| Lasso | 0.92 | 0.258 | 0.219 | 124.74 | 0.917 | 0.576 | 0.494 | 66.79 | 0.002 | (0.884, 0.946) | −4.855 | ±1.0690 | 0.002 | 0.002 | 0.004 |
| EN | 0.909 | 0.275 | 0.238 | 132.22 | 0.84 | 0.802 | 0.703 | 61.37 | 0.069 | (0.772, 0.879) | −3.8 | ±1.2196 | 0.002 | 0.002 | 0.004 |
| Ridge | 0.9 | 0.288 | 0.246 | 131.92 | 0.761 | 0.98 | 0.864 | 109.93 | 0.139 | (0.642, 0.834) | −2.889 | ±1.2033 | 0.002 | 0.002 | 0.004 |
| Foundation F4 | |||||||||||||||
| ERH | 0.944 | 0.326 | 0.19 | 56.67 | 0.881 | 0.522 | 0.319 | 8.12 | 0.063 | (0.713, 0.940) | 0.763 | ±0.9770 | 0.016 | 0 | 0.017 |
| Huber | 0.946 | 0.32 | 0.191 | 57.15 | 0.872 | 0.542 | 0.355 | 8.9 | 0.074 | (0.698, 0.934) | 0.767 | ±0.9893 | 0.01 | 0.002 | 0.011 |
| LR | 0.95 | 0.308 | 0.2 | 58.01 | 0.801 | 0.676 | 0.536 | 12.45 | 0.149 | (0.591, 0.873) | 0.776 | ±1.1731 | 0.002 | 0.002 | 0.004 |
| BR | 0.95 | 0.308 | 0.201 | 58.06 | 0.799 | 0.679 | 0.541 | 12.58 | 0.151 | (0.589, 0.872) | 0.771 | ±1.1688 | 0.002 | 0.002 | 0.004 |
| Lasso | 0.935 | 0.351 | 0.272 | 60.97 | 0.539 | 1.028 | 0.904 | 20.27 | 0.396 | (0.266, 0.650) | −0.179 | ±1.0228 | 0.002 | 0.002 | 0.004 |
| EN | 0.923 | 0.382 | 0.308 | 63.62 | 0.326 | 1.243 | 1.13 | 24.78 | 0.597 | (−0.079, 0.501) | −0.319 | ±1.0636 | 0.002 | 0.002 | 0.004 |
| Ridge | 0.916 | 0.398 | 0.32 | 67.25 | 0.218 | 1.339 | 1.248 | 27.18 | 0.698 | (−0.284, 0.412) | −0.628 | ±0.9530 | 0.002 | 0.002 | 0.004 |
References
- Chen, F.H. Foundations on Expansive Soils; Elsevier: Amsterdam, The Netherlands, 2012; Volume 12. [Google Scholar]
- Nelson, J.; Miller, D.J. Expansive Soils: Problems and Practice in Foundation and Pavement Engineering; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Jones, L.D.; Jefferson, I. Expansive soils. In ICE Manual of Geotechnical Engineering. Volume 1, Geotechnical Engineering Principles, Problematic Soils and Site Investigation; Burland, J., Ed.; ICE Publishing: London, UK, 2012; pp. 413–441. [Google Scholar]
- Fredlund, D.G.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; John Wiley & Sons: Hoboken, NJ, USA, 1993. [Google Scholar]
- Hu, J.; Li, X. A novel prediction model construction and result interpretation method for slope deformation of deep excavated expansive soil canals. Expert Syst. Appl. 2024, 236, 121326. [Google Scholar] [CrossRef]
- Ibrahim, H.H.; Hummadi, R.A. Dataset on the long-term monitoring of foundation vertical deformations on medium-expansive soil. Data Brief 2025, 59, 111422. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, Y.; Jamhiri, B.; Wang, L.; Li, T. Predicting uniaxial tensile strength of expansive soil with ensemble learning methods. Comput. Geotech. 2022, 150, 104904. [Google Scholar] [CrossRef]
- Tiwari, N.; Satyam, N. Coupling effect of pond ash and polypropylene fiber on strength and durability of expansive soil subgrades: An integrated experimental and machine learning approach. J. Rock Mech. Geotech. Eng. 2021, 13, 1101–1112. [Google Scholar] [CrossRef]
- Habib, M.; Habib, A.; Alibrahim, B. Prediction and parametric assessment of soil one-dimensional vertical free swelling potential using ensemble machine learning models. Adv. Model. Simul. Eng. Sci. 2024, 11, 26. [Google Scholar] [CrossRef]
- Abden, A.; Al-Shamrani, M.; Dafalla, M.; Siddiqui, N. Assessment of the performance of spread footings and mat foundations on expansive soils. Results Eng. 2024, 23, 102782. [Google Scholar] [CrossRef]
- Ikeagwuani, C.C.; Nwonu, D.C. Stability analysis and prediction of coconut shell ash modified expansive soil as road embankment material. Transp. Infrastruct. Geotechnol. 2023, 10, 329–358. [Google Scholar] [CrossRef]
- Laporte, S.; Eichhorn, G.; Kingswood, J.; Siemens, G.; Beddoe, R. Physical modelling of climate-soil-infrastructure interactions of paved roadways constructed in expansive soil. Transp. Geotech. 2023, 43, 101126. [Google Scholar] [CrossRef]
- Davar, S.; Nobahar, M.; Khan, M.S.; Amini, F. The development of PSO-ANN and BOA-ANN models for predicting matric suction in expansive clay soil. Mathematics 2022, 10, 2825. [Google Scholar] [CrossRef]
- Jalal, F.E.; Xu, Y.; Iqbal, M.; Javed, M.F.; Jamhiri, B. Predictive modeling of swell-strength of expansive soils using artificial intelligence approaches: ANN, ANFIS and GEP. J. Environ. Manag. 2021, 289, 112420. [Google Scholar] [CrossRef]
- Eyo, E.U.; Abbey, S.J.; Lawrence, T.T.; Tetteh, F.K. Improved prediction of clay soil expansion using machine learning algorithms and meta-heuristic dichotomous ensemble classifiers. Geosci. Front. 2022, 13, 101296. [Google Scholar] [CrossRef]
- Li, C.; Wang, L.; Li, J.; Chen, Y. Application of multi-algorithm ensemble methods in high-dimensional and small-sample data of geotechnical engineering: A case study of swelling pressure of expansive soils. J. Rock Mech. Geotech. Eng. 2024, 16, 1896–1917. [Google Scholar] [CrossRef]
- Zhou, Q.; Ge, Y.; Zhou, P.; Ge, H.; Wang, Y.; Chen, J.; Mei, D. Short-term prediction of vertical deformation in tidal flat terrains based on PSO-VMD-LSTM. IEEE Trans. Instrum. Meas. 2024, 73, 2521214. [Google Scholar] [CrossRef]
- Zhang, J.; Qiao, G.; Feng, T.; Zhao, Y.; Zhang, C. Dynamic back analysis of soil deformation during the construction of deep cantilever foundation pits. Sci. Rep. 2022, 12, 13112. [Google Scholar] [CrossRef]
- Nobahar, M.; Khan, S. Proactive measures for preventing highway embankment failures on expansive soil: Developing an early warning protocol. Appl. Sci. 2024, 14, 9381. [Google Scholar] [CrossRef]
- Ikeagwuani, C.C.; Nwonu, D.C. Influence of dilatancy behavior on the numerical modeling and prediction of slope stability of stabilized expansive soil slope. Arab. J. Sci. Eng. 2021, 46, 11387–11413. [Google Scholar] [CrossRef]
- Ikeagwuani, C.C. Estimation of modified expansive soil CBR with multivariate adaptive regression splines, random forest and gradient boosting machine. Innov. Infrastruct. Solut. 2021, 6, 199. [Google Scholar] [CrossRef]
- Ahmad, M.; Al-Mansob, R.A.; Ramli, A.B.B.; Ahmad, F.; Khan, B.J. Unconfined compressive strength prediction of stabilized expansive clay soil using machine learning techniques. Multiscale Multidiscip. Model. Exp. Des. 2024, 7, 217–231. [Google Scholar] [CrossRef]
- Chen, W.; Wan, X.; Ding, J.; Wang, T. Enhancing clay content estimation through hybrid CatBoost-GP with model class selection. Transp. Geotech. 2024, 45, 101232. [Google Scholar] [CrossRef]
- Onyelowe, K.C.; Moghal, A.A.B.; Ahmad, F.; Rehman, A.U.; Hanandeh, S. Numerical model of debris flow susceptibility using slope stability failure machine learning prediction with metaheuristic techniques trained with different algorithms. Sci. Rep. 2024, 14, 19562. [Google Scholar] [CrossRef] [PubMed]
- Wei, S.H.; Hwang, C. Land subsidence near Hanford and Corcoran, California, from Cryosat-2 altimetry and Sentinel-1A SAR imagery. Terr. Atmos. Ocean. Sci. 2025, 36, 6. [Google Scholar] [CrossRef]
- Nguyen, D.D.; Roussis, P.C.; Pham, B.T.; Ferentinou, M.; Mamou, A.; Vu, D.Q.; Bui, Q.A.T.; Trong, D.K.; Asteris, P.G. Bagging and multilayer perceptron hybrid intelligence models predicting the swelling potential of soil. Transp. Geotech. 2022, 36, 100797. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R; Springer: New York, NY, USA, 2013; Volume 103. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach; Springer: New York, NY, USA, 2002. [Google Scholar]
- Hair, J.F.; Black, W.C.; Babin, B.J.; Anderson, R.E. Multivariate Data Analysis, 7th ed.; Pearson: Boston, MA, USA, 2010. [Google Scholar]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Raudys, S.J.; Jain, A.K. Small sample size effects in statistical pattern recognition: Recommendations for practitioners. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 252–264. [Google Scholar] [CrossRef]
- Cawley, G.C.; Talbot, N.L. On over-fitting in model selection and subsequent selection bias in performance evaluation. J. Mach. Learn. Res. 2010, 11, 2079–2107. [Google Scholar]
- Vapnik, V.N. Statistical Learning Theory; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Puppala, A.J.; Manosuthikij, T.; Chittoori, B.C. Swell and shrinkage characterizations of unsaturated expansive clays from Texas. Eng. Geol. 2013, 164, 187–194. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman & Hall/CRC: Boca Raton, FL, USA, 1993. [Google Scholar]
- Bergmeir, C.; Benítez, J.M. On the use of cross-validation for time series predictor evaluation. Inf. Sci. 2012, 191, 192–213. [Google Scholar] [CrossRef]
- ASCE/SEI 7-16; Minimum Design Loads and Associated Criteria for Buildings and Other Structures. American Society of Civil Engineers: Reston, VA, USA, 2017.
- EN 1997-1:2004; Eurocode 7. Geotechnical Design—Part 1: General Rules. European Committee for Standardization: Brussels, Belgium, 2004.
- Ang, A.H.S.; Tang, W.H. Probability Concepts in Engineering: Emphasis on Applications to Civil and Environmental Engineering; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Farrar, C.R.; Worden, K. An introduction to foundation monitoring. Philos. Trans. R. Soc. A 2007, 365, 303–315. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 2002, 1, 67–82. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-based neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice, 3rd ed.; OTexts: Melbourne, Australia, 2018. [Google Scholar]




| Study | ML Methods | Dataset | Feature Categories | Target Variable | Best R2 | Key Contribution |
|---|---|---|---|---|---|---|
| Hu & Li [5] | Baseline: XGBoost, RF, LS-SVM; Hybrid: XGBoost-SHAP | Long-term monitoring, 4-year series | canal water level components, groundwater level components, time dependent effect, displacement increment of previous month data, lag features, VMD trend/periodic decomposition, atmospheric precipitation, evaporation, | Slope deformation | 0.908–0.993 | Interpretable ML with actionable reinforcement insights |
| Chen et al. [7] | Baseline: XGBoost, RF, ANN, SVM, MARS; Hybrid: Stacked Generalization | Manual collection, 125 records | dry density, water content, matric suction, unconfined compressive strength, failure compressive/tensile strains | Uniaxial tensile strength | 0.88 | Ensemble approach outperforming individual models |
| Habib et al. [9] | Baseline: SGD, DT, RF, AB, GB; Hybrid: ERT, XGB | Laboratory testing, 210 samples | dry unit weight, liquid limit, plasticity index, clay content, initial moisture content, etc. | Soil swelling potential | 0.97 | ~49% error reduction over baseline methods |
| Davar et al. [13] | Baseline: ANN-BR; Hybrid: PSO-ANN, BOA-ANN | Real-time monitoring, 13,690 hourly points | volumetric soil moisture content, 18-month hourly time series, air temperature, soil temperature, rainfall | Soil matric suction | 0.9949 | Hybrid optimization achieving temporal prediction |
| Eyo et al. [15] | Baseline: BLR, REG, LR, ANN, SVM, RDF, BDT; Hybrid: Voting/Stacking ensembles | Literature compilation, 517 records | void ratio, unit weight, liquid limit, plasticity index, clay content, maximum dry unit weight, coarse content, cation exchange capacity, activity, moisture content | Soil expansion | 0.94 | Meta-heuristic ensembles with 2–10 fold improvement |
| Zhou et al. [17] | Baseline: SVR, BPNN, RBFNN, LSTM; Hybrid: PSO-VMD-LSTM | MEMS sensors, 7-day hourly | cumulative displacement, lag features 8–24 h, temporal dependencies, rainfall, water level, tide height | Vertical deformation | >0.90 | Time series decomposition for tidal environments |
| Nguyen et al. [26] | Baseline: GP, MLP, ANN, SVM; Hybrid: Bagging-MLP | Field collection, 214 samples | gravel content, coarse/fine sand content, silt clay content, liquid/plastic limits, plasticity index, maximum dry density, organic content, optimum water content | Swelling potential | 0.90 | Bootstrap aggregation for variance reduction |
| Present study, 2025 | Baseline: LR, Ridge, Lasso, EN, Huber, BR, RF; Hybrid: Residual-Clustering, Elastic Net Fusion, Residual Correction, Enhanced Robust Huber | Foundation monitoring, 974 days, 4 foundations | raw monitoring variables, physics-based features (swelling/deformation potentials), statistical transformations (normalized and nonlinear terms), temporal features, seasonal encodings, and lag variables | Foundation deformation | 0.881–0.963 | Foundation-specific modeling with statistical validation and early warning |
| Variable Group | Variable | N | Mean | Std | Min | 25% | Median | 75% | Max | Range | Skewness | Kurtosis | CV (%) | Missing |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Deformation (mm) | F1 | 140 | −1.01 | 1.39 | −3.99 | −1.83 | −1.34 | 0.35 | 1.67 | 5.66 | 0.09 | −0.77 | −137.64 | 0 |
| F2 | 140 | 0.72 | 1.84 | −2.83 | −0.55 | 0.98 | 1.95 | 4.86 | 7.69 | −0.23 | −0.56 | 255.35 | 0 | |
| F3 | 140 | −0.80 | 1.21 | −3.38 | −1.70 | −0.65 | 0.04 | 2.89 | 6.27 | 0.17 | 0.06 | −150.66 | 0 | |
| F4 | 140 | 0.70 | 2.61 | −3.15 | −1.23 | 0.12 | 1.51 | 7.43 | 10.58 | 0.93 | 0.20 | 370.74 | 0 | |
| Soil Moisture (%) | F1 | 140 | 9.79 | 1.68 | 6.07 | 8.26 | 10.05 | 10.86 | 14.64 | 8.57 | 0.18 | −0.20 | 17.11 | 0 |
| F2 | 140 | 11.96 | 2.49 | 6.46 | 9.59 | 11.88 | 13.29 | 18.60 | 12.14 | 0.53 | 0.39 | 20.84 | 0 | |
| F3 | 140 | 8.33 | 2.03 | 4.49 | 7.10 | 8.28 | 9.39 | 13.65 | 9.16 | 0.47 | 0.04 | 24.39 | 0 | |
| F4 | 140 | 8.63 | 3.22 | 3.24 | 7.58 | 8.40 | 9.87 | 16.48 | 13.24 | 0.28 | 0.11 | 37.29 | 0 | |
| Environmental | Temp (°C) | 140 | 22.48 | 10.02 | 3.30 | 13.40 | 21.55 | 32.65 | 39.40 | 36.10 | 0.11 | −1.35 | 44.56 | 0 |
| Rainfall (mm) | 140 | 7.66 | 18.29 | 0.00 | 0.00 | 0.00 | 5.20 | 146.30 | 146.30 | 4.25 | 23.96 | 238.77 | 0 |
| Category | Variable | Foundation | Mean | Std | Min | Max | Trend/Net Change | Status | Notes (From Figure 1) |
|---|---|---|---|---|---|---|---|---|---|
| Environmental | Temperature (°C) | – | 22.48 | 10.02 | 3.30 | 39.40 | – | – | Seasonal cycles |
| Rainfall (mm) | – | 7.66 | 18.29 | 0.00 | 146.30 | 5 extreme events | – | Episodic spikes | |
| Soil Moisture (%) | Moisture | F1 | 9.79 | 1.68 | 6.07 | 14.64 | Decreasing | – | Matches settlement |
| F2 | 11.96 | 2.49 | 6.46 | 18.60 | Increasing | – | Matches heave | ||
| F3 | 8.33 | 2.03 | 4.49 | 13.65 | Decreasing | – | Matches settlement | ||
| F4 | 8.63 | 3.22 | 3.24 | 16.48 | Increasing | – | Matches heave | ||
| Deformation (mm) | Vertical disp. | F1 | −1.01 | 1.39 | −3.99 | 1.67 | −3.99 | Settlement | Long-term decline |
| F2 | 0.72 | 1.84 | −2.83 | 4.86 | +1.52 | Heave | Episodic rise | ||
| F3 | −0.80 | 1.21 | −3.38 | 2.89 | −3.38 | Settlement | Sustained decline | ||
| F4 | 0.70 | 2.61 | −3.15 | 7.43 | +3.36 | Heave | Strong episodic rise | ||
| Dial Gauge (mm) | Position | F1 | 5.32 | 1.40 | 2.34 | 8.00 | −3.99 | – | Corroborates disp. |
| F2 | 5.06 | 1.85 | 1.51 | 9.20 | −1.52 | – | – | ||
| F3 | 3.95 | 1.21 | 1.37 | 7.64 | −3.38 | – | – | ||
| F4 | 5.35 | 2.62 | 1.50 | 12.08 | +3.36 | – | – |
| Rank | Foundation F1 | Foundation F2 | Foundation F3 | Foundation F4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Variable | r | Sig. | Variable | r | Sig. | Variable | r | Sig. | Variable | r | Sig. | |
| 1 | Target_lag1_F1 | 0.96 | *** | Target_lag1_F2 | 0.97 | *** | Target_lag1_F3 | 0.96 | *** | Target_lag1_F4 | 0.98 | *** |
| 2 | NormMoist_F1 | 0.41 | *** | Month_sin | 0.65 | *** | Swell_F3 | 0.60 | *** | Moist2_F4 | 0.84 | *** |
| 3 | Swell_F1 | 0.41 | *** | TempLag1 | −0.38 | *** | %moist_F3 | 0.60 | *** | NormMoistLag1_F4 | 0.78 | *** |
| 4 | DefPot_F1 | 0.41 | *** | Moist2_F2 | 0.38 | *** | NormMoist_F3 | 0.60 | *** | SwellLag1_F4 | 0.78 | *** |
| 5 | %moist_F1 | 0.41 | *** | Temp | −0.34 | *** | DefPot_F3 | 0.60 | *** | DefPotLag1_F4 | 0.78 | *** |
| 6 | Moist2_F1 | 0.39 | *** | %moist_F2 | 0.33 | *** | Moist2_F3 | 0.59 | *** | MoistLag1_F4 | 0.78 | *** |
| 7 | MoistLag1_F1 | 0.38 | *** | NormMoist_F2 | 0.33 | *** | TempLag1 | −0.59 | *** | %moist_F4 | 0.78 | *** |
| 8 | Temp | −0.30 | *** | DefPot_F2 | 0.33 | *** | Temp | −0.58 | *** | Rain | 0.30 | *** |
| 9 | Rain | 0.16 | NS | Rain | 0.23 | ** | Rain | 0.35 | *** | Temp | −0.17 | * |
| Foundation | Hybrid Model | Baseline Comparison | t-Statistic | p-Value | Cohen’s d | Effect Size | Performance Gain |
|---|---|---|---|---|---|---|---|
| F1 | Residual-Clustering Hybrid | Ridge | 5.366 | 0.001279 * | 0.711 | Medium | ΔR2 = +0.063 |
| EN | 4.834 | 0.005326 * | 0.669 | Medium | ΔR2 = +0.061 | ||
| F2 | Elastic Net Fusion | (No significant improvements) | - | >0.05 | <0.05 | Negligible | - |
| F3 | Residual Correction | Ridge | 5.710 | 0.000510 * | 1.507 | Very Large | ΔR2 = +0.202 |
| EN | 5.627 | 0.000636 * | 1.135 | Large | ΔR2 = +0.123 | ||
| F4 | Enhanced Robust Huber | Ridge | 7.396 | 0.000007 * | 1.494 | Very Large | ΔR2 = +0.663 |
| EN | 6.238 | 0.000127 * | 1.201 | Very Large | ΔR2 = +0.555 | ||
| RF | 6.576 | 0.000053 * | 1.805 | Very Large | ΔR2 = +0.431 | ||
| Lasso | 5.408 | 0.001141 * | 0.854 | Large | ΔR2 = +0.342 | ||
| LR | 4.185 | 0.030339 * | 0.259 | Small | ΔR2 = +0.080 | ||
| BR | 4.274 | 0.023901 * | 0.264 | Small | ΔR2 = +0.082 |
| Foundation | Full Model R2 | −Physics Features | −Temporal Features | −Environmental Features | Critical Feature Group |
|---|---|---|---|---|---|
| F1 | 0.945 | 0.945 (0.000) | 0.000 (−0.945) | 0.855 (−0.090) | Temporal |
| F2 | 0.947 | 0.947 (0.000) | 0.000 (−0.947) | 0.897 (−0.050) | Temporal |
| F3 | 0.963 | 0.963 (0.000) | 0.108 (−0.855) | 0.913 (−0.050) | Temporal |
| F4 | 0.881 | 0.881 (0.000) | 0.000 (−0.881) | 0.843 (−0.038) | Temporal |
| Foundation | Model | Warning Events | Critical Events | Precision | Recall | F1-Score | Prediction Accuracy | Thresholds Used |
|---|---|---|---|---|---|---|---|---|
| F1 | Residual-Clustering Hybrid | 9/28 (32.1%) | 7/28 (25.0%) | 1.000 | 0.818 | 0.900 | 0.765 | 4 |
| F2 | Elastic Net Fusion | 11/28 (39.3%) | 6/28 (21.4%) | 0.909 | 1.000 | 0.952 | 0.771 | 4 |
| F3 | Residual Correction | 17/28 (60.7%) | 13/28 (46.4%) | 0.941 | 1.000 | 0.970 | 0.807 | 4 |
| F4 | Enhanced Robust Huber | 27/28 (96.4%) | 26/28 (92.9%) | 1.000 | 0.964 | 0.982 | 0.655 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saeheaw, T. Foundation-Specific Hybrid Models for Expansive Soil Deformation Prediction and Early Warning. Buildings 2025, 15, 3497. https://doi.org/10.3390/buildings15193497
Saeheaw T. Foundation-Specific Hybrid Models for Expansive Soil Deformation Prediction and Early Warning. Buildings. 2025; 15(19):3497. https://doi.org/10.3390/buildings15193497
Chicago/Turabian StyleSaeheaw, Teerapun. 2025. "Foundation-Specific Hybrid Models for Expansive Soil Deformation Prediction and Early Warning" Buildings 15, no. 19: 3497. https://doi.org/10.3390/buildings15193497
APA StyleSaeheaw, T. (2025). Foundation-Specific Hybrid Models for Expansive Soil Deformation Prediction and Early Warning. Buildings, 15(19), 3497. https://doi.org/10.3390/buildings15193497






