A Potential Outlier Detection Model for Structural Crack Variation Using Big Data-Based Periodic Analysis

Abstract

Cracks in concrete structures, caused by aging, adjacent construction, and seismic activity, pose critical risks to structural integrity, durability, and serviceability. Traditional monitoring methods based solely on absolute thresholds are inadequate for detecting progressive crack growth at early stages. This study proposes a big data-driven anomaly detection model that combines absolute threshold evaluation with periodic trend analysis to enable both real-time monitoring and early anomaly identification. By incorporating relative comparisons, the model captures subtle variations within allowable limits, thereby enhancing sensitivity to incipient defects. Validation was conducted using approximately 2700 simulated datasets with an increase–hold–increase pattern and 470,000 real-world crack measurements. The model successfully detected four major anomalies, including abrupt shifts and cumulative deviations, and time series visualizations identified the exact onset of abnormal behavior. Through periodic fluctuation analysis and the Isolation Forest algorithm, the model effectively classified risk trends and supported proactive crack management. Rather than defining fixed labels or thresholds for the detected results, this study focused on verifying whether the analysis of detected crack data accurately reflected actual trends. To support interpretability and potential applicability, the detection outcomes were presented using quantitative descriptors such as anomaly count, anomaly score, and persistence. The proposed framework addresses the limitations of conventional digital monitoring by enabling early intervention below predefined thresholds. This data-driven approach contributes to structural health management by facilitating timely detection of potential risks and strengthening preventive maintenance strategies.

1. Introduction

The need for systematic management of structural cracks has been increasing due to factors such as building deterioration, adjacent construction activities, and earthquakes [1]. Cracks can lead to reduced durability of concrete members, decreased load-bearing capacity caused by reinforcement corrosion, loss of water- and airtightness, and aesthetic degradation, thereby requiring thorough monitoring and management [2]. In particular, precise monitoring is essential not only to detect the occurrence of cracks but also to assess their implications and progression in order to ensure structural safety.

Currently, most crack inspections rely on visual surveys and manual record-keeping [3], which involve significant limitations. For instance, inspections may expose workers to hazardous environments such as ladder operations, and results can vary depending on the inspector’s subjective judgment. Moreover, manually recorded data are unsuitable for long-term monitoring and systematic analysis. Periodic inspection methods are also inefficient in terms of time and cost, while being vulnerable to missing sudden changes.

To overcome these drawbacks, automated monitoring using digital crack measurement devices has been introduced. However, most of these approaches still focus only on determining whether the absolute crack width exceeds a predefined threshold. While absolute value-based methods are useful for assessing a crack’s state at a given point in time, they cannot capture temporal variations or progressive deterioration. As a result, early-stage defects that gradually expand may not be detected in time, leading to delayed repair or reinforcement and increased maintenance costs [4].

Cracks typically progress gradually, compromising structural durability and, if left unaddressed, potentially leading to critical failure. Therefore, even small deformations below allowable thresholds can pose risks if they accumulate over time, highlighting the importance of observing crack width variations across a temporal dimension. In aging structures especially, continuous monitoring of cracks—regardless of whether they exceed the threshold—is essential to enable early detection of potentially anomalous behavior. Traditional methods based solely on visual inspection or fixed thresholds are insufficient for identifying early-stage defects. Instead, tracking time-dependent changes is necessary for timely recognition of underlying risks.

Crack behavior is governed by nonlinear and cumulative interactions among material properties, loading histories, and environmental conditions, producing complex and evolving patterns that challenge traditional evaluation methods. Such characteristics limit the effectiveness of static threshold-based approaches, which cannot adequately capture the progressive and context-dependent nature of deterioration. This inherent complexity provides a clear rationale for employing data-driven methods capable of detecting patterns within large, heterogeneous time series datasets.

By leveraging variation-based data, it becomes possible to understand the context and flow of crack behavior over time, thereby improving the accuracy of anomaly detection [5]. To detect subtle, progressive crack growth, a big data-based periodic analysis framework offers significant advantages. Analyzing large-scale, time series crack data enables the identification of hidden growth trends that remain within allowable limits yet signal future deterioration, thus providing a stronger basis for timely and informed maintenance decisions.

This study proposes a big data-driven framework for detecting potential crack anomalies by computing three variation metrics—long-term variation, short-term variation, and instantaneous variation—followed by normalization using a Robust Scaler and anomaly detection with the Isolation Forest algorithm. The proposed framework consists of a sequence of procedures: data transformation, normalization, and visualization during preprocessing; candidate anomaly detection during the anomaly detection stage; and redundancy-based classification of anomalies. Furthermore, by incorporating periodic analysis, the framework evaluates risk-level transitions over time, addressing the limitations of absolute value-based approaches and enabling earlier recognition of crack growth patterns. Ultimately, the framework aims to reduce labor and cost requirements for crack inspections while preventing damage caused by undetected anomalies.

The remainder of this paper is organized as follows. Section 2 reviews prior studies on crack monitoring, big data-based anomaly detection, and the Isolation Forest algorithm. Section 3 details the step-by-step procedures of the proposed framework. Section 4 validates the model using both simulated and real-world datasets. Finally, Section 5 presents the conclusions and implications of this research.

2. Literature Review

2.1. Trends in Concrete Crack Monitoring

Conventional crack inspection methods can be categorized into visual inspection, crack gauges, electronic crack meters, core sampling, and non-destructive testing (NDT), as summarized in

Table 1. Conventional methods for concrete crack inspection.

Method	Description	Advantages	Disadvantages
Visual Inspection	Inspectors visit the site and measure/record the width and length of concrete cracks by visual observation.	Low cost, quick measurement	Subjective results, low accuracy
Crack Gauge	A gauge is attached to the crack to visually check changes in crack width.	Easy installation, relatively inexpensive	Inefficient for long-term monitoring
Electronic Crack Monitoring Device	Sensors are installed to precisely measure crack displacement.	High precision, real-time monitoring possible	Requires data processing, high initial installation cost
Core Test	Core samples are taken from suspicious areas to examine and measure defects.	High accuracy in measuring crack size and depth	Labor- and time-intensive
Non-Destructive Testing (NDT)	Internal defects and crack depth are measured using radiation or ultrasonic testing.	Able to detect deep internal defects	Expensive equipment required, skilled operators needed

. Visual inspection is low-cost and quick but suffers from subjectivity, limited accessibility, and low accuracy due to reliance on human judgment [6]. Crack gauges are simple and economical to install but are unsuitable for long-term monitoring and systematic record-keeping. Electronic crack meters allow precise displacement measurements through sensors and enable real-time monitoring; however, they require data processing and involve higher initial installation costs. Core sampling and NDT provide higher accuracy but demand costly equipment and skilled operators.

In this study, electronic crack meters were adopted because of their suitability for quantitative and long-term monitoring. These devices are attached directly to crack surfaces, measuring variations in crack width based on changes in electrical resistance, and are well-suited for large-scale data collection and long-term analysis.

Traditional crack management procedures rely on inspection–recording–observation cycles, where structural safety is assessed based on whether crack widths exceed allowable limits, followed by detailed safety evaluations when necessary. However, such approaches are highly labor-dependent, lack real-time monitoring capabilities, and are limited in cumulative data analysis. Furthermore, many monitoring devices simply determine whether an absolute threshold is exceeded, leaving sub-threshold cracks to manual inspection. Even when large datasets are collected, systematic data-driven analysis is rarely attempted.

Against this background, various studies have investigated concrete crack monitoring. Representative works from 2017 to 2024, retrieved using the keyword “concrete crack monitoring” on Google Scholar, are summarized in

Table 2. Representative studies on concrete crack monitoring (2017–2024).

Author	Description	Objective	Data Acquisition Method
[7] Arbaoui et al.	Proposed an automatic crack type classification system using CNN to monitor crack progression and detect cracks before they become visible.	Crack detection and automatic classification.	Vision (ultrasonic image collection).
[8] Wu, et al.	Developed a simulation test platform for crack monitoring based on fiber optic sensing, providing theoretical and technical guarantees.	Crack growth monitoring	Sensor (fiber optic sensing network, micro-bending principle)
[9] Richter et al.	Applied distributed fiber optic sensors (DFOS) to locate crack damage and measure width, proposing an automated framework for DFOS-based width calculation.	Crack width measurement.	Sensor (distributed fiber optic sensor, DFOS).
[10] Jung et al.	Developed a CNT-based polymer composite crack sensor that detects cracks through electrical property changes under tensile load.	Crack detection and growth monitoring.	Sensor (CNT-based self-sensing surface-attached sensor).
[11] Jin, et al.	Monitored crack initiation and growth using a soft elastomer capacitor (SEC) detecting strain via capacitance changes.	Crack detection and quantification.	Sensor (soft elastomer capacitor, SEC-based sensing skin).
[12] Zhang, et al.	Proposed a method to monitor and evaluate repaired cracks using piezoelectric smart aggregates (SA), analyzing stress wave propagation.	Monitoring and evaluation of repaired cracks.	Sensor (piezoelectric smart aggregate, SA).
[13] Domaneschi, et al.	Conducted multi-sensor monitoring: degradation via NDT, deformation via embedded fiber optic sensors (FOS), and crack initiation via acoustic emission (AE) sensors.	Structural damage assessment up to reinforcement yield, crack monitoring.	Sensor (FOS, AE sensors); Vision (digital image correlation, DIC).
[14] Chakraborty, et al.	Demonstrated ultrasonic sensors can detect cracks with 100% probability before visible, validated with embedded/external sensors and advanced signal processing.	Early crack detection.	Sensor (ultrasonic, embedded/external sensors).
[15] Cha et al.	Deep learning-based crack detection using CNN and sliding window.	Automate crack detection under varying lighting/shadow conditions.	40k labeled crack images; field test images under varying conditions.
[16] Dorafshan et al.	Comparison of edge detectors vs. DCNN for image-based crack detection.	Evaluate performance differences between edge detection and DCNN.	High-definition concrete images (3420 sub-images).
[17] Duan et al.	CNN-based damage identification for bridge hanger cables using FAS data.	Improve robustness of damage detection in bridges using raw spectral data.	Numerical simulations with wind vibration data for bridge cables.
[18] Ewald et al.	DeepSHM: CNN with guided Lamb waves for ultrasonic SHM.	Develop an end-to-end DL framework for ultrasonic SHM.	Ultrasonic guided wave signals from FEM + experimental testing.
[19] Zhang et al.	Context-aware semantic segmentation for crack detection in complex conditions.	Enhance segmentation accuracy for cracks under complex infrastructure conditions.	Multiple datasets: CFD, TRIMMD, and CFTD crack images.
This study	Proposed a big data-based crack anomaly detection model using Isolation Forest with long-term, short-term, and instantaneous variations. Real-time monitoring uses absolute thresholds, while periodic monitoring applies time series variation.	Early anomaly detection and risk crack monitoring.	Sensor (electronic crack monitoring device).

. Recent research has predominantly focused on physical measurements using sensors and imaging technologies, with an emphasis on condition assessment based on observed values. Notably, vision-based deep learning approaches have demonstrated high accuracy in crack detection and classification using image data. However, while effective, most of these methods remain limited in practice because they rely heavily on large-scale labeled datasets, lack integration with long-term or real-time monitoring systems, and struggle to detect sub-threshold or gradually growing cracks that are not yet visually apparent. As a result, most existing studies provide only snapshot assessments of crack conditions at specific moments in time and rarely address predictive evaluation of progressive deterioration. In addition, prior big data-driven SHM approaches often face challenges of generalizability across different structural contexts, limited explainability of detection outcomes, and computational scalability when handling massive time series datasets. In particular, there is a scarcity of big data-based approaches that analyze time-dependent crack variations to detect early-stage risks.

In response, this study proposes a time series-based anomaly detection framework that computes and utilizes three crack variation metrics—long-term, short-term, and instantaneous—as core analytical indicators. The aim is to detect subtle or abnormal trends even when the crack width remains within allowable limits. By focusing on trend behavior rather than absolute thresholds, the proposed method complements vision-based deep learning approaches and supports continuous, real-time structural health monitoring.

2.2. Research Trends in Big Data-Based Anomaly Detection

An observation which deviates so much from other observations as to arouse suspicions that it was generated by a different mechanism is referred to as an outlier [20]. In big data environments, anomaly detection requires the design of algorithms that are both efficient and scalable, considering the volume, variety, and velocity of the data.

Traditional statistical approaches, such as Statistical Process Control (SPC) methods—including Shewhart, EWMA, and CUSUM charts—have long been used to detect structural anomalies by monitoring deviations from predefined thresholds. These methods are widely recognized for their simplicity, interpretability, and computational efficiency. However, because they rely on assumptions of stationarity and fixed control limits, their performance is limited in complex structural health monitoring (SHM) environments, particularly in capturing subtle variations or progressive deterioration [21,22].

In recent years, machine learning (ML)-based anomaly detection techniques capable of handling multidimensional data and irregular distributions have been introduced. ML models have been successfully applied across various domains, including SHM benchmark datasets such as SHMnet, demonstrating improved adaptability compared to traditional control charts [23,24,25]. Among these, the Isolation Forest algorithm has drawn attention for its ability to isolate anomalies by recursively partitioning the data space, offering robustness to noise and scalability to large datasets.

Deep learning (DL)-based methods, such as convolutional neural networks (CNNs), recurrent neural networks (RNNs), and autoencoders, have also achieved strong performance in anomaly detection, particularly for high-dimensional or unstructured data [26,27,28]. However, these approaches are constrained in practice by their dependence on large-scale labeled datasets, high computational demands, and challenges in integration with long-term monitoring systems.

In contrast, this study applies an Isolation Forest-based anomaly detection framework that incorporates time series crack variation metrics (long-term, short-term, and instantaneous). Unlike conventional SPC methods or DL-based techniques, this framework enables early detection of potential sub-threshold anomalies without requiring extensive labeled datasets, thereby offering a practical and scalable solution for real-time structural health monitoring.

Table 3. Categories of outlier detection methods in big data environments.

Category	Description	Advantages	Limitations
Statistical	Detect outliers using statistical measures (Z-score, IQR).	Simple, intuitive.	Limited with uneven distributions or threshold setting.
Distance-based	Use distances between data points (e.g., k-NN).	Effective in multidimensional data.	Sensitive to parameters, performance drops in high dimensions.
Density-based	Detect sparse regions via density (e.g., LOF).	Considers data distribution.	Poor performance with uneven density.
Deep learning	Learn abnormal patterns (Autoencoder, CNN).	Flexible across data types.	Time- and expertise-intensive.
Machine learning	Classify using ML algorithms (SVM, RF, IF).	Efficient for high-dimensional data.	Performance depends on parameters.

summarizes the representative categories of outlier detection methods in big data environments, together with their advantages and limitations: statistical, distance-based, density-based, and machine learning-based approaches [29]. Statistical methods are simple and intuitive but sensitive to distributional assumptions and threshold selection. Distance-based methods can be applied in high-dimensional data but often suffer from performance degradation as dimensionality increases. Density-based methods enable precise detection by considering data distribution, but their performance decreases when data density is uneven. Machine learning and deep learning approaches allow for complex pattern learning and advanced anomaly detection but are highly dependent on data quality and parameter tuning.

Recently, numerous studies have explored anomaly detection using big data across various industries.

Table 4. Representative studies on big data-based anomaly detection (2024–present).

Category	Author	Description	Data
Machine learning	[23] Shiva et al.	Reviewed and improved anomaly detection methods for predictive maintenance in industrial environments by applying ML algorithms to sensor data.	Industrial sensor data
	[24] Theodorakopoulos et al.	Developed a real-time credit card fraud detection system. Compared multiple ML models (Logistic Regression, Decision Trees, Random Forests, XGBoost), with XGBoost achieving the highest accuracy.	Credit card transaction data
	[25] Ofoegbu et al.	Built a real-time cyber threat detection system using ML and big data analytics. Employed adaptive models for continuous learning and accurate threat prediction.	Security and threat pattern data
Deep learning	[26] Wong et al.	Developed an anomaly detection model for big data environments by combining CNN and LSTM to detect real-time network traffic anomalies.	Network flow data
	[27] Wang et al.	Implemented an autoencoder-based anomaly detection model integrating kernel methods and neural networks to improve detection in abnormal industrial processes.	High-dimensional industrial/process data
	[28] Song et al.	Predicted and evaluated battery conditions using a big data platform with deep learning.	Battery operation data
Statistical	[21] Entezami et al.	Detected structural anomalies using statistical pattern recognition and ARMA modeling of vibration data.	Vibration data
	[22] Silik et al.	Analyzed abnormal structural data and extracted features using wavelet transform.	Structural dynamic data
Density-based	[30] Lin et al.	Predicted relief supply demand during floods by analyzing population density and distribution with MLP neural networks and big data.	Population distribution, flood case data
	[31] Sarker et al.	Proposed disaster response strategies and resilience improvement using big data, GIS, and social media analysis.	Disaster, GIS, social media data
Distance-based	[32] Sun et al.	Evaluated structural health by analyzing distance and temporal data using AI and big data techniques.	Structural condition, SHM data

presents representative studies published since 2024, highlighting the adoption of advanced models that combine machine learning and deep learning in domains such as industry, finance, cybersecurity, and network management. However, research focusing on structural anomalies involving long-term and gradual changes, such as concrete cracks, remains limited.

In particular, cracks may continue to propagate even after their initial occurrence, making it difficult to achieve early risk recognition based solely on threshold-based evaluations at single time points. To address this gap, this study proposes a model that incorporates time-dependent crack variations (long-term, short-term, and instantaneous changes) as key variables and leverages accumulated large-scale datasets to enable relative anomaly detection and risk trend analysis. This approach allows the early identification of risk patterns even below allowable crack thresholds and supports more proactive decision-making in structural health management.

2.3. Isolation Forest-Based Approaches for Anomaly Detection

The Isolation Forest algorithm detects anomalies by generating multiple binary trees, where each tree recursively partitions the data based on randomly selected features and split values (see Figure 1). The anomaly score is determined by the average path length required to isolate a given data point. Typically, anomalies can be isolated with fewer partitions, resulting in shorter path lengths, whereas normal data points require longer paths.

A key parameter of the algorithm, contamination, represents the expected proportion of anomalies within the dataset and influences the final decision threshold. In this study, the Isolation Forest was applied to detect anomalies in big data-based crack variation values, for the following reasons:

• Performance with high-dimensional data: The model uses three crack variation metrics—long-term (relative to the initial value), instantaneous (relative to the previous value), and short-term (daily cumulative variation). These multidimensional variables can be effectively handled by Isolation Forest.
• Computational efficiency: Crack data are continuously collected in real time, requiring rapid analysis of large-scale datasets. Isolation Forest requires less computational effort compared to clustering-based methods, making it suitable for large-scale monitoring.
• Overcoming the limitations of absolute thresholds: Conventional crack monitoring methods rely on fixed allowable width limits, making it difficult to detect gradual growth or subtle variations. Isolation Forest, however, isolates data points based on relative separability, enabling the detection of abnormal patterns even within values below the threshold, thus allowing early identification of potential risks.

Building on these strengths, this study proposes a crack management framework that leverages temporal variation metrics to detect anomalies and assess risk at an early stage.

Isolation Forest has been widely applied in various domains of anomaly detection.

Table 5. Representative studies applying Isolation Forest for anomaly detection.

Author	Description	Purpose	Variables/Data
[33] Ahn et al.	Developed anomaly detection and rapid failure response system for securities data	Real-time alerts during failures	Multivariate features of futures/options and stock data
[34] Xu, et al.	Improved Isolation Forest for higher accuracy and efficiency	Enhanced tree efficiency and optimized detection	Characteristics of diverse datasets, simulation data
[35] Kim et al.	Detected anomalies in water quality data	Compared with distance-based methods for water management improvement	Multi-parameter water quality data
[36] Jin et al.	Applied anomaly detection to manufacturing quality control	Identified abnormal patterns in welding process time series	Welding process time series data
[37] Wan, et al.	Computer vision-based defect detection in mechanical components	Detected crack-type and bulging defects in air springs	Small image features, crack and bulging defects
[29] Chen, et al.	Integrated anomaly detection with key operational attributes	Improved machine reliability	Operating conditions, performance data
[38] Takanashi et al.	Automated pavement deterioration detection using vibration sensors and ML	Detected road deterioration via vibration analysis	Vibration data, pavement condition
[39] Devi, et al.	Applied modified Isolation Forest for IoT sensor networks	Automatic detection and recovery of network issues	Sensor data patterns
[40] McKinnon et al.	Used SCADA data for predictive maintenance in wind turbines	Predicted pitch system failures 12–18 months in advance	SCADA data, hydraulic/electrical pitch data
[41] Antonini, et al.	Developed edge computing-based anomaly detection for extreme industrial environments	Real-time on-site data processing and detection	Sensor data
[42] Feng, et al.	Detected abnormal behavior in student data	Improved Isolation Forest with logistic regression and particle swarm optimization	Student behavioral data, educational big data
[43] Yepmo, et al.	Enhanced explainability of anomaly detection results	Differentiated local/global anomalies and provided contextual explanations	Dataset structure, local/global anomalies
[44] Wang, et al.	Improved anomaly detection in power consumption	Integrated Canopy-Kmeans with Isolation Forest	Electricity consumption patterns

summarizes representative studies that adopted this method. While recent works have demonstrated its effectiveness in finance, manufacturing, IoT, and infrastructure monitoring, its application to anomaly detection in crack variation data remains limited. To address this gap, the present study employs time series variation metrics to complement conventional absolute-threshold approaches, providing an early-warning framework for crack management.

3. Potential Anomaly Detection Model for Structural Cracks Based on Periodic Big Data Analysis

3.1. Overview of the Proposed Model

This study first reviewed the current status and limitations of concrete crack monitoring, the applicability of big data-based anomaly detection methods, and the characteristics of the Isolation Forest algorithm. Conventional crack monitoring has primarily focused on measuring crack width and length at specific time points, without adequately reflecting time series variability. As a result, it is difficult to identify potential risks that may occur even when cracks remain below allowable thresholds.

Big data-driven anomaly detection has been actively applied to early-warning systems across various industries; however, its application to long-term crack variation analysis remains limited. Although Isolation Forest offers strong computational efficiency and the ability to process high-dimensional data, few studies have employed it using time series crack variation metrics as primary variables.

To address this gap, this study proposes an anomaly detection model that incorporates time-dependent crack variation values and applies the Isolation Forest algorithm. The model aims to overcome the limitations of absolute-threshold monitoring by enabling early detection of potential anomalies and contributing to efficient crack data management and the development of an automated early-warning system.

This section provides an overview of the proposed anomaly detection model. Section 3.1.1 introduces the dual framework for real-time and periodic crack monitoring. Section 3.1.2 describes the classification scheme for crack anomalies. Finally, Section 3.1.3 outlines the implementation and application strategies of the proposed model.

3.1.1. Real-Time and Periodic Crack Monitoring Framework

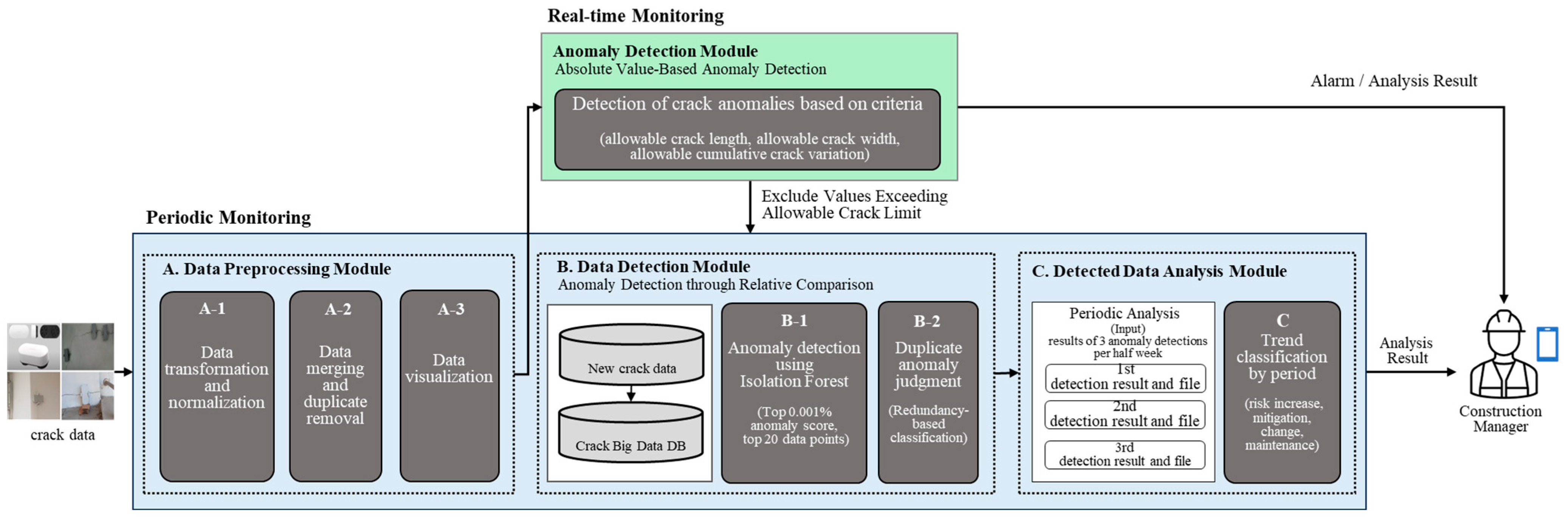
This study proposes a big data-based anomaly detection model designed to enable early detection of structural crack anomalies and long-term risk assessment (see Figure 2). The model employs a dual framework consisting of real-time and periodic monitoring, each serving distinct purposes as summarized in

Table 6. Comparison between real-time and periodic monitoring methods.

Category	Criterion	Method	Detected Data
Real-time monitoring	Absolute value threshold	Anomalies are detected when the measured crack width exceeds predefined allowable limits	Data exceeding allowable crack width
Periodic monitoring	Relative comparison	Anomalies are detected based on time series variability and relative comparison within accumulated data	Data within allowable range but identified as potential anomalies (high anomaly score)

:

• Real-time monitoring: Crack width data continuously collected from electronic sensors installed on the structure are analyzed in real time. Any data exceeding predefined allowable thresholds or exhibiting sudden fluctuations are immediately detected and flagged as anomalies.
• Periodic monitoring: Accumulated time series data over a given period are analyzed to evaluate relative variability. Even if data remain within allowable thresholds, values with a high anomaly probability are identified, and long-term risk trends are assessed.

In addition, Figure 3 illustrates the overall conceptual flow of crack management, integrating both real-time and periodic monitoring. Unlike conventional field inspection-oriented approaches, the proposed model is based on an automated data collection–analysis–decision framework. This enables the quantitative evaluation of risk trends through time series analysis, providing a more systematic and objective approach to structural crack management.

Table 7. Comparison of conventional crack inspection and the proposed model.

Category	Conventional Crack Inspection	Proposed Anomaly Detection Model
Real-time capability	Periodic on-site inspection; real-time evaluation difficult	Continuous data collection via electronic sensors enables real-time monitoring
Record management efficiency	Manual recording with risk of data loss	Automated storage in big-data systems; consistent and continuous accumulation without omission
Objectivity of evaluation	Subjective assessments; difficult to ensure consistency	Quantitative and time series data visualization allow objective, data-driven evaluation
Data detection: above threshold	Detection of cracks exceeding allowable width	Detection of cracks exceeding allowable width (real-time analysis)
Data detection: below threshold	Not detectable	Detection of sub-threshold anomalies through periodic analysis
Risk trend analysis	Continuous tracking of crack growth not feasible	Combined real-time and periodic monitoring enables tracking of crack progression and risk trend analysis

provides a detailed comparision between conventional crack inspection methods and the proposed model.

3.1.2. Classification of Crack Anomalies

(1)

Crack Anomaly Classification

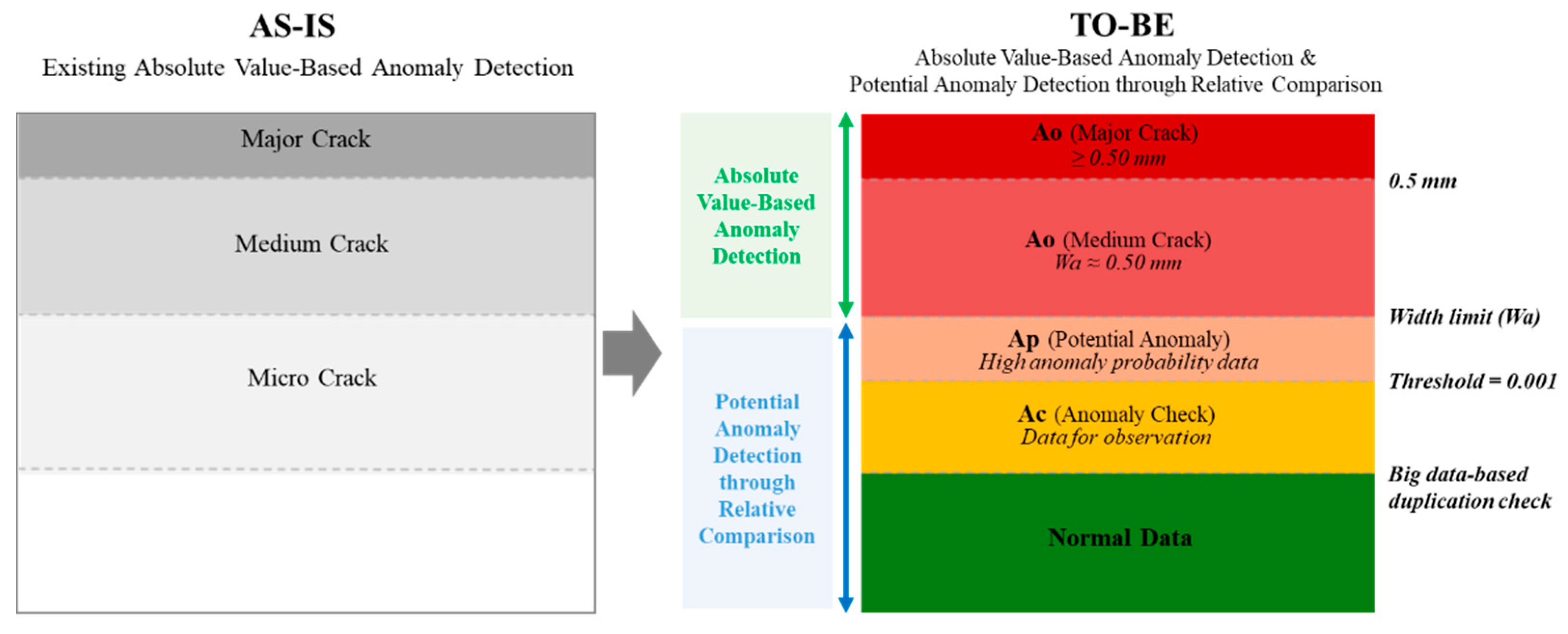
In this study, crack data were classified according to two detection approaches: absolute value criteria and relative comparison criteria, as illustrated in Figure 4.

• Absolute Value-Based Anomaly Detection: Anomalies are identified by determining whether the measured crack width exceeds the allowable crack width (Wa).
• Potential Anomaly Detection through Relative Comparison: Among data within the allowable width, anomalies are identified if time series analysis reveals recurring abnormal patterns with high anomaly probability.

This classification framework enables the quantitative assessment of risks associated with cracks below the allowable limit and supports the prioritization of resources for intensive monitoring. The definitions for each category are as follows:

• Ao (Anomaly Data): Data that clearly exceed or approach the structural criteria.

  -

  Major Crack: Crack width ≥ 0.50 mm

  -

  Medium Crack: Crack width approaching the allowable width (Wa ≈ 0.50 mm)

• Ap (Potential Anomaly): Data within the allowable limit but repeatedly identified with high anomaly probability through relative comparison.
• Ac (Anomaly Check): Data within the allowable limit that exhibit single-instance or low-level anomalies requiring observation.
• Normal Data: Data within the threshold range without abnormal features.

(2)

Crack Data Structure and Variation Metrics

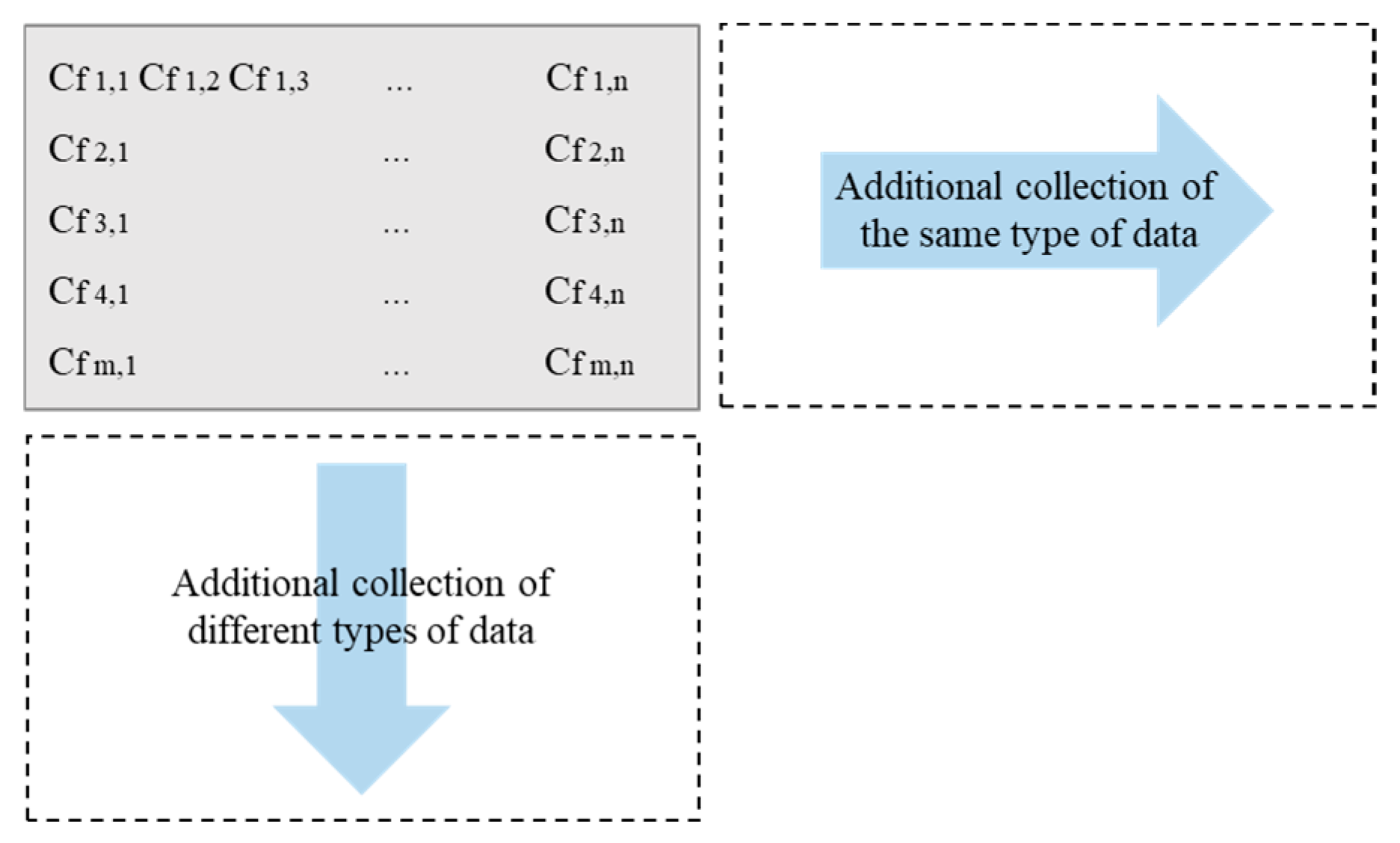
The crack data used in this study were automatically collected at fixed intervals using electronic crack monitoring devices and stored as time series information at the structural unit level. Each dataset is organized in three dimensions: facility ID (f), crack type (i), and observation time (t).

Figure 5 provides an example visualization of repeated observations (t) of multiple crack types (i) in the same facility (f). Data for the same crack type accumulates along the horizontal axis in chronological order, while data for different crack types expand along the vertical axis. This structure serves as a fundamental dataset not only for real-time monitoring but also for periodic analysis and anomaly detection.

To analyze crack progression, the following derived metrics were defined from the raw data and used as key input variables for the Isolation Forest algorithm:

• Δ (Variation): Change in crack width between consecutive time points.
• ΣΔ (Accumulated Variation): Cumulative crack variation over a defined period.

3.1.3. Implementation and Application Strategy

The anomaly detection framework consists of two complementary logics: real-time and periodic analysis (see

Table 8. Detection criteria and feature mapping for real-time and periodic analysis.

Category	Detection Criteria	Description
Real-time monitoring	Crack width	An anomaly is detected when real-time data exceed the allowable crack width (0.20–0.40 mm), as defined by KDS 14 20 30.
	Variation amplitude	If the difference from the previous value exceeds ±0.10 mm, the data are considered highly anomalous. The variation is evaluated by relative comparison.
	Accumulated variation	When the cumulative variation continuously exceeds the allowable crack width (0.20–0.40 mm), the data are classified as highly anomalous. This reflects the progressive state of crack growth.
Periodic monitoring	Isolation Forest	Detects relatively anomalous data through comparative analysis. The threshold is set to 0.001 to reduce sensitivity. Detections are further assessed for duplication and anomaly patterns.
	Risk trend analysis	Evaluates risk trend (increase, mitigation, fluctuation, stable) based on detected anomalies, enabling proactive response through periodic assessment.

).

• Real-Time Analysis Logic: Crack width data collected from sensors are classified as anomalies (Ao) when they exceed the allowable threshold (Wa, e.g., 0.20–0.40 mm), when an abrupt fluctuation of ±0.10 mm or more occurs compared to the previous value, or when the accumulated variation surpasses the allowable threshold. In such cases, an immediate warning is triggered (see Figure 6).
• Periodic Analysis Logic: For cumulative data excluded from real-time analysis, the Isolation Forest algorithm is applied to perform anomaly detection based on relative distinctiveness. Detected data are further classified as Ap or Ac depending on redundancy checks, and time series-based risk trend analysis is then conducted to quantitatively evaluate risk levels (escalation, mitigation, fluctuation, stable).

3.2. Data Preprocessing

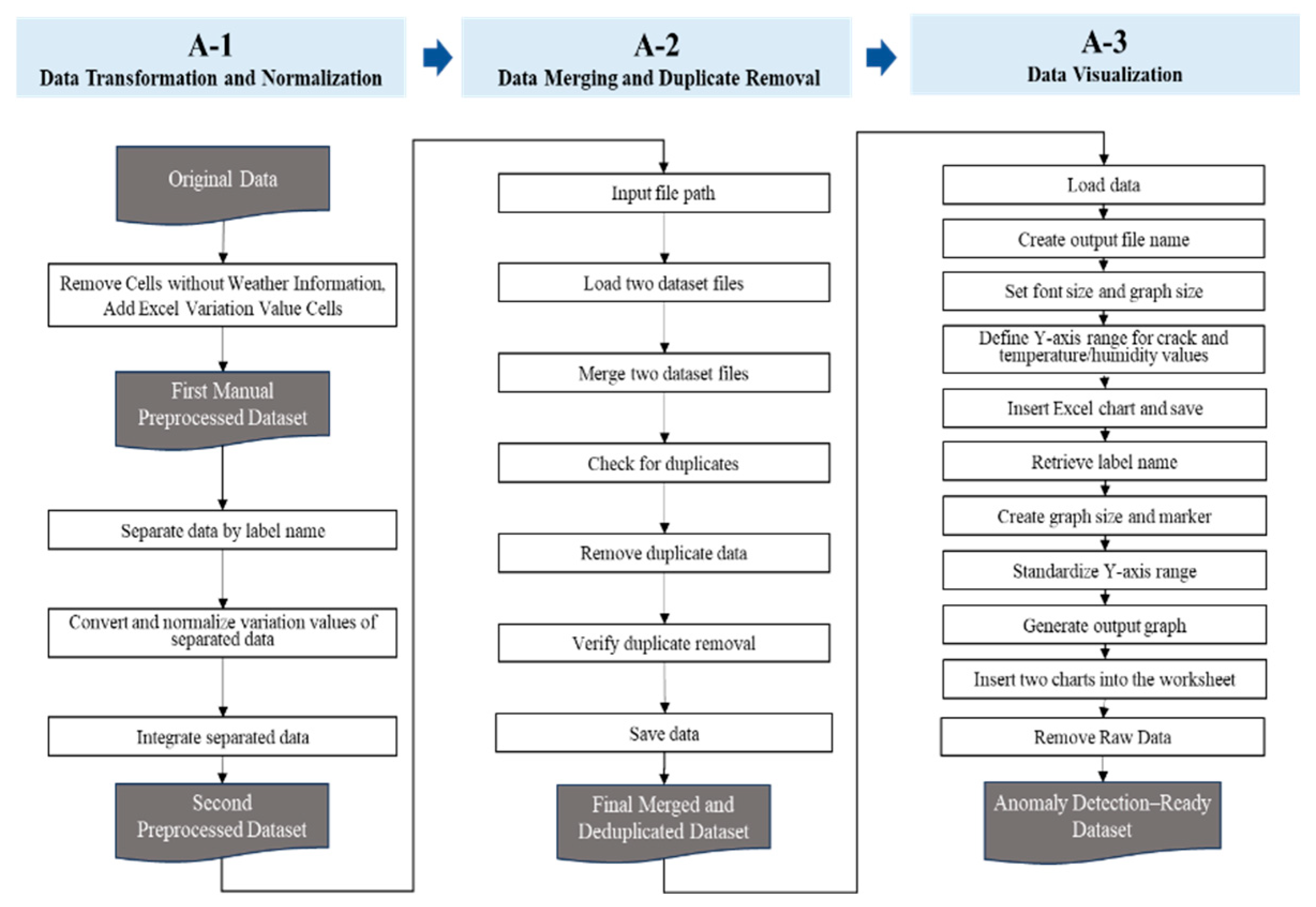
In this study, prior to applying the Isolation Forest anomaly detection algorithm, a data preprocessing procedure was conducted to transform the raw crack data into an analysis-ready format and to ensure its quality. The procedure consisted of three stages: Data Transformation and Normalization (A-1), Data Merging and Duplicate Removal (A-2), and Data Visualization (A-3).

First, in the Data Transformation and Normalization (A-1) stage, the raw data were grouped by measurement label (label name), and difference values were calculated for crack variations as well as for environmental variables (temperature and humidity). A Robust Scaler normalization method was then applied to minimize the influence of outliers and to adjust for scale differences among variables. The normalized data were subsequently reintegrated, resulting in the second preprocessed dataset.

Second, in the Data Merging and Duplicate Removal (A-2) stage, datasets collected from different sources were merged, and duplicate entries were identified and removed. This process yielded a final integrated dataset with reduced missing values and redundancy.

Third, in the Data Visualization (A-3) stage, time series graphs of crack and environmental variables were generated with standardized Y-axis ranges based on the preprocessed dataset. Two charts were inserted into each worksheet to enable intuitive validation of data variability. This visualization step allowed researchers to confirm whether preprocessing was properly executed and whether the dataset was fully prepared for anomaly detection.

Figure 7 illustrates the entire preprocessing workflow, showing the sequential steps from raw data to the anomaly detection-ready dataset. This process enhances the reliability and reproducibility of the proposed framework.

(1)

Data Transformation and Normalization

Because the performance of Isolation Forest depends on the input features, the raw crack data $C_{fi,t}$ were reorganized and three variation metrics across different temporal scales were defined as the main analytical variables. These metrics capture different aspects of crack progression and enhance the accuracy of anomaly detection. These three metrics were normalized to correct for scale differences and then combined into a three-dimensional feature vector, which served as the input to the Isolation Forest model. By simultaneously incorporating variation trends across different temporal contexts, this representation enhanced the model’s ability to detect potential anomalies with greater sensitivity and interpretive precision.

(2)

Long-Term Variation (Crack Variation Compared to Initial Value, ${\mathit{C}}_{\mathit{f}\mathit{i},\mathit{t}}$): Represents the change in crack width relative to the initial measurement, reflecting the long-term progression of structural cracks.

• Instantaneous Variation (Crack Variation Compared to Previous Value, $\mathsf{\Delta }{\mathit{C}}_{\mathit{f}\mathit{i},\mathit{t}}$): Represents the change relative to the immediately preceding observation, capturing sudden variations caused by load or environmental effects.

  $$\mathsf{\Delta }{C}_{fi,t}=C_{fi,t}-C_{fi,t-1},(C_{fi,t-1}:\mathrm{previous}\mathrm{observation}\mathrm{value}),$$

  (1)
• Short-Term Variation (Daily Cumulative Crack Variation, $\sum ∆{\mathit{C}}_{\mathit{f}\mathit{i},\mathit{t}}$): Represents the cumulative variation within a day, capturing short-term fluctuation patterns and subtle accumulations that may indicate crack growth.

  $${\sum }_{t=a}^b∆C_{fi,t}(\mathrm{a}\sim \mathrm{b}=\mathrm{daily}\mathrm{interval})$$

To correct scale differences among variables, Robust Scaler was applied for normalization. This method uses the median and interquartile range (IQR) instead of mean and standard deviation, reducing sensitivity to outliers while improving model stability and efficiency.

(3)

Data Merging and Duplicate Removal

Preprocessed files were consolidated, and duplicate records were eliminated to build the final dataset for analysis. This procedure followed general data processing practices rather than specialized algorithms.

(4)

Data Visualization

To verify preprocessing quality and detect potential conversion errors, a visualization step was carried out. Signals collected by the electronic crack gauge were digitized through analog-to-digital conversion (ADC), as described in Equation (2). The corresponding crack length was then calculated using Equation (3).

$$ADCvalue=\left({\displaystyle \frac{V_0}{V_r}}\right)\ast \left(2^n-1\right),$$

(2)

$$CrackLength={\displaystyle \frac{ADCvalue\ast 25}{1023}},$$

(3)

where $V_0=\left({\displaystyle \frac{measuredlength}{25mm}}\right)\times V_r$($V_r=3.3V,\mathrm{and}n=10$).

In some cases, abnormal values were produced during the conversion process. Therefore, data points with instantaneous variations exceeding ±1 mm, or with variation values outside the range of −0.62 mm to 0.53 mm, were treated as errors and removed. This visualization process allowed intuitive identification of abnormal data and provided the basis for excluding unsuitable records from model training.

3.3. Anomaly Detection

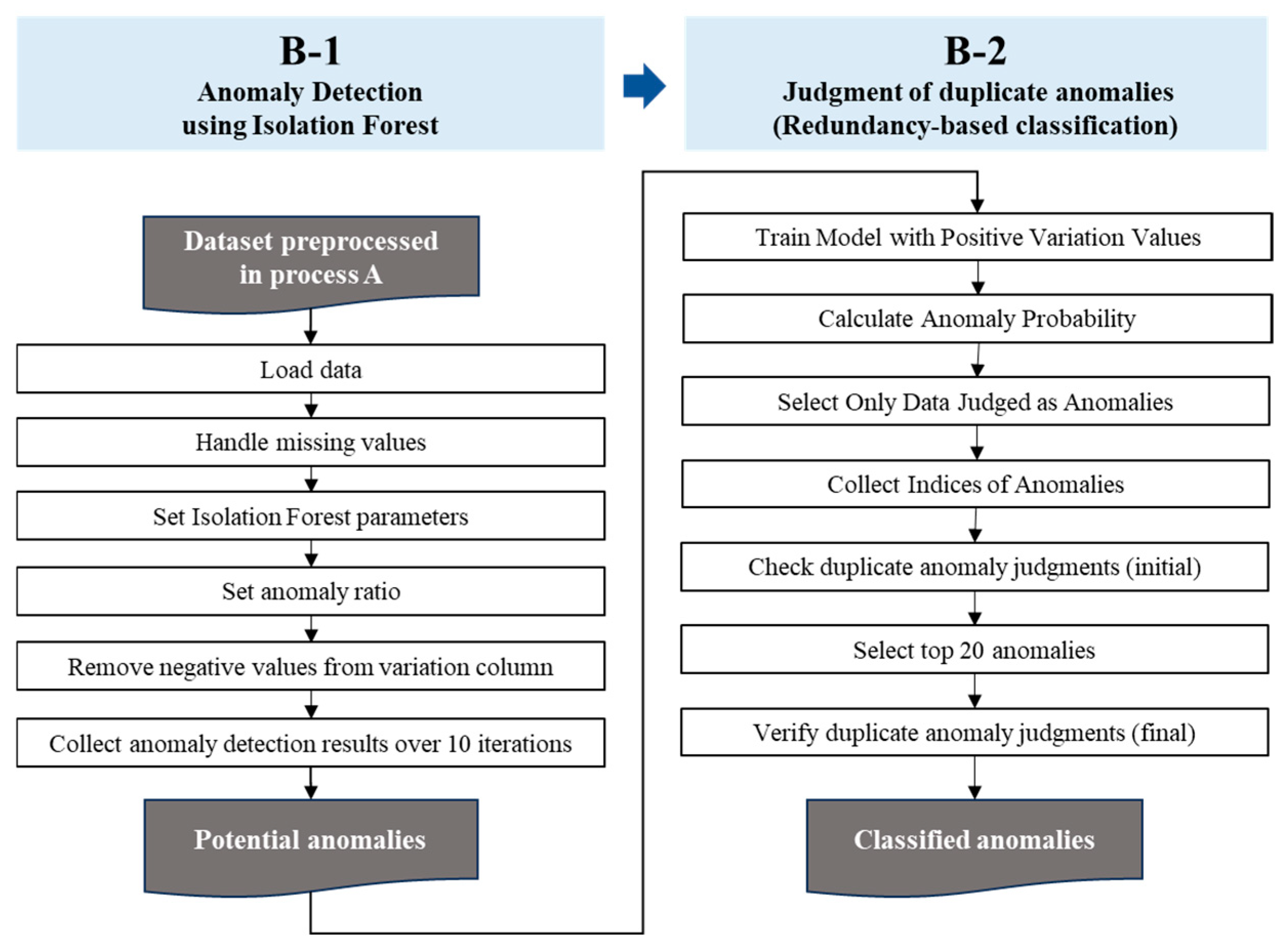
The anomaly detection and classification process proposed in this study consists of two stages. First, potential anomalies are detected from time series crack data using the Isolation Forest algorithm. Second, the redundancy of detection results is verified to classify anomalies based on reliability. Figure 8 presents the code implementation process of the proposed anomaly detection framework.

(1)

Potential Anomaly Detection using Isolation Forest

This study applies the Isolation Forest algorithm to time series crack data to identify potential anomalies. Isolation Forest is well-suited for high-dimensional multivariate data, with its sensitivity influenced by the choice of input variables. In this study, the main variables are indicators that reflect crack variability across different time scales: Long-Term Variation, Instantaneous Variation, and Short-Term Accumulated Variation.

The detection process follows a dual procedure of big data-based detection and new data-based detection. First, historical crack datasets are analyzed to identify records with high relative variability, establishing a reference distribution of anomalies across the data base. Subsequently, the same algorithm is applied to newly collected data, where anomalies are detected through internal relative comparisons. This two-step process provides both a stable benchmark for evaluation and the basis for redundancy verification in the classification stage. The big data-based detection and new data-based detection in this study serve distinct but complementary purposes within the same analytical framework. Big data-based detection involves training the model on approximately 470,000 real-world crack measurements to establish a reference baseline and evaluate anomaly detection performance over long-term trends. In contrast, new data-based detection applies the same algorithm to newly incoming data to assess how reliably the model can detect potential anomalies under controlled conditions. Although both approaches rely on the Isolation Forest algorithm, their datasets and objectives differ: the big data establish the baseline, while the new data validate the model’s generalizability and robustness.

(2)

Redundancy-Based Classification of Detected Anomalies

The results of the Isolation Forest are generated independently from big data-based detection and new data-based detection. These results are then compared to determine redundancy. If the same data point is consistently identified as an anomaly in both analyses, it is classified as Ap (Potential Anomaly), representing high potential risk and requiring prioritized monitoring. Conversely, if an anomaly is detected in only one analysis or shows low distinctiveness, it is classified as Ac (Anomaly Check), which denotes lower priority but still warrants continued observation.

This redundancy-based classification enhances the reliability and accuracy of anomaly detection results and supports the establishment of priority-based inspection strategies in structural maintenance.

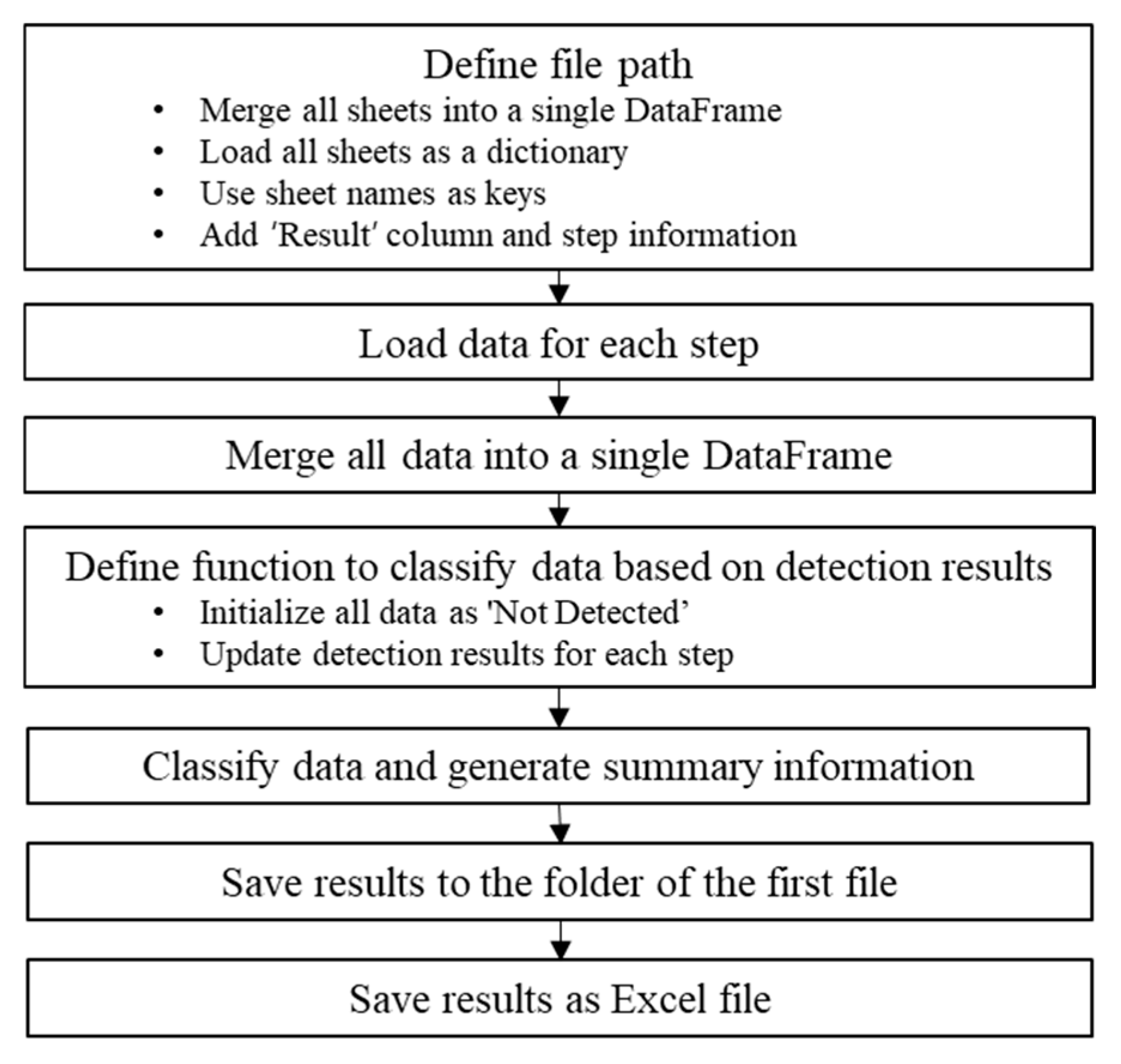
3.4. Analysis of Detected Anomalies

To evaluate the long-term risk of structural cracks, this study conducted a cumulative comparison of anomaly detection results based on periodic analysis. Periodic analyses were performed repeatedly according to a user-defined cycle, and for case validation, anomalies were detected at three intervals with a one-month gap. Figure 9 summarizes the code implementation workflow of this periodic analysis.

The detection results were constructed from anomaly classifications at the first, second, and third cycles. Each cycle produced three categories of outcomes: data with high anomaly probability (Ap), data requiring observation (Ac), and undetected data. As shown in

Table 9. Risk level classification based on anomaly detection categories.

Data Category	Risk Level	Description
High anomaly probability (Ap)	3	Detected as anomalies in both new-data and big-data combined analyses, consistently showing high relative distinctiveness.
Observation required (Ac)	2	Detected as an anomaly in new-data analysis but not in the big-data combined analysis, indicating the need for continued observation.
Not detected (X)	1	Not detected as an anomaly in either analysis, considered normal with low anomaly probability.

, Ap refers to data identified as anomalies in both big data-based and new data-based detection, Ac denotes anomalies detected only in new data, and undetected data are those not identified as anomalies in either analysis. Risk levels were assigned to each category: Ap corresponds to risk level 3, Ac to risk level 2, and undetected data to risk level 1.

Based on this classification, risk trend transitions were derived and visualized in Figure 10. Risk trends were divided into four categories: Mitigation, Escalation, Fluctuation, and Stable, each with further subtypes. Mitigation includes rapid mitigation, mitigation, and mitigation maintained; escalation includes rapid escalation, escalation, and escalation maintained; fluctuation is subdivided into rapid fluctuation and minor fluctuation depending on the degree of change; and stable is further classified into observation maintained or normal maintained depending on the data type (see

Table 10. Classification and interpretation of risk trends.

Category	Sub-Type	Interpretation
Mitigation	Rapid mitigation	Initially classified as risky, but stabilized quickly thereafter.
	Mitigation	Crack risk gradually decreases. Regular monitoring required.
	Sustained mitigation	Low-risk condition continues. Intensive observation can be terminated.
Escalation	Rapid escalation	Transitions abruptly from normal/observation to a risky state. Immediate action required.
	Escalation	Crack risk gradually increases. Regular inspections needed.
	Sustained escalation	High risk persists. Long-term repair planning necessary.
Fluctuation	Rapid fluctuation	Risk fluctuates sharply, indicating instability. Cause analysis required.
	Minor fluctuation	Small-scale variations occur. Continuous monitoring necessary.
Stable	Observation sustained	Observation-required data (Ac) recurs, indicating mid-level risk remains unchanged.
	Normal sustained	Non-detected data (X) recurs, indicating stable normal condition.

). This risk trend analysis quantitatively evaluates the evolution of anomalies, thereby improving diagnostic reliability for crack progression and supporting the establishment of priority-based maintenance strategies.

By combining classification results across the first, second, and third cycles, a total of 27 possible cases were generated. Each combination was mapped to one of the risk trends (Mitigation, Escalation, Fluctuation, Stable), enabling a systematic interpretation of periodic anomaly detection outcomes (see

Table 11. Possible combinations of anomaly detection results across three periodic cycles.

1st Status	2nd Status	3rd Status	Risk Trend and Interpretation
Ap	Ap	Ap	Sustained Escalation: Risk level remains consistently high.
		Ac	Mitigation: Risk gradually decreases.
		Not detected	Rapid Mitigation: Risk rapidly decreases.
	Ac	Ap	Rapid Fluctuation: Risk fluctuates significantly across cycles.
		Ac	Sustained Mitigation: Mitigated state is consistently maintained.
		Not detected	Mitigation: Risk gradually decreases.
	Not detected	Ap	Rapid Fluctuation: Risk fluctuates sharply.
		Ac	Minor Fluctuation: Small-scale variations occur.
		Not detected	Sustained Mitigation: Normalization trend is consistently maintained.
Ac	Ap	Ap	Rapid Escalation: Risk level rises sharply.
		Ac	Minor Fluctuation: Temporary variation in risk observed.
		Not detected	Rapid Fluctuation: Rapid changes in risk level.
	Ac	Ap	Escalation: Risk gradually increases.
		Ac	Observation Sustained: Medium-level risk consistently maintained.
		Not detected	Mitigation: Risk gradually decreases.
	Not detected	Ap	Rapid Fluctuation: Risk fluctuates sharply.
		Ac	Minor Fluctuation: Small-scale variations occur.
		Not detected	Sustained Mitigation: Risk mitigation trend consistently maintained.
Not Detected	Ap	Ap	Rapid Escalation: Risk sharply increases.
		Ac	Minor Fluctuation: Limited variation in risk observed.
		Not detected	Rapid Fluctuation: Significant sudden changes in risk level.
	Ac	Ap	Escalation: Risk gradually increases.
		Ac	Observation Sustained: Observation-required state consistently maintained
		Not detected	Minor Fluctuation: Small-scale variation in risk level.
	Not detected	Ap	Rapid Escalation: Risk rapidly increases.
		Ac	Escalation: Risk gradually increases.
		Not detected	Normal Sustained: Normal state consistently maintained.

).

4. Case Study

4.1. Overview

To evaluate the anomaly detection performance of the proposed big data-based crack variation analysis model, a simulation-based validation scenario was designed. Validation was conducted by comparing the overlap between anomalies detected from new data alone and those identified through big data-based analysis. The datasets used are summarized in

Table 12. Datasets used for model validation.

Category	Description	Data Size	Collection Period
New Data	Simulated dataset with an increase–hold–increase trend	2720	1 April–23 July 2023
Big Data	Field-collected dataset from actual construction sites	470,000	13 April 2023–14 June 2024

. In this study, synthetic crack data exhibiting an increase–hold–increase pattern were generated to simulate potential risk scenarios. The intention was not to prescribe fixed ground truth labels or thresholds, but rather to evaluate whether the model could correctly detect the timing and progression of anomalies with high anomaly probabilities. Because the definition of “true” anomalies is strongly dependent on threshold criteria, we deliberately created visually distinguishable data to facilitate intuitive comparison between the simulated patterns and the model’s detection results. This approach enabled straightforward validation of whether the framework can recognize anomaly-like behaviors, while future studies will focus on applying the method to real-world crack monitoring data.

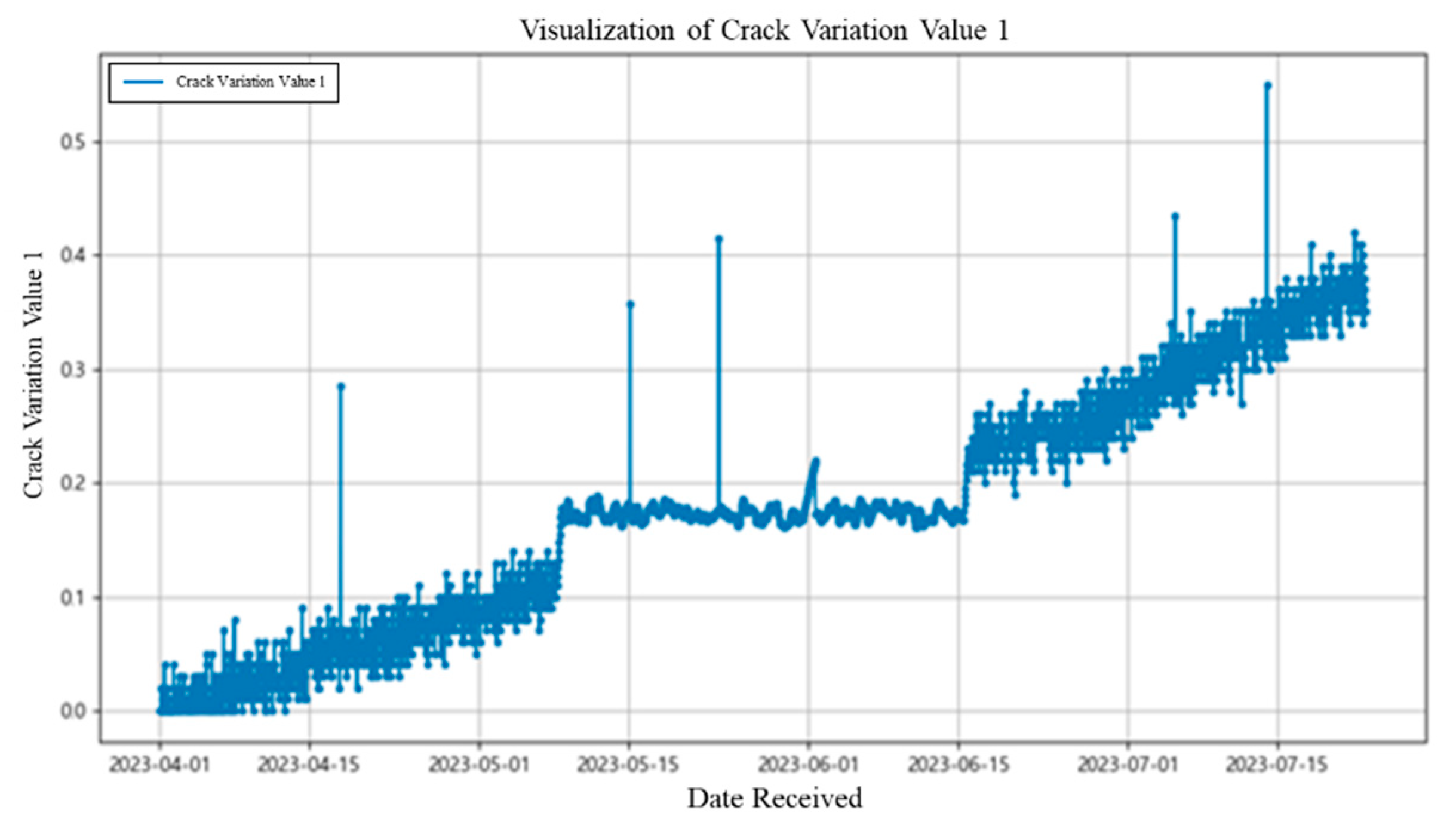
The new dataset consisted of 2720 synthetic records collected at one-hour intervals from 1 April to 23 July 2023, designed to follow an increase–hold–increase pattern (Figure 11). This scenario reflects diverse time series variations—including long-term, short-term, and instantaneous changes—and simulates the processes of initial deformation → temporary stabilization → risk accumulation and potential sudden escalation. Its purpose was to assess whether the anomaly detection model could identify abnormal patterns beyond absolute threshold exceedance. Furthermore, periodic analysis was employed to quantify the timing and magnitude of risk evolution, thereby validating both the real-time and cumulative evaluation capabilities of the proposed model.

The big data used for validation were collected with an electronic crack monitoring device. The device is attached to crack surfaces and measures crack width precisely by detecting changes in electrical resistance (see Figure 12). This method overcomes the subjectivity of visual inspection and the physical limitations of manual access, enabling continuous and automated collection of quantitative data.

The real dataset comprised approximately 470,000 records collected from 64 cracks across 12 sites in Seoul. Each record included crack location, width, timestamp, and environmental parameters (e.g., temperature, humidity). The detailed structure of the dataset is provided in Appendix A.

For anomaly detection, the Isolation Forest algorithm was applied with the contamination parameter set to 0.001, reflecting the rarity of anomalies in structural crack data and ensuring higher detection sensitivity. The number of trees was maintained at the default of 100. For the dataset of ~470,000 records, preprocessing required approximately 5 min, and anomaly detection required about 10 min.

4.2. Model Validation

4.2.1. Data Preprocessing

The proposed model’s periodic anomaly detection process consists of three steps: data preprocessing → anomaly detection → risk analysis.

The collected crack data were first standardized through preprocessing, during which three variation metrics were derived: long-term variation (relative to the initial value), instantaneous variation (relative to the previous value), and short-term variation (daily cumulative change).

Table 13. Raw data after manual preprocessing.

No	Site	ID	Received Date	Long-Term Variation	Instantaneous Variation	Short-Term Variation	Temperature	Humidity
437	Yongsan Site	21F-12C-1	22 June 2023 16:59:35	−0.01			27.2	67
437	Yongsan Site	21F-12C-1	22 June 2023 17:59:45	0			25.7	74
437	Yongsan Site	21F-12C-1	22 June 2023 18:59:37	−0.01			24.2	82
437	Yongsan Site	21F-12C-1	22 June 2023 19:59:38	−0.01			24	85
437	Yongsan Site	21F-12C-1	22 June 2023 20:59:43	0			22.5	91
437	Yongsan Site	21F-12C-1	22 June 2023 21:59:39	−0.01			22.5	95

presents an example of raw data after the first stage of manual preprocessing. In this stage, records with missing meteorological data were removed, and additional fields (e.g., temperature/humidity differences, variation values) were created for subsequent analysis.

The data were then transformed and normalized to produce an input format suitable for anomaly detection, as shown in

Table 14. Data after transformation and normalization.

No	Site	ID	Received Date	Long-Term Variation	Instantaneous Variation	Short-Term Variation	Temperature	Humidity
437	Yongsan Site	21F-12C-1	22 June 2023 16:59:35	−0.01	0	0	27.2	67
437	Yongsan Site	21F-12C-1	22 June 2023 17:59:45	0	0.01	0	25.7	74
437	Yongsan Site	21F-12C-1	22 June 2023 18:59:37	−0.01	−0.01	0	24.2	82
437	Yongsan Site	21F-12C-1	22 June 2023 19:59:38	−0.01	0	0	24	85
437	Yongsan Site	21F-12C-1	22 June 2023 20:59:43	0	0.01	0	22.5	91
437	Yongsan Site	21F-12C-1	22 June 2023 21:59:39	−0.01	−0.01	0	22.5	95

. For normalization, a Robust Scaler was applied, which scales data based on the median and interquartile range. This method is less sensitive to outliers than mean–standard deviation scaling, ensuring stability in the anomaly detection process.

4.2.2. Anomaly Detection

Based on the preprocessed data, the Isolation Forest algorithm was applied to perform anomaly detection across three monitoring cycles. At each cycle, the detected anomalies were recorded with their corresponding anomaly scores, and the results were later compared to evaluate redundancy across cycles. This redundancy formed the basis for subsequent risk trend analysis.

The validation consisted of three periodic detection cycles, with the following key findings:

• 1st detection result (

  Table 15. Potential anomalies detected in the first cycle.

  Site	Received Date	Long-Term Variation	Instantaneous Variation	Short-Term Variation	Weather Data Date	Temperature	Humidity	Anomaly Probability
  D site	18 April 2023 00:00:00	0.284663	0.245	0.01	2023-04-18 00:00:00	21.05	53.67	0.815857

  ): In the first analysis, anomalies with scores above 0.80 were identified. Notably, the data collected on 18 April 2023 exhibited both a large long-term variation (compared to the initial value) and a significant instantaneous variation (compared to the previous value). Although the absolute crack width threshold was not exceeded, this data point showed a distinct abnormal pattern, making it a meaningful detection.
• 2nd detection result (

  Table 16. Potential anomalies detected in the second cycle.

  Site	Received Date	Long-Term Variation	Instantaneous Variation	Short-Term Variation	Weather Data Date	Temperature	Humidity	Anomaly Probability
  D site	18 April 2023 00:00:00	0.285	0.245	0.01	2023-04-18 00:00:00	21.05	53.67	0.8193
  D site	28 June 2023 20:00:00	0.3	0.05	0.03	2023-06-28 20:00:00	23.76	50.88	0.708407

  ): In the second analysis, a new anomaly was detected on 28 June 2023. This record showed a high long-term variation but relatively small instantaneous and short-term variations, resulting in an anomaly score below 0.80. Meanwhile, the 18 April data was repeatedly detected in this cycle, with its anomaly score increasing compared to the first cycle. This persistence demonstrates that the abnormality remained significant despite data accumulation, indicating the need for continued observation.
• 3rd detection result (

  Table 17. Potential anomalies detected in the third cycle.

  Site	Received Date	Long-Term Variation	Instantaneous Variation	Short-Term Variation	Weather Data Date	Temperature	Humidity	Anomaly Probability
  D site	05 July 2023 10:00:00	0.434964	0.155	0.04	2023-07-05 10:00:00	23.65	50.35	0.771721
  D site	18 April 2023 00:00:00	0.284663	0.245	0.01	2023-04-18 00:00:00	21.05	53.67	0.762079
  D site	22 July 2023 07:00:00	0.42	0.07	0.02	2023-07-22 07:00:00	23.71	50.61	0.694886

  ): In the third analysis, the 18 April anomaly was once again detected, alongside two new anomalies identified on 5 July and 22 July 2023. Among these, the 5 July data showed the highest anomaly score across all cycles, with both long-term and instantaneous variations substantially larger than other records. This case was therefore assessed as more critical than the previously recurring April 18 anomaly, suggesting the need for prioritized on-site inspection and root-cause investigation.

4.2.3. Analysis of Detected Anomalies

The results of the three periodic detection cycles were integrated to analyze the variation patterns and risk levels of the detected anomalies. As summarized in

Table 18. Summary of detection results across three periodic cycles.

1st Status	2nd Status	3rd Status	Count	Risk Trend
Ac	Ac	Ac	1	Observation Sustained
Not Detected	Ac	Not Detected	1	Minor Fluctuation
Not Detected	Not Detected	Ac	2	Escalation

, one anomaly was repeatedly detected across all three cycles, one anomaly was detected in the first two cycles only, and two anomalies were newly identified in the third cycle.

Based on these detection patterns, the risk trends were categorized into three types: Stable, Fluctuation, and Escalation. An anomaly detected consistently in all three cycles was interpreted as Stable, indicating a persistent abnormal condition in the corresponding crack segment. An anomaly detected only in the first two cycles but absent in the third was classified as a case of Minor Fluctuation, suggesting that the abnormal pattern had subsided over time. In contrast, anomalies that newly appeared in the third cycle were interpreted as Escalation, indicating a worsening crack condition in those segments.

This risk trend analysis provides a quantitative interpretation of temporal changes in crack behavior and serves as a useful tool for prioritizing inspection and maintenance strategies in structural health management.

4.3. Results and Discussion

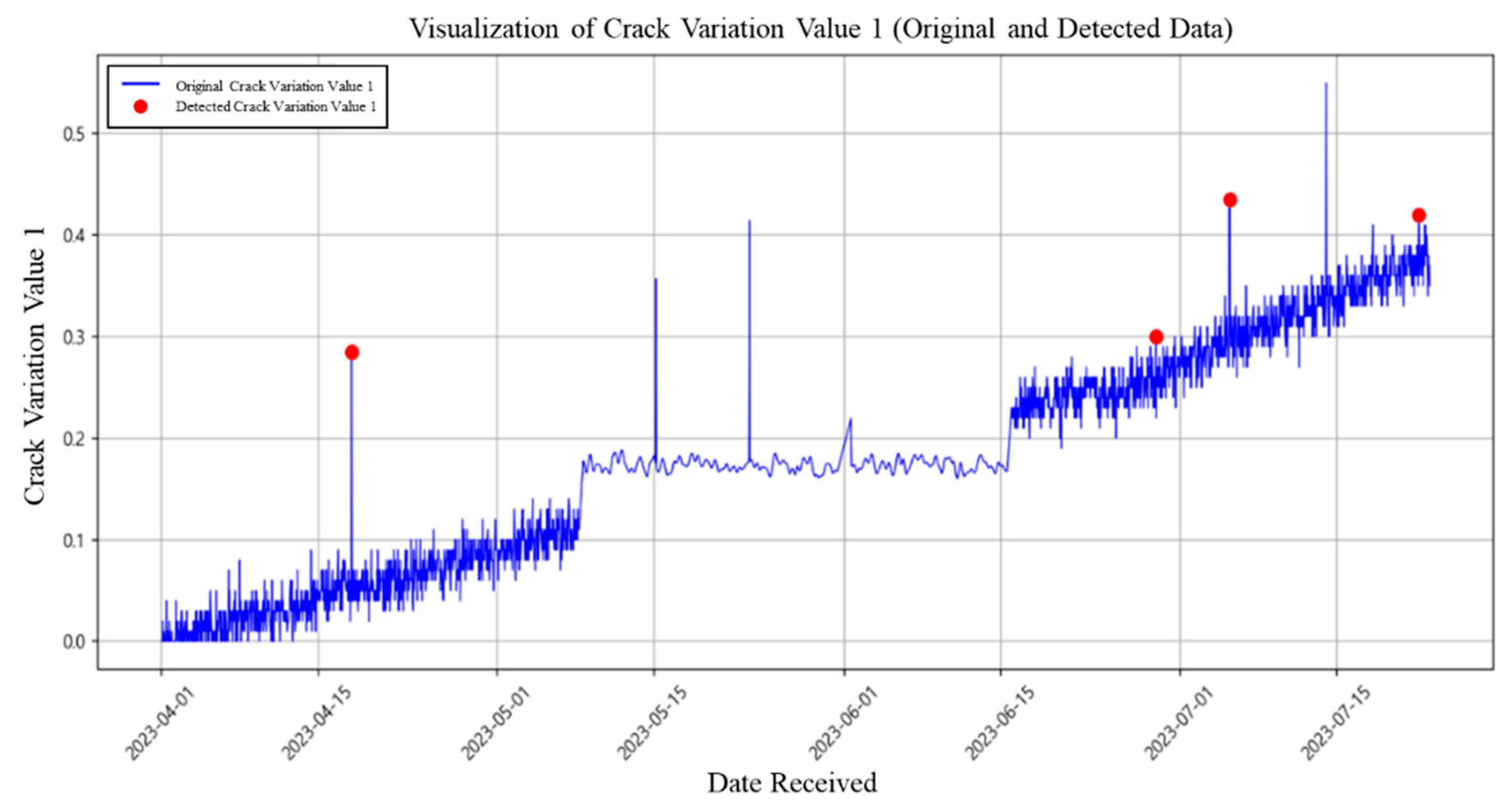
In this study, a total of four data points with high anomaly probabilities were detected. The analysis did not emphasize the absolute number of anomalies, but rather the alignment between the detection timing and the observed crack progression. To enhance interpretability, the detection threshold was intentionally set high, thereby extracting only data points with strong anomaly characteristics. This design allowed the evaluation to focus on whether the framework could effectively identify meaningful changes in crack behavior, rather than on the sheer quantity of anomalies detected.

Table 19. Interpretation of risk level transitions across anomaly detection cycles.

Risk Trend	Count	Interpretation
Sustained Escalation	1	High risk level persists. Regular data collection and continuous monitoring required.
Minor Fluctuation	1	Temporary change followed by risk reduction. Ongoing monitoring necessary to confirm stability.
Escalation	2	New anomalies emerged, leading to increased risk. Regular inspection and intensive management required.

and Figure 13 summarize the crack conditions and corresponding risk trends identified through periodic analysis. The dataset collected on 18 April 2023, was detected as an anomaly across all three cycles, showing a continuous increase in both long-term and instantaneous variations. This segment was therefore classified as “Stable with sustained escalation”, indicating the need for ongoing data collection and continuous monitoring.

By contrast, the dataset from 28 June 2023 was detected as an anomaly during the second cycle but not in the third. This indicates a reduced level of risk and was classified as “Mitigation with long-term observation”, suggesting that while the immediate risk has decreased, periodic monitoring remains necessary.

The datasets from 5 July and 22 July 2023, were newly identified as anomalies in the third cycle. Among these, the 5 July dataset recorded the highest anomaly score across all detections, with both long-term and instantaneous variations significantly exceeding those of other entries. These cases were classified as “Escalation”, signifying priority targets for additional inspection and management.

Overall, four anomalous crack datasets were detected, primarily influenced by long-term and instantaneous variation values. However, despite the overall increase–hold–increase trend embedded in the simulated data, abrupt anomalies within the hold phase were not detected. This outcome highlights a limitation of the Isolation Forest algorithm: as it relies on relative distributional characteristics, it may overlook subtle abnormal changes during stable intervals.

These results confirm that the proposed approach is effective for early anomaly detection during crack escalation phases, but also underscore the need to improve sensitivity during stable phases. To address this, further studies should consider optimizing algorithm parameters (e.g., contamination levels) and validating them with experimental datasets that reflect diverse distributional properties.

4.4. Limitations and Robustness Analysis

The current experiment was based on a synthetic data scenario, which imposes constraints on real-world applicability. Since cracks in actual structures often progress gradually before reaching a critical state, future research should incorporate long-term field data to enhance model validation and practical relevance. With more realistic datasets, the model could achieve more robust trend analysis and anomaly interpretation.

In addition, the robustness of the proposed framework is closely tied to the quality of data preprocessing. Since anomaly detection results can be significantly affected by noise, missing values, or duplicated entries, systematic preprocessing—such as normalization, duplicate removal, and visualization—becomes essential for ensuring reliable outcomes. In this study, preprocessing was performed under the assumption of complete and error-free data; however, in real-world applications, device-induced errors or missing data are unavoidable. Recent studies have explicitly demonstrated the critical role of preprocessing in structural health monitoring, such as handling missing monitoring data with advanced recovery models [45] and integrating multi-source monitoring information for robust prediction [46]. Building on these insights, future research should develop and incorporate advanced preprocessing techniques capable of distinguishing true structural anomalies from sensor-related noise, thereby further enhancing the robustness, reproducibility, and practical applicability of the proposed framework.

This study confirmed that the proposed framework can detect potential anomalies in crack progression, even when crack widths remain within allowable limits. By emphasizing trend-based interpretation rather than fixed thresholds, the framework demonstrated its capability for identifying early abnormal variations. Although validation was performed on a single dataset, the framework is model-agnostic and can be extended to other SHM datasets where time series crack variation data are available. Future research should focus on validating the framework with diverse field datasets to further demonstrate its robustness and practical applicability.

Although ground-truth labels were not available in this study, making it infeasible to evaluate false positives and false negatives in the conventional sense, the concept can be reframed in terms of anomaly probability. A false negative may correspond to the model’s failure to detect data points with high anomaly probability, whereas a false positive may involve labeling low-probability data as anomalous. Such errors could create ambiguity in anomaly interpretation and, in practice, may affect maintenance decisions. To reduce this risk, the proposed framework applies three rounds of periodic detection and integrates their outcomes, thereby focusing on consistent trend behavior rather than isolated detections. This redundancy-based strategy lowers the likelihood of both missed detections and false alarms under uncertain conditions. Nevertheless, future research should incorporate labeled datasets with confirmed structural damage events, enabling parameter optimization and a quantitative evaluation of false positives and false negatives in real-world scenarios.

Finally, expanding the framework to account for different crack types and growth patterns, and developing classification-based detection models tailored to these patterns, would enhance both the accuracy and applicability of potential anomaly detection. This study does not aim to define absolute ground-truth labels or fixed thresholds. Instead, the proposed framework focuses on analyzing the trends of detected data based on relative comparisons, providing an interpretable structure for anomaly detection. For example, in the case of the Isolation Forest algorithm, detection outcomes may vary depending on the distribution of the input data and parameter settings. Accordingly, the evaluation did not attempt to determine whether each detected point was definitively correct or incorrect, but rather whether the anomalies consistently reflected meaningful changes in crack progression trends. To enhance interpretability, the detection results were reported alongside quantitative descriptors such as anomaly count, anomaly score, and persistence. These descriptors allowed for relative comparison and provided practical insights into the model’s utility. Future research should aim to incorporate datasets with confirmed structural damage events and labeled ground truth, enabling validation through conventional metrics such as precision, recall, and F1-score.

5. Conclusions

This study proposed a periodic anomaly detection model for structural crack monitoring based on big data analysis, designed to overcome the limitations of conventional absolute threshold-based approaches. Most existing studies have focused on vision-based approaches that achieve high accuracy in detecting visible cracks, yet they remain constrained by their dependence on large-scale labeled data, the lack of validation using long-term monitoring data, and their inability to capture subtle or progressive anomalies below allowable thresholds.

In contrast, the present study does not aim to classify images at a single point in time but instead proposes an anomaly detection framework based on large-scale time series crack data. Specifically, by quantifying long-term, short-term, and instantaneous variations, the framework identifies time points with high anomaly probability, thereby enabling the early recognition of progressive crack growth patterns. Traditional monitoring methods often fail to reflect the temporal progression of crack growth, making it difficult to detect early signs of developing defects. The proposed model combines real-time anomaly detection with periodic analysis to identify both explicit anomalies and potential anomalies based on relative variations and accumulated changes, thereby enabling a more systematic assessment of structural safety.

To validate the model, approximately 2700 simulated data points following an increase–hold–increase pattern and about 470,000 field-collected crack data records were utilized. Using long-term, short-term, and instantaneous variation metrics, the model successfully detected four anomalies, demonstrating its ability to capture both sudden and cumulative risks. The results confirm that the model supports quantitative evaluation of risk trends and extends anomaly detection beyond simple threshold exceedance.

The main contributions of this study can be summarized as follows: First, the model expands analytical efficiency and applicability by utilizing large-scale crack datasets and enhances data utility through relative anomaly detection. Second, variation-based analysis enables the early detection of risks even when crack widths remain below allowable thresholds, thereby supporting preventive crack management. Third, periodic analysis facilitates the quantitative assessment of crack progression and risk levels over time, contributing to improved long-term structural stability and maintenance strategies.

Nevertheless, this study has several limitations and future research directions: First, the analysis interval was fixed at one month, and performance sensitivity to different cycle lengths was not examined. Future work should compare various intervals to establish an optimal cycle for anomaly detection. In addition, further experiments are required to ensure generalizability and statistical stability. The proposed framework could be enhanced by adjusting model parameters and defining thresholds based on real-world crack data exhibiting gradual progression, thereby improving reproducibility. Second, this study was conducted under the assumption that the collected data were input without device-related errors. However, in real-world applications, missing values or noise may occur during the preprocessing stage. Future research should focus on developing preprocessing techniques or pre-filtering models that can distinguish whether abnormal data arise from physical crack progression or from sensor malfunctions. Third, the current model focuses solely on anomaly detection and does not include predictive capabilities. Incorporating deep learning-based forecasting models could allow for the prediction of anomaly progression and risk propagation. Fourth, external environmental factors such as temperature, humidity, and vibration were not analyzed. Future frameworks should integrate multi-sensor environmental data to quantify their effects on crack occurrence and growth. Such integration would further enhance the practical applicability and robustness of the proposed framework in real-world monitoring scenarios. Fifth, anomaly detection in this study was limited to numerical crack data without considering crack shape or visual features. Combining vision-based image analysis could provide a more comprehensive assessment of crack development. Finally, the interpretation and reporting of anomaly detection results were conducted manually. Future work should employ large language models (LLMs) to automate interpretation and reporting, thereby improving accessibility and efficiency. This study confirmed that the proposed framework can detect potential anomalies in crack progression, even when crack widths remain within allowable limits. By emphasizing trend-based interpretation rather than fixed thresholds, the framework demonstrated its capability for identifying early abnormal variations. Although validated on one dataset, the framework is model-agnostic and can be applied to other SHM datasets if time series crack variation is available. Future research should extend this validation to diverse field datasets to further confirm its robustness and practical applicability.

This study proposed a data-driven framework for detecting potential crack anomalies through periodic time series analysis. The framework goes beyond simple anomaly detection by enabling quantitative assessment of crack progression and risk trends over time, thereby providing meaningful insights into structural condition. In the future, integrating this framework with sensor-based monitoring systems could facilitate real-time decision-making for structural maintenance. Moreover, there is potential to extend this approach to robotic platforms. For example, if detected anomalies are linked to robotic systems capable of conducting targeted inspections or interventions, a fully automated detection–diagnosis–response workflow could be realized. Therefore, the proposed model may serve as a core data analytics component in intelligent structural management systems. When combined with robotics, it could contribute to the development of more efficient, autonomous, and proactive maintenance solutions for buildings and civil infrastructure.