Investigation on Static Performance of Piers Assembled with Steel Cap Beams and Single Concrete Columns
Abstract
1. Introduction
2. Test Scheme
2.1. Background Project
2.2. Scale Ratios
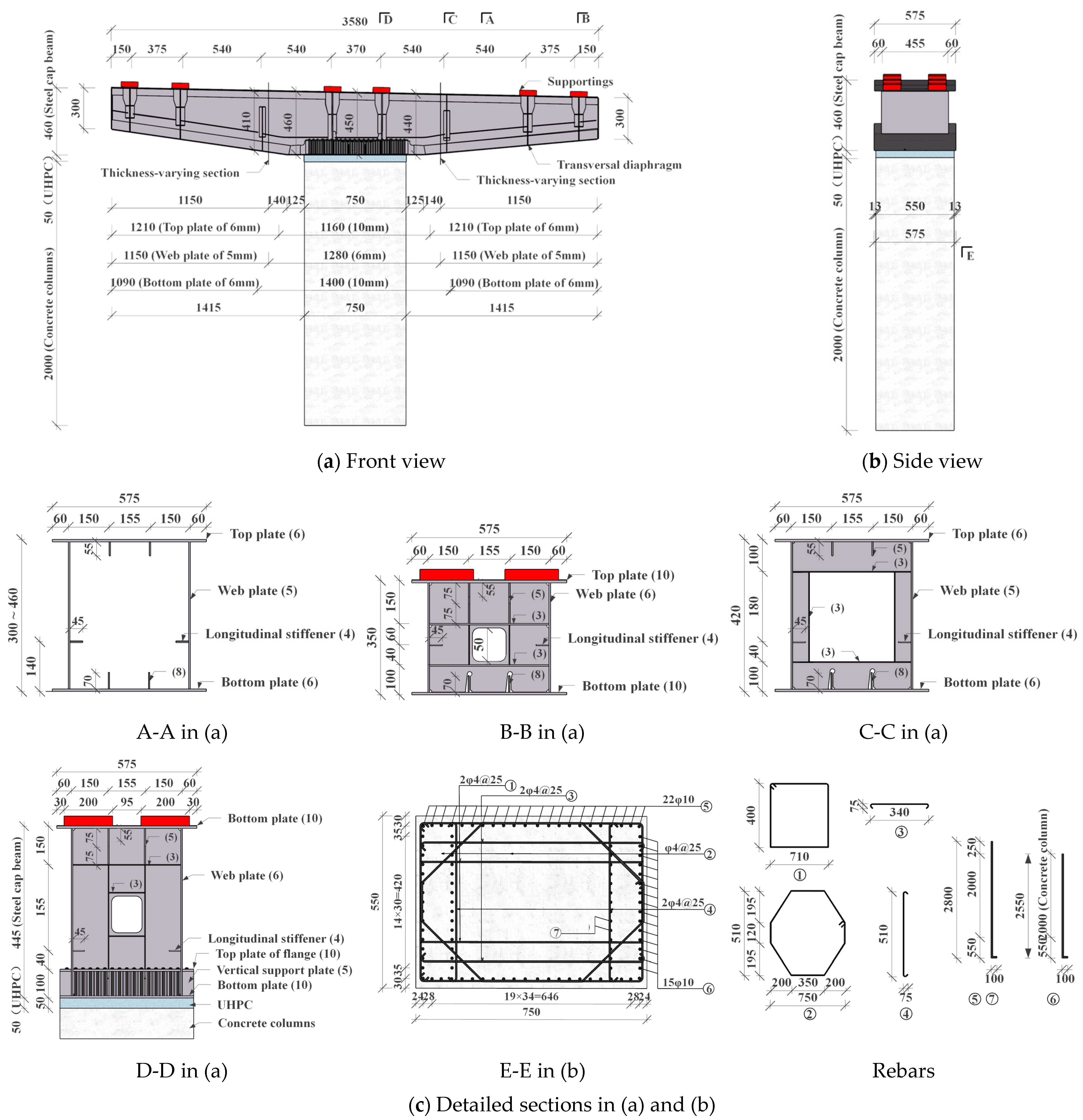
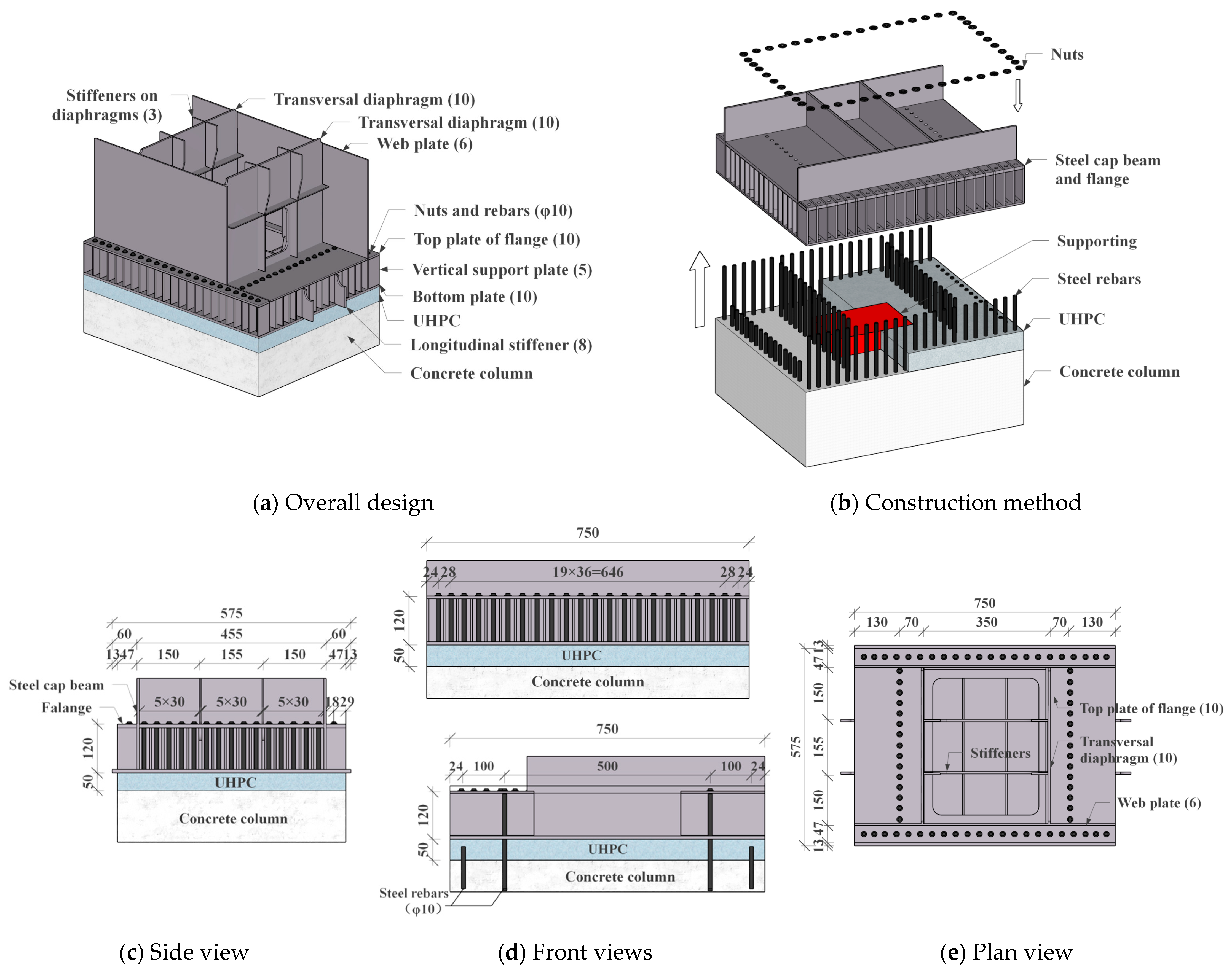
2.3. Specimen Design
- (1)
- Steel cap beam
- (2)
- Reinforced-concrete column
- (3)
- Connection joint
2.4. Specimen Fabrication
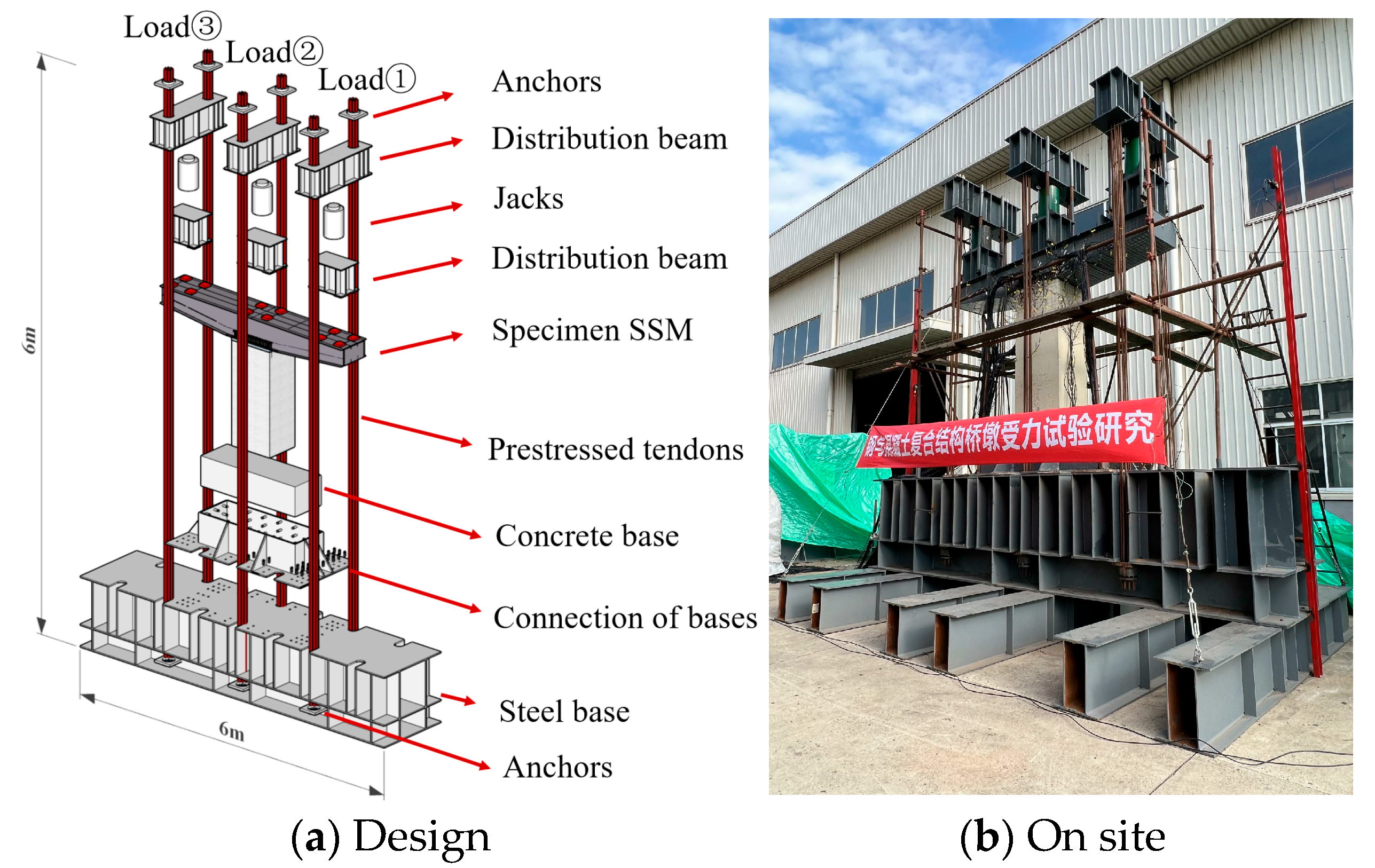
2.5. Test System and Scheme
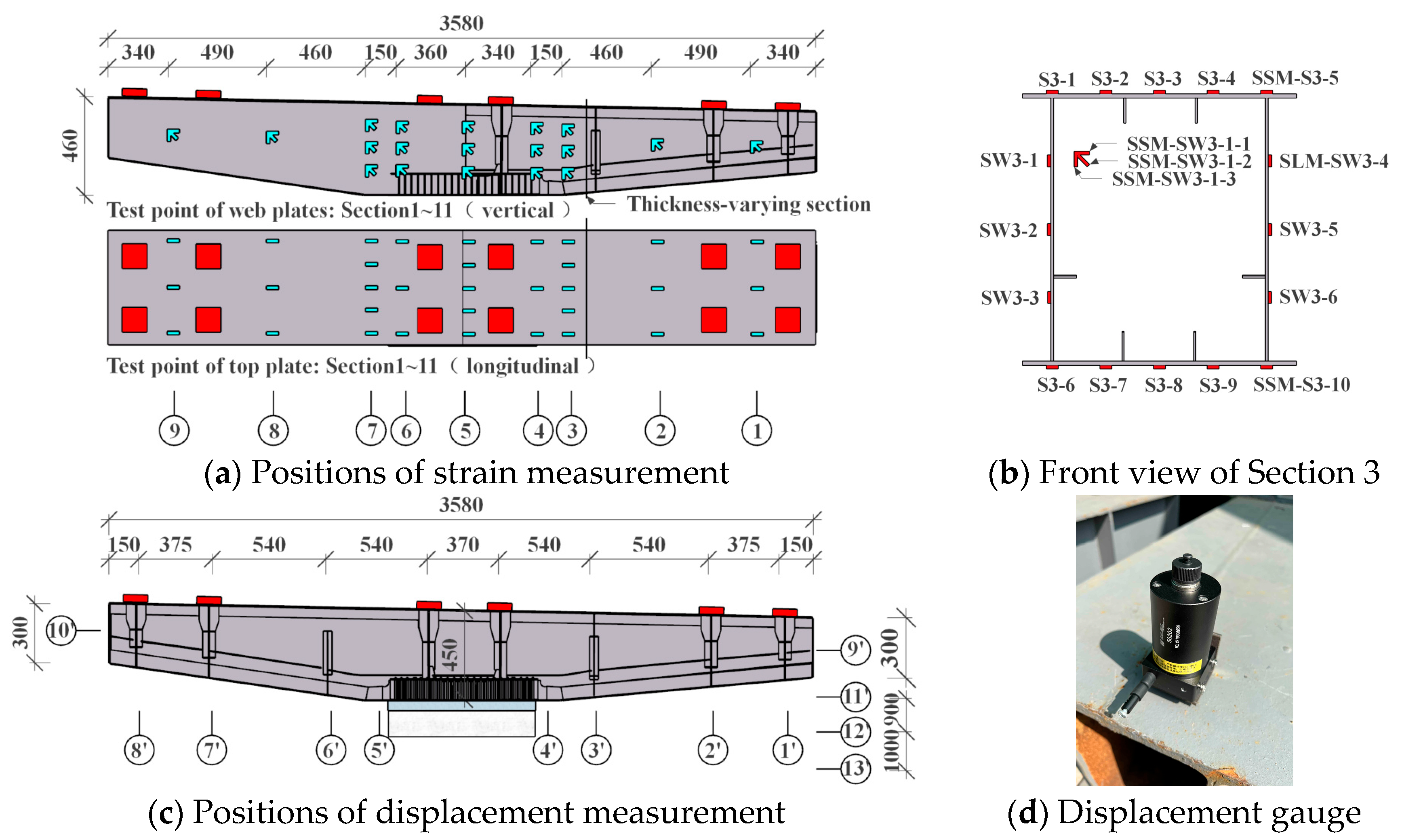
2.6. Measurement Scheme
3. Test Results
3.1. Material Property Testing
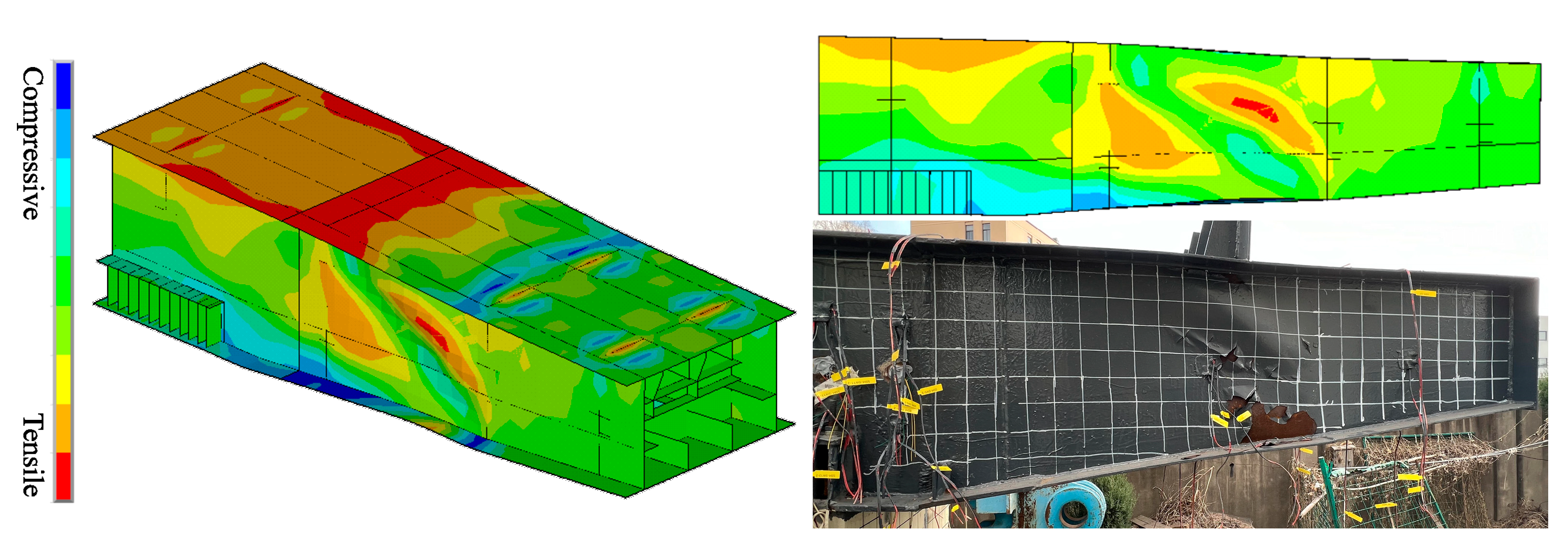
3.2. Experimental Phenomenon and Failure Mode
3.3. Load–Displacement Response
3.4. Load–Strain Response
- (1)
- Steel cap beam
- (2)
- Connection joint
- (3)
- Reinforced-concrete column
4. Numerical Study
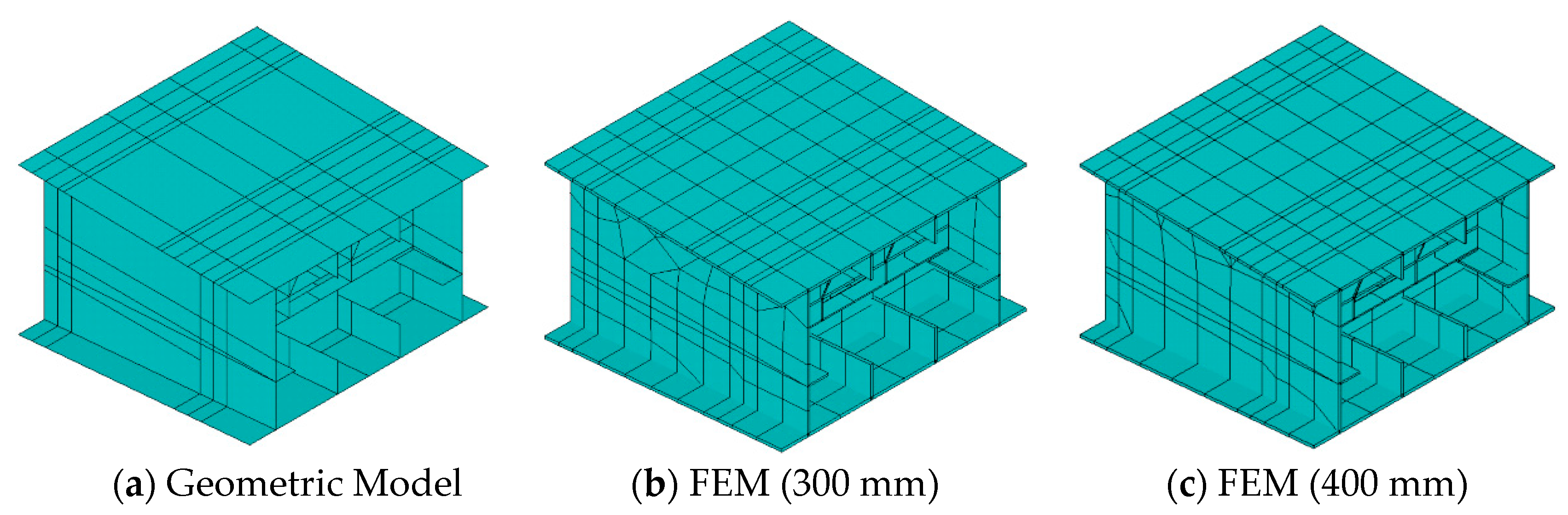
4.1. Finite Element Model
4.2. Comparison Between Experiment and Finite Element Analysis
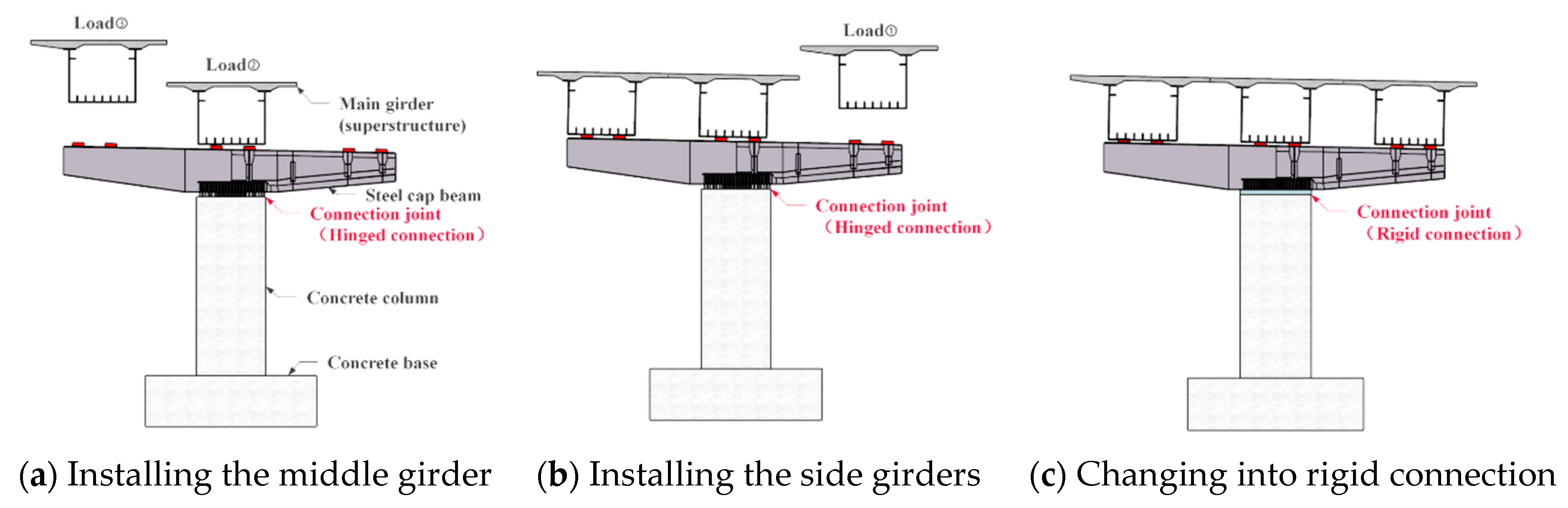
4.3. The Hinged-to-Rigid Construction Method
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Li, W.S.; Liu, Z. Experimental investigation and fragility analysis on seismic performance of precast UHPC hollow piers under varying axial load. Soil Dyn. Earthq. Eng. 2025, 196, 109420. [Google Scholar] [CrossRef]
- Xie, W.; Zhang, B.J.; Yu, L.T.; Su, Q.; Matanmi, F.O. Flexural Performance of an Innovative Girder-to-Pier Joint for Composite Bridges with Integral Piers: Full-Scale Test. Materials 2025, 18, 1157. [Google Scholar] [CrossRef]
- Wang, S.Z.; Su, Q.T.; Jiang, X.; Michels, J.; Ghafoori, E. Fully bonded iron-based shape memory alloy for retrofitting large-scale bridge girders: Thermal and mechanical behavior. Structures 2024, 65, 106710. [Google Scholar] [CrossRef]
- Ge, J.P.; Mei, D.L.; Yan, X.F.; Wang, Z.Q. Comparison and analysis of construction method of precast pier cap. J. Technol. 2018, 18, 56–62. [Google Scholar] [CrossRef]
- Shao, X.D.; Zeng, H.Q.; Cao, J.H. Flexural behavior of fully prefabricated large-cantilevered high strength steel-UHPC composite bent caps. J. Constr. Steel Res. 2023, 204, 107856. [Google Scholar] [CrossRef]
- Hu, H.; Wang, J.W.; Yan, X.F.; Ge, J.; Zhang, D. Experimental research and numerical analysis on mechanical behavior of lightweight-design precast bent caps with large cantilevers. Structures 2022, 40, 536–554. [Google Scholar] [CrossRef]
- Hu, F.J.; Yang, C.H.; Zhou, P.M.; Hu, H.; Wang, Y.C. Experimental study on mechanical behavior of precast large-cantilevered UHPC bent caps with π-shaped cross-sections. Structures 2024, 62, 106333. [Google Scholar] [CrossRef]
- McKee, C.D.; Lee, J.D.; Birely, A.C.; Mander, J.B. Experimental Behavior of Pretensioned Bent Caps with Internal Voids for Weight Reduction. J. Bridge Eng. 2020, 25, 04019123. [Google Scholar] [CrossRef]
- Birely, A.C.; Yole, K.J.; Lee, J.D.; McKee, C.D.; Mander, J.B. Experimental Behavior of Reinforced Concrete and Pretensioned Concrete Bent Caps. J. Bridge Eng. 2019, 25, 04019137. [Google Scholar] [CrossRef]
- Ye, M.; Li, L.; Hu, F.J.; Wang, L.; Shao, X. UHPC-based precast large-cantilevered thin-walled bent caps: Design and experiments. Eng. Struct. 2022, 272, 114909. [Google Scholar] [CrossRef]
- Khan, M.; Uy, B.; Tao, Z.; Mashiri, F. Behaviour and design of short high-strength steel welded box and concrete-filled tube (CFT) sections. Eng. Struct. 2017, 147, 458–472. [Google Scholar] [CrossRef]
- Deng, E.; Zhang, Z.; Zhang, C.; Tang, Y.; Wang, W.; Du, Z.; Gao, J. Experimental study on flexural behavior of UHPC wet joint in prefabricated multi-girder bridge. Eng. Struct. 2023, 275, 115314. [Google Scholar] [CrossRef]
- Li, L.; Ye, M.; Hu, F.; Liao, R.; Tang, J.; Shao, X. Experimental study on the flexural behavior of a prefabricated large-cantilevered prestressed UHPC thin-walled bent cap. China Civ. Eng. J. 2020, 53, 92–104. [Google Scholar] [CrossRef]
- Li, J.W.; Xia, Z.H.; Sun, M.S.; Xia, J. Experimental Study on Mechanical Performance of UHPC Formwork-RC Composite Cap Beam. China J. Highw. Transp. 2021, 34, 157–167. [Google Scholar]
- Hayashi, H.; Horie, Y.; Mizobuchi, S.; Kamijo, T.; Abe, Y.; Kobayash, Y. The Behavior of Hybrid Pier with RC Column and Steel Beam under Quasi Practical Load. J. Struct. Eng. 1998, 44A, 1459–1466. [Google Scholar]
- Zhou, W.J. Analysis on Application of Steel Capping Beam in Municipal Elevated Bridge. Urban Roads Bridges Flood Control. 2021, 6, 313–317. [Google Scholar] [CrossRef]
- Lang, Y.; Yan, L. Design and Research on Composite Portal Piers with Railway Steel Cap Beams and Concrete Columns. High-Speed Railw. Technol. 2020, 11, 80–84. [Google Scholar]
- Yan, B.; Liu, C.; Du, K.; Dai, G. Bridge-rail Interaction of High-speed Railway Continuous Beams on Portal Piers. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2012, 40, 81–84. [Google Scholar] [CrossRef]
- Liang, Q.; Guo, W. Optimal Design of Connection Structure Between Steel Cap Beam and Concrete Pier Column Based on the Integral Joint Concept. Bridge Constr. 2024, 54, 129–134. [Google Scholar] [CrossRef]
- Nie, X.; Yang, Y.; Fan, J.; Mo, Y.L.; Nie, J. Experimental Study on Steel Jacket–Concrete Composite Connections. J. Bridge Eng. 2016, 22, 04016138. [Google Scholar] [CrossRef]
- Rahnavard, R.; Rebelo, C.; Craveiro, H.D.; Napolitano, R. Understanding the Cyclic Performance of Composite Steel-concrete Connections on Steel Bridges. Eng. Struct. 2020, 224, 111213. [Google Scholar] [CrossRef]
- Chen, X. Study on Design Method and Mechanical Performance of Temporary Hinged Device for Composite Piers with Steel Cap Beams and Concrete Columns. Master’s Thesis, Nanchang University, Nanchang, China, 2023. [Google Scholar]
- JTG D60-2015; General Specifications for Design of Highway Bridge and Culvert. Ministry of Transport of the People’s Republic of China: Beijing, China, 2015.
- GB/T 228.1-2021; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. Standardization Administration of the People’s Republic of China: Beijing, China, 2021.
- GB 50017-2017; Code for Design of Steel Structures. China Architecture & Building Press: Beijing, China, 2017.
- GB/T 50081-2019; Standard for Test Methods of Physical and Mechanical Properties of Concrete. China Architecture & Building Press: Beijing, China, 2019.



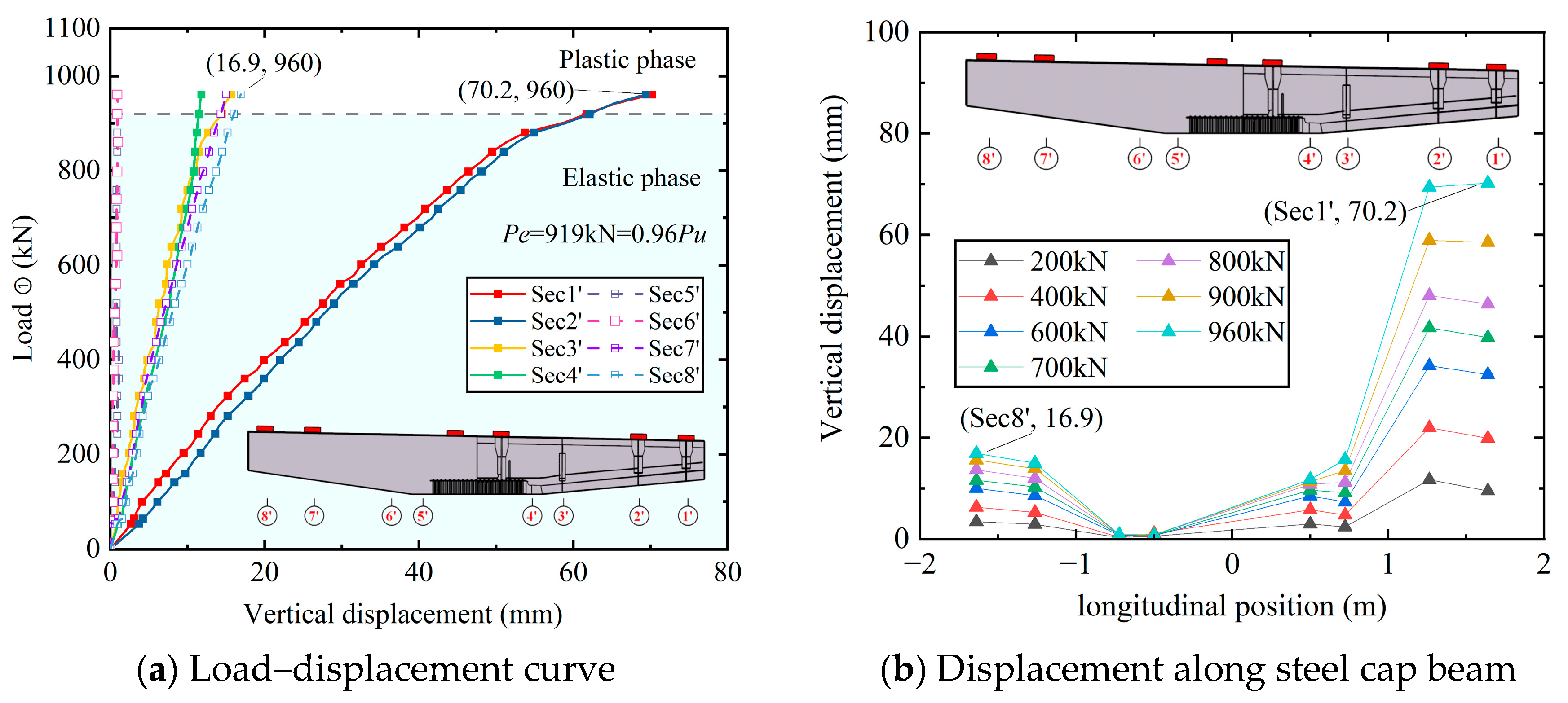
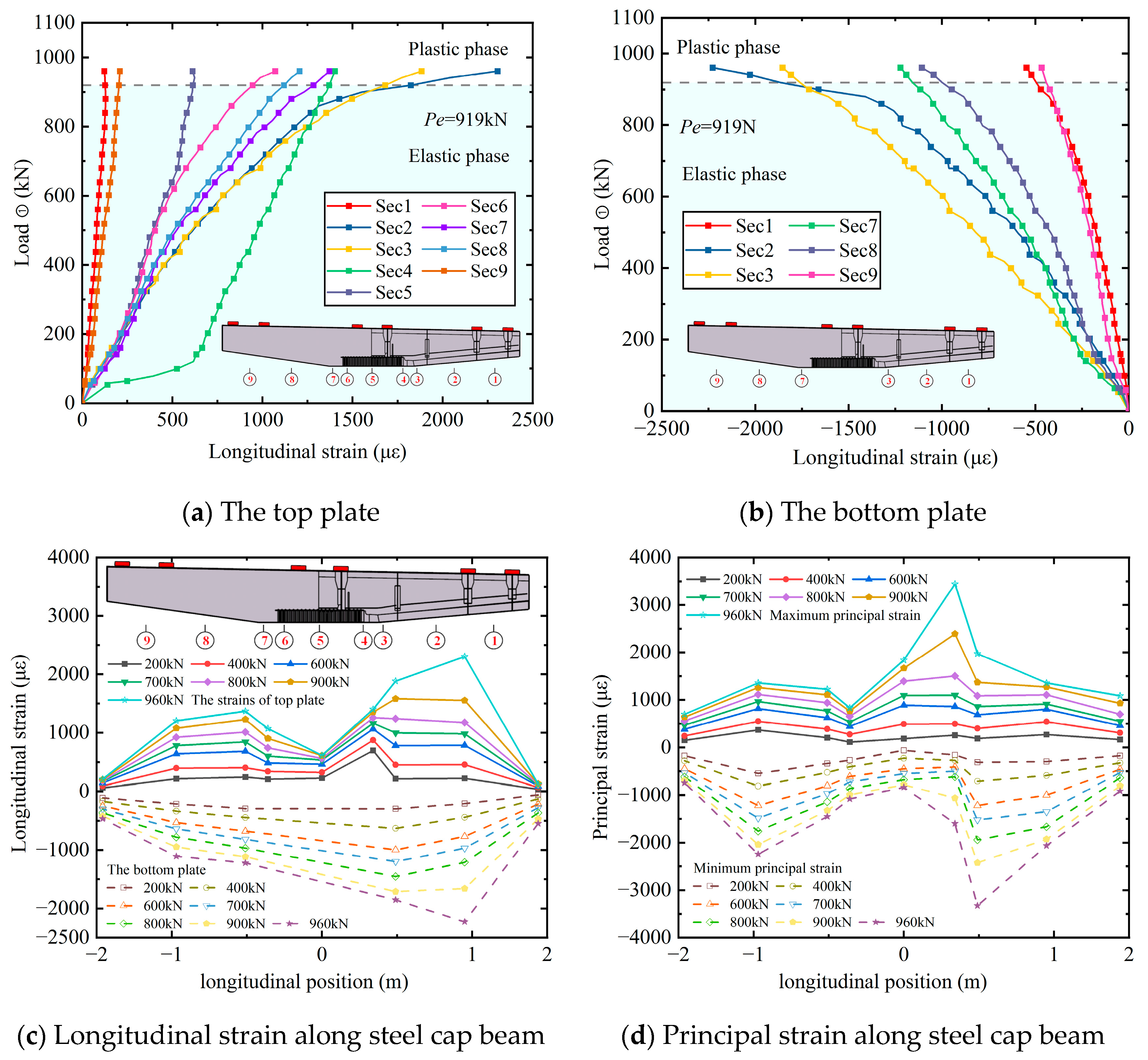
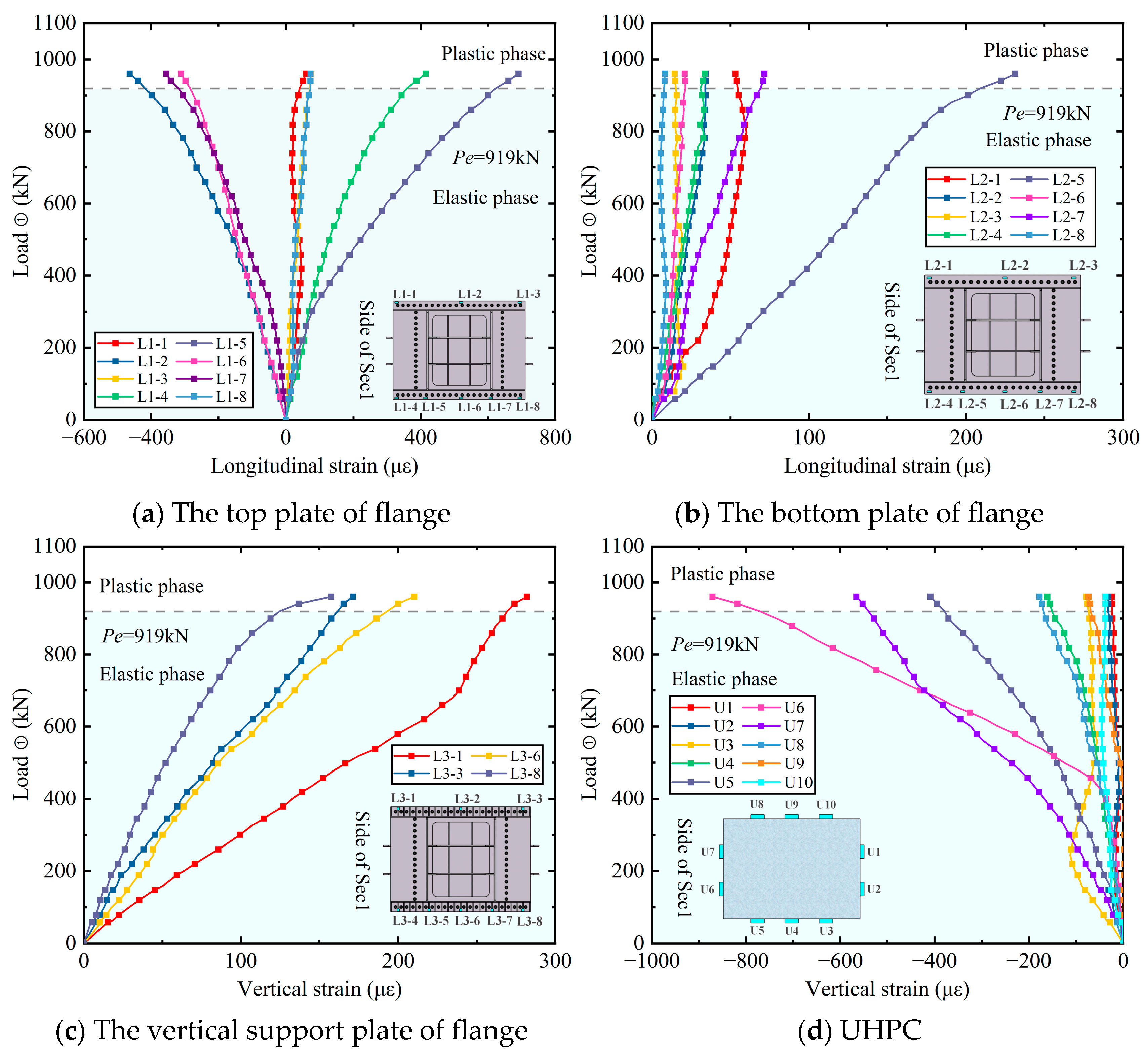


| Step | Load ① (kN) | Load ② and ③ (kN) | Remark | Loads | ||
|---|---|---|---|---|---|---|
| Dead Loads of Main Girders | Dead Loads of Auxiliary Structures | Live Load (Only Load ①) | ||||
| 0 | 40 | 40 | * | |||
| 1 | 148 | 148 | ✓ | |||
| 2 | 364 | 208 | ✓ | ✓ | ✓ | |
| 3 | 740 | 432 | ✓ | ✓ | ✓ | |
| 4 | +17 kN/step | +10 kN/step | ✓ | ✓ | ✓ | |
| Steel | Thickness in Actual (mm) | Yield Strength (MPa) | Ultimate Strength (MPa) | Ultimate Strain (με) | |
|---|---|---|---|---|---|
| Steel plates | 3 mm | 2.69 | 477 | 582 | 132,600 |
| 4 mm | 3.62 | 419 | 566 | 137,000 | |
| 5 mm | 4.59 | 423 | 533 | 136,000 | |
| 6 mm | 5.50 | 474 | 634 | 111,000 | |
| 8 mm | 7.60 | 411 | 578 | 136,300 | |
| 10 mm | 9.55 | 443 | 615 | 103,000 | |
| Rebars | D 10 mm | - | 400 | - | - |
| D 4 mm | - | 400 | - | - | |
| Concrete | Position | Size (mm) | Contents | Results (MPa) |
|---|---|---|---|---|
| C40 | Column | 150 × 150 × 150 | Compressive strength | 27.5 |
| 150 × 150 × 150 | Flexural strength | 5.1 | ||
| UHPC | Connection joint | 100 × 100 × 100 | Compressive strength | 150.4 |
| 100 × 100 × 300 | Flexural strength | 139.0 | ||
| 100 × 100 × 300 | Elastic modulus | 47,700 | ||
| Dog-bone | Tensile strength | 14.2 |
| Loading Steps | Mesh Sizes | 300 mm | 400 mm | |||
|---|---|---|---|---|---|---|
| Maximum Stress/MPa | Compressive | Tensile | Compressive | Tensile | ||
| 1 | Pw | −117 | 93 | −1117 | 93 | |
| 2 | Ps | −161 | 129 | −1162 | 129 | |
| 3 | Pe | −282 | 207 | −1282 | 202 | |
| 4 | Pu | Ultimate load/kN | 988 | 1003 | ||
| Loading Scheme | Hinged-to-Rigid | Directly Rigid | ||||||
|---|---|---|---|---|---|---|---|---|
| Concrete | Steel Mises | Concrete | Steel Mises | |||||
| Compression | Tension | Compression | Tension | |||||
| Installing main beams | 1 | Load ② = 148 kN | −10.5 | 0.25 | 37 | −10.34 | 0.24 | 36 |
| 2 | Load ③ = 148 kN | −13.2 | 1.6 | 178 | −13.9 | 1.8 | 140 | |
| 3 | Load ① = 148 kN | −11.6 | 0.9 | 98 | −13.5 | 2.2 | 108 | |
| Constructing auxiliary facilities | 4 | Load ①②③ = 60 kN | −12.8 | 1 | 137 | −14.9 | 3.1 | 151 |
| Live load | 5 | Load ① = 138 kN | −14.8 | 3.4 | 261 | −17 | 4.9 | 293 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, C.; Su, Q.; Wang, S.; Matanmi, F.O. Investigation on Static Performance of Piers Assembled with Steel Cap Beams and Single Concrete Columns. Buildings 2025, 15, 3476. https://doi.org/10.3390/buildings15193476
Shen C, Su Q, Wang S, Matanmi FO. Investigation on Static Performance of Piers Assembled with Steel Cap Beams and Single Concrete Columns. Buildings. 2025; 15(19):3476. https://doi.org/10.3390/buildings15193476
Chicago/Turabian StyleShen, Chong, Qingtian Su, Sizhe Wang, and Fawas. O. Matanmi. 2025. "Investigation on Static Performance of Piers Assembled with Steel Cap Beams and Single Concrete Columns" Buildings 15, no. 19: 3476. https://doi.org/10.3390/buildings15193476
APA StyleShen, C., Su, Q., Wang, S., & Matanmi, F. O. (2025). Investigation on Static Performance of Piers Assembled with Steel Cap Beams and Single Concrete Columns. Buildings, 15(19), 3476. https://doi.org/10.3390/buildings15193476








