Porosity and Permeability in Construction Materials as Key Parameters for Their Durability and Performance: A Review
Abstract
1. Introduction
2. Porosity and Permeability: Fundamental Definitions and Characterization Methods
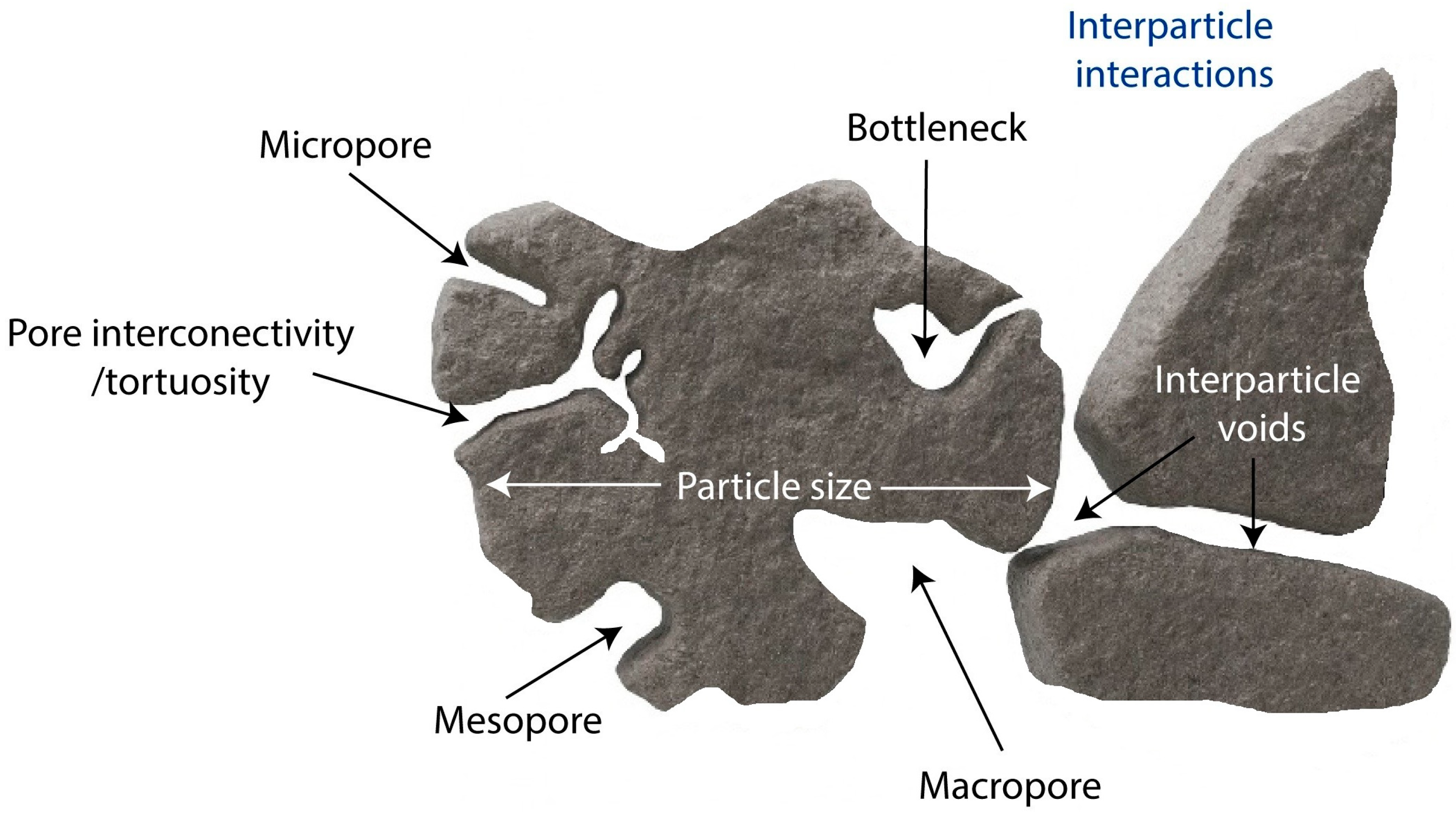
2.1. Porosity
2.2. Principal Techniques for Determining the Porosity of Porous Materials (Rocks, Mortars, and Concrete)
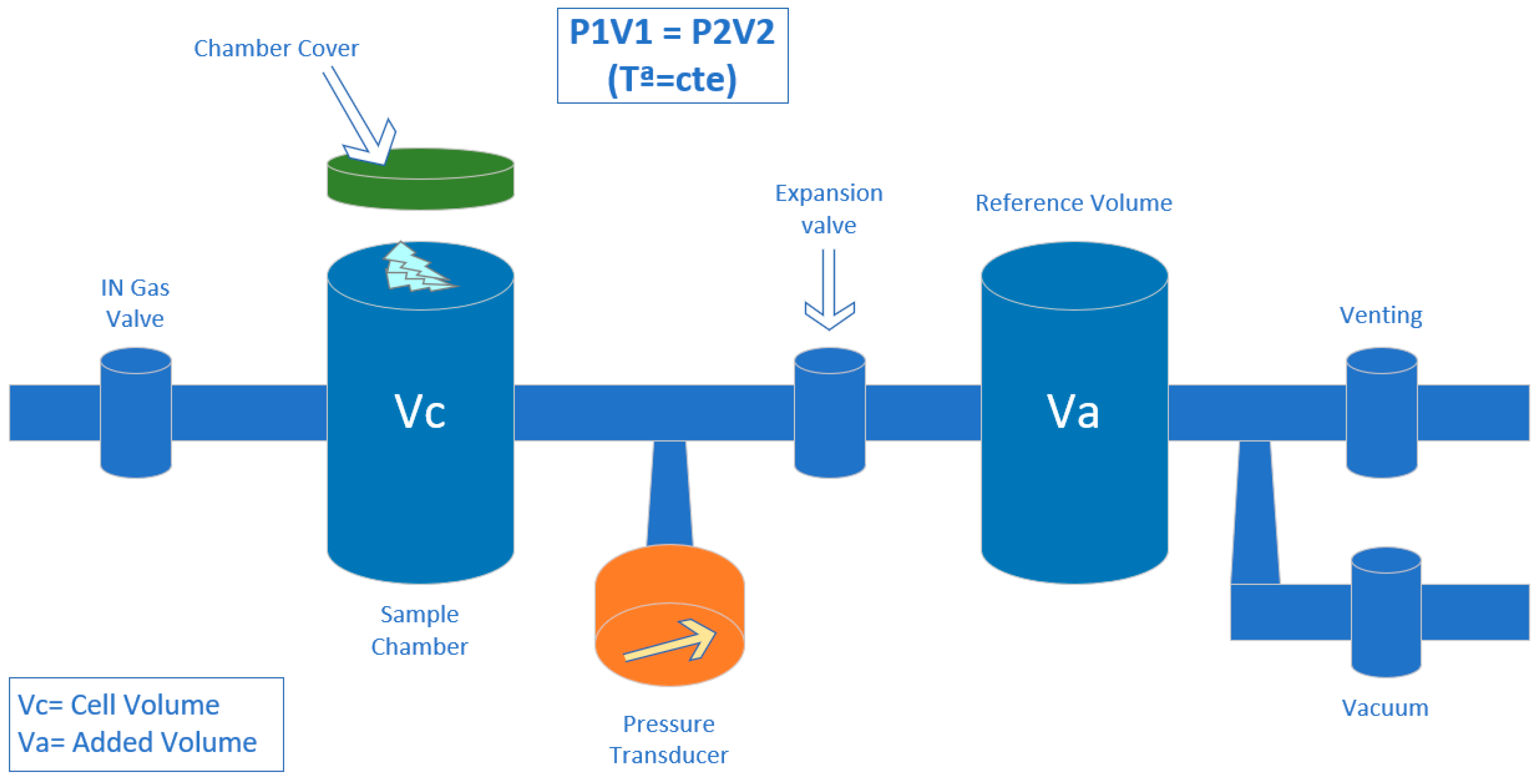
2.2.1. Helium Pycnometry
2.2.2. Mercury Intrusion Porosimetry (MIP)
2.2.3. Gas Adsorption–Desorption Characterization (Typically N2 at 77 K) and BET/BJH Analysis Methods
2.2.4. T2/T1 Relaxation NMR for Porosity Characterization
2.2.5. Imaging Techniques and Digital Analysis
Optical Microscopy
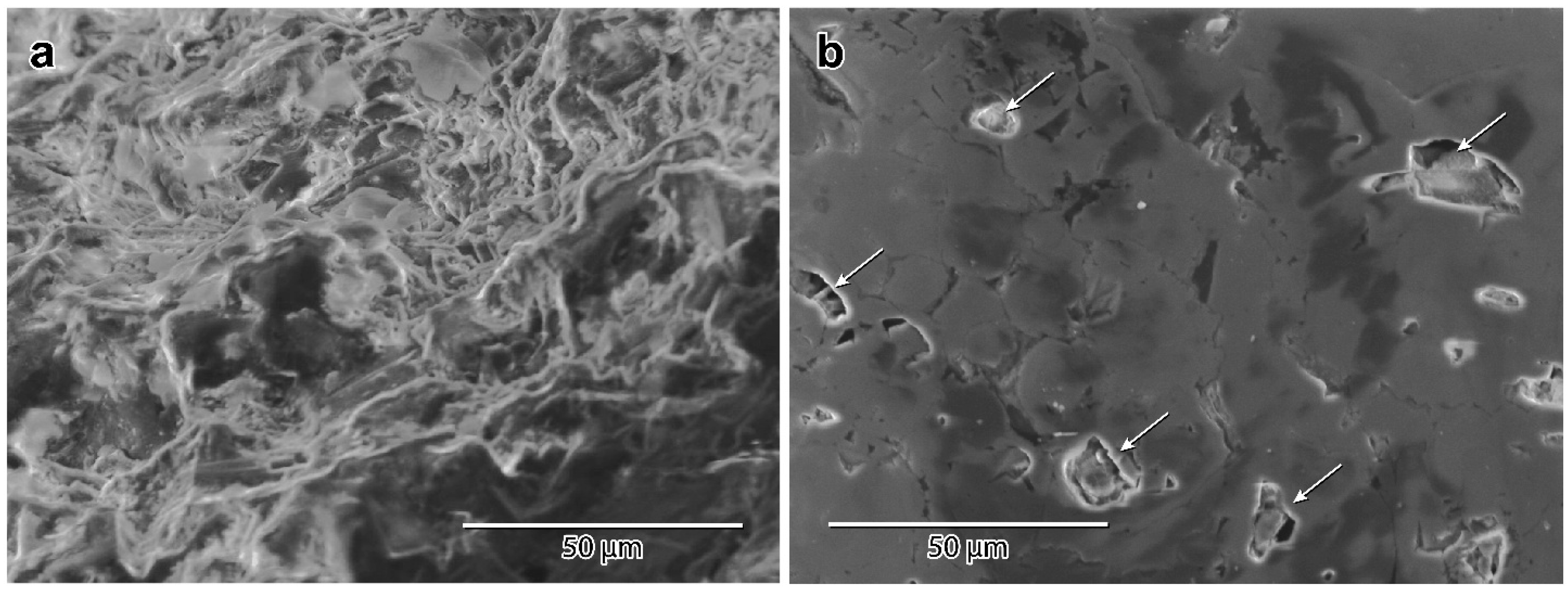
SEM
Focused Ion Beam–SEM (FIB-SEM)
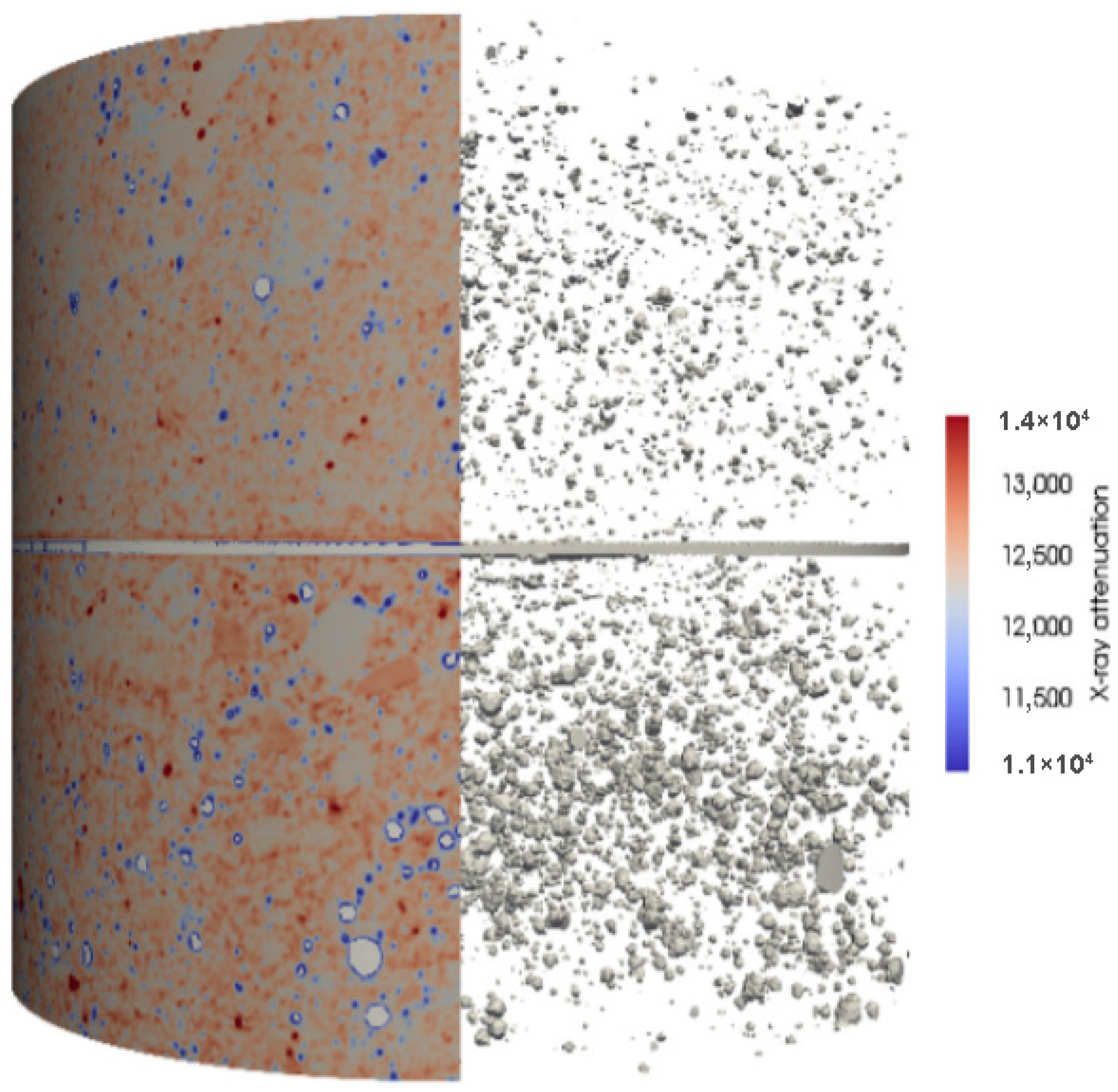
X-Ray Micro-Computed Tomography (Micro-CT)
Confocal Laser Scanning Microscopy (CLSM)
Deep Learning-Assisted Segmentation
2.3. Permeability (k)
2.4. Tortuosity, Capillary Suction, and the Mechanisms Governing Fluid Transport in Porous Media
2.4.1. Tortuosity
2.4.2. Capillary Suction
2.4.3. Mechanisms of Fluid Transport in Porous Media
Advection
Diffusion
Dispersion
Capillary Flow
Osmosis and Electro-Osmosis
2.5. Principal Techniques for Measuring the Permeability of Porous Materials (Rocks, Mortars, and Concrete)
2.5.1. Permeability Determination Under Steady-State Flow Conditions (Darcy’s Law)
2.5.2. Classical Hydraulic Permeametry (Steady-State Flow with Water or Brine)
2.5.3. Transient-Pressure Methods (Gas or Liquid)
2.5.4. Imaging and Indirect Correlations
- Acquisition of X-ray micro-computed tomography (μCT) in accordance with ISO 15708-3, performing geometric calibration of the system and verifying the effective resolution using reference standards.
- Document the preprocessing and segmentation stages, maintaining a reproducible record of all parameters used.
- Generate the computational domain and define boundary conditions consistent with the planned experimental comparison.
- Solve the Stokes–Brinkman model to determine the full permeability tensor, verifying convergence with respect to the representative elementary volume (REV) size and the mesh discretization.
- Benchmark the numerical results against physical tests performed in accordance with ASTM and API standards (e.g., core permeametry per API RP 40), matching, as far as possible, the stress state, saturation, temperature, and flow regime, including the Klinkenberg correction for gas flow. This coherently closes the image → simulation → experiment loop.
- A consistent alignment of the assumptions applied in the digital model and laboratory experiments.
- Comparability across laboratories and experimental campaigns.
- Cross-validation that uncovers segmentation or boundary-definition biases in the simulation and deviations arising from experimental sample preparation.
- Industrial and regulatory acceptance by placing the digital twin and the experimental data within recognized standards frameworks.
2.5.5. Field Infiltration Testing Technique
2.6. Knowledge Gaps in the Characterization and Fundamental Understanding of Porosity and Permeability
2.6.1. Three-Dimensional Connectivity and Tortuosity of the Pore Network
2.6.2. Thermo-Hydro-Mechanical-Chemical (THMC) Coupling
2.6.3. Temporal Scales and Transitions
2.6.4. Long-Term Effects of Nano- and Microstructural Additives
2.6.5. Standardization and Comparability of Testing
2.6.6. Influence of Salts, Climatic Cycles, and Biocolonization
2.6.7. Upscaling
3. Influence on the Material’s Durability and Performance
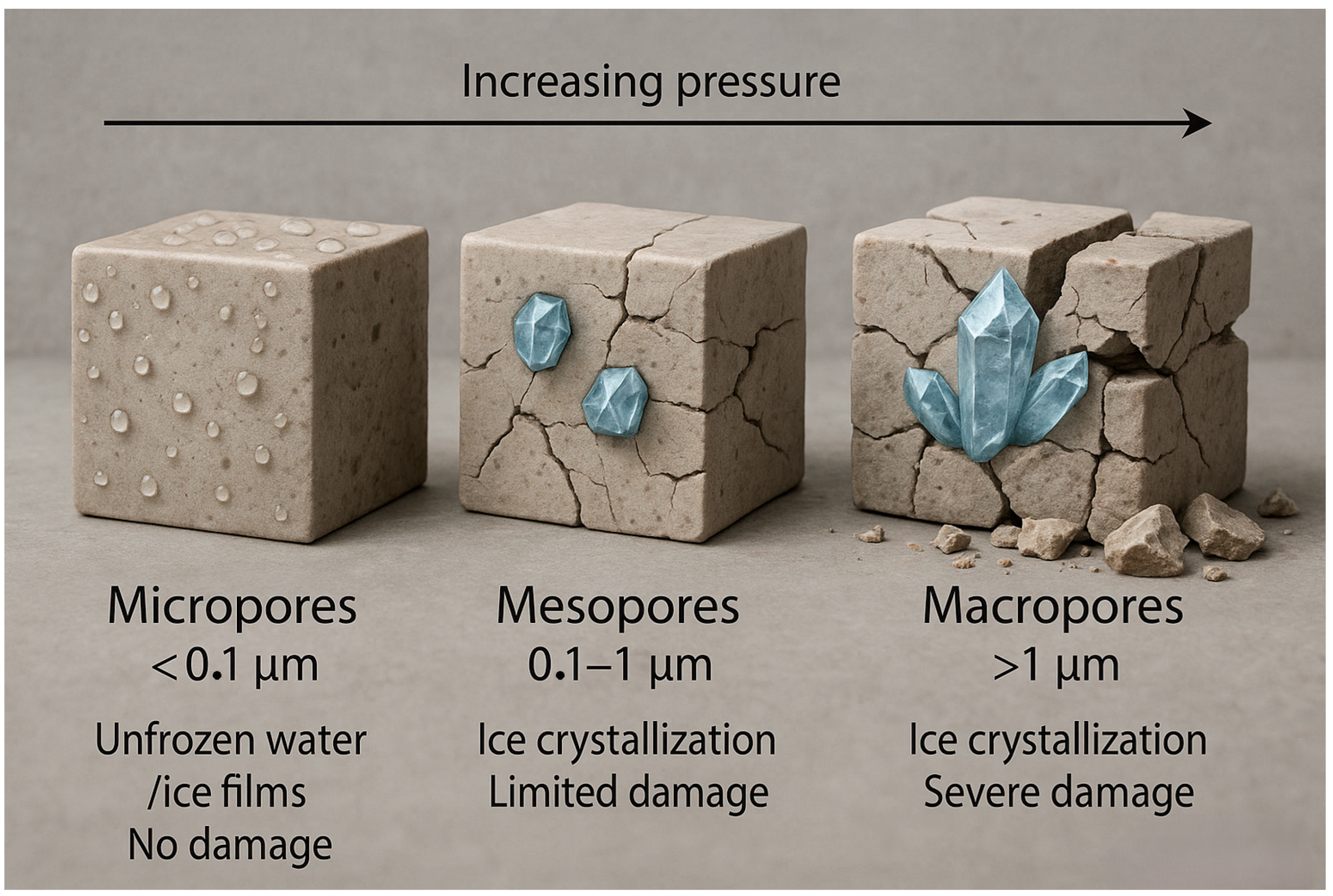
3.1. Water Absorption and Freeze–Thaw Resistance
3.2. Degradation Under Corrosive Media
4. Case Studies of Natural and Cementitious Materials
4.1. Natural Stones
4.2. Concrete and Cement-Based Materials
5. Recent Advances: Nanomaterials and Pore System Engineering
- Improvement in total porosity through filler effect;
- Positive influence on hydration reaction which also reduces porosity;
- Creation of physical barrier for intruding harmful ions.
- Possible high costs despite relatively low dosages;
- Problems with scaling up the production, including dispersion in cement matrix;
- Not enough data on long-term behaviour under natural corrosive conditions.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Viles, H.A. The Dynamic Setting for 21st Century Stone Deterioration and Conservation. Available online: http://qjegh.lyellcollection.org/ (accessed on 21 August 2025).
- Deprez, M.; De Kock, T.; De Schutter, G.; Cnudde, V. A Review on Freeze-Thaw Action and Weathering of Rocks. Earth Sci. Rev. 2020, 203, 103143. [Google Scholar] [CrossRef]
- Zhou, D.; Liu, J.; Cheng, L.; An, S.; Huo, L. Pore Structures and Deterioration Mechanism of Concrete after Cryogenic Freeze-Thaw Cycles: Effects of Moisture Contents and Aggregates. J. Build. Eng. 2024, 96, 110620. [Google Scholar] [CrossRef]
- Liu, B.; Liu, Q.; Liu, X.; Liu, Q.; Wang, X. Mechanical and Microstructural Characteristics and Damage Constitutive Model of Limestone under Acid Corrosion. J. Build. Eng. 2025, 108, 112903. [Google Scholar] [CrossRef]
- Kudasik, M.; Anioł, Ł.; Gajda, A.; Pajdak, A. Influence of Confining Pressure on Permeability and Structural Properties of Selected Sedimentary, Igneous, and Metamorphic Rocks. Bull. Eng. Geol. Environ. 2023, 82, 455. [Google Scholar] [CrossRef]
- Hoseini, M.; Bindiganavile, V.; Banthia, N. The Effect of Mechanical Stress on Permeability of Concrete: A Review. Cem. Concr. Compos. 2009, 31, 213–220. [Google Scholar] [CrossRef]
- Li, W.; Zhou, Y.; Yin, J.; Peng, Y.; Wang, Y.; Tang, S.; Shi, Y.; Wang, Y.; Wang, L. Thermodynamics-Based Simulations of the Hydration of Low-Heat Portland Cement and the Compensatory Effect of Magnesium Oxide Admixtures. J. Zhejiang Univ. Sci. A 2025, 26, 305–319. [Google Scholar] [CrossRef]
- Yu, W.; Zhou, Y.; Zhao, Z.; Li, Y.; Long, Y.; Tang, S. Simulation of Low-Heat Portland Cement Permeability and Thermal Conductivity Using Thermodynamics. Proc. Inst. Civ. Eng.-Transp. 2025, in press. [Google Scholar] [CrossRef]
- Broomfield, J.P. Corrosion of Steel in Concrete; CRC Press: London, UK, 2022. [Google Scholar] [CrossRef]
- Abreu Araujo, L.; Rebolledo Ramos, N.; Torres Martín, J.E.; Chinchón-Payá, S.; Sánchez Montero, J.; Lample Carreras, R.M.; Vera-Agullo, J.; Jimenez-Vicaria, J.D. Concrete Gas Permeability: Implications for Hydrogen Storage Applications. Appl. Sci. 2024, 14, 6408. [Google Scholar] [CrossRef]
- van der Merwe, J.E. Towards the Estimation of Concrete Intrinsic Permeability. Cem. Concr. Res. 2022, 159, 106885. [Google Scholar] [CrossRef]
- Wang, J.; Lu, S.; Zhang, P.; Zhi, Q.; Huang, H. Pore Distribution Characteristics of Different Lithofacies Shales: Evidence from Scanning Electron Microscopy. Processes 2023, 11, 1120. [Google Scholar] [CrossRef]
- Ali, A.; Zhang, N.; Santos, R.M. Mineral Characterization Using Scanning Electron Microscopy (SEM): A Review of the Fundamentals, Advancements, and Research Directions. Appl. Sci. 2023, 13, 12600. [Google Scholar] [CrossRef]
- Dullien, F.A.L.; Brenner, H. Porous Media: Fluid Transport and Pore Structure; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Beck, K.; Rozenbaum, O.; Al-Mukhtar, M.; Plançon, A. Multi-Scale Characterisation of monument limestones. In Proceedings of the 6th International Symposium on the Conservation of Monuments in the Mediterranean Basin, Lisbon, Portugal, 7–10 April 2004; pp. 1–6. [Google Scholar]
- Instrument Models. Poremaster® & Poremaster® GT User Guide (Operating Manual); Quantachrome Instruments: Boynton Beach, FL, USA, 2009. [Google Scholar]
- Wang, L.; Song, X.; Yang, H.; Wang, L.; Tang, S.; Wu, B.; Mao, W. Pore Structural and Fractal Analysis of the Effects of MgO Reactivity and Dosage on Permeability and F–T Resistance of Concrete. Fractal Fract. 2022, 6, 113. [Google Scholar] [CrossRef]
- Ordóñez, S.; Fort, R.; Garcia del Cura, M.A. Pore Size Distribution and the Durability of a Porous Limestone. Q. J. Eng. Geol. 1997, 30, 221–230. [Google Scholar] [CrossRef]
- ASTM D4404; Standard Test Method for Determination of Pore Volume and Pore Volume Distribution of Soil and Rock by Mercury Intrusion Porosimetry. ASTM International: West Conshohocken, PA, USA, 2025.
- Muller, A.C.A.; Scrivener, K.L. A Reassessment of Mercury Intrusion Porosimetry by Comparison with 1H NMR Relaxometry. Cem. Concr. Res. 2017, 100, 350–360. [Google Scholar] [CrossRef]
- Chatterji, S. A Discussion of the Paper “Mercury Porosimetry: An Inappropriate Method for the Measurement of Pore Size Distributions in Cement-Based Materials” by S. Diamond. Cem. Concr. Res. 2001, 31, 1657–1658. [Google Scholar] [CrossRef]
- Rigby, S.P. Uses of Gas Sorption and Mercury Porosimetry Methods in Studies of Heritage Materials. Heritage 2025, 8, 132. [Google Scholar] [CrossRef]
- Zeng, Q.; Chen, S.; Yang, P.; Peng, Y.; Wang, J.; Zhou, C.; Wang, Z.; Yan, D. Reassessment of Mercury Intrusion Porosimetry for Characterizing the Pore Structure of Cement-Based Porous Materials by Monitoring the Mercury Entrapments with X-Ray Computed Tomography. Cem. Concr. Compos. 2020, 113, 103726. [Google Scholar] [CrossRef]
- ASTM D4222-20; Standard Test Method for Determination of Nitrogen Adsorption and Desorption Isotherms of Catalysts and Catalyst Carriers by Static Volumetric Measurements. ASTM International: West Conshohocken, PA, USA, 2020.
- ASTM D3663-20; Standard Test Method for Surface Area of Catalysts and Catalyst Carriers. ASTM International: West Conshohocken, PA, USA, 2020.
- ASTM D4641-17; Standard Practice for Calculation of Pore Size Distributions of Catalysts and Catalyst Carriers from Nitrogen Desorption Isotherms. ASTM International: West Conshohocken, PA, USA, 2017.
- Zhao, L.; Feng, P.; Hong, J.; Liu, Q.; Geng, G. Improved Low-Field NMR Porosity Characterization of Cementitious Materials Containing Water-Soluble Organic Admixtures. Cem. Concr. Compos. 2024, 153, 105732. [Google Scholar] [CrossRef]
- Robert, E.; Saleh, F.K.; Teodoriu, C. Revolutionizing Reservoir Management: Real-Time Petrophysical Analysis with NMR Technology of Drill Cuttings. Available online: https://pangea.stanford.edu/ERE/db/GeoConf/papers/SGW/2024/Robert.pdf (accessed on 21 August 2025).
- Tang, Y.J.; Shan, Z.Q.; Yin, G.J.; Miao, L.; Wang, S.S.; Zhang, Z.Y. Low-Field Nuclear Magnetic Resonance Investigation on Early Hydration Characterization of Cement Paste Mixed with Mineral Admixtures. Buildings 2023, 13, 2318. [Google Scholar] [CrossRef]
- Stroeven, P.; Le, N.L.; Sluys, L.J.; He, H. Porosimetry by Double-Random Multiple Tree Structuring in Virtual Concrete. Image Anal. Ster. Stereol. 2012, 31, 55–63. [Google Scholar] [CrossRef]
- Zhu, P.; Dong, Y.; Chen, M.; Li, Z.; Han, B.; Wang, J.; Cui, Y. Quantitative Evaluation of Pore Structure from Mineralogical and Diagenetic Information Extracted from Well Logs in Tight Sandstone Reservoirs. J. Nat. Gas. Sci. Eng. 2020, 80, 103376. [Google Scholar] [CrossRef]
- Ulusay, R.; Hudson, J.A. The Complete ISRM Suggested Methods for Rock Characterization, Testing and Monitoring: 1974–2006; Ulusay, R., Hudson, J.A., Eds.; International Society for Rock Mechanics (ISRM): Ankara, Turkey, 2007. [Google Scholar]
- Scrivener, K.L. The Use of Backscattered Electron Microscopy and Image Analysis to Study the Porosity of Cement Paste. In Material Research Society Symposium; Roberts, L.R., Skalny, J.P., Eds.; Materials Research Society (MRS): Boston, MA, USA, 1989; Volume 137, pp. 129–140. [Google Scholar]
- Scrivener, K.L.; Lyon, A.K.C.; Laugesen, F.P. The Interfacial Transition Zone (ITZ) Between Cement Paste and Aggregate in Concrete. Interface Sci. 2004, 12, 411–421. [Google Scholar] [CrossRef]
- Sorbier, L.; Poncet, H.; Lecocq, V.; Maillet, G.; Moula, M.; Le Corre, V. Local Porosity Measurement from Scanning Electron Microscopy Images in the Backscattered Electrons Mode. Microsc. Microanal. 2021, 27, 20–27. [Google Scholar] [CrossRef]
- Żak, A.M.; Wieczorek, A.; Chowaniec, A.; Sadowski, Ł. Segmentation of Pores in Cementitious Materials Based on Backscattered Electron Measurements: A New Proposal of Regression-Based Approach for Threshold Estimation. Constr. Build. Mater. 2023, 368, 130419. [Google Scholar] [CrossRef]
- Salvini, S.; Coletti, C.; Maritan, L.; Massironi, M.; Balsamo, F.; Mazzoli, C. Exploring the Pore System of Carbonate Rocks through a Multi-Analytical Approach. Environ. Earth Sci. 2023, 82, 564. [Google Scholar] [CrossRef]
- Buckman, J.; Bankole, S.A.; Zihms, S.; Lewis, H.; Couples, G.; Corbett, P.W.M. Quantifying Porosity through Automated Image Collection and Batch Image Processing: Case Study of Three Carbonates and an Aragonite Cemented Sandstone. Geosciences 2017, 7, 70. [Google Scholar] [CrossRef]
- Scrivener, K.; Snellings, R.; Lothenbach, B. (Eds.) A Practical Guide to Microstructural Analysis of Cementitious Materials, 1st ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar] [CrossRef]
- ASTM C1721-22; Standard Guide for Petrographic Examination of Dimension Stone. ASTM International: West Conshohocken, PA, USA, 2022.
- Liu, Y.; King, H.E.; van Huis, M.A.; Drury, M.R.; Plümper, O. Nano-Tomography of Porous Geological Materials Using Focused Ion Beam-Scanning Electron Microscopy. Minerals 2016, 6, 104. [Google Scholar] [CrossRef]
- Schmid, T.; Ruffray, N.; Griffa, M.; Zhang, Z.; Isgor, O.B.; Angst, U.M. Probing the Steel-Concrete Interface Microstructure Using FIB-SEM Nanotomography. Mater. Struct. Mater. Constr. 2025, 58, 75. [Google Scholar] [CrossRef]
- Reedy, C.L.; Reedy, C.L. High-Resolution Micro-CT with 3D Image Analysis for Porosity Characterization of Historic Bricks. Herit. Sci. 2022, 10, 83. [Google Scholar] [CrossRef]
- De Kock, T.; Boone, M.A.; De Schryver, T.; Van Stappen, J.; Derluyn, H.; Masschaele, B.; De Schutter, G.; Cnudde, V. A Pore-Scale Study of Fracture Dynamics in Rock Using X-Ray Micro CT Under Ambient Freeze–Thaw Cycling. Environ. Sci. Technol. 2015, 49, 2867–2874. [Google Scholar] [CrossRef]
- Hassan, A.; Yutkin, M.; Chandra, V.; Patzek, T. Quality Evaluation of Epoxy Pore Casts Using Silicon Micromodels: Application to Confocal Imaging of Carbonate Samples. Appl. Sci. 2021, 11, 5557. [Google Scholar] [CrossRef]
- Phan, J.; Ruspini, L.C.; Lindseth, F. Automatic Segmentation Tool for 3D Digital Rocks by Deep Learning. Sci. Rep. 2021, 11, 19123. [Google Scholar] [CrossRef]
- Niu, Y.; Mostaghimi, P.; Shabaninejad, M.; Swietojanski, P.; Armstrong, R.T. Digital Rock Segmentation for Petrophysical Analysis With Reduced User Bias Using Convolutional Neural Networks. Water Resour. Res. 2020, 56, e2019WR026597. [Google Scholar] [CrossRef]
- Shen, Y.; Su, J.; Qin, Q.; Chen, H. Comparative Study on Applicability of Permeability Testing Methods in Shale Reservoirs. ACS Omega 2021, 6, 24176–24184. [Google Scholar] [CrossRef]
- Carles, P.; Egermann, P.; Lenormand, R.; Lombard, J.M. Sca2007-07 Low Permeability Measurements using steady-state and transient methods. In Proceedings of the International Symposium of the SCA, Calgary, AB, Canada, 10–13 September 2007. [Google Scholar]
- Tanikawa, W.; Shimamoto, T. Klinkenberg Effect for Gas Permeability and Its Comparison to Water Permeability for Porous Sedimentary Rocks. Hydrol. Earth Syst. Sci. Discuss. 2006, 3, 1315–1338. [Google Scholar] [CrossRef]
- Xiao, W.; Bernabé, Y.; Evans, B.; Mok, U.; Zhao, J.; Ren, X.; Chen, M. Klinkenberg Effect and Effective Pressure for Gas Permeability of Tight Sandstones. J. Geophys. Res. Solid Earth 2019, 124, 1412–1429. [Google Scholar] [CrossRef]
- Ahmad, I.; Ahmad, M.; Ali, I. Klinkenberg-Corrected and Water Permeability Correlation for a Sarawak Carbonate Field. Fluids 2021, 6, 339. [Google Scholar] [CrossRef]
- ISO 4022:2018; Permeable sintered metal materials—Determination of fluid permeability. ISO (International Organization for Standardization): Geneva, Switzerland, 2018.
- API RP 40; Recommended Practices for Core Analysis. American Petroleum Institute (API): Washington, DC, USA, 1998.
- RILEM TC 116-PCD: Permeability of Concrete as a Criterion of Its Durability. Available online: https://www.rilem.net/groupe/116-pcd-permeability-of-concrete-as-a-criterion-of-its-durability-116 (accessed on 21 August 2025).
- Tanikawa, W.; Shimamoto, T. Comparison of Klinkenberg-Corrected Gas Permeability and Water Permeability in Sedimentary Rocks. Int. J. Rock Mech. Min. Sci. 2009, 46, 229–238, Correction to Int. J. Rock Mech. Min. Sci. 2009, 46, 1394–1395. http://doi.org/10.1016/j.ijrmms.2009.08.001. [Google Scholar] [CrossRef]
- Shi, J.; Qian, R.; Wang, D.; Liu, Z.; Chun, Q.; Zhang, Y. Experimental Study on Gas Permeability of Cement-Based Materials. Cem. Concr. Compos. 2022, 129, 104491. [Google Scholar] [CrossRef]
- Gao, J.; Li, Z.; Wei, M.; Zhang, C. Experimental Study on the Klinkenberg Effect for Gas Permeability in Carboniferous Shales, Eastern Qaidam Basin, China. Energy Explor. Exploit. 2024, 42, 1386–1407. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Torres-Verdín, C.; Lake, L.W.; Marder, M. Gas Permeability in Unconventional Tight Sandstones: Scaling up from Pore to Core. J. Pet. Sci. Eng. 2019, 173, 1163–1172. [Google Scholar] [CrossRef]
- ISO 17892-11:2019; Geotechnical Investigation and Testing—Laboratory Testing of Soil—Part 11: Permeability Tests. ISO (International Organization for Standardization): Geneva, Switzerland, 2019.
- ASTM D5084-24; Standard Test Methods for Measurement of Hydraulic Conductivity of Saturated Porous Materials Using a Flexible Wall Permeamete. ASTM International: West Conshohocken, PA, USA, 2024.
- D2434-68; Standard Test Method for Permeability of Granular Soils (Constant Head). ASTM International: West Conshohocken, PA, USA, 2020.
- ASTM D5856-15; Standard Test Method for Measurement of Hydraulic Conductivity of Porous Material Using a Rigid-Wall, Compaction-Mold Permeameter. ASTM International: West Conshohocken, PA, USA, 2015.
- EN 12390-8:2019; Testing hardened concrete—Part 8: Depth of Penetration of Water Under Pressure. The European Committee for Standardization (CEN): Brussels, Belgium, 2019.
- Nijp, J.J.; Metselaar, K.; Limpens, J.; Gooren, H.P.A.; van der Zee, S.E.A.T.M. A Modification of the Constant-Head Permeameter to Measure Saturated Hydraulic Conductivity of Highly Permeable Media. MethodsX 2017, 4, 134–142. [Google Scholar] [CrossRef]
- Singh, K.; Camulli, H.; Bradley, J. Sediment Size Effects on Non-Darcy Flow: Insights from Izbash Equation and Forchheimer Inertial Coefficient Analysis. Hydrogeol. J. 2024, 32, 1853–1871. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, K.; Wang, C.; Bi, J. A Large Pressure Pulse Decay Method to Simultaneously Measure Permeability and Compressibility of Tight Rocks. J. Nat. Gas. Sci. Eng. 2022, 98, 104395. [Google Scholar] [CrossRef]
- Zhang, T.; Hu, Q.; Ghanbarian, B.; Elsworth, D.; Lu, Z. A Pulse-Decay Method for Low (Matrix) Permeability Analyses of Granular Rock. Hydrol. Earth Syst. Sci. 2023, 27, 4453–4465. [Google Scholar] [CrossRef]
- ASTM D4104/D4104M-20; Standard Practice (Analytical Procedures) for Determining Transmissivity of Nonleaky Confined Aquifers by Overdamped Well Response to Instantaneous Change in Head (Slug Tests). ASTM International: West Conshohocken, PA, USA, 2020.
- ASTM D5912-20; Standard Practice for Determining Hydraulic Conductivity of an Unconfined Aquifer by Overdamped Well Response to Instantaneous Change in Head. ASTM International: West Conshohocken, PA, USA, 2020.
- ISO 22282-1:2012; Geotechnical Investigation and Testing—Geohydraulic Testing—Part 1: General Rules. ISO (International Organization for Standardization): Geneva, Switzerland, 2012.
- Wang, Y.; Nolte, S.; Gaus, G.; Tian, Z.; Amann-Hildenbrand, A.; Krooss, B.; Wang, M. An Early-Time Solution of Pulse-Decay Method for Permeability Measurement of Tight Rocks. J. Geophys. Res. Solid. Earth 2021, 126, e2021JB022422. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, Z.; Nolte, S.; Amann-Hildenbrand, A.; Krooss, B.M.; Wang, M. Reassessment of Transient Permeability Measurement for Tight Rocks: The Role of Boundary and Initial Conditions. J. Nat. Gas. Sci. Eng. 2021, 95, 104173. [Google Scholar] [CrossRef]
- Liu, Q.; Hu, L.; Bayer, P.; Xing, Y.; Qiu, P.; Ptak, T.; Hu, R. A Numerical Study of Slug Tests in a Three-Dimensional Heterogeneous Porous Aquifer Considering Well Inertial Effects. Water Resour. Res. 2020, 56, e2020WR027155. [Google Scholar] [CrossRef]
- ISO 15708-3; Non-Destructive Testing—Radiation Methods for Computed Tomography—Part 3: Operation and Interpretation. ISO (International Organization for Standardization): Geneva, Switzerland, 2025.
- E1814; Standard Practice for Computed Tomographic (CT) Examination of Castings. ASTM International: West Conshohocken, PA, USA, 2025.
- Arns, C.H.; Knackstedt, M.A.; Pinczewski, W.V.; Martys, N.S. Virtual Permeametry on Microtomographic Images. J. Pet. Sci. Eng. 2004, 45, 41–46. [Google Scholar] [CrossRef]
- Timur, A. Pulsed Nuclear Magnetic Resonance Studies of Porosity, Movable Fluid, and Permeability of Sandstones. J. Pet. Technol. 1969, 21, 775–786. [Google Scholar] [CrossRef]
- SoilMoisture Equipment Corp. Operating Instructions Guelph Permeameter. 2012. Available online: https://www.soilmoisture.com (accessed on 21 August 2025).
- Reynolds, W.D.; Elrick, D.E. In Situ Measurement of Field-Saturated Hydraulic Conductivity, Sorptivity, and the α-Parameter Using the Guelph Permeameter. Soil. Sci. 1985, 140, 292–302. [Google Scholar] [CrossRef]
- Mohanty, B.P.; Kanwar, R.S.; Everts, C.J. Comparison of Saturated Hydraulic Conductivity Measurement Methods for a Glacial-Till Soil. Soil Sci. Soc. Am. J. 1994, 58, 672–677. [Google Scholar] [CrossRef]
- Ghibus, T.; Gaitanaru, D. A Statistical Approach for the Assessment of Saturated Hydraulic Conductivity Values of Unsaturated Urban Soils Obtained by Field Infiltration Tests. Water 2024, 16, 1908. [Google Scholar] [CrossRef]
- Benavente, D.; Pla, C.; Cueto, N.; Galvañ, S.; Martínez-Martínez, J.; García-del-Cura, M.A.; Ordóñez, S. Predicting Water Permeability in Sedimentary Rocks from Capillary Imbibition and Pore Structure. Eng. Geol. 2015, 195, 301–311. [Google Scholar] [CrossRef]
- Alves, C.; Figueiredo, C.A.M.; Sanjurjo-Sánchez, J.; Hernández, A.C. Effects of Water on Natural Stone in the Built Environment—A Review. Geosciences 2021, 11, 459. [Google Scholar] [CrossRef]
- Chen, L.; Li, K.; Song, G.; Zhang, D.; Liu, C. Effect of Freeze–Thaw Cycle on Physical and Mechanical Properties and Damage Characteristics of Sandstone. Sci. Rep. 2021, 11, 12315. [Google Scholar] [CrossRef]
- Török, Á.; Szemerey-Kiss, B. Freeze-Thaw Durability of Repair Mortars and Porous Limestone: Compatibility Issues. Prog. Earth Planet. Sci. 2019, 6, 42. [Google Scholar] [CrossRef]
- Vercher, J.; Borràs, J.G.; Lerma, C.; Mas, Á.; Gil, E. Estimation by Capillary Water Absorption Method to Building Natural Stones’ Durability against Freeze-Thaw. Constr. Build. Mater. 2024, 427, 136215. [Google Scholar] [CrossRef]
- Li, B.; Zhang, L.; Wei, J.; Ren, Y. Pore Damage Properties and Permeability Change of Coal Caused by Freeze-Thaw Action of Liquid Nitrogen. Adv. Civ. Eng. 2018, 2018, 5076391. [Google Scholar] [CrossRef]
- Gökçe, M.V.; Ince, I.; Fener, M.; Taşkiran, T.; Kayabali, K. The Effects of Freeze-Thaw (F-T) Cycles on the Gödene Travertine Used in Historical Structures in Konya (Turkey). Cold Reg. Sci. Technol. 2016, 127, 65–75. [Google Scholar] [CrossRef]
- Draebing, D.; Krautblatter, M. P-Wave Velocity Changes in Freezing Hard Low-Porosity Rocks: A Laboratory-Based Time-Average Model. Cryosphere 2012, 6, 1163–1174. [Google Scholar] [CrossRef]
- Hori, M.; Hidenori, M. Micromechanical Analysis on Deterioration Due to Freezing and Thawing in Porous Brittle Materials. Int. J. Eng. Sci. 1998, 36, 511–522. [Google Scholar] [CrossRef]
- Rusheng, Q.; Yunsheng, Z.; Yu, Z.; Chuanqing, F.; Cheng, L.; Lin, Y.; Guojian, L. Various Gas Transport Properties in Concrete Considering Transporting Mechanisms and Testing Methods-A Review. Constr. Build. Mater. 2023, 389, 131636. [Google Scholar] [CrossRef]
- Shah, V.; Mackechnie, J.; Scott, A. Determination of Carbonation Resistance of Concrete through a Combination of Cement Content and Tortuosity. J. Build. Eng. 2022, 60, 105176. [Google Scholar] [CrossRef]
- Andrade, C. Concepts on the Chloride Diffusion Coefficient. In Proceedings of the Third International RILEM Workshop on Testing and Modelling Chloride Ingress into Concrete, Madrid, Spain, 9–10 September 2002; pp. 1–15. [Google Scholar]
- Zhang, J.; Bian, F.; Zhang, Y.; Fang, Z.; Fu, C.; Guo, J. Effect of Pore Structures on Gas Permeability and Chloride Diffusivity of Concrete. Constr. Build. Mater. 2018, 163, 402–413. [Google Scholar] [CrossRef]
- Dehwah, O.H.A.; Xi, Y. Theoretical Model for the Coupling Effect of Moisture Transport on Chloride Penetration in Concrete. Cem. Concr. Res. 2024, 177, 107431. [Google Scholar] [CrossRef]
- Ragoug, R.; Metalssi, O.O.; Barberon, F.; Torrenti, J.M.; Roussel, N.; Divet, L.; d’Espinose de Lacaillerie, J.B. Durability of Cement Pastes Exposed to External Sulfate Attack and Leaching: Physical and Chemical Aspects. Cem. Concr. Res. 2019, 116, 134–145. [Google Scholar] [CrossRef]
- Feng, P.; Garboczi, E.J.; Miao, C.; Bullard, J.W. Microstructural Origins of Cement Paste Degradation by External Sulfate Attack. Constr. Build. Mater. 2015, 96, 391–403. [Google Scholar] [CrossRef]
- Yu, C.; Sun, W.; Scrivener, K. Mechanism of Expansion of Mortars Immersed in Sodium Sulfate Solutions. Cem. Concr. Res. 2013, 43, 105–111. [Google Scholar] [CrossRef]
- Zhang, C.; Li, J.; Yu, M.; Lu, Y.; Liu, S. Mechanism and Performance Control Methods of Sulfate Attack on Concrete: A Review. Materials 2024, 17, 4836. [Google Scholar] [CrossRef]
- Shah, V.; Bishnoi, S. Understanding the Process of Carbonation in Concrete Using Numerical Modeling. J. Adv. Concr. Technol. 2021, 19, 1148–1161. [Google Scholar] [CrossRef]
- Chen, W.; Wang, P.; Liang, Y. Experimental Study on the Influence of Low Temperature on the Gas Permeability of Granite. Appl. Sci. 2025, 15, 5447. [Google Scholar] [CrossRef]
- Wu, J. Experimental Study on Gas Permeability Semiempirical Model of Granite after Heat Treatment. Adv. Civ. Eng. 2022, 2022, 2812413. [Google Scholar] [CrossRef]
- García-del-Cura, M.A.; Benavente, D.; Bernabéu, A.; Martínez-Martínez, J. The Effect of Surface Finishes on Outdoor Granite and Limestone Pavers. Mater. Construcción 2007, 58, 289–290. [Google Scholar] [CrossRef]
- Laskaridis, K.; Arapakou, A.; Patronis, M.; Papatrechas, C.; Kouseris, I. Effect of Freeze–Thaw Cycles on the Flexural Strength of Greek Natural Stones. Mater. Proc. 2024, 15, 72. [Google Scholar] [CrossRef]
- Al-Harthi, A.A.; Al-Amri, R.M.; Shehata, W.M. The Porosity and Engineering Properties of Vesicular Basalt in Saudi Arabia. Eng. Geol. 1999, 54, 313–320. [Google Scholar] [CrossRef]
- Wang, L.; Chen, X.; Zhang, W.; Tian, Y.; Xu, S. Study on Changes in Physical and Mechanical Properties and Integrity Decay of Sandstone Subjected to Freeze–Thaw Cycling. Appl. Sci. 2023, 13, 7316. [Google Scholar] [CrossRef]
- Xiong, X.; Gao, F.; Li, J.; Zhou, K.; Yang, C. Pore Structure Evolution Characteristics and Damage Mechanism of Sandstone Subjected to Freeze–Thaw Cycle Treatment: Insights from Low-Field Nuclear Magnetic Resonance Testing and Fractal Theory. Fractal Fract. 2025, 9, 293. [Google Scholar] [CrossRef]
- Lifshitz Sherzer, G.; Ye, G.; Schlangen, E.; Kovler, K. The Role of Porosity on Degradation of Concrete under Severe Internal and External Brine Attack in Confined Conditions. Constr. Build. Mater. 2022, 341, 127721. [Google Scholar] [CrossRef]
- Gan, L.; Xu, W.; Shen, Z.; Xu, L.; Zhang, W.; Zhang, H.; Abbas, M.A.; Chen, G. Experimental and Numerical Investigations on Damage Evolution of Concrete under Sulfate Attack and Freeze-Thaw Cycles. J. Build. Eng. 2023, 71, 106469. [Google Scholar] [CrossRef]
- Ren, F.; Chen, X.; Zeng, Q.; Zhou, C. Effects of Pure Carbonation on Pore Structure and Water Permeability of White Cement Mortars. Cement 2022, 9, 8. [Google Scholar] [CrossRef]
- Tong, Y.; Li, Z.; Li, M.; Wang, J.; Seibou, A.-O.; Ye, J. Study on Effect of Pore Structure on the Permeability of Concrete after a Century Natural Carbonation. J. Asian Archit. Build. Eng. 2023, 22, 2867–2875. [Google Scholar] [CrossRef]
- Huang, Z.; Luo, Y.; Zhang, W.; Ye, Z.; Li, Z.; Liang, Y. Thermal Insulation and High-Temperature Resistant Cement-Based Materials with Different Pore Structure Characteristics: Performance and High-Temperature Testing. J. Build. Eng. 2025, 101, 111839. [Google Scholar] [CrossRef]
- Peng, Y.; Tang, S.; Huang, J.; Tang, C.; Wang, L.; Liu, Y. Fractal Analysis on Pore Structure and Modeling of Hydration of Magnesium Phosphate Cement Paste. Fractal Fract. 2022, 6, 337. [Google Scholar] [CrossRef]
- Lü, Q.; Qiu, Q.; Zheng, J.; Wang, J.; Zeng, Q. Fractal Dimension of Concrete Incorporating Silica Fume and Its Correlations to Pore Structure, Strength and Permeability. Constr. Build. Mater. 2019, 228, 116986. [Google Scholar] [CrossRef]
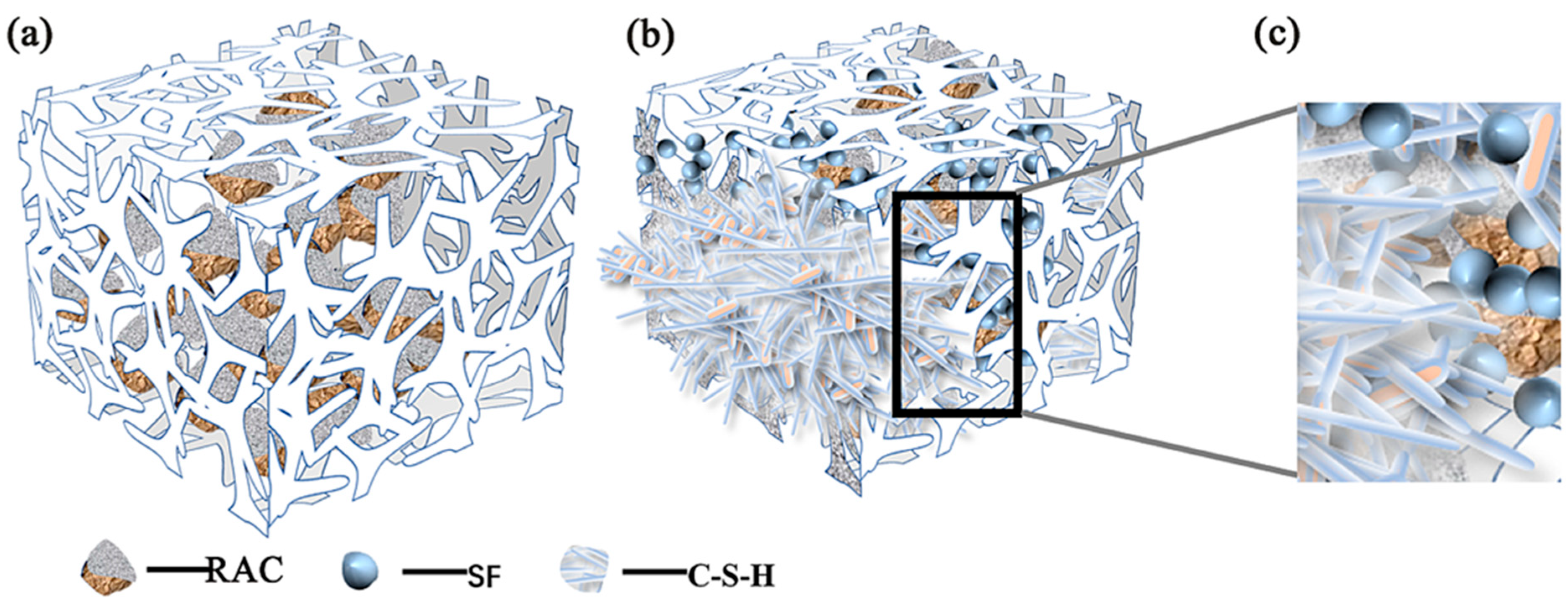
- Gao, S.; Ji, Y.; Qin, Z.; Zhang, H.; Xing, F.; Liu, A. A Comprehensive Analysis of Pore Structures and Performances of Mineral Admixtures Modified Recycled Aggregate Concrete Based on Experiment and Theory. Constr. Build. Mater. 2022, 358, 129451. [Google Scholar] [CrossRef]
- Saha, A.K. Effect of Class F Fly Ash on the Durability Properties of Concrete. Sustain. Environ. Res. 2018, 28, 25–31. [Google Scholar] [CrossRef]
- Kewalramani, M.; Khartabil, A. Porosity Evaluation of Concrete Containing Supplementary Cementitious Materials for Durability Assessment through Volume of Permeable Voids and Water Immersion Conditions. Buildings 2021, 11, 378. [Google Scholar] [CrossRef]
- Zhang, B.; Tan, H.; Shen, W.; Xu, G.; Ma, B.; Ji, X. Nano-Silica and Silica Fume Modified Cement Mortar Used as Surface Protection Material to Enhance the Impermeability. Cem. Concr. Compos. 2018, 92, 7–17. [Google Scholar] [CrossRef]
- Chao, Z.; Wang, H.; Hu, S.; Wang, M.; Xu, S.; Zhang, W. Permeability and Porosity of Light-Weight Concrete with Plastic Waste Aggregate: Experimental Study and Machine Learning Modelling. Constr. Build. Mater. 2024, 411, 134465. [Google Scholar] [CrossRef]
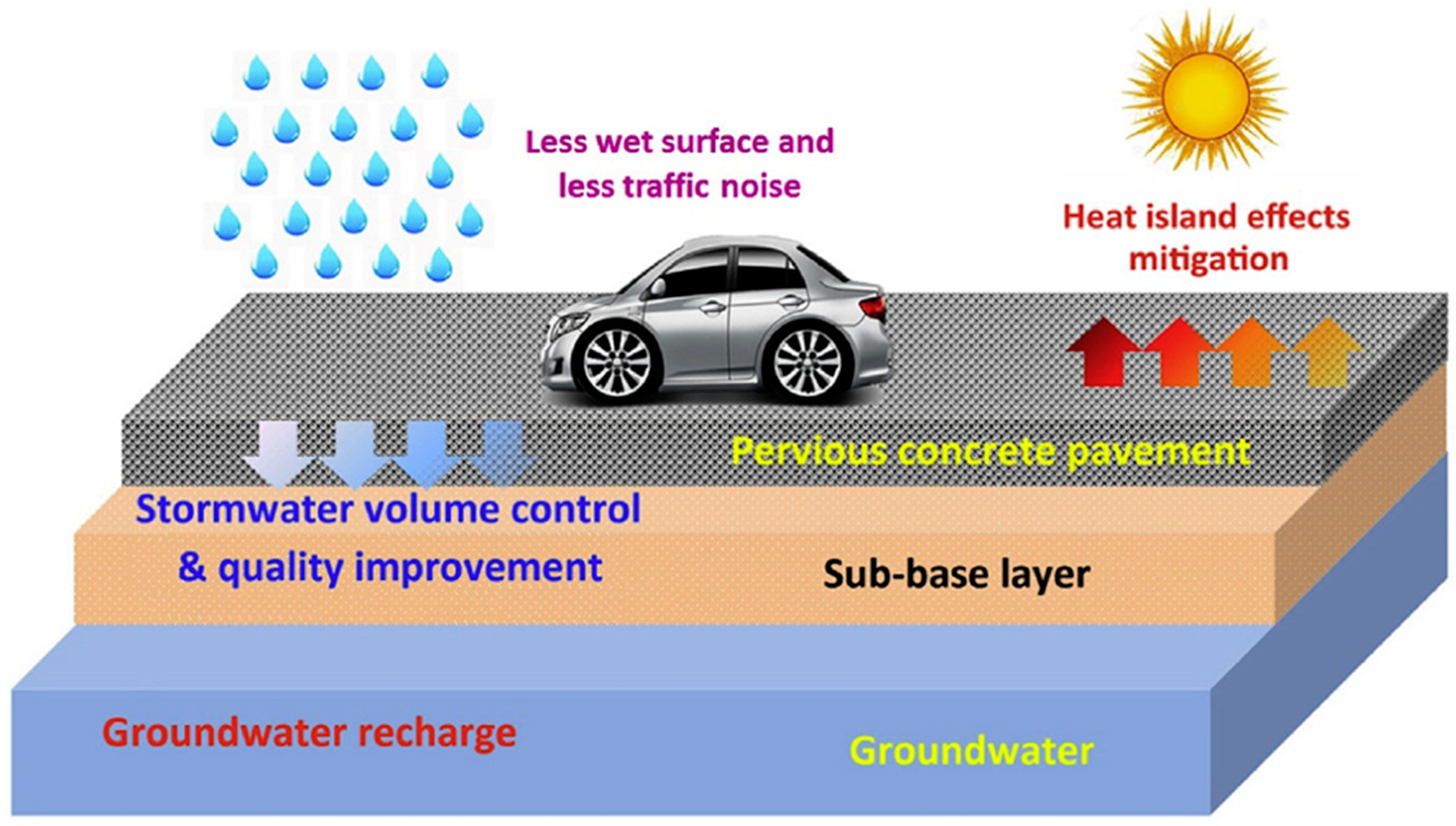
- Xie, N.; Akin, M.; Shi, X. Permeable Concrete Pavements: A Review of Environmental Benefits and Durability. J. Clean. Prod. 2019, 210, 1605–1621. [Google Scholar] [CrossRef]
- Shan, J.; Zhang, Y.; Wu, S.; Lin, Z.; Li, L.; Wu, Q. Pore Characteristics of Pervious Concrete and Their Influence on Permeability Attributes. Constr. Build. Mater. 2022, 327, 126874. [Google Scholar] [CrossRef]
- Mehrabi, P.; Shariati, M.; Kabirifar, K.; Jarrah, M.; Rasekh, H.; Trung, N.T.; Shariati, A.; Jahandari, S. Effect of Pumice Powder and Nano-Clay on the Strength and Permeability of Fiber-Reinforced Pervious Concrete Incorporating Recycled Concrete Aggregate. Constr. Build. Mater. 2021, 287, 122652. [Google Scholar] [CrossRef]
- Jiang, Z.; Atilhan, M.; Ozbulut, O.E. Exploring Optimal Dispersion Process Parameters for Fabrication of Graphene-Reinforced Cement Composites. Constr. Build. Mater. 2023, 372, 130805. [Google Scholar] [CrossRef]
- Zeng, H.; Lai, Y.; Qu, S.; Yu, F. Effect of Graphene Oxide on Permeability of Cement Materials: An Experimental and Theoretical Perspective. J. Build. Eng. 2021, 41, 102326. [Google Scholar] [CrossRef]
- Yang, J.; Ye, C.; Wen, L.; Yu, B.; Tao, W.; Yang, Z.; Yuan, S. Study on the Microscale Structure and Sulfate Attack Resistance of Cement Mortars Containing Graphene Oxide Nanoplatelets. J. Build. Eng. 2023, 78, 107727. [Google Scholar] [CrossRef]
- Luo, J.; Zhou, C.; Li, W.; Chen, S.; Korayem, A.H.; Duan, W. Using Graphene Oxide to Improve Physical Property and Control ASR Expansion of Cement Mortar. Constr. Build. Mater. 2021, 307, 125006. [Google Scholar] [CrossRef]
- Du, H.; Pang, S.D. Enhancement of Barrier Properties of Cement Mortar with Graphene Nanoplatelet. Cem. Concr. Res. 2015, 76, 10–19. [Google Scholar] [CrossRef]
- Win, T.T.; Prasittisopin, L.; Jongvivatsakul, P.; Likitlersuang, S. Investigating the Synergistic Effect of Graphene Nanoplatelets and Fly Ash on the Mechanical Properties and Microstructure of Calcium Aluminate Cement Composites. J. Build. Eng. 2023, 78, 107710. [Google Scholar] [CrossRef]
- Alafogianni, P.; Dassios, K.; Tsakiroglou, C.D.; Matikas, T.E.; Barkoula, N.M. Effect of CNT Addition and Dispersive Agents on the Transport Properties and Microstructure of Cement Mortars. Constr. Build. Mater. 2019, 197, 251–261. [Google Scholar] [CrossRef]
- Li, L.; Jing, H.; Gao, Y.; Hu, T.; Meng, Y.; Fu, G. Influence of Methylcellulose on the Impermeability Properties of Carbon Nanotube-Based Cement Pastes at Different Water-to-Cement Ratios. Constr. Build. Mater. 2020, 244, 118403. [Google Scholar] [CrossRef]
- Gao, Y.; Jing, H.; Zhou, Z.; Shi, X.; Li, L.; Fu, G. Roles of Carbon Nanotubes in Reinforcing the Interfacial Transition Zone and Impermeability of Concrete under Different Water-to-Cement Ratios. Constr. Build. Mater. 2021, 272, 121664. [Google Scholar] [CrossRef]
- Gao, Y.; Jing, H.; Zhou, Z.; Chen, W.; Du, M.; Du, Y. Reinforced Impermeability of Cementitious Composites Using Graphene Oxide-Carbon Nanotube Hybrid under Different Water-to-Cement Ratios. Constr. Build. Mater. 2019, 222, 610–621. [Google Scholar] [CrossRef]
- Chen, H.; Feng, P.; Du, Y.; Jiang, J.; Sun, W. The Effect of Superhydrophobic Nano-Silica Particles on the Transport and Mechanical Properties of Hardened Cement Pastes. Constr. Build. Mater. 2018, 182, 620–628. [Google Scholar] [CrossRef]
- Bai, S.; Yu, L.; Guan, X.; Li, H.; Ou, J. Study on the Long-Term Chloride Permeability of Nano-Silica Modified Cement Pastes Cured at Negative Temperature. J. Build. Eng. 2022, 57, 104854. [Google Scholar] [CrossRef]
- Ramezanianpour, A.A.; Mortezaei, M.; Mirvalad, S. Synergic Effect of Nano-Silica and Natural Pozzolans on Transport and Mechanical Properties of Blended Cement Mortars. J. Build. Eng. 2021, 44, 102667. [Google Scholar] [CrossRef]
- Bai, S.; Yu, L.; Guan, X.; Li, H.; Ou, J. Comparative Study on Effects of Pozzolanic Nano-SiO2 and Non-Pozzolanic Nano-TiO2 on the Microstructure and Macro Properties of Cement Paste Subjected to Early-Age Frost Attack. Cold Reg. Sci. Technol. 2023, 210, 103841. [Google Scholar] [CrossRef]
- Shafaei, D.; Yang, S.; Berlouis, L.; Minto, J. Multiscale Pore Structure Analysis of Nano Titanium Dioxide Cement Mortar Composite. Mater. Today Commun. 2020, 22, 100779. [Google Scholar] [CrossRef]

| Assumption | Implication/Potential Deviation |
|---|---|
| Cylindrical pore (or circular throat) | The Washburn equation is strictly valid only for cylindrical pore throats, because complex geometries modify the pressure-to-radius P → r conversion |
| Constant contact angle and surface tension γ | θ and γ are assumed invariant with pressure and surface chemistry. Coatings, impurities, or heterogeneous surface energies alter θ |
| Rigid structure | The solid matrix is assumed incompressible. In soft solids (e.g., silica gels and aerogels), elastic compression modifies the intrusion curve |
| Nonwetting condition. Quasistatic flow | Partial wetting phenomena are neglected, and capillary equilibrium is assumed. At high intrusion-pressurization rates, hysteresis increases |
| Mercury assumed incompressible | Introduces a small error (<1%) at 400 MPa, generally neglected |
| Effect | Interpretational Consequence |
|---|---|
| Ink-bottle effect | If a wide pore communicates with the exterior through a narrow throat, the intrusion pressure records the throat (small r), whereas the wider portion fills a much larger volume. Upon depressurization, extrusion is governed by the throat and hysteresis appears. The actual cavity size remains hidden. |
| Interparticle porosity intrusion | Interparticle voids fill first and can mask the intraparticle porosity distribution. This is usually mitigated by applying a pressure cutoff (e.g., 30–100 kPa) to exclude that volume. |
| Hysteresis and entrapped mercury | A fraction of Hg remains trapped during pressure decrease (“entrapment”), particularly under rapid depressurization. This complicates the determination of the extruded volume and the quantification of open versus blind (dead-end) pores. |
| Compressibility of the sample | Powders or foams may compact prior to intrusion, artificially reducing the accessible volume and shifting the intrusion curve. |
| Lower pore size limit (≈3–4 nm) | Micropores are not detected. Complement with gas adsorption (N2, Ar, CO2). |
| Assumption of homogeneous wettability | Surface-treated materials (e.g., silanes and organics) locally alter θ, introducing a systematic error in r. |
| Technique | Type of Technique | Applicable Pore Size and Type | Strengths | Limitations | Destructive |
|---|---|---|---|---|---|
| Helium Pycnometry | Skeletal Density by Gas Displacement | ~0.1 nm–100 µm (Micropores to Macropores) | High precision; non-destructive; indirect method | No pore size distribution; excludes open voids | No |
| Mercury Intrusion Porosimetry (MIP) | Pore Size by Mercury Pressure Invasion | ~3.6 nm–950 µm (Mesopores to Macropores) | Wide pore range; connectivity characterization | Destructive; toxic; assumes cylindrical pores; no info on closed porosity | Yes |
| N2 Adsorption (BET/BJH) | Surface Area and Mesopores by Gas Adsorption | ~2–50 nm (Mesopores) | High sensitivity; surface area and pore volume; non-destructive | Not suitable for macropores; degassing required; limited in micropores (<2 nm) | No |
| NMR Relaxometry | Pore Distribution by Magnetic Resonance | ~10 nm–100 µm (Mesopores to Macropores) | Non-destructive; total porosity and distribution | Expensive equipment; complex interpretation; no info on closed pores | No |
| Optical Microscopy | Surface Pore Observation by Light Microscopy | >1 µm (Macropores) | Simple; low cost; visual and digital analysis; mineral ID | No 3D info; polish quality affects results; limited to visible pores | Yes (thin-section preparation) |
| SEM (Scanning Electron Microscopy) | Pore Geometry by Electron Imaging | ~0.05 µm–100s µm (Mesopores to Macropores) | High-resolution 2D imaging; shape and orientation analysis; automatable | Small field of view; 2D only; sample prep required; no closed pores | Yes (sample preparation) |
| FIB-SEM Tomography | 3D Serial Sectioning by Focused Ion Beam + SEM | ~10 nm–50 µm (Micro- to Mesopores) | Nanometre 3D resolution; pore morphology and connectivity; closed pores visualized | Small sample volume; time-consuming; destructive | Yes |
| Synchrotron µCT (SRµCT) | X-ray Tomography with Synchrotron Radiation | ~50 nm–100 µm (Micro- to Macropores) | High-resolution 3D imaging; phase contrast; non-destructive; in situ studies possible | Limited access to synchrotron; data-intensive; sample size limited | No |
| CLSM (Confocal Laser Scanning Microscopy) | Optical 3D Imaging by Laser Scanning | ~0.3–5 µm (Visible Pores) | Optical 3D imaging; hydrated sample possible; non-destructive; fast | Limited depth penetration; resolution limited by optics | No |
| Deep Learning Segmentation | Digital Image Analysis by Neural Networks | Varies (depends on image input) | Robust, automated pore segmentation; adaptable to noisy data; minimal user bias | Requires training data; model generalization varies | No (applies to image post-processing) |
| X-ray Ptychography/Nano-CT | Coherent Diffraction/Nano-resolution CT | ~10–100 nm (Micropores) | Ultra-high resolution; access to closed pores; no sectioning required | Very limited availability; sample size very small; complex data processing | No |
| Technique | Type of Technique | Applicable Pore Size and Type | Strengths | Limitations | Destructive |
|---|---|---|---|---|---|
| Gas Permeametry (N2, He) | Steady-State Flow via Darcy’s Law (with Klinkenberg Correction) | ~10−21 to 10−14 m2 (Nanopores to Micropores) | High sensitivity and resolution; ideal for dense, dry specimens; provides intrinsic permeability; rapid testing | Assumes cylindrical pores and laminar flow; inaccurate for cracked or saturated materials; not reliable below ~10−18 m2 without advanced setups | No |
| Classical Hydraulic Permeametry | Steady-State Flow with Water or Brine | ~10−18 to 10−12 m2 (Micropores to Mesopores) | Direct measurement; applicable to soils, rocks, concretes; standardized across materials | Requires full saturation; sensitive to air bubbles; very slow for low-k materials | No |
| Transient Pressure Methods (Pulse/Slug Tests) | Pressure–Relaxation Analysis (Gas or Liquid) | ~10−22 to 10−13 m2 (Ultralow to Low Permeability) | Rapid and sample-efficient; ideal for tight materials; no steady-state needed | Loses accuracy for high-k materials; non-unique response in fractured or heterogeneous media; lacks mass-balance check | No |
| Image-Based (e.g., µCT + Simulation) | Digital Twin via Stokes–Brinkman Simulation | <10−20 m2 (Nanopores to Micropores) | Non-invasive; resolves anisotropy; works with very small or damaged samples | Depends on image quality, segmentation accuracy, and assumptions; validation required | No |
| NMR Relaxometry and Indirect Correlations | Magnetic Relaxation Mapping + Empirical Models | Material dependent; calibrated to known samples | Fast; no real flow required; applicable to microporous rocks and concrete | Requires calibration dataset; not direct; lower reliability for certification | No |
| Field Infiltration (e.g., Guelph, Ring Infiltrometer) | In situ Quasi-Steady Flow | ~10−14 to 10−10 m2 (Soils to Aggregates) | Minimal disturbance; captures real-field conditions; fast for shallow layers | Sensitive to soil heterogeneity, surface conditions, and water level control | No |
| Degradation Mechanism | Influence of Porosity | Influence of Permeability |
|---|---|---|
| Freeze–thaw |
|
|
| Chloride attack |
|
|
| Sulphate attack |
|
|
| Carbonation |
|
|
| Concept | Benefits | Challenges |
|---|---|---|
| Fractal theory in modelling porosity | A detailed mathematical model which provides clear numerical comparison | More experimental evidence is needed to make models more robust |
| Considering porosity in modelling of concrete degradation | A more complex model including an important factor of porosity | Optimization of modelling approaches, more experimental evidence |
| Controlling of porosity through mix design | Multiple well-established and reliable additions | Mix design of ecological concretes with waste materials is complex |
| Pervious concrete | A way of using high permeability in a beneficial way | A more complex mix design to combine high permeability with other properties |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ortiz-Marqués, A.; Caldevilla, P.; Goldmann, E.; Safuta, M.; Fernández-Raga, M.; Górski, M. Porosity and Permeability in Construction Materials as Key Parameters for Their Durability and Performance: A Review. Buildings 2025, 15, 3422. https://doi.org/10.3390/buildings15183422
Ortiz-Marqués A, Caldevilla P, Goldmann E, Safuta M, Fernández-Raga M, Górski M. Porosity and Permeability in Construction Materials as Key Parameters for Their Durability and Performance: A Review. Buildings. 2025; 15(18):3422. https://doi.org/10.3390/buildings15183422
Chicago/Turabian StyleOrtiz-Marqués, Almudena, Pablo Caldevilla, Eryk Goldmann, Małgorzata Safuta, María Fernández-Raga, and Marcin Górski. 2025. "Porosity and Permeability in Construction Materials as Key Parameters for Their Durability and Performance: A Review" Buildings 15, no. 18: 3422. https://doi.org/10.3390/buildings15183422
APA StyleOrtiz-Marqués, A., Caldevilla, P., Goldmann, E., Safuta, M., Fernández-Raga, M., & Górski, M. (2025). Porosity and Permeability in Construction Materials as Key Parameters for Their Durability and Performance: A Review. Buildings, 15(18), 3422. https://doi.org/10.3390/buildings15183422









