Study on Maximum Temperature Under Multi-Factor Influence of Tunnel Fire Based on Machine Learning
Abstract
1. Introduction
2. Theoretical Analysis
3. Data Collection
3.1. Experimental Model
3.2. FDS Numerical Simulation Model
3.2.1. Fire Source Setting
3.2.2. Boundary Condition Setting
3.2.3. Grid Sensitivity Analysis
3.2.4. Verification of Model Accuracy
3.3. Fire Scenarios
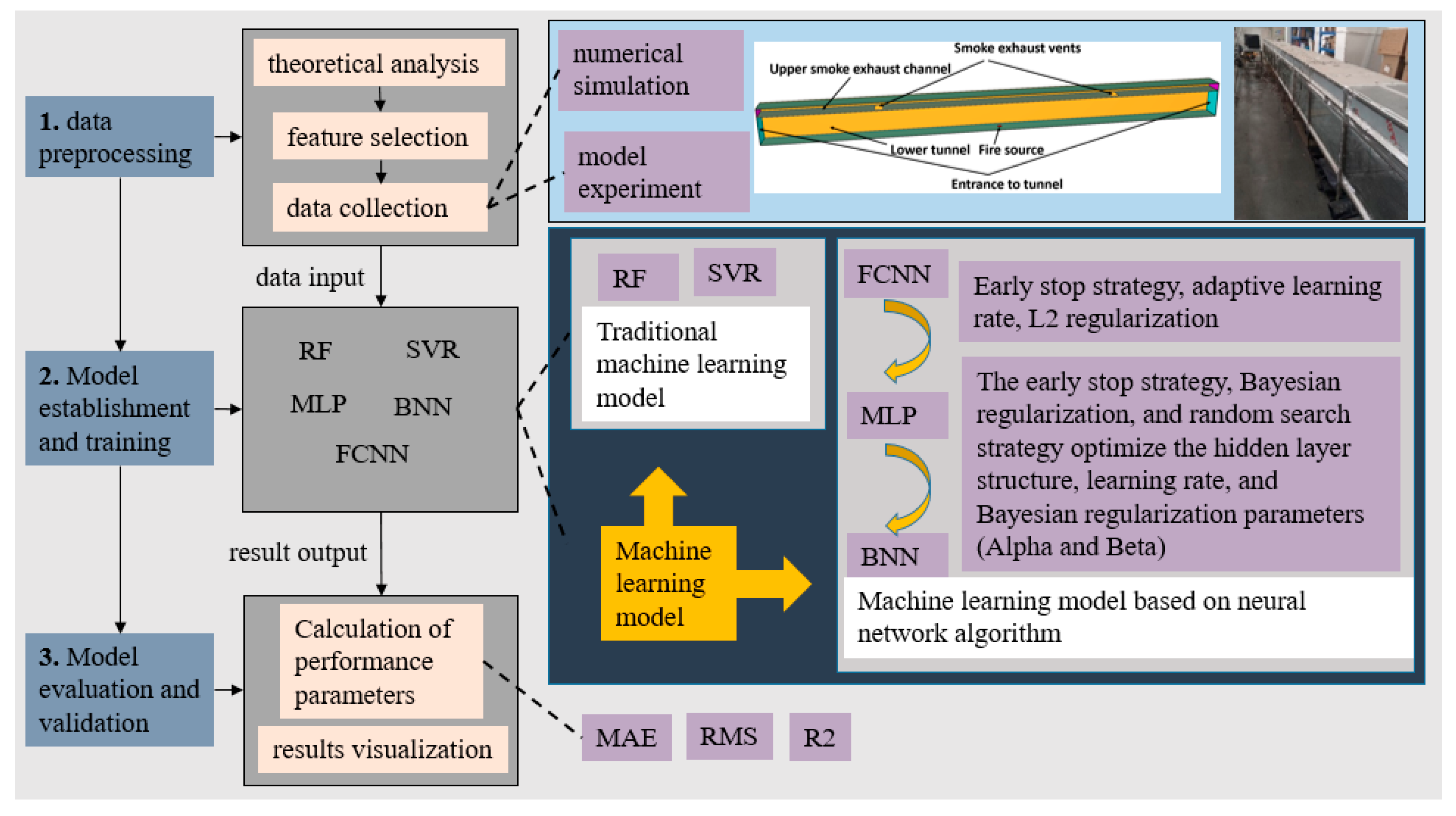
4. Establishment of Machine Learning Regression Prediction Models
4.1. Data Preprocessing
- (1)
- Feature selection
- (2)
- Standardization processing
- (3)
- Dataset partitioning
4.2. Model Establishment and Training
- (1)
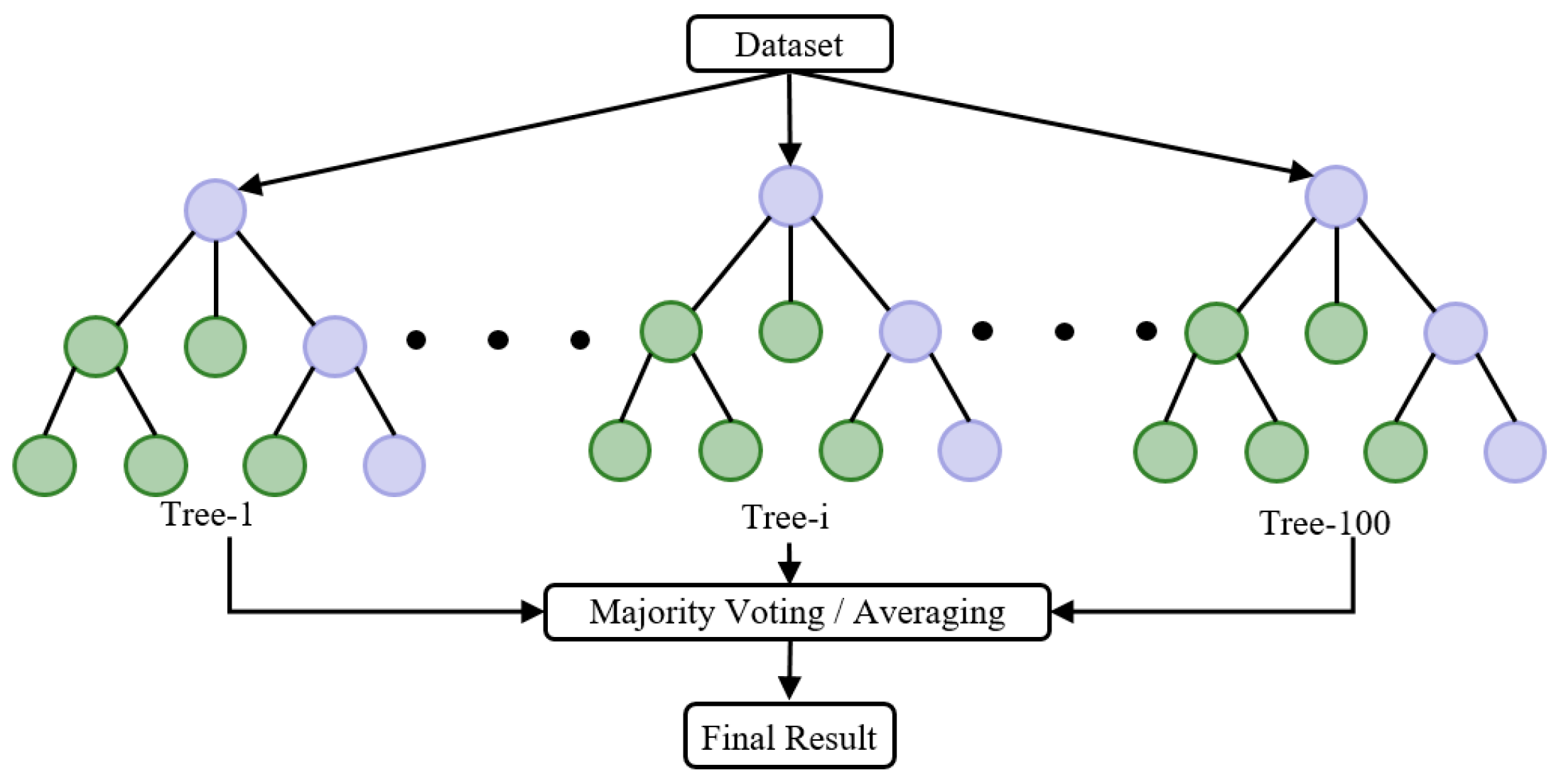
- Random Forest (RF) model
- (2)
- Support Vector Regression (SVR) model
- (3)
- Fully Connected Neural Network (FCNN) model
- (4)
- Multilayer Perceptron (MLP) model
- Increase the maximum number of iterations to 2000.
- Increase the early stopping patience value, and terminate training when the validation set error does not decrease 50 consecutive times to prevent overfitting.
- Adaptive learning rate: initial rate = 0.01, increase factor = 1.05, decrease factor = 0.7.
- L2 regularization with weight decay = 0.001.
- (5)
- Bayesian Neural Network (BNN) model
- Parameter search: a stochastic search strategy optimizes the hidden layer architecture, learning rate, and Bayesian regularization parameters (α, β). Stochastic search is chosen for its superior efficiency in high-dimensional parameter spaces, which is particularly well-suited for multi-parameter optimization. The hyperparameter search space encompasses:
- b.
- BNN Training with Bayesian regularization: The BNN model is trained using the Bayesian regularization training algorithm (trainbr). In scenarios with limited data, manual tuning of the L2 regularization parameter (λ) often leads to overfitting or underfitting. Bayesian regularization addresses this challenge by treating model parameters as random variables, introducing prior distributions, and maximizing the posterior probability to constrain model complexity automatically. The objective function is formulated as:
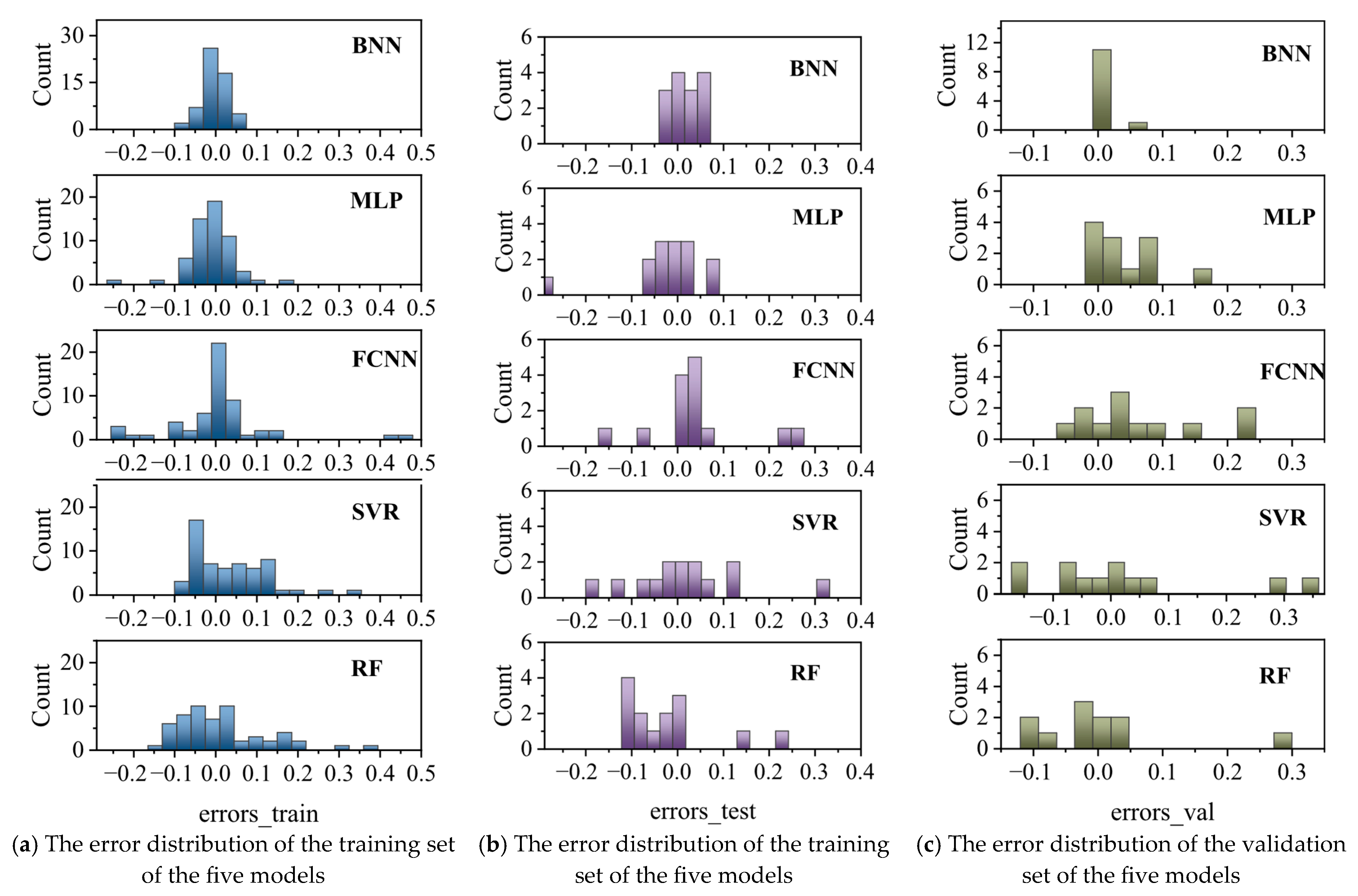
4.3. Model Evaluation
4.4. Model Application and Expansion
- (1)
- Fire source: Single fire source;
- (2)
- Smoke exhaust layout: Tunnel with symmetric two-point smoke exhaust;
- (3)
- Environmental and structural parameters: Ambient pressure (40–100 kPa), tunnel slope (0–6%), rectangular cross-section, full-scale height (5–15 m), and width (5 m).
- (1)
- Incorporate scenario-specific physical features and refine the feature vector system to align model inputs with the new scenario’s physical mechanisms;
- (2)
- Supplement experimental/simulation data of out-of-bound scenarios to expand training sample coverage, thus mitigating increased generalization errors caused by data distribution shift.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alarie, Y. Toxicity of fire smoke. Crit. Rev. Toxicol. 2002, 32, 259–289. [Google Scholar] [CrossRef]
- Javadi, P.; Askari, M.; Vahedi, S.; GhafourianHesami, A.; Tizchang, A. Retrofit of RC buildings using vertical shear links and hybrid connections. Structures 2023, 48, 1788–1807. [Google Scholar] [CrossRef]
- Islam, R.; Lattimer, B.Y. Understanding the Impact of Fuel on Surfactant Microstructure of Firefighting Foam. Fire Technol. 2024, 60, 3413–3441. [Google Scholar] [CrossRef]
- Zhong, W.; Liu, L.; Han, N.; Gao, Z.; Zhao, J. Investigation on the maximum ceiling temperature of the weak plume impingement flow in tunnel fires under longitudinal ventilation. Tunn. Undergr. Space Technol. 2023, 131, 104821. [Google Scholar] [CrossRef]
- Alpert, R.L. Calculation of Response Time of Ceiling-Mounted Fire Detectors. Fire Technol. 1972, 8, 181–195. [Google Scholar] [CrossRef]
- Kurioka, H.; Oka, Y.; Satoh, H.; Sugawa, O. Fire properties in near field of square fire source with longitudinal ventilation in tunnels. Fire Saf. J. 2003, 38, 319–340. [Google Scholar] [CrossRef]
- Hu, L.H.; Huo, R.; Peng, W.; Chow, W.K.; Yang, R.X. On the maximum smoke temperature under the ceiling in tunnel fires. Tunn. Undergr. Space Technol. 2006, 21, 650–655. [Google Scholar] [CrossRef]
- Li, Y.Z.; Lei, B.; Ingason, H. The maximum temperature of buoyancy-driven smoke flow beneath the ceiling in tunnel fires. Fire Saf. J. 2011, 46, 204–210. [Google Scholar] [CrossRef]
- Li, Y.Z.; Ingason, H. The maximum ceiling gas temperature in a large tunnel fire. Fire Saf. J. 2012, 48, 38–48. [Google Scholar] [CrossRef]
- Liu, F.; Yu, L.X.; Weng, M.C.; Lu, X.L. Study on longitudinal temperature distribution of fire-induced ceiling flow in tunnels with different sectional coefficients. Tunn. Undergr. Space Technol. 2016, 54, 49–60. [Google Scholar] [CrossRef]
- Ji, J.; Wang, Z.; Ding, L.; Yu, L.; Gao, Z.; Wan, H. Effects of ambient pressure on smoke movement and temperature distribution in inclined tunnel fires. Int. J. Therm. Sci. 2019, 145, 106006. [Google Scholar] [CrossRef]
- Wang, Y. Study of Combustion Characteristics and Smoke Flow Control Method of Highway Tunnel in Very High Altitude Area. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, 2019. [Google Scholar]
- Wang, Q.; Wang, S.; Liu, H.; Shen, J.; Shang, F.; Shi, C.; Tang, F. Characterization of ceiling smoke temperature profile and maximum temperature rise induced by double fires in a natural ventilation tunnel. Tunn. Undergr. Space Technol. 2020, 96, 103233. [Google Scholar] [CrossRef]
- He, K.; Li, Y.Z.; Ingason, H.; Shi, L.; Cheng, X. Experimental study on the maximum ceiling gas temperature driven by double fires in a tunnel with natural ventilation. Tunn. Undergr. Space Technol. 2024, 144, 105550. [Google Scholar] [CrossRef]
- Beya, O.; Hittawe, M.; Sidibe, D.; Meriaudeau, F. Automatic detection and tracking of animal sperm cells in microscopy images. In Proceedings of the 2015 11th International Conference on Signal-Image Technology & Internet-Based Systems (SITIS), Bangkok, Thailand, 23–27 November 2015; pp. 155–159. [Google Scholar]
- Hittawe, M.M.; Harrou, F.; Sun, Y.; Knio, O. Stacked Transformer Models for Enhanced Wind Speed Prediction in the Red Sea. In Proceedings of the 2024 IEEE 22nd International Conference on Industrial Informatics (INDIN), Beijing, China, 18–20 August 2024. [Google Scholar]
- Wang, Z.; Zhang, T.; Wu, X.; Huang, X. Predicting transient building fire based on external smoke images and deep learning. J. Build. Eng. 2022, 47, 103823. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, X.; Huang, X.; Xiao, F.; Usmani, A. A real-time forecast of tunnel fire based on numerical database and artificial intelligence. Build. Simul. 2022, 15, 511–524. [Google Scholar] [CrossRef]
- Cheng, J.; Yang, N.; Jiang, S.; Xiong, C. Real-time forecast of tunnel fire scenario and hazard based on external smoke images. Tunn. Undergr. Space Technol. 2025, 158, 106377. [Google Scholar] [CrossRef]
- Yan, F.; Jiang, Y.; Chen, Y.; Xu, Z.-D. A data-driven model for tunnel fire scenario deduction based on optimized informer. Meas. Sci. Technol. 2025, 36, 108102. [Google Scholar] [CrossRef]
- Sun, B.; Liu, X.; Xu, Z.-D.; Xu, D. Temperature data-driven fire source estimation algorithm of the underground pipe gallery. Int. J. Therm. Sci. 2022, 171, 107247. [Google Scholar] [CrossRef]
- Guo, C.; Guo, Q.; Zhang, T.; Li, W.; Zhu, H.; Yan, Z. Study on real-time heat release rate inversion for dynamic reconstruction and visualization of tunnel fire scenarios. Tunn. Undergr. Space Technol. 2022, 122, 104333. [Google Scholar] [CrossRef]
- Hu, P.; Peng, X.; Tang, F. Prediction of maximum ceiling temperature of rectangular fire against wall in longitudinally ventilation tunnels: Experimental analysis and machine learning modeling. Tunn. Undergr. Space Technol. 2023, 140, 105275. [Google Scholar] [CrossRef]
- Liu, W.; Deng, L.; Li, H.; Li, X.; Shi, C.; Meng, N.; Tang, F. Experimental study and machine learning on the maximum temperature beneath tunnel ceiling induced by adjacent tandem fires in longitudinally ventilated tunnel. Int. J. Therm. Sci. 2023, 187, 108169. [Google Scholar] [CrossRef]
- Li, M.; Jiang, Y.; Wu, Z.; Fan, R. Real-Time Prediction of Smoke Spread Affected by Multiple Factors in Subway Tunnel Using CAERES-DNN Model. Fire Technol. 2021, 57, 2025–2059. [Google Scholar] [CrossRef]
- Sun, B.; Liu, X.; Xu, Z.-D.; Xu, D. BP neural network-based adaptive spatial-temporal data generation technology for predicting ceiling temperature in tunnel fire and full-scale experimental Verification. Fire Saf. J. 2022, 130, 103577. [Google Scholar] [CrossRef]
- Sun, B.; Xu, Z.-D.; Zhou, H. A multiple back propagation neural network fusion algorithm for ceiling temperature prediction in tunnel fires. Eng. Struct. 2023, 280, 115601. [Google Scholar] [CrossRef]
- Liu, X.; Sun, B.; Xu, Z.-D.; Liu, X.; Xu, D. Identification of Multiple Fire Sources in the Utility Tunnel Based on a Constrained Particle Swarm Optimization Algorithm. Fire Technol. 2022, 58, 2825–2845. [Google Scholar] [CrossRef]
- Yang, W.; Chen, Z.; Zhao, H.; Chen, S.; Shi, C. Feature fusion method for rock mass classification prediction and interpretable analysis based on TBM operating and cutter wear data. Tunn. Undergr. Space Technol. 2025, 157, 106351. [Google Scholar] [CrossRef]
- Zukoski, E.E.; Kubota, T.; Cetegen, B. Entrainment in Fire Plumes. Fire Saf. J. 1980, 107–121. [Google Scholar] [CrossRef]
- Karlsson, B.; Quintiere, J.G. Enclosure Fire Dynamics; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Zhao, P.; Yuan, Z.; Liang, C.; Yuan, Y.; Xie, Y.; Yu, N. Experimental investigation on ceiling temperature characteristics induced by weak and strong fire plumes in tunnel fires equipped with two-point extraction ventilation using smoke extraction channel. Tunn. Undergr. Space Technol. 2022, 124, 104487. [Google Scholar] [CrossRef]
- Yan, G.; Wang, M.; Yu, L.; Tian, Y. Effects of ambient pressure on the critical velocity and back-layering length in longitudinal ventilated tunnel fire. Indoor Built Environ. 2020, 29, 1017–1027. [Google Scholar] [CrossRef]
- Hu, L.; Wang, Q.; Delichatsios, M.; Tang, F.; Zhang, X.; Lu, S. Flame height and liftoff of turbulent buoyant jet diffusion flames in a reduced pressure atmosphere. Fuel 2013, 109, 234–240. [Google Scholar] [CrossRef]
- Xu, T.; Tang, F.; Xu, X.; He, Q. Impacts of ambient pressure on the stability of smoke layers and maximum smoke temperature under ceiling in ventilated tunnels. Indoor Built Environ. 2023, 32, 85–97. [Google Scholar] [CrossRef]
- Tan, T.; Yu, L.; Ding, L.; Gao, Z.; Ji, J. Numerical investigation on the effect of ambient pressure on mechanical smoke extraction efficiency in tunnel fires. Fire Saf. J. 2021, 120, 103136. [Google Scholar] [CrossRef]
- Yang, Y.; Long, Z.; Cheng, H.; Chen, J.; Liu, C.; Zhong, M. Experimental and numerical study of smoke temperature distribution characteristics in a sloped tunnel. Sustain. Cities Soc. 2021, 73, 103091. [Google Scholar] [CrossRef]
- Qu, H. Study on Natural Ventilation Smoke Gas Characteristics and Smoke Control of Sloped Tunnel Fires with Roof Openings. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2022. [Google Scholar]
- Zhao, P.; Yuan, Z.; Yu, N.; Liang, C. Effect of heat release rate and exhaust vent settings on the occurrence of plug-holing during tunnel fires with two-point extraction ventilation. Tunn. Undergr. Space Technol. 2020, 106, 103617. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, R.; Xia, Z.; Ren, F.; Zhao, J.; Zhu, H.; Cheng, X. Numerical study of the characteristics of smoke spread in tunnel fires during construction and method for improvement of smoke control. Case Stud. Therm. Eng. 2022, 34, 102043. [Google Scholar] [CrossRef]
- Li, L.; Du, F.; Yang, Y.; Wei, L.; Huang, F.; Gao, Z.; Song, Y. Research on the smoke mass flow rate in one-dimensional spreading stage in tunnel with multiple fire sources. Case Stud. Therm. Eng. 2022, 31, 101801. [Google Scholar] [CrossRef]
- Kazemipour, A.; Afshin, H.; Farhanieh, B. Numerical-Analytical Assessment of Fire and Ventilation Interaction in Longitudinally Ventilated Tunnels Using Jet Fans. Heat Transf. Eng. 2017, 38, 523–537. [Google Scholar] [CrossRef]
- Liu, J.; He, Y.; Zhou, Z.; Yao, W.; Yuen, R.; Wang, J. The burning behaviors of pool fire flames under low pressure. Fire Mater. 2014, 40, 318–334. [Google Scholar] [CrossRef]
- McGrattan, K.; Hostikka, S.; McDermott, R.; Floyd, J.; Vanella, M. Fire Dynamics Simulator User’s Guide, 6th ed.; NIST: Gaithersburg, MD, USA, 2018. [Google Scholar]
- Ishwaran, H. Theory and Applications of Random Forests; Technical Report; University of Miami: Miami, FL, USA, 2011. [Google Scholar]
- Rhodes, J.S.; Cutler, A.; Moon, K.R. Geometry- and Accuracy-Preserving Random Forest Proximities. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 10947–10959. [Google Scholar] [CrossRef]
- Keshtegar, B.; Piri, J.; Abdullah, R.A.; Hasanipanah, M.; Sabri, M.M.S.; Le, B.N. Intelligent ground vibration prediction in surface mines using an efficient soft computing method based on field data. Front. Public Health 2023, 10, 1094771. [Google Scholar] [CrossRef]
- Lewenstein, M.; Nowak, A. Fully connected neural networks with self-control of noise levels. Phys. Rev. Lett. 1989, 62, 225–228. [Google Scholar] [CrossRef] [PubMed]
- Altunkaynak, A. Prediction of significant wave height using geno-multilayer perceptron. Ocean Eng. 2013, 58, 144–153. [Google Scholar] [CrossRef]
- Thimm, G.; Fiesler, E. High-order and multilayer perceptron initialization. IEEE Trans. Neural Netw. 1997, 8, 349–359. [Google Scholar] [CrossRef] [PubMed]
- Fila, R.J.J.; Attri, S.H.; Sharma, V. Mitigating Overfitting in Deep Learning: Insights from Bayesian Regularization. In Proceedings of the 2024 IEEE Region 10 Symposium (TENSYMP), New Delhi, India, 5–7 April 2024. [Google Scholar]

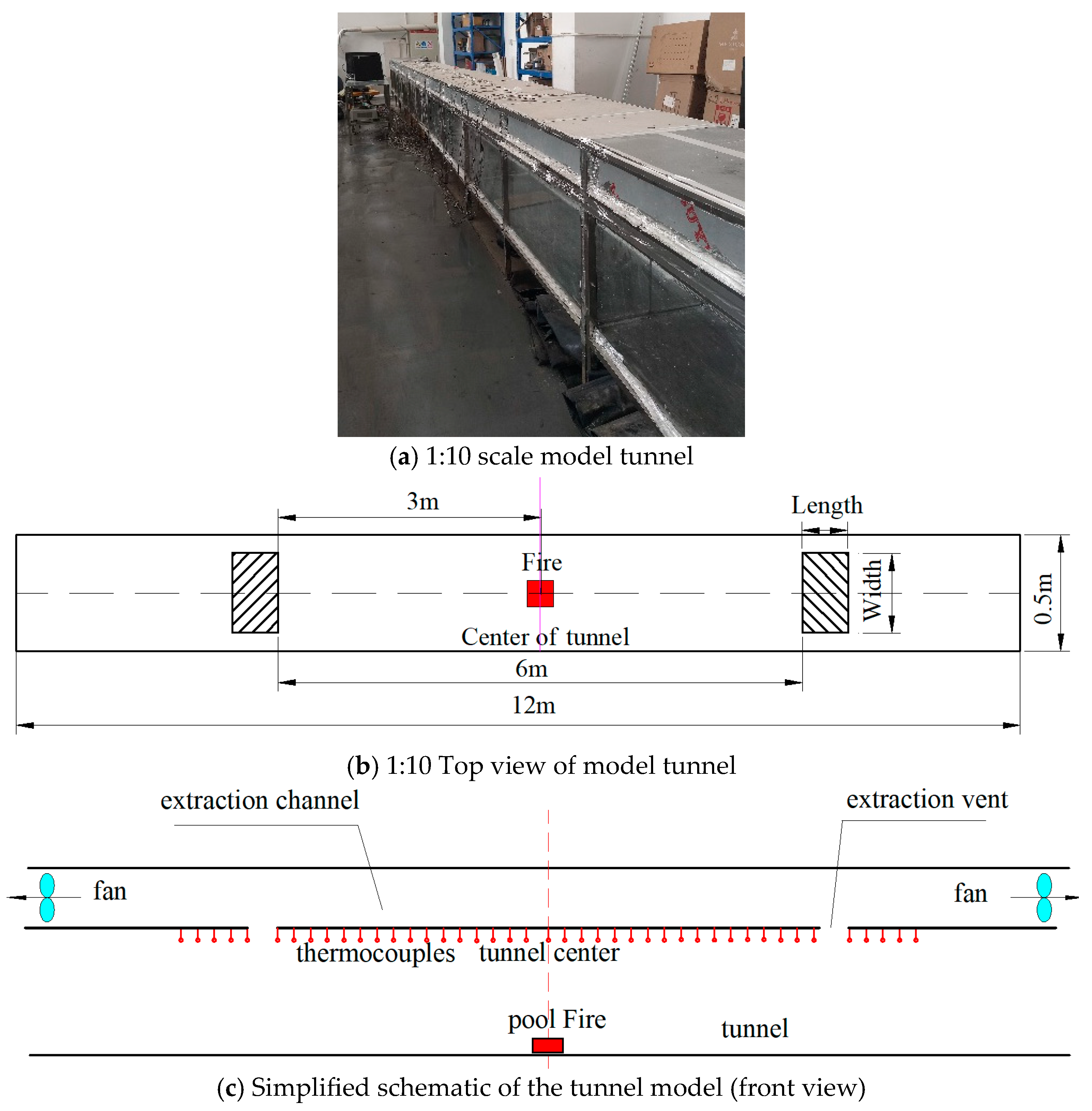


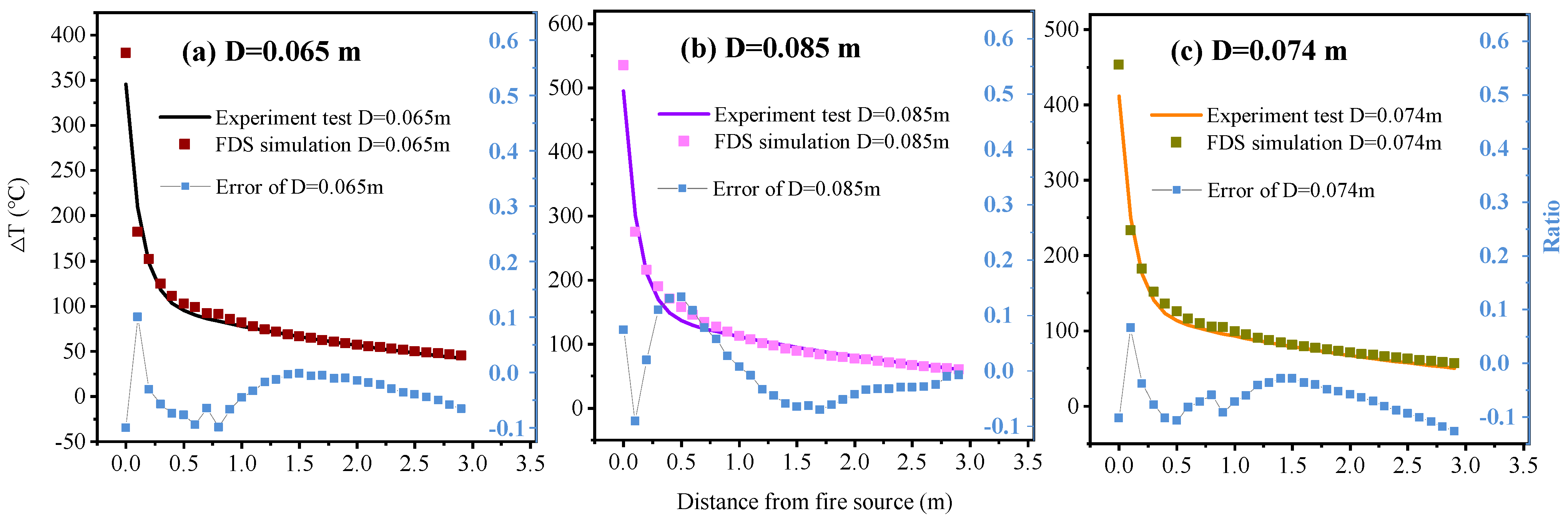
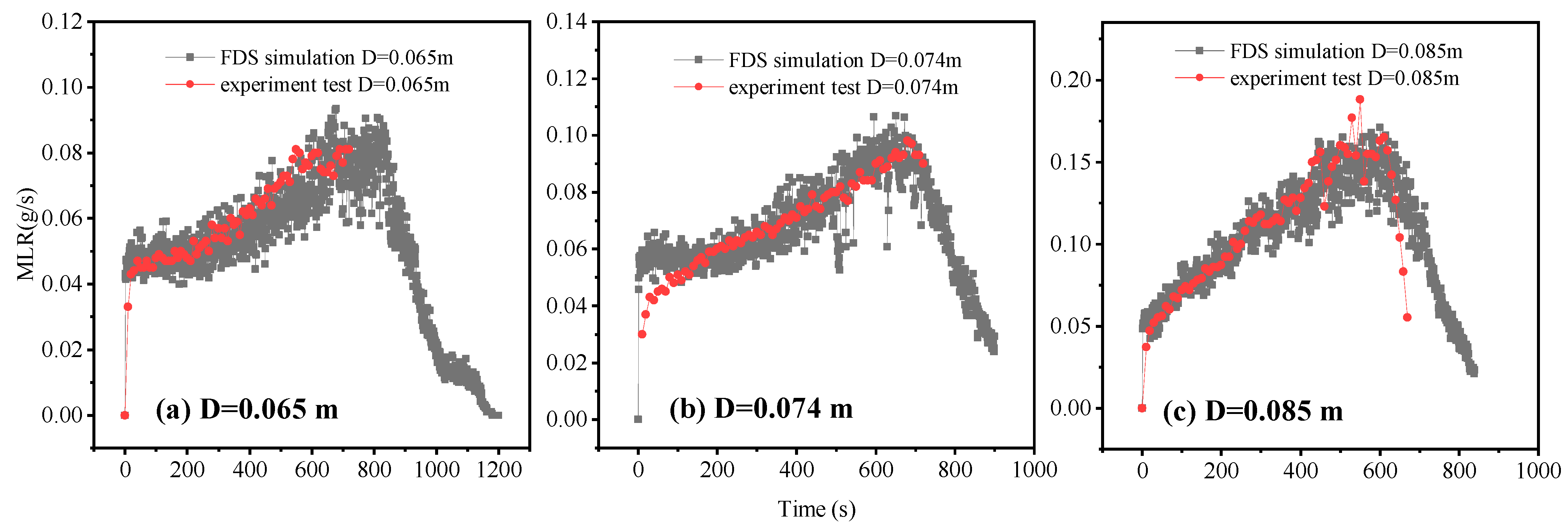


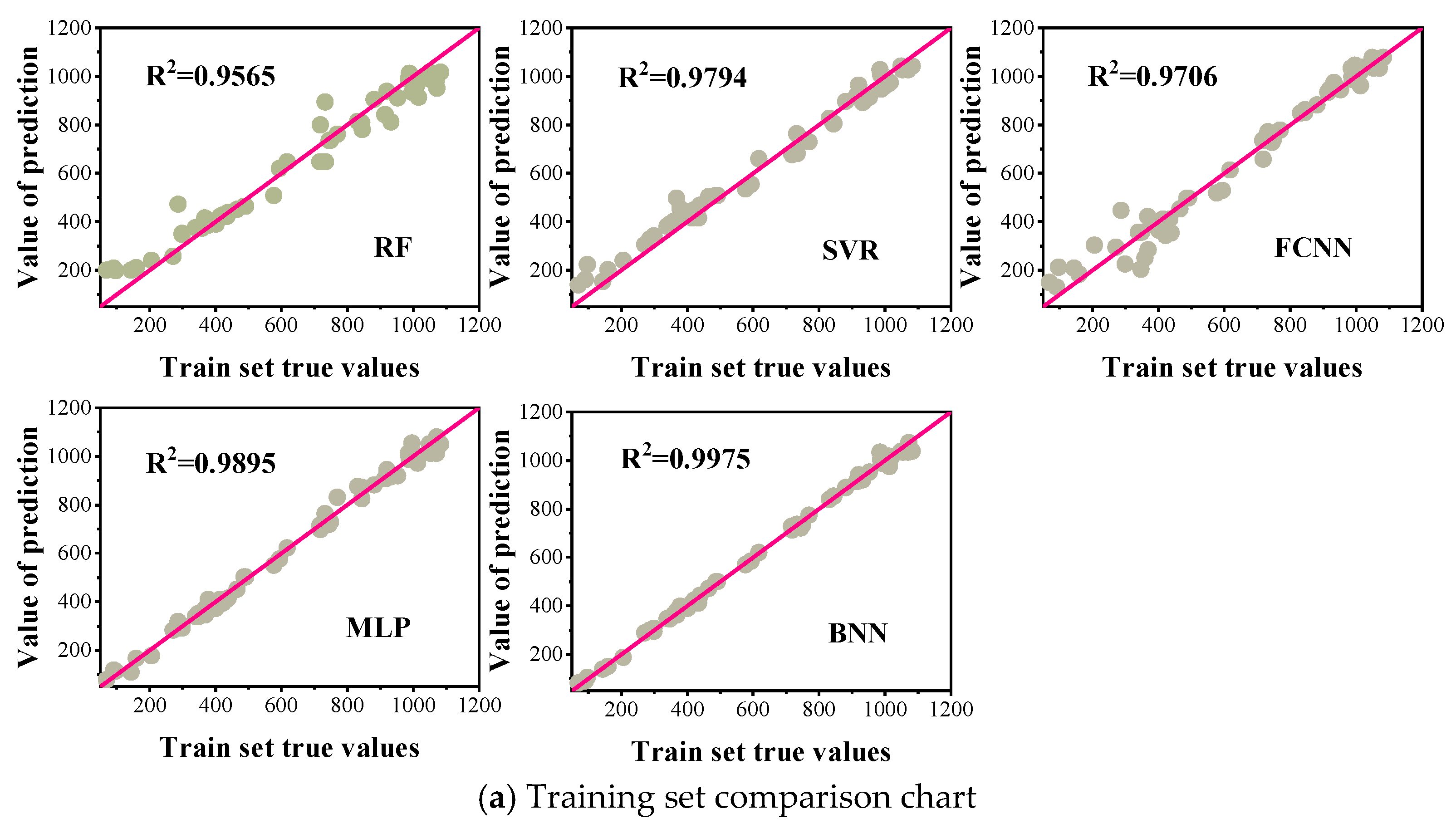
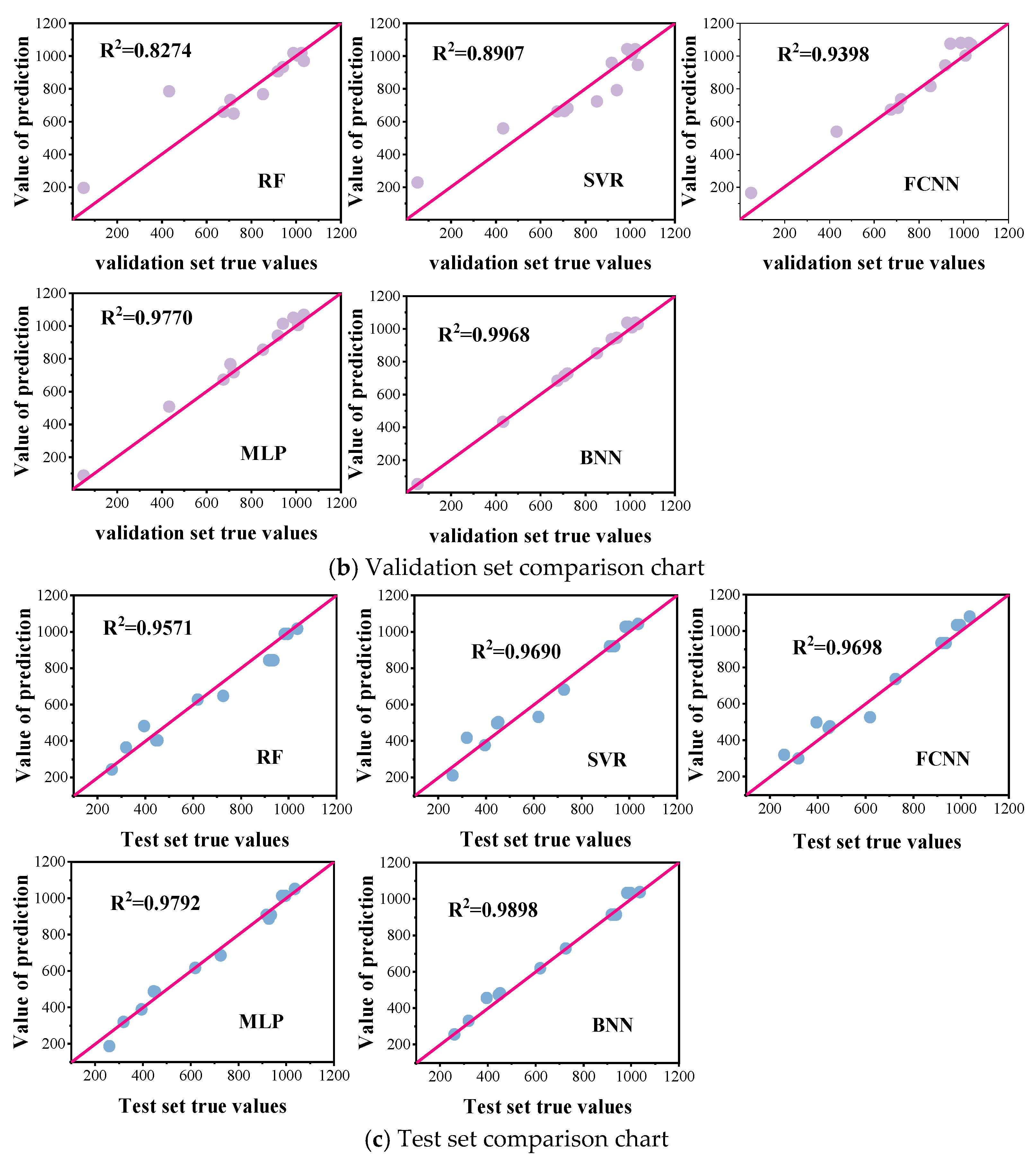
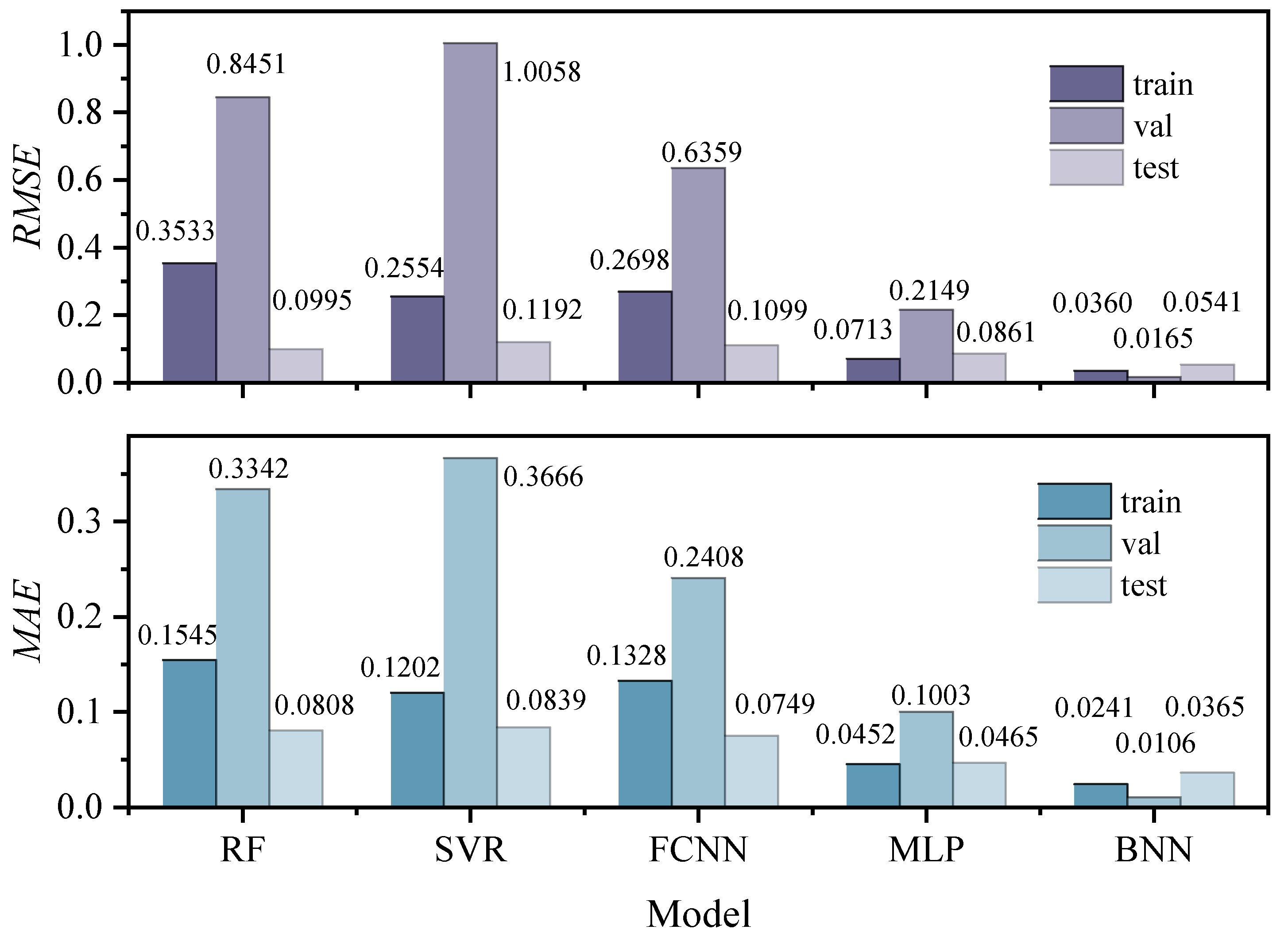

| No. | Series | Research Contents | Tunnel Size (H × W) | Fire Source Setting (HRR/kW, D/m) | P /kPa | Slope i |
|---|---|---|---|---|---|---|
| 1–3 | Normal pressure horizontal tunnel experiment | HRR, P | 0.5 m × 0.5 m | HRR: 4.37/5.68/7.5 D: 0.065/0.074/0.085 | 100 | 0 |
| 3–6 | Low-pressure horizontal tunnel experiment | HRR, P | 0.5 m × 0.5 m | HRR: Obtained from experiments D: 0.065/0.074/0.085 | 66.2 | 0 |
| 7–18 | Multi-pressure horizontal tunnel simulation | HRR, P | 0.5 m × 0.5 m | HRR: Obtained from simulations D: 0.065/0.074/0.085 | 100/80 /60/40 | 0 |
| 19–34 | Multi-pressure horizontal tunnel simulation | HRR, P | 5 m × 5 m | HRR: Obtained from simulations D: 1.15/1.58/2.24/2.72 | 100/80 /60/40 | 0 |
| 35–50 | Simulation of the Inclined Tunnel at H1 | HRR, P, i, H | 7 m × 5 m | HRR: 5000/10,000/20,000/30,000 D: 1.15/1.58/2.24/2.72 | 100 | 0/2%/ 4%/6% |
| 51–62 | Simulation of the Inclined Tunnel at H2 | HRR, P, i, H | 5 m × 5 m | HRR: 5000/10,000/20,000/30,000 D: 1.15/1.58/2.24/2.72 | 100 | 2%/4% /6% |
| 63–70 | Simulation of the Inclined Tunnel at H3 | HRR, P, i, H | 8 m × 5 m | HRR: 5000/10,000/20,000/30,000 D: 1.15/1.58/2.24/2.72 | 100 | 0/2%/ 4%/6% |
| 71–78 | Simulation of the Inclined Tunnel at H4 | HRR, P, i, H | 10 m × 5 m | HRR: 5000/10,000 D: 1.15/1.58 | 100 | 0/2%/ 4%/6% |
| 79–82 | Simulation of the Inclined Tunnel at H5 | P, i, H | 15 m × 5 m | HRR: 5000 D: 1.15 | 100 | 0/2%/ 4%/6% |
| Model | RF | SVR | FCNN | MLP | BNN |
|---|---|---|---|---|---|
| Training time (s) | 0.2288 | 0.1058 | 2.6382 | 2.6382 | 0.6458 |
| Inference time (s) | 0.0957 | 0.0364 | 0.0610 | 0.0151 | 0.0143 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; Yao, G.; Yuan, Z. Study on Maximum Temperature Under Multi-Factor Influence of Tunnel Fire Based on Machine Learning. Buildings 2025, 15, 3401. https://doi.org/10.3390/buildings15183401
Xie Y, Yao G, Yuan Z. Study on Maximum Temperature Under Multi-Factor Influence of Tunnel Fire Based on Machine Learning. Buildings. 2025; 15(18):3401. https://doi.org/10.3390/buildings15183401
Chicago/Turabian StyleXie, Yuanyi, Guanghui Yao, and Zhongyuan Yuan. 2025. "Study on Maximum Temperature Under Multi-Factor Influence of Tunnel Fire Based on Machine Learning" Buildings 15, no. 18: 3401. https://doi.org/10.3390/buildings15183401
APA StyleXie, Y., Yao, G., & Yuan, Z. (2025). Study on Maximum Temperature Under Multi-Factor Influence of Tunnel Fire Based on Machine Learning. Buildings, 15(18), 3401. https://doi.org/10.3390/buildings15183401







