Study on the Ultimate Bearing Capacity Performance of Composite Stiffened Tubular Joints
Abstract
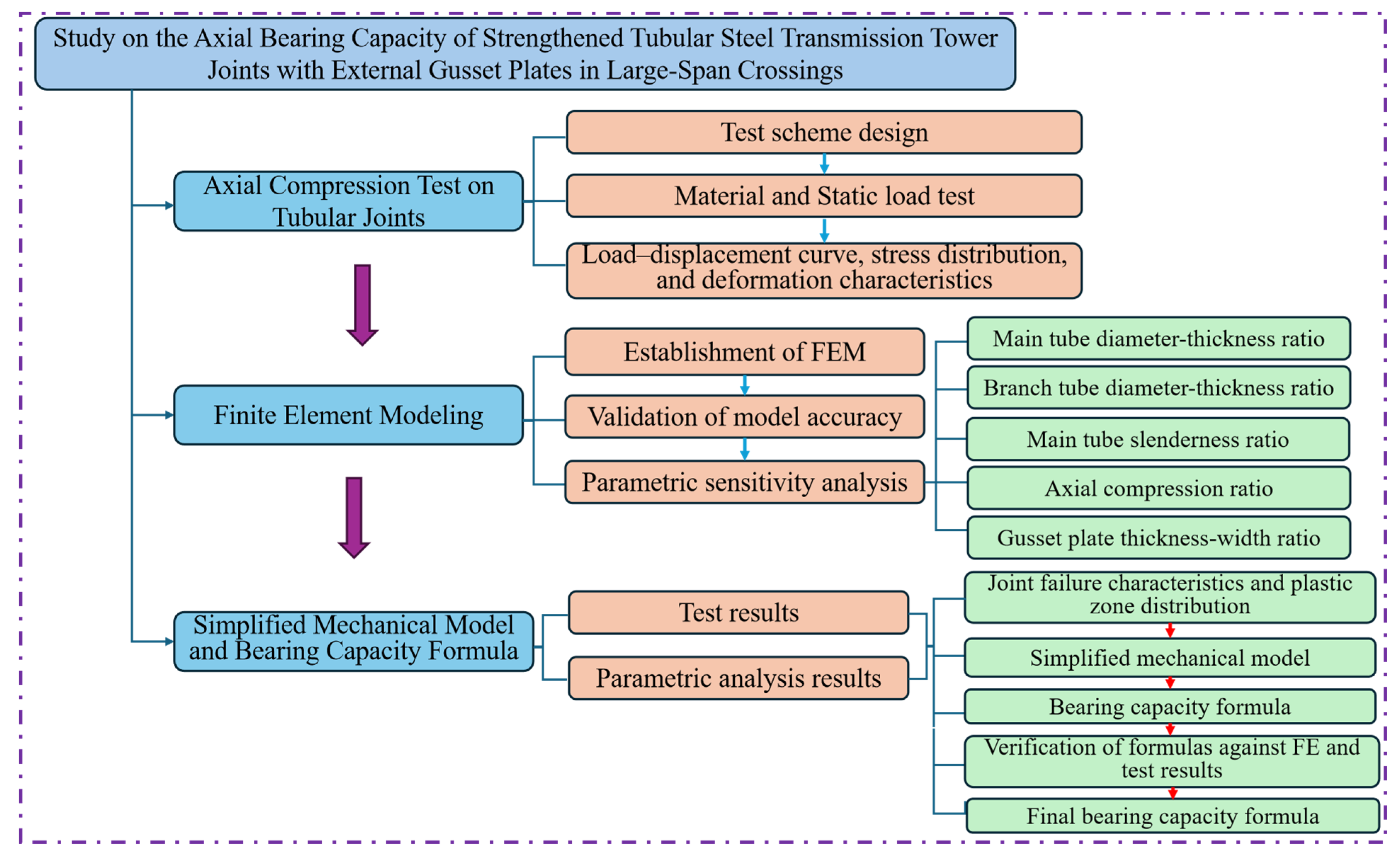
1. Introduction
2. Experimental Program
2.1. Test Units
2.2. Material Property Test
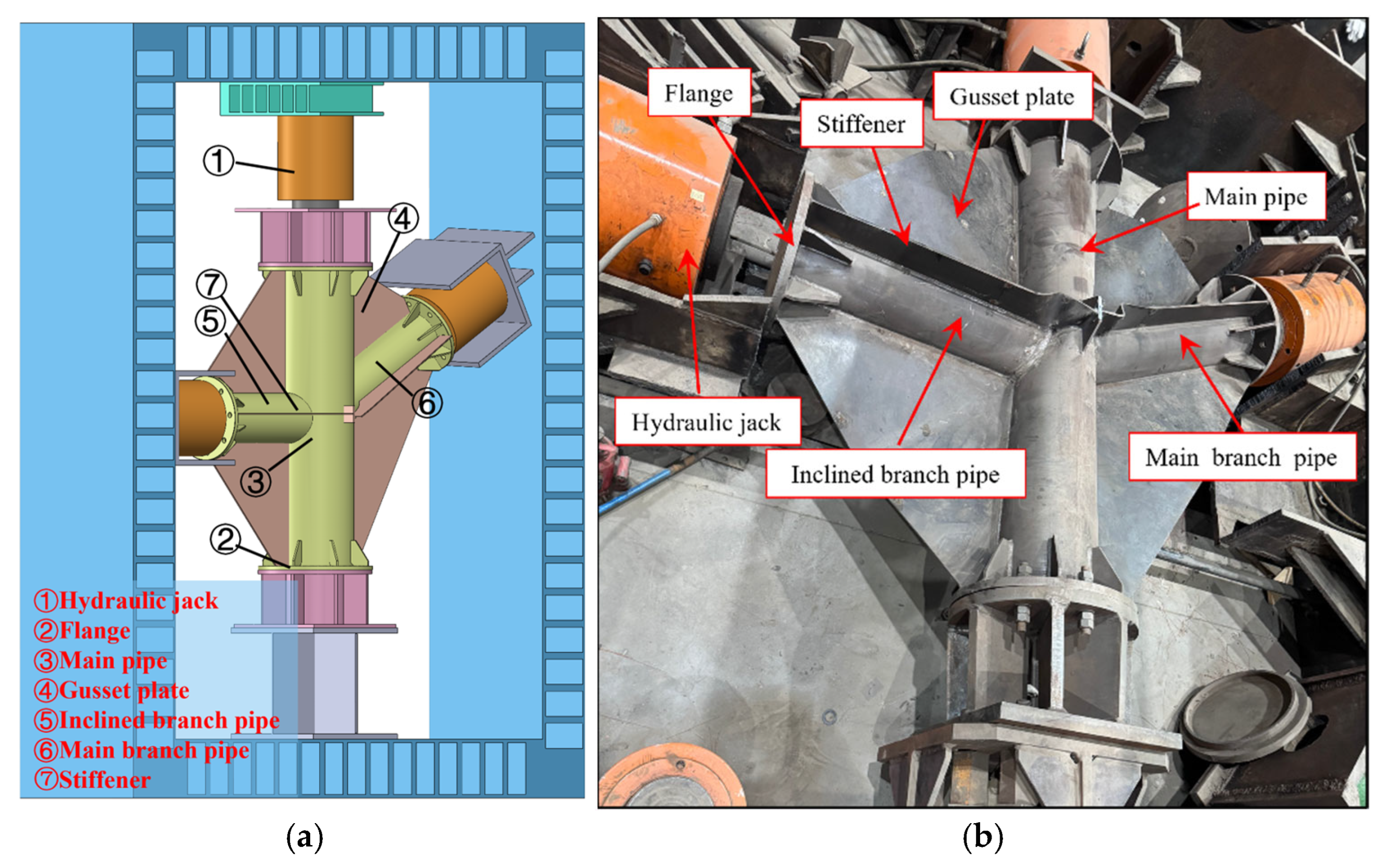
2.3. Loading Device and Loading Scheme
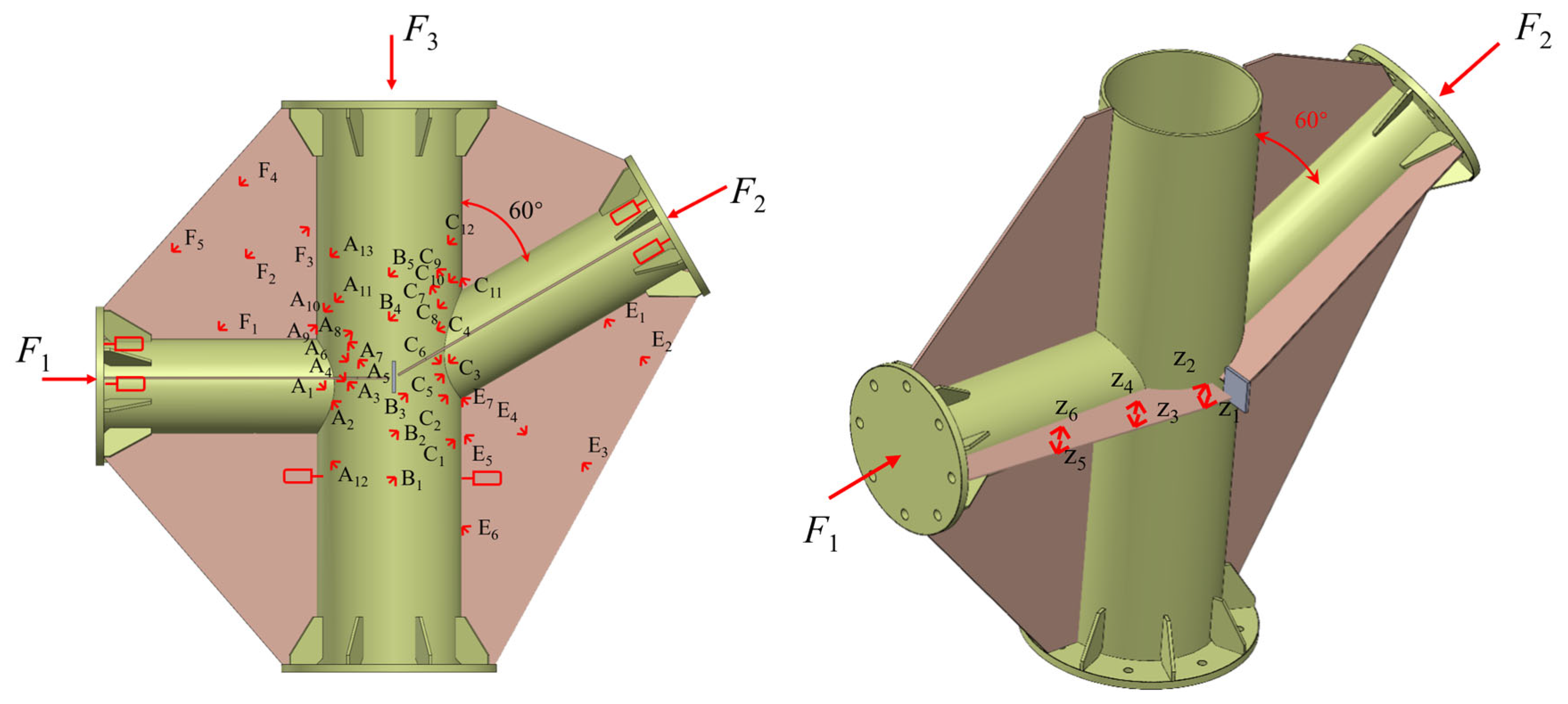
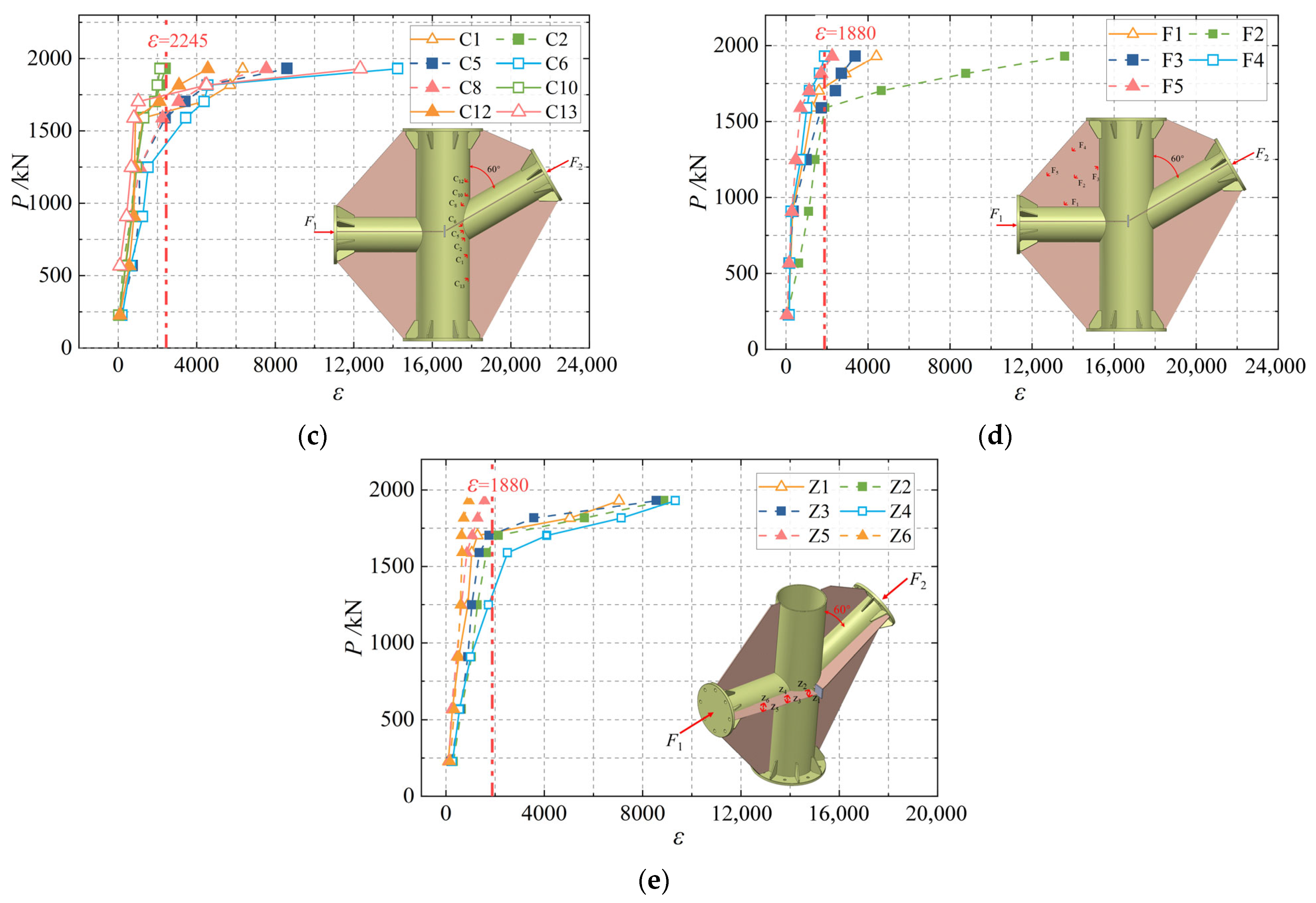
2.4. Arrangement of Displacement Transducers and Strain Gauges
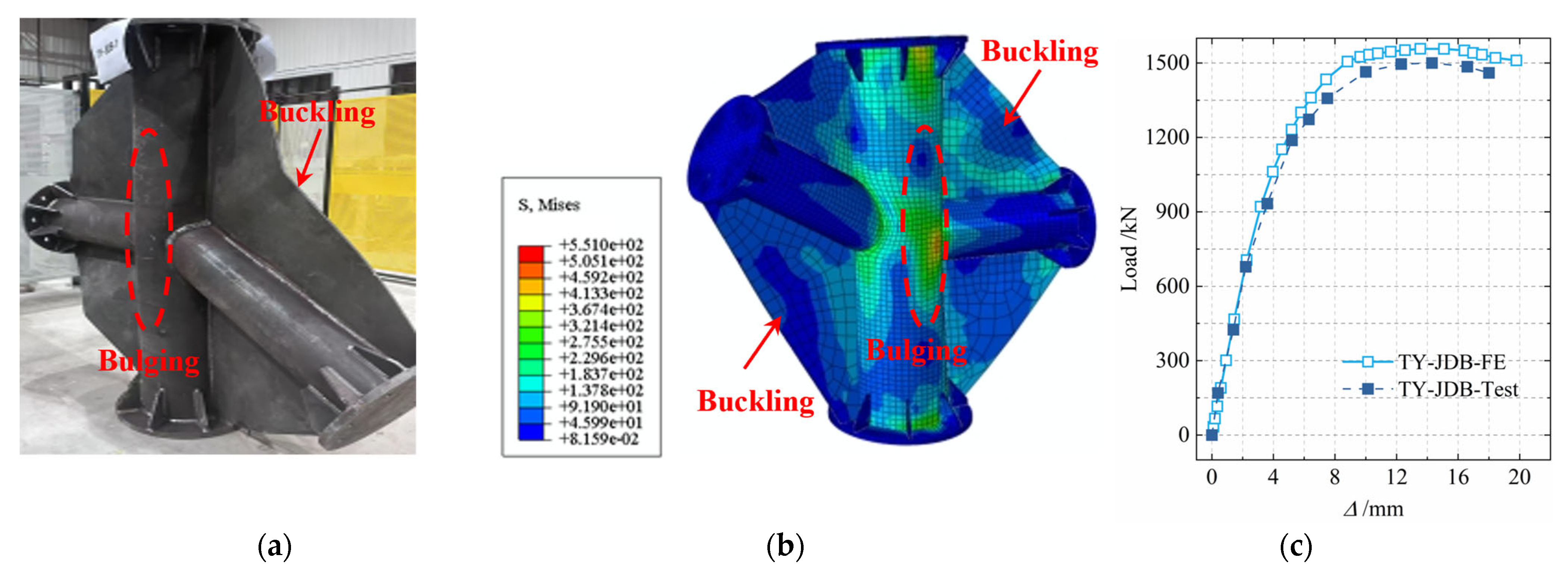
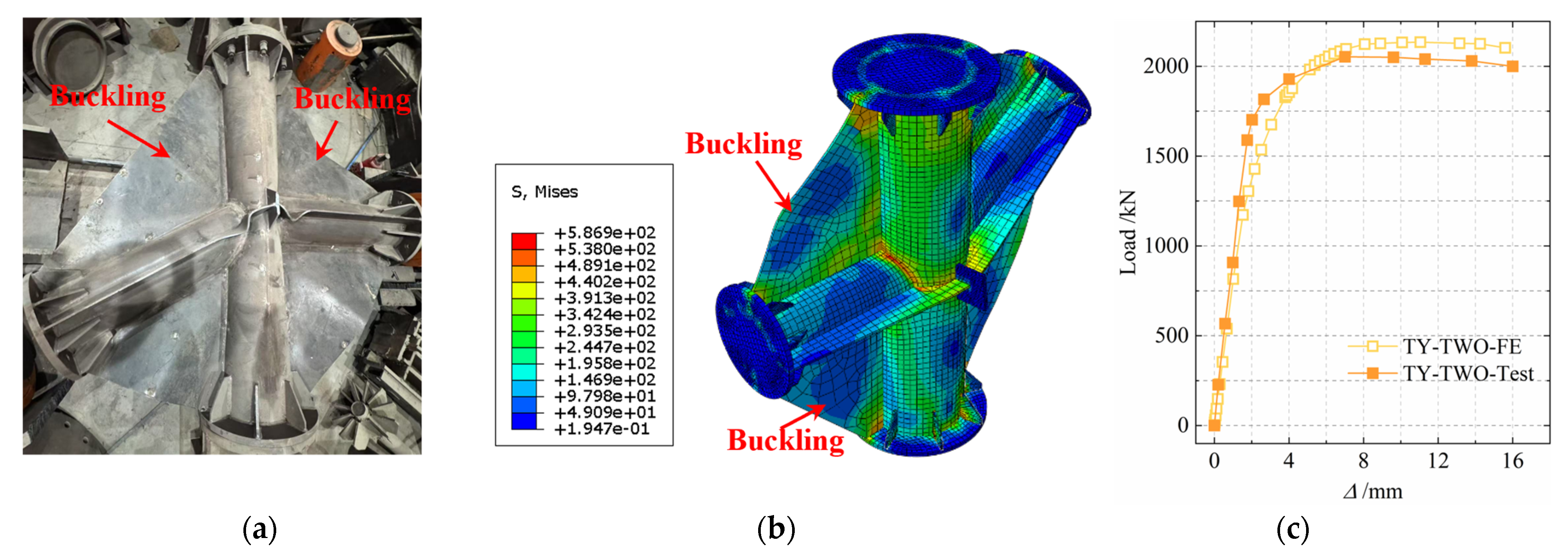
3. Test Phenomena and Failure Modes
4. Test Results and Analysis
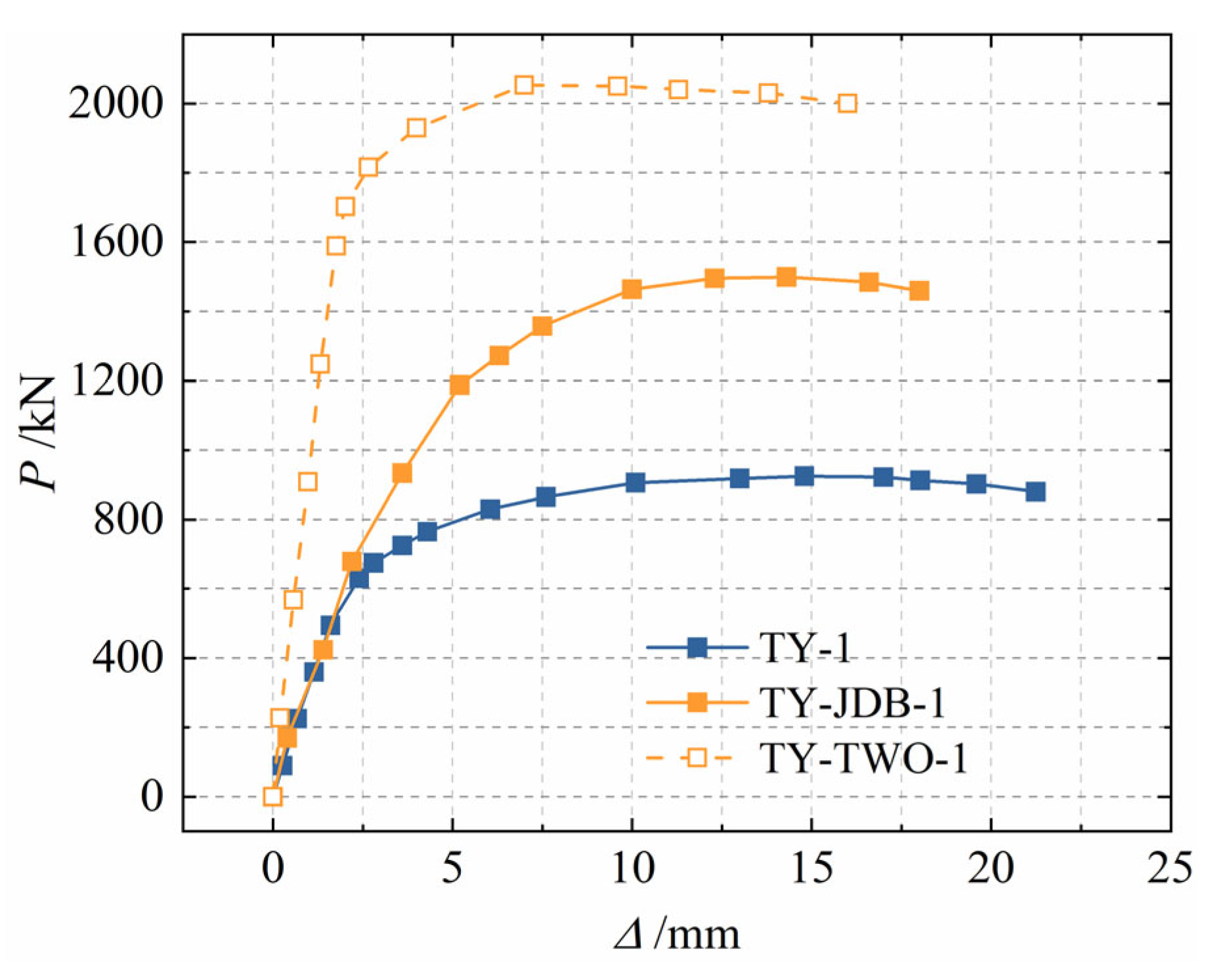
4.1. Analysis of Joint Ultimate Bearing Capacity
- (1)
- Specimen TY-1 is a pure steel joint, and Specimen TY-JDB-1 is a joint with gusset plates. Compared with Specimen TY-1, the initial stiffness of Specimen TY-JDB-1 remains basically unchanged, the loading displacement in the elastic stage is increased by 50%, and the ultimate bearing capacity is increased by 63.6%. It can be seen that the gusset plates can effectively increase the ultimate bearing capacity of the joint and extend the elastic stage of the joint, but have little impact on the initial stiffness of the joint.
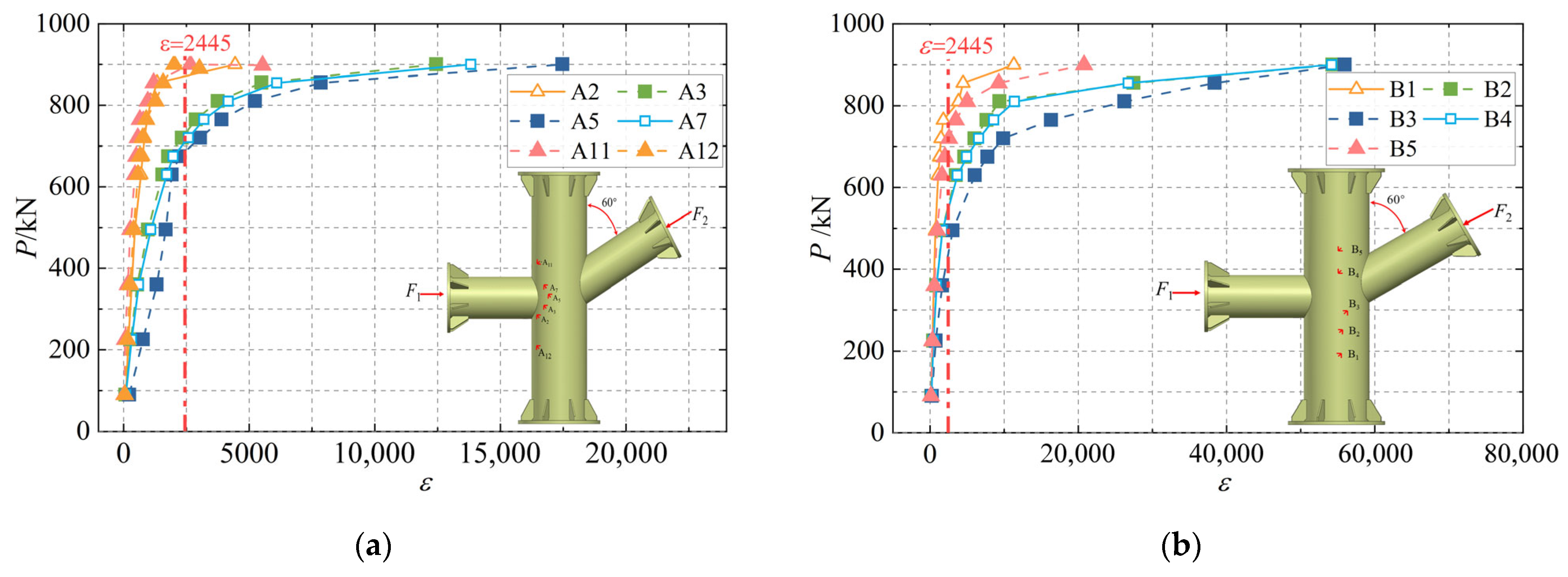
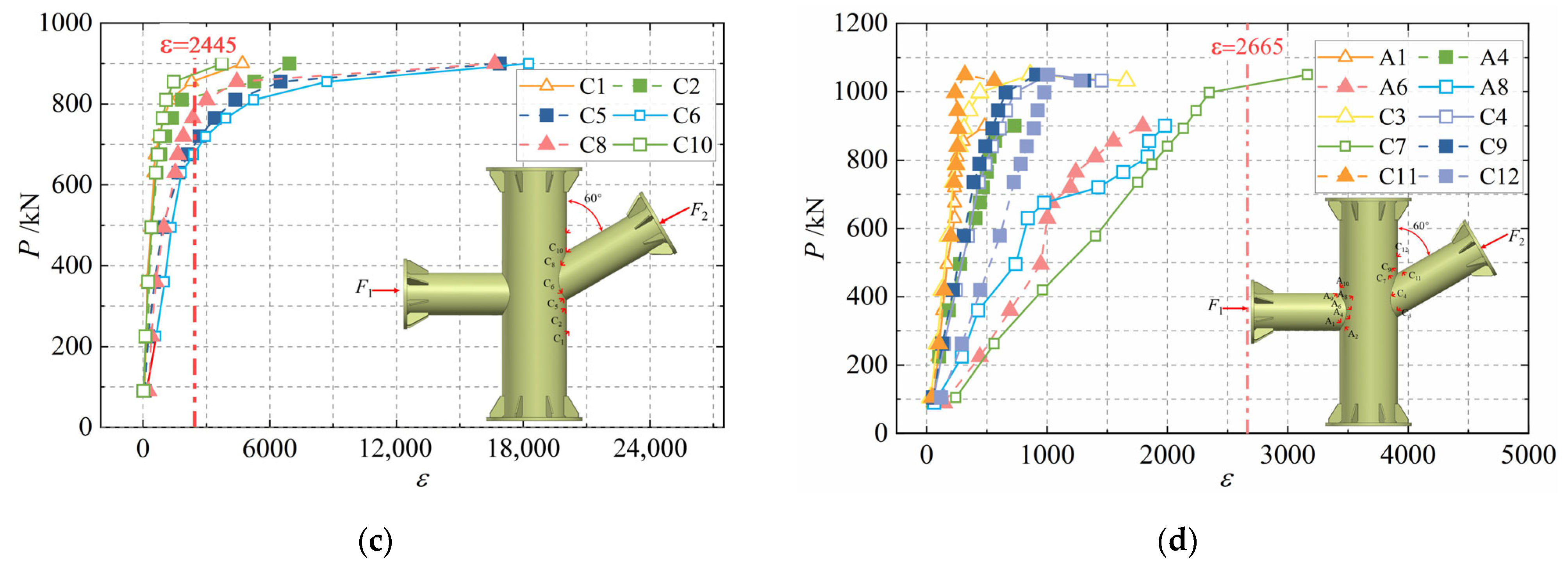
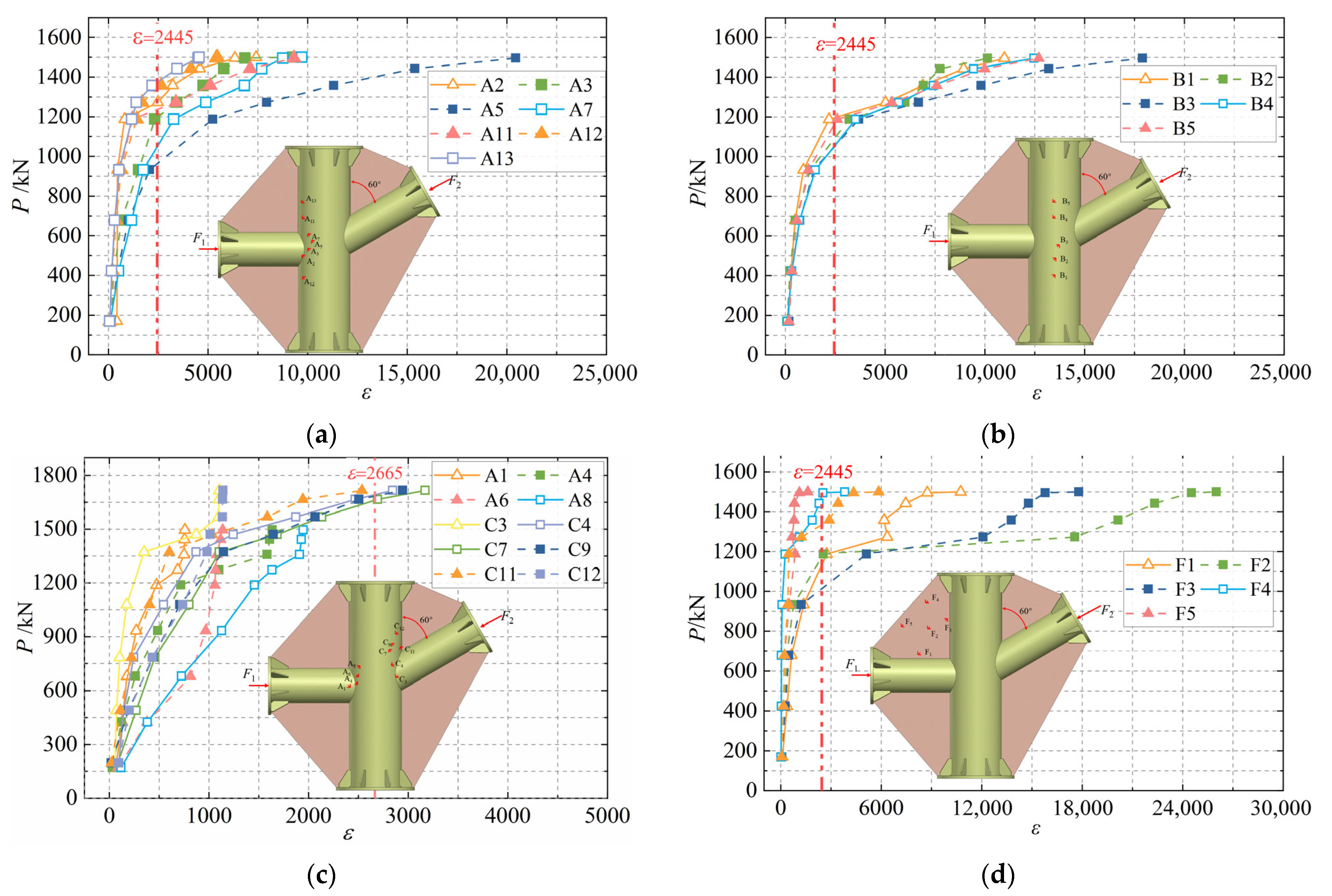
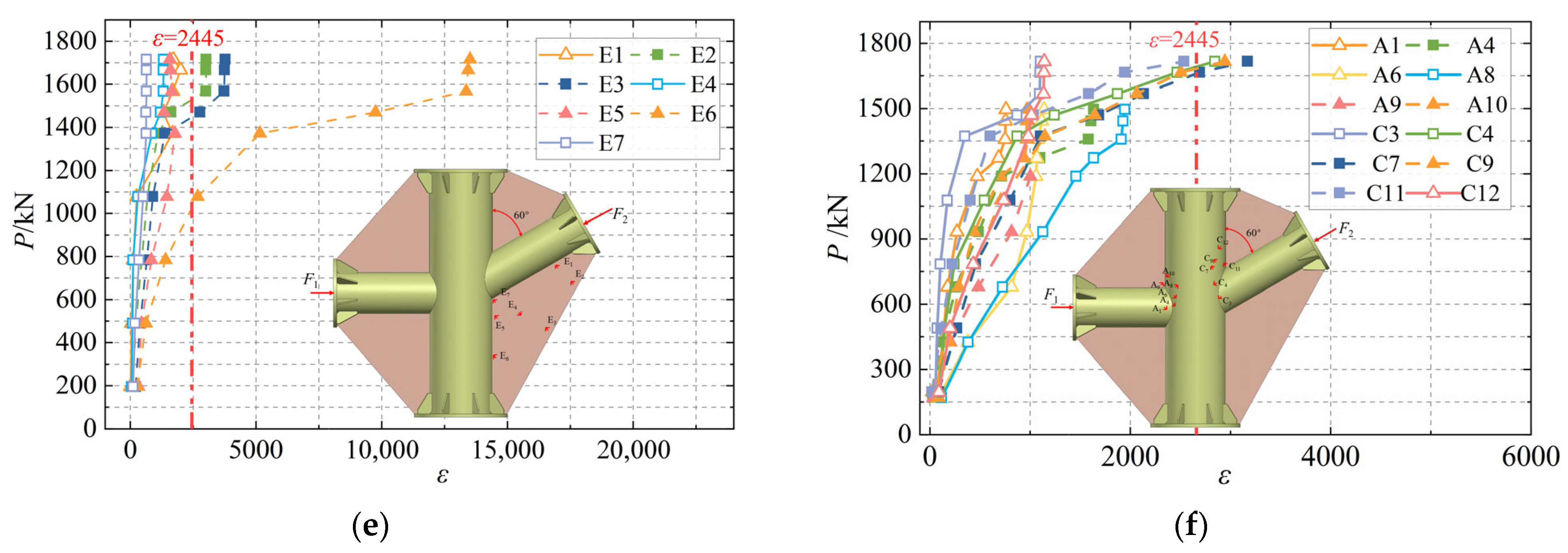
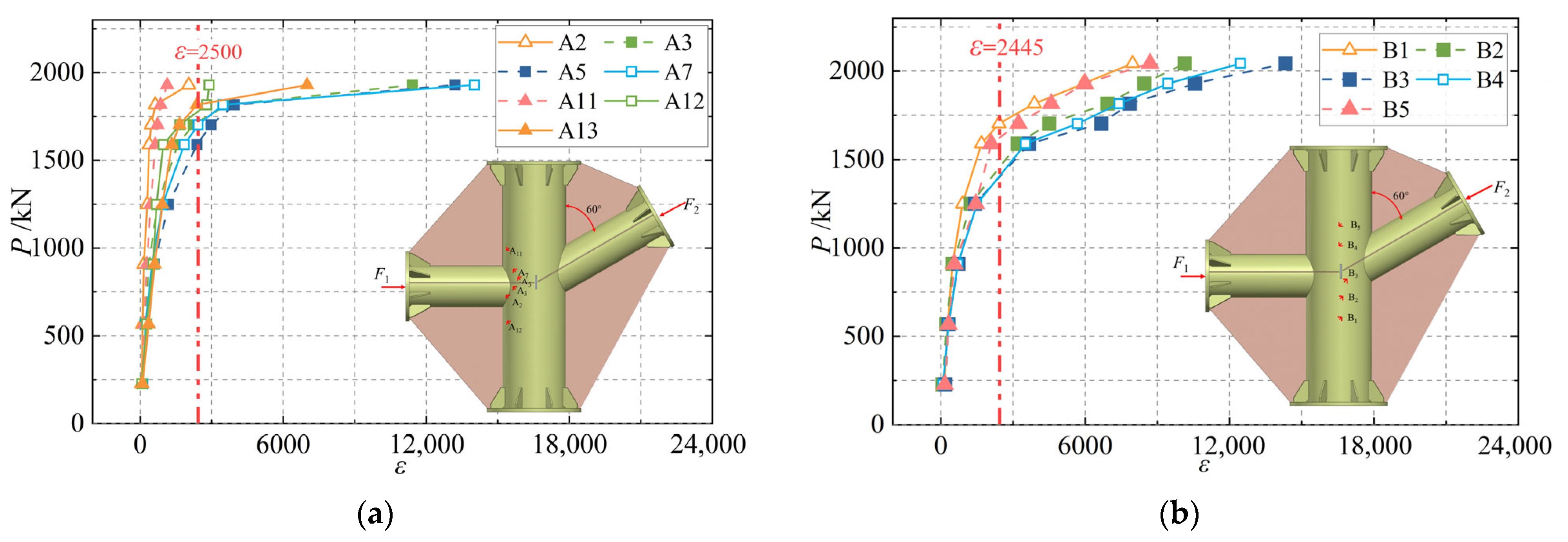
4.2. Analysis of Strain and Plasticity Results
5. Finite Element Model Analysis
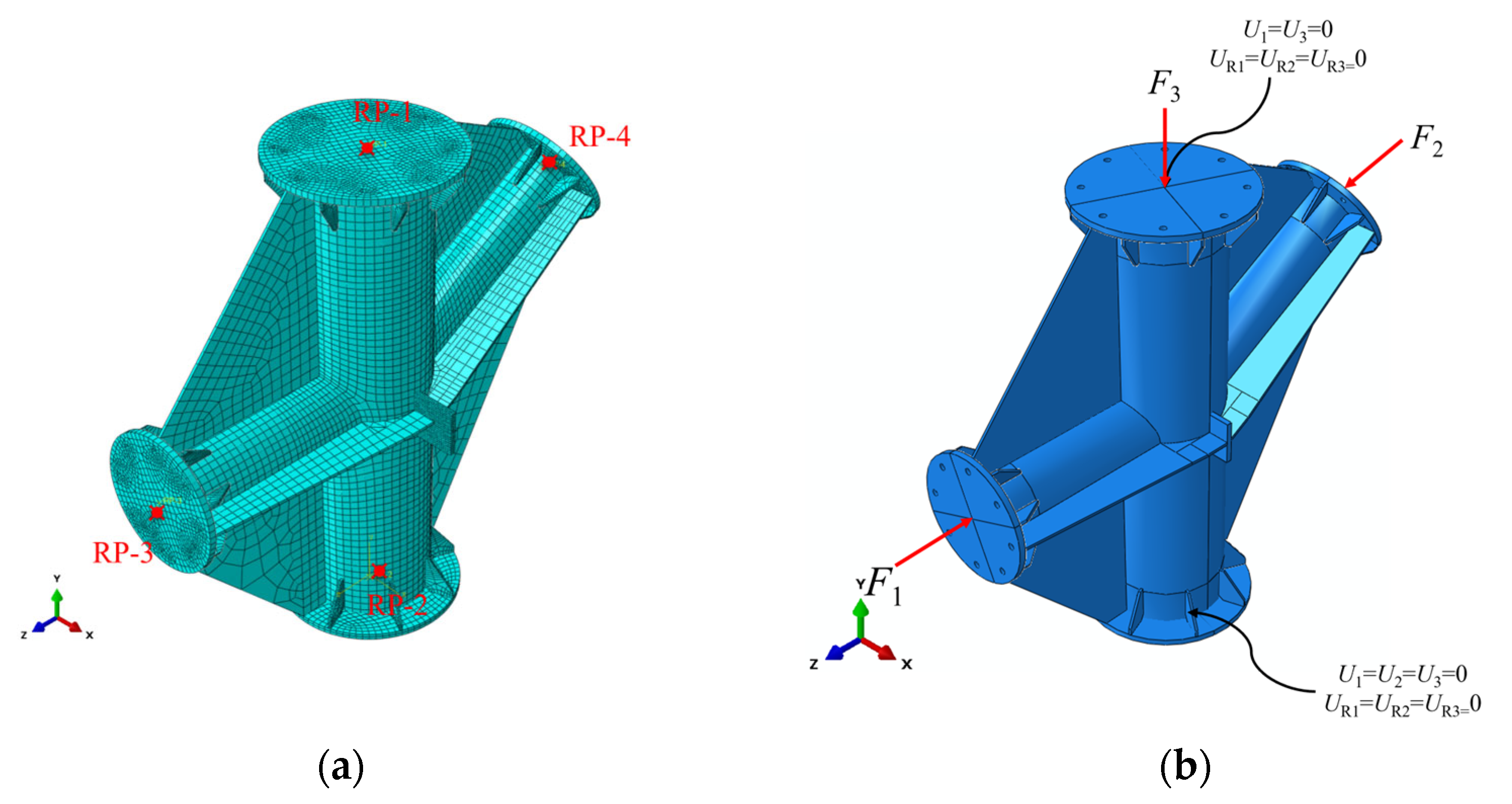
5.1. Finite Element Model Establishment
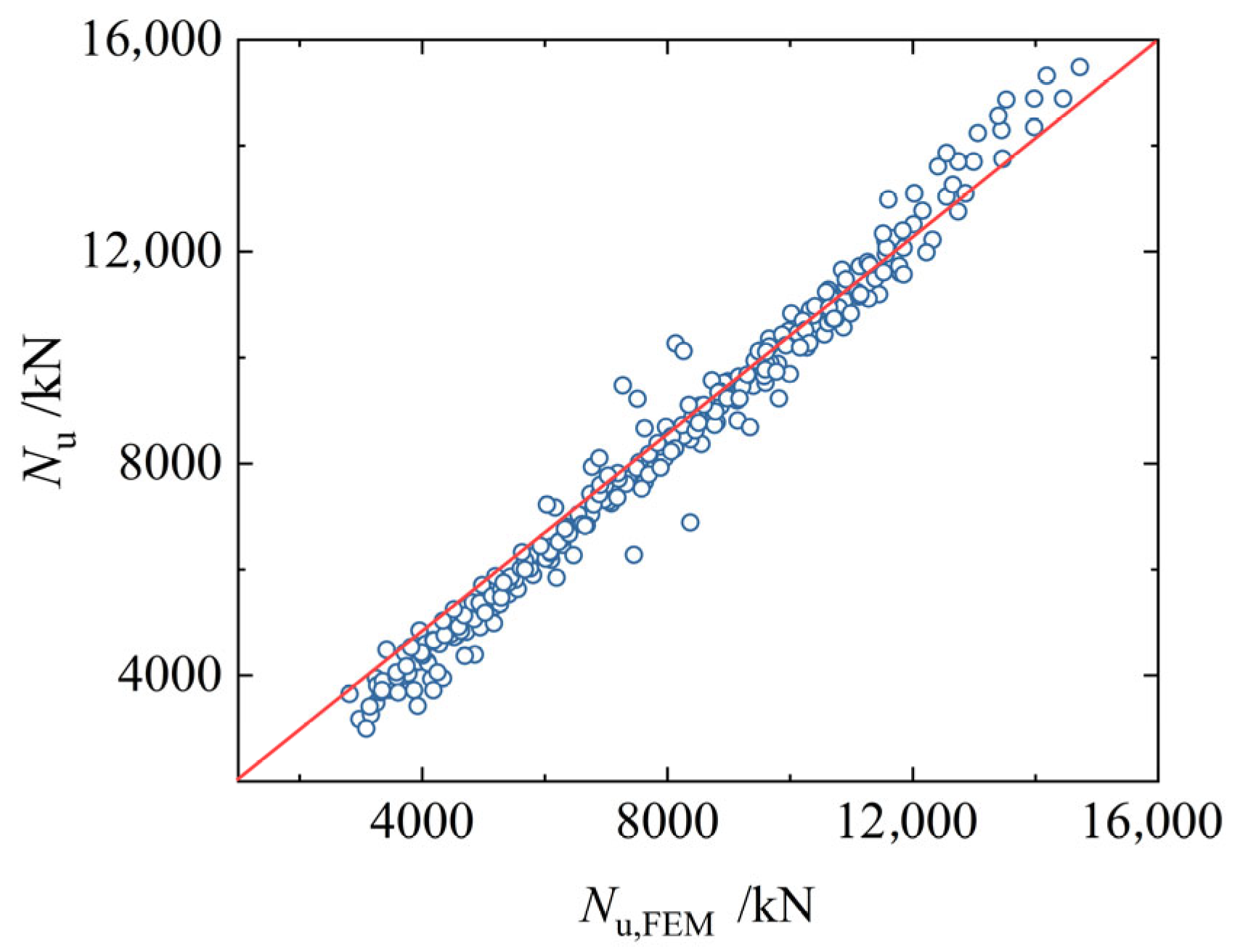
5.2. Finite Element Model Validation
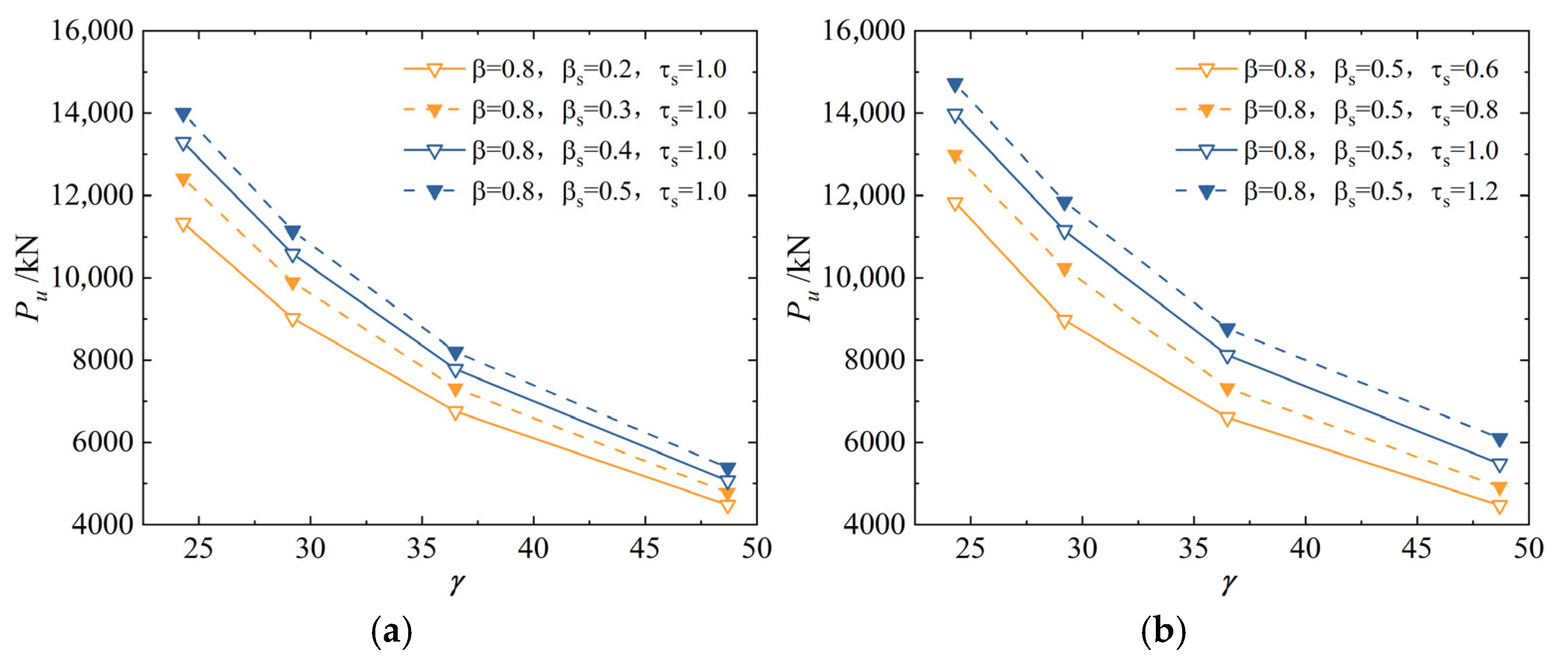
6. Analysis of Influencing Factors on Bearing Capacity
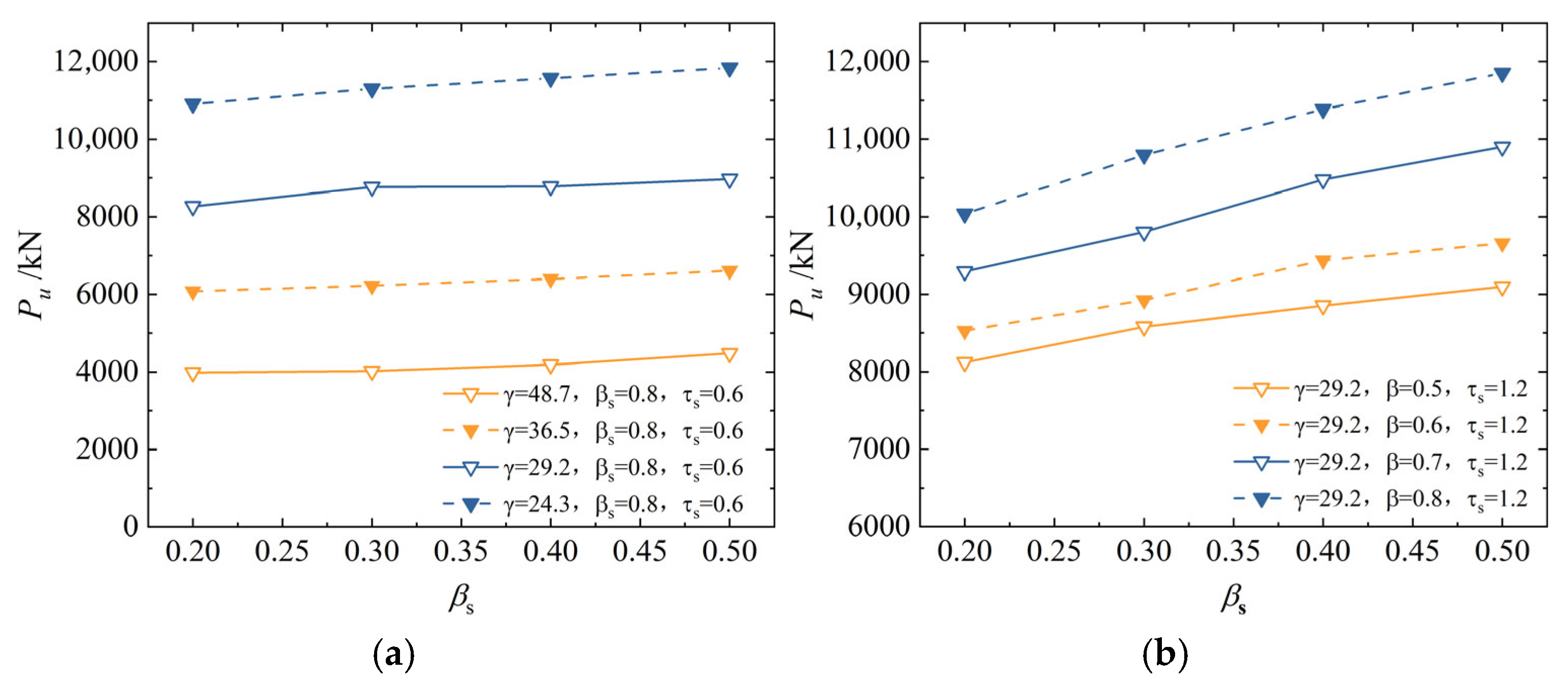
6.1. Influence of Diameter-to-Thickness Ratio of Main Pipe γ
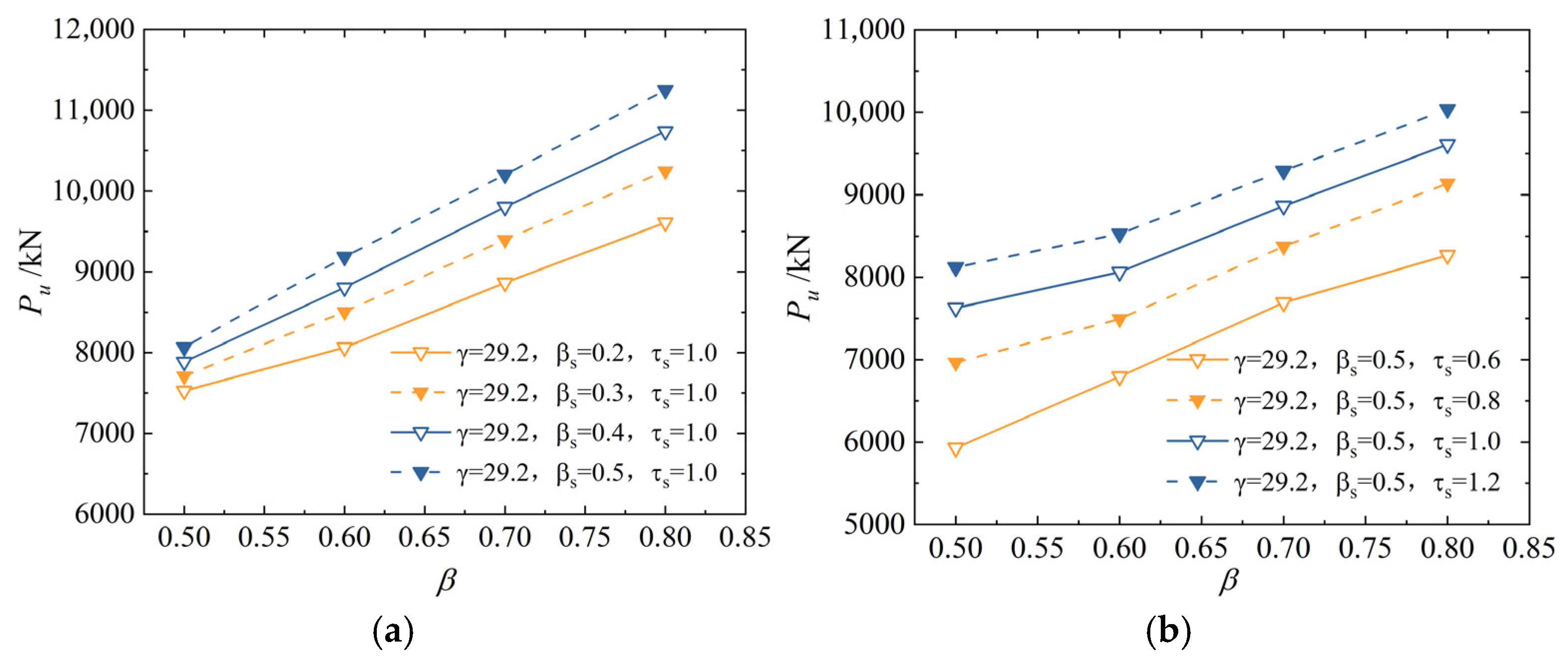
6.2. Influence of Main Pipe to Branch Pipe Diameter Ratio β
6.3. Influence of Gusset Plate Thickness Ratio τ
6.4. Influence of Stiffener Thickness Ratio τs
6.5. Influence of Stiffener Height Ratio βs
6.6. Influence of Angle Ratio Between Inclined Branch Pipe and Main Pipe θ
6.7. Influence of Axial Compression Ratio of Main Pipe n
7. Calculation of Ultimate Bearing Capacity
8. Engineering Implications
9. Conclusions
- (1)
- Through static tests on three types of intersecting joints: unstiffened, gusset plate stiffened, and composite stiffened, it is found that stiffening measures can effectively enhance the ultimate bearing capacity and initial stiffness of the joints. Among them, the ultimate bearing capacity of the composite stiffened specimen (TY-TWO-1) is increased by 126.8% compared with the unstiffened specimen (TY-1). The failure form of the joint presents a failure mechanism dominated by local buckling of the main pipe caused by the transition of force transmission from the branch pipe to the main pipe. Stiffening components play a role in delaying the expansion of the buckling surface and sharing the load.
- (2)
- The failure modes of unstiffened and composite externally stiffened joints are basically similar, both failing due to excessive plastic deformation caused by yielding at the intersecting area and side walls of the main pipe surface. Specifically, the gusset plate buckles when it fails, and the external stiffener undergoes local out-of-plane buckling when it fails. The overall failure form meets the design principle of “strong joint and weak member”. The improvement in the ultimate bearing capacity of externally stiffened joints is attributed to the combined action of gusset plates and external stiffeners, which increases the overall stiffness of the joint and restricts local deformation on the main pipe surface.
- (3)
- Analysis of finite element results with different geometric parameters shows that: the diameter–thickness ratio of the main pipe, the diameter ratio of branch pipe to main pipe, the thickness ratio of gusset plate, the width ratio and height ratio of external stiffeners, and the axial compression ratio of the main pipe all have significant impacts on the ultimate bearing capacity of the joint. The ultimate bearing capacity of the joint increases with the increase of main pipe thickness, branch-to-main pipe diameter ratio, stiffener thickness and height, and gusset plate thickness. The constraint effect of gusset plates and stiffeners can reduce the influence of the angle between the branch pipe and main pipe on the ultimate bearing capacity.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dong, Y.; Ning, X.; Han, T.; Hou, H.; Zang, M.; Lu, H.; He, X. Triethanolamine assisted ball milling activation of high alumina fly ash: Grinding kinetics, activation mechanism. Ceram. Int. 2025, 51, 4168–4177. [Google Scholar] [CrossRef]
- Tong, L.; Wang, Y.; Gao, L.; Shi, W.; Gao, F. Comparative study of different strengthening methods for circular hollow section K-joints. J. Constr. Steel Res. 2024, 217, 108668. [Google Scholar] [CrossRef]
- Nassiraei, H.; Rezadoost, P. Local joint flexibility of tubular X-joints stiffened with external ring or external plates. Mar. Struct. 2021, 80, 103085. [Google Scholar] [CrossRef]
- Zhu, H.; Shao, Y.; Chi, G.; Gao, X.; Li, K. Simplified bar-system model for tubular structures by considering local joint flexibility. Mar. Struct. 2022, 81, 103122. [Google Scholar] [CrossRef]
- Iqbal, M.; Karuppanan, S.; Perumal, V.; Ovinis, M.; Rasul, A. Rehabilitation techniques for offshore tubular joints: A review. J. Mar. Sci. Eng. 2023, 11, 461. [Google Scholar] [CrossRef]
- Karuppanan, S.; Perumal, V.; Iqbal, M.; Ovinis, M.; Rasul, A. Ultimate Strength of Internal Ring-Reinforced KT-Joints under Brace Axial Compression. Civil Eng. J. 2024, 10, 1543–1560. [Google Scholar]
- Ahmadi, H.; Alinezhad, R.; Atalo, A.A. Stress Concentration Analysis of Internally Ring-Stiffened Two-Planar Tubular KK-Joints. Ships Offshore Struct. 2022, 17, 2203–2217. [Google Scholar] [CrossRef]
- Sun, Q.; Qu, S.; Wu, X. Ultimate Load Capacity Analysis of Q690 High-Strength Steel KK-Type Tube-Gusset Plate Connections. J. Struct. Eng. 2019, 145, 04019074. [Google Scholar] [CrossRef]
- Deng, P.; Chen, Y.; Zhu, Z.; Liu, Y.; Zhao, S.; Guo, J. Structural behaviour of FRP-reinforced tubular T-joint subjected to combined in-plane bending and axial load. Buildings 2024, 14, 412. [Google Scholar] [CrossRef]
- Osman, A.; Gerguis, P.; Gaawan, S. Performance of externally reinforced CHS X-joints subjected to axial loads. J. Eng. Appl. Sci. 2023, 70, 38. [Google Scholar] [CrossRef]
- Nassiraei, H.; Rezadoost, P. Stress concentration factors in tubular T-joints reinforced with external ring under in-plane bending moment. Ocean Eng. 2022, 266, 112551. [Google Scholar] [CrossRef]
- Diao, Y.; He, S.; Wang, Y.; Tu, L. Experimental and numerical investigations on stress concentration factors of concrete filled steel tube X-joints. Sci. Rep. 2024, 14, 11415. [Google Scholar] [CrossRef]
- Nassiraei, H.; Rezadoost, P. Probabilistic analysis of the ultimate strength of tubular X-joints stiffened with outer ring at ambient and elevated temperatures. Ocean Eng. 2022, 248, 110744. [Google Scholar] [CrossRef]
- Nassiraei, H.; Yara, A. Local joint flexibility of tubular K-joints reinforced with external plates under in-plane bending loads. Mar. Struct. 2022, 84, 103199. [Google Scholar] [CrossRef]
- Nassiraei, H.; Rezadoost, P. Static capacity of tubular X-joints reinforced with fiber reinforced polymer subjected to compressive load. Eng. Struct. 2021, 236, 112041. [Google Scholar] [CrossRef]
- Wang, K.; Wang, Y.; Gao, S.; Wang, B.; Chen, J.; Luo, P. Experimental study of hot spot stress for spatial CHS KK-joints. J. Mar. Sci. Eng. 2023, 11, 1432. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.; Zheng, S.; Liu, L.; Wu, D. Parametric Modeling and Interpretable Machine-Learning Prediction on Ultimate Load-Carrying Capacity of a Circular Hollow Section X-Joint. Front. Struct. Civ. Eng. 2025, 19, 1287–1304. [Google Scholar] [CrossRef]
- GB/T 228.1-2021; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. Standards Press of China: Beijing, China, 2022. (In Chinese)
- Gao, C.; Zhang, D.; Cui, M.; Peng, P. Bearing Capacity Test and Calculation Theory on CHS X-Joints Stiffened with Joint-Plates. KSCE J. Civ. Eng. 2022, 26, 848–864. [Google Scholar] [CrossRef]
- Asgari, M.; Kouchakzadeh, M.A. An equivalent von Mises stress and corresponding equivalent plastic strain for elastic-plastic ordinary peridynamics. Meccanica 2019, 54, 1001–1014. [Google Scholar] [CrossRef]
- Wu, Y.; Li, J. Temperature and stress of RC T-beam under different heating curves. J. Build. Eng. 2022, 46, 103620. [Google Scholar] [CrossRef]
- Qu, H.; Shi, W.; Li, G. Experimental Study on Tubular K-Joints under Impact Loadings. J. Constr. Steel Res. 2015, 110, 136–150. [Google Scholar] [CrossRef]
- Sawada, Y.; Idogaki, S.; Sekita, K. Static and fatigue tests on T-joints stiffened by an internal ring. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 30 April–3 May1979; One Petro: Richardson, TX, USA, 1979. [Google Scholar]

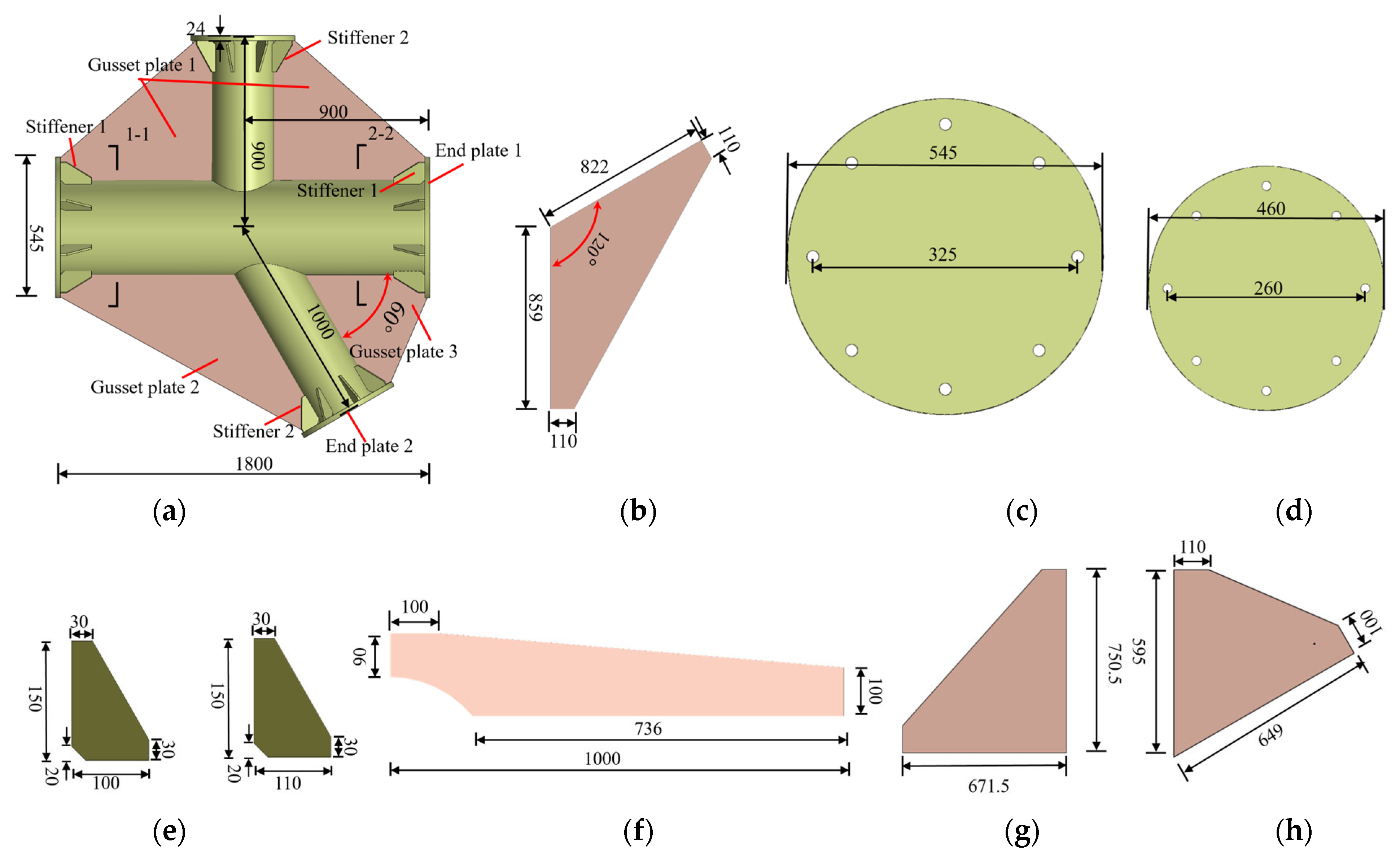


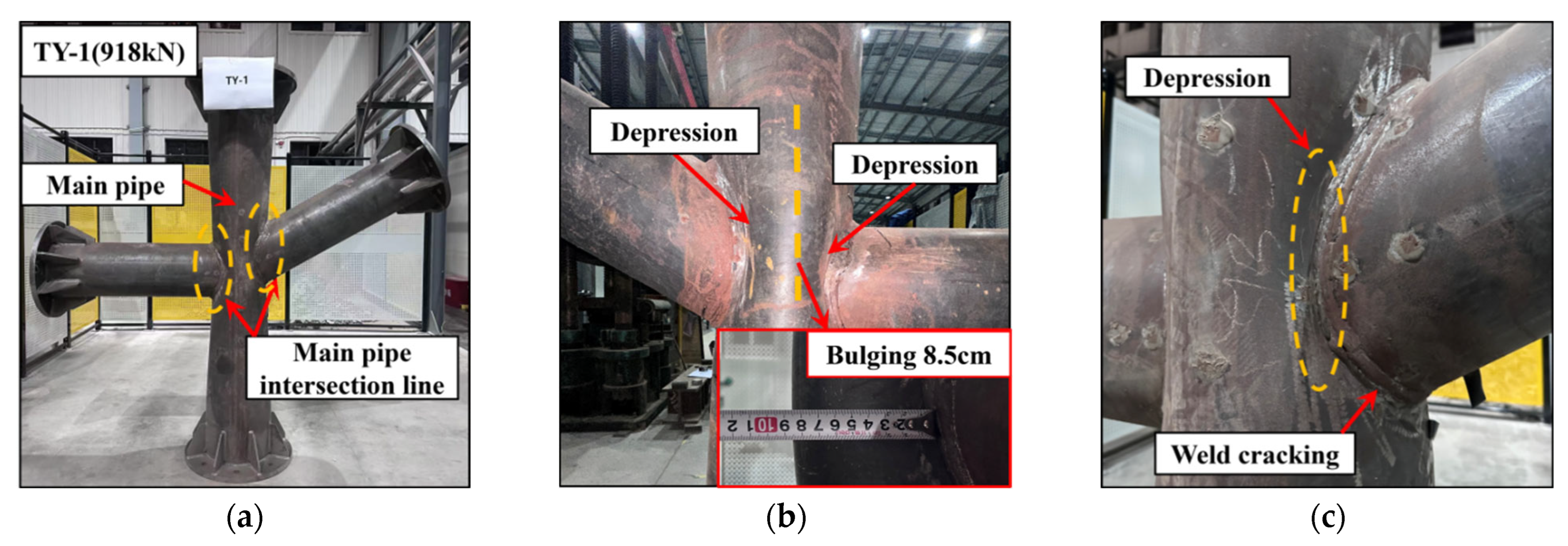
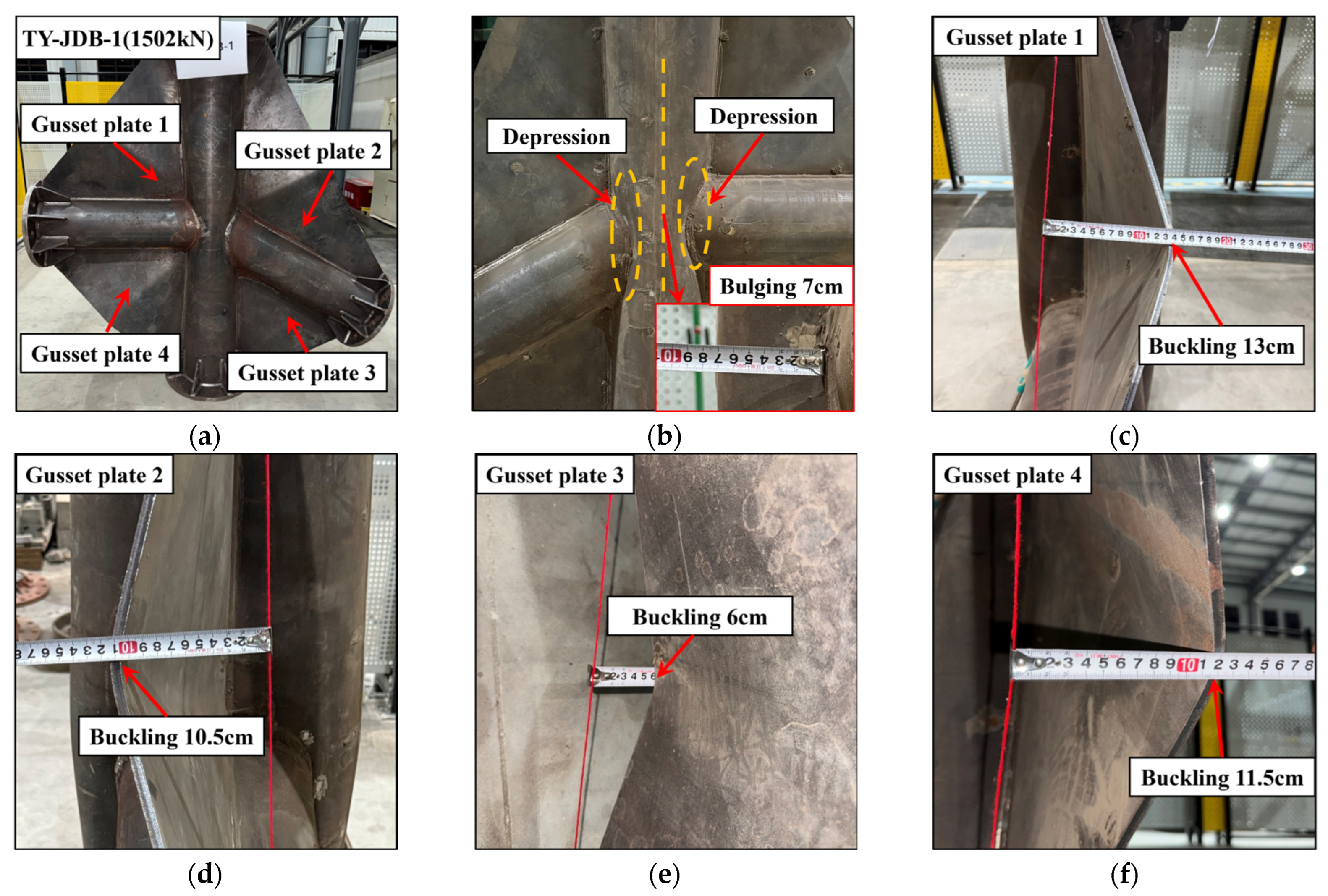





| Specimen Number | D (mm) | t (mm) | d (mm) | t1 (mm) | tp (mm) | ts (mm) | hs (mm) |
|---|---|---|---|---|---|---|---|
| TY-1 | 325 | 10 | 260 | 8 | - | - | - |
| TY-JDB-1 | 8 | - | - | ||||
| TY-TWO-1 | 8 | 8 | 8 |
| Steel Type | Yield Strength fy (MPa) | Tensile Strength fu (MPa) | Elastic Modulus Es (105 MPa) | Elongation After Fracture δ (%) |
|---|---|---|---|---|
| Q420-10 mm | 459.9 | 589.7 | 188.2 | 23.3 |
| Q420-8 mm | 549.2 | 604.7 | 208.3 | 21.3 |
| Q355-8 mm | 409.2 | 559.6 | 218.1 | 25.5 |
| Specimen Number | Ultimate Bearing Capacity (kN) | Improvement Ratio Compared to Unstiffened Specimen | Improvement Ratio Compared to Gusset Plate-Stiffened Specimen |
|---|---|---|---|
| TY-1 | 918 | - | - |
| TY-JDB-1 | 1502 | 63.6% | - |
| TY-TWO-2 | 2082 | 126.8% | 38.6% |
| Geometric Parameters | Parameter Range |
|---|---|
| β = d/D | 0.5, 0.6, 0.7, 0.8 |
| γ = D/T | 24.3, 29.2, 36.5, 48.7 |
| τ = tp/T | 0.6, 0.8, 1.0, 1.2 |
| βs = hs/D | 0.2, 0.3, 0.4, 0.5 |
| τs = ts/T | 0.6, 0.8, 1.0, 1.2 |
| θ | 45, 60, 75, 90 |
| n | 0, 0.2, 0.4, 0.6, 0.8, 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Q.; Zhu, M.; Lu, Y.; Guo, X.; Wen, F.; Du, Q.; Sun, Q. Study on the Ultimate Bearing Capacity Performance of Composite Stiffened Tubular Joints. Buildings 2025, 15, 3397. https://doi.org/10.3390/buildings15183397
Gao Q, Zhu M, Lu Y, Guo X, Wen F, Du Q, Sun Q. Study on the Ultimate Bearing Capacity Performance of Composite Stiffened Tubular Joints. Buildings. 2025; 15(18):3397. https://doi.org/10.3390/buildings15183397
Chicago/Turabian StyleGao, Qian, Mengwei Zhu, Yiyang Lu, Xianda Guo, Fan Wen, Qiongfei Du, and Qing Sun. 2025. "Study on the Ultimate Bearing Capacity Performance of Composite Stiffened Tubular Joints" Buildings 15, no. 18: 3397. https://doi.org/10.3390/buildings15183397
APA StyleGao, Q., Zhu, M., Lu, Y., Guo, X., Wen, F., Du, Q., & Sun, Q. (2025). Study on the Ultimate Bearing Capacity Performance of Composite Stiffened Tubular Joints. Buildings, 15(18), 3397. https://doi.org/10.3390/buildings15183397






