Shear Behavior of Large Keyed Dry Joints in Segmental Precast Bridges: Experiment, Numerical Modeling, and Capacity Prediction

Abstract

The mechanical properties of the joint are a key factor influencing the overall structural performance of segmental precast beams. This study investigates the shear performance of large keyed dry joints in segmental precast beam specimens under six different conditions, including variations in the base height of the key, depth-to-height ratio, number of keys, and prestressing reinforcement ratio, using direct shear tests and numerical simulations. The mechanical performance of the joints in segmental precast bridges under combined bending and shear forces is also studied using finite element analysis software. Additionally, a prediction model for the shear strength of the large keyed dry joints is established using machine learning methods. The results show that increasing the base height, depth-to-height ratio, and overall dimensions of the key can enhance the shear strength of dry joints. The depth-to-height ratio of the key not only affects the shear strength of the dry joint but also determines the failure mode of the joint. Furthermore, the shear bearing capacity and displacement stiffness of the keyed dry joint increase with the reinforcement ratio of the prestressing tendons. Compared to smaller keyed joints, larger keyed dry joints exhibit higher shear bearing capacity, smaller relative slip at failure, and a simpler casting process, making them more suitable for application in segmental precast bridges. The influence of bending moment on the shear bearing capacity of the joint section is limited, with the relative variation compared to the pure shear condition being less than 10%. The shear bearing capacity of the joint section in segmental precast bridges can be designed based on its direct shear performance. The developed interface shear strength prediction model effectively captures the nonlinear relationship between various parameters and shear strength, demonstrating strong adaptability and accuracy.

1. Introduction

Prefabricated Bridge Elements and Systems (PBES) originated in France in the 1940s and has been increasingly applied in recent years due to its advantages, such as shortened construction cycles, reduced impact on the surrounding construction site, and lower lifecycle costs. Examples include the Severn Second Crossing in the UK, the Northumberland Strait Bridge in Canada, and the Hongtang Bridge in Fujian, China [1,2]. The key distinction of segmental precast bridges lies in the presence of joints between segments, where the concrete interface separates and the longitudinal reinforcement is discontinuous. Given the severe consequences of structural failure [3], the mechanical properties of the joints are a critical factor affecting the overall load-bearing performance of segmental precast bridges [4].

Based on the type of joint connecting materials, joints are classified into wet joints, adhesive joints, and dry joints. Wet joints are formed by casting in situ concrete between precast segments, adhesive joints are assembled with epoxy applied to the interface before prestressing, while dry joints rely solely on mechanical interlock and prestressing without epoxy. While wet joints offer better durability, they have slower construction speeds. Most segmental precast bridges use epoxy and dry joints [5]. Epoxy joints effectively eliminate the defects of discontinuities in the concrete structure at the joints [6,7,8], but the epoxy layer contributes limitedly to the shear bearing capacity [9]. It is also susceptible to the negative effects of uneven coating thickness, low environmental temperatures, and harsh weather conditions [10,11]. Dry joints have significant advantages in terms of ease of construction and reduced environmental disruption [12], making them suitable for fast-track construction, and have garnered widespread attention from researchers [13,14,15,16].

Bu et al. [17] conducted monotonic direct shear tests on 10 dry joint specimens for precast assembly bridge piers. The failure mode involved shear of the protruding keys and the development of inclined cracks toward the nearest free surface. As confining pressure increased, the protruding keys were almost completely sheared off, and significant interface grinding occurred. Zhan et al. [18] studied the shear performance of “Z”-shaped dry joint specimens through direct shear tests and numerical simulations, examining the effects of geometric shape, size, and internal reinforcement. The primary failure mode was “direct shear,” and adding internal reinforcement helped strengthen the joint connection, causing the main failure mode to shift to a “fracture” mode. Yuan et al. [19] found that fibers significantly affected the shear performance of the specimens. Adding fibers improved the cracking stress, ultimate stress, and ductility of the specimens. Shamass et al. [20] confirmed that the shear strength of dry joints predicted by the AASHTO standard equation differed from the shear strength results obtained through numerical simulations under high confining pressure. They recommended reducing the friction coefficient used in the AASHTO equation when high confining pressure is applied. Chen et al. [21] developed a finite element model for the shear performance of single-key joints, obtaining their crack modes, ultimate shear strength, and load–displacement curves.

A series of studies have been conducted on the shear bearing capacity of keyed dry joints [22,23,24,25], but most existing research focuses on small keys (with base heights of 50 mm to 200 mm). The traditional methods based on ACI 318-14 [26], PCI Manual [27], and AASHTO LRFD standards [28] cannot accurately predict the shear bearing capacity of concrete dry joints [29,30,31]. Subsequent experimental and analytical studies also confirmed the limitations of these code provisions. Billington et al. [32] reported discrepancies between design assumptions and observed shear transfer in precast substructures. Koseki and Breen [33] demonstrated through exploratory tests that ACI code values may overestimate friction for plain joints while underestimating key and corbel shear strength. More recently, Jiang et al. [34] showed that the AASHTO formula tends to overpredict the shear capacity of multi-key joints and recommended a reduction factor, while Gao [35] highlighted that the brittle shear behavior of large cantilever precast cap beams cannot be reliably captured by current specifications. These findings reinforce that while design codes provide useful references, direct application to large keyed dry joints can lead to significant errors, and more effective analytical or data-driven approaches are needed. With the development of machine learning technology and improved computational capabilities, more researchers are applying it to the study of complex, multivariate problems [36]. Machine learning offers significant advantages in handling large-scale datasets and capturing nonlinear relationships [37,38]. In recent years, machine learning has been increasingly applied in civil engineering [39], covering a wide range of areas, including material fracture characteristics [40], concrete splitting strength [41], shear and buckling capacities of beams [42], seismic performance of reinforced concrete columns [43], shear strength of concrete joints [44], and structural seismic response [45], demonstrating its excellent adaptability.

In the practical engineering of large cantilever segmental precast beams, the cross-section height of segmental precast beams for six- to eight-lane expressways can reach 3–4 m, with overall cap beam lengths of 27–40 m and cantilever ends extending 8–10 m. Under such conditions, the joint section is far larger than those investigated in previous studies, and traditional small keys with base heights of only 50–200 mm are not suitable, as they not only increase the difficulty of casting but also raise the probability of mismatch at both ends of the keyed joint, making it more likely that the preset shear bearing capacity will not be achieved. Therefore, for the application scenarios of large cantilever segmental precast bridges, the effects of key base height, key depth, key quantity, and reinforcement ratio on the shear performance of dry joints are studied. Additionally, the mechanical performance of joints in segmental precast bridges under combined bending and shear forces is investigated using finite element analysis software. Furthermore, machine learning methods are introduced, and various regression models are established to analyze the relationship between the shear bearing capacity of keyed dry joints and various influencing factors. A prediction method for their shear bearing capacity is proposed.

2. Experimental Program

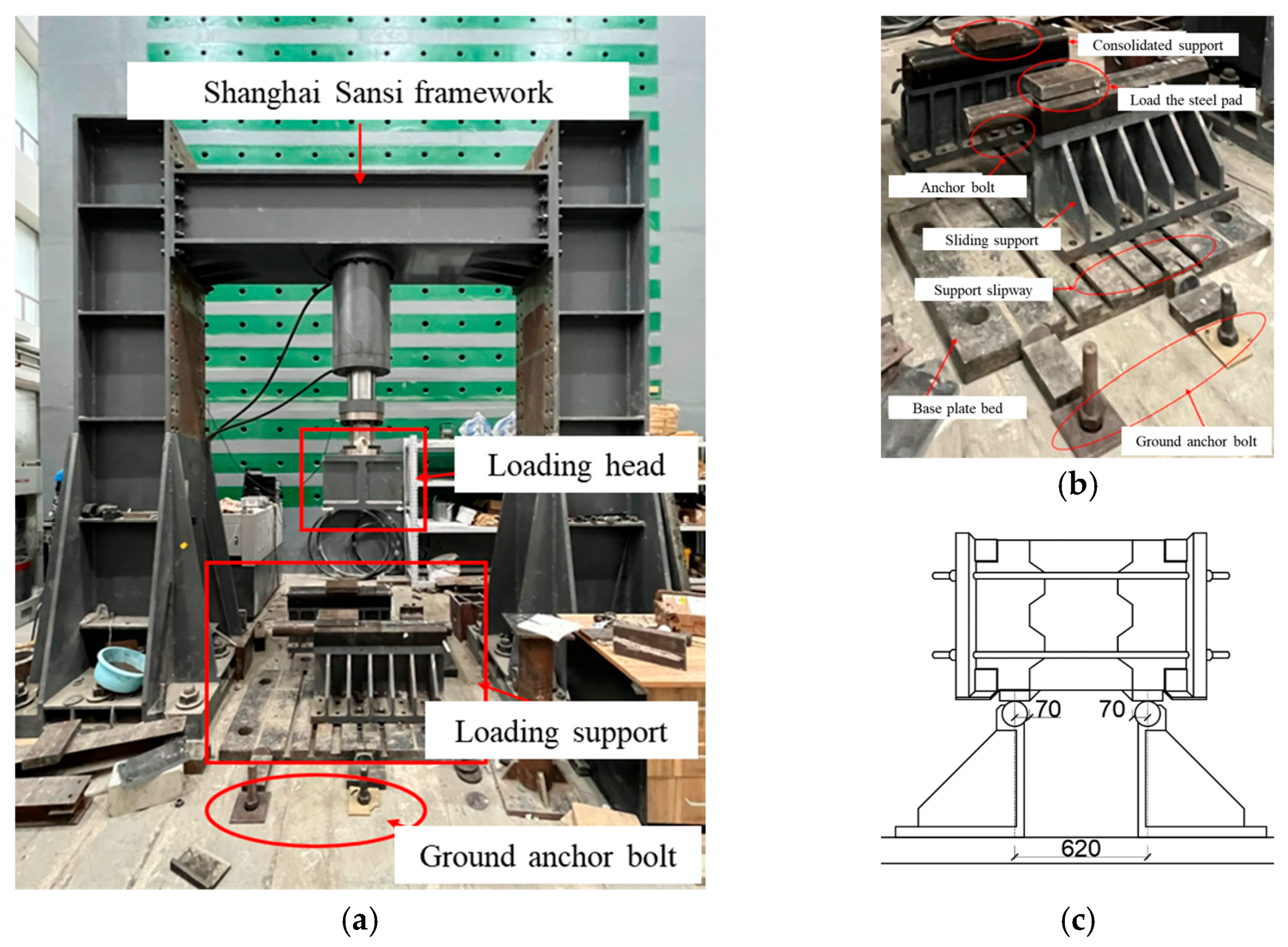
2.1. Specimens and Parameters

The keyed dry joint specimens and a two-key dry joint specimen are shown in Figure 1, with parameters provided in

Table 1. Parameters of shear specimens of key tooth dry joint.

Specimen Number	Thickness /mm	h/d	Concrete Grade	Prestressing Tendon Diameter/mm	Number of Tendons	Tensile Force per Tendon /kN
K1-1	250	0.467	C50	14	2	50
K1-2	250	0.253	C50	14	4	43.75
K1-3-1	250	0.467	C50	14	4	43.75
K1-3-2	250	0.467	C50	20	4	43.75
K1-3-3	250	0.467	C50	30	4	43.75
K2-1	250	0.467	C50	14	4	43.75

Note: The specimen number in the table is KX-Y-Z, where “K” is the Key tooth; “X” is the number of key teeth; “Y” is the key tooth type (1-small key tooth with base height of 200 mm, h:d = 0.467; 2-Large key teeth with base height of 400 mm, h:d = 0.233; 3 is the key tooth with a base height of 400 mm and h:d = 0.467) and “Z” is the reinforcement ratio (1-reinforcement ratio is 0.31%, 2-reinforcement ratio is 0.63%, 3-reinforcement ratio is 1.42%). It should be emphasized that all specimens were subjected to horizontal prestressing using threaded steel bars.

.

The vertical load loading device for the keyed dry joint shear performance test is shown in Figure 2. This device includes a vertical reaction frame (Shanghai Sansi Electronic Engineering Co., Ltd., Shanghai, China), a 200 t vertical loading head, a pair of loading supports, and four steel pads measuring 140 mm × 250 mm × 60 mm. The steel reaction frame was fabricated from welded structural sections, with a clear span of 3.5 m, and was designed to provide a safe load capacity exceeding 3000 kN to ensure structural stiffness during testing. The vertical actuator, with a rated capacity of 200 t and an accuracy within ±1%, was mounted at the top of the frame to apply displacement-controlled vertical loading. The loading supports are connected to the base plate using pins, and when the anchor bolts are not tightened, the supports can slide relative to the base plate. When tightened, they act as a fixed connection. In this case, one side is secured by tightening bolts to form a solid connection, while the other side allows the supports to slide relative to the base plate, as shown in Figure 2b. Additionally, the base plate of the supports is connected to the test ground using ground anchor bolts (Φ24 mm, embedded depth ≥ 300 mm), ensuring the stability of the shear test specimens and supports.

During specimen preparation, foil strain gauges (type BF120-50AA250(11)-P150-D, Xingdongfang Strain Gauge Enterprise Store, Sichuan, China) were mounted on the concrete surface in the key regions to monitor local strain development. In addition, YHD-100 displacement transducers (Liyang Jincheng Testing Instrument Factory, Jiangsu China) were installed across the joint interfaces to measure the relative slip between segments. The strain gauge data were mainly used for auxiliary monitoring, while the displacement transducer readings formed the primary basis for load–slip and shear performance analysis.

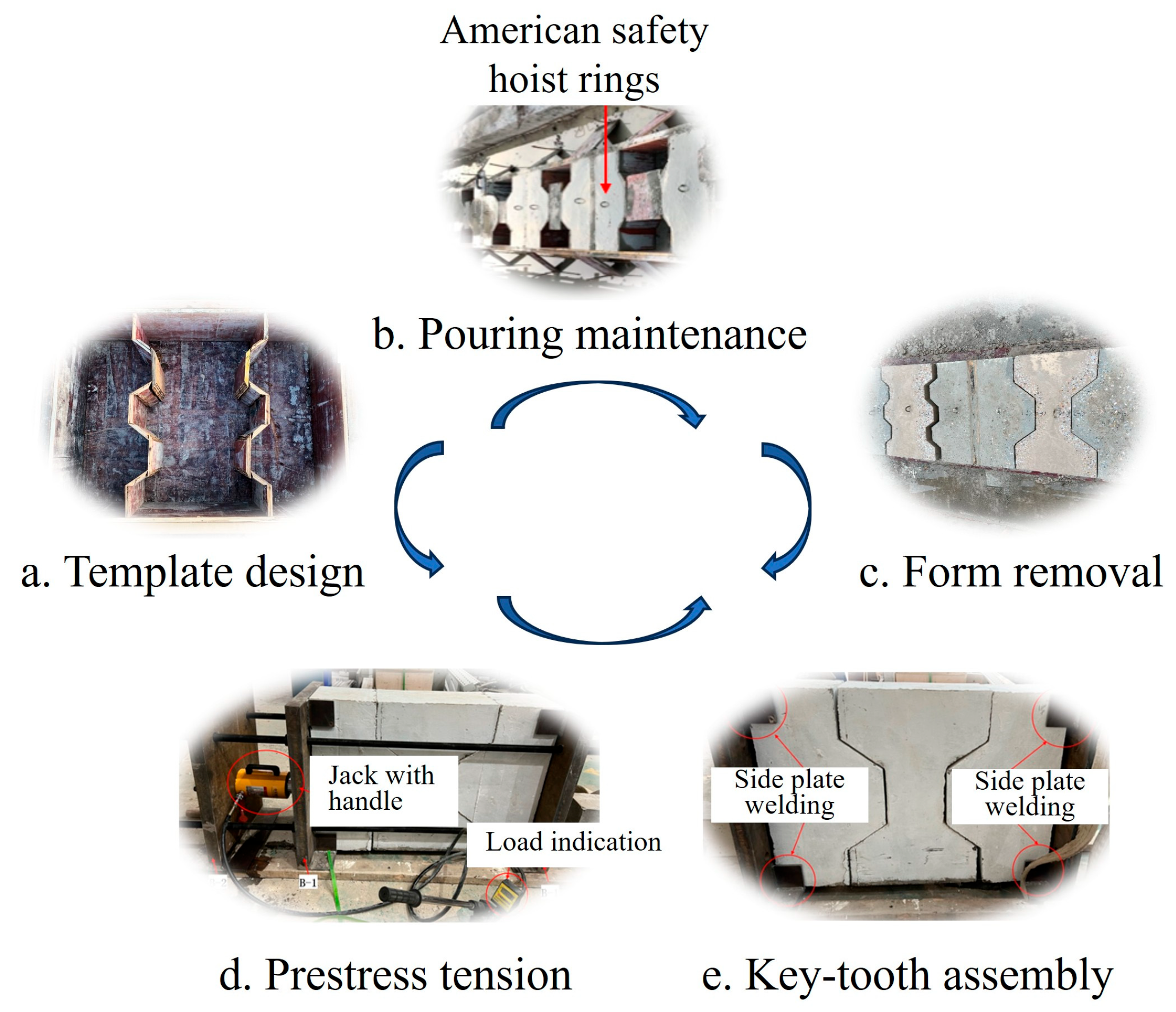
2.2. Production of Key Tooth Joint Specimen

The keyed dry joint specimens were cast using the matching pouring method. This method, applied to segmental precast assembly components, ensures minimal assembly errors in the prefabricated components. The pouring process for the specimens is shown in Figure 3.

To ensure casting accuracy and matching between segments, and to minimize dimensional errors in all specimens, the following steps were followed during fabrication: (1) Formwork was set, and the concrete for the side positive keyed specimens was poured, with the keying template arranged based on the parameters of the side positive keyed specimens. (2) After curing for 14 days, the formwork was removed, while the remaining formwork was kept. The completed positive keyed specimens were used as templates for casting the middle segments. (3) Specimens were painted, and strain gauges were applied to the keyed specimens. (4) The keyed specimens were assembled and prestressed.

2.3. Material Property

In this experiment, a total of six C50 concrete cube specimens with dimensions of 150 mm × 150 mm × 150 mm were tested for compressive strength using the Wance electro-hydraulic servo testing machine. The average compressive strength was 50.02 MPa. According to the empirical equation recommended by GB/T 50081-2019 Standard [46] for Test Methods of Physical and Mechanical Properties of Concrete, the elastic modulus of concrete E_c can be calculated as: $E_c={\displaystyle \frac{1\times {10}^5}{2.2+\frac{34.7}{f_{cu,k}}}}$, where f_cu,k is the cubic compressive strength of concrete (MPa). Based on this formula and the measured compressive strength, the average elastic modulus of the concrete was calculated to be 34.55 GPa.

3. Analysis and Discussion of Test Results

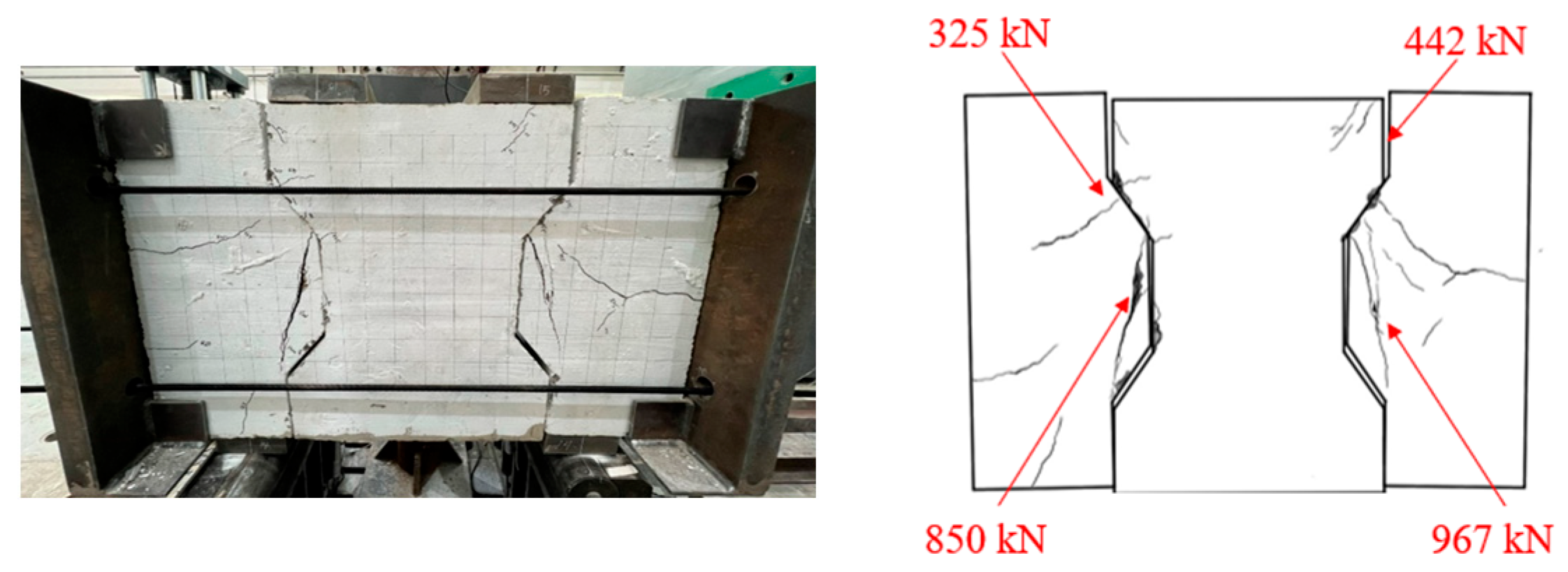
3.1. Failure Mode of Specimens

The shear failure process of specimen K1-1 is illustrated in Figure 4. Initially, vertical cracks and surface spalling appeared near the bottom support of the left-side positive keyed joint. As 285 kN–343 kN, a 45° inclined crack formed at the root of the left-side negative keyed joint, which then extended toward the left support. A nearly horizontal crack also developed and propagated toward the right support. When the load reached about 80% of the ultimate capacity, a small crack emerged at the root of the left-side positive keyed joint. At the peak load of 571 kN, a “clicking” sound was heard, followed by a rapid widening of cracks and sudden shear failure of the left keyed joint.

The shear failure mode of specimen K1-2 is shown in Figure 5. Initially, small vertical cracks appeared at the right-side loading end of the middle negative keyed joint. At 325 kN, cracks and spalling occurred at the top corner of the left negative keyed joint. At 442 kN, a continuous sound and load fluctuation were observed. When the load reached 850 kN, a large, inclined crack formed in the left positive keyed joint with a loud noise, but the joint still maintained bearing capacity. At 967.43 kN, a similar crack appeared in the right positive keyed joint, followed by two loud noises, and both keyed joints failed almost simultaneously.

Specimens K1-3-1, K1-3-2, and K1-3-3 have prestressing reinforcement ratios of 0.31%, 0.63%, and 1.42%, respectively, all with a key depth-to-height ratio of 0.467 and a base height of 400 mm. The shear failure process of K1-3-1 is shown in Figure 6. At 30% of peak load, a crack formed from the support to the lower root of the left keyed joint. At 977 kN, inclined cracks appeared on both positive keyed joints. As the load increased, the left crack widened with concrete spalling. At 1076.8 kN, a loud sound marked sudden shear failure of the left joint. After the capacity dropped to 917.3 kN, the right-side crack widened, accompanied by further spalling.

The failure modes of K1-3-2 and K1-3-3 are similar and represented by K1-3-3, as shown in Figure 7. At 30% of the ultimate load, initial cracks and minor spalling occurred at the positive keyed support. Small cracks formed at the negative keyed loading point. When the load reached 80–90% of the peak, diagonal cracks formed on both positive keyed joints with cracking sounds. Shortly after, both joints failed almost simultaneously with two loud sounds and large concrete spalling from the keyed region.

The two-keyed specimen K2-1 shares the same key parameters as K1-1, with a base height of 200 mm and a depth-to-height ratio of 0.467. At 453 kN, cracks appeared at the upper part of the right-side positive keyed joint, gradually forming two major 1 mm wide cracks. As loading progressed, more cracks developed at the joint’s upper edge. At 655.6 kN, a loud crack marked the extension of the upper crack to the joint root. Around 750 kN, a 0.1 mm-wide crack formed at the lower part and extended upward. When the load reached 941 kN, both cracks widened significantly, extending to the support, with heavy spalling at the keyed joint root, as shown in Figure 8.

3.2. Load-Slip Curves

Figure 9 presents the load-slip curves, where the horizontal axis shows the average vertical relative slip between the positive keyed joints and the middle negative keyed joint, and the vertical axis indicates the applied load. Specimens K1-1, K1-3-1, and K2-1 exhibit similar trends. Initially, the curves rise steadily with minor fluctuations due to early cracking. As the load increases, one side of the keyed joint is damaged, causing a sharp load drop. After a partial recovery, further loading leads to failure on the other side, resulting in a second rapid drop in the curve.

Specimens K1-3-2 and K1-3-3 follow a similar load-slip trend. Early loading produces small cracks with slight curve fluctuations, but the overall trend is linear. When the load reaches its peak, both sides of the keyed joint fail nearly simultaneously. This leads to severe concrete spalling in the keyed region and complete loss of bearing capacity, causing the load-slip curve to drop sharply without any residual strength.

Specimen K1-2 shows a different pattern. The load-slip curve initially rises linearly. At 442 kN, a “clicking” sound and widening joint gaps occur, and the load fluctuates with displacement. After a brief slip and stabilization, the load increases again until final failure. Upon reaching the ultimate load, both sides shear almost simultaneously, and the curve drops sharply with no recovery, indicating complete failure of the keyed joints.

3.3. Analysis of Test Parameters

The shear test results of keyed dry joint specimens with different parameters are summarized in

Table 2. Summary of shear test results.

Specimen Number	Cracking Load/kN	Ultimate Load/kN	Average Shear Stress/MPa	AASHTO Calculated Values/MPa	The Ultimate Relative Slip/mm	Failure Mode
K1-1	366.47	571.35	5.71	9.20	4.74	The key teeth are not completely broken
K1-2	602.14	967.43	5.53	11.55	12.46	The key teeth are cut and there is large slip
K1-3-1	855.56	1078.90	6.17	10.36	6.68	Key teeth cut
K1-3-2	905.58	1118.79	6.39	10.34	6.17	Key teeth cut
K1-3-3	996.67	1186.52	6.78	10.35	5.58	Key teeth cut
K2-1	453.55	941.78	5.38	10.35	7.85	Key teeth cut

. The crack load indicated in the table represents the load at which one of the keyed joints first cracks, and the relative slip corresponding to the ultimate bearing capacity is the average relative slip between the positive keyed joints on both sides and the middle negative keyed joint (similarly, the load–displacement curve uses the average relative slip of both sides).

The keyed load and stress in Table 2 represent the average performance of each keyed joint after subtracting the frictional effects of the non-keyed regions. The average shear stress is calculated by Equations (1)–(3). Equation (1) defines the shear load carried by each key after deducting the contribution of the non-keyed plane, Equation (2) follows the shear-friction expression for non-keyed interfaces as specified in the AASHTO LRFD Bridge Design Specifications (2024)—Section 5.7.4.2 [28], and Equation (3) calculates the average shear stress on the base area of the key.

$$F_{\mathrm{k}}={\displaystyle \frac{V-V_{\mathrm{sm}}}{2}}$$

(1)

$$V_{\mathrm{sm}}=0.6\times A_{\mathrm{sm}}\times {\sigma }_{\mathrm{n}}$$

(2)

$${\tau }_{\mathrm{k}}={\displaystyle \frac{F_{\mathrm{k}}}{A_{\mathrm{k}}}}$$

(3)

where F_k is the shear load on each side of the key tooth (kN), V_sm is the friction provided by the plane of the non-keyed tooth region of the joint (kN), A_sm is the plane area of the non-keyed tooth region of the joint (mm²), τ_k is the average shear stress of the key tooth according to the basal area of the key tooth, and A_k is the basal area of the key tooth.

The current AASHTO standard provides a calculation method for the shear capacity of keyed dry joints, as shown in Formula (4), which is directly adopted from the AASHTO LRFD Bridge Design Specifications (2024)—Section 5.7.4.3 [28].

$$V_{\mathrm{j}}=A_{\mathrm{k}}\sqrt{f_c^{\prime }}(0.9961+0.2048{\sigma }_{\mathrm{n}})+0.6A_{\mathrm{k}}{\sigma }_{\mathrm{n}}$$

(4)

where A_k is the area of the base of the key teeth (m²), f_c’ is the compressive strength of the concrete (MPa), σ_n is the horizontal pre-compressive stress applied to the member (MPa), and A_sm is the planar area of the non-keyed teeth region (m²).

The load–slip curves show that increasing the key base height, depth-to-height ratio, and overall key size improves the shear performance of keyed joints. Raising the base height from 200 mm to 400 mm increases the cracking and ultimate loads by 67.1% and 62.1%, respectively, but reduces average shear stress by 19%. Increasing the depth-to-height ratio from 0.233 to 0.467 raises the cracking load by 49.5%, ultimate load by 12.8%, and shear stress by 12.8%, demonstrating enhanced load-bearing capacity.

Test results reveal that higher prestressing reinforcement ratios enhance initial stiffness, cracking load, and ultimate load, while reducing relative displacement at peak load. However, the AASHTO formula greatly overestimates shear capacity under typical reinforcement ratios. For example, the calculated value for K1-3-3 exceeds the experimental result by 50.7%, indicating the formula is not applicable for accurately predicting the shear performance of keyed dry joints.

For single-key specimens with a 200 mm base height and 0.467 depth-to-height ratio, the cracking and ultimate loads are 366.47 kN and 571.35 kN. Increasing the number of keys from one to two raises these values to 453.55 kN and 941.78 kN—an increase of 23.8% and 64.8%, respectively. This shows that adding keys improves shear capacity but may slightly reduce shear efficiency due to interaction effects.

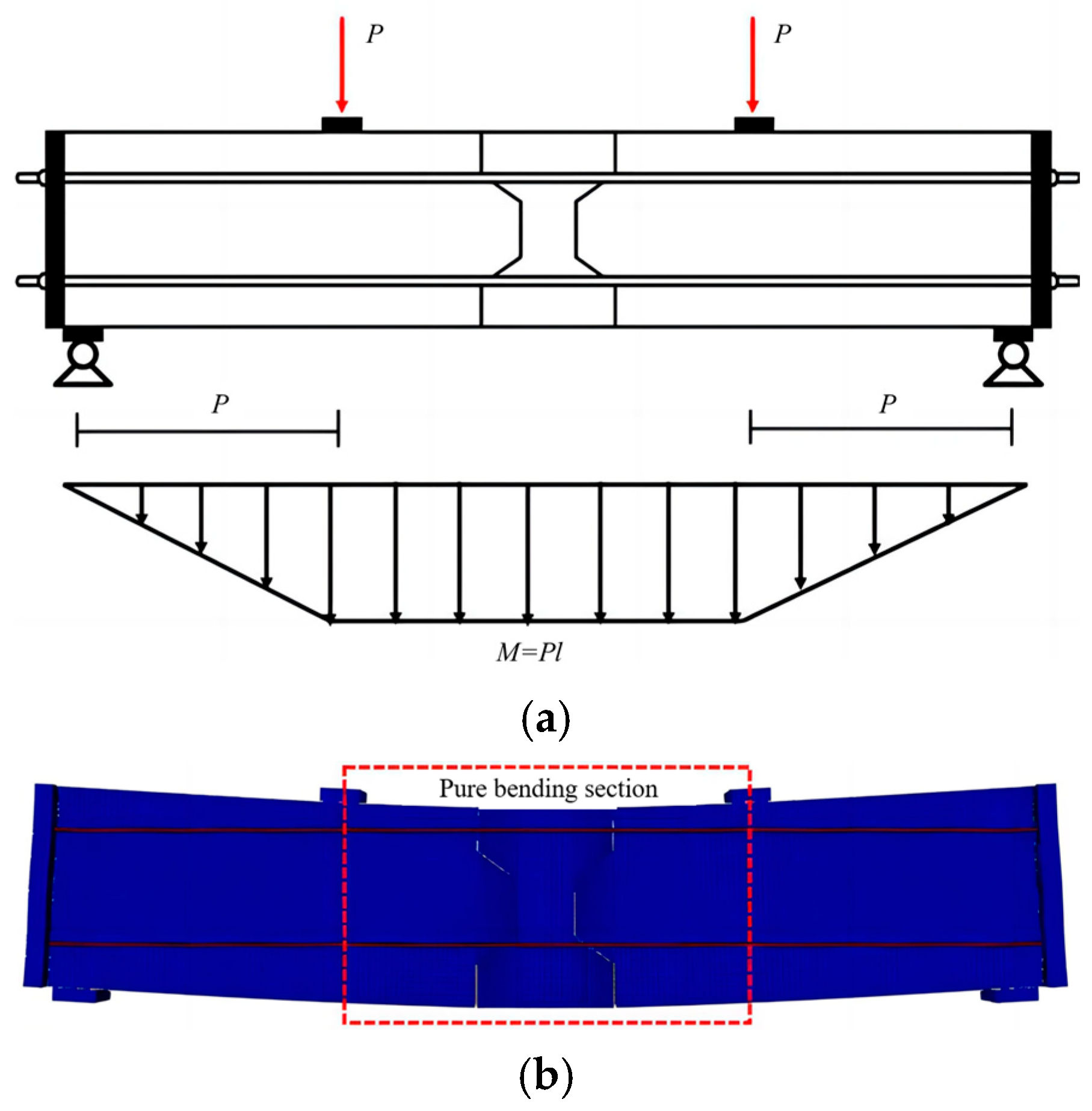
4. Research on Joint Flexural Shear Performance of Segmental Cap Beam

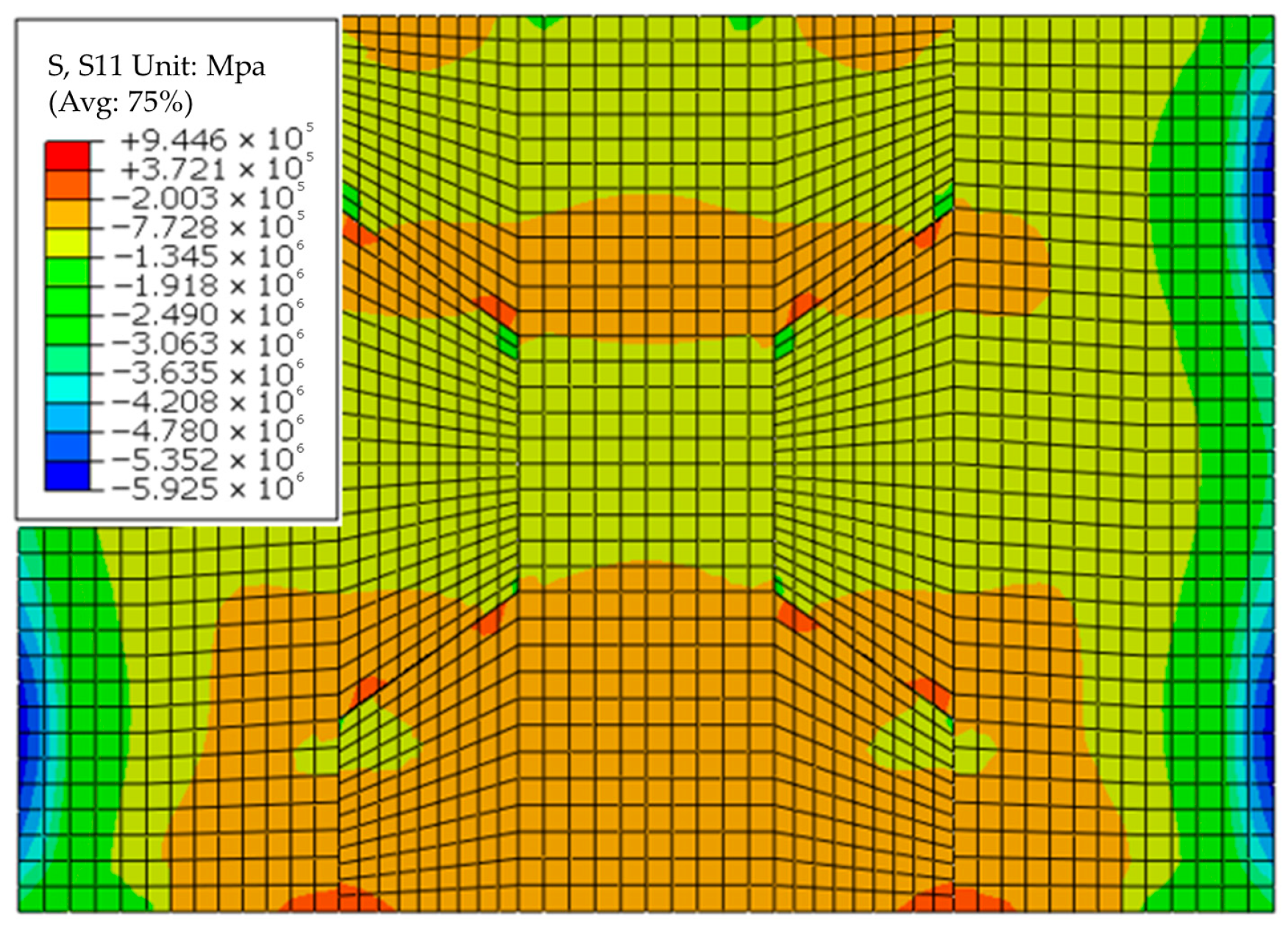
4.1. Establishment and Result Verification of Three-Segment Splicing Key Tooth Model

The finite element model adopts the Concrete Damage Plasticity (CDP) model to simulate the nonlinear elastoplastic behavior of concrete, which ensures reliable convergence under various loading conditions. Key CDP parameters include a dilation angle of 36, flow potential eccentricity of 0.1, and viscosity parameter of 0.0015 [22]. The biaxial-to-uniaxial compressive yield strength ratio is 1.16, and the tensile-compressive meridian ratio K_c is 0.6667 [47,48]. In the CDP model, the damage evolution laws for concrete were defined based on the experimentally obtained C50 cubic compressive strength (50.02 MPa) and the elastic modulus (34.55 GPa) calculated according to GB/T 50081-2019. A bilinear softening function was employed for compressive damage, where the response increases linearly up to the peak stress and then softens with descending stiffness, calibrated to reflect the strain characteristics of high-strength concrete. For tensile damage, an exponential softening function was adopted, linking crack opening displacement to energy dissipation and thus representing the brittle cracking behavior of high-strength concrete. Both damage functions are consistent with the constitutive relations in GB50010-2010 [49] and were implemented in ABAQUS (v2021) through tabular stress–strain input. The reinforcement is modeled with a bilinear elastoplastic constitutive law.

The specimen consists of C50 concrete and four M8 threaded steel bars (14 mm diameter), with a thickness of 250 mm, key height of 700 mm, and depth of 140 mm. In the numerical model, the concrete segments of the keyed joint were discretized using three-dimensional 8-node solid elements (C3D8). Internal steel bars and prestressing tendons were modeled with truss elements (T3D2). A mesh convergence study revealed that the mesh size of the key teeth had a significant effect on the results. After trial analyses, an element size of 20 mm was adopted for both single-key and multi-key specimens, balancing accuracy in capturing concrete damage evolution with computational efficiency. Reinforcement was embedded in the concrete ends of the key segments using the Embedded technique.

The top and bottom loading plates were modeled with an elastic modulus of 200 GPa. The loading plates were tied (Tie constraint) to the adjacent concrete, while the top surface of the upper plate was kinematically coupled to reference point Rp-1, where displacements and rotations were controlled. The joint interfaces between key teeth were defined using Surface-to-Surface Contact to simulate shear transfer and frictional behavior. Tangential and normal contact behaviors were both modeled using the penalty method to enhance convergence, with a tangential friction coefficient of 0.618 obtained from experimental results and finite sliding allowed.

Boundary conditions were imposed by fully constraining the bottom loading plate in all translational and rotational directions. Additionally, Rp-1 was restricted from horizontal displacements to stabilize the model. The loading procedure consisted of two steps: (1) application of prestress, and (2) shear loading. Prestress was applied to tendons using the cooling method, where thermal contraction was imposed along the tendon axis. The thermal expansion coefficient in the longitudinal direction was set to 1.2 × 10⁻⁵, with orthotropic material definition and local coordinate orientations specified. After the prestress step, shear load was applied through displacement control at Rp-1. The stress distribution following prestress application is shown in Figure 10, illustrating the initial stress state of the specimen.

$$C={\displaystyle \frac{\sigma }{E\times 1.2\times {10}^{-5}}}={\displaystyle \frac{F}{EA\times 6.158\times {10}^{-4}}}=-118.417°$$

(5)

Based on the finite element model parameters and loading methods set above, the comparison results of the bearing capacity and failure modes of the key segment specimens are shown in Figure 11.

As shown in Figure 11c, the shear load–displacement curves from experiment and simulation for specimen K1-3-1 match well. At peak load point A, the experimental shear load is 1078.90 kN with 6.68 mm displacement, while the simulation gives 983.5 kN and 6.66 mm, showing an 8.84% error. The failure modes observed at points A and C also align closely with the simulated results, as shown in Figure 11a,b. The remaining discrepancy of approximately 100 kN in ultimate shear load and about 1 mm in relative slip between the FE and test results can be attributed to the simplification of concrete damage laws, the assumption of constant frictional contact behavior, and the adopted mesh resolution. Nevertheless, the overall agreement is satisfactory. Specimen K1-3-1 was selected for FE verification because it represents the standard configuration (base height 400 mm, depth-to-height ratio 0.467, prestressing reinforcement ratio 0.31%), making it a suitable benchmark for validating the numerical model prior to conducting further parametric studies.

4.2. Simulation of Segmental Precast Beams

Under the working load, the large cantilever segmental precast beam’s key joints simultaneously bear both shear load and bending moment, as shown in Figure 12. Under the combined effects of prestress, bending moment, and shear force, the stress state of the key joints in the assembled segmental precast beam is not purely shear. The horizontal pre-compression stress on the keys is also not evenly distributed. Based on the assumption of a plane section, the stress distribution in the segmental precast beam’s joints under the combined effect of bending moment and prestress is triangular or trapezoidal. Whether the bearing capacity of the segmental precast beam’s joints will decrease under the action of bending moment still requires further investigation, thus providing design standards for the shear bearing capacity design of the segmental precast beam’s joints.

4.2.1. Finite Element Model Overview

Section 4.1 of this paper verifies the correctness of the finite element model by comparing the finite element simulation results with the experimental results. The length of the K1-3-1 specimen’s segmental key test pieces was extended from 0.25 m to 1.5 m, transforming the specimen from a key joint specimen into a prestressed segmental precast beam with a rectangular cross-section. The parameters and loading method are shown in Figure 13 and Figure 14.

According to the current design standards for segmental precast beams and the JTG3362-2018 Bridge Code [50], the cap beams are considered prestressed concrete components that are not allowed to crack. Therefore, after applying a horizontal pre-compression stress of 1 MPa on the concrete cross-section, the release bending moment at the joint is first calculated, as shown below:

$$M_0={\sigma }_{\mathrm{pc}}{W}_0$$

(6)

$$P={\displaystyle \frac{M_0}{l}}$$

(7)

where σ_pc is the horizontal pre-compressive stress applied to the concrete section with the magnitude of 1 MPa, and W₀ is the elastic resistance moment at the tensile edge of the converted section.

The specific simulation parameter settings are shown in

Table 3. Finite element simulation parameter.

Specimen Number	Joint Pattern	Key Tooth Size	Prestress/MPa	Shear Span Ratio	Vertical Load/kN
M-S-1	Single key tooth	400 × 200 × 140	1	1.43	0
M-S-2					22.075
M-S-3					45
M-S-4					−22.075

, where M-S-1 is used to verify that the shear performance of the key joint under this loading condition is consistent with the shear capacity test results of the key joint model K1-3-1, ensuring the reliability of the finite element simulation results. M-S-2 tests the shear performance of the key joint when the compressive stress at the lower edge of the segmental joint cross-section is 0, i.e., when the segmental precast beam is under a release bending moment condition. M-S-3 tests the shear performance of the key joint when the lower edge of the beam is under tensile opening. M-S-4 tests the shear performance of the key joint when the compressive stress at the upper edge of the segmental joint cross-section is 0. The difference between M-S-2 and M-S-4 is shown in Figure 15. The compression surface of the key joint is the upper sloping surface of the key joint. The shear performance of the key joint is related to the magnitude of pre-stress. M-S-2 and M-S-4 correspond to different horizontal pre-compression stresses depending on the location of the compression surface.

4.2.2. Analysis of Simulation Results and Design of Shear Bearing Capacity

The failure modes of the four specimens are consistent. Taking M-S-1 as an example, the load–displacement curve and the joint key failure mode are shown in Figure 16. From the load–displacement curve, it can be observed that the stiffness of K1-3-1 and M-S-1 is essentially the same when the shear capacity of the key joint reaches point A. The corresponding ultimate loads for the two are 983.5 kN and 1002 kN, with a relative error of 0.93%, indicating that the shear performance of the key joint in both models is quite similar. However, as loading continues, after the key joint failure at point A, there is a noticeable difference between the load–displacement curves of the two. In the key joint failure stage, the stiffness of M-S-1 decreases more rapidly, and the failure of the key joint is more brittle compared to K1-3-1, but overall, this does not affect the ultimate shear capacity result of the key joint. As shown in Figure 16b, the key joint failure modes of K1-3-1 and M-S-1 are also basically the same. In both cases, the key joints fail from the root section, but M-S-1 shows more diagonal damage points at the root of the key joint compared to K1-3-1.

The finite element analysis results of the key components of the four segmental precast beam key joint specimens are shown in

Table 4. Finite element simulation result.

Specimen Number	Vertical Load/kN	Bending Moment at the Seam/kN·m	Key Tooth Limit Load/kn	Relative Displacement/mm
M-S-1	0	0	1002	6.60
M-S-2	22.075	22.075	1019.63	6.65
M-S-3	45	45	1058.19	6.83
M-S-4	−22.075	−22.075	1008.29	6.00

. The four segmental precast beam key joint specimens can be divided into two groups: 1-3 (denoted as 1 for M-S-1, 2 for M-S-2, and so on) form one group; 1, 2, and 4 form another group. By observing Figure 17a, it can be seen that with the increase in the positive bending moment at the key joint surface, the shear performance of the key joint slightly improves. Similarly, as shown in Figure 17b, when the positive bending moment is changed to a negative bending moment, the shear performance of the segmental precast beam joint slightly improves compared to the condition where there is no bending moment in the section. The above research shows that the bending moment present in the joint section of the segmental precast beam has a negligible effect on the shear performance of the key joint, indicating that the shear capacity of the segmental precast beam key joint can be designed based on its direct shear performance.

5. The Predicting Method for Shear Capacity of Segmental Precast Bridges

The research in Section 4.2 demonstrates that the shear performance of the key joint at the segmental beam joint is essentially unaffected by the bending moment, and the shear capacity design of the joint can be based on its direct shear performance. Therefore, a machine learning-based method is proposed to predict the shear strength of concrete key joint specimens, which will be validated using experimental data.

To improve the model’s predictive performance, a broad collection of experimental data from researchers in various countries was compiled, including 442 key joint specimens obtained from the literature [8,15,18,41,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79], and all experimental data are presented in Appendix A. The output parameter is the interface shear strength Y, and six variables were selected: concrete compressive strength X 1, key depth X 2, the ratio of the total area of the key root surface to the shear interface area X 3, the ratio of the total area in the plane to the shear interface area X 4, the normal compressive stress perpendicular to the shear plane X 5, and the shear interface area X 6. Figure 18 illustrates the data distribution of the six variables and shear strength Y. The linear fitting results show that variable X 6 has the strongest correlation with Y, with an R² value of 0.50. Following closely is variable X 1, with an R² value of 0.21. Overall, the correlation between the variables and shear strength is relatively weak, with the highest being only 0.50.

The high correlation between input variables may lead to overfitting of the model and poor model interpretability, making the predictions unreliable [80,81]. To determine the correlation between these variables, correlation analysis was conducted using Spearman’s correlation coefficient. Spearman’s correlation coefficient is capable of capturing both linear and nonlinear relationships between variables, which has an advantage over the traditional Pearson correlation coefficient, which can only quantify linear relationships. Figure 19 shows the results of the correlation analysis between the variables. The results indicate that there is relatively high correlation between X 2 and X 3, X 2 and X 4, X 2 and X 6, and X 3 and X 4, with correlation coefficients not exceeding 0.53. It can be observed that there exists a complex nonlinear relationship between the input parameters and the interface shear strength.

5.1. Comparison of Prediction Models

This study selected four commonly used regression models for predicting shear bearing capacity: (1) XGBoost (Extreme Gradient Boosting): An efficient implementation based on gradient boosting trees, with strong predictive capabilities and the ability to handle missing values [82]. (2) LightGBM (Light Gradient Boosting Machine): Based on the gradient boosting framework, optimized for training speed and memory usage, suitable for large-scale datasets [83]. (3) CatBoost (Categorical Boosting): Optimized for categorical features, reducing the bias in handling categorical variables during the gradient boosting process [84]. (4) RF (Random Forest): By integrating multiple decision trees, it reduces model variance and improves generalization ability [85]. Based on the optimized hyperparameters, the four regression models were trained separately, and the models were evaluated using four performance metrics: R² (coefficient of determination), MAE (mean absolute error), RMSE (root mean square error), and MAPE (mean absolute percentage error), as shown in the following expressions [86,87].

$$R^2=1-{\displaystyle \frac{{\displaystyle \sum _{i=1}^n}{(y_i-{\widehat{y}}_i)}^2}{{\displaystyle \sum _{i=1}^n}{(y_i-\overline{y})}^2}}$$

(8)

$$\mathrm{MAE}={\displaystyle \frac{1}{n}}{\displaystyle {\displaystyle \sum _{i=1}^n}|}{y}_i-{\widehat{y}}_i|$$

(9)

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2}}$$

(10)

$$\mathrm{MAPE}={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n|}(y_i-{\widehat{y}}_i)/y_i|\times 100\%$$

(11)

In the equations, y_i represents the true values, ${\widehat{y}}_i$ represents the predicted values, $\overline{y}$ is the mean value, and n is the number of samples used for calculation. The higher the R², and the lower the RMSE, MAE, and MAPE, the better the model performance, indicating that the predicted values are closer to the true values.

Table 5. Predicted values of each model on the test set.

Model	Train				Test
	R2	MAE	RMSE	MAPE	R2	MAE	RMSE	MAPE
XGBoost	0.91	0.69	1.13	16.16	0.87	0.93	1.54	20.34
LightGBM	0.92	0.59	1.09	14.56	0.89	0.94	1.64	21.91
CatBoost	0.91	0.71	1.15	16.57	0.90	0.88	1.47	19.56
RF	0.90	0.74	1.19	16.73	0.88	1.08	1.60	21.48

shows the evaluation metrics for the four machine learning models. Compared to other methods, in the training set, the CatBoost algorithm achieved the highest R², and the lowest RMSE, MAE, and MAPE, yielding the highest prediction accuracy. The XGBoost algorithm also performed well, while the prediction results of LightGBM and RF algorithms were similar, slightly inferior to the other two models, but with stable prediction accuracy within a certain range; in the test set, the CatBoost algorithm performed the best, followed by LightGBM, RF, and XGBoost algorithms.

Based on the four models XGBoost, LightGBM, CatBoost, and RF, the correlation between the predicted values and the actual values was analyzed, as shown in Figure 20. By comparing the scatter distribution of the training and test sets, the prediction accuracy and error distribution of each model can be quantified. The results indicate that the predicted values of XGBoost are highly consistent with the actual values, with the point distribution almost strictly along the diagonal line of y = x, showing the smallest deviation and error. The performance of LightGBM is similar to XGBoost, with a slightly higher mean squared error (MSE) in the test set, but it has an advantage in training speed. CatBoost performs well in capturing nonlinear features, but some test samples show significant deviations from the diagonal line. The point distribution of RF is relatively scattered, with larger errors in the test set, indicating that its fitting ability for complex nonlinear relationships is weaker than the previous three models. In conclusion, XGBoost and LightGBM are the models with the best prediction accuracy.

The comparison highlights that tree-based ensemble learning methods, especially CatBoost and RF, exhibit superior stability and generalization capability when dealing with nonlinear parameter interactions. This indicates that machine learning can provide more accurate and robust predictions than conventional empirical formulas.

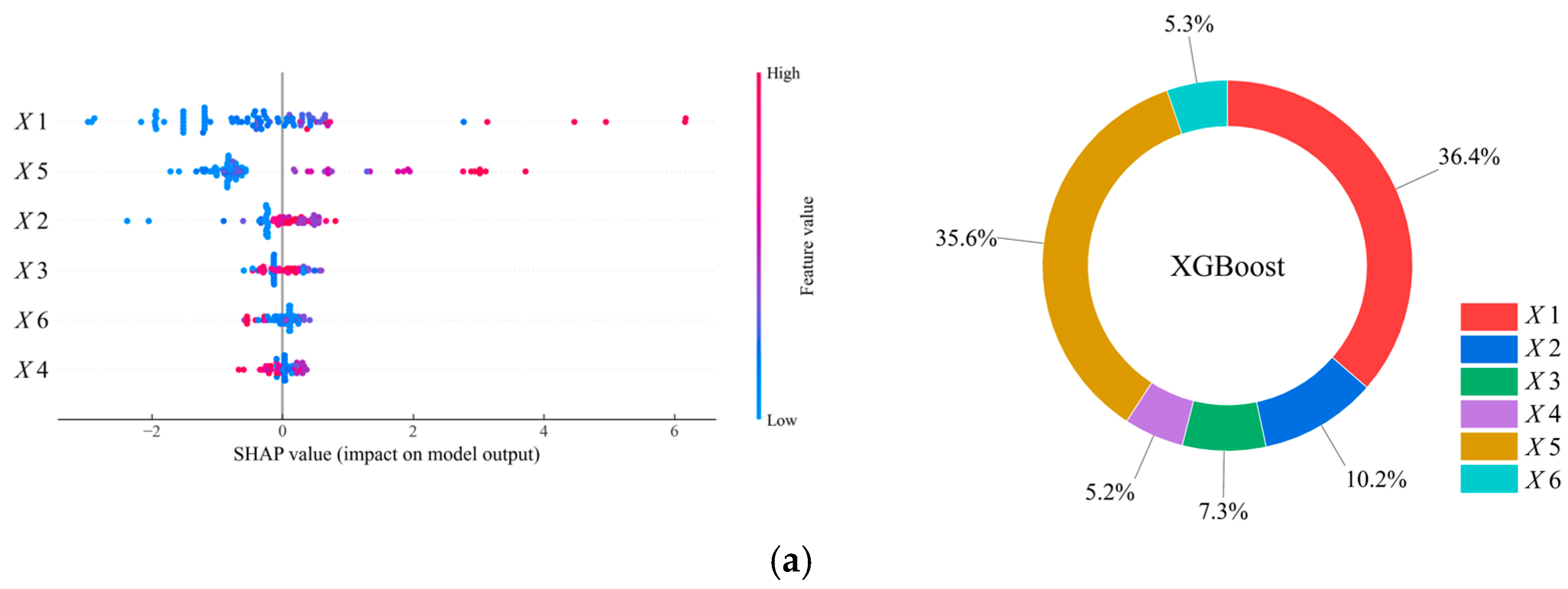
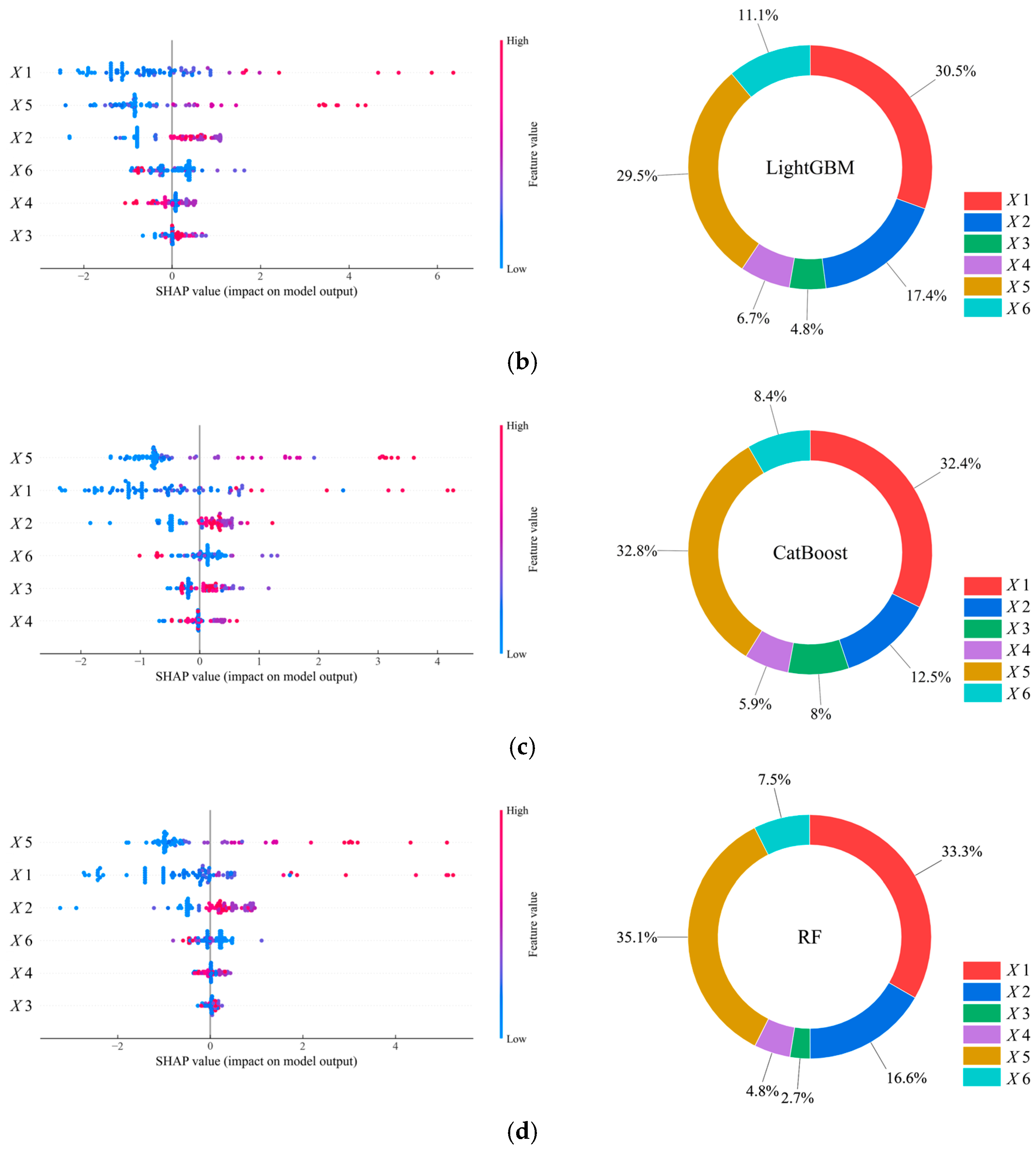
5.2. Interpretability Analysis Based on SHAP

Poor interpretability is a major factor hindering the application of machine learning algorithms in practical engineering [88]. Understanding why the model predicts the interface shear strength of large keyed dry joints based on the feature values is crucial for the credibility of the model’s predictions. Therefore, it is necessary to conduct an interpretability analysis of the prediction results. Lundberg et al. [89] proposed a unified interpretability method for machine learning called Shapley Additive Explanations (SHAP). SHAP constructs an additive explanation model, treating all features as contributors and calculating their contribution values. The sum of the contribution values of all features equals the final prediction of the model.

$$f(x)=g\left(z^{*}\right)={\varphi }_0+{\displaystyle \sum _{i=1}^M{\varphi }_i}{z}_i^{*}$$

(12)

$${\varphi }_i={\displaystyle \sum _{S\subseteq N\backslash i}\frac{\left|S\right|!(M-|S|-1)!}{M!}}[f(S\cup \{i\})-f(S)]$$

(13)

In the equation, f(x) is the machine learning model, z* = {0, 1}, where z* = 0 when feature i is observed, and otherwise, it is 0; if i is involved in the prediction process, M is the number of features; φ_i is the contribution of feature i, N is the set of all input features, and S is the set containing non-zero indices in z*.

Based on the four models—CatBoost, LightGBM, RF, and XGBoost—SHAP values and feature importance analysis were used to reveal the influence of each feature on the model’s prediction results, as shown in Figure 21. The results show that X 1 and X 5 are the core features in all models, with their contribution to prediction performance exceeding 60%. Among them, CatBoost and XGBoost are particularly dependent on these two features, while Random Forest has a more balanced feature importance distribution, making it more suitable for tasks that require a balance of feature dependence. The SHAP Summary plot further shows that high feature values of X 1 and X 5 usually contribute positively to the model output, while the contributions of other features (such as X 2 and X 6) are weaker and more dispersed. The feature importance circular chart shows that XGBoost performs excellently in capturing nonlinear relationships, with its importance ranking for feature X 3 slightly higher than that of other models.

5.3. Model Verification

After completing the training and optimization of the model, this study conducted a predictive analysis on the test dataset in Section 3.3 and compared the calculated values (AASHTO specification) in Formula (4). The results are shown in

Table 6. Comparison of predicted and experimental values.

Type	XGBoost		LightGBM		CatBoost		RF		AASHTO		Test Values /MPa
	Values /MPa	Error /%	Values /MPa	Error /%	Values /MPa	Error /%	Values /MPa	Error /%	Values /MPa	Error /%
K1-1	4.93	13.66	5.85	−2.40	5.65	1.07	5.26	7.89	9.20	61.12	5.71
K1-2	3.67	33.69	5.79	−4.75	5.45	1.50	5.76	−4.28	11.55	108.79	5.53
K1-3-1	3.86	37.32	8.09	−31.16	6.11	0.87	6.35	−3.05	10.36	67.87	6.17
K1-3-2	3.86	39.56	8.09	−26.48	6.11	4.40	6.35	0.62	10.34	61.88	6.39
K1-3-3	3.86	43.01	8.09	−19.26	6.11	9.86	6.35	6.30	10.35	52.64	6.78
K2-1	3.67	31.89	5.79	−7.61	5.45	−1.18	5.76	−7.12	10.35	92.31	5.38

. The calculation value of AASHTO standard is much higher than the test result, and the maximum error is 108.79%. The actual shear bearing capacity of the key tooth joint is far less than the calculated result of the current standard, which makes the structural design of segmental precast bridges unsafe.

A comparison shows that the CatBoost and RF models perform excellently in predicting the interface shear strength. The CatBoost model has the smallest error, with the prediction errors for different specimens controlled within 10%, demonstrating very high prediction accuracy and stability. The overall performance of the RF model is close to that of CatBoost, with a smaller error distribution, and the predicted values are in good agreement with the experimental values. In contrast, the XGBoost and LightGBM models have larger errors, with XGBoost showing significantly higher errors for certain specimens, and LightGBM also exhibiting relatively higher errors for some specimens. Overall, the CatBoost and RF models outperform other models in both accuracy and stability and can be used to predict the interface shear strength of keyed dry joints.

These findings demonstrate the potential of machine learning methods to serve as a practical supplement to code-based formulas in design and safety evaluation of segmental precast bridges, offering both improved accuracy and reliability.

6. Conclusions

Direct shear tests were conducted on large keyed dry joints used in segmental precast bridges, with the experimental parameters covering the base height of the key, the depth-to-height ratio of the key, the overall size of the key, the prestress reinforcement ratio, and the number of keys. Additionally, finite element analysis was used to investigate the effect of the bending moment in the segmental precast beam joint section on the shear performance of the keyed dry joints. The main conclusions obtained are as follows:

(1)

The base height, depth-to-height ratio, and overall size of the key have an impact on the shear performance of the keyed dry joints. Increasing the overall size of the key most significantly improves its shear performance. As the base height of the key increases, the improvement in shear capacity shows a certain reduction. When the depth-to-height ratio of the key is too low, excessive relative slip may occur at the joint due to insufficient friction during shear.

(2)

The AASHTO specifications calculation formula for the shear capacity of keyed dry joints significantly overestimates the shear performance of the joints in beam-type structures for the given reinforcement ratios. Increasing the prestress reinforcement ratio improves both the shear capacity and displacement stiffness of the keyed dry joints. For the same joint section, a large key results in much better cracking and ultimate load capacity compared to using multiple small keys. In practical engineering, cap beams are components where cracking is not allowed, and using large keys offers better shear performance than small keys.

(3)

Finite element results show that the relative change in ultimate shear capacity of the segmental precast beam joint section under bending moment is less than 10% compared with the pure shear case. Moreover, the presence of bending moment slightly enhances the shear resistance of the keyed dry joint. Therefore, the shear capacity of the joint section can be reasonably designed based on its direct shear performance.

(4)

Comparison with experimental results reveals that the AASHTO specification formula significantly overestimates the shear strength of keyed dry joints, with the maximum error reaching 108.79%. In contrast, the machine learning models—particularly CatBoost and RF—achieve prediction errors within 10% and effectively capture nonlinear parameter interactions. Furthermore, the SHAP-based interpretability analysis identifies concrete strength and prestress level as the dominant parameters, together contributing over 60% to prediction performance. These findings confirm that ML methods not only provide higher accuracy but also deliver transparent and reliable insights, serving as a practical supplementary tool for the design and safety assessment of segmental precast bridges.