Seismic Fragility Analysis of Double-Column Bridge Piers Under Freeze–Thaw Cycles

Abstract

This study investigates the influence of freeze–thaw (F–T) cycles on the seismic fragility of double-column bridge piers. Mechanical tests were conducted on standard concrete specimens subjected to 0, 25, 50, 75, and 100 F–T cycles using an HC-HDK9/F rapid freeze–thaw testing machine. The experimental results were used to calibrate and validate the applicability of the selected concrete constitutive model. A nonlinear finite element model of a double-column bridge pier was developed in the OpenSees platform, incorporating material degradation parameters corresponding to varying F–T cycles. Incremental dynamic analysis (IDA) was performed to derive seismic demand curves and quantify fragility corresponding to multiple damage states. The results indicate that the failure probability of the piers increases significantly with the number of F–T cycles, particularly for slight and moderate damage levels. In the low to moderate peak ground acceleration (PGA) range, the exceedance probabilities for slight and moderate damage states show a sharp rise, highlighting the sensitivity of early-stage damage to F–T degradation. It is worth noting that under the extreme condition of PGA = 1.0 g and 100 freeze–thaw cycles, the piers still exhibit a certain degree of redundancy against severe and complete damage, which to some extent reflects the certain rationality of the current seismic design in freeze–thaw environments. These findings underscore the robustness of current seismic design provisions in cold regions and provide theoretical and data-driven support for performance assessment, service life prediction, and maintenance planning of bridges exposed to freeze–thaw environments.

1. Introduction

Twin-column piers, characterized by their simple structure and excellent seismic performance, are widely used in various bridge constructions such as urban viaducts and river-crossing bridges, and have become an indispensable key component in modern bridge structural systems [1]. However, in cold regions, these piers face more complex environmental challenges—in addition to withstanding the impact of seismic loads, they also have to bear the continuous effect of freeze–thaw cycles, a natural phenomenon, for a long time [2]. In cold climatic conditions, bridge structures are often under the combined influence of freeze–thaw cycle erosion and seismic action. The erosion caused by freeze–thaw cycles is a long-term and gradual process, and each alternation of freezing and thawing will have a non-negligible impact on the strength and stiffness of concrete [3]. Specifically, freeze–thaw cycles will lead to an increase in the internal porosity of concrete, promote the continuous initiation and expansion of microcracks, thereby weakening the durability of concrete, accelerating the process of carbonation and chloride ion penetration, and even adversely affecting the impermeability of concrete [4].

At present, the academic community has carried out extensive research at the material and component levels to explore the impact of freeze–thaw cycles on the mechanical properties of concrete and the mechanical behavior of reinforced concrete (RC) components. Hasan et al. [5] conducted experimental research on concrete cube specimens after freeze–thaw action; Duan [6] explored the relationship between the number of freeze–thaw cycles and the compressive strength of plain concrete and hoop-reinforced concrete; Cao et al. [7,8] conducted an in-depth analysis of the effect of concrete freeze–thaw damage on the flexural bearing capacity of beams and the stress process of prestressed beams. Xu et al. [9], Zheng et al. [10], and Zheng et al. [11], respectively, analyzed the influence law of concrete freeze–thaw damage on the seismic performance of reinforced concrete frame columns, shear walls, and beam–column joints through quasi-static tests. The results of these studies all show that with the increase in the number of freeze–thaw cycles, the bearing capacity, stiffness, and energy dissipation capacity of reinforced concrete components will be weakened, and their seismic performance will also decrease significantly. The superposition of many factors makes the seismic performance of piers gradually degrade, and thus, the safety of the overall structure is threatened [12].

With the development of finite element technology and the deepening of research on concrete freeze–thaw deterioration, more and more scholars use numerical simulation methods to analyze the impact of concrete freeze–thaw deterioration on bridge seismic performance. Gong et al. [13] used ABAQUS software to simulate RC columns that had undergone 0–300 freeze–thaw cycles and were reinforced with basalt fiber-reinforced composite materials. The results showed that the strength attenuation rate of the reinforced components slowed down, the hysteretic curves were fuller, and the energy dissipation capacity was also improved. Liu [14] proposed a uniaxial compressive stress–strain model of concrete for RC beam–column joints considering freeze–thaw damage, which was verified to be reasonable through ABAQUS seismic simulation. He et al. [15] conducted full-scale elastic-plastic time-history analysis on the freeze–thawed RC frame based on OPENSEES software, confirming that its bearing capacity decreased and displacement response increased. Du [16] pointed out that if numerical simulation ignores the uneven distribution of freeze–thaw damage in the component section, it may underestimate the bearing capacity of continuous beam bridges. Yang [17] established a calculation method for river piers affected by freeze–thaw and carried out seismic vulnerability analysis combined with damage depth and height; Sun [18] found that freeze–thaw cycles would lead to performance degradation of Y-shaped piers of urban viaducts, such as reduced bearing capacity and accelerated stiffness degradation. Li et al. [19] and Yang [20] both emphasized that material deterioration caused by freeze–thaw will affect the seismic performance of bridges, and ignoring the coupling effect of deterioration (such as corrosion, carbonation, etc.) will seriously overestimate the seismic performance of bridges. Xiong et al. [21] proposed a seismic resilience evaluation method for steel–concrete composite beam bridges in cold regions considering freeze–thaw damage; Dong [22] constructed a bridge vulnerability analysis method based on deterioration and found that freeze–thaw deterioration would increase the curvature at the bottom of piers and reduce the relative displacement of supports. Studies by Wang [23] showed that freeze–thaw deterioration would increase the displacement at the top of offshore bridge piers, leading to early structural yielding and reduced safety factors. Peng et al. [24] proposed a micro-scale concrete freeze–thaw damage prediction method and a multi-scale pier equivalent simulation model, and found that the peak load of piers decreases with the increase in the number of freeze–thaw cycles; Sun et al. [25] found that the seismic vulnerability of bridges shows a “increase-decrease-increase” trend with the number of freeze–thaw cycles. Huang et al. [26] developed a comprehensive numerical model to simulate the gradual degradation from the material level to the component level and its cumulative impact on structural seismic performance. The model integrates beam–column fiber elements and joint elements; they also used ground motions scaled by amplitude to conduct probabilistic seismic demand analysis and defined damage thresholds based on freeze–thaw degraded RC columns. Wang et al. [27] established a finite element model of PC bridges through OpenSees software to analyze the time-varying deterioration effect. On the basis of considering the uncertainty of seismic loads, they carried out time-varying seismic response and vulnerability analysis of prestressed concrete bridges; using a method combining seismic vulnerability curves and seismic hazard curves to evaluate the time-varying seismic hazard of concrete bridges, the results showed that the seismic risk probability of PC bridges under different damage states first increases and then decreases, reaching the maximum when the seismic fortification intensity is VIII. Cui et al. [28] developed a seismic vulnerability analysis framework for degraded RC columns considering the impact of freeze–thaw damage, and conducted probabilistic seismic vulnerability analysis on aging RC columns. The results showed that the impact of freeze–thaw damage cannot be ignored when studying the seismic performance of aging RC structures, and the seismic vulnerability of degraded RC columns increases nonlinearly with the increase in the number of freeze–thaw cycles and the severity of damage states.

Although the above studies have clarified the deterioration effect of freeze–thaw cycles on the seismic performance of concrete materials, RC components, and some bridge types, there are still two key shortcomings: Firstly, existing numerical simulations and vulnerability analyses mostly focus on frame columns, Y-shaped piers, or composite beam bridges, etc. Special research on twin-column piers, which are widely used in engineering, is relatively scarce, especially the lack of targeted analysis on their damage mechanism under the coupling effect of freeze–thaw cycles and seismic loads. Secondly, most studies only consider the macroscopic impact of freeze–thaw damage alone, and do not systematically reveal the regulatory mechanism of the interaction between the number of freeze–thaw cycles and seismic intensity on the failure mode of twin-column piers, making it difficult to directly provide accurate support for the design and maintenance of twin-column piers in cold regions.

In view of this, this study takes twin-column piers as the research object and systematically explores the seismic response law under the action of freeze–thaw cycles through numerical simulation and theoretical analysis. It aims to reveal the damage mechanism and failure mode of piers under the interaction of the number of freeze–thaw cycles and seismic intensity, so as to provide more targeted decision support for the design, maintenance, and management of bridges in cold regions.

2. Freeze–Thaw Damaged Pier Model

Freeze–thaw (F–T) cycles exert a significant negative impact on the mechanical properties and durability of concrete. During each F–T cycle, the water within the concrete undergoes a phase change and expands in volume, inducing additional internal stress in the material. The repeated action of freezing and thawing progressively reduces both the compressive strength and elastic modulus of concrete, with strength typically decreasing by approximately 1–3% per cycle [29]. As the number of F–T cycles increases, the internal porosity of the concrete rises, and microcracks initiate, propagate, and eventually interconnect, resulting in increasingly complex internal damage structures.

This degradation of the microstructure directly affects the macroscopic mechanical behavior of concrete, leading to a continuous decline in its compressive strength and stiffness. Furthermore, the increase in porosity and the expansion of microcracks significantly accelerate carbonation and chloride ion penetration. Carbonation reduces the alkalinity of the concrete, thereby weakening its protective environment for embedded reinforcement. Meanwhile, chloride ingress can trigger reinforcement corrosion, further compromising the load-carrying capacity of reinforced concrete components.

In addition, F–T cycles impair the impermeability of concrete, diminishing its ability to resist the ingress of water and aggressive substances. This exacerbates the formation and propagation of internal voids and cracks, which in turn accelerates the deterioration of the concrete under harsh environmental conditions and reduces its overall durability.

2.1. Constitutive Models of Concrete and Reinforcement Under Freeze–Thaw Cycles

For ordinary concrete, its mechanical properties exhibit a generally linear degradation trend with increasing freeze–thaw (F–T) cycles. Zhang et al. [30] conducted F–T tests on concrete specimens and established a quantitative relationship between the mechanical properties of concrete and the number of F–T cycles. The empirical expression describing this degradation is given as follows:

$${\displaystyle \frac{f_{c,d}}{f_c}}=1-200N\times f_{cu}^{-3.0355}$$

(1)

$${\displaystyle \frac{f_{cc,d}}{f_{cc}}}=1-51800\times f_{cu}^{-4.7}(1-1.2884\lambda )N$$

(2)

where

$f_c$ and $f_{c,d}$—Compressive strength of plain concrete after freeze–thaw damage;

$f_{cu}$—Compressive strength of plain concrete cube;

$\lambda$—characteristic value of stirrup reinforcement;

$f_{cc}$ and $f_{cc,d}$—Compressive strength of concrete confined by stirrups before and after freeze–thaw damage.

The constitutive model for reinforcing steel used in this study is expressed by the following equation:

$$f_s=\left\{\begin{array}{l}{E}_s{\epsilon }_s,{\epsilon }_s\le {\epsilon }_y\\ f_y+b_s{E}_s({\epsilon }_s-{\epsilon }_y),{\epsilon }_s>{\epsilon }_y\end{array}\right.$$

(3)

where

$f_s$ and ${\epsilon }_s$—stress and strain of the reinforcing steel, respectively;

$f_y$ and ${\epsilon }_y$—yield strength and yield strain of the reinforcing steel, respectively;

$E_s$ and $b_s$—elastic modulus and strain hardening ratio of the reinforcing steel, respectively.

2.2. Slip Model of Longitudinal Reinforcement Considering Freeze–Thaw Damage

Under freeze–thaw (F–T) cycles, the bond performance between concrete and reinforcing steel is also adversely affected, resulting in increased longitudinal reinforcement slip. Sezen and Setzler [31] developed a slip model for longitudinal reinforcement that accounts for freeze–thaw damage based on experimental investigations and numerical analyses. This model incorporates the effect of the number of F–T cycles on the bond–slip relationship, enabling a more accurate simulation of longitudinal reinforcement slip behavior under freeze–thaw-induced deterioration.

$$S=\left\{\begin{array}{l}{\displaystyle \frac{f_s^{2}d}{8E_s\sqrt{f_{c,d}}}},0\le f_s\le f_y\\ {\displaystyle \frac{(4f_s-3f_y)f_{y}d}{8E_s\sqrt{f_{c,d}}}}+{\displaystyle \frac{(f_s-f_d{)}^{2}d}{4E_s{b}_s\sqrt{f_{c,d}}}},f_s>f_y\end{array}\right.$$

(4)

where

$\mathrm{s}$—slip displacement of the longitudinal reinforcement;

d—diameter of the longitudinal reinforcement.

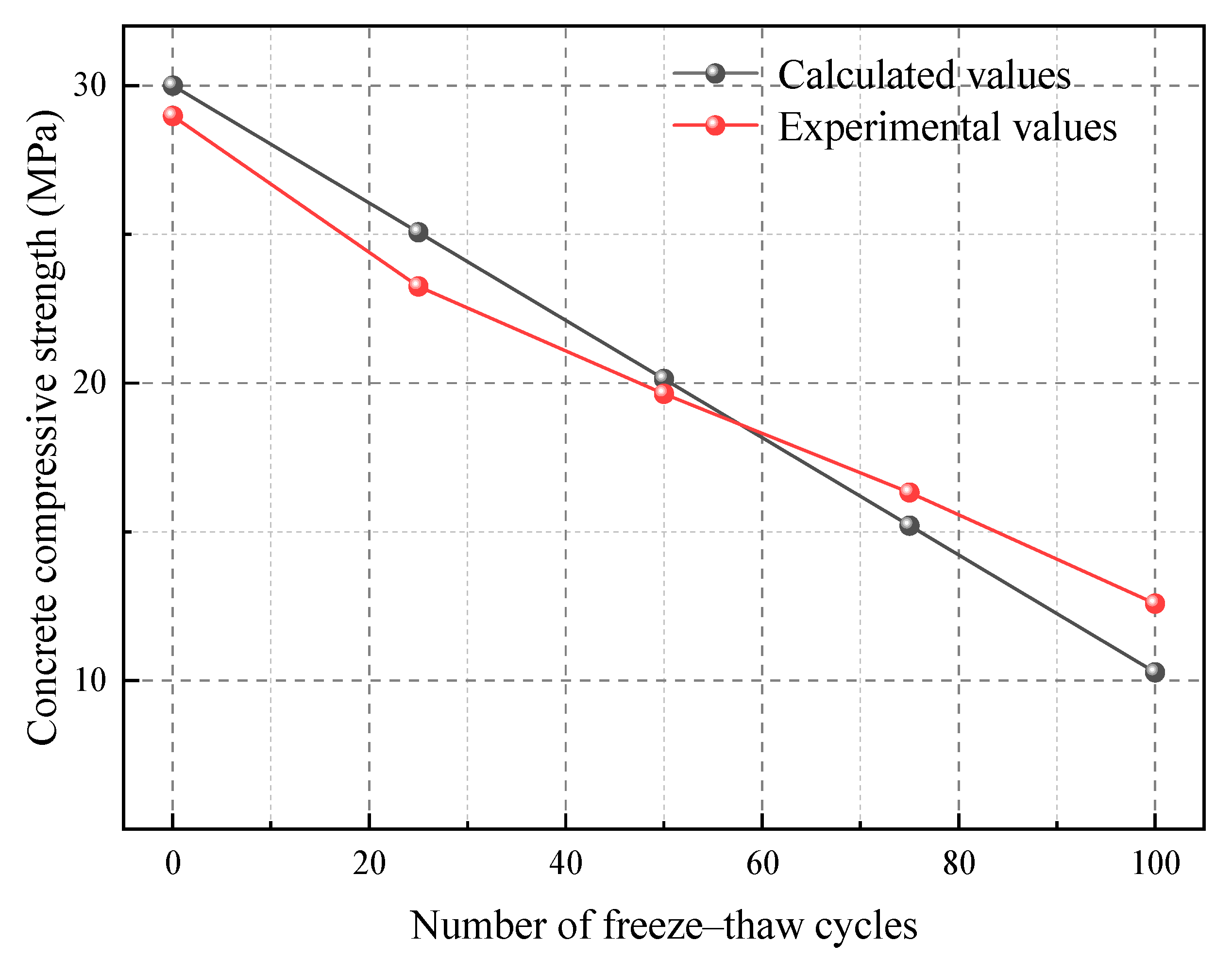
2.3. Constitutive Model Validation

To verify the accuracy and reliability of the adopted concrete constitutive model, a series of standard-sized concrete specimens were specially prepared and subjected to freeze–thaw (F–T) cycles using the HC-HDK9/F rapid freeze–thaw (Hangzhou Huaguan Technology, Hangzhou, China) testing machine, as shown in Figure 1. The specimens were exposed to 25, 50, 75, and 100 F–T cycles, respectively, simulating the material performance variations at different freeze–thaw stages. Each F–T cycle was conducted strictly following the relevant testing standards to ensure consistency and control of the experimental conditions. Upon completion of the prescribed number of cycles, compressive strength tests were immediately performed on the specimens, as illustrated in Figure 2, to obtain mechanical property data of concrete at different freeze–thaw degradation levels.

After completing the compressive strength tests on the concrete specimens, measured data reflecting the influence of different numbers of freeze–thaw (F–T) cycles on concrete compressive strength were obtained. These experimental results were systematically compared with the calculated values predicted by the concrete constitutive model introduced in Section 2.1, as illustrated in Figure 3.

The comparison reveals that both the experimental and predicted values exhibit a consistent trend of decreasing compressive strength with increasing F–T cycles. The experimental data show a more rapid decline in the early stages of cycling, while the predicted values decrease more gradually overall. In the initial phase (0–25 cycles), the experimental results are slightly lower but close to the predicted values; during the mid-phase (25–75 cycles), the discrepancy widens somewhat; and in the later phase (75–100 cycles), the two sets of data converge again. These observations indicate that the adopted concrete constitutive model effectively captures the degradation pattern of compressive strength due to freeze–thaw cycling, providing reliable theoretical support for related studies.

3. Seismic Fragility Analysis Method Based on Incremental Dynamic Analysis (IDA)

Incremental Dynamic Analysis (IDA) is a nonlinear dynamic time-history analysis method developed in recent years, often described metaphorically as a dynamic pushover analysis [32]. IDA not only clearly depicts the full progression of damage in bridges—from initial yielding to complete collapse—under seismic excitations of varying intensities from the same earthquake record, but also retains the advantages of both nonlinear time-history analysis and pushover methods. Furthermore, it can be applied to multi-degree-of-freedom (MDOF) structural systems, accounting for higher mode effects on the seismic performance of bridge piers. Therefore, IDA provides a more comprehensive and realistic evaluation of seismic performance, especially suitable for high piers and long-span structures.

Compared with static nonlinear pushover analysis, IDA simulates the dynamic response process of structures under earthquake loading, effectively overcoming many limitations caused by the static simplification inherent in pushover methods.

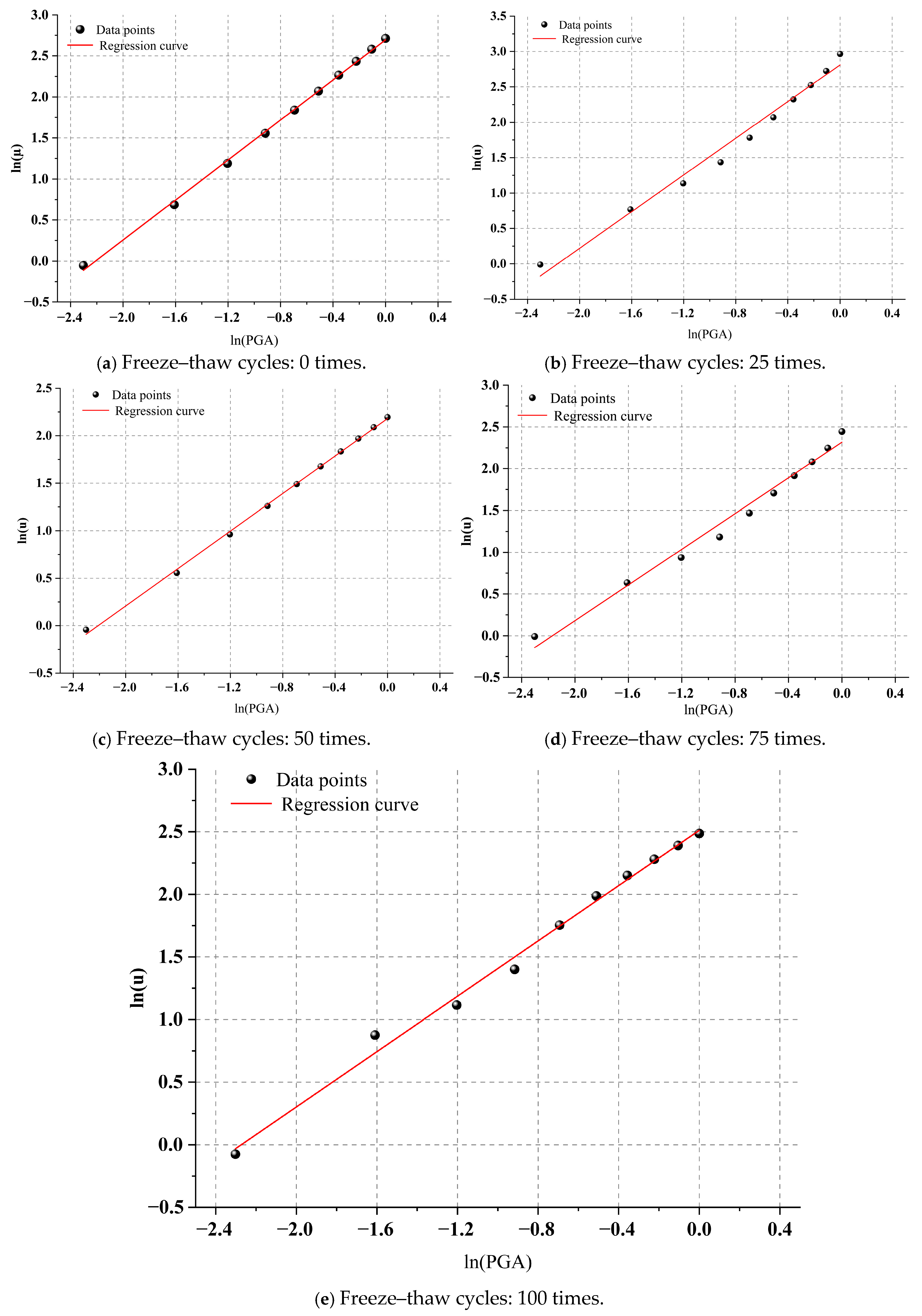
3.1. Log-Linear Probabilistic Seismic Demand Model

In earthquake engineering, peak ground acceleration (PGA) and the structural displacement ductility ratio generally exhibit an exponential regression relationship. To establish fragility curves, logarithmic transformations are typically applied to both PGA and the displacement ductility ratio. A log-linear regression is then performed to determine the relationship between these two variables.

$$\ln (\mu )=a+b\ln (PGA)$$

(5)

where

$\mu$—displacement ductility ratio of the structure;

$a,b$—value predicted by linear regression.

Seismic fragility refers to the probability that a component or system sustains a certain level of damage or exceeds a specified damage state under different seismic intensities [33]. In this study, the seismic fragility of bridge piers is calculated using the Incremental Dynamic Analysis (IDA) method, and is expressed as follows:

$$P_f=P\left[\ln ({\displaystyle \frac{S_d}{S_c}})\right]\ge 0\left|IM\right.$$

(6)

As previously stated, when both the seismic demand and structural capacity follow a lognormal distribution, the probability of failure also conforms to a lognormal distribution. Accordingly, the fragility function can be transformed into the following expression:

$$P_f=\mathsf{\Phi }\left[{\displaystyle \frac{a+b\ln (IM)-\ln (S_c)}{\sqrt{{\beta }_d^2+{\beta }_c^2}}}\right]$$

(7)

where

$\mathsf{\Phi }\left[\right]$—standard normal cumulative distribution function;

$S_d$—seismic demand;

$S_c$—seismic capacity;

${\beta }_d$—logarithmic standard deviation $S_d$ of seismic demand;

${\beta }_c$—logarithmic standard deviation $S_c$ of seismic capacity.

3.2. Development of Theoretical Seismic Fragility Curves Based on IDA

The procedure for establishing theoretical seismic fragility curves for structural components using Incremental Dynamic Analysis (IDA) is outlined as follows:

• Based on local site conditions, a set of appropriate ground motion records is selected. A suitable ground motion intensity measure, typically the peak ground acceleration (PGA), is chosen. Each selected ground motion is scaled using a series of amplitude scaling factors to cover a PGA range from 0.1 g to 1.0 g, with increments of 0.05 g or 0.1 g.
• Reasonable damage states and corresponding damage indices are defined and quantified. A nonlinear finite element dynamic analysis model of the component is then established. Nonlinear time history analyses are performed under the selected ground motions, and structural response data are extracted to construct probabilistic seismic demand models (PSDMs) through regression analysis.
• Based on the regression results, the probability that seismic demand exceeds capacity is calculated for each damage state. Fragility curves are then plotted to represent these exceedance probabilities as a function of seismic intensity.

3.3. Damage Index for Bridge Piers

In the seismic vulnerability analysis of bridges, it is necessary to define different damage states for structures or components and select appropriate damage indices to quantify these states. In this study, the displacement ductility ratio suggested by Hwang [34] is adopted as the damage index for bridge piers. The displacement ductility ratio is defined as the ratio of the maximum pier-top displacement under seismic action to the pier-top displacement corresponding to the first yielding of the tension reinforcement. When using this damage index, the damage states of bridge piers are categorized into five levels: no damage, slight damage, moderate damage, severe damage, and complete damage, as shown in Table 1.

$$\mu ={\displaystyle \frac{\mathsf{\Delta }}{{\mathsf{\Delta }}_{cy1}}}$$

(8)

where

$\mu$—displacement ductility ratio;

${\mathsf{\Delta }}_{cy1}$—relative pier-top displacement when tension reinforcement first yields;

$\mathsf{\Delta }$—maximum relative pier-top displacement under seismic action.

Table 1. Displacement ductility ratio damage index.

Damage State	Displacement Ductility Ratio Threshold	Damage Characteristics
No Damage	$\mu \le {\mu }_{\mathrm{c}\mathrm{y}1}$	Minor cracks appear
Slight Damage	${\mu }_{cy1}\le \mu \le {\mu }_{\mathrm{cy}}$	Minor cracks are widely distributed
Moderate Damage	${\mu }_{cy}\le \mu \le {\mu }_{\mathrm{c}\mathrm{y}4}$	Concrete cover begins to spall
Severe Damage	${\mu }_{cy4}\le \mu \le {\mu }_{\max }$	Concrete is crushed
Complete Damage	${\mu }_{\max }\le \mu$	Structural collapse

Table 1. Displacement ductility ratio damage index.

Damage State	Displacement Ductility Ratio Threshold	Damage Characteristics
No Damage	$\mu \le {\mu }_{\mathrm{c}\mathrm{y}1}$	Minor cracks appear
Slight Damage	${\mu }_{cy1}\le \mu \le {\mu }_{\mathrm{cy}}$	Minor cracks are widely distributed
Moderate Damage	${\mu }_{cy}\le \mu \le {\mu }_{\mathrm{c}\mathrm{y}4}$	Concrete cover begins to spall
Severe Damage	${\mu }_{cy4}\le \mu \le {\mu }_{\max }$	Concrete is crushed
Complete Damage	${\mu }_{\max }\le \mu$	Structural collapse

3.4. Selection of Ground Motion Records

The input of seismic ground motion is crucial for conducting structural seismic response analysis, and different ground motions can have a significant impact on structural response. Due to the uncertainty of seismic ground motion, a large number of earthquake records are usually required to simulate this uncertainty when performing seismic vulnerability analysis. Referring to the Seismic Design Code for Highway Bridges (JTGT2231-01-2020) [35] and previous research [36], this study considered factors such as the intensity, spectrum, duration of the seismic ground motion, and the number of selected ground motions. Earthquake records were selected from the Pacific Earthquake Engineering Research Center Strong Motion Database (PEER Strong Motion Database) based on seismic intensity, frequency, duration, and quantity. Existing research has shown that when using the Incremental Dynamic Analysis (IDA) method to assess structural performance, selecting 10 to 20 earthquake records can achieve a certain level of accuracy [37]. Therefore, this study selected 10 appropriate seismic records that cover a range of seismic intensities and frequency characteristics to ensure the reliability and representativeness of the analysis results, as shown in

Table 2. Ten Selected Ground Motion Records.

No.	Earthquake Name	Duration (s)	Characteristic Period (s)	PGA (g)
1	RH3TG045	19.92	0.49	0.11
2	San Fernando-291	22.07	0.49	0.26
3	ImperialValley, #10 V	32.64	0.48	0.10
4	Landers	42.92	0.48	0.12
5	Chi-Chi_Taiwan	39.62	0.46	0.28
6	Morgan Hill	23.68	0.48	0.16
7	Borrego	36.26	0.46	0.23
8	Point Mugu	40.26	0.50	0.36
9	Kent country	28.65	0.49	0.12
10	Gulf of Aqabaa	30.68	0.48	0.18

.

4. Seismic Vulnerability Analysis of Bridge Piers

4.1. Development of Finite Element Model for Bridge Pier

In this study, a finite element model of the bridge pier was developed using the OpenSees simulation platform. The flexural responses of the cap beam and pier columns were modeled using fiber beam–column elements. Zero-length rotational spring elements were employed to simulate the plastic hinge behavior and bond-slip deformation of longitudinal reinforcement at the connections between the piers and cap beam, as well as at the base. The joint region between the cap beam and pier was idealized using rigid arms to represent the rigid connection behavior [38]. The detailed numerical model is illustrated in Figure 4.

In the numerical model, the concrete behavior was modeled using the Concrete01 constitutive relationship available in OpenSees, which effectively captures the strength enhancement and increased peak strain characteristics of confined core concrete due to transverse reinforcement. For the longitudinal reinforcement, the Steel02 model in OpenSees was adopted, which accurately reflects the Bauschinger effect of reinforcing steel [39].

Furthermore, to simulate the plastic hinge formation and bond–slip deformation of the longitudinal reinforcement at the base, zero-length rotational spring elements (Bond_SP01) were employed in conjunction with a pullout force–slip displacement model for the rebar. The yield slip, a key parameter in this model, is calculated using the following formula during the simulation process [40]:

$$S_y=2.54{\left({\displaystyle \frac{d_b}{8437}}{\displaystyle \frac{f_y}{f_c^{\prime }}}(2\alpha +1)\right)}^{1/\alpha }+0.34$$

(9)

where

$d_b$—diameter of the reinforcement bar;

$f_y$—yield stress of the reinforcement;

$\alpha$—local bond–slip parameter, taken as 0.4 according to recommended values.

4.2. Seismic Demand Function of Bridge Piers

Incremental Dynamic Analysis (IDA) was conducted on the structural model using the selected ground motion records individually. For each seismic record, the maximum pier-top displacement was obtained, and the corresponding displacement ductility ratio was calculated. Using conventional reliability methods, a log-linear regression was performed on the displacement ductility ratios derived from each ground motion to develop seismic demand functions for the double-column bridge pier subjected to 0, 25, 50, 75, and 100 freeze–thaw cycles [41]. The log-linear regression fitting processes for freeze–thaw cycles ranging from 0 to 100 are illustrated in the corresponding Figure 5. Through statistical analysis and regression fitting, seismic demand functions were established for different freeze–thaw cycle counts, providing a foundation for subsequent fragility analysis.

Seismic Demand Function of the Bridge Pier under 0 Freeze–Thaw Cycles:

$$\ln (\mu )=2.5632+1.0265\ln (PGA)$$

(10)

Seismic Demand Function of the Bridge Pier under 25 Freeze–Thaw Cycles:

$$\ln (\mu )=2.6369+1.0569\ln (PGA)$$

(11)

Seismic Demand Function of the Bridge Pier under 50 Freeze–Thaw Cycles:

$$\ln (\mu )=2.7526+0.9965\ln (PGA)$$

(12)

Seismic Demand Function of the Bridge Pier under 75 Freeze–Thaw Cycles:

$$\ln (\mu )=2.6529+1.5965\ln (PGA)$$

(13)

Seismic Demand Function of the Bridge Pier under 100 Freeze–Thaw Cycles:

$$\ln (\mu )=2.4896+1.3696\ln (PGA)$$

(14)

4.3. Seismic Fragility of Bridge Piers

Based on the constructed seismic demand functions of the bridge piers, seismic fragility functions corresponding to different numbers of freeze–thaw cycles can be obtained. These fragility functions enable the calculation of the probability that the bridge pier exceeds various damage states under different freeze–thaw cycle counts, as summarized in

Table 3. Seismic Fragility Functions of Bridge Piers under Different Freeze–Thaw Cycles.

Number of Freeze–Thaw Cycles	Seismic Fragility Function
0	$P_f=\mathsf{\Phi }\left[{\displaystyle \frac{2.5632+1.0265\ln (IM)-\ln (S_c)}{0.5}}\right]$
25	$P_f=\mathsf{\Phi }\left[{\displaystyle \frac{2.6369+1.0569\ln (IM)-\ln (S_c)}{0.5}}\right]$
50	$P_f=\mathsf{\Phi }\left[{\displaystyle \frac{2.7526+0.9965\ln (IM)-\ln (S_c)}{0.5}}\right]$
75	$P_f=\mathsf{\Phi }\left[{\displaystyle \frac{2.6529+1.5965\ln (IM)-\ln (S_c)}{0.5}}\right]$
100	$P_f=\mathsf{\Phi }\left[{\displaystyle \frac{2.4896+1.3696\ln (IM)-\ln (S_c)}{0.5}}\right]$

.

To thoroughly investigate the effect of the number of freeze–thaw cycles on the seismic fragility of bridge piers, a comparative analysis of the fragility curves was conducted for the bridge pier at four distinct damage states under varying seismic intensities, as shown in Figure 6.

The vulnerability curve for slight damage indicates that as the number of freeze–thaw cycles increases, the probability of slight damage to the pier exceeds a certain threshold, generally showing an upward trend. This effect is particularly significant in the lower PGA range (0.1 g to 0.3 g). For instance, at a PGA of 0.2 g, the probability of slight damage for a pier that has undergone zero freeze–thaw cycles is approximately 0.1, while after 100 freeze–thaw cycles, this probability rises to around 0.3. This suggests that freeze–thaw cycles have a noticeable impact on the accumulation of initial damage in piers, reducing their load-bearing capacity under lower seismic intensities. This phenomenon is likely due to material property degradation caused by freeze–thaw cycles, such as reduced compressive strength and elastic modulus of concrete. These degradations make piers more susceptible to initial damage under the same seismic excitation. Moreover, freeze–thaw cycles may also lead to the expansion of microcracks within the pier, further diminishing its seismic performance.

In the vulnerability curve for moderate damage, the increase in freeze–thaw cycles similarly leads to a significant rise in the probability of exceeding the threshold for moderate damage. In the moderate PGA range (0.3 g to 0.6 g), the impact of freeze–thaw cycles is more pronounced. For example, at a PGA of 0.5 g, the probability of moderate damage for a pier that has undergone zero freeze–thaw cycles is about 0.2, while after 100 freeze–thaw cycles, this probability increases to around 0.45. This indicates that as the number of freeze–thaw cycles increases, the extent of damage to piers under moderate seismic intensity intensifies, and the seismic performance of the structure deteriorates significantly. This degradation is likely due to material fatigue and microcrack expansion caused by freeze–thaw cycles. These microcracks further expand under seismic action, leading to increased damage severity. Additionally, freeze–thaw cycles may reduce the stiffness of the pier, making it more prone to larger deformations under seismic excitation, thereby increasing the probability of moderate damage.

The probability of complete damage exceeding a certain threshold remains at a low level in all cases. Even under extreme conditions with a PGA of 1.0 g and 100 freeze–thaw cycles, the probability of complete damage is only about 0.3. This indicates that piers have a high safety margin in terms of design and material selection, effectively resisting the risk of complete damage. Although freeze–thaw cycles increase the probability of complete damage, their impact is relatively small, and the overall structure of the pier remains relatively reliable. This low probability of complete damage is likely due to the high safety margin in the design and material selection of piers. Even under extreme conditions, the structural performance of piers can still maintain a certain level of integrity, effectively resisting the risk of complete damage. Moreover, although freeze–thaw cycles increase the probability of complete damage, their impact is relatively small, indicating that the design and material selection of piers can to some extent resist such effects.

The exceedance probability for complete failure remains low across all scenarios. Even under extreme conditions—PGA of 1.0 g and 100 freeze–thaw cycles—the probability of complete failure is only about 0.3. This demonstrates that the bridge piers possess substantial safety reserves in terms of both design and material selection, effectively resisting the risk of total collapse. Although freeze–thaw cycles slightly increase the likelihood of complete failure, the overall impact is limited, and the structural integrity remains largely intact.

In summary, the increase in freeze–thaw cycles significantly elevates the seismic fragility of bridge piers across different levels of earthquake intensity, particularly in the slight and moderate damage states. This highlights the importance of accounting for freeze–thaw effects in bridge design and maintenance. Nonetheless, the piers exhibit strong resistance to severe and complete damage, reflecting rational design choices and a high level of structural safety.

5. Conclusions and Outlook

5.1. Conclusions

This study systematically investigates the influence of freeze–thaw (F–T) cycles on the seismic fragility of twin-column bridge piers using the Incremental Dynamic Analysis (IDA) method implemented in the OpenSees finite element platform. The main findings are summarized as follows:

(1)

The increase in the number of freeze–thaw cycles significantly enhances the vulnerability of bridge piers under different seismic intensities, particularly evident in the slight and moderate damage levels. In the lower to moderate PGA range, the effect of freeze–thaw cycles markedly increases the probability of exceeding the thresholds for slight and moderate damage. This indicates that freeze–thaw cycles accelerate the accumulation of initial damage in piers, reducing their load-bearing capacity under moderate to low seismic intensities. This result underscores the importance of considering freeze–thaw effects in the design of bridges in cold regions, especially in seismic design. The acceleration of initial damage accumulation due to freeze–thaw cycles should be given full attention to enhance the seismic performance of piers under moderate to low seismic intensities.

(2)

At the severe and complete damage levels, the piers demonstrate strong resistance, reflecting the rationality of structural design in terms of durability and safety margin. Even under extreme conditions with PGA = 1.0 g and 100 freeze–thaw cycles, the probability of complete damage remains around 30%. This suggests that the impact of freeze–thaw degradation on the ultimate state is relatively small, and the overall structure of the pier still has good seismic redundancy and reliability. This indicates that the current bridge design codes can, to some extent, ensure the seismic performance of piers under extreme conditions. However, in cold regions, further refinement of design codes is still needed to better address the impact of freeze–thaw cycles on the seismic performance of piers.

5.2. Outlook

(1)

In this study, the displacement ductility ratio was selected as the damage assessment index for transverse non-equal-height twin-column piers in mountainous areas. However, structural damage assessment is a complex process. In future research, it is possible to consider introducing composite parameters, such as curvature, as damage indices to complement the displacement ductility ratio.

(2)

The number of seismic records selected in this study is limited. In the future, it is possible to consider introducing more seismic records from different regions, with different magnitudes and different focal mechanisms, to more comprehensively evaluate the response characteristics and vulnerability of piers under various seismic conditions, thereby enhancing the universality and accuracy of the research results.