Mechanical Performance and Parameter Sensitivity Analysis of Small-Diameter Lead-Rubber Bearings
Abstract
1. Introduction
2. Design and Testing of Seismic Isolation Bearings
2.1. Design of Small-Diameter Bearings
2.2. Compression–Shear Test
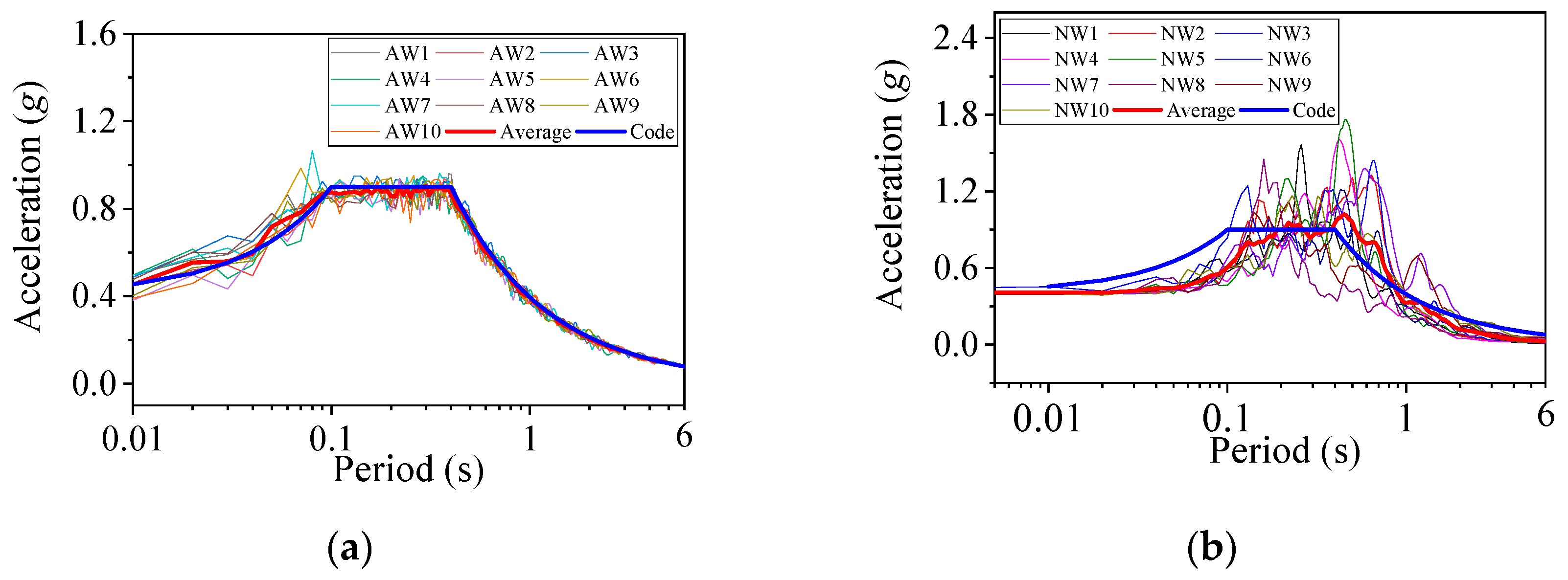
2.3. Dynamic Testing of Bearings
3. Mechanical Properties of Small-Diameter Bearings
3.1. Analysis of Quasi-Static Test Results
3.2. Analysis of Dynamic Test Results
4. Restoring Force Model of Small-Diameter Bearing
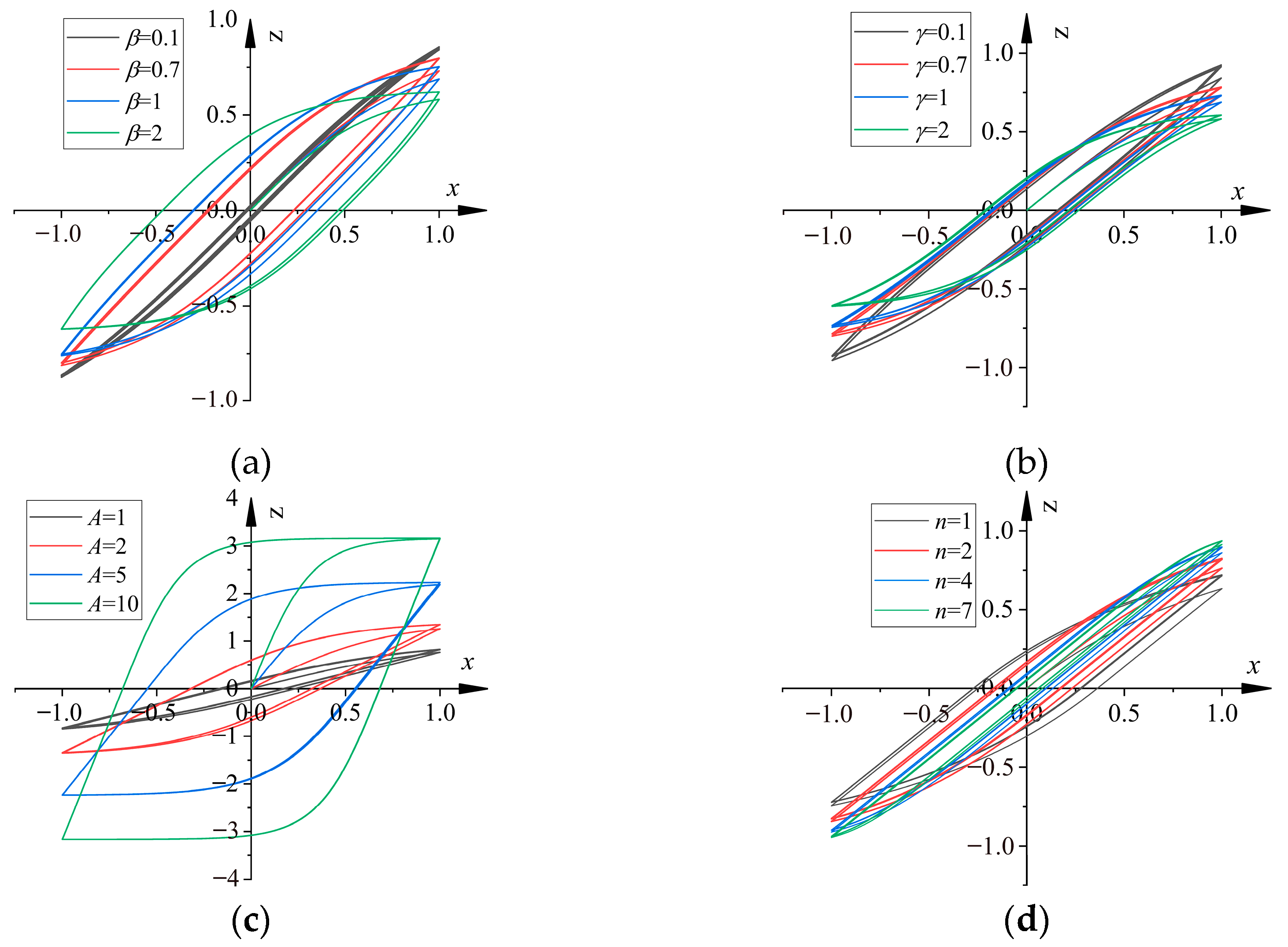
4.1. Identification of Restoring Force Model Parameters
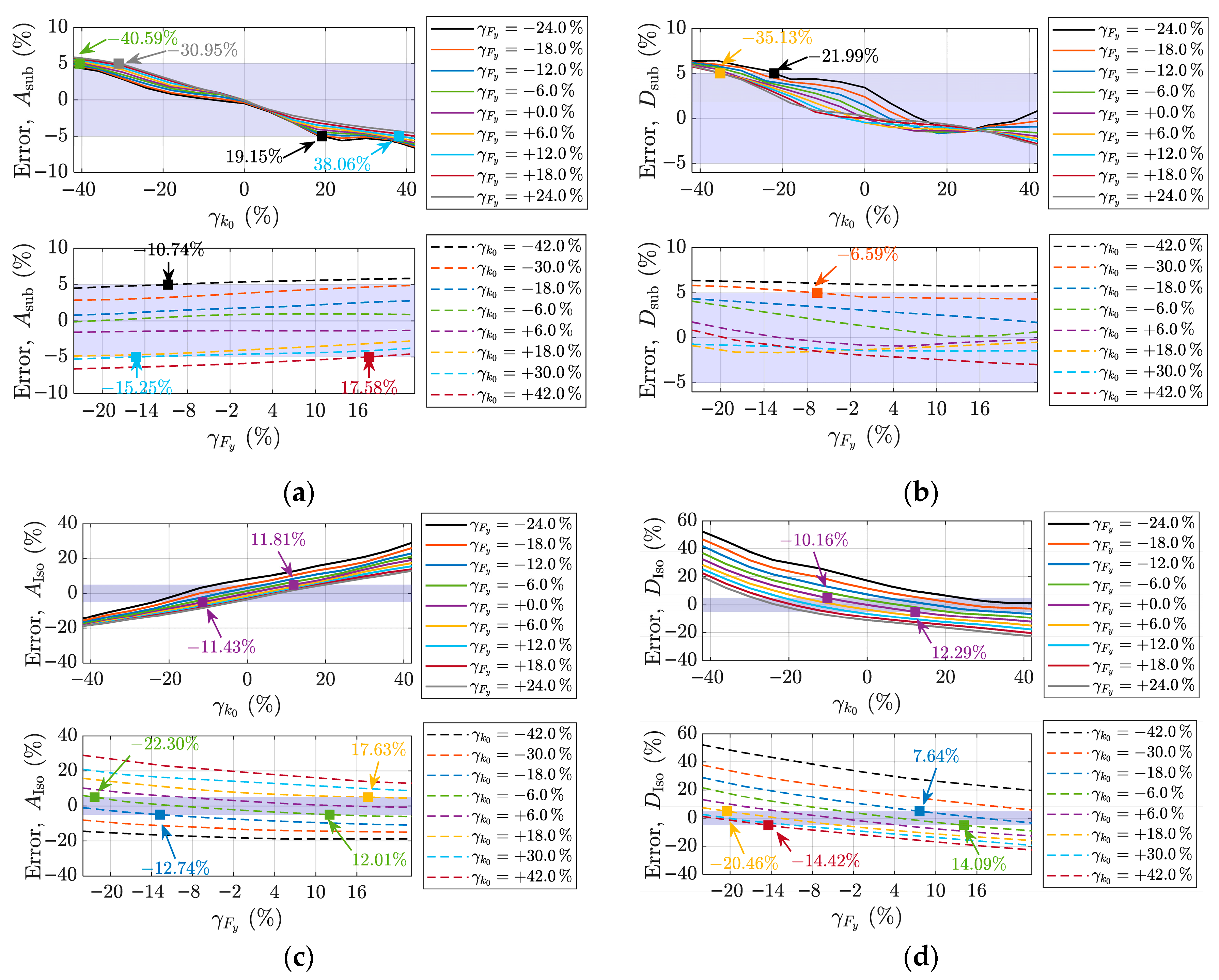
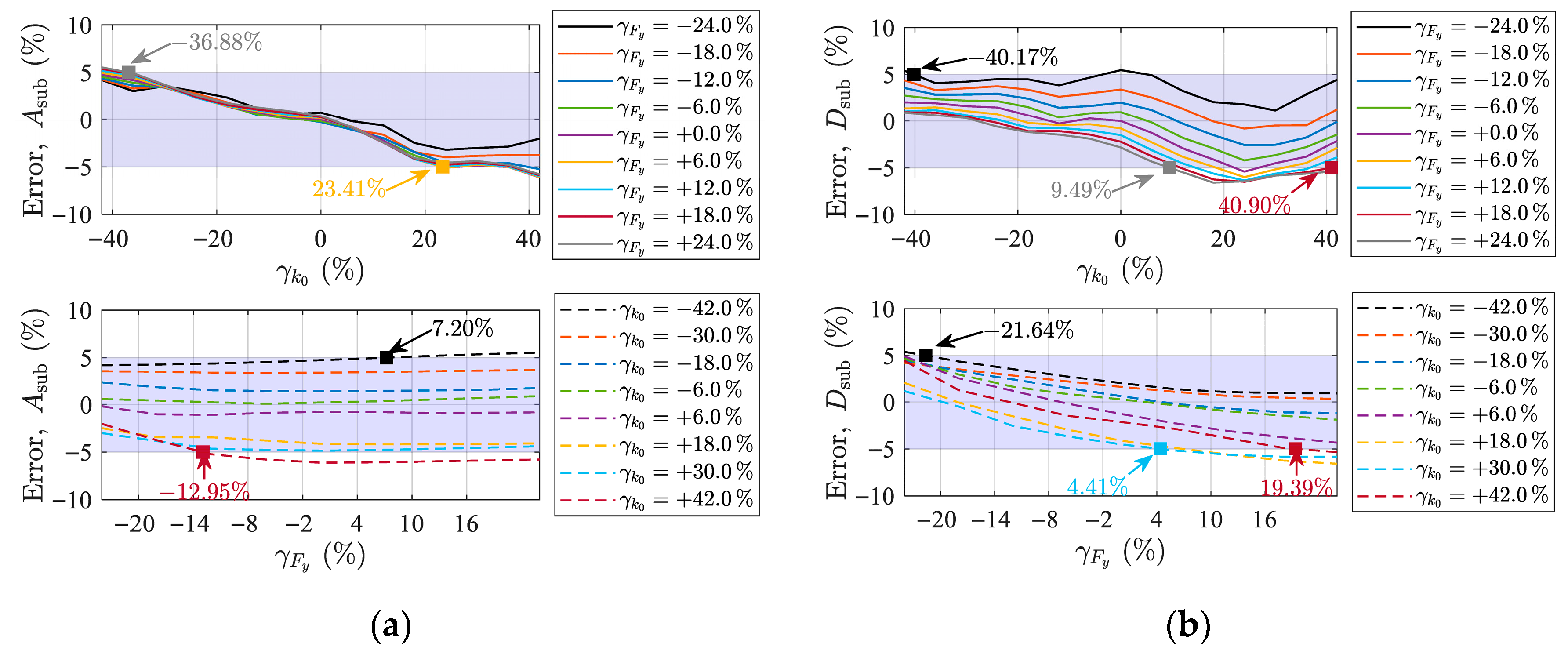
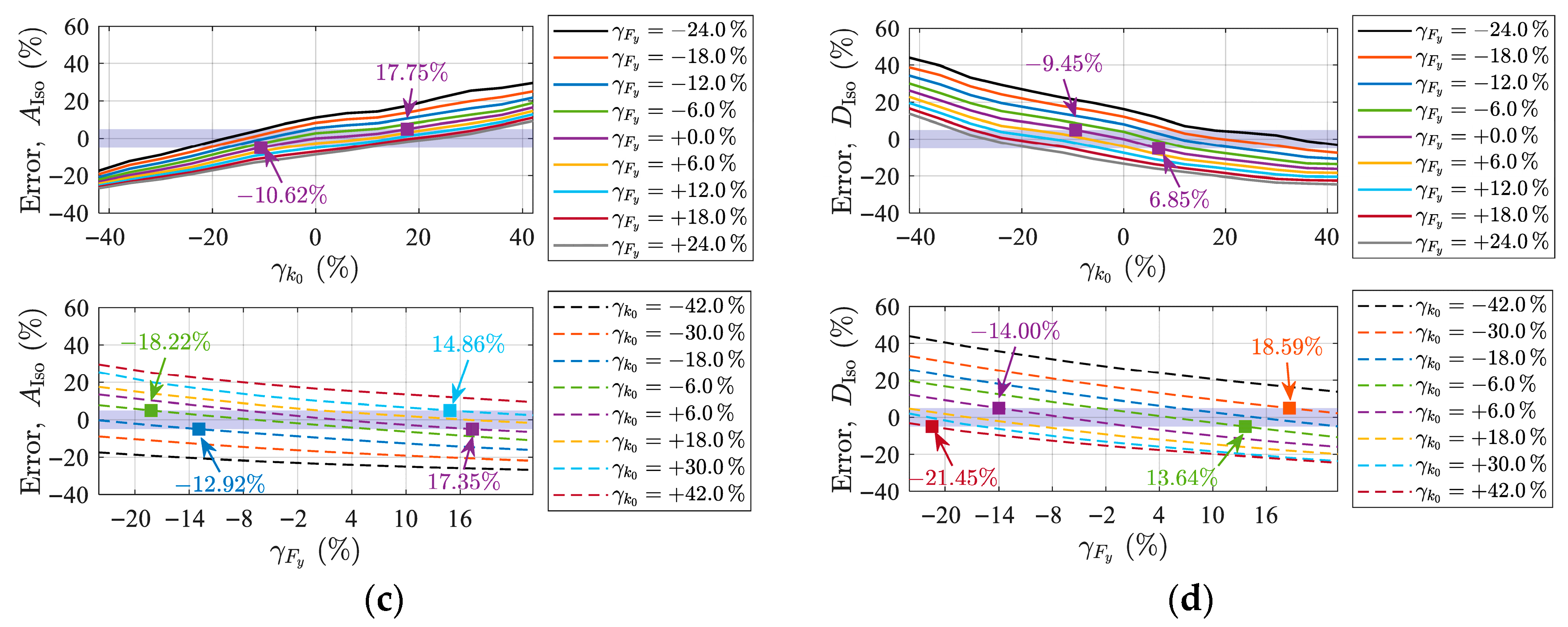
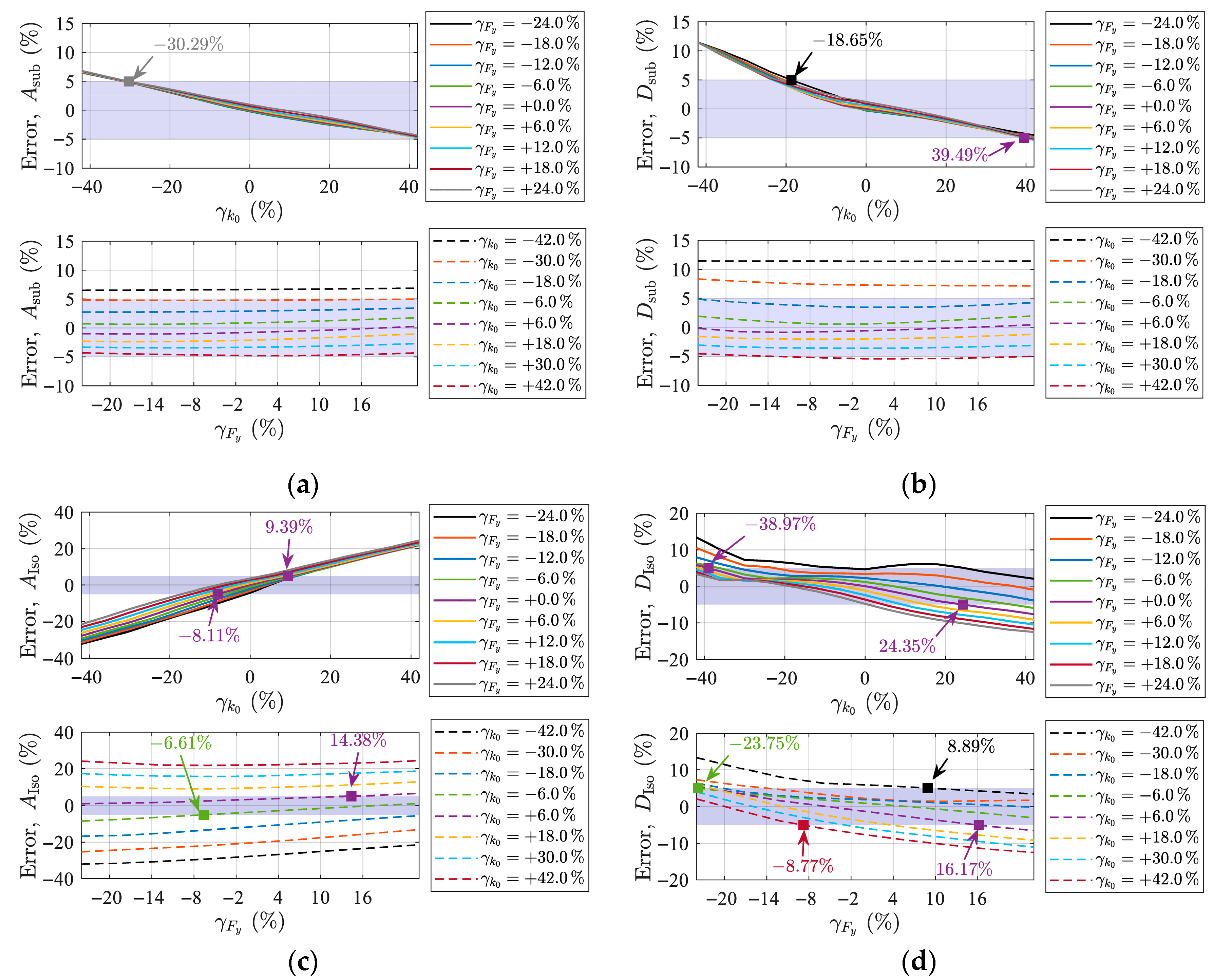
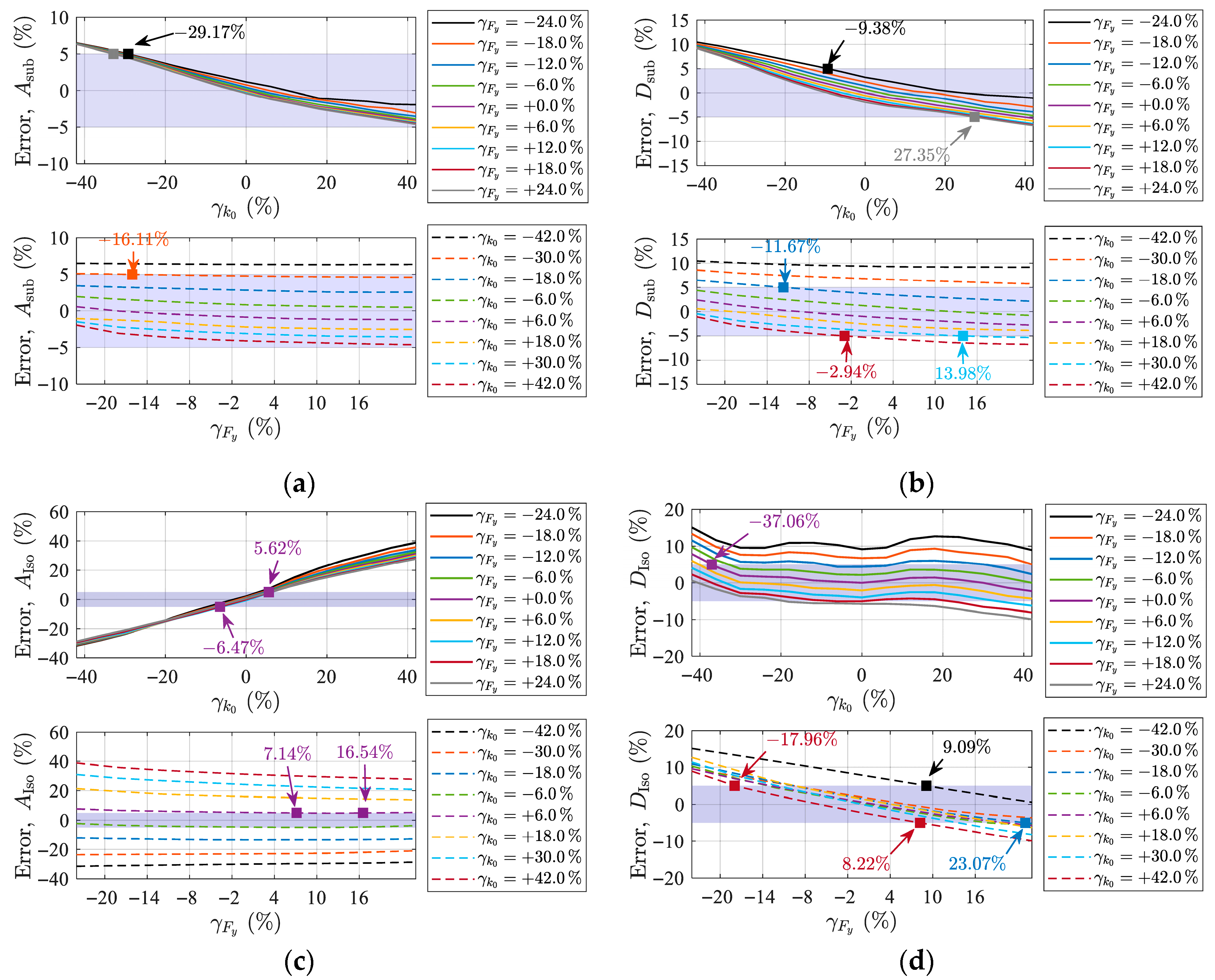
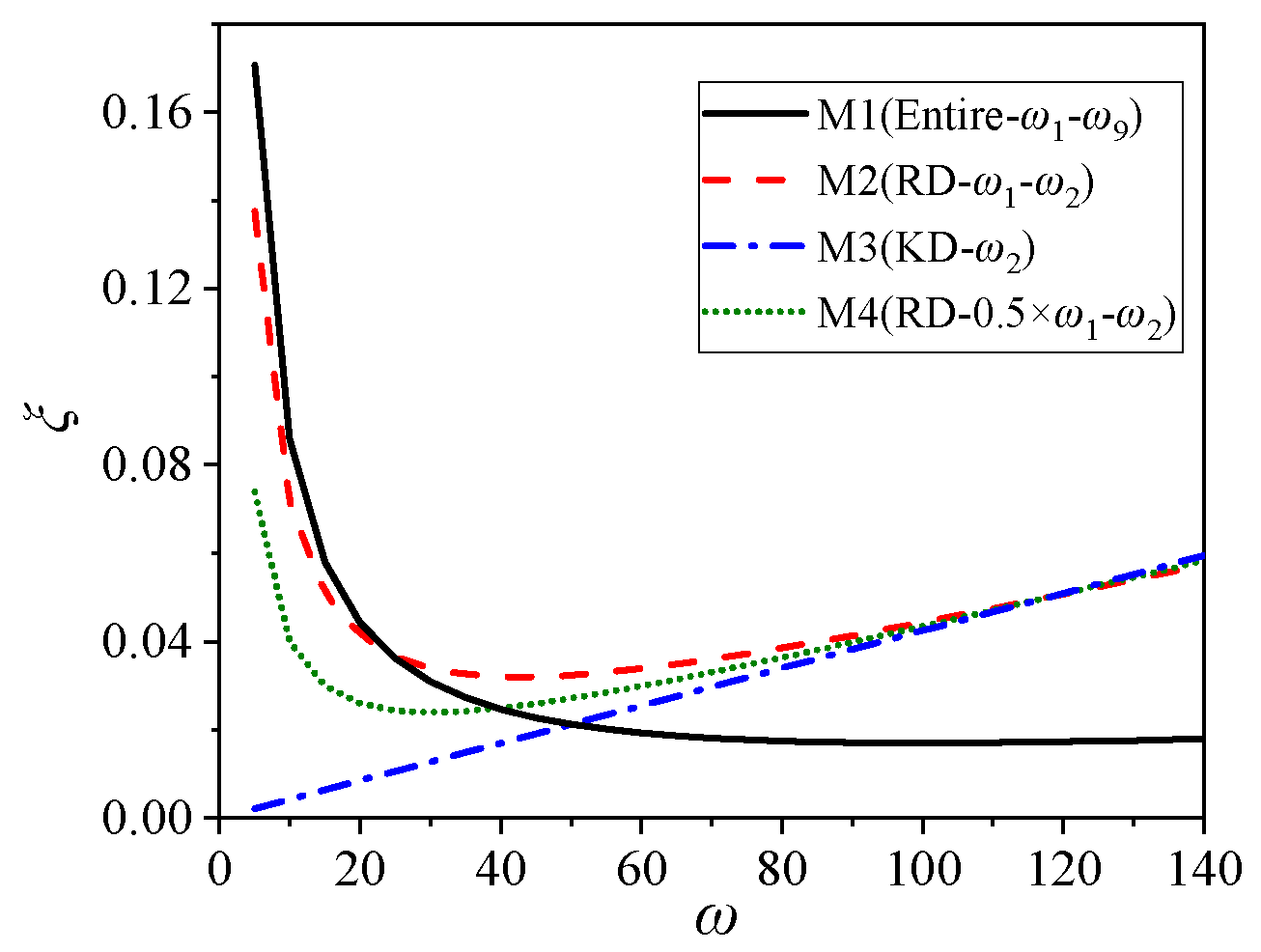
4.2. Sensitivity Analysis of Restoring Force Model Parameters
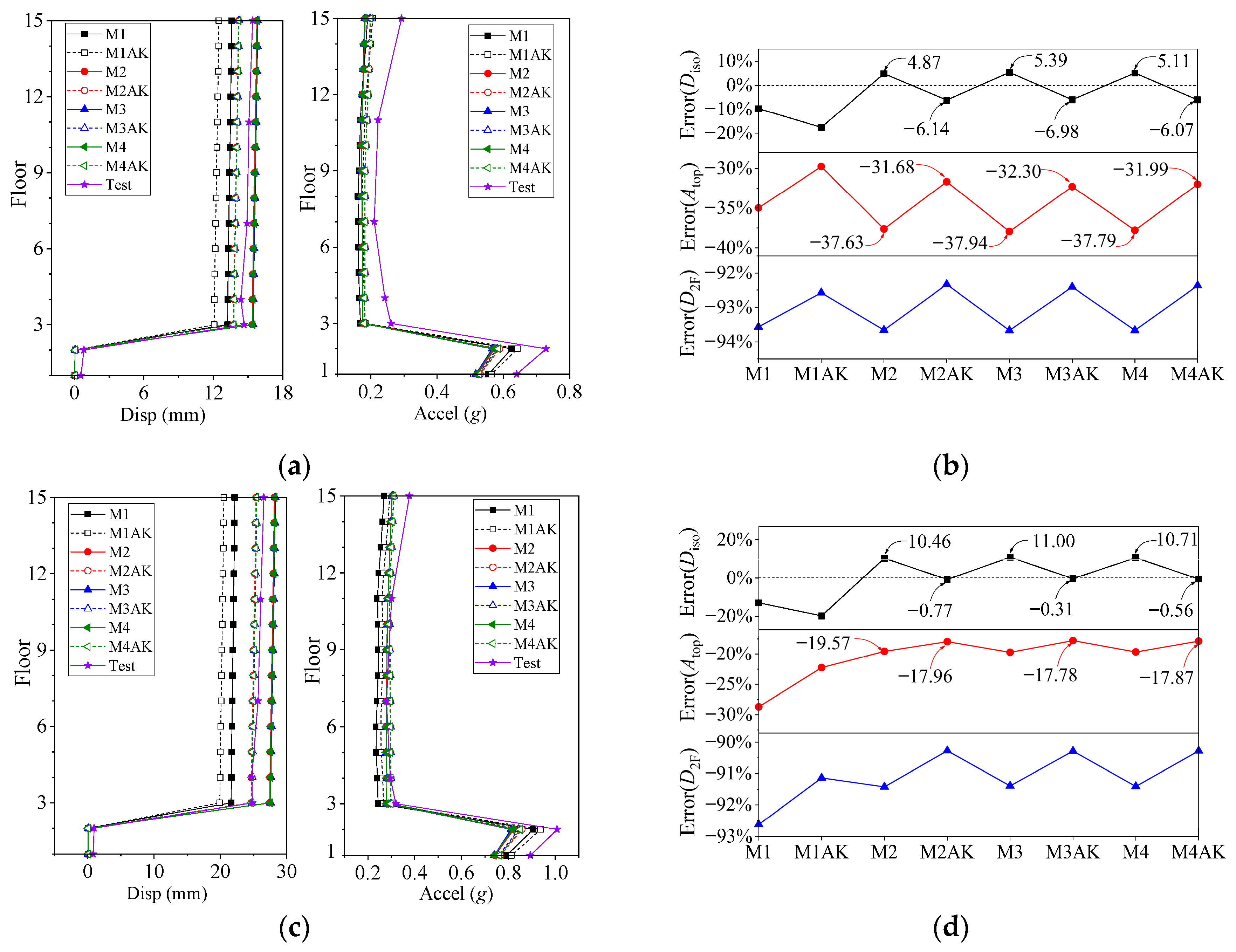
4.3. Structural Seismic Response Analysis Based on the Finite Element Model
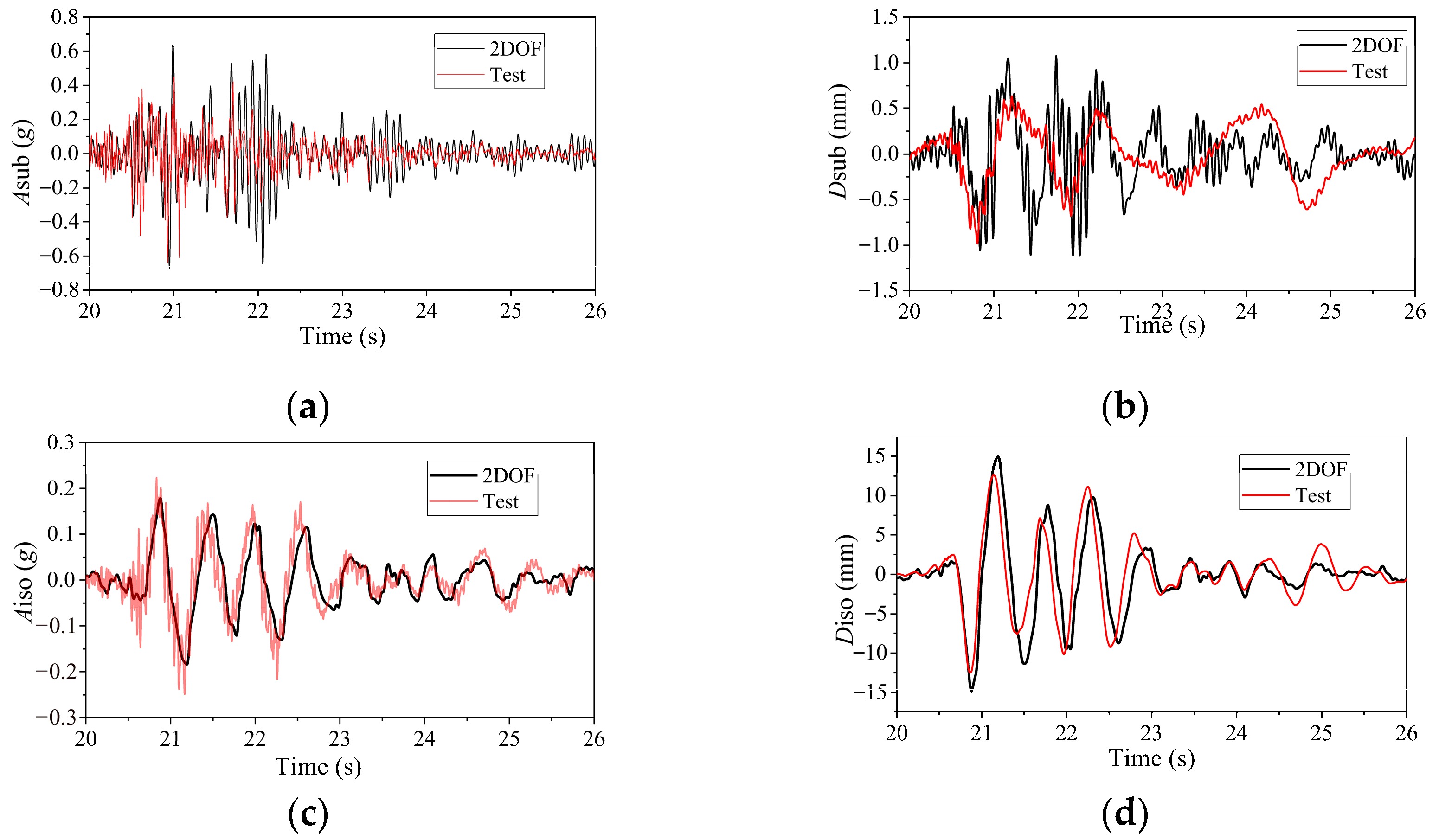
4.3.1. Numerical Modeling
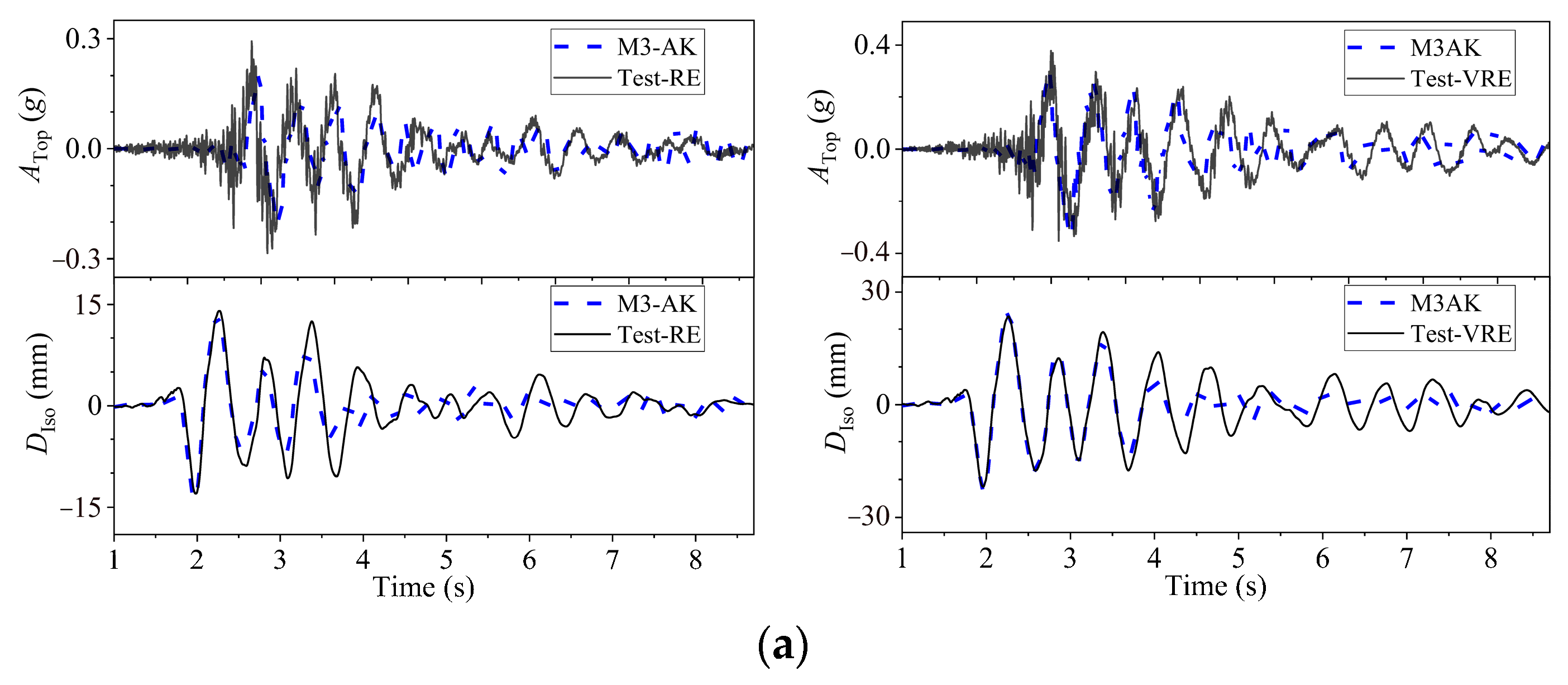
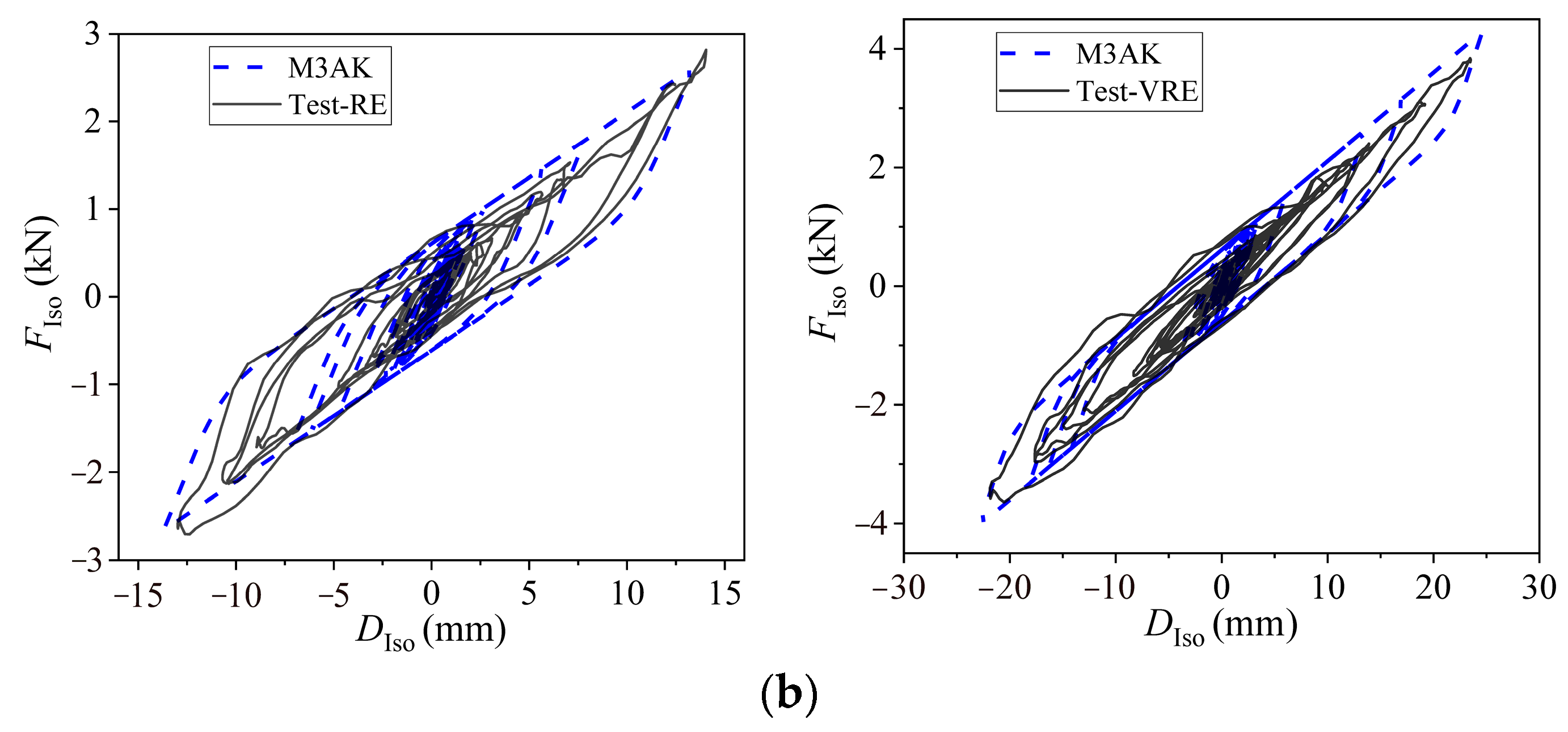
4.3.2. Seismic Response Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xiao, J.; Huang, L.; Weng, R.; Murong, Y.; Liu, L.; Zeng, H.; Jiang, H. Mechanism of chloride ion transport and associated damage in ultra-high-performance concrete subjected to hydrostatic pressure. J. Build. Eng. 2025, 112, 113700. [Google Scholar] [CrossRef]
- Weng, R.; He, Z.; Liu, J.; Lei, B.; Huang, L.; Xu, J.; Liu, L.; Xiao, J. Shear Performance of UHPC-NC Composite Structure Interface Treated with Retarder: Quantification by Fractal Dimension and Optimization of Process Parameters. Buildings 2025, 15, 2591. [Google Scholar] [CrossRef]
- Xiao, J.; Shuai, J.; Deng, W.; Liu, L.; Wang, P.; Li, L. Low-Carbon and Green Materials in Construction: Latest Advances and Prospects. Buildings 2025, 15, 1508. [Google Scholar] [CrossRef]
- Zucca, M.; Longarini, N.; Simoncelli, M.; Aly, A.M. Tuned Mass Damper Design for Slender Masonry Structures: A Framework for Linear and Nonlinear Analysis. Appl. Sci. 2021, 11, 3425. [Google Scholar] [CrossRef]
- Wang, S.J.; Chang, K.C.; Hwang, J.S.; Lee, B.H. Simplified analysis of mid-story seismically isolated buildings. Earthq. Eng. Struct. Dyn. 2011, 40, 119–133. [Google Scholar] [CrossRef]
- Li, Z.H.; Huang, G.Q.; Chen, X.Z.; Zhou, X.H. Seismic Response and Parametric Analysis of Inter-Story Isolated Tall Buildings Based on Enhanced Simplified Dynamic Model. Int. J. Struct. Stab. Dyn. 2022, 22, 2240008. [Google Scholar] [CrossRef]
- Faiella, D.; Mele, E. Vibration characteristics and higher mode coupling in intermediate isolation systems (IIS): A parametric analysis. Bull. Earthq. Eng. 2019, 17, 4347–4387. [Google Scholar] [CrossRef]
- Bhandari, M.; Bharti, S.D.; Shrimali, M.K.; Datta, T.K. Seismic Fragility Analysis of Base-Isolated Building Frames Excited by Near- and Far-Field Earthquakes. J. Perform. Constr. Facil. 2019, 33, 04019029. [Google Scholar] [CrossRef]
- Saha, A.; Mishra, S.K. Implications of inter-storey-isolation (ISI) on seismic fragility, loss and resilience of buildings subjected to near fault ground motions. Bull. Earthq. Eng. 2022, 20, 899–939. [Google Scholar] [CrossRef]
- Tamari, M.; Yoshihara, T.; Miyashita, M.; Ariyama, N.; Nonoyama, M. Structural Design and Performance Evaluation of a Mid-story Seismic Isolated High-Rise Building. Int. J. High-Rise Build. 2017, 6, 227–235. [Google Scholar] [CrossRef]
- Li, J.R.; Luo, W.L.; Liang, Q.H.; Wang, D.Y.; Zhou, Y.; He, Z.M. Shaking table test of seismic performance of high-rise over-track building with base isolation. J. Build. Eng. 2023, 75, 106749. [Google Scholar] [CrossRef]
- Liang, Q.H.; Zhou, Y.; Wang, D.Y.; Luo, W.L.; Li, J.R.; He, Z.M. Shaking table test of vertical isolation performances of super high-rise structure under metro train-induced vibration. J. Build. Eng. 2024, 82, 108323. [Google Scholar] [CrossRef]
- Liu, X.T.; Wang, W.; Li, J.L. Full-scale shaking table tests and numerical studies of structural frames with a hybrid isolation system. Eng. Struct. 2023, 292, 116545. [Google Scholar] [CrossRef]
- JG/T 118-2018; Rubber Isolation Bearings for Buildings. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2018.
- Haringx, J.A. On highly compressible helical springs and rubber rods and their application for vibration-free mountings. II. Philips Res. Rep. 1949, 4, 49–80. [Google Scholar]
- Haringx, J.A. On highly compressible helical springs and rubber rods and their application for vibration-free mountings. III. Philips Res. Rep. 1949, 4, 206–220. [Google Scholar]
- Gent, A.N. Elastic stability of rubber compression springs. J. Mech. Eng. Sci. 1964, 6, 318–326. [Google Scholar] [CrossRef]
- Nishi, T.; Suzuki, S.; Aoki, M.; Sawada, T.; Fukuda, s. International investigation of shear displacement capacity of various elastomeric seismic-protection isolators for buildings. J. Rubber Res. 2019, 22, 33–41. [Google Scholar] [CrossRef]
- Cardone, D.; Perrone, G. Critical load of slender elastomeric seismic isolators: An experimental perspective. Eng. Struct. 2012, 40, 198–204. [Google Scholar] [CrossRef]
- Montuori, G.M.; Mele, E.; Marrazzo, G.; Brandonisio, G.; De Luca, A. Stability issues and pressure–shear interaction in elastomeric bearings: The primary role of the secondary shape factor. Bull. Earthq. Eng. 2015, 14, 569–597. [Google Scholar] [CrossRef]
- Yabana, S.; Matsuda, A. Mechanical properties of laminated rubber bearings for three-dimensional seismic isolation. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000. [Google Scholar]
- Vemuru, V.S.M.; Nagarajaiah, S.; Mosqueda, G. Coupled horizontal–vertical stability of bearings under dynamic loading. Earthq. Eng. Struct. Dyn. 2016, 45, 913–934. [Google Scholar] [CrossRef]
- Orfeo, A.; Tubaldi, E.; Muhr, A.H.; Losanno, D. Dynamic behaviour and seismic response of structures isolated with low shape factor bearings. Earthq. Eng. Struct. Dyn. 2023, 52, 3765–3787. [Google Scholar] [CrossRef]
- Sanchez, J.; Masroor, A.; Mosqueda, G.; Ryan, K. Static and Dynamic Stability of Elastomeric Bearings for Seismic Protection of Structures. J. Struct. Eng. 2013, 139, 1149–1159. [Google Scholar] [CrossRef]
- Rahnavarda, R.; Craveiroa, H.D.; Napolitano, R. Static and dynamic stability analysis of a steel-rubber isolator with rubber cores. Structures 2020, 26, 441–455. [Google Scholar] [CrossRef]
- Akazawa, M.; Kurata, M.; Yamazaki, S.; Kawamata, Y.; Matsuo, S. Test and sensitivity analysis of base-isolated steel frame with low-friction spherical sliding bearings. Earthq. Eng. Struct. Dyn. 2024, 54, 100–118. [Google Scholar] [CrossRef]
- Wu, Y.X.; Lu, J.F.; Qi, A. Shaking table test and numerical analysis of mid-story isolation eccentric structure with tower-podium. Adv. Mech. Eng. 2019, 11, 1687814018819562. [Google Scholar] [CrossRef]
- GB 50011-2010; Code for Seismic Design of Buildings. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2016.
- Xing, G.H.; Cao, G.R.; Chang, Z.Q.; Huang, Y.A.; Lu, Z.; Li, Y.Y.; Ma, X.F. Shaking Table Test and Dynamic Analysis on the Metro depot Over-Track Isolated Structure in High Seismic Intensity Regions; Chang’an University: Xi’an, China, 2025. [Google Scholar]
- Ismail, M.; Ikhouane, F.; Rodellar, J. The hysteresis Bouc-Wen model, a survey. Arch. Comput. Methods Eng. 2009, 16, 161–188. [Google Scholar] [CrossRef]
- Chen, P.; Wang, B.; Zhang, A.H.; Li, T.; Dai, K.S. A generalized model of lead rubber bearing considering large strain stiffening and degradation. Eng. Struct. 2023, 275, 115264. [Google Scholar] [CrossRef]
- Mansouri, I.; Ghodrati Amiri, G.; Hu, J.W.; Khoshkalam, M.; Soori, S.; Shahbazi, S. Seismic Fragility Estimates of LRB Base Isolated Frames Using Performance-Based Design. Shock Vib. 2017, 3, 5184790. [Google Scholar] [CrossRef]
- Zheng, W.Z.; Chen, J.L.; Wang, H.; Tan, P.; Li, J.; Wang, S.Q. A novel damping adaptive pendulum isolation system for seismic resilience enhancement of continuous bridges. Eng. Struct. 2025, 339, 120465. [Google Scholar] [CrossRef]
- PEER Ground Motion Database Pacific Earthquake Engineering Research Center. University of California, Berkeley. Available online: https://ngawest2.berkeley.edu/ (accessed on 3 March 2018).[Green Version]
- Skandalos, K.; Chakraborty, S.; Tesfamariam, S. Seismic reliability analysis using a multi-fidelity surrogate model: Example of base-isolated buildings. Struct. Saf. 2022, 97, 102222. [Google Scholar] [CrossRef]
- Anajafi, H.; Medina, R.A.; Santini-Bell, E. Effects of the improper modeling of viscous damping on the first-mode and higher-mode dominated responses of base-isolated buildings. Earthq. Eng. Struct. Dyn. 2020, 49, 51–73. [Google Scholar] [CrossRef]
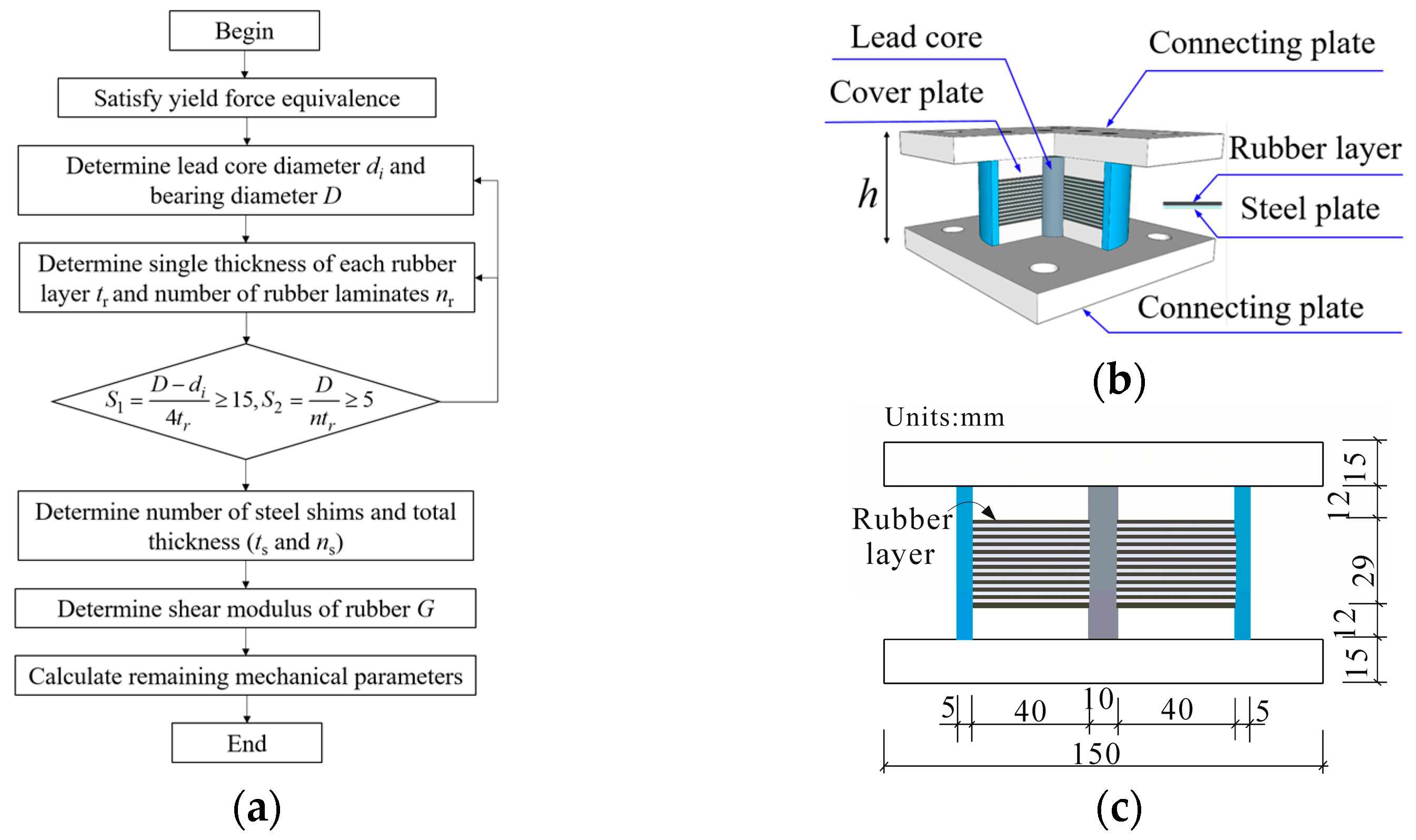
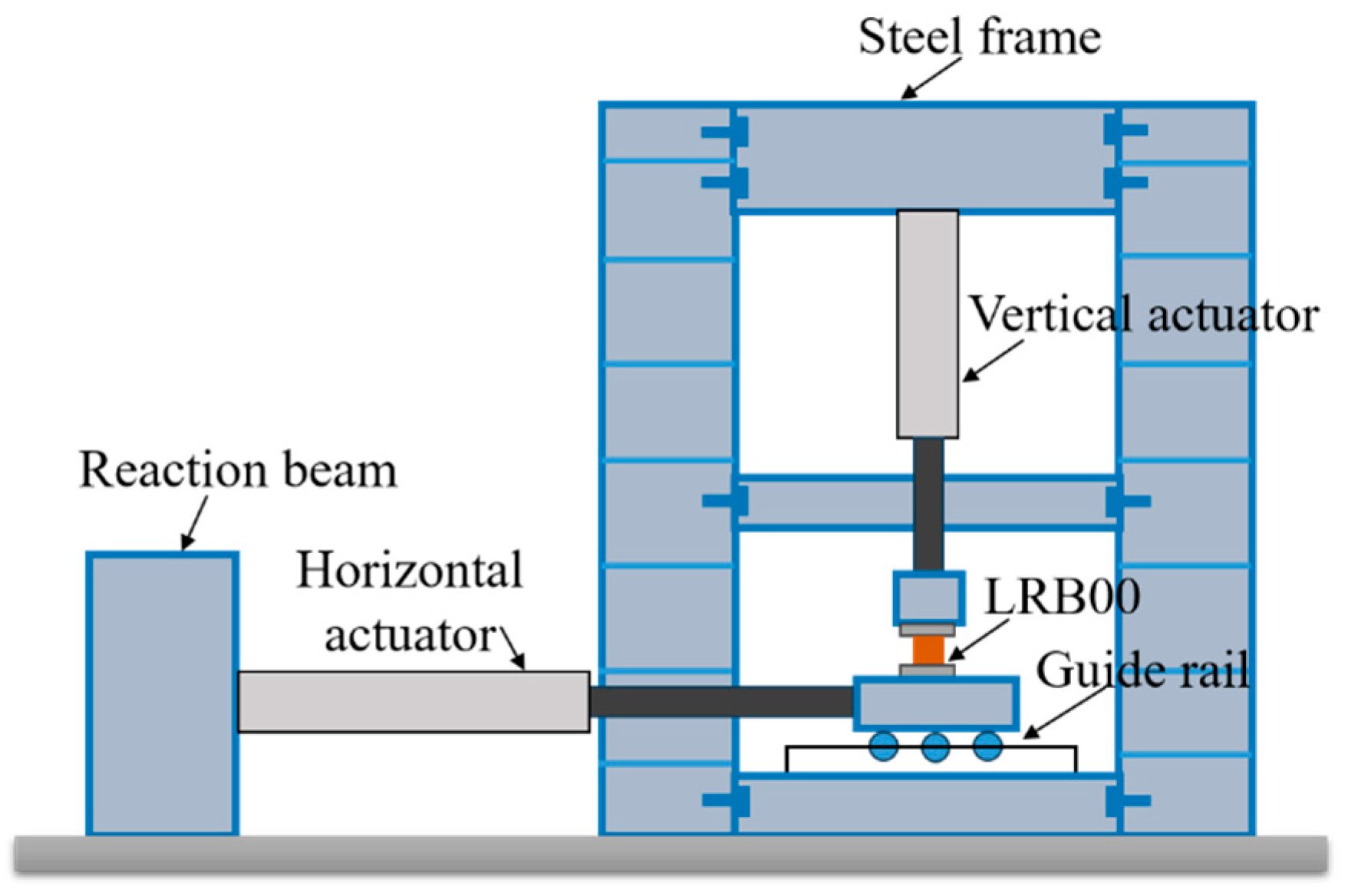
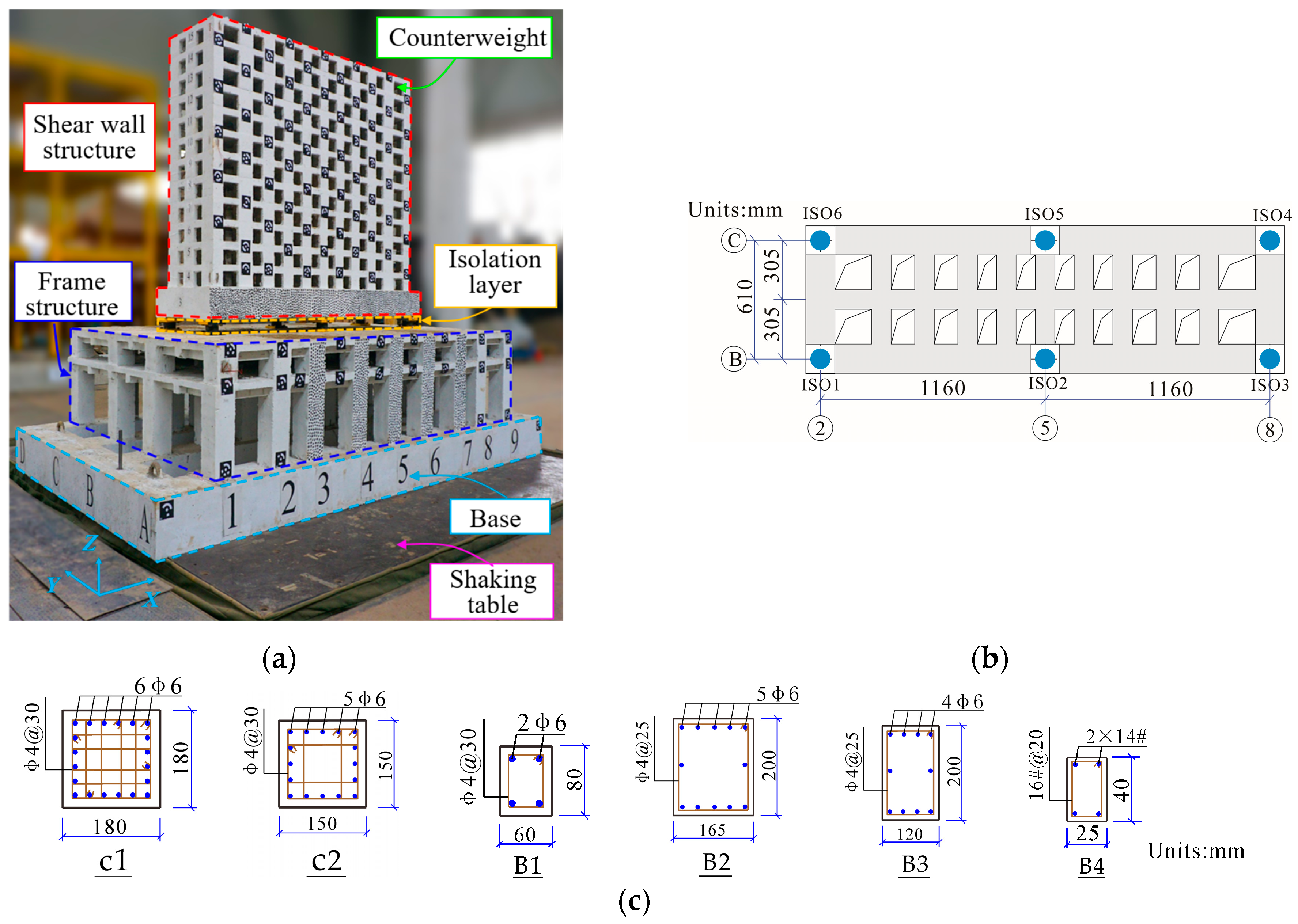
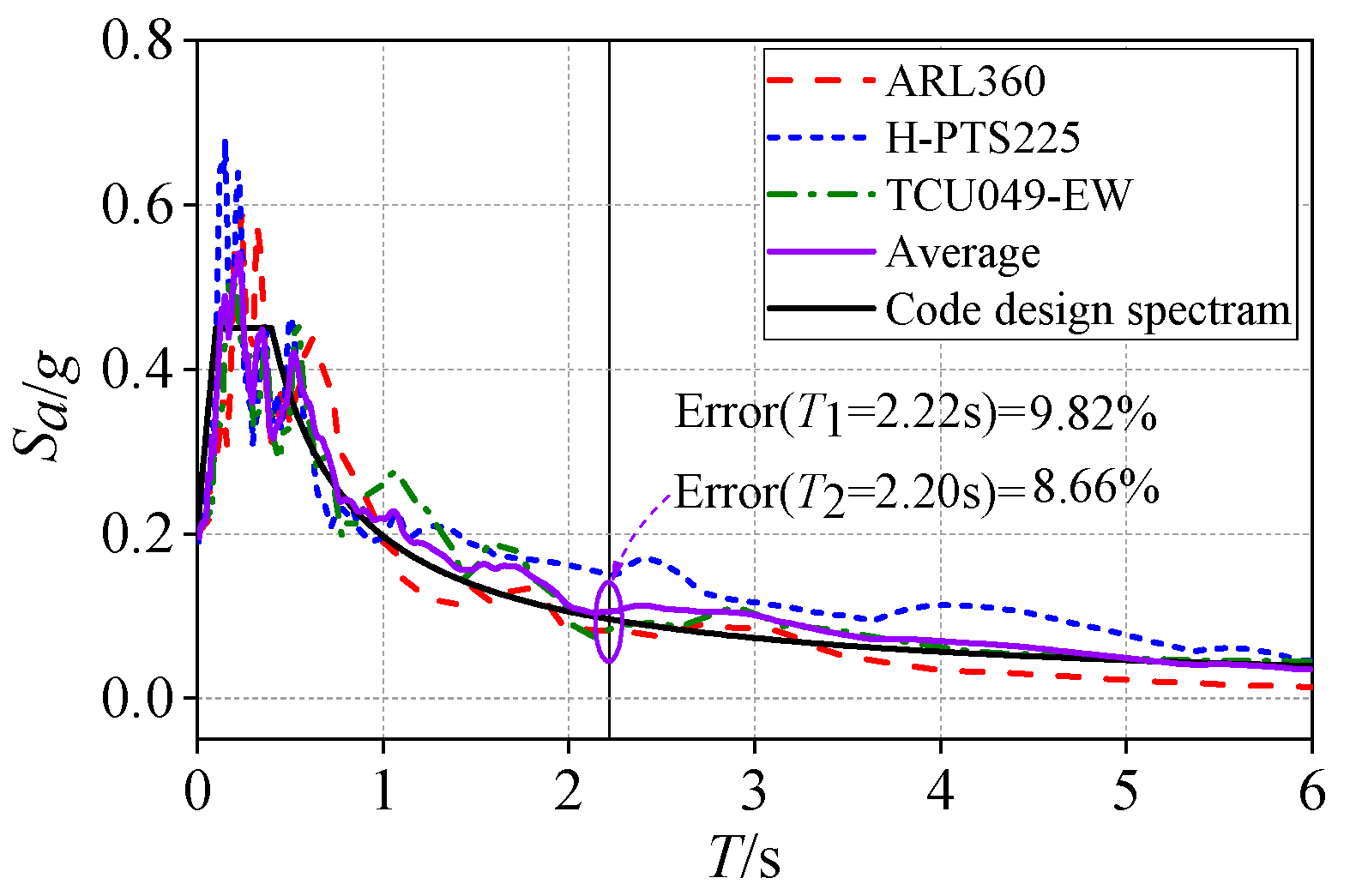


| Geometrical Parameters | LRB100 | Mechanical Properties | Value |
|---|---|---|---|
| Outer diameter D (mm) | 100 | Shear modulus of rubber, G (MPa) | 0.392 |
| Height (mm) | 53 | Yield strength of lead, τp (MPa) | 8.5 |
| Effective diameter, d0 (mm) | 90 | First shape factor, S1 | 15 |
| Core diameter, di (mm) | 10 | Second shape factor, S2 | 5 |
| Thickness of single rubber layer, tr (mm) | 1.5 | Vertical stiffness, Kv (kN/mm) | 163 |
| Number of rubber layers, nr | 12 | Yield force, Fy (kN) | 0.57 |
| Total rubber thickness, Tr (mm) | 18 | Post-yield stiffness (100%), Kd (kN/mm) | 0.137 |
| Lead core area, Ap (mm2) | 78.5 | Equivalent horizontal stiffness (100%), Kh (kN/mm) | 0.175 |
| Thickness of thin steel plate, ts (mm) | 1 | Equivalent damping ratio (100%), heq (%) | 13.5 |
| Number of steel plates, ns | 11 | - | - |
| End plate thickness (mm) | 12 | - | - |
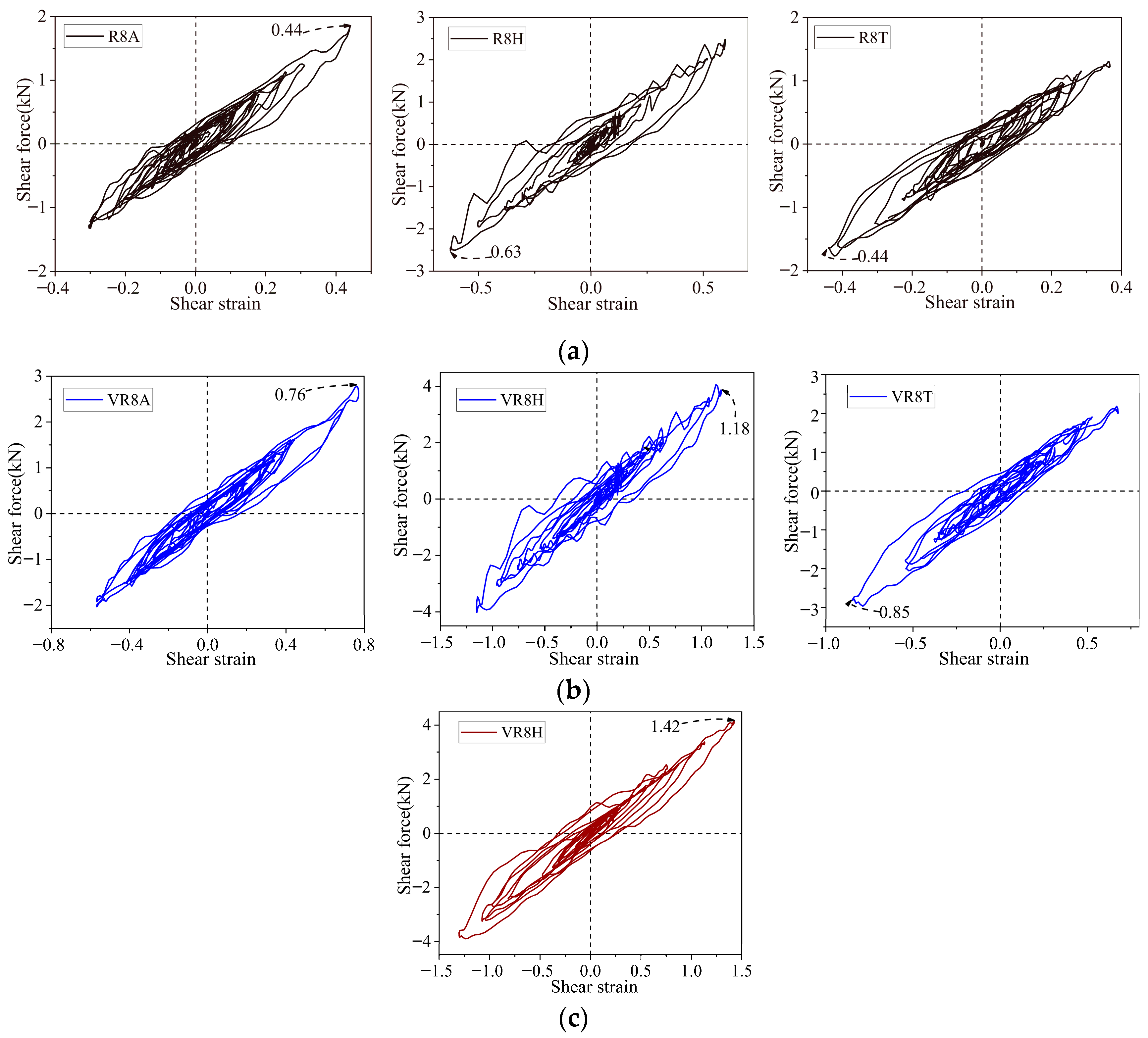
| Case | Vertical Load P (kN) | Displacement Amplitude u1 (mm) | Shear Strain γ (%) | Loading Frequency f (Hz) | Number of Cycles |
|---|---|---|---|---|---|
| 1 | 16 | ±9 | ±50% | 0.05 | 5 |
| 2 | 16 | ±18 | ±100% | 0.05 | 5 |
| 3 | 16 | ±27 | ±150% | 0.05 | 5 |
| 4 | 16 | ±36 | ±200% | 0.05 | 5 |
| 5 | 16 | ±18 | ±100% | 0.2 | 5 |
| 6 | 16 | ±27 | ±150% | 0.2 | 5 |
| 7 | 16 | ±36 | ±200% | 0.2 | 5 |
| 8 | 16 | ±18 | ±100% | 0.5 | 5 |
| 9 | 16 | ±27 | ±150% | 0.5 | 5 |
| 10 | 16 | ±36 | ±200% | 0.5 | 5 |
| Physical Quantity | Value | Physical Quantity | Value |
|---|---|---|---|
| Length | 1/20 | Period | 0.224 |
| Elastic modulus | 1/4 | Frequency | 4.47 |
| Stress | 0.25 | Time | 0.224 |
| Mass | 6.25 × 10−4 | Gravity | 1 |
| Stiffness | 0.0125 | Velocity | 0.224 |
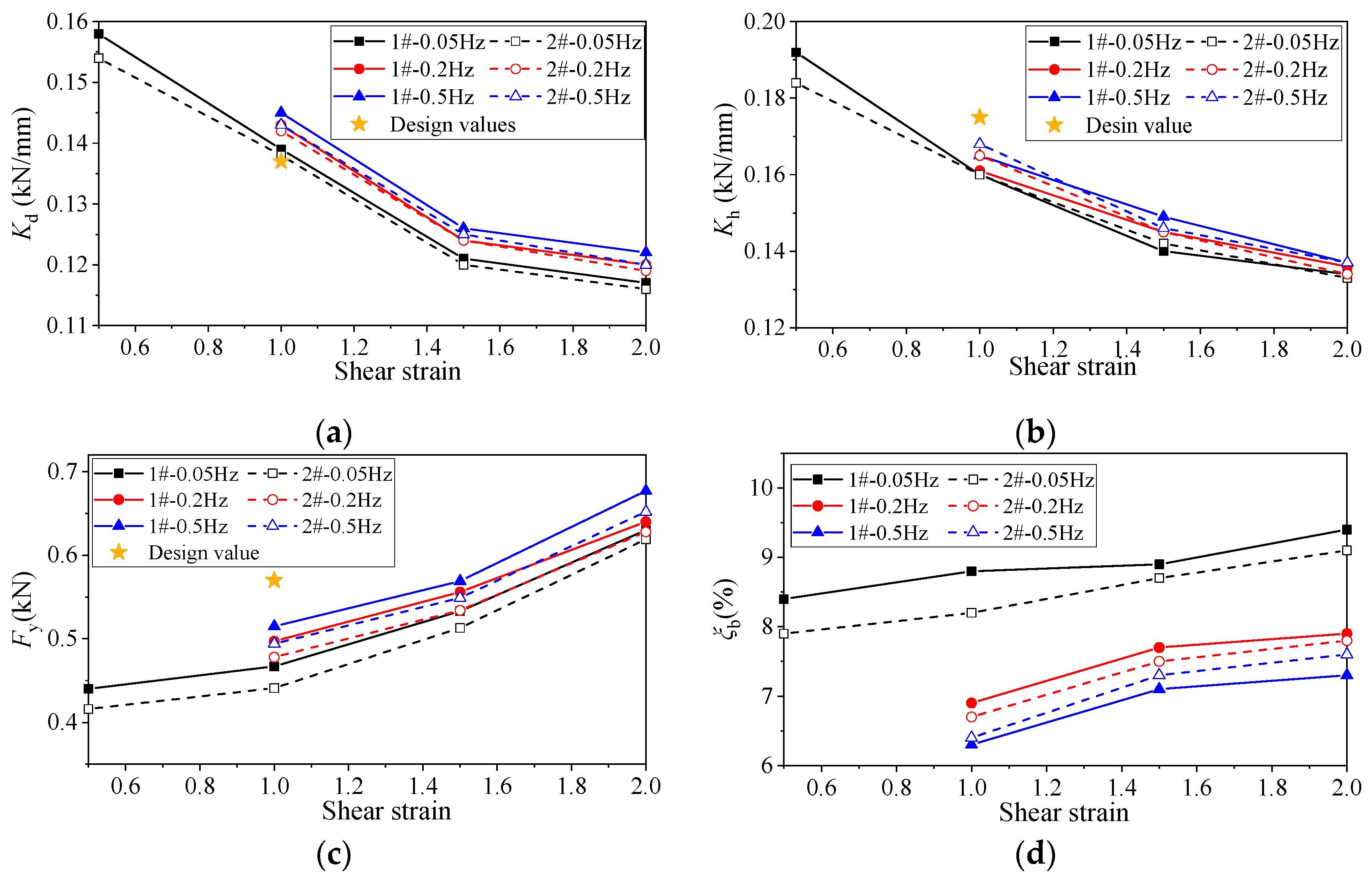
| Case | γ | f1 | Kd (kN/mm) | Fy (kN) | Kh (kN/mm) | heq (%) |
|---|---|---|---|---|---|---|
| 1 | 50% | 0.05 Hz | 0.158 | 0.440 | 0.192 | 8.4 |
| 2 | 100% | 0.05 Hz | 0.139 | 0.467 | 0.160 | 8.8 |
| 3 | 150% | 0.05 Hz | 0.121 | 0.533 | 0.140 | 8.9 |
| 4 | 200% | 0.05 Hz | 0.117 | 0.630 | 0.134 | 9.4 |
| 5 | 100% | 0.2 Hz | 0.143 | 0.497 | 0.161 | 6.9 |
| 6 | 150% | 0.2 Hz | 0.124 | 0.556 | 0.145 | 7.7 |
| 7 | 200% | 0.2 Hz | 0.120 | 0.640 | 0.136 | 7.9 |
| 8 | 100% | 0.5 Hz | 0.145 | 0.515 | 0.165 | 6.3 |
| 9 | 150% | 0.5 Hz | 0.126 | 0.569 | 0.149 | 7.1 |
| 10 | 200% | 0.5 Hz | 0.122 | 0.677 | 0.137 | 7.3 |
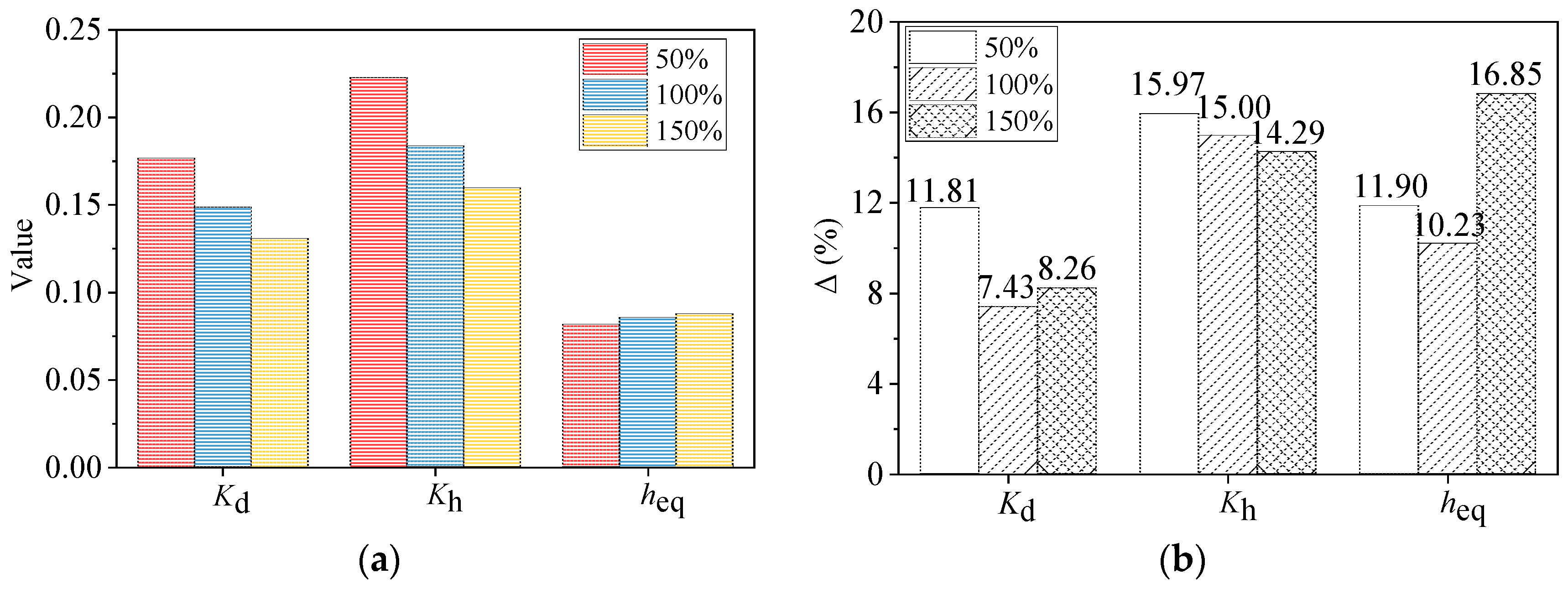
| γ | Property | ARL | H-PTS | TCU0489 | Mean Value | Compression–Shear Test Value | Increase Ratio (%) |
|---|---|---|---|---|---|---|---|
| 50% | Kd (kN/mm) | 0.182 | 0.175 | 0.173 | 0.177 | 0.158 | 11.81 |
| 50% | Kh (kN/mm) | 0.228 | 0.224 | 0.216 | 0.223 | 0.192 | 15.97 |
| 50% | heq (%) | 9.1 | 9.7 | 9.4 | 9.400 | 8.4 | 11.90 |
| 100% | Kd (kN/mm) | 0.155 | 0.148 | 0.145 | 0.149 | 0.139 | 7.43 |
| 100% | Kh (kN/mm) | 0.186 | 0.182 | 0.184 | 0.184 | 0.160 | 15.00 |
| 100% | heq (%) | 9.4 | 10.1 | 9.6 | 9.700 | 8.8 | 10.23 |
| 150% | Kd (kN/mm) | - | 0.131 | - | 0.131 | 0.121 | 8.26 |
| 150% | Kh (kN/mm) | - | 0.160 | - | 0.160 | 0.140 | 14.29 |
| 150% | heq (%) | - | 10.4 | - | 10.400 | 8.9 | 16.85 |
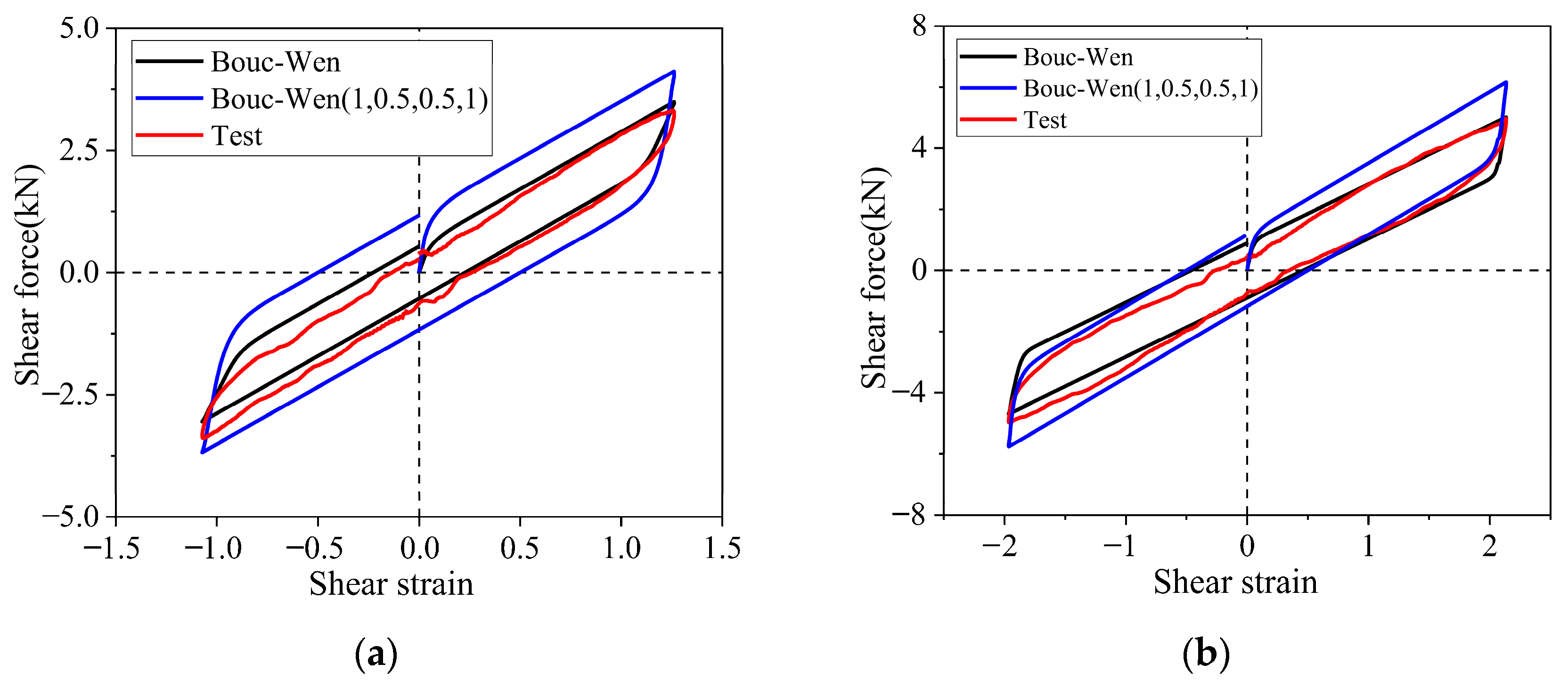
| Parameter | Initial Parameters | Modify Parameters | ||
|---|---|---|---|---|
| γ = 100% | Error 1 (%) | γ = 100% | Error 2 (%) | |
| Kd (kN/mm) | 0.131 | −5.76 | 0.151 | 1.12 |
| Fy (kN) | 0.510 | 9.21 | - | - |
| Kh (kN/mm) | 0.155 | −3.13 | 0.180 | 2.17 |
| heq (%) | 9.3 | 5.68 | 9.3 | 4.12 |
| No. | Name | Year | Recorder Station | Component | PGA (g) | PGV (cm/s) | Duration (s) |
|---|---|---|---|---|---|---|---|
| 1 | Friuli | 1976 | Tolmezzo | A-TMZ000 | 0.35 | 31 | 36.34 |
| 2 | Friuli | 1976 | Tolmezzo | A-TMZ 270 | 0.31 | 31 | 36.34 |
| 3 | Loma prieta | 1989 | Capitola | CAP 090 | 0.53 | 35 | 39.95 |
| 4 | Cape Mendocino | 1992 | Rio Dell Overpass | RIO 360 | 0.55 | 44 | 35.98 |
| 5 | Kobe, Japan | 1995 | Nishi-Akashi | NIS000 | 0.51 | 37 | 40.95 |
| 6 | Kobe, Japan | 1995 | Nishi-Akashi | NIS900 | 0.50 | 38 | 40.95 |
| 7 | Kobe, Japan | 1995 | Shin-Osaka | SHI 090 | 0.24 | 38 | 40.95 |
| 8 | Kocaeli, Turkey | 1999 | Arcelik | ARC 000 | 0.22 | 40 | 30.00 |
| 9 | Hector Mine | 1999 | Hector | HEC 000 | 0.34 | 42 | 45.3 |
| 10 | Northridge-01 | 1944 | Arleta -Nordhoff Fire Sta | NGA_no_949 _ARL360 | 0.31 | 23 | 39.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, G.; Chang, Z.; Deng, G.; Ma, W.; Liu, B. Mechanical Performance and Parameter Sensitivity Analysis of Small-Diameter Lead-Rubber Bearings. Buildings 2025, 15, 3284. https://doi.org/10.3390/buildings15183284
Cao G, Chang Z, Deng G, Ma W, Liu B. Mechanical Performance and Parameter Sensitivity Analysis of Small-Diameter Lead-Rubber Bearings. Buildings. 2025; 15(18):3284. https://doi.org/10.3390/buildings15183284
Chicago/Turabian StyleCao, Guorong, Zhaoqun Chang, Guizhi Deng, Wenbo Ma, and Boquan Liu. 2025. "Mechanical Performance and Parameter Sensitivity Analysis of Small-Diameter Lead-Rubber Bearings" Buildings 15, no. 18: 3284. https://doi.org/10.3390/buildings15183284
APA StyleCao, G., Chang, Z., Deng, G., Ma, W., & Liu, B. (2025). Mechanical Performance and Parameter Sensitivity Analysis of Small-Diameter Lead-Rubber Bearings. Buildings, 15(18), 3284. https://doi.org/10.3390/buildings15183284




