New Insight into the Phenomenon of Buckling in Compressed Beams with Firm Support
Abstract
1. Introduction
2. Compressed Beams with Firm Support and Sinusoidal Directrix
2.1. Expressions of First-Order and Second-Order Effects
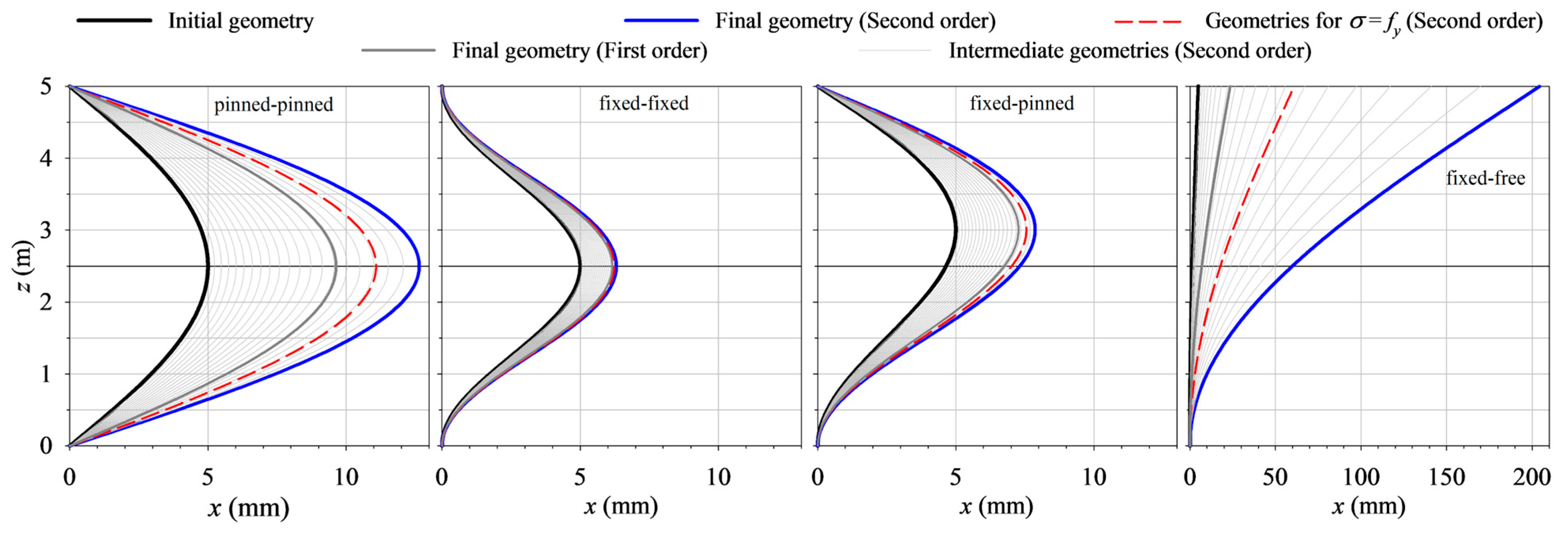
2.2. Numerical Example of a Compression Beam
2.3. Maximum Normal Stress of First- and Second-Order Effects
2.4. Analysis of the Type Beam with Different Sag-to-Span Ratios
3. Compressed Beams with Firm Support and Initial Deformation Generated by Transverse Loads
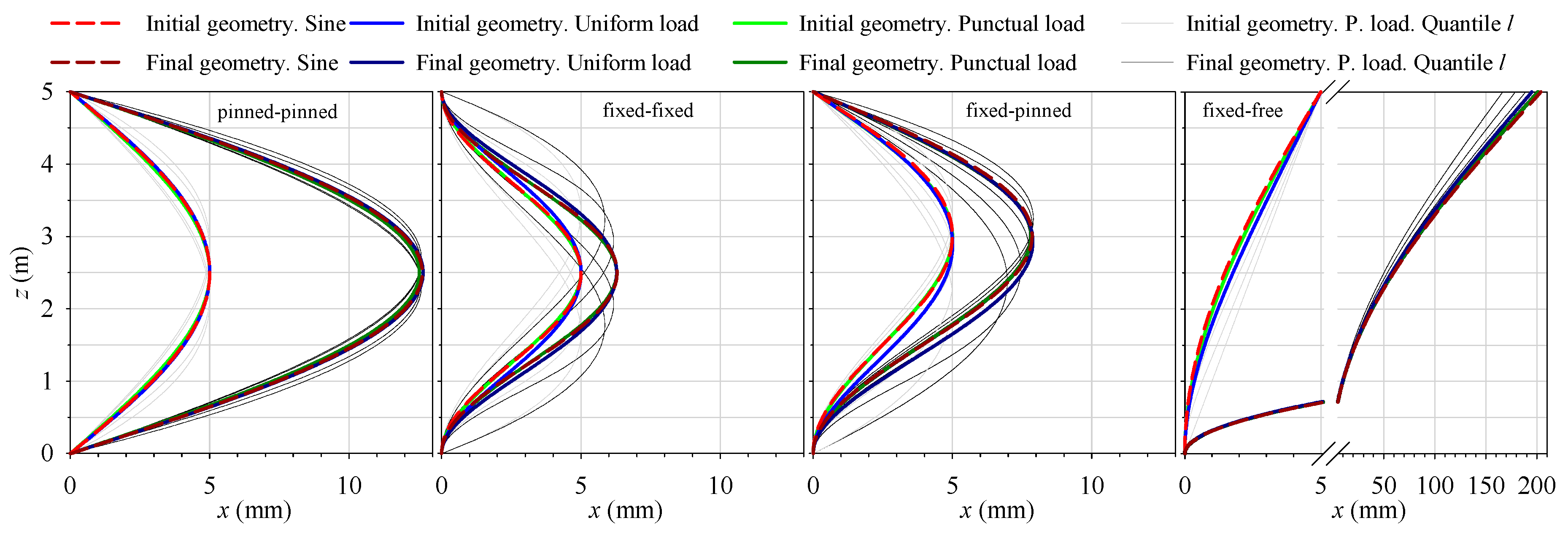
3.1. Beams with Initial Deformation Produced by a Punctual Transverse Load
3.2. Beam with Initial Deformation Produced by a Uniform and Constant Transverse Load
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lahuerta Vargas, J. Estructuras de Edificación; Escuela Técnica Superior de Arquitectura de la Universidad de Navarra: Pamplona, Spain, 1985. [Google Scholar]
- Ortiz Berrocal, L. Resistencia de Materiales; McGraw-Hill: Madrid, Spain, 2007. [Google Scholar]
- Ikeda, K.; Murota, K. Imperfect Bifurcation in Structures and Materials; Springer: New York, NY, USA, 2002. [Google Scholar]
- Areiza-Hurtado, M.; Aristizábal-Ochoa, J.D. Second-order analysis of a beam-column on elastic foundation partially restrained axially with initial deflections and semirigid connections. Structures 2019, 20, 134–146. [Google Scholar] [CrossRef]
- Ikeda, K.; Murota, K. Bifurcation and Buckling in Structures; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity; Dover Publications Inc.: Garden City, NY, USA, 1944. [Google Scholar]
- Horton, W.H.; Bailey, S.C.; McQuilkin, B.H. An introduction to instability. In Proceedings of the ASTM Annual Meeting, Atlantic City, NJ, USA, June 1966. Stanford University Paper No. 219. [Google Scholar]
- Euler, L. Sur la force des colonnes. Mémoires L’acad. Sci. Berl. 1759, 13, 252–282. [Google Scholar]
- Aroca Hernández-Ros, R. Flexión Compuesta y Pandeo en Barras Rectas. In Cuadernos de Apoyo a la Docencia del Instituto Juan de Herrera; Instituto Juan de Herrera, ETS de Arquitectura: Madrid, Spain, 2001. [Google Scholar]
- Todhunter, I. A History of the Theory of Elasticity and of the Strength of Materials from Galilei to the Present Time; The Syndics of the University Press: Cambridge, UK, 1893. [Google Scholar]
- Timoshenko, S.P. History of Strength of Materials; McGraw-Hill: Tokyo, Japan, 1953. [Google Scholar]
- Komarakul-na-Nakorn, A.; Arora, J.S. Stability criteria: A review. Comput. Struct. 1990, 37, 35–49. [Google Scholar] [CrossRef]
- Johnston, B.G. Column buckling theory: Historic highlights. J. Struct. Eng. 1993, 109, 2086–2096. [Google Scholar] [CrossRef]
- Elishakoff, I. Uncertain buckling: Its past, present and future. Int. J. Solids Struct. 2000, 37, 6869–6889. [Google Scholar] [CrossRef]
- Elishakoff, I. Essay on the Contributors to the Elastic Stability Theory. Meccanica 2005, 40, 75–110. [Google Scholar] [CrossRef]
- Ortega, M.A.; Romero, J.L.; de la Rosa, E. Un estudio histórico del problema de las piezas prismáticas rectas sometidas a compresión. parte I. Inf. Constr. 2007, 59, 69–81. [Google Scholar]
- Ortega, M.A.; Romero, J.L.; de la Rosa, E. Un estudio histórico del problema de las piezas prismáticas rectas sometidas a compresión. parte II. Inf. Constr. 2007, 59, 61–71. [Google Scholar]
- Melissianos, V.E.; Gantes, C.J. Buckling and post-buckling behavior of beams with internal flexible joints resting on elastic foundation modeling buried pipelines. Structures 2016, 7, 138–152. [Google Scholar] [CrossRef]
- Shen, C.H.; Yu, H.S.; Wang, X.J.; Tang, K.; Asiedu-Kwakyewaa, C.; Zhang, H.Y. Determining the critical buckling load of locally stiffened U-shaped steel sheet pile using dynamic correlation coefficient method. Sci. Rep. 2022, 12, 12970. [Google Scholar] [CrossRef]
- Rodrigues, M.A.C.; Burgos, R.B.; Martha, L.F.C.R. A unified approach to the Timoshenko 3D beam-column element tangent stiffness matrix considering higher-order terms in the strain tensor and large rotations. Int. J. Solids Struct. 2021, 222, 111003. [Google Scholar] [CrossRef]
- Sun, Y.; Song, D.A.; Sun, S.; Guo, Y. Behavior of large-size and high-strength steel angle subjected to eccentric load. Structures 2023, 57, 105161. [Google Scholar] [CrossRef]
- Barszcz, A.M.; Giżejowski, M.A.; Papangelis, J.P. Investigations into the Flexural-Torsional Buckling Behavior of Steel Open-Section Beam-Columns. Buildings 2023, 13, 307. [Google Scholar] [CrossRef]
- Emam, S.; Lacarbonara, W. A review on buckling and postbuckling of thin elastic beams. Eur. J. Mech. A/Solids 2022, 92, 104449. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Gere, J.M. Theory of Elastic Stability; McGraw-Hill: Tokyo, Japan, 1961. [Google Scholar]
- Zeeman, E.C. Euler Buckling. In Structural Stability, the Theory of Catastrophes, and Applications in the Sciences; Springer: Berlin, Germany, 1976. [Google Scholar]
- Trahair, N.S.; Bradford, M.A.; Nethercot, D.; Gardner, L. The Behaviour and Design of Steel Structures to EC3; Springer: Berlin, Germany, 2008. [Google Scholar]
- Luo, L.; Zhang, Y. A new method for establishing the total potential energy equations of steel members based on the principle of virtual work. Structures 2023, 52, 904–920. [Google Scholar] [CrossRef]
- Falope, F.O.; Lanzoni, L.; Tarantino, A.M. Lateral buckling of the compressed edge of a beam under finite bending. Eur. J. Mech. A/Solids 2024, 107, 105373. [Google Scholar] [CrossRef]
- Hussein, A.B. Structural behaviour of built-up I-shaped CFS columns. Sci. Rep. 2024, 14, 25628. [Google Scholar] [CrossRef]
- Botis, M.; Imre, L.; Conțiu, M. Numerical method of increasing the critical buckling load for straight beam-type elements with variable cross-sections. Appl. Sci. 2023, 13, 1460. [Google Scholar] [CrossRef]
- Trahair, N.S. Flexural–Torsional Buckling of Structures; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Yang, Y.B.; Kuo, S.R. Theory and Analysis of Nonlinear Framed Structures; Prentice Hall: Singapore, 1994. [Google Scholar]
- Eslami, M.R. Buckling and Postbuckling of Beams, Plates, and Shells; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar]
- Gimena, F.N.; Goñi, M.; Gonzaga, P.; Valdenebro, J.V. Alternative approach to the buckling phenomenon by means of a second-order incremental analysis. Sci. Rep. 2023, 13, 16146. [Google Scholar] [CrossRef]
- Gimena, F.N.; Gonzaga, P.; Gimena, L. Numerical transfer-method with boundary conditions for arbitrary curved beam elements. Eng. Anal. Bound. Elem. 2009, 33, 249–257. [Google Scholar] [CrossRef]
- Sarria, F.; Gimena, F.N.; Gonzaga, P.; Goñi, M.; Gimena, L. Formulation and Solution of Curved Beams with Elastic Supports. Teh. Vjesn. 2018, 25 (Suppl. S1), 56–65. [Google Scholar] [CrossRef]
- Gimena, F.N.; Gonzaga, P.; Valdenebro, J.V.; Goñi, M.; Reyes-Rubiano, L.S. Curved beam through matrices associated with support conditions. Struct. Eng. Mech. 2020, 76, 395–412. [Google Scholar] [CrossRef]
- Gimena, L.; Gonzaga, P.; Gimena, F.N. Boundary equations in the finite transfer method for solving differential equation systems. Appl. Math. Model. 2014, 38, 2648–2660. [Google Scholar] [CrossRef]
- European Committee for Standardization. Eurocode 3: Design of Steel Structures-Part 1-1: General Rules and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2005. [Google Scholar]
- Real Decreto 470/2021, de 29 de Junio, por el que se Aprueba el Código Estructural. Available online: https://www.boe.es/eli/es/rd/2021/06/29/470 (accessed on 10 September 2025).
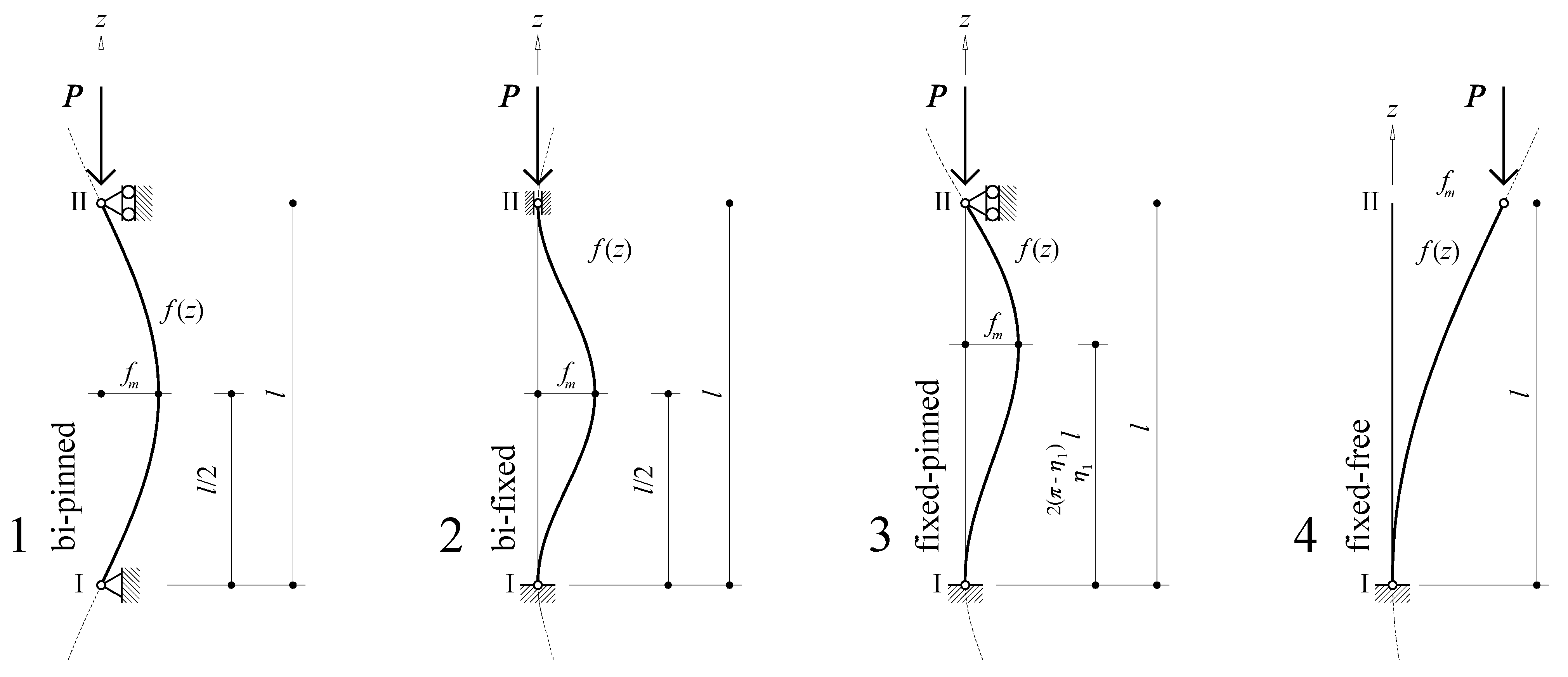


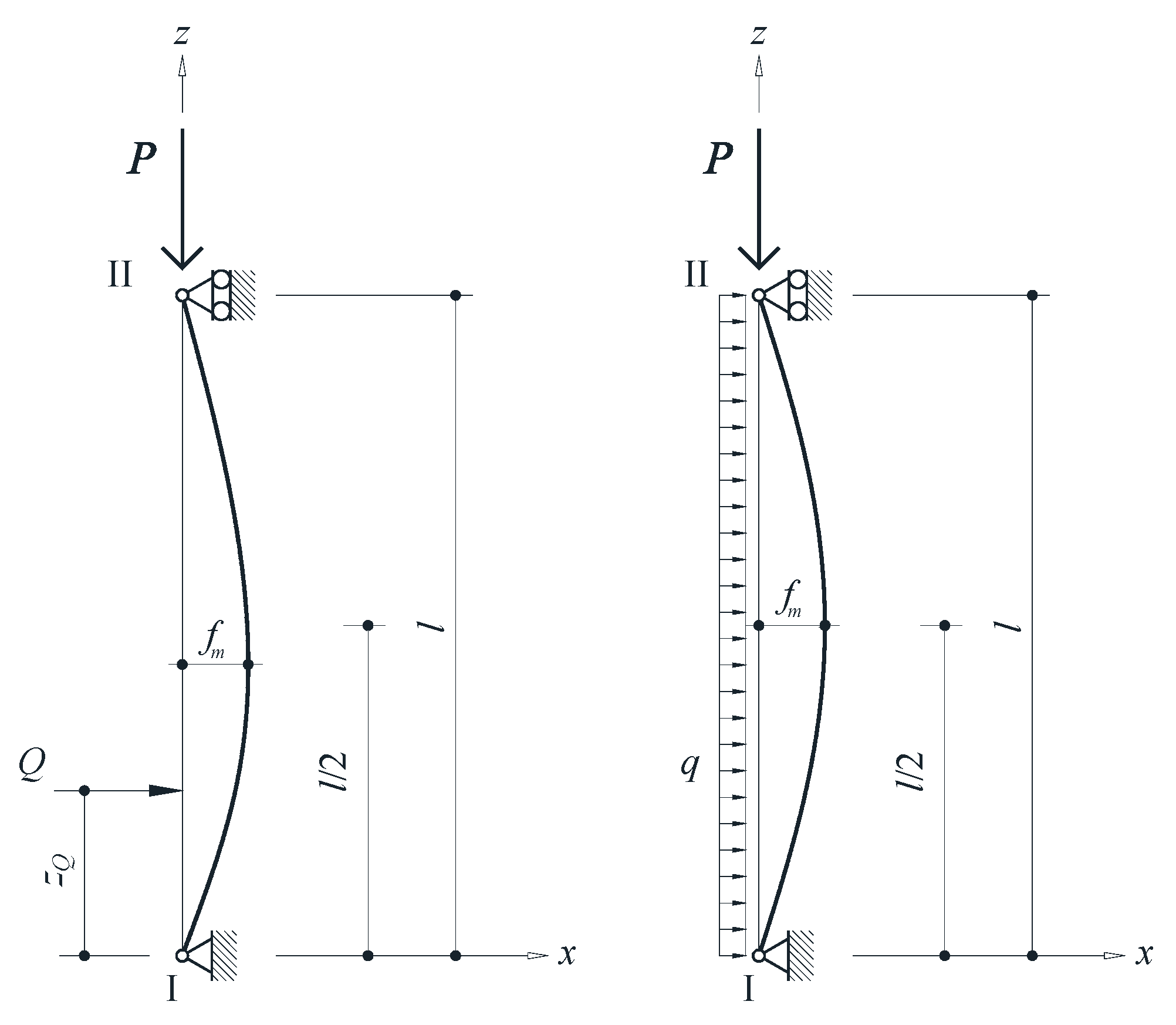

| η | η | η | η | η | |
|---|---|---|---|---|---|
| bi-pinned | −1 | π | π | 0 | 0 |
| bi-fixed | −0.5 | 2π | π/2 | 0 | −1 |
| fixed-pinned | −0.73264413 | 4.49340947 | 1.78977584 | 0.97611964 | −0.97611964 |
| η1/(2πsin(η1)) | η1 + tan(2π − η1) = 0 | 2π − η1 | sin(2π − η1) | sin(η1) | |
| fixed-free | −1 | π/2 | π/2 | 0 | −1 |
| Beam | l (m) | fm (mm) | Steel | E (kN/mm2) | G (kN/mm2) |
| 5 | 5 | S355 | 210 | 81 | |
| Circular hollow sections | de (mm) | di (mm) | A (cm2) | W (cm3) | I = Ib = Iy (cm4) |
| ϕ200.8 | 200 | 184 | 48.25 | 222.74 | 2227.44 |
| My (kN·m) | Bi-Pinned | Bi-Fixed | Fixed-Pinned | Fixed-Free | ||||
|---|---|---|---|---|---|---|---|---|
| z (m) | First Order | Second Order | First Order | Second Order | First Order | Second Order | First Order | Second Order |
| 0 | 0.00 | 0.00 | 4.28 | 4.82 | 6.13 | 7.75 | 8.57 | 92.05 |
| 0.625 | −3.28 | −5.40 | 3.03 | 3.41 | 4.46 | 5.64 | 8.40 | 90.28 |
| 1.25 | −6.06 | −9.98 | 0.00 | 0.00 | 1.42 | 1.80 | 7.91 | 85.04 |
| 1.875 | −7.91 | −13.04 | −3.03 | −3.41 | −2.05 | −2.60 | 7.12 | 76.54 |
| 2.5 | −8.57 | −14.11 | −4.28 | −4.82 | −4.90 | −6.19 | 6.06 | 65.09 |
| 3.125 | −7.91 | −13.04 | −3.03 | −3.41 | −6.23 | −7.89 | 4.76 | 51.14 |
| 3.25 | −7.63 | −12.57 | −2.52 | −2.83 | −6.28 | −7.94 | 4.48 | 48.10 |
| 3.75 | −6.06 | −9.98 | 0.00 | 0.00 | −5.66 | −7.16 | 3.28 | 35.23 |
| 4.375 | −3.28 | −5.40 | 3.03 | 3.41 | −3.34 | −4.23 | 1.67 | 17.96 |
| 5 | 0.00 | 0.00 | 4.28 | 4.82 | 0.00 | 0.00 | 0.00 | 0.00 |
| My (kN·m) | Bi-Pinned | Bi-Fixed | Fixed-Pinned | Fixed-Free | ||||
|---|---|---|---|---|---|---|---|---|
| z (m) | First Order | Second Order | First Order | Second Order | First Order | Second Order | First Order | Second Order |
| 0 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 0.625 | 1.77 | 2.92 | 0.17 | 0.19 | 0.24 | 0.30 | 0.36 | 3.83 |
| 1.25 | 3.27 | 5.39 | 0.58 | 0.65 | 0.84 | 1.06 | 1.41 | 15.16 |
| 1.875 | 4.28 | 7.05 | 0.98 | 1.11 | 1.55 | 1.96 | 3.13 | 33.55 |
| 2.5 | 4.63 | 7.63 | 1.15 | 1.30 | 2.10 | 2.66 | 5.43 | 58.31 |
| 3.01 | 4.39 | 7.24 | 1.04 | 1.17 | 2.26 | 2.86 | 7.69 | 82.56 |
| 3.125 | 4.28 | 7.05 | 0.98 | 1.11 | 2.25 | 2.85 | 8.24 | 88.47 |
| 3.75 | 3.27 | 5.39 | 0.58 | 0.65 | 1.90 | 2.40 | 11.45 | 122.87 |
| 4.375 | 1.77 | 2.92 | 0.17 | 0.19 | 1.08 | 1.37 | 14.93 | 160.20 |
| 5 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 18.55 | 199.02 |
| Second-Order | Bi-Pinned | Bi-Fixed | Fixed-Pinned | Fixed-Free | |||||
|---|---|---|---|---|---|---|---|---|---|
| My (kN.m) | δx (mm) | My (kN.m) | δx (mm) | My (kN.m) | δx (mm) | My (kN.m) | δx (mm) | ||
| l/100 | analytical | −141.14 | 76.43 | −48.20 | 13.05 | −79.40 | 28.69 | −920.51 | 1993.91 |
| numeric | −141.11 | 76.22 | −48.20 | 12.96 | −79.40 | 28.58 | 898.78 | 1857.41 | |
| l/250 | analytical | −56.45 | 30.57 | −19.28 | 5.22 | −31.76 | 11.48 | −368.21 | 797.56 |
| numeric | −56.53 | 30.62 | −19.28 | 5.18 | −31.76 | 11.43 | 366.55 | 787.50 | |
| l/500 | analytical | −28.23 | 15.29 | −9.64 | 2.61 | −15.88 | 5.74 | −184.10 | 398.78 |
| numeric | −28.23 | 15.26 | −9.64 | 2.59 | −15.88 | 5.72 | 183.80 | 397.17 | |
| l/750 | analytical | −18.82 | 10.19 | −6.43 | 1.74 | −10.59 | 3.83 | −122.74 | 265.85 |
| numeric | −18.82 | 10.17 | −6.43 | 1.73 | −10.59 | 3.81 | 122.60 | 265.20 | |
| l/1000 | analytical | −14.11 | 7.64 | −4.82 | 1.31 | −7.94 | 2.87 | −92.05 | 199.39 |
| numeric | −14.11 | 7.63 | −4.82 | 1.30 | −7.94 | 2.86 | 91.96 | 199.02 | |
| Second Order | Bi-Pinned | Bi-Fixed | Fixed-Pinned | Fixed-Free | ||||
|---|---|---|---|---|---|---|---|---|
| P2 (kN) | P2/P0 (%) | P2 (kN) | P2/P0 (%) | P2 (kN) | P2/P0 (%) | P2 (kN) | P2/P0 (%) | |
| l/100 | 735.07 | 42.91% | 1081.97 | 63.16% | 903.27 | 52.73% | 553.74 | 32.32% |
| l/250 | 1078.42 | 62.95% | 1383.44 | 80.76% | 1244.95 | 72.67% | 794.63 | 46.39% |
| l/500 | 1302.98 | 76.06% | 1529.04 | 89.26% | 1435.80 | 83.82% | 979.12 | 57.16% |
| l/750 | 1408.05 | 82.20% | 1585.35 | 92.55% | 1515.72 | 88.48% | 1083.19 | 63.23% |
| l/1000 | 1469.73 | 85.80% | 1615.26 | 94.29% | 1559.80 | 91.05% | 1154.02 | 67.37% |
| zQ (m) | Bi-Pinned | Bi-Fixed | Fixed-Pinned | Fixed-Free | ||||
|---|---|---|---|---|---|---|---|---|
| z (fm) (m) | |MyMax| (kN.m) | z (fm) (m) | |MyMax| (kN.m) | z (fm) (m) | |MyMax| (kN.m) | z (fm) (m) | |MyMax| (kN.m) | |
| 0 | 2.113 | 14.07 | 1.667 | 8.20 | 2.113 | 10.24 | 5.000 | 76.39 |
| 0.25 | 2.117 | 14.07 | 1.724 | 7.83 | 2.163 | 10.01 | 5.000 | 77.50 |
| 0.5 | 2.128 | 14.07 | 1.786 | 7.45 | 2.215 | 9.78 | 5.000 | 78.58 |
| 0.75 | 2.146 | 14.07 | 1.852 | 7.09 | 2.269 | 9.55 | 5.000 | 79.61 |
| 1 | 2.172 | 14.06 | 1.923 | 6.73 | 2.327 | 9.32 | 5.000 | 80.61 |
| 1.25 | 2.205 | 14.06 | 2.000 | 6.38 | 2.389 | 9.09 | 5.000 | 81.57 |
| 1.5 | 2.246 | 14.05 | 2.083 | 6.04 | 2.454 | 8.87 | 5.000 | 82.49 |
| 1.75 | 2.296 | 14.05 | 2.174 | 5.71 | 2.524 | 8.65 | 5.000 | 83.37 |
| 2 | 2.354 | 14.04 | 2.273 | 5.40 | 2.598 | 8.44 | 5.000 | 84.20 |
| 2.25 | 2.422 | 14.04 | 2.381 | 5.10 | 2.678 | 8.25 | 5.000 | 85.00 |
| 2.5 | 2.500 | 14.04 | 2.500 | 4.81 | 2.764 | 8.07 | 5.000 | 85.75 |
| 2.75 | 2.578 | 14.04 | 2.619 | 5.10 | 2.857 | 7.91 | 5.000 | 86.45 |
| 3 | 2.646 | 14.04 | 2.727 | 5.40 | 2.958 | 7.80 | 5.000 | 87.11 |
| 3.25 | 2.704 | 14.05 | 2.826 | 5.71 | 3.008 | 7.98 | 5.000 | 87.73 |
| 3.5 | 2.754 | 14.05 | 2.917 | 6.04 | 3.050 | 8.13 | 5.000 | 88.30 |
| 3.75 | 2.795 | 14.06 | 3.000 | 6.38 | 3.127 | 8.25 | 5.000 | 88.82 |
| 4 | 2.828 | 14.06 | 3.077 | 6.73 | 3.191 | 8.34 | 5.000 | 89.30 |
| 4.25 | 2.854 | 14.07 | 3.148 | 7.09 | 3.243 | 8.41 | 5.000 | 89.74 |
| 4.5 | 2.872 | 14.07 | 3.214 | 7.45 | 3.283 | 8.46 | 5.000 | 90.13 |
| 4.75 | 2.883 | 14.07 | 3.276 | 7.83 | 3.311 | 8.49 | 5.000 | 90.48 |
| 5 | 2.887 | 14.07 | 3.333 | 8.20 | 3.328 | 8.50 | 5.000 | 90.79 |
| Initial Directrix Shape | |||||
|---|---|---|---|---|---|
| Second Order | Firm Support | Punctual Transverse Load zQ(sin) | Uniform Transverse Load | Sinusoidal (Numerical) | Sinusoidal (Analytical) |
| bi-pinned | 7.656 | 7.525 | 7.628 | 7.643 | |
| δx | bi-fixed | 1.278 | 1.278 | 1.296 | 1.305 |
| (mm) | fixed-pinned | 2.883 | 2.820 | 2.858 | 2.869 |
| fixed-free | 190.174 | 196.172 | 199.015 | 199.391 | |
| bi-pinned | −14.13 | −14.04 | −14.11 | −14.11 | |
| MyMin | bi-fixed | −4.52 | −4.81 | −4.82 | −4.82 |
| (kN·m) | fixed-pinned | −7.02 | −7.90 | −7.94 | −7.94 |
| fixed-free | 0.00 | 0.00 | 0.00 | 0.00 | |
| bi-pinned | 0.00 | 0.00 | 0.00 | 0.00 | |
| MyMax | bi-fixed | 5.11 | 4.81 | 4.82 | 4.82 |
| (kN·m) | fixed-pinned | 8.49 | 7.71 | 7.75 | 7.75 |
| fixed-free | 88.30 | 90.79 | 91.96 | 92.05 | |
| bi-pinned | 418.45 | 418.02 | 418.36 | 418.36 | |
| σMax | bi-fixed | 377.92 | 376.61 | 376.64 | 376.64 |
| (N/mm2) | fixed-pinned | 393.135 | 390.459 | 390.645 | 390.646 |
| fixed-free | 751.401 | 762.573 | 767.87 | 768.26 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goñi, M.; Gimena, F.N.; Valdenebro, J.-V. New Insight into the Phenomenon of Buckling in Compressed Beams with Firm Support. Buildings 2025, 15, 3279. https://doi.org/10.3390/buildings15183279
Goñi M, Gimena FN, Valdenebro J-V. New Insight into the Phenomenon of Buckling in Compressed Beams with Firm Support. Buildings. 2025; 15(18):3279. https://doi.org/10.3390/buildings15183279
Chicago/Turabian StyleGoñi, Mikel, Faustino N. Gimena, and José-Vicente Valdenebro. 2025. "New Insight into the Phenomenon of Buckling in Compressed Beams with Firm Support" Buildings 15, no. 18: 3279. https://doi.org/10.3390/buildings15183279
APA StyleGoñi, M., Gimena, F. N., & Valdenebro, J.-V. (2025). New Insight into the Phenomenon of Buckling in Compressed Beams with Firm Support. Buildings, 15(18), 3279. https://doi.org/10.3390/buildings15183279






