Acoustic Emission Assisted Inspection of Punching Shear Failure in Reinforced Concrete Slab–Column Structures
Abstract
1. Introduction
2. Experimental Test
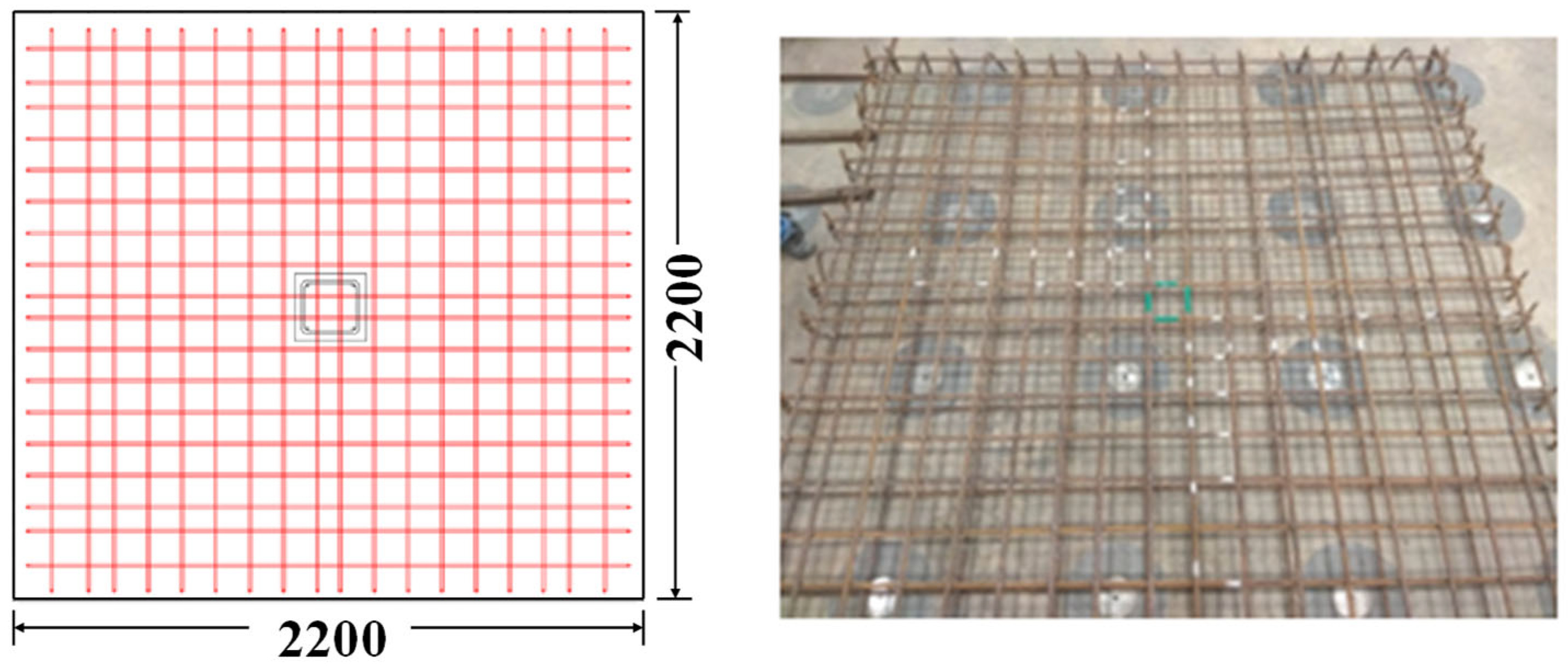
2.1. Specimen Specification
2.2. Loading Setup
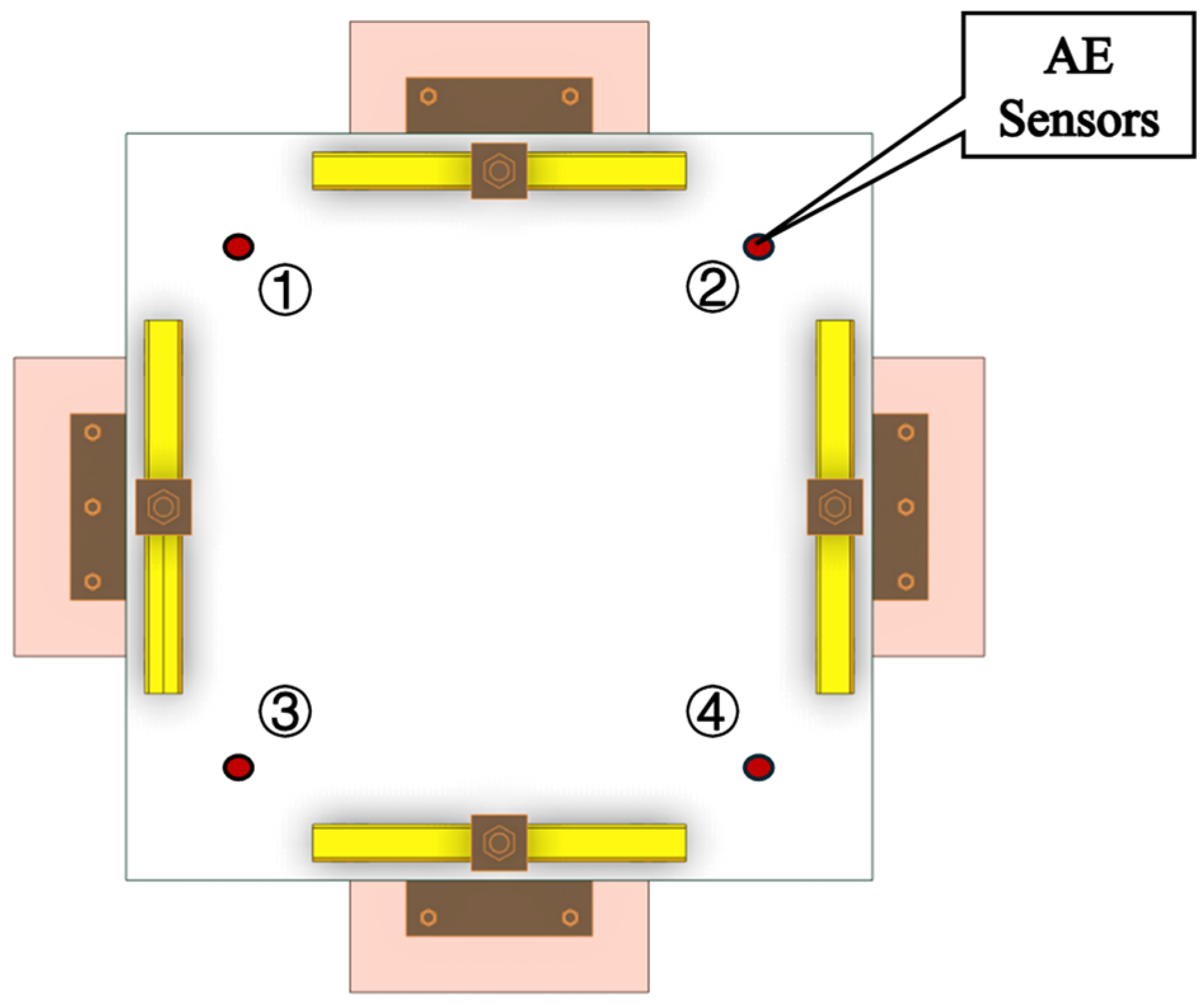
2.3. AE System
3. Experiment Results and Analysis
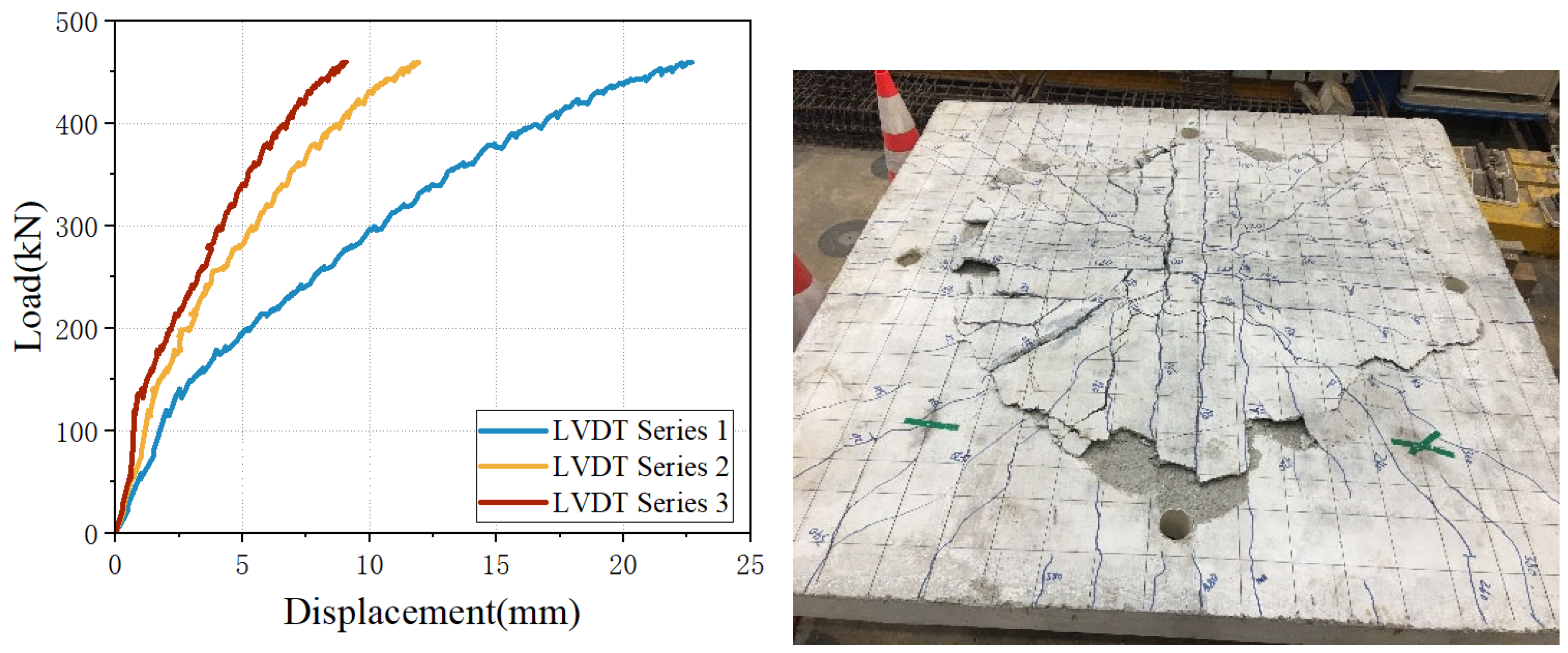
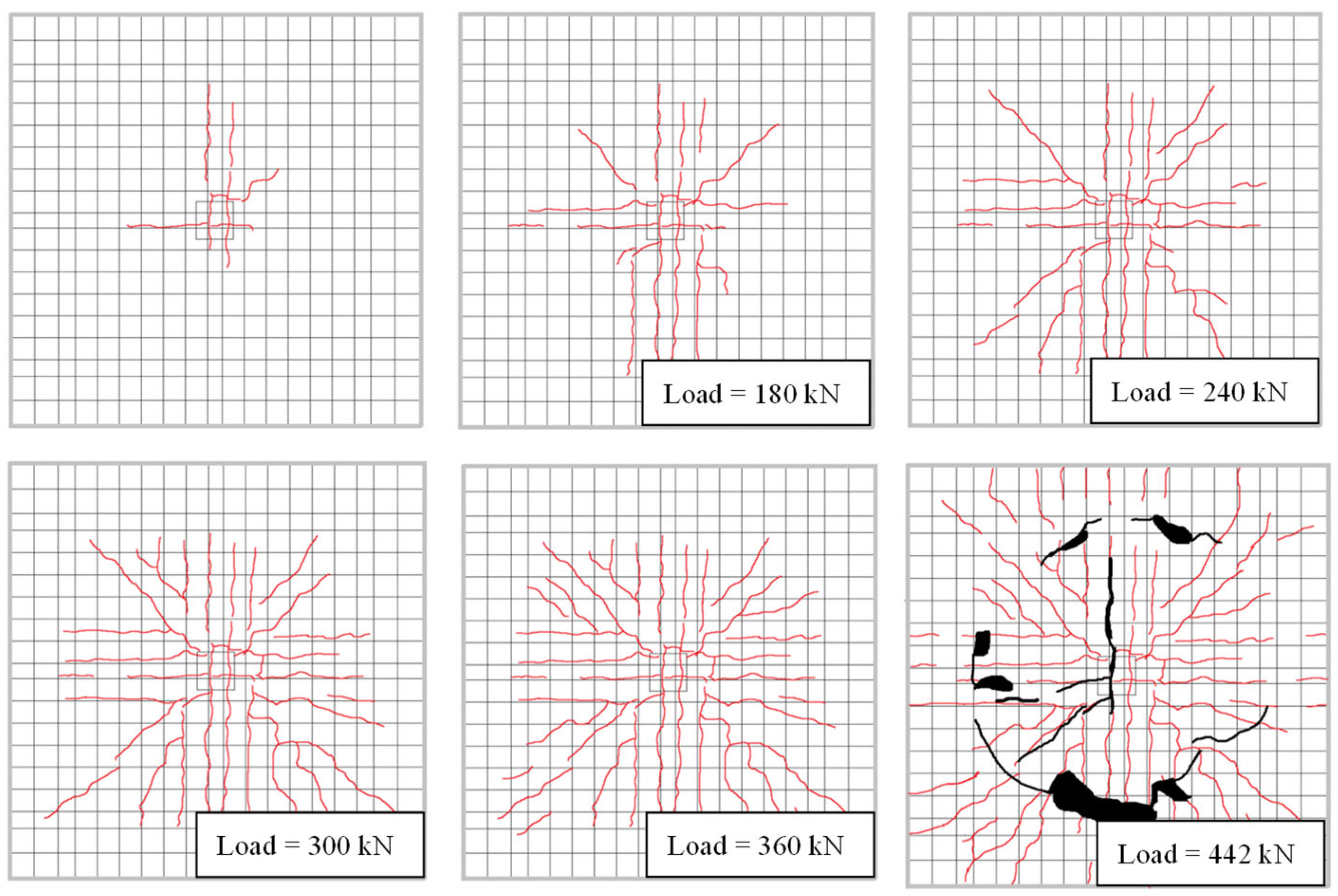
3.1. Load–Displacement Curve and Observed Cracks
3.2. AE Parameters Analysis and Damage Assessment
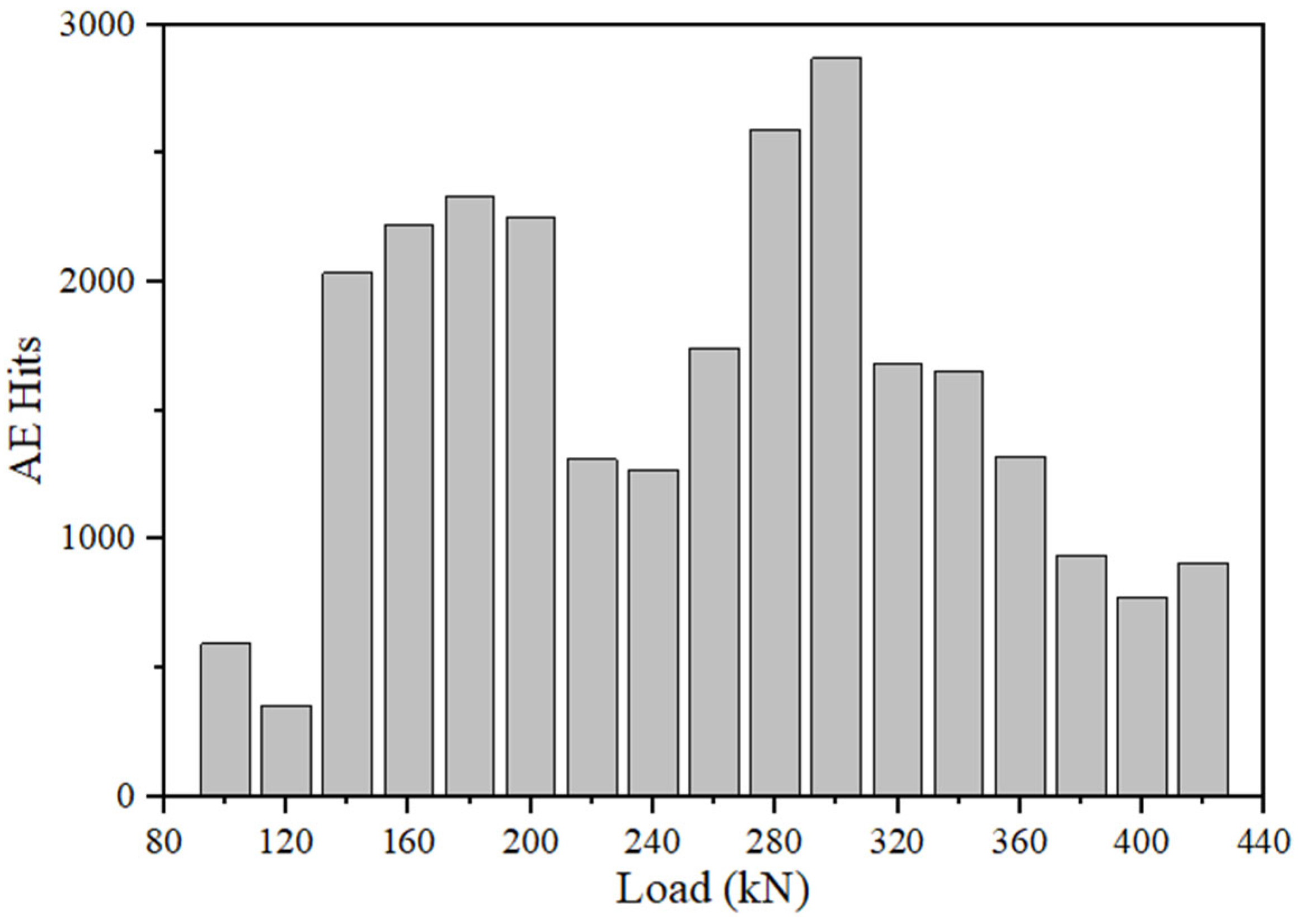
3.2.1. AE Hits Analysis
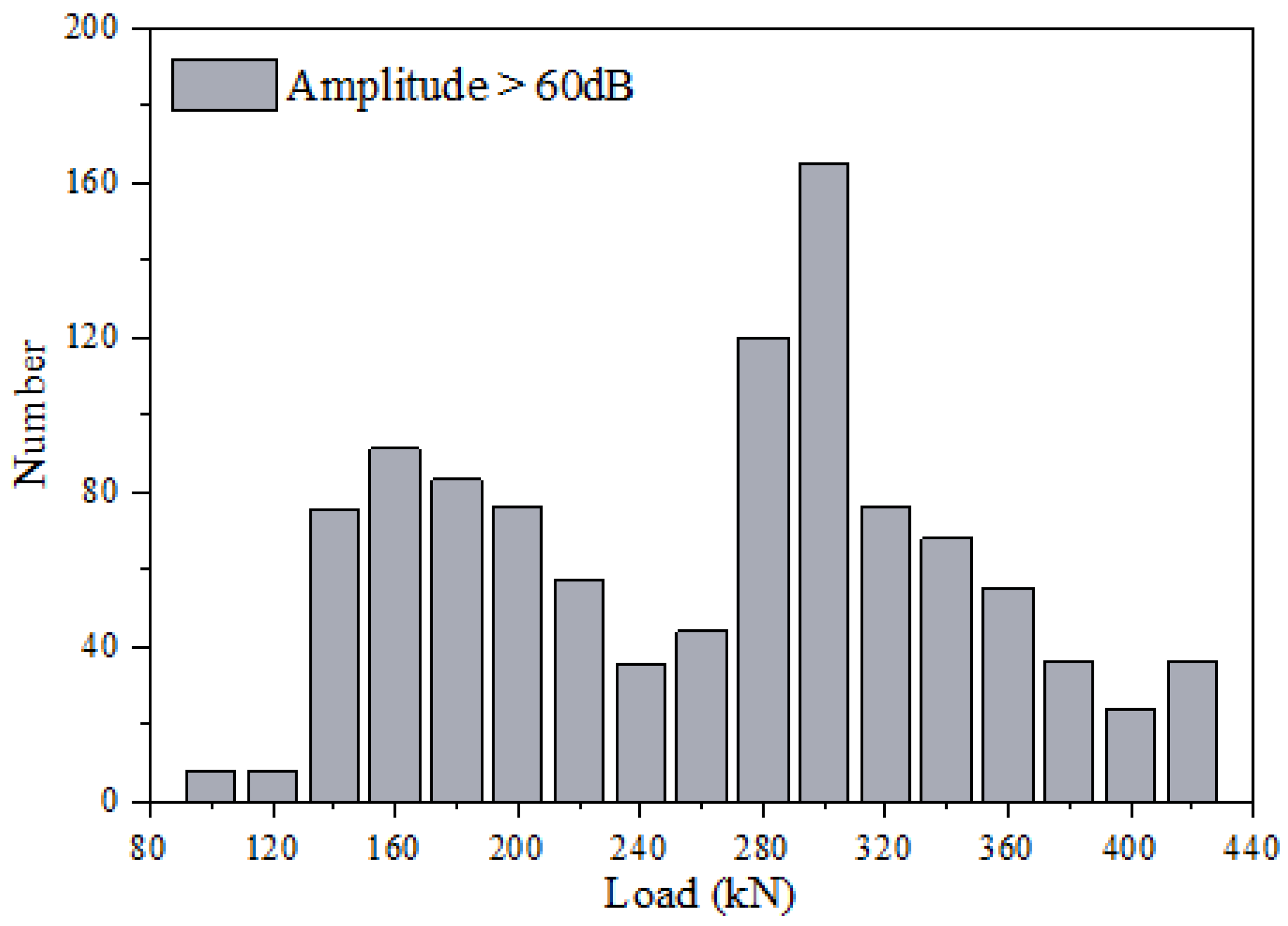
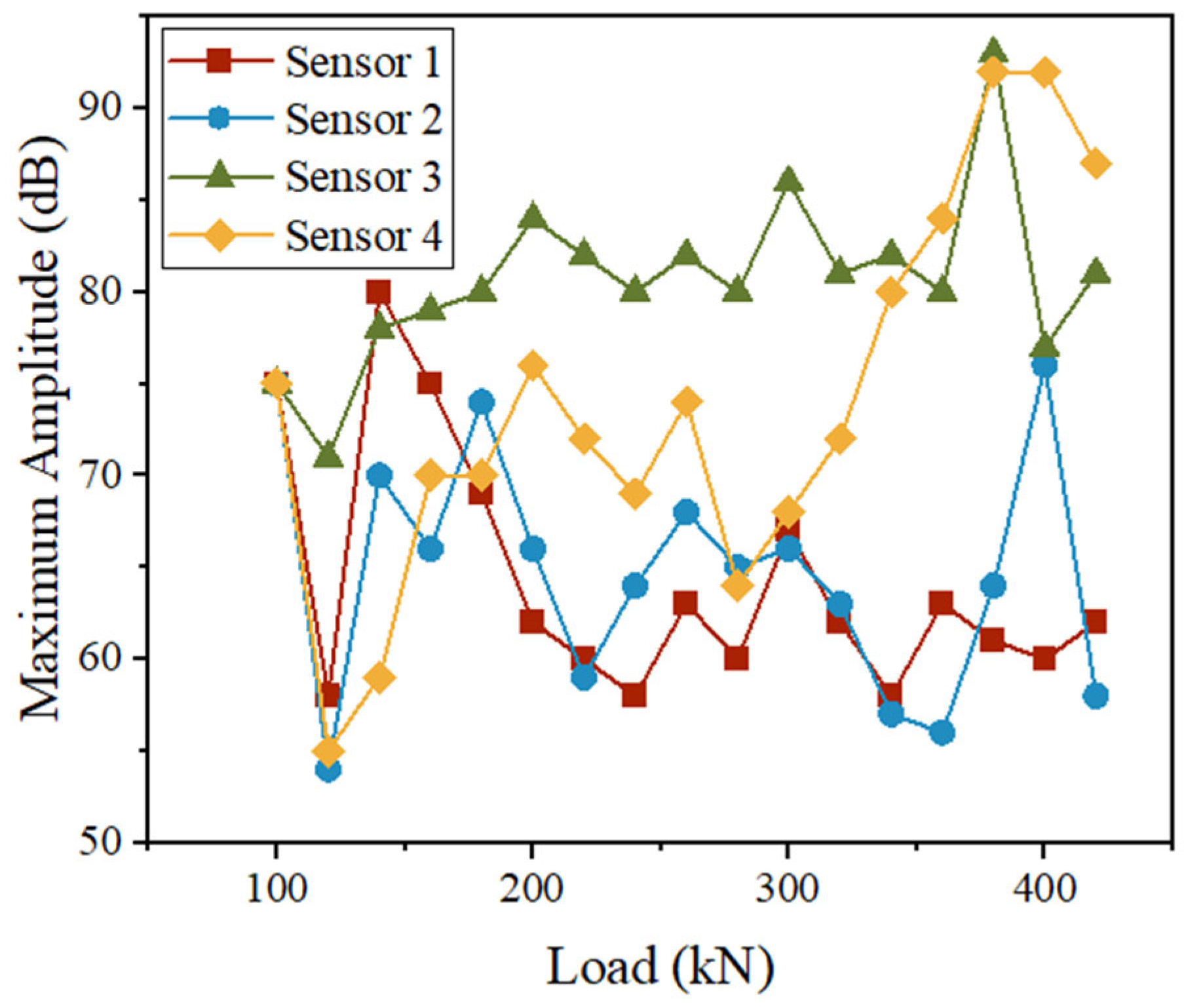
3.2.2. AE Amplitude Analysis
4. Dagame Development Process and Assessment
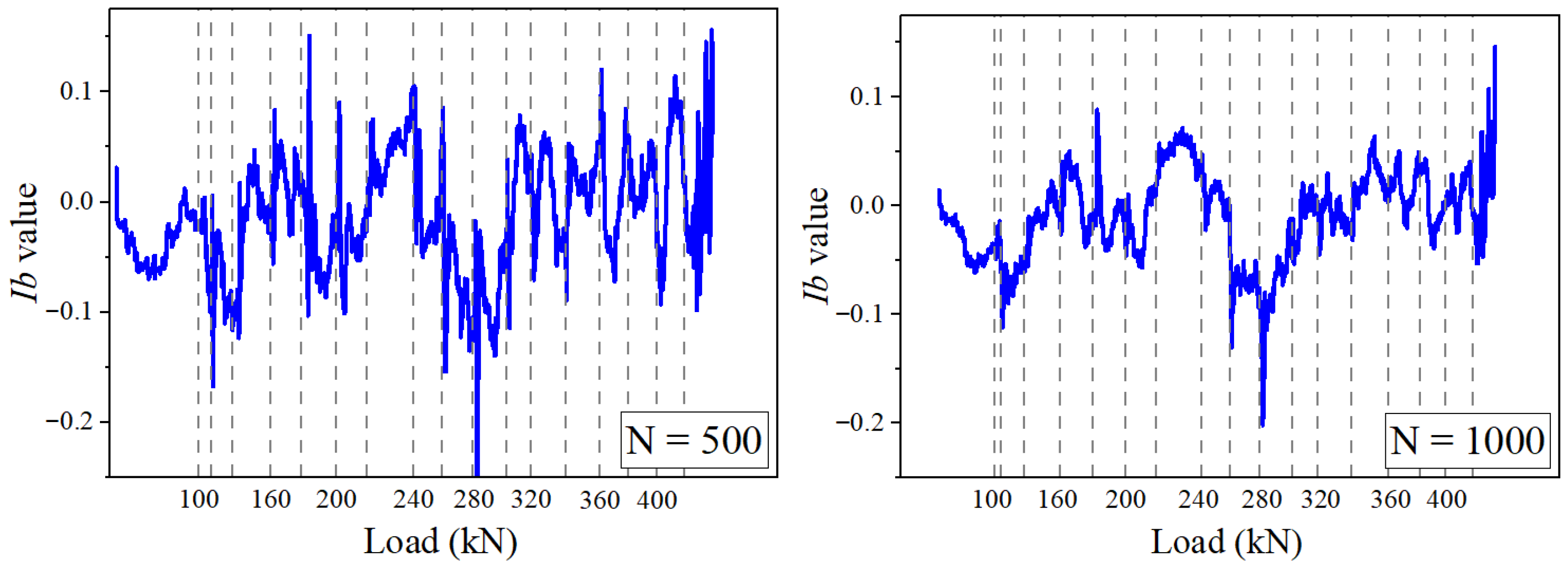
4.1. Ib-Value Analysis
4.2. Energy Analysis
4.3. Failure Mode Evaluation
5. Conclusions
- Obvious punching shear failure was revealed in the specimens by the mechanical experiment results. Through analysis of basic acoustic emission parameters, namely AE hits and amplitude, significant crack development was identified during the loading stage from 120 kN to 200 kN and around 300 kN. This observation was found to be in good agreement with the experimental phenomena.
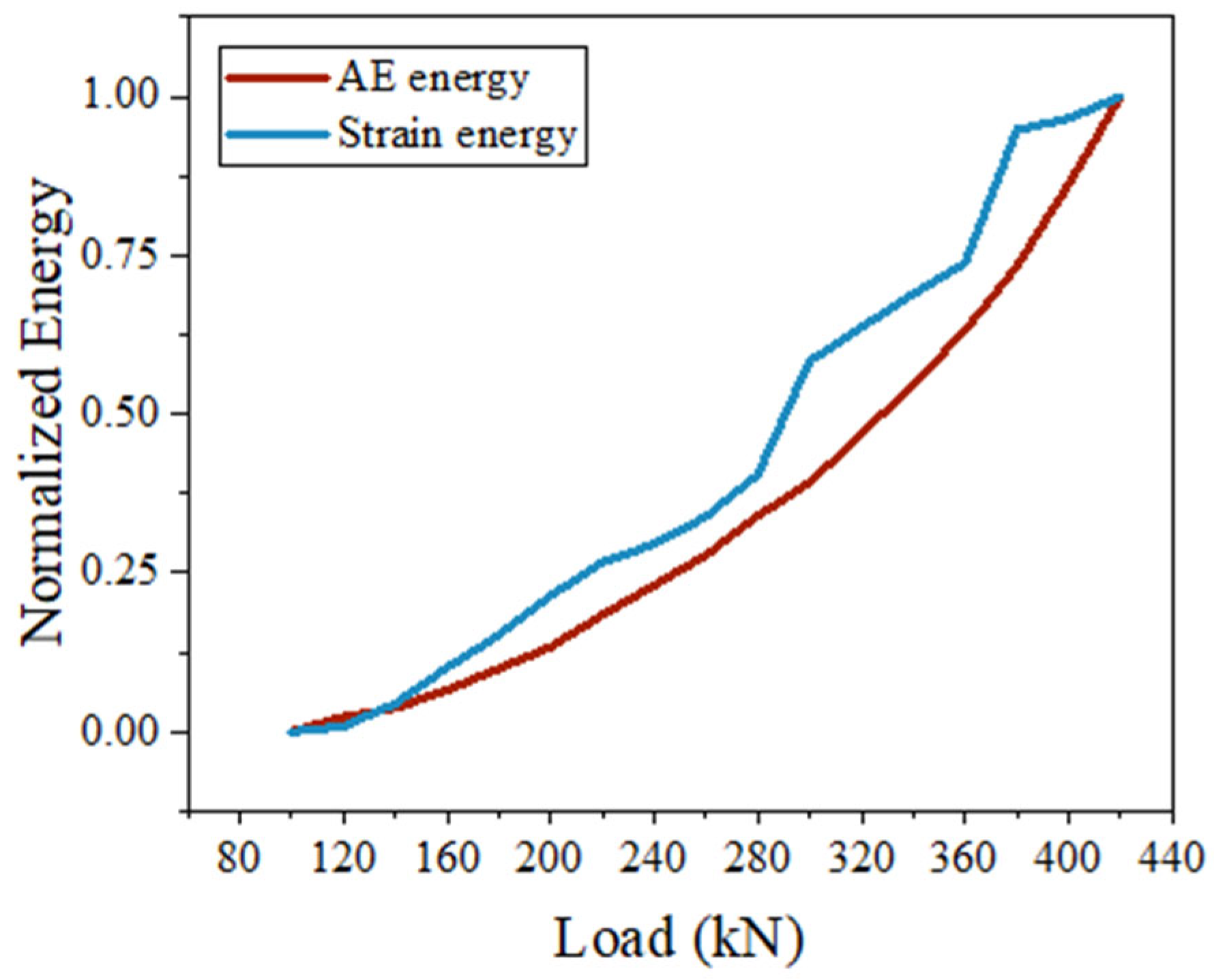
- Analysis of the Ib-value indicates that at 280–300 kN, the transition from micro-crack propagation to macro-crack widening occurs, which aligns with the accelerated development of crack width. The synchronization between AE energy and structural strain energy demonstrates their capability to reflect structural damage. When the load is less than or equal to 220 kN, the damage level remains below 0.25; conversely, when the load reaches or exceeds 340 kN, the damage level surpasses 0.6. This indicates that the structure enters an accelerated failure stage, providing a quantitative basis for safety early-warning systems.
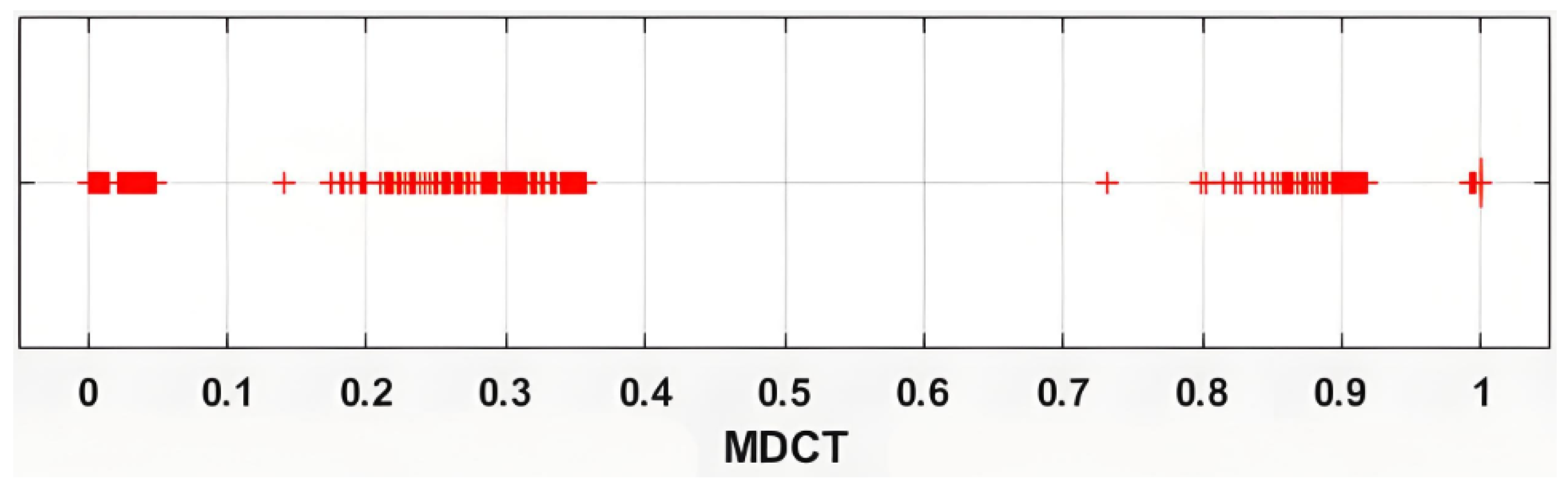
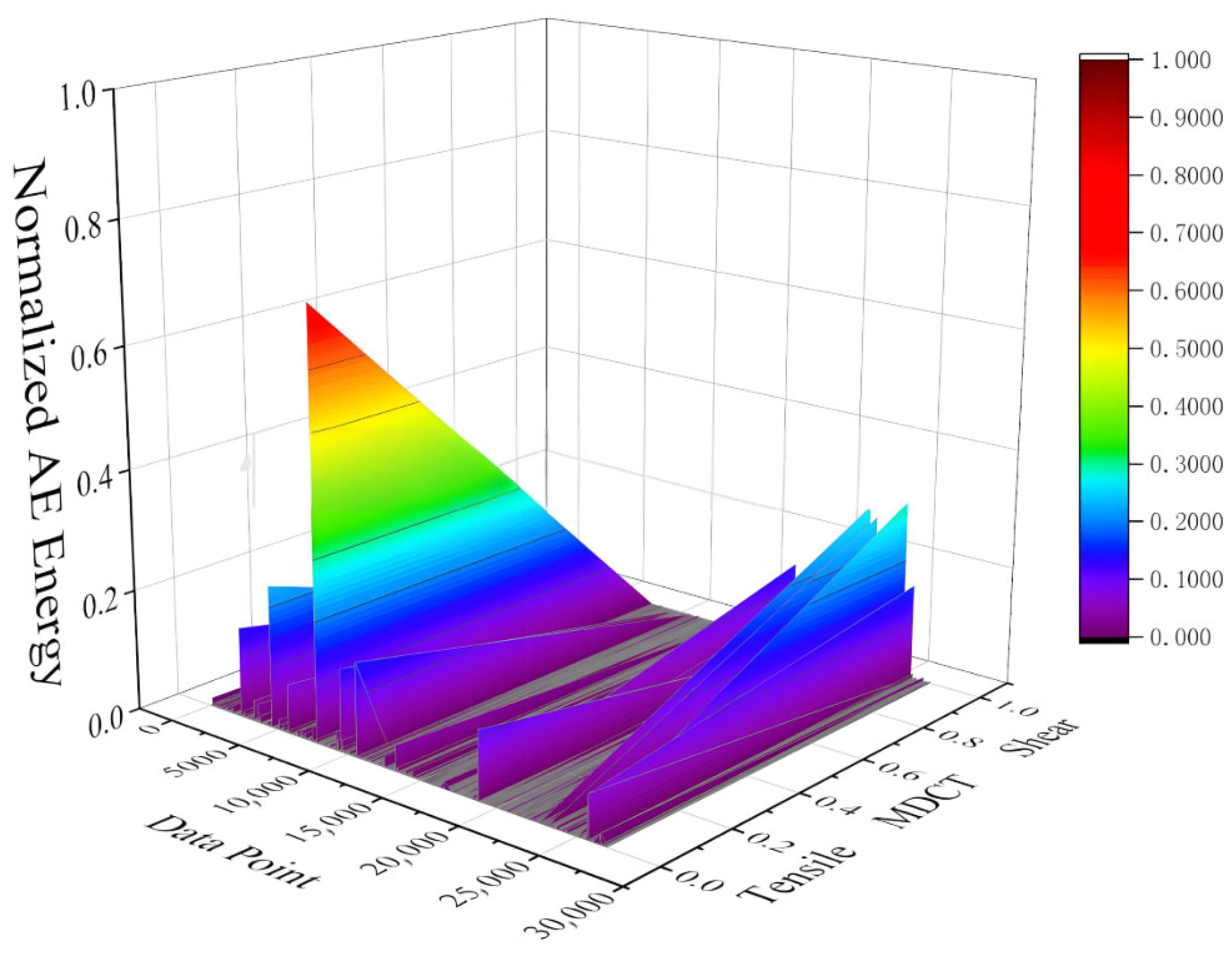
- RA–AF analysis confirms tensile cracks dominate below 200 kN, while shear cracks surge beyond 400 kN, validating the bending-to-punching shear failure transition. A GMM clustering method was employed to convert RA–AF features into a unified Crack-Type membership index. Synchronized MDCT-AE energy analysis was proposed to comprehensively reflect the damage process and intensity, demonstrating exceptional consistency with the experimental damage progression and highlighting substantial potential for real-time structural health monitoring.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Ramana, N.V. Review on punching shear strength of slabs. Int. Eng. J. Res. Dev. 2017, 13, 1–25. [Google Scholar]
- Rankin, G.; Long, A. Punching strength of conventional slab-column specimens. Eng. Struct. 2019, 178, 37–54. [Google Scholar] [CrossRef]
- Hamoda, A.; Abadel, A.A.; Ahmed, M.; Wang, V.; Vrcelj, Z.; Liang, Q.Q. Punching shear performance of reinforced concrete slab-to-steel column connections incorporating ECC and UHPECC. Eng. Struct. 2025, 322, 119145. [Google Scholar] [CrossRef]
- Elstner, R.C.; Hognestad, E. Shearing strength of reinforced concrete slabs. J. Proc. 1956, 53, 29–58. [Google Scholar]
- Muttoni, A. Punching shear strength of reinforced concrete slabs without transverse reinforcement. ACI Struct. J. 2008, 105, 440. [Google Scholar]
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures–Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2004.
- ACI Committee 318; Building Code Requirements for Structural Concrete (ACI 318-14) and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2014.
- Yang, Z.; Ma, J.; Li, B. Investigating the impact of corrosion on behavior and failure modes of reinforced concrete slabs: An experimental and analytical study. Eng. Struct. 2024, 321, 118983. [Google Scholar] [CrossRef]
- Inácio, M.; Isufi, B.; Lapi, M.; Ramos, A.P. Rational use of high-strength concrete in flat slab-column connections under seismic loading. ACI Struct. J. 2020, 117, 297–310. [Google Scholar]
- Ozden, S.; Ersoy, U.; Ozturan, T. Punching shear tests of normal-and high-strength concrete flat plates. Can. J. Civ. Eng. 2006, 33, 1389–1400. [Google Scholar] [CrossRef]
- Gouveia, N.D.; Lapi, M.; Orlando, M.; Faria, D.M.V.; Ramos, A.M.P. Experimental and theoretical evaluation of punching strength of steel fiber reinforced concrete slabs. Struct. Concr. 2018, 19, 217–229. [Google Scholar] [CrossRef]
- Michels, J.; Waldmann, D.; Maas, S.; Zürbes, A. Steel fibers as only reinforcement for flat slab construction–Experimental investigation and design. Constr. Build. Mater. 2012, 26, 145–155. [Google Scholar] [CrossRef]
- Bastien-Masse, M.; Brühwiler, E. Experimental investigation on punching resistance of R-UHPFRC–RC composite slabs. Mater. Struct. 2016, 49, 1573–1590. [Google Scholar] [CrossRef]
- Afefy, H.M.; El-Tony, E.-T.M. Punching shear resistance of strengthened reinforced concrete interior slab–column connections using ultra-high-performance strain-hardening cementitious composite material. Adv. Struct. Eng. 2019, 22, 1799–1816. [Google Scholar] [CrossRef]
- Zhang, X.; Li, B. Damage characteristics and assessment of corroded RC beam-column joint under cyclic loading based on acoustic emission monitoring. Eng. Struct. 2020, 205, 110090. [Google Scholar] [CrossRef]
- Benavent-Climent, A.; Castro, E.; Gallego, A. AE monitoring for damage assessment of RC exterior beam-column subassemblages subjected to cyclic loading. Struct. Health Monit. 2009, 8, 175–189. [Google Scholar] [CrossRef]
- Farhidzadeh, A.; Salamone, S.; Luna, B.; Whittaker, A. Acoustic emission monitoring of a reinforced concrete shear wall by b-value–based outlier analysis. Struct. Health Monit. 2013, 12, 3–13. [Google Scholar] [CrossRef]
- Zhang, X.; Shan, W.; Zhang, Z.; Li, B. AE monitoring of reinforced concrete squat wall subjected to cyclic loading with information entropy-based analysis. Eng. Struct. 2018, 165, 359–367. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhu, Z.; Accornero, F. Tensile-to-shear crack transition in the compression failure of steel-fibre-reinforced concrete: Insights from acoustic emission monitoring. Buildings 2024, 14, 2039. [Google Scholar] [CrossRef]
- Yuyama, S.; Li, Z.-W.; Yoshizawa, M.; Tomokiyo, T.; Uomoto, T. Evaluation of fatigue damage in reinforced concrete slab by acoustic emission. NDT E Int. 2001, 34, 381–387. [Google Scholar] [CrossRef]
- Shan, W.; Liu, J.; Li, J.; Hu, H.; Chen, Y.F. Characterization of damage on precast pre-stressed concrete composite slabs under static loading based on acoustic emission parameters. Struct. Health Monit. 2020, 19, 2091–2106. [Google Scholar] [CrossRef]
- Raghu Prasad, B.K.; Vidya Sagar, R. Relationship between AE energy and fracture energy of plain concrete beams: Experimental study. J. Mater. Civ. Eng. 2008, 20, 212–220. [Google Scholar] [CrossRef]
- Ma, G.; Du, Q. Structural health evaluation of the prestressed concrete using advanced acoustic emission (AE) parameters. Constr. Build. Mater. 2020, 250, 118860. [Google Scholar] [CrossRef]
- Colombo, I.S.; Main, I.G.; Forde, M.C. Assessing damage of reinforced concrete beam using “b-value” analysis of acoustic emission signals. J. Mater. Civ. Eng. 2003, 15, 280–286. [Google Scholar] [CrossRef]
- Zeng, H.; Hartell, J.A.; Soliman, M. Damage evaluation of prestressed beams under cyclic loading based on acoustic emission monitoring. Constr. Build. Mater. 2020, 255, 119235. [Google Scholar] [CrossRef]
- Colombo, S.; Forde, M.; Main, I.G.; Shigeishi, M. Predicting the ultimate bending capacity of concrete beams from the “relaxation ratio” analysis of AE signals. Constr. Build. Mater. 2005, 19, 746–754. [Google Scholar] [CrossRef]
- Ziehl, P.; Ridge, A. Evaluation of strengthened reinforced concrete beams: Cyclic load test and acoustic emission methods. ACI Struct. J. 2006, 103, 832. [Google Scholar]
- Prem, P.R.; Verma, M.; Ambily, P.S. Damage characterization of reinforced concrete beams under different failure modes using acoustic emission. Structures 2021, 30, 174–187. [Google Scholar] [CrossRef]
- Muir, C.; Swaminathan, B.; Fields, K.; Almansour, A.S.; Sevener, K.; Smith, C.; Presby, M.; Kiser, J.D.; Pollock, T.M.; Daly, S. A machine learning framework for damage mechanism identification from acoustic emissions in unidirectional SiC/SiC composites. NPJ Comput. Mater. 2021, 7, 146. [Google Scholar] [CrossRef]
- Calabrese, L.; Campanella, G.; Proverbio, E. Use of cluster analysis of acoustic emission signals in evaluating damage severity in concrete structures. J. Acoust. Emiss. 2010, 1, 28. [Google Scholar]
- Ma, G.; Li, H. Acoustic emission monitoring and damage assessment of FRP-strengthened reinforced concrete columns under cyclic loading. Constr. Build. Mater. 2017, 144, 86–98. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Earthquake magnitude, intensity, energy, and acceleration. Bull. Seismol. Soc. Am. 1942, 32, 163–191. [Google Scholar] [CrossRef]
- Shiotani, T.; Fujii, K.; Aoki, T.; Amou, K. Evaluation of progressive failure using AE sources and improved b-value on slope model tests. Prog. Acoust. Emiss. 1994, 7, 529–534. [Google Scholar]
- JCMS–III B5706; Monitoring Method for Active Cracks in Concrete by Acoustic Emission. Federation of Construction Materials Industries: Tokyo, Japan, 2003.
- Prem, R.; Murthy, A.R. Acoustic emission monitoring of reinforced concrete beams subjected to four-point-bending. Appl. Acoust. 2017, 117, 28–38. [Google Scholar] [CrossRef]
- Bi, J.; Zhao, Y.; Wu, Z.; Li, J.; Wang, C. Research on crack classification method and failure precursor index based on RA-AF value of brittle rock. Theor. Appl. Fract. Mech. 2024, 129, 104179. [Google Scholar] [CrossRef]


| Rebar | Yield Strength (MPa) | Ultimate Strength (MPa) |
|---|---|---|
| T10 | 564 | 708 |
| T14 | 571 | 721 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Yang, Z.; Ying, G. Acoustic Emission Assisted Inspection of Punching Shear Failure in Reinforced Concrete Slab–Column Structures. Buildings 2025, 15, 3226. https://doi.org/10.3390/buildings15173226
Zhang X, Yang Z, Ying G. Acoustic Emission Assisted Inspection of Punching Shear Failure in Reinforced Concrete Slab–Column Structures. Buildings. 2025; 15(17):3226. https://doi.org/10.3390/buildings15173226
Chicago/Turabian StyleZhang, Xinchen, Zhihong Yang, and Guogang Ying. 2025. "Acoustic Emission Assisted Inspection of Punching Shear Failure in Reinforced Concrete Slab–Column Structures" Buildings 15, no. 17: 3226. https://doi.org/10.3390/buildings15173226
APA StyleZhang, X., Yang, Z., & Ying, G. (2025). Acoustic Emission Assisted Inspection of Punching Shear Failure in Reinforced Concrete Slab–Column Structures. Buildings, 15(17), 3226. https://doi.org/10.3390/buildings15173226







