SMA-Activated Double-Stage Yielding BRB: Experimental and FEM Insights
Abstract
1. Introduction
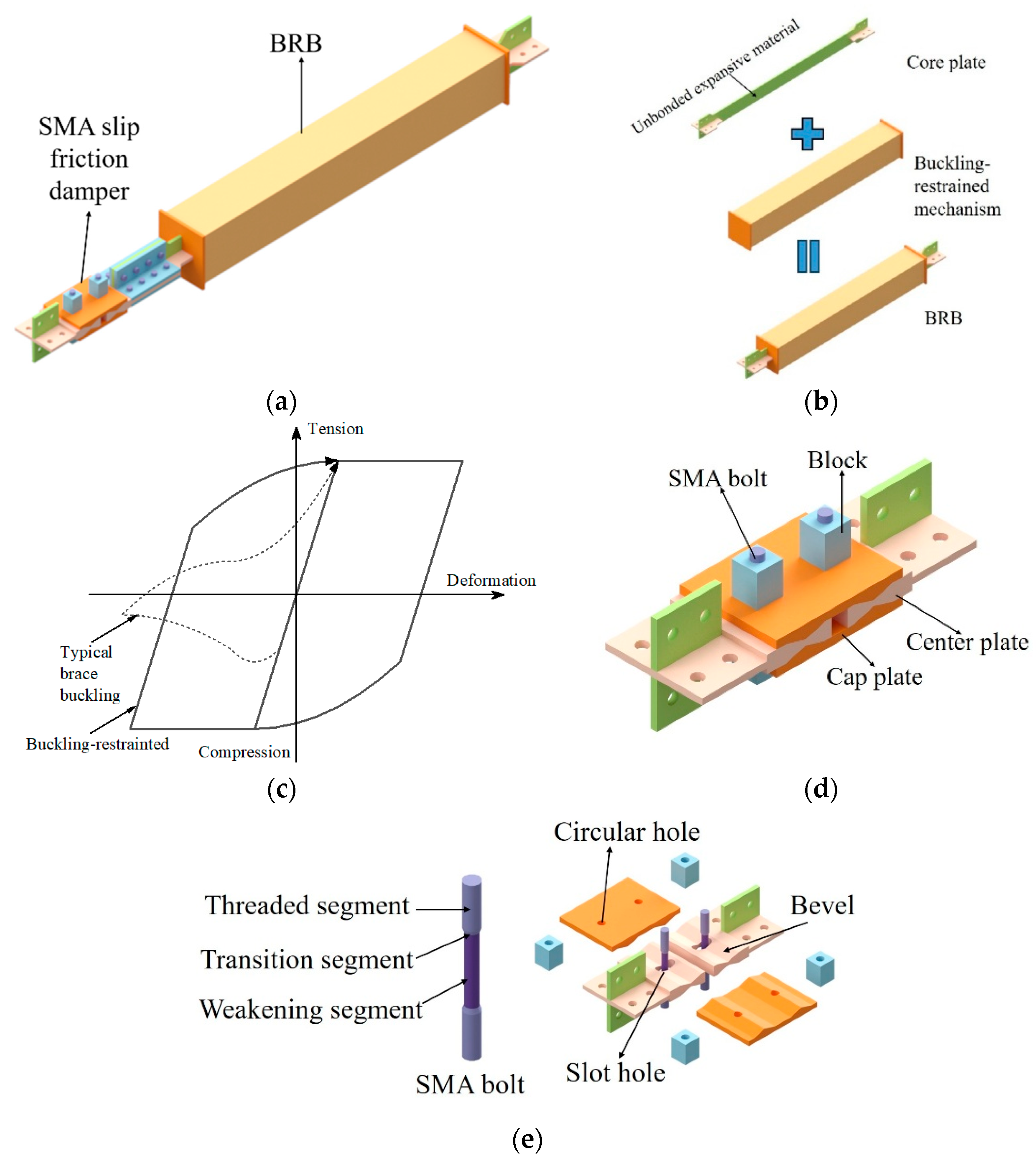
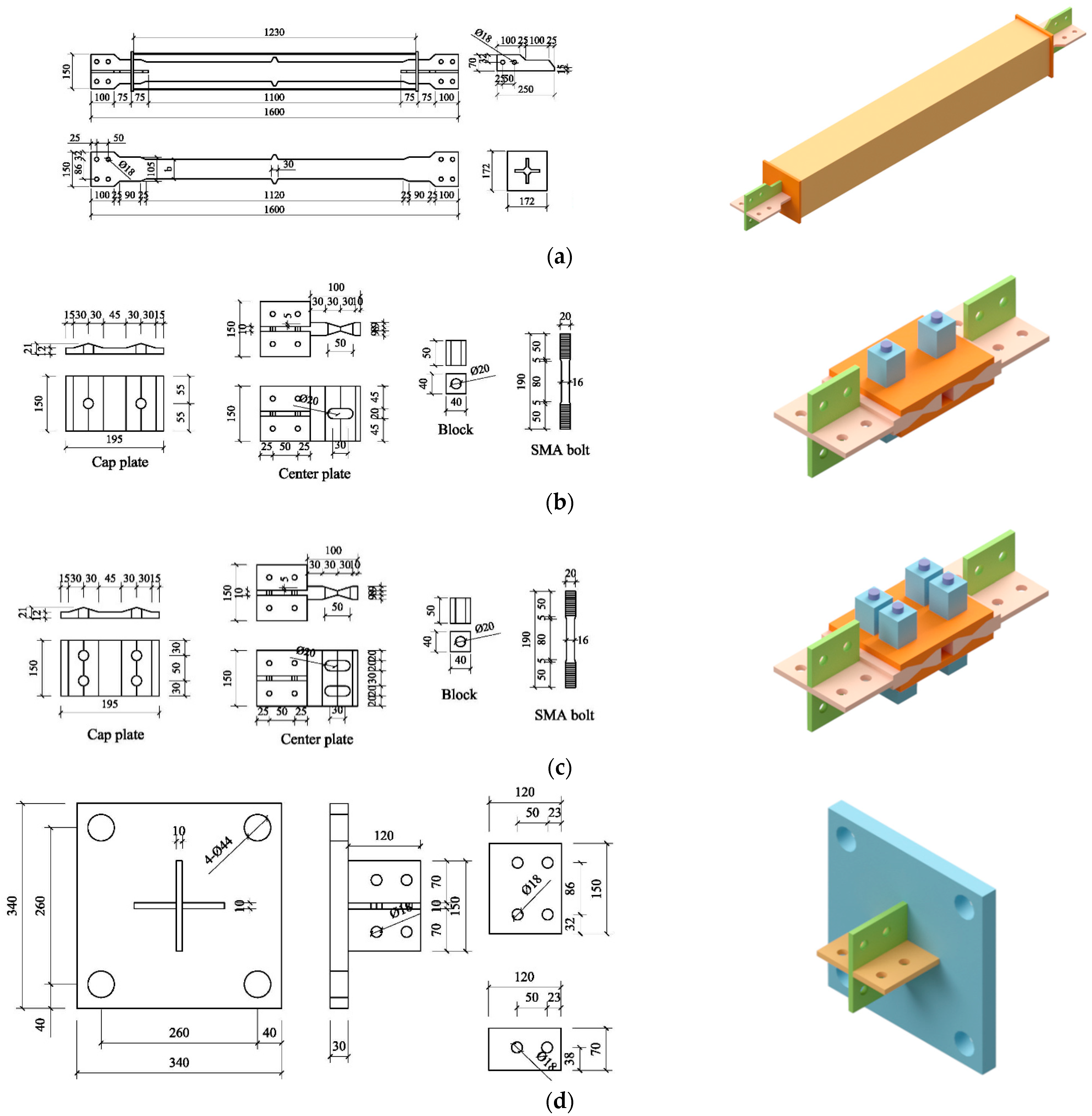
2. Design Principle of Double-Stage Yielding BRB
2.1. Basic Configuration
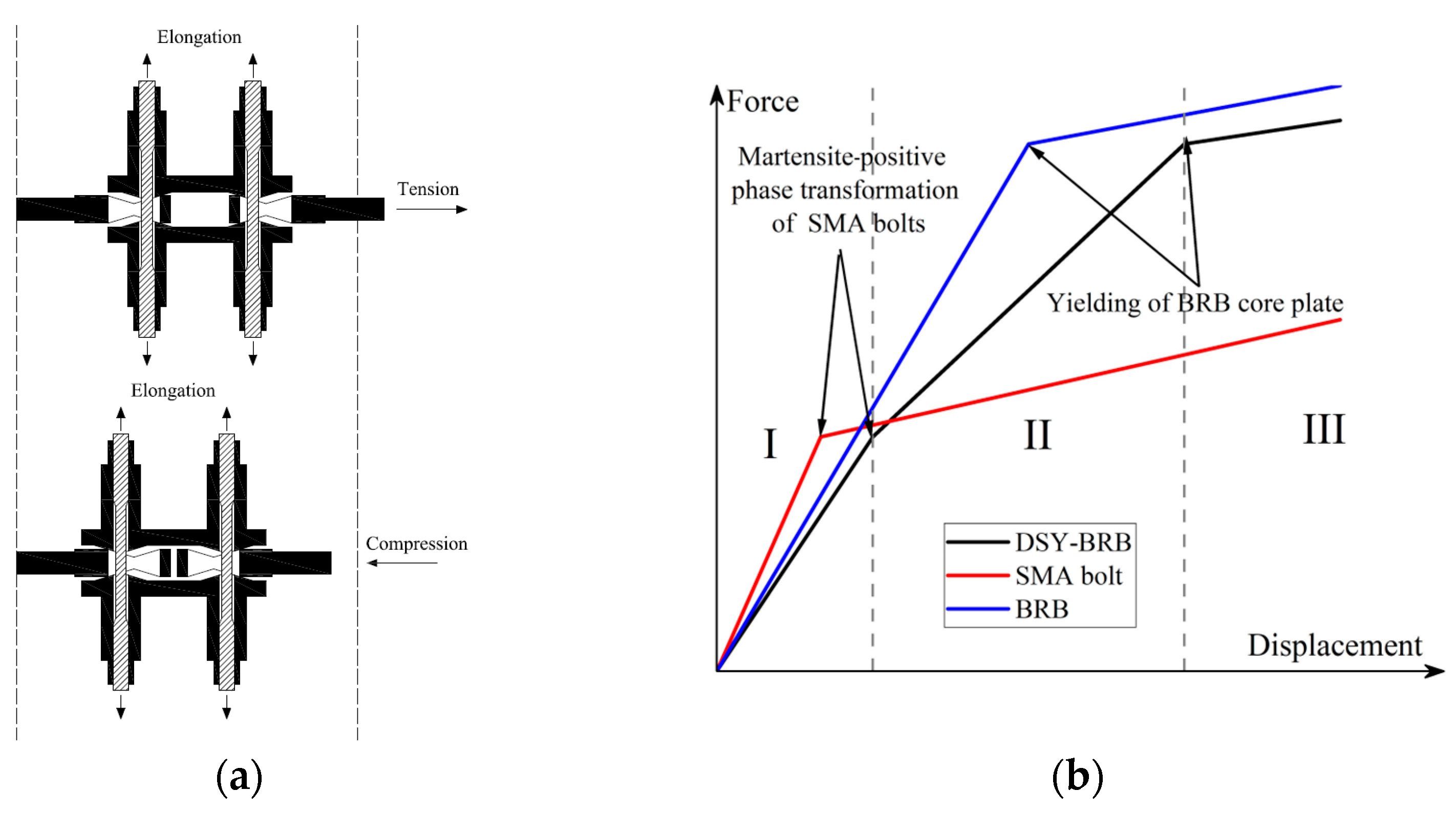
2.2. Working Mechanism
3. Experimental Program
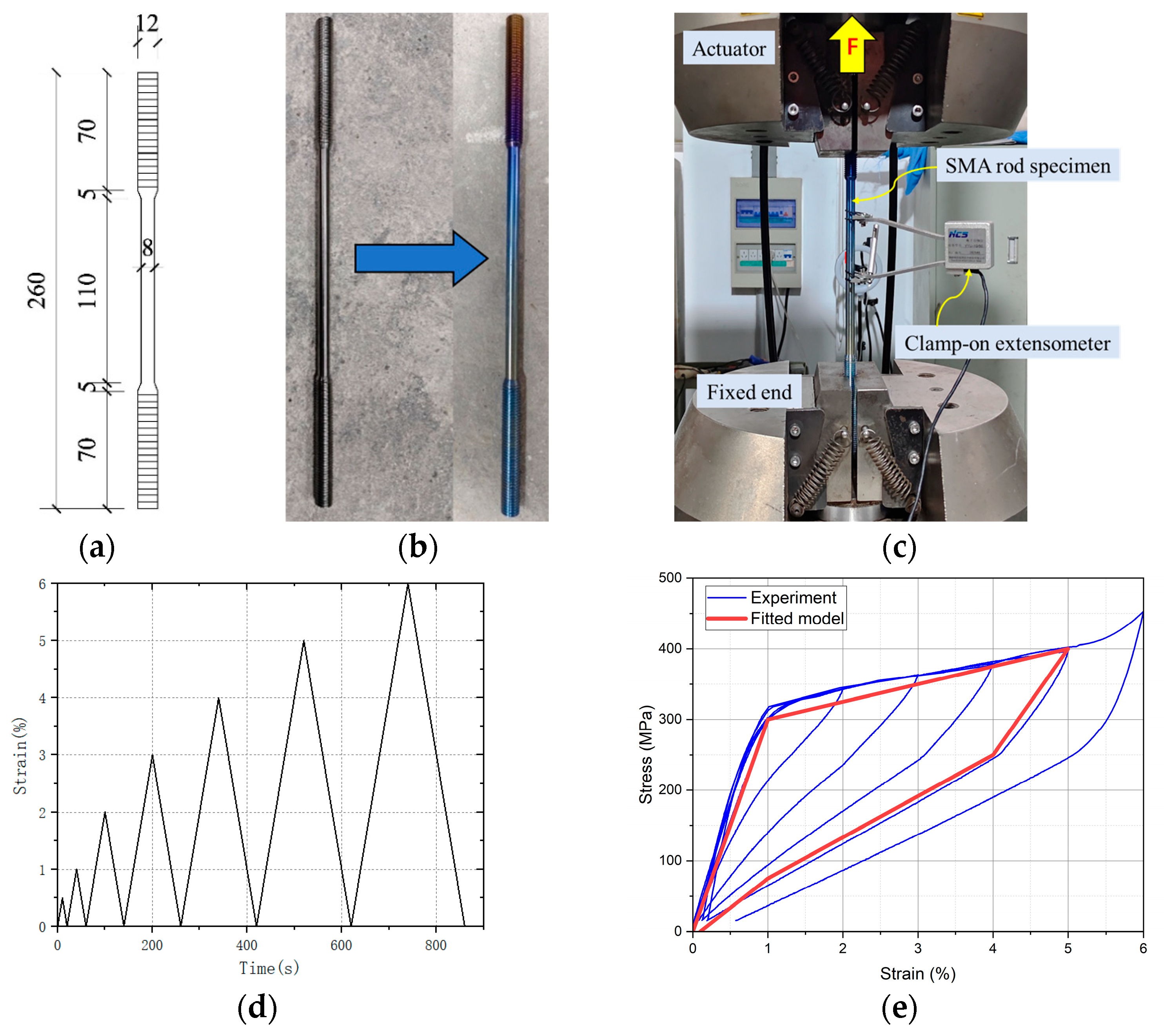
3.1. Pre-Testing of SMA Phase Transition
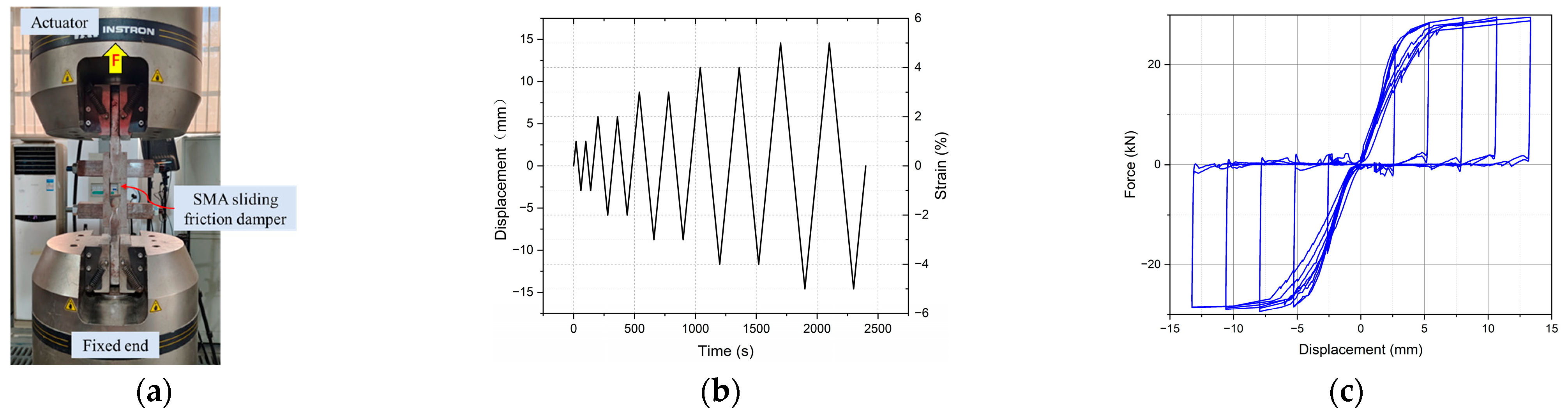
3.2. Mechanical Properties of SMA Slip Friction Damper
3.3. Mechanical Properties of SMA-Activated DSY-BRB Damper
3.3.1. Specimen Details
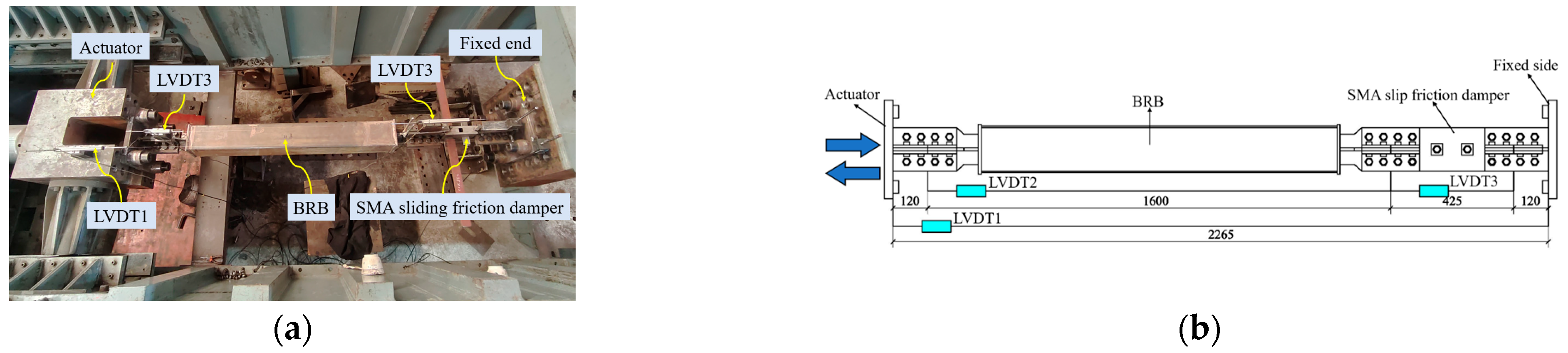
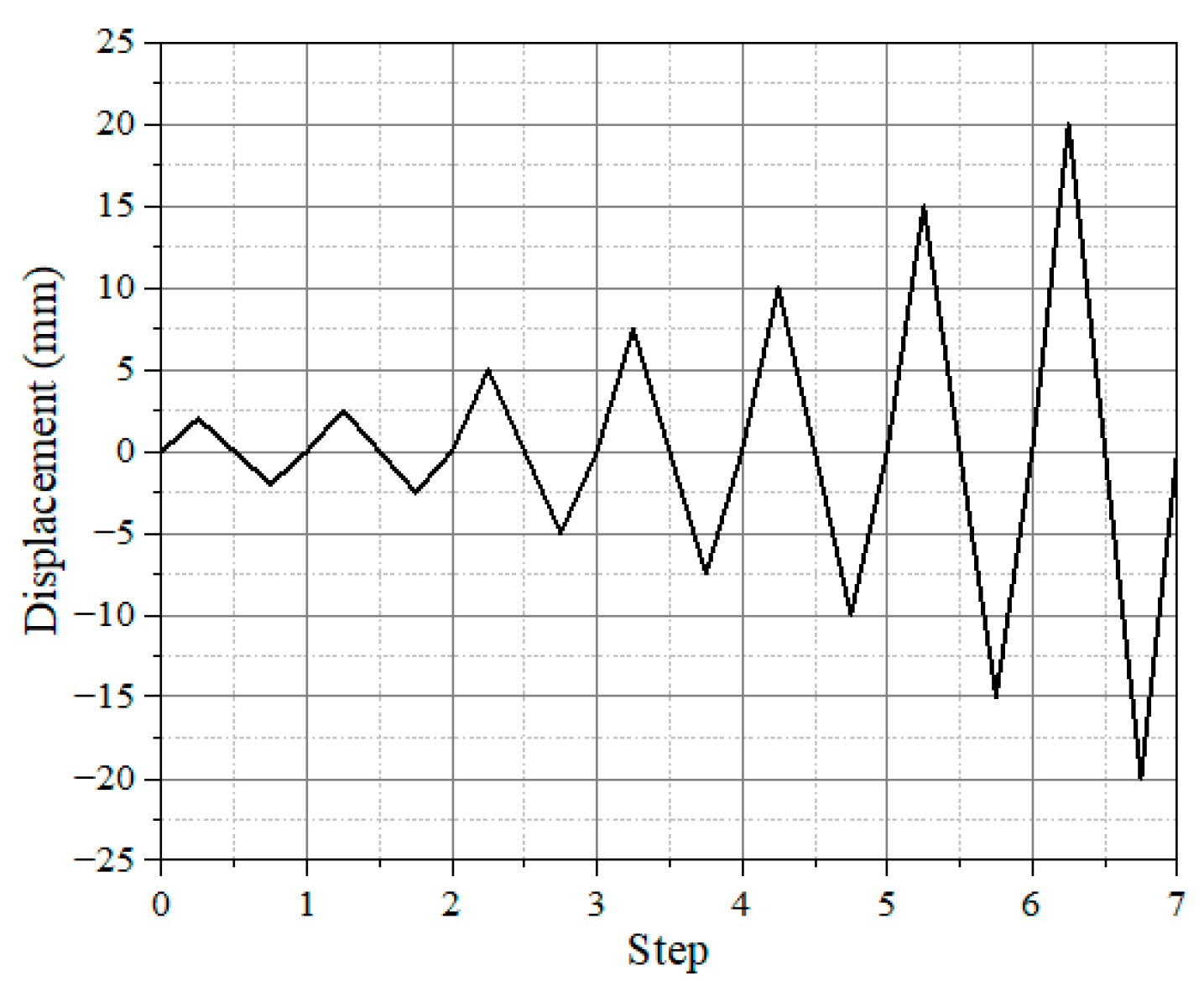
3.3.2. Test Setup and Loading Protocol
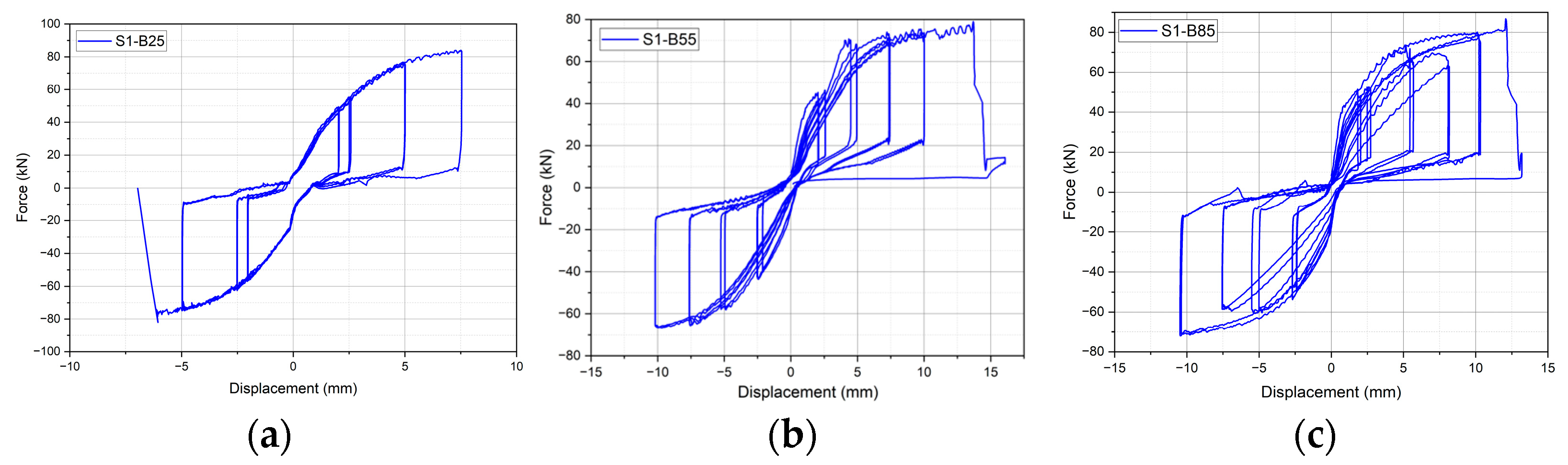
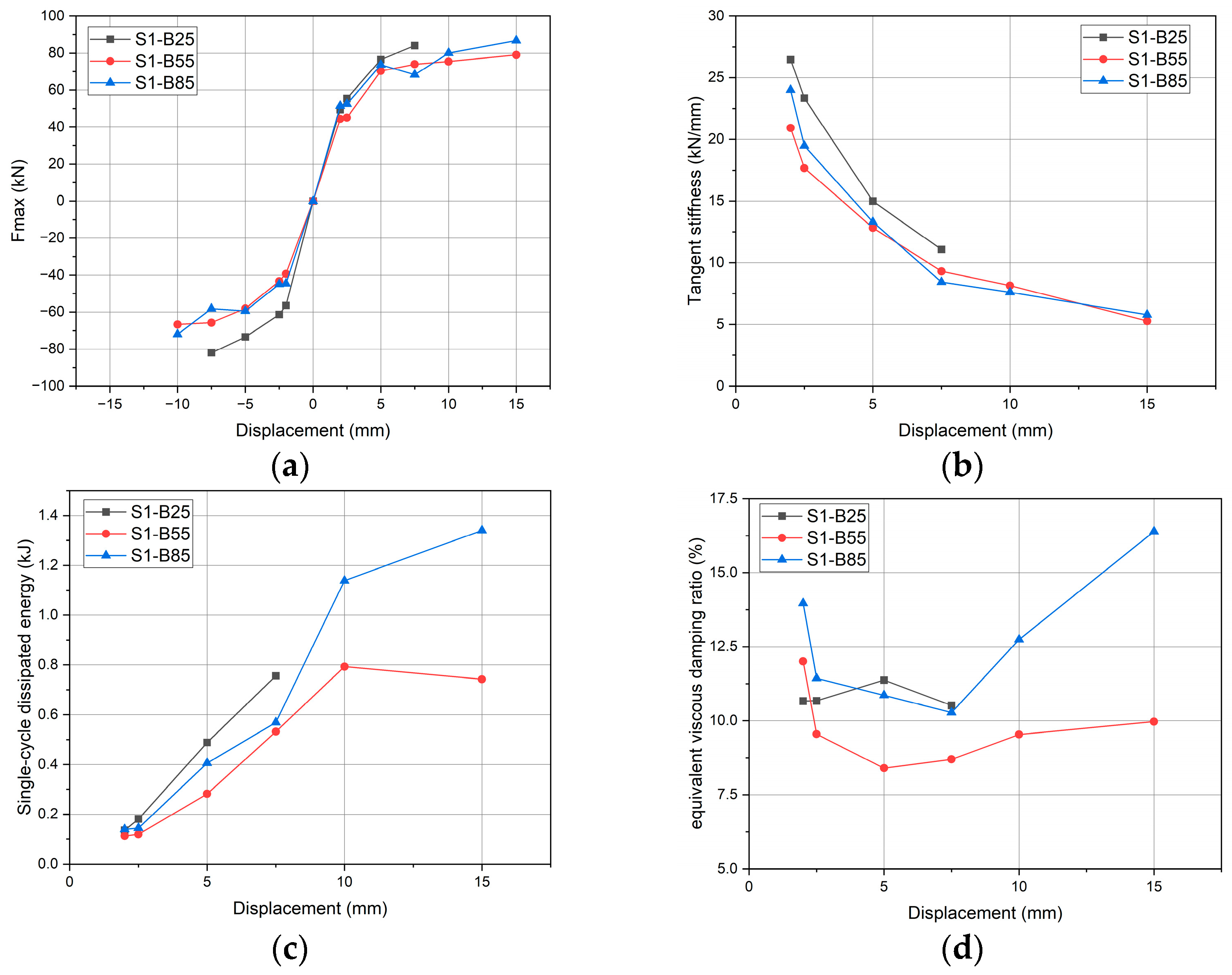
3.3.3. Test Results
4. Numerical Simulations
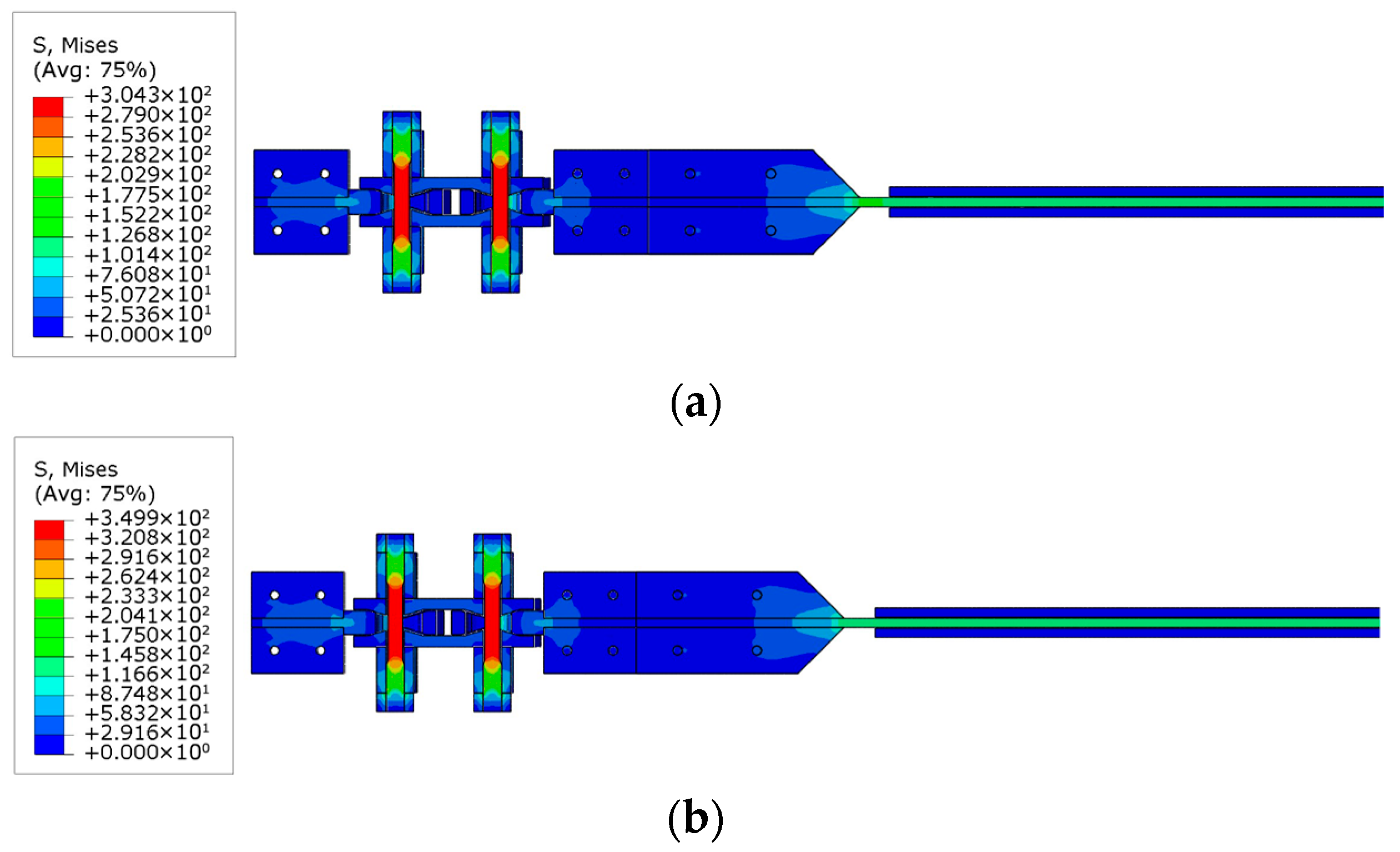
4.1. Finite Element Model
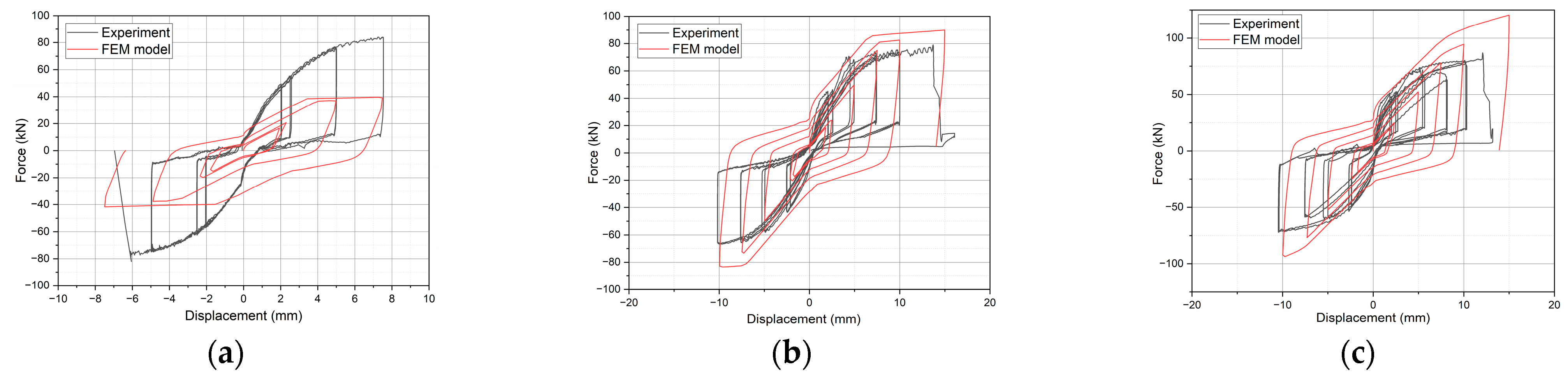
4.2. Verification of FEM Simulation
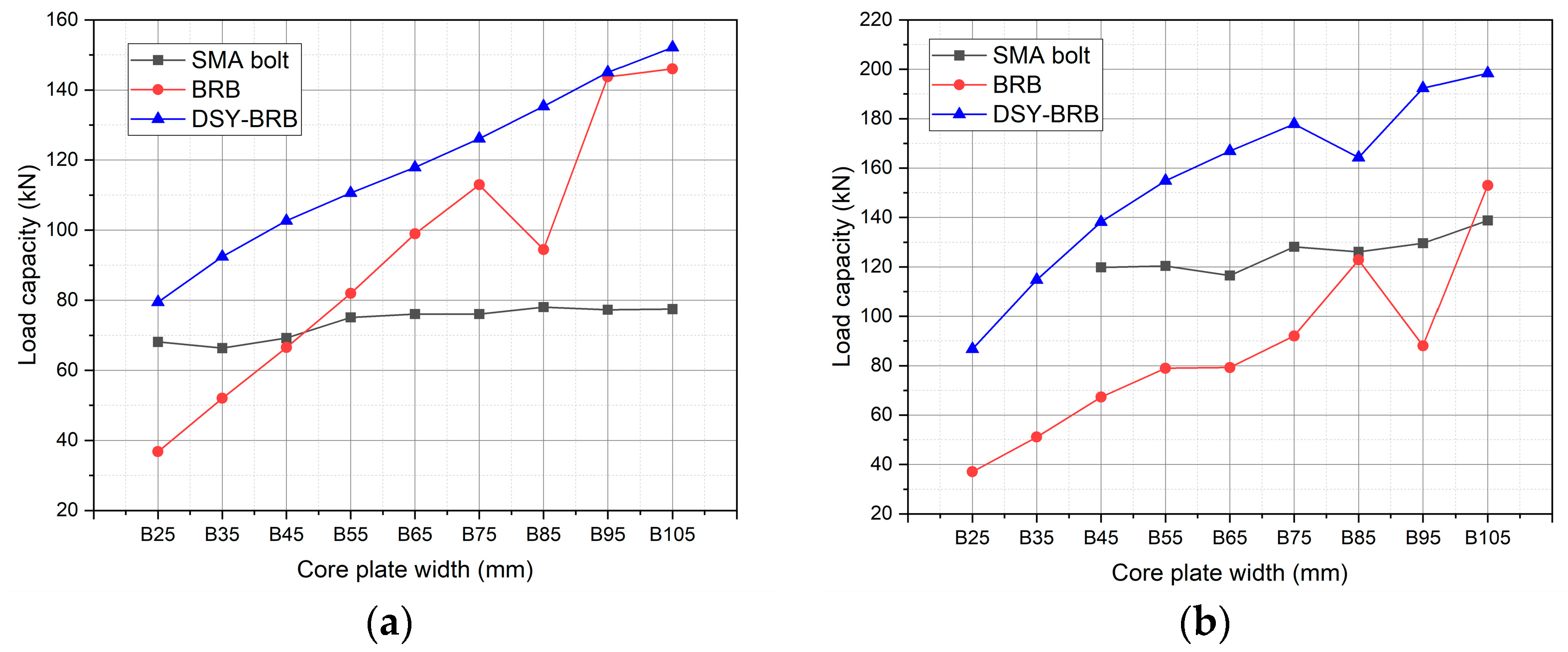
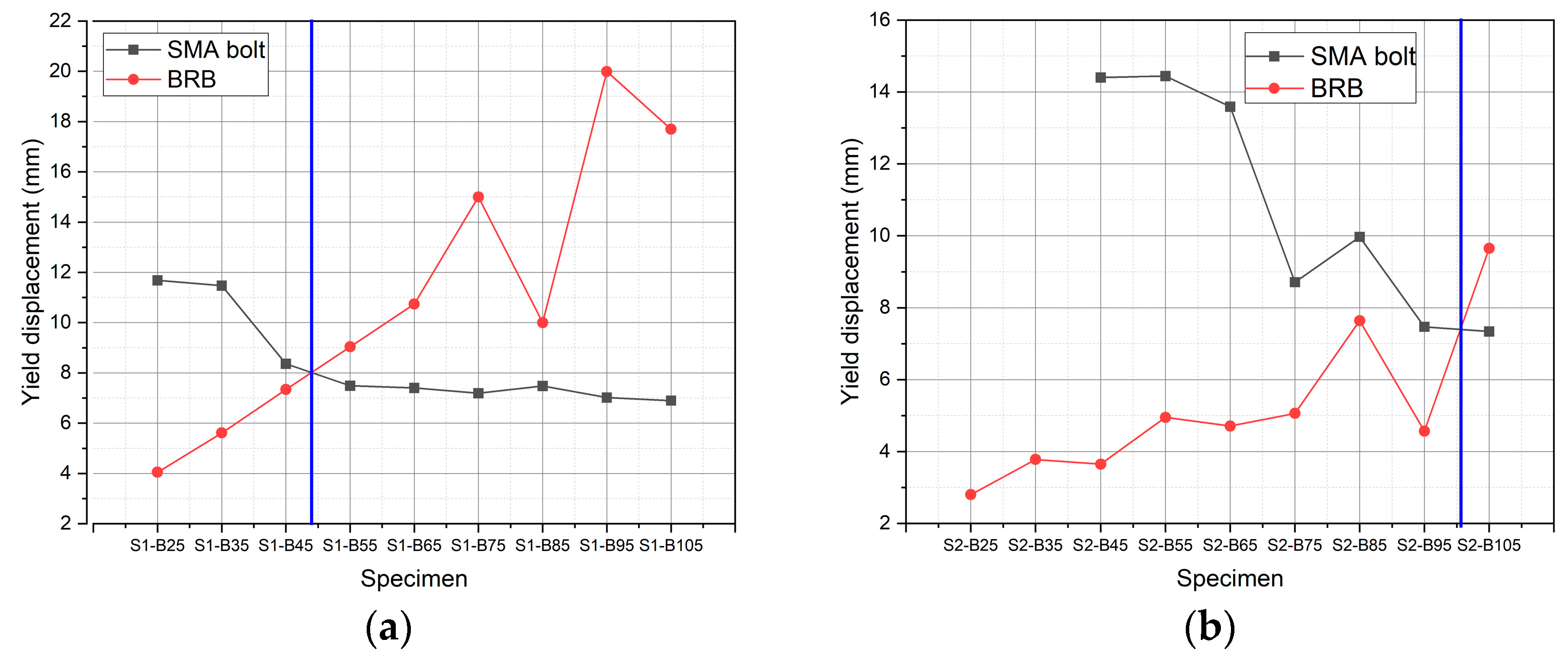
4.3. Parameter Analysis of FEM Simulation
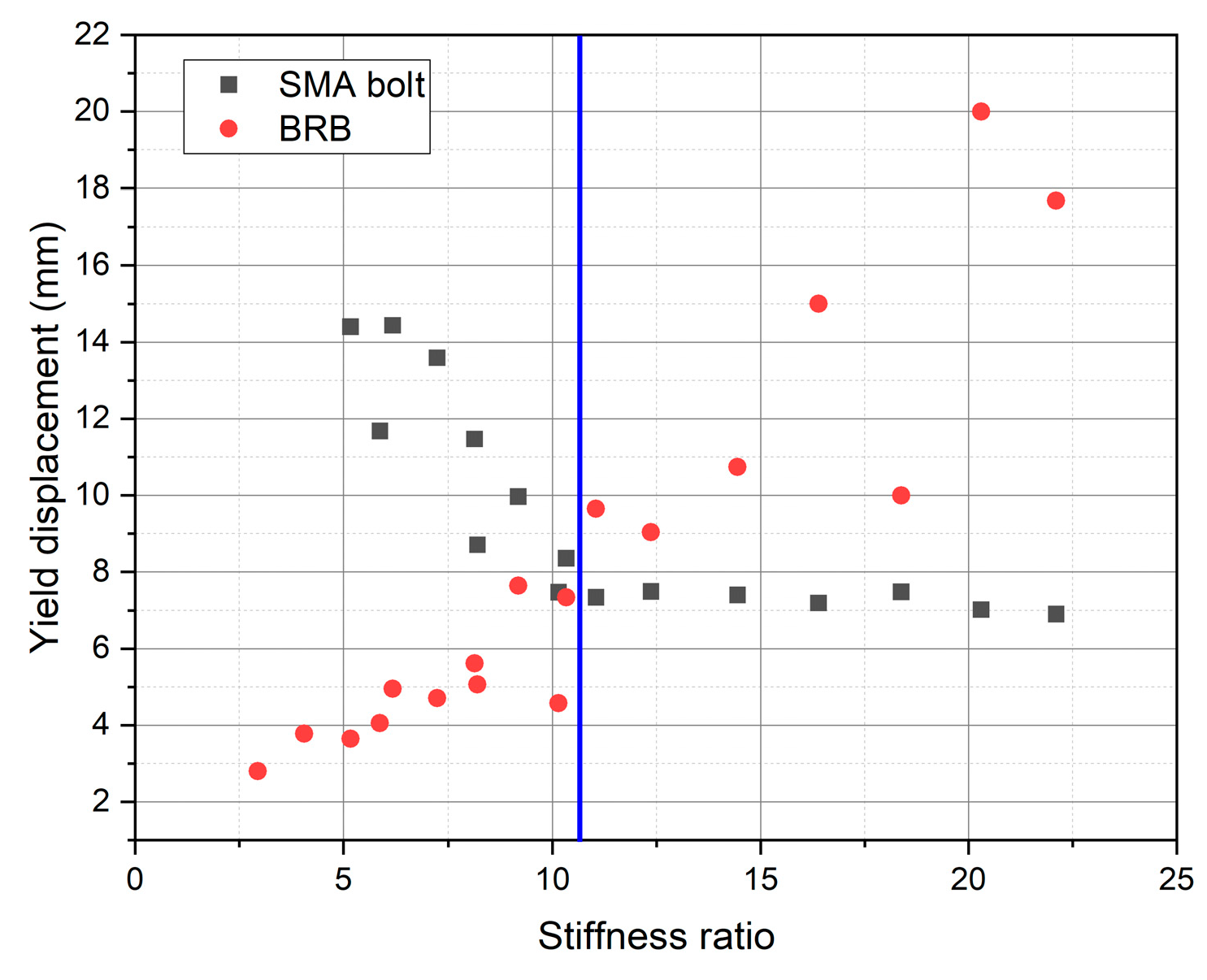
4.4. Discussion
5. Conclusions
- (1)
- The SMA sliding friction damper, designed based on phase-change SMA subjected to high-temperature pre-treatment, demonstrates negligible residual deformation. The incorporation of sliding friction not only enhances the damper’s energy dissipation ability under large deformations but also endows it with reliable self-centering performance.
- (2)
- Quasi-static testing of DSY-BRB specimens revealed that failure predominantly occurred at the threaded end of the SMA bolt. The specimens exhibited stable, full, flag-shaped hysteresis loops with excellent tension–compression symmetry and clear double-stage yielding characteristics, indicating outstanding energy dissipation and self-centering capacities.
- (3)
- FEM simulations, with varied core plate widths and SMA bolt numbers, showed that the stiffness ratio of the DSY-BRB is a critical parameter influencing the yield order of the BRB and the SMA sliding damper. Specifically, a higher stiffness ratio causes the SMA damper to yield before the BRB, while a stiffness ratio between 10.33 and 11.05 results in simultaneous yielding.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sok, A.; Yamada, S.; Iyama, J. Displacement Control of Existing Steel Moment-Resisting Frame Structures Using Buckling-Restrained Braces. J. Earthq. Eng. 2024, 28, 1–21. [Google Scholar] [CrossRef]
- Xu, L.Y.; Nie, X.; Fan, J.S. Cyclic behaviour of low-yield-point steel shear panel dampers. Eng. Struct. 2016, 126, 391–404. [Google Scholar] [CrossRef]
- Mualla, I.H.; Belev, B. Performance of steel frames with a new friction damper device under earthquake excitation. Eng. Struct. 2002, 24, 365–371. [Google Scholar] [CrossRef]
- Zhang, R.H.; Soong, T. Seismic design of viscoelastic dampers for structural applications. J. Struct. Eng. 1992, 118, 1375–1392. [Google Scholar] [CrossRef]
- Martinez-Rodrigo, M.; Romero, M.L. An optimum retrofit strategy for moment resisting frames with nonlinear viscous dampers for seismic applications. Eng. Struct. 2003, 25, 913–925. [Google Scholar] [CrossRef]
- Sabelli, R.; Mahin, S.; Chang, C. Seismic demands on steel braced frame buildings with buckling-restrained braces. Eng. Struct. 2003, 25, 655–666. [Google Scholar] [CrossRef]
- Özkılıç, Y.O.; Bozkurt, M.B. Experimentally investigation of replaceable reduced beam section utilizing beam splice connection. Steel Compos. Struct. 2024, 52, 109. [Google Scholar]
- Özkılıç, Y.O.; Bozkurt, M.B. Numerical validation on novel replaceable reduced beam section connections for moment-resisting frames. Structures 2023, 50, 63–79. [Google Scholar] [CrossRef]
- Özkılıç, Y.O.; Ün, E.M.; Topkaya, C. Frictional mid-spliced shear links for eccentrically braced frames. Earthq. Eng. Struct. Dyn. 2023, 52, 5050–5071. [Google Scholar] [CrossRef]
- Afsar Dizaj, E.; Fanaie, N.; Zarifpour, A. Probabilistic seismic demand assessment of steel frames braced with reduced yielding segment buckling restrained braces. Adv. Struct. Eng. 2018, 21, 1002–1020. [Google Scholar] [CrossRef]
- Mirtaheri, S.M.; Nazeryan, M.; Bahrani, M.K.; Nooralizadeh, A.; Montazerian, L.; Naserifard, M. Local and global buckling condition of all-steel buckling restrained braces. Steel Compos. Struct. 2017, 23, 217–228. [Google Scholar] [CrossRef]
- Hoveidae, N. Numerical investigation of seismic response of hybrid buckling restrained braced frames. Period. Polytech Civ. Eng. 2019, 63, 130–140. [Google Scholar] [CrossRef]
- Ebadi Jamkhaneh, M.; Homaioon Ebrahimi, A.; Shokri Amiri, M. Seismic performance of steel-braced frames with an all-steel buckling restrained brace. Pract. Period. Struct. Des. Constr. 2018, 23, 04018016. [Google Scholar] [CrossRef]
- Kim, D.H.; Yoo, J.H. Analytical Study on a Prototype of Buckling Restrained Braces Reinforced with Steel Plate. Int. J. Steel Struct. 2022, 22, 1841–1849. [Google Scholar] [CrossRef]
- Takeuchi, T.; Hajjar, J.F.; Matsui, R.; Nishimoto, K.; Aiken, I.D. Effect of local buckling core plate restraint in buckling restrained braces. Eng. Struct. 2012, 44, 304–311. [Google Scholar] [CrossRef]
- Yazdi, H.M.; Mosalman, M.; Soltani, A.M. Seismic study of buckling restrained brace system without concrete infill. Int. J. Steel Struct. 2018, 18, 153–162. [Google Scholar] [CrossRef]
- Pandikkadavath, M.S.; Sahoo, D.R. Development and subassemblage cyclic testing of hybrid buckling-restrained steel braces. Earthq. Eng. Eng. Vib. 2020, 19, 967–983. [Google Scholar] [CrossRef]
- Oh, S.; Kurama, Y.C.; Mohle, J.; Polster, L.; Manning, M.; Weldon, B.D. A novel reinforced-concrete buckling-restrained brace for precast concrete lateral-load-resisting frames. PCI J. 2023, 68, 95–116. [Google Scholar] [CrossRef]
- Pan, P.; Li, W.; Nie, X.; Deng, K.; Sun, J. Seismic performance of a reinforced concrete frame equipped with a double-stage yield buckling restrained brace. Struct. Des. Tall Spec. Build. 2017, 26, e1335. [Google Scholar] [CrossRef]
- Li, G.; Sun, Y.; Jiang, J.; Sun, F.; Ji, C. Experimental study on two-level yielding buckling-restrained braces. J. Constr. Steel Res. 2019, 159, 260–269. [Google Scholar] [CrossRef]
- Hu, B.; Min, Y.; Wang, C.; Xu, Q.; Keleta, Y. Design, analysis and application of the double-stage yield buckling restrained brace. J. Build. Eng. 2022, 48, 103980. [Google Scholar] [CrossRef]
- Yang, C.; Xie, L.; An, N.; Li, A.; Liu, Q.; Wang, X. Development of a novel parallel double-stage yielding buckling restrained brace: Theoretical, experimental, and numerical investigations. J. Build. Eng. 2023, 68, 106089. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, Q.; Gong, C.; Li, D.; Zhang, Y.; Chen, Z. A double-stage buckling restrained brace with progressive failure pattern: Experimental verification and numerical calibration. Structures 2024, 62, 106242. [Google Scholar] [CrossRef]
- Zhai, Z.; Liu, Y.; Mercan, O.; Zou, S.; Zhou, F. A hybrid buckling-restrained brace for enhancing the seismic performance of steel moment resisting frames. Soil Dyn. Earthq. Eng. 2024, 178, 108464. [Google Scholar] [CrossRef]
- Yang, C.; Xie, L.; Liu, Q.; Li, A.; Liu, Q.; Wang, X. Dual-objective control of braced steel frame using asynchronized parallel two-stage yielding BRB. Soil Dyn. Earthq. Eng. 2024, 179, 108522. [Google Scholar] [CrossRef]
- Xiong, C.; Cao, Y.; Wang, T.; Xie, L.; Wu, D. Experimental and numerical studies of a core plate repairable double-stage yield buckling-restrained brace. J. Constr. Steel Res. 2024, 223, 109006. [Google Scholar] [CrossRef]
- Kawashima, K.; MacRae, G.A.; Hoshikuma, J.; Nagaya, K. Residual displacement response spectrum. J. Struct. Eng. 1998, 124, 523–530. [Google Scholar] [CrossRef]
- McCormick, J.; Aburano, H.; Ikenaga, M.; Nakashima, M. Permissible residual deformation levels for building structures considering both safety and human elements. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008; Seismological Press: Beijing, China, 2008. [Google Scholar]
- Özkılıç, Y.O.; Bozkurt, M.B.; Topkaya, C. Mid-spliced end-plated replaceable links for eccentrically braced frames. Eng. Struct. 2021, 237, 112225. [Google Scholar] [CrossRef]
- Hui, D.; Yu, B.; Qiang, H.; Xiu, D. Mechanical performance of new type of self-centering energy dissipation brace and its application in double-column bridge structures. China J. Highw. Transp. 2017, 30, 196–204. (In Chinese) [Google Scholar]
- Qing, Y.; Wang, C.L.; Zhou, Z.; Zeng, B. Seismic responses of multistory buildings with self-centering buckling-restrained braces: Influence of the pretension force. Eng. Struct. 2021, 238, 112249. [Google Scholar] [CrossRef]
- Zhang, C.; Guo, X.; Luo, J.; Chen, S. Seismic design and performance evaluation of steel braced frames with post-tensioned and disc-spring-based self-centering buckling-restrained braces. Soil Dyn. Earthq. Eng. 2024, 180, 108602. [Google Scholar] [CrossRef]
- Han, Y.L.; Xing, D.J.; Xiao, E.T.; Li, A.Q. NiTi-wire shape memory alloy dampers to simultaneously damp tension, compression, and torsion. J. Vib. Control 2005, 11, 1067–1084. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, Z.; Wang, S.; Yang, T.; Zhan, M. Design and analysis of an innovative hybrid shape memory alloys viscous damper. J. Earthq. Eng. Eng. Vib. 2016, 36, 72–78. [Google Scholar]
- Alipour, A.; Kadkhodaei, M.; Safaei, M. Design, analysis, and manufacture of a tension–compression self-centering damper based on energy dissipation of pre-stretched superelastic shape memory alloy wires. J. Intell. Mater. Syst. Struct. 2017, 28, 2129–2139. [Google Scholar] [CrossRef]
- Liu, M.; Li, H.; Fu, X. Experimental and numerical analysis of an innovative re-centering shape memory alloys-shearing lead damper. Eng. Mech. 2018, 35, 52–57, 67. [Google Scholar]
- NourEldin, M.; Naeem, A.; Kim, J. Life-cycle cost evaluation of steel structures retrofitted with steel slit damper and shape memory alloy–based hybrid damper. Adv. Struct. Eng. 2019, 22, 3–16. [Google Scholar] [CrossRef]
- Tian, L.; Gao, G.; Qiu, C.; Rong, K. Effect of hysteresis properties of shape memory alloy-tuned mass damper on seismic control of power transmission tower. Adv. Struct. Eng. 2019, 22, 1007–1017. [Google Scholar] [CrossRef]
- Yang, W.; Cao, S.; Liu, W.; Dang, X. Mechanical properties of a novel friction dampers incorporated with buckling restrained shape memory alloy bars. Adv. Bridge Eng. 2024, 5, 21. [Google Scholar] [CrossRef]
- Gur, S.; Xie, Y.; DesRoches, R. Seismic fragility analyses of steel building frames installed with superelastic shape memory alloy dampers: Comparison with yielding dampers. J. Intell. Mater. Syst. Struct. 2019, 30, 2670–2687. [Google Scholar] [CrossRef]
- Qiu, C.; Liu, J.; Du, X. Cyclic behavior of SMA slip friction damper. Eng. Struct. 2022, 250, 113407. [Google Scholar] [CrossRef]
- Qiu, C.; Liu, J.; Jiang, T.; Du, X. Tests of double-stage SMA slip friction damper. Eng. Struct. 2023, 288, 116171. [Google Scholar] [CrossRef]
- Wang, W.; Fang, C.; Liu, J. Large size superelastic SMA bars: Heat treatment strategy, mechanical property and seismic application. Smart Mater. Struct. 2016, 25, 075001. [Google Scholar] [CrossRef]
- Qiu, C.; Yang, Y.; Liu, J.; Jiang, T. Test of a novel self-centering brace using SMA slip friction damper. J. Constr. Steel Res. 2023, 204, 107872. [Google Scholar] [CrossRef]


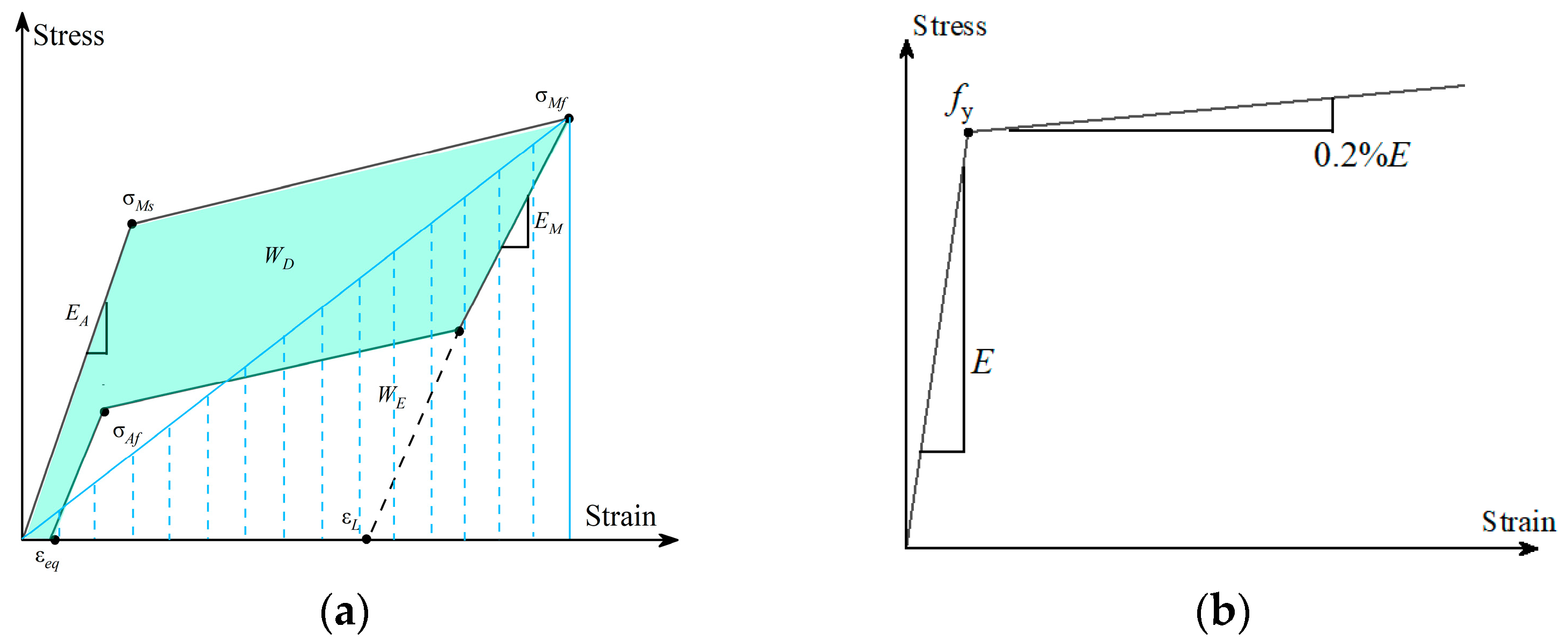


| σMs (MPa) | σMf (MPa) | σAs (MPa) | σAf (MPa) | EA (GPa) | EM (GPa) |
|---|---|---|---|---|---|
| 300 | 400 | 250 | 75 | 30 | 15 |
| Specimen ID | BRB | SMA Slip Friction Damper | ||
|---|---|---|---|---|
| Center Plate Width b (mm) | Overall Length L (mm) | Yield Section Length l (mm) | Number of SMA Bolts | |
| S1-B25 | 25 | 1600 | 1100 | 2 |
| S1-B55 | 55 | |||
| S1-B85 | 85 | |||
| Specimen ID. | Yield Displacement (mm) | Fmax (kN) | ksec (kN/mm) | WD (kJ) | ξeq (%) | Residual Displacement (mm) | |
|---|---|---|---|---|---|---|---|
| S1-B25 | 1.86 | 3.13 | 84.06 | 11.20 | 0.42 | 10.51 | 1.55 |
| S1-B55 | 1.94 | 4.78 | 79.06 | 5.27 | 0.74 | 9.97 | 0.28 |
| S1-B85 | 1.83 | 5.70 | 86.78 | 5.79 | 1.34 | 16.39 | 0.46 |
| Study Source | WD (kJ) | ξeq (%) |
|---|---|---|
| (This study) | 1.34 * | 16.39 |
| Alipour et al. 2017 [35] | ~0.023 | 11.60 |
| Liu et al. 2018 [36] | ~0.0051 | 4.22 |
| Yang et al. 2024 [39] | ~0.96 | ~12.00 |
| Qiu et al. 2022 [41] | ~0.30 | 16.40 |
| Qiu et al. 2023 [42] | ~0.23 | 15.80 |
| Qiu et al. 2023 [44] | ~2.00 | ~14.00 |
| Specimen ID | BRB | SMA Slip Friction Damper | Stiffness Ratio | Normalized Stiffness Ratio | ||
|---|---|---|---|---|---|---|
| b (mm) | Stiffness (kN/mm) | n | Stiffness (kN/mm) | |||
| S1-B25 | 25 | 42.5 | 1 | 7.23 | 5.88 | 2 |
| S1-B35 | 35 | 58.8 | 1 | 7.23 | 8.13 | 2.75 |
| S1-B45 | 45 | 74.7 | 1 | 7.23 | 10.33 | 3.5 |
| S1-B55 | 55 | 89.4 | 1 | 7.23 | 12.37 | 4.25 |
| S1-B65 | 65 | 104.5 | 1 | 7.23 | 14.45 | 5 |
| S1-B75 | 75 | 118.5 | 1 | 7.23 | 16.39 | 5.5 |
| S1-B85 | 85 | 132.9 | 1 | 7.23 | 18.38 | 6.25 |
| S1-B95 | 95 | 146.8 | 1 | 7.23 | 20.30 | 7 |
| S1-B105 | 105 | 159.8 | 1 | 7.23 | 22.10 | 7.5 |
| S2-B25 | 25 | 42.5 | 2 | 14.47 | 2.94 | 1 |
| S2-B35 | 35 | 58.8 | 2 | 14.47 | 4.06 | 1.375 |
| S2-B45 | 45 | 74.7 | 2 | 14.47 | 5.17 | 1.75 |
| S2-B55 | 55 | 89.4 | 2 | 14.47 | 6.18 | 2.125 |
| S2-B65 | 65 | 104.5 | 2 | 14.47 | 7.23 | 2.5 |
| S2-B75 | 75 | 118.5 | 2 | 14.47 | 8.20 | 2.75 |
| S2-B85 | 85 | 132.9 | 2 | 14.47 | 9.18 | 3.125 |
| S2-B95 | 95 | 146.8 | 2 | 14.47 | 10.15 | 3.5 |
| S2-B105 | 105 | 159.8 | 2 | 14.47 | 11.05 | 3.75 |
| Specimen ID | Peak Load | Secant Stiffness | ||||
|---|---|---|---|---|---|---|
| Simulated (kN) | Experimental (kN) | Error (%) | Simulated (kN/mm) | Experimental (kN/mm) | Error (%) | |
| S1-B25 | 39.69 | 84.06 | 52.8 | 5.45 | 11.21 | 51.4 |
| S1-B55 | 75.11 | 73.95 | 1.6 | 10.01 | 10.25 | 2.3 |
| S1-B85 | 78.05 | 69.72 | 11.9 | 10.43 | 9.94 | 4.9 |
| Specimen ID. | Stiffness Ratio | First-Stage Yield Force (kN) | First-Stage Yield Displacement (mm) | Second-Stage Yield Force (kN) | Second-Stage Yield Displacement (mm) | Maximum Force (kN) | Yield Sequence |
|---|---|---|---|---|---|---|---|
| S1-B25 | 5.88 | 36.79 | 4.05 | 68.12 | 11.68 | 79.47 | B → S |
| S1-B35 | 8.13 | 52.02 | 5.61 | 66.35 | 11.47 | 92.42 | B → S |
| S1-B45 | 10.33 | 66.50 | 7.34 | 69.20 | 8.36 | 102.68 | B → S |
| S1-B55 | 12.37 | 75.11 | 7.49 | 81.94 | 9.04 | 110.60 | S → B |
| S1-B65 | 14.45 | 76.06 | 7.40 | 98.96 | 10.74 | 117.91 | S → B |
| S1-B75 | 16.39 | 76.06 | 7.19 | 112.95 | 15.00 | 126.13 | S → B |
| S1-B85 | 18.38 | 78.05 | 7.48 | 94.46 | 10.00 | 135.33 | S → B |
| S1-B95 | 20.30 | 77.30 | 7.02 | 143.73 | 19.99 | 145.06 | S → B |
| S1-B105 | 22.10 | 77.48 | 6.90 | 146.03 | 17.69 | 152.14 | S → B |
| S2-B25 | 2.94 | 37.04 | 2.80 | - | - | 86.77 | B |
| S2-B35 | 4.06 | 51.12 | 3.78 | - | - | 114.75 | B |
| S2-B45 | 5.17 | 67.29 | 3.65 | 119.79 | 14.40 | 138.19 | B → S |
| S2-B55 | 6.18 | 78.98 | 4.95 | 120.4 | 14.44 | 154.87 | B → S |
| S2-B65 | 7.23 | 79.26 | 4.71 | 116.49 | 13.59 | 166.92 | B → S |
| S2-B75 | 8.20 | 92.06 | 5.06 | 128.16 | 8.71 | 177.86 | B → S |
| S2-B85 | 9.18 | 122.81 | 7.64 | 126.08 | 9.97 | 164.28 | B → S |
| S2-B95 | 10.15 | 88.07 | 4.57 | 129.61 | 7.47 | 192.40 | B → S |
| S2-B105 | 11.05 | 138.80 | 7.34 | 152.98 | 9.65 | 198.38 | S → B |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Wang, J.; Yao, D.; Zhou, P.; Zhao, S. SMA-Activated Double-Stage Yielding BRB: Experimental and FEM Insights. Buildings 2025, 15, 3225. https://doi.org/10.3390/buildings15173225
Huang H, Wang J, Yao D, Zhou P, Zhao S. SMA-Activated Double-Stage Yielding BRB: Experimental and FEM Insights. Buildings. 2025; 15(17):3225. https://doi.org/10.3390/buildings15173225
Chicago/Turabian StyleHuang, Huijie, Jiyang Wang, Dong Yao, Pinghuai Zhou, and Senlin Zhao. 2025. "SMA-Activated Double-Stage Yielding BRB: Experimental and FEM Insights" Buildings 15, no. 17: 3225. https://doi.org/10.3390/buildings15173225
APA StyleHuang, H., Wang, J., Yao, D., Zhou, P., & Zhao, S. (2025). SMA-Activated Double-Stage Yielding BRB: Experimental and FEM Insights. Buildings, 15(17), 3225. https://doi.org/10.3390/buildings15173225







