Fragility Analysis of Prefabricated RCS Hybrid Frame Structures Based on IDA
Abstract
1. Introduction
2. Frame Structure Model Design
2.1. Model Validation
2.2. Establishment of the Prefabricated RCS Hybrid Structure Model
3. Simulation Results and Analysis
3.1. IDA Analysis
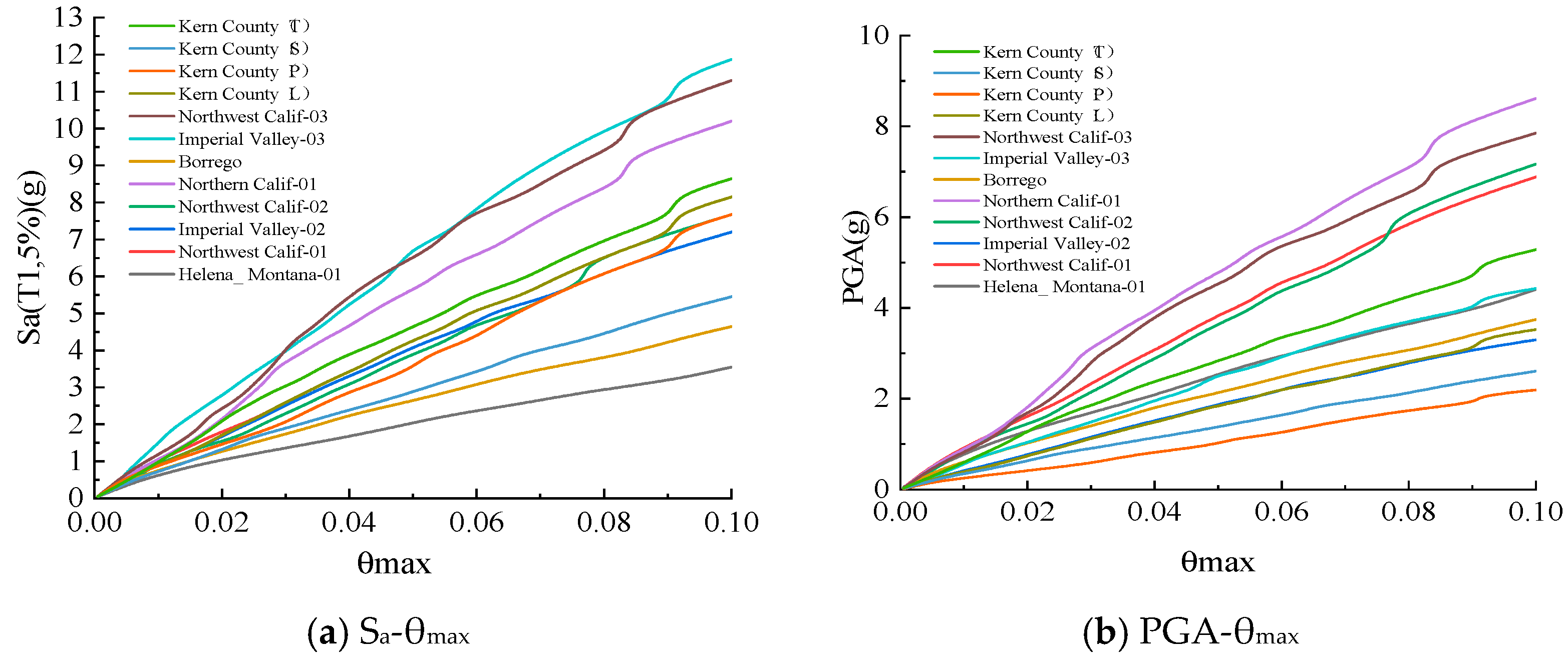
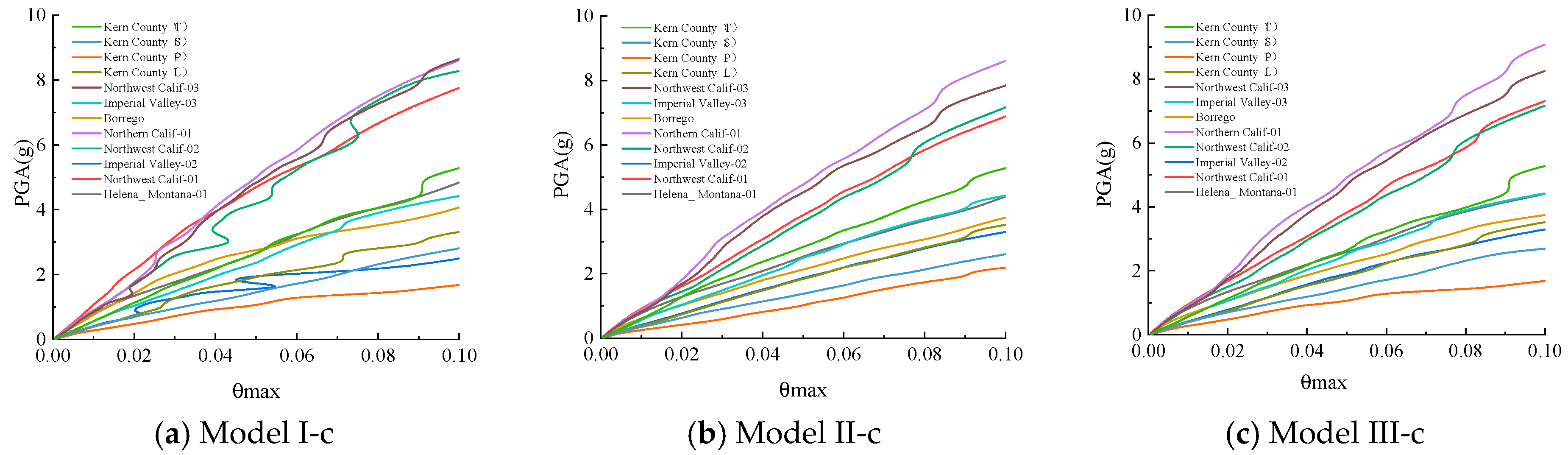
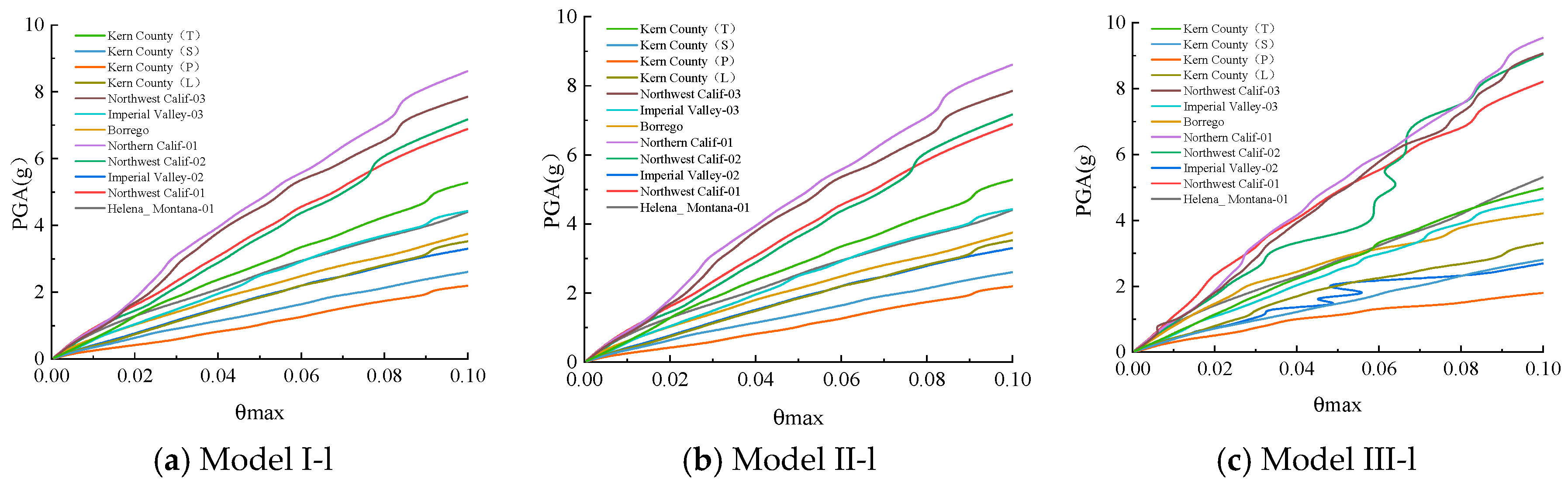
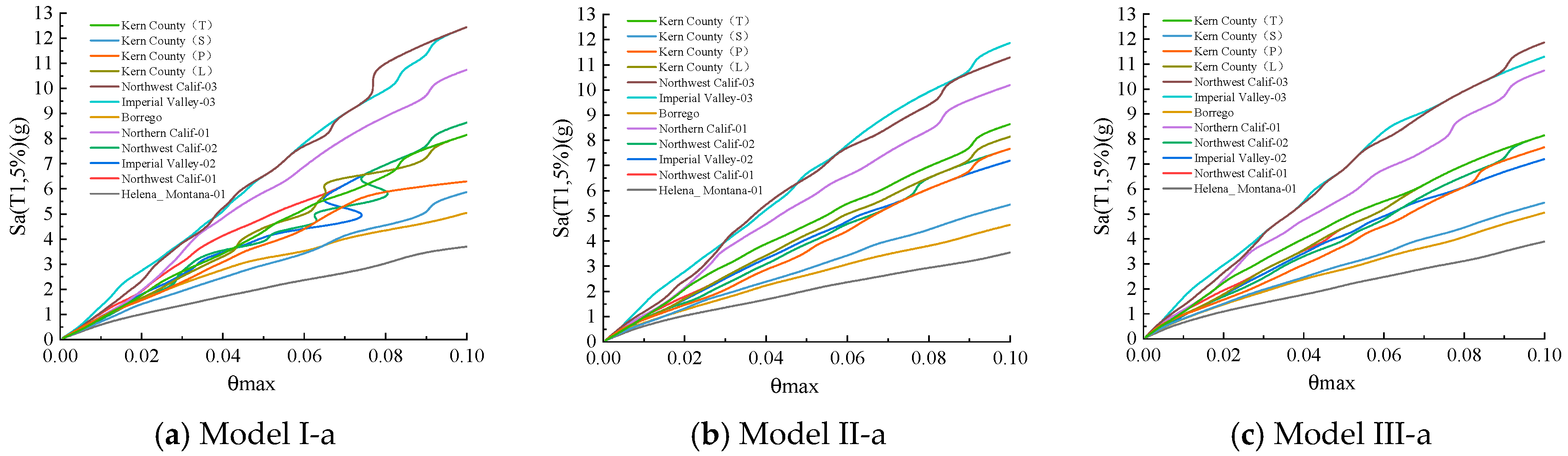
3.1.1. IDA Analysis Under a Single Ground Vibration
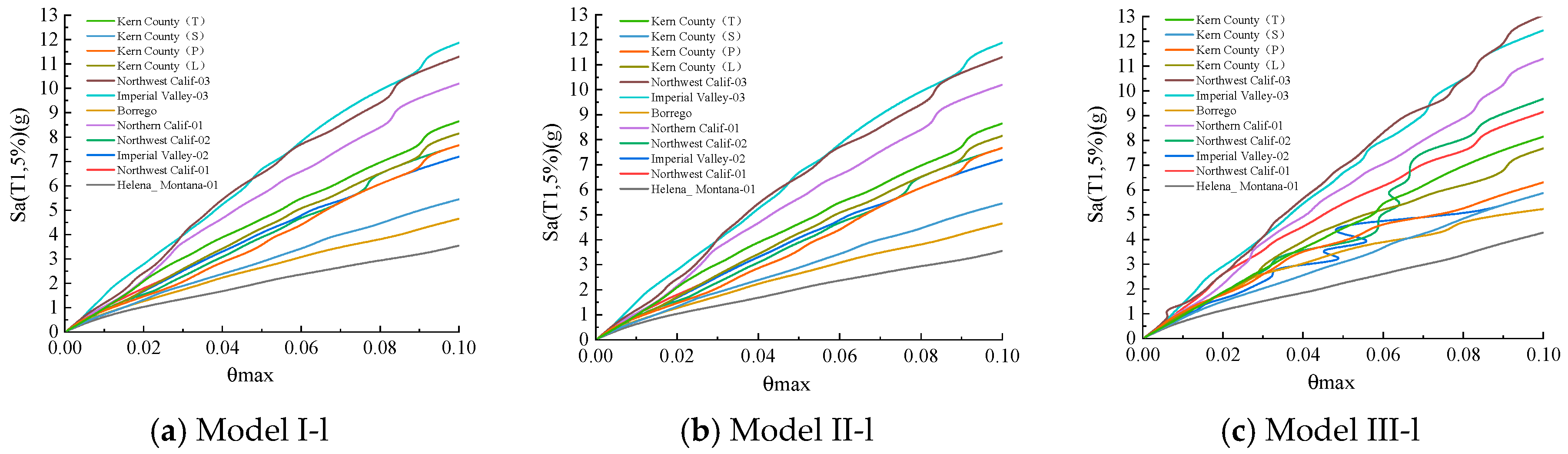
3.1.2. IDA Analysis Under Multiple Ground Vibration
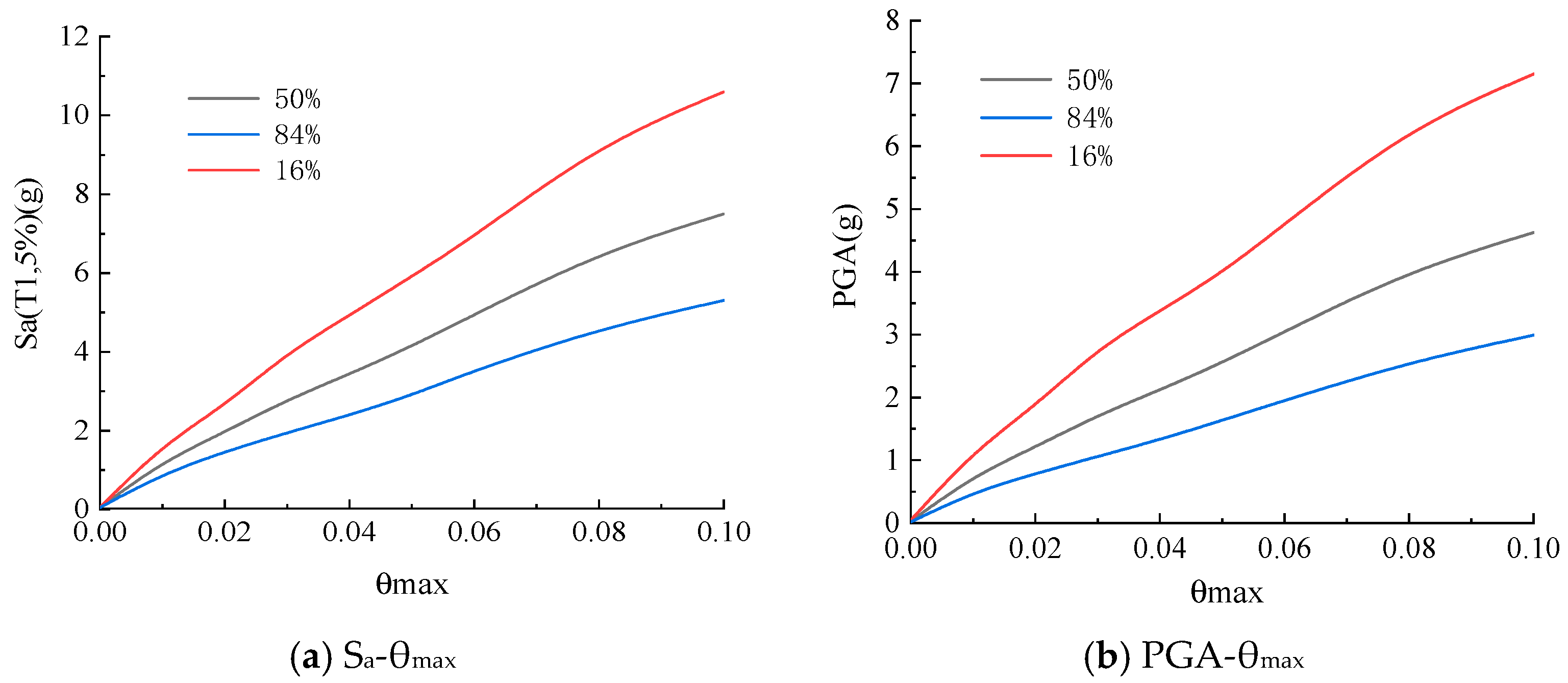
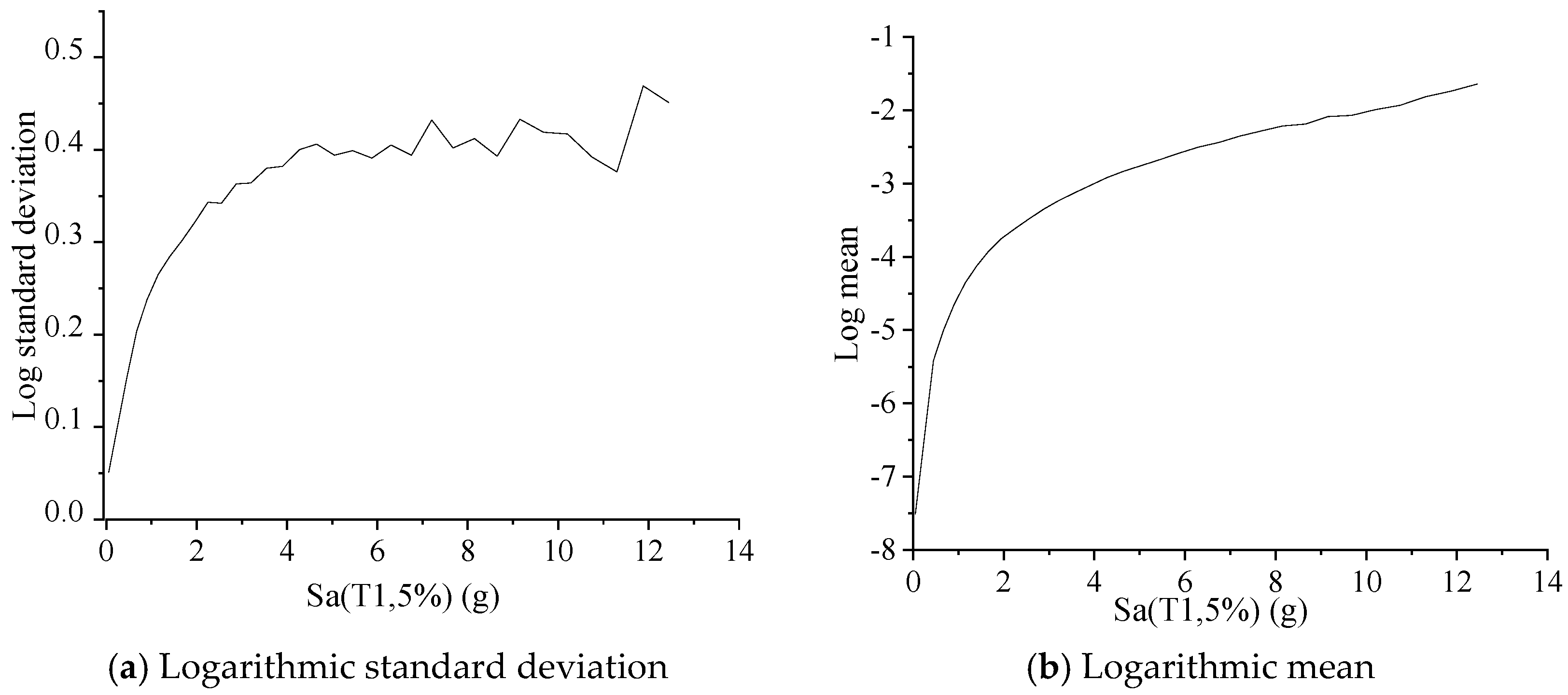
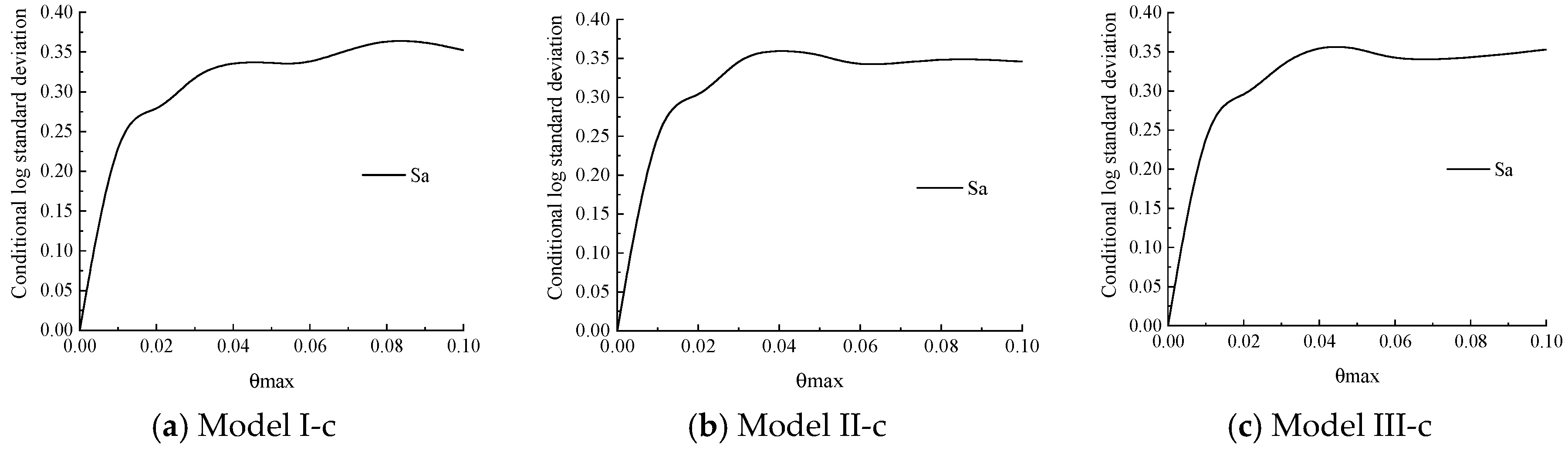
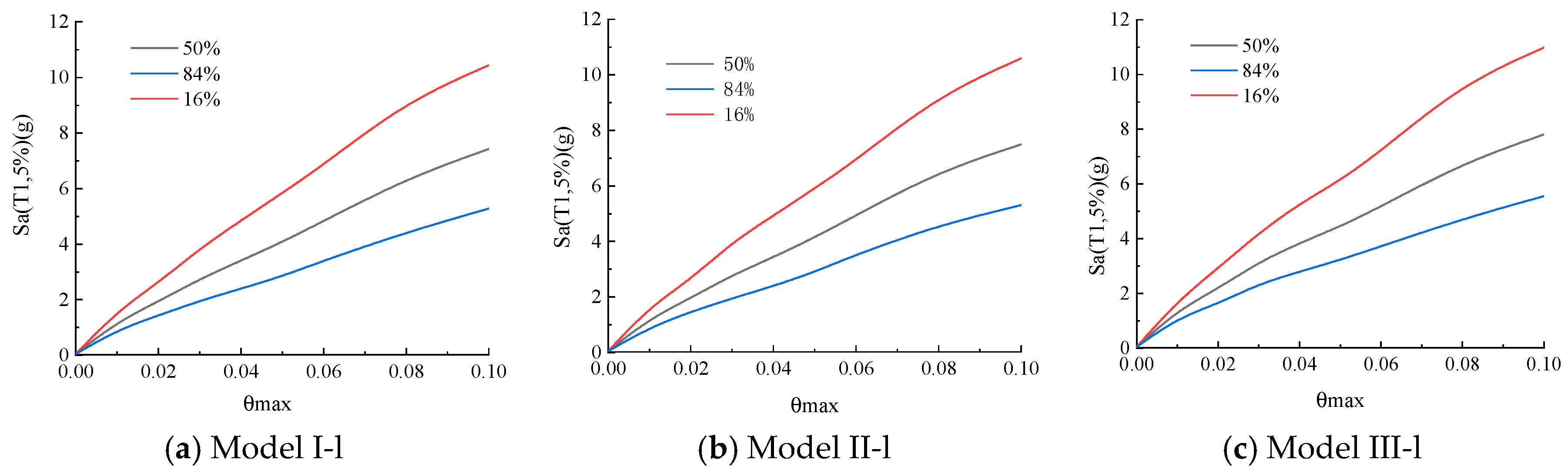
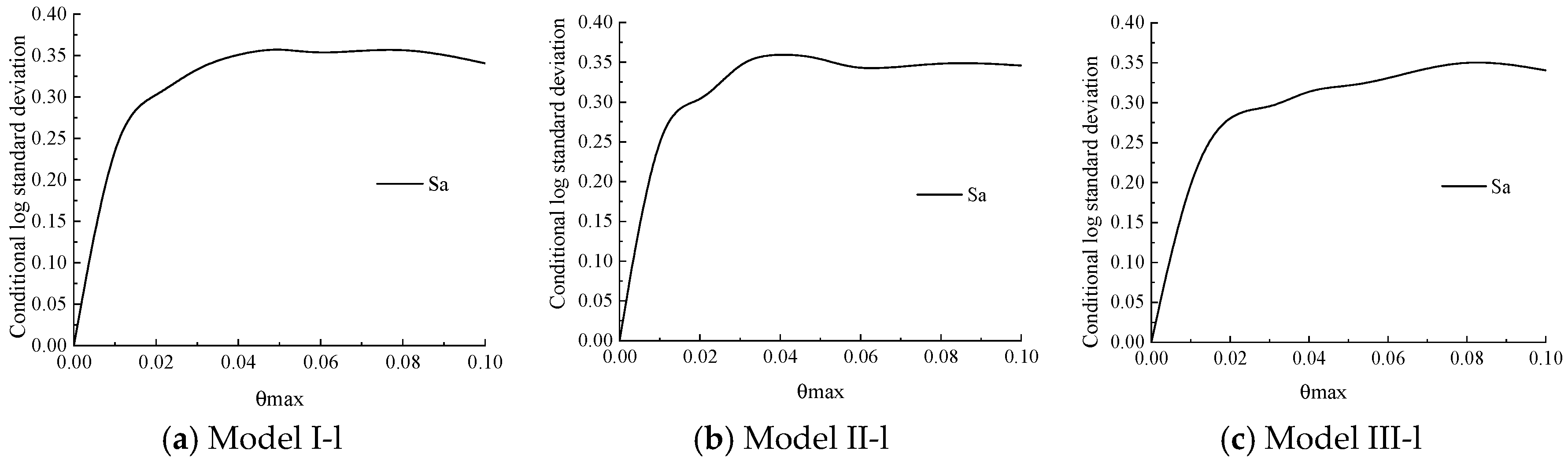
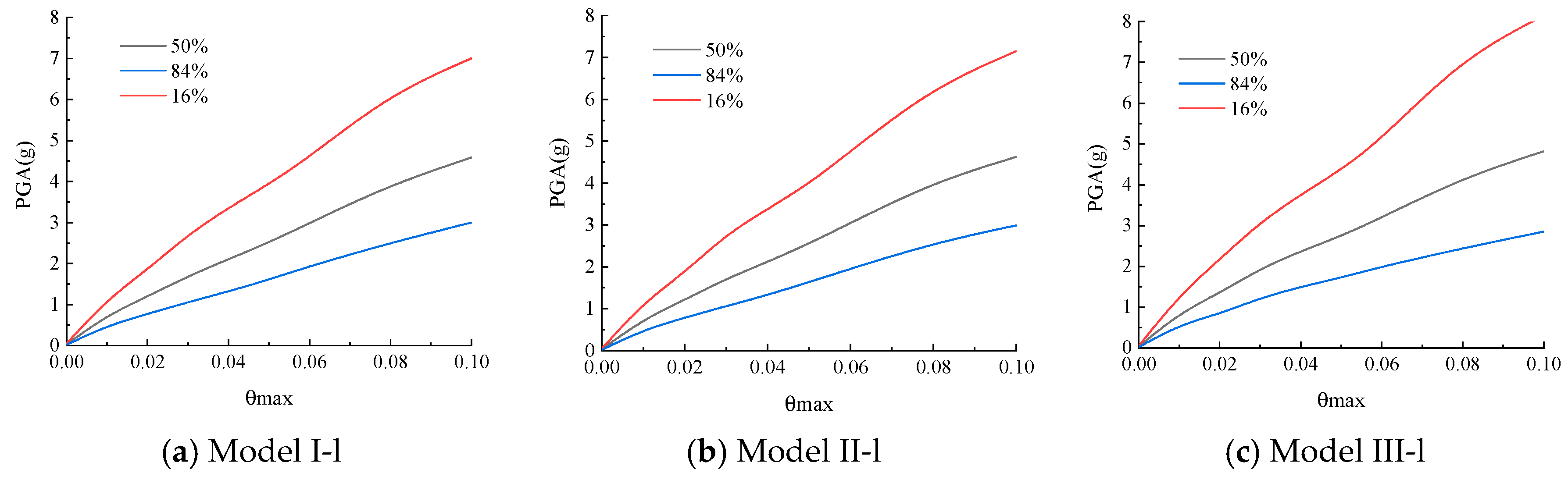
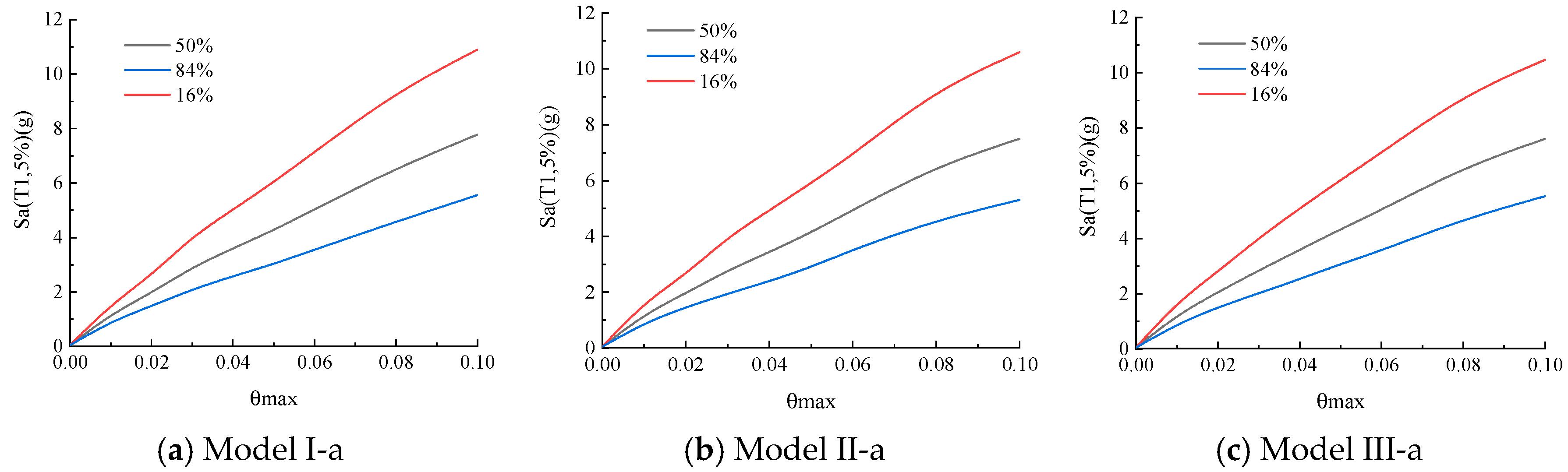
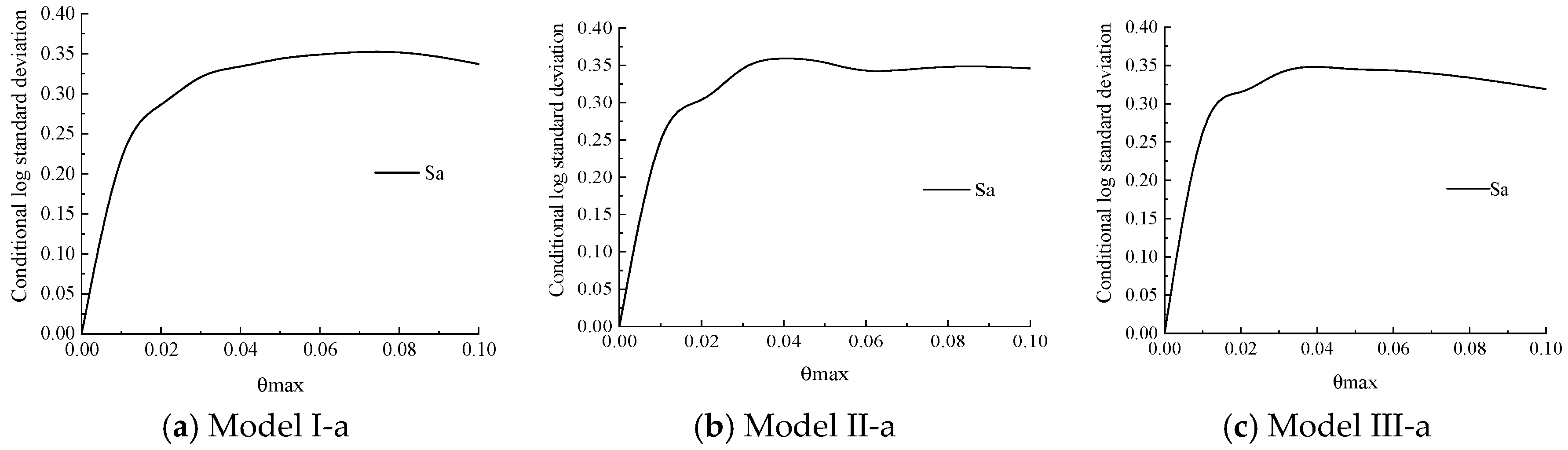
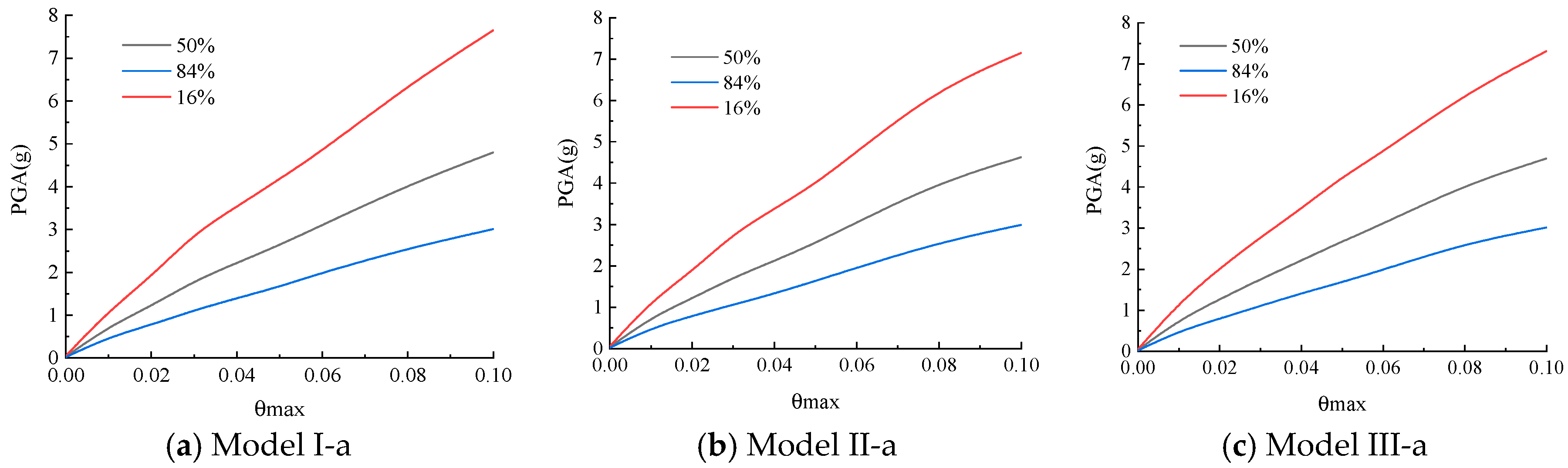
3.1.3. IDA Curve Cluster Statistics and Analysis
3.2. Seismic Fragility Analysis
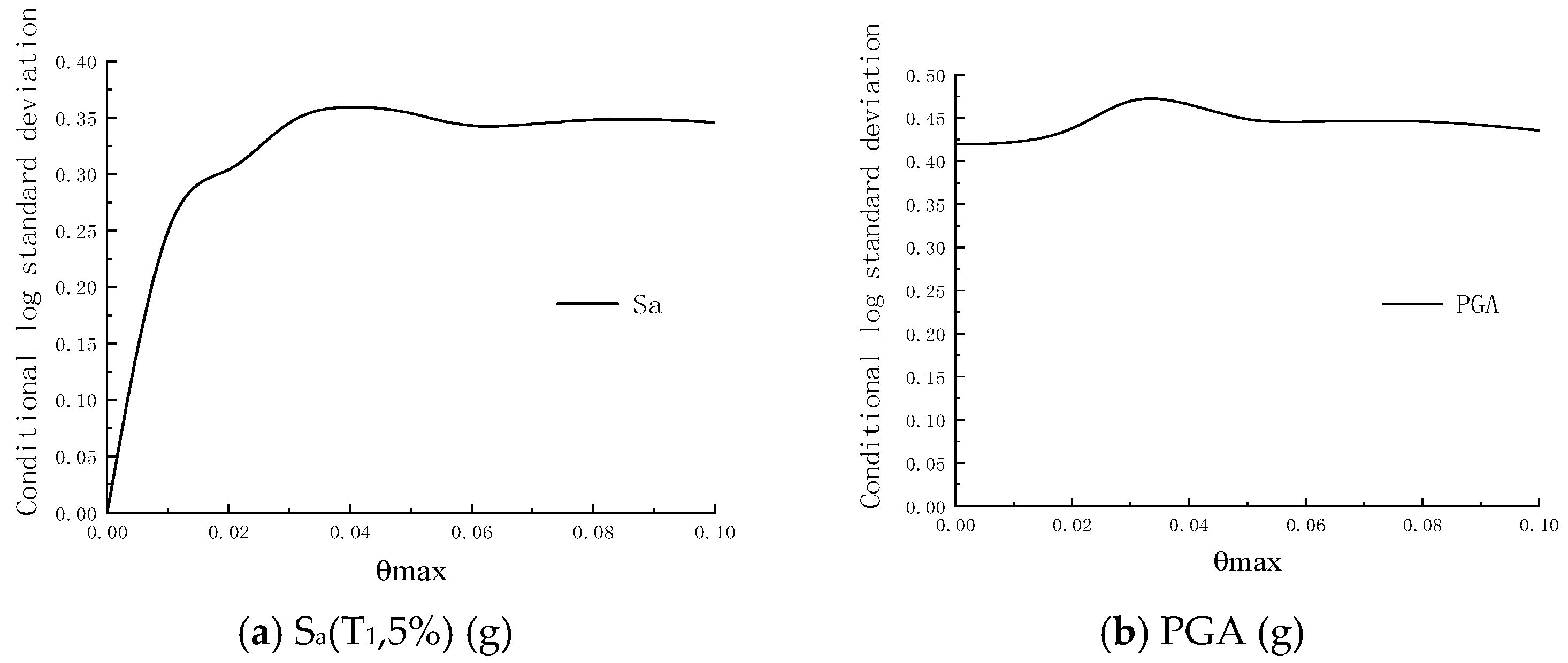
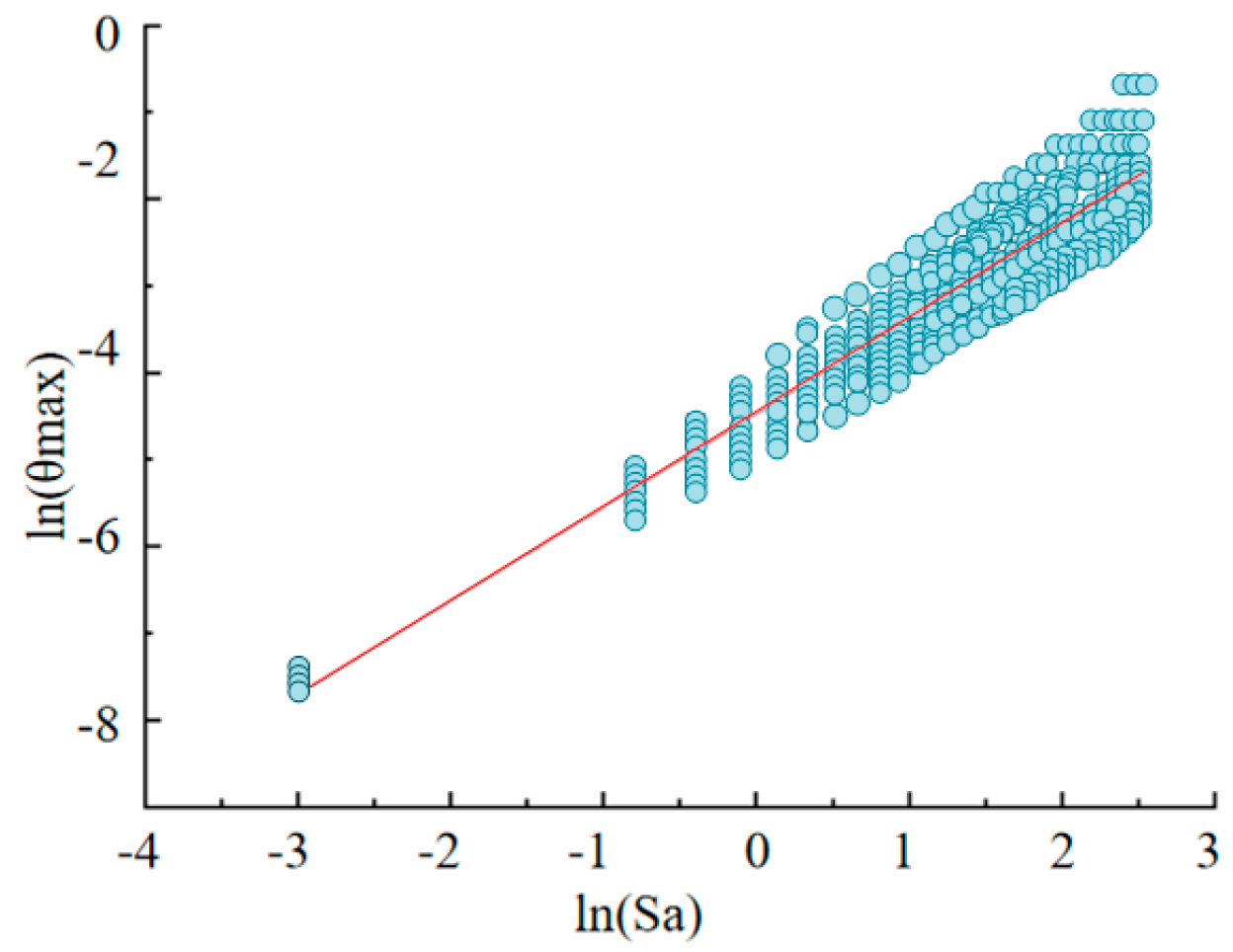
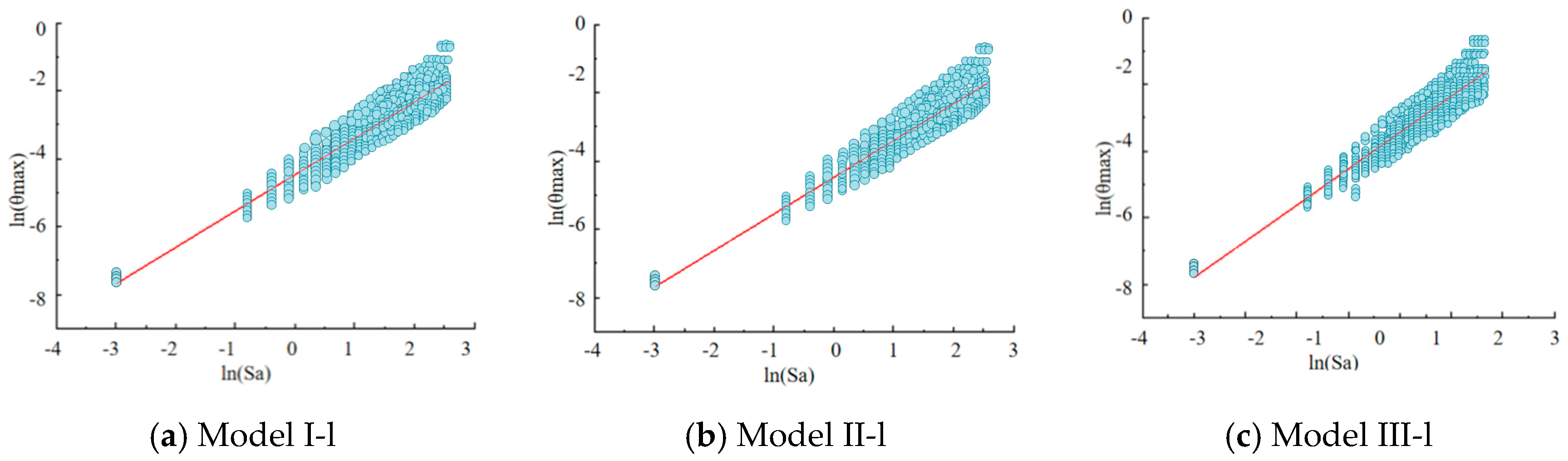
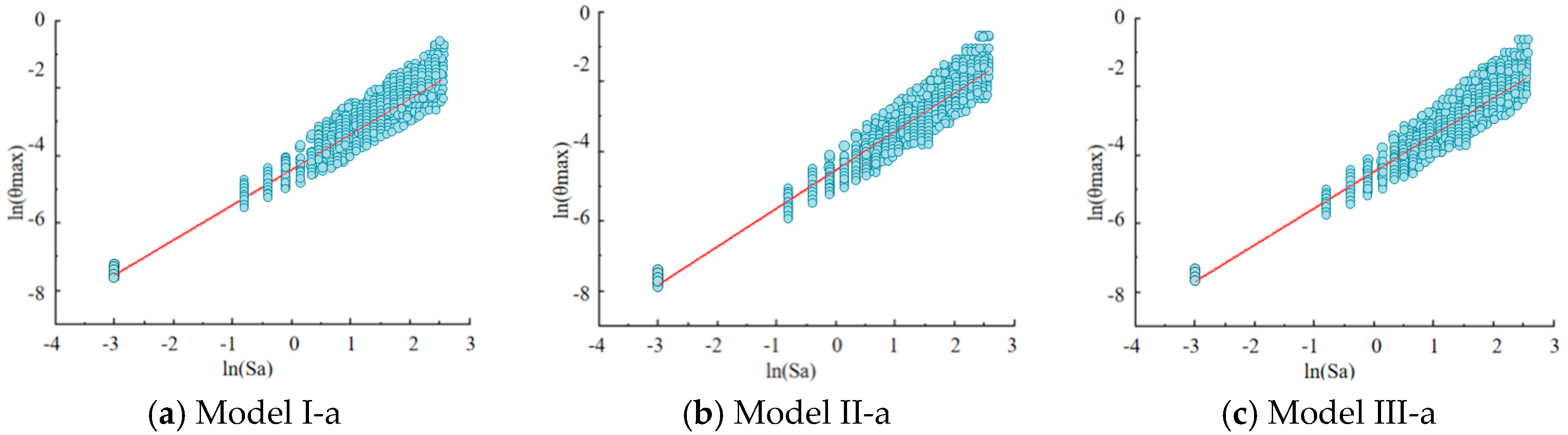
3.2.1. Seismic Probability Demand Model Parameterized by Sa
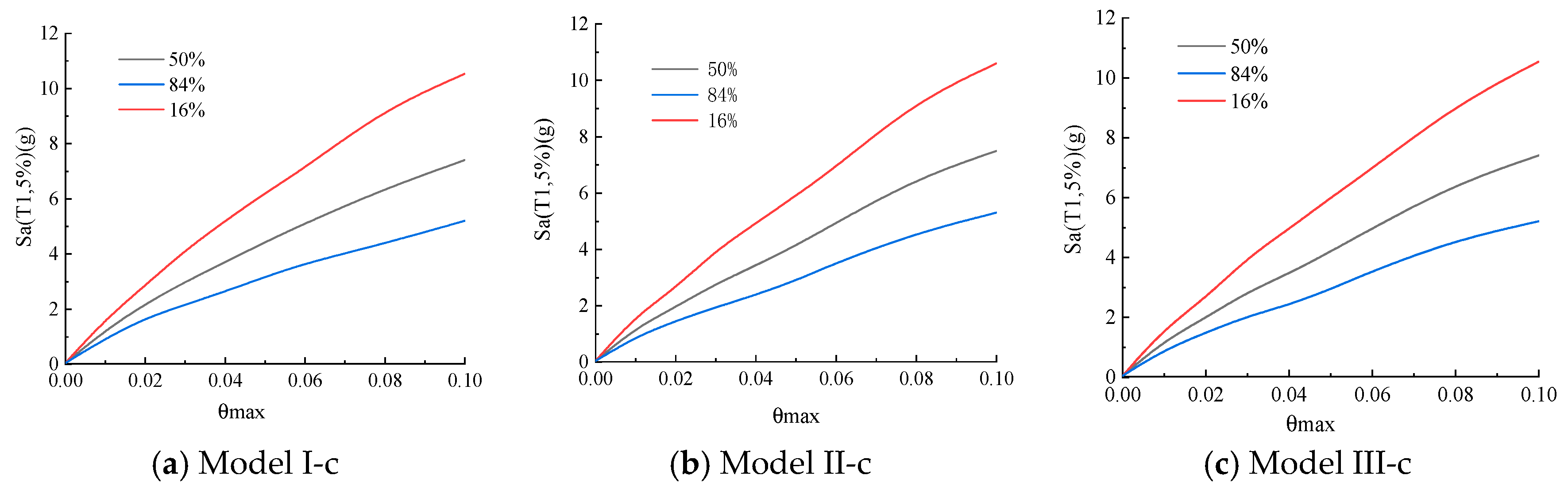
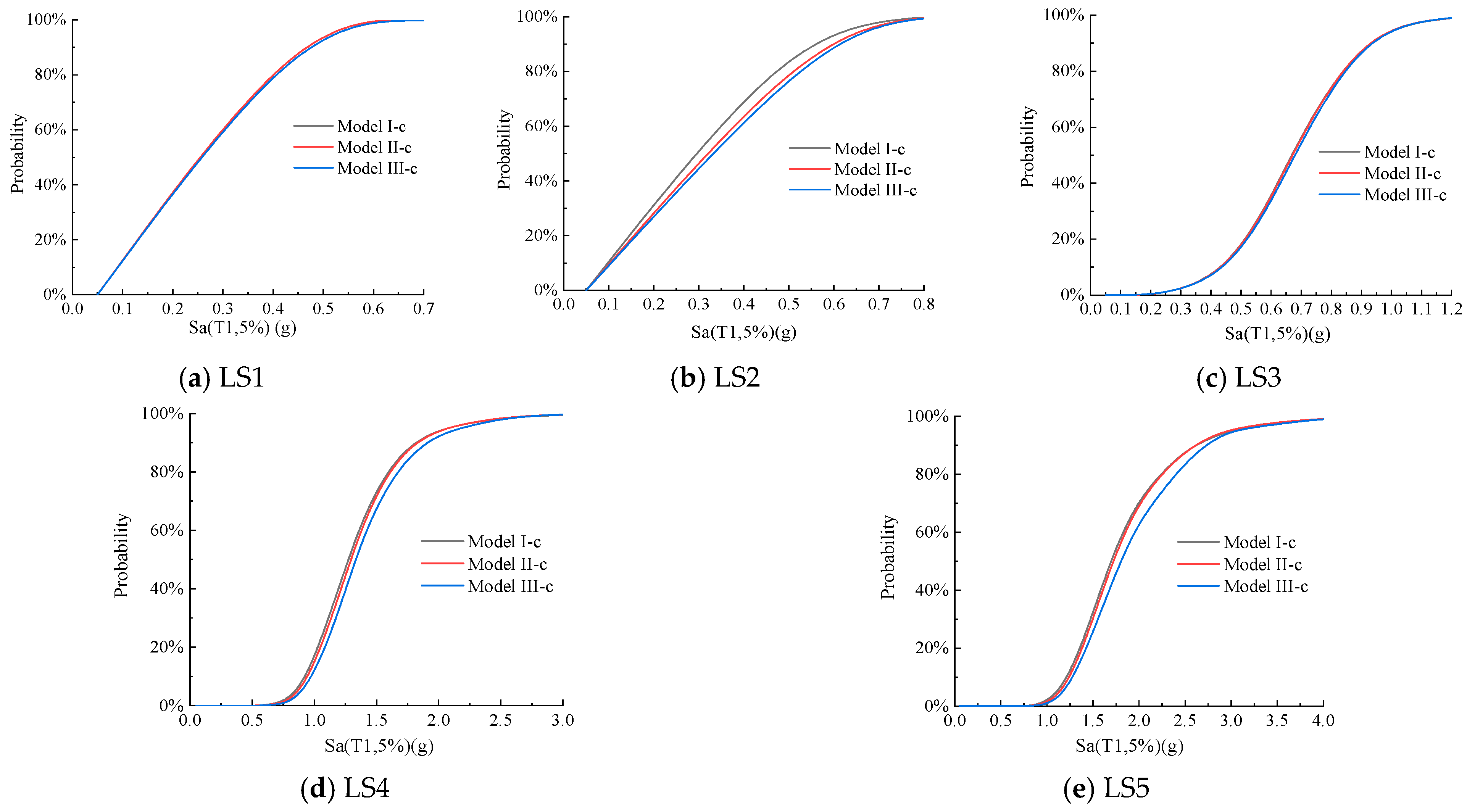
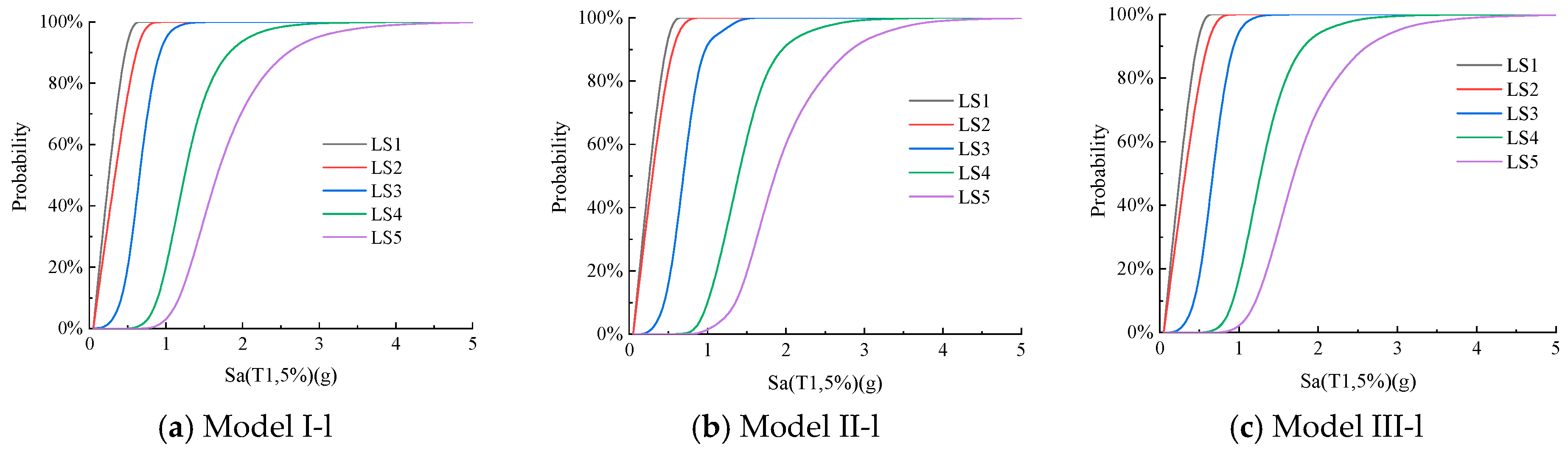
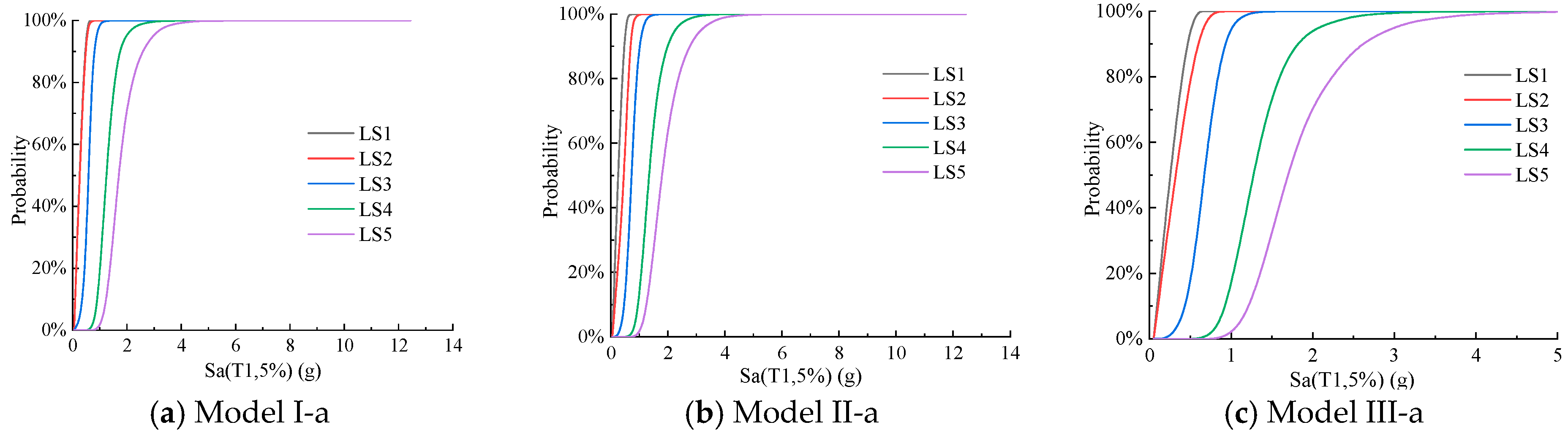
3.2.2. The Fragility Curves Parameterized by Sa
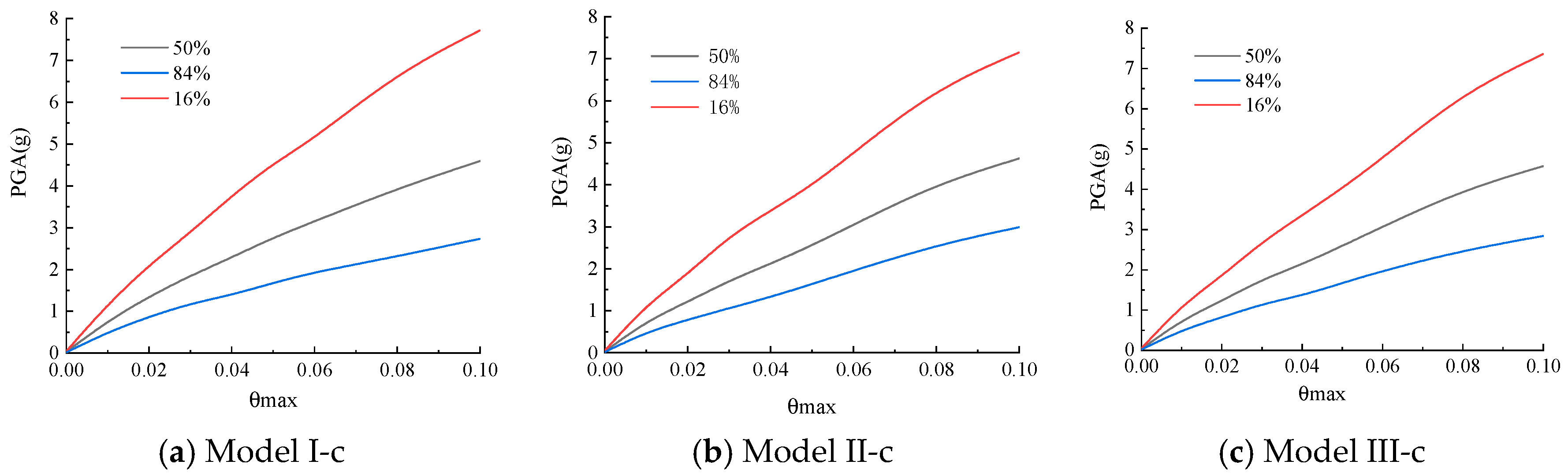
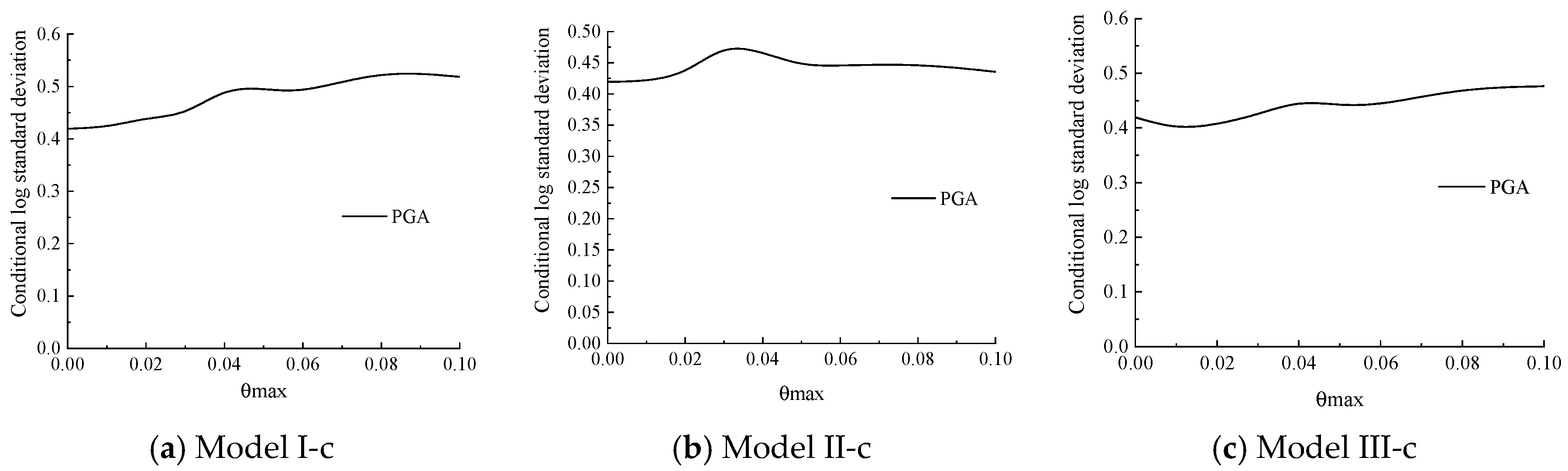
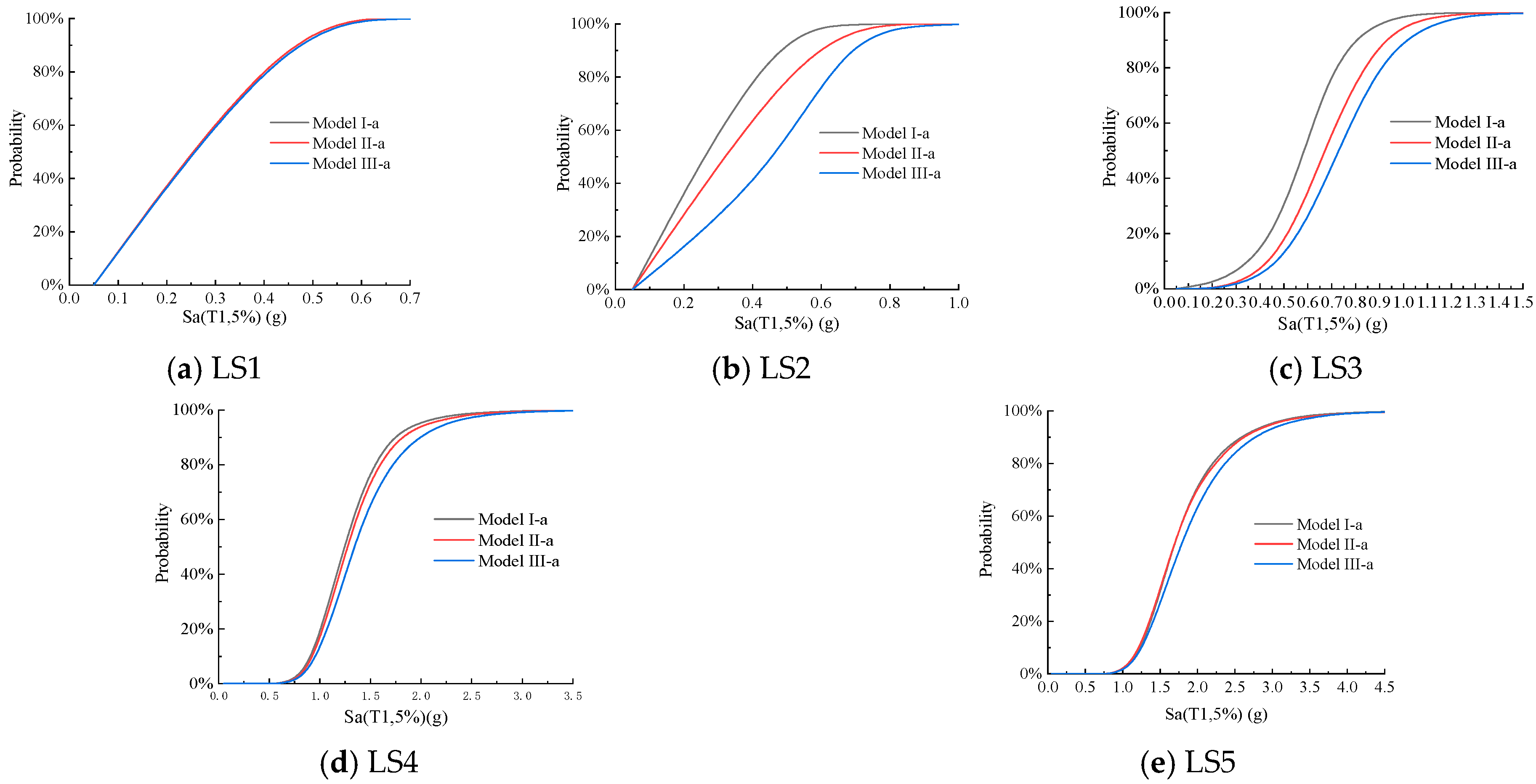
4. Influencing Factors of Seismic Fragility of Structure
4.1. Concrete Strength
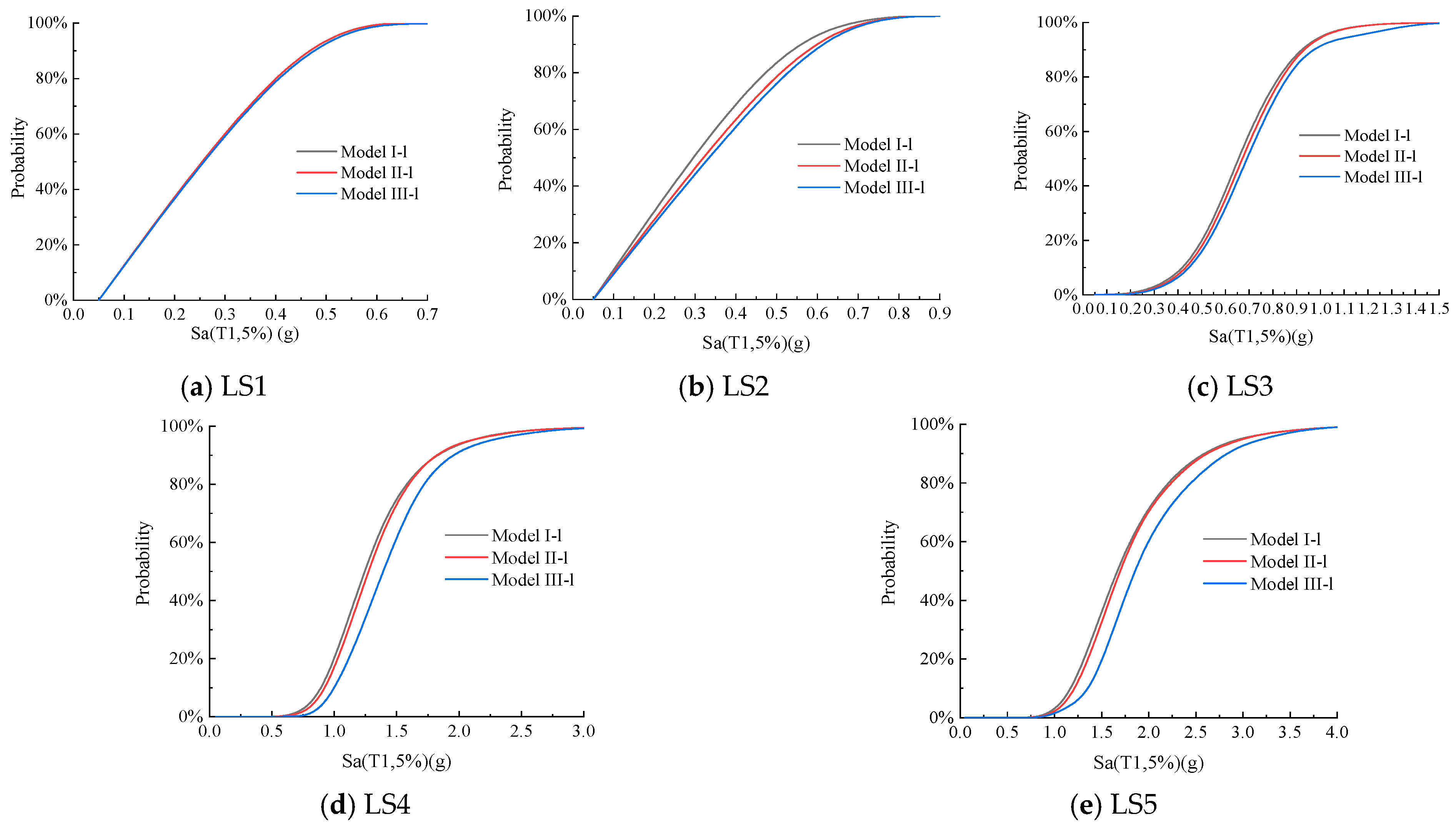
4.2. Longitudinal Tendon Strength
4.3. Axial Compression Ratio
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jian, Z. Study on Vulnerability Analysis and Seismic Risk of Reinforced Concrete Structures; Xi’an University of Architecture and Technology: Xi’an, China, 2010. [Google Scholar]
- Vamvatsikos, D.; Cornell, C.A. Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- Beitz, W.; Pahl, G.; Grote, K. Engineering design: A systematic approach. Mrs Bulletin. 1996, 71, 30. [Google Scholar]
- Fazli, H. Optimal performance-based seismic design of composite building frames with RC columns and steel beams. Int. J. Optim. Civ. Eng. 2019, 9, 611–628. [Google Scholar]
- Fan, D.; Jinjie, M.; Zhang, Z.; Wenye, T.; Yunlong, L. Seismic Performance and Replaceability Analysis of RCS Hybrid Frame with Energy Dissipation Beams; SSRN: Rochester, NY, USA; p. 5114963.
- Si, Q.; Pan, Z.; Zhu, Y.; Ying, H. Seismic design method based on limit state for prefabricated RCS frames. Structures 2024, 59, 105747. [Google Scholar] [CrossRef]
- Murari, K.; Kumar, P.C.A.; Shiradhonkar, S. Analytical investigations of seismic performance of different joint details for composite RCS frames. CE/papers 2023, 6, 46–52. [Google Scholar] [CrossRef]
- Dai, H.; Wang, B. Seismic Analysis of steel solid web girder-RC tubular column hybrid structure. Appl. Sci. 2018, 8, 2095. [Google Scholar] [CrossRef]
- Ghezeljeh, J.; Mirghaderi, S.R.; Kavei, S. Comparison of the seismic performance of Reinforced Concrete-Steel (RCS) frames with steel and reinforced concrete moment frames in low, mid, and high-rise structures. Steel Compos. Struct. 2024, 50, 249–263. [Google Scholar]
- Men, J.J.; Huo, W.W.; Lan, T.; Lei, M.K.; Shi, Q.X. Mechanical behavior and seismic design method of RCS hybrid frame structure with replaceable components. China Civ. Eng. J. 2020, 53, 42–52. [Google Scholar]
- Pan, Z.; Si, Q.; Zhu, Y.; Ying, H.; Wang, X.; Du, D. Seismic performance of prefabricated semi-rigid RCS structures. Structures 2022, 43, 1369–1379. [Google Scholar] [CrossRef]
- Cai, J.; Li, W. Seismic performance of demountable RCS frame structures. Earthq. Eng. Eng. Vib. 2025, 45, 205–216. (In Chinese) [Google Scholar]
- Bertero, V.V. Strength and deformation capacities of buildings under extreme environments. Struct. Eng. Struct. Mech. 1977, 53, 29–79. [Google Scholar]
- Vamvatsikos, D.; Cornell, C.A. Applied incremental dynamic analysis. Earthq. Spectra 2004, 20, 523–553. [Google Scholar] [CrossRef]
- Dolsek, M. Incremental dynamic analysis with consideration of modeling uncertainties. Earthq. Eng. Struct. Dyn. 2009, 38, 805–825. [Google Scholar] [CrossRef]
- Cheng, Y.; Dong, Y.R.; Bai, G.L.; Wang, Y.Y. IDA-based seismic fragility of high-rise frame-core tube structure subjected to multi-dimensional long-period ground motions. J. Build. Eng. 2021, 43, 102917. [Google Scholar] [CrossRef]
- Jouneghani, H.G.; Haghollahi, A. Assessing the seismic behavior of steel moment frames equipped by elliptical brace through incremental dynamic analysis (IDA). Earthq. Eng. Eng. Vib. 2020, 19, 435–449. [Google Scholar] [CrossRef]
- Fanaie, N.; Ezzatshoar, S. Studying the seismic behavior of gate braced frames by incremental dynamic analysis (IDA). J. Constr. Steel Res. 2014, 99, 111–120. [Google Scholar] [CrossRef]
- Wu, C.; Pan, Z.; Jin, C.; Meng, S. Evaluation of deformation-based seismic performance of RECC frames based on IDA method. Eng. Struct. 2020, 211, 110499. [Google Scholar] [CrossRef]
- Ren, H.; Tian, Q.H.; Zhang, W.C.; Zhou, C.F.; Shao, D. Seismic fragility analysis of reinforced concrete frame structures based on IDA method. Build. Struct. 2019, 49, 350–355. (In Chinese) [Google Scholar]
- Li, G.; Dong, Z.Q.; Li, H.N.; Yang, Y.B. Seismic collapse analysis of concentrically-braced frames by the IDA method. Adv. Steel Constr. 2017, 13, 273–292. [Google Scholar]
- Xu, W.; Zhao, Y.; Yang, W.; Yu, D.; Zhao, Y. Seismic fragility analysis of RC frame structures based on IDA analysis and machine learning. Structures 2024, 65, 106774. [Google Scholar] [CrossRef]
- Liu, X.; Xu, C. IDA-Based Seismic fragility analysis of a concrete-filled square tubular frame. Buildings 2024, 14, 2686. [Google Scholar] [CrossRef]
- Qiu, Y.C.; Zhou, J.Z.; Yang, G.X. Ductility analysis of RC frames based on IDA. J. Hefei Univ. Technol. (Nat. Sci. Ed.) 2015, 38, 377–382. (In Chinese) [Google Scholar]
- Li, J.; Chen, P.; Wei, W.; Li, Q.N. Seismic behavior research of steel plate hoop-bolt prefabricated column confined by high-strength composite spiral stirrups. Ind. Constr. 2014, 44, 7–10. (In Chinese) [Google Scholar]
- Huang, S.M.; Wang, Y.Y.; Dai, G.Y.; Fu, S.C.; Luo, K.H.; Li, X.J.; Ke, C.H.; Yu, Y.Q.; Lou, Y.; Xue, H.L. Seismic Design Code for Buildings (GB 50011-2016). China Build. Ind. Press 2016, 8. [Google Scholar]
- Mander, J.B. Theoretical Stress-Strain Model or for Confined Concrete. J. Struct. Devision 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Azarbakht, A. Minimum magnitude boundaries in probabilistic seismic hazard analysis: An insight from structural engineering. Bull. Earthq. Eng. 2024, 22, 5299–5320. [Google Scholar] [CrossRef]
- Applied Technology Council; National Earthquake Hazards Reduction Program (US). Seismic Performance Assessment of Buildings; Federal Emergency Management Agency: Washington, DC, USA, 2012.
- Iervolino, I.; Cornell, C.A. Record Selection for Nonlinear Seismic Analysis of Structures. Earthq. Spectra 2005, 21, 685–713. [Google Scholar] [CrossRef]
- Baker, J.W. Efficient analytical fragility function fitting using dynamic structural analysis. Earthq. Spectra 2015, 31, 579–599. [Google Scholar] [CrossRef]
- Kazemi, F.; Asgarkhani, N.; Jankowski, R. Machine learning-based seismic fragility and seismic vulnerability assessment of reinforced concrete structures. Soil Dyn. Earthq. Eng. 2023, 166, 107761. [Google Scholar] [CrossRef]
- Wang, L. Effectiveness of New Ground Motion Intensity Measures Based on IDA and Seismic Fragility Analysis of Structures; Lanzhou University of Technology: Lanzhou, China, 2020. [Google Scholar]
- Men, J.J.; Zhou, T.T.; Zhang, Y.R.; Shi, Q.X. Performance-based seismic design method and quantitative index for reinforced concrete column-steel beam composite frame structures. J. Build. Struct. 2015, 36, 28–34. (In Chinese) [Google Scholar]
- FEMA-356; Prestandard and Commentary for the Seismic Rehabilitation of Buildings. Federal Emergency Management Agency: Washington, DC, USA, 2000.
- Zhao, K.D.; Liu, L.X.; Qiu, H.X.; Huang, X.K.; Zhu, A.P.; Wang, X.F.; Fu, J.P.; Ke, C.H.; Zhang, F.X.; Zuo, J. Code for design of concrete structures (GB 50010-2010). Constr. Sci. Technol. 2015, 3. [Google Scholar]
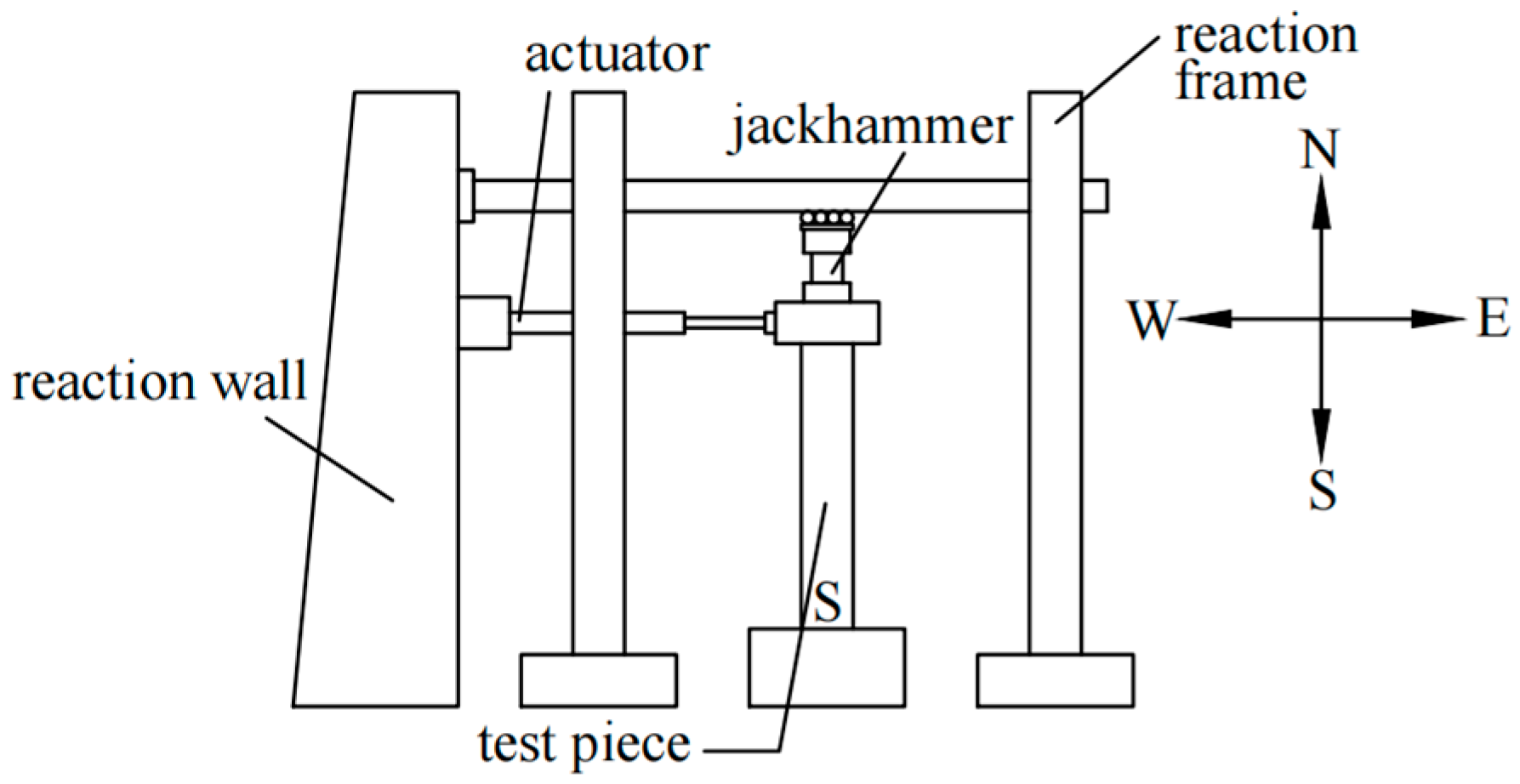



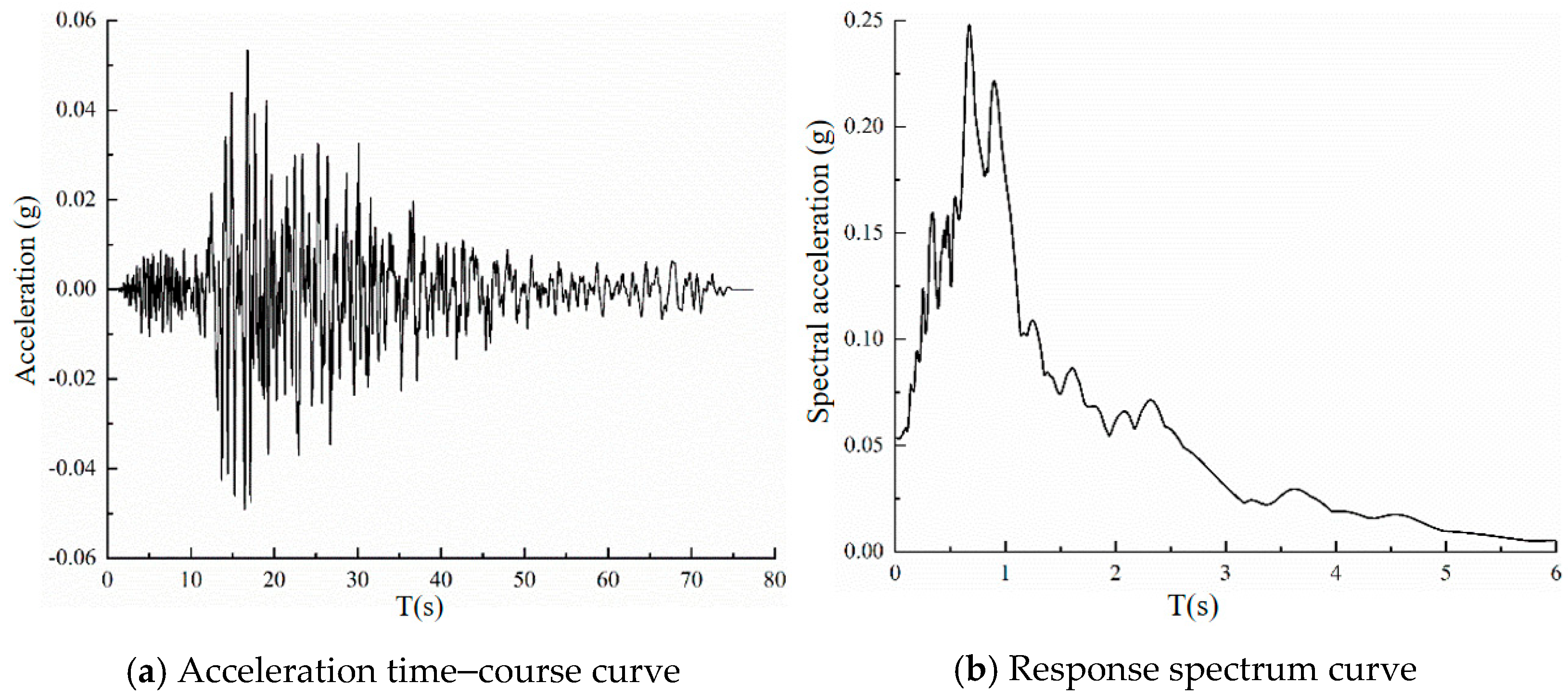
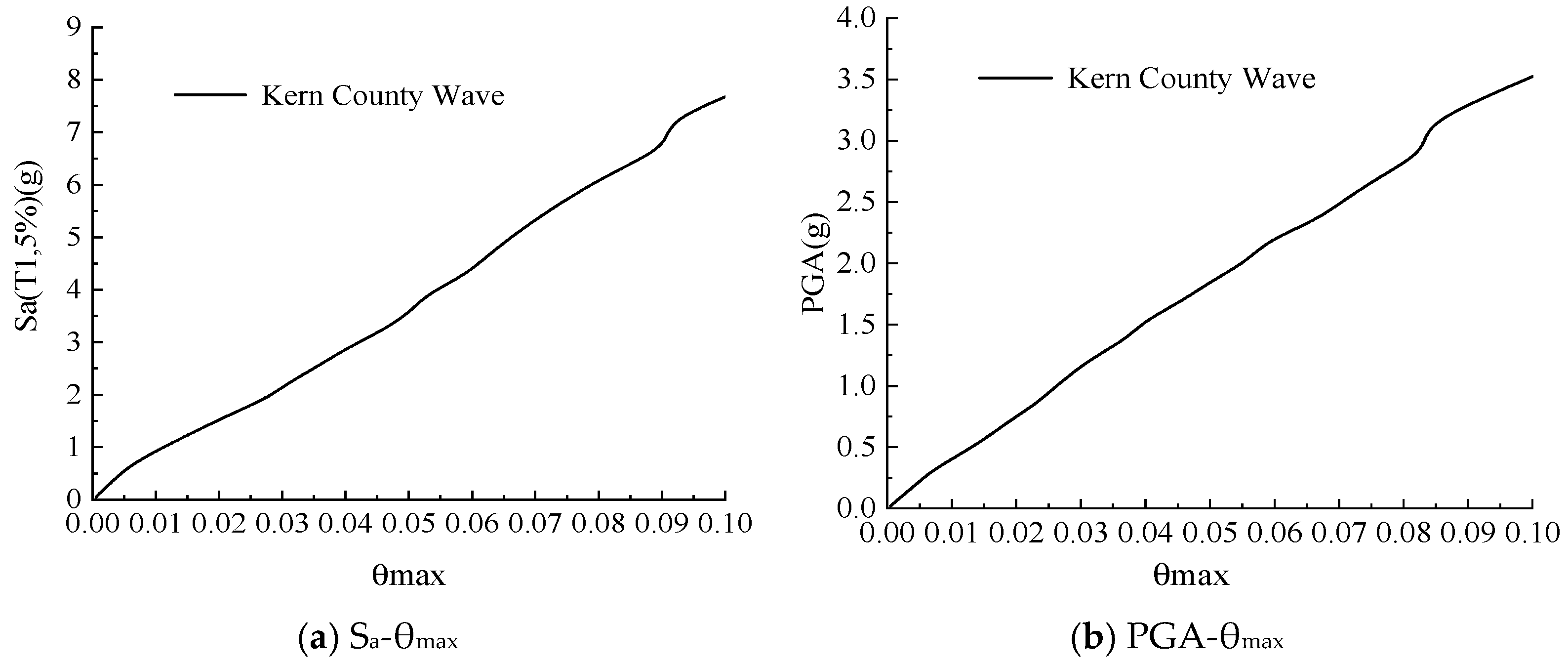







| Specimen Number | Ratio of Axial Compression Stress to Strength | Axial Pressure (kN) | Shear-span Ratio | Maximum Horizontal Load (kN) | Loading Method |
|---|---|---|---|---|---|
| PRCC-01 | 0.2 | 857.6 | 4.5 | 249.3 | low-cyclic recurrence |
| Cycle Number | Displacement (mm) | Test Value (kN) | Value of Simulation (kN) | Difference (%) |
|---|---|---|---|---|
| 1 | 14.57 | 223.15 | 208.13 | 0.15 |
| 2 | 22.83 | 234.57 | 220.43 | 0.14 |
| 3 | 35.18 | 210.13 | 198.79 | 0.11 |
| 4 | 47.96 | 203.35 | 186.55 | 0.16 |
| 5 | 59.17 | 187.65 | 175.34 | 0.12 |
| 6 | 75.62 | 177.48 | 164.21 | 0.13 |
| Modal Order | Period (s) | Modal Shapes |
|---|---|---|
| 1 | 0.7767 | Y-direction translational motion |
| 2 | 0.2190 | X-direction translational motion |
| 3 | 0.1840 | Torsion |
| Serial Number | Step Size Calculation Method | Sa(T1,5%)/g | Amplitude Modulation Index λ | |
|---|---|---|---|---|
| 1 | 0.05 | 0.2680 | 0.0006 | |
| 2 | 0.05 + 0.4 | 0.45 | 2.4121 | 0.0039 |
| 3 | 0.45 + 0.4 + 0.05 | 0.90 | 4.8242 | 0.0095 |
| 4 | 0.90 + 0.4 + 2 × 0.05 | 1.40 | 7.5043 | 0.0179 |
| 5 | 1.40 + 0.4 + 3 × 0.05 | 1.95 | 10.4524 | 0.0278 |
| 6 | 1.95 + 0.4 + 4 × 0.05 | 2.55 | 13.6685 | 0.0357 |
| 7 | 2.55 + 0.4 + 5 × 0.05 | 3.20 | 17.1527 | 0.0455 |
| 8 | 3.20 + 0.4 + 6 × 0.05 | 3.90 | 20.9048 | 0.0526 |
| 9 | 3.90 + 0.4 + 7 × 0.05 | 4.65 | 24.9250 | 0.0625 |
| 10 | 4.65 + 0.4 + 8 × 0.05 | 5.45 | 29.2131 | 0.0714 |
| 11 | 5.45 + 0.4 + 9 × 0.05 | 6.30 | 33.7693 | 0.0833 |
| 12 | 6.30 + 0.4 + 10 × 0.05 | 7.20 | 38.5935 | 0.0909 |
| 13 | 7.20 + 0.4 + 11 × 0.05 | 8.15 | 43.6857 | 0.1111 |
| 14 | (0.45 + 0.90)/2 | 0.675 | 3.6181 | 0.0064 |
| 15 | (0.90 + 1.40)/2 | 1.15 | 6.1642 | 0.0137 |
| 16 | (1.40 + 1.95)/2 | 1.675 | 8.9783 | 0.0227 |
| 17 | (1.95 + 2.55)/2 | 2.25 | 12.0605 | 0.0313 |
| 18 | (2.55 + 3.20)/2 | 2.875 | 15.4106 | 0.0400 |
| 19 | (3.20 + 3.90)/2 | 3.55 | 19.0287 | 0.0500 |
| 20 | (3.90 + 4.65)/2 | 4.275 | 22.9149 | 0.0588 |
| 21 | (4.65 + 5.45)/2 | 5.05 | 27.0690 | 0.0667 |
| 22 | (5.45 + 6.30)/2 | 5.875 | 31.4912 | 0.0769 |
| 23 | (6.30 + 7.20)/2 | 6.75 | 36.1814 | 0.0909 |
| 24 | (7.20 + 8.15)/2 | 7.675 | 41.1396 | 0.10000 |
| Performance Level | Normal Operation (LS1) | Temporary Use (LS2) | Use After Repair (LS3) | Life Safety (LS4) | Preventing Collapse (LS5) |
|---|---|---|---|---|---|
| Limit value of inter-story displacement angle | 1/400 | 1/250 | 1/150 | 1/70 | 1/50 |
| Model Number | Model I-c | Model II-c | Model III-c |
|---|---|---|---|
| Concrete strength class | C30 | C40 | C50 |
| Average concrete strength (MPa) | 33.05 | 42.51 | 52.33 |
| Modulus of elasticity (MPa) | 3.30 × 104 | 3.51 × 104 | 3.67 × 104 |
| Model Number | Model I-l | Model II-l | Model III-l |
|---|---|---|---|
| Strength grade of longitudinal reinforcement | HRB335 | HRB400 | HRB500 |
| Average strength of longitudinal reinforcement (MPa) | 378.60 | 452.05 | 565.07 |
| Model Number | Model I-a | Model II-a | Model III-a |
|---|---|---|---|
| Beam section dimension | H400 × 146 × 14.5 × 14.5 | ||
| Column section dimension | 500 × 500 | 600 × 600 | 700 × 700 |
| Maximal axial compression ratio | 0.57 | 0.38 | 0.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Sun, G.; Wang, X.; Zhang, X.; Miedziałowski, C. Fragility Analysis of Prefabricated RCS Hybrid Frame Structures Based on IDA. Buildings 2025, 15, 3207. https://doi.org/10.3390/buildings15173207
Wang Y, Sun G, Wang X, Zhang X, Miedziałowski C. Fragility Analysis of Prefabricated RCS Hybrid Frame Structures Based on IDA. Buildings. 2025; 15(17):3207. https://doi.org/10.3390/buildings15173207
Chicago/Turabian StyleWang, Yuliang, Guocan Sun, Xuyue Wang, Xinyue Zhang, and Czesław Miedziałowski. 2025. "Fragility Analysis of Prefabricated RCS Hybrid Frame Structures Based on IDA" Buildings 15, no. 17: 3207. https://doi.org/10.3390/buildings15173207
APA StyleWang, Y., Sun, G., Wang, X., Zhang, X., & Miedziałowski, C. (2025). Fragility Analysis of Prefabricated RCS Hybrid Frame Structures Based on IDA. Buildings, 15(17), 3207. https://doi.org/10.3390/buildings15173207






