Abstract
In China, most of the ancient wooden structure mortise and tenon buildings, under the long-term upper load, have columns with surface surfaces that have varying degrees of damage, which need to be repaired and strengthened urgently, but the theory related to CFRP, mortise size, and pre-damage simulation still needs to be deeply studied. To investigate the effects of CFRP reinforcement layers, cross-sectional area of concealed tenons as the projected area after installation, and tenon engagement length as the axial length after installation on the axial compressive mechanical properties of pre-damaged quad-segment spliced Pinus sylvestris var. mongolia composited wooden columns, axial compression failure tests were conducted on 10 specimens following pre-damage simulation and CFRP strengthening. The experimental program yielded comprehensive data, including observations, mechanical analyses, load-displacement curves, load-strain curves, ultimate load-bearing capacities, ductility coefficients, and stiffness values. The results demonstrate that with consistent tenon cross-sectional area and engagement length, increasing CFRP layers from 1 to 3 raises the ultimate bearing capacity from 472.3 kN to 620.3 kN and improves the ductility coefficient from 4.67 to 7.95, clearly indicating that CFRP reinforcement significantly enhances axial compressive performance while effectively mitigating brittle failure. When maintaining constant CFRP layers and tenon cross-sectional area, extending the tenon engagement length from 30 mm to 90 mm elevates the bearing capacity from 494.95 kN to 546.3 kN and boosts the ductility coefficient from 5.58 to 7.95. In contrast, with fixed CFRP layers and engagement length, expanding the tenon cross-sectional area from 360 mm2 to 810 mm2 produces only marginal bearing capacity improvement from 548.2 kN to 556.2 kN with ductility coefficients ranging between 4.67 and 5.56, conclusively revealing that tenon engagement length has substantially greater influence on mechanical properties than cross-sectional area. The optimal axial compressive performance configuration combines 3 CFRP layers, an 810 mm2 tenon cross-section, and a 90 mm engagement length.
1. Introduction
1.1. Background
Timber structures are extensively utilized worldwide owing to their elegant aesthetics and favorable seismic performance, with modern timber constructions being particularly prevalent in earthquake-prone regions where they effectively mitigate building collapse and reduce casualties during seismic events [1]. However, timber components such as columns subjected to sustained loads, including compression, are prone to damage accumulation, and such progressive deterioration may ultimately trigger structural instability or even catastrophic collapse [2]. Spliced timber columns, composed of multiple wood blocks interconnected by mortise-tenon joints, represent a quintessential element in ancient Chinese large-scale timber architecture as exemplified by historically significant buildings like the Main Hall of Baoguo Temple in Ningbo. Concealed drum-shaped tenons are joint components inserted into corresponding mortises to connect structural elements and are characterized by their fully or partially hidden profiles [3]. Wedge keys serve as wooden blocks that secure these tenons within mortises [4]. Nevertheless, over extended periods, these columns exhibit cracks, loosening of mortise-tenon joints, and other forms of degradation that severely compromise structural stability and necessitate urgent reinforcement [5]. Therefore, research on repair and strengthening techniques for timber structures to enhance their mechanical performance and durability is critically important for both preserving architectural heritage and ensuring the safety of contemporary timber constructions.
Multiple reinforcement techniques exist for historic building restoration, including fiber reinforcement and in situ timber structure repair methods, with this study primarily employing carbon fiber reinforcement [6]. Recent years have witnessed extensive research on fiber-reinforced polymer-strengthened timber components. Fernando et al. [7] investigated basalt FRP for enhancing timber mechanical properties and reported stiffness increases reaching 26% alongside strength improvements, achieving 65%. Francisco et al. [8] conducted axial compression tests and numerical simulations on thin-walled glass FRP-wood composite short columns across six specimen groups, with their findings demonstrating that increasing GFRP layers effectively enhances structural strength. Cui et al. [9] performed axial compression tests and numerical simulations on six groups of thin-walled GFRP-confined wood composite stub columns, establishing that specimen strength improves proportionally with increasing GFRP layer quantity. Huang et al. [10] studied CFRP-reinforced wooden columns, and the results showed that the enhancement of CFRP can significantly improve the mechanical properties of wood and inhibit the occurrence of brittle failure. With the increase in the number and angle of CFRP winding layers, the ultimate bearing capacity of the wood members increased from 112.63 kN to 161.21 kN, and the displacement ductility coefficient also increased from 1.44 to 1.72. Wang et al. [11] executed axial compression tests on AFRP-confined laminated bamboo columns featuring varying slenderness ratios. The collective body of existing research confirms that FRP reinforcement successfully overcomes the inherent complexities of wood anisotropy and specialized structural mechanics while effectively mitigating stress concentrations and redistributing internal stresses, thereby enhancing load-bearing capacity and prolonging the service life of structural components [12,13]. However, different reinforcement polymers exhibit distinct strengthening efficiencies, with CFRP demonstrating superior load-bearing capacity compared with other FRP materials despite its higher implementation costs. These comprehensive findings substantiate CFRP’s exceptional mechanical properties, particularly its lightweight nature and high strength, which significantly augment timber’s mechanical performance when rehabilitating damaged wooden structures.
1.2. Research Significance
This study makes significant contributions to understanding the axial compression behavior of CFRP-confined damaged quad-segment spliced Pinus sylvestris var. mongolia composited wooden columns. The research systematically investigates the synergistic mechanisms between CFRP confinement and tenon joint parameters, revealing that CFRP reinforcement combined with extended tenon length can enhance both ultimate bearing capacity and ductility while effectively inhibiting brittle failure modes. Comprehensive parametric analysis of failure characteristics and load-deformation responses provides new insights into the structural performance optimization of traditional timber components. The experimental results demonstrate that the optimal combination of CFRP layers and tenon geometry establishes an effective balance between load transfer efficiency and confinement effects, offering a scientifically validated approach for historical timber structure conservation and modern timber engineering applications.
2. Experimental Progress
2.1. Specimen Designed
Following the Standard for Design of Timber Structures (GB 50005-2017) [14], fifteen quad-segment spliced Pinus sylvestris var. mongolia composited wooden columns were manufactured. Subsequent procedures included damage simulation, CFRP reinforcement application, and axial compression failure testing on CFRP-strengthened specimens. These ten columns were systematically divided into five groups containing two specimens each (named a and b), with experimental variables consisting of tenon cross-sectional area, mortise joint length, and CFRP reinforcement layers. All specimens shared identical geometric parameters with an effective height of 360 mm and a cylindrical radius of 90 mm; in compliance with the Technical Code for Application of Fiber Reinforced Composites in Construction Engineering (GB 50608-2010) [15], CFRP lap length was maintained at 100 mm, winding layers were limited to either 1 or 3 layers, and reinforcement followed a standardized 100 mm width with consistent 30 mm spacing. Complete dimensional specifications of reinforced components and tenon configurations are systematically presented in Table 1, while the internal mortise-tenon structural arrangement is visually detailed in Figure 1.

Table 1.
Parameters of specimen.
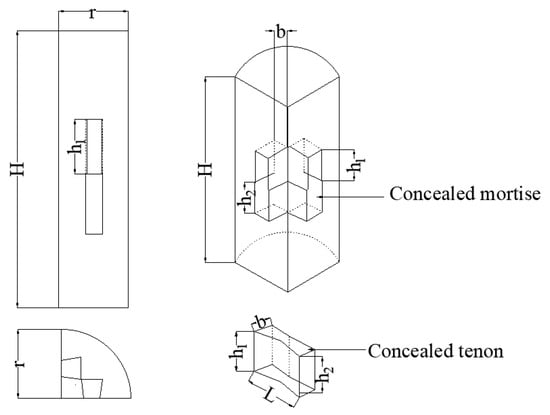
Figure 1.
Diagram of internal tenon.
2.2. Material Setting
Quad-segment composite column shafts and mortise-tenon connectors utilized Pinus sylvestris var. mongolica timber, known for its superior insect resistance and decay resistance characteristics. This timber species demonstrates inherent compressive strength combined with moderate density and hardness that collectively confer excellent workability, offering significant advantages in timber structure applications [16]. The main mechanical properties of wood are measured according to the Chinese standard “Standard for Test Methods for Wood Structures” [GB/T 50329–2012] [17]. The engineering elastic constants for Pinus sylvestris var. mongolica are documented in Table 2, with timber moisture content measured at 10.3 percent and density recorded as 0.46 g per cubic centimeter. For reinforcement materials, the study employed T300 3k high-strength carbon fiber along with impregnating resin. According to the Technical Specification for the Application of Fiber-Reinforced Composite Materials (GB50608-2010) [13], the main performance parameters of CFRP are measured, and the results are shown in Table 3.

Table 2.
Material property of Pinus sylvestris var. Mongolica.

Table 3.
Material property of CFRP and epoxy resin.
To minimize test errors caused by internal moisture variations within different sections of homogeneous timber while accounting for the substantial impact of moisture content on wood’s physical characteristics [18], all timber components received desiccation treatment before CFRP reinforcement following the Standard for Test Methods of Timber Structures. Each specimen was first weighed and then positioned in a drying oven maintained at 100 degrees Celsius with a 2-degree variation [14]. Every four hours, specimens were extracted from the oven, allowed to cool to room temperature, measured using an electronic balance, and subsequently returned to the heating chamber. This cyclical process continued systematically until successive weight measurements showed less than 0.2 percent variation, confirming achievement of complete dryness, with the full desiccation procedure visually represented in Figure 2.

Figure 2.
Diagram of drying and weighing process.
The pre-damage simulation replicating mechanical actions typical of historic structures was conducted using an electro-hydraulic servo universal testing machine. Loading progressed at rates specified in the Standard for Test Methods of Timber Structures until achieving 80 percent of the specimens’ ultimate bearing capacity [15], at which point loading terminated. The unreinforced specimen groups received designations ranging from A1 to A5. Documented specimen damage patterns consisted of transverse crushing, longitudinal cracking, and localized shear cracking. Principal tenon failure types involved tenon-head shear cracking, mortise extrusion deformation, and mortise cracking, with visual documentation provided in Figure 3.


Figure 3.
Failure mode of pre-damaged loads.
To guarantee optimal CFRP-to-timber bonding, according to the Technical Code for Application of Fiber Reinforced Composites in Construction Engineering (GB 50608-2010) [14], the surface of the wooden column is sanded with sandpaper. Resins A and B underwent mixing in a 2-to-1 proportion, thorough homogenization, and a prescribed resting period prior to implementation. CFRP sheet application occurred along predetermined alignment paths using brush-deposited adhesive layers, succeeded by specimen curing in controlled ventilation conditions, with the complete reinforcement methodology visually presented in Figure 4.
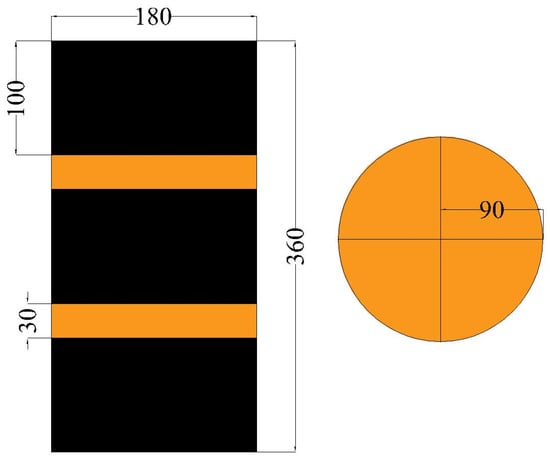
Figure 4.
Diagram of CFRP wrapping.
2.3. Data Collection and Loading Device
Strain gauges were installed transversely at both ends and mid-height positions of the specimens with two gauges per location for a total of six gauges to monitor lateral deformation, while four additional gauges were arranged longitudinally at the specimen mid-height to record axial deformation, bringing the total number of gauges to ten [18]. Two displacement transducers oriented perpendicularly to each other were mounted at matching elevations on the column to measure mid-span lateral displacement. The data collection system utilized a uT7110Y static resistance strain indicator, and the loading process was carried out using a 3000 kN long-column testing machine [19], with the complete loading setup shown in Figure 5.
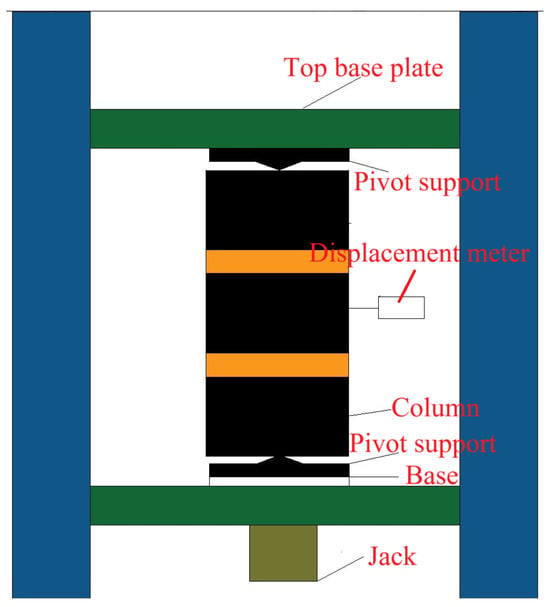
Figure 5.
Strain gauge position diagram and loading device.
2.4. Measurement Procedure
Before applying any load, precise mechanical alignment was established between the long-column testing machine and specimens to ensure coaxial pressure application. Loading rates and procedures were determined in accordance with the Standard for Test Methods of Timber Structures [15]. The loading process consisted of two distinct stages: initial preloading advanced at a constant rate of 0.1 kN per second up to 15 kN to remove any clearance between specimens and supporting structures; subsequent formal loading maintained the identical 0.1 kN per second rate until specimens exhibited complete structural failure, at which point the test was concluded [17].
3. Analysis of Test Results
3.1. Test Phenomenon
In the initial loading phase up to 300 kN, no notable experimental phenomena were detected. When the load exceeded this threshold, compressive sounds from wood fibers became increasingly frequent, accompanied by sporadic CFRP fracture noises. As the load approached its peak, CFRP fracture sounds grew significantly more pronounced. At maximum load capacity, a sudden rupture occurred across large CFRP surface areas. With diminishing specimen load-bearing capacity, extensive splitting cracks formed at joint interfaces, considerable lateral displacement became evident at mid-column positions, and localized bulging deformations emerged on CFRP surfaces [20]. Wood columns exposed to simulated historical structural loading conditions showed severe damage characteristics, including cracking and crushing failures with noticeable timber extrusion and dislocation around affected areas. Clear differences in failure patterns appeared between single-layer and triple-layer CFRP-reinforced specimens: Single-layer specimens mainly displayed clean fractures at joints with systematic CFRP rupture and tenon failure at mid-column connections, while triple-layer specimens showed irregular CFRP fractures concentrated in lower mid-column sections, with timber reduced to fragmented particles showing fiber extrusion deformation and extensive CFRP separation from the wood substrate.
3.2. Destruction Phenomenon
As shown in Figure 6 for specimens MC-1 and MC-2, the CFRP displayed brittle fracture simultaneously with the specimens attaining ultimate stress, mainly caused by localized shear cracks at simulated damage areas and tenon shear cracks that aggravated transverse displacement under growing load while reducing the mortise-tenon joint’s restraining capability, thus precipitating sudden CFRP failure. Regarding specimen MC-3, localized crushing appeared, probably resulting from stress concentration caused by hardened epoxy-bonded CFRP acting as a force-transfer plate, leading to localized wood fiber fracture and final compressive failure. For specimens MC-4 and MC-5, irregular CFRP cracking at mid-column originated from initial simulated damage, including partial transverse crushing, mortise extrusion deformation, and mortise cracking, which gradually weakened load transfer via mortise-tenon joints under increasing load, with amplified deformation at previously damaged crushed areas causing rapid CFRP stress increase and resulting in asymmetrical fracture.
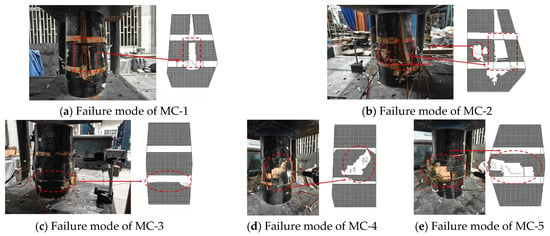
Figure 6.
Diagram of failure modes.
3.3. Load-Displacement Curve Analysis
As shown in Figure 7, all specimen groups display comparable three-stage development in their load-displacement curves: elastic phase, elastoplastic transition phase, and plastic failure phase. The initial loading stage demonstrates nonlinear elastic behavior linked to stiffness reduction from simulated damage, indicating accumulated damage effects from upper structural loads on timber columns. When approaching the proportional limit load, the curves progress into the second stage, where epoxy resin-mediated adhesive interaction at CFRP-wood interfaces becomes active: deformation dynamics of compressed wood fibers slow under CFRP restraint, evidenced by smaller displacement increments and substantially improved load-carrying capacity relative to the elastic phase. The final failure stage spans from peak load to complete structural failure; CFRP-reinforced timber specimens initially achieve maximum load capacity, then experience simultaneous wood fiber breakdown and CFRP separation when the CFRP reaches its strain limit. This terminal phase shows sudden intensification of deformation displacement paired with rapid strength decline.
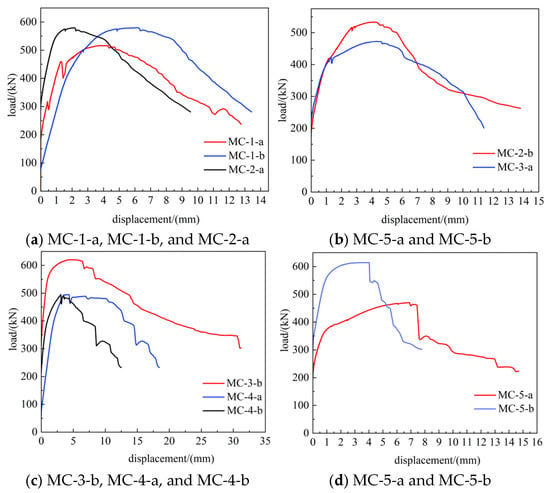
Figure 7.
Load-displacement curves.
3.4. Stress-Strain Behavior Analysis
3.4.1. Loading Longitudinal Strain
As demonstrated in Figure 8, showing load-longitudinal strain relationships, all specimen groups display similar developmental patterns. The uniform CFRP deformation verifies dependable interfacial bonding between reinforcement materials and timber surfaces [21]. Although simulated damage causes mortise-tenon shear cracks and longitudinal fractures at mid-column locations, transverse CFRP confinement preserves essentially linear load-strain behavior throughout all specimens. Examination of tenon length parameters in Figure 8d,e shows decreasing CFRP strain variation rates and improved load-bearing capacity as tenon dimensions increase, suggesting the structural impact of tenon size. Comparison between single-layer CFRP specimens in Figure 8a,b and triple-layer specimens in Figure 8d,e indicates lower final surface strains with additional CFRP layers, demonstrating significantly improved confinement effectiveness. For specimens with identical reinforcement layers, Equation (1), developed from experimental data fitting, shows the relationship between hidden tenon cross-sectional area and CFRP ultimate strain variation rate, demonstrating that larger tenon sections quicken surface strain development, consequently decreasing load-bearing capacity. The resulting fitted curve appears in Figure 9.
where ξ represents the change rate of CFRP ultimate surface strain, and A corresponds to the cross-sectional area of the specimen’s hidden tenon.
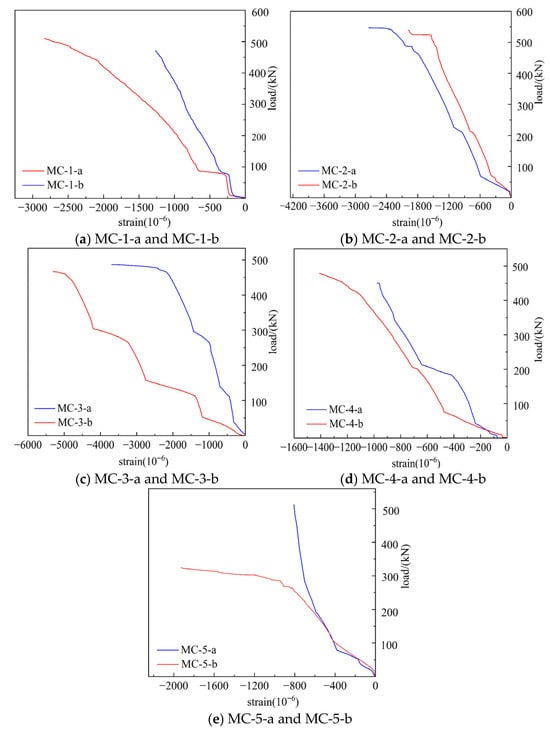
Figure 8.
Load-longitudinal strain.
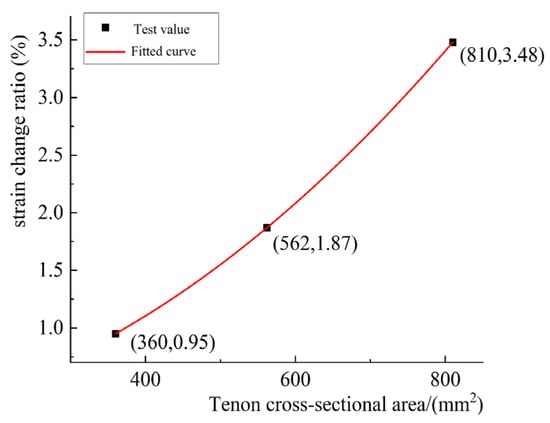
Figure 9.
The rate of ultimate stress-strain of tenon cross-sectional area.
3.4.2. Transverse Strain
As shown in Figure 10, presenting load-transverse strain relationships among specimen groups, all curves display fundamentally similar developmental patterns. During initial loading stages, CFRP surfaces show minimal strain development; as applied loads increase, stress gradually concentrates downward to compress timber components, consequently increasing transverse strain at mid-column locations [22]. The combination of mortise-tenon joints and CFRP confinement slows transverse displacement dynamics, thereby stabilizing CFRP surface strain development. Comparative examination between Figure 10b,d shows reduced final CFRP surface strain with additional reinforcement layers, verifying improved confinement effectiveness through CFRP layer addition. Assessment of Figure 10c through Figure 10e under triple-layer CFRP reinforcement with consistent hidden tenon cross-sectional area demonstrates stabilized CFRP surface strain as tenon length decreases from 90 mm to 60 mm and 30 mm, identifying 60 mm as the optimal parameter for mortise-tenon design. The strain irregularity visible in Figure 10c likely originates from diverse failure mechanisms caused by pre-existing simulated damage and intermittent CFRP bonding, where insufficient reinforcement coverage across extended shear cracks may have triggered stress-focused failure, appearing as localized strain decrease and sudden strain changes.
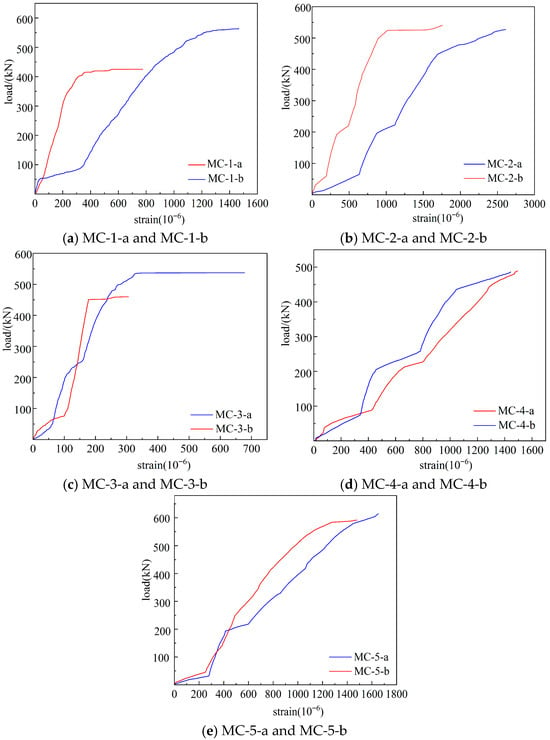
Figure 10.
Diagram of load-lateral strain.
4. Quantitative Analysis
4.1. Calculation of Compressive Strength of CFRP-Confined Wooden Columns
In studies investigating the load-bearing capacity calculation of composite-reinforced timber columns, Andre et al. [23] applied CFRP-confined concrete theory to develop stress–strain models for CFRP-strengthened wood columns, establishing an axial compression capacity calculation formula where force equilibrium at the timber-CFRP interface is defined by Equation (2).
(1) The stress–strain relationship of CFRP is assumed to be a linear elasticity relationship; (2) It is assumed that wood exhibits a linear stress–strain relationship during the elastic phase.
where fcfrp represents the tensile stress of CFRP sheets; tf and bf correspond to the thickness and width of CFRP sheets, respectively; f1 denotes the confining stress provided by CFRP; Scj indicates the bonding spacing of CFRP sheets; and D represents the cylindrical diameter.
The calculation formula for the lateral confining stress f1 applied by CFRP sheets to timber columns is presented in Equation (3) [24].
where ECFRP and εCFRP represent the tensile elastic modulus and ultimate tensile strain of CFRP sheets, respectively; the effective confinement coefficient ks is introduced for critical sections due to weakened CFRP confinement in discretely wrapped regions; ks is determined by Equation (4), with ks = 1 when CFRP sheets are continuously bonded to the timber column surface [18].
where Acj represents the effective confined area of CFRP sheets, and Ac denotes the confined area; the expression for calculating the effective confining stress applied by CFRP sheets to timber columns is presented in Equation (5).
Classical theories for calculating the strength of CFRP-confined concrete establish that the peak stress of confined specimens correlates with the effective confining stress of CFRP sheets, as expressed by the computational relationship in Equation (6).
where fcc denotes the confined peak stress and fco represents the unconfined specimen strength; the axial compressive calculation formulas for compression-strengthened timber columns are provided in Equations (7) and (8), which yield the theoretical axial compressive capacity Nu of timber columns when substituting experimental data, as shown in Table 4.
where Ag denotes the gross cross-sectional area of the timber columns.

Table 4.
Theoretical calculations and comparison of results.
By comparing the model proposed by Togay et al. [25], the model has great limitations, and the fitting effect is not ideal due to the different failure forms of the pre-damage simulation of wooden columns.
It can be seen from the table data that the model is more suitable for one-layer CFRP-reinforced specimens, and the deviation is large for three-layer CFRP-reinforced specimens; the enhancement in compressive bearing capacity of strengthened specimens relative to unstrengthened specimens appears in Table 5.

Table 5.
The ultimate bearing capacity of CFRP-confined specimen.
4.2. Ductility Analysis
To compare the axial stiffness of specimens during the elastic phase, the initial nonlinear segment of load-displacement curves is excluded to eliminate its influence; the initial axial stiffness, K, of specimens is determined by the slope of load-displacement curves between 20% and 40% of peak load [26], with corresponding data for each specimen group presented in Table 6; the elastoplastic deformation capacity of timber columns is characterized by displacement ductility coefficient µ, calculated as follows:
where Δμ and Δv represent displacements corresponding to failure load and yield load, respectively; this study employs the Equivalent Elastoplastic Energy (EEEP) method to determine the ductility coefficient of timber columns, defining the displacement at which the load decreases to 80% of the ultimate load as failure displacement Δμ; the yield displacement is calculated using Equations (10) and (11):
where Pv represents the yield load of the specimen, K denotes the initial axial stiffness, and ω indicates the energy dissipated before failure, specifically the area enclosed by the load-displacement curve prior to failure; analysis of the ductility coefficient for each specimen group demonstrates values consistently exceeding 4, directly correlated with wood’s inherent fiber extensibility as a natural composite material.

Table 6.
Mechanical properties of specimens.
The impact of experimental variables on ductility coefficients varies significantly, where increasing CFRP reinforcement layers from 1 to 3 yields a 10.5% enhancement in ductility coefficient when comparing specimens MC-4 and MC-1, confirming that additional CFRP layers improve plastic deformation capacity, but the ducility coefficient was not significantly improved because the specimen was reinforced at intervals, which reduced the restraint ability of CFRP on the wooden column specimen MC-4 with 60 mm mortise dimensions displays a 9.2% greater ductility coefficient than specimen MC-5 with 30 mm mortise dimensions, whereas specimen MC-2 with 562 mm2 tenon cross-section shows 16% lower ductility coefficient relative to specimen MC-1 with 360 mm2 tenon cross-section, establishing that strategic mortise enlargement combined with controlled tenon cross-section effectively enhances plastic performance; reference data for unreinforced specimens’ stiffness and ductility coefficients originate from Reference [15].
5. Conclusions
Most historical wooden structures have sustained varying degrees of damage due to long-term upper load effects. To investigate the effect of CFRP reinforcement on damaged wooden structures, five sets of pre-damaged reinforced axial compression tests were conducted on four-segment spliced specimens. The study analyzed the enhancing effect of CFRP on the load-bearing capacity of wooden columns and summarized the distribution patterns of stress–strain curves of wooden columns under different parameters. The main research conclusions are as follows:
(1) CFRP reinforcement effectively enhances the mechanical properties of damaged timber columns; single-layer CFRP strengthening increases specimen load-bearing capacity by 41.0 to 49.2 percent, elevates ductility coefficient by 12.0 to 15.1 percent, and improves stiffness by 63.59 to 80.3 percent, while triple-layer CFRP reinforcement achieves load-bearing capacity improvements of 56.6 to 74.5 percent, ductility coefficient increments of 3.7 to 4.3 percent, and stiffness enhancements of 58.56 to 138.8 percent, demonstrating that increasing CFRP layers effectively augments specimen mechanical performance.
(2) Mortise dimensions and tenon cross-sectional area differentially influence specimen load-bearing capacity: within specimens featuring single-layer CFRP reinforcement and fixed 90 mm mortise size, load-bearing capacity exhibits a negative correlation with tenon cross-sectional area where a 30.6 percent average reduction in tenon area corresponds to a 17.8 percent capacity increase; in specimens with triple-layer CFRP reinforcement and fixed 810 mm2 tenon area, every 10 mm increase in tenon length yields approximately 43 kN of load-bearing capacity gain, though capacity variation plateaus when tenon length is below 60 mm, suggesting tenon length should serve as the primary controllable design parameter to fulfill load-bearing requirements.
(3) This study simulates upper-load damage in ancient architectural components followed by reinforcement, effectively demonstrating CFRP’s multifaceted beneficial impacts on restoring damaged heritage structures. This study is limited by the constraints of the sample size, and the generalizability of the conclusions requires further validation through the expansion of the types and numbers of experimental samples. Subsequent research should employ environmental simulation techniques replicating temperature-humidity fluctuations and biological erosion for in-depth exploration of natural factors’ effects on timber structural systems, which holds significant research implications for refining CFRP reinforcement theories applicable to ancient timber columns with varying damage severities.
Author Contributions
S.P.: Writing—original draft, visualization, validation, software, methodology, investigation, formal analysis, data curation, conceptualization. W.L.: Supervision, resources, software, project administration. Y.Q., L.L., and H.L.: Methodology, investigation. D.W.: Writing—review and editing, investigation, funding acquisition, formal analysis, conceptualization. All authors have read and agreed to the published version of the manuscript.
Funding
The authors would like to acknowledge the financial support provided by the Natural Science Foundation of Hubei Province (Grant No. 2022CFB662), the Scientific Research Fund of the Institute of Engineering Mechanics, China Earthquake Administration (Grant No. 2024D30), and the Wuhan Knowledge Innovation Special Dawn Plan Project of China (Grant No. 2023020201020403).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lee, M.G.; Huang, Y.S.; Kan, Y.C.; Wang, Y.C.; Chen, Y.S.; Kao, S.C. Experimental study on durability of CFRP-strengthened wood member. J. Mater. Res. Technol. 2023, 24, 3704–3716. [Google Scholar] [CrossRef]
- Li, H.M.; Qiu, H.X.; Lu, Y. An analytical model for the loading capacity of splice-retrofitted slender timber columns. Eng. Struct. 2020, 225, 111274. [Google Scholar] [CrossRef]
- Han, Y.D.; Chun, Q.; Xu, X.M.; Teng, Q.; Dong, Y.; Lin, Y. Wind effects on Chinese traditional timber buildings in complex terrain: The case of Baoguo Temple. J. Build. Eng. 2022, 59, 105088. [Google Scholar] [CrossRef]
- Ji, W.; Ding, Y.; Hu, C.K. Research on einforcement and repair method of wood structure of ancient buildings in Huizhou. Sci. Technol. Innov. 2019, 10, 120–126. [Google Scholar]
- Corradi, M.; Vemury, C.M.; Edmondson, V.; Poologanathan, K.; Nagaratnam, B. Local FRP reinforcement of existing timber beams. Compos. Struct. 2021, 258, 113363. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, Z.; He, L.; Tam, L.-H. Experimental study on the static and fatigue performances of GFRP-timber bolted connections. Compos. Struct. 2023, 304, 116435. [Google Scholar] [CrossRef]
- Fernando, D.; Frangi, A.; Kobel, P. Behaviour of basalt fibre reinforced polymer strengthened timber laminates under tensile loading. Eng. Struct. 2016, 117, 437–465. [Google Scholar] [CrossRef]
- Rescalvo, F.J.; Valverde-Palacios, I.; Suarez, E.; Gallego, A. Experimental and analytical analysis for bending load capacity of old timber beams with defects when reinforced with carbon fiber strips. Compos. Struct. 2018, 186, 29–38. [Google Scholar] [CrossRef]
- Cui, W.Q.; Fernando, D.; Heitzmann, M.; Gattas, J.M. Manufacture and structural performance of modular hybrid FRP-timber thin-walled columns. Compos. Struct. 2021, 260, 113506. [Google Scholar] [CrossRef]
- Huang, J.; She, Y.; He, J. Effect of CFRP winding modes on axial compressive damage performance of wood components. Constr. Build. Mater. 2024, 426, 136148. [Google Scholar] [CrossRef]
- Wang, Z.; Li, H.T.; Fei, B.H.; Ashraf, M.; Xiong, Z.; Lorenzo, R.; Fang, C. Axial compressive performance of laminated bamboo column with aramid fiber reinforced polymer. Compos. Struct. 2021, 258, 113398. [Google Scholar] [CrossRef]
- Hugo, C.B.; David, C.; Carlos, C. Analysis of the debonding process of CFRP-to-timber interfaces. Constr. Build. Mater. 2016, 113, 96–112. [Google Scholar]
- Abbas, V.; Rijun, S.; Keith, C. Effective bond length and bond behaviour of FRP externally bonded to timber. Constr. Build. Mater. 2017, 151, 742–754. [Google Scholar] [CrossRef]
- GB 50005-2017; Standard for Design of Timber Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2017.
- GB 50608-2010; Technical code for infrastrucure application of FRP composites. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2010.
- Liu, S.W.; Lei, Y.X.; Zhang, J.W.; Zhao, J.; Bai, C.; Hu, Q. Experimental study and analysis on bonding strength of CFRP-wood interface. Int. J. Adhes. Adhes. 2023, 123, 103335. [Google Scholar] [CrossRef]
- GB/T 50329-2012; Standard for Test Methods of Timber Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2012.
- Xie, Q.F.; Zhang, M.; Zhang, L.F. Mechanical properties test and degradation model of naturally cracked wooden columns. J. Build. Struct. 2022, 43, 210–222. [Google Scholar]
- Hosseinihashemi, S.K.; Arwinfar, F.; Najafi, A.; Nemli, G.; Ayrilmis, N. Long-term water absorption behavior of thermoplastic composites produced with thermally treated wood. Measurement 2016, 86, 202–208. [Google Scholar] [CrossRef]
- Asha, Y.; Zhou, C.D.; Yang, L. Experimental study on axial compression behavior of composite reinforced timber columns. China Civ. Eng. J. 2021, 54, 1–9. [Google Scholar]
- Peng, S.; Qiao, Y.; Song, Y. Analysis of mechanical properties of four-section composite columns of Pinus sylvestris var. mongolia of ancient wooden architecture under axial compression load. Buildings 2024, 14, 24–38. [Google Scholar] [CrossRef]
- Kia, L.; Valipour, H.R. Composite timber-steel encased columns subjected to concentric loading. Eng. Struct. 2021, 232, 111825. [Google Scholar] [CrossRef]
- Andre, J.; Massimo, F. General notes on ductility in timber structures. Eng. Struct. 2011, 33, 2987–2997. [Google Scholar] [CrossRef]
- Karkoodi, S.; Karampour, H.; Gilbert, B.P.; Gunalan, S. A study on enhanced mechanical properties of wood in the parallel-to-grain direction in timber-filled-steel tubular columns. Eng. Struct. 2025, 331, 119973. [Google Scholar] [CrossRef]
- Ozbakkaloglu, T.; Lim, J.C.; Vincent, T. FRP-confined concrete in circular sections: Review and assessment of stress–strain models. Eng. Struct. 2013, 49, 1068–1088. [Google Scholar] [CrossRef]
- Kia, L.; Hamid, R.V.; Tohid, G.G. Experimental and numerical investigation of concentric axial loading on bar-reinforced composite timber columns at a large scale. Structures 2024, 60, 105920. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).