Enhanced Convolutional Neural Network–Transformer Framework for Accurate Prediction of the Flexural Capacity of Ultra-High-Performance Concrete Beams
Abstract
1. Introduction
2. Design Code for Flexural Capacity
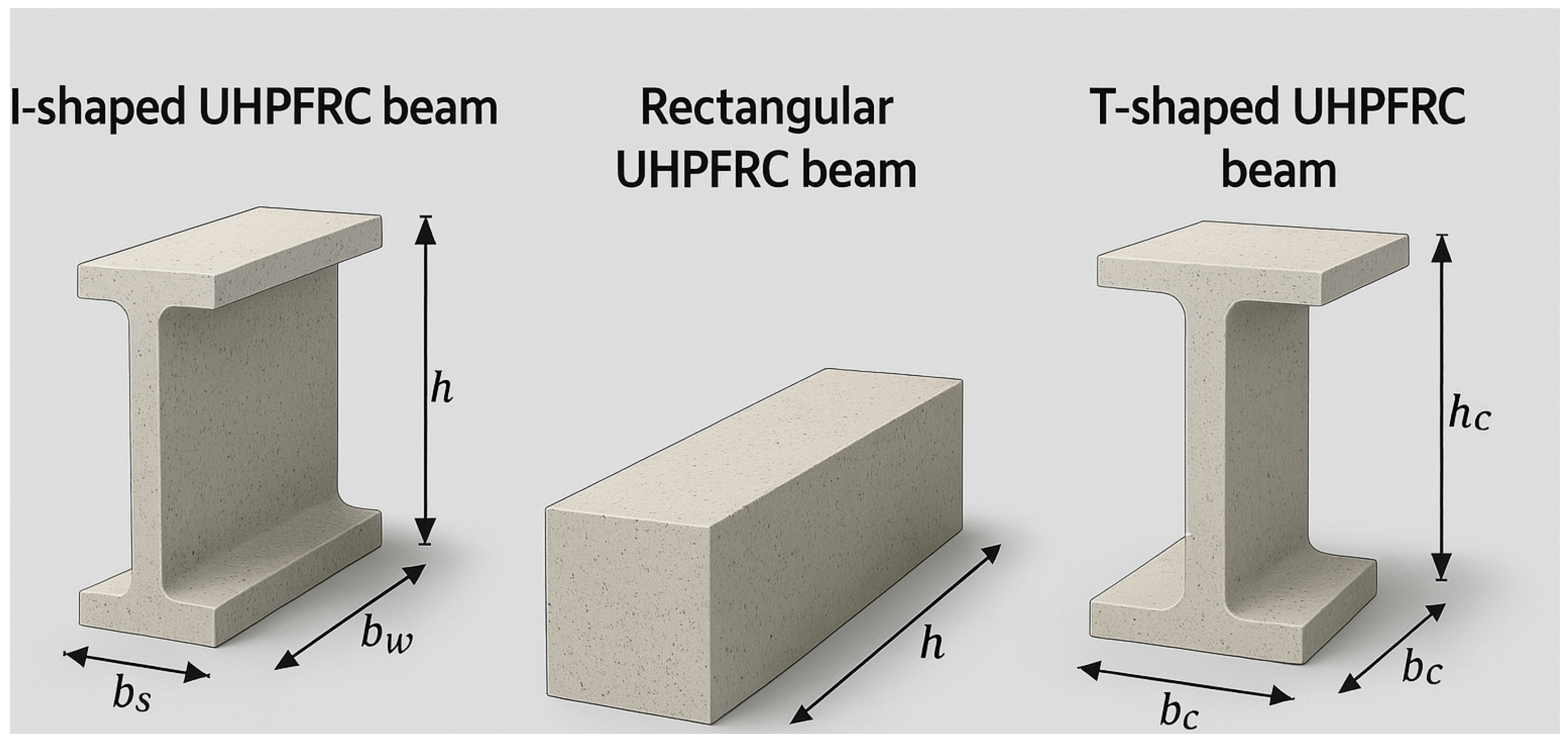
2.1. I-Shaped UHPFRC Beams
2.2. Rectangular UHPFRC Beam
2.3. T-Shaped UHPFRC Beams
3. Methodology
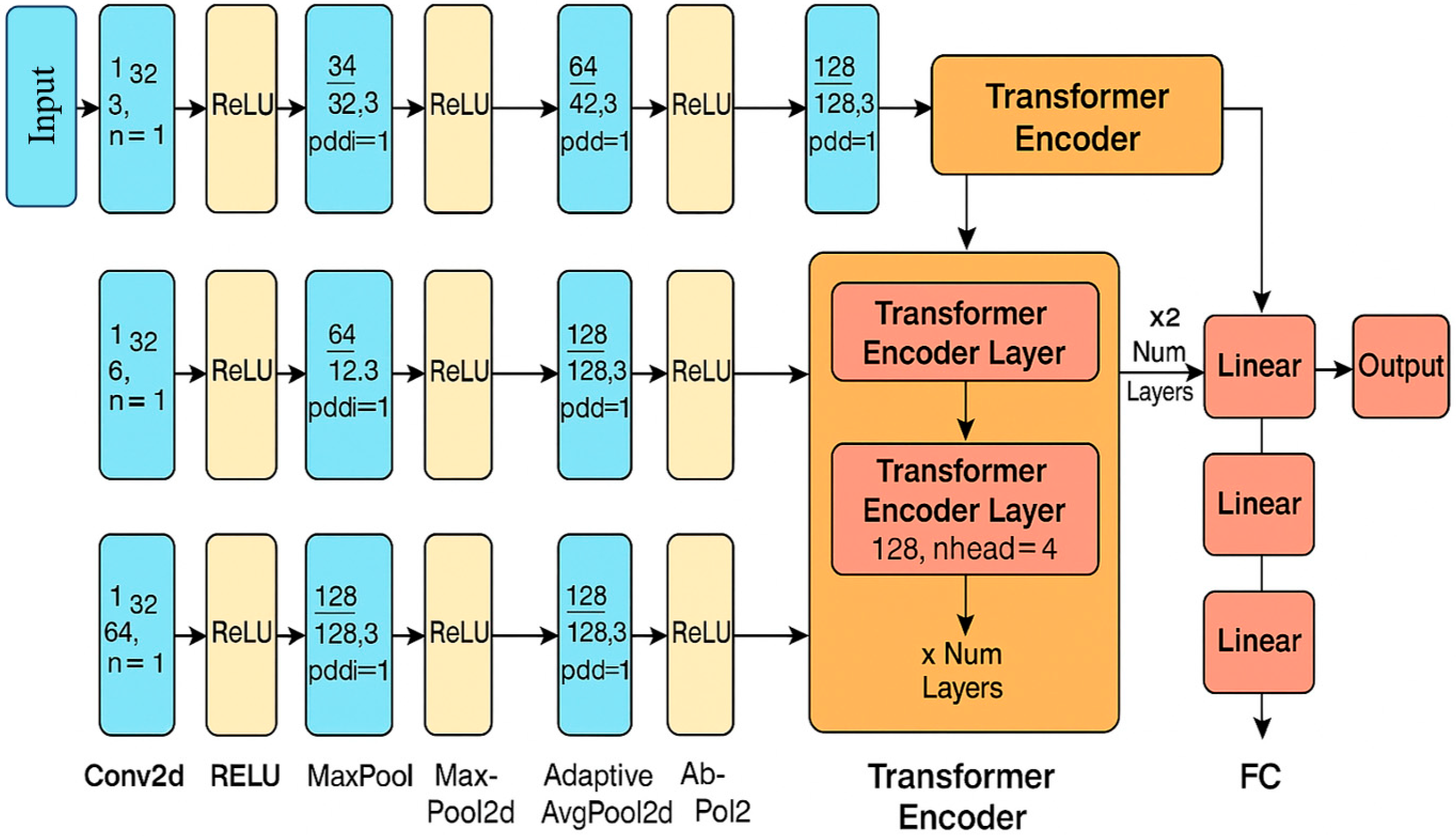
3.1. The Proposed CNN-Transformer Framework
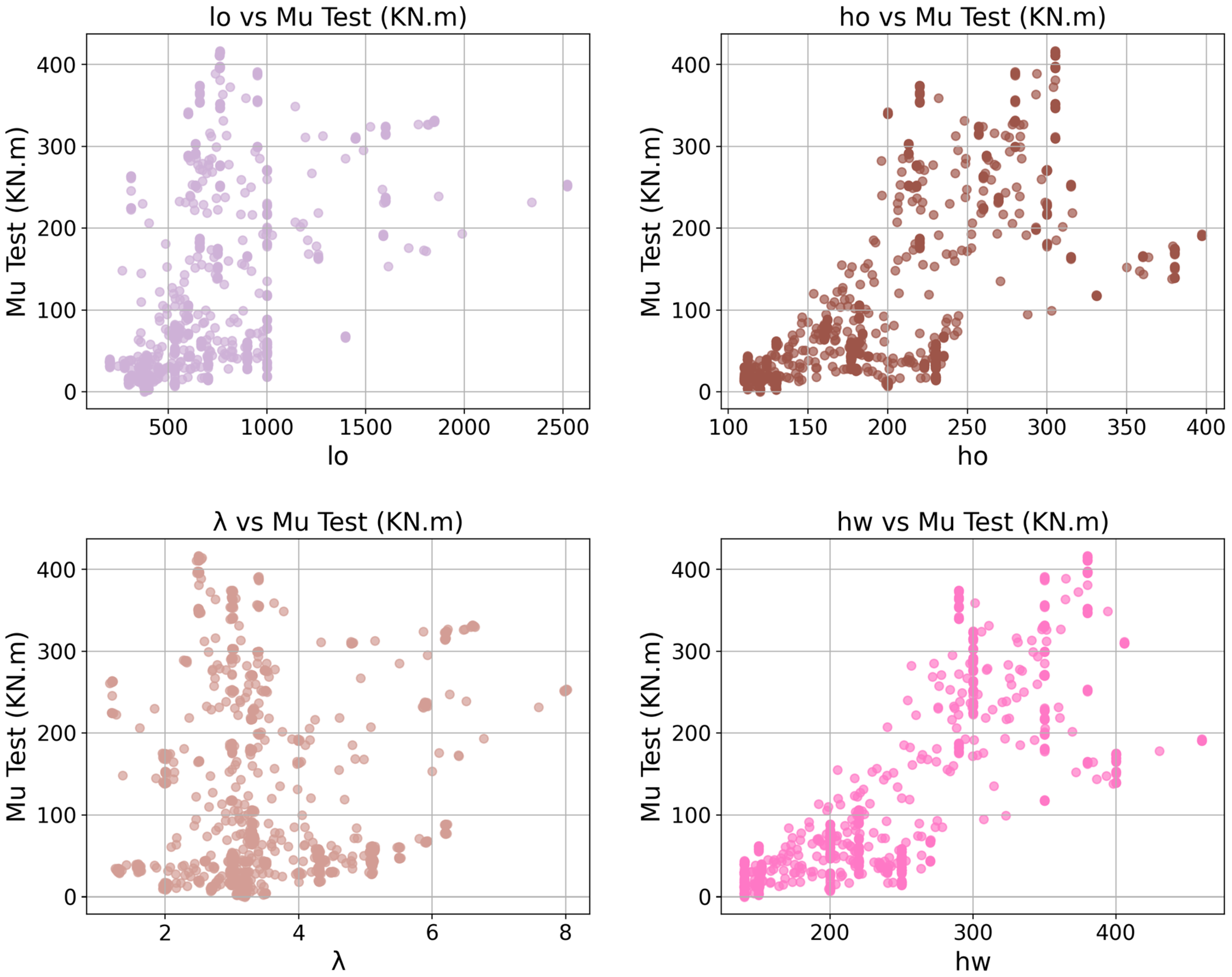
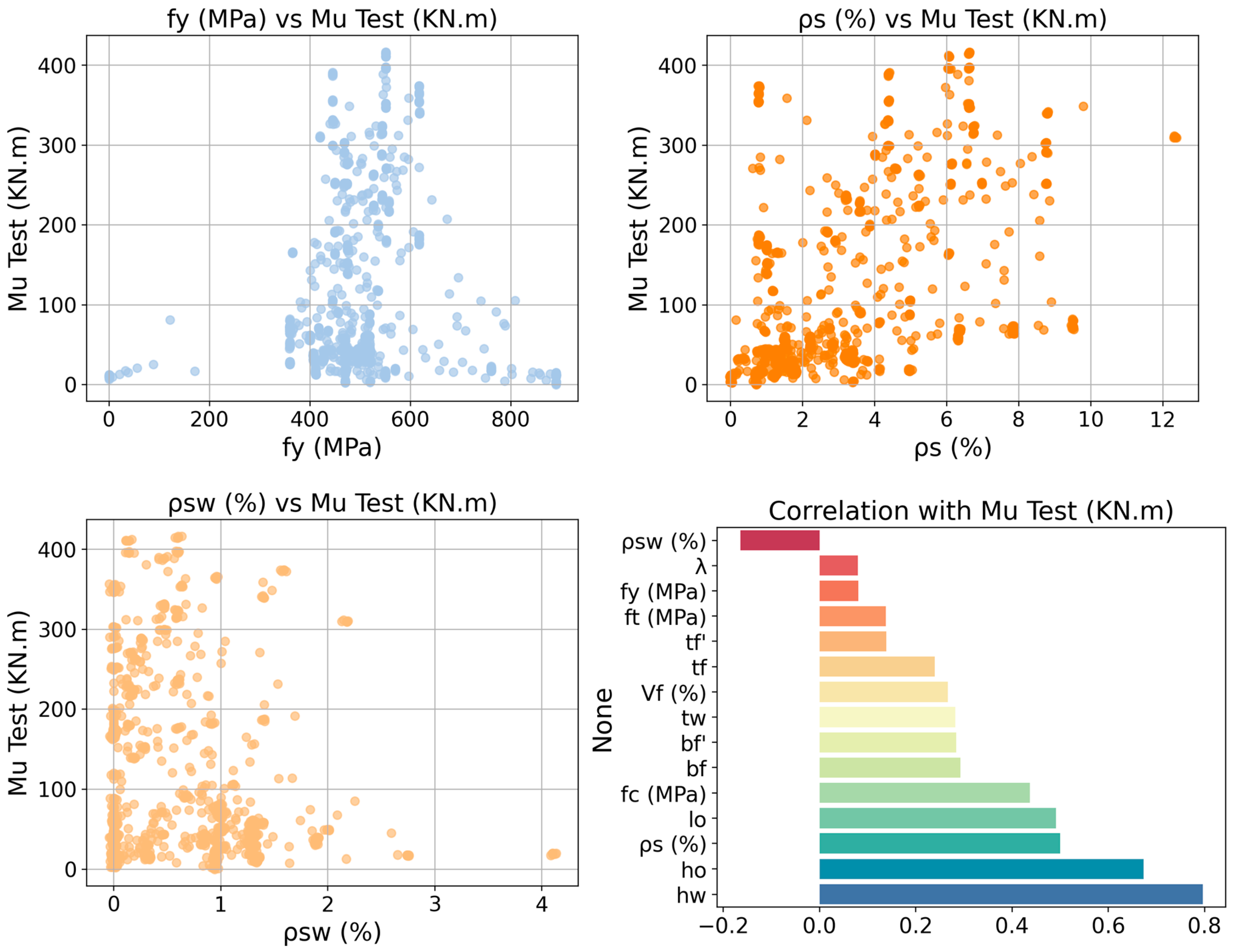
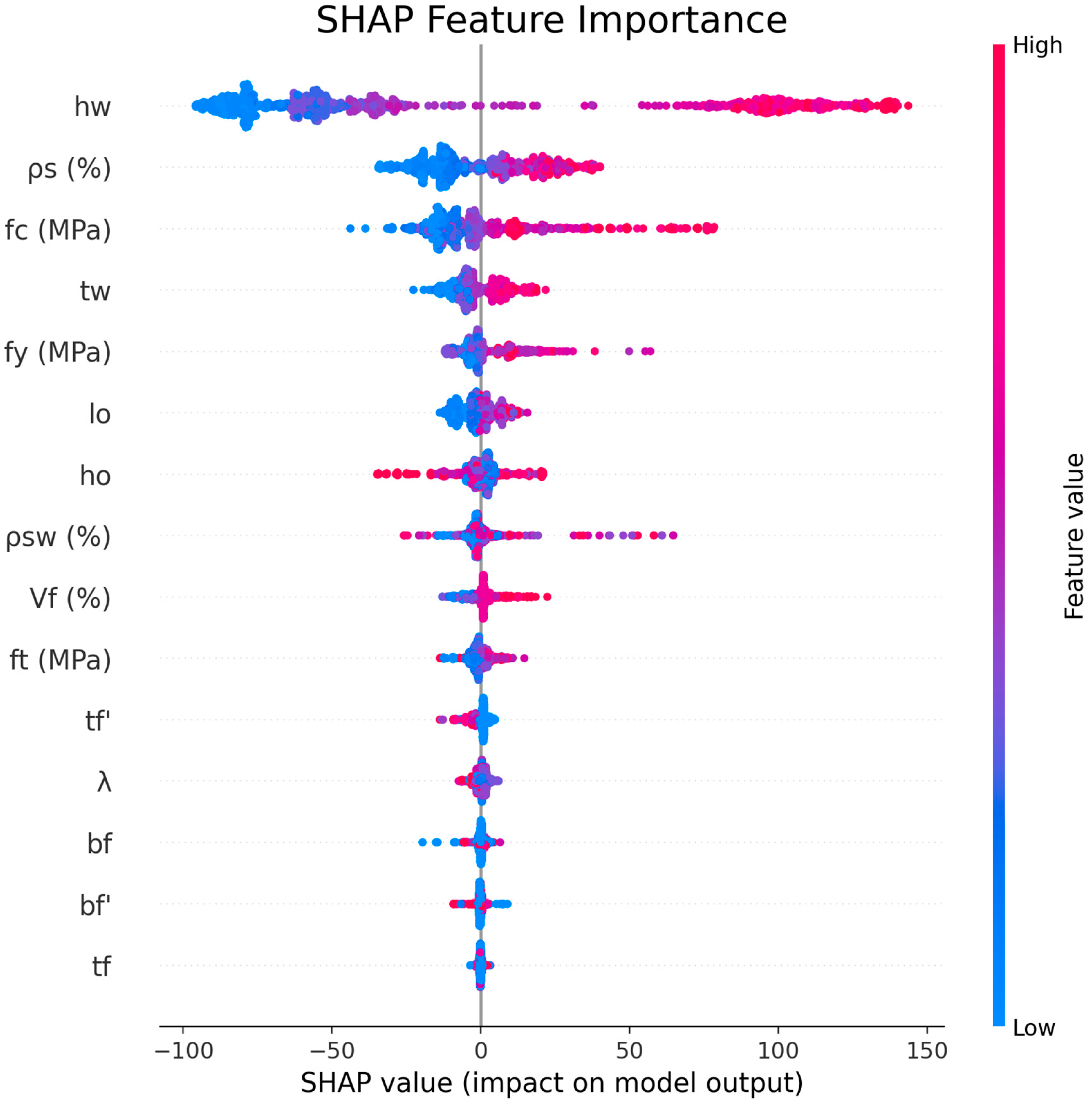
3.2. Data Collection and Analysis
3.3. Experimental Data Scope
4. Results and Discussion
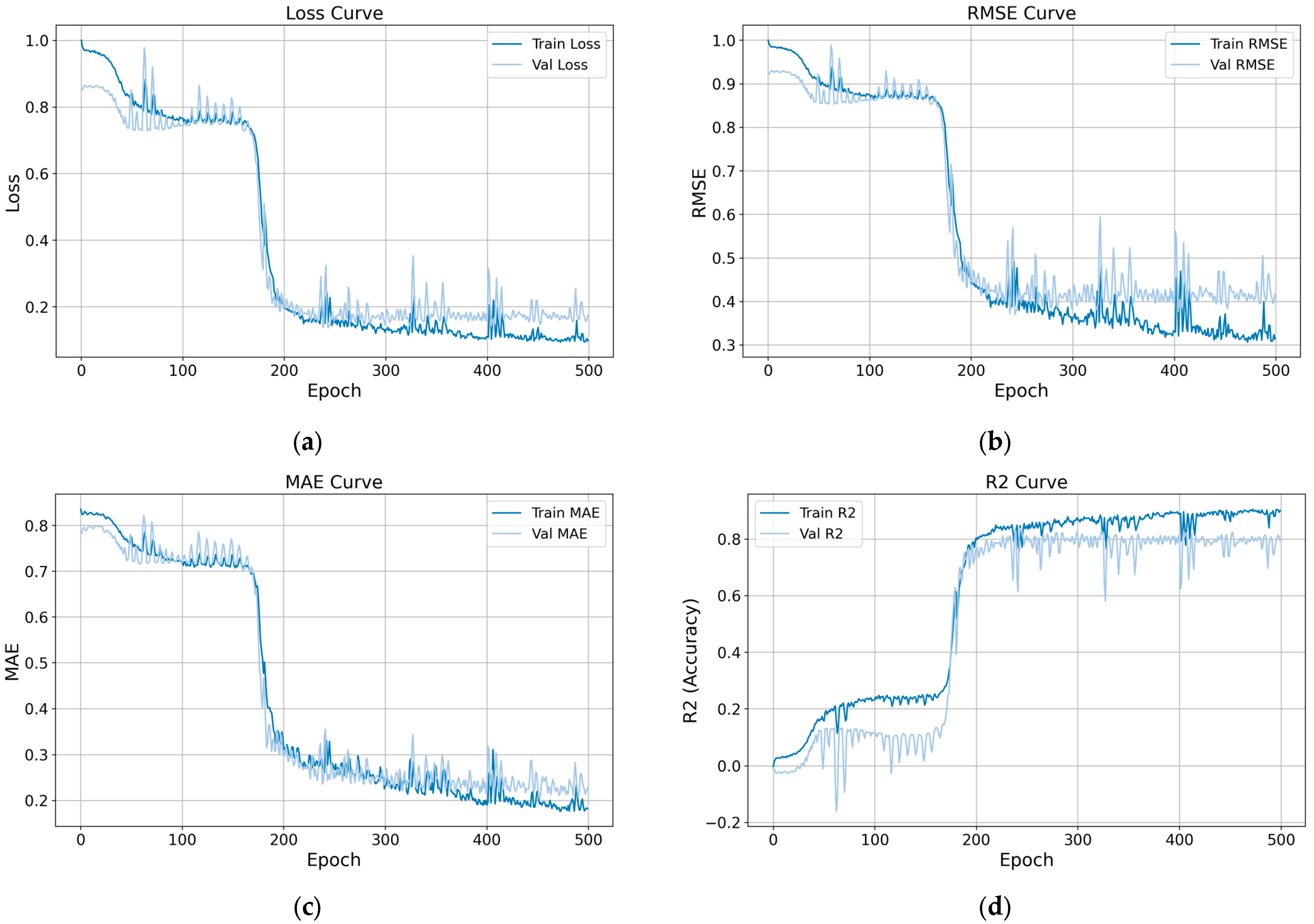
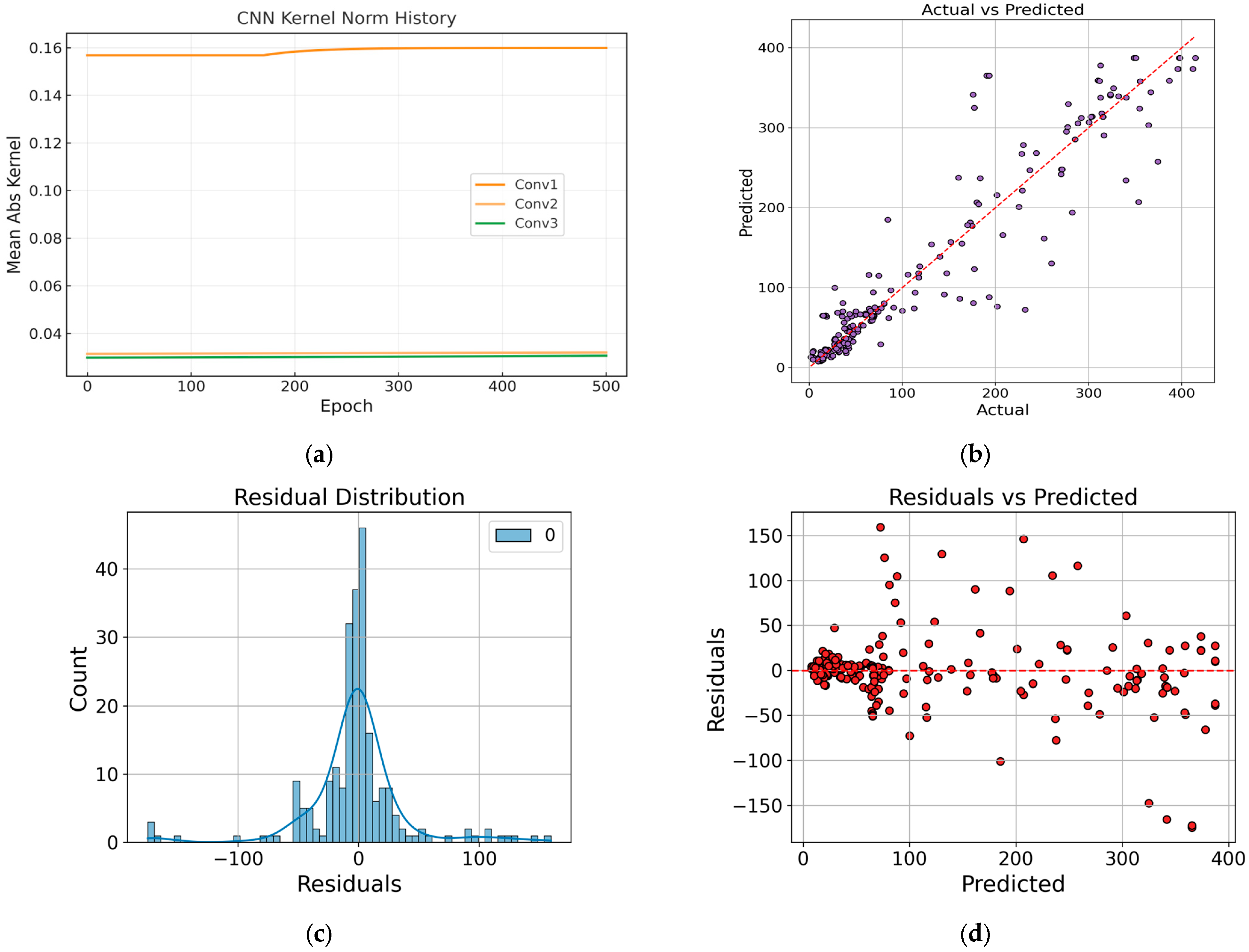
4.1. Evaluation of Training Process
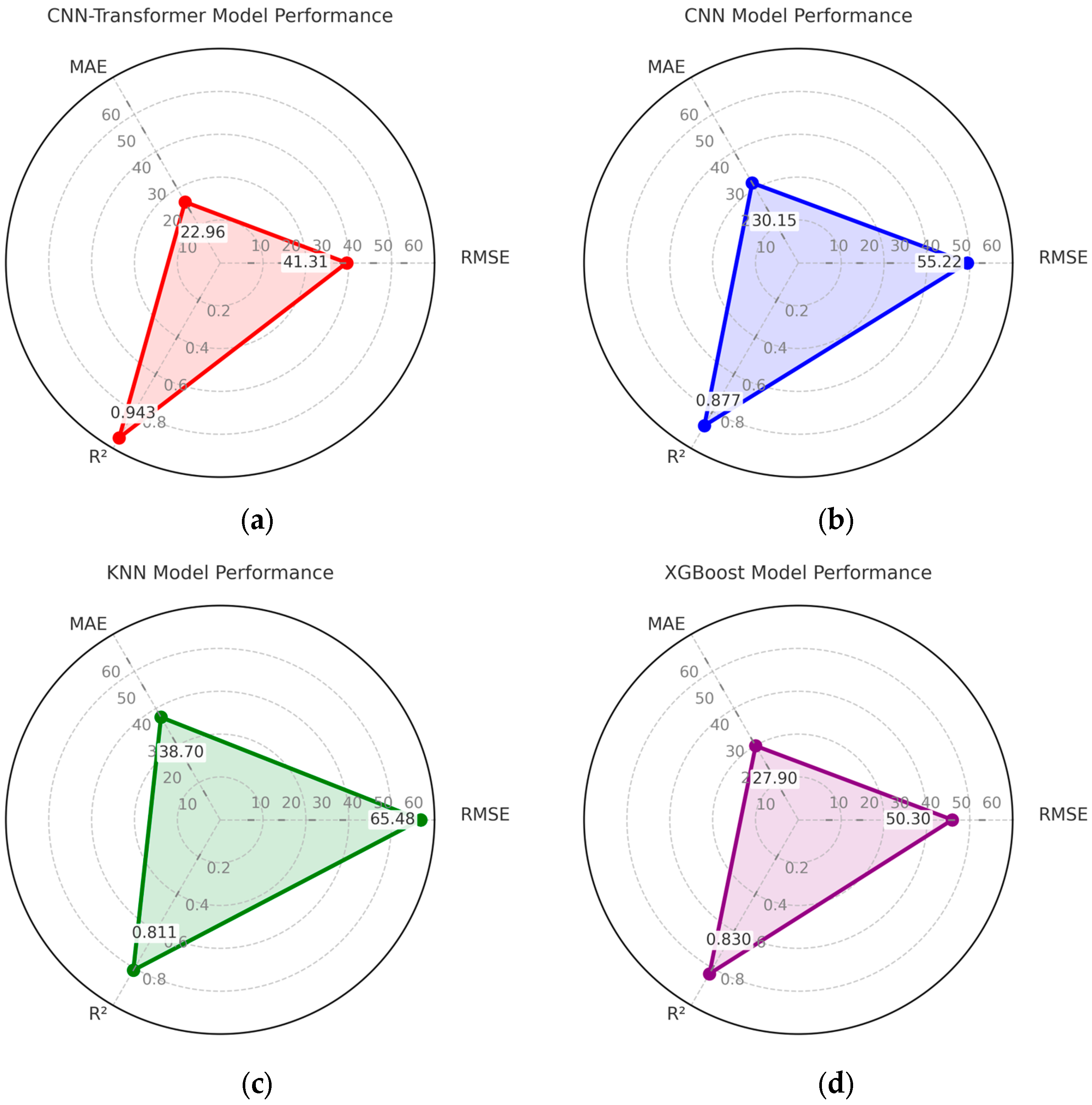
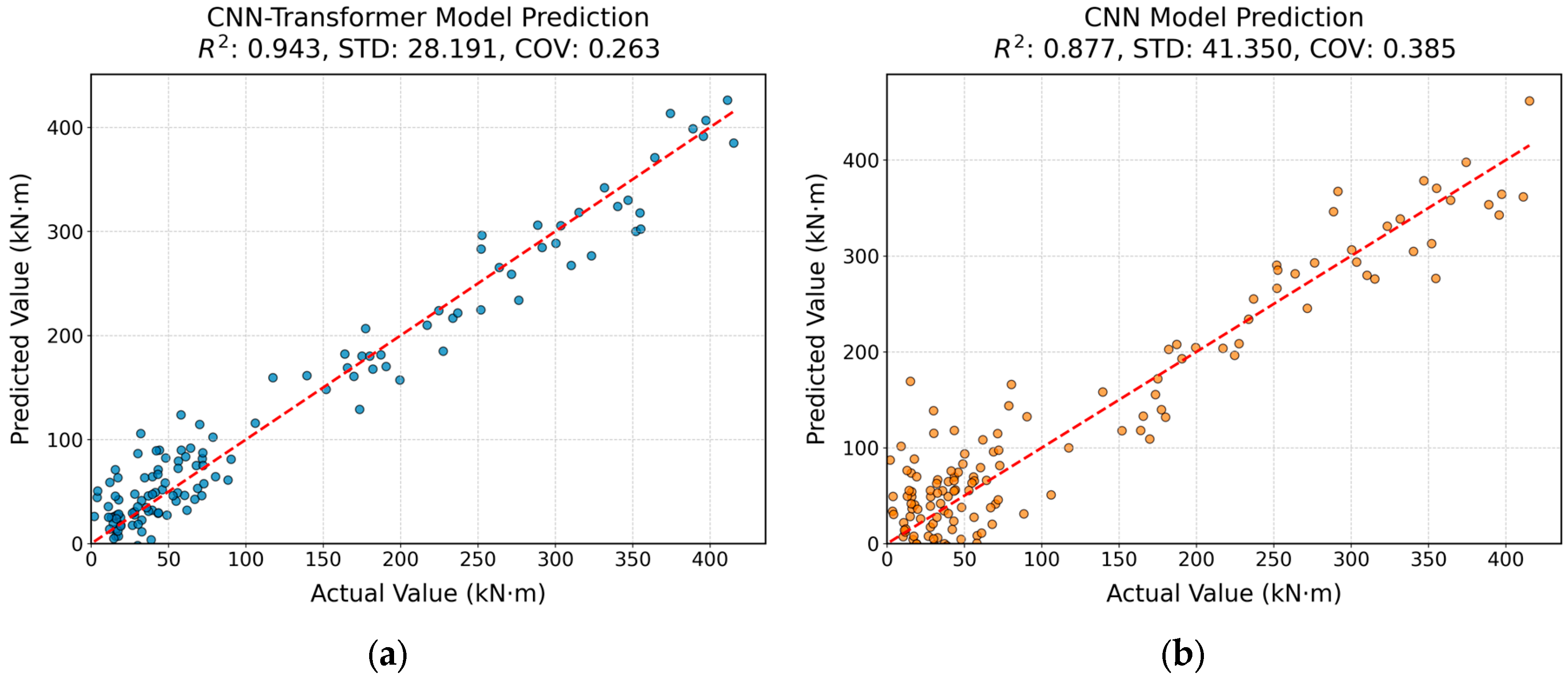
4.2. Model Performance
5. Conclusions
- (1)
- The CNN-Transformer model achieved the highest prediction accuracy, with a test RMSE of 41.310, MAE of 22.963, and an R2 value of 0.943, significantly outperforming traditional models.
- (2)
- Among the benchmarked methods, KNN exhibited the lowest predictive accuracy, indicating its limited capability in modeling complex UHPC beam behaviors.
- (3)
- Both CNN and XGBoost provided relatively satisfactory results; however, their accuracy was notably inferior to the proposed CNN-Transformer model, underscoring the advantage of integrating spatial feature extraction with global context modeling.
- (4)
- The proposed CNN-Transformer framework demonstrates high robustness and generalizability, making it a promising and reliable tool for structural engineers in the design optimization and safety assessment of UHPC beams.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Amran, M.; Huang, S.-S.; Onaizi, A.M.; Makul, N.; Abdelgader, H.S.; Ozbakkaloglu, T. Recent trends in ultra-high performance concrete (UHPC): Current status, challenges, and future prospects. Constr. Build. Mater. 2022, 352, 129029. [Google Scholar] [CrossRef]
- Zhou, M.; Lu, W.; Song, J.; Lee, G.C. Application of ultra-high performance concrete in bridge engineering. Constr. Build. Mater. 2018, 186, 1256–1267. [Google Scholar] [CrossRef]
- Sharma, R.; Jang, J.G.; Bansal, P.P. A comprehensive review on effects of mineral admixtures and fibers on engineering properties of ultra-high-performance concrete. J. Build. Eng. 2022, 45, 103314. [Google Scholar] [CrossRef]
- Murali, G. Recent research in mechanical properties of geopolymer-based ultra-high-performance concrete: A review. Def. Technol. 2024, 32, 67–88. [Google Scholar] [CrossRef]
- Li, Y.-Y.; Nie, J.-G.; Ding, R.; Fan, J.-S. Seismic performance of squat UHPC shear walls subjected to high-compression shear combined cyclic load. Eng. Struct. 2023, 276, 115369. [Google Scholar] [CrossRef]
- Xue, J.; Briseghella, B.; Huang, F.; Nuti, C.; Tabatabai, H.; Chen, B. Review of ultra-high performance concrete and its application in bridge engineering. Constr. Build. Mater. 2020, 260, 119844. [Google Scholar] [CrossRef]
- Ravichandran, D.; Prem, P.R.; Kaliyavaradhan, S.K.; Ambily, P. Influence of fibers on fresh and hardened properties of Ultra High Performance Concrete (UHPC)—A review. J. Build. Eng. 2022, 57, 104922. [Google Scholar] [CrossRef]
- Deng, Z.; Liu, X.; Zhou, X.; Yang, Q.; Chen, P.; de la Fuente, A.; Ren, L.; Du, L.; Han, Y.; Xiong, F.; et al. Main engineering problems and countermeasures in ultra-long-distance rock pipe jacking project: Water pipeline case study in Chongqing. Tunn. Undergr. Space Technol. 2022, 123, 104420. [Google Scholar] [CrossRef]
- Abid, M.; Hou, X.; Zheng, W.; Hussain, R.R. Effect of fibers on high-temperature mechanical behavior and microstructure of reactive powder concrete. Materials 2019, 12, 329. [Google Scholar] [CrossRef]
- Yong, W.T.L.; Thien, V.Y.; Misson, M.; Chin, G.J.W.L.; Hussin, S.N.I.S.; Chong, H.L.H.; Yusof, N.A.; Ma, N.L.; Rodrigues, K.F. Seaweed: A bioindustrial game-changer for the green revolution. Biomass Bioenergy 2024, 183, 107122. [Google Scholar] [CrossRef]
- El-Abbasy, A.A. Tensile, flexural, impact strength, and fracture properties of ultra-high-performance fiber-reinforced concrete–a comprehensive review. Constr. Build. Mater. 2023, 408, 133621. [Google Scholar] [CrossRef]
- Min, W.; Jin, W.; He, X.; Wu, R.; Chen, K.; Chen, J.; Xia, J. Experimental study on the flexural fatigue performance of slag/fly ash geopolymer concrete reinforced with modified basalt and PVA hybrid fibers. J. Build. Eng. 2024, 94, 109917. [Google Scholar] [CrossRef]
- Regalla, S.S.; Kumar, N.S. Investigation of hydration kinetics, microstructure and mechanical properties of multiwalled carbon nano tubes (MWCNT) based future emerging ecological economic ultra high-performance concrete (E3 UHPC). Results Eng. 2024, 23, 102432. [Google Scholar] [CrossRef]
- Zaid, O.; El Ouni, M.H. Advancements in 3D printing of cementitious materials: A review of mineral additives, properties, and systematic developments. Constr. Build. Mater. 2024, 427, 136254. [Google Scholar] [CrossRef]
- Khayat, K.H.; Meng, W.; Vallurupalli, K.; Teng, L. Rheological properties of ultra-high-performance concrete—An overview. Cem. Concr. Res. 2019, 124, 105828. [Google Scholar] [CrossRef]
- Wu, C.; Yu, Z.; Shao, R.; Li, J. A comprehensive review of extraterrestrial construction, from space concrete materials to habitat structures. Eng. Struct. 2024, 318, 118723. [Google Scholar] [CrossRef]
- Deng, Z.; Chen, P.; Liu, X.; Du, L.; Tan, J.; Liang, N. Study on the tensile and compressive mechanical properties of multi-scale fiber-reinforced concrete: Laboratory test and mesoscopic numerical simulation. J. Build. Eng. 2024, 86, 108852. [Google Scholar] [CrossRef]
- Deng, Z.; Liu, X.; Chen, P.; de la Fuente, A.; Zhao, Y.; Liang, N.; Zhou, X.; Du, L.; Han, Y. Basalt-polypropylene fiber reinforced concrete for durable and sustainable pipe production. Part 2: Numerical and parametric analysis. Struct. Concr. 2022, 23, 328–345. [Google Scholar] [CrossRef]
- Deng, Z.; Liu, X.; Chen, P.; de la Fuente, A.; Zhou, X.; Liang, N.; Han, Y.; Du, L. Basalt-polypropylene fiber reinforced concrete for durable and sustainable pipe production. Part 1: Experimental program. Struct. Concr. 2022, 23, 311–327. [Google Scholar] [CrossRef]
- Bischof, P.; Mata-Falcón, J.; Kaufmann, W. Fostering innovative and sustainable mass-market construction using digital fabrication with concrete. Cem. Concr. Res. 2022, 161, 106948. [Google Scholar] [CrossRef]
- Abellán-García, J.; Carvajal-Muñoz, J.S.; Ramírez-Munévar, C. Application of ultra-high-performance concrete as bridge pavement overlays: Literature review and case studies. Constr. Build. Mater. 2024, 410, 134221. [Google Scholar] [CrossRef]
- Qian, Y.; Yang, J.; Yang, W.; Alateah, A.H.; Alsubeai, A.; Alfares, A.M.; Sufian, M. Prediction of ultra-high-performance concrete (UHPC) properties using gene expression programming (GEP). Buildings 2024, 14, 2675. [Google Scholar] [CrossRef]
- Qiu, M.; Shao, X.; Wille, K.; Yan, B.; Wu, J. Experimental investigation on flexural behavior of reinforced ultra high performance concrete low-profile T-beams. Int. J. Concr. Struct. Mater. 2020, 14, 5. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, Y.; Hussein, H.H.; Chen, G. Flexural strengthening of reinforced concrete beams or slabs using ultra-high performance concrete (UHPC): A state of the art review. Eng. Struct. 2020, 205, 110035. [Google Scholar] [CrossRef]
- Solhmirzaei, R.; Salehi, H.; Kodur, V. Predicting flexural capacity of ultrahigh-performance concrete beams: Machine learning–based approach. J. Struct. Eng. 2022, 148, 04022031. [Google Scholar] [CrossRef]
- Ergen, F.; Katlav, M. Machine and deep learning-based prediction of flexural moment capacity of ultra-high performance concrete beams with/out steel fiber. J. Civ. Eng. 2024, 25, 4541–4562. [Google Scholar] [CrossRef]
- Safdar, M.; Matsumoto, T.; Kakuma, K. Flexural behavior of reinforced concrete beams repaired with ultra-high performance fiber reinforced concrete (UHPFRC). Compos. Struct. 2016, 157, 448–460. [Google Scholar] [CrossRef]
- Abellan-Garcia, J.; Fernandez, J.; Khan, M.I.; Abbas, Y.M.; Carrillo, J. Uniaxial tensile ductility behavior of ultrahigh-performance concrete based on the mixture design–Partial dependence approach. Cem. Concr. Compos. 2023, 140, 105060. [Google Scholar] [CrossRef]
- Khaoula, E.; Amine, B.; Mostafa, B.; Deifalla, A.; El-Said, A.; Salama, M.; Awad, A. Machine learning-based prediction of torsional behavior for ultra-high-performance concrete beams with variable cross-sectional shapes. Case Stud. Constr. Mater. 2025, 22, e04136. [Google Scholar] [CrossRef]
- Schmidt, J.; Marques, M.R.; Botti, S.; Marques, M.A.L. Recent advances and applications of machine learning in solid-state materials science. npj Comput. Mater. 2019, 5, 83. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.; Zhu, Y.; Shao, X. Experimental study on flexural behavior of damaged reinforced concrete (RC) beam strengthened by toughness-improved ultra-high performance concrete (UHPC) layer. Compos. Part B Eng. 2020, 186, 107834. [Google Scholar] [CrossRef]
- Abuodeh, O.R.; Abdalla, J.A.; Hawileh, R.A. Assessment of compressive strength of Ultra-high Performance Concrete using deep machine learning techniques. Appl. Soft Comput. 2020, 95, 106552. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, Y.; Qu, S.; Kumar, A.; Shao, X. Improvement of flexural and tensile strength of layered-casting UHPC with aligned steel fibers. Constr. Build. Mater. 2020, 251, 118893. [Google Scholar] [CrossRef]
- Li, W.-W.; Li, Z.-C.; Chen, H.-D.; Zhou, Y.-W.; Mansour, W.; Wang, X.-Q.; Wang, P. Effects of concrete-stirrup interaction on shear behavior of RC beams under varying shear span-depth ratio scenarios. Structures 2024, 61, 106071. [Google Scholar] [CrossRef]
- Amin, A.; Foster, S.J. Shear strength of steel fibre reinforced concrete beams with stirrups. Eng. Struct. 2016, 111, 323–332. [Google Scholar] [CrossRef]
- Wei, F.; Chen, H.; Xie, Y. Experimental study on seismic behavior of reinforced concrete shear walls with low shear span ratio. J. Build. Eng. 2022, 45, 103602. [Google Scholar] [CrossRef]
- Gu, J.; Li, L.; Huang, X.; Chen, H. Experimental study on the reinforced concrete beams with varied stirrup reinforcement ratio under static and impact loads. Struct. Concr. 2025, 26, 3124–3145. [Google Scholar] [CrossRef]
- Ye, M.; Li, L.; Yoo, D.-Y.; Li, H.; Zhou, C.; Shao, X. Prediction of shear strength in UHPC beams using machine learning-based models and SHAP interpretation. Constr. Build. Mater. 2023, 408, 133752. [Google Scholar] [CrossRef]
- Ombres, L.; Aiello, M.A.; Cascardi, A.; Verre, S. Modeling of steel-reinforced grout composite system-to-concrete bond capacity using artificial neural networks. J. Compos. Constr. 2024, 28, 04024034. [Google Scholar] [CrossRef]
- Jasmine, P.H.; Arun, S. Machine learning applications in structural engineering—A review. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1114, 012012. [Google Scholar] [CrossRef]
- Xiong, J.; Guo, S.; Wu, Y.; Yan, D.; Xiao, C.; Lu, X. Predicting the response of heating and cooling demands of residential buildings with various thermal performances in China to climate change. Energy 2023, 269, 126789. [Google Scholar] [CrossRef]
- Phoeuk, M.; Kwon, M. Accuracy prediction of compressive strength of concrete incorporating recycled aggregate using ensemble learning algorithms: Multinational dataset. Adv. Civ. Eng. 2023, 2023, 5076429. [Google Scholar] [CrossRef]
- Ray, P.; Reddy, S.S.; Banerjee, T. Various dimension reduction techniques for high dimensional data analysis: A review. Artif. Intell. Rev. 2021, 54, 3473–3515. [Google Scholar] [CrossRef]
- Huang, F.; Li, Y.; Wu, J.; Dong, J.; Wang, Y. Identification of repeatedly frozen meat based on near-infrared spectroscopy combined with self-organizing competitive neural networks. Int. J. Food Prop. 2016, 19, 1007–1015. [Google Scholar] [CrossRef]
- Chin, Y.-H.; Wang, J.-C.; Huang, C.-L.; Wang, K.-Y.; Wu, C.-H. Speaker identification using discriminative features and sparse representation. IEEE Trans. Inf. Forensics Secur. 2017, 12, 1979–1987. [Google Scholar] [CrossRef]
- Zhao, L.; Liu, Y.; Zhao, J.; Zhang, Y.; Xu, L.; Xiang, Y.; Liu, J. Robust PCA-deep belief network surrogate model for distribution system topology identification with DERs. Int. J. Electr. Power Energy Syst. 2021, 125, 106441. [Google Scholar] [CrossRef]
- Ajin, R.S.; Segoni, S.; Fanti, R. Optimization of SVR and CatBoost models using metaheuristic algorithms to assess landslide susceptibility. Sci. Rep. 2024, 14, 24851. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. Adv. Neural Inf. Process. Syst. 2018, 31, 6639–6649. [Google Scholar] [CrossRef]
- Mohan, M.; Jetti, K.D.; Smith, M.D.; Demerdash, O.N.; Kidder, M.K.; Smith, J.C. Accurate machine learning for predicting the viscosities of deep eutectic solvents. J. Chem. Theory Comput. 2024, 20, 3911–3926. [Google Scholar] [CrossRef]
- D’Amico, B.; Myers, R.J.; Sykes, J.; Voss, E.; Cousins-Jenvey, B.; Fawcett, W.; Richardson, S.; Kermani, A.; Pomponi, F. Machine learning for sustainable structures: A call for data. Structures 2019, 19, 1–4. [Google Scholar] [CrossRef]


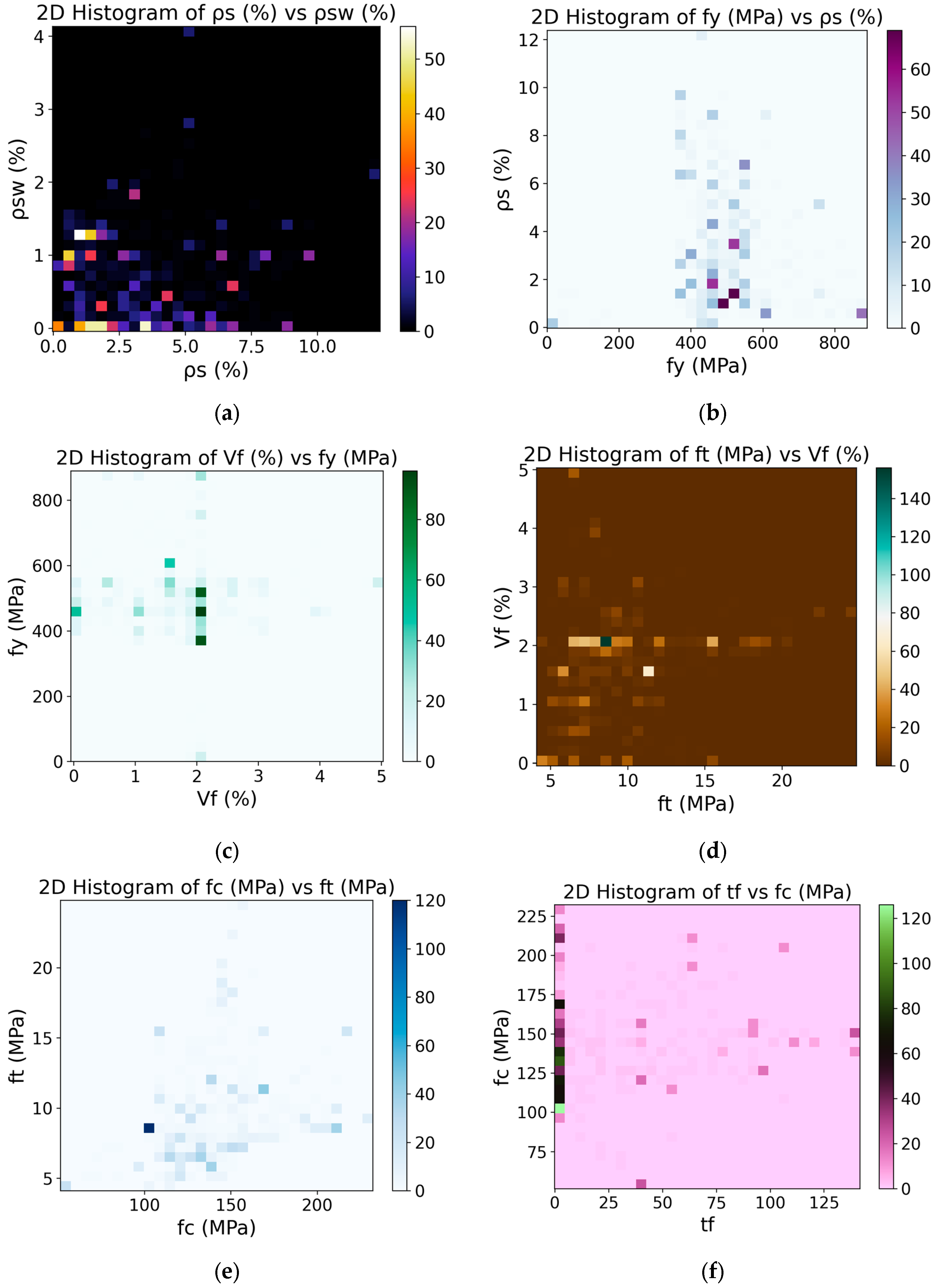
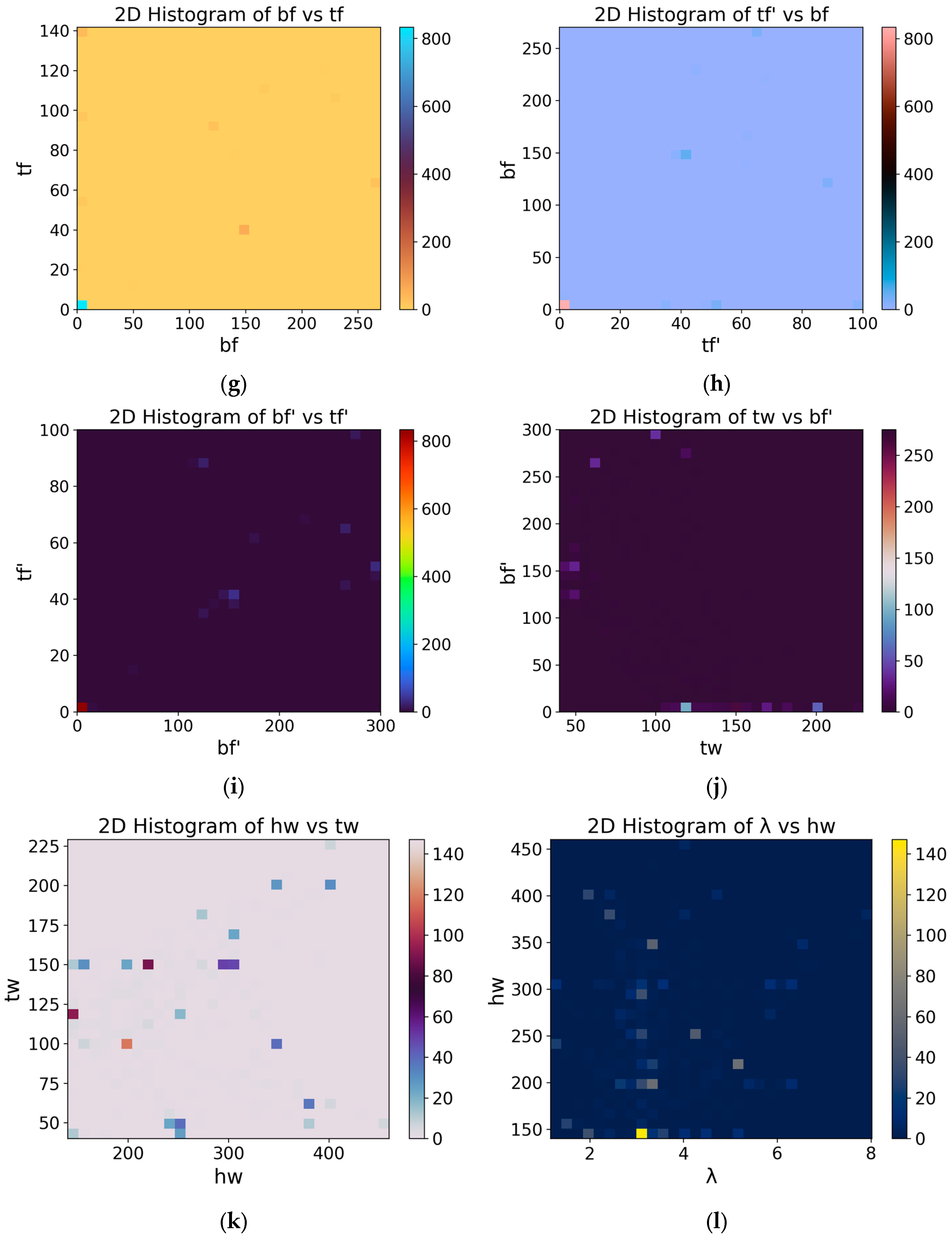
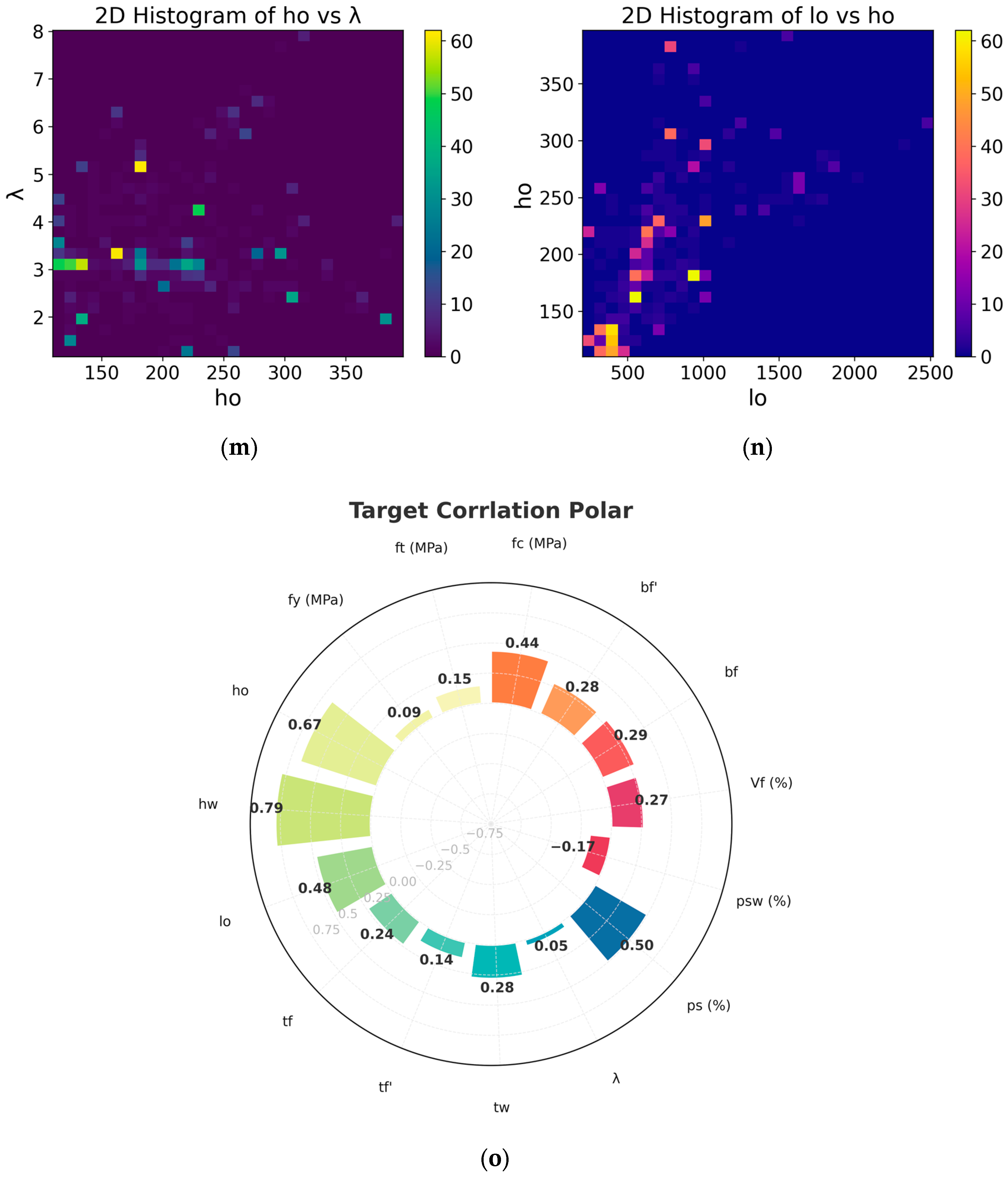
| Test No. | Data | lo (mm) | ho (mm) | λ | hw (mm) | tw (mm) | bf’(mm) | tf’(mm) | bf (mm) | tf (mm) | fc (MPa) | ft (MPa) | Vf (%) | fy (MPa) | ρs(%) | ρsw(%) | Mu(kN·m) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 760 | 305 | 2.5 | 380 | 65 | 270 | 45 | 230 | 105 | 203–205 | 8.55–8.59 | 2–2.5 | 551 | 6.06 | 0.14 | 395.58–411.16 |
| 2 | 10 | 900 | 177 | 5.1 | 220 | 150 | 0 | 0 | 0 | 0 | 200.9–232.1 | 8.5–9.14 | 0–2 | 495–510 | 0.94–1.5 | 1.31 | 28.17–60.26 |
| 3 | 2 | 610–1397 | 235 | 2.6–5.9 | 270 | 180 | 0 | 0 | 0 | 0 | 167 | 15.3 | 0 | 436 | 0.94–1.26 | 0 | 43.34–67.82 |
| 4 | 4 | 762.5 | 305 | 2.5 | 380 | 65 | 270 | 65 | 270 | 65 | 195–212 | 9.5–9.8 | 2–2.5 | 551 | 6.62 | 0–0.6 | 346.94–415.18 |
| 5 | 2 | 763 | 218 | 3.5 | 300 | 150 | 0 | 0 | 0 | 0 | 153–159 | 7.42–7.57 | 1–2 | 474 | 6.12 | 0 | 251.79–276.21 |
| 6 | 3 | 639 | 213 | 3 | 300 | 150 | 0 | 0 | 0 | 0 | 153–154 | 7.42–7.45 | 1–2 | 468 | 8.76 | 0 | 252.41–303.53 |
| 7 | 3 | 600–1448.8 | 200–360 | 2.5–4.8 | 290–406 | 60–229 | 0–140 | 0–60 | 0–140 | 0–80 | 137.6–167 | 7.22–12.2 | 1–3 | 365–618 | 1.28–12.34 | 0–2.18 | 165.6–340.2 |
| 8 | 6 | 300 | 130 | 2 | 150 | 100 | 0 | 0 | 0 | 0 | 127–135 | 6.76–6.97 | 0–0.5 | 550 | 1.2–1.7 | 1.34 | 10.37–15.87 |
| 9 | 4 | 392–504 | 112 | 3.5–4.5 | 140 | 100 | 0 | 0 | 0 | 0 | 110–151 | 15.4–18.5 | 2 | 520 | 3.4 | 0 | 4.31–39.59 |
| 10 | 4 | 1000 | 230 | 4.3 | 250 | 40 | 150 | 40 | 150 | 40 | 51.3 | 4.3 | 0 | 467–470 | 0.8–2.2 | 1.26 | 18.84–45.98 |
| 11 | 5 | 750 | 380 | 2 | 400 | 200 | 0 | 0 | 0 | 0 | 106.4–117 | 5–11 | 0–1 | 475 | 1 | 0–0.28 | 139.35–174.94 |
| 12 | 3 | 1000 | 230 | 4.3 | 250 | 50 | 150 | 40 | 150 | 40 | 145–159 | 5.3–10.7 | 0–2.5 | 470 | 2.2 | 0–2.01 | 48.91–58.2 |
| 13 | 4 | 952–1848 | 280 | 3.4–6.6 | 350 | 200 | 0 | 0 | 0 | 0 | 117–217 | 7.84–15.48 | 2 | 445 | 4.38 | 0–0.47 | 300.2–388.8 |
| 14 | 3 | 1260–2520 | 315–397 | 4–8 | 380–460 | 50 | 170–230 | 60–70 | 165–220 | 110–120 | 146 | 19–20 | 2 | 450 | 2.69–6.98 | 0 | 163.8–252 |
| 15 | 4 | 600 | 182–188 | 3.2–3.3 | 220 | 150 | 0 | 0 | 0 | 0 | 141.5 | 12 | 2 | 417–461 | 1.09–4.99 | 0.45–1.12 | 43.26–105.93 |
| 16 | 6 | 660–700 | 220–230 | 3 | 250–290 | 50–150 | 0–150 | 0–40 | 0–150 | 0–40 | 121–166.9 | 6.71–9.98 | 0–1.5 | 470–617.7 | 0.78–1.76 | 0–1.4 | 3.48–187.11 |
| 17 | 8 | 400 | 130 | 3.1 | 150 | 100 | 0 | 0 | 0 | 0 | 124.9–176.9 | 6.71–7.98 | 1–4 | 470 | 0–1.74 | 0 | 3.48–19.06 |
| 18 | 4 | 278.75 | 223 | 1.3 | 240 | 50 | 120 | 90 | 120 | 90 | 148–155 | 7.35–24.8 | 2–2.55 | 512 | 1.37 | 0 | 30.38–34.43 |
| 19 | 3 | 700 | 230 | 3 | 250 | 120 | 280 | 100 | 0 | 0 | 98.913 | 125.3 | 9.3 | 424.6–427.9 | 0.21–0.74 | 0.84 | 32.2–41.3 |
| 20 | 4 | 1000 | 300 | 3.3 | 350 | 100 | 300 | 50 | 0 | 0 | 141.67 | 148.6–149.8 | 9.7–11.5 | 551.8–557 | 2.9–4.59 | 0.15 | 180–271.5 |
| 21 | 8 | 361.38–350 | 110–114 | 3.1–3.2 | 140–150 | 40–120 | 0–120 | 0–35 | 0 | 0 | 52.5–127.33 | 4.11–116 | 0–7.1 | 411.4–760.9 | 0.8–4.96 | 0.31–4.1 | 12.95–30.08 |
| 22 | 8 | 203–312.5 | 124–260 | 1.2–1.6–2.5 | 150–300 | 100–152 | 0 | 0 | 0 | 0 | 113.3–164.8 | 4.75–10.52 | 0–3 | 406.2–570 | 3.2–5.23 | 0–1.89 | 19.06–263.64 |
| 23 | 6 | 1000 | 162–331 | 3–6.2–3.4 | 200–350 | 100–150 | 0–300 | 0–50 | 0 | 0 | 140.1–141.67 | 5.6–140.1 | 1.5–… | 518.3–535.7 | 1.18–4.96 | 0 | 48.1–199.35 |
| 24 | 4 | 1600 | 257–269.5 | 5.9–6.2 | 300 | 170 | 0 | 0 | 0 | 0 | 119.7–135.6 | 5.63–6.26 | 3–5 | 543.4 | 3.21–6.74 | 0.59 | 233.6–323.2 |
| 25 | 3 | 599.98–666.7 | 130–262 | 2.3–5.1 | 150–300 | 150 | 0 | 0 | 0 | 0 | 130.5–138.1 | 6.79–9.8 | 2–5 | 400–543 | 4–6.31 | 0–1.4 | 58–288.5 |
| 26 | 4 | 1600 | 257–269.5 | 5.9–6.2 | 300 | 170 | 0 | 0 | 0 | 0 | 119.7–135.6 | 5.63–6.26 | 3–5 | 543.4 | 3.21–6.74 | 0.59 | 233.6–323.2 |
| 27 | 8 | 380 | 120 | 3.2 | 140 | 120 | 0 | 0 | 0 | 0 | 94.3–135.6 | 5.83–6.99 | 0.5–2 | 760.9–889.7 | 0.7–1.57 | 0.94 | 1.86–21.5 |
| 28 | 3 | 660 | 220 | 3 | 290 | 150 | 0 | 0 | 0 | 0 | 166.9 | 11.5 | 1.5 | 617.7 | 0.78 | 0.63–1.59 | 354.62–374.22 |
| 29 | 4 | 392–504 | 112 | 3.5–4.5 | 140 | 100 | 0 | 0 | 0 | 0 | 110–151 | 15.4–18.5 | 2 | 520 | 3.4 | 0 | 28–43.12 |
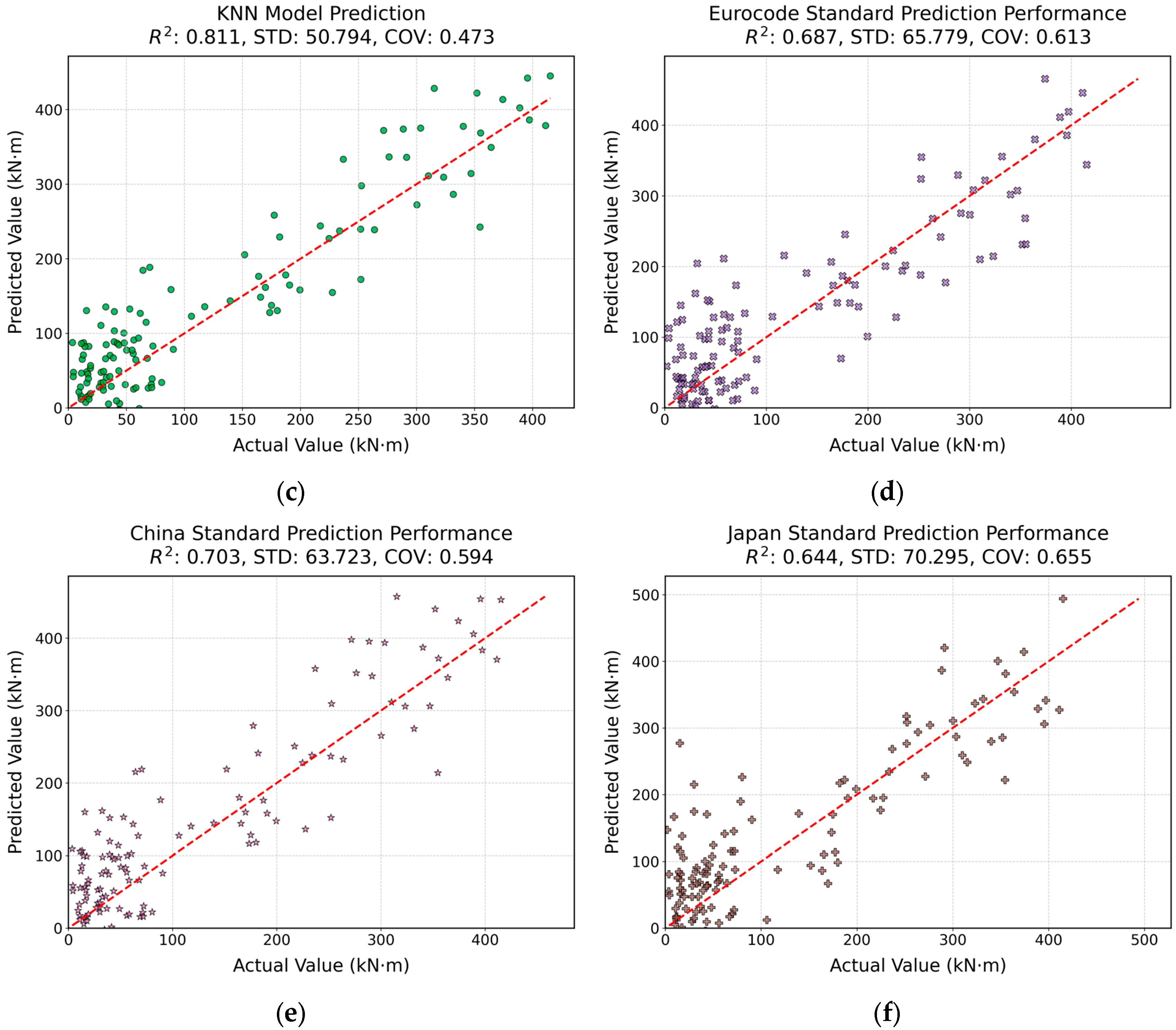
| Model/Standard | RMSE | MAE | R2 | STD | COV |
|---|---|---|---|---|---|
| CNN-Transformer | 41.31 | 22.963 | 0.943 | 28.191 | 0.263 |
| CNN | 55.22 | 30.15 | 0.877 | 41.35 | 0.385 |
| XGBoost | 50.3 | 27.9 | 0.83 | 47.21 | 0.453 |
| KNN | 65.48 | 38.7 | 0.811 | 50.794 | 0.473 |
| Eurocode 2 | — | — | 0.703 | 63.723 | 0.594 |
| Chinese JTG 3362 | — | — | 0.671 | 67.48 | 0.627 |
| Japanese JSCE | — | — | 0.644 | 70.295 | 0.655 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, L.; Liu, P.; Yang, F.; Feng, X. Enhanced Convolutional Neural Network–Transformer Framework for Accurate Prediction of the Flexural Capacity of Ultra-High-Performance Concrete Beams. Buildings 2025, 15, 3138. https://doi.org/10.3390/buildings15173138
Yan L, Liu P, Yang F, Feng X. Enhanced Convolutional Neural Network–Transformer Framework for Accurate Prediction of the Flexural Capacity of Ultra-High-Performance Concrete Beams. Buildings. 2025; 15(17):3138. https://doi.org/10.3390/buildings15173138
Chicago/Turabian StyleYan, Long, Pengfei Liu, Fan Yang, and Xu Feng. 2025. "Enhanced Convolutional Neural Network–Transformer Framework for Accurate Prediction of the Flexural Capacity of Ultra-High-Performance Concrete Beams" Buildings 15, no. 17: 3138. https://doi.org/10.3390/buildings15173138
APA StyleYan, L., Liu, P., Yang, F., & Feng, X. (2025). Enhanced Convolutional Neural Network–Transformer Framework for Accurate Prediction of the Flexural Capacity of Ultra-High-Performance Concrete Beams. Buildings, 15(17), 3138. https://doi.org/10.3390/buildings15173138






