Settlement Characteristics and Control Parameters for the Integrated Construction of Large-Section Underground Structures and Airport Terminals: A Case Study
Abstract
1. Introduction
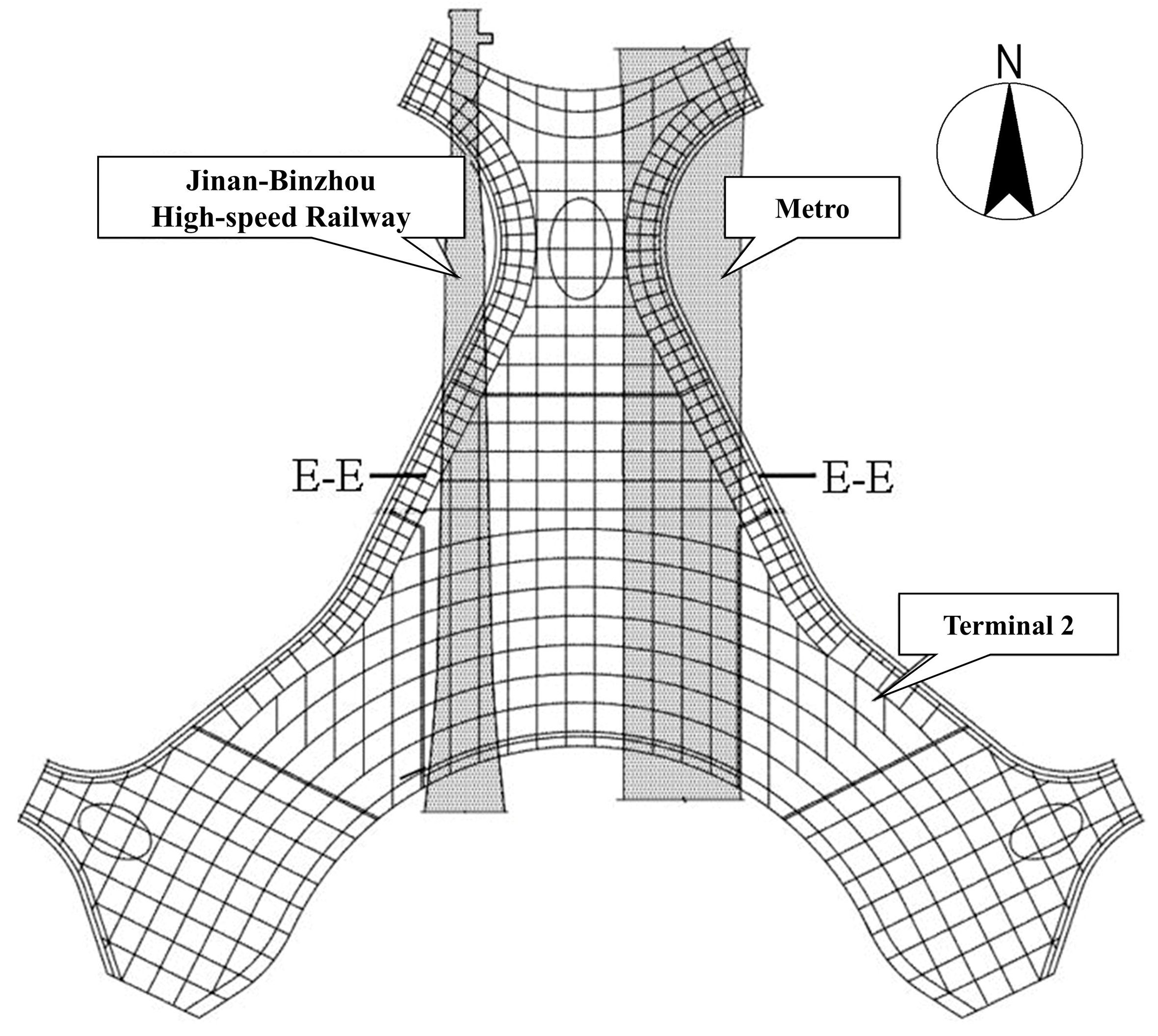
2. Project Background
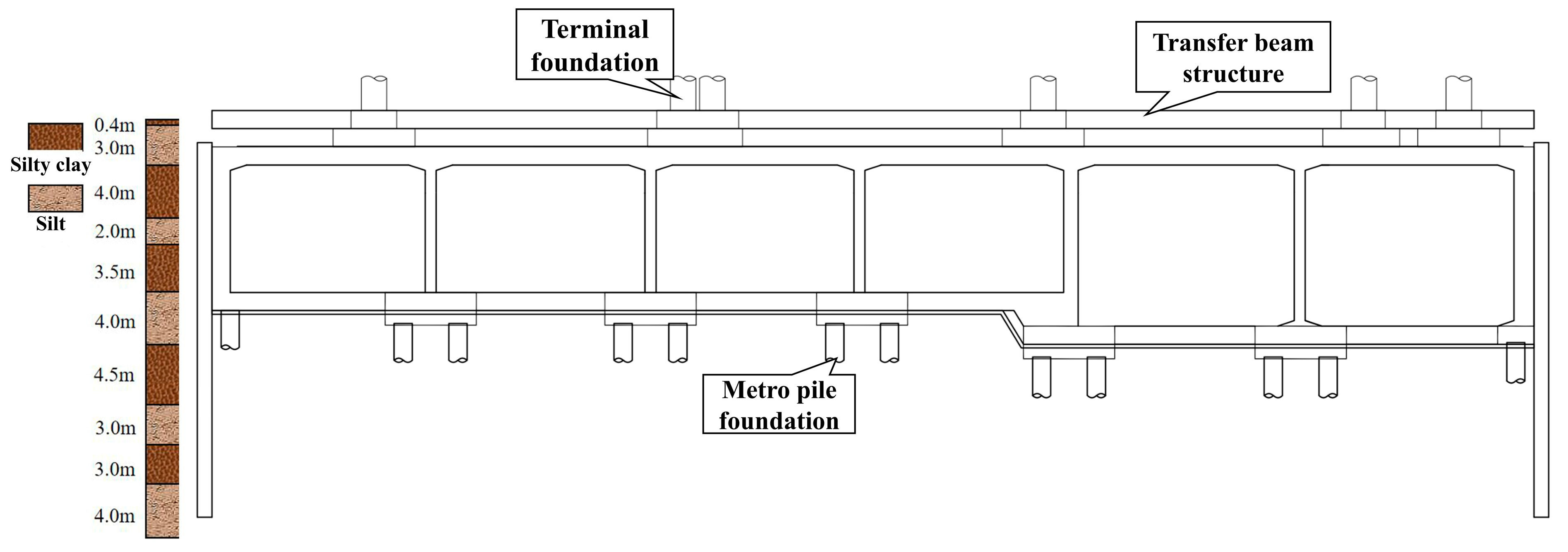
2.1. Project Overview
2.2. Engineering Geology and Hydrogeology
3. Settlement Control Standard Analysis
3.1. Frame Structure Deformation Standards
3.2. Deformation Standards for Existing Tunnel Structures in Crossing Engineering
3.3. Deformation Standards of High-Speed Railway and Metro Structures After Construction
4. Analysis of Settlement Characteristics of Underground Structures Subjected to Uneven Loading from Terminal Buildings
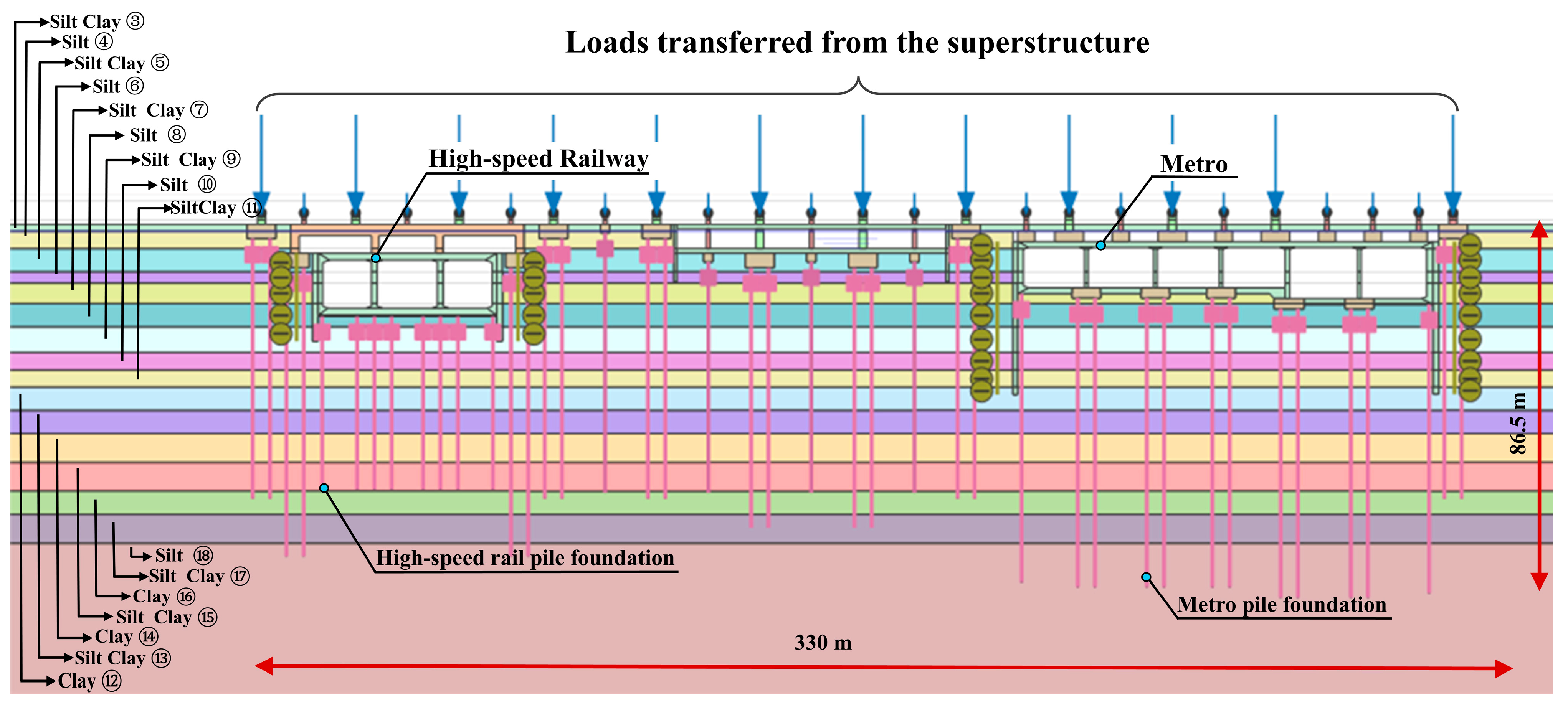
4.1. Numerical Model
4.2. Constitutive Model and Parameters
4.3. Simulation of Construction Process
5. Results and Discussion
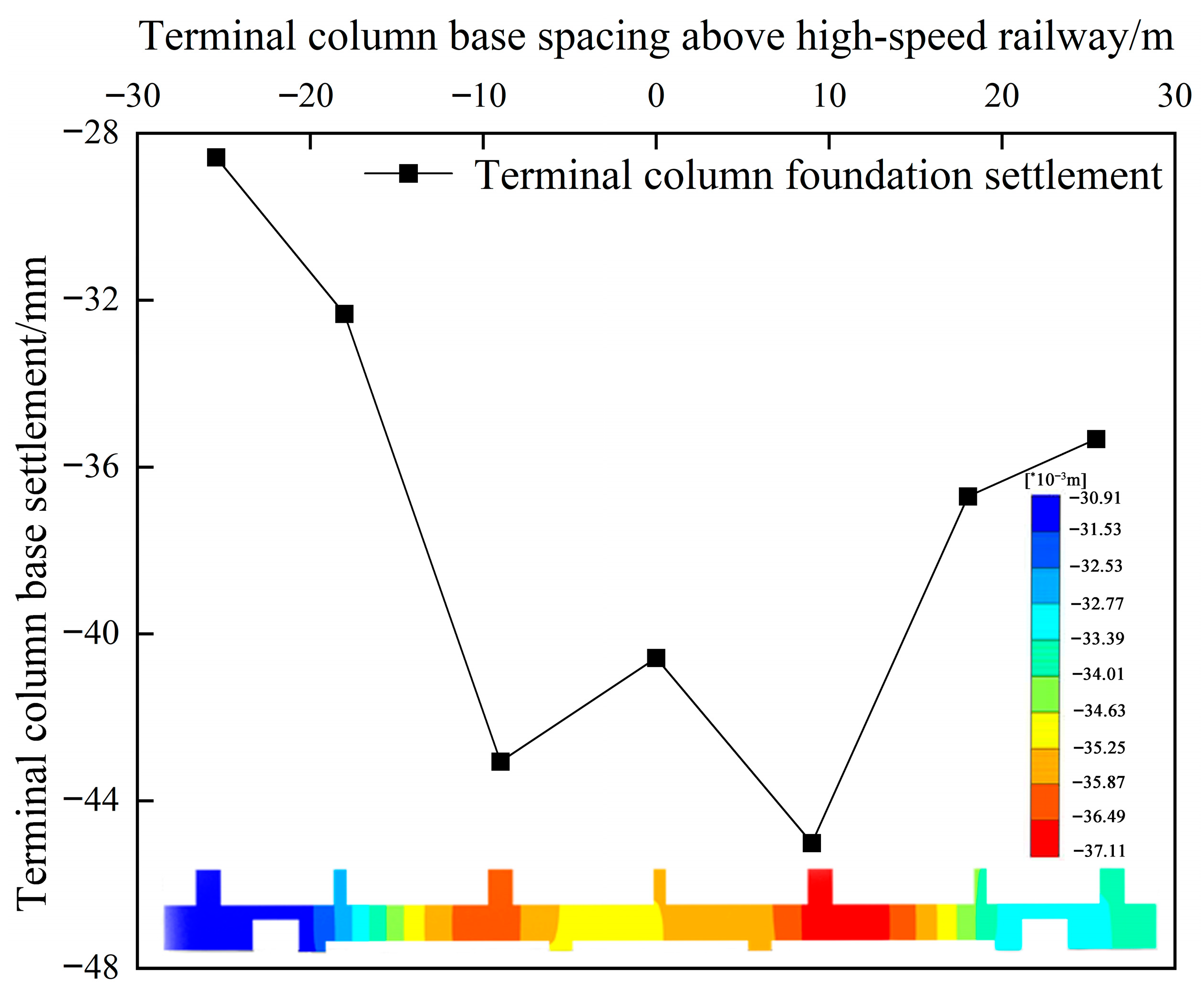
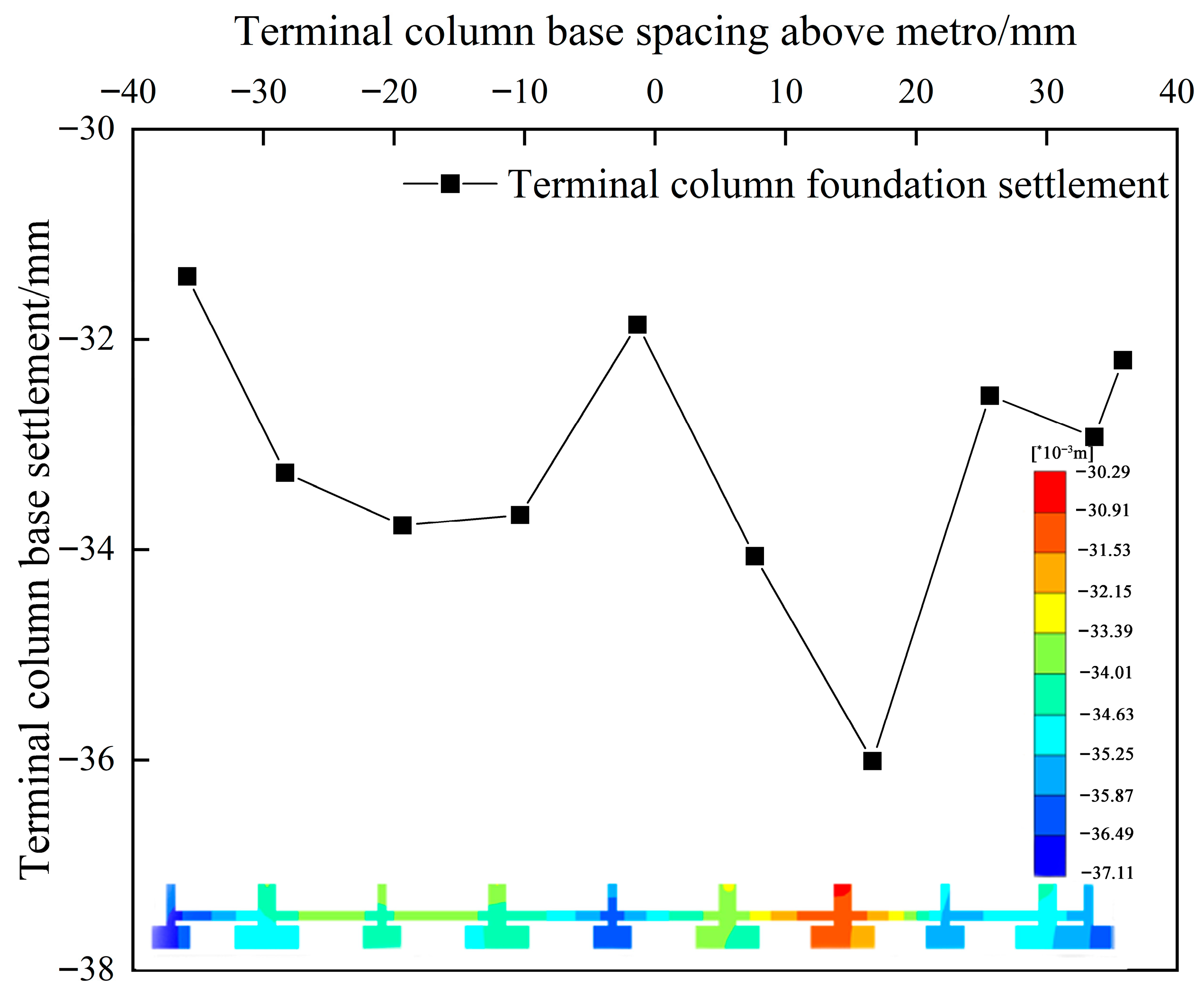
5.1. Settlement Behaviors of Terminal Slabs and Column Foundations
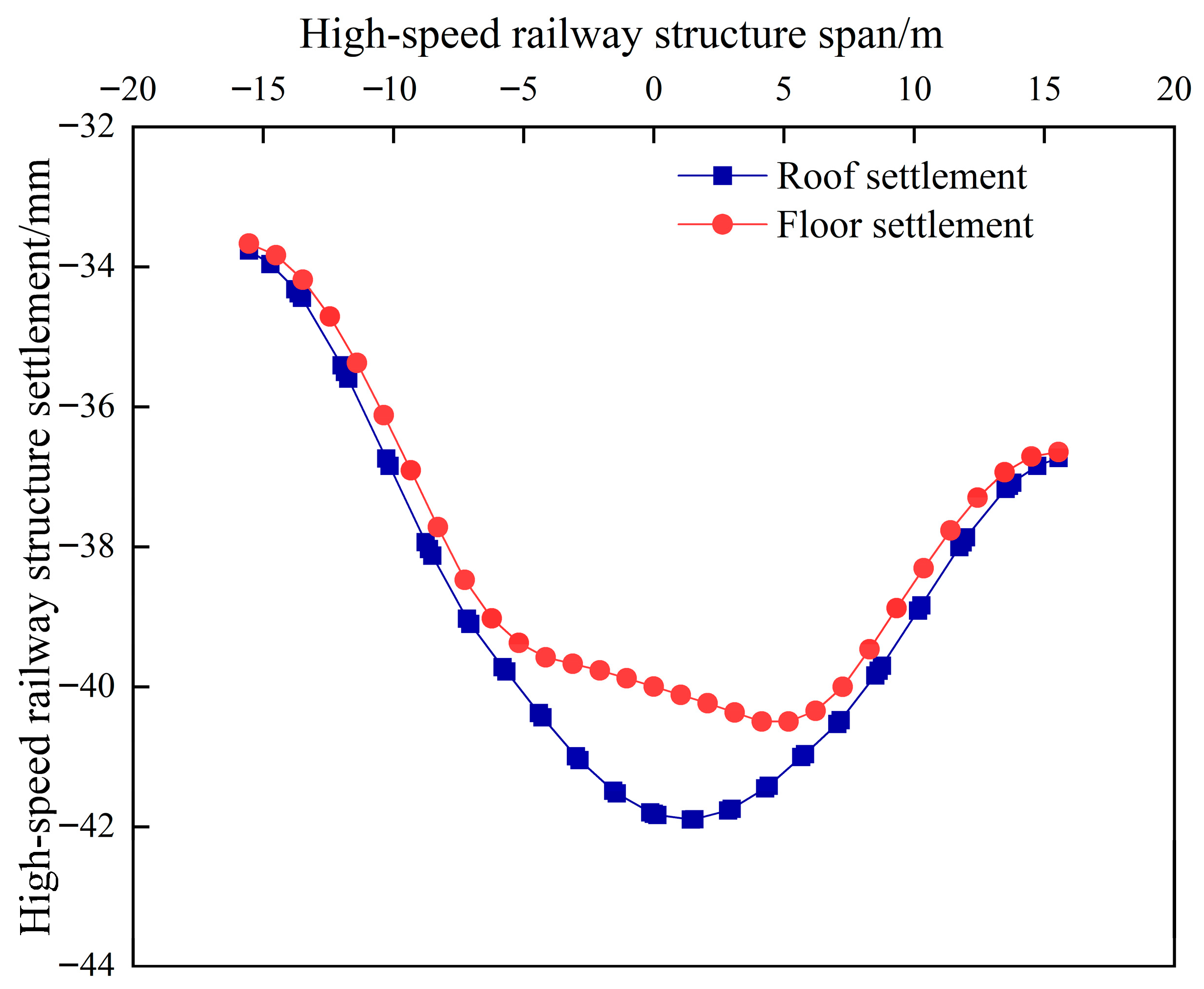
5.2. Settlement Behaviors of High-Speed Railway Structure
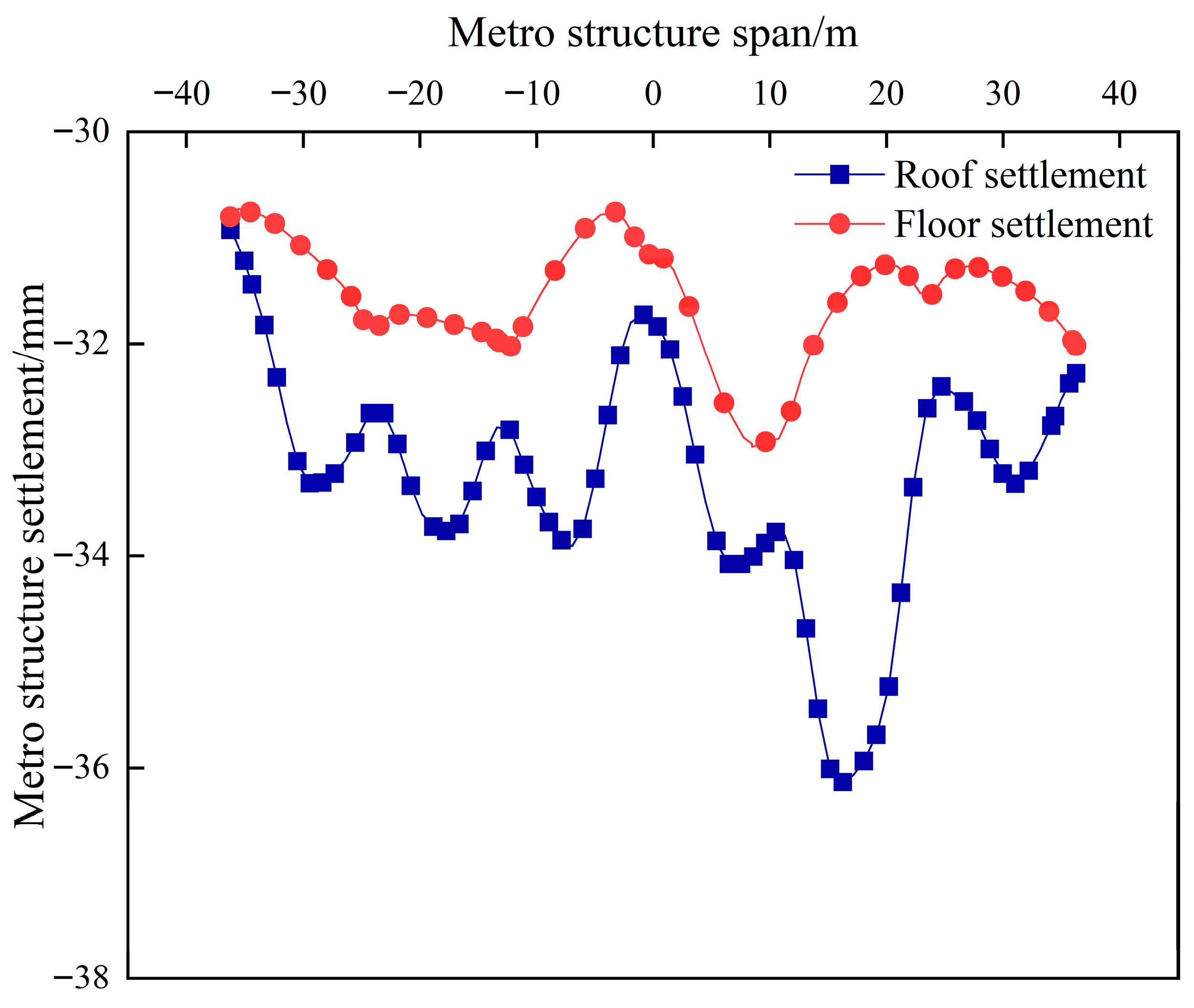
5.3. Settlement Behaviors of Metro Structure
5.4. Sensitivity Analysis of Model Boundary Dimensions
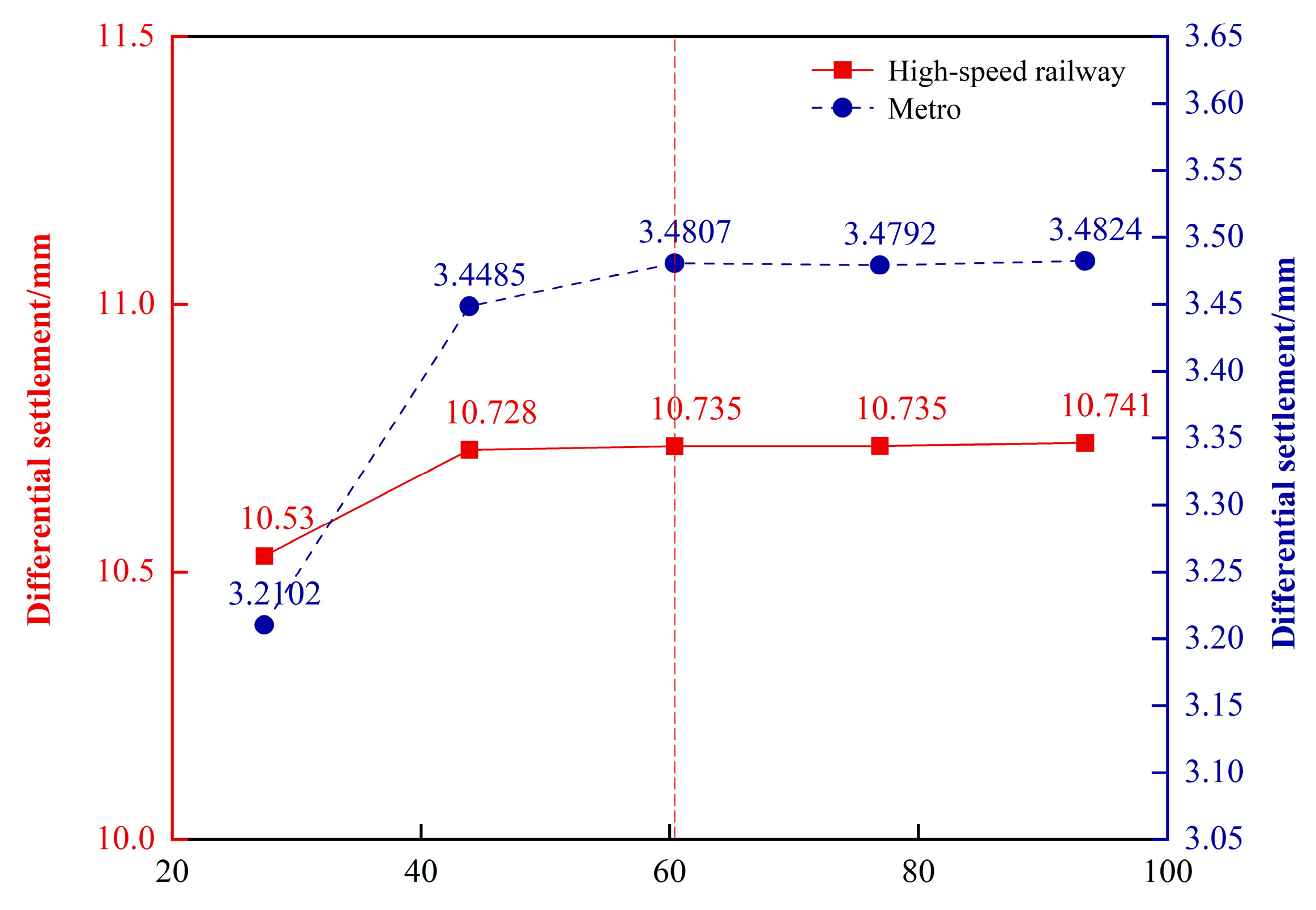
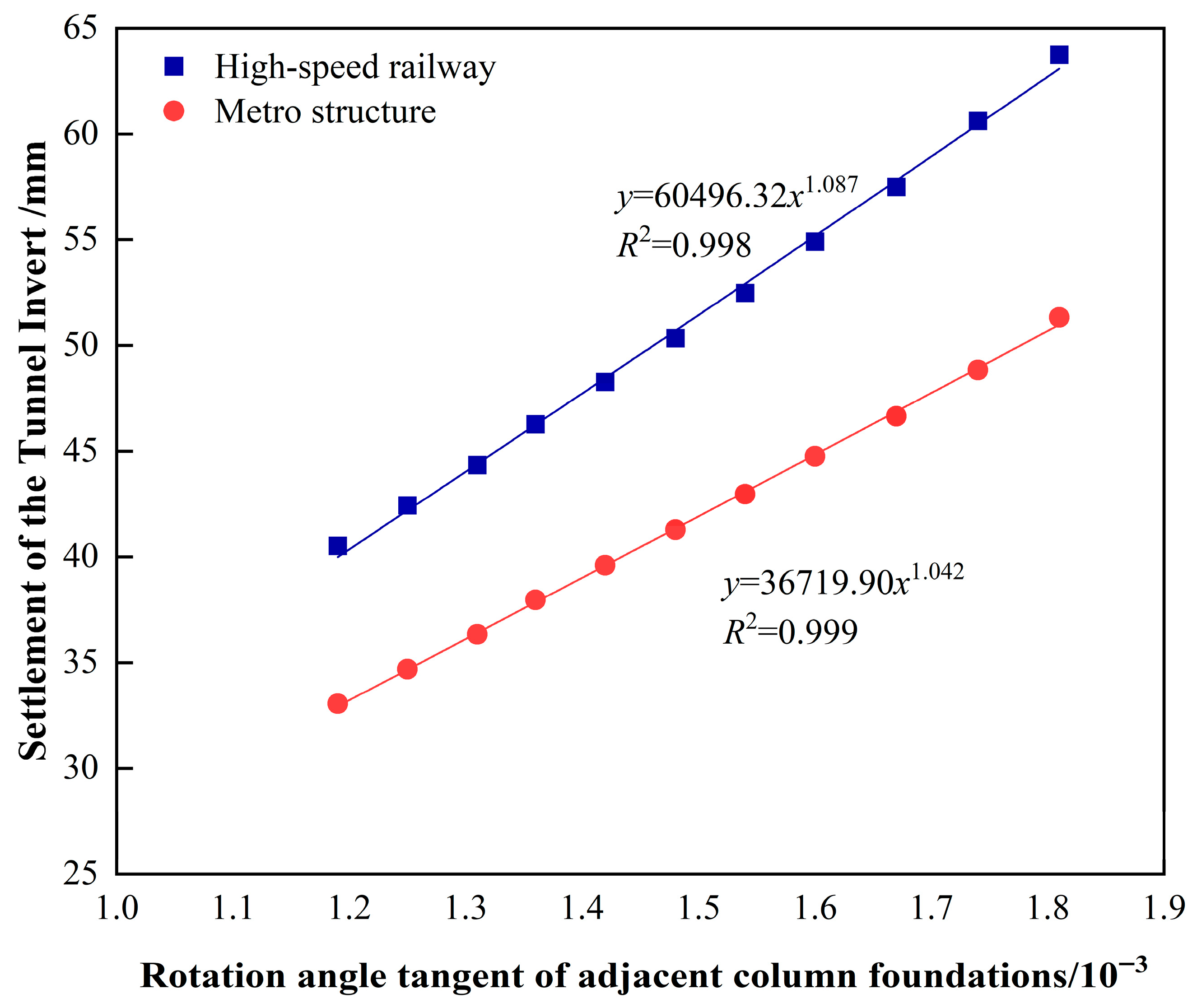
6. Prediction and Analysis of Co-Construction Structure Settlement
7. Conclusions
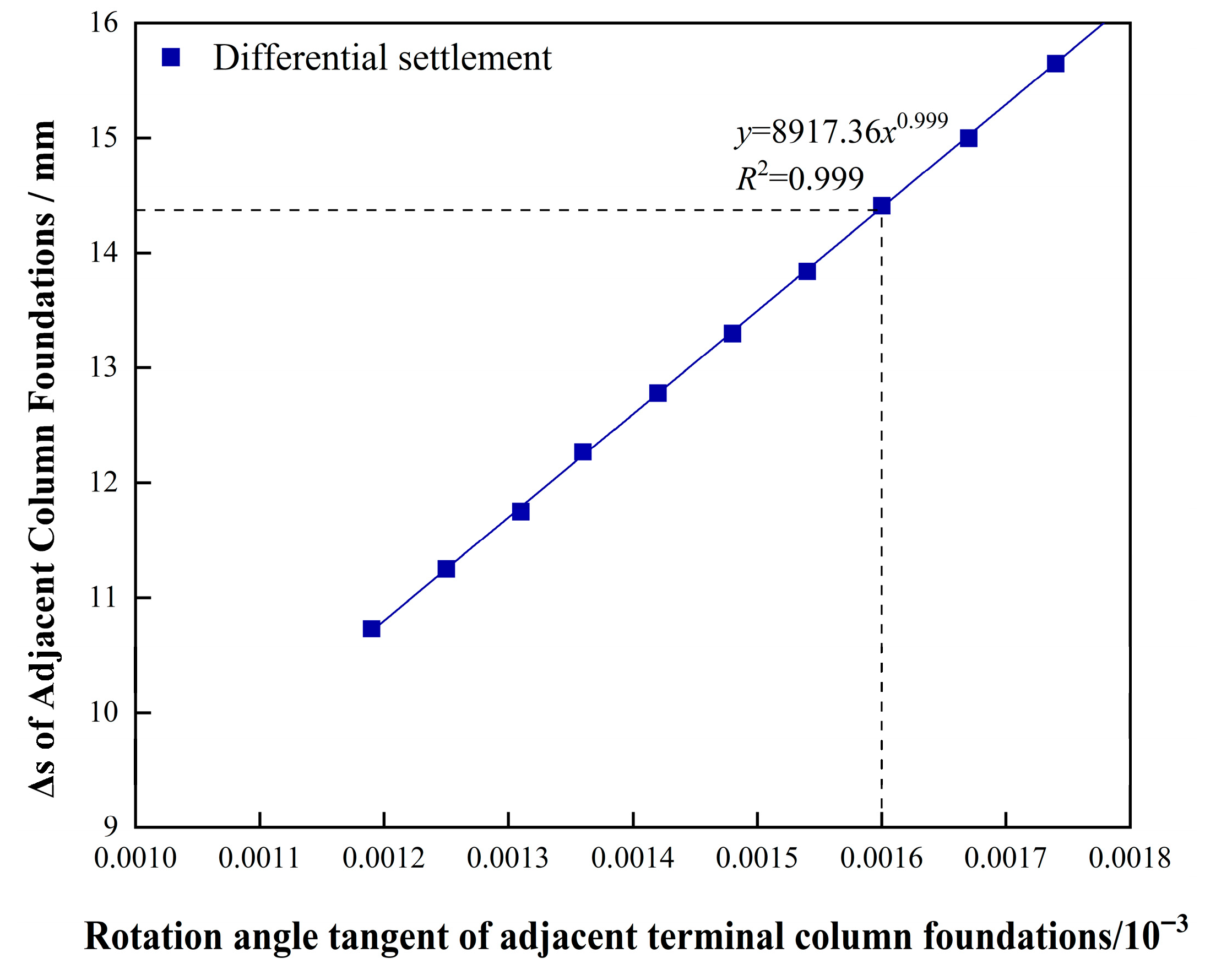
- A settlement control criterion for the adjacent column foundations of the terminal structure, defined by a rotation angle tangent of 1/625, was established to ensure normal serviceability by controlling the differential settlements of the column foundations.
- At cross-section E-E, the maximum differential settlement and tangent rotation angle for the adjacent terminal column foundations occurred at the columns above the left span of the transfer structure, with a differential settlement of 10.73 mm and a rotation angle tangent of 1/839.
- The settlements of the high-speed railway and metro tunnel slabs were lower at mid-span locations and higher at the internal partition walls. The maximum differential settlements between adjacent partition walls at cross-section E-E are 5.49 mm for the high-speed railway and 1.76 mm for the metro structure, corresponding to rotation angle tangent of 1/1712 and 1/6591, respectively.
- When the rotation angle tangent between adjacent terminal column foundations reaches the specified limit of 1/625, the allowable maximum differential settlement for adjacent terminal foundations at cross-section E-E is approximately 14.37 mm. Under these conditions, the maximum allowable settlements of the base slabs for the high-speed railway and metro structures at cross-section E-E are limited to 55.28 mm and 44.83 mm, respectively, with corresponding allowable differential settlements limited to 7.5 mm and 3.13 mm.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Luo, Q.Y.; Jia, H.F.; Sun, B.F. Research on evaluating functions and structures of comprehensive passenger transport hub. In Proceedings of the 1st International Conference on Sustainable Construction & Risk Management, Beijing, China, 16–18 October 2010; Wu, D., Xu, M.Z., Zhang, Z.J., Fang, Y., Eds.; China Architecture & Building Press: Beijing, China, 2010; pp. 184–188. [Google Scholar]
- Yatskiv, I.; Budilovich, E. A comprehensive analysis of the planned multimodal public transportation HUB. Transp. Res. Procedia 2017, 24, 50–57. [Google Scholar] [CrossRef]
- Pshinko, O.; Charkina, T.; Martseniuk, L.; Orlovska, O. Hubs as a key tool for improving the quality of the service and development of multimodal passenger traffic. Transp. Probl. 2022, 17, 201–214. [Google Scholar] [CrossRef]
- Jia, J.; Fang, Y.G. Underground space development in comprehensive transport hubs in China. In Underground Urbanisation as a Prerequisite for Sustainable Development, Proceedings of the 15th World Conference of the Associated Research Centers for the Urban Underground Space (ACUUS), Saint Petersburg, Russia, 12–15 September 2016; Alpatov, S., Prentkovskis, O., Sterling, R.L., Kaliampakos, D., Eds.; Elsevier: Amsterdam, The Netherlands, 2016; Volume 165, pp. 404–417. [Google Scholar]
- Sun, X.; Zheng, C.; Li, J.; Jiang, C.; Zhang, A.; Wandelt, S. A review on research regarding HSR interactions with air transport and outlook for future research challenges. Transp. Policy 2024, 157, 74–85. [Google Scholar] [CrossRef]
- Huan, N.; Yamamoto, T.; Yao, E. Seamless air-HSR intermodal solution: Behavioural model-based scheduling of airline timetable and airfare. Transp. Res. Part A Policy Pract. 2023, 176, 103821. [Google Scholar] [CrossRef]
- Zang, Y.W.; Liu, C.B.; Yan, J.J.; Yu, J.L.; Yu, T.C.; Zhu, H.D.; Ding, P.; Zhu, J.C.; Xu, R.Q. Study on the Influence and Control Methods of Shield Tunneling through the Sensitive Buildings. In Proceedings of the 8th International Conference on Hydraulic and Civil Engineering—Deep Space Intelligent Development and Utilization Forum (ICHCE), Xi’an, China, 25–27 November 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 311–316. [Google Scholar]
- Liu, Y.; Zhou, Y.; Suo, X.; Fan, H.; Cao, Y.; Du, Z. Model test on the deformation law of shield tunnel underpassing high speed railway roadbed. Yantu Lixue Rock Soil Mech. 2023, 44, 941–951. [Google Scholar] [CrossRef]
- Zhang, X.; Tan, H.; Liu, Z.; Dong, J.; Liu, S. Study on the Influence of Subway Tunnel Induced by Under-Crossing Tunnel Based on Monitor Data in Shenzhen, China. Sustainability 2023, 15, 13232. [Google Scholar] [CrossRef]
- Ding, Z.; Wei, X.J.; Wei, G. Prediction methods on tunnel-excavation induced surface settlement around adjacent building. Geomech. Eng. 2017, 12, 185–195. [Google Scholar] [CrossRef]
- Gong, C.J.; Xie, C.R.; Lin, Z.Q.; Xie, D.W.; Zhou, Z. Ground deformation prediction induced by shield tunnelling considering existing multi-story buildings. J. Cent. South Univ. 2023, 30, 1373–1387. [Google Scholar] [CrossRef]
- Ma, B.L.; Wu, S.Z.; Chen, Q.H.; Liang, E.B.; Li, X.D. The influence of existing piles on station settlement during the construction of a tunnel undercrossing under existing stations. Sci. Rep. 2024, 14, 14024. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Wu, K.; Sun, J.; Chen, R.; Li, Y.; Yang, S. Study on the Influence of Close Distance Construction of Urban Tunnel on the Existing Station. Geotech. Geol. Eng. 2021, 39, 4765–4780. [Google Scholar] [CrossRef]
- Nematollahi, M.; Dias, D. Interaction between an underground parking and twin tunnels—Case of the Shiraz subway line. Tunn. Undergr. Space Technol. 2020, 95, 103150. [Google Scholar] [CrossRef]
- Zhang, M. Options selection and impact study of intercity railway tunnel construction under airport interzone. Stavební Obz.-Civ. Eng. J. 2024, 33, 275–293. [Google Scholar] [CrossRef]
- Williams, I. Heathrow terminal 5: Tunnelled underground infrastructure. Proc. Inst. Civ. Eng. Civ. Eng. 2008, 161, 30–37. [Google Scholar] [CrossRef]
- Li, X.; Yuan, D.; Jin, D.; Yu, J.; Li, M. Twin neighboring tunnel construction under an operating airport runway. Tunn. Undergr. Space Technol. 2018, 81, 534–546. [Google Scholar] [CrossRef]
- Fang, Y.; Wang, Y.; Lu, P. New Airport Design and verification of pile foundation of Terminal Area of Beijing. Build. Struct. 2017, 47, 21–25. [Google Scholar] [CrossRef]
- Clark, M.; Pe, C.M. Challenges of design and construction of passenger terminal building foundation, New International Airport of Mexico, Mexico City. In Proceedings of the 17th European Conference on Soil Mechanics and Geotechnical Engineering, ECSMGE 2019—Proceedings, Reykjavík, Iceland, 1–6 September 2019. [Google Scholar]
- Asadoullahtabar, S.R.; Asgari, A.; Tabari, M.M.R. Assessment, identifying, and presenting a plan for the stabilization of loessic soils exposed to scouring in the path of gas pipelines, case study: Maraveh-Tappeh city. Eng. Geol. 2024, 342, 107747. [Google Scholar] [CrossRef]
- Meyerhof, G.G. The settlement analysis of building frames. Struct. Eng. 1947, 25, 369–409. [Google Scholar]
- Aw, S.; Dh, M. The allowable settlement of buildings. Proc. Inst. Civ. Eng. 1956, 5, 727–784. [Google Scholar]
- Polshin, D.E.; Tokar, R.A. Maximum allowable non-uniform settlement of structures. In Proceedings of the Fourth International Conference on Soil Mechanics and Foundation Engineering, London, UK, 12–14 August 1957; pp. 402–405. [Google Scholar]
- Jia, Q.; Cheng, L.; Zhang, X. Experimental study of the influence of differential settlement on RCframe structures. China Civ. Eng. J. 2011, 44, 79–86. (In Chinese) [Google Scholar] [CrossRef]
- Hakam, A.; Ismail, F.A.; Al Jauhari, Z.; Chairani, C. Evaluation of an RC frame building exposed to differential settlement in Padang City, Indonesia. Geomate J. 2024, 27, 125–132. [Google Scholar]
- ASCE 7-16; Minimum Design Loads and Associated Criteria for Buildings and Other Structures. American Society of Civil Engineers: Reston, VA, USA, 2016.
- GB 50669-2011; Code for Design of Building Foundation. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2011. (In Chinese)
- National Research Council Canada. National Building Code of Canada 2015; Institute for Research in Construction: Ottawa, ON, Canada, 2015.
- American Concrete Institute. Building Code Requirements for Reinforced Concrete—ACI 318-89. In ACI 318-17; American Concrete Institute: Farmington Hills, MI, USA, 2017. [Google Scholar]
- Duarte, J.; Chanquini, C.V.; Garcia, F.A.; Simmonds, A.J. On-line settlement monitoring in a subway tunnel crossing in São Paulo, Brazil. In Proceedings of the ITA-AITES World Tunnel Congress, Budapest, Hungary, 23–28 May 2009. [Google Scholar]
- Liu, G.; Li, Z.; Wu, X. 3D FEM Analysis on Surroundings Influence due to the Construction of Transverse Section for Shanghai Stadium Station of Pearl Line Phase II. Chin. J. Undergr. Space Eng. 2005, 1, 460–463. (In Chinese) [Google Scholar] [CrossRef]
- Cao, W.; Yao, Y. The Impact Analysis of Shield Tunnel Boring Machine Crossing Line 2 for the Section of Shanghai Metro Line 8 (Qufu Road to People’s Square). Undergr. Eng. Tunn. 2005, 11–16. (In Chinese) [Google Scholar]
- Li, X.G.; Yuan, D.J. Response of a double-decked metro tunnel to shield driving of twin closely under-crossing tunnels. Tunn. Undergr. Space Technol. 2012, 28, 18–30. [Google Scholar] [CrossRef]
- Li, X.; Chen, X. Using grouting of shield tunneling to reduce settlements of overlying tunnels: Case study in Shenzhen metro construction. J. Constr. Eng. Manag. 2012, 138, 574–584. [Google Scholar] [CrossRef]
- Lei, M.F.; Lin, D.Y.; Huang, Q.Y.; Shi, C.H.; Huang, L.C. Research on the construction risk control technology of shield tunnel underneath an operational railway in sand pebble formation: A case study. Eur. J. Environ. Civ. Eng. 2020, 24, 1558–1572. [Google Scholar] [CrossRef]
- Li, X.; Zhang, C.; Yuan, D. An in-tunnel jacking above tunnel protection methodology for excavating a tunnel under a tunnel in service. Tunn. Undergr. Space Technol. 2013, 34, 22–37. [Google Scholar] [CrossRef]
- Zheng, Y.; Yan, J.; Su, R.; Ma, S.; Li, Y.; Wang, X.; Zheng, J.; Zhu, Y.; Yu, Y. Investigation of the settlement mechanism and control measures of a super-large section tunnel in a giant karst cave using ultra-thick backfill method. Tunn. Undergr. Space Technol. 2023, 137, 104956. [Google Scholar] [CrossRef]
- Ren, Y.; Zhou, S.; Jia, J.; Yuan, Q.; Liu, M.; Song, S.; Zhou, Z.; Wang, Z. The Influence of Construction Methods on the Stability of Tunnels and Ground Structures in the Construction of Urban Intersection Tunnels. Sustainability 2023, 15, 14720. [Google Scholar] [CrossRef]
- Wang, Y. Analysis of settlement and deformation of subway double line shield beneath existing railway roadbeds. Discov. Appl. Sci. 2025, 7, 353. [Google Scholar] [CrossRef]
- GB 50911-2013; Code for Monitoring Measurement of Urbanrail Transit Engineering. China Architecture Publishing Media Co., Ltd.: Beijing, China, 2013. (In Chinese)
- CJJ/T 202–2013; Technical Code for Protection Structures of Urban Rail Transit. China Architecture Publishing Media Co., Ltd.: Beijing, China, 2013. (In Chinese)
- Soeung, S.; Lee, S.; Lee, S.J.; Kim, B.; Yune, C. Causing factors of additional settlement in high-speed railways in Korea. KSCE J. Civ. Eng. 2018, 22, 3843–3851. [Google Scholar] [CrossRef]
- Fiamingo, A.; Abate, G.; Chiaro, G.; Massimino, M.R. HS-Small Constitutive Model for Innovative Geomaterials: Effectiveness and Limits. Int. J. Geomech. 2024, 24, 04024118. [Google Scholar] [CrossRef]
- Wang, D.; Lin, Y.; Wu, Y.; Lin, C.; Zong, C. Numerical modeling of ground surface settlement due to tunneling in urban areas. Multiscale Multidiscip. Model. Exp. Des. 2024, 7, 1679–1692. [Google Scholar] [CrossRef]
- Cudny, M.; Truty, A. Refinement of the Hardening Soil model within the small strain range. Acta Geotech. 2020, 15, 2031–2051. [Google Scholar] [CrossRef]
- Asgari, A.; Ranjbar, F.; Bagheri, M. Seismic resilience of pile groups to lateral spreading in liquefiable soils: 3D parallel finite element modeling. Structures 2025, 74, 108578. [Google Scholar] [CrossRef]
- Pei, S.-F.; Zhao, J.-S.; Chen, B.-R.; Li, S.-J.; Jiang, Q.; Xu, D.-P.; Wang, Z.-N. Deformation warning and microseismicity assessment of the collapse in the fault development area of the Yebatan Hydropower Station. J. Cent. South Univ. 2025. [Google Scholar] [CrossRef]
- Zhao, J.-S.; Chen, B.-R.; Jiang, Q.; Xu, D.-P.; He, B.-G.; Duan, S.-Q. In-situ comprehensive investigation of deformation mechanism of the rock mass with weak interlayer zone in the Baihetan Hydropower Station. Tunn. Undergr. Space Technol. 2024, 148, 105690. [Google Scholar] [CrossRef]
- Zhao, J.-S.; Duan, S.-Q.; Chen, B.-R.; Li, L.; He, B.-G.; Li, P.-X.; Liu, G.-F. Failure mechanism of rock masses with complex geological conditions in a large underground cavern: A case study. Soil. Dyn. Earthq. Eng. 2024, 177, 108439. [Google Scholar] [CrossRef]
- Jahangiri, V.; Akbarzadeh, M.R.; Shahamat, S.A.; Asgari, A.; Naeim, B.; Ranjbar, F. Machine learning-based prediction of seismic response of steel diagrid systems. Structures 2025, 80, 109791. [Google Scholar] [CrossRef]






| Soil Layer | Layer Thickness/m | γ (Unit Weight)/(kN/m3) | Es (Modulus of Elasticity)/MPa | Ea1–2 (Compression Index)/MPa−1 | C (Cohesion)/kPa | LL (Liquid Limit)/% | φ (Internal Friction Angle)/° | PL (Plastic Limit)/% | K (Permeability)/cm/s |
|---|---|---|---|---|---|---|---|---|---|
| Plain Fill | 1.2 | 19 | 2 | 15 | 15 | ||||
| Silt ② | 3.3 | 18.9 | 9.56 | 0.215 | 15 | 27.5 | 21.7 | 18 | 1.71 × 10−4 |
| Silt Clay ③ | 2 | 18.3 | 4.78 | 0.485 | 24.8 | 43.1 | 10.3 | 25.2 | 7.17 × 10−5 |
| Silt ④ | 3 | 19.2 | 9.46 | 0.239 | 15.6 | 29.7 | 19.9 | 19.0 | 1.97 × 10−4 |
| Silt Clay ⑤ | 4 | 19.2 | 4.96 | 0.39 | 27.8 | 36.9 | 13.5 | 22.0 | 1.01 × 10−4 |
| Silt ⑥ | 2 | 19.6 | 10.03 | 0.19 | 18.8 | 29.2 | 29.6 | 28.6 | 3.40 × 10−4 |
| Silt Clay ⑦ | 3.5 | 19.9 | 5.29 | 0.31 | 29.4 | 33.0 | 13.7 | 20.0 | |
| Silt ⑧ | 4 | 20 | 8.55 | 0.193 | 15.8 | 29.4 | 21.6 | 18.6 | |
| Silt Clay ⑨ | 4.5 | 19.8 | 6.24 | 0.283 | 27.2 | 34.0 | 13.2 | 20.7 | |
| Silt ⑩ | 3 | 19.9 | 8.23 | 0.210 | 19.4 | 28.3 | 27.8 | 18.1 | |
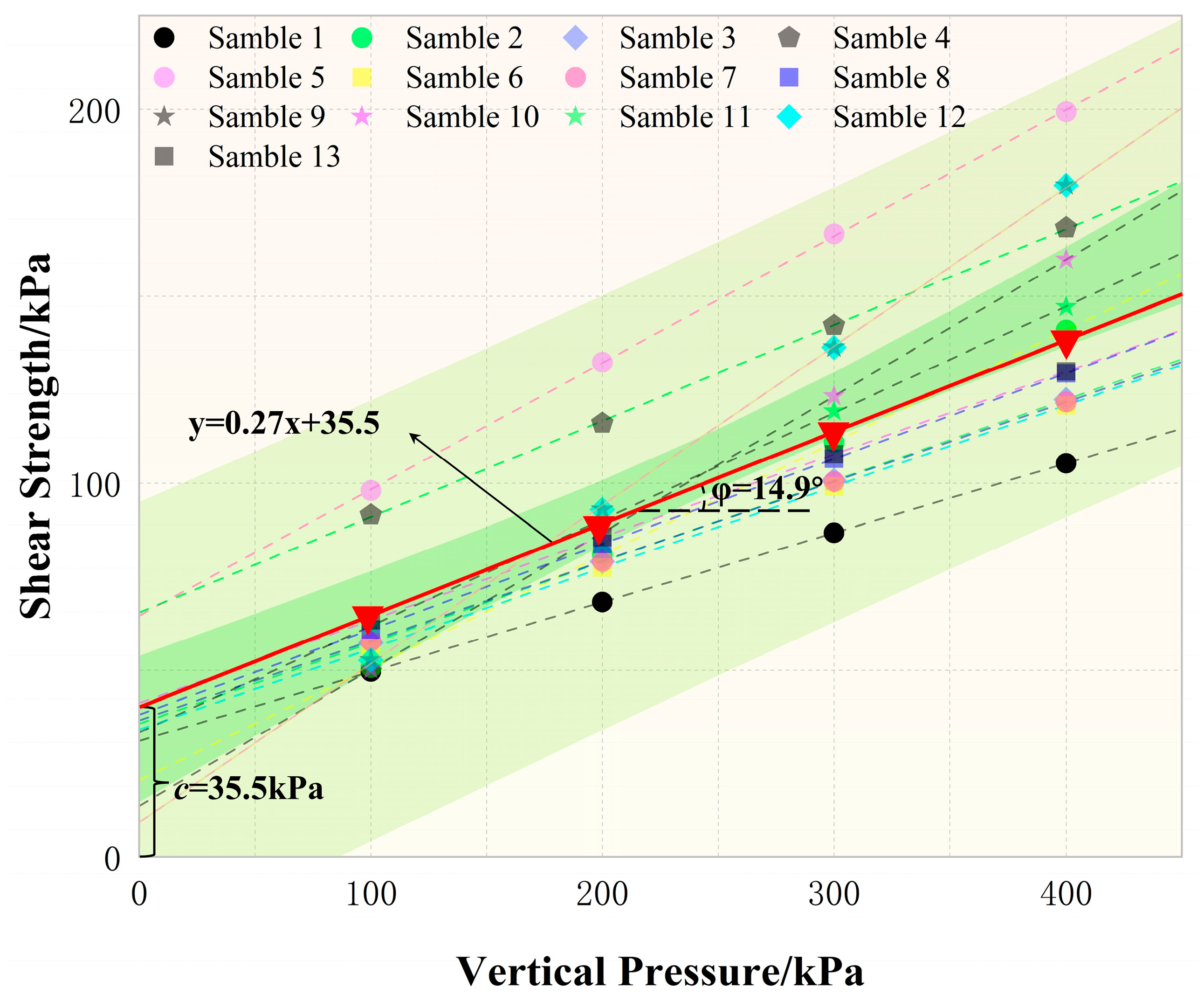
| Silt Clay ⑪ | 3 | 19.5 | 6.8 | 0.277 | 35.5 | 37.1 | 14.9 | 22.1 | |
| Clay ⑫ | 4 | 19.4 | 6.36 | 0.295 | 33.3 | 38.4 | 11.9 | 22.7 | |
| Silt Clay ⑬ | 4 | 19.5 | 6.37 | 0.288 | 34.1 | 36.1 | 13 | 21.6 | |
| Clay ⑭ | 5 | 19.1 | 6.66 | 0.282 | 40.3 | 39.2 | 14.6 | 23.3 | |
| Silt Clay ⑮ | 5 | 19.4 | 6.76 | 0.268 | 43.1 | 37.5 | 15.2 | 22.3 | |
| Clay ⑯ | 4 | 19.3 | 7.23 | 0.267 | 47 | 39.9 | 16.2 | 23.6 | |
| Silt Clay ⑰ | 5 | 19.4 | 7.04 | 0.255 | 38.8 | 37.2 | 15 | 22.3 | |
| Clay ⑱ | 26 | 19 | 8.01 | 0.260 | 23.9 | 37.8 | 18.8 | 22.7 |
| Scholar | Publication Year | Research Findings |
|---|---|---|
| Meyerhof GG [21] | 1947 | δ/L < 1/300 |
| Skempton and MacDonald [22] | 1956 | δ/L < 1/150 |
| Polshin and Tokar [23] | 1957 | δ/L < 1/200 |
| Jia Qiang [24] | 2011 | δ/L < 1/625 |
| Hakam [25] | 2023 | δ/L < 1/300 |
| Issuing Organization | Year of Issue | Settlement Limit |
|---|---|---|
| American Association of State Highway and Transportation Officials [26] | 2010 | δ/L < 1/125 to 1/250 |
| China Academy of Building Research [27] | 2011 | δ/L < 3/1000 to 1/500 |
| National Building Code of Canada [28] | 2015 | δ/L < 1/250 to 1/150 |
| American Concrete Institute [29] | 2017 | Δ < 0.75 in |
| Material Name | EA/GN·m−1 | EI/GN·m | Spacing/m | ν |
|---|---|---|---|---|
| Terminal Building Columns ① | 22.75 | / | 9 | 0.2 |
| Terminal Building Columns ② | 45.5 | / | 9 | 0.2 |
| Foundation Slab | 162.5 | / | 9 | 0.2 |
| Transfer Structure | / | 59.45 | 9 | 0.2 |
| Different Locations of Cross-Section | Maximum Settlement/mm | Minimum Settlement/mm | Maximum Differential Settlement Between Adjacent Columns (Walls)/mm | Maximum Tangent of Rotation Angle Between Adjacent Columns (Walls) |
|---|---|---|---|---|
| Terminal | 45.45 | 28.75 | 10.73 | 1/839 |
| High-Speed Railway | 40.52 | 33.67 | 5.49 | 1/1712 |
| Metro | 33.05 | 30.73 | 1.76 | 1/6591 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Liu, W.; Wei, Z.; Han, J.; Shao, G.; Li, S. Settlement Characteristics and Control Parameters for the Integrated Construction of Large-Section Underground Structures and Airport Terminals: A Case Study. Buildings 2025, 15, 3139. https://doi.org/10.3390/buildings15173139
Zhang R, Liu W, Wei Z, Han J, Shao G, Li S. Settlement Characteristics and Control Parameters for the Integrated Construction of Large-Section Underground Structures and Airport Terminals: A Case Study. Buildings. 2025; 15(17):3139. https://doi.org/10.3390/buildings15173139
Chicago/Turabian StyleZhang, Rongzhen, Wei Liu, Zekun Wei, Jianyong Han, Guangbiao Shao, and Shenao Li. 2025. "Settlement Characteristics and Control Parameters for the Integrated Construction of Large-Section Underground Structures and Airport Terminals: A Case Study" Buildings 15, no. 17: 3139. https://doi.org/10.3390/buildings15173139
APA StyleZhang, R., Liu, W., Wei, Z., Han, J., Shao, G., & Li, S. (2025). Settlement Characteristics and Control Parameters for the Integrated Construction of Large-Section Underground Structures and Airport Terminals: A Case Study. Buildings, 15(17), 3139. https://doi.org/10.3390/buildings15173139







