Experimental and Numerical Investigations on Shear Performance of Large-Scale Stirrup-Free I-Shaped UHPC Beams
Abstract
1. Introduction
2. Research Significance
3. Experimental Programs
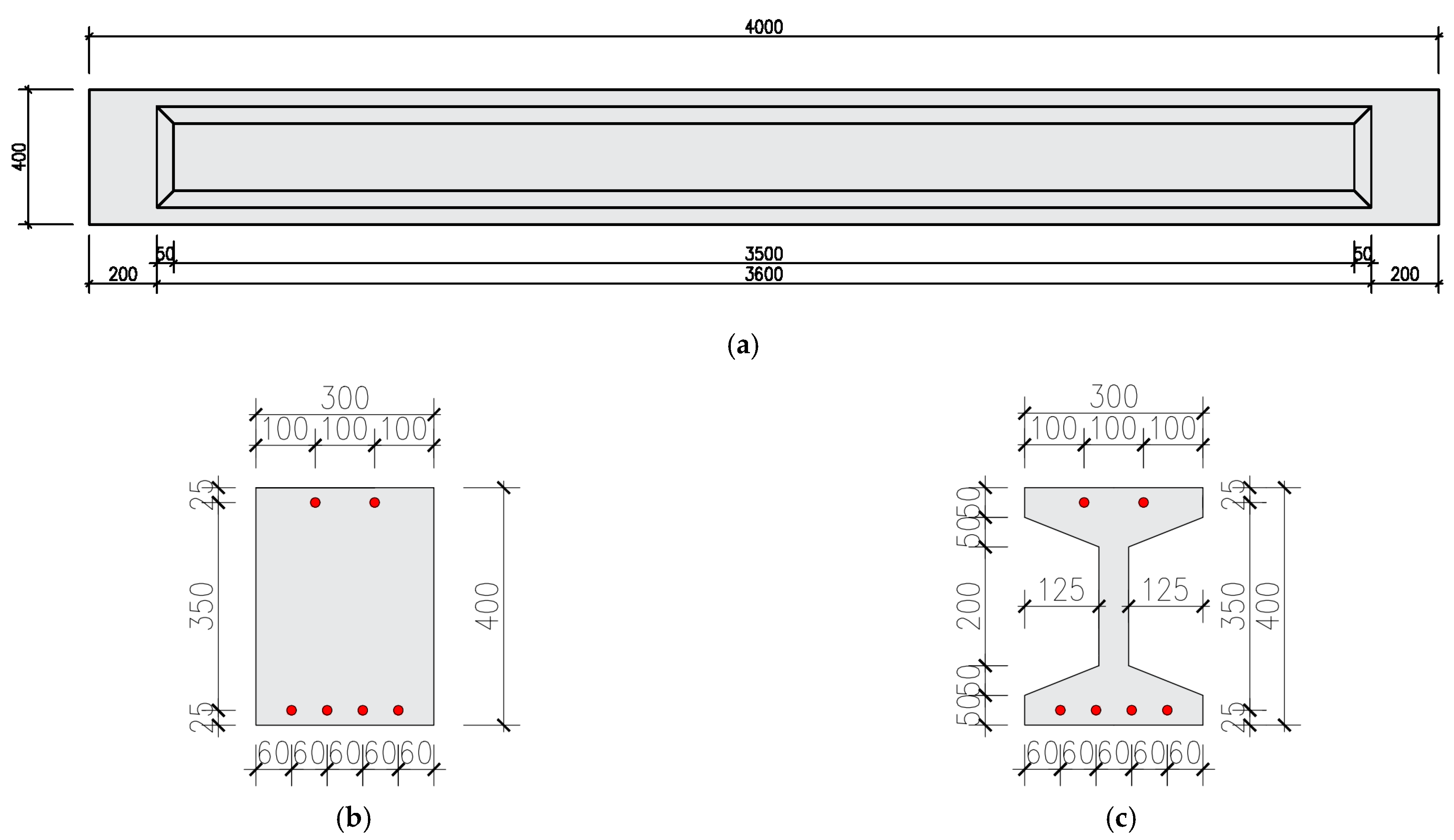
3.1. Experimental Specimen Design
3.2. Material Properties
3.2.1. Preparation and Mechanical Properties of UHPC and Steel Reinforcement
3.2.2. Specimen Fabrication and Curing
3.3. Test Loading
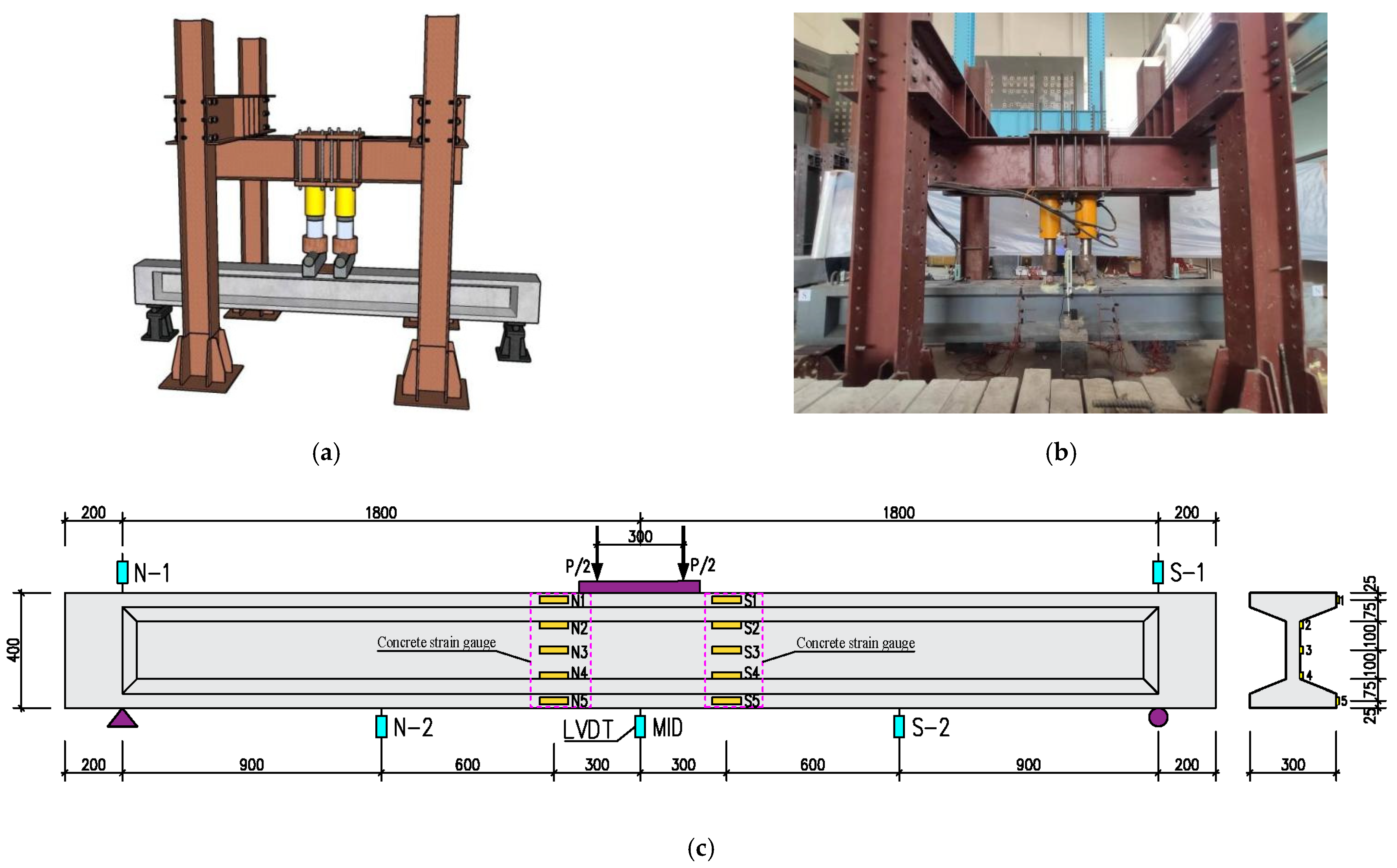
3.3.1. Flexural Test Loading
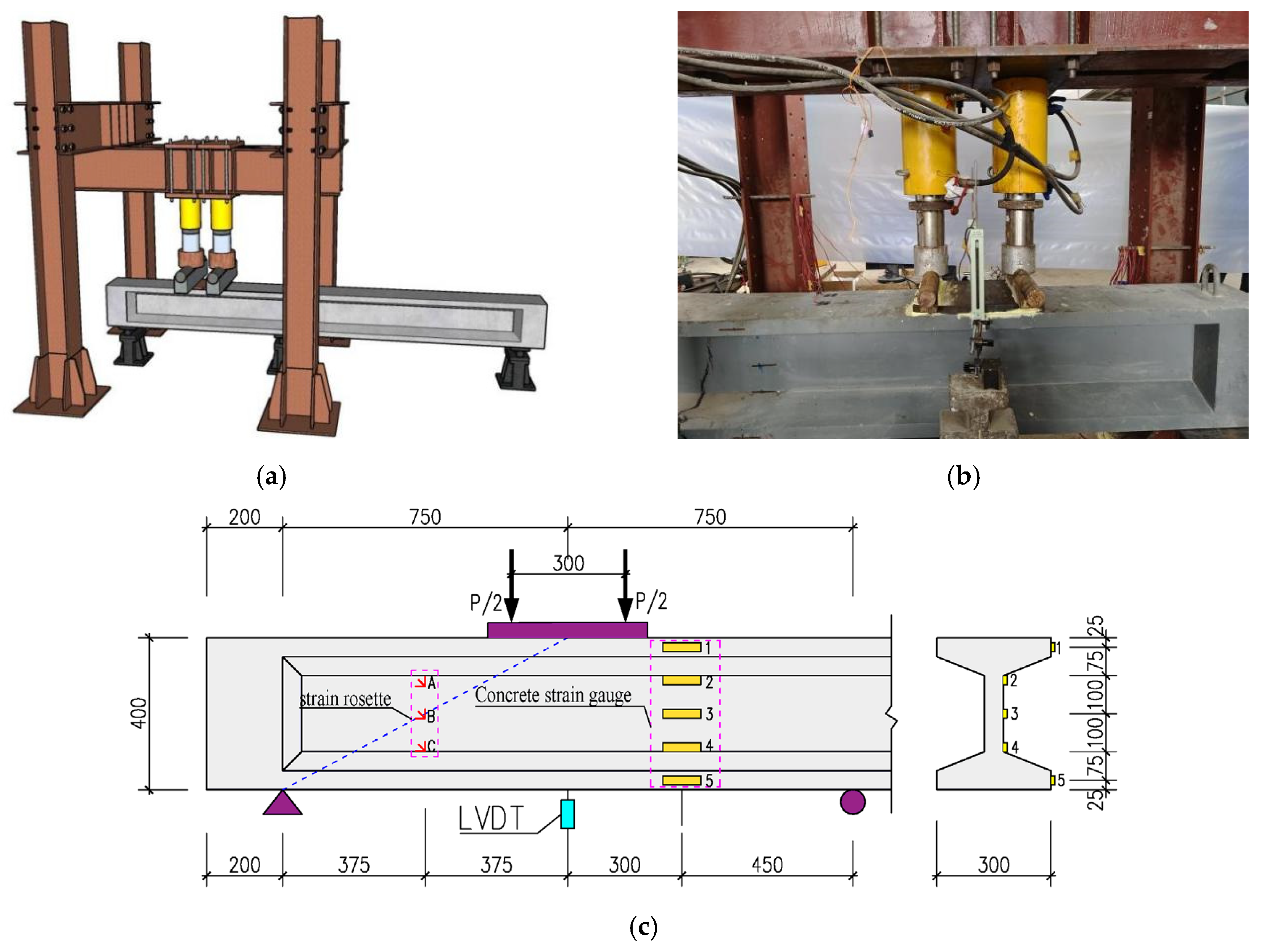
3.3.2. Shear Test Loading
3.4. Test Instrumentation Layout
3.4.1. Instrumentation Layout for Flexural Tests
3.4.2. Instrumentation Layout for Shear Tests
3.5. Test Results and Analysis
3.5.1. Summary and Comparison of Test Results
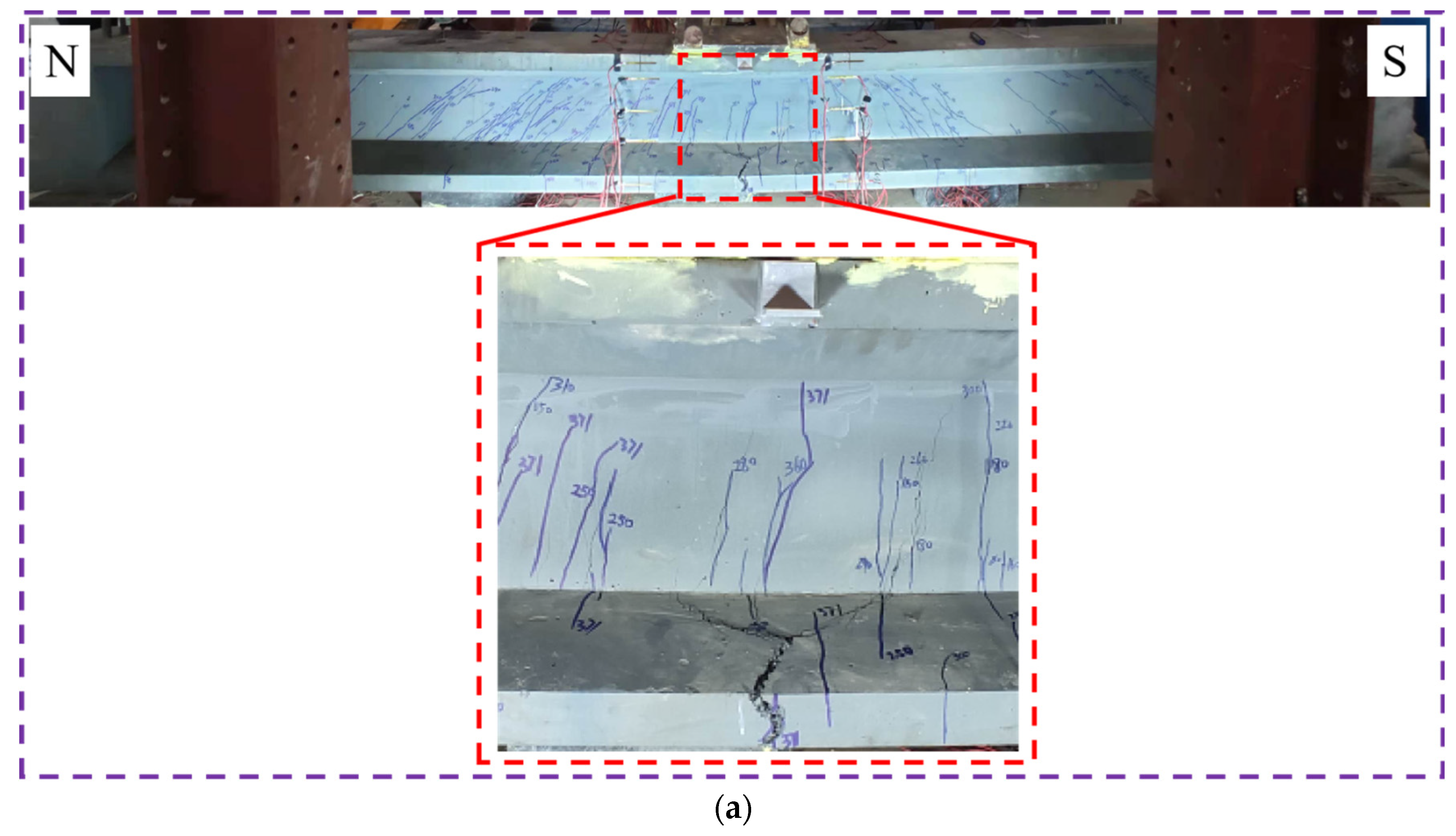
3.5.2. Test Observations and Failure Modes
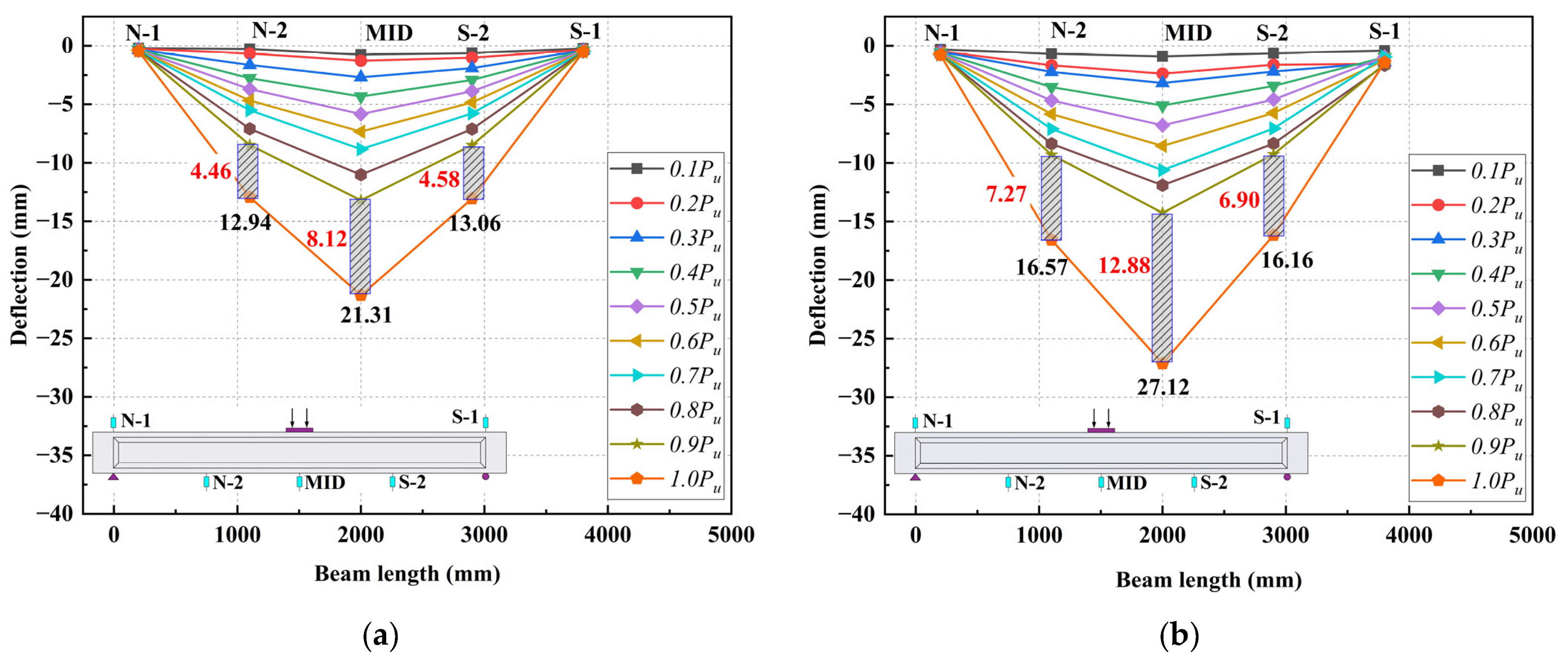
3.5.3. Deflection Development in Flexural Test Beams
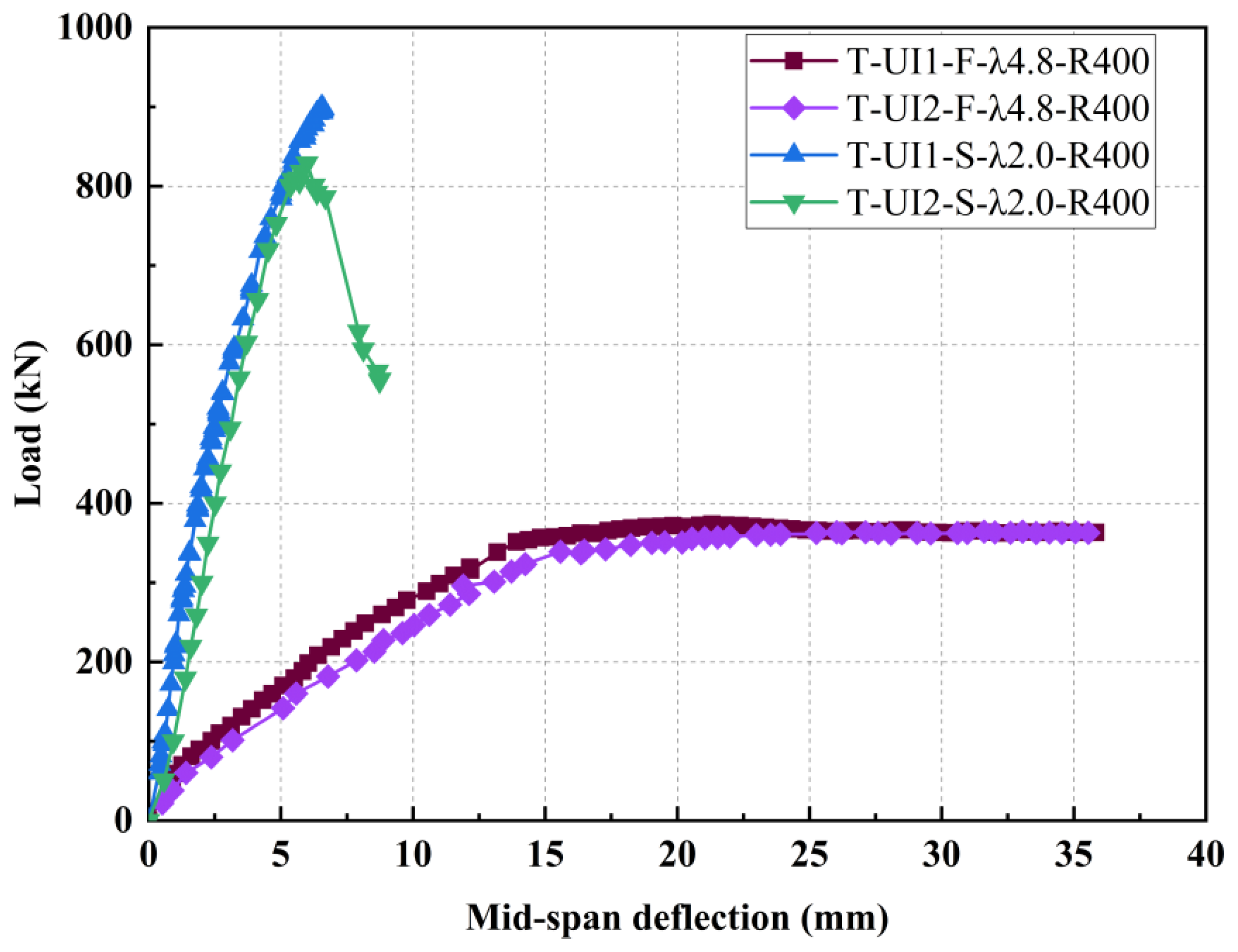
3.5.4. Analysis of Load Versus Mid-Span Deflection Curves
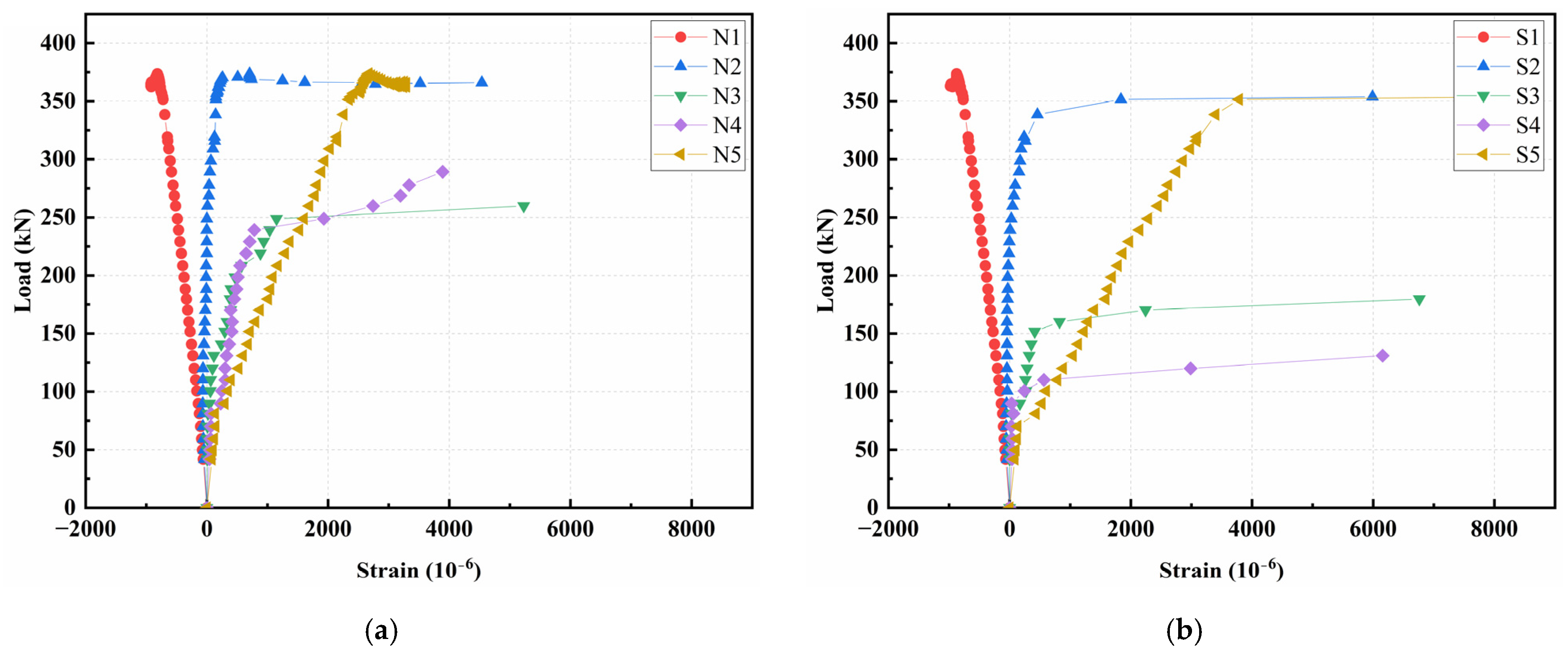
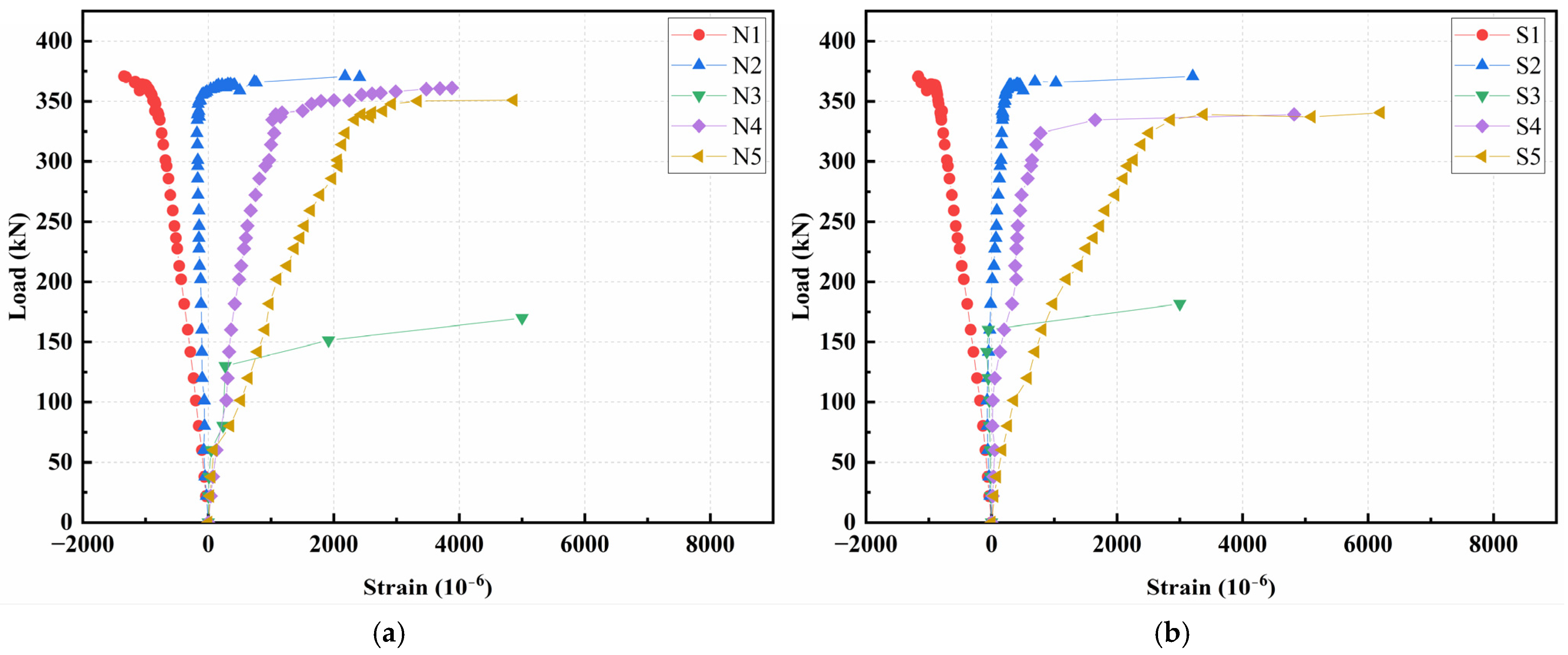
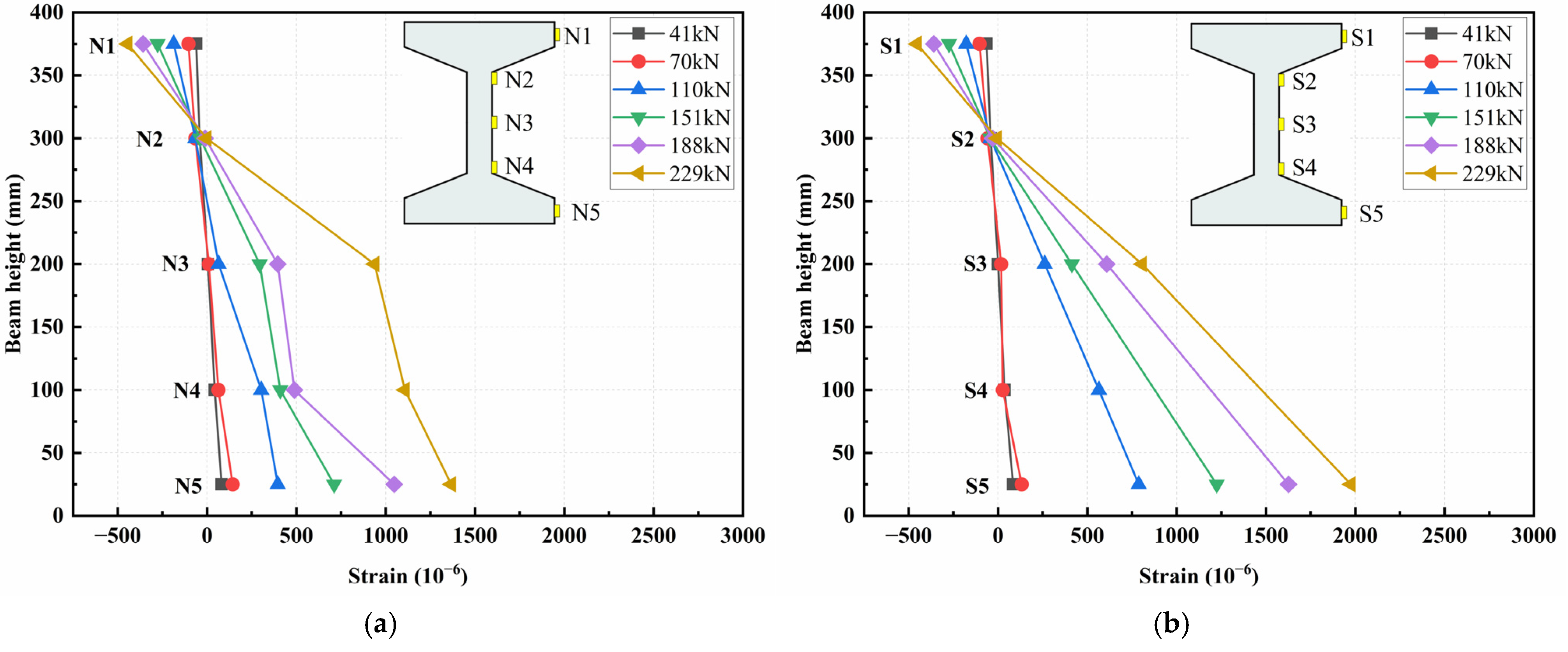
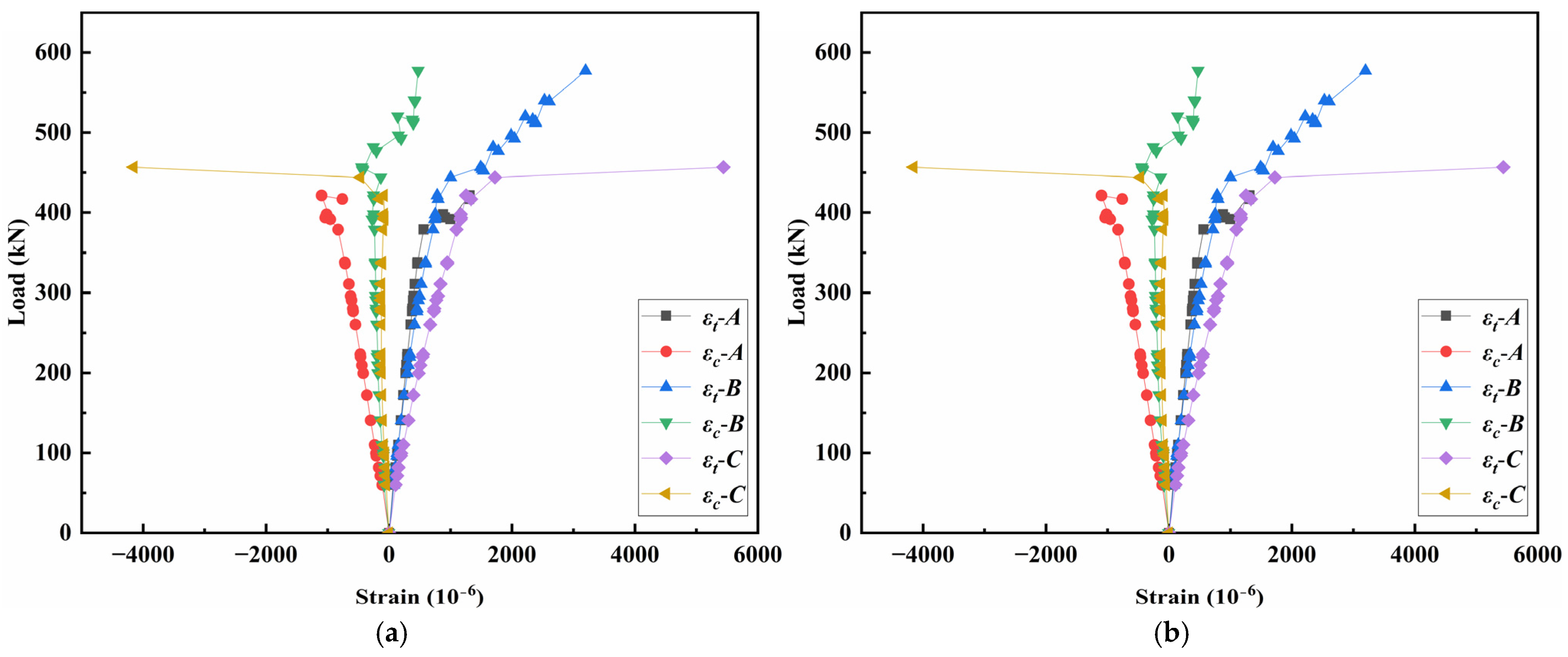
3.5.5. Concrete Strain Analysis
- (1)
- Flexural tests
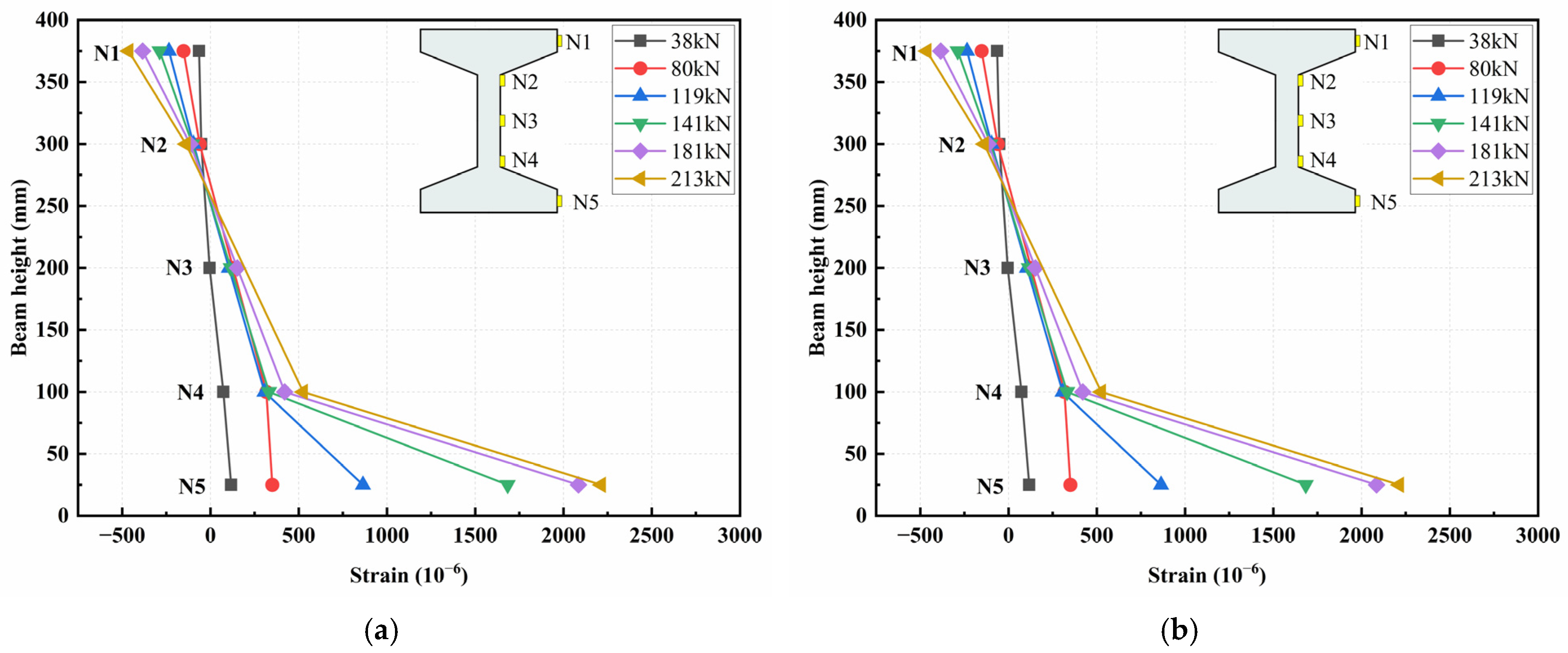
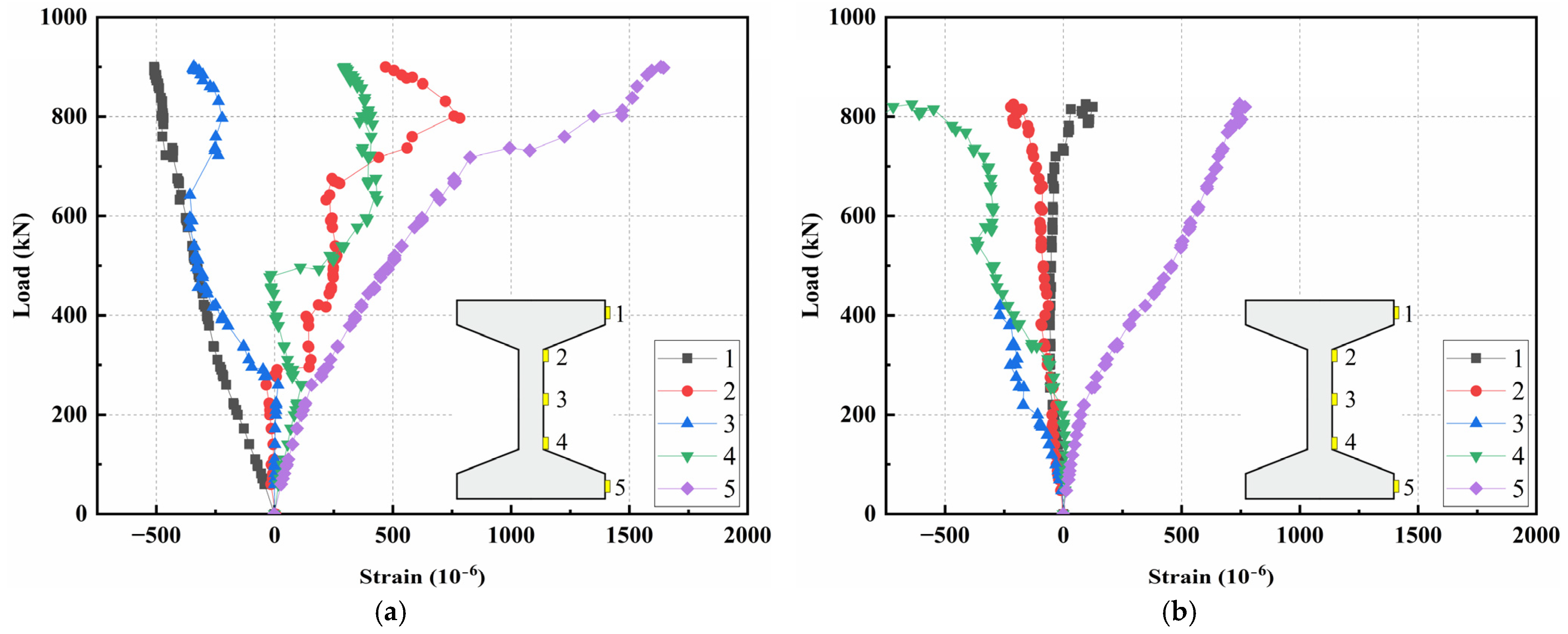
- (2)
- Shear tests
4. Finite Element Analysis on Shear Behaviors of Stirrup-Free I-Shaped UHPC Beams
4.1. Abaqus Finite Element Models
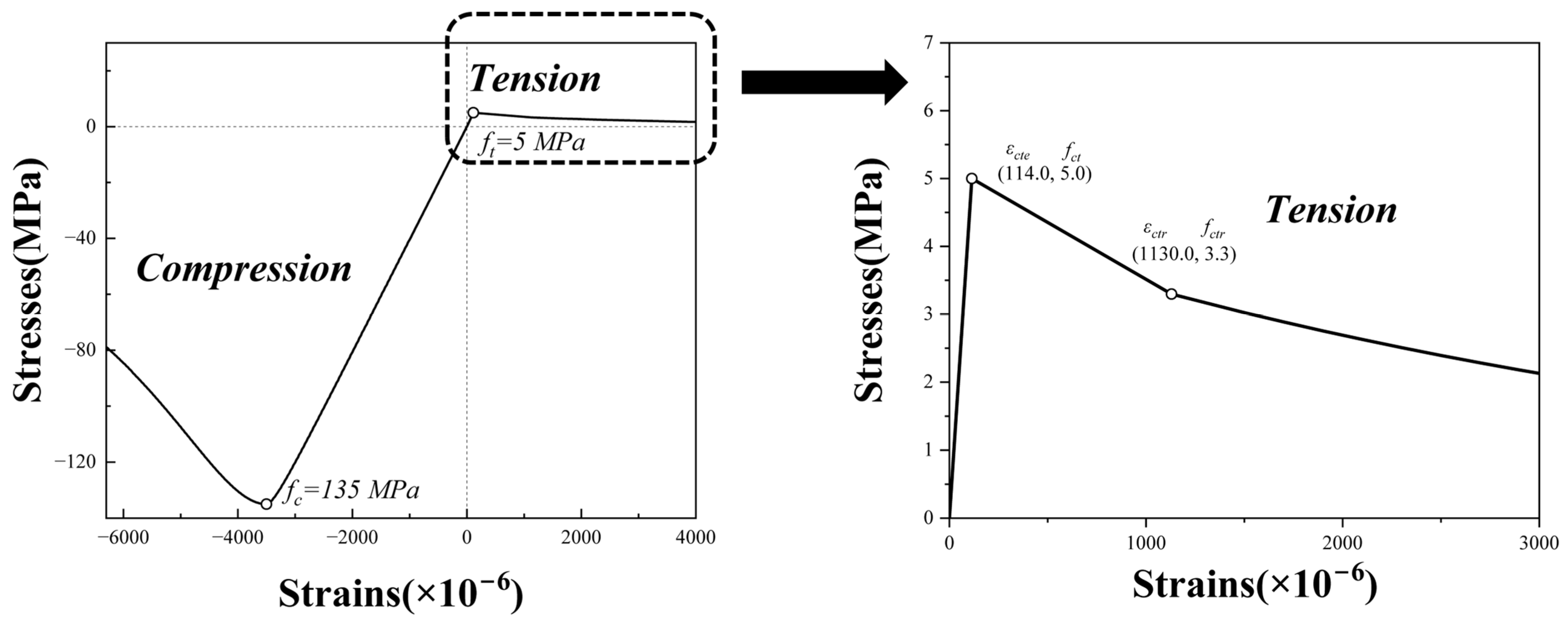
4.1.1. Material Constitutive Relationships
- (1)
- Concrete material
- (2)
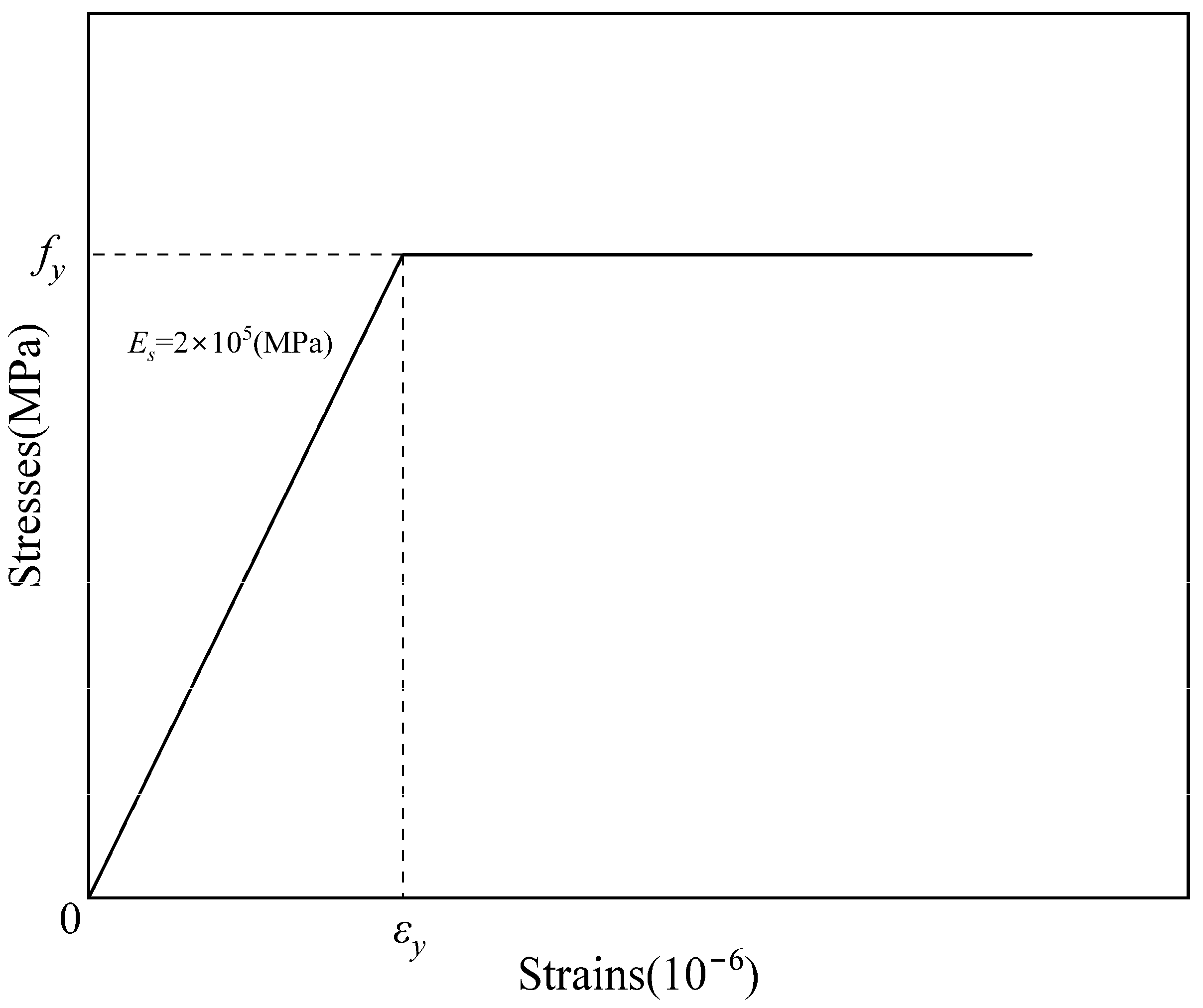
- Reinforcing steel material
- —Elastic modulus of reinforcing steel;
- —Yield strain of reinforcing steel;
- —Yield stress of reinforcing steel.
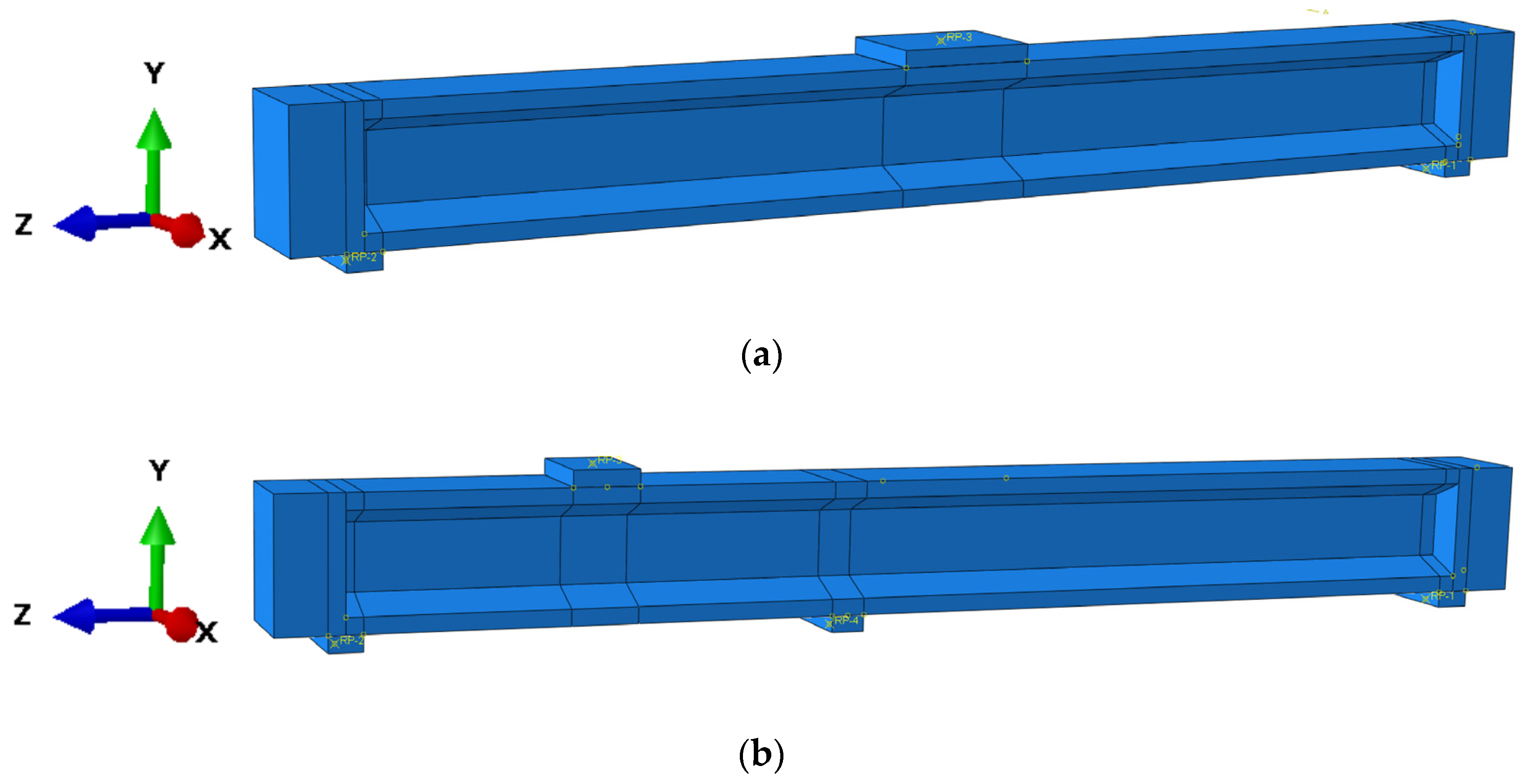
4.1.2. Model Establishing
- (1)
- Element type selection
- (2)
- Contact definitions
- (3)
- Boundary conditions and loading protocol
- (4)
- Mesh generation
4.2. Finite Element Model Verification
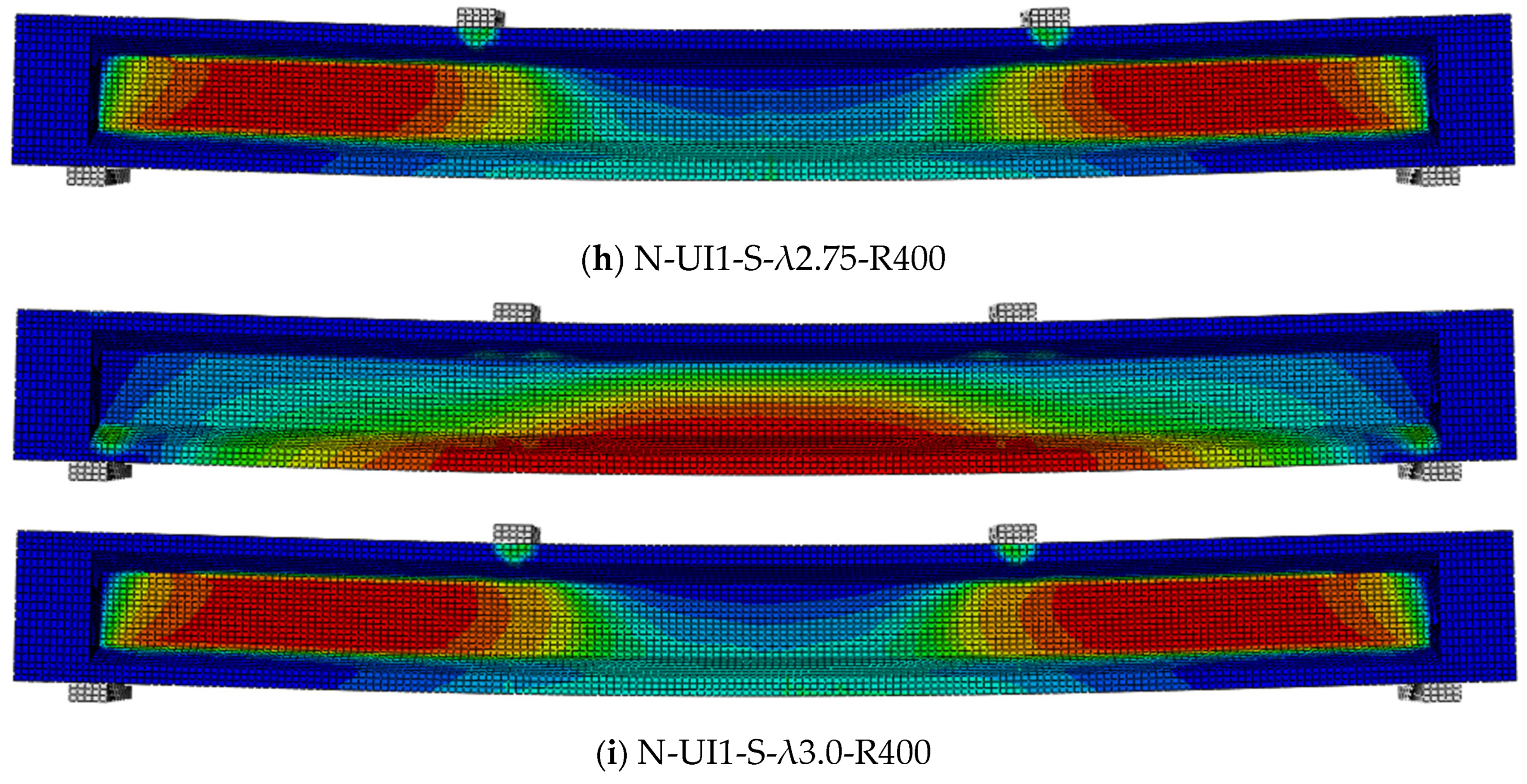
4.2.1. Comparison of Failure Patterns
4.2.2. Ultimate Load and Mid-Span Deflection Comparison
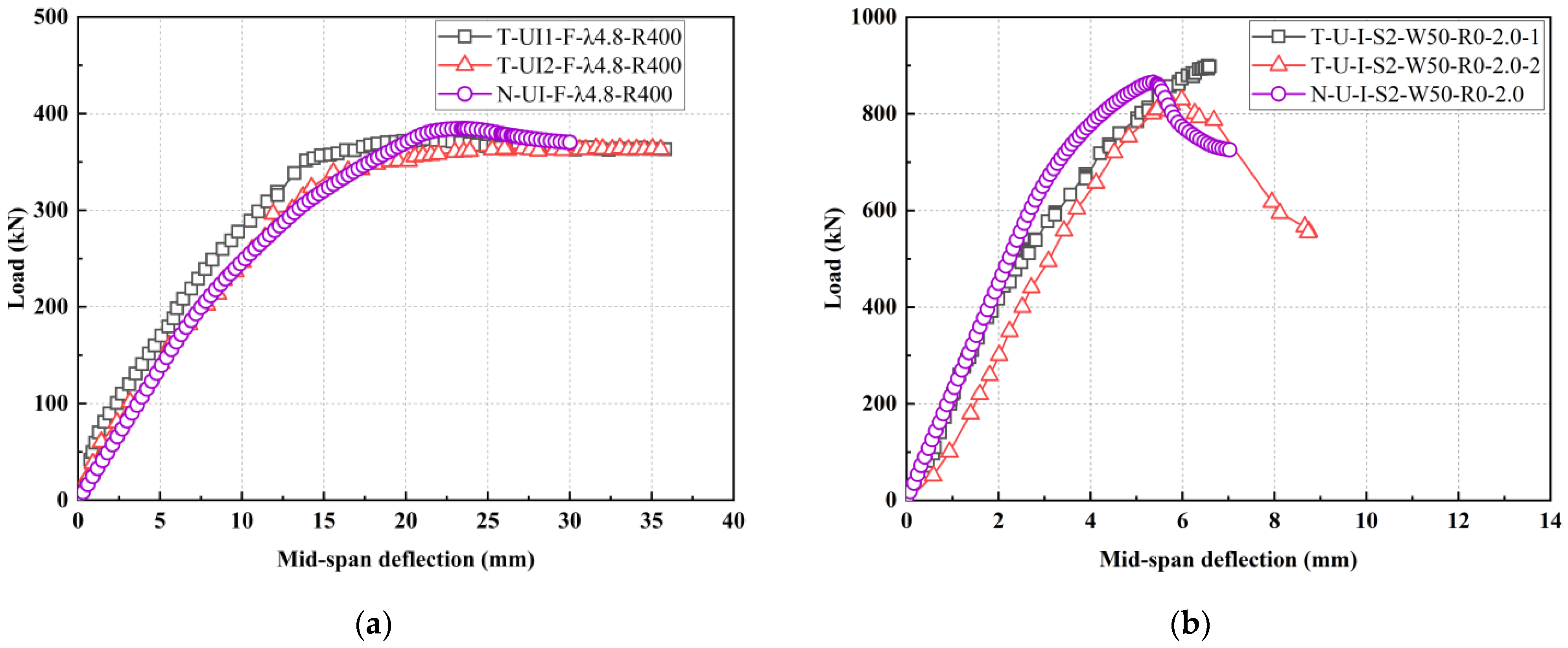
4.2.3. Comparison of Load-Mid-Span Deflection Curves
4.3. Finite Element Simulation Parameter Expansion
4.3.1. Effects of Span-to-Depth Ratio
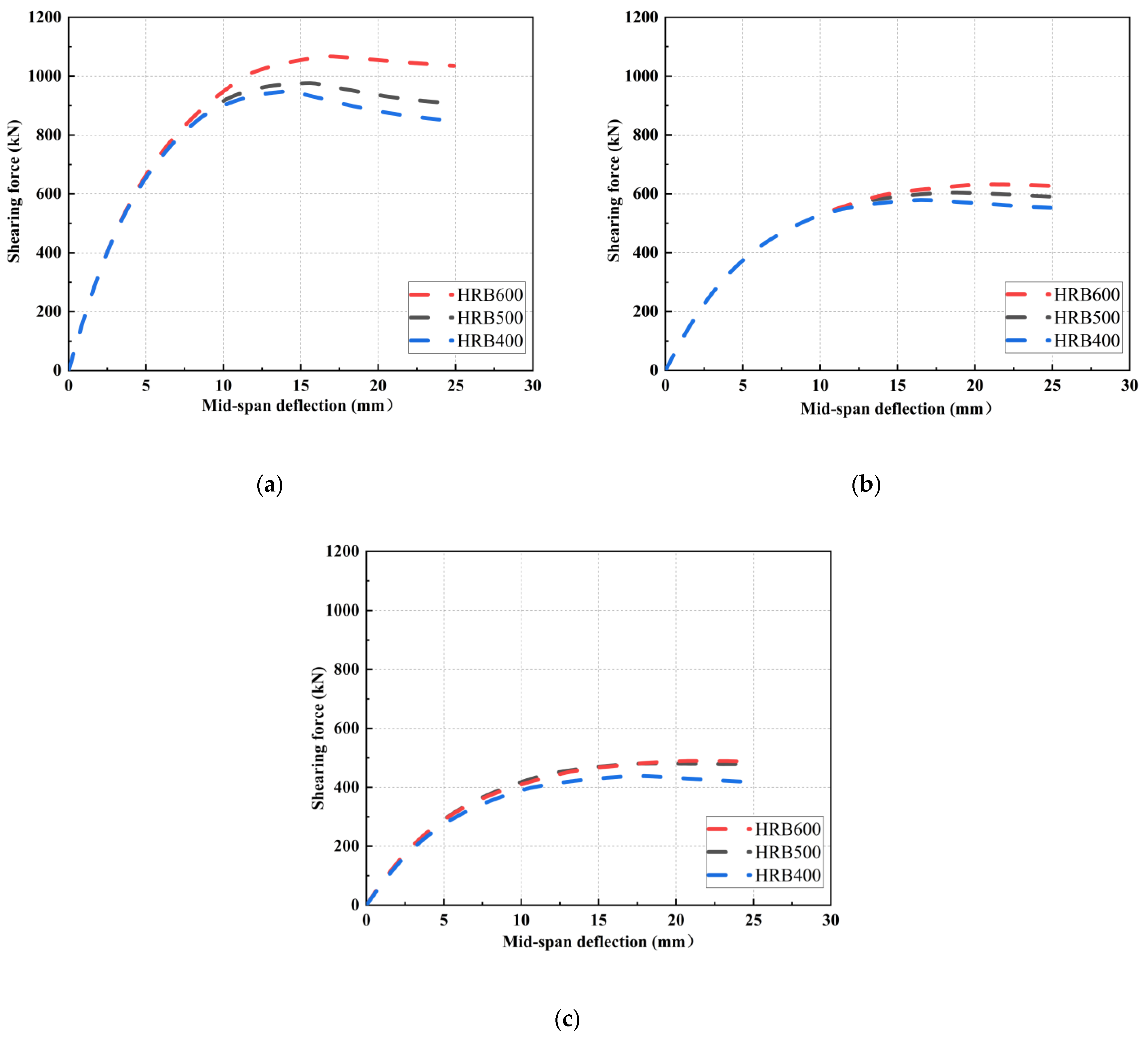
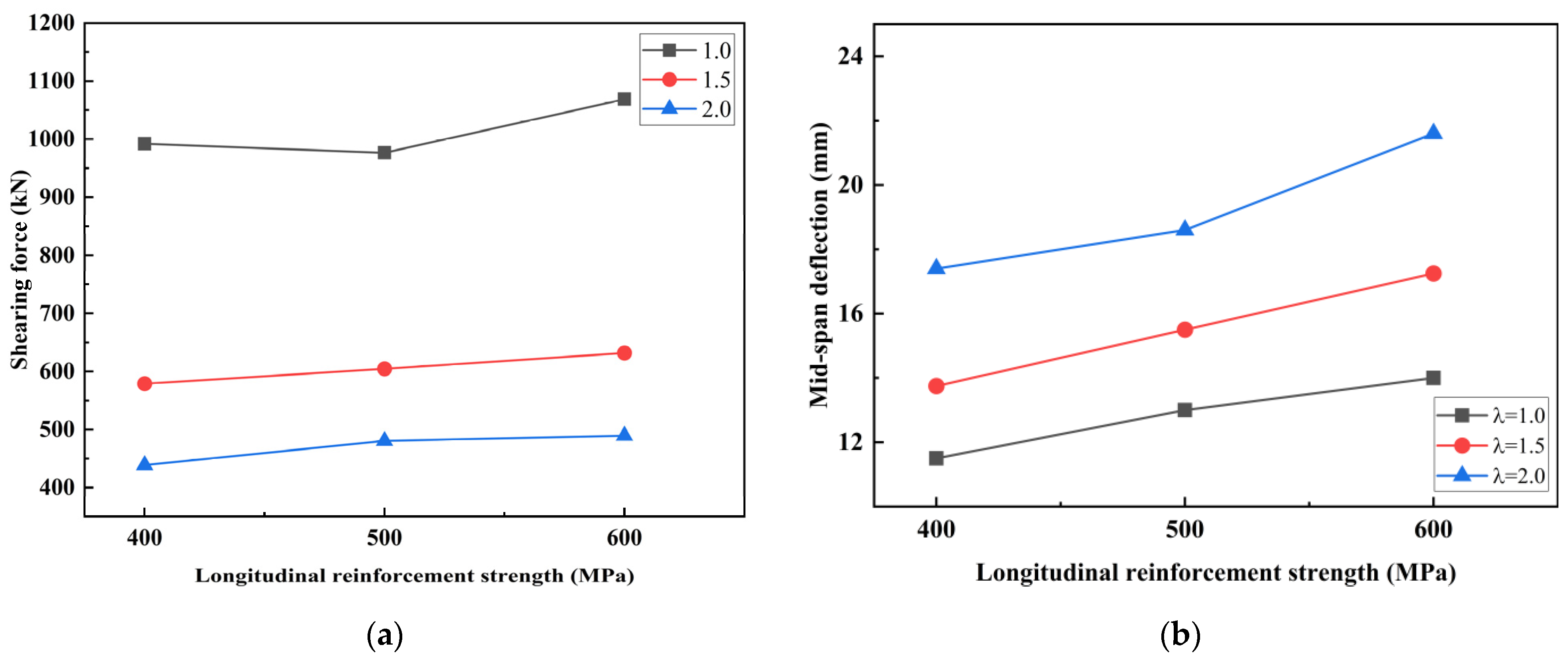
4.3.2. Effects of Longitudinal Reinforcement Strength
5. Comparison of Code-Based Shear Capacity Calculations and Experimental Results for Test Beams
5.1. Comparison of Code-Based Shear Capacity Calculations and Experimental Results for Test Beams
5.1.1. Shear Capacity Calculations Based on French Code
5.1.2. Shear Capacity Calculation Based on PCI Report
5.1.3. Shear Capacity Calculation Based on Feng’s Modified Compression Field Theory (MCFT)
5.1.4. Shear Capacity Calculation Based on Ye’s Regression Analysis Method
5.1.5. Summary and Analysis of UHPC Code Formula Calculations and Experimental Results
6. Conclusions
- (1)
- The UHPC beams have a bending load of approximately 369.00 kN and a shear load of approximately 864.58 kN. The UHPC beams exhibited good post-cracking performance, with indexes of post-cracking capacities in bending and shear tests ranging from 56.1% to 59.9% and 68.9% to 78.3%, respectively.
- (2)
- Cracks are likely to appear on the web during bending and shear tests, mainly due to the thin web and stress concentration at the intersection of the web and flange. For the two bending tests, the first vertical cracks emerged at the inferior portion of mid-span at around 155 kN. For the two shear tests, all cracks were diagonal cracks in the shear span. As load enhancing, cracks in shear span average nominal diagonal stress was 6.15 MPa. As load enhancing, one crack evolved into the critical diagonal crack, until typical shear-compression failure was exhibited. The angles of critical diagonal cracks were 37.2°and 36.4°, respectively.
- (3)
- In two bending tests, the beam’s deflection increases linearly and symmetrically with respect to the mid-span along the beam length. When the load exceeds 0.9, the deflection grows rapidly from the load-mid-span deflection curves. Due to the steel fiber bridging effect and longitudinal reinforcement, the beam demonstrates excellent ductility. The maximum deflections were 21.31 mm and 27.12 mm respectively. The load-deflection curves of two shear tests illustrated a distinctly precipitous descent after peak loads, indicating brittle failure.
- (4)
- In the bending test, strain variations along the vertical section basically conformed to the plane section assumption, with the neutral axis approximately at the junction of the top flange and the web. In the shear test, the strains along the vertical section and principal strain at the shear span were complex, due to the irregular propagation of cracks and stress distributions.
- (5)
- The cracking patterns and cracking failures simulated by FEMs aligned with the experimental observation. According to extensive parameter analysis of FEMs, the shear load of stirrup-free I-shaped UHPC beams significantly decreased with the increase in shear span–depth ratios. Otherwise, the influence of longitudinal rebars was limited.
- (6)
- Comparisons of FEMs outcomes and predicting values of four formulas corroborated that Ye’s formula yielded the most accurate. In the scenario of design practice of stirrup-free I-shape UHPC beams at high shear span-depth ratio (≥2.0), two formulations of the French code and PCI reports were recommended, owing to the rationally conservative predictions, and explicit physical indication.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Olivito, R.S.; Zuccarello, F.A. An experimental study on the tensile strength of steel fiber reinforced concrete. Compos. Part B Eng. 2010, 41, 246–255. [Google Scholar] [CrossRef]
- Yu, R.; Spiesz, P.; Brouwers, H.J.H. Mix design and properties assessment of Ultra-High Performance Fibre Reinforced Concrete (UHPFRC). Cem. Concr. Res. 2014, 56, 29–39. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, J.; Liu, J.; Zhang, P.; Zhang, Q.; Jiang, L. Experimental studies and modeling of creep of UHPC. Constr. Build. Mater. 2018, 175, 643–652. [Google Scholar] [CrossRef]
- Hung, C.-C.; Chen, Y.-T.; Yen, C.-H. Workability, fiber distribution, and mechanical properties of UHPC with hooked end steel macro-fibers. Constr. Build. Mater. 2020, 260, 119944. [Google Scholar] [CrossRef]
- Li, J.; Wu, Z.; Shi, C.; Yuan, Q.; Zhang, Z. Durability of ultra-high performance concrete—A review. Constr. Build. Mater. 2020, 255, 119296. [Google Scholar] [CrossRef]
- Kang, S.-T.; Kim, J.-K. Investigation on the flexural behavior of UHPCC considering the effect of fiber orientation distribution. Constr. Build. Mater. 2012, 28, 57–65. [Google Scholar] [CrossRef]
- Xue, J.; Briseghella, B.; Huang, F.; Nuti, C.; Tabatabai, H.; Chen, B. Review of ultra-high performance concrete and its application in bridge engineering. Constr. Build. Mater. 2020, 260, 119844. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, L.; Deng, B.; Gao, X.; Xie, S.; Sha, Z.; Chen, M. The direct shear behavior of the ultra-high performance concrete-filled socket connections between the bridge piers and footings. Structures 2024, 66, 106888. [Google Scholar] [CrossRef]
- Jiang, H.; Chen, Z.; Fang, Z.; Fang, S.; Tu, W.; Mo, F.; Xie, S.; Liu, J. Rapid hardening high performance concrete (RHHPC) for bridge expansion joints: From material properties to interfacial shear performance. Constr. Build. Mater. 2025, 458, 139638. [Google Scholar] [CrossRef]
- Shafieifar, M.; Farzad, M.; Azizinamini, A. Experimental and numerical study on mechanical properties of Ultra High Performance Concrete (UHPC). Constr. Build. Mater. 2017, 156, 402–411. [Google Scholar] [CrossRef]
- Abdal, S.; Mansour, W.; Agwa, I.; Nasr, M.; Abadel, A.; Özkılıç, Y.O.; Akeed, M.H. Application of Ultra-High-Performance Concrete in Bridge Engineering: Current Status, Limitations, Challenges, and Future Prospects. Buildings 2023, 13, 185. [Google Scholar] [CrossRef]
- Peng, Y.; Zhang, J.; Liu, J.; Ke, J.; Wang, F. Properties and microstructure of reactive powder concrete having a high content of phosphorous slag powder and silica fume. Constr. Build. Mater. 2015, 101, 482–487. [Google Scholar] [CrossRef]
- Kunieda, M.; Choonghyun, K.; Ueda, N.; Nakamura, H. Recovery of Protective Performance of Cracked Ultra High Performance-Strain Hardening Cementitious Composites (UHP-SHCC) Due to Autogenous Healing. J. Adv. Concr. Technol. 2012, 10, 313–322. [Google Scholar] [CrossRef]
- Binard, J.P. UHPC: A game-changing material for PCI bridge producers. PCI J. 2017, 62, 34–46. [Google Scholar] [CrossRef]
- Estefanía, C.; Francesco, L.M.; Marina, M.; Andrea, S.; Liberato, F. Effects of Autogenous and Stimulated Self-Healing on Durability and Mechanical Performance of UHPFRC: Validation of Tailored Test Method through Multi-Performance Healing-Induced Recovery Indices. Sustainability 2021, 13, 11386. [Google Scholar]
- Estefania, C.; Valentin, P.; Liberato, F. Cellulose nanofibers to improve the mechanical and durability performance of self-healing Ultra-High Performance Concretes exposed to aggressive waters. Constr. Build. Mater. 2023, 374, 130785. [Google Scholar]
- Zhou, M.; Lu, W.; Song, J.; Lee, G.C. Application of Ultra-High Performance Concrete in bridge engineering. Constr. Build. Mater. 2018, 186, 1256–1267. [Google Scholar] [CrossRef]
- Amran, M.; Huang, S.-S.; Onaizi, A.M.; Makul, N.; Abdelgader, H.S.; Ozbakkaloglu, T. Recent trends in ultra-high performance concrete (UHPC): Current status, challenges, and future prospects. Constr. Build. Mater. 2022, 352, 129029. [Google Scholar] [CrossRef]
- Voo, Y.L.; Foster, S.J.; Voo, C.C. Ultrahigh-Performance Concrete Segmental Bridge Technology: Toward Sustainable Bridge Construction. J. Bridge Eng. 2014, 20, B5014001. [Google Scholar] [CrossRef]
- Hung, C.-C.; El-Tawil, S.; Chao, S.-H. A Review of Developments and Challenges for UHPC in Structural Engineering: Behavior, Analysis, and Design. J. Struct. Eng. 2021, 1479, 03121001. [Google Scholar] [CrossRef]
- Feng, Z.; Li, C.; Ke, L.; Yoo, D.-Y. Experimental and numerical investigations on flexural performance of ultra-high-performance concrete (UHPC) beams with wet joints. Structures 2022, 45, 199–213. [Google Scholar] [CrossRef]
- Randl, N.; Mészöly, T.; Harsányi, P. Shear Behaviour of UsHPC Beams with Varying Degrees of Fibre and Shear Reinforcement. In High Tech Concrete—Where Technology and Engineering Meet, Proceedings of the Fib Symposium, Maastricht, The Netherlands, 12–14 June 2017; Springer International Publishing: Cham, Switzerland, 2017; pp. 500–507. [Google Scholar]
- Feng, J.; Li, P.; Wu, J.; Jiang, H.; Tian, Y.; Sun, X. Shear behavior of externally prestressed UHPC beams without stirrups. Case Stud. Constr. Mater. 2023, 18, e01766. [Google Scholar] [CrossRef]
- Feng, W.; Feng, H.; Zhou, Z.; Shi, X. Analysis of the Shear Capacity of Ultrahigh Performance Concrete Beams Based on the Modified Compression Field Theory. Adv. Mater. Sci. Eng. 2021, 2021, 5569733. [Google Scholar]
- Ye, M.; Li, L.; Pei, B.; Yoo, D.Y.; Li, H. Shear behavior of externally prestressed ultra-high-performance concrete (UHPC) T-beams without stirrups. Eng. Struct. 2023, 288, 116217. [Google Scholar]
- Jiang, H.; Hu, Z.; Cao, Z.; Gao, X.; Tian, Y.; Sun, X. Experimental and numerical study on shear performance of externally prestressed precast UHPC segmental beams without stirrups. Structures 2022, 46, 1134–1153. [Google Scholar] [CrossRef]
- Voo, Y.L.; Poon, W.K.; Foster, S.J. Shear Strength of Steel Fiber-Reinforced Ultrahigh-Performance Concrete Beams without Stirrups. J. Struct. Eng. 2010, 136, 1393–1400. [Google Scholar] [CrossRef]
- Lee, J.W.; Joh, C.; Choi, E.S.; Kwak, I.J.; Kim, B.S. Estimation of Shear Behavior of Ultra High Performance Concrete I Girder without Shear Stirrups. Key Eng. Mater. 2013, 525, 557–560. [Google Scholar]
- El-Helou, R.G.; Graybeal, B.A. Shear Behavior of Ultrahigh-Performance Concrete Pretensioned Bridge Girders. J. Struct. Eng. 2022, 148, 04022017. [Google Scholar] [CrossRef]
- El-Helou, R.G.; Graybeal, B.A. Shear Design of Strain-Hardening Fiber-Reinforced Concrete Beams. J. Struct. Eng. 2022, 149, 04022234. [Google Scholar] [CrossRef]
- Tu, W.; Cheng, Q.; Zhang, L.; Li, P.; Jiang, H.; Tian, Y.; Fang, J. Shear performance of 25 m full-scale prestressed UHPC-NC composite I-beam without stirrups. Case Stud. Constr. Mater. 2024, 21, e03942. [Google Scholar] [CrossRef]
- Ahmad, S.; Bahij, S.; Al-Osta, M.A.; Adekunle, S.K.; Al-Dulaijan, S.U. Shear Behavior of Ultra-High-Performance Concrete Beams Reinforced with High-Strength Steel Bars. ACI Struct. J. 2019, 116, 3–14. [Google Scholar] [CrossRef]
- Deng, B.; Zhang, L.; Wu, S.; Jiang, H.; Tian, Y.; Fang, J.; Zhou, C. Shear Behavior of Non-Stirrup Ultra-High-Performance Concrete Beams: Contribution of Steel Fibers and UHPC. Buildings 2024, 14, 2705. [Google Scholar] [CrossRef]
- Zhang, L.; Deng, B.; He, B.; Jiang, H.; Xiao, J.; Tian, Y.; Fang, J. Experimental Investigation on Shear Behavior of Non-Stirrup UHPC Beams under Larger Shear Span–Depth Ratios. Buildings 2024, 14, 1374. [Google Scholar] [CrossRef]
- Li, P.; Cheng, Q.; Chen, N.; Tian, Y.; Fang, J.; Jiang, H. Experimental Study on Shear Behavior of Non-Stirrup Ultra-High Performance Concrete Beams. Materials 2023, 16, 4177. [Google Scholar] [CrossRef]
- NFP 18 470:2016; Concrete-Ultra-High Performance Fibre-Reinforced Concrete-Specifications, Performance, Production and Conformity. French Standardization Association: Paris, France, 2016.
- Tadros, M.; Lawler, J.; El-Khier, M.A.; Gee, D.; Kurt, A.; Lucier, G.; Wagner, E. Implementation of Ultra-High-Performance Con crete in Long-Span Precast Pretensioned Elements for Concrete Buildings and Bridges; Precast/Prestressed Concrete Institute (PCI): Chicago, IL, USA, 2021. [Google Scholar]
- GB/T50448—2015; Technical Code for Application of Cementitious Grout. China Architecture and Building Press: Beijing, China, 2015.
- Yang, J.; Fang, Z. Research on stress-strain relation of ultra-high-performance concrete. Concrete 2008, 7, 11–15. [Google Scholar]
- Shi, Z.C.; Su, Q.T.; Kavoura, F.; Veljkovic, M. Uniaxial tensile response and tensile constitutive model of ultra-high performance concrete containing coarse aggregate (CA-UHPC). Cem. Concr. Compos. 2023, 136, 136104878. [Google Scholar] [CrossRef]
- Birtel, V.; Mark, P. Parameterised finite element modelling of RC beam shear failure. In Proceedings of the ABAQUS Users’ Conference; Ruhr-University Bochture: Bochum, Germany, 2006. [Google Scholar]
- Chuanbo, Z. Research on Uniaxial Compressive Strength of Reactive Powder Concrete; Hunan University: Changsha, China, 2017. [Google Scholar]
- Fang, Z.; Zhang, S.; Wu, J.; Ma, Y.; Fang, S.; Zhao, G.; Jiang, H. Experimental and numerical study on shear performance of grouped bolt-UHPC pocket connections under static loading. J. Build. Eng. 2023, 76, 106966. [Google Scholar] [CrossRef]
- Fang, S.; Ma, F.; Xian, B.; Fang, Z.; Jiang, H.; Ma, Y.; Zhao, G. Numerical and theoretical investigation on interfacial shear performance of prefabricated steel-UHPC composite beams with grouped stud-UHPC pocket connections. Structures 2024, 69, 107300. [Google Scholar] [CrossRef]
- Luo, J.; Wu, G.; Zhao, G.; Ma, Y.; Fang, Z.; Fang, S. Experimental and numerical analysis on shear performance of single embedded nut bolted shear connectors in prefabricated steel-UHPC composite structures under cyclic loading. Structures 2025, 73, 108446. [Google Scholar] [CrossRef]
- Zou, S.; Chen, R.; Wang, H.; Fang, Z.; Qu, C.; Zhang, C. Effect of shear key geometrical dimensions on seismic performance of prefabricated concrete piers with shallow socket connections. Structures 2025, 71, 107975. [Google Scholar] [CrossRef]
- Collins, M.P.; Mitchell, D. Shear and Torsion Design of Prestressed and Non-Prestressed Concrete Beams. PCI J. 1980, 25, 32–100. [Google Scholar] [CrossRef]
- Vecchio, F.J.; Collins, M.P. The modified compression-field theory for reinforced concrete elements subjected to shear. ACI J. 1986, 83, 219–231. [Google Scholar]
- Collins, M.P.; Mitchell, D. Rational Approach to Shear Design—The 1984 Canadian Code Provisions. J. Proc. 1986, 83, 925–933. [Google Scholar]
- Gamble, W.L.; Ramirez, J.A. Recent approaches to shear design of structural concrete. J. Struct. Eng. 2000, 126, 853. [Google Scholar] [CrossRef]






| Type | Cement | Silica Fume | Microsphere Powder | Quartz Sand | Steel Fiber | Water Reducer | Water |
|---|---|---|---|---|---|---|---|
| UHPC-2% | 868 | 181 | 102 | 941 | 161 | 46 | 153 |
| Concrete Type | Steel Fiber Content | (MPa) | (MPa) | (MPa) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| UHPC-2% | 2% | 158.8 | 142.0 | 8.7 | 5.4 | 28.1 | 10.54 | 9.29 | 43.62 | 0.23 |
| Reinforcing Steel Bar Samples | (MPa) | (MPa) | |
|---|---|---|---|
| HRB-400-16 | 425.16 | 611.29 | 199 |
| Test Specimen Name | MPa | MPa | kN | mm | MPa | Post-Cracking Performance | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 4.8-R400 | 150 | 4.32 | 12.3 | 240 | 7.77 | 6.4 | 373.67 | 21.31 | 10.0 | 59.9% | 336.3 |
| 4.8-R400 | 160 | 5.58 | 12.4 | 200 | 7.87 | 5.3 | 364.33 | 27.12 | 9.70 | 56.1% | 327.9 |
| 2.0-R400 | -- | -- | -- | 280 | 1.26 | 7.5 | 900.03 | 6.55 | 24.0 | 68.9% | 337.5 |
| 2.0-R400 | -- | -- | -- | 180 | 1.39 | 4.8 | 829.13 | 5.99 | 22.1 | 78.3% | 310.9 |
| Concrete | Dilation Angle | Eccentricity Rate | K | Viscosity Coefficient | |
|---|---|---|---|---|---|
| UHPC | 36 | 0.1 | 1.16 | 0.667 | 0.005 |
| Reinforcing Steel Type | ) | Young’s Modulus (MPa) | Poisson’s Ratio | Yield Strength (MPa) |
|---|---|---|---|---|
| HRB400 | 7800 | 200,000 | 0.3 | 420 |
| HRB500 | 7800 | 200,000 | 0.3 | 520 |
| HRB600 | 7800 | 200,000 | 0.3 | 620 |
| Specimen | (kN) | (mm) | ||||
|---|---|---|---|---|---|---|
| 4.8-R400 | 373.67 | 21.31 | 386.0 | 25.28 | 1.03 | 1.19 |
| 4.8-R400 | 364.33 | 27.12 | 386.0 | 25.28 | 1.06 | 0.93 |
| 2.0-R400 | 900.03 | 6.55 | 865.1 | 5.36 | 0.97 | 0.82 |
| 2.0-R400 | 829.13 | 5.99 | 865.1 | 5.36 | 1.05 | 0.89 |
| Mean | 1.03 | 0.96 | ||||
| Standard Deviation | 0.04 | 0.16 | ||||
| Extended Parameter | Test Beam | Condition |
|---|---|---|
| Span-to-depth ratio | 4-m I-section UHPC beam without stirrups | λ = 1.0, 1.25, 1.5, 1.75, 2.0, 2.25, 2.5, 2.75, 3.0 |
| Longitudinal reinforcement strength | UHPC beam without stirrups | HRB500, HRB600 |
| Category | Specimen Name | (kN) | Deflection at Loading Point (mm) | Bending Moment Mu (kN·m) |
|---|---|---|---|---|
| ① | T-UI1-S-λ2.0-R400 | 450.02 | 6.55 | 337.51 |
| T-UI2-S-λ2.0-R400 | 414.57 | 5.99 | 310.92 | |
| ② | N-UI1-S-λ2.0-R400 | 432.55 | 5.40 | 324.41 |
| ③ | N-UI1-S-λ1.0-R400 | 947.7 | 11.50 | 355.39 |
| N-UI1-S-λ1.25-R400 | 652.95 | 12.40 | 306.07 | |
| N-UI1-S-λ1.5-R400 | 578.99 | 13.75 | 325.68 | |
| N-UI1-S-λ1.75-R400 | 480.30 | 15.00 | 315.20 | |
| N-UI1-S-λ2.0-R400 | 438.83 | 17.40 | 329.12 | |
| N-UI1-S-λ2.25-R400 | 382.27 | 18.30 | 322.54 | |
| N-UI1-S-λ2.50-R400 | 339.10 | 18.90 | 317.91 | |
| N-UI1-S-λ2.75-R400 | 305.74 | 19.50 | 315.29 | |
| N-UI1-S-λ3.0-R400 | 279.00 | 20.10 | 313.88 | |
| ④ | N-UI1-S-λ1.0-R500 | 976.74 | 13.00 | 366.28 |
| N-UI1-S-λ1.5-R500 | 604.74 | 15.50 | 340.17 | |
| N-UI1-S-λ2.0-R500 | 480.58 | 18.60 | 360.44 | |
| N-UI1-S-λ1.0-R600 | 1068.80 | 14.00 | 400.80 | |
| N-UI1-S-λ1.5-R600 | 631.94 | 17.25 | 355.47 | |
| N-UI1-S-λ2.0-R600 | 489.56 | 21.60 | 367.17 |
| Category | Specimen Name | ° | (MPa) | (MPa) | b (mm) | z (mm) | (kN) | (kN) | (kN) | (kN) | (kN) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ① | T-UI1-S-λ2.0-R400 | 37.20 | 158.80 | 8.70 | 50.00 | 337.50 | 49.62 | 0.00 | 193.42 | 243.04 | 450.015 | 0.54 |
| T-UI2-S-λ2.0-R400 | 36.40 | 158.80 | 8.70 | 50.00 | 337.50 | 49.62 | 0.00 | 199.13 | 248.75 | 414.565 | 0.60 | |
| ② | N-UI1-S-λ2.0-R400 | 40.19 | 158.80 | 8.70 | 50.00 | 337.50 | 49.62 | 0.00 | 173.78 | 223.40 | 432.55 | 0.52 |
| ③ | N-UI1-S-λ1.0-R400 | 42.35 | 158.80 | 8.70 | 50.00 | 337.50 | 49.62 | 0.00 | 161.06 | 210.68 | 947.71 | 0.22 |
| N-UI1-S-λ1.25-R400 | 44.11 | 158.80 | 8.70 | 50.00 | 337.50 | 49.62 | 0.00 | 151.43 | 201.05 | 652.95 | 0.31 | |
| N-UI1-S-λ1.5-R400 | 40.34 | 158.80 | 8.70 | 50.00 | 337.50 | 49.62 | 0.00 | 172.87 | 222.49 | 578.99 | 0.38 | |
| N-UI1-S-λ1.75-R400 | 40.99 | 158.80 | 8.70 | 50.00 | 337.50 | 49.62 | 0.00 | 168.95 | 218.57 | 480.3 | 0.46 | |
| N-UI1-S-λ2.0-R400 | 39.75 | 158.80 | 8.70 | 50.00 | 337.50 | 49.62 | 0.00 | 176.52 | 226.14 | 438.83 | 0.52 | |
| N-UI1-S-λ2.25-R400 | 39.64 | 158.80 | 8.70 | 50.00 | 337.50 | 49.62 | 0.00 | 177.20 | 226.82 | 382.27 | 0.59 | |
| N-UI1-S-λ2.50-R400 | 39.46 | 158.80 | 8.70 | 50.00 | 337.50 | 49.62 | 0.00 | 178.34 | 227.95 | 339.1 | 0.67 | |
| N-UI1-S-λ2.75-R400 | 39.65 | 158.80 | 8.70 | 50.00 | 337.50 | 49.62 | 0.00 | 177.17 | 226.79 | 305.74 | 0.74 | |
| N-UI1-S-λ3.0-R400 | 40.29 | 158.80 | 8.70 | 50.00 | 337.50 | 49.62 | 0.00 | 173.19 | 222.81 | 279 | 0.80 | |
| ④ | N-UI1-S-λ1.0-R500 | 42.68 | 158.80 | 8.70 | 50.00 | 337.50 | 49.62 | 0.00 | 159.20 | 208.82 | 976.74 | 0.21 |
| N-UI1-S-λ1.5-R500 | 41.51 | 158.80 | 8.70 | 50.00 | 337.50 | 49.62 | 0.00 | 165.86 | 215.48 | 604.74 | 0.36 | |
| N-UI1-S-λ2.0-R500 | 39.40 | 158.80 | 8.70 | 50.00 | 337.50 | 49.62 | 0.00 | 178.74 | 228.35 | 480.58 | 0.48 | |
| N-UI1-S-λ1.0-R600 | 42.84 | 158.80 | 8.70 | 50.00 | 337.50 | 49.62 | 0.00 | 158.30 | 207.92 | 1068.8 | 0.19 | |
| N-UI1-S-λ1.5-R600 | 41.35 | 158.80 | 8.70 | 50.00 | 337.50 | 49.62 | 0.00 | 166.80 | 216.41 | 631.94 | 0.34 | |
| N-UI1-S-λ2.0-R600 | 39.67 | 158.80 | 8.70 | 50.00 | 337.50 | 49.62 | 0.00 | 177.03 | 226.65 | 489.56 | 0.46 | |
| Overall mean: 0.47; Standard deviation: 0.18; Coefficient of variation: 0.38 ① Test beams: I—section, λ = 2.0; ② Simulated beams: I—section, λ = 2.0; ③ Simulated I—section beams, varying λ (4—point loading); ④ Simulated I—section beams, varying λ and reinforcement strength. | ||||||||||||
| Category | Specimen Name | ° | (MPa) | b (mm) | z (mm) | (kN) | (kN) | (kN) | (kN) | |
|---|---|---|---|---|---|---|---|---|---|---|
| ① | T-UI1-S-λ2.0-R400 | 36° | 10.50 | 50.00 | 337.50 | 325.17 | 0.00 | 325.17 | 450.015 | 0.72 |
| T-UI2-S-λ2.0-R400 | 36° | 10.50 | 50.00 | 337.50 | 325.17 | 0.00 | 325.17 | 414.565 | 0.78 | |
| ② | N-UI1-S-λ2.0-R400 | 36° | 10.50 | 50.00 | 337.50 | 325.17 | 0.00 | 325.17 | 432.55 | 0.75 |
| ③ | N-UI1-S-λ1.0-R400 | 36° | 10.50 | 50.00 | 337.50 | 325.17 | 0.00 | 325.17 | 947.71 | 0.34 |
| N-UI1-S-λ1.25-R400 | 36° | 10.50 | 50.00 | 337.50 | 325.17 | 0.00 | 325.17 | 652.95 | 0.50 | |
| N-UI1-S-λ1.5-R400 | 36° | 10.50 | 50.00 | 337.50 | 325.17 | 0.00 | 325.17 | 578.99 | 0.56 | |
| N-UI1-S-λ1.75-R400 | 36° | 10.50 | 50.00 | 337.50 | 325.17 | 0.00 | 325.17 | 480.3 | 0.68 | |
| N-UI1-S-λ2.0-R400 | 36° | 10.50 | 50.00 | 337.50 | 325.17 | 0.00 | 325.17 | 438.83 | 0.74 | |
| N-UI1-S-λ2.25-R400 | 36° | 10.50 | 50.00 | 337.50 | 325.17 | 0.00 | 325.17 | 382.27 | 0.85 | |
| N-UI1-S-λ2.50-R400 | 36° | 10.50 | 50.00 | 337.50 | 325.17 | 0.00 | 325.17 | 339.1 | 0.96 | |
| N-UI1-S-λ2.75-R400 | 36° | 10.50 | 50.00 | 337.50 | 325.17 | 0.00 | 325.17 | 305.74 | 1.06 | |
| N-UI1-S-λ3.0-R400 | 36° | 10.50 | 50.00 | 337.50 | 325.17 | 0.00 | 325.17 | 279 | 1.17 | |
| ④ | N-UI1-S-λ1.0-R500 | 36° | 10.50 | 50.00 | 337.50 | 325.17 | 0.00 | 325.17 | 976.74 | 0.33 |
| N-UI1-S-λ1.5-R500 | 36° | 10.50 | 50.00 | 337.50 | 325.17 | 0.00 | 325.17 | 604.74 | 0.54 | |
| N-UI1-S-λ2.0-R500 | 36° | 10.50 | 50.00 | 337.50 | 325.17 | 0.00 | 325.17 | 480.58 | 0.68 | |
| N-UI1-S-λ1.0-R600 | 36° | 10.50 | 50.00 | 337.50 | 325.17 | 0.00 | 325.17 | 1068.8 | 0.30 | |
| N-UI1-S-λ1.5-R600 | 36° | 10.50 | 50.00 | 337.50 | 325.17 | 0.00 | 325.17 | 631.94 | 0.51 | |
| N-UI1-S-λ2.0-R600 | 36° | 10.50 | 50.00 | 337.50 | 325.17 | 0.00 | 325.17 | 489.56 | 0.66 | |
| Overall mean: 0.67; Standard deviation: 0.24; Coefficient of variation: 0.36 ① Test beams: I—section, λ = 2.0; ② Simulated beams: I—section, λ = 2.0; ③ Simulated I—section beams, varying λ (4—point loading); ④ Simulated I—section beams, varying λ and reinforcement strength. | ||||||||||
| Category | Specimen Name | (MPa) | b (mm) | d (mm) | (kN) | (kN) | (kN) | (kN) | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ① | T-UI1-S-λ2.0-R400 | 2 | 158.80 | 50.00 | 375.00 | 0.00% | 314.25 | 0.00 | 314.25 | 450.02 | 0.70 |
| T-UI2-S-λ2.0-R400 | 2 | 158.80 | 50.00 | 375.00 | 0.00% | 314.25 | 0.00 | 314.25 | 414.57 | 0.76 | |
| ② | N-UI1-S-λ2.0-R400 | 2 | 158.80 | 50.00 | 375.00 | 0.00% | 314.25 | 0.00 | 314.25 | 432.55 | 0.73 |
| ③ | N-UI1-S-λ1.0-R400 | 1.5 | 158.80 | 50.00 | 375.00 | 0.00% | 448.93 | 0.00 | 448.93 | 947.71 | 0.47 |
| N-UI1-S-λ1.25-R400 | 1.5 | 158.80 | 50.00 | 375.00 | 0.00% | 448.93 | 0.00 | 448.93 | 652.95 | 0.69 | |
| N-UI1-S-λ1.5-R400 | 1.5 | 158.80 | 50.00 | 375.00 | 0.00% | 448.93 | 0.00 | 448.93 | 578.99 | 0.78 | |
| N-UI1-S-λ1.75-R400 | 1.75 | 158.80 | 50.00 | 375.00 | 0.00% | 371.97 | 0.00 | 371.97 | 480.30 | 0.77 | |
| N-UI1-S-λ2.0-R400 | 2 | 158.80 | 50.00 | 375.00 | 0.00% | 314.25 | 0.00 | 314.25 | 438.83 | 0.72 | |
| N-UI1-S-λ2.25-R400 | 2.25 | 158.80 | 50.00 | 375.00 | 0.00% | 269.36 | 0.00 | 269.36 | 382.27 | 0.70 | |
| N-UI1-S-λ2.50-R400 | 2.5 | 158.80 | 50.00 | 375.00 | 0.00% | 233.44 | 0.00 | 233.44 | 339.10 | 0.69 | |
| N-UI1-S-λ2.75-R400 | 2.75 | 158.80 | 50.00 | 375.00 | 0.00% | 204.06 | 0.00 | 204.06 | 305.74 | 0.67 | |
| N-UI1-S-λ3.0-R400 | 3 | 158.80 | 50.00 | 375.00 | 0.00% | 179.57 | 0.00 | 179.57 | 279.00 | 0.64 | |
| ④ | N-UI1-S-λ1.0-R500 | 1.5 | 158.80 | 50.00 | 375.00 | 0.00% | 448.93 | 0.00 | 448.93 | 976.74 | 0.46 |
| N-UI1-S-λ1.5-R500 | 1.5 | 158.80 | 50.00 | 375.00 | 0.00% | 448.93 | 0.00 | 448.93 | 604.74 | 0.74 | |
| N-UI1-S-λ2.0-R500 | 2 | 158.80 | 50.00 | 375.00 | 0.00% | 314.25 | 0.00 | 314.25 | 480.58 | 0.65 | |
| N-UI1-S-λ1.0-R600 | 1.5 | 158.80 | 50.00 | 375.00 | 0.00% | 448.93 | 0.00 | 448.93 | 1068.80 | 0.42 | |
| N-UI1-S-λ1.5-R600 | 1.5 | 158.80 | 50.00 | 375.00 | 0.00% | 448.93 | 0.00 | 448.93 | 631.94 | 0.71 | |
| N-UI1-S-λ2.0-R600 | 2 | 158.80 | 50.00 | 375.00 | 0.00% | 314.25 | 0.00 | 314.25 | 489.56 | 0.64 | |
| Overall mean: 0.66; Standard deviation: 0.11; Coefficient of variation: 0.16 ① Test beams: I—section, λ = 2.0; ② Simulated beams: I—section, λ = 2.0; ③ Simulated I—section beams, varying λ (4—point loading); ④ Simulated I—section beams, varying λ and reinforcement strength. | |||||||||||
| Category | Specimen Name | (MPa) | b (mm) | d (mm) | (kN) | (kN) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| ① | T-UI1-S-λ2.0-R400 | 2 | 2.00 | 158.80 | 50.00 | 375.00 | 4.30% | 361.48 | 450.015 | 0.80 |
| T-UI2-S-λ2.0-R400 | 2 | 2.00 | 158.80 | 50.00 | 375.00 | 4.30% | 361.48 | 414.565 | 0.87 | |
| ② | N-UI1-S-λ2.0-R400 | 2 | 2.00 | 158.80 | 50.00 | 375.00 | 4.30% | 361.48 | 432.55 | 0.84 |
| ③ | N-UI1-S-λ1.0-R400 | 1 | 2.00 | 158.80 | 50.00 | 375.00 | 4.30% | 545.76 | 947.71 | 0.58 |
| N-UI1-S-λ1.25-R400 | 1.25 | 2.00 | 158.80 | 50.00 | 375.00 | 4.30% | 475.39 | 652.95 | 0.73 | |
| N-UI1-S-λ1.5-R400 | 1.5 | 2.00 | 158.80 | 50.00 | 375.00 | 4.30% | 426.33 | 578.99 | 0.74 | |
| N-UI1-S-λ1.75-R400 | 1.75 | 2.00 | 158.80 | 50.00 | 375.00 | 4.30% | 389.85 | 480.3 | 0.81 | |
| N-UI1-S-λ2.0-R400 | 2 | 2.00 | 158.80 | 50.00 | 375.00 | 4.30% | 361.48 | 438.83 | 0.82 | |
| N-UI1-S-λ2.25-R400 | 2.25 | 2.00 | 158.80 | 50.00 | 375.00 | 4.30% | 338.66 | 382.27 | 0.89 | |
| N-UI1-S-λ2.50-R400 | 2.5 | 2.00 | 158.80 | 50.00 | 375.00 | 4.30% | 319.82 | 339.1 | 0.94 | |
| N-UI1-S-λ2.75-R400 | 2.75 | 2.00 | 158.80 | 50.00 | 375.00 | 4.30% | 303.95 | 305.74 | 0.99 | |
| N-UI1-S-λ3.0-R400 | 3 | 2.00 | 158.80 | 50.00 | 375.00 | 4.30% | 290.36 | 279 | 1.04 | |
| ④ | N-UI1-S-λ1.0-R500 | 1 | 2.00 | 158.80 | 50.00 | 375.00 | 4.30% | 545.76 | 976.74 | 0.56 |
| N-UI1-S-λ1.5-R500 | 1.5 | 2.00 | 158.80 | 50.00 | 375.00 | 4.30% | 426.33 | 604.74 | 0.70 | |
| N-UI1-S-λ2.0-R500 | 2 | 2.00 | 158.80 | 50.00 | 375.00 | 4.30% | 361.48 | 480.58 | 0.75 | |
| N-UI1-S-λ1.0-R600 | 1 | 2.00 | 158.80 | 50.00 | 375.00 | 4.30% | 545.76 | 1068.8 | 0.51 | |
| N-UI1-S-λ1.5-R600 | 1.5 | 2.00 | 158.80 | 50.00 | 375.00 | 4.30% | 426.33 | 631.94 | 0.67 | |
| N-UI1-S-λ2.0-R600 | 2 | 2.00 | 158.80 | 50.00 | 375.00 | 4.30% | 361.48 | 489.56 | 0.74 | |
| Overall mean: 0.787; Standard deviation: 0.14; Coefficient of variation: 0.19 ① Test beams: I—section, λ = 2.0; ② Simulated beams: I—section, λ = 2.0; ③ Simulated I—section beams, varying λ (4—point loading); ④ Simulated I—section beams, varying λ and reinforcement strength. | ||||||||||
| Category | Specimen Name | ||||
|---|---|---|---|---|---|
| ① | T-UI1-S-2.0-R400 | 0.54 | 0.72 | 0.70 | 0.80 |
| T-UI2-S-2.0-R400 | 0.60 | 0.78 | 0.76 | 0.87 | |
| ② | N-UI1-S-2.0-R400 | 0.52 | 0.75 | 0.73 | 0.84 |
| ③ | N-UI1-S-1.0-R400 | 0.22 | 0.34 | 0.47 | 0.58 |
| N-UI1-S-1.25-R400 | 0.31 | 0.50 | 0.69 | 0.73 | |
| N-UI1-S-1.5-R400 | 0.38 | 0.56 | 0.78 | 0.74 | |
| N-UI1-S-1.75-R400 | 0.46 | 0.68 | 0.77 | 0.81 | |
| N-UI1-S-2.0-R400 | 0.52 | 0.74 | 0.72 | 0.82 | |
| N-UI1-S-λ2.25-R400 | 0.59 | 0.85 | 0.70 | 0.89 | |
| N-UI1-S-λ2.50-R400 | 0.67 | 0.96 | 0.69 | 0.94 | |
| N-UI1-S-λ2.75-R400 | 0.74 | 1.06 | 0.67 | 0.99 | |
| N-UI1-S-λ3.0-R400 | 0.80 | 1.17 | 0.64 | 1.04 | |
| ④ | N-UI1-S-1.0-R500 | 0.21 | 0.33 | 0.46 | 0.56 |
| N-UI1-S-1.5-R500 | 0.36 | 0.54 | 0.74 | 0.70 | |
| N-UI1-S-2.0-R500 | 0.48 | 0.68 | 0.65 | 0.75 | |
| N-UI1-S-1.0-R600 | 0.19 | 0.30 | 0.42 | 0.51 | |
| N-UI1-S-1.5-R600 | 0.34 | 0.51 | 0.71 | 0.67 | |
| N-UI1-S-2.0-R600 | 0.46 | 0.66 | 0.64 | 0.74 | |
| Mean | 0.47 | 0.67 | 0.66 | 0.78 | |
| Standard Deviation | 0.18 | 0.24 | 0.11 | 0.14 | |
| Coefficient of Variation | 0.38 | 0.36 | 0.16 | 0.19 |
| Category | Specimen Name | ||||
|---|---|---|---|---|---|
| ③ | N-UI1-S-λ2.25-R400 | 0.59 | 0.85 | 0.7 | 0.89 |
| N-UI1-S-λ2.50-R400 | 0.67 | 0.96 | 0.69 | 0.94 | |
| N-UI1-S-λ2.75-R400 | 0.74 | 1.06 | 0.67 | 0.99 | |
| N-UI1-S-λ3.0-R400 | 0.8 | 1.17 | 0.64 | 1.04 | |
| Mean | 0.70 | 1.01 | 0.68 | 0.97 | |
| Standard Deviation | 0.09 | 0.14 | 0.03 | 0.06 | |
| Coefficient of Variation | 0.13 | 0.14 | 0.04 | 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.; Zhou, C.; Mo, F.; Zhang, L.; Jiang, H.; Tian, Y.; Fang, J. Experimental and Numerical Investigations on Shear Performance of Large-Scale Stirrup-Free I-Shaped UHPC Beams. Buildings 2025, 15, 3129. https://doi.org/10.3390/buildings15173129
Wu S, Zhou C, Mo F, Zhang L, Jiang H, Tian Y, Fang J. Experimental and Numerical Investigations on Shear Performance of Large-Scale Stirrup-Free I-Shaped UHPC Beams. Buildings. 2025; 15(17):3129. https://doi.org/10.3390/buildings15173129
Chicago/Turabian StyleWu, Shengze, Chengan Zhou, Fan Mo, Lifeng Zhang, Haibo Jiang, Yueqiang Tian, and Junfa Fang. 2025. "Experimental and Numerical Investigations on Shear Performance of Large-Scale Stirrup-Free I-Shaped UHPC Beams" Buildings 15, no. 17: 3129. https://doi.org/10.3390/buildings15173129
APA StyleWu, S., Zhou, C., Mo, F., Zhang, L., Jiang, H., Tian, Y., & Fang, J. (2025). Experimental and Numerical Investigations on Shear Performance of Large-Scale Stirrup-Free I-Shaped UHPC Beams. Buildings, 15(17), 3129. https://doi.org/10.3390/buildings15173129








