Deteriorated Cyclic Behaviour of Corroded RC Framed Elements: A Practical Proposal for Their Modelling
Abstract
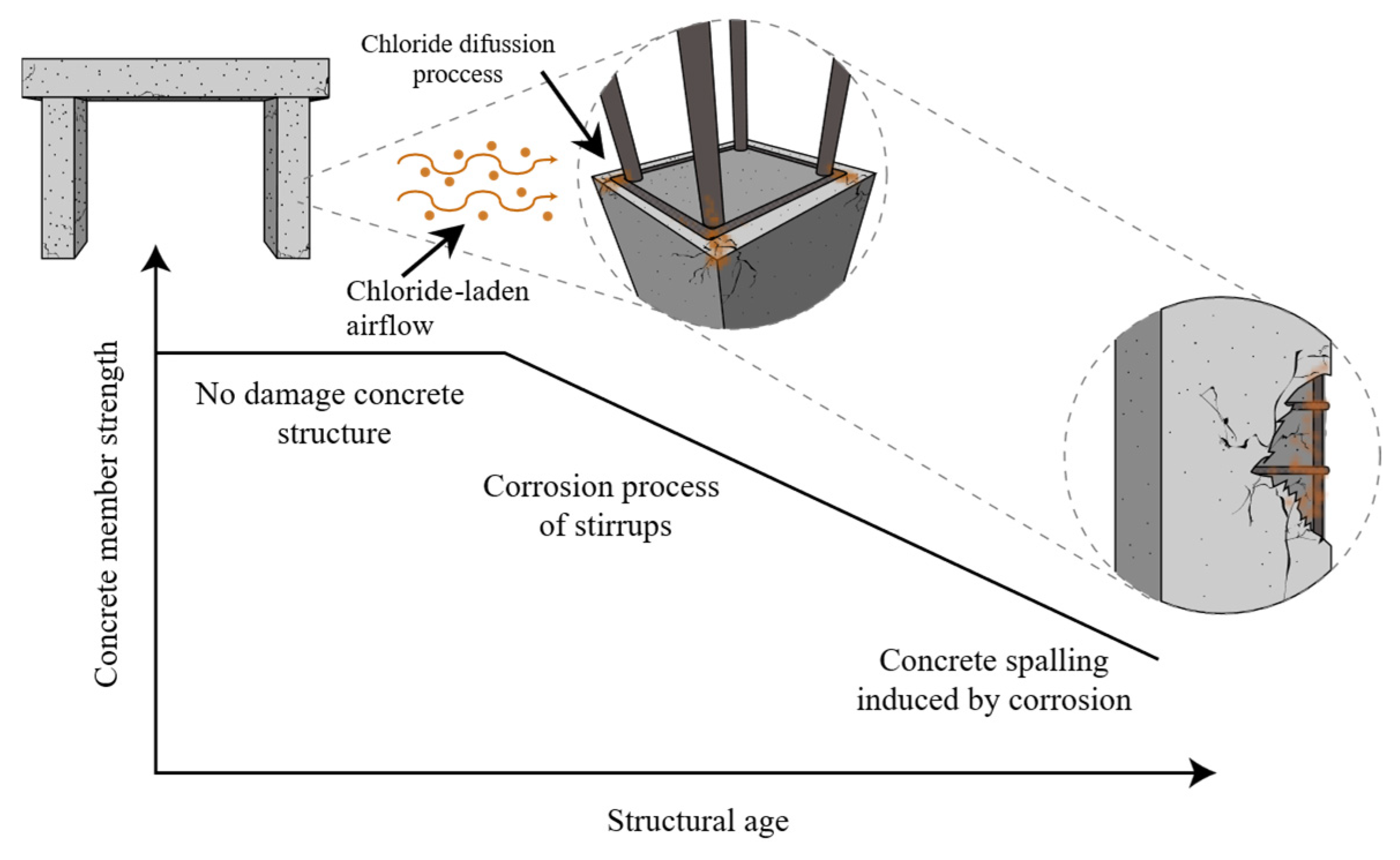
1. Introduction
2. Modelling Considerations and Experimental Tests
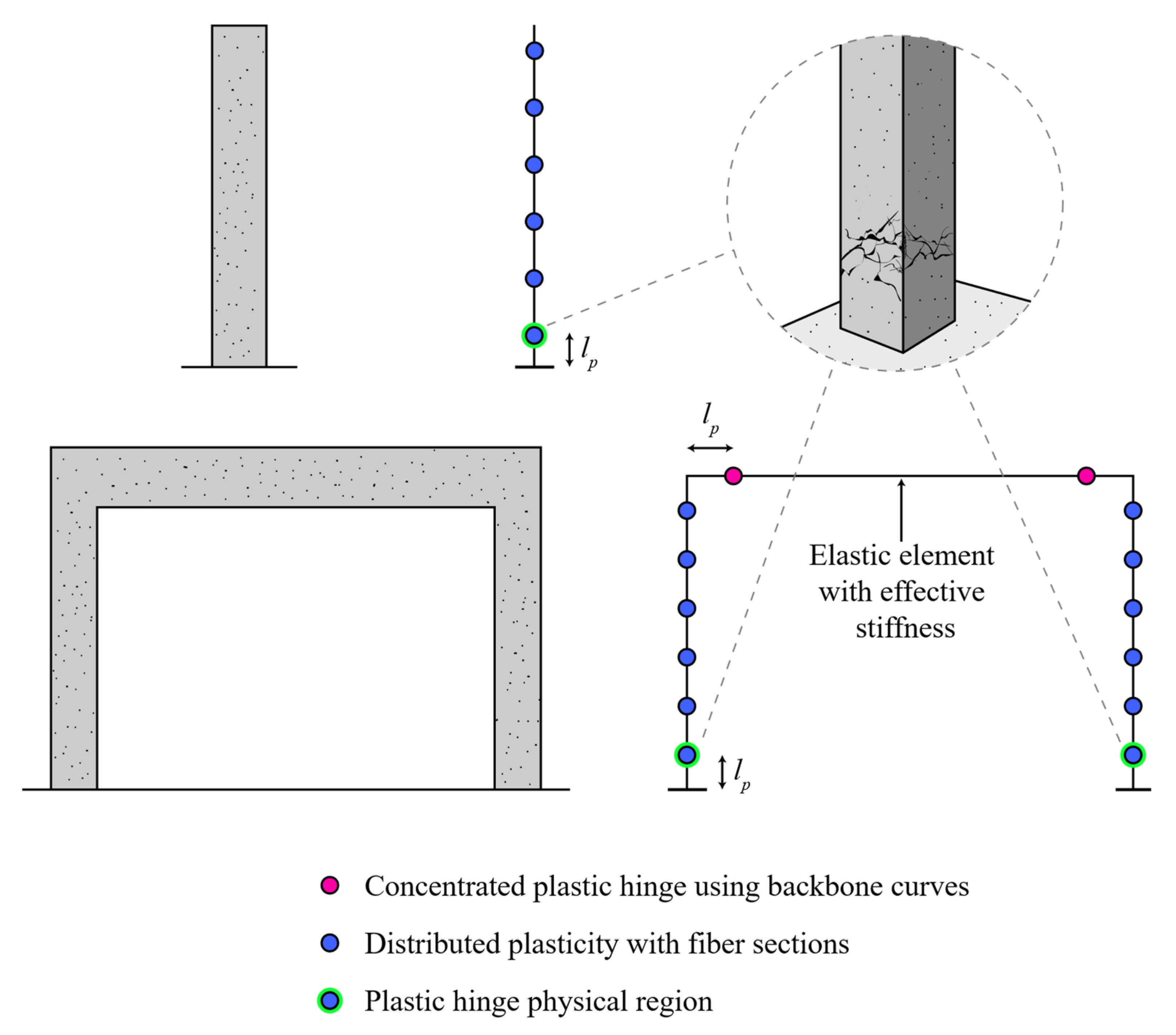
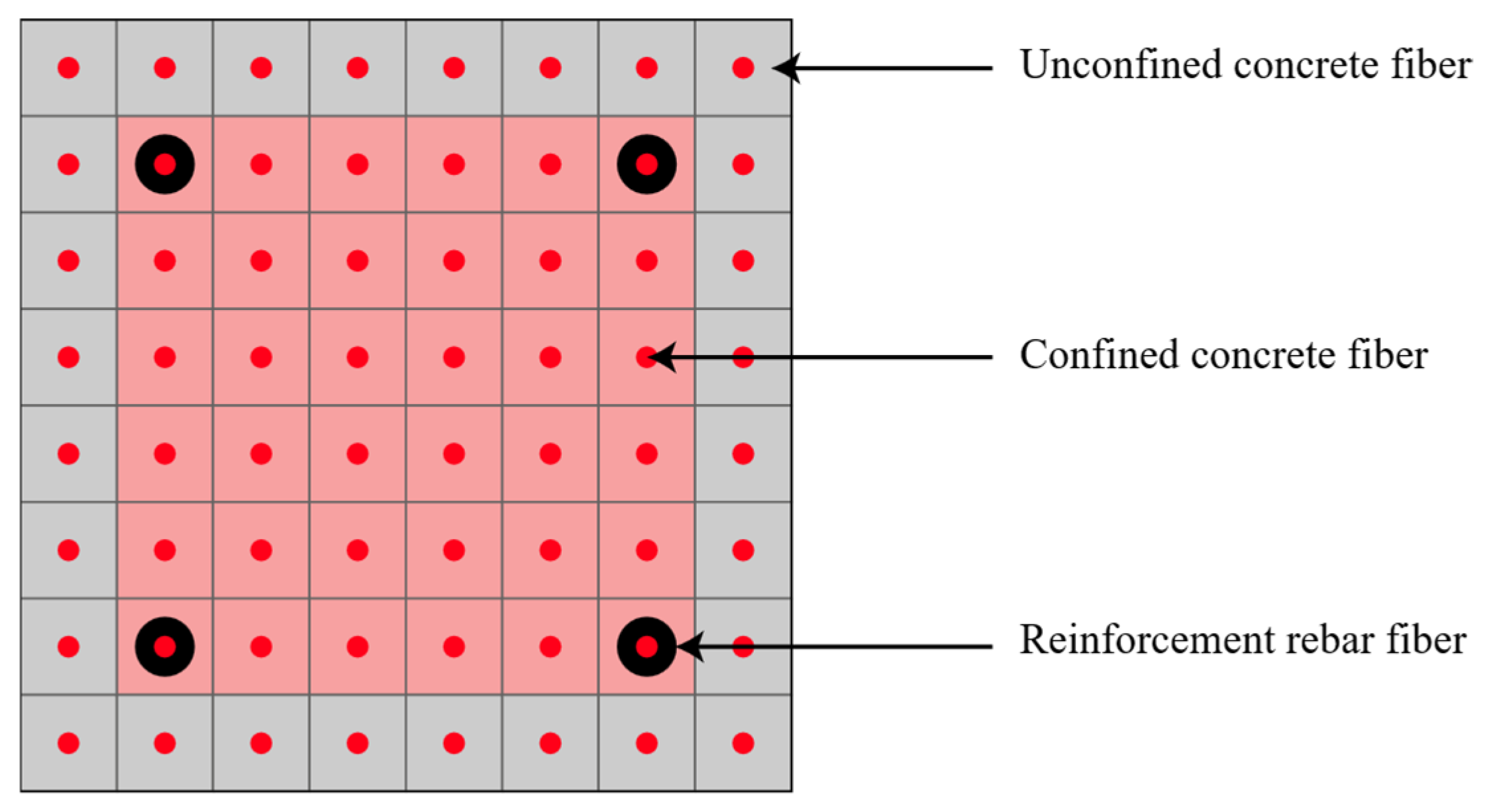
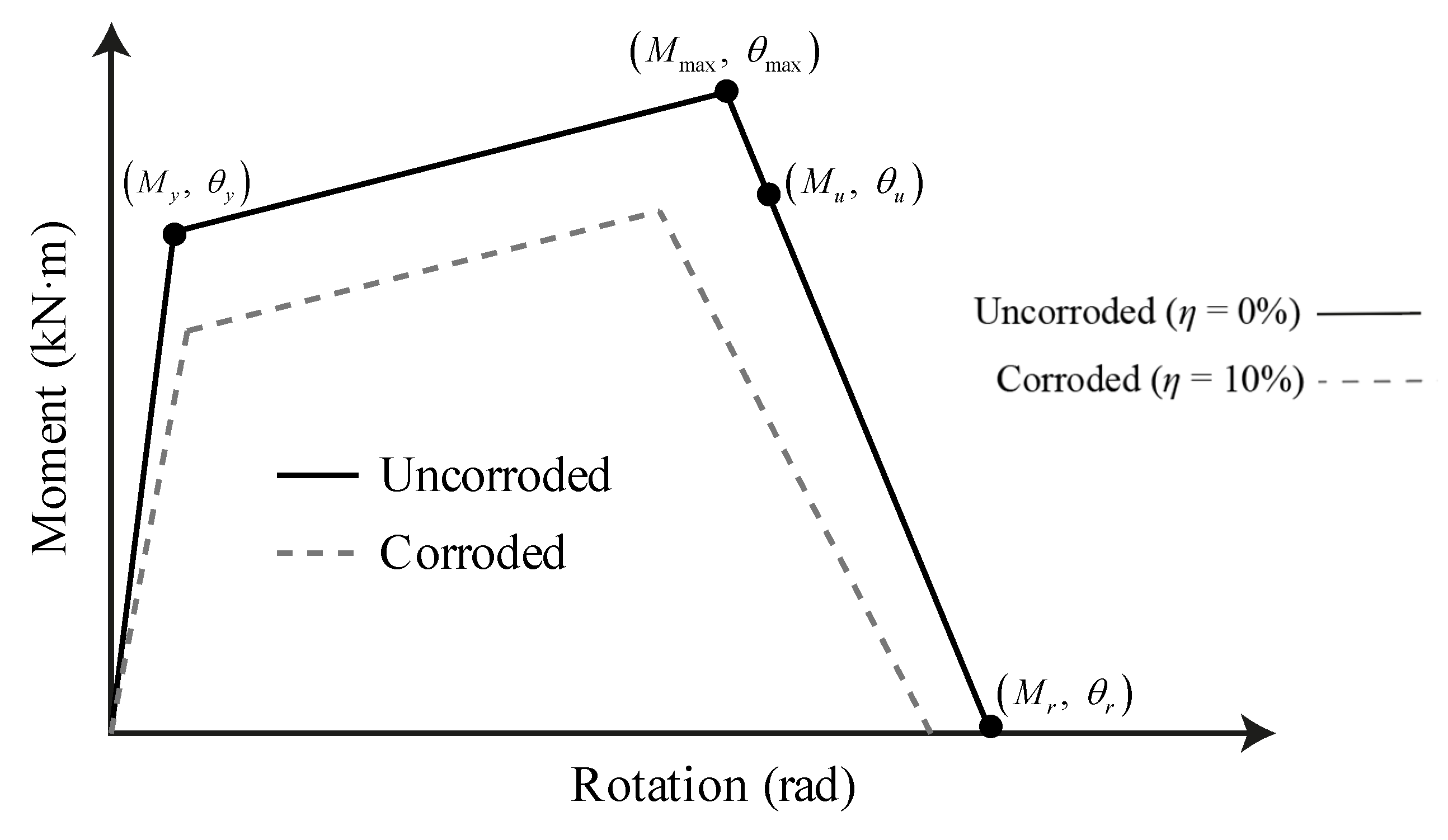
2.1. Description of the Proposed Modelling
2.2. Procedure for the Validation of the Proposed Modelling
2.3. Considerations for Isolated Columns
2.4. Considerations for Frames
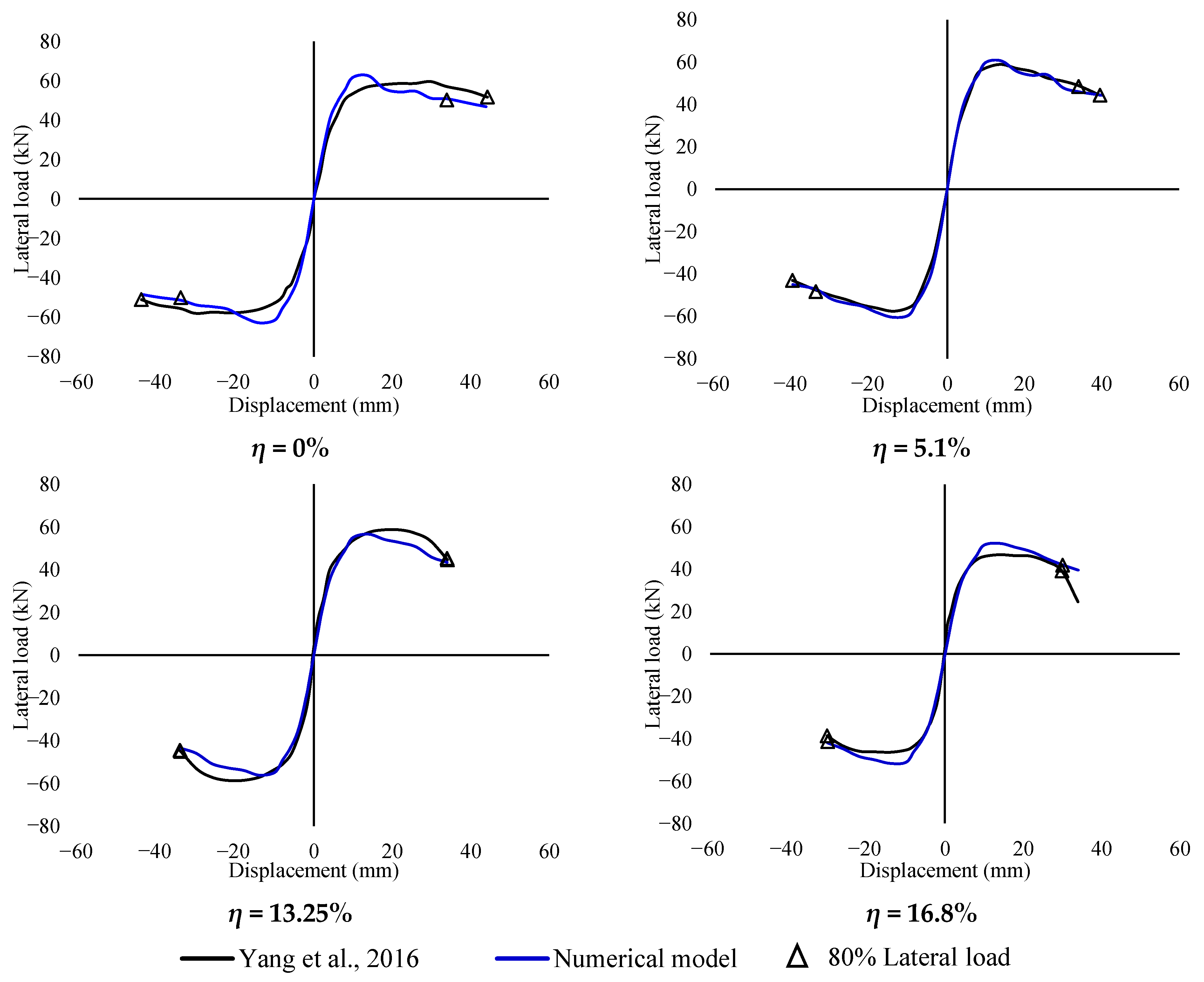
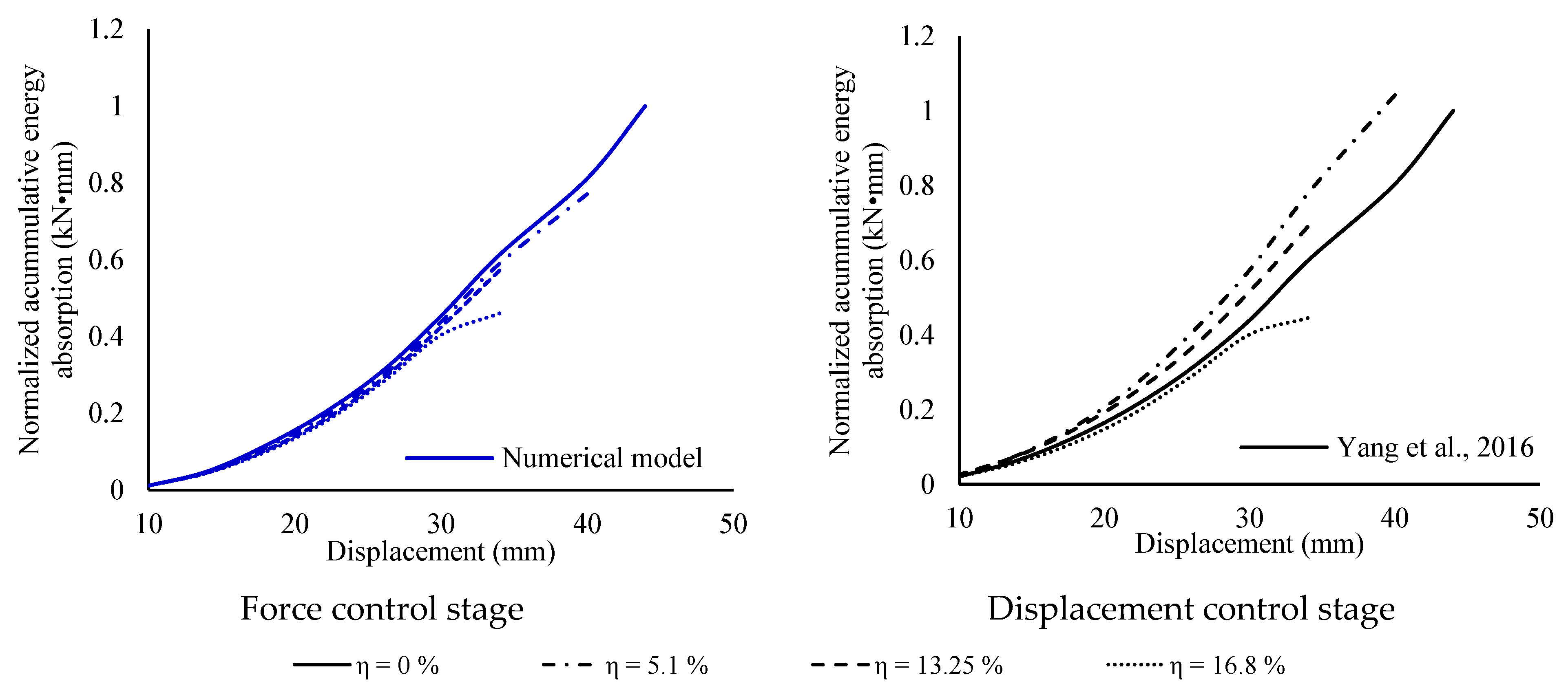
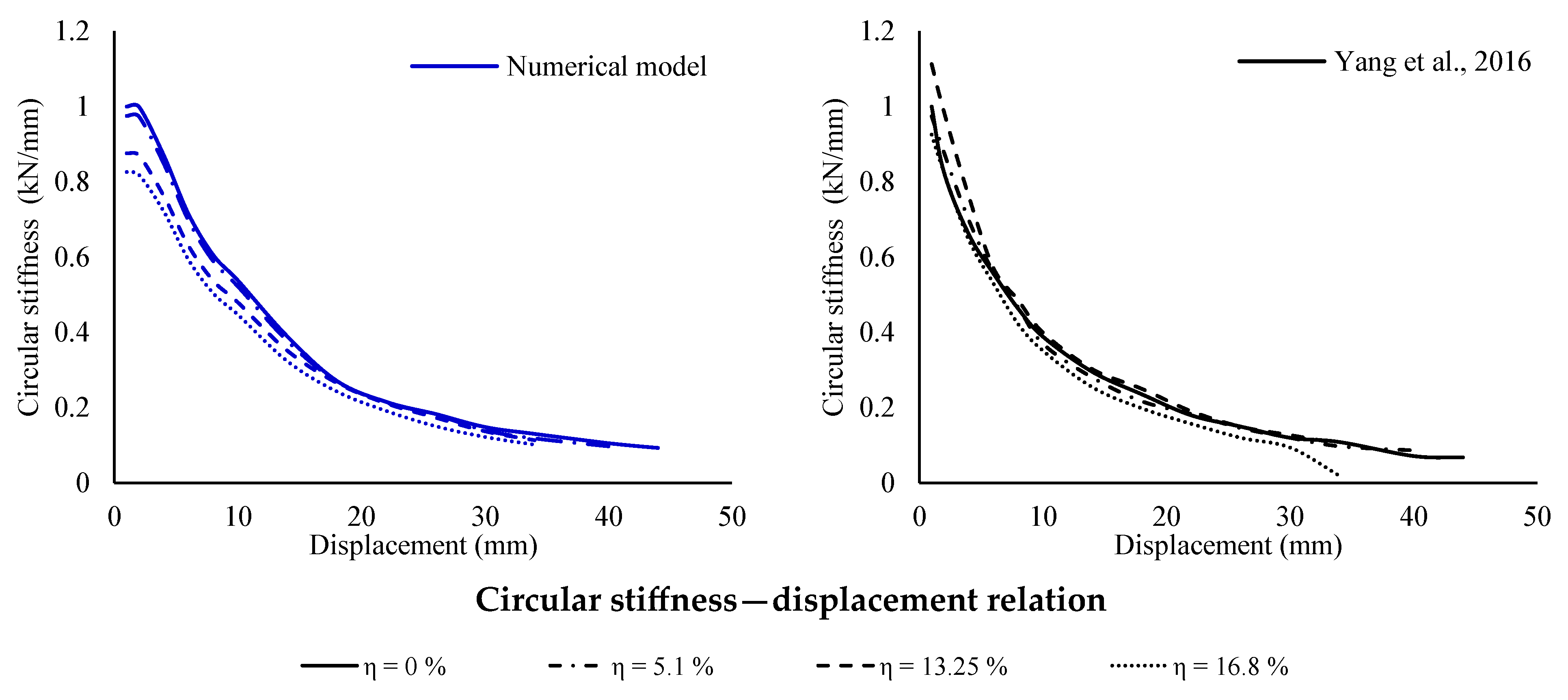
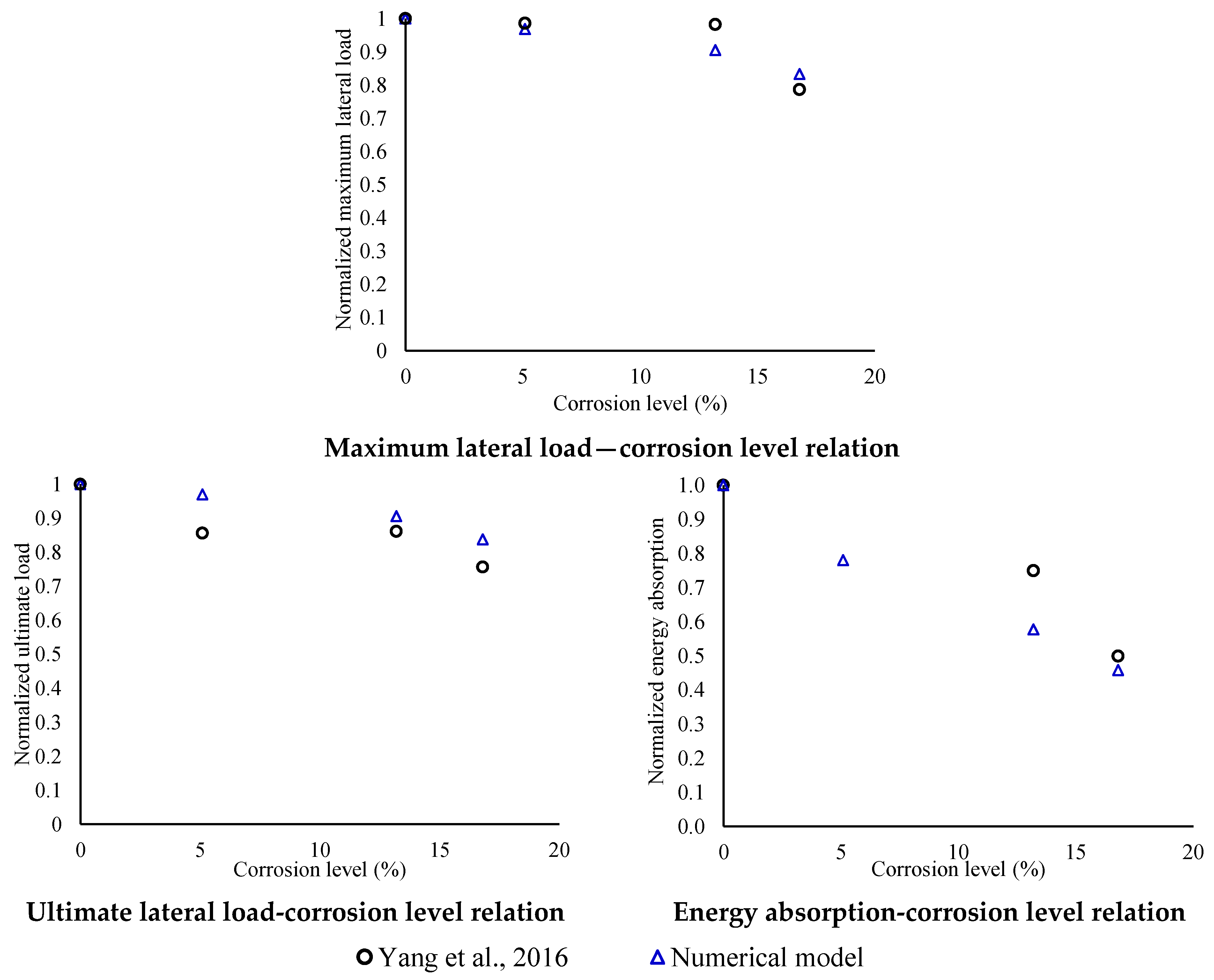
3. Column Behaviour
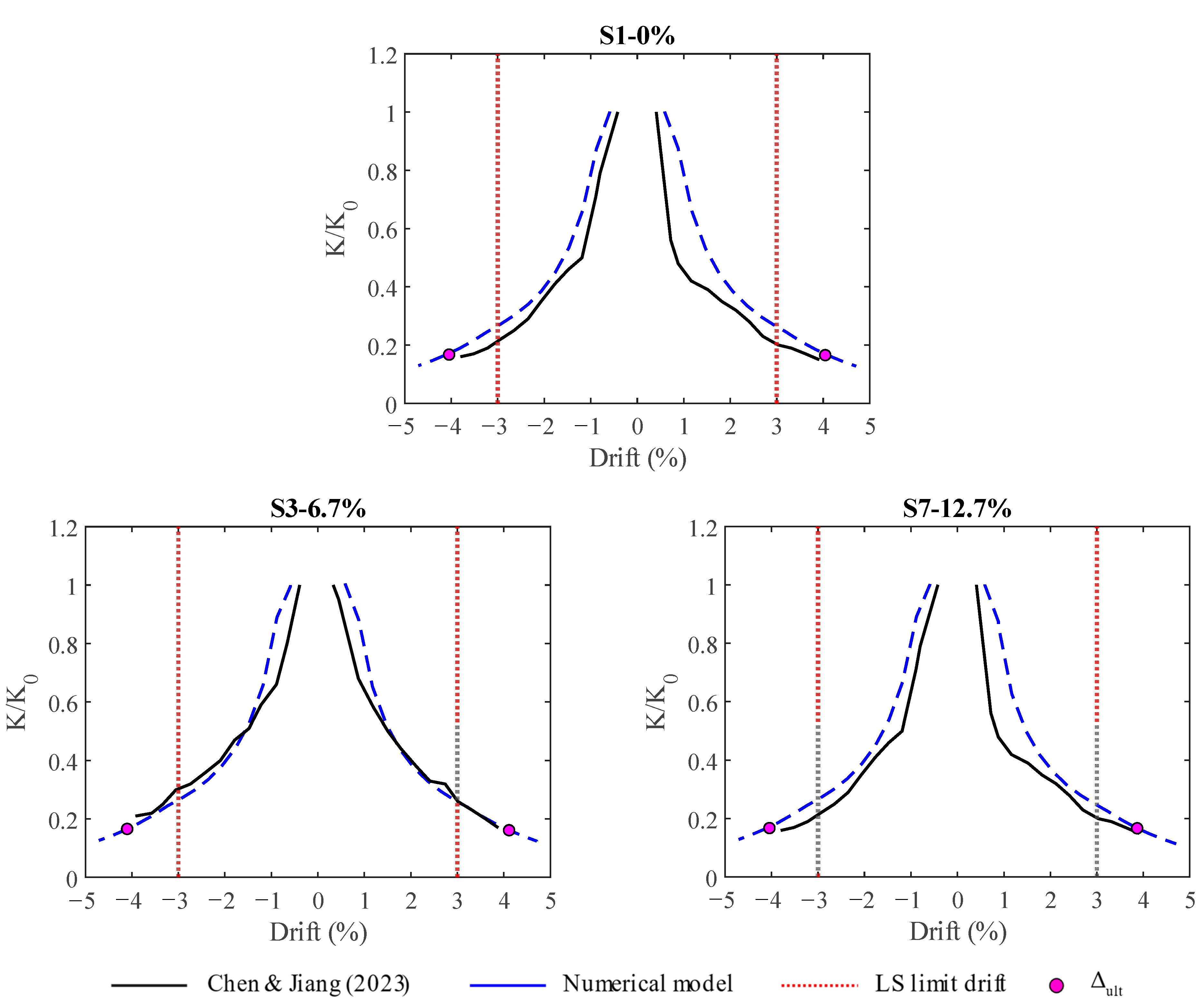
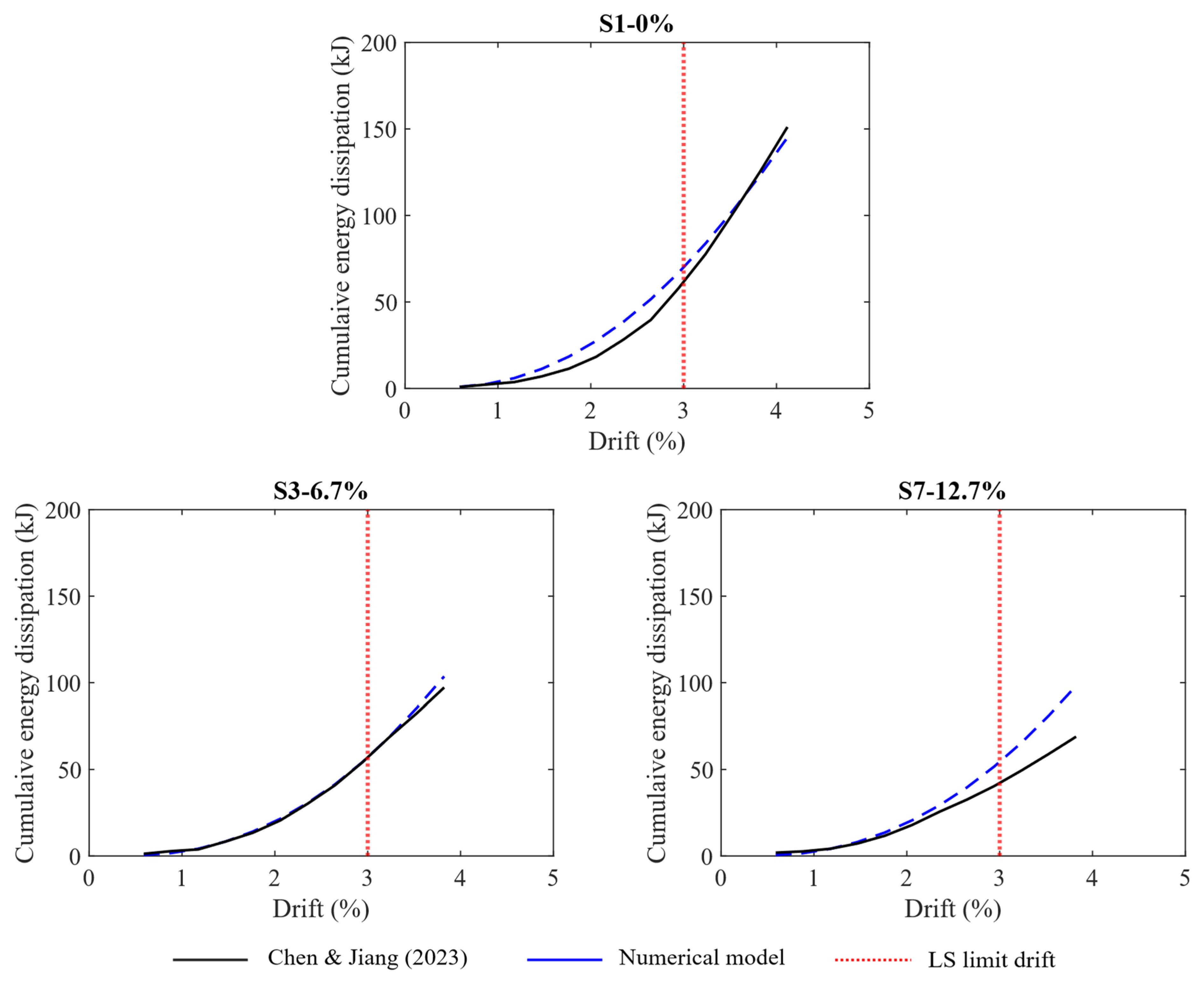
4. Frame Behaviour
5. Conclusions
- -
- For non-corroded columns: The dissipated energy and circular stiffness presented errors lower than 30%. The differences of the maximum and ultimate lateral load were lower than 5 and 3%, respectively.
- -
- With regard to corroded columns: The dissipated energy and circular stiffness showed errors lower than 30%. The differences of the maximum and ultimate lateral load were found to be less than 11 and 12%, respectively.
- -
- For non-corroded frames in LS: The dissipated energy and circular stiffness errors were found to be less than 23%. The differences in the maximum and ultimate lateral loads were found to be 6.8 and 7%, respectively.
- -
- With regard to corroded frames in LS: The dissipated energy and circular stiffness exhibited errors lower than 30%. The differences in the maximum and ultimate lateral loads were 15 and 12%, respectively.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lin, H.; Zhao, Y.; Yang, J.Q.; Feng, P.; Ozbolt, J.; Ye, H. Effects of the Corrosion of Main Bar and Stirrups on the Bond Behavior of Reinforcing Steel Bar. Constr. Build Mater. 2019, 225, 13–28. [Google Scholar] [CrossRef]
- Angst, U.M. Predicting the Time to Corrosion Initiation in Reinforced Concrete Structures Exposed to Chlorides. Cem. Concr. Res. 2019, 115, 559–567. [Google Scholar] [CrossRef]
- Leporace-Guimil, B.; Conforti, A.; Zerbino, R.; Plizzari, G.A. Chloride-Induced Corrosion in Reinforced Concrete and Fiber Reinforced Concrete Elements under Tensile Service Loads. Cem. Concr. Compos. 2021, 124, 104245. [Google Scholar] [CrossRef]
- Cruz, C. Enemigo Número Uno de la Infraestructura Nacional; en Países Industrializados Provoca Pérdidas de Entre el Tres y Cinco Por Ciento del PIB. Available online: https://www.uv.mx/universo-hemeroteca/237/reportaje/reportaje.html (accessed on 16 January 2025).
- Valdez, B.; Ramirez, J.; Eliezer, A.; Schorr, M.; Ramos, R.; Salinas, R. Corrosion Assessment of Infrastructure Assets in Coastal Seas. J. Mar. Eng. Technol. 2016, 15, 124–134. [Google Scholar] [CrossRef]
- Baltazar-García, B.P.; Baltazar-Zamora, D.F.; Santiago-Hurtado, G.; Moreno-Landeros, V.; Lozano, D.; Landa-Ruiz, L.; Shukla, S.; Baltazar-Zamora, M.A. Behavior of Potential of Half-Cell AISI 1018 and GS in Concrete Buried in Sand in the Presence of MgSO4. Eur. J. Eng. Technol. Res. 2024, 9, 32–36. [Google Scholar] [CrossRef]
- Cook, D.C.; Van Orden, A.C.; Reyes, J.; Oh, S.J.; Balasubramanian, R.; Carpio, J.J.; Townsend, H.E. Atmospheric Corrosion in Marine Environments Along the Gulf of México; ASTM Special Technical Publication: West Conshohocken, PA, USA, 2000; pp. 75–97. [Google Scholar] [CrossRef]
- Yu, X.H.; Dai, K.Y.; Li, Y.S. Variability in Corrosion Damage Models and Its Effect on Seismic Collapse Fragility of Aging Reinforced Concrete Frames. Constr. Build Mater. 2021, 295, 123654. [Google Scholar] [CrossRef]
- Moodi, Y.; Sohrabi, M.R.; Mousavi, S.R. Corrosion Effect of the Main Rebar and Stirrups on the Bond Strength of RC Beams. Structures 2021, 32, 1444–1454. [Google Scholar] [CrossRef]
- Tondolo, F. Bond Behaviour with Reinforcement Corrosion. Constr. Build. Mater 2015, 93, 926–932. [Google Scholar] [CrossRef]
- Shunmuga Vembu, P.R.; Ammasi, A.K. A Comprehensive Review on the Factors Affecting Bond Strength in Concrete. Buildings 2023, 13, 577. [Google Scholar] [CrossRef]
- Zhang, K.; Xiao, J.; Zhao, Y.; Zhang, Q. Analytical Model for Critical Corrosion Level of Reinforcements to Cause the Cracking of Concrete Cover. Constr. Build Mater 2019, 223, 185–197. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y.; Liu, B.; Liu, B.; Wu, W.; Yang, C. Corrosion-Induced Spalling of Concrete Cover and Its Effects on Shear Strength of RC Beams. Eng. Fail Anal. 2021, 127, 105538. [Google Scholar] [CrossRef]
- Chen, H.P.; Jiang, Y.; Markou, G. Structural Performance Deterioration of Corroding Reinforced Concrete Columns in Marine Environments. Ocean. Eng. 2022, 262, 112155. [Google Scholar] [CrossRef]
- Zhang, G.; Cao, X.; Fu, Q. Experimental Study on Residual Strength of Concrete Confined with Corroded Stirrups. Can. J. Civ. Eng. 2016, 43, 583–590. [Google Scholar] [CrossRef]
- De Domenico, D.; Lamberto, G.; Messina, D.; Recupero, A. Seismic Vulnerability Assessment of Reinforced Concrete Bridge Piers Exposed to Chloride-Induced Corrosion. Procedia Struct. Integr. 2022, 44, 633–640. [Google Scholar] [CrossRef]
- Miao, Z.; Liu, Y.; Chen, K.; Niu, X. Modification of Uniaxial Stress–Strain Model of Concrete Confined by Pitting Corroded Stirrups. Materials 2024, 17, 6014. [Google Scholar] [CrossRef] [PubMed]
- Berto, L.; Caprili, S.; Saetta, A.; Salvatore, W.; Talledo, D. Corrosion Effects on the Seismic Response of Existing Rc Frames Designed According to Different Building Codes. Eng. Struct. 2020, 216, 110397. [Google Scholar] [CrossRef]
- Kordtabar, B.; Dehestani, M. Effect of Corrosion in Reinforced Concrete Frame Components on Pushover Behavior and Ductility of Frame. Struct. Concr. 2021, 22, 2665–2687. [Google Scholar] [CrossRef]
- Al-Huri, M.A.; Al-Osta, M.A.; Ahmad, S. Finite Element Modelling of Corrosion-Damaged RC Beams Strengthened Using the UHPC Layers. Materials 2022, 15, 7606. [Google Scholar] [CrossRef]
- Arunkumar, Y.M.; Prashanth, S.; Pandit, P.; Girish, M.G.; Shetty, A. Finite Element Analysis Of Bond Behavior In Corroded Reinforced Concrete Beams: State-Of-The-Art. J. Appl. Eng. Sci. 2023, 21, 1031–1042. [Google Scholar] [CrossRef]
- Zaghian, S.; Martín-Pérez, B.; Almansour, H. Nonlinear Finite Element Modeling of the Impact of Reinforcement Corrosion on Bridge Piers under Concentric Loads. Struct. Concr. 2022, 23, 138–153. [Google Scholar] [CrossRef]
- Castorena-González, J.H.; Martin, U.; Gaona-Tiburcio, C.; Núñez-Jáquez, R.E.; Almeraya-Calderón, F.M.; Bastidas, J.M.; Bastidas, D.M. Modeling Steel Corrosion Failure in Reinforced Concrete by Cover Crack Width 3D FEM Analysis. Front Mater 2020, 7, 483965. [Google Scholar] [CrossRef]
- Sæther, I.; Sand, B. FEM Simulations of Reinforced Concrete Beams Attacked by Corrosion. Nord. Concr. Res. 2012, 39, 15–31. [Google Scholar]
- Gaceta del Gobierno de la Ciudad de México NTC-Concrete; México, 2023. Available online: https://www.isc.cdmx.gob.mx/directores-res/cursos-de-actualizacion-2022/normas-tecnicas-complementarias-2023 (accessed on 10 July 2025).
- Rodríguez, J.; Andrade, C.; Izquierdo, D.; Tanner, P. El Eurocódigo 2 y La Evaluación de Estructuras de Hormigón Armado Con Armaduras Corroídas. Hormigón Y Acero 2014, 65, 123–132. [Google Scholar] [CrossRef]
- Instituto Nacional de la Infraestructura Física Educativa Normatividad Técnica, Ciudad de México, México, 2024. Available online: https://www.gob.mx/inifed/acciones-y-programas/normatividad-tecnica (accessed on 10 July 2025).
- Gaceta del Gobierno de la Ciudad de México NTC- Evaluation and Rehabilitation; Ciudad de México, México, 2023. Available online: https://www.isc.cdmx.gob.mx/directores-res/cursos-de-actualizacion-2022/normas-tecnicas-complementarias-2023 (accessed on 10 July 2025).
- CSi America ETABS V22 2024. Available online: https://www.csiespana.com/software/5/etabs (accessed on 10 July 2025).
- Arias, D.; Rodriguez, D.; Pérez, K.; Muria, D. Análisis de Estrategias Numéricas Para El Modelado No Lineal de Muros de Concreto Reforzado. In Proceedings of the XXIV Congreso Nacional De Ingeniería Sísmica, Guadalajara, Mexico, 1–4 November 2023; Available online: https://www.researchgate.net/publication/378740048_Analisis_de_estrategias_numericas_para_el_modelado_no_lineal_de_muros_de_concreto_reforzado (accessed on 10 July 2025).
- Mostafaei, H.; Barmchi, M.A.; Bahmani, H. Seismic Resilience and Sustainability: A Comparative Analysis of Steel and Reinforced Structures. Buildings 2025, 15, 1613. [Google Scholar] [CrossRef]
- Inel, M.; Ozmen, H.B. Effects of Plastic Hinge Properties in Nonlinear Analysis of Reinforced Concrete Buildings. Eng. Struct. 2006, 28, 1494–1502. [Google Scholar] [CrossRef]
- Panandikar Hede, N.; Narayan, K.S.B. Sensitivity of Pushover Curve to Material and Geometric Modelling—An Analytical Investigation. Structures 2015, 2, 91–97. [Google Scholar] [CrossRef]
- Park, R.; Paulay, T. Reinforced Concrete Structures; John Wiley & Sons: Hoboken, NJ, USA, 1975; p. 769. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical Stress Strain Model for Confined Concrete. J. Struct. Eng.-Asce 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Du, Y.; Clark, L.A.; Chan, A.H.C. Impact of Reinforcement Corrosion on Ductile Behavior of Reinforced Concrete Beams. Struct. J. 2007, 104, 285–293. [Google Scholar] [CrossRef]
- Kashani, M.M.; Lowes, L.N.; Crewe, A.J.; Alexander, N.A. Phenomenological Hysteretic Model for Corroded Reinforcing Bars Including Inelastic Buckling and Low-Cycle Fatigue Degradation. Comput. Struct 2015, 156, 58–71. [Google Scholar] [CrossRef]
- Lee, H.S.; Cho, Y.S. Evaluation of the Mechanical Properties of Steel Reinforcement Embedded in Concrete Specimen as a Function of the Degree of Reinforcement Corrosion. Int. J. Fract. 2009, 157, 81–88. [Google Scholar] [CrossRef]
- Zhao, G.; Zhang, M.; Li, Y.; Li, D. The Hysteresis Performance and Restoring Force Model for Corroded Reinforced Concrete Frame Columns. J. Eng. 2016, 2016, 7615385. [Google Scholar] [CrossRef]
- Shayanfar, M.A.; Barkhordari, M.A.; Ghanooni-Bagha, M. Effect of Longitudinal Rebar Corrosion on the Compressive Strength Reduction of Concrete in Reinforced Concrete Structure. Adv. Struct. Eng. 2016, 19, 897–907. [Google Scholar] [CrossRef]
- Dowell, R.K.; Seible, F.; Wilson, E.L. Pivot Hysteresis Model for Reinforced Concrete Members. Struct. J. 1998, 95, 607–617. [Google Scholar] [CrossRef]
- Son, J.K.; Lee, C.H. Evaluation of Appropriate Hysteresis Model for Nonlinear Dynamic Analysis of Existing Reinforced Concrete Moment Frames. Materials 2021, 14, 524. [Google Scholar] [CrossRef]
- Ling, Y.C.; Mogili, S.; Hwang, S.J. Parameter Optimization for Pivot Hysteresis Model for Reinforced Concrete Columns with Different Failure Modes. Earthq. Eng. Struct. Dyn. 2022, 51, 2167–2187. [Google Scholar] [CrossRef]
- Lepage, A.; Hopper, M.W.; Delgado, S.A.; Dragovich, J.J. Best-Fit Models for Nonlinear Seismic Response of Reinforced Concrete Frames. Eng. Struct 2010, 32, 2931–2939. [Google Scholar] [CrossRef]
- Sharma, A.; Eligehausen, R.; Reddy, G.R. Pivot Hysteresis Model Parameters for Reinforced Concrete Columns, Joints, and Structures. ACI Struct. J. 2013, 110, 217–227. [Google Scholar] [CrossRef]
- Yang, S.Y.; Song, X.B.; Jia, H.X.; Chen, X.; Liu, X. La Experimental Research on Hysteretic Behaviors of Corroded Reinforced Concrete Columns with Different Maximum Amounts of Corrosion of Rebar. Constr. Build Mater. 2016, 121, 319–327. [Google Scholar] [CrossRef]
- Chen, S.; Jiang, H. Experimental Investigation on Seismic Performance of Non-Uniformly Corroded RC Moment-Resisting Frames. Materials 2023, 16, 2649. [Google Scholar] [CrossRef]
- GB 50011-2010; Code for Seismic Design of Buildings. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2016. Available online: https://www.codeofchina.com/standard/GB50011-2010(2016).html (accessed on 10 July 2025).
- ACI-318; Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2025. Available online: https://www.concrete.org/store/productdetail.aspx?ItemID=318U19&Language=English&Units=US_Units (accessed on 10 July 2025).

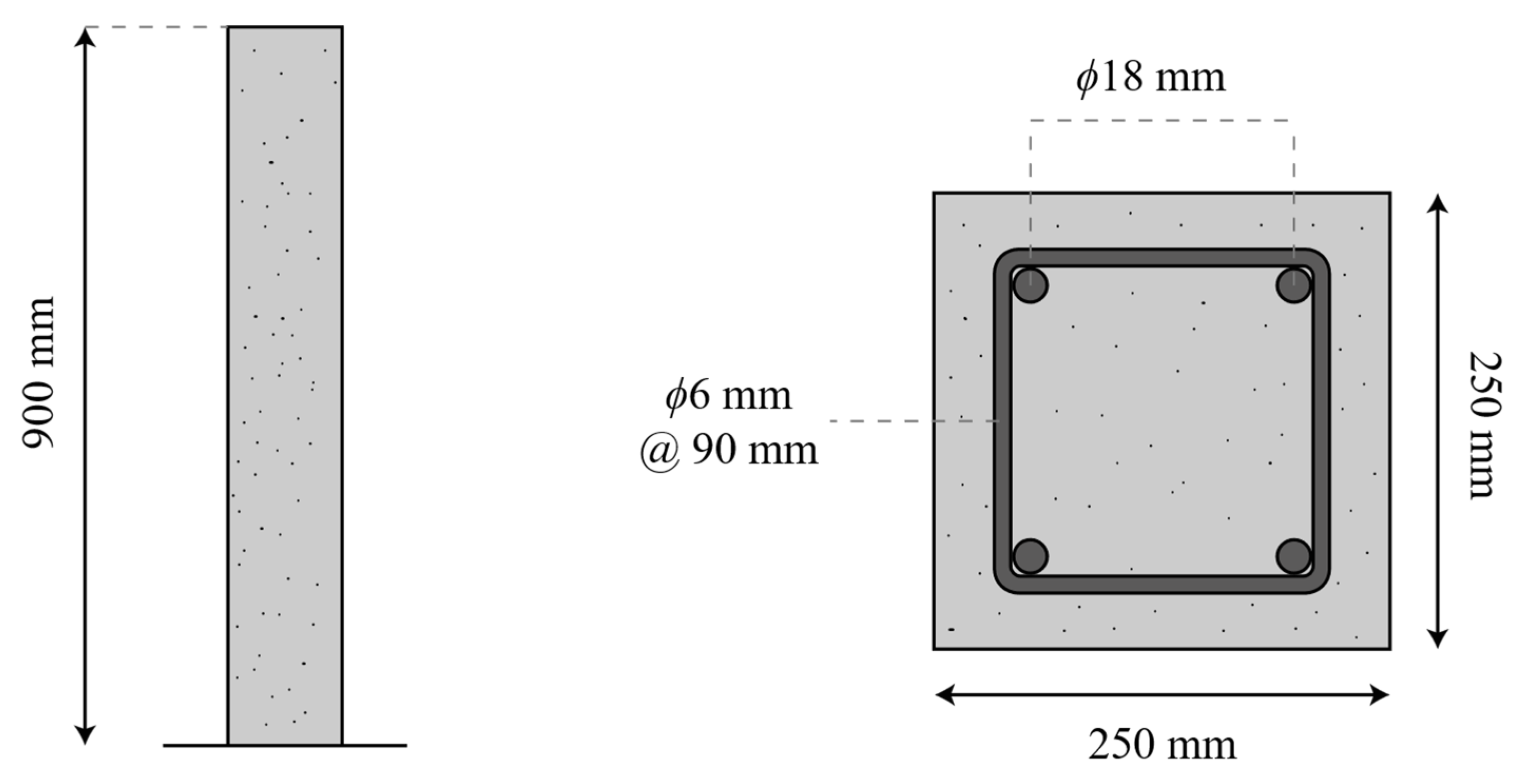
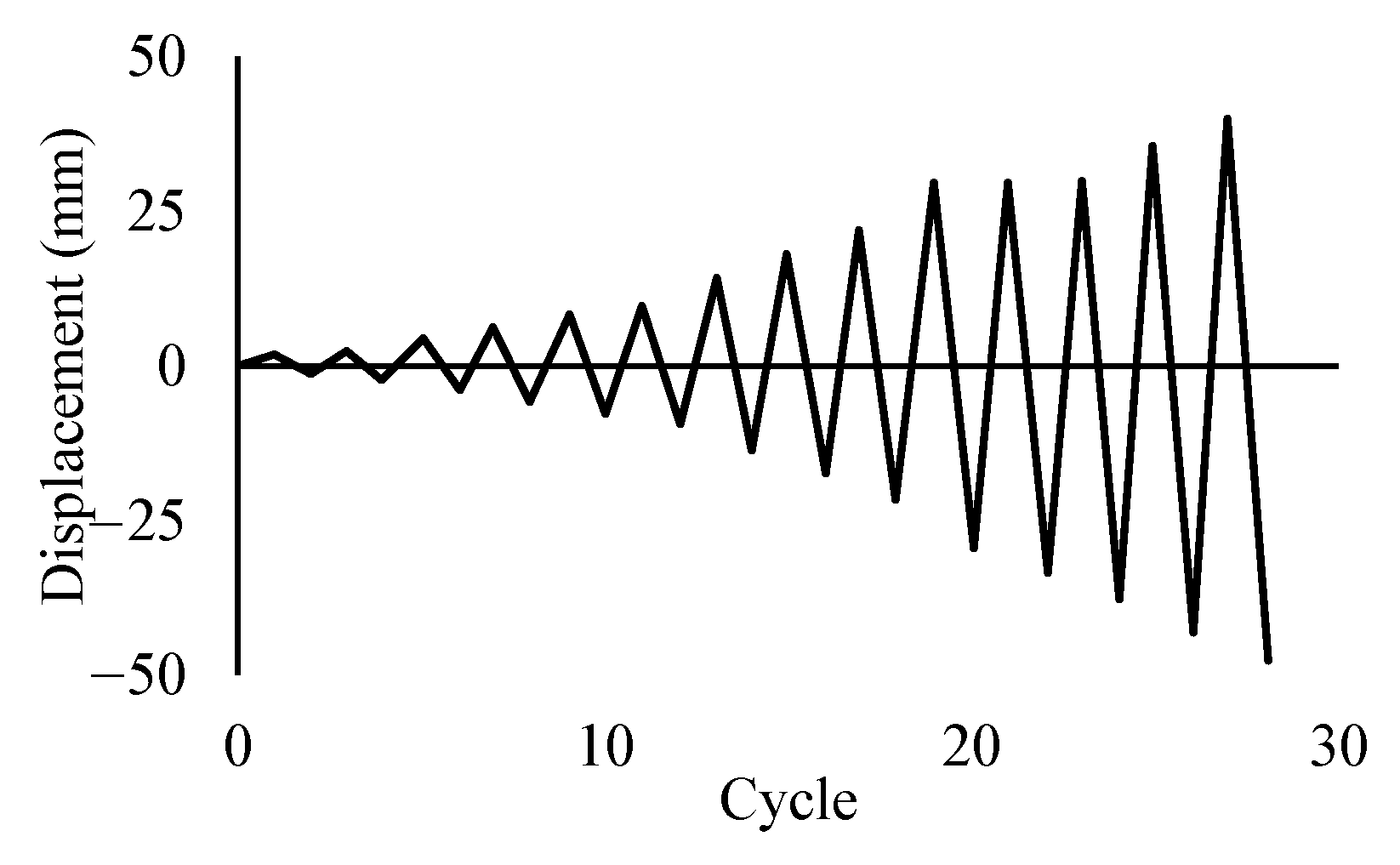
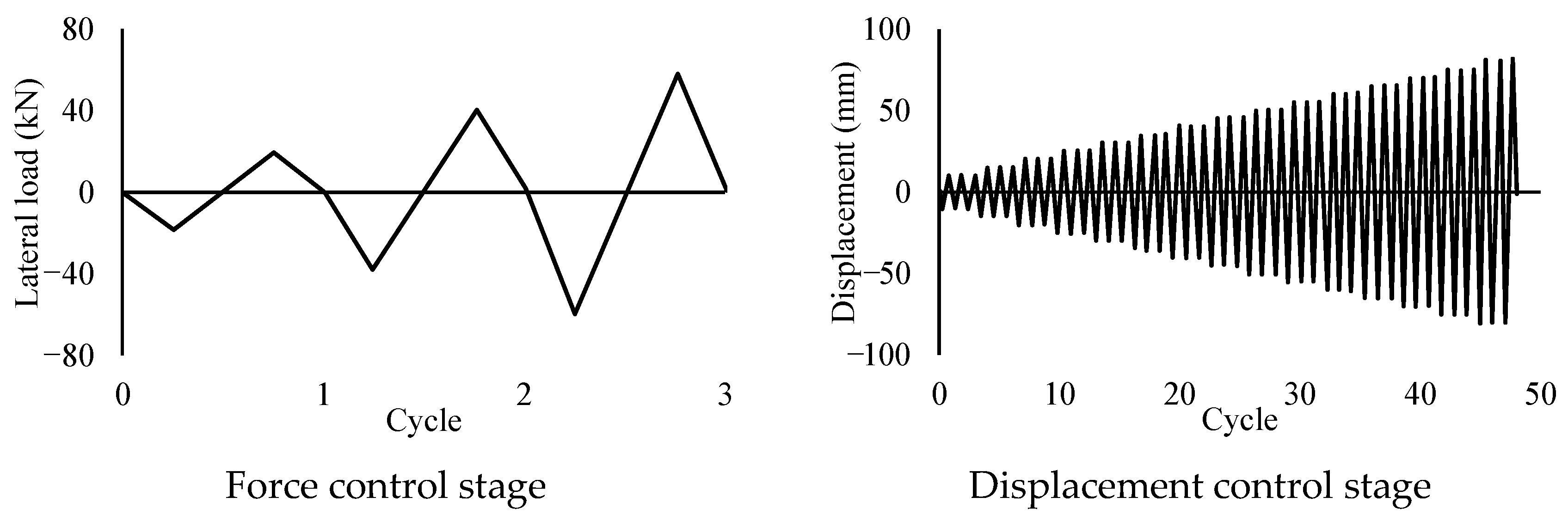

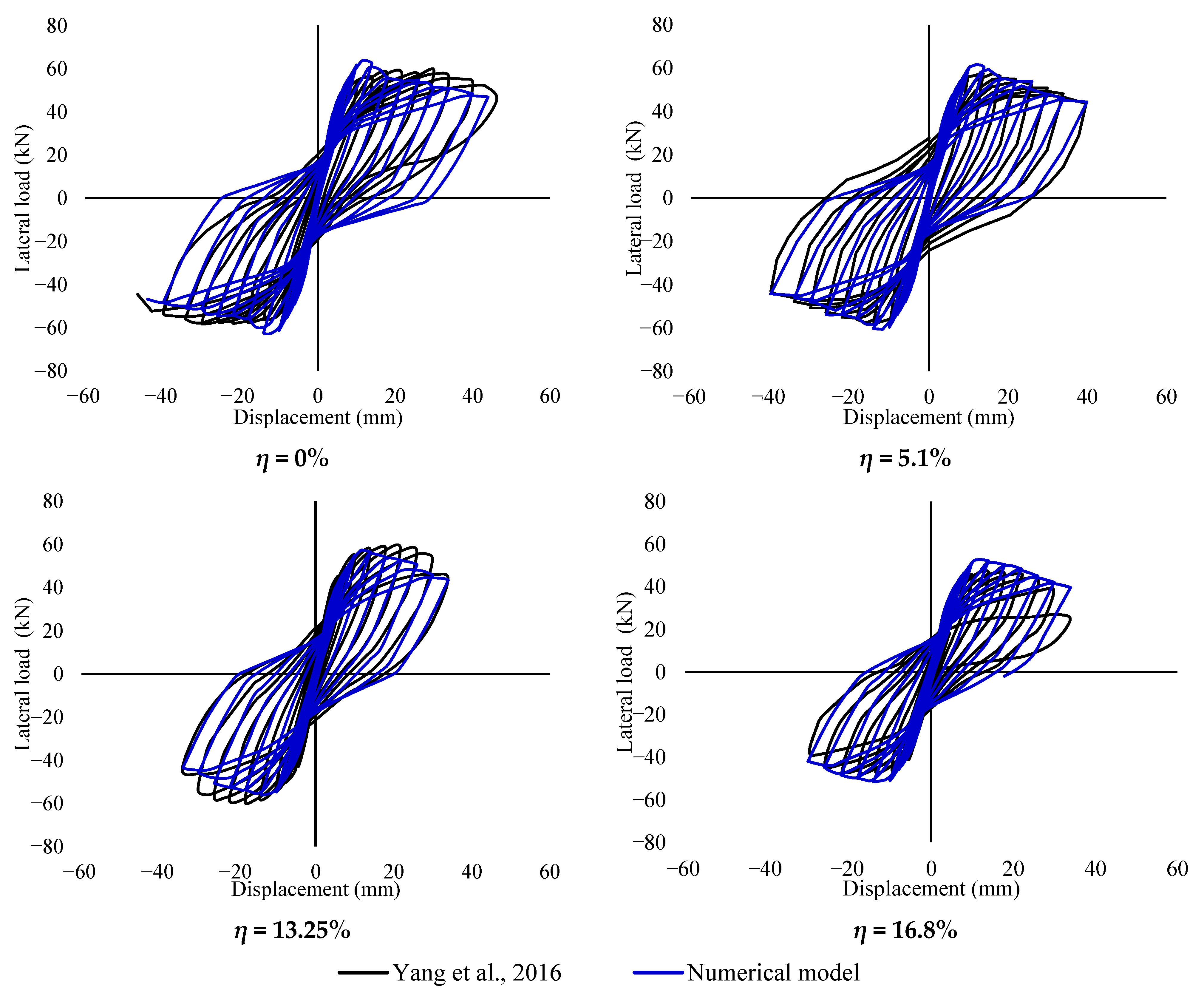

| Material | Property | Columns | ||||
|---|---|---|---|---|---|---|
| Reinforcing steel | Corrosion level (%) | 0 | 5.1 | 13.2 | 16.8 | |
| Φ = 6 mm | Cross-section area (mm2) | 28.2 | 28.1 | 27.7 | 26.1 | |
| Φ = 18 mm | Cross-section area (mm2) | 254.4 | 241.4 | 220.7 | 211.7 | |
| Concrete | Young’s modulus (MPa) | 30,100.0 | 28,254.2 | 24,467.9 | 22,582.3 | |
| Unconfined compressive strength (MPa) | 46.8 | 41.2 | 30.9 | 26.3 | ||
| Confined compressive strength (MPa) | 52.0 | 50.7 | 48.7 | 47.3 | ||
| Tensile strength (MPa) | 3.2 | 3.0 | 2.6 | 2.4 | ||
| Material | Property | Frame | |||
|---|---|---|---|---|---|
| S1 | S3 | S7 | |||
| Reinforcing steel | Corrosion level (%) | 0 | 6.7 | 12.7 | |
| Φ = 6 mm | Cross-section area (mm2) | 113.0 | 105.4 | 98.7 | |
| Ultimate strain | 0.09 | 0.07 | 0.06 | ||
| Φ = 18 mm | Cross-section area (mm2) | 153.9 | 143.6 | 134.4 | |
| Ultimate strain | 0.09 | 0.07 | 0.06 | ||
| Concrete | Young’s modulus (MPa) | 27,407.4 | 25,083.9 | 22,504.6 | |
| Unconfined compressive strength (MPa) | 38.8 | 32.5 | 26.1 | ||
| Confined compressive strength (MPa) | 43.6 | 38.8 | 33.2 | ||
| Tensile strength (MPa) | 2.9 | 2.6 | 2.4 | ||
| Capacity | Corrosion Level (η) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0% | 5.1% | 13.25% | 16.8% | |||||||||
| E | N | ε (%) | E | N | ε (%) | E | N | ε (%) | E | N | ε (%) | |
| Maximum load (kN) (+) | 59.6 | 62.6 | 5.0 | 58.7 | 60.6 | 3.2 | 58.6 | 56.6 | 3.4 | 46.9 | 52.1 | 11.1 |
| Ultimate load (kN) (+) | 51.7 | 50.0 | 3.3 | 44.2 | 48.5 | 9.7 | 44.5 | 45.3 | 1.8 | 39.1 | 41.9 | 7.2 |
| Ultimate displacement (mm) (+) | 44.37 | 34.0 | 23.4 | 39.6 | 34.0 | 14.1 | 34.0 | 34.0 | 0.0 | 29.8 | 30.0 | 0.7 |
| Ultimate load (kN) (−) | 51.1 | 50.2 | 1.8 | 43.1 | 48.4 | 12.3 | 44.5 | 44.8 | 0.7 | 38.6 | 41.3 | 7.0 |
| Ultimate displacement (mm) (−) | 44.0 | 33.9 | 23.0 | 43.1 | 48.5 | 12.5 | 34.0 | 33.9 | 0.3 | 30.1 | 29.9 | 0.7 |
| Energy absorption (kN∙mm) | 14,861.0 | 15,055.0 | 1.3 | 14,947.1 | 11,748.0 | 21.4 | 11,145.9 | 8684.0 | 22.1 | 7407.0 | 6890.0 | 7.0 |
| Capacity | Corrosion Level (η) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0% | 6.7% | 12.7% | |||||||
| E | N | ε | E | N | ε | E | N | ε | |
| Yield load (kN) (+) | 105.3 | 110.5 | 4.9 | 102.2 | 102.7 | 0.5 | 91.8 | 94.1 | 2.5 |
| Yield load (kN) (−) | 95.6 | 109.4 | 14.4 | 68.2 | 101.85 | 49.3 | 57.7 | 98.0 | 69.8 |
| Maximum load (kN) (+) | 119.6 | 113.8 | 4.8 | 118.4 | 103.4 | 12.7 | 109.5 | 93.0 | 15.1 |
| Maximum load (kN) (−) | 121.9 | 113.6 | 6.8 | 105.5 | 104.2 | 1.2 | 93.3 | 100.2 | 7.4 |
| Ultimate displacement (mm) (+) | 73.0 | 68.8 | 5.8 | 62.0 | 69.9 | 12.7 | 62.1 | 65.7 | 5.8 |
| Ultimate load (kN) (+) | 101.6 | 96.2 | 5.3 | 100.6 | 88.1 | 12.4 | 93.0 | 81.0 | 12.9 |
| Ultimate displacement (mm) (−) | 76.4 | 68.8 | 9.9 | 70.1 | 69.7 | 0.6 | 51.2 | 68.8 | 34.4 |
| Ultimate load (kN) (−) | 103.6 | 96.3 | 7.0 | 89.6 | 89.3 | 0.3 | 79.3 | 85.1 | 7.3 |
| Total cumulative energy dissipation (kJ) | 151.1 | 145.1 | 4.0 | 97.2 | 100.5 | 3.4 | 69.0 | 97.1 | 40.7 |
| Parameter | Corrosion Level (η) | ||
|---|---|---|---|
| 0% | 6.7% | 12.7% | |
| Positive stiffness error (%) | 30 | 0.4 | 25.0 |
| Negative stiffness error (%) | 23.8 | 13.3 | 28.5 |
| Accumulative dissipated energy (%) | 13.8 | 0.0 | 29.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barradas-Hernández, J.; Barrera-Jiménez, D.; Ramírez-González, I.; Carpio-Santamaría, F.; Vargas-Colorado, A.; Márquez-Domínguez, S.; Salgado-Estrada, R.; Piña-Flores, J.; Zamora-Hernández, A. Deteriorated Cyclic Behaviour of Corroded RC Framed Elements: A Practical Proposal for Their Modelling. Buildings 2025, 15, 3110. https://doi.org/10.3390/buildings15173110
Barradas-Hernández J, Barrera-Jiménez D, Ramírez-González I, Carpio-Santamaría F, Vargas-Colorado A, Márquez-Domínguez S, Salgado-Estrada R, Piña-Flores J, Zamora-Hernández A. Deteriorated Cyclic Behaviour of Corroded RC Framed Elements: A Practical Proposal for Their Modelling. Buildings. 2025; 15(17):3110. https://doi.org/10.3390/buildings15173110
Chicago/Turabian StyleBarradas-Hernández, José, Dariniel Barrera-Jiménez, Irving Ramírez-González, Franco Carpio-Santamaría, Alejandro Vargas-Colorado, Sergio Márquez-Domínguez, Rolando Salgado-Estrada, José Piña-Flores, and Abigail Zamora-Hernández. 2025. "Deteriorated Cyclic Behaviour of Corroded RC Framed Elements: A Practical Proposal for Their Modelling" Buildings 15, no. 17: 3110. https://doi.org/10.3390/buildings15173110
APA StyleBarradas-Hernández, J., Barrera-Jiménez, D., Ramírez-González, I., Carpio-Santamaría, F., Vargas-Colorado, A., Márquez-Domínguez, S., Salgado-Estrada, R., Piña-Flores, J., & Zamora-Hernández, A. (2025). Deteriorated Cyclic Behaviour of Corroded RC Framed Elements: A Practical Proposal for Their Modelling. Buildings, 15(17), 3110. https://doi.org/10.3390/buildings15173110










