Seismic Damage Assessment of SRC Frame-RC Core Tube High-Rise Structure Under Long-Period Ground Motions

Abstract

To accurately assess the seismic damage of high-rise structures under long-period ground motions (LPGMs), a 36-story SRC frame-RC core tube high-rise structure was designed. Twelve groups of LPGMs and twelve groups of ordinary ground motions (OGMs) were selected and bidirectionally input into the structure. The spectral acceleration S_90c considering the effect of higher-order modes was adopted as the intensity measure (IM) of ground motions, and the maximum inter-story drift angle θ_max under bidirectional ground motions was taken as the engineering demand parameter (EDP). Structural Incremental Dynamic Analysis (IDA) was conducted, the structural vulnerability was investigated, and seismic vulnerability curves, damage state probability curves, vulnerability index curves, as well as the probabilities of exceeding performance levels and vulnerability index of the structure during 8-degree frequent, design, and rare earthquakes were obtained, respectively. The results indicate that structural damage is significantly aggravated under LPGMs, and the exceeding probabilities for all performance levels are greater than those under OGMs, failing to meet the seismic fortification target specified in the code. When encountering an 8-degree frequent earthquake, the structure is in a moderate or severe damage state under LPGMs and is basically intact or in a slight damage state under OGMs. When encountering an 8-degree design earthquake, the structure is in a severe damage or near-collapse state under LPGMs and is in a moderate damage state under OGMs. When encountering an 8-degree rare earthquake, the structure is in a near-collapse state under LPGMs and in a severe damage state under OGMs.

1. Introduction

Strong earthquakes of magnitude 6 or above can easily generate long-period ground motions (LPGMs), with the predominant period ranging from several seconds to over ten seconds in distant sedimentary basins or alluvial plains [1]. LPGMs are special seismic motions with an abundant low-frequency component, which can cause severe damage to high-rise structures and pin the connected or cantilever types of industrial facilities with long natural periods. In recent decades, severe damage to high-rise buildings induced by LPGMs has been observed during major earthquakes, such as the 2004 Kii peninsula earthquake (M7.3) [2], the 2008 Wenchuan earthquake (M8.0) [3], and the 2011 East Japan earthquake (M9.0) [4]. Computational results also indicate that most seismic response indicators of high-rise structures under LPGMs exceed those under OGMs [5,6,7,8,9,10]. Accurate assessment of seismic damage to high-rise structures under LPGMs has become a focal point of concern for scholars worldwide.

The seismic vulnerability analysis method based on Incremental Dynamic Analysis (IDA) is widely applied in structural damage assessment. Different seismic intensity measures (IMs) will result in different IDA curves, thereby affecting the accuracy of seismic damage assessment. Research conducted by our team shows that the peak ground acceleration (PGA) correlates well with the seismic response of short-period structures under LPGMs, while the fundamental-period spectral acceleration S_a(T₁) correlates well with the seismic response of mid- to long-period structures and is more suitable as the IM for the IDA of high-rise structures [11]. Zhou et al. [12] also points out that S_a(T₁) used for IDA of high-rise structures is more effective than PGA. For high-rise structures, to fully consider the effect of higher-order modes, IMs, such as S₁₂ [12,13], S₁₂₃ [12,13], S_a,avg [14], ${\overline{S}}_{\mathrm{a}}$ [15] and S₉₀ [16], have been proposed. The analyses indicate that the more vibration modes considered, the better the effectiveness of the IMs. Scholars have conducted vulnerability studies on various types of high-rise structures, such as reinforced concrete frame structures [17,18], reinforced concrete frame–core tube structures [19], steel frame structures [20,21], steel frame–shear wall structures [22], steel frame-RC core tube structures [23], and SRC frame-RC core tube structure [24,25], quantitatively assessing the structural damage degree. However, most of the analysis results are based on OGMs, with few considering the influence of LPGMs. The vulnerability of a reinforced concrete frame–shear wall high-rise building under LPGMs has been explored by our team [11] but without considering the bidirectional input of LPGMs. Analysis of the spectral characteristics of LPGMs shows that the two horizontal ground motions obtained from the same station may both be LPGMs, and the seismic response of high-rise structures under bidirectional ground motions is significantly different from that under unidirectional ground motions [8]. Therefore, the vulnerability analysis and seismic damage assessment of high-rise structures under bidirectional LPGMs need to be carried out urgently.

In view of this, twelve groups of LPGMs and twelve groups of OGMs were selected and bidirectionally input into an SRC frame-RC core tube high-rise structure. The spectral acceleration S_90c considering the effect of higher-order modes and bidirectional ground motion input was adopted as the IM, and the maximum inter-story drift angle θ_max under bidirectional ground motions was taken as the engineering demand parameter. Then, the IDA of the high-rise structure was conducted. Subsequently, the seismic vulnerability of the high-rise structure was assessed. Finally, the seismic damage degree of the high-rise structure was comparatively assessed based on the probabilities of exceeding performance levels and vulnerability index under LPGMs and OGMs at 8-degree seismic levels.

2. Design of High-Rise Structure and Selection of Ground Motions

2.1. High-Rise Structure Design

In accordance with current Chinese structural design codes, a 36-story SRC frame-RC core tube high-rise structure was designed with a story height of 4.0 m. Figure 1 shows the standard floor plan of the structure. The seismic fortification intensity is 8 degrees (0.2 g), the design earthquake group is class three, and the site category is Class II. The dead load on the floors and roof is 5.0 kN/m² and 6.0 kN/m², respectively, and the live load on the floors and roof is 2.0 kN/m². The basic wind pressure is 0.5 kN/m², and the ground roughness is Class C. For SRC columns and RC core tube walls, the concrete strength grades are C60 (1–12 floors), C50 (13–24 floors), and C40 (25–36 floors), respectively. For the beams and slabs, the concrete strength grade is C30. The steel sections are of Q345 grade, and the reinforcing bars are of HRB400 grade. The thickness of slabs is 120 mm, and the cross-sectional dimensions and reinforcement details of the RC beams, SRC columns, and shear walls are detailed in Reference [26].

The structure was modeled and analyzed by using the nonlinear analysis software Perform-3D (Version 7), with the modeling principles outlined in Reference [26]. To verify the reliability of the structural model, the vibration period, mass and seismic response of the structure were calculated in Perform-3D and YJK (Version 4.0), and a comparative analysis was conducted. The vibration period, mode characteristics and structural mass corresponding to the first six-order modes of the structure are listed in

Table 1. Comparison of vibration mode, vibration period and mass of high-rise structure.

Analysis Software	Vibration Period (s) Corresponding to Each Mode						Mass (t)
	T1	T2	T3	T4	T5	T6
Perform-3D	3.352	2.951	2.495	0.907	0.844	0.819	69,922
YJK	3.285	2.942	2.429	0.907	0.811	0.805	70,052
Error	2.00%	0.31%	2.65%	0	3.91%	1.71%	0.19%
Mode characteristics	Y-direction 1st-order Translation	X-direction 1st-order Translation	Z-direction 1st-order Torsion	Y-direction 2nd-order Translation	X-direction 2nd-order Translation	Z-direction 2nd-order Torsion	Y-direction 1st-order Translation

. It can be seen that the vibration periods of each order obtained by Perform-3D are close to those of YJK, with a maximum difference of no more than 4.0%. The mode characteristics of each order are the same as that of YJK, and the mass of the structure only differs by 0.19%, indicating good consistency between the modal characteristics and the total mass of the structure.

The ground motion NBI000 from the 1994 Northridge earthquake, whose peak acceleration was adjusted to 400 gal, was selected and input into the structure for elastic–plastic time–history analysis. The calculated seismic response is listed in

Table 2. Comparison of seismic response of high-rise structure.

Analysis Software	Maximum Inter-Story Drift Angle	Weak Floors	Maximum Displacement of Top Floor (mm)	Base Shear Force (kN)
Perform-3D	0.0067	27	546	66,780
YJK	0.0071	28	617	74,307
Error	5.63%	—	11.51%	10.13%

. It can be seen that the maximum inter-story drift angle, the maximum displacement of the top floor, and the base shear force obtained by Perform-3D modeling are all relatively close to those of YJK, with differences of 5.63%, 11.51%, and 10.13%, respectively. The positions of the weak floors are roughly the same, indicating that the elastic–plastic properties of the structure are also highly comparable.

Therefore, the finite element model established by using Perform-3D software is reliable.

2.2. Ground Motion Selection

Appropriate ground motions are selected based on principles such as similar or close site categories and matching the elastic acceleration response spectrum with the design response spectrum specified in seismic code in certain frequency bands. However, since the current design response spectrum cannot adequately consider the impact of LPGMs, it is inappropriate to select LPGMs with the design response spectrum as the matching target [27]. Based on the calculation results of the response spectrum of LPGMs, scholars have fitted the response spectrum that can reflect the characteristics of LPGMs (hereinafter referred to as “fitted response spectrum”) [28,29]. In this study, the fitted response spectrum proposed in Reference [29] is used to select LPGMs.

Firstly, LPGMs were selected. When the weighted average value β_l of the amplification coefficient spectrum curve of ground motions in the range of 2–10 s is greater than or equal to 0.4, the ground motions can be regarded as LPGMs [30]. Research shows that based on the average shear-wave velocity of soil layers as the measurement basis, the Class II site classified according to the “Code for seismic design of buildings” [31] in China corresponds to the Class C site classified according to the NEHRP code in the United States [32]. Therefore, the selection principle for LPGMs was as follows: magnitude ≥ 6, β_l ≥ 0.4, epicentral distance ≥ 200 km, and the site category is Class II or Class C.

Secondly, the PGA of each selected ground motion was uniformly adjusted to 70 gal, and its elastic acceleration response spectrum was calculated. The fitted response spectrum was determined based on the response spectrum and spectral parameters of LPGMs proposed in Reference [29]. Finally, appropriate LPGMs were selected by ensuring that the average acceleration response spectrum values in the [0.1, T_g] segment (T_g is site characteristic period) and the acceleration response spectrum value in the fundamental period T₁ do not deviate by more than 20% from the corresponding values in the fitted response spectrum. To comparatively analyze the differences in the seismic damage to the high-rise structure, OGMs were also selected following the same procedure but using the design response spectrum as the matching target.

For high-rise structures, selecting 10 to 20 ground motions for IDA can provide a relatively accurate assessment of seismic demand [33]. Therefore, twelve groups of LPGMs and twelve groups of OGMs were selected following the aforementioned method and input bidirectionally. During ground motion input, for each group, one ground motion with the closest acceleration response spectrum value in the fundamental period T₁ to the fitted or design response spectrum was selected and input along the Y-axis of the structure, and the other ground motion was selected and input along the X-axis of the structure. Based on the provisions of “Code for seismic design of buildings”, the peak acceleration of the input ground motions is adjusted according to PGA_y/PGA_x = 1:0.85. Basic information and the input direction of the selected ground motions are presented in

Table 3. Basic information and input direction of selected ground motions.

Type of Ground Motion	№	Earthquake Name	Magnitude	Recording Station	Ground Motion	Site Category	PGA (cm/s2)	βl	Input Direction
LPGMs	1	Wen chuan	8.0	14HTG	14HTG-NS	II	16.47	0.78	Y
					14HTG-EW	II	16.13	0.95	X
	2			62QSY	62QSY-NS	II	17.18	0.65	Y
					62QSY-EW	II	18.08	0.84	X
	3			62CJA	62CJA-NS	II	13.19	1.00	Y
					62CJA-EW	II	12.24	1.22	X
	4			62KLE	62KLE-NS	II	14.82	0.91	Y
					62KLE-EW	II	15.14	0.83	X
	5			62DAT	62DAT-EW	II	14.71	1.35	Y
					62DAT-NS	II	12.40	0.94	X
	6	Tokachi	8.0	HKD130	HKD130-NS	C	56.16	0.52	Y
					HKD130-EW	C	51.41	0.65	X
	7			SRCH04	SRCH04-EW	C	11.97	1.04	Y
					SRCH04-NS	C	14.17	1.13	X
	8	East Japan	9.0	AKT013	AKT013-EW	C	28.59	0.47	Y
					AKT013-NS	C	44.20	0.25	X
	9			CHBH16	CHBH16-EW	C	11.83	1.04	Y
					CHBH16-NS	C	10.52	0.84	X
	10			HKD083	HKD083-NS	C	14.34	0.77	Y
					HKD083-EW	C	13.31	1.00	X
	11			AOM018	AOM018-NS	C	14.91	0.65	Y
					AOM018-EW	C	15.74	0.85	X
	12			NIG015	NIG015-EW	C	23.62	0.44	Y
					NIG015-NS	C	19.85	0.55	X
OGMs	1	Kobe	6.9	MZH	MZH090	C	52.38	0.06	Y
					MZH000	C	69.65	0.04	X
	2	Kocaeli	7.5	Bursa Sivil	BRS180	C	57.50	0.22	Y
					BRS090	C	45.31	0.19	X
	3			Hava Alani	DHM090	C	83.23	0.27	Y
					DHM000	C	89.96	0.38	X
	4			Maslak	MSK000	C	41.67	0.29	Y
					MSK090	C	37.81	0.22	X
	5			Eregli	ERG180	C	89.69	0.18	Y
					ERG090	C	106.06	0.09	X
	6	Wen chuan	8.0	51AXT	51AXT-EW	II	309.39	0.11	Y
					51AXT-NS	II	220.13	0.19	X
	7			51JYC	51JYC-EW	II	304.76	0.08	Y
					51JYC-NS	II	280.46	0.09	X
	8	Duzce	7.4	Lamont362	362-N	C	42.08	0.32	Y
					362-E	C	25.80	0.38	X
	9			Mudurnu	MDR000	C	120.38	0.14	Y
					MDR090	C	56.08	0.29	X
	10	Northridge	6.7	LB-City	LBC360	C	51.17	0.05	Y
					LBC090	C	36.46	0.09	X
	11			LA-W 15th	W15090	C	104.02	0.10	Y
					W15180	C	159.11	0.04	X
	12			Newport Bch-Irvine	NBI000	C	41.24	0.08	Y
					NBI090	C	60.72	0.05	X

.

Figure 2 presents the average acceleration amplification coefficient β spectra of the selected ground motions. The peak values of β spectra of two types of ground motions generally exhibit little difference, but the prominent period of the β spectrum of LPGMs significantly increases, reaching 1.44 s. After the prominent period, as the vibration period of the structure increases, the β spectrum value of OGMs decays rapidly, while the β spectrum value of LPGMs decays relatively slowly and is greater than that of OGMs. Among them, the β spectrum values in the fundamental period T₁ and the second period T₂ are 4.7-times and 4.0-times those of OGMs, respectively. The spectral characteristics of ground motions are the main reason for the significant differences in the seismic responses of high-rise structures under two types of ground motions [26].

3. Selection of Ground Motion Intensity Measure and Engineering Demand Parameter

3.1. Intensity Measure (IM)

The spectral acceleration S_a exhibits good correlation with the seismic response of long-period structures under LPGMs and is suitable to be used as IM for IDA of high-rise structures. Research indicates that only when the modal participation mass coefficient reaches over 90% can its contribution to the seismic response of high-rise structures be better considered [16]. Therefore, to take into account the influences of higher-order mode participation and bidirectional ground motion input, the spectral acceleration S_90c is defined as IM for IDA and is calculated according to Equation (1):

$$S_{90c}=\sqrt{{({[S_a(T_{1y})]}^{{\alpha }_1}.{[S_a(T_{2y})]}^{{\alpha }_2}\dots {[S_a(T_{ny})]}^{{\alpha }_n})}^2+{({[S_a(T_{1x})]}^{{\beta }_1}.{[S_a(T_{2x})]}^{{\beta }_2}\dots {[S_a(T_{nx})]}^{{\beta }_n})}^2}$$

(1)

where T_1y, T_2y, ⋯, T_ny are the first n-order natural periods of the structure in the Y direction; S_a(T_1y), S_a(T_2y), ⋯, S_a(T_ny) are the spectral acceleration values corresponding to the T_1y, T_2y, ⋯, T_ny, respectively; T_1x, T_2x, ⋯, T_nx are the first n-order natural periods of the structure in the X direction; S_a(T_1x), S_a(T_2x), ⋯, S_a(T_nx) are the spectral acceleration values corresponding to the T_1x, T_2x, ⋯, T_nx, respectively; α₁, α₂, ⋯, α_n are the modal participation mass coefficient ratios of the first n-order modes in the Y direction, calculated as α₁ = m_1y/(m_1y + m_2y + … +m_ny), α₂ = m_2y/(m_1y + m_2y + … + m_ny), ⋯, α_n = m_ny/(m_1y + m_2y + … + m_ny), where m_1y, m_2y,⋯, m_ny are the modal participation mass coefficients of the first n-order modes in the Y direction, respectively; β₁, β₂, ⋯, β_n are the modal participation mass coefficient ratios of the first n-order modes in the X direction, calculated as β₁ = m_1x/(m_1x + m_2x + … + m_nx), β₂ = m_2x/(m_1x + m_2x + … + m_nx), ⋯, β_n = m_nx/(m_1x + m_2x + … + m_nx), where m_1x, m_2x, ⋯, m_nx are the modal participation mass coefficients of the first n-order modes in the X direction, respectively; n is the number of modes when the sum of the modal participation mass coefficients is greater than or equal to 90%.

The dynamic characteristics of the high-rise structure in this study were analyzed using Perform-3D, the natural period and modal participation mass coefficients of each mode of the structure were obtained, and the modal participation mass coefficient ratios α_i and β_i are listed in

Table 4. Modal participation mass coefficient ratio α_i and β_i of high-rise structure.

Mode Order	Y Direction				X Direction
	Natural Vibration Period (s)	Modal Participation Mass Coefficient	Sum of Modal Participation Mass Coefficient	αi	Natural Vibration Period (s)	Modal Participation Mass Coefficient	Sum of Modal Participation Mass Coefficient	βi
1	3.352	62.7%	90.3%	0.694	2.951	68.1%	90.1%	0.756
2	0.907	18.7%		0.207	0.844	16.8%		0.186
3	0.363	8.9%		0.099	0.473	5.2%		0.058

. Analysis reveals that the sum of the modal participation mass coefficients of the first three-order modes in the Y and X directions of the structure is greater than 90%. By substituting the ratios of the mode participation mass coefficients into Equation (1), S_90c is obtained:

$$S_{90c}=\sqrt{{({[S_a(T_{1y})]}^{0.694}.{[S_a(T_{2y})]}^{0.207}.{[S_a(T_{3y})]}^{0.099})}^2+{({[S_a(T_{1x})]}^{0.756}.{[S_a(T_{2x})]}^{0.186}.{[S_a(T_{3x})]}^{0.058})}^2}$$

(2)

3.2. Engineering Demand Parameter (EDP)

The selected EDP should be capable of characterizing the seismic response and damage degree of the structure and being directly extracted or derived from the results of time–history analysis. The maximum inter-story drift angle θ_max can effectively reflect the structural damage degree and collapse capacity and is commonly used as the EDP for IDA. Considering the seismic response in two axial directions, θ_max under bidirectional ground motions is defined as:

$${\theta }_{\max }=\underset{i\in (0,\mathrm{N})}{\max }\left(\underset{t\in (0,T_{90})}{\max }\left(\sqrt{{\theta }_{ix}^2(t)+{\theta }_{iy}^2(t)}\right)\right)$$

(3)

where θ_ix(t) and θ_iy(t) represent the time histories of inter-story drift angles in X and Y directions of the i-th floor, respectively; N denotes the total number of floors; T₉₀ is the energy duration of ground motions, defined as the difference in the times corresponding to 95% and 5% of cumulative total energy on the Hilbert time-domain cumulative energy spectrum curve. Research shows that θ_max can more effectively reduce the dispersion in structural IDA results under bidirectional ground motions, thereby improving the accuracy of the structural damage assessment [34]. Therefore, the θ_max of the high-rise structure under bidirectional ground motions is adopted as the EDP for IDA in this study.

In seismic vulnerability analysis, it is essential to pre-define the limit states between different damage levels of the structure, which are referred to as performance levels in performance-based seismic design. The performance levels of the structure are divided into four grades: normal usability/LS₁, basic usability/LS₂, repairable usability/LS₃, and life safety/LS₄. Based on the research findings of SRC frame-RC core tube high-rise structures [24,25], the limit values of the θ_max for each performance level are presented in

Table 5. Quantitative limits of performance levels of SRC frame-RC core tube high-rise structure.

Performance Indicator	Performance Level
	Normal Usability/LS1	Basic Usability/LS2	Repairable Usability/LS3	Life Safety/LS4
θmax	1/800	1/400	1/200	1/100

.

4. Seismic Vulnerability Analysis and Damage Assessment of SRC Frame-RC Core Tube High-Rise Structure Under LPGMs

4.1. IDA of the Structure

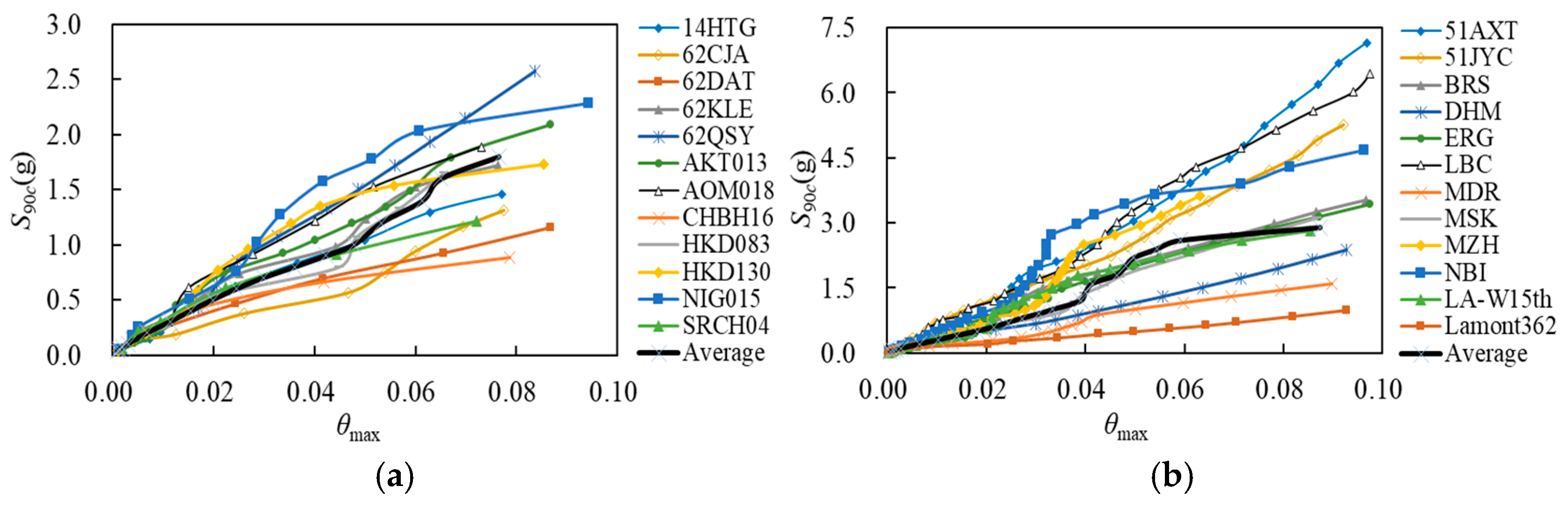
To analyze the seismic vulnerability of the SRC frame-RC core tube high-rise structure, the IDA of the structure was first conducted with bidirectional ground motions input. For each group, the PGA_y of the selected ground motion along the structural Y-axis is sequentially scaled to 0.02 g, 0.07 g, 0.1 g, 0.2 g, 0.3 g, …, 1.0 g, 1.2 g, 1.4 g, 1.6 g, …, while maintaining the ratio of PGA_y/PGA_x = 1:0.85 constant. The elastic or elastic–plastic time–history analysis of the structure was conducted one by one, and the scaling and calculation were terminated when the slope between two adjacent performance points was less than 0.2K_e or the θ_max exceeded 0.1. The PGA_yi was converted into corresponding S_90ci. Taking θ_max as the seismic response indicator, a series of performance points (θ_maxi, S_90ci) were obtained, and connecting these performance points forms a single IDA curve. By varying the ground motions and repeating the above procedure, additional IDA curves were obtained. Finally, the IDA curve clusters of the structure under LPGMs and OGMs were obtained, as shown in Figure 3.

4.2. Structural Damage Assessment Based on Seismic Vulnerability Curves

The structural seismic vulnerability is the conditional probability P(LS|IM) that the EDP reaches or exceeds the quantitative limit value corresponding to a certain performance level under ground motions of different intensities [34], which is usually represented by a seismic vulnerability curve, that is, the relationship curve between IM and exceeding probability P(LS|IM).

Assuming that the limit value of EDP corresponding to the performance level LS_i is edp_i, the conditional probability $P({\mathrm{LS}}_{\mathrm{i}}|\mathrm{IM}=im)$ can be expressed as:

$$P({\mathrm{LS}}_{\mathrm{i}}|\mathrm{IM}=im)=P(\mathrm{EDP}\ge ed{p}_i|\mathrm{IM}=im)$$

(4)

Assuming that $P(\mathrm{EDP}\ge ed{p}_i|\mathrm{IM}=im)$ follows a logarithmic standard normal distribution, that is:

$$P(\mathrm{EDP}\ge ed{p}_i|\mathrm{IM}=im)=1-P(\mathrm{EDP}<ed{p}_i|\mathrm{IM}=im)=1-\mathsf{\Phi }\left({\displaystyle \frac{\ln ed{p}_i-{\mu }_{\ln \mathrm{EDP}|\mathrm{IM}=im}}{{\sigma }_{\ln \mathrm{EDP}|\mathrm{IM}=im}}}\right)$$

(5)

where μ_{lnEDP|IM = im} and σ_{lnEDP|IM = im} are the logarithmic mean and logarithmic standard deviation of EDP given IM = im, respectively, and Φ(x) is the standard normal distribution function.

Based on the IDA results of the structure under LPGMs and OGMs in Section 4.1, the conditional probability P(LS_i) that the θ_max exceeds each performance level LS_i was calculated according to Equation (5). Taking S_90c as the horizontal axis and P(LS_i|S_90c) as the vertical axis, the seismic vulnerability curve of the structure, that is, the exceeding probability curve of each performance level, was drawn.

The calculation process of the vulnerability curve of the basic usability performance level was illustrated as an example. Firstly, according to the structural IDA results, the corresponding θ_max under the same S_90c for each group of ground motions was obtained, and the μ_lnθmax and σ_lnθmax of θ_max were calculated. Secondly, μ_lnθmax, σ_lnθmax, and the limit value of θ_max for a basic usability performance level of 1/400 were substituted into Equation (5) to calculate the exceeding probability as:

$$P({\theta }_{\max }\ge 1/400|S_{90c})=1-P({\theta }_{\max }<1/400|S_{90c})=1-\mathsf{\Phi }\left({\displaystyle \frac{\ln (1/400)-{\mu }_{\ln {\theta }_{\max }|S_{90c}}}{{\sigma }_{\ln {\theta }_{\max }|S_{90c}}}}\right)$$

(6)

Finally, taking S_90c as the horizontal axis and P(θ_max ≥ 1/400|S_90c) as the vertical axis, the seismic vulnerability curve of the basic usability performance level for the structure was drawn.

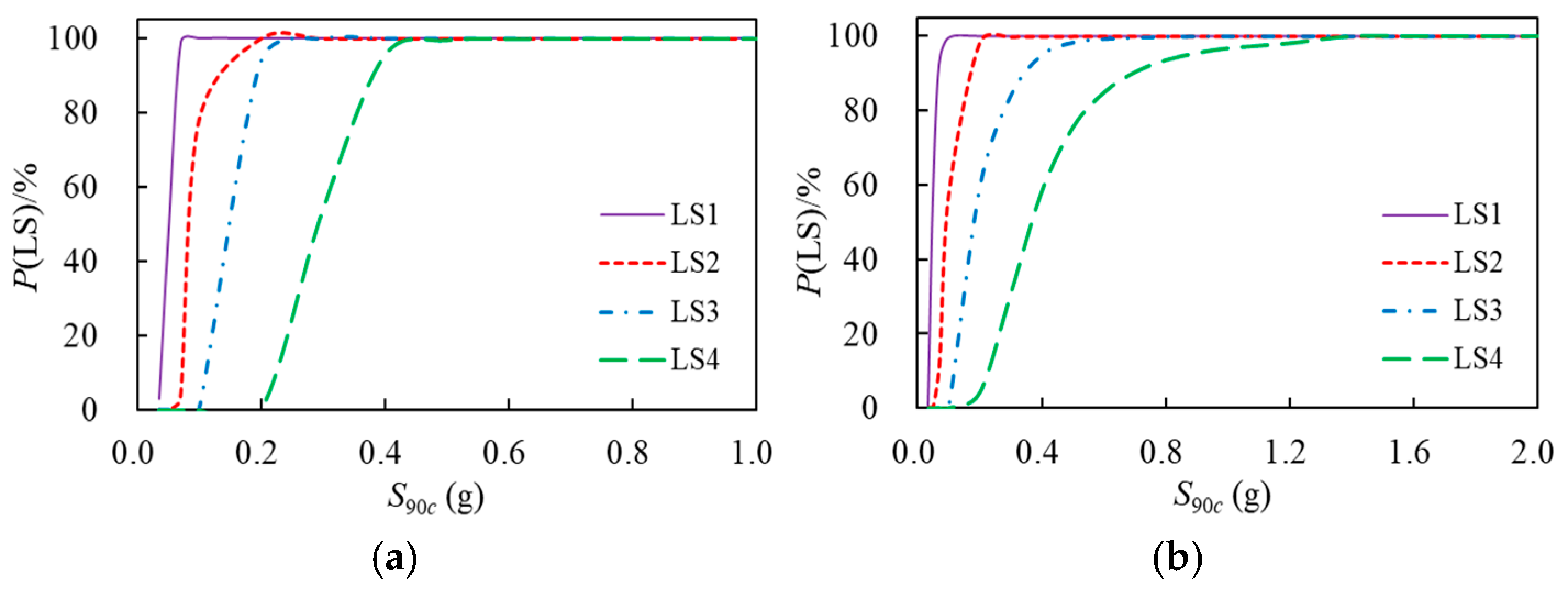
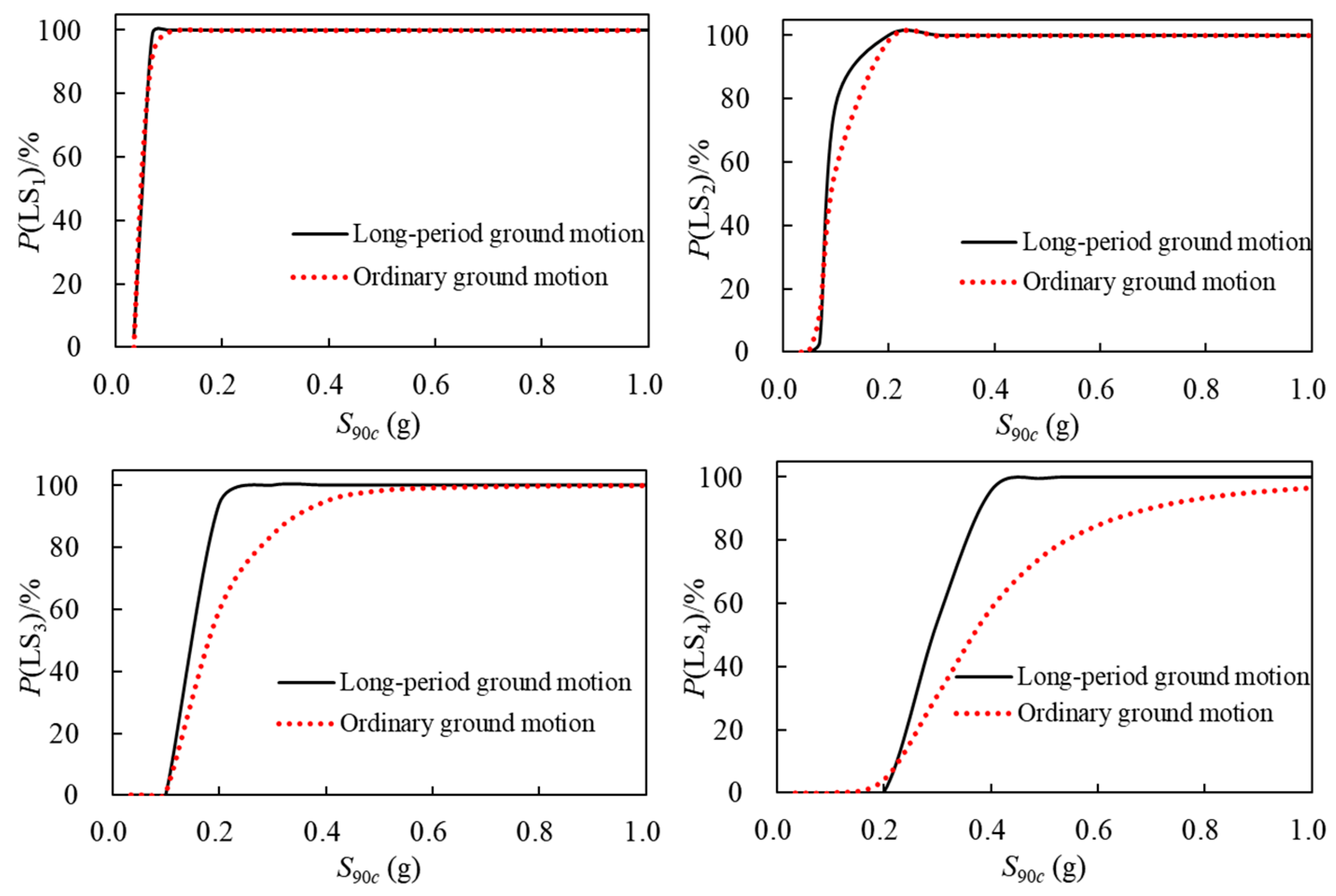
Figure 4 represents the seismic vulnerability curves of the structure under LPGMs and OGMs. As observed from Figure 4, the vulnerability curve of the normal usability performance level LS₁ is the steepest, indicating that maintaining normal performance levels without structural damage during earthquakes is challenging; that is, it is relatively easy for the structure to exceed the limit of the elastic inter-story drift angle and enter the plastic state. As S_90c increases, the structural damage gradually accumulates, and the vulnerability curves of the basic usability performance level LS₂, repairable usability performance level LS₃, and life safety performance level LS₄ gradually become flatter, indicating that the exceeding probability of the above performance levels under the ground motions of the same intensity continuously decreases, and the range of ground motion intensity changes required increases. This is because the ductility of the structure entering the elastic–plastic stage gradually comes into play, thereby enhancing seismic resistance.

To further evaluate the differences in structural seismic damage under LPGMs and OGMs, the seismic vulnerability curves of each performance level of the structure under two types of ground motions were compared, as shown in Figure 5. The vulnerability curves of the normal usability performance level LS₁ of the structure are basically coincident, indicating that the probability of exceeding the normal usability performance level under LPGMs and OGMs with the same intensity S_90c is similar, and the influence of ground motion type is relatively minimal. However, the differences in the vulnerability curves of the basic usability performance level LS₂ and the repairable usability performance level LS₃ of the structure gradually increase. The conditional probabilities of exceeding the above performance levels under LPGMs with the same intensity S_90c are generally larger than those under OGMs, especially for life safety performance level LS₄, indicating that it is much more difficult to control the structural damage at the life safety performance level under LPGMs than under OGMs.

The high-rise structure in this study was located in an area with a seismic fortification intensity of 8 degrees (0.2 g). Based on Figure 4, the exceeding probabilities of the performance levels of the structure under LPGMs and OGMs at 8-degree seismic levels were calculated, thereby assessing the seismic damage of the structure. The S_90c of each group of ground motions under the 8-degree frequent earthquake, design earthquake, and rare earthquake was calculated using the “average value method” [34], and then the average value of S_90c was used to calculate the exceeding probabilities of each performance level. The results are listed in

Table 6. Exceeding probabilities of different performance levels of the structure under LPGMs during 8-degree earthquake.

Seismic Level	PGA (gal)	S90c (g)	Exceeding Probability
			LS1	LS2	LS3	LS4
8-degree Frequent Earthquake	70	0.162	100%	94.08%	49.79%	5.19%
8-degree Design Earthquake	200	0.464	100%	100%	100%	97.25%
8-degree Rare Earthquake	400	0.927	100%	100%	100%	99.99%

and

Table 7. Exceeding probabilities of different performance levels of the structure under OGMs during 8-degree earthquake.

Seismic Level	PGA (gal)	S90c (g)	Exceeding Probability
			LS1	LS2	LS3	LS4
8-degree Frequent Earthquake	70	0.049	51.42%	0.04%	0.00%	0.00%
8-degree Design Earthquake	200	0.139	99.74%	69.68%	23.56%	4.88%
8-degree Rare Earthquake	400	0.278	99.96%	97.94%	78.71%	33.45%

. Specific analyses are as follows:

• During an 8-degree frequent earthquake, under LPGMs, the structure reaches normal usability performance level LS₁; the exceeding probability of the basic usability performance level LS₂ is 94.08%, indicating it is very difficult to maintain a basic usability performance level. However, the exceeding probability of life safety performance level LS₄ is very low, only 5.19%. Under OGMs, the probability of reaching normal usability performance level LS₁ is significantly reduced to 51.42%, and the exceeding probabilities of basic usability LS₂, repairable usability LS₃, and life safety LS₄ performance levels are nearly zero.
• During an 8-degree design earthquake, under LPGMs, the structure definitely reaches the performance levels of normal usability LS₁, basic usability LS₂, and repairable usability LS₃, and the probability of reaching life safety performance level LS₄ is 97.25%. Under OGMs, the probabilities of reaching the performance levels of basic usability LS₂ and repairable usability LS₃ are greatly reduced to 69.68% and 23.56%, respectively; the possibility of continued use after repair is relatively large, and the probability of reaching the life safety performance level LS₄ drops further to 4.88%.
• During an 8-degree rare earthquake, under LPGMs, the structure definitely exceeds all performance levels. Under OGMs, although the structure is also basically determined to exceed the performance levels of normal usability LS₁ and basic usability LS₂, the probability of reaching the life safety state and subsequent collapse is less than that under LPGMs, only 33.45%.

4.3. Structural Damage Assessment Based on Vulnerability Index

Although seismic vulnerability curves can evaluate structural damage under ground motions of different intensities, the damage assessment results are expressed as conditional probabilities of exceeding various performance levels, which are not intuitive and difficult to be widely accepted by engineering personnel [35]. Therefore, it is more appropriate to adopt a single quantitative value to assess structural damage performance. To address this issue, the “vulnerability index” is used to further assess the seismic damage of a high-rise structure under LPGMs.

The damage states of the high-rise structure are classified into five grades based on the four defined performance levels: basically intact, slight damage, moderate damage, severe damage, and near collapse. According to the vulnerability curves of each performance level, the differences in the exceeding probabilities between two adjacent performance levels are calculated sequentially to obtain the probabilities of the structure being in different damage states, denoted as P(DS_i|S_90c), which can be expressed using the following formula:

$$P({\mathrm{DS}}_i|S_{90c})=\left\{\begin{array}{l}1-P({\mathrm{LS}}_1|S_{90c})\\ P({\mathrm{LS}}_{i-1}|S_{90c})-P({\mathrm{LS}}_i|S_{90c})\\ P({\mathrm{LS}}_4|S_{90c})\end{array}\right.\begin{array}{l}i=1\\ i=2,3,4\\ i=5\end{array}$$

(7)

where DS_i (i = 1, 2, 3, 4, 5) represents the five damage states of basically intact, slight damage, moderate damage, severe damage, and near collapse, respectively.

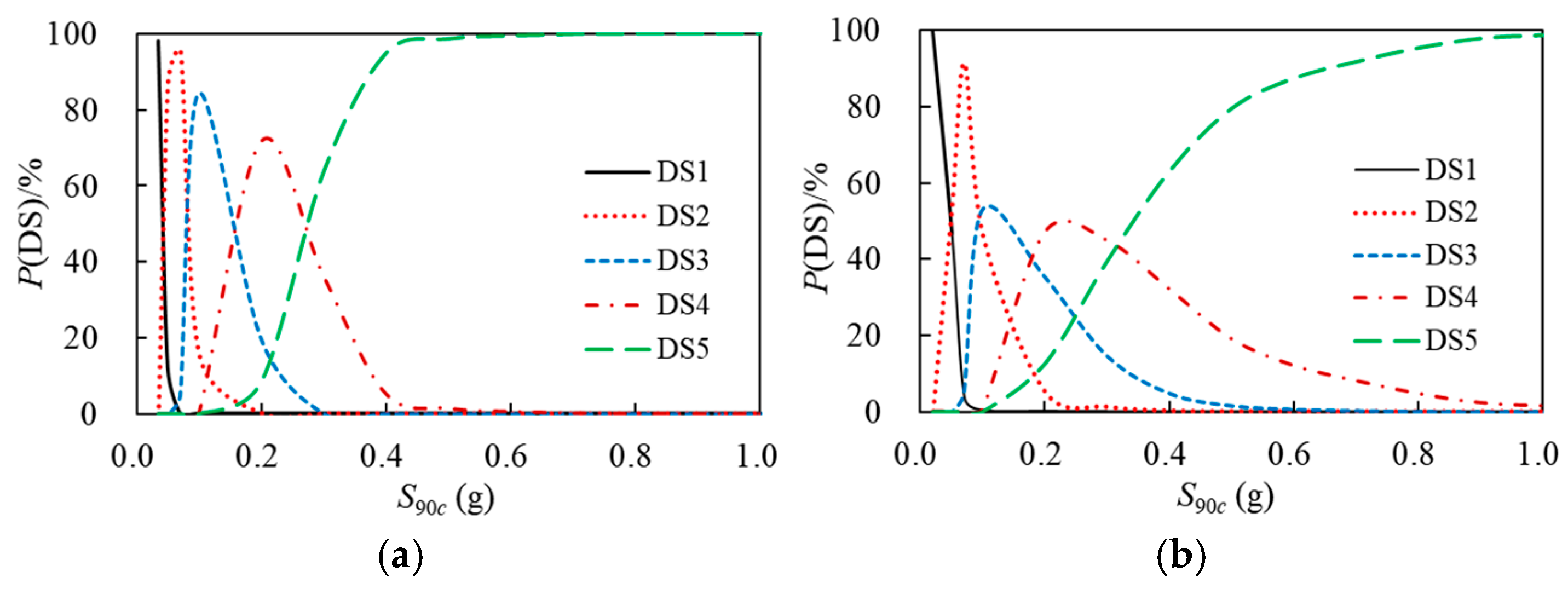
The probabilities of damage states of the high-rise structure under LPGMs and OGMs were calculated based on Equation (7), and the probability curves of the damage states of the structure were plotted taking S_90c as the horizontal axis and P(DS_i|S_90c) as the vertical axis, as shown in Figure 6. It can be observed that under two types of ground motions, as S_90c increases, the probability of remaining basically intact decreases rapidly, while the probability of being in a near-collapse state gradually increases. Meanwhile, the probabilities of being in slight damage, moderate damage, and severe damage states first increase and then decrease, reaching the peak exceeding probability at S_90c of 0.07 g, 0.1 g, and 0.2 g, respectively. In addition, the probability of different damage states varies across different seismic intensities.

The vulnerability index (VI), drawing on the concept of the average damage index in the seismic damage assessment of group structures and combining the probabilities of damage states of the structures, is defined as the mathematical expectation of DI, calculated by multiplying the probability of each damage state by the corresponding DI and then summing the results [35]. The mathematical expression is as follows:

$$\mathrm{VI}={\displaystyle \sum _{i=1}^5{\mathrm{DF}}_i}\times P({\mathrm{DS}}_i|S_{90c})$$

(8)

where DF_i (i = 1, 2, 3, 4, 5) is the damage index corresponding to the five damage states of basically intact, slight damage, moderate damage, severe damage, and near collapse, respectively, as listed in

Table 8. Damage index corresponding to damage grade.

Damage Index	Damage Grade
	Basically Intact	Slight Damage	Moderate Damage	Severe Damage	Near Collapse
Lower- and Upper-Limit Value (%)	(0,10]	(10,30]	(30,55]	(55,85]	(85,100]
Average Value (%)	5	20	42.5	70	92.5

.

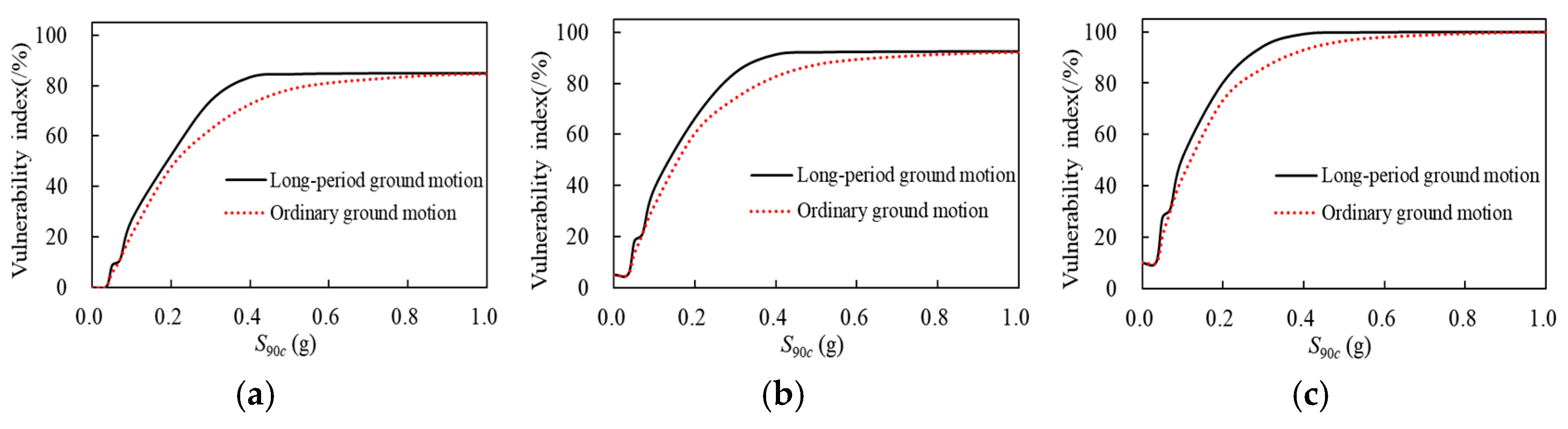
By substituting the probabilities of damage states of the high-rise structure under LPGMs and OGMs, along with the damage index limit values from Table 8, into Equation (8), the lower-limit values, average values, and upper-limit values of the vulnerability index of the structure under the two types of ground motions were obtained. Taking S_90c as the horizontal axis and the vulnerability index as the vertical axis, the corresponding vulnerability index curves were plotted, as shown in Figure 7. Furthermore, the vulnerability index curves were compared, as shown in Figure 8. The vulnerability index curves provide the interval range of vulnerability index of the structure under ground motions of different intensities. For any given ground motion intensity, the corresponding vulnerability index can be calculated and compared with the damage index in Table 8 to determine the damage state grade and seismic damage of the structure.

From Figure 7 to Figure 8, it can be observed that as S_90c increases, the vulnerability index of the structure increases rapidly, which ceases to increase at approximately 0.4 g and 0.5 g under LPGMs and OGMs, respectively. Within the range of ground motion intensity, the structure sequentially experiences basically intact, slight damage, moderate damage, severe damage, and ultimately overall instability, leading to collapse. The vulnerability index of the structure under LPGMs is generally greater than that under OGMs, indicating that LPGMs cause more severe damage to the structure. This is because, compared to OGMs, the pronounced low-frequency characteristics of LPGMs significantly amplify the internal forces, deformations, and energy responses of the high-rise structure [26], leading to more severe damage and failure.

To more comprehensively assess the structural damage and whether the expected seismic fortification target can be achieved, the vulnerability index of the structure under two types of ground motions during an 8-degree frequent earthquake, design earthquake, and rare earthquake was calculated. The results are detailed in

Table 9. Vulnerability index of high-rise structure during 8-degree earthquake.

Seismic Level	PGA (gal)	S90c (g)	Vulnerability Index (%)
			LPGMs			OGMs
			Lower Limit Value	Average Value	Upper Limit Value	Lower Limit Value	Average Value	Upper Limit Value
8-degree Frequent Earthquake	70	0.049	42.82	56.03	69.24	5.15	12.72	20.29
8-degree Design Earthquake	200	0.139	84.18	91.88	99.59	31.26	43.22	54.17
8-degree Rare Earthquake	400	0.278	85.00	92.50	100.00	59.30	71.20	83.11

.

Based on the damage index in Table 8 and the vulnerability index in Table 9, the following judgements can be made:

• When subjected to an 8-degree frequent earthquake, the structure is in a moderate damage or severe damage state under LPGMs, while the structure is basically intact or the damage is controlled at a slight damage level under OGMs, with the basic functions unaffected and normal operation resumable after minor repairs.
• When subjected to an 8-degree design earthquake, the structure enters the severe damage or near-collapse state under LPGMs, endangering human life, while the structural damage under OGMs is controlled at a moderate damage level, and the structure remains stable, which can still be used after appropriate repairs or reinforcement.
• When subjected to an 8-degree rare earthquake, the structure is in the near-collapse state under LPGMs, while the structure suffers severe damage and is in a relatively dangerous state but will not collapse under OGMs.

The above analysis results indicate that under OGMs, the SRC frame-RC core tube high-rise structure can meet the seismic fortification target of “no damage in minor earthquake, repairable damage in moderate earthquake, and no collapse in major earthquake”. However, the structural seismic damage under major earthquakes is very severe, and the structure can only continue to be used after extensive risk elimination and major repairs. Under LPGMs, the damage degree of the structure is significantly aggravated. The structure suffers moderate or even severe damage under frequent earthquakes and is in the near-collapse state under the design earthquake and rare earthquake, failing to meet the seismic design objectives required by the codes. This also indicates that the current Chinese design codes cannot fully consider the impact of LPGMs on the seismic performance of SRC frame-RC core tube high-rise structures and still need to be further improved.

Research shows that significant differences in seismic damage assessment results of structures can arise from the selection of different calculation methods for the probabilities of damage states and damage index [36]. Therefore, to reliably evaluate the seismic damage of high-rise structures, it is necessary to adopt appropriate methods that account for the uncertainties of the calculation methods for the probability of damage states and the damage index.

5. Conclusions

Twelve groups of LPGMs and twelve groups of OGMs were selected and bidirectionally input into the SRC frame-RC core tube high-rise structure for seismic vulnerability analysis according to the IDA results. Based on the exceeding probabilities of performance levels and vulnerability index of the high-rise structure, the structural damage degree under an 8-degree frequent, design and rare earthquake was evaluated, and the following conclusions were obtained:

• When subjected to an 8-degree frequent earthquake, the structure reaches the normal usability performance level and it is difficult to maintain the basic usability performance level under LPGMs, while the probability of reaching the normal usability performance level under OGMs is significantly reduced and cannot reach the basic usability performance level. When subjected to an 8-degree design earthquake, the structure almost certainly reaches all performance levels under LPGMs, while the probabilities of reaching the performance levels of basic usability, repairable usability, and life safety under OGMs decrease to 69.68%, 23.56%, and 4.88%, respectively. When subjected to an 8-degree rare earthquake, the structure definitely exceeds all performance levels under LPGMs, while the probability of reaching the life safety performance level under OGMs is only 33.45%.
• When subjected to an 8-degree frequent earthquake, the structure is in the moderate damage or severe damage state under LPGMs, while it is basically intact or in the slight damage state under OGMs. When subjected to an 8-degree design earthquake, the structure is in the severe damage or near-collapse state under LPGMs, while it is in the moderate damage state under OGMs. When subjected to an 8-degree rare earthquake, the structure is in the near-collapse state under LPGMs, while it is in the severe damage state under OGMs.
• Under LPGMs, the damage degree of the SRC frame-RC core tube high-rise structure designed in accordance with the Chinese codes is significantly aggravated, failing to meet the seismic fortification target of “no damage in minor earthquake, repairable damage in moderate earthquake, and no collapse in major earthquake”.