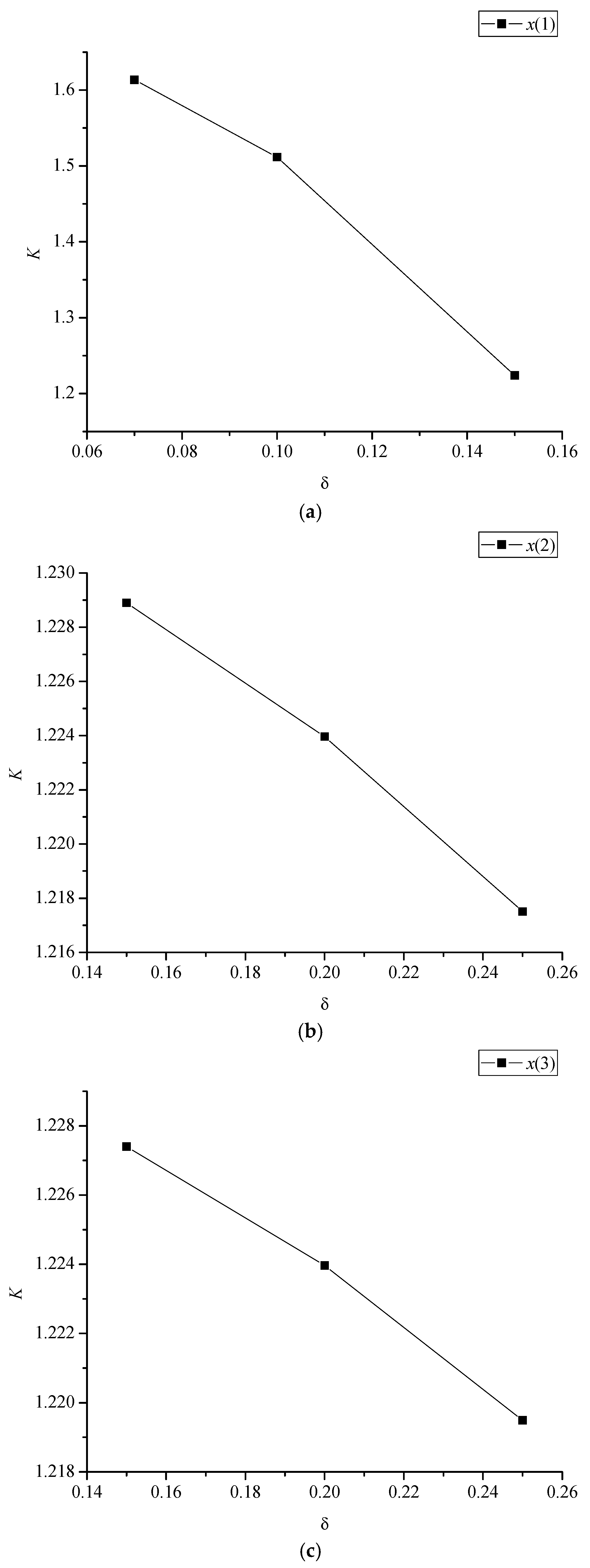Probabilistic Safety Factor Assessment of Composite Pile Foundation Using Symmetrical FEM Reliability Method

Abstract

Composite pile foundation, as a new structural form in foundation engineering, has been widely used in the field of bridge engineering due to its overall superiority. This article focuses on the specific randomness problems encountered in the practical application of composite pile foundations, and uses probability based forward and backward reliability theory combined with finite element technology to study the safety of pile foundation structures. The safety of composite pile foundation structures needs to meet the requirements of established target reliability indicators while considering parameter randomness. The method proposed in this paper can verify whether it meets the established target reliability indicators while calculating the safety factor of composite pile foundations. This method has good operability. Through the engineering application and parameter sensitivity analysis of a specific case, the study shows that the variability of parameters has a significant impact on the calculation results of the probability safety factor, and the safety factor decreases with the increase in parameter variability. The target reliability index will also directly affect the value of the probability safety factor. The iterative initial value has no effect on the calculation results, indicating the applicability of the method proposed in this paper. The research results of this paper can provide theoretical and technical support for the safety design of composite pile foundations.

1. Introduction

Composite pile foundation is widely used in the field of bridge engineering construction, and its superiority is significant [1,2,3]. In terms of application, it can adapt to complex geological conditions, such as those in soft soil foundations, sandy soils, and other formations. By combining different types of piles, the advantages of each pile type can be fully utilized. In the construction of some cross river and cross sea bridges, cast-in-place piles are often combined with prefabricated piles. The cast-in-place piles are responsible for bearing large vertical loads, while the prefabricated piles enhance lateral stability [4,5,6]. From the perspective of superiority, composite pile foundations can effectively improve the bearing capacity. Compared with a single pile type, it can greatly enhance the support of the bridge foundation for the upper structure, ensuring the stability of the bridge [7]. At the same time, it also performs well in terms of economy by reasonably matching pile types, reducing the excessive use of expensive pile materials and lowering engineering costs. In addition, its construction flexibility is high, and the combination of piles can be flexibly adjusted according to the actual situation on site, shortening the construction period. This greatly improves the construction efficiency of large-scale bridge projects and effectively promotes the development of bridge engineering.

The random factors encountered during the structural bearing process of composite pile foundations include earthquakes [8,9,10], erosion slip [11,12,13], displacement [14], etc. During an earthquake, the characteristics, magnitude, and duration of seismic waves are random, which can cause complex dynamic loads on pile foundations and potentially lead to pile damage. The water flow erosion will randomly change the mechanical properties of the soil around the pile and the depth of the pile entering the soil, weaken the lateral support force of the pile, and affect the bearing performance. Basic displacement also has uncertainty, which may be caused by uneven settlement of the foundation soil, adjacent construction projects, etc., leading to changes in the stress state of the pile body, additional internal forces, increasing the complexity and uncertainty of structural bearing, and threatening the stability and safety of the pile foundation.

When studying the safety factor from a probabilistic perspective for the randomness problem in the practical application of composite pile foundations, the commonly used methods and theories include reliability theory [15,16,17,18,19]. This theory considers various uncertain factors of pile foundations, such as material properties, geometric dimensions, loads, etc., as random variables. By establishing limit state equations and using probability statistical methods to calculate the failure probability or reliability index of the structure, the safety factor is evaluated [20,21]. There is also Monte Carlo simulation method, which generates a large number of samples that conform to the probability distribution of various random variables through random sampling, inputs them into the pile foundation model for calculation, and statistically analyzes the results to obtain the probability distribution of the safety factor [22,23,24,25,26]. In addition, the first-order second-moment method is also an important method, which linearizes the nonlinear limit state equation at the design verification point, calculates the reliability index and safety factor of the structure based on the mean and variance of random variables, effectively considers the randomness and correlation of variables, and provides a more accurate theoretical basis for the safety assessment of composite pile foundations [27,28,29,30,31].

The traditional research methods for the probabilistic safety of pile foundations have many shortcomings in considering the symbiotic relationship with target reliability indicators. Firstly, traditional methods are often based on simplified assumptions and empirical formulas, which do not fully consider complex pile–soil interactions and various random factors in practical engineering, resulting in deviations between the calculation of safety factors and actual reliability. Traditional research methods usually use deterministic analysis models, which are difficult to adapt to changes in different geological conditions and engineering environments. They lack effective quantification and processing of uncertainty, making it difficult to accurately grasp the symbiotic relationship between safety factors and target reliability indicators, thereby affecting the safety and economy of pile foundation optimization design [32,33,34].

This study attempts to use the method of positive and negative reliability to study the safety performance of pile foundations from a probabilistic perspective. This article adopts a probabilistic finite element method based on the reliability theory of positive and negative systems to evaluate the safety of composite pile foundations. The innovation of this article is mainly reflected in the following aspects: firstly, establishing a quantitative relationship between the safety factor and the randomness of influencing factors; secondly, directly converting the safety factor to the target reliability index of the structure; thirdly, the use of probabilistic finite element method combined with symmetric reliability theory can achieve parallel operations for calculating and verifying probabilistic safety factors.

The remainder of this paper is structured as follows. Firstly, a description of the forward and inverse symmetrical reliability methods used in this study is given. Based on this, a reliability-based probabilistic safety factor evaluation method for pile foundations is proposed. Finally, a practical engineering case is used to illustrate the correctness of the research method in this paper, providing theoretical guidance for the safe construction and optimization design of pile foundations.

2. Symmetrical Reliability Method

The system reliability [35] used in this study has the following assumptions and limitations: (1) system reliability refers to the combination of positive reliability and inverse reliability, especially the use of positive reliability in the inverse reliability algorithm; (2) in the iterative process of reliability, the relevant random variables must satisfy both position parameters and scale parameters, that is, conform to a normal distribution, lognormal distribution, and extremum distribution; (3) the iterative process of finite element reliability requires attention to the selection of iteration step size, which cannot be too small, otherwise it is easy to fall into local oscillations and cannot achieve final convergence. In this case, the step size needs to be updated until the final global convergence is achieved.

2.1. Forward Reliability Theory

Structural reliability is of great significance for ensuring the safety of pile foundation structures, improving economic benefits, and achieving sustainable development. In the process of designing, constructing, and maintaining pile foundations, attention should be paid to improving the reliability of the structure to ensure the stability and safety of the system or structure.

Reliability refers to the probability of a system operating normally within a certain period of time, usually described by a reliability function. The reliability function is a function of influencing factors that represent the probability of a system operating normally within a given constraint condition. According to the characteristics and requirements of the system, suitable functional functions can be selected to calculate the system’s reliability, and corresponding optimization and improvement can be conducted based on the calculation results. The limit state of a structure can be described using the limit state equation, which is expressed as follows:

g = g(R,S) = R − S = 0

(1)

where g is the limit state function;

R is the resistance;

S is the effect of action.

The calculation of the reliability index is as follows:

$$\beta ={\displaystyle \frac{{\mu }_R-{\mu }_S}{\sqrt{{\sigma }_R^2+{\sigma }_S^2}}}$$

(2)

where ${\mu }_R$—the mean value of random variables of resistance;

${\mu }_S$—the mean value of random variables of effect;

${\sigma }_R$—the standard deviation of random variables of resistance;

${\sigma }_S$—the standard deviation of random variables of effect.

2.2. Inverse Reliability Theory

The safety factor, as a deterministic variable, is a very important parameter in the evaluation and design of pile foundation structures. The probability safety factor is the correlation between the value of the safety factor and the reliability index, and the safety factor is calculated through the reliability index.

For a target reliability index ${\mathit{\beta }}^{\mathrm{T}}$, the inverse problem can then be stated as follows [23,24]:

$$\begin{gathered} \mathrm{Given}{\mathit{\beta }}^{\mathrm{T}} \\ \mathrm{Find}:\mathbf{d}\mathrm{or}/\mathrm{and}\mathbf{r} \\ \mathrm{Subject}\mathrm{to}\beta (\mathbf{X},k,r)={\beta }^{\mathrm{T}}\mathrm{and}\mathrm{G}(\mathbf{X},k,r)=0 \end{gathered}$$

(3)

where G—the limit state function;

X—the vector of basic random variables;

k—the vector of design deterministic parameters;

r—the vector of the design parameters of random variables.

The equation $\beta (\mathbf{X},k,r)={\beta }^{\mathrm{T}}$ can be written as an ordinary nonlinear equation:

$$f=\beta (\mathbf{X},k,r)-{\beta }^{\mathrm{T}}$$

(4)

with the Newton–Raphson iterations applied to arrive at $f=0$.

The iterative formula for the safety factor can be obtained from Formula (2) as follows:

$$K^{j+1}=K^j+{\displaystyle \frac{{\beta }_T-{\beta }^j}{{\left.\frac{\partial \beta }{\partial K}\right|}_{K^j}}}$$

(5)

Equation (8) is selected as the convergence criterion of the reliability inverse analysis method adopted in this study:

$$\left|K^{j+1}-K^j\right|\le \epsilon$$

(6)

where $\epsilon$ is the convergence criterion value.

2.3. Implementation Steps

Step 1: Set the initial values for random variables and the iteration of surrogate parameters. The initial value of a random variable is generally chosen as the mean, while the initial value of an iterative parameter is generally chosen as the calculated value of a deterministic model.

Step 2: Set j = 1, and calculate ${\beta }^j$ and ${\left.{\displaystyle \frac{\partial \beta }{\partial K}}\right|}_{K^j}$.

Step 3: Use ${\beta }^j$ and ${\left.{\displaystyle \frac{\partial \beta }{\partial K}}\right|}_{K^j}$ to calculate the safety factor of the pile foundation and update the K value.

Step 4: Check whether the convergence criterion is met according to Equation (6). If it does not meet the convergence criterion, set j = j + 1 and proceed to step 2; otherwise, output the calculation result.

3. Reliability Model of the Safety Factor of the Pile Foundation

The expression of the deterministic safety factor of the pile foundation is as follows:

$$K={\displaystyle \frac{R}{S}}$$

(7)

where $K$—the safety factor of the pile foundation;

$R$—the characteristic value of the pile;

$S$—the combination of the standard value of the action effect of the pile.

The standard value of the vertical ultimate load-carrying capacity of a single pile is calculated using the following Formula (8):

$$Q_k=Q_{sk}+Q_{pk}=u{\displaystyle \sum q_{sik}{l}_i+p_{sk}{A}_p}$$

(8)

where $Q_k$—the standard value of the pile;

$Q_{sk}$—the standard value of the total ultimate lateral friction resistance;

$Q_{pk}$—the standard value of the total ultimate end resistance;

$u$—the perimeter of the pile;

$q_{sik}$—the standard value of the unit limit friction resistance of the $i$-layer soil on the pile side;

$l_i$—the thickness of the $i$-layer soil on the pile side;

$p_{sk}$—the standard value of the unit limit end resistance of the soil;

$A_p$—the area of the bottom of the pile.

As the ultimate load-carrying capacity of a single pile is related to various uncertain factors, Equation (8) cannot cover all the uncertain factors, so a random variable is introduced to describe the uncertainty of the calculation model, as shown in Equation (9):

$$Q_u=\chi Q_k$$

(9)

where $Q_u$—the measured value of the vertical ultimate load-carrying capacity of the single pile of bridge structures;

$\chi$—the random variable coefficients of the uncertainty calculation model.

According to the inverse reliability theory, when evaluating the safety factor of the vertical load-carrying capacity of the pile foundation of bridges, the load-carrying capacity safety factor is considered an unknown parameter. Equations (7) and (9) show that the calculation expression of the pile foundation of the bridge stability safety factor is as follows:

$$K={\displaystyle \frac{Q_u}{S}}$$

(10)

Then,

$$Z=Q_u-KS$$

(11)

Combining Equations (8) and (11), the functional function for the analysis of the probabilistic safety factor of the vertical load-carrying capacity of the pile foundation can be constructed as follows:

$$Z=\chi (u{\displaystyle \sum q_{sik}{l}_i+p_{sk}{A}_p)}-KS$$

(12)

4. Probabilistic Analysis Process of the Safety Factor of Combination Piles

In this research paper, the analysis approach for determining the safety factors of combination piles grounded on the symmetrical reliability method is effectively implemented through the integration of the finite element analysis software ANSYS 15.0 and the probabilistic analysis software MATLAB 2023b. The comprehensive and detailed analysis steps regarding the safety factor of combination piles based on the symmetrical reliability method are elaborated as follows:

Step 1: Initially, the initial value of the random variable needs to be set. Generally speaking, in most practical scenarios, the mean value of the random variable can be prudently chosen as the initial iteration value. This is because the mean value represents the central tendency of the random variable to a certain extent. By using it as the starting point for iteration, it can provide a relatively reasonable initial reference for the subsequent iterative calculations, which is conducive to approaching the final accurate result more quickly.

Step 2: Subsequently, the limit state function is established. Once it is set up, the initial iteration value obtained in the previous step is then adopted as the search point for the normal quantization probability transformation. The establishment of the limit state function is based on the mechanical characteristics of the combination pile structure and the actual engineering requirements. It reflects the relationship among various factors when the structure is in a limited state. Selecting the initial iteration value as the search point aims to seek the optimal solution that satisfies the limit state conditions in the probability space, thereby providing a clear direction for the subsequent calculations.

Step 3: Next, the value of the random variable is inputted into the ANSYS software. After that, the bearing capacity of the combination piles is calculated using the deterministic method. ANSYS software possesses powerful finite element analysis capabilities, enabling it to accurately simulate the mechanical behavior of combination piles under various complex working conditions. By inputting the random variable values and leveraging its deterministic algorithms, the accurate bearing capacity values of the combination piles under the current set conditions can be obtained. These values serve as fundamental data for the subsequent analysis.

Step 4: Then, the loads calculated in Step 3 are inputted into the MATLAB software. MATLAB is then utilized to calculate the value of the limit state function. MATLAB software has unique advantages in numerical calculation and probability analysis. By importing the load data calculated by ANSYS into it, according to the established limit state function model, the corresponding function value can be accurately computed. This function value reflects the degree of deviation between the current structural state and the limit state, and it is an important basis for judging the safety of the structure.

Step 5: In ANSYS, the difference method is employed to analyze the sensitivity of the bearing capacity. Simultaneously, the gradient value of the limit state function is calculated. The difference method analyzes the minute changes in the bearing capacity under different working conditions. Through this analysis, it can clearly understand the degree of influence of each factor on the bearing capacity, that is, the sensitivity. At the same time, calculating the gradient value of the limit state function can determine the change direction and rate of the function value in the space. This provides crucial information for the subsequent iterative optimization and helps to find the solution that satisfies the convergence condition more rapidly.

Step 6: Subsequently, the probability safety factor is calculated. Based on the various data obtained from the previous steps, specific probability calculation methods are utilized. By comprehensively considering factors such as the uncertainty of random variables, bearing capacity, and the limit state function, the probability safety factor of the combination piles is ultimately calculated. This factor can more realistically reflect the safety level of the structure when facing various random factors during the actual service process.

Step 7: Finally, a judgment is made as to whether convergence has been achieved. If convergence is attained, the calculation is terminated. Conversely, if convergence has not been achieved, the process returns to Step 2 to continue the iterative calculations. The convergence judgment is a crucial part of the entire calculation process. It ensures the accuracy and reliability of the calculation results. When the calculation results meet the pre-set convergence conditions, it indicates that a relatively accurate solution has been found, and the calculation can be stopped at this time. If not, the search point needs to be adjusted, and the iterative calculations need to be continued until the convergence requirements are met.

5. Application

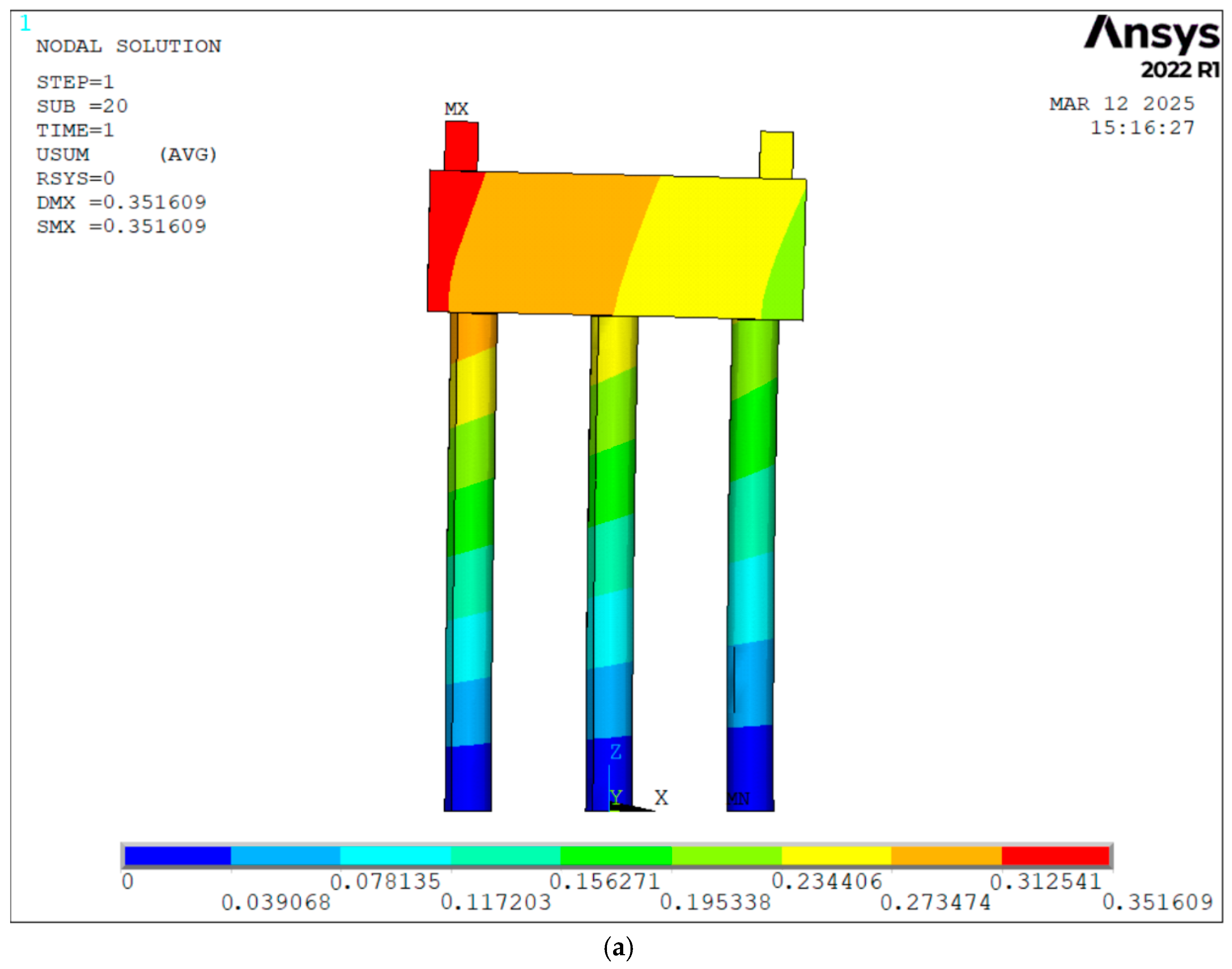
The ultra-high-performance concrete composite pile foundation was used under the pier columns in an actual bridge engineering case. A solid model of the pile foundation and bearing platform was established using the universal finite element software ANSYS and simulated using SOLID45 elements; the elastic modulus of the SOLID45 element was 33,000 Mpa. The soil spring was simulated using the COMBIN14 element; the soil spring stiffnesses were 5520 kN/m, 13,220 kN/m, and 20,200 kN/m, with each soil spring element using a single degree of freedom analysis option. The two nodes of the element coincide and are located at the same position as the peripheral nodes of the pile foundation. The spring element stiffness is calculated based on the soil investigation results. In order to facilitate the application of loads and boundary conditions, reference points were established at the top section of the column and the bottom section of the pile cap, and rigid coupling constraints were established between all points in the corresponding section and the reference points. The finite element model is shown in Figure 1; the entire model has 2927 nodes and 10,033 elements with the minimize element size 5 cm, balancing the efficiency and accuracy of multiple structural response calculations required for reliability calculation.

The ultimate bearing capacity of the foundation soil under the cushion cap can be calculated using the modified Hansen formula, as follows:

$$f_d=0.5\psi N_{\gamma }{\zeta }_{\gamma }\gamma B+N_q{\zeta }_q{\gamma }_{0}D+\psi N_c{\zeta }_c{c}_d$$

(13)

where

$$c_d={\displaystyle \frac{\lambda c_k}{{\gamma }_c}}$$

(14)

$${\phi }_d={\displaystyle \frac{\lambda {\phi }_k}{{\gamma }_{\phi }}}$$

(15)

and $\psi$ is a correction factor related to the design value of the internal friction angle ${\phi }_d$; $N_{\gamma }$, $N_q$, and $N_c$ are bearing capacity factors related to the design value of the internal friction angle ${\phi }_d$; ${\zeta }_{\gamma }$, ${\zeta }_q$, and ${\zeta }_c$ are the shape coefficients of the cushion cap; $B$ is the width of the cushion cap; $D$ is the burying depth for bearing platform; $\gamma$ is the weight of the soil below the bottom surface of the bearing platform; ${\gamma }_0$ is the weighted average weight of each layer of soil above the bottom surface of the bearing platform; $c_d$ is the design value of the cohesive force of foundation soil; $c_k$ is the standard value of foundation soil cohesion; ${\phi }_k$ is the standard value of the internal friction angle of foundation soil; $\lambda$ is the correction coefficient for the standard value of the shear strength index of soil, which is 0.8; ${\gamma }_c$ is the partial coefficient of soil cohesion, which is 2.7; and ${\gamma }_{\phi }$ is the partial coefficient of the internal friction angle of the soil, which is 1.2.

Among the above parameters, the geometric parameters of the pile cap and pile body, the coefficients related to the geometric parameters, the thickness of each layer of soil, and the weight of the soil layer and pile cap can be regarded as deterministic. The correction coefficients and bearing capacity coefficients related to $c$ and $\phi$, as well as the load indicators of each soil layer $f_{si}$ and $f_p$, have significant variability, and both are considered random variables.

The settlement control expressed by various basic random variables conforms to the limit state equation for checking the overall bearing capacity of the pile foundation as follows:

$$\begin{array}{c}Z=\chi [n(U_P{\displaystyle \sum f_{si}{l}_i}+f_p{A}_p)+(0.5\psi N_{\gamma }{\zeta }_{\gamma }\gamma B+N_q{\zeta }_q{\gamma }_{0}D+\psi N_c{\zeta }_c{c}_d)A_c]\\ -K[(\overline{S_G}+\overline{S_Q})-G]\end{array}$$

(16)

A bridge-bored pile has a diameter of 1.2 m and a length of 22 m. The load effect on the top of the pile is 3000 kN calculated theoretically based on actual specifications [36]. The design parameters of each soil layer are shown in

Table 1. The design parameters of soil layers.

Structural Layer	Thickness/m	Ultimate Pile Side Friction Resistance/kPa	Ultimate Pile End Friction Resistance/kPa
Soil layer 1	6	60	-
Soil layer 2	6	50	-
Soil layer 3	10	80	-
Pile end soil	-	-	2000

. The statistical characteristics of random variable indicators [37] for foundation soil are shown in

Table 2. Statistical properties of random variables of foundation soil.

Layer Order	$\mathit{c}/\mathbf{kPa}$		φ/∘		${\mathit{f}}_{\mathit{s}\mathit{i}}/\mathbf{kPa}$		${\mathit{f}}_{\mathit{p}}/\mathbf{kPa}$
	Mean Value	Coefficient of Variation	Mean Value	Coefficient of Variation	Mean Value	Coefficient of Variation	Mean Value	Coefficient of Variation
2	16.8	0.45	10.4	0.20	12	0.11	-	-
3	9.1	0.33	15.3	0.15	12	0.26	-	-
4	7.0	-	7.5	-	12	0.16	-	-
51	11.2	-	12.0	-	33.6	0.18	800	0.25
52	5.0	-	25.0	-	40	0.23	1100	0.31
6	30.8	-	19.5	-	48	0.20	1200	0.29

.

Putting the above parameter values into Formula (16), the structural overturning stability function can be obtained as follows:

$$Z=x(1)\cdot (1492.88x(2)+1244.07x(3)+3317.52x(4)+2488.14x(5))-3000\cdot K\cdot x(6)$$

(17)

The values of the statistical parameters of each random variable in Formula (19) are shown in

Table 3. Random variables.

No.	Random Variable	Probability Distribution Type	Mean	Coefficients of Variation
x(1)	$\chi$	Normal	1	0.15
x(2)	$q_{s1k}/\mathrm{kPa}$	Normal	1	0.2
x(3)	$q_{s2k}/\mathrm{kPa}$	Normal	1	0.2
x(4)	$q_{s3k}/\mathrm{kPa}$	Normal	1	0.2
x(5)	$p_{sk}/\mathrm{kPa}$	Normal	1	0.2
x(6)	$S/\mathrm{kN}$	Normal	1	0.07

[38].

5.1. Finite Element Simulation Process

In the process of calculating the safety factor of pile foundation using the method proposed in this article, it is necessary to simultaneously iterate the calculation of positive and negative reliability indicators. Each iteration of the reliability indicators requires the calculation of structural response and gradient values, with the core being the simulation of stress and displacement calculation of the pile foundation structure. By selecting initial iteration parameters, the mean of statistical parameters is generally chosen as the initial iteration value, and the iteration step size is set at 5% of the mean until the calculation results converge. The following Figure 2 shows the operating conditions of the finite element calculation process, the finite element analysis calculation results are consistent with the actual test results based on deterministic model.

5.2. Analysis Results of Safety Factor

In this example, the target reliability index of the bridge is 3.5 [28], the calculated safety factor of the vertical load-carrying capacity of the pile foundation of bridges is 1.224, and the safety factor calculated based on the deterministic model is 2.848.

Comparing the safety factor calculation results of probabilistic safety factors and deterministic models, it can be found that using the principle of reliability to calculate the safety factor from a probability perspective can fully consider the randomness of parameters, which significantly impacts the calculation results of probabilistic safety factors, mainly reflected in the fact that the variability of parameters directly reduces the safety reserve of the structure. Therefore, the result of the probability safety factor is smaller than the calculation result of the deterministic model. This will prompt us to consider the impact when designing and evaluating pile safety.

5.3. Impact of Target Reliability Indicators

The target reliability index is used to ensure the safety of bridge pile foundation reliability, and the size of the target reliability index has a significant impact on the value of the pile foundation safety coefficient. In order to study the quantitative impact of target reliability indicators on the safety factor of pile foundations, different values of target reliability indicators are taken, and each type of target reliability indicator is calculated separately. The value range of the structural target reliability index is 1~4, in order to analyze the influence of the target reliability on the safety factor of the vertical load-carrying capacity of the pile foundation of bridges. The specific calculation results are shown in

Table 4. The influence of the reliability index on the safety factor of the vertical load-carrying capacity of bridges’ pile foundations.

Target Reliability Index	1	1.5	2	2.5	3	3.5	4
Safety factor	2.3174	2.0745	1.8449	1.6275	1.4212	1.2240	1.0332

.

The analysis showed that the target reliability index has a significant impact on the value of the safety coefficient of pile foundation structures, and the size of the safety coefficient is inversely proportional to the target reliability index; that is, the larger the value of the target reliability index, the smaller the calculated safety factor, and the magnitude of the safety factor correspond in a one-to-one manner with the structural reliability index. The calculation results of the relationship between safety factor and reliability index are consistent with the ref. [39,40,41]. The reason for this calculation result is that when the safety factor and load term are combined, the load term will show an inverse proportional result with the change in reliability index compared to the resistance term. Therefore, determining the probability safety coefficient of pile foundation structures and the functional relationship between the target reliability indicators can provide an effective means for structural safety assessment and design.

5.4. Influence of Parameter Uncertainty on Safety Factor

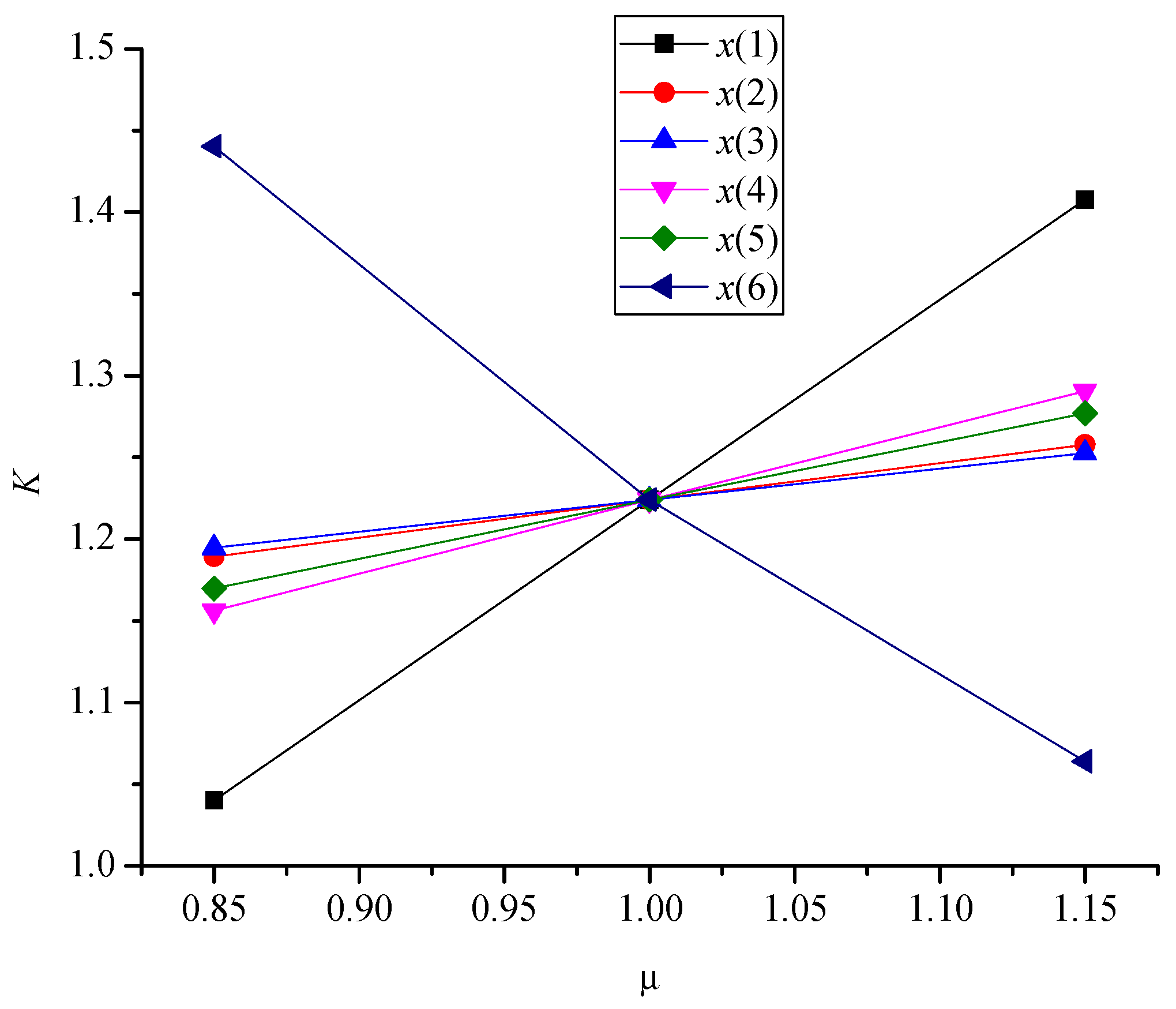
In order to study the impact of parameter randomness on the safety factor of pile foundation structures, the mean and variability of random variables are changed when the target reliability index is set. The structural target reliability index is taken as 3.5, the mean value of each random variable is increased by −15% to +15%, and the variation coefficients δ (which was the ratio of the standard deviation to mean value of random variables) are taken as 0.07, 0.1, 0.15, 0.2, and 0.25; the calculation results of the overturning stability safety factor are shown in

Table 5. The effect of the mean value of random variables.

Mean	Safety Factor
	x(1)	x(2)	x(3)	x(4)	x(5)	x(6)
	$\mathit{\chi }$	${\displaystyle {\mathit{q}}_{\mathit{s}1\mathit{k}}/kPa}$	${\displaystyle {\mathit{q}}_{\mathit{s}2\mathit{k}}/kPa}$	${\displaystyle {\mathit{q}}_{\mathit{s}3\mathit{k}}/kPa}$	${\displaystyle {\mathit{p}}_{\mathit{s}\mathit{k}}/kPa}$	${\displaystyle \mathit{S}/kN}$
−15%	1.0401	1.1894	1.1947	1.1561	1.1698	1.4402
0	1.2240	1.2240	1.2240	1.2240	1.2240	1.2240
+15%	1.4078	1.2577	1.2526	1.2905	1.2771	1.0640

and

Table 6. The effect of coefficients of variation in random variables.

Coefficients of Variation δ	Safety Factor
	x(1)	x(2)	x(3)	x(4)	x(5)	x(6)
	$\mathit{\chi }$	${\displaystyle {\mathit{q}}_{\mathit{s}1\mathit{k}}/kPa}$	${\displaystyle {\mathit{q}}_{\mathit{s}2\mathit{k}}/kPa}$	${\displaystyle {\mathit{q}}_{\mathit{s}3\mathit{k}}/kPa}$	${\displaystyle {\mathit{p}}_{\mathit{s}\mathit{k}}/kPa}$	${\displaystyle \mathit{S}/kN}$
0.07	1.6135	-	-	-	-	1.2240
0.1	1.5117	-	-	-	-	1.1945
0.15	1.2240	1.2289	1.2274	1.2478	1.2377	1.1342
0.2	-	1.2240	1.2240	1.2240	1.2240	-
0.25	-	1.2175	1.2195	1.1907	1.2057	-

and Figure 3 and Figure 4.

When analyzing the influence of the mean value of random variables on the safety factor, the safety factor increases with the increase in the mean value of $\chi$, $q_{s1k}$, $q_{s2k}$, $q_{s3k}$, and $p_{sk}$ and decreases with the increase in the mean value $S$. From the essence of safety factor analysis, the safety factor is directly proportional to the mean of resistance and load. Therefore, the larger the mean term of resistance, the greater the safety factor, and the larger the mean term of load, the greater the safety factor.

When analyzing the influence of random variable coefficients of variation on the safety factor, the safety factor decreases with the increase in the variability of $\chi$, $q_{s1k}$, $q_{s2k}$, $q_{s3k}$, $p_{sk}$, and $S$. From the essence of safety factor analysis, the safety factor is directly proportional to the variability of resistance and load. Therefore, the larger the variation coefficient term of resistance, the smaller the safety factor, and the larger the variation coefficient term of load, the smaller the safety factor.

A comprehensive analysis of the influence of parameter uncertainty on the safety factor shows that the random variable coefficients $\chi$ that describe the uncertainty have the greatest influence on the safety factor, which needs to be determined carefully. From the essence of safety factor analysis, the safety factor is directly proportional to the overall calculation term of resistance, so the calculation mode of resistance has the greatest impact on the value of the safety factor.

5.5. The Influence of the Initial Iteration Value of the Safety Factor

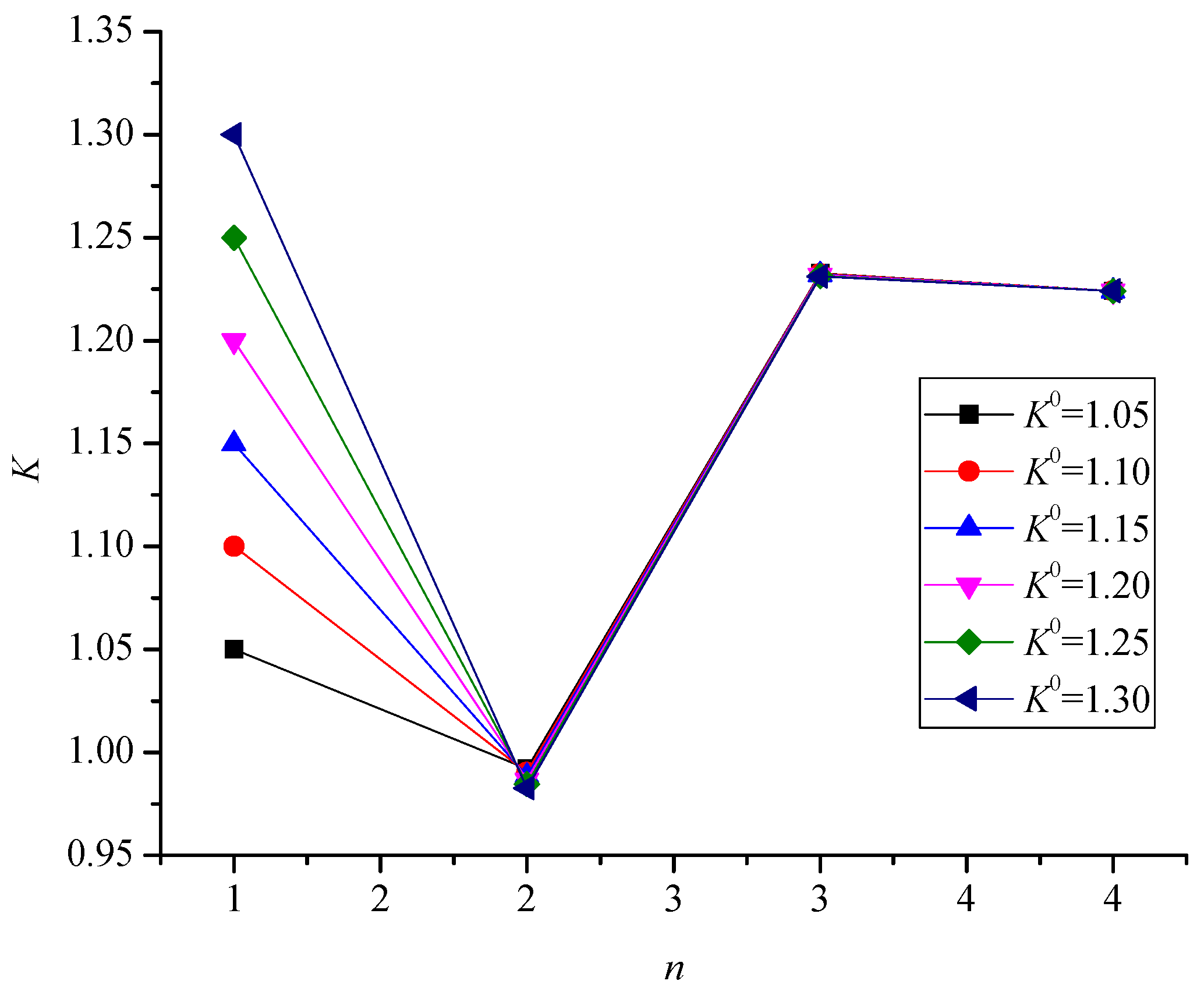
As the initial value $K^0$ of the safety factor of the vertical load-carrying capacity of the pile foundation of bridges is arbitrarily selected in the process of reliability inverse analysis, it is necessary to analyze the influence of the initial value $K$ on the safety factor of the vertical load-carrying capacity of the pile foundation of bridges. Figure 5 shows the corresponding safety factor calculation results when the initial values of $K$ are 1.05, 1.10, 1.15, 1.20, 1.25, and 1.30 (the abscissa in the figure represents the number of iterations).

The analysis showed that calculating the safety factor of pile foundation structures requires multiple iterations. When setting different initial iteration values, the final results all converge to the same value. This indicates that the setting of the initial iteration value only affects the iteration process and the number of iterations, and has no effect on the final result. Through iterative calculations, it can be found that the symmetric reliability method used in this paper has good stability in calculating the probability safety factor of composite pile foundations. It can achieve a significant impact on the calculation of the corresponding quantity relationship between the safety factor and the target reliability index without considering the choice of disposal, ensuring the stability of the calculation process.

6. Conclusions

This study proposed a probability analysis method based on the symmetrical reliability method for the safety evaluation of pile foundation structures. This method calculates the probability safety factor by combining forward and inverse reliability theory. The calculated safety factor can simultaneously consider the randomness of the target reliability index and design parameters of the structure. The method proposed in this article was analyzed through an engineering example, and the following conclusions were obtained:

(1)

By integrating a deterministic calculation model and a probabilistic evaluation model, a calculation expression is established between the probability safety factor and reliability index of composite pile foundation, which can achieve quantitative calculation of safety factor under the premise of established reliability index, while considering the randomness of design parameters. This calculation model meets the practical application requirements of engineering.

(2)

By comprehensively using the deterministic finite element calculation method and reliability programmed iteration, it is possible to achieve automated operation in the calculation process of the probability safety factor of composite pile foundation, and automatically meet the requirements of the target reliability index while calculating the probability safety factor result.

(3)

Analysis shows the target reliability index significantly impacts the pile foundation safety coefficient. They are inversely proportional: a larger index means a smaller safety coefficient, with a one-to-one correspondence. This is because, when combined with the safety factor, the load term is inversely proportional to the reliability index relative to the resistance term. Thus, determining this relationship aids structural safety assessment and design.

(4)

In safety factor analysis, the safety factor is directly proportional to the mean of resistance and load. A larger resistance mean leads to a greater safety factor, and the same for load. Also, it is inversely proportional to the variability of resistance and load. A larger resistance or load variation coefficient results in a smaller safety factor. Moreover, as the safety factor is directly proportional to the overall resistance calculation term, the resistance calculation mode has the greatest impact on its value.

(5)

Analysis reveals that calculating pile foundation safety factors needs multiple iterations. Different initial values lead to the same final result, meaning they only affect the iteration process and count. The symmetric reliability method in this paper shows good stability in computing composite pile foundation safety factors. It impacts the calculation of the relationship between safety factors and target reliability indexes without disposal choice concerns, ensuring calculation stability.

In the process of this study, due to limitations in research funding and experimental conditions, there are still the following issues that need further research. Firstly, the specific probability and statistical model of random variables should follow interval distribution instead of the real number set distribution described by traditional probability equations. Secondly, further research is needed to extend the method proposed in this article to the calculation of probability safety factors based on interval random variables. The correlation coupling between random variables will also have a significant impact on the calculation results of the probability safety factor. Finally, a more comprehensive multi-load condition should be considered for the safety of composite pile foundations, which can better conform to practical engineering. In summary, this study only provides a technical means for the safety assessment of composite pile foundations, which can achieve automated verification between safety factors and structural reliability.