Investigation of Screw Layout and Hole Geometry on Cold-Formed Steel Bending Performance Using Finite Element Model and Statistical Methods
Abstract
1. Introduction
2. Experimental Studies in the Literature
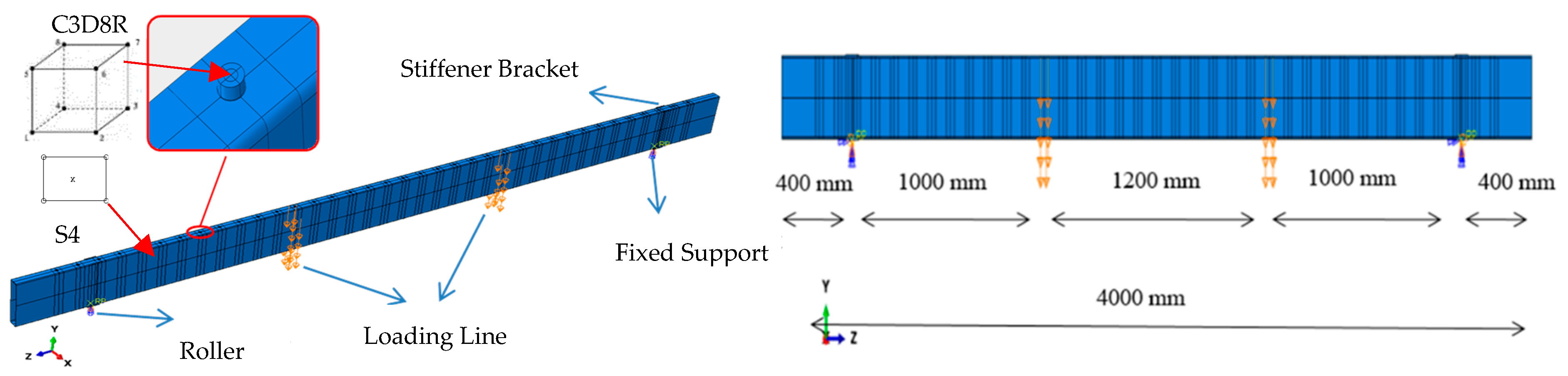
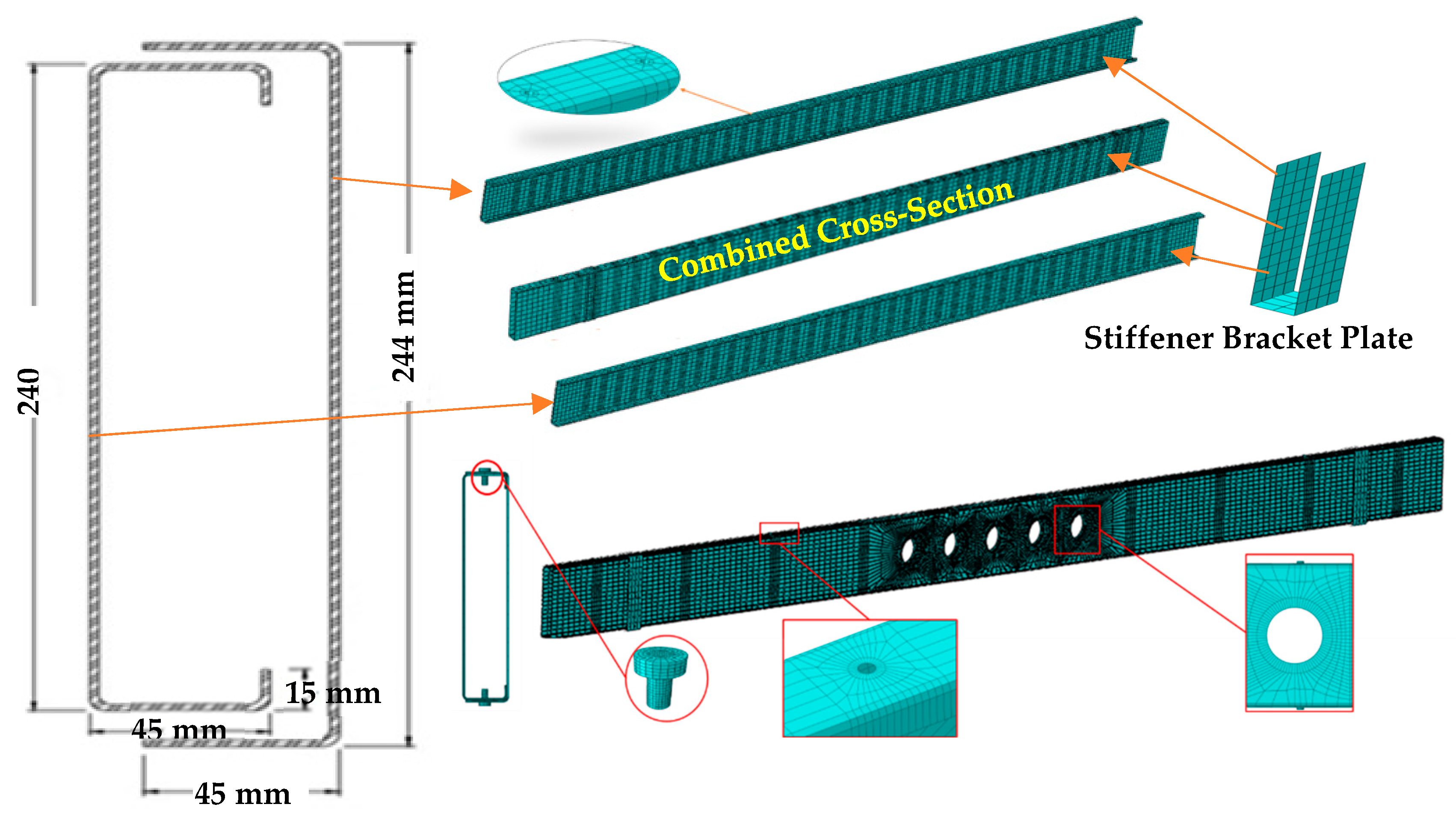
3. Finite Element Study
3.1. Material Properties
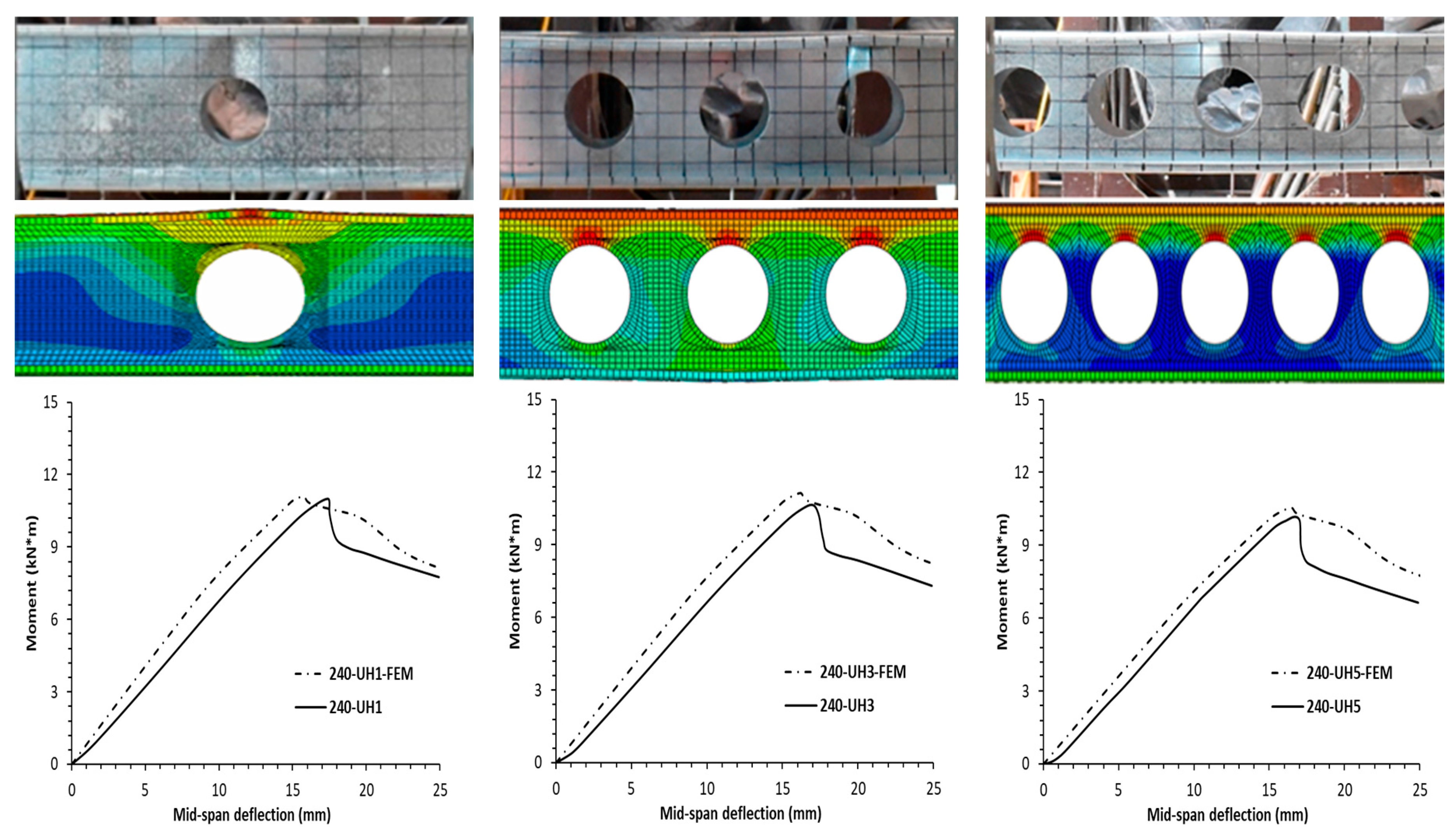
3.2. Model Verification
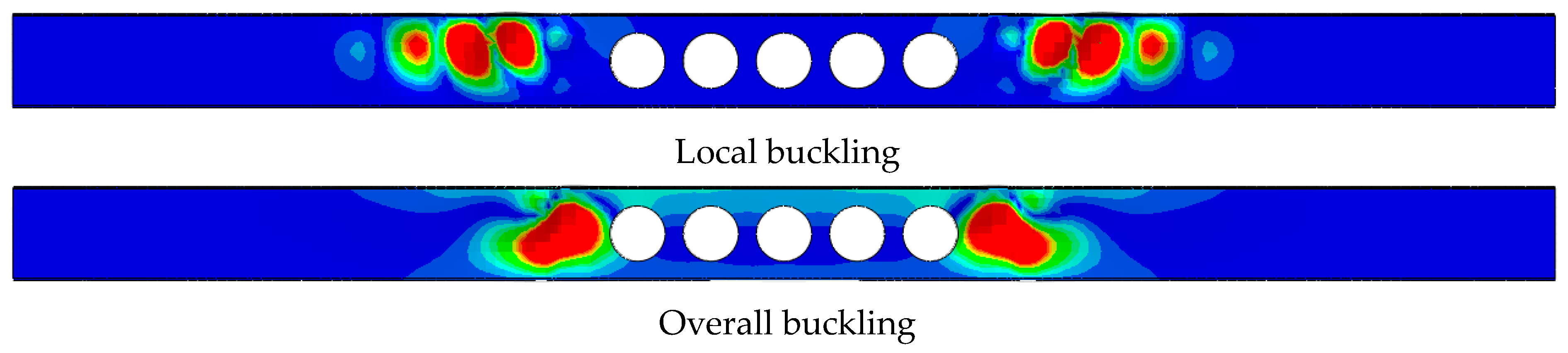
3.3. Initial Geometric Imperfections
4. Parametric Study
5. Findings and Discussions
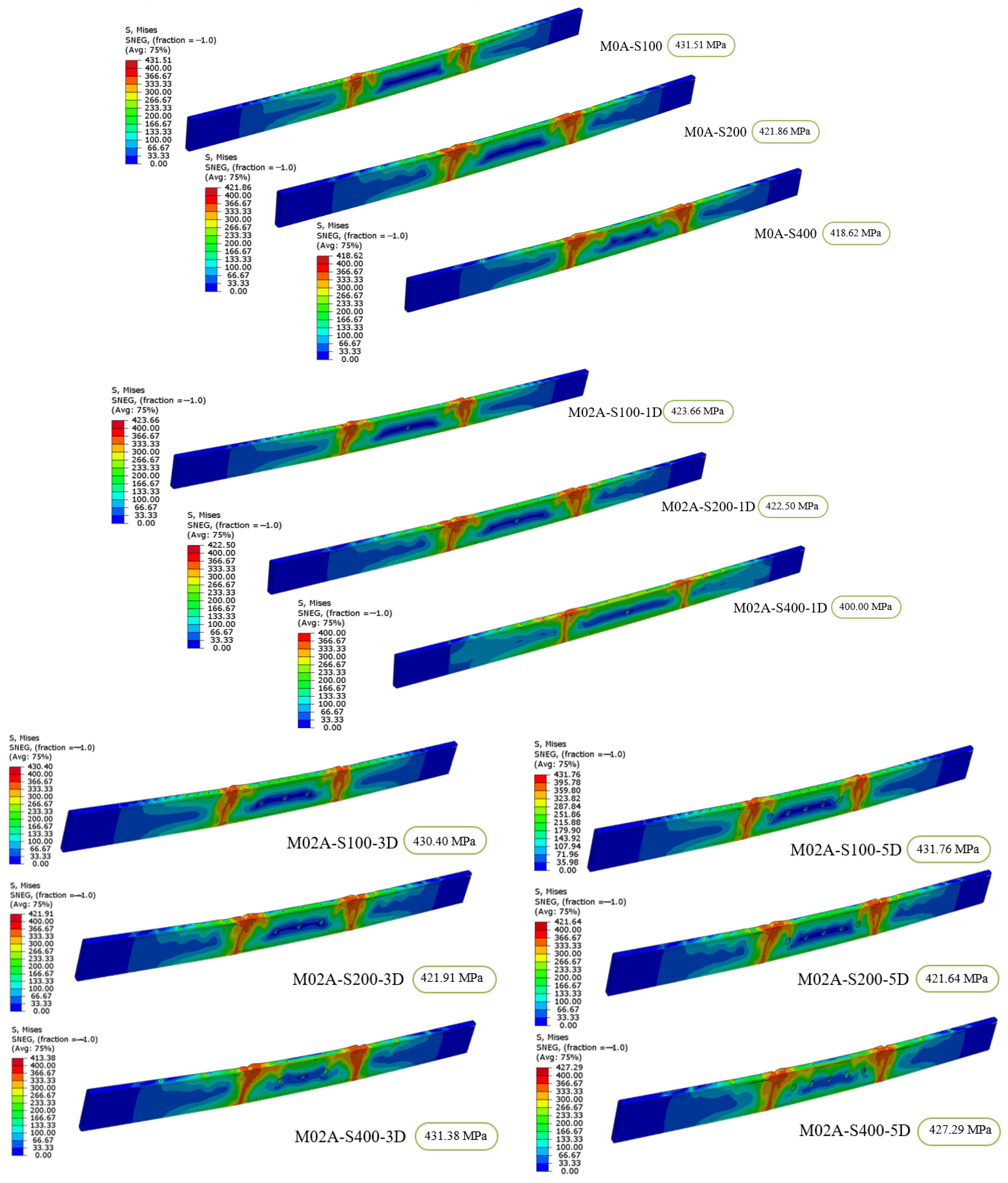
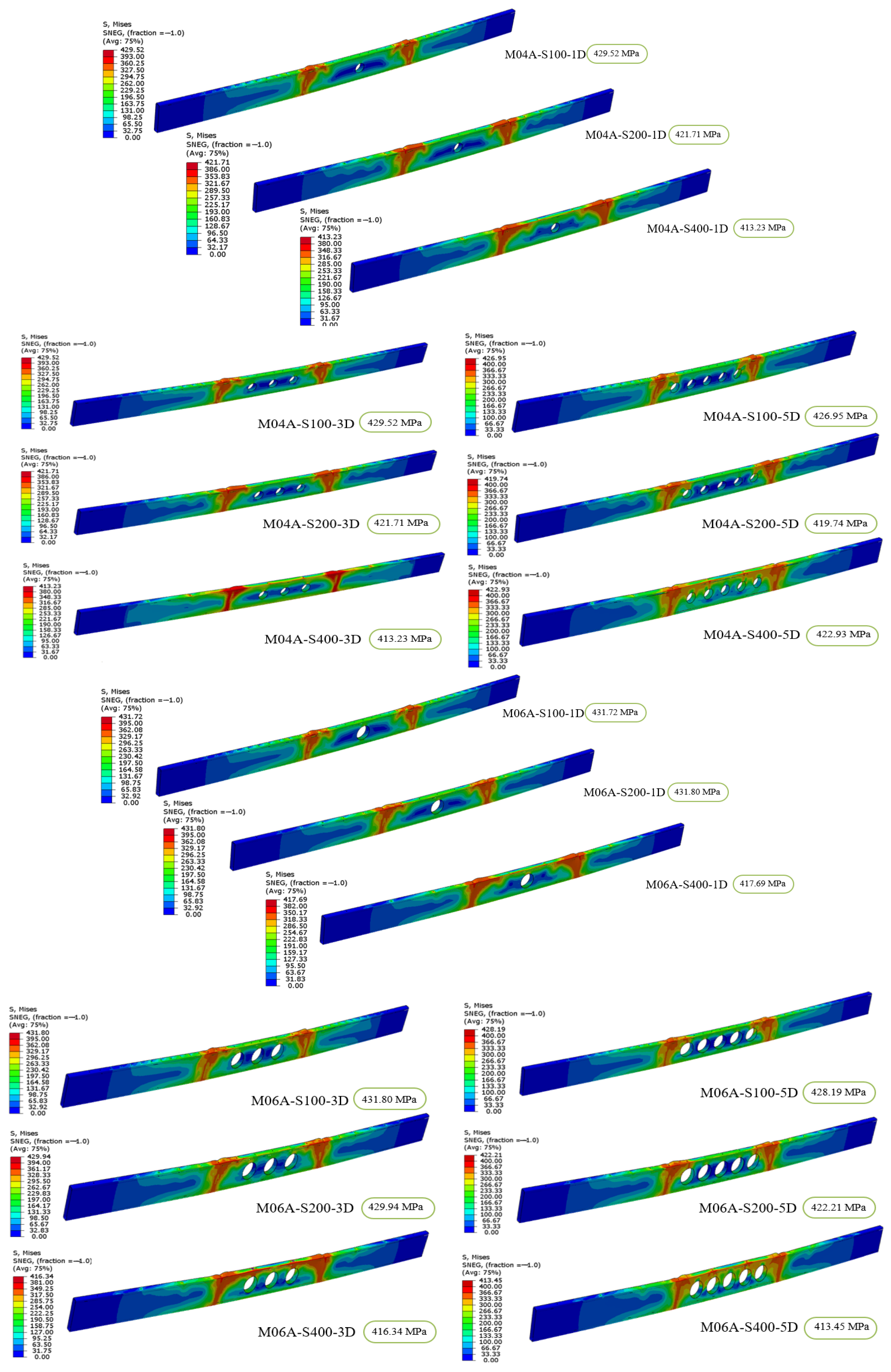
5.1. Von Mises Stress
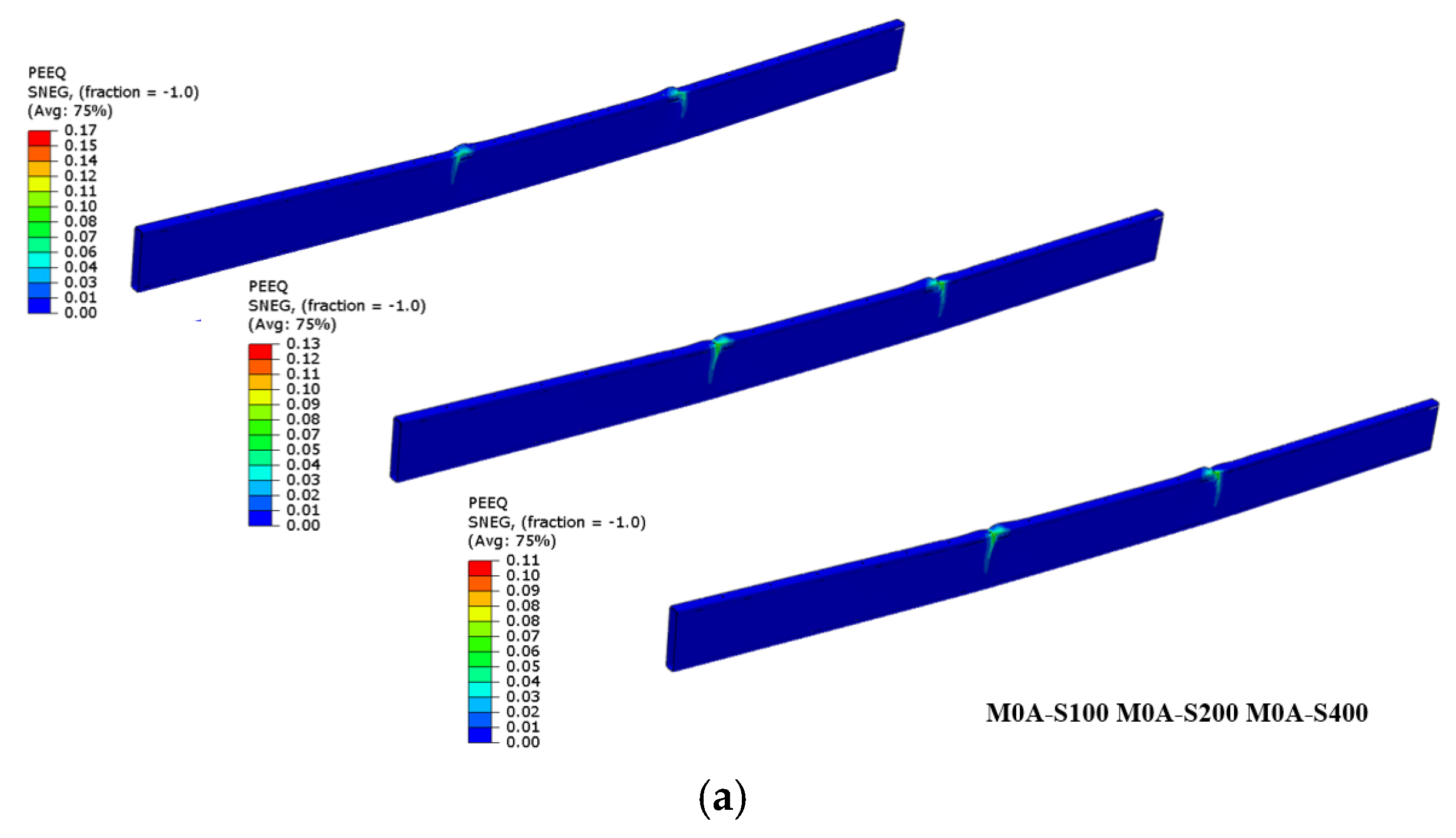
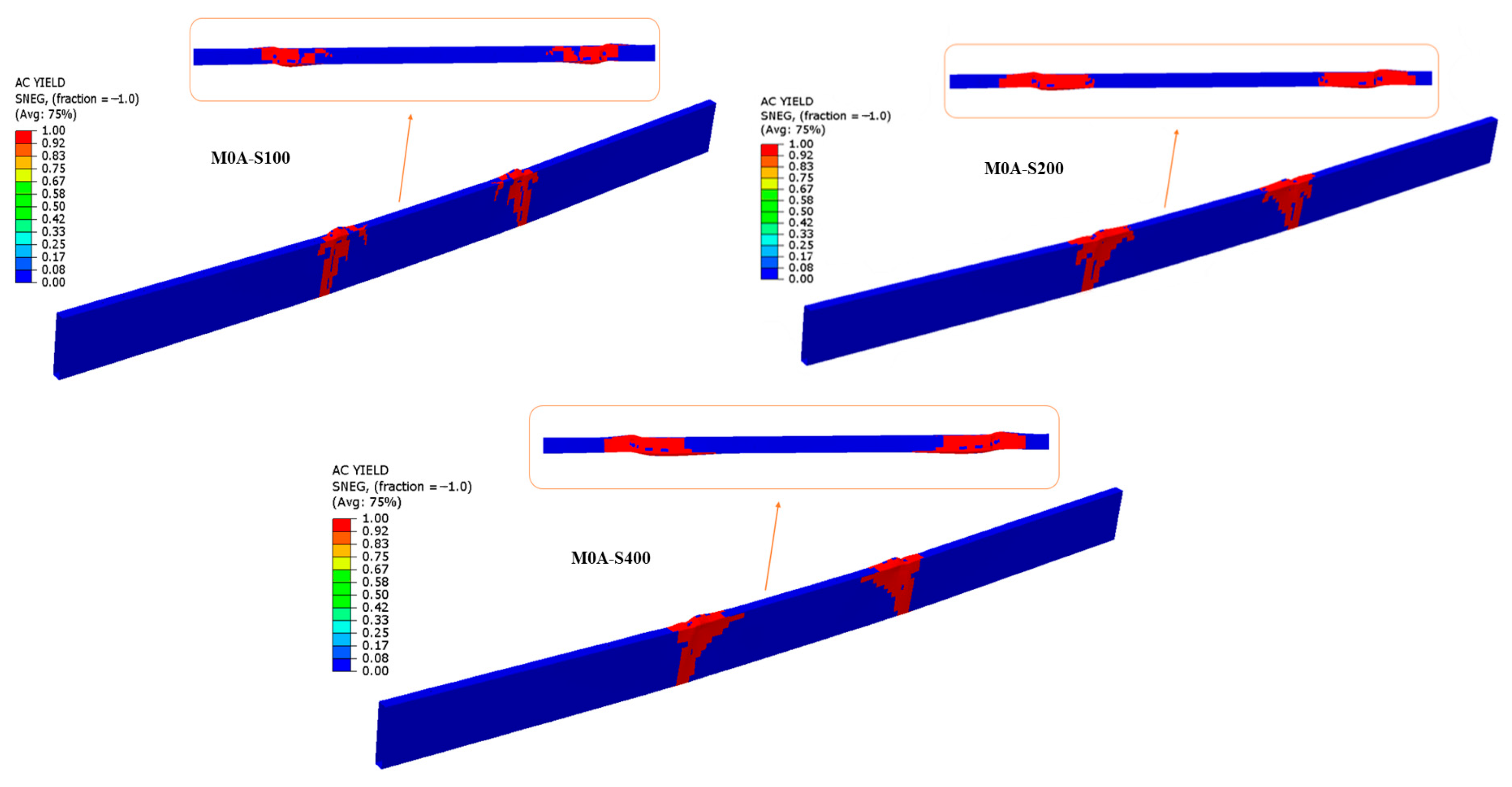
5.2. PEEQ Values and Yield Behavior
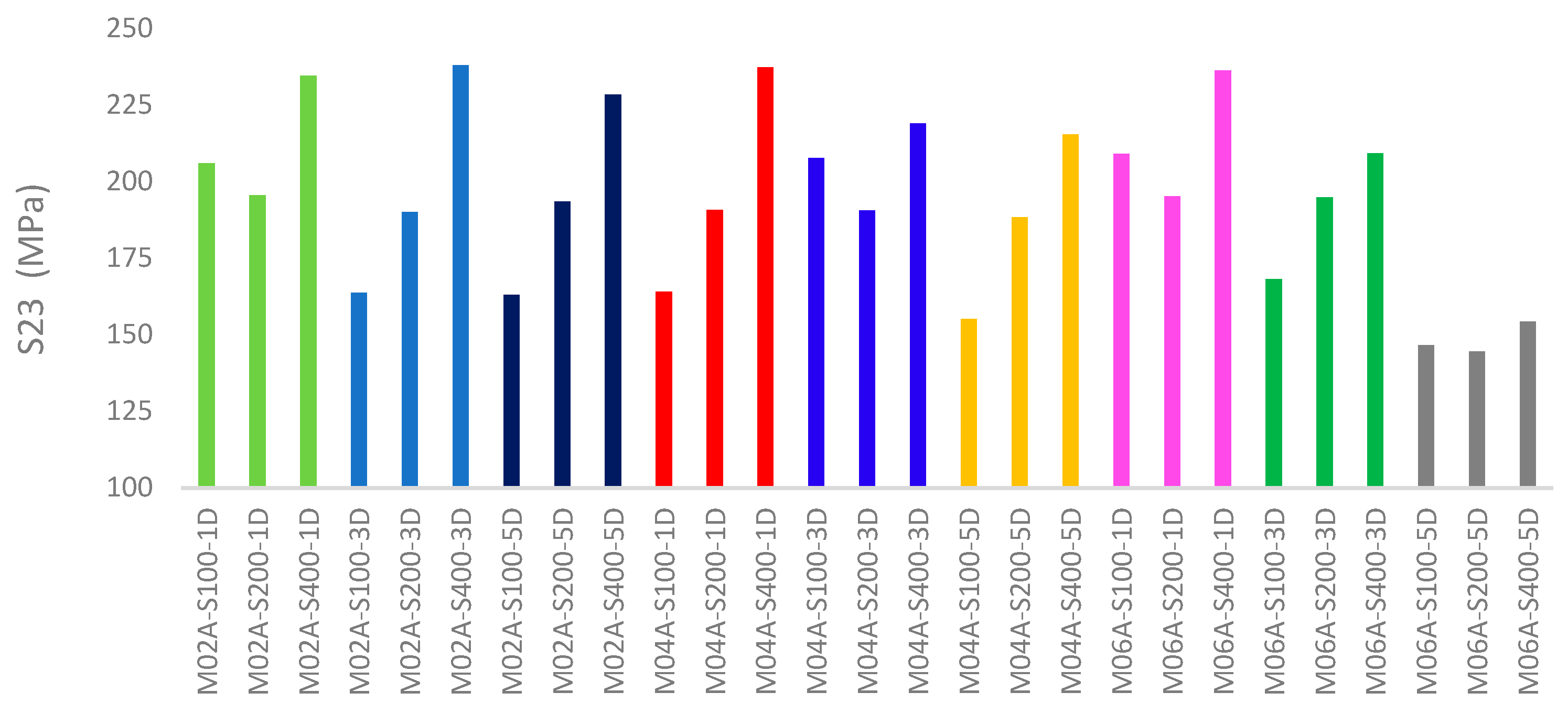
5.3. Shear Stress
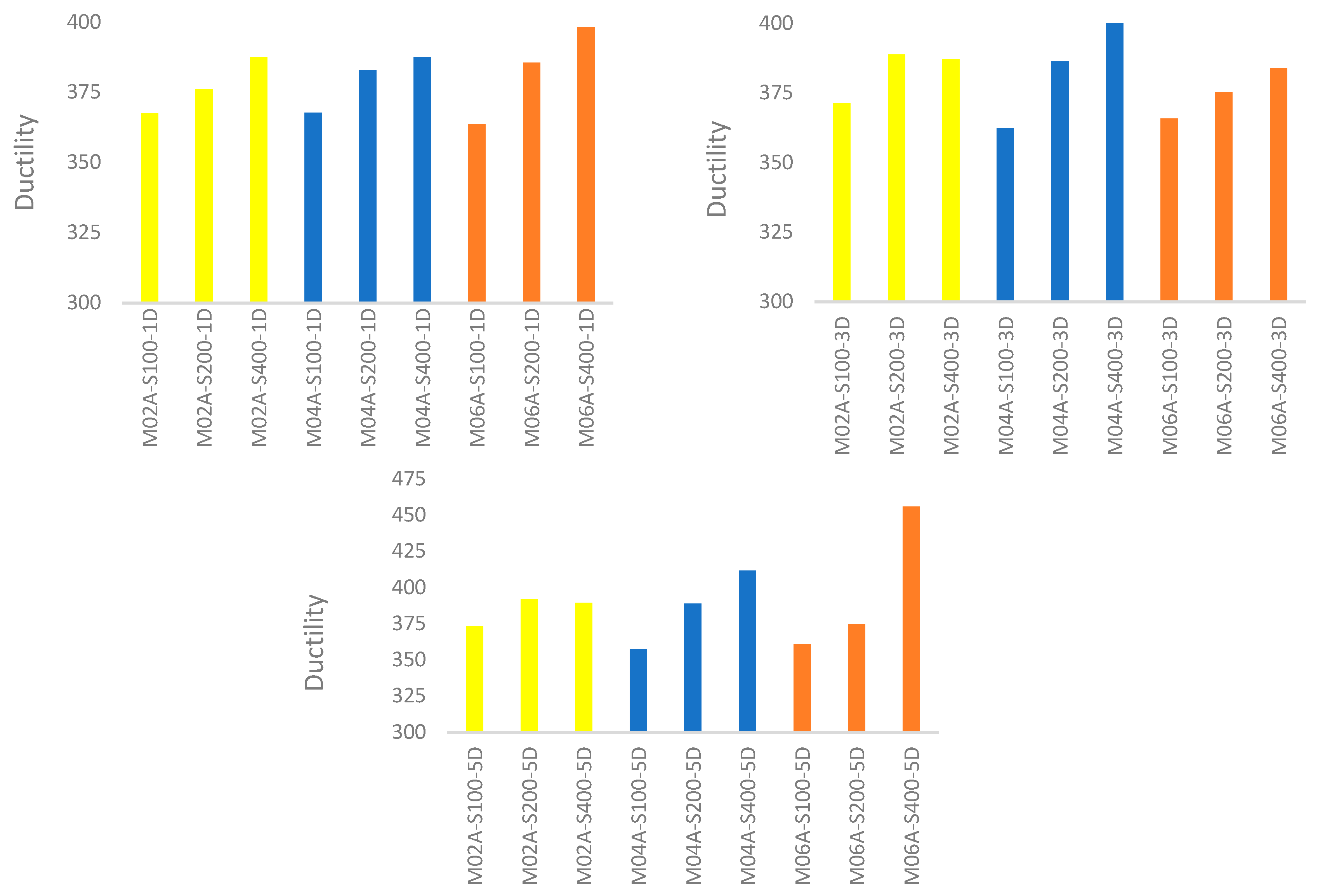
5.4. Ductility
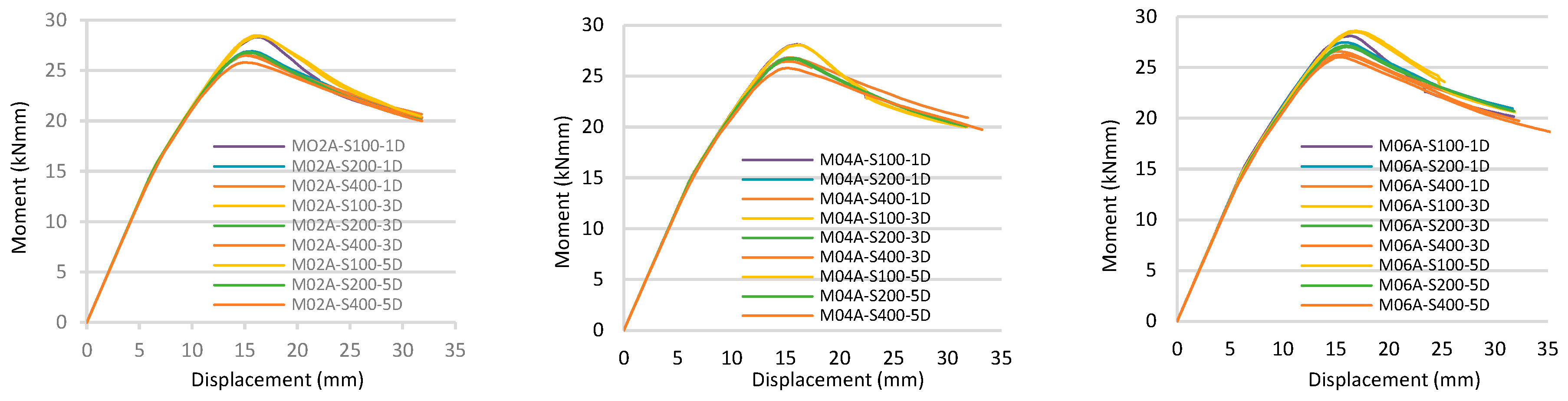
5.5. Moment–Displacement Graphs
6. Moment Estimation of Statistical Evaluation
7. Conclusions
- An increase in the spacing of the self-drilling screw resulted in significant changes in the Von Mises stress values within the element, whereas an increase in the number of holes in the web led to relatively minor variations in stress.
- In the M0A, M02A, M04A, and M06A series, it was observed that variations in the a/d ratio had an impact of less than 2% on the stress distribution within the cross-section. These results indicate that screw spacing has a more pronounced effect on the stress values in the element compared to the a/d ratio.
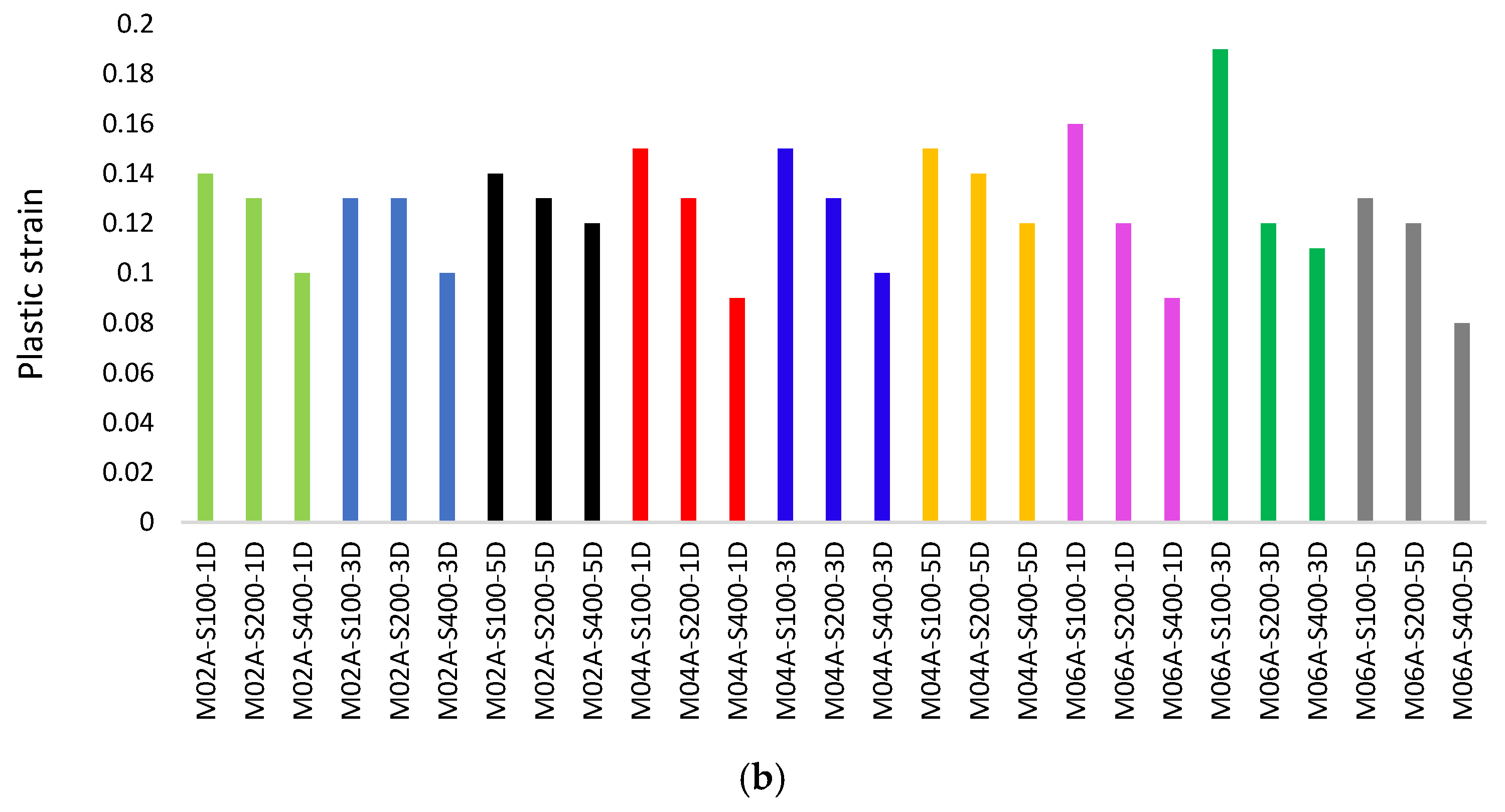
- Changes in PEEQ values based on screw spacing and hole configurations were minimal in elements with S100 and S200 screw spacing, whereas variations ranged from 10% to 33% for the S400 spacing. Additionally, as the a/d ratio increased, the PEEQ ratio exhibited an average variation of approximately 10% across the S100, S200, and S400 series.
- An examination of the models used in this study reveals that plastic hinges tend to concentrate in the regions subjected to loading.
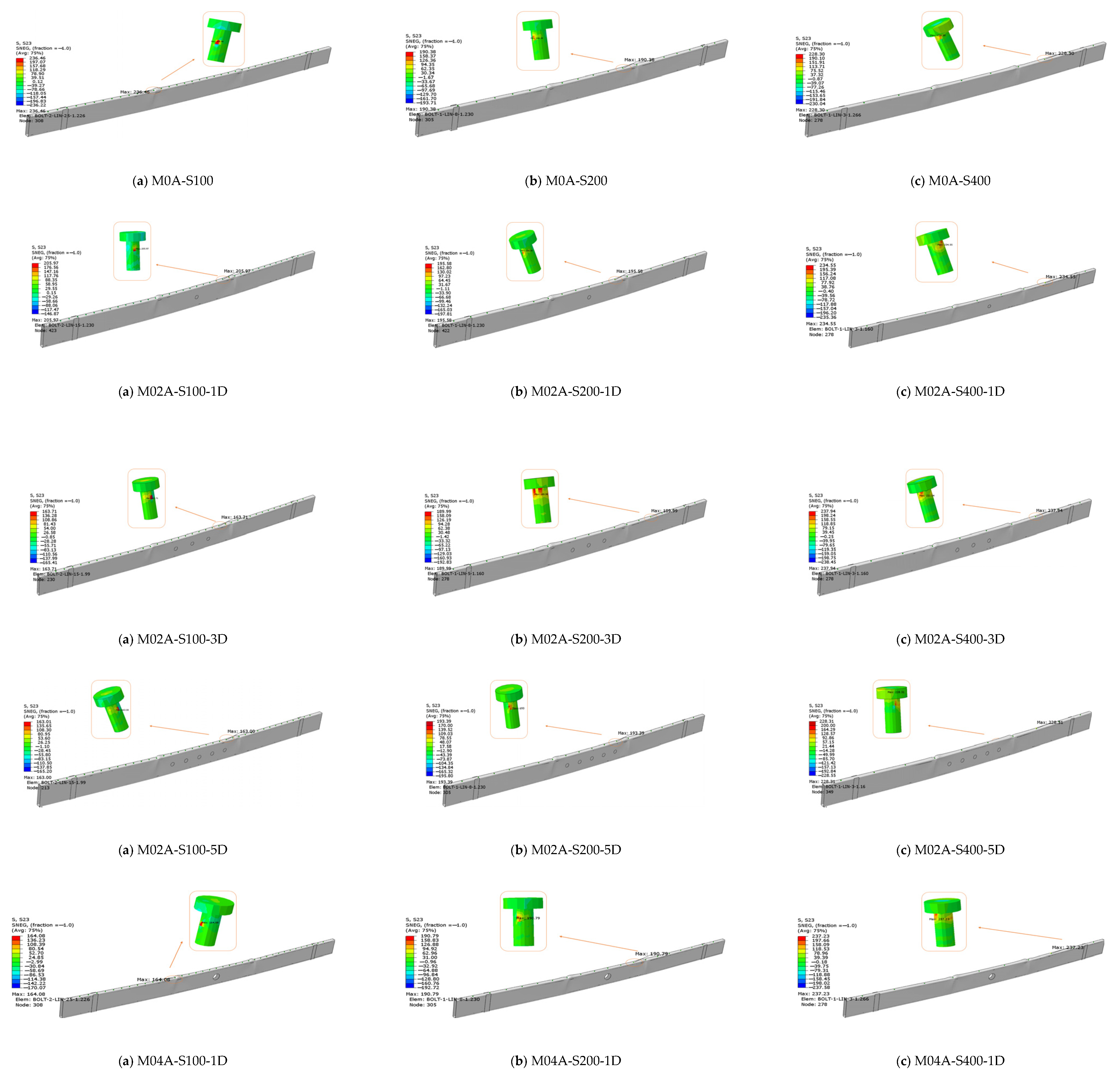
- In the M02A, M04A, and M06A series, as the spacing between the smart screws increases, the S23 stress value in the smart screws also increases. Conversely, as the a/d ratio increases in these series, the S23 stress values decrease. An examination of the models used in the study indicates that S23 stress values vary inversely with the Von Mises and PEEQ values.
- In the model series analyzed in the study, an increase in screw spacing led to a 3.5% reduction in ductility in the M0A series, while the M02A series exhibited an increase in ductility ranging from 4% to 5%. The M04A series showed increases between 5% and 13%, and the M06A series demonstrated increases ranging from 5% to 20%.
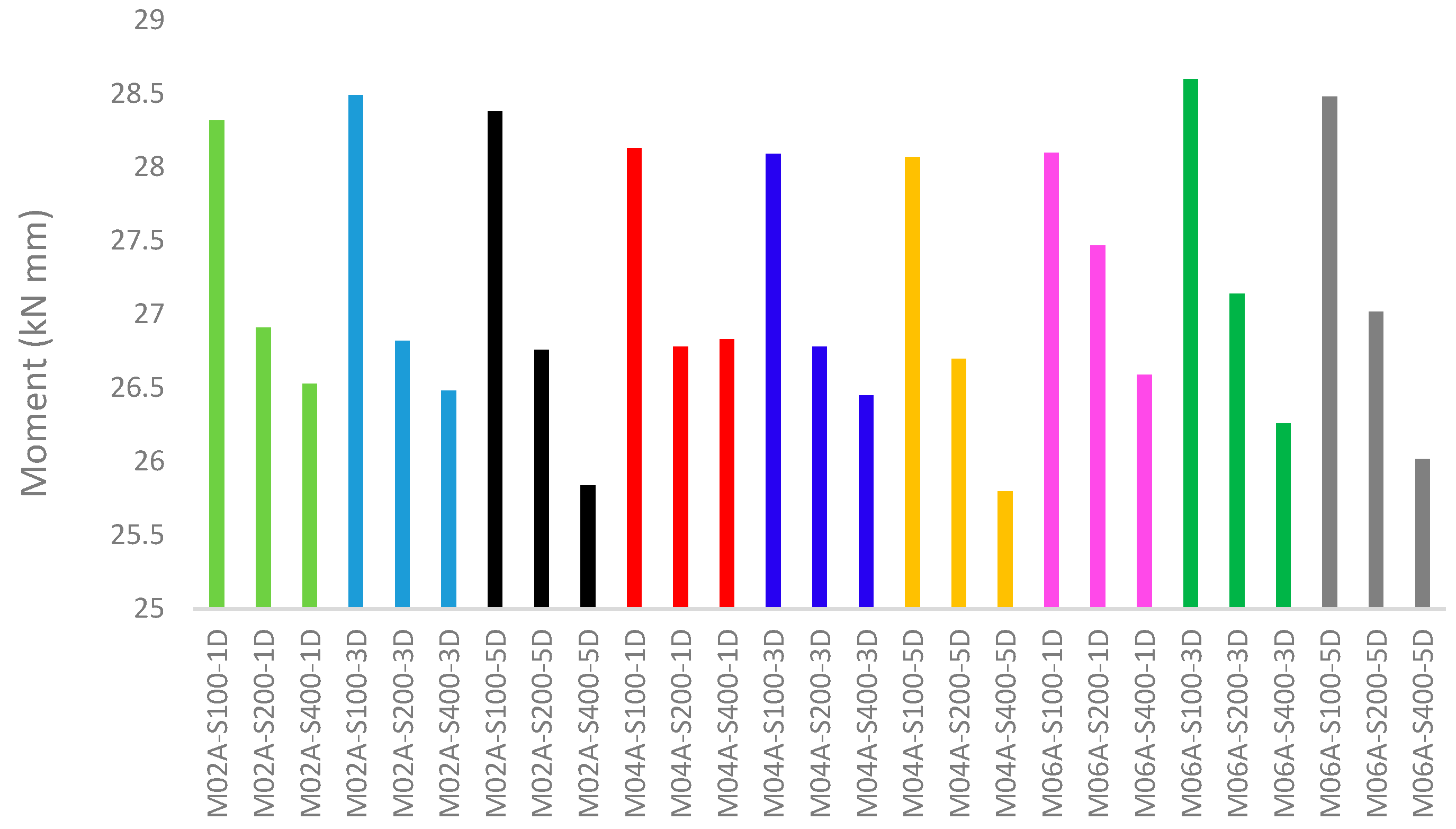
- In the M02A, M04A, and M06A series, as the spacing between the smart screws increases, the maximum moment capacity decreases by varying amounts in the range of 5% to 10%. It was observed that changes in the a/d ratio had an impact of less than 2% on the maximum moment values in the M02A, M04A, and M06A series. Similarly, increases in the number of web holes in these series resulted in a variation of less than 2% in the maximum moment values within the elements.
- Increasing screw spacings led to a reduction in estimated moment capacity across all screw spacing configurations, with the most significant error deviations observed at the 200 mm spacing. This indicates reduced structural stiffness and decreased prediction accuracy. In contrast, the 400 mm spacing provided more stable estimations with lower variance.
- Increasing the number of holes from 1 to 3 results in an approximate reduction of 7% to 10% in the numerical moment capacity. This decrease is primarily attributed to the loss of effective cross-sectional area and the stress concentrations around the holes, clearly demonstrating the negative impact of higher hole numbers on flexural performance.
- The numerical results demonstrate that increasing the number of holes leads to a decrease in moment capacity due to the reduction in effective cross-sectional area and an increase in local stress concentrations. Additionally, a smaller screw distance generally results in higher moment capacities, as closer screw spacing enhances the composite action and stiffness of the built-up sections. Conversely, larger screw distances slightly reduce the moment capacity, especially when combined with a higher number of holes. These findings highlight the combined effect of connection detailing and web perforations on the flexural behavior of the sections.
- Considering the design conditions, it was found that a screw spacing of 200 mm provides an optimal design. In lightweight steel beam elements, the number of holes in the web was not identified as a highly influential parameter on the bending behavior; however, it is recommended that such modifications be made as necessary.
8. Recommendations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, H.; Sui, L.; Liu, X.; Liang, S.; Zhou, T. Shear-slip constitutive model of screw-fastened connections and application in numerical analysis of built-up back-to-back cold-formed steel columns. Thin-Walled Struct. 2023, 186, 110710. [Google Scholar] [CrossRef]
- Li, Y.; Yao, X. Shear behavior of screw connections for cold-formed thin-walled steel structures. Thin-Walled Struct. 2010, 48, 897–906. [Google Scholar]
- Yan, S.; Young, B. Screwed connections of thin sheet steels at elevated temperatures—Part I: Steady state tests. Eng. Struct. 2012, 35, 234–243. [Google Scholar] [CrossRef]
- Moen, C.D.; Padilla-Llano, D.A.; Corner, S.; Ding, C. Towards Load-Deformation Models for Screw-Fastened Cold-Formed Steel-to-Steel Shear Connections. In Proceedings of the International Specialty Conference on Cold-Formed Steel Structures, St. Louis, MO, USA, 5–6 November 2014; p. 6. Available online: https://scholarsmine.mst.edu/isccss/22iccfss/session10/6 (accessed on 1 June 2024).
- Huynh, M.T.; Pham, C.H.; Hancock, G.J. On the finite element modeling of the screwed connections of cold-formed steel. In Congrès International de Géotechnique-Ouvrages-Structures; Springer: Singapore, 2017; pp. 224–232. [Google Scholar] [CrossRef]
- Roy, K.; Lau, H.H.; Ting, T.C.H.; Masood, R.; Kumar, A.; Lim, J.B. Experiments and finite element modelling of screw pattern of self-drilling screw connections for high strength cold-formed steel. Thin-Walled Struct. 2019, 145, 106393. [Google Scholar] [CrossRef]
- Chen, W.; Ye, J.; Zhao, M. Steady- and transient-state response of cold-formed steel-to-steel screwed connections at elevated temperatures. J. Constr. Steel Res. 2018, 144, 13–20. [Google Scholar] [CrossRef]
- American Iron and Steel Institute (AISI). AISI S240, North American Standard for Cold-Formed Steel Structural Framing; AISI: Washington, DC, USA, 2015. [Google Scholar]
- Chung, K.F.; Lau, L. Experimental investigation on bolted moment connections among cold-formed steel members. Eng. Struct. 1999, 21, 898–911. [Google Scholar] [CrossRef]
- Zhao, J.; Sun, K.; Yu, C.; Wang, J. Tests and direct strength design on cold-formed steel channel beams with web holes. Eng. Struct. 2019, 184, 434–446. [Google Scholar] [CrossRef]
- Chen, B.; Roy, K.; Uzzaman, A.; Lim, J.B. Moment capacity of cold-formed channel beams with edge-stiffened web holes, un-stiffened web holes and plain webs. Thin-Walled Struct. 2020, 157, 107070. [Google Scholar] [CrossRef]
- Dissanayake, D.M.M.P.; Poologanathan, K.; Gunalan, S.; Tsavdaridis, K.D.; Wanniarachchi, K.S.; Nagaratnam, B. Bending-shear interaction of cold-formed stainless steel lipped channel sections. Structures 2021, 30, 1042–1055. [Google Scholar] [CrossRef]
- Fang, Z.; Roy, K.; Uzzaman, A.; Lim, J.B. Numerical simulation and proposed design rules of cold-formed stainless steel channels with web holes under interior-one-flange loading. Eng. Struct. 2022, 252, 113566. [Google Scholar] [CrossRef]
- Wang, L.; Li, J.; Luo, C.; Cao, X.; Wang, H. Experimental and numerical study on the shear behavior of web perforated cold-formed steel beams. Structures 2022, 45, 2117–2136. [Google Scholar] [CrossRef]
- Öztürk, F.; Mojtabaei, S.M.; Şentürk, M.; Pul, S.; Hajirasouliha, I. Buckling behaviour of cold-formed steel sigma and lipped channel beam–column members. Thin-Walled Struct. 2022, 173, 108963. [Google Scholar] [CrossRef]
- British Standards Institution. BS EN 10002-1:2001 Tensile Testing of Metallic Materials—Method of Test at Ambient Temperature; BSI: London, UK, 2001. [Google Scholar]
- Aktepe, R.; Erkal, B.G. State-of-the-art review on measurement techniques and numerical modeling of geometric imperfections in cold-formed steel members. J. Constr. Steel Res. 2023, 207, 107942. [Google Scholar] [CrossRef]
- Aktepe, R.; Erkal, B.G. Prediction of the initial geometric imperfection magnitudes for numerical modeling of cold-formed steel channel sections. Structures 2024, 60, 105869. [Google Scholar] [CrossRef]
- Mei, Y.; Cui, Y.; Ma, C.; Sun, Y.; Su, A. Tests, numerical simulations and design of G550 high strength cold-formed steel lipped channel section columns failing by interactive buckling. Thin-Walled Struct. 2023, 192, 111172. [Google Scholar] [CrossRef]
- Selvam, J.; Vajravelu, A.; Nagapan, S.; Arumugham, B.K. Analyzing the Flexural Performance of Cold-Formed Steel Sigma Section Using ABAQUS Software. Sustainability 2023, 15, 4085. [Google Scholar] [CrossRef]
- Samuel, J.; Nair, S.R.; Joanna, P.S.; Gurupatham, B.G.A.; Roy, K.; Lim, J.B.P. Composite Cold-Formed Steel Beams with Diagonal Rebars for Earthquake-Resistant Buildings. Materials 2023, 16, 3002. [Google Scholar] [CrossRef]
- Liu, R.-G.; Xu, B.; Zhang, F.; Peng, S.-N.; Yang, C.; Chen, M.-W.; Chen, S.-H.; Xie, M.-Z. Experimental Study of the Bending Performance of Cold-Formed Steel Channel Beams Considering the Corner Hardening Effect. Buildings 2023, 13, 2149. [Google Scholar] [CrossRef]
- Chen, T.; Chen, Z.; Liu, J.; Zhang, A. Bending Properties of Cold-Formed Thin-Walled Steel/Fast-Growing Timber Composite I-Beams. Forests 2024, 15, 857. [Google Scholar] [CrossRef]
- Sato, A.; Kitagawa, H. Seismic Design Procedure for Low-Rise Cold-Formed Steel–Special Bolted Moment Frames. Appl. Sci. 2024, 14, 4520. [Google Scholar] [CrossRef]
- Dubina, D.; Ungureanu, V. Effect of imperfections on numerical simulation of instability behaviour of cold-formed steel members. Thin-Walled Struct. 2002, 40, 239–262. [Google Scholar] [CrossRef]
- Peköz, T.; Schafer, B.W. Computational Modeling of Cold-Formed Steel: Characterizing Geometric Imperfections and Residual Stresses. J. Constr. Steel Res. 1998, 47, 193–210. [Google Scholar] [CrossRef]
- Dassault Systèmes Simulia Corp. ABAQUS/CAE, version 6.12; Dassault Systèmes: Providence, RI, USA, 2016. [Google Scholar]
- Wang, W.; Roy, K.; Rezaeian, H.; Fang, Z.; Lim, J.B. Experimental and numerical investigation of cold-formed steel telescopic studs under compression. J. Constr. Steel Res. 2024, 212, 108279. [Google Scholar] [CrossRef]
- Abanoz, E. Effect of Flexural Behavior of Circular Holes Opened in the Body of Cold-Formed Beams: Finite Element Analyzes. Master’s Thesis, Science Institute-Sakarya University, Sakarya, Turkiye, 2024. [Google Scholar]
- Sayed, A.M. Numerical study of the effects of web openings on the load capacity of steel beams with corrugated webs. J. Constr. Steel Res. 2022, 196, 107418. [Google Scholar] [CrossRef]
- Sayed, A.M.; Aljarbou, M.H. Numerical study of the effect of circular openings in the upper surface of rectangular hollow flange steel beams on the sectional moment capacity. Results Eng. 2024, 24, 103620. [Google Scholar] [CrossRef]
- Chen, W.F.; Lui, E.M. Principles of Structural Design; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar] [CrossRef]
- Ding, B.; Zhao, Y.; Huang, Z.; Cai, L.; Wang, N. Tensile bearing capacity for bolted spherical joints with different screwing depths of high-strength bolts. Eng. Struct. 2020, 225, 111255. [Google Scholar] [CrossRef]
- Coelho, A.M.G.; Bijlaard, F.S. Experimental behaviour of high strength steel end-plate connections. J. Constr. Steel Res. 2007, 63, 1228–1240. [Google Scholar] [CrossRef]
- EN 1993-1-8; Eurocode 3: Design of Steel Structures—Part 1–8: Design of Joints. European Committee for Standardization: Brussels, Belgium, 2005.
- Federal Emergency Management Agency (FEMA). FEMA 350, Recommended Seismic Design Criteria for New Steel Moment-Frame Buildings; FEMA: Washington, DC, USA, 2000.


 |  | Coupon | Young’s Modulus (MPa) | Yield Stress (MPa) | Ultimate Strength (MPa) | Poisson’s Ratio |
| Corner Coupon | 210,052 | 363.4 | 431.8 | 0.3 | ||
| Web Coupon | 192,057 | 332.8 | 420.5 | 0.3 | ||
| G500- Self-drilling screws | 208,000 | 500 | 520 |
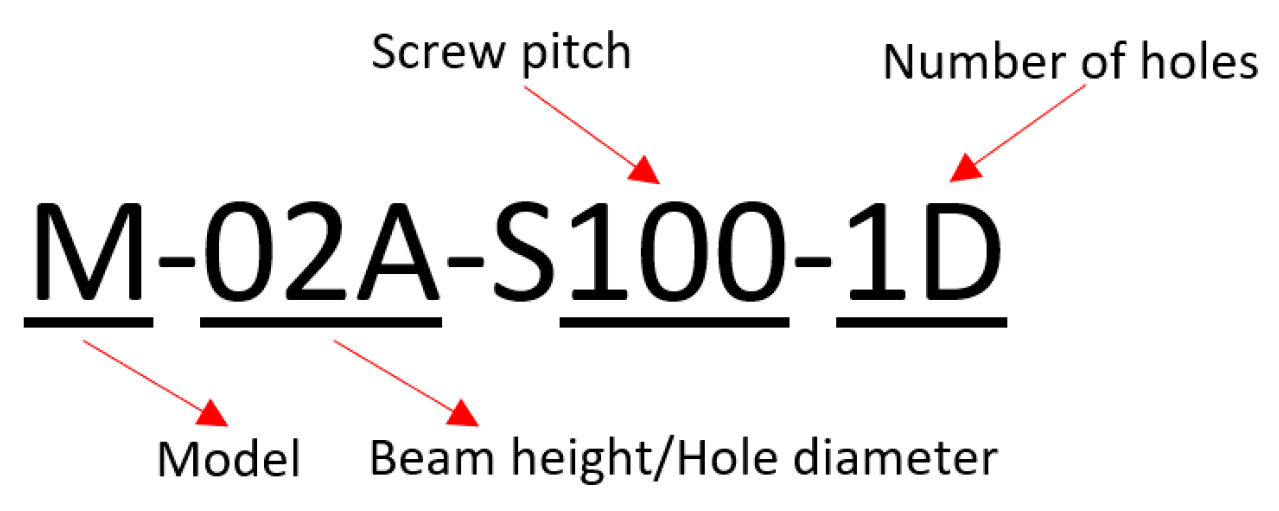
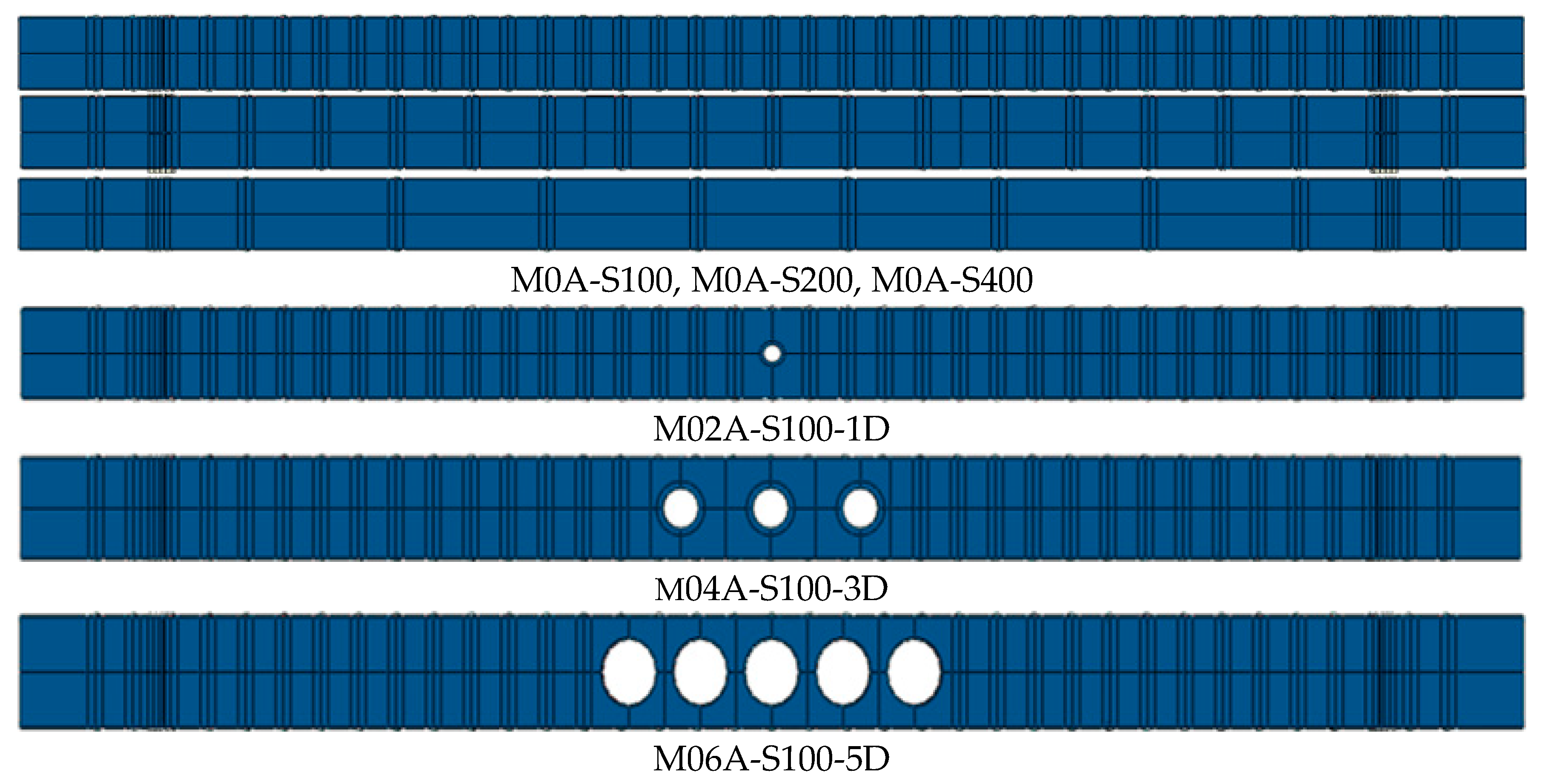
| Model | a/d | Number of Web Holes | Web Diameter (mm) | Diameter (mm) | Spacing (mm) | Number of Screws (For a Single Head of a Built-Up Box Profile) |
|---|---|---|---|---|---|---|
| M0A-S100 | - | - | - | 3.14 | 100 | 37 |
| M0A-S200 | - | - | - | 200 | 19 | |
| M0A-S400 | - | - | - | 400 | 10 | |
| M02A-S100-1D | 0.2 | 1 | 48 | 100 | 37 | |
| M02A-S200-1D | 0.2 | 1 | 48 | 200 | 19 | |
| M02A-S400-1D | 0.2 | 1 | 48 | 400 | 10 | |
| M02A-S100-3D | 0.2 | 3 | 48 | 100 | 37 | |
| M02A-S200-3D | 0.2 | 3 | 48 | 200 | 19 | |
| M02A-S400-3D | 0.2 | 3 | 48 | 400 | 10 | |
| M02A-S100-5D | 0.2 | 5 | 48 | 100 | 37 | |
| M02A-S200-5D | 0.2 | 5 | 48 | 200 | 19 | |
| M02A-S400-5D | 0.2 | 5 | 48 | 400 | 10 | |
| M04A-S100-1D | 0.4 | 1 | 96 | 100 | 37 | |
| M04A-S200-1D | 0.4 | 1 | 96 | 200 | 19 | |
| M04A-S400-1D | 0.4 | 1 | 96 | 400 | 10 | |
| M04A-S100-3D | 0.4 | 3 | 96 | 100 | 37 | |
| M04A-S200-3D | 0.4 | 3 | 96 | 200 | 19 | |
| M04A-S400-3D | 0.4 | 3 | 96 | 400 | 10 | |
| M04A-S100-5D | 0.4 | 5 | 96 | 100 | 37 | |
| M04A-S200-5D | 0.4 | 5 | 96 | 200 | 19 | |
| M04A-S400-5D | 0.4 | 5 | 96 | 400 | 10 | |
| M06A-S100-1D | 0.6 | 1 | 96 | 100 | 37 | |
| M06A-S200-1D | 0.6 | 1 | 96 | 200 | 19 | |
| M06A-S400-1D | 0.6 | 1 | 96 | 400 | 10 | |
| M06A-S100-3D | 0.6 | 3 | 96 | 100 | 37 | |
| M06A-S200-3D | 0.6 | 3 | 96 | 200 | 19 | |
| M06A-S400-3D | 0.6 | 3 | 96 | 400 | 10 | |
| M06A-S100-5D | 0.6 | 5 | 96 | 100 | 37 | |
| M06A-S200-5D | 0.6 | 5 | 96 | 200 | 19 | |
| M06A-S400-5D | 0.6 | 5 | 96 | 400 | 10 |
| Model | Von Mises Stress (MPa) | Equivalent Plastic Deformation | S23 Stress at Self-Drilling Screws— (MPa) | Toughness | Ductility | Moment (kN.mm) |
|---|---|---|---|---|---|---|
| M0A-S100 | 431.51 | 0.17 | 236.46 | 637.37 | 378.24 | 28.29 |
| M0A-S200 | 421.86 | 0.13 | 190.38 | 617.65 | 388.24 | 26.77 |
| M0A-S400 | 418.62 | 0.11 | 228.3 | 607.62 | 392.11 | 26.48 |
| M02A-S100-1D | 423.66 | 0.14 | 205.97 | 628.46 | 367.43 | 28.32 |
| M02A-S200-1D | 422.5 | 0.13 | 195.58 | 620.5 | 376.15 | 26.91 |
| M02A-S400-1D | 400 | 0.1 | 234.55 | 613.3 | 387.49 | 26.53 |
| M02A-S100-3D | 430.4 | 0.13 | 163.71 | 634.76 | 371.21 | 28.49 |
| M02A-S200-3D | 421.91 | 0.13 | 189.99 | 616.23 | 388.83 | 26.82 |
| M02A-S400-3D | 413.38 | 0.1 | 237.94 | 609.44 | 387.19 | 26.48 |
| M02A-S100-5D | 431.76 | 0.14 | 163 | 637.38 | 372.97 | 28.38 |
| M02A-S200-5D | 427.29 | 0.13 | 193.39 | 617.68 | 391.75 | 26.76 |
| M02A-S400-5D | 421.64 | 0.12 | 228.31 | 607.89 | 389.42 | 25.84 |
| M04A-S100-1D | 429.52 | 0.15 | 164.08 | 624.46 | 367.68 | 28.13 |
| M04A-S200-1D | 421.71 | 0.13 | 190.79 | 618.68 | 382.72 | 26.78 |
| M04A-S400-1D | 413.23 | 0.09 | 237.23 | 613.71 | 387.45 | 26.83 |
| M04A-S100-3D | 429.67 | 0.15 | 207.68 | 627.17 | 362.37 | 28.09 |
| M04A-S200-3D | 421.82 | 0.13 | 190.52 | 618.38 | 386.32 | 26.78 |
| M04A-S400-3D | 375.49 | 0.1 | 219.04 | 285.39 | 403.47 | 26.45 |
| M04A-S100-5D | 426.95 | 0.15 | 155.13 | 617.15 | 357.54 | 28.07 |
| M04A-S200-5D | 422.93 | 0.14 | 188.26 | 616.15 | 388.88 | 26.7 |
| M04A-S400-5D | 419.74 | 0.12 | 215.45 | 632.12 | 411.76 | 25.8 |
| M06A-S100-1D | 431.72 | 0.16 | 209.02 | 625.17 | 363.71 | 28.1 |
| M06A-S200-1D | 431.8 | 0.12 | 195.24 | 620.87 | 385.6 | 27.47 |
| M06A-S400-1D | 417.69 | 0.09 | 236.21 | 613.71 | 398.32 | 26.59 |
| M06A-S100-3D | 431.8 | 0.19 | 168.21 | 646.06 | 365.81 | 28.6 |
| M06A-S200-3D | 429.94 | 0.12 | 194.78 | 619.37 | 375.34 | 27.14 |
| M06A-S400-3D | 416.34 | 0.11 | 209.27 | 620.18 | 383.76 | 26.26 |
| M06A-S100-5D | 428.19 | 0.13 | 146.58 | 639.59 | 360.77 | 28.48 |
| M06A-S200-5D | 422.21 | 0.12 | 144.53 | 618.95 | 374.62 | 27.02 |
| M06A-S400-5D | 413.45 | 0.08 | 154.27 | 672.25 | 455.85 | 26.02 |
| M02A | Screw Distance | Hole Number | Numerical Moment | Estimated Moment | Error (e) | Mean Error | Standard Deviation | E.Q. Distribution Standard Deviation | T Table | Lower Limit | Upper Limit |
| 100 | 1 | 28.62 | 28.617 | 0.003 | −1.18E-15 | 5.77E-03 | 4.08E-03 | 9.92E+00 | −4.05E-02 | 4.05E-02 | |
| 2 | 28.49 | 28.497 | −0.007 | ||||||||
| 3 | 28.38 | 28.377 | 0.003 | ||||||||
| 200 | 1 | 29.61 | 26.905 | 0.005 | −2.38E-15 | 8.66E-03 | 6.12E-03 | 9.92E+00 | −6.08E-02 | 6.08E-02 | |
| 2 | 26.82 | 26.830 | −0.01 | ||||||||
| 3 | 26.76 | 26.755 | 0.005 | ||||||||
| 400 | 1 | 26.53 | 26.528 | 0.002 | −1.18E-15 | 2.89E-03 | 2.04E-03 | 9.92E+00 | −2.03E-02 | 2.03E-02 | |
| 2 | 26.18 | 26.183 | −0.003 | ||||||||
| 3 | 25.84 | 25.838 | 0.002 | ||||||||
| M04A | Screw Distance | Hole Number | Numerical Moment | Estimated Moment | Error (e) | Mean Error | Standard Deviation | E.Q. Distribution Standard Deviation | T Table | Lower Limit | Upper Limit |
| 100 | 1 | 28.13 | 28.127 | 0.003 | −3.55E-15 | 5.77E-03 | 4.08E-03 | 9.92E+00 | −4.05E-02 | 4.05E-02 | |
| 2 | 28.09 | 28.097 | −0.007 | ||||||||
| 3 | 28.07 | 28.067 | 0.003 | ||||||||
| 200 | 1 | 26.78 | 26.783 | −0.003 | −3.55E-15 | 5.77E-03 | 4.08E-03 | 9.92E+00 | −4.05E-02 | 4.05E-02 | |
| 2 | 26.75 | 26.743 | 0.007 | ||||||||
| 3 | 26.70 | 26.703 | −0.003 | ||||||||
| 400 | 1 | 26.83 | 26.858 | −0.028 | 0.00E+00 | 4.91E-02 | 3.47E-02 | 9.92E+00 | −3.44E-01 | 3.44E-01 | |
| 2 | 26.40 | 26.343 | 0.057 | ||||||||
| 3 | 25.80 | 25.828 | 0.028 | ||||||||
| M06A | Screw Distance | Hole Number | Numerical Moment | Estimated Moment | Error (e) | Mean Error | Standard Deviation | E.Q. Distribution Standard Deviation | T Table | Lower Limit | Upper Limit |
| 100 | 1 | 29.10 | 29.073 | 0.027 | 0.00E+00 | 4.62E-02 | 3.27E-02 | 9.92E+00 | −3.24E-01 | 3.24E-01 | |
| 2 | 28.71 | 28.763 | −0.053 | ||||||||
| 3 | 28.48 | 28.453 | 0.027 | ||||||||
| 200 | 1 | 27.47 | 27.488 | −0.018 | −2.37E-15 | 3.18E-02 | 2.25E-02 | 9.92E+00 | −2.23E-01 | 2.23E-01 | |
| 2 | 27.30 | 27.263 | 0.037 | ||||||||
| 3 | 27.02 | 27.038 | −0.018 | ||||||||
| 400 | 1 | 26.59 | 26.575 | 0.015 | −1.18E-15 | 2.60E-02 | 1.84E-02 | 9.92E+00 | −1.82E-01 | 1.82E-01 | |
| 2 | 26.26 | 26.290 | −0.030 | ||||||||
| 3 | 26.02 | 26.005 | 0.015 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yaman, Z.; Maali, M.; Abanoz, E.; Ağcakoca, E.; Sadid, M.S.; Çavuş, T.F. Investigation of Screw Layout and Hole Geometry on Cold-Formed Steel Bending Performance Using Finite Element Model and Statistical Methods. Buildings 2025, 15, 3101. https://doi.org/10.3390/buildings15173101
Yaman Z, Maali M, Abanoz E, Ağcakoca E, Sadid MS, Çavuş TF. Investigation of Screw Layout and Hole Geometry on Cold-Formed Steel Bending Performance Using Finite Element Model and Statistical Methods. Buildings. 2025; 15(17):3101. https://doi.org/10.3390/buildings15173101
Chicago/Turabian StyleYaman, Zeynep, Mahyar Maali, Ekin Abanoz, Elif Ağcakoca, Mohammad Saber Sadid, and Türker Fedai Çavuş. 2025. "Investigation of Screw Layout and Hole Geometry on Cold-Formed Steel Bending Performance Using Finite Element Model and Statistical Methods" Buildings 15, no. 17: 3101. https://doi.org/10.3390/buildings15173101
APA StyleYaman, Z., Maali, M., Abanoz, E., Ağcakoca, E., Sadid, M. S., & Çavuş, T. F. (2025). Investigation of Screw Layout and Hole Geometry on Cold-Formed Steel Bending Performance Using Finite Element Model and Statistical Methods. Buildings, 15(17), 3101. https://doi.org/10.3390/buildings15173101








