Random Wind Vibration Control of Transmission Tower-Line Systems Using Shape Memory Alloy Damper
Abstract
1. Introduction
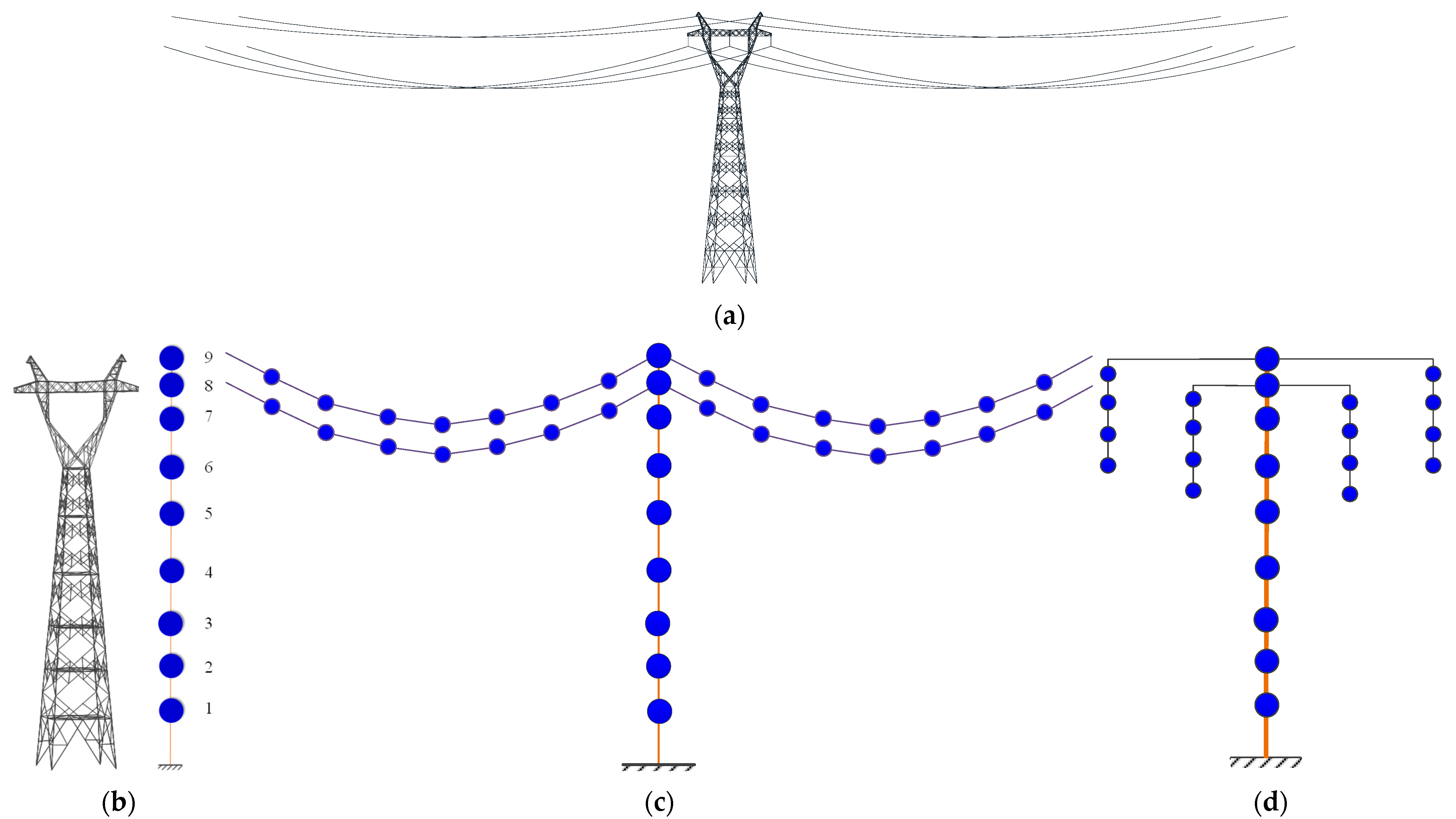
2. TTL–SMAD System Model
2.1. TTL-Coupled System Model
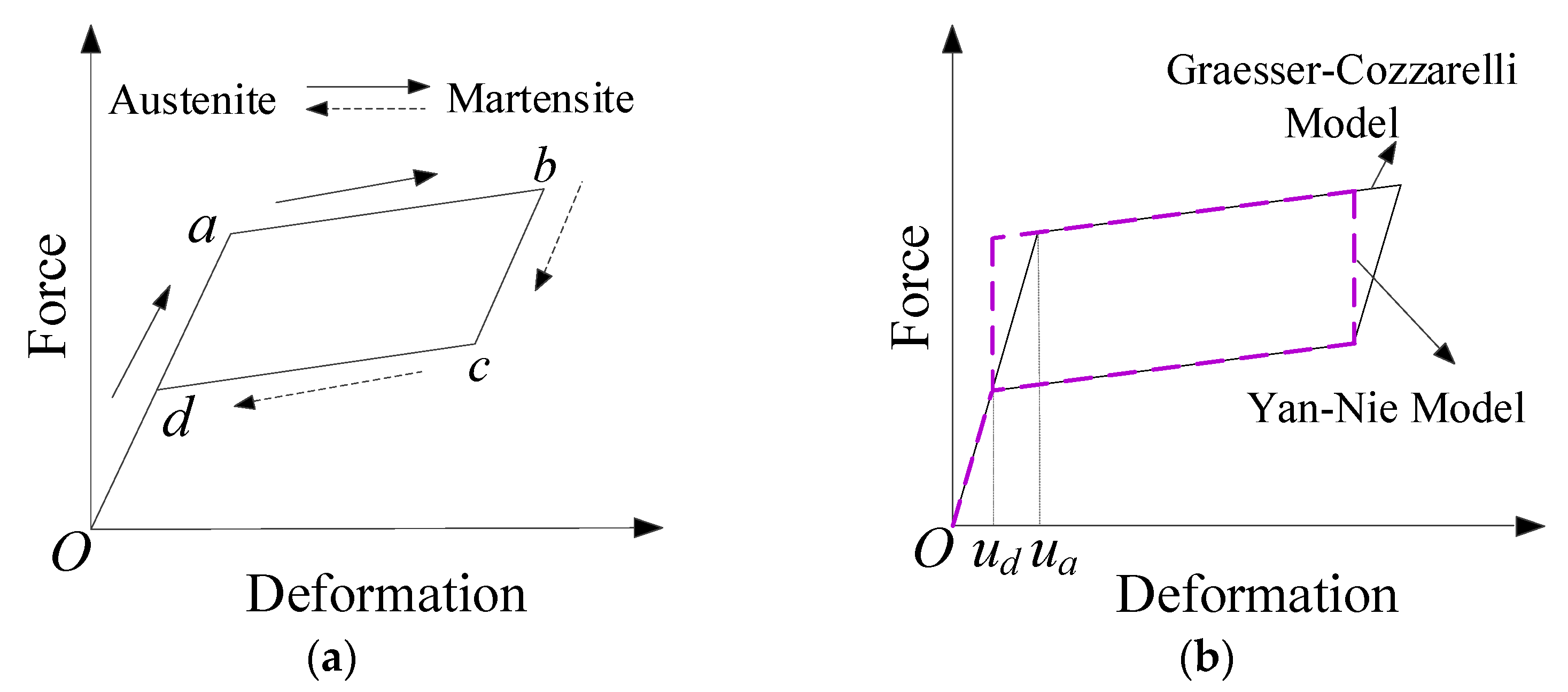
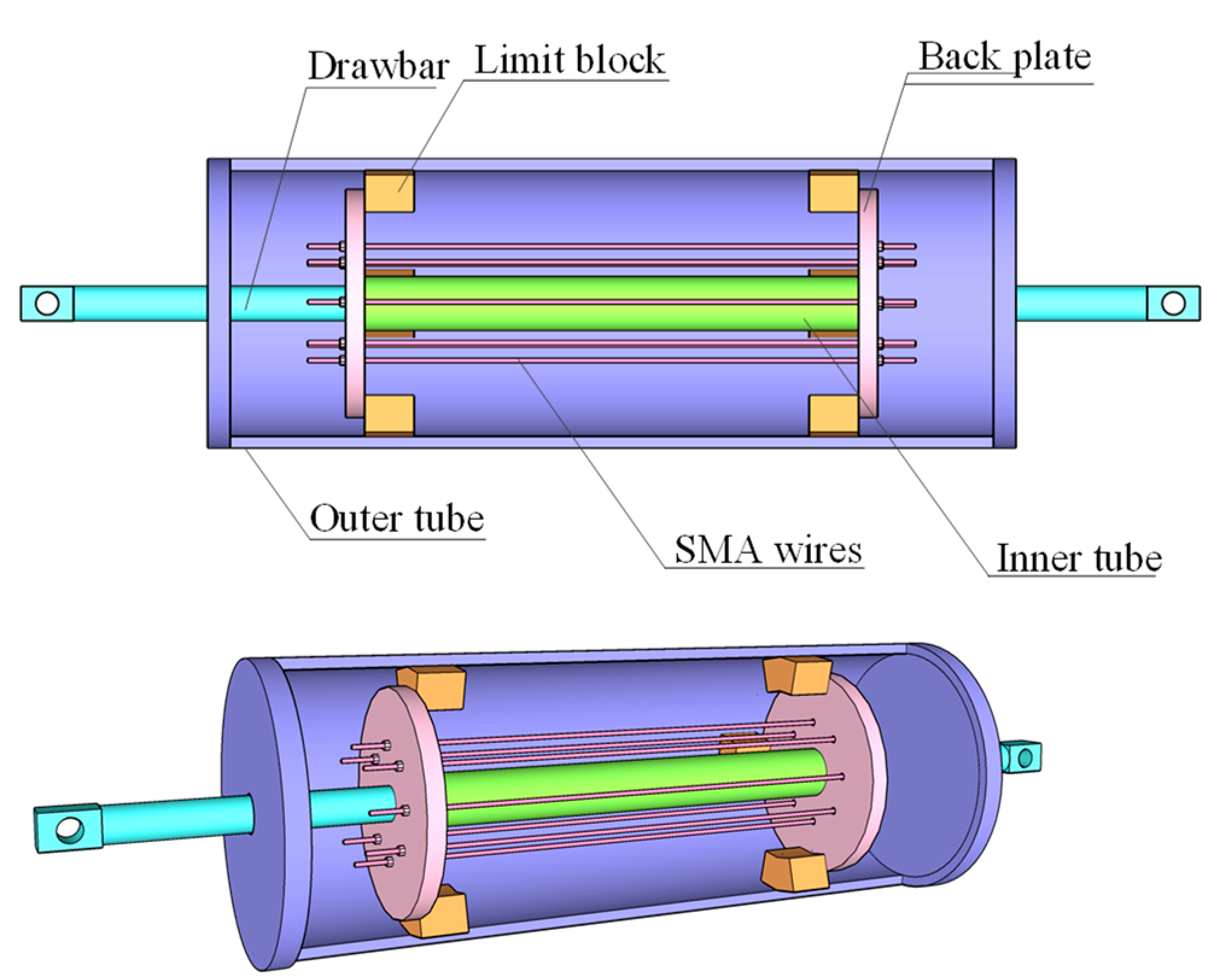
2.2. Constitutive Relationship of SMAD
3. The TTL–SMAD System’s Motion Equation
4. Random Wind-Induced Vibration Response of TTL–SMAD System
4.1. Random Wind Load
4.2. Random Wind-Induced Vibration Response
4.3. Extreme Response of the Control System
5. Case Study
5.1. Structural and Wind Field Parameters
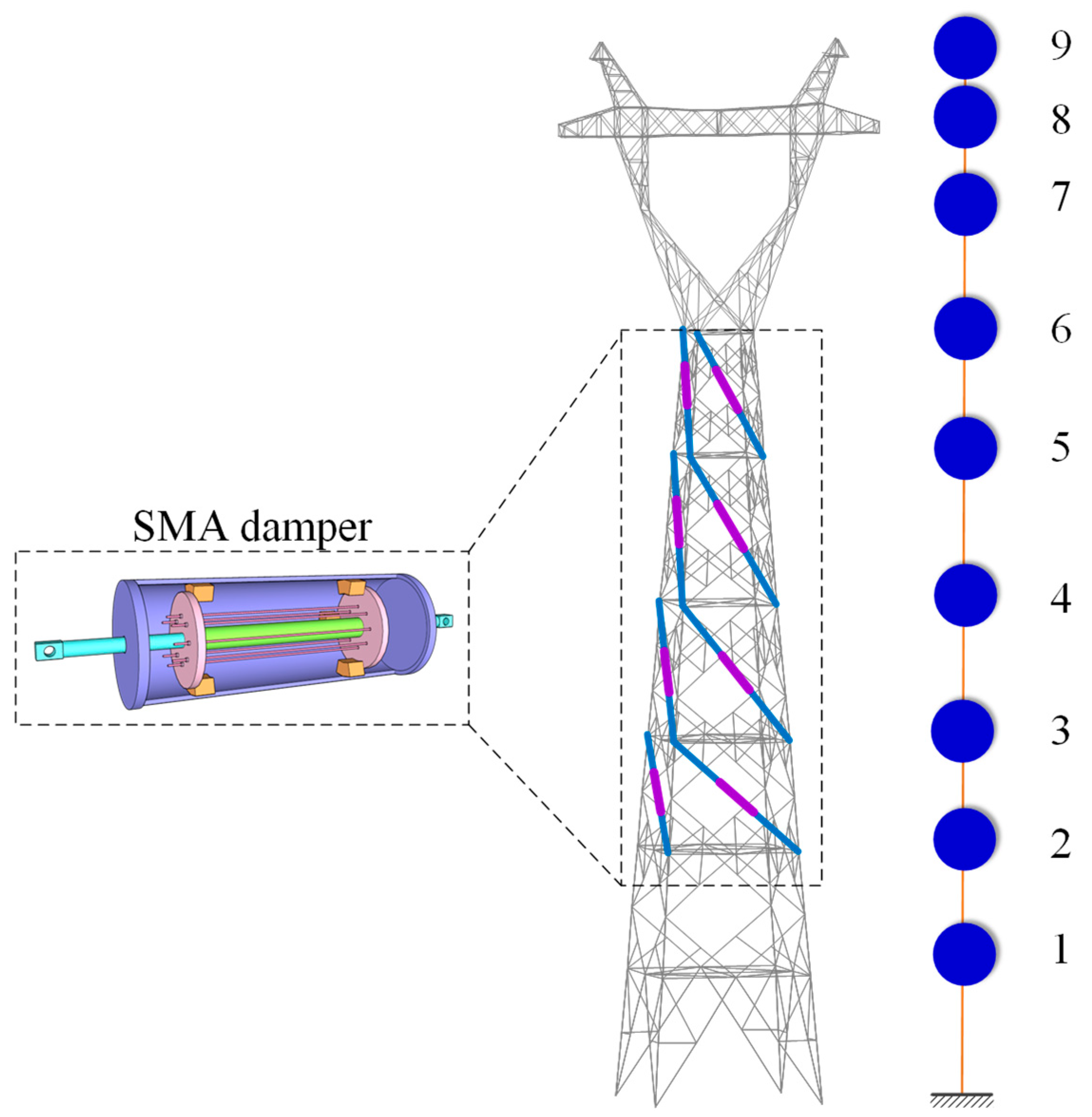
5.2. Damper Parameters and Installation
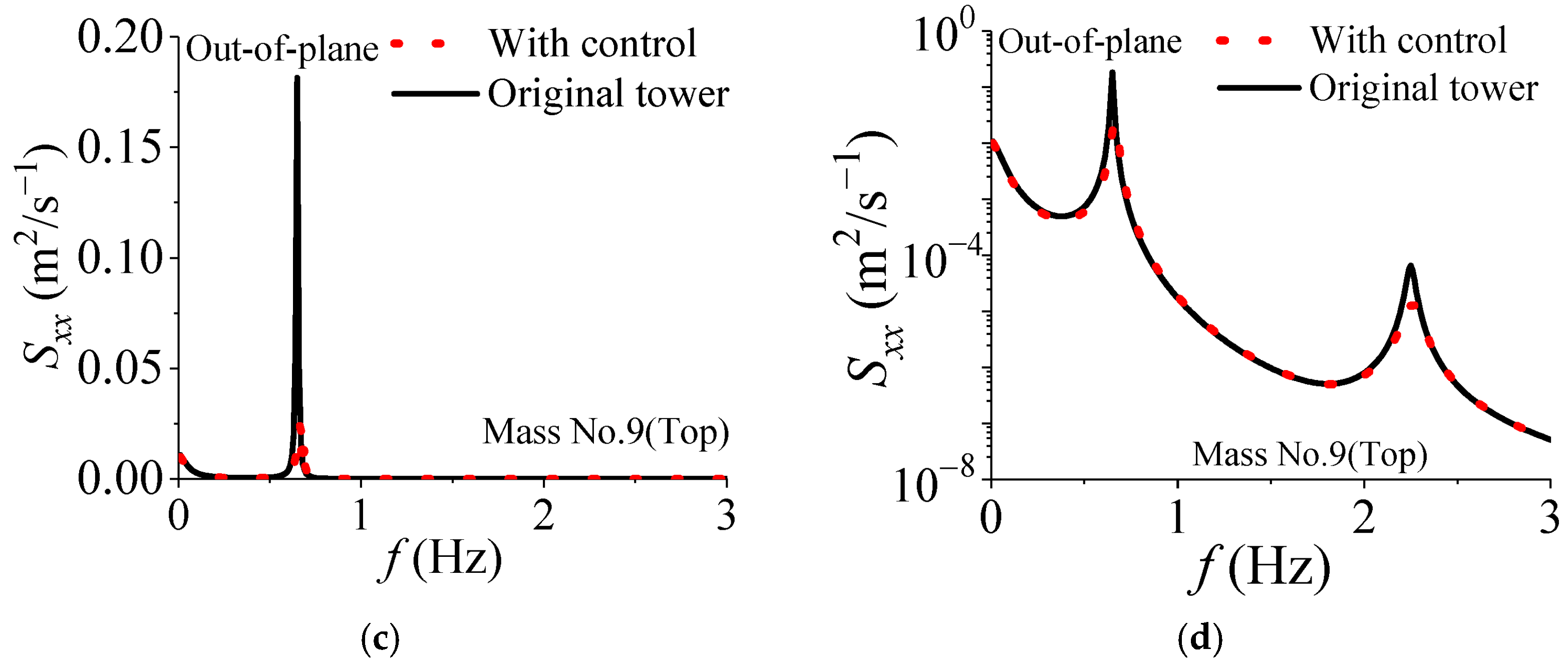
5.3. PSD Analysis
6. Parametric Study
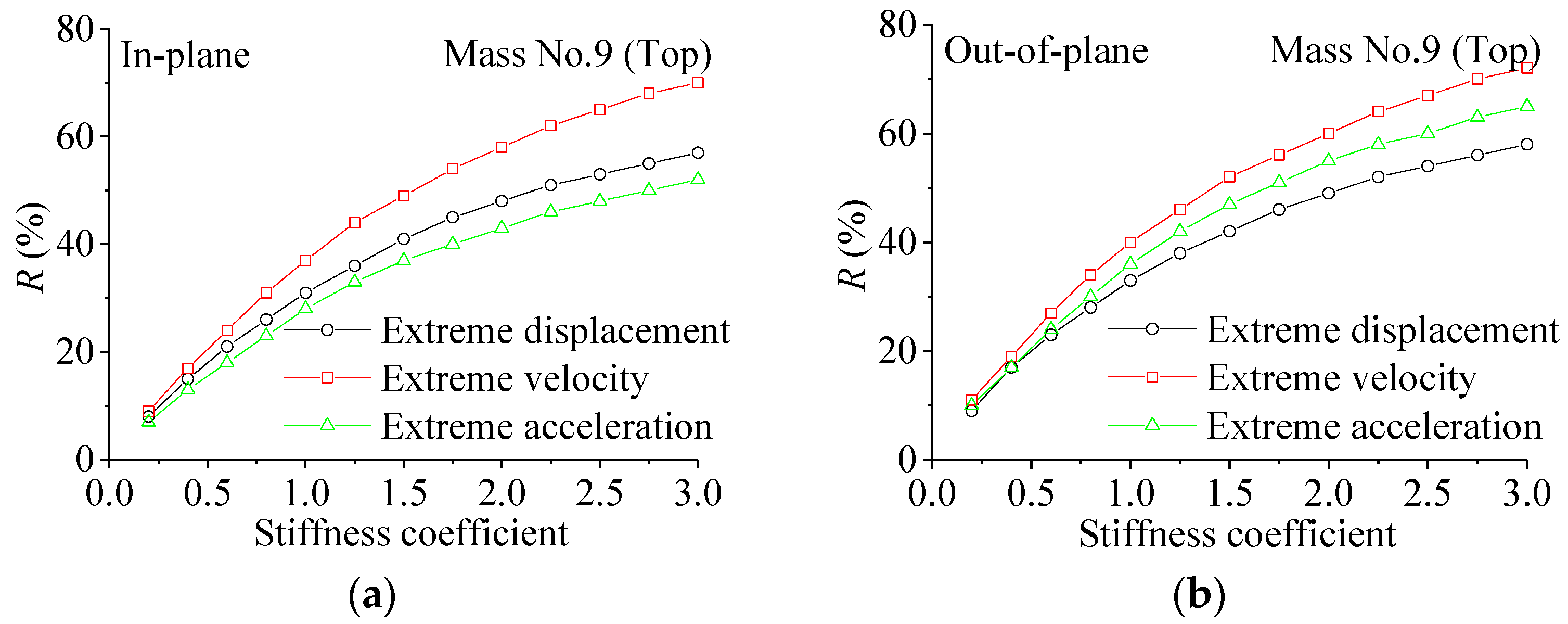
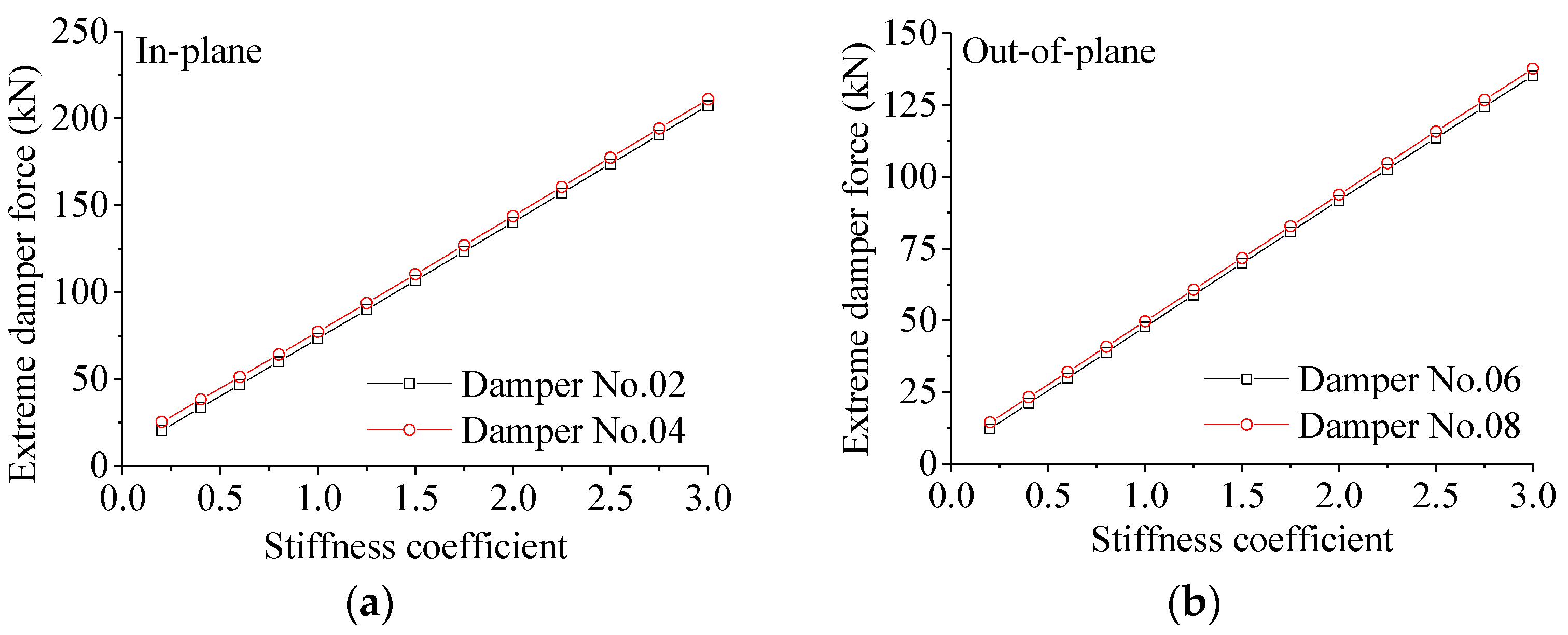
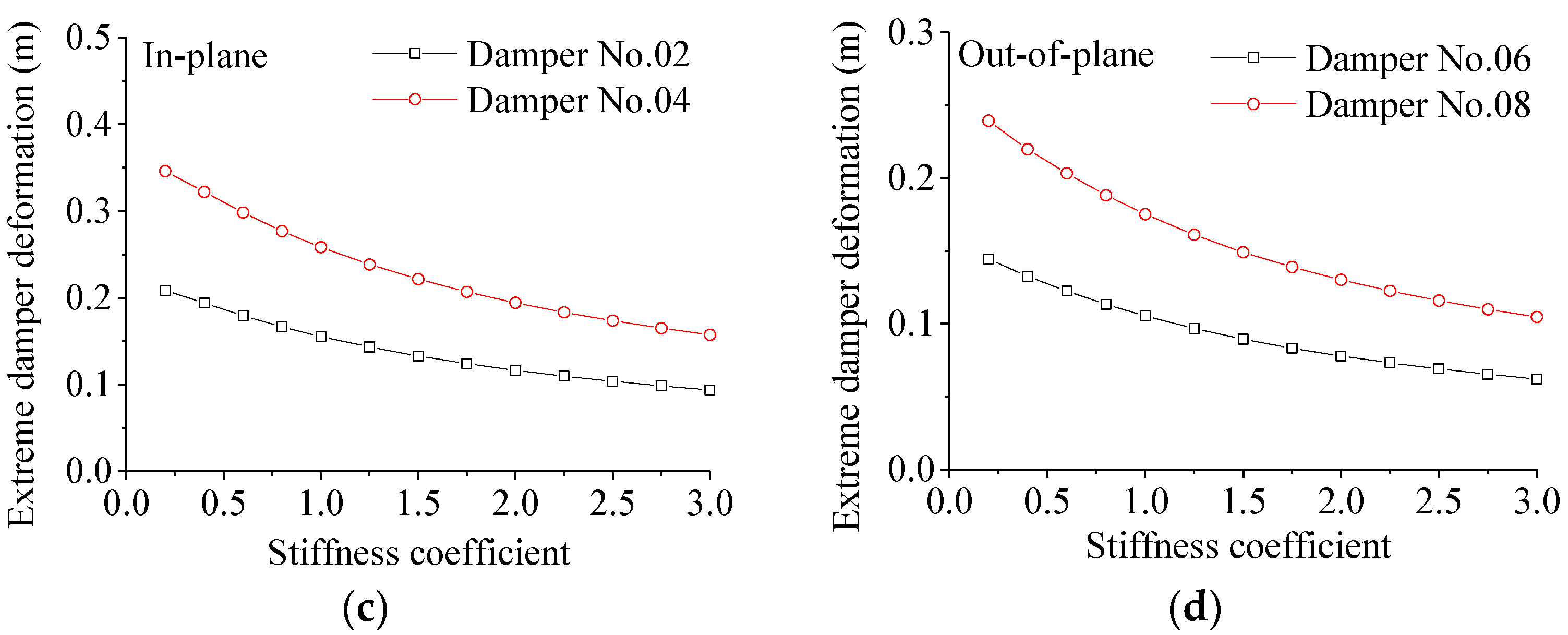
6.1. Influence of Stiffness
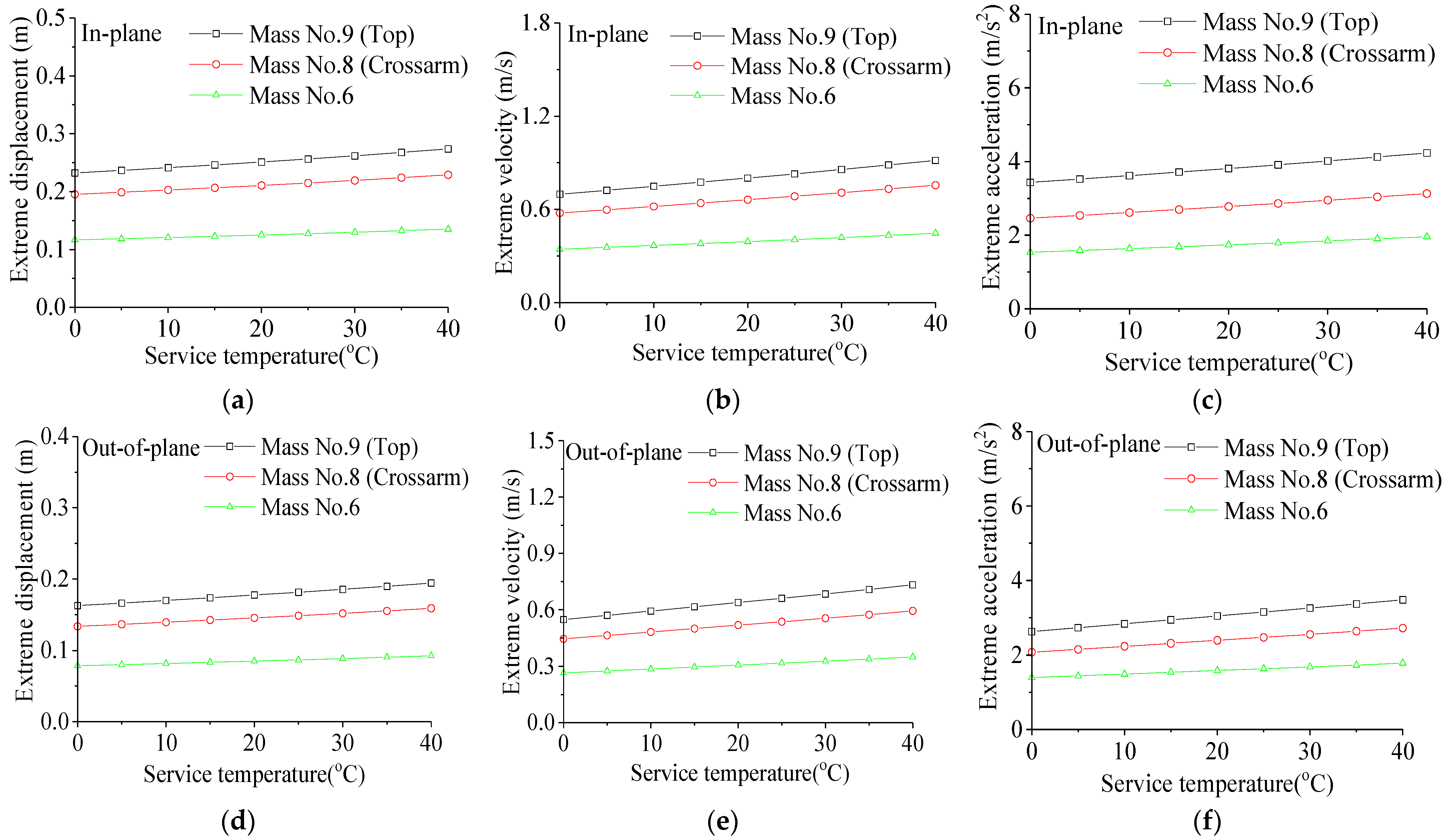
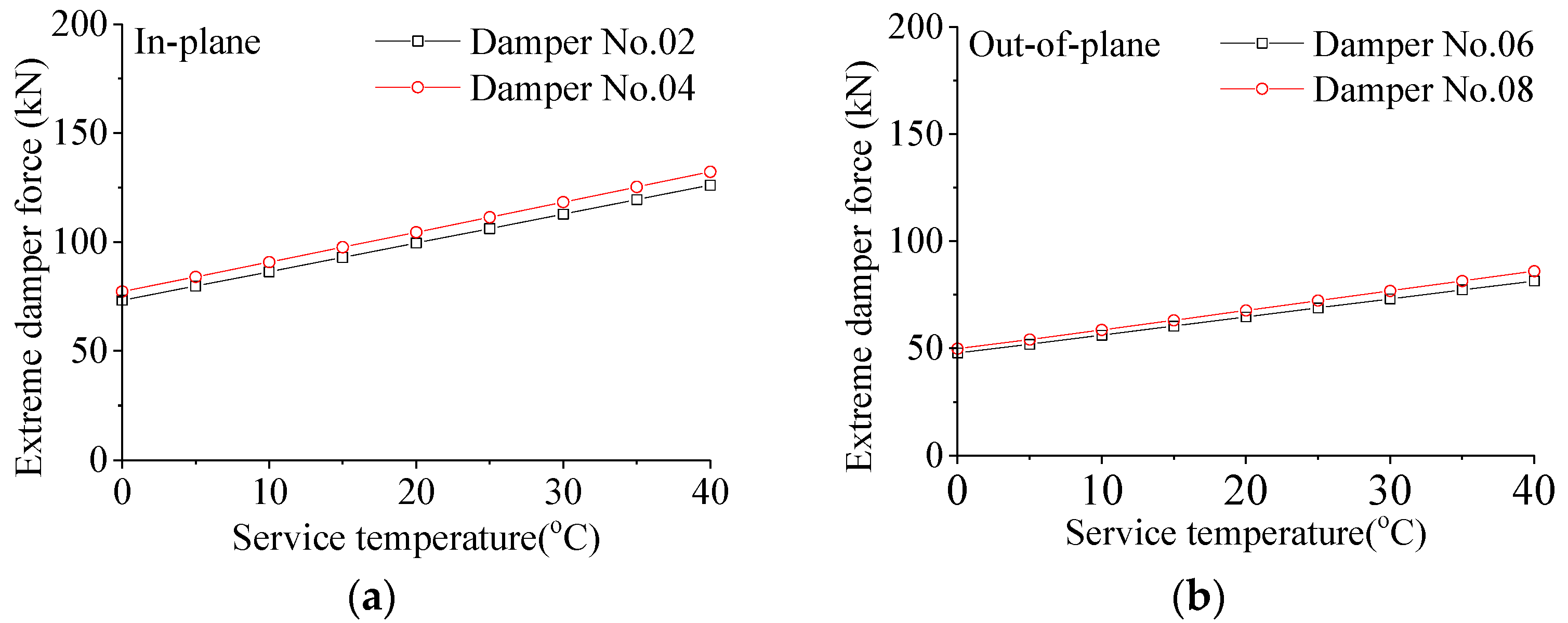
6.2. Influence of Service Temperature
7. Conclusions
- (1)
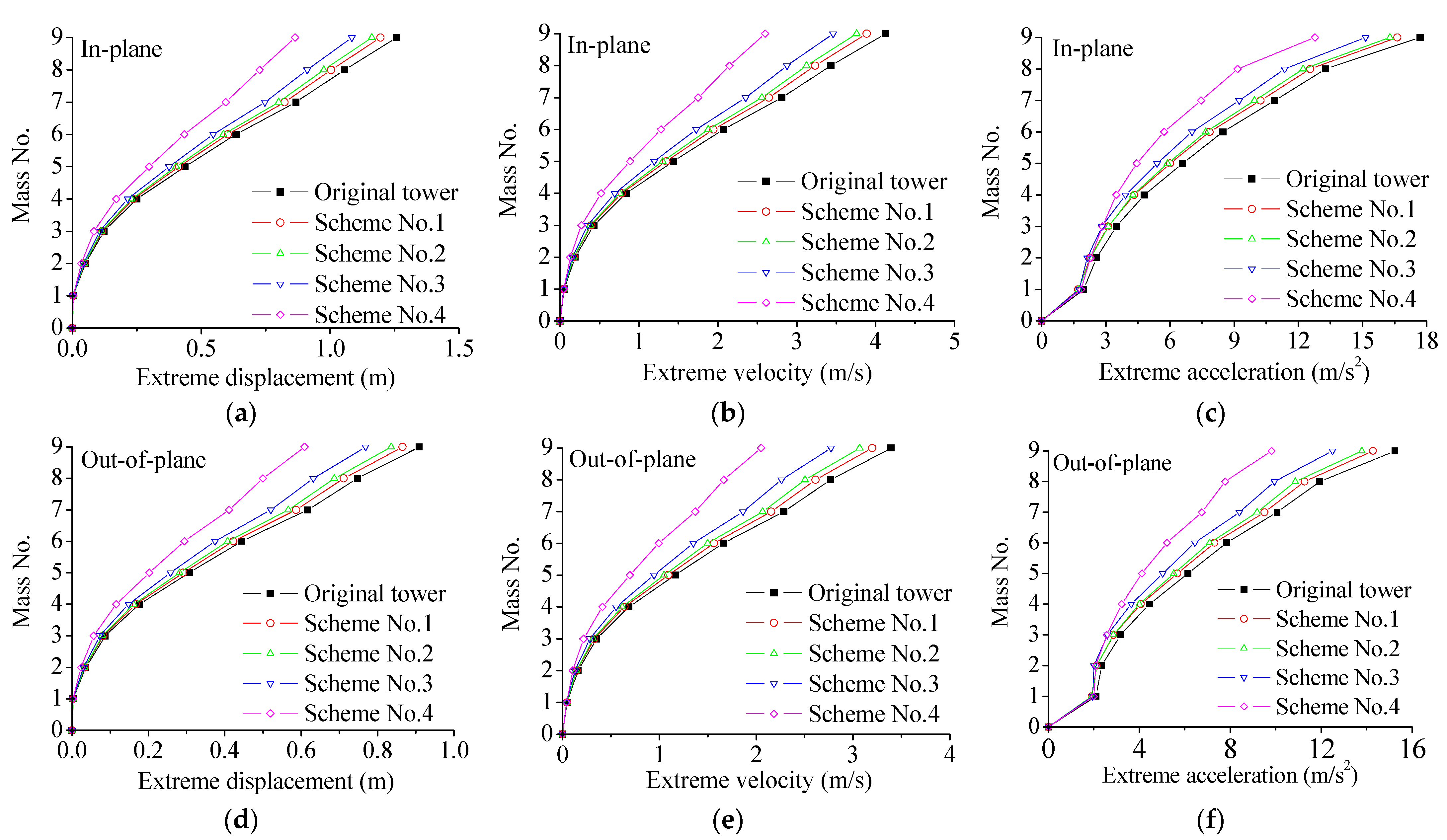
- All four installation schemes effectively mitigate the random wind-induced vibration response of the TTL system. However, Scheme No. 4, where the SMA damper is installed concentrically at the upper part of the tower body, demonstrates the best control performance, with a damping rate exceeding 30%, significantly outperforming the other schemes. In comparison, the damping effects of the other schemes, particularly those using distributed installation or lower tower placements, are relatively lower, and the control performance is less effective than that of Scheme No. 4.
- (2)
- The first two modes contribute mainly to the system’s response, with the first mode contributing the most. The PSD peak corresponding to the first mode of the control system is reduced by approximately 80%. SMAD does not change the inherent vibration characteristics of the system.
- (3)
- Damper stiffness significantly affects the damper’s control performance. Increasing the damper stiffness leads to a significant reduction in the extreme response of the transmission tower. A recommended value of Cs is 1.0. For different damper stiffness values, the control effect on extreme velocity is relatively better.
- (4)
- Service temperature affects the damper’s control performance. As the temperature increases, the control performance of the transmission tower decreases. At 0 °C, the control performance of SMAD is the best in both the in-plane and out-of-plane directions, with velocity reduction rates of 37.09% and 39.55%, respectively. The control effect on extreme velocity is relatively better at different service temperatures.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SMA | Shape memory alloy |
| SMAD | Shape memory alloy damper |
| TTL | Transmission tower-line |
| TTL–SMAD | Transmission tower-line with shape memory alloy damper |
| TMD | Tuned mass damper |
| MDOF | Multi-degree-of-freedom |
| PEM | Pseudo Excitation Method |
| PSD | Power spectral density |
References
- Li, J.-X.; Yang, T.; Zhang, C.; Sun, L.; Qu, C.-X. Typhoon fragility analysis of transmission tower-line system considering wind-induced fatigue. Eng. Struct. 2025, 338, 120572. [Google Scholar] [CrossRef]
- Jin, Q.; Liu, J.; Rong, K.; Zhang, R.; Tian, L.; Meng, X. Enhancing the wind-resistant performance of transmission towers with cross-shield non-destructive continuous strengthening measure. Thin-Walled Struct. 2025, 216, 113703. [Google Scholar] [CrossRef]
- Tian, L.; Luo, J.Y.; Zhou, M.Y.; Bi, W.Z.; Liu, Y.P. Research on vibration control of a transmission tower-line system using SMA-BTMD subjected to wind load. Struct. Eng. Mech. 2022, 82, 571–585. [Google Scholar]
- Xue, J.; Xiang, Z.; Ou, G. Predicting single freestanding transmission tower time history response during complex wind input through a convolutional neural network based surrogate model. Eng. Struct. 2021, 233, 111859. [Google Scholar] [CrossRef]
- Roy, S.; Kundu, C.K. State of the art review of wind induced vibration and its control on transmission towers. Structures 2021, 29, 254–264. [Google Scholar] [CrossRef]
- Chen, B.; Guo, W.H.; Li, P.Y.; Xie, W.P. Dynamic responses and vibration control of the transmission tower-line system: A state-of-the-art review. Sci. World J. 2014, 2014, 538457. [Google Scholar] [CrossRef]
- Chen, B.; Zheng, J.; Qu, W.L. Control of wind-induced response of transmission tower-line system by using magnetorheological dampers. Int. J. Struct. Stab. Dyn. 2009, 9, 661–685. [Google Scholar] [CrossRef]
- Sheng, Z.Y.; Xia, C.; Xu, W.P.; Li, P.Y. Analytical study on wind-induced vibration and its control of transmission towers in mountainous area. Appl. Mech. Mater. 2011, 105–107, 635–639. [Google Scholar] [CrossRef]
- Zeng, C.; Hao, D.X.; Hou, L.Q. Research on calculation of equivalent damping ratio of electrical transmission tower-line system with viscoelastic dampers. Adv. Mater. Res. 2014, 1064, 115–119. [Google Scholar] [CrossRef]
- Chen, B.; Weng, S.; Zhi, L.H.; Li, D.M. Response control of a large transmission tower-line system under seismic excitations using friction dampers. Adv. Struct. Eng. 2016, 20, 1155–1173. [Google Scholar] [CrossRef]
- Zhang, P.; Song, G.; Li, H.N.; Lin, Y.X. Seismic control of power transmission tower using pounding TMD. J. Eng. Mech. 2013, 139, 1395–1406. [Google Scholar] [CrossRef]
- Koutsoloukas, L.; Nikitas, N.; Aristidou, P. Passive, semi-active, active and hybrid mass dampers: A literature review with associated applications on building-like structures. Dev. Built Environ. 2022, 12, 100094. [Google Scholar] [CrossRef]
- An, Z.; Wang, W.; Wang, H.; Li, Z.; Wang, D.; Xie, G. Seismic performance research on a graded-yielding metal brace with self-centering functions. Buildings 2024, 14, 3940. [Google Scholar] [CrossRef]
- Song, G.; Ma, N.; Li, H.N. Applications of shape memory alloys in civil structures. Eng. Struct. 2006, 28, 1266–1274. [Google Scholar] [CrossRef]
- Tabrizikahou, A.; Kuczma, M.; Łasecka-Plura, M. Application and modelling of shape-memory alloys for structural vibration control: State-of-the-art review. Constr. Build. Mater. 2022, 342, 127975. [Google Scholar] [CrossRef]
- Zuo, X.B.; Li, A.Q. Numerical and experimental investigation on cable vibration mitigation using shape memory alloy damper. Struct. Control Health Monit. 2011, 18, 20–39. [Google Scholar] [CrossRef]
- Casciati, F.; Faravelli, L. A passive control device with SMA components: From the prototype to the model. Struct. Control Health Monit. 2009, 16, 751–765. [Google Scholar] [CrossRef]
- Shi, F.; Zhou, Y.; Ozbulut, O.E.; Ren, F.M. Hysteretic response and failure behavior of an SMA cable-based self-centering brace. Struct. Control Health Monit. 2022, 29, e2847. [Google Scholar] [CrossRef]
- Huang, H.Y.; Chang, W.S. Application of pre-stressed SMA-based tuned mass damper to a timber floor system. Eng. Struct. 2018, 167, 143–150. [Google Scholar] [CrossRef]
- Huang, H.Y.; Chang, W.S. Re-tuning an off-tuned tuned mass damper by adjusting temperature of shape memory alloy: Exposed to wind action. Structures 2020, 25, 180–189. [Google Scholar] [CrossRef]
- Chen, B.; Song, X.X.; Li, W.B.; Wu, J.B. Vibration control of a wind-excited transmission tower-line system by shape memory alloy dampers. Materials 2022, 15, 1790. [Google Scholar] [CrossRef]
- Wu, J.B.; Chen, B.; Zhi, L.H.; Song, X.X. Seismic response mitigation of a television transmission tower by shape memory alloy dampers. Materials 2021, 14, 6987. [Google Scholar] [CrossRef]
- Lin, J.H.; Zhang, Y.H.; Zhao, Y. Pseudo Excitation Method and Some Recent Developments. Procedia Eng. 2011, 14, 2453–2458. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Lin, J.; Zhao, Y.; Howson, W.P.; Williams, F.W. Random vibration of a train traversing a bridge subjected to traveling seismic waves. Eng. Struct. 2011, 33, 3546–3558. [Google Scholar] [CrossRef]
- Hu, L.; Xu, Y.L.; Huang, W.F. Typhoon-induced nonstationary buffeting response of long-span bridges in complex terrain. Eng. Struct. 2013, 57, 406–415. [Google Scholar] [CrossRef]
- Zhao, Y.; Si, L.T.; Ouyang, H. Frequency domain analysis method of nonstationary random vibration based on evolutionary spectral representation. Eng. Comput. 2018, 35, 1098–1127. [Google Scholar] [CrossRef]
- Zhong, Y.L.; Li, S.; Jin, W.C.; Yan, Z.T.; Liu, X.P.; Li, Y. Frequency domain analysis of along-wind response and study of windloads for transmision tower subjected to downbursts. Buildings 2022, 12, 148. [Google Scholar] [CrossRef]
- Li, H.N.; Shi, W.L.; Wang, G.X.; Jia, L.G. Simplified models and experimental verification for coupled transmission tower-line system to seismic excitations. J. Sound Vib. 2005, 286, 569–585. [Google Scholar] [CrossRef]
- Andrawes, B.; Desroches, R. Effect of ambient temperature on the hinge opening in bridges with shape memory alloy seismic restrainers. Eng. Struct. 2007, 29, 2294–2301. [Google Scholar] [CrossRef]
- Araya, R.; Marivil, M.; Mir, C.; Moroni, O.; Sepulveda, A. Temperature and grain size effects on the behavior of CuAlBe SMA wires under cyclic loading. Mater. Sci. Eng. A 2008, 496, 209–213. [Google Scholar] [CrossRef]
- Graesser, E.J.; Cozzarelli, F.A. Shape-memory alloys as new materials for aseismic isolation. J. Eng. Mech. (ASCE) 1991, 117, 2590–2608. [Google Scholar] [CrossRef]
- Graesser, E.J.; Cozzarelli, F.A. A proposed three-dimensional constitutive model for shape memory alloys. J. Intell. Mater. Syst. Struct. 1994, 5, 78–89. [Google Scholar] [CrossRef]
- Jia, Y.Q.; Wang, C.; Zhang, R.F.; Li, L.Z.; Lu, Z.D. A double shape memory alloy damper for structural vibration control. Int. J. Struct. Stab. Dyn. 2021, 21, 2150098. [Google Scholar] [CrossRef]
- Du, X.W.; Sun, G.; Sun, S.S. Piecewise linear constitutive relation for pseudo-elasticity of shape memory alloy (SMA). Mater. Sci. Eng. A 2005, 393, 332–337. [Google Scholar] [CrossRef]
- Yan, X.; Nie, J. Response of SMA superelastic systems under random excitation. J. Sound Vib. 2000, 238, 893–901. [Google Scholar] [CrossRef]
- Wen, Y.K. Equivalent linearization for hysteretic systems under random excitation. J. Appl. Mech. 1980, 47, 150–154. [Google Scholar] [CrossRef]
- Guo, Z.; Hou, W.; Yao, H.; Liu, Y.; Zhang, Y. Dynamic responses of monopile offshore wind turbines under different wind-wave misalignment angles. Structures 2024, 69, 107454. [Google Scholar] [CrossRef]
- Yang, H.; Yang, M.; Lu, X.; Song, M. Analysis of the dynamic characteristics of corroded offshore wind turbine steel piles under extreme wind, wave, and current loads. Ocean Eng. 2025, 332, 121298. [Google Scholar] [CrossRef]
- Tang, J.; Cai, Q.; Dai, K.; Liu, Y.; Heng, J.; Luo, Y. A cable-based tuned inerter damper for edgewise vibration control of the wind turbine blade. Eng. Struct. 2025, 323, 119248. [Google Scholar] [CrossRef]
- Xing, L.; Gardoni, P.; Zhou, Y.; Zhang, P. Optimal models of outrigger locations and damping parameters for combined energy dissipation outrigger systems subject to seismic and wind loads. J. Build. Eng. 2023, 76, 107209. [Google Scholar] [CrossRef]
- Miao, Q.; Low, Y.M. Efficient long-term extreme response and fatigue analysis of offshore structures under stochastic wave, current, and wind loads. Mar. Struct. 2025, 103, 103815. [Google Scholar] [CrossRef]
- Zhao, Z.; Low, Y.M. Extreme value analysis of multivariate gaussian processes with wave-passage effects. J. Sound Vib. 2025, 596, 118703. [Google Scholar] [CrossRef]
- China Ministry of Construction. GB 50009-2012; Load Code for the Design of Building Structures. Chinese Architectural Industry Press: Beijing, China, 2012. (In Chinese)




| Force | Displacement | Stiffness |
|---|---|---|
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| Mf | −46 °C | CM | 10 MPa/°C | 120 MPa | |
| As | −18.5 °C | CA | 15.8 MPa/°C | 190 MPa | |
| Ms | −37.4 °C | DA | 75,000 MPa | εL | 0.079 |
| Af | −6 °C | DM | 29,300 MPa |
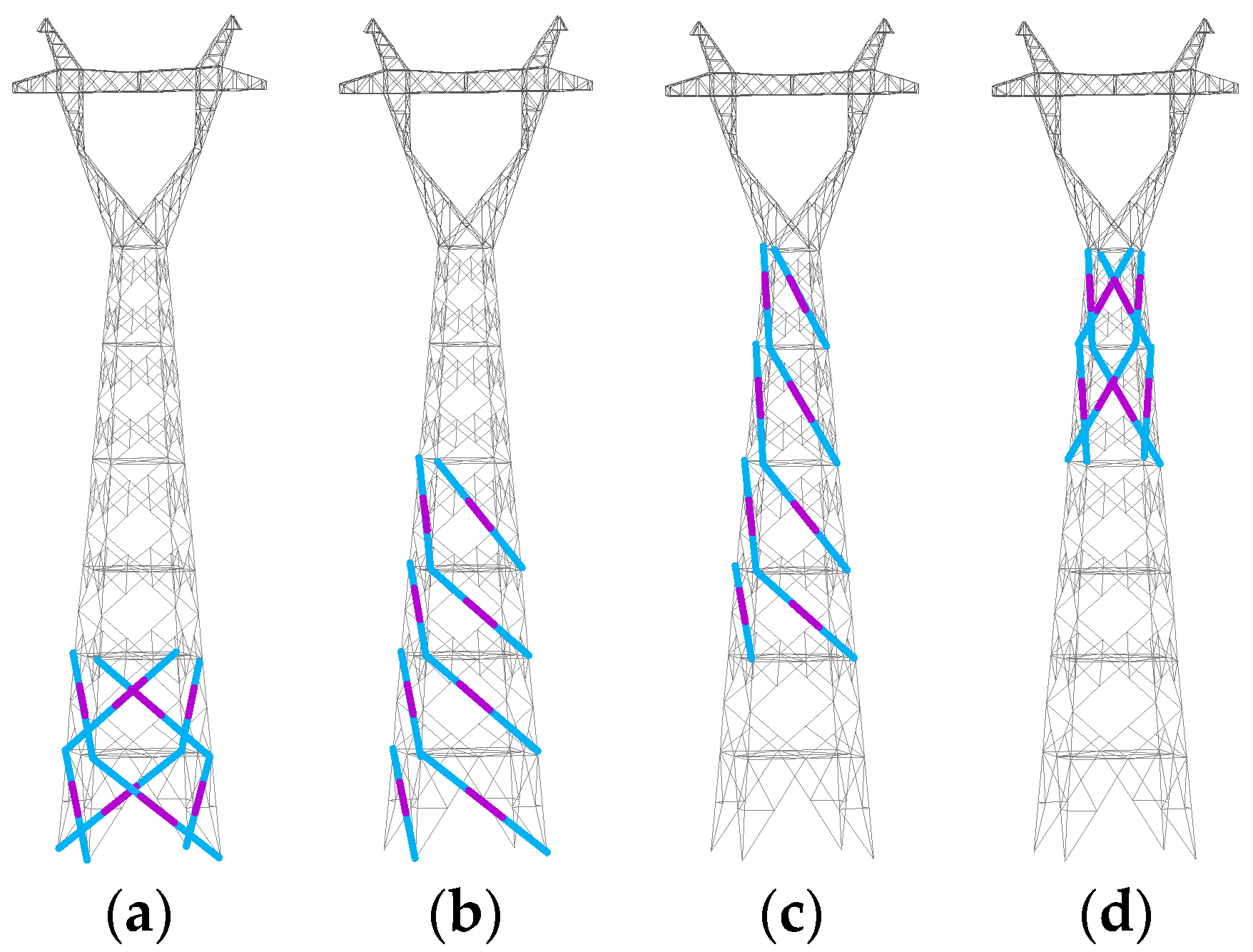
| Scheme | Installation Layers | Dampers per Layer | Total Dampers | Installation Type |
|---|---|---|---|---|
| No. 1 | Mass No. 1, 2 | 2 per mass layer | 4 | Lower part, concentrated |
| No. 2 | Mass No. 1, 2, 3, 4 | 1 per mass layer | 4 | Lower half, uniform |
| No. 3 | Mass No. 3, 4, 5, 6 | 1 per mass layer | 4 | Upper half, uniform |
| No. 4 | Mass No. 5, 6 | 2 per mass layer | 4 | Upper part, concentrated |
| Direction | Location | Extreme Response | Scheme No. 1 | Scheme No. 2 | Scheme No. 3 | Scheme No. 4 |
|---|---|---|---|---|---|---|
| In-plane | Mass No. 6 (Top of tower body) | Displacement | 5.07 | 7.78 | 13.95 | 31.62 |
| Velocity | 6.05 | 9.23 | 16.58 | 38.09 | ||
| Acceleration | 7.31 | 9.51 | 17.06 | 32.50 | ||
| Mass No. 8 (Cross arm) | Displacement | 4.98 | 7.65 | 13.76 | 31.18 | |
| Velocity | 5.83 | 8.99 | 16.19 | 37.46 | ||
| Acceleration | 5.43 | 7.93 | 14.45 | 30.99 | ||
| Mass No. 9 (Tower top) | Displacement | 4.99 | 7.67 | 13.80 | 31.29 | |
| Velocity | 5.86 | 8.97 | 16.15 | 37.09 | ||
| Acceleration | 6.05 | 7.99 | 14.42 | 27.82 | ||
| Out-of-plane | Mass No. 6 (Top of tower body) | Displacement | 4.95 | 8.29 | 15.75 | 33.76 |
| Velocity | 5.86 | 9.75 | 18.62 | 40.21 | ||
| Acceleration | 6.68 | 9.50 | 17.79 | 33.39 | ||
| Mass No. 8 (Cross arm) | Displacement | 4.82 | 8.11 | 15.46 | 33.08 | |
| Velocity | 5.65 | 9.55 | 18.31 | 39.83 | ||
| Acceleration | 5.58 | 9.03 | 16.69 | 34.86 | ||
| Mass No. 9 (Tower top) | Displacement | 4.81 | 8.09 | 15.43 | 32.99 | |
| Velocity | 5.69 | 9.55 | 18.28 | 39.55 | ||
| Acceleration | 6.35 | 9.57 | 18.02 | 35.62 |
| Direction | Response | Service Temperature | ||||
|---|---|---|---|---|---|---|
| 0 °C | 10 °C | 20 °C | 30 °C | 40 °C | ||
| In-plane | Displacement | 31.29 | 28.53 | 25.56 | 22.32 | 18.73 |
| Velocity | 37.09 | 32.42 | 27.61 | 22.60 | 17.26 | |
| Acceleration | 27.82 | 23.85 | 19.72 | 15.36 | 10.73 | |
| Out-of-plane | Displacement | 32.99 | 29.83 | 26.50 | 23.12 | 19.31 |
| Velocity | 39.55 | 34.39 | 29.19 | 24.05 | 18.52 | |
| Acceleration | 35.62 | 30.30 | 24.92 | 19.59 | 13.94 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, M.; Fang, X.; Zhang, S.; Xie, D. Random Wind Vibration Control of Transmission Tower-Line Systems Using Shape Memory Alloy Damper. Buildings 2025, 15, 3091. https://doi.org/10.3390/buildings15173091
Chang M, Fang X, Zhang S, Xie D. Random Wind Vibration Control of Transmission Tower-Line Systems Using Shape Memory Alloy Damper. Buildings. 2025; 15(17):3091. https://doi.org/10.3390/buildings15173091
Chicago/Turabian StyleChang, Mingjing, Xibing Fang, Shanshan Zhang, and Dingkun Xie. 2025. "Random Wind Vibration Control of Transmission Tower-Line Systems Using Shape Memory Alloy Damper" Buildings 15, no. 17: 3091. https://doi.org/10.3390/buildings15173091
APA StyleChang, M., Fang, X., Zhang, S., & Xie, D. (2025). Random Wind Vibration Control of Transmission Tower-Line Systems Using Shape Memory Alloy Damper. Buildings, 15(17), 3091. https://doi.org/10.3390/buildings15173091






