1. Introduction
For centuries, shell structures have been used in architecture due to their high weight-to-span ratio and structural effectiveness [
1]. These 3D surface-like shapes have a thickness much smaller than other dimensions, and their performance depends on the double curved surface geometry [
2]. While digital design enables easy formal exploration, constructing double-curved surfaces poses significant challenges. In this regard, recent developments in computer-aided design have made double-curved surfaces more accessible. However, their complex geometry creates design, fabrication, and assembly challenges. Studies have focused on rationalization to simplify the construction of complex surfaces [
3,
4,
5], with a key approach being surface discretization into smaller members. Thus, architectural rationalization has gained attention to design shell geometries that are practical and cost-effective to fabricate.
Discrete shells are geometric tiling arrangements on shell surfaces that utilize connected members without overlap [
6]. The resultant assembly consists of uniquely shaped elements. Discretizing double-curved surfaces into equivalent elements requires a complex design study. These structures are characterized by polygonal meshes for numerical accuracy, with edges as beams and faces as panels. Various methods exist to reduce the number of unique edges in architectural structures [
7,
8] and sphere tessellations [
9,
10].
Architectural works with double-curved surfaces comprise uniquely shaped elements, often requiring customized fabrication [
11], while design variables and objectives are influenced by manufacturing technologies and materials. Several discrete shell design studies utilize prefabrication techniques and simple joining methods, including timber plates [
12], cross-laminated timber plates [
13], and timber cassettes [
14]. The Armadillo Vault demonstrates a compression-only discrete shell using shaped limestone voussoirs [
15]. Concrete discrete shell examples include the ribbed concrete shell prototype [
16] and a discrete shell with post-tensioned precast members [
17].
Reducing unique elements simplifies CNC machining and 3D printing setups [
18] and enables mold-based prefabrication through the reuse of molds. Using identical elements allows backup creation and reduces transportation costs if waste occurs [
19]. One approach to reducing the geometric variety in double-curved architectural surfaces is modeling with discrete equivalence classes. Studies often simplify geometry using fixed topology with triangular or quadrilateral faces to explore equivalent elements through clustering and vertex optimization [
20,
21]. Alternatively, increasing formwork reusability is investigated to fabricate curved surface panels [
22] or triangular folding elements [
23], where congruent elements are manufactured and reshaped to different sizes. A recent study [
24] presents a method to discretize double-curved freeform surfaces into congruent polyhedral members with gaps.
Finding the overall form is crucial in shell design. Several numerical form-finding methods exist, including the
Force Density Method [
25],
Particle-spring Method [
26],
Dynamic Relaxation Method [
27], and
Thrust Network Analysis [
28]. The initial step is finding a shape that satisfies the structural equilibrium; additional constraints for feasibility and buildability can be included through optimization [
29,
30]. Several studies focus on shape optimization for structural performance [
31,
32,
33]. Others use geometry processing for self-supporting forms [
34,
35,
36,
37,
38,
39]. Also, artificial neural networks are employed to address complex structural design challenges [
40], such as physics-informed neural networks [
41] and mechanics-informed models [
42]. Self-supporting structures are not our focus; however, integrating computational form-finding methods into the initial formal exploration process of shell geometry provides a plausible starting point for load-bearing shells.
The assembly of discrete shells remains complex, particularly when scaffolding systems are avoided [
43,
44]. A staged block insertion method using suspension cables reduces costs and ensures structural stability [
45]. Robotic assembly can support specific block configurations [
46]. Assembly sequence optimization depends on block count, discretization pattern, and shape, requiring equilibrium calculations and temporary support considerations [
24]. The assembly process is outside the scope of this study and will be addressed separately.
The novelty of this work lies in combining relaxation-based form-finding, similarity-driven clustering, and fabrication-oriented optimization into a unified parametric workflow, specifically targeting mold-based prefabrication for discrete shells. Unlike [
24,
47], which address clustering or panelization separately, our method integrates surface approximation control, facing angle alignment, and cluster congruency optimization within a single optimization framework. In this study, we find the relaxed mesh and continuum surface approximation considering boundary conditions, supports, loads, and topological relationships. Planarized quad faces are grouped by geometrical similarities, calculated through vertex correspondences and alignment. An optimization procedure transforms faces within sets into congruent shapes while preserving topology. The 3D discrete shell elements are generated and optimized for buildability by minimizing dihedral angle deviations between neighboring elements. The proposed methodology provides architects and engineers with an adaptive computational tool that optimizes shell structures, considering both their architectural expression and fabrication efficiency. The method accounts for buildability by controlling the dihedral angles between contact faces and ensures geometric similarity within a user-defined error threshold. This study presents a novel approach to discrete shell design by integrating computational form generation with geometric simplification, while also incorporating geometry processing procedures that enable the use of efficient and scalable fabrication strategies.
3. Results
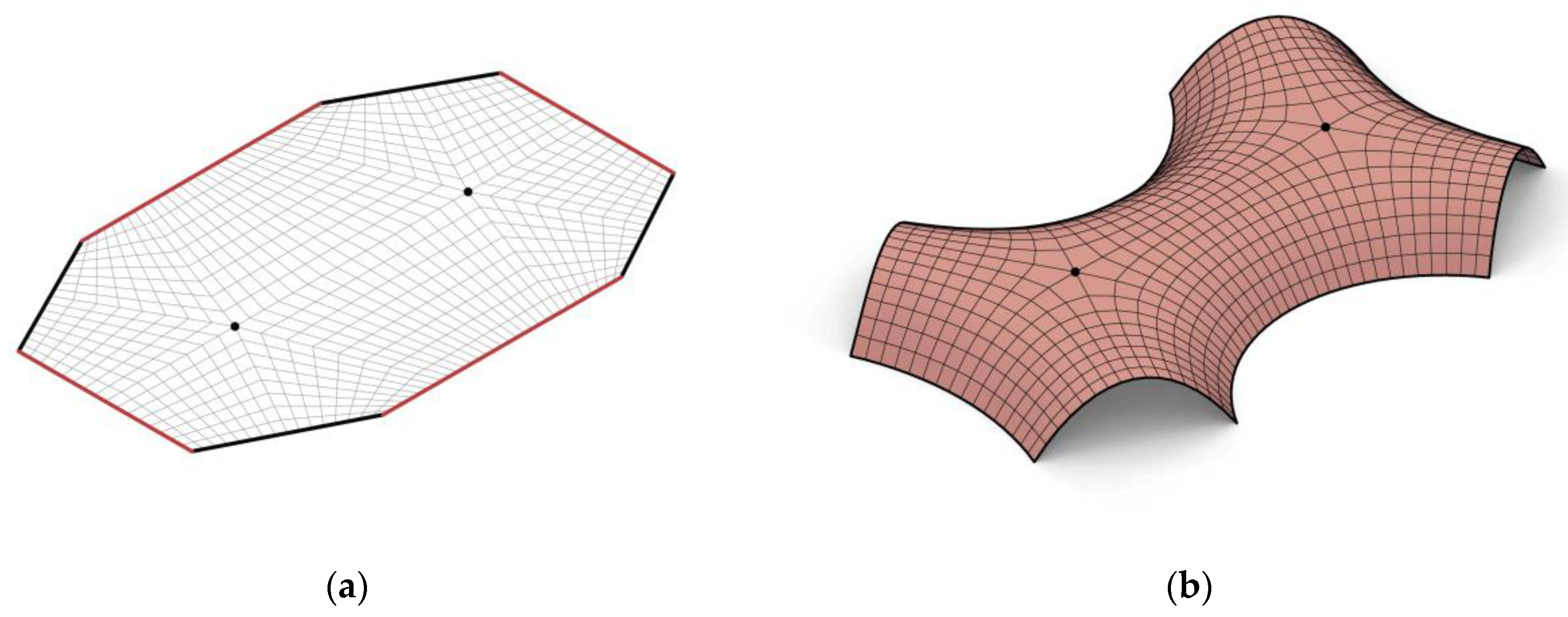
We actualize our methodological investigation in the Grasshopper–Rhino 7.38 (Robert McNeel & Associates, Seattle, WA, USA) environment on a desktop computer with a 5.0 GHz CPU and 64GB of memory. All numerical inputs (boundary conditions, face counts, support settings) are generated parametrically in Grasshopper. Data for the figures and tables are directly exported from the optimization output logs. Our approach involves computational form finding for a discrete shell structure, based on a 2D boundary mesh definition and quadrilateral discretization. This is followed by clustering the faces based on their similarity and optimizing the 3D discrete shell elements by minimizing the angle deviation of dihedral angles between contacting faces and the optimal intersection plane. Three error metrics are introduced to evaluate the efficiency of our approach, namely the similarity error for assessing the intra-cluster similarities by normalizing the largest volume of the element with the average volume in the relative cluster, the facing angle error to evaluate the largest deviation of elements’ contacting side faces from the relative optimal intersection plane, and the surface approximation error to calculate the maximum distance between the discretized mesh and the smooth surface approximation. The similarity error is expressed in cubic centimeters () since it is based on normalized volume differences. The facing angle error is expressed in radians (). The surface approximation error is expressed in meters () as a maximum Euclidean distance. The optimization is concluded when , and are reached by the user-defined thresholds considering architectural design requirements and fabrication error margins of 0.005, 0.035 and 0.05, respectively.
To evaluate the performance of our modeling approach, we tested two distinct cases on 2D topologies. As described comprehensively in [
52], a key criterion in topology design is the number of singularities (vertices with irregular valency).
Structured meshes with fewer singularities are preferred for identifying structural patterns, whereas
unstructured meshes result in disorganized element flows. In this regard, Case 1 involved varying boundary conditions, number of singularities, support vertex settings, and mesh face counts to assess our approach’s adaptability to different geometrical settings. On the other hand, Case 2 focused on varying mesh face count under consistent boundary conditions and support vertex settings. We defined the thickness of discrete shell elements
as 10 cm. The weights of the relative objectives regarding the similarity of the sets
, surface approximation of discretized mesh
, and facing angle deviation
are defined as
since
has a relatively higher influence on the convergence by restraining the similarity-based clustering process. The form-found discrete geometry and its double curved surface approximation are supplied to the optimization process. The optimization of each shape starts with the lowest possible target set number 1, and the set number
is incrementally raised until the user-defined thresholds are satisfied. We characterized the minimum set number
as the lowest number of sets of equivalent discrete members that satisfy the constraints of
,
and
.
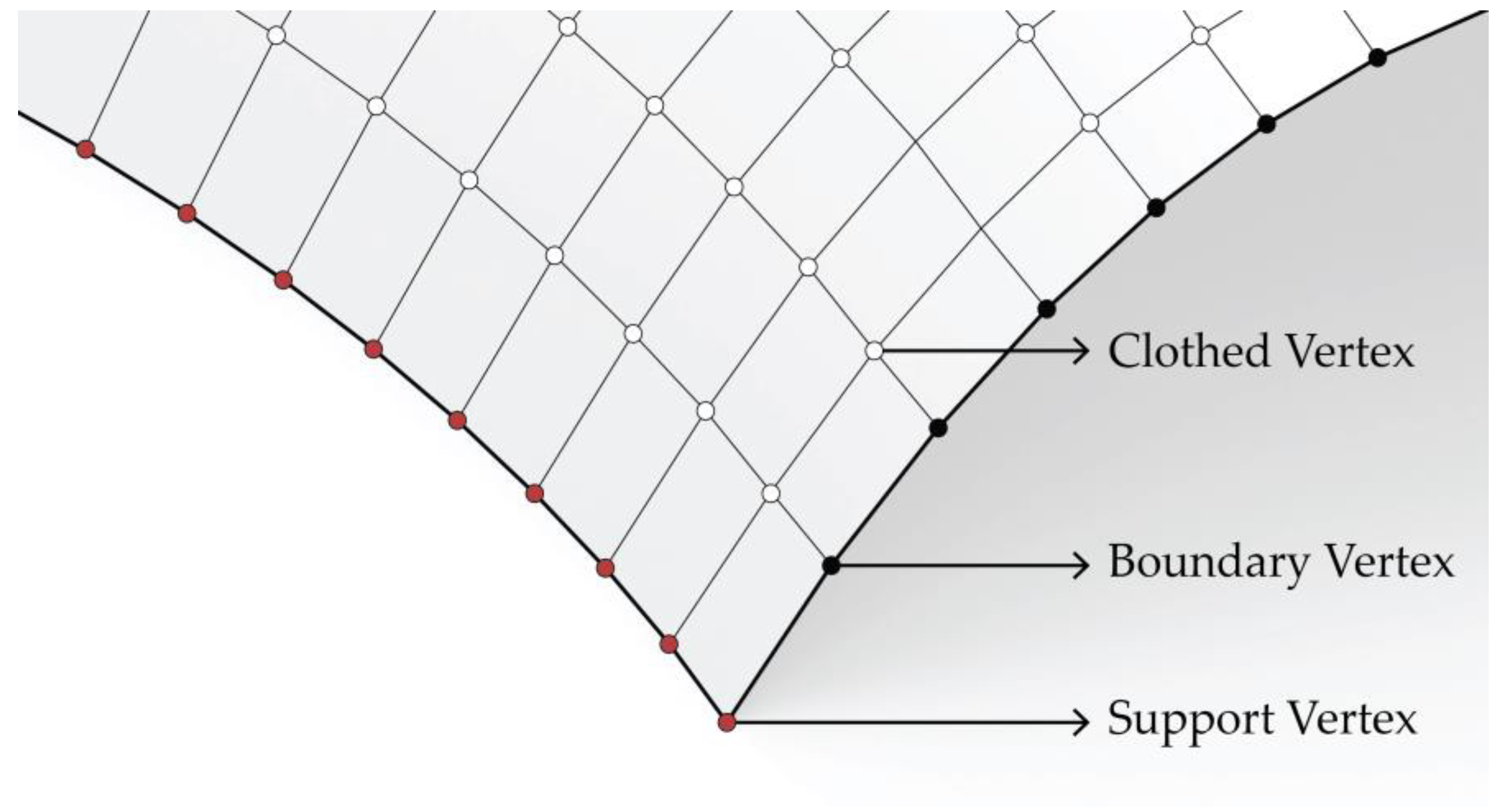
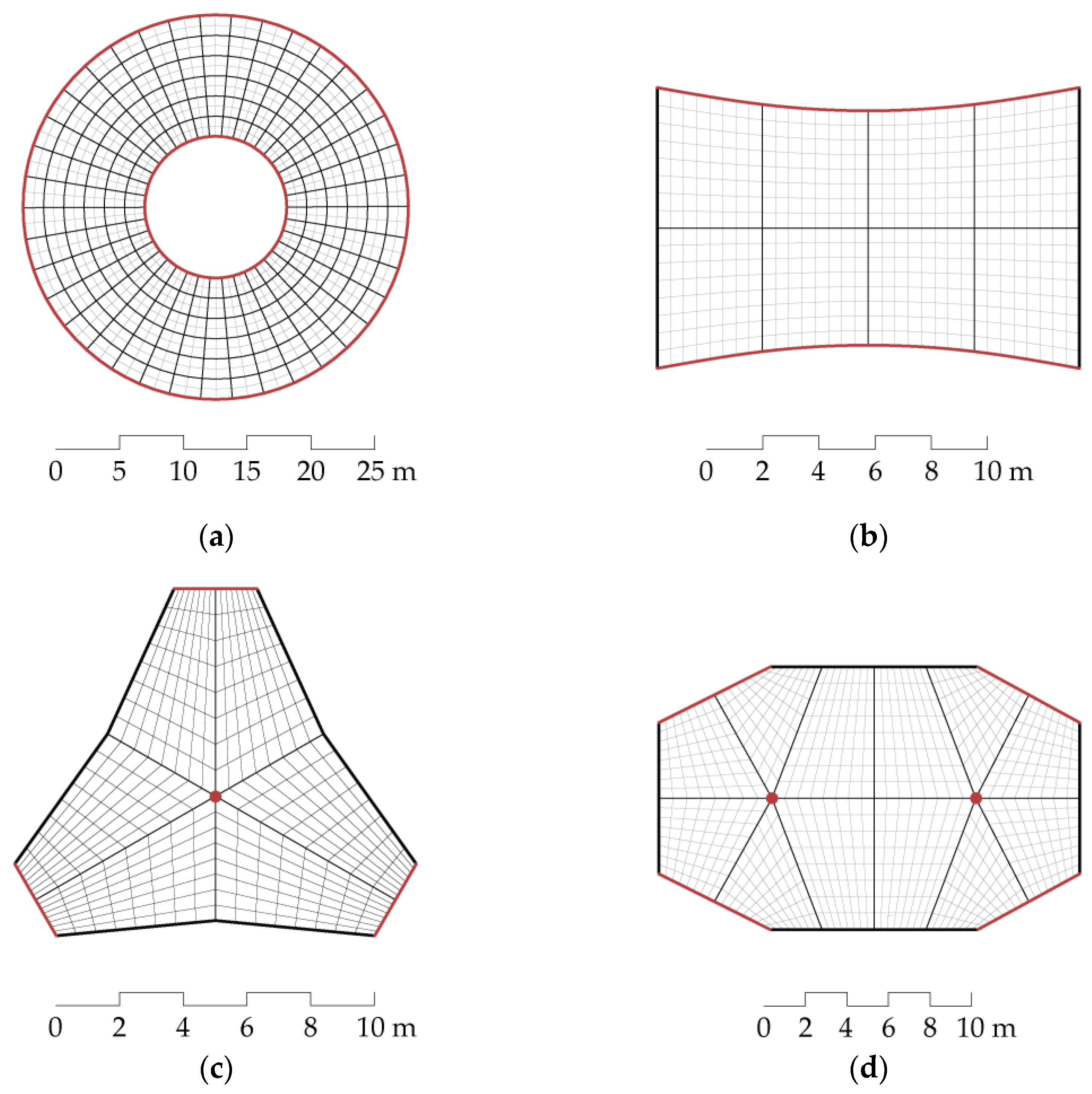
In the first part of our experiments, we tested the adaptability of our approach. We applied our method to 2D structured quad meshes with different topological settings in terms of number of singularities and number of faces, and different boundary conditions and support vertex settings as shown in
Figure 5. In this regard, we employed a shape with no singularities and no boundary vertices (
Figure 6a), a shape with no singularities (
Figure 6b), a shape with only a single singularity (
Figure 6c), and a shape with multiple singularities (
Figure 6d). The resultant discrete shell alternatives are presented in
Figure 7, and the numerical data of our implementation is outlined in
Table 1.
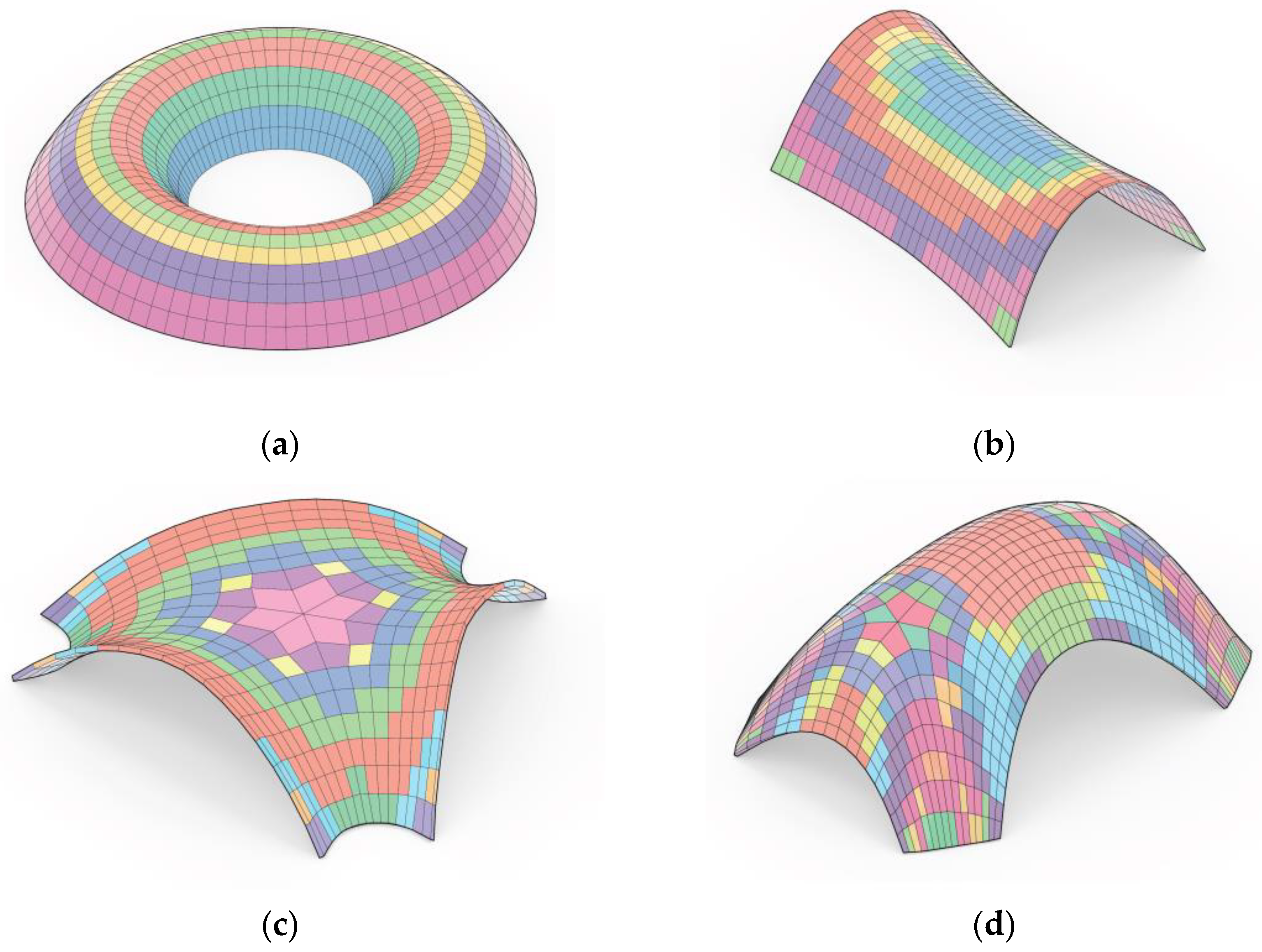
The results of Case 1 indicate that the surface curvature’s complexity significantly affects both the
and runtime of the optimization. The resultant discrete shell alternatives in
Figure 7a,b resulted in lower
numbers compared to the other shapes while satisfying the error metrics due to their relatively less complex surface curvature characteristics. Also, the discrete shell alternatives with singularities (
Figure 7c,d) resulted in higher
values since the number of singularities significantly increases the geometrical differences in initial mesh faces. In addition, the distribution of discrete shells into relative sets depends on the geometrical variety in the faces of discretized geometries. The initial geometrical variety among the discrete faces caused by the singularities affects the element distribution within the sets. Therefore, the optimization of the shapes that included initial singularities in their geometries resulted in relatively small sets to satisfy the similarity threshold. The element distribution within the sets for each shape is outlined in
Table 2.
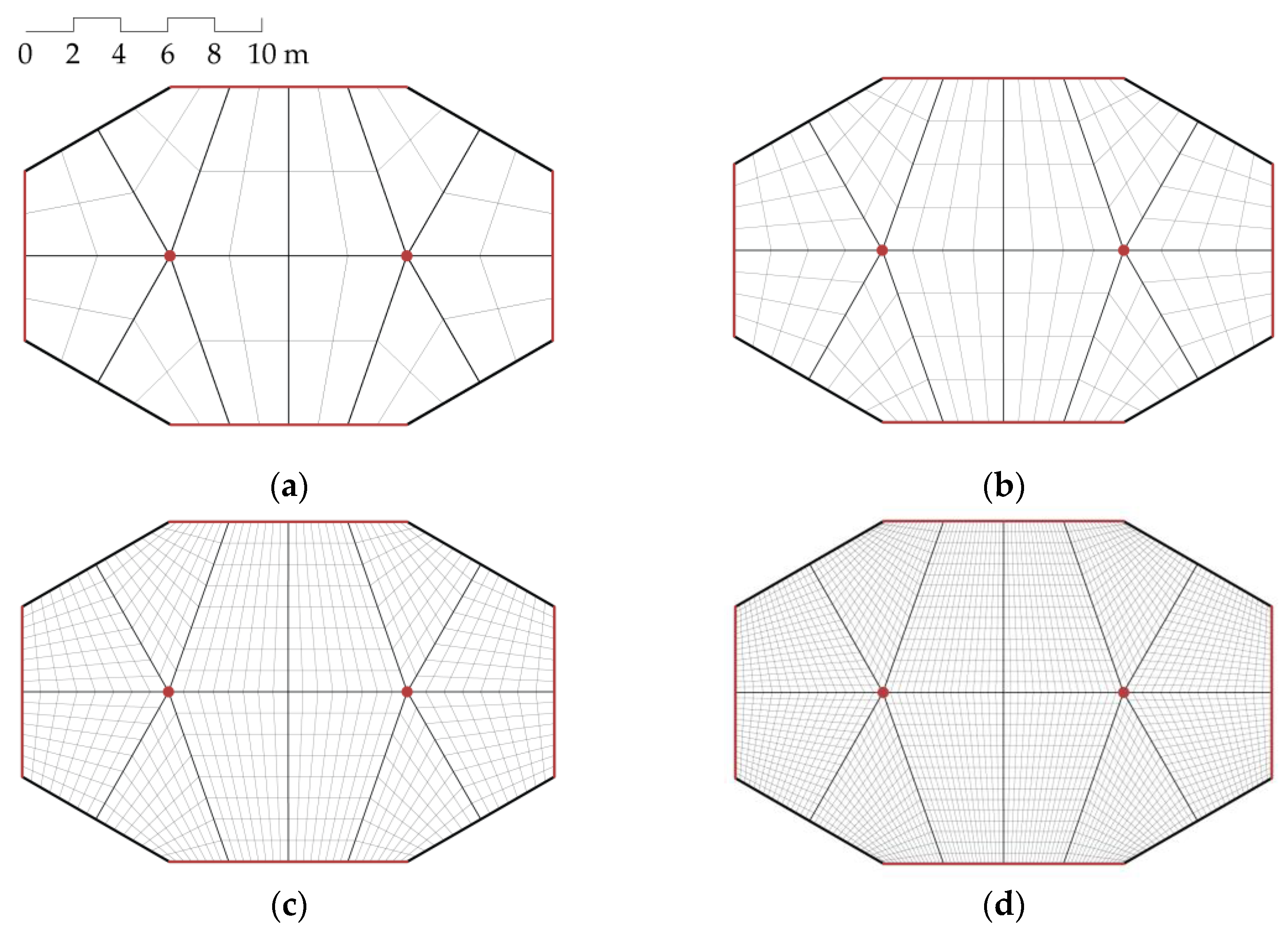
In the second part of our experiments, we employed similar structured meshes except for their face count to test the effect of the number of faces. To achieve this, we employed a 2D structured mesh and we applied a recursive subdivision procedure to generate alternatives with the same boundary conditions and support settings while only having different face counts. The resultant geometries of subdivision implementation are presented in
Figure 8 with their resultant face counts. The subdivision process is guided by predefined edges to generate only quadrilateral mesh faces. Also, each shape has the same number of singularities. The optimized discrete shell alternatives for Case 2 are presented in
Figure 8, and the numerical data of our implementation is outlined in
Table 3.
The resultant discrete topologies have support vertices and boundary vertices as well as singularities in their geometries while their smooth surface approximation has relatively complex curvature characteristics. Besides the surface complexity, we confirmed that the face count also directly affects the convergence time and error metrics. The optimization algorithm was able to find suitable design alternatives that satisfy the error metrics starting from
for the shape with the lowest face count (
Figure 9a) in comparison to the other alternatives. The number of sets that include equivalent elements has a proportional relationship to the total face count; the geometry with the largest face count of (
) satisfied the error metrics with the largest
, comparatively. Also, the increase in the number of faces resulted in lower surface approximation and the maximum facing angle deviation error metrics while requiring more computation time to satisfy the similarity metric. In addition, we confirmed that the initial geometrical variety of the discrete geometry highly influences the distribution of elements in their respective sets based on similarity. The resultant element distribution is outlined in
Table 4.
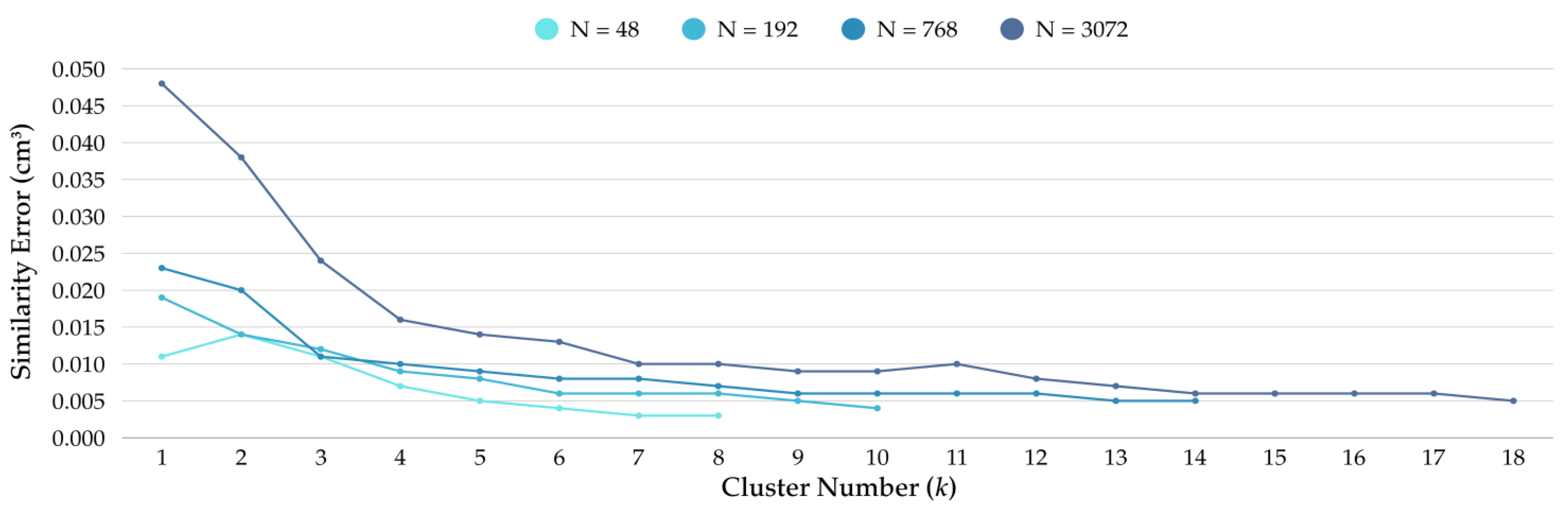
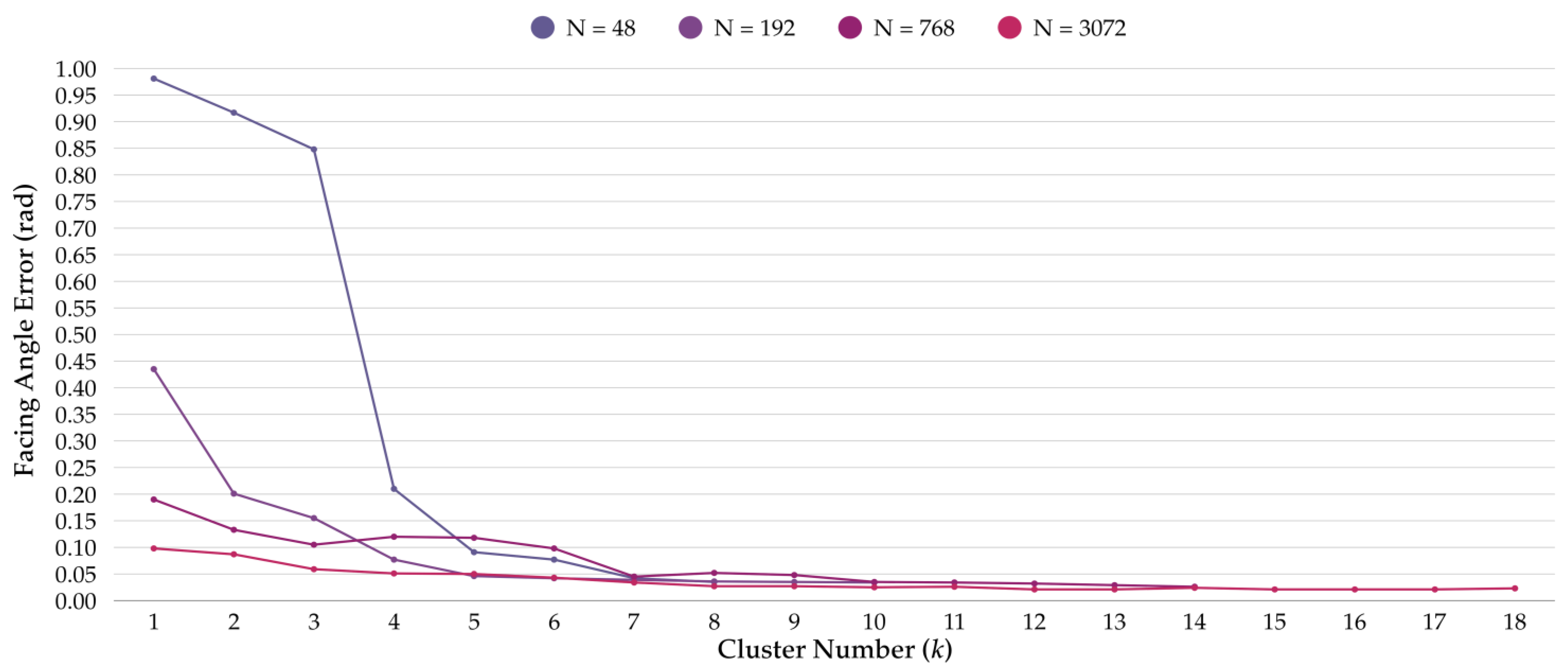
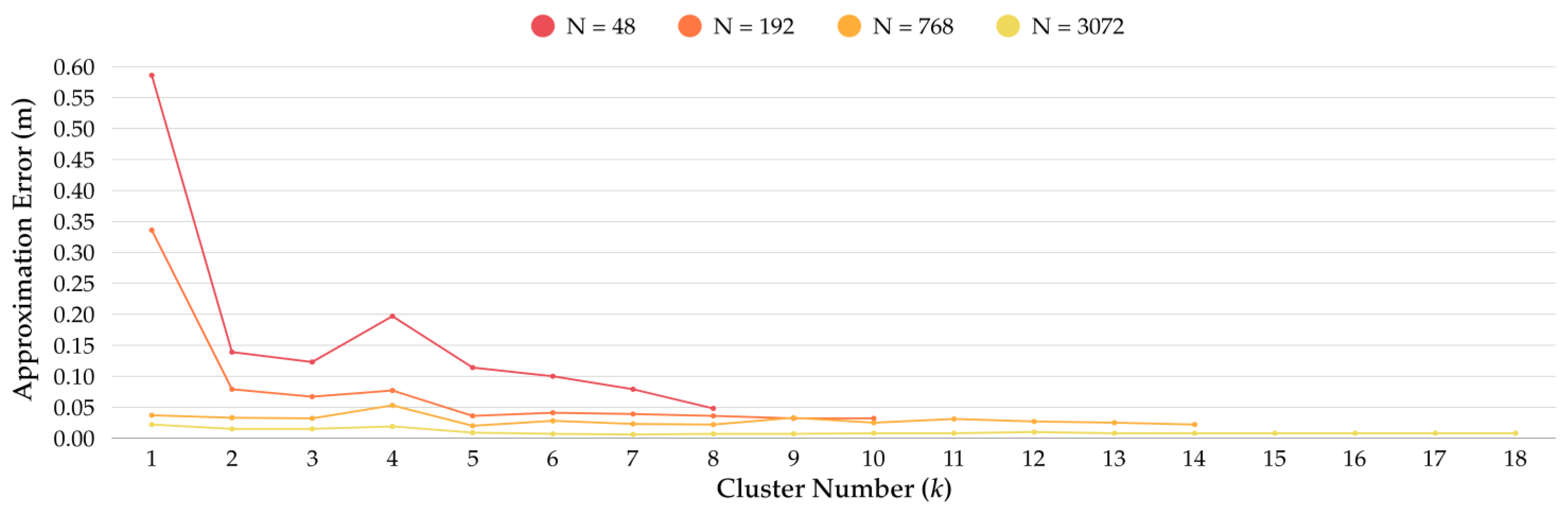
Figure 10,
Figure 11 and
Figure 12 present the convergence histories for the error metrics regarding the similarity error
, the facing angle error
, and the surface approximation error
in relation to the number of sets
. The performance of these metrics was evaluated across multiple mesh densities. These plots address both the optimization performance and the influence of mesh refinement on the results. In the plots, the curves show a steep initial decrease in error values during the early iterations, followed by a gradual stabilization, indicating consistent convergence behavior. Coarser meshes exhibit higher starting errors and more substantial early reductions, whereas finer meshes begin with lower errors and converge more gradually, reflecting a smaller margin for improvement. This pattern highlights a fundamental trade-off: coarse meshes offer greater computational efficiency but may fail to capture important geometric and structural details. In contrast, finer meshes provide higher fidelity at the cost of longer processing times. In the context of shell structures, these observations are structurally relevant since mesh size directly affects the accuracy of curvature representation, the identification of potential stress concentrations, and the precision of assembly tolerances. The presented convergence plots thus provide both a quantitative record of optimization progress and a practical reference for selecting mesh densities that balance geometric accuracy, computational cost, and fabrication constraints.
The runtime results in
Table 1 and
Table 3 reflect the direct influence of mesh density on computational costs. Higher mesh resolutions lead to longer runtimes due to the quadratic growth of pairwise similarity calculations during clustering. Despite this, convergence plots in
Figure 10,
Figure 11 and
Figure 12 indicate that the majority of optimization progress occurs within the first 30–40% of iterations, after which improvements taper off. This trend suggests that early termination strategies could be implemented to improve computational efficiency without significantly compromising solution quality. Furthermore, the algorithm generated a nearly uniform distribution of elements within the sets when the input discrete topologies had no singularities and their double-curved surface approximations had relatively simple surface curvatures. In contrast, optimizing geometries with singularities resulted in significant deviations in the number of elements in their respective sets, as the algorithm prioritizes the separation of significantly different geometries into their respective sets. In addition, the geometries that possess inherent symmetries are employed in this study. It was observed that, although there is no integration of symmetry recognition procedures in the workflow, the approach was efficient enough to create nearly symmetrical discrete shell results, as shown in
Figure 13.
4. Discussion
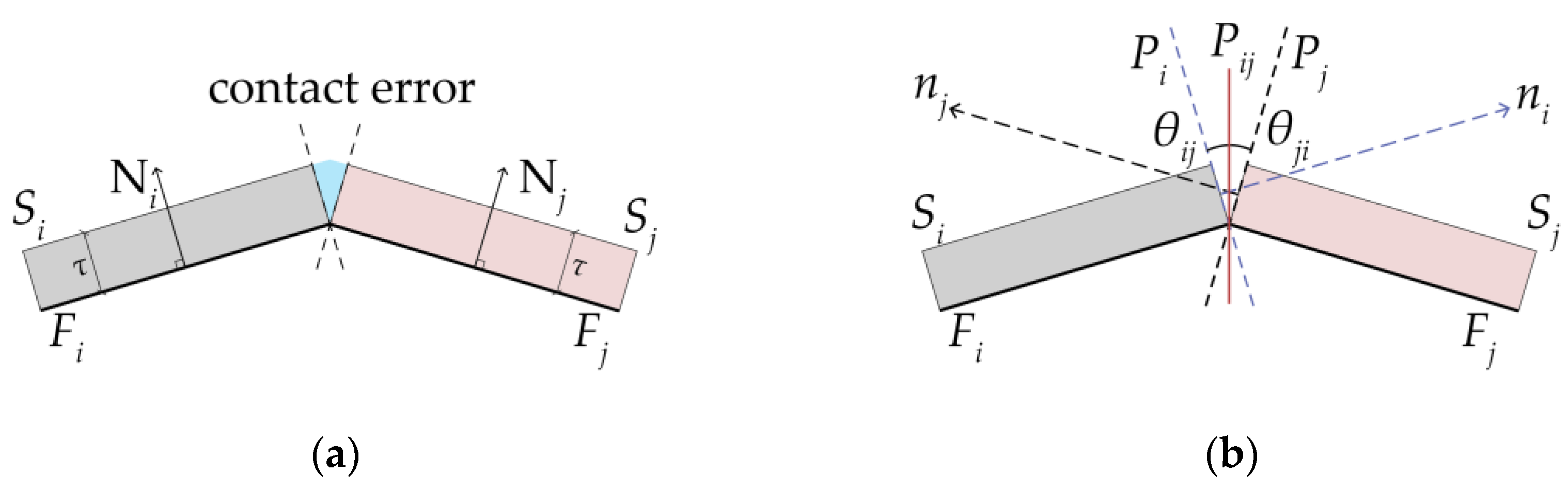
This study addresses the prominent rationalization challenge of utilizing geometries with discrete equivalence classes in architectural discrete shell design problems. Unlike existing methodologies, our approach focuses on minimizing the geometrical variety of discrete shell elements through a computational workflow that integrates relaxation-based form-finding, similarity-based clustering, and geometric optimization of discrete shell elements, considering user-defined thresholds for architectural appearance and fabrication constraints. The proposed method departs from prior work through three primary innovations. First, rather than operating solely at the surface/panel level, we generate 3D elements with explicit thickness and assess contact geometry between neighboring elements. Second, we introduce a facing angle objective (Equations (16)–(18)) that prioritizes assembly ready interfaces within prescribed tolerances. Third, the optimization jointly enforces cluster congruency (Equation (14)) and surface fidelity (Equation (15)) together with contact alignment in a single objective (Equation (19)), targeting mold reuse and repeatable fabrication. This combination is specifically oriented to prefabrication logistics (mold count reduction and tolerance management), which extends beyond the primary goals of prior clustering/panelization frameworks.
We applied quadrilateral discretization to the geometries to reduce the difference in the initial shape of elements and to prevent the generation of irregular shapes, especially near the boundaries. Our findings confirmed the hypothesis that employing planar quadrilateral meshes simplifies the initial geometric complexity and effectively reduces the shape variety in discrete members. The results demonstrate that discretization using structured quadrilateral meshes generated by the computational form-finding process allows the creation of element groups with minimal variation. As the comparative tests demonstrate, meshes without singularities and with relatively simple boundary conditions require fewer discrete equivalence classes and converge faster, aligning with prior studies that emphasize the benefits of structured meshing in reducing geometric complexity. The face count of the discrete meshes directly affects the complexity and efficiency of the optimization process. The results show a clear correlation between increased mesh density, improved double-curved surface approximation, and reduced facing angle deviation in the expanse of increased computation time. Also, an interesting aspect of the research was the observed optimization accuracy to preserve inherent symmetries in optimized discrete shell design alternatives. Despite complex geometric configurations, the optimization process consistently resulted in near-symmetrical outputs, which contributed to further reducing the set numbers. This implicit recognition of symmetry is a byproduct of the clustering procedure rather than a targeted optimization objective. Integrating explicit symmetry metrics or symmetry-aware optimization methods could further enhance repetition rates and mold reusability, and is identified as a promising direction for future development.
In practical terms, the cluster count produced by our method directly specifies the mold count required for prefabrication. At the same time, the per-cluster element lists define production batches and reuse schedules. The facing angle metric serves as a tolerance proxy for assembly that indicates whether dry-fit contact is feasible or whether shimming/adjustable joints are required. The surface approximation metric informs finishing and machining allowances. Furthermore, the optimized geometries can be directly exported from Rhino as surface or solid meshes and imported into standard FEA software in STEP or IGES format. For discrete element analysis, each panel is exported as an individual solid with defined contact interfaces. This allows structural engineers to perform FEA on the same discretization and, if necessary, request targeted mesh refinement in critical regions.
Several limitations arise from our study that necessitate further exploration. Although clustering and optimization effectively reduce geometric variety, inherent complexities associated with structures featuring singularities or complex boundaries remain. Such cases increase computational time and the minimum number of discrete equivalence sets. While the method has been successfully applied to meshes with up to 3072 faces, scalability remains a challenge, as the computational cost increases non-linearly with mesh size. Large or highly irregular meshes require longer runtimes and more memory resources due to the similarity assessment step, which involves calculating pairwise distances between elements. The quality of the initial mesh is also a factor in achieving stable convergence since poorly shaped or irregularly proportioned meshes may slow optimization and lead to less efficient clustering outcomes. Future research could focus on advanced clustering algorithms or adaptive discretization strategies to handle such complexities more efficiently by creating fewer sets with a uniform distribution of elements. Furthermore, the approach depends on user-defined thresholds for similarity tolerances, which are case-specific. While this flexibility enables adaptation to various fabrication contexts, it also means that the results are sensitive to these input parameters. In this regard, the presented convergence histories (
Figure 10,
Figure 11 and
Figure 12) and runtime data (
Table 1 and
Table 3) offer guidance for selecting practical mesh densities and stopping criteria.
The facing angle optimization evaluates the planarity of the transverse faces of the neighboring discrete shell elements. However, minor curvature or fabrication deviations could cause local misalignments in practice. This limitation could be mitigated by tolerance-based clustering or adjustable joint interfaces. Also, the practical challenges of assembling discrete shell structures without temporary scaffolding or support elements remain unresolved within the scope of our current study. Although we have optimized geometric alignment and minimized facing angles, physical assembly feasibility and structural stability during assembly require further in-depth investigation, which opens up interesting directions for research that include integrated robotic fabrication techniques or automated assembly sequencing strategies.
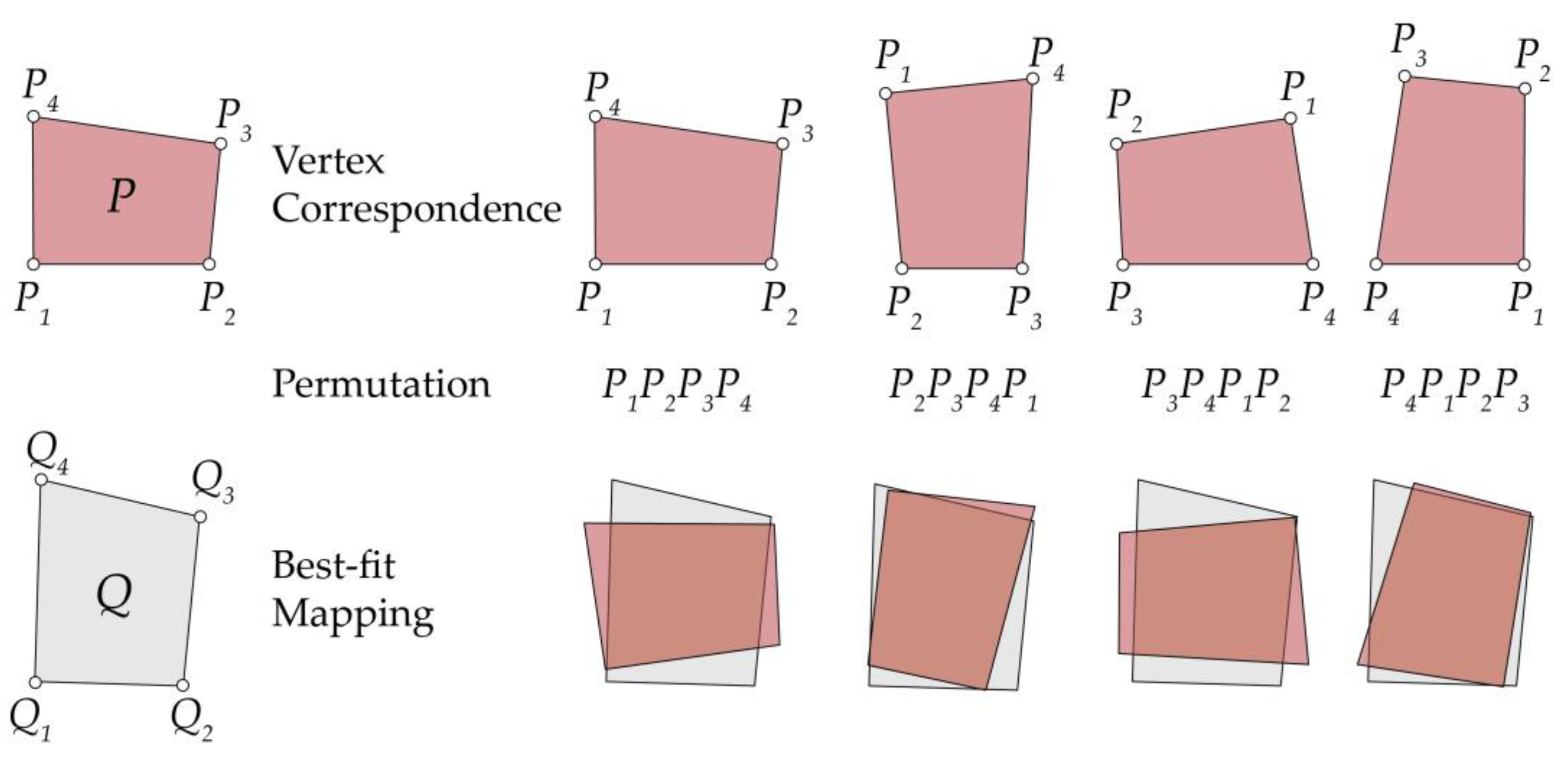
The similarity metric in Equation (12) is defined in terms of Euclidean vertex-to-vertex distances between corresponding mesh faces. This choice ensures computational efficiency and maintains a consistent, material-independent basis for geometric comparison, which is essential for evaluating element congruency across varied mesh topologies. While this approach effectively captures geometric alignment, it does not directly account for fabrication-related factors such as angular deviations between face normals, variations in element thickness, or tolerance margins that may arise during manufacturing and assembly. Therefore, the introduced error metrics incorporate user-defined thresholds, which serve as case-specific specifications of allowable geometric deviation. These thresholds can be adjusted according to material thickness and fabrication precision requirements. Furthermore, flipping of mesh faces is not permitted during similarity-based optimization to ensure that surface normal directions remain consistent across all elements, preserving correct orientation for assembly. While the current framework allows for the adjustment of user-defined thresholds to reflect material thickness and tolerance requirements, future work could expand this capability to infer threshold values from material and process constraints automatically. In addition, embedding material anisotropy constraints, such as grain direction in timber or formwork-induced shrinkage in concrete, would allow the workflow to account for directional performance and deformation risks. Maintaining consistent surface normal orientation is already enforced in the current workflow to avoid geometric inconsistencies during assembly, and this constraint will remain critical in material-specific extensions.
While explicit structural analysis and physical prototyping are beyond the scope of the present work, several aspects of the proposed workflow inherently support structural plausibility and fabrication readiness. The form-finding stage produces geometries in static equilibrium, providing an efficient starting point for shell action. Low dihedral-angle deviations and a close approximation of the smooth surface suggest that the optimized forms can maintain efficient force flow under typical shell loading conditions. However, their self-supporting behavior may require further investigation and adjustments once integrated with structural analysis workflows. Although the mesh size here is chosen based on geometric rationalization goals, finer meshes can better capture stress gradients in structural analysis. Our method can accommodate varying mesh densities; however, the trade-off between fabrication simplification and structural accuracy requires further study. Due to minor contact errors, the relative structural performance assessment can be challenging using analysis methods such as the rigid-block equilibrium methods [
31,
32,
44]. Therefore, further studies could explore combined optimization frameworks incorporating structural performance criteria to enhance practical applicability. In addition, the proposed method can effectively reduce the geometrical variety in discrete shell members and allows the utilization of mold-based fabrication techniques. Testing the structural behavior and suitability of a specific material can be a direction for another study. Lastly, the fabrication of shell elements and physical experimentation could provide understanding to improve the proposed discrete shell design method.
5. Conclusions
This study addresses the prominent rationalization challenge of utilizing geometries with discrete equivalence classes in architectural discrete shell design problems. We formulated a clustering-based optimization procedure to generate sets of equivalent discrete shell members corresponding to a form-found discretized shell topology and its double-curved architectural surface approximation. We characterized several metrics to assess the similarity of elements within each set, evaluate the relationship between planar quad mesh faces and smooth surface approximation, and their buildability by minimizing the dihedral angle between shell elements’ contacting side faces and their optimal intersection plane. We tested our proposed algorithm by employing various 2D structured meshes with different characteristics, including boundary conditions, singularity and support definitions, and quad face counts. Our approach effectively allows the creation of discrete shell design alternatives based on sets of equivalent shell members corresponding to the decision variables and user-defined constraints. Across all tested cases, the proposed method reduced the number of unique element geometries by 68–92% relative to the initial mesh, while maintaining surface approximation errors below 0.05 m and facing angle deviations below 0.035 rad.
The methodological workflow consisted of relaxation-based computational form-finding, ensuring equilibrium-based geometries, followed by quad mesh planarization to generate a viable baseline for clustering. Subsequently, similarity-based clustering and optimization stages were executed to categorize and refine mesh faces into minimal groups of geometrically congruent elements. The final optimization stage addressed a crucial fabrication constraint by controlling the dihedral angles between neighboring shell elements, ensuring seamless assembly within defined fabrication tolerances. This optimization strategy successfully balanced the objectives of geometric approximation accuracy and element congruency.
We validated our approach through computational experimentation across multiple scenarios characterized by differing boundary conditions, support vertex settings, face counts, and singularities in discrete mesh topologies. The experiments showed the methodology’s adaptability, successfully optimizing geometries from simpler meshes without singularities to more complex configurations with multiple irregularities. Notably, structured quadrilateral discretization allowed the reduction in the geometric diversity, which is crucial in practical architectural applications that utilize prefabrication and mold-based manufacturing techniques. The quad-based discretization was proven to be especially effective, as it inherently minimizes geometric variance and supports symmetrical clustering patterns. The computational experiments highlighted the inherent capability of the proposed optimization methodology to recognize symmetry. This feature significantly reduced the number of unique prefabricated molds required, further minimizing manufacturing complexity and cost.
Overall, the proposed method contributes to computational design studies in architecture by providing a viable strategy for rationalizing and simplifying discrete shell structures. This study presents an innovative computational design approach to address the complexities associated with discrete shell structures, with a primary aim of significantly reducing the number of unique geometric elements. The results clearly demonstrate the method’s effectiveness in managing geometric complexity and systematically minimizing variations among discrete shell elements, which not only contributes to more practical and economical fabrication processes but also allows the utilization of mold-based prefabrication techniques in the discrete shell design problems.