Dynamic BIM-Driven Framework for Adaptive and Optimized Construction Projects Scheduling Under Uncertainty
Abstract
1. Introduction
1.1. BIM for Cost Estimation and Scheduling
1.2. Simulation-Based Scheduling in Construction
1.3. System Dynamics in Construction Management
1.4. Labor Productivity
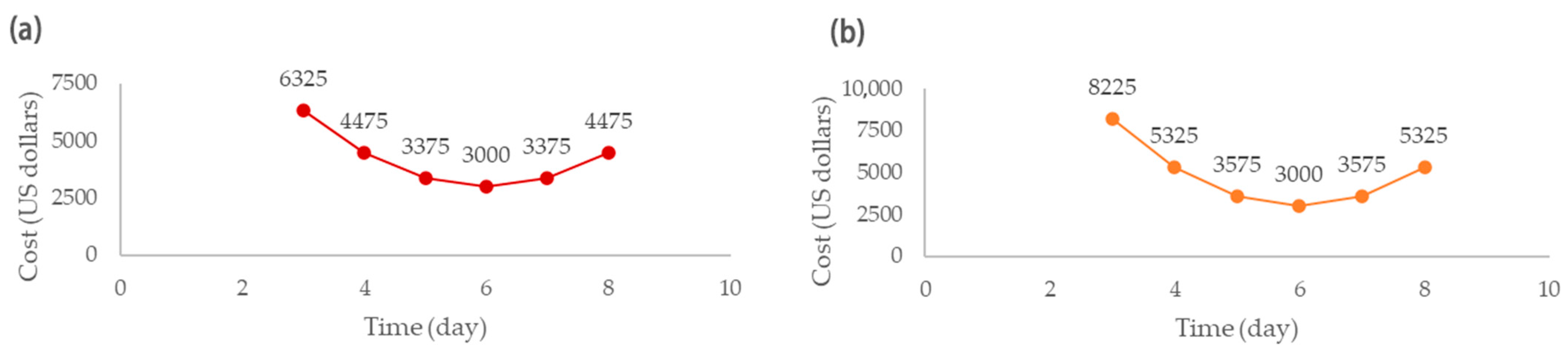
1.5. Nonlinear Relationship Between Time and Cost
1.6. ACOR Optimization Algorithm for Scheduling
2. Research Significance and Identified Gaps
- Development of a dynamic construction scheduling framework that integrates BIM, Discrete Event Simulation (DES), system dynamics (SD), and the ACOR optimization algorithm.
- Modeling and incorporating nonlinear time–cost relationships that evolve dynamically based on real-time productivity and budget constraints.
- Seamless integration of productivity-driven SD simulations into scheduling processes, enabling adaptive decision-making in uncertain construction environments.
- Demonstrating the effectiveness of the proposed model through validation using real project data, showing measurable improvements in scheduling accuracy and cost control.
- Addressing the limitations of static BIM optimization frameworks by enabling real-time schedule reoptimization based on project-specific changes.
3. Methodology
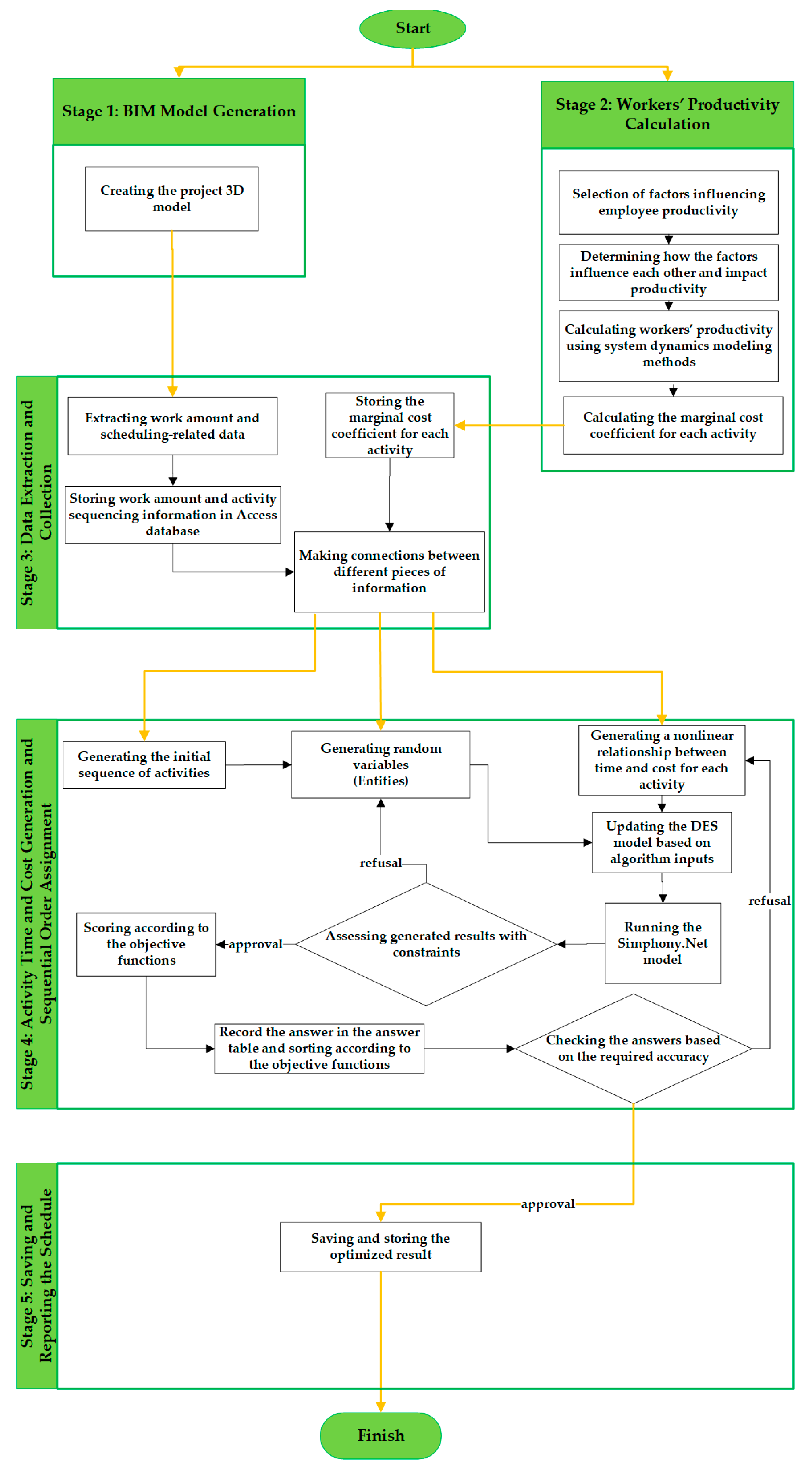
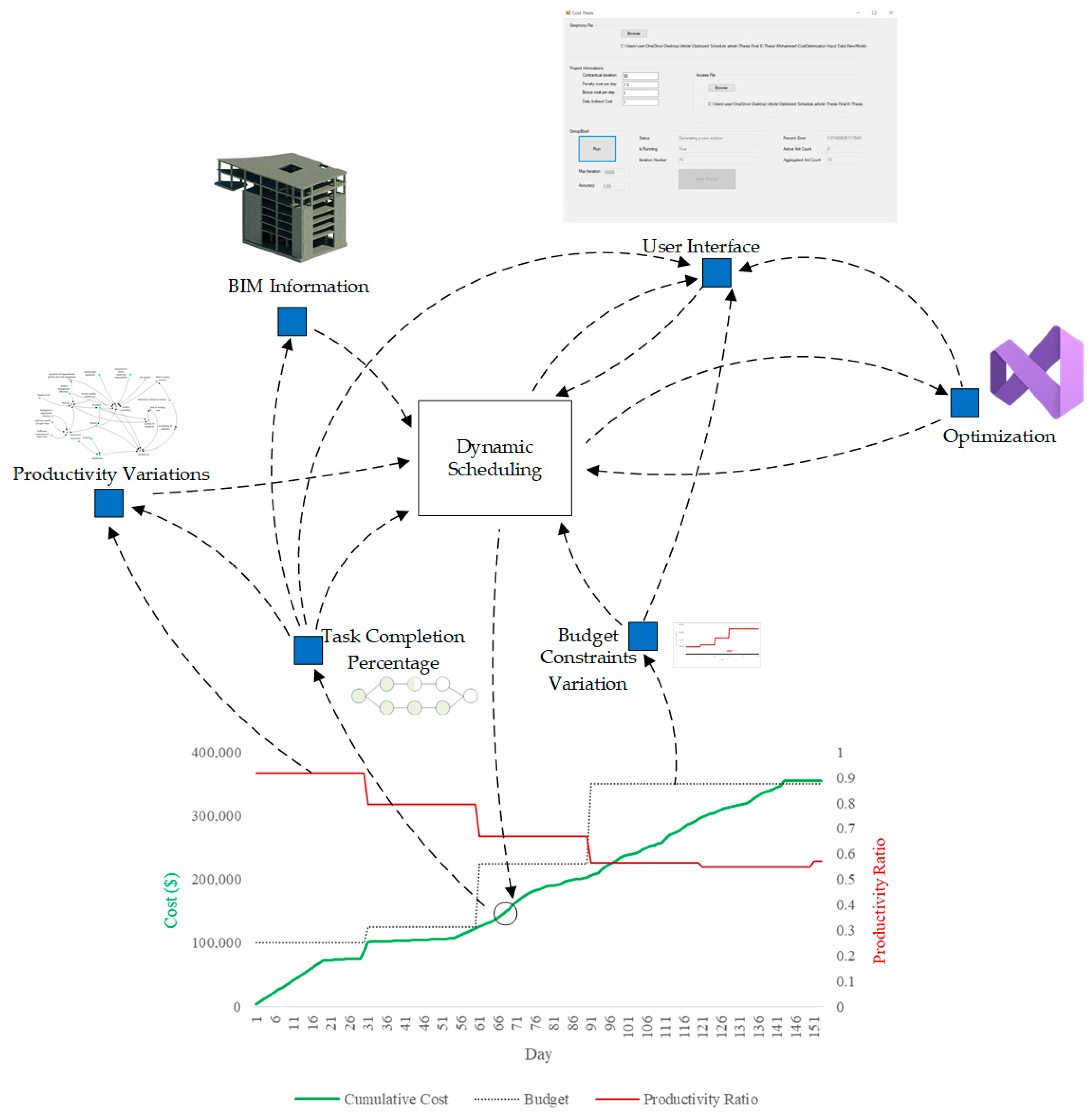
3.1. The Process of Tool Implementation
BIM Model Generation
3.2. Calculation of Workers’ Productivity
System Dynamics Modeling
3.3. Data Extraction and Collection
3.4. Activities’ Time, Cost, and Sequential Order
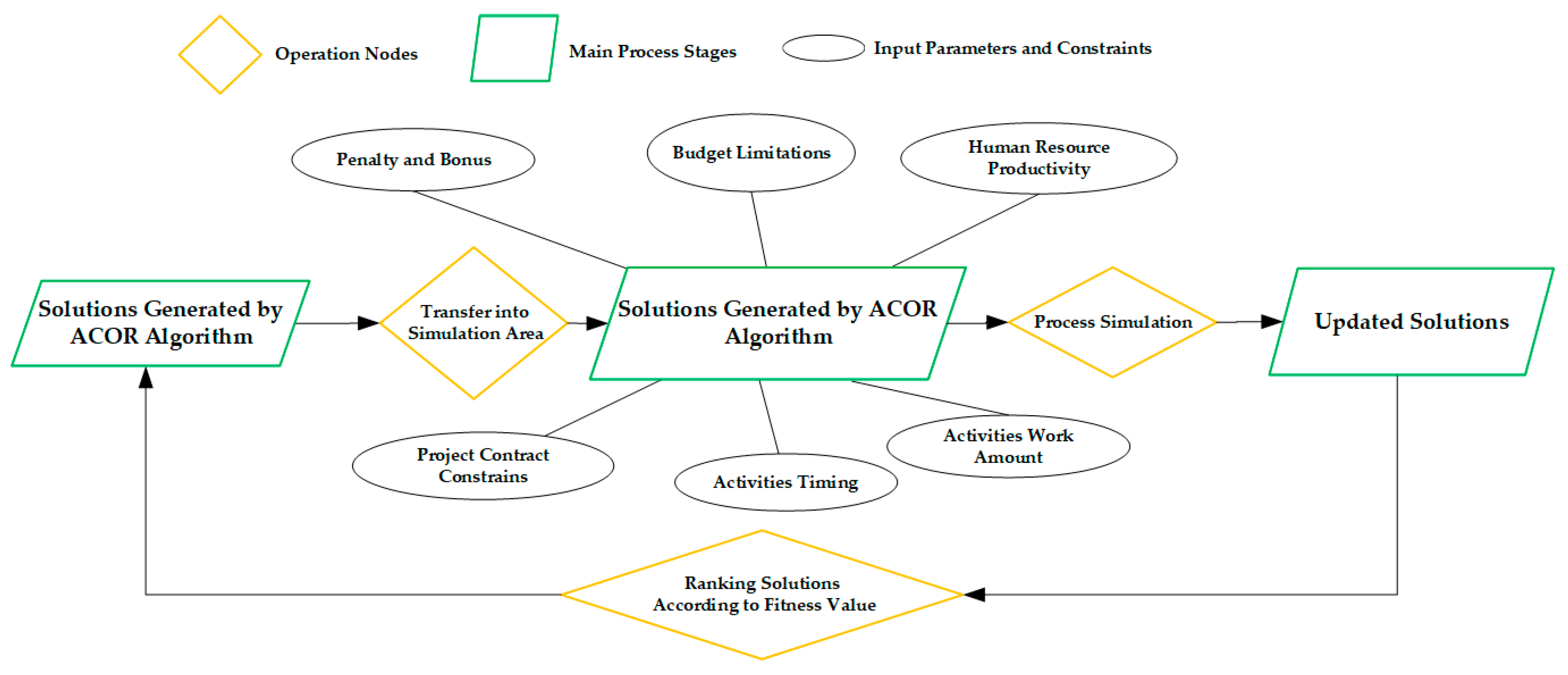
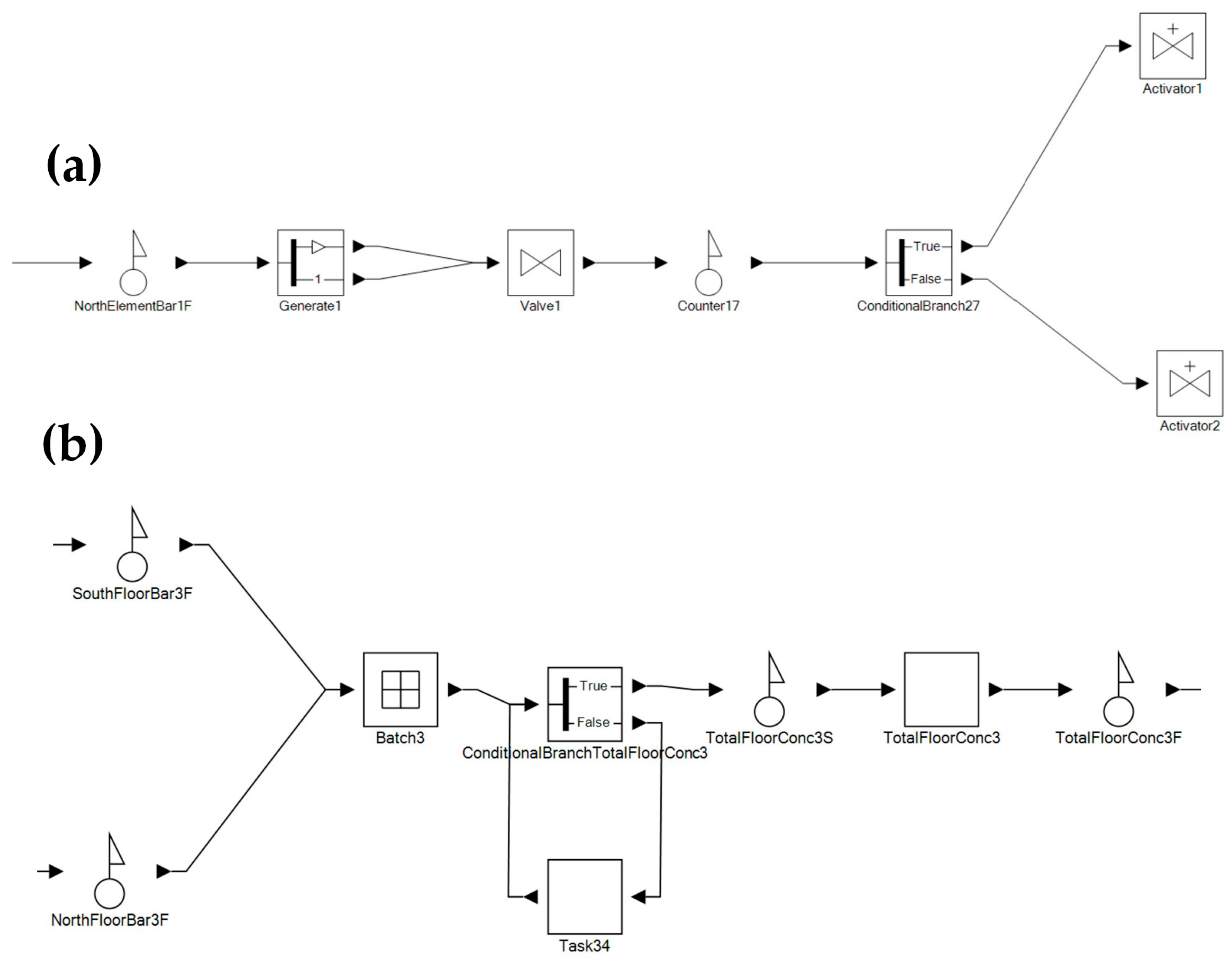
3.5. Process Simulation and ACOR Integrated Performance
3.6. Implementation of ACOR Algorithm
- 1-
- No valid solution: If all solutions are invalid, the optimization stops to prevent the propagation of invalid results, improving speed and performance.
- 2-
- Distribution-based criteria: In population-based algorithms, termination occurs when solutions cluster near the optimum. This can be measured using decision variables, objective function, or both [48]. Given that ACOR is a population-based algorithm, such a criterion is used for termination [49]. ACOR takes the following approach: when the normalized improvement of the best solution falls below a defined threshold, the population is considered converged and optimization stops. In this study, convergence was assessed using Formula (4), with a threshold (Acc set at 5%).
- 3-
- Exhaustion-based criteria: A maximum iteration limit is set to prevent excessive computational load. Once this limit is reached, the algorithm terminates. In this study, the maximum number of iterations was set to 10,000.
4. Results
4.1. Model Validation
4.2. Estimation of Workers’ Productivity over Time
4.3. Optimization Results
4.4. Improved Scheduling Accuracy and Dynamic Scheduling
5. Discussion
6. Conclusions
- The use of enriched data from a BIM model significantly improves the accuracy of work quantity evaluations, which in turn improves the precision of activity duration estimates at each stage of the project. Integrating BIM with construction process simulation allows constraints such as budget limits and activity sequences to be seamlessly incorporated, giving stakeholders a clearer understanding of project progress and planning.
- The inclusion of the factors that affect productivity and accounting for monthly budget limits improved the accuracy of estimating the overall project completion time by 33%. In addition, the use of SD allows both direct and indirect factors influencing productivity over time to be considered, providing greater flexibility in identifying the causes of productivity fluctuations throughout the project.
- Through the integration of system dynamics, BIM, process simulation, and optimization produced notable improvements, including a 4% reduction in total costs compared with real-world execution and a 9% decrease in project duration. The optimization process proved highly effective, reducing the error margin to 6.7% after 10,000 iterations, with project duration shortened by 3% and costs reduced by 15%.
- The integration of BIM, SD, and process simulation with optimization improved project management by utilizing enriched data, dynamically incorporating productivity factors, and efficiently integrating constraints and optimization steps. This resulted in a more efficient and accurate project execution.
- Despite the demonstrated benefits of the proposed dynamic BIM-driven scheduling framework, several limitations must be acknowledged. First, the model requires accurate and high-resolution productivity data, which may not always be readily available in all construction contexts. Second, the implementation assumes a certain level of BIM maturity and technical expertise, which could be a barrier for small- to mid-scale firms. Third, the model’s computational demands are relatively high due to the simulation of complex project activities across multiple zones, which may limit its real-time deployment for very large or complex projects.
- Future research could explore the integration of machine learning techniques to predict productivity trends and automate parameter tuning in the ACOR algorithm. Additionally, expanding the model’s applicability to different types of construction projects (e.g., infrastructure or residential housing) and validating it across various geographic and regulatory contexts would enhance its generalizability. Lastly, cloud-based deployment and user-interface simplification could help make the tool more accessible to practitioners in the industry.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BIM | Building Information Modeling |
| ACOR | Continuous Ant Colony Optimization |
| DES | Discrete Event Simulation |
| GA | Genetic Algorithm |
| QTO | Quantity Take-Off |
| PERT | Program Evaluation and Review Technique |
| CPM | Critical Path Method |
| SD | System Dynamics |
| QPI | Quality Performance Index |
References
- Love, P.E. Auditing the indirect consequences of rework in construction: A case based approach. Manag. Audit. J. 2002, 17, 138–146. [Google Scholar] [CrossRef]
- AlSehaimi, A.O.; Tzortzopoulos, P.; Koskela, L.J. Improving construction management practice with the Last Planner System: A case study. Eng. Constr. Archit. Manag. 2014, 21, 51–64. [Google Scholar] [CrossRef]
- Newell, A.; Simon, H.A. Human Problem Solving; Prentice-Hall: Englewood Cliffs, NJ, USA, 1972; ISBN 9781635617924. [Google Scholar]
- Chaarvika, I.; Bhatnagar, A.; Sammeta, R.; Balasubramanian, M.; Monisha, R. Comparison of Energy Analysis in a Residential Building Using Building Information Modeling. In Sustainable Construction Materials: Select Proceedings of ACMM 2021; Springer: Singapore, 2021; pp. 239–255. [Google Scholar]
- Haji, M.D.; Taghaddos, H.; Sebt, M.; Chokan, F.; Zavari, M. The effects of bim maturity level on the 4d simulation performance: An empirical study. Int. J. Eng. 2021, 34, 606–614. [Google Scholar] [CrossRef]
- Valinejadshoubi, M.; Moselhi, O.; Iordanova, I.; Valdivieso, F.; Bagchi, A. Automated system for high-accuracy quantity takeoff using BIM. Autom. Constr. 2023, 157, 105155. [Google Scholar] [CrossRef]
- Wang, W.-C.; Weng, S.-W.; Wang, S.-H.; Chen, C.-Y. Integrating building information models with construction process simulations for project scheduling support. Autom. Constr. 2014, 37, 68–80. [Google Scholar] [CrossRef]
- Khant, L.P.; Widjaja, D.D.; Kwon, K.; Kim, S. A BIM-Based Bar Bending Schedule Generation Algorithm with Enhanced Accuracy. Buildings 2024, 14, 1207. [Google Scholar] [CrossRef]
- Madihi, M.H.; Tafazzoli, M.; Javid, A.A.S.; Nasirzadeh, F. Probabilistic Cash Flow Analysis Considering Risk Impacts by Integrating 5D-Building Information Modeling and Bayesian Belief Network. Buildings 2025, 15, 1774. [Google Scholar] [CrossRef]
- Choi, J.; Kim, H.; Kim, I. Open BIM-based quantity take-off system for schematic estimation of building frame in early design stage. J. Comput. Des. Eng. 2014, 2, 16–25. [Google Scholar] [CrossRef]
- Wu, Z.; Ma, G. Automatic generation of BIM-based construction schedule: Combining an ontology constraint rule and a genetic algorithm. Eng. Constr. Arch. Manag. 2022, 30, 5253–5279. [Google Scholar] [CrossRef]
- Preece, C.N.; Barati, R.; Charehzehi, A. Enhancing planning and scheduling program by using benefits of BIM-based applications. Civ. Environ. Res. 2013, 3, 41–48. [Google Scholar]
- Wainer, G. Discrete-Event Modeling and Simulation: A Practitioner’s Approach; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Lu, W.; Olofsson, T. Building information modeling and discrete event simulation: Towards an integrated framework. Autom. Constr. 2014, 44, 73–83. [Google Scholar] [CrossRef]
- Abbasi, S.; Taghizade, K.; Noorzai, E. BIM-based combination of takt time and discrete event simulation for implementing just in time in construction scheduling under constraints. J. Constr. Eng. Manag. 2020, 146, 04020143. [Google Scholar] [CrossRef]
- AbouRizk, S.M.; Wales, R.J. Combined discrete-event/continuous simulation for project planning. J. Constr. Eng. Manag. 1997, 123, 11–20. [Google Scholar] [CrossRef]
- AbouRizk, S.; Halpin, D.; Mohamed, Y.; Hermann, U. Research in modeling and simulation for improving construction engineering operations. J. Constr. Eng. Manag. 2011, 137, 843–852. [Google Scholar] [CrossRef]
- AbouRizk, S. Role of simulation in construction engineering and management. J. Constr. Eng. Manag. 2010, 136, 1140–1153. [Google Scholar] [CrossRef]
- Dashti, M.S.; RezaZadeh, M.; Khanzadi, M.; Taghaddos, H. Integrated BIM-based simulation for automated time-space conflict management in construction projects. Autom. Constr. 2021, 132, 103957. [Google Scholar] [CrossRef]
- Lu, M.; Lam, H.-C.; Dai, F. Resource-constrained critical path analysis based on discrete event simulation and particle swarm optimization. Autom. Constr. 2008, 17, 670–681. [Google Scholar] [CrossRef]
- Konig, M.; Koch, C.; Habenicht, I.; Spieckermann, S. Intelligent BIM-based construction scheduling using discrete event simulation. In Proceedings of the 2012 Winter Simulation Conference (WSC), Berlin, Germany, 9–12 December 2012; pp. 1–12. [Google Scholar]
- Peña-Mora, F.; Han, S.; Lee, S.; Park, M. Strategic-operational construction management: Hybrid system dynamics and discrete event approach. J. Constr. Eng. Manag. 2008, 134, 701–710. [Google Scholar] [CrossRef]
- Wang, W.-C.; Demsetz, L.A. Model for evaluating networks under correlated uncertainty—NETCOR. J. Constr. Eng. Manag. 2000, 126, 458–466. [Google Scholar] [CrossRef]
- Haji, M.D.; Behnam, B.; Sebt, M.H.; Ardeshir, A.; Katooziani, A. BIM-based safety leading indicators measurement tool for construction sites. Int. J. Civ. Eng. 2022, 21, 265–282. [Google Scholar] [CrossRef]
- Barbosa, F.; Woetzel, J.; Mischke, J.; Ribeirinho, M.J.; Sridhar, M.; Parsons, M.; Bertram, N.; Brown, S. Reinventing Construction: A Route of Higher Productivity; McKinsey Global Institute: New York, NY, USA, 2017. [Google Scholar]
- Imagining Construction’s Digital Future McKinsey & Company. Available online: https://www.mckinsey.com/capabilities/operations/our-insights/imagining-constructions-digital-future (accessed on 18 January 2024).
- Ashcraft, H. Transforming project delivery: Integrated project delivery. Oxf. Rev. Econ. Policy 2022, 38, 369–384. [Google Scholar] [CrossRef]
- Al-Kofahi, Z.G.; Mahdavian, A.; Oloufa, A. System dynamics modeling approach to quantify change orders impact on labor productivity 1: Principles and model development comparative study. Int. J. Constr. Manag. 2020, 22, 1355–1366. [Google Scholar] [CrossRef]
- Leon, H.; Osman, H.; Georgy, M.; Elsaid, M. System dynamics approach for forecasting performance of construction projects. J. Manag. Eng. 2018, 34, 04017049. [Google Scholar] [CrossRef]
- Nasirzadeh, F.; Nojedehi, P. Dynamic modeling of labor productivity in construction projects. Int. J. Proj. Manag. 2013, 31, 903–911. [Google Scholar] [CrossRef]
- Yao, H.; Shen, L.; Tan, Y.; Hao, J. Simulating the impacts of policy scenarios on the sustainability performance of infrastructure projects. Autom. Constr. 2011, 20, 1060–1069. [Google Scholar] [CrossRef]
- Porwal, A.; Parsamehr, M.; Szostopal, D.; Ruparathna, R.; Hewage, K. The integration of building information modeling (BIM) and system dynamic modeling to minimize construction waste generation from change orders. Int. J. Constr. Manag. 2020, 23, 156–166. [Google Scholar] [CrossRef]
- John, S. System Dynamics: Systems Thinking and Modeling for a Complex World; Massachusetts Institute of Technology: Cambridge, MA, USA, 2002. [Google Scholar]
- Ballesteros-Pérez, P.; Elamrousy, K.M.; González-Cruz, M.C. Non-linear time-cost trade-off models of activity crashing: Application to construction scheduling and project compression with fast-tracking. Autom. Constr. 2019, 97, 229–240. [Google Scholar] [CrossRef]
- Deckro, R.F.; Hebert, J.E.; Verdini, W.A.; Grimsrud, P.H.; Venkateshwar, S. Nonlinear time/cost tradeoff models in project management. Comput. Ind. Eng. 1995, 28, 219–229. [Google Scholar] [CrossRef]
- Zhang, L.; Du, J.; Zhang, S. Solution to the time-cost-quality trade-off problem in construction projects based on immune genetic particle swarm optimization. J. Manag. Eng. 2014, 30, 163–172. [Google Scholar] [CrossRef]
- Sigalov, K.; König, M. Recognition of process patterns for BIM-based construction schedules. Adv. Eng. Inform. 2017, 33, 456–472. [Google Scholar] [CrossRef]
- ElMenshawy, M.; Marzouk, M. Automated BIM schedule generation approach for solving time–cost trade-off problems. Eng. Constr. Arch. Manag. 2021, 28, 3346–3367. [Google Scholar] [CrossRef]
- Faghihi, V.; Reinschmidt, K.F.; Kang, J.H. Construction scheduling using genetic algorithm based on building information model. Expert Syst. Appl. 2014, 41, 7565–7578. [Google Scholar] [CrossRef]
- Faghihi, V. Automated and Optimized Scheduling Using BIM. Ph.D. Thesis, Texas A&M U niversity, College Station, TX, USA, 2014. [Google Scholar]
- Wefki, H.; Elnahla, M.; Elbeltagi, E. BIM-based schedule generation and optimization using genetic algorithms. Autom. Constr. 2024, 164, 105476. [Google Scholar] [CrossRef]
- Long, L.D. A non-unit repetitive construction project scheduling with uncertainties. Autom. Constr. 2024, 164, 105428. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, J.; Ning, W.; Yu, H.; Lin, S.; Wang, Z.; Pang, G.; Chen, C. A time-sensitive network scheduling algorithm based on improved ant colony optimization. Alex. Eng. J. 2021, 60, 107–114. [Google Scholar] [CrossRef]
- Li, H.; Zhang, H. Ant colony optimization-based multi-mode scheduling under renewable and nonrenewable resource constraints. Autom. Constr. 2013, 35, 431–438. [Google Scholar] [CrossRef]
- Socha, K.; Dorigo, M. Ant colony optimization for continuous domains. Eur. J. Oper. Res. 2008, 185, 1155–1173. [Google Scholar] [CrossRef]
- Tavakolan, M.; Chokan, F.; Haji, M.D. Simultaneous project portfolio selection and scheduling from contractor perspective. Int. J. Constr. Manag. 2023, 24, 298–313. [Google Scholar] [CrossRef]
- Mawdesley, M.J.; Al-Jibouri, S. Modelling construction project productivity using systems dynamics approach. Int. J. Prod. Perform. Manag. 2009, 59, 18–36. [Google Scholar] [CrossRef]
- Fernández-Vargas, J.A.; Bonilla-Petriciolet, A.; Rangaiah, G.P.; Fateen, S.-E.K. Performance analysis of stopping criteria of population-based metaheuristics for global optimization in phase equilibrium calculations and modeling. Fluid Phase Equilibria 2016, 427, 104–125. [Google Scholar] [CrossRef]
- Omran, M.G.; Al-Sharhan, S. Improved continuous Ant Colony Optimization algorithms for real-world engineering optimization problems. Eng. Appl. Artif. Intell. 2019, 85, 818–829. [Google Scholar] [CrossRef]

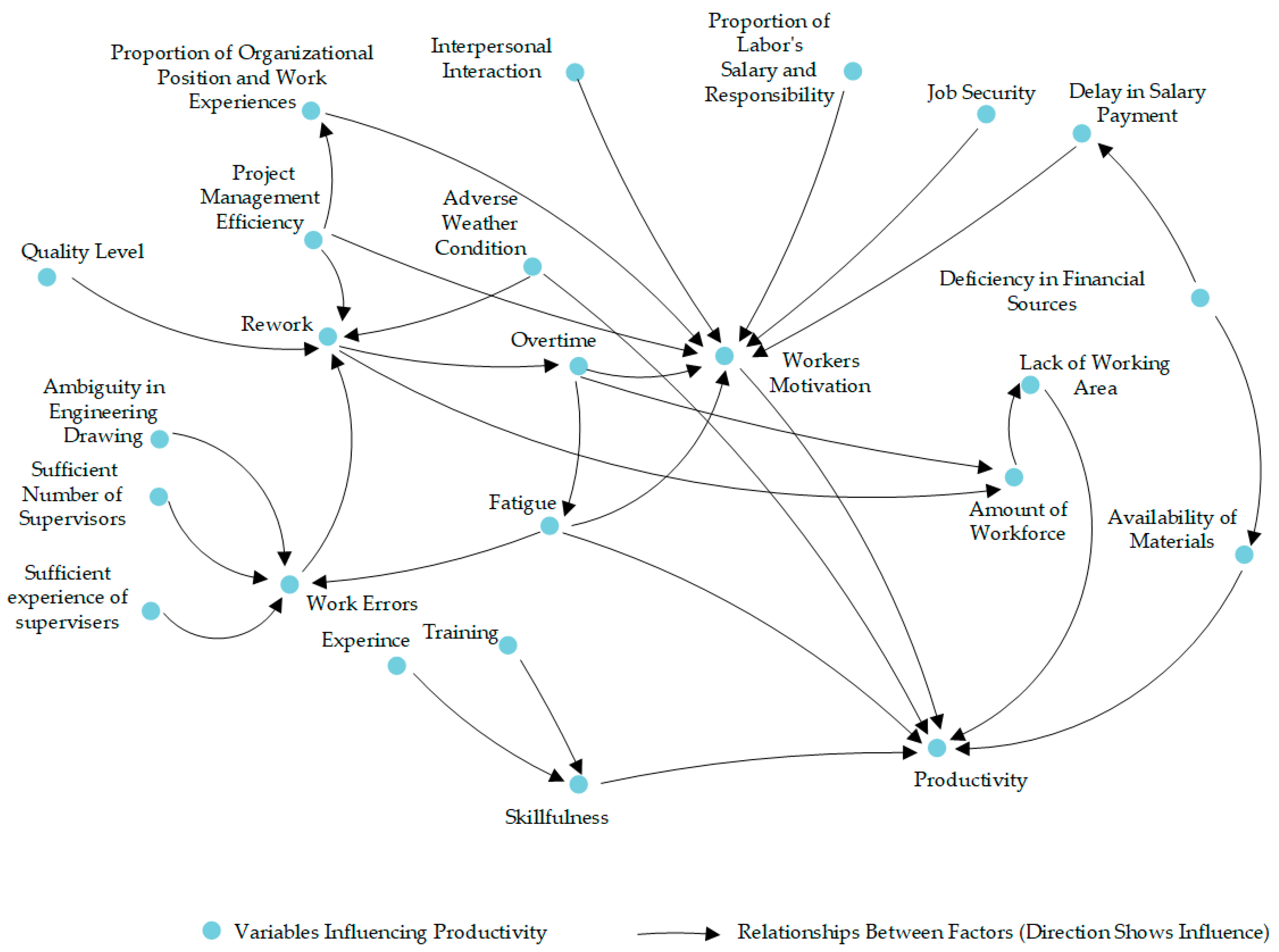

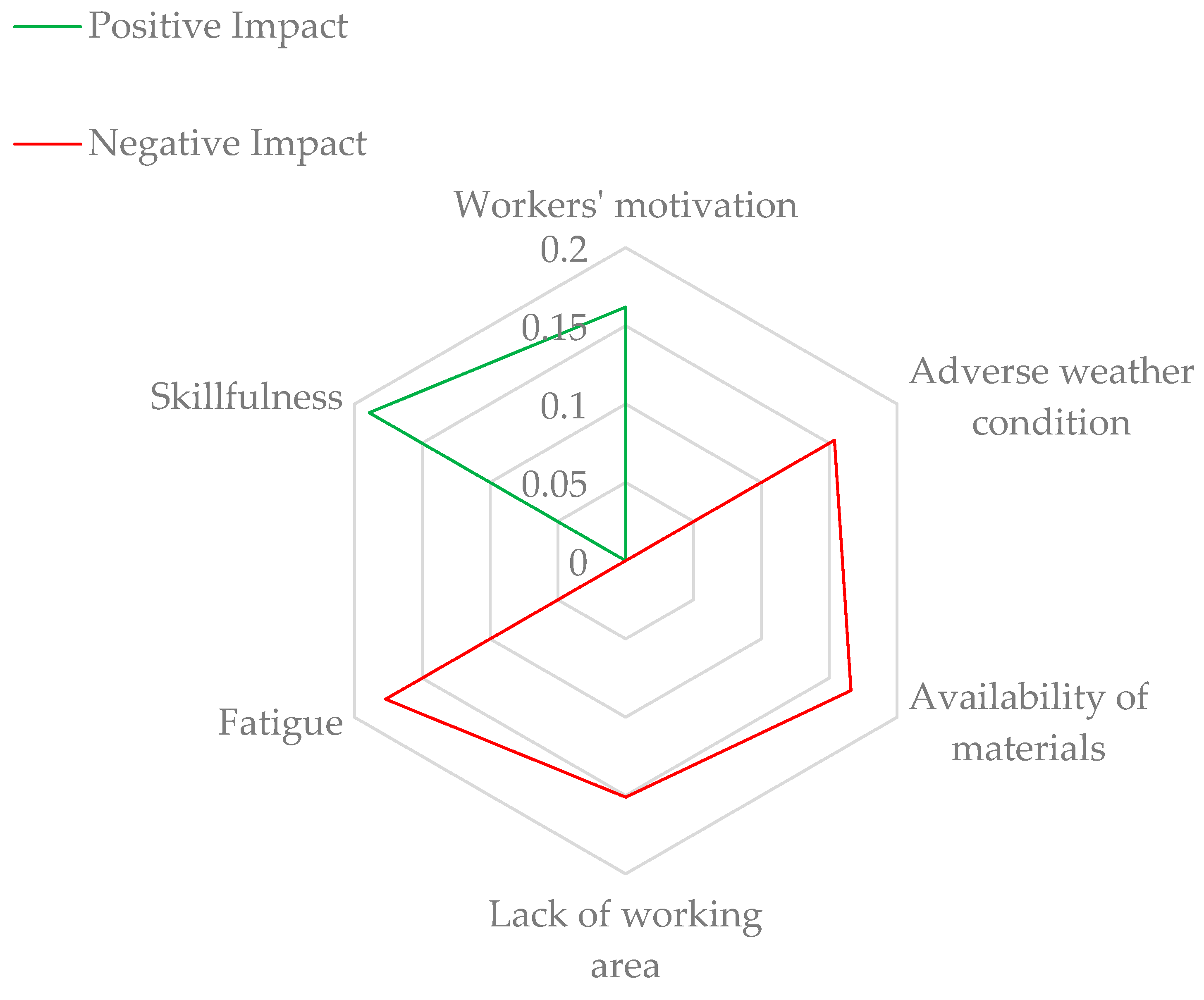
| Factors Affecting Employee Productivity | Worker Enthusiasm | Delays in Salary Payments | Fatigue | Workers’ Productivity |
|---|---|---|---|---|
| Workers’ Motivation | 0 | 0 | 0 | 0.162 |
| Job Security | 0 | 0.458 | 0 | 0 |
| Project Management Efficiency | 0.133 | 0 | 0 | 0 |
| Delays in Salary Payments | 0.145 | 0 | 0.469 | 0 |
| Skillfulness | 0 | 0 | 0 | 0.189 |
| Fatigue | 0.135 | 0 | 0 | 0.177 |
| Adverse Weather Conditions | 0 | 0 | 0 | 0.154 |
| Lack of Working Area | 0 | 0 | 0 | 0.151 |
| Availability of Materials | 0 | 0 | 0 | 0.166 |
| Month | Concrete Pouring (m3/Day) | Formwork (m2/Day) | Reinforcement (Tons/Day) |
|---|---|---|---|
| 1 | 27.87 | 9.19 | 0.38 |
| 2 | 24.18 | 7.95 | 0.33 |
| 3 | 20.38 | 6.70 | 0.28 |
| 4 | 17.20 | 5.64 | 0.23 |
| 5 | 16.78 | 5.49 | 0.23 |
| 6 | 17.49 | 5.72 | 0.24 |
| 7 | 17.53 | 5.76 | 0.24 |
| 8 | 17.59 | 5.77 | 0.24 |
| 9 | 17.53 | 5.82 | 0.24 |
| Scheduling Scenario | Total Cost (USD) | Total Time (Day) | Closure (Day) | Time Error Relative to the Actual Time | Cost Error Relative to the Actual Cost |
|---|---|---|---|---|---|
| Baseline Plan (Initial Prediction) | 300,750 | 90 | 0 | 41% | 16.5% |
| Actual Project Performance | 360,504 | 152 | 33 | 0% | 0% |
| Model Prediction—Without Optimization | 407,175 | 146 | 31 | 4% | 13% |
| Model Prediction—With Optimization | 347,686 | 142 | 28 | 6.6% | 3.5% |
| Scheduling Scenario | Total Cost (USD) | Total Time (Days) | ΔCost vs. Base Optimized | ΔTime vs. Base Optimized | Key Observations |
|---|---|---|---|---|---|
| Base Optimized Model | 347,686 | 142 | – | – | Balance of cost and time; continuous reoptimization |
| Model—Without Optimization | 407,175 | 146 | +17.1% | +2.8% | Static sequencing; higher cost despite slight time reduction vs. actual |
| Optimized Model (Productivity +10%) | 374,013 | 133 | +7.6% | −6.3% | Schedule compression; slight cost rise from resource acceleration |
| Optimized Model (Productivity −10%) | 376,645 | 147 | +8.3% | +3.5% | Cost increase from indirect costs and extended duration |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gandomkar Armaki, M.E.; Shirzadi Javid, A.A.; Omrani, S. Dynamic BIM-Driven Framework for Adaptive and Optimized Construction Projects Scheduling Under Uncertainty. Buildings 2025, 15, 3004. https://doi.org/10.3390/buildings15173004
Gandomkar Armaki ME, Shirzadi Javid AA, Omrani S. Dynamic BIM-Driven Framework for Adaptive and Optimized Construction Projects Scheduling Under Uncertainty. Buildings. 2025; 15(17):3004. https://doi.org/10.3390/buildings15173004
Chicago/Turabian StyleGandomkar Armaki, Mohammad Esmaeil, Ali Akbar Shirzadi Javid, and Shahrzad Omrani. 2025. "Dynamic BIM-Driven Framework for Adaptive and Optimized Construction Projects Scheduling Under Uncertainty" Buildings 15, no. 17: 3004. https://doi.org/10.3390/buildings15173004
APA StyleGandomkar Armaki, M. E., Shirzadi Javid, A. A., & Omrani, S. (2025). Dynamic BIM-Driven Framework for Adaptive and Optimized Construction Projects Scheduling Under Uncertainty. Buildings, 15(17), 3004. https://doi.org/10.3390/buildings15173004






