Study on Finite Element Modeling Method and Seismic Performance of Hybrid Connection Joints of Large-Span Frames
Abstract
1. Introduction
2. Comparison Between the CZM Method and Conventional Modeling Methods
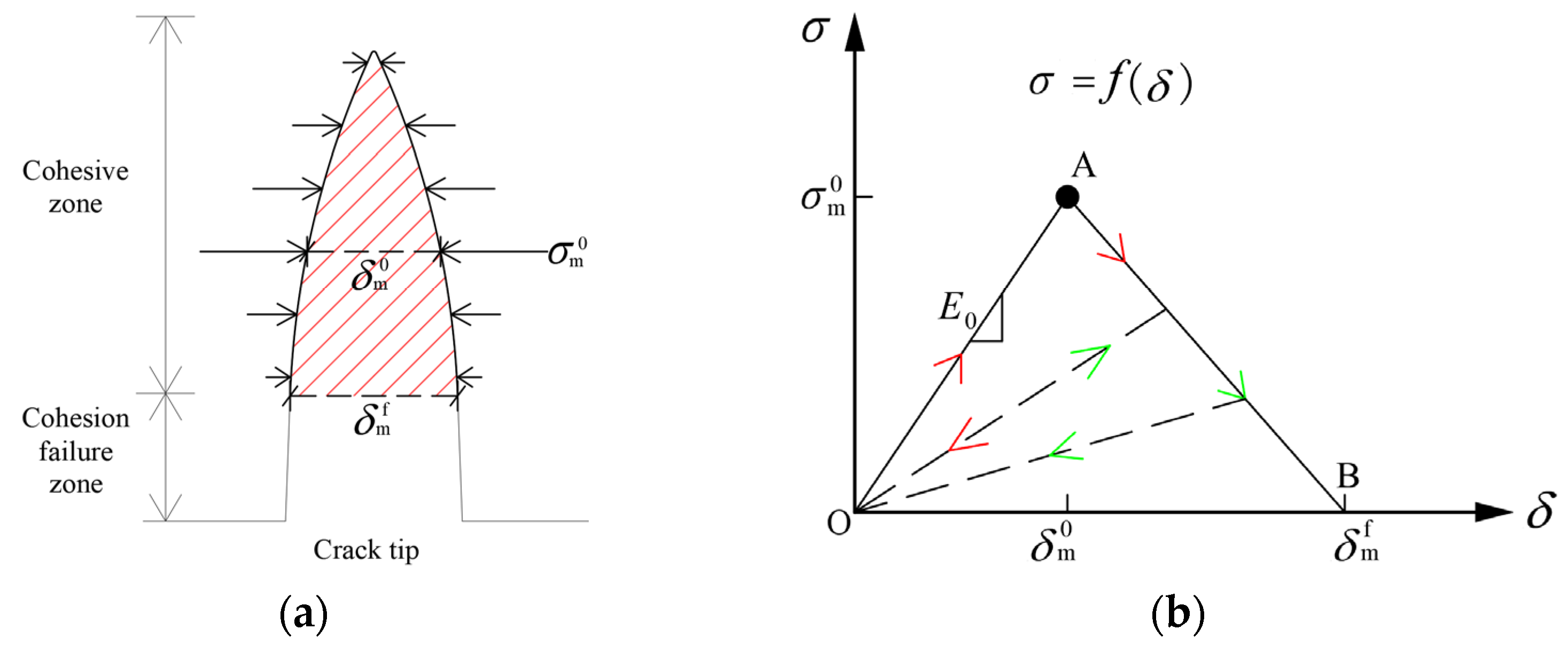
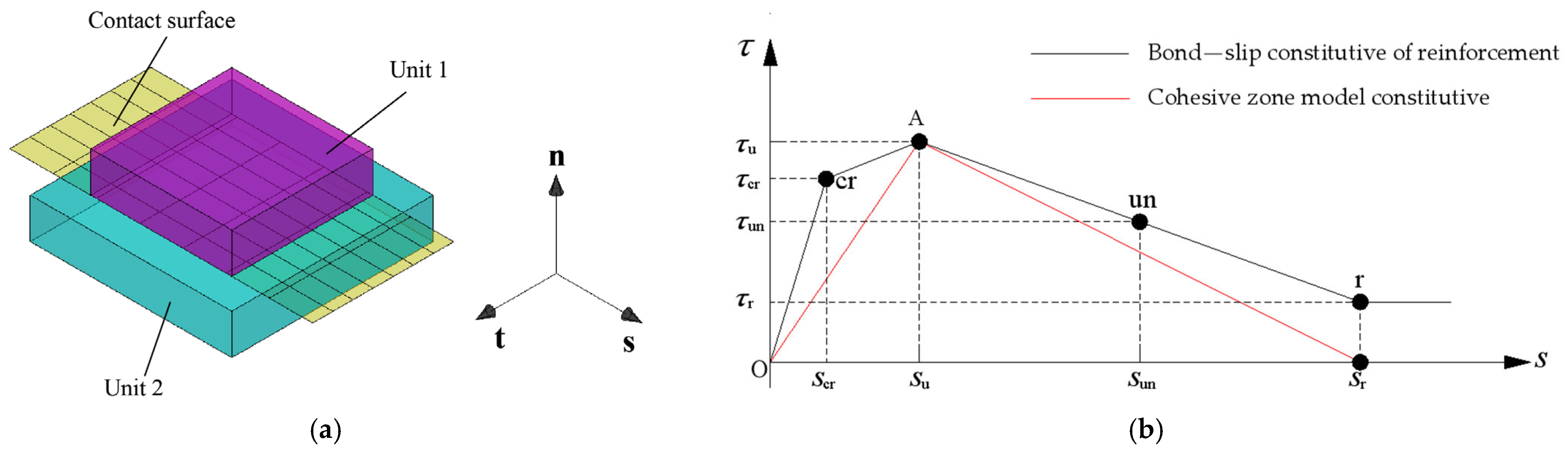
2.1. Introduction to the CZM Theory
2.2. Introduction to the CZM Method and Conventional Modeling Methods
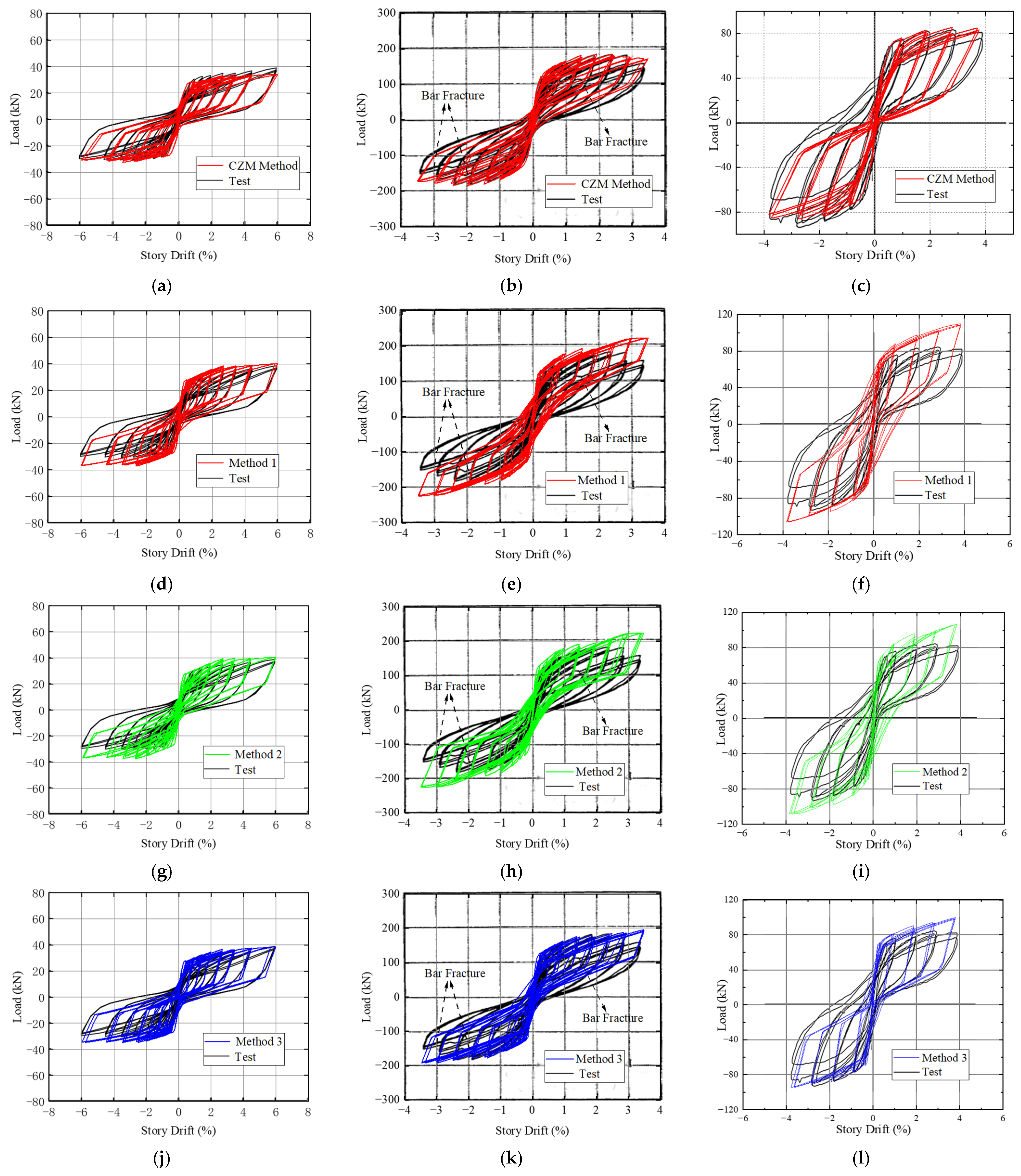
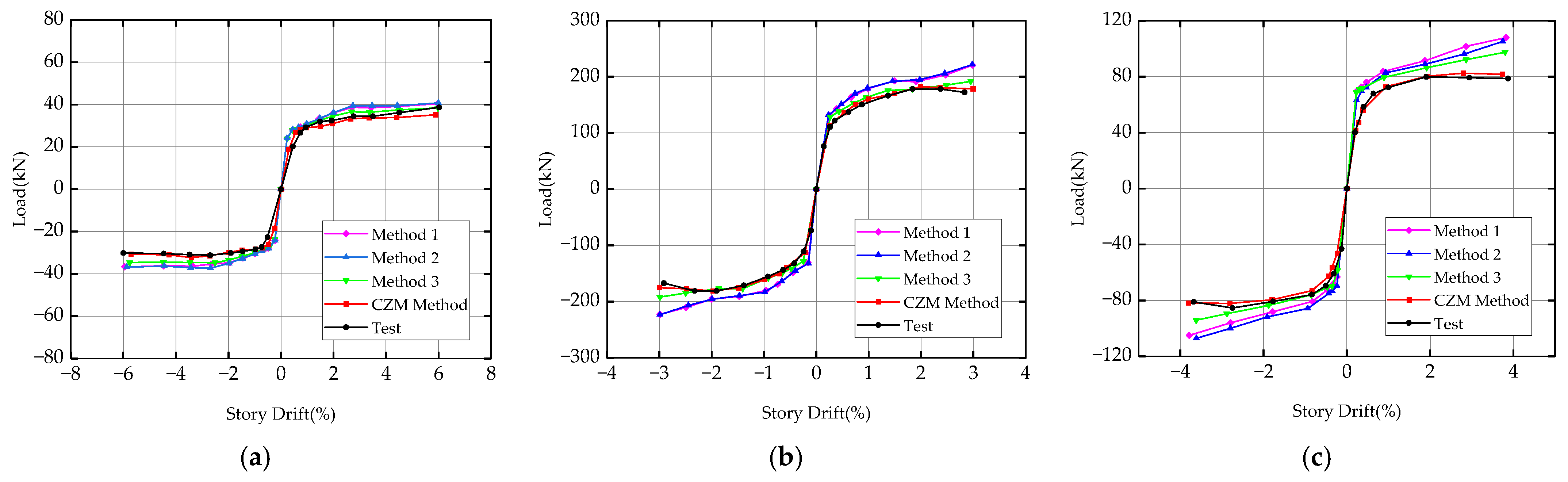
2.3. Simulation Results and Analysis
2.3.1. Hysteresis and Skeleton Curves
2.3.2. Residual Deformation
2.3.3. Energy Dissipation Performance
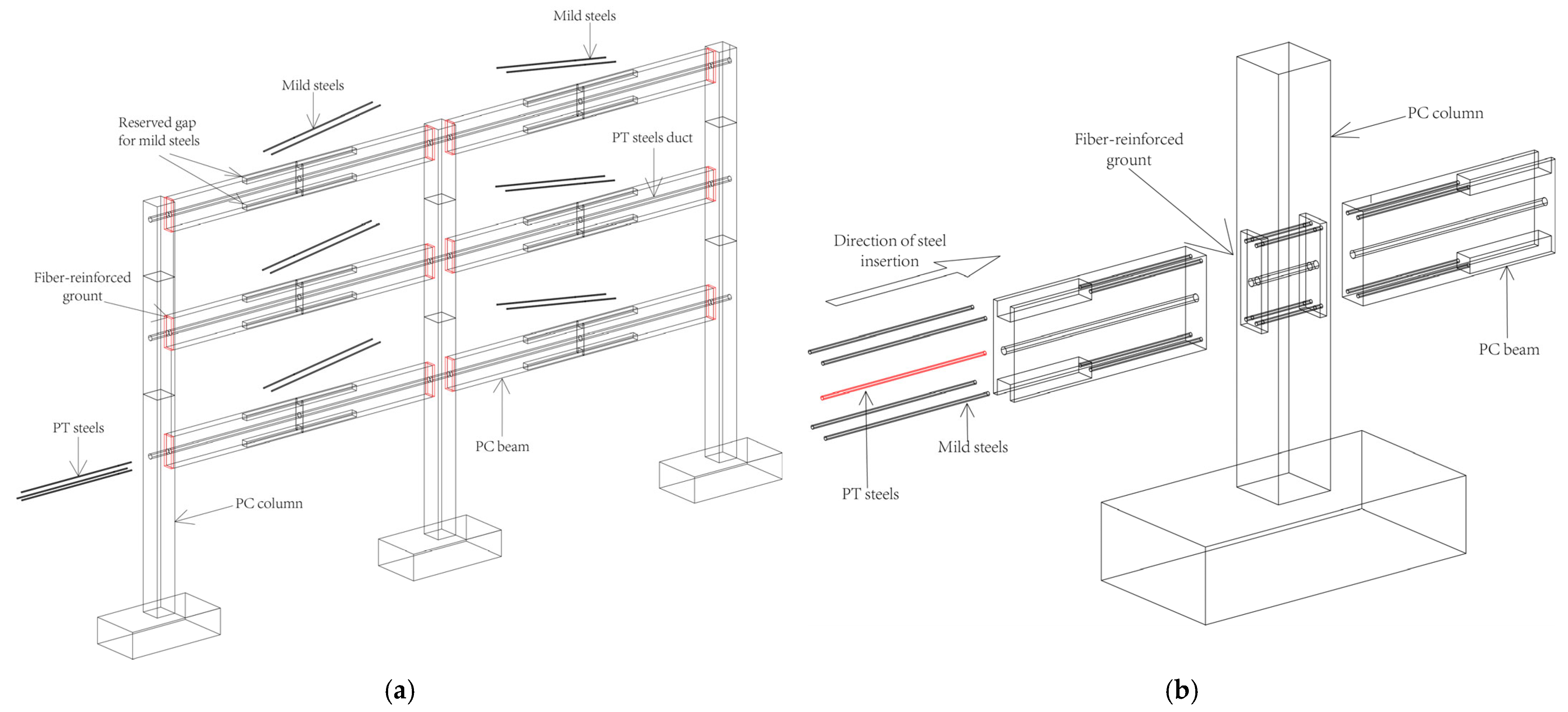
3. Example Design of the Hybrid Connection Joints of Large-Span Frames
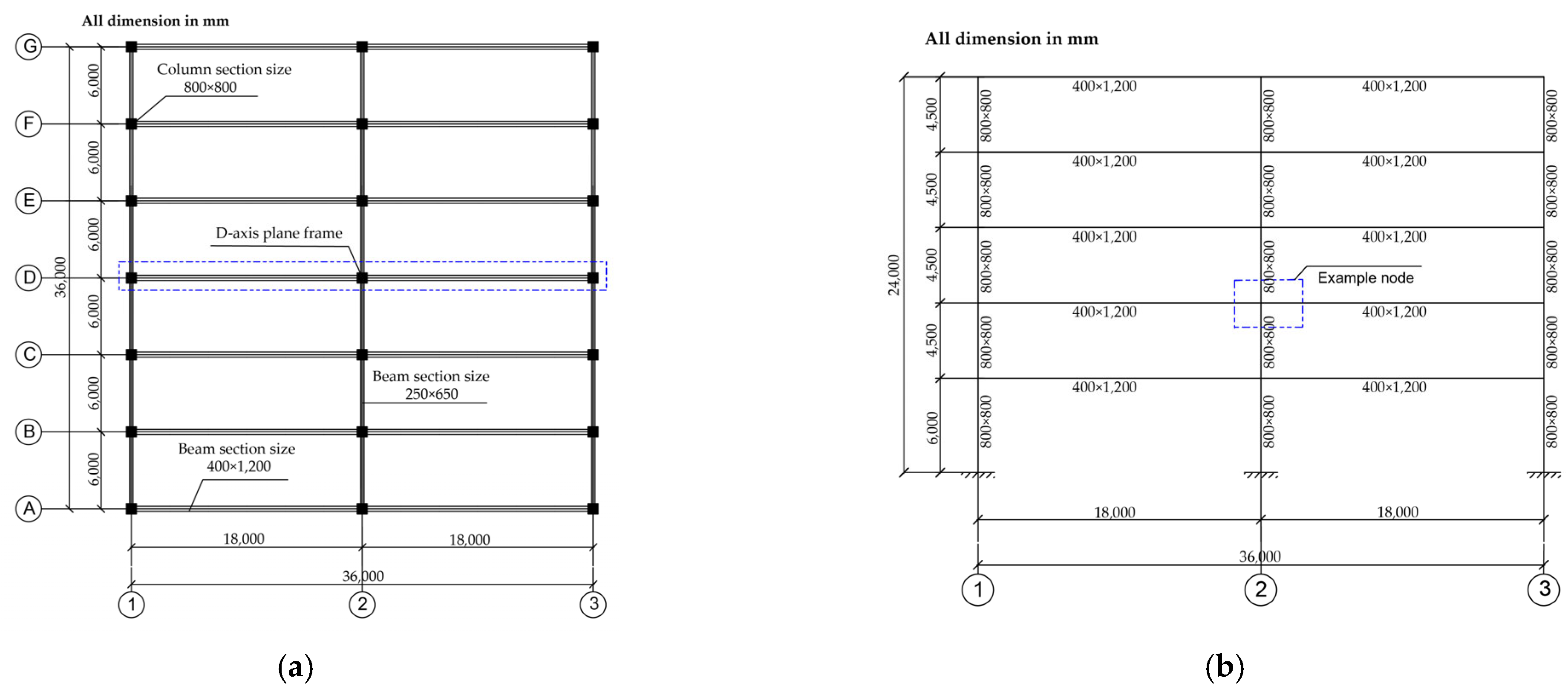
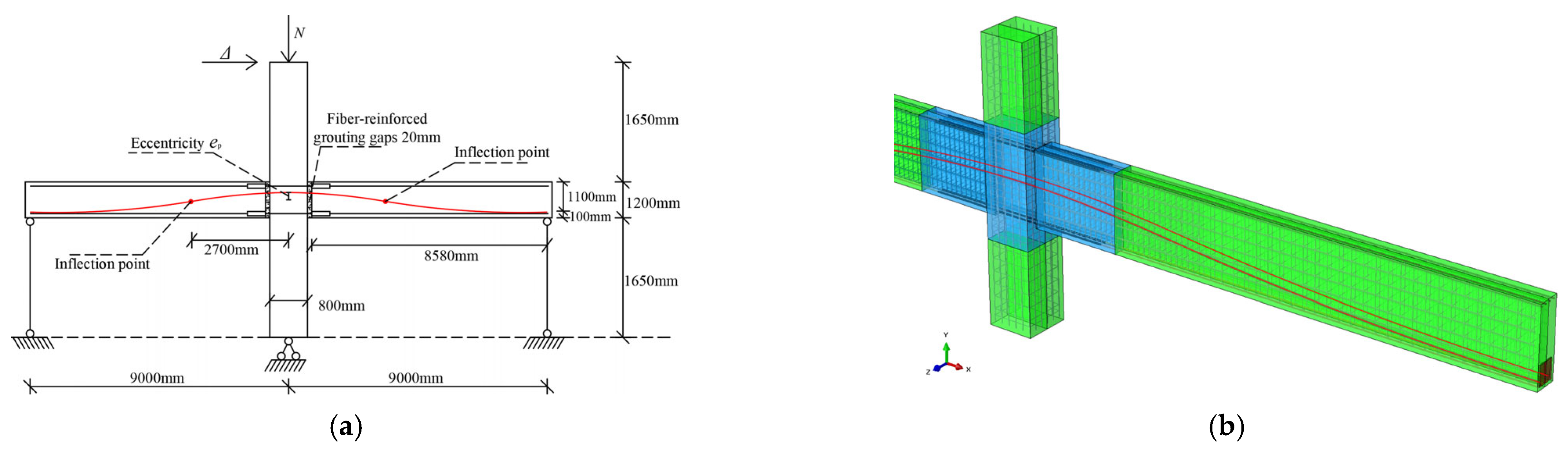
3.1. Basic Information
3.2. Load Distribution
3.3. Load Combinations
3.4. Material Properties
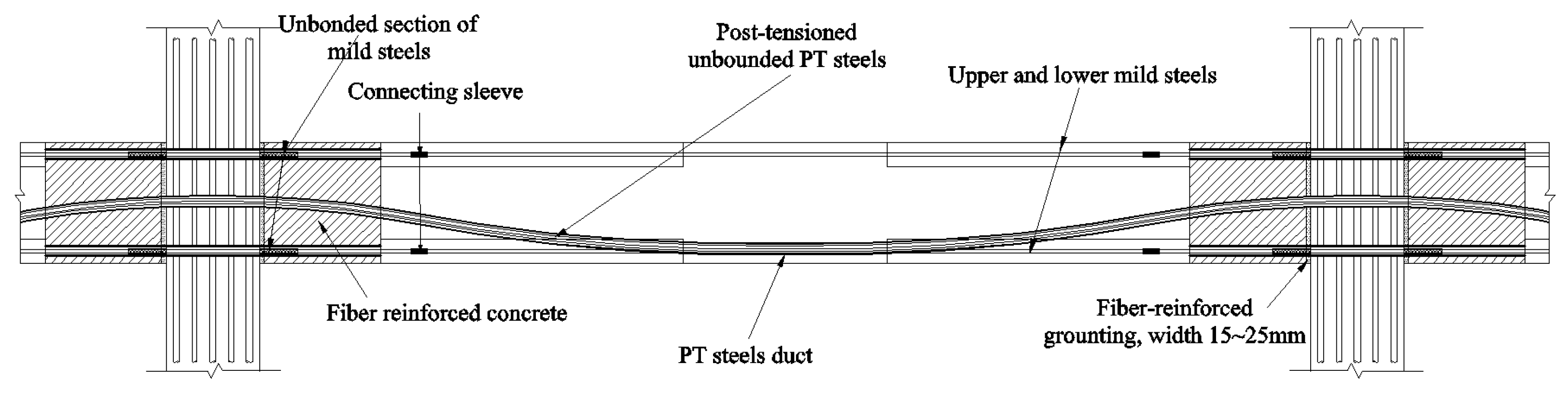
3.5. Design of Joint Examples
4. Seismic Performance Analysis of the Hybrid Connection Joints of Large-Span Frames
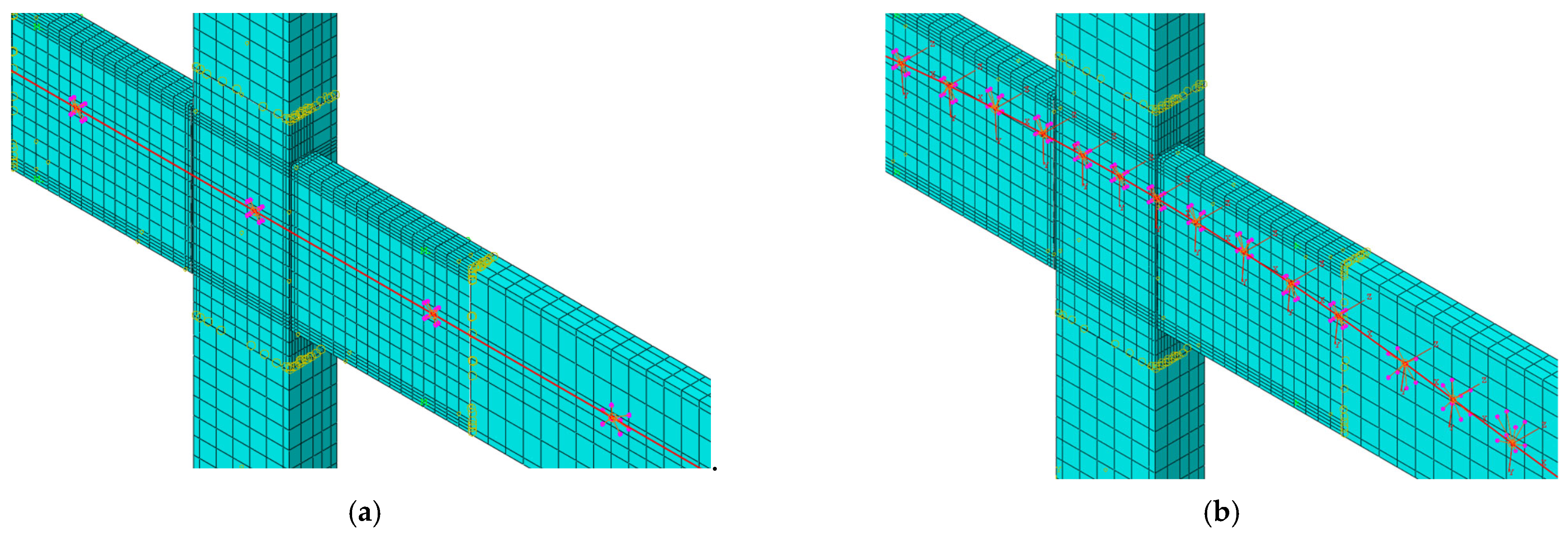
4.1. Establishment of FEM
4.2. Self-Centering Performance
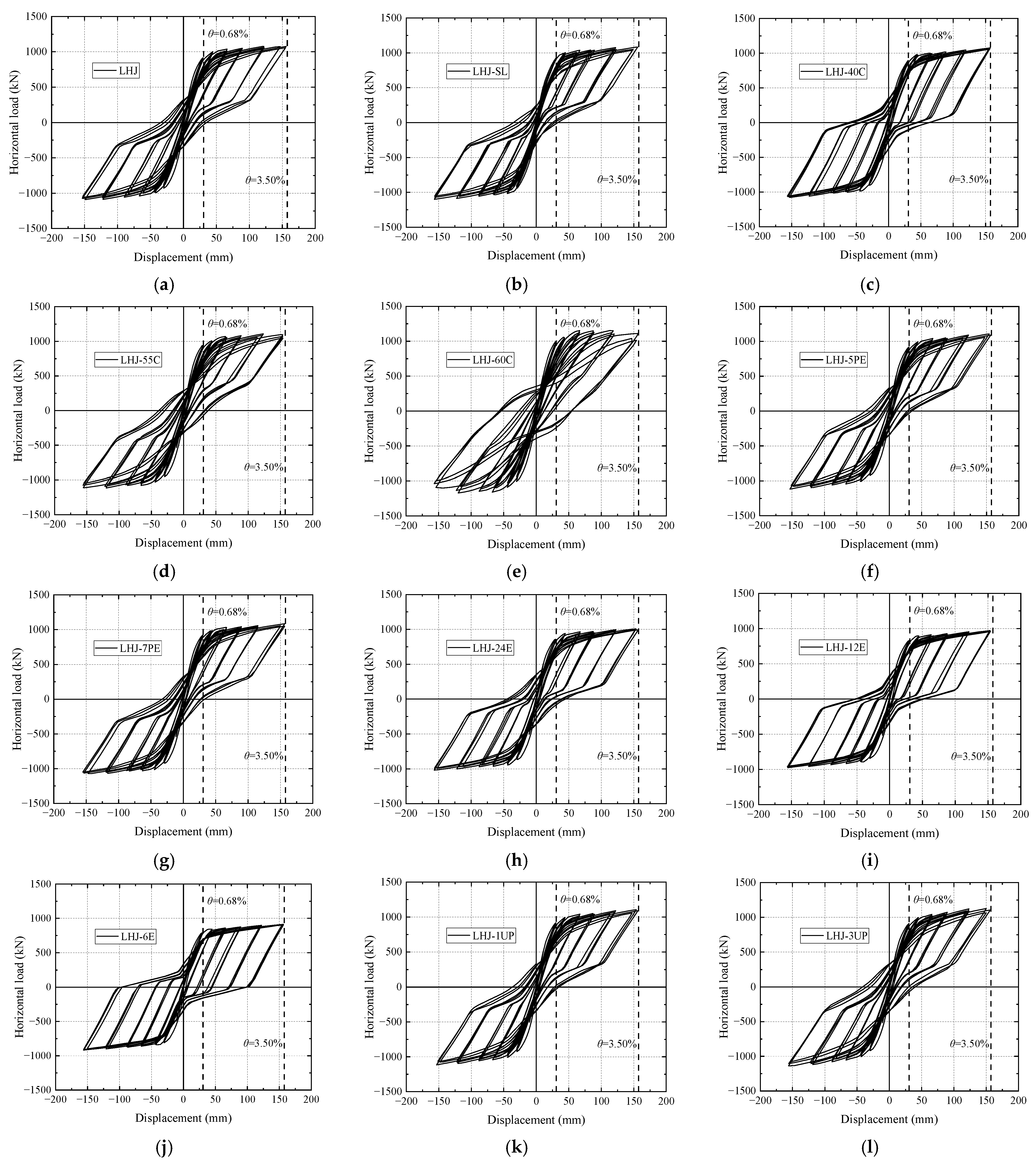
4.2.1. Hysteresis Curves
- (1)
- Bending bearing capacity ratio of PT steels . Comparing Figure 10a, Figure 10c, Figure 10d, and Figure 10e with the decrease in , the figures show a more obvious flag feature. Meanwhile, the unloading stiffness of the two-fold line is more notable, and the unloading of the two-fold line reflects the stress characteristics of the hybrid connection joint.
- (2)
- (3)
- Calculation of the PT steel eccentricity . Comparing Figure 10a, Figure 10b, Figure 10h, Figure 10i, and Figure 10j, when , the mechanical performance of the joint is almost the same, regardless of whether the PT steels are placed in a curved or straight manner. The pinch trend, stiffness, and bearing capacity of the hysteresis curve are basically the same. For the joint which PT steels is placed in a curve manner, as increases, there are obvious differences in the hysteresis curve among the joint examples, such as the reduction in bearing capacity, the degradation of unloading stiffness, and the weakening of pinch.
- (4)
- Unbonded length of the PT steels. Comparing Figure 10a, Figure 10k, and Figure 10l, as increases from to , this does not cause significant changes in the mechanical properties of the joints, and the pinching trend of the hysteresis curve, bearing capacity, and loading and unloading stiffness are basically the same.
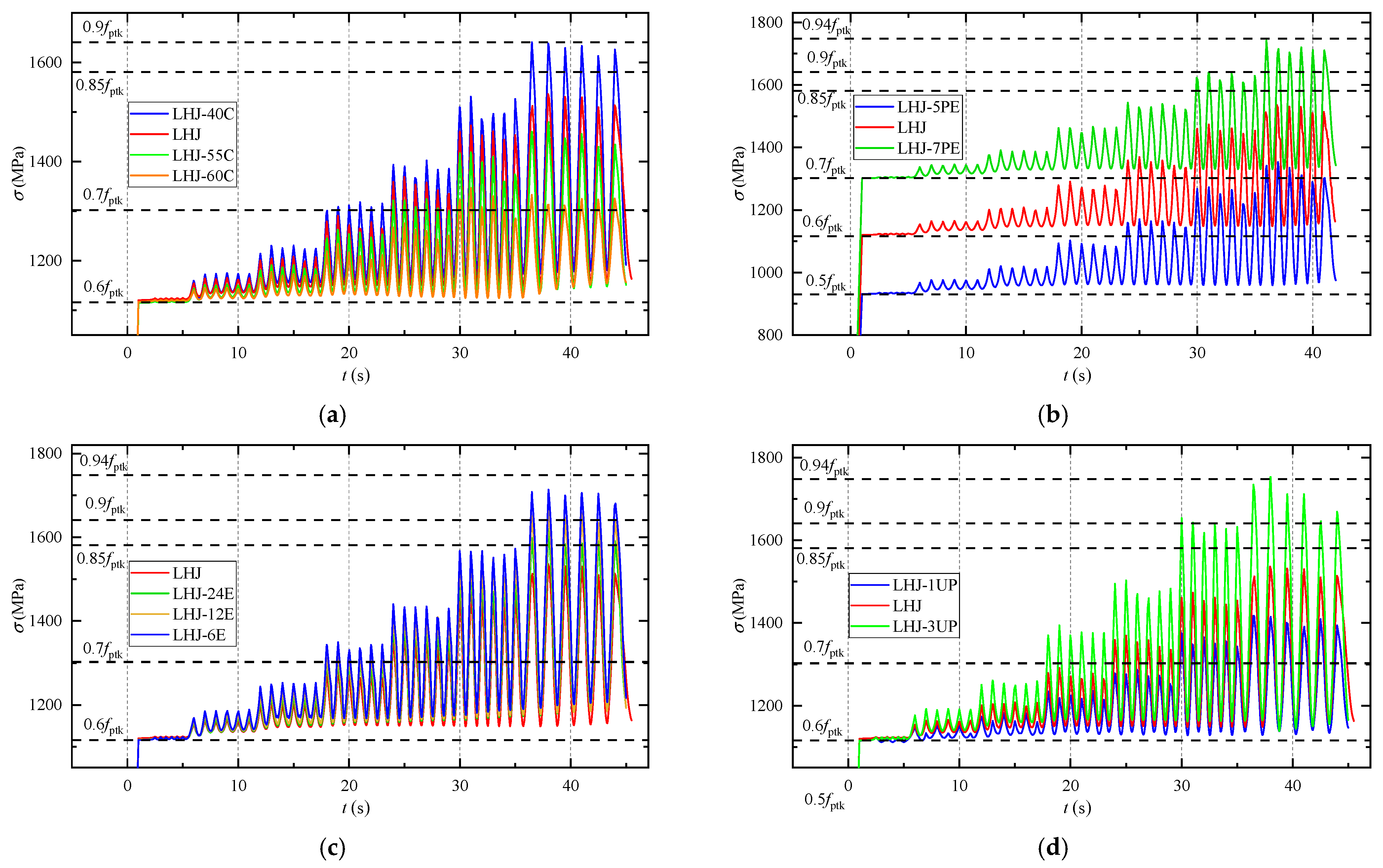
4.2.2. Stress Growth of PT Steels
4.2.3. Residual Deformation
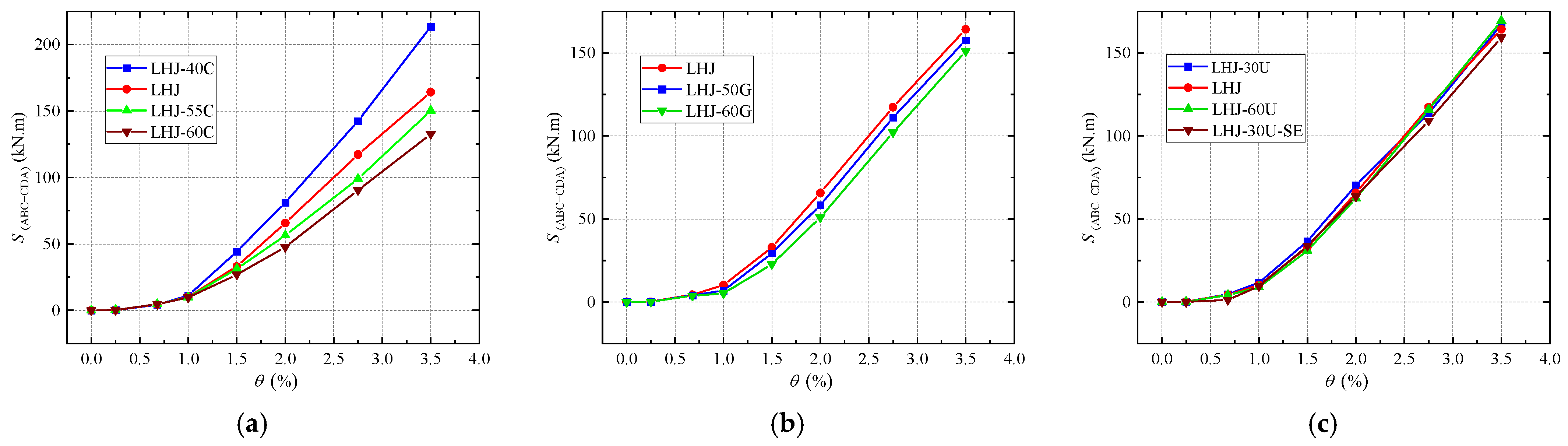
4.3. Energy Dissipation Reinforcement
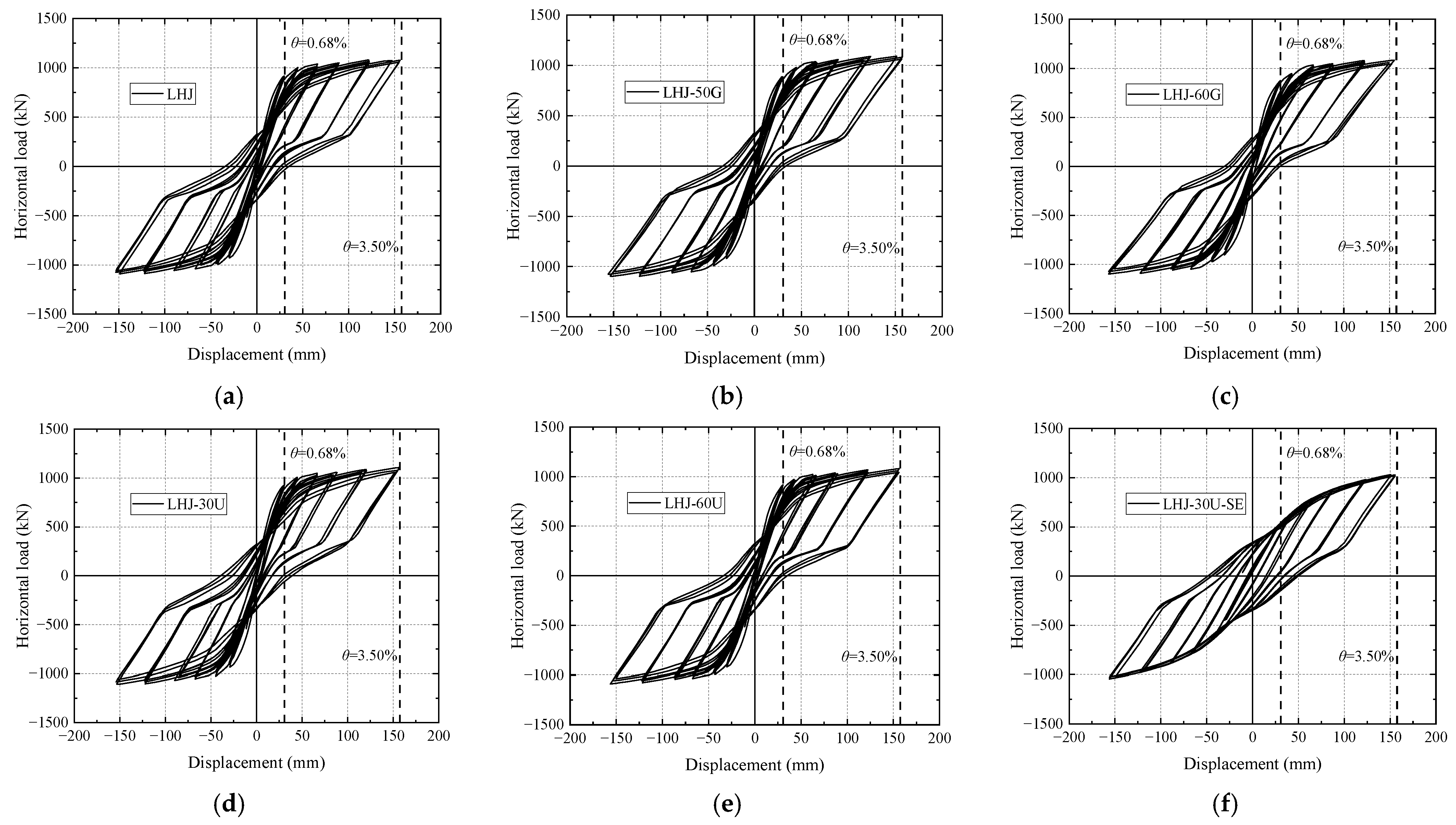
4.3.1. Hysteresis Curves
- (1)
- Bending-bearing capacity ratio of PT steel (). Compared with LHJ, LHJ-40C, LHJ-55C, and LHJ-60C, with an increase in , the hysteresis loop area gradually decreased because the increase in led to a decrease in the reinforcement area of the mild steel.
- (2)
- Strength grade of the mild steel. Compared with LHJ, LHJ-50G, and LHJ-60G, the strength grade of the mild steel had little effect on the hysteretic energy dissipation of the joints; however, with an increase in the strength grade of the mild steel, the area surrounded by the hysteretic loop of the joints decreased slightly.
- (3)
- Unbonded mild-steel length (). Compared with LHJ, LHJ-30U, and LHJ-60U, increased from 300 to 600 mm, and there was no significant difference in the hysteretic curve of each joint. Its bearing capacity, hysteretic shape, pinching trend, and loading and unloading stiffness are basically the same.
4.3.2. Damage of Mild Steel
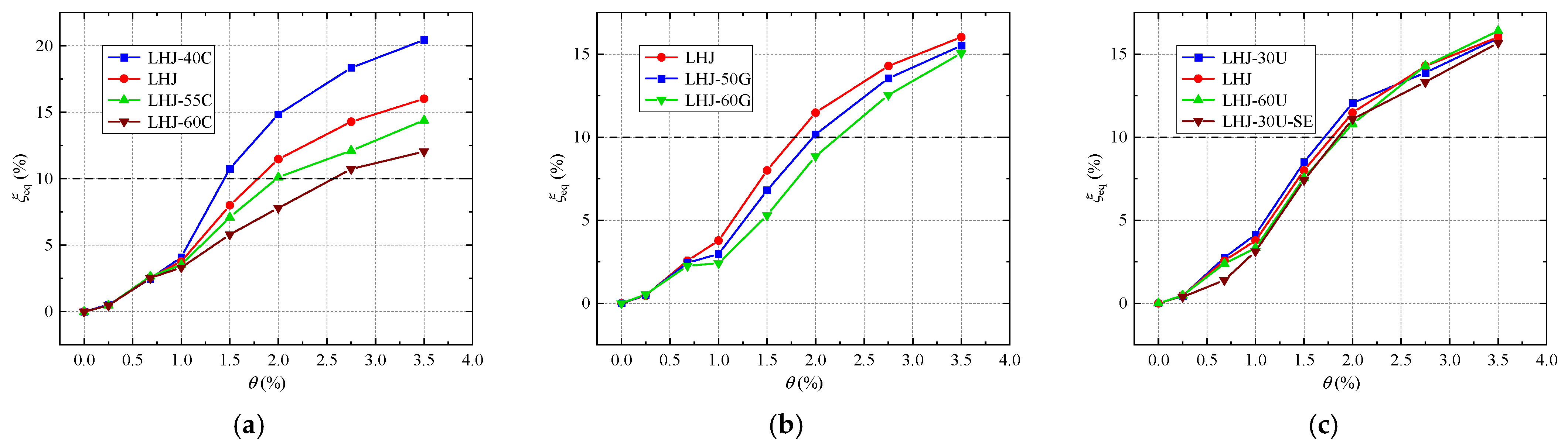
4.3.3. One-Cycle Energy Dissipation Area and Equivalent Viscous Damping Coefficient
- (1)
- At the level of a large earthquake (), the and of each joint are similar, and the energy dissipation capacity is weak. With the increase in , the energy dissipation capacity of the joints is continuously improved.
- (2)
- Compared with the LHJ-40 C, LHJ, LHJ-55 C, and LHJ-60 C in group A, with the increase in , the and of the joints decrease, and the energy dissipation performance is obviously weakened. When , is in the range of 7.8% to 14.85%.
- (3)
- Compared with the LHJ, LHJ-50G, and LHJ-60G in group E, with the increase in the strength grade of mild steel, the and of the joints decrease, and the energy dissipation performance is obviously weakened. However, with the increase in , the energy dissipation difference of the joints gradually decreases. When , is in the range of 8.86% to 11.47%.
- (4)
- Comparing the LHJ-30U, LHJ, and LHJ-60U in group F, when , with the increase in , the and of the joints decrease slightly, indicating that the energy dissipation capacity is weakened. When , has little effect on the energy dissipation performance of the joints. For , is in the range of 10.79% to 12.06%.
5. Conclusions
- (1)
- For the bond–slip of mild steel, the three existing conventional FEM methods cannot effectively simulate the seismic response. The CZM method proposed in this study can effectively simulate the bond–slip mechanism of mild steel and the crack development mechanism of the beam–column joint surface and can more accurately reflect the seismic performance indicators of such joints. It can also meet the requirements of finite element analysis of the seismic performance of hybrid connection joints.
- (2)
- For the hybrid connection joint of a large-span frame, when the bending capacity ratio of the PT steels is 0.4 to 0.6, the effective stress of the PT steels is 0.5 fptk to 0.7 fptk, the unbonded length of the PT steels is L/3 to L, and the eccentricity of the PT steels ; the residual deformation is small, showing good self-resetting performance. Before the loading level of large earthquakes (), the damage to the joint is small, and energy dissipation is not evident. However, with an increase in , the mild steels undergo yield strengthening, and the energy dissipation performance is significantly improved. When subjected to large earthquakes, it does not affect the overall function of the structure, and the entire structure can be used without treatment. Even if it reaches the limit for large earthquakes (), it does not affect the overall bearing capacity of the structure.
- (3)
- At the same level of , with an increase in , the residual deformation obviously decreases; however, when is close to 0.6, the residual deformation may increase. With an increase in , the stress growth of the PT steels accelerates. When is 0.5 fptk to 0.7 fptk, even if reaches 3.5%, the PT steels of hybrid connection joints in the large-span frame still have no large plastic strain. When decreases from to , there is no evident plastic strain on the PT steels, which has little effect on the self-resetting performance of the joints.
- (4)
- At the same level of , with an increase in , the energy dissipation capacity of the joint is weakened, and with an increase in the strength grade of the mild steels, the energy dissipation capacity of the joint decreases; however, with an increase in , the energy dissipation difference gradually decreases. When the unbonded length of the mild steels increases from 300 to 600 mm, the energy dissipation capacity decreases at a small level of , but when increases further, the increase in has little effect on the energy dissipation performance of the joint.
- (5)
- After the first earthquake, the concrete damage in the core area of precast beams, precast columns, and joints (beam–column overlap area) is small, the maximum strain of mild steels is less than 0.065, and there is a deformation reserve of 22.31% to 59.84%. After experiencing a large earthquake action of the displacement limit value () again, no joint failure occurs, and the bearing capacity of the joint is not significantly reduced in the later period. The maximum strain of the mild steels is still less than 0.065, and there is no risk of fracture.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Notation list | |||
| Length of the bond–slip | Average value of axial tensile strength of concrete | ||
| , | The opening displacement of the joint surface | Average value of axial compressive strength of concrete | |
| Maximum value the cohesive force | Bending capacity ratio of the PT steel | ||
| , | The stiffnesses in the viscous behavior | Effective stress of the PT steel | |
| , | The maximum stress in the damage initiation | Unbonded length of the PT steel | |
| The representative value of the uniaxial tensile strength of concrete, which can be taken as , , or according to the actual structural analysis requirements | Eccentricity of the PT steel | ||
| Concrete peak tensile strain corresponding to the single-axis tensile strength representative value | Unbonded length of the mild steel | ||
| The reduction factor for the tensile strength of concrete at the joint surface | L | Length of the precast beam span | |
| Diameter of steel reinforcement | h | Height of the precast beam span | |
| The residual deformation rate | As | Calculated area of mild steel. | |
| The maximum displacement of the current cyclic loading | Ap | Calculation area of the PT steel | |
| The residual deformation after unloading of the current cyclic loading | Interstory displacement angle | ||
| The relative error between the simulated value and the experimental value | Interstory displacement corresponding to the | ||
| Average value of the | Maximum stress of the PT steel | ||
| The equivalent viscous damping coefficient | Stress increments of the PT steel | ||
| The relative error between the simulated value and the experimental value | Residual stress of the PT steel | ||
| Average value of the | Maximum strain of the mild steel obtained by the simulation analysis under the current | ||
| Standard value of yield strength of steel reinforcement | Ultimate strain of mild steel calculated according to the prestressed seismic code | ||
| Standard value of ultimate strength of steel reinforcement | Relative error between and | ||
| Standard value of ultimate strength of the PT steel | Percentage of the safety reserve of mild steel | ||
| Average value of yield strength of steel reinforcement | Value of the strain permeability coefficient | ||
| Average value of ultimate strength of steel reinforcement | Residual strain of mild steel | ||
| Standard value of the axial tensile strength of concrete | Area of the one-cycle energy dissipation | ||
| Standard value of axial compressive strength of concrete | |||
References
- Song, S.; Chen, G.; Li, P.; Ying, Z.; Zhang, T. Investigation into wind resistance performance of cable-stiffened spherical latticed shells. J. Constr. Steel Res. 2025, 229, 109507. [Google Scholar] [CrossRef]
- Xiong, X.; Ge, Y.; Yao, G. Experimental study on flexural behavior of full-scale precast prestressed concrete double-tee members. J. Build. Struct. 2022, 43, 127–136, 172. [Google Scholar]
- Fan, J.; Wu, G.; Xu, A.; Feng, D.; Chen, Z. Experimental study on the seismic performance of novel precast reinforced concrete grid moment-resisting frames. Struct. Concr. 2020, 21, 2028–2043. [Google Scholar] [CrossRef]
- Yooprasertchai, E.; Warnitchai, P. Seismic performance of precast hybrid moment-resisting frame/rocking wall systems. Mag. Concr. Res. 2018, 70, 1118–1134. [Google Scholar] [CrossRef]
- Priestley, M.; Sritharan, S.; Conley, J.; Pampanin, S. Preliminary results and conclusions from the PRESSS five-story precast concrete test building. PCI J. 1999, 44, 42–67. [Google Scholar] [CrossRef]
- Nakaki, S.; Stanton, J.; Sritharan, S. An Overview of the PRESSS Five-Story Precast Test Building. PCI J. 1999, 44, 26–39. [Google Scholar] [CrossRef]
- GB/T 50011-2010; Seismic Design Standard for Building Structures. China National Standards: Beijing, China, 2010.
- Stone, W.; Cheek, G.; Stanton, J. Performance of hybrid moment-resisting precast beam-column concrete connections subjected to cyclic loading. ACI Struct. J. 1995, 92, 229–249. [Google Scholar]
- Cheok, G.; Stone, W. Performance of 1/3-Scale Model Precast Concrete Beam-Column Connections Subjected to Cyclic Inelastic Loads. Report. No. 4; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1994.
- Stanton, J.; Stone, W.; Cheok, G. A hybrid reinforced precast frame for seismic regions. PCI J. 1997, 42, 20–23. [Google Scholar] [CrossRef]
- Li, P.; Li, H.; Song, S.; Zhang, T.; Zhang, Y. Seismic response analysis of cable-stiffened latticed shells with buckling-restrained braces. J. Constr. Steel Res. 2025, 228, 109437. [Google Scholar] [CrossRef]
- Nicoletti, V.; Carbonari, S.; Gara, F. Nomograms for the pre-dimensioning of RC beam-column joints according to Eurocode 8. Structures 2022, 39, 958–973. [Google Scholar] [CrossRef]
- Shen, X.; Li, B.; Chen, Y.; Tizani, W.; Jiang, Y. Relocating plastic hinges in reinforced concrete beam-column joints by mechanically anchored diagonal bars. Eng. Struct. 2021, 251, 113468. [Google Scholar] [CrossRef]
- Yooprasertchai, E.; Warnitchai, P. An application of precast hybrid moment-resisting frames for seismic improvement. Mag. Concr. Res. 2016, 68, 1051–1069. [Google Scholar] [CrossRef]
- Li, P.; Chu, S.; Qin, S.; Ding, H.; Luo, N.; Yu, Y.; Zhang, T.; Xiong, G. Optimisation of prestressed stayed steel columns based on strengthen elitist genetic algorithm. J. Constr. Steel Res. 2025, 227, 109324. [Google Scholar] [CrossRef]
- Fan, J.; Wu, G.; Cao, Y. Seismic behavior of a precast prestressed beam-column joint with energy dissipation bars. Mag Concr. Res. 2019, 72, 365–378. [Google Scholar] [CrossRef]
- Girgin, S.; Misir, I.; Kahraman, S. Seismic performance factors for precast buildings with hybrid beam-column connections. Procedia Eng. 2017, 199, 3540–3545. [Google Scholar] [CrossRef]
- Li, P.; Chen, G.; Qiu, J.; Qian, J.; Ding, D.; Jian, B.; Zhang, X.; Xiong, G. Experimental and numerical investigation into the load-carrying capacity of aluminium alloy H-sectional stocky columns under axial compression. J. Build. Eng. 2024, 87, 108777. [Google Scholar] [CrossRef]
- JGJ/T 140-2019; China Association for Engineering Construction Standardization. Seismic Design Standard for Prestressed Concrete Structures. China Architecture & Building Press: Beijing, China, impending publication.
- Huang, M.; Gul, M.; Zhu, H. Vibration-based structural damage identification under varying temperature effects. J. Aerosp. Eng. 2018, 31, 3. [Google Scholar] [CrossRef]
- Huang, M.; Ling, Z.; Sun, C.; Lei, Y.; Xiang, C.; Wan, Z.; Gu, J. Two-stage damage identification for bridge bearings based on sailfish optimization and element relative modal strain energy. Struct. Eng. Mech. 2023, 86, 715–730. [Google Scholar]
- Huang, M.; Zhang, J.; Li, J.; Deng, Z.; Luo, J. Damage identification of steel bridge based on data augmentation and adaptive optimization neural network. Struct. Health Monit. 2024, 24, 1674–1699. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, M.; Wan, N.; Deng, Z.; He, Z.; Luo, J. Missing measurement data recovery methods in structural health monitoring: The state, challenges and case study. Measurement 2024, 231, 114528. [Google Scholar] [CrossRef]
- Dong, J.; Chen, M.; Jin, Y.; Hong, G.; Zaman, M.; Li, Y. Study on micro-scale properties of cohesive zone in shale. Int. J. Solids Struct. 2019, 163, 178–193. [Google Scholar] [CrossRef]
- Xie, H. Study on Failure Process and Mechanism of Concrete with Mesostructure Based on Cohesive Zone Model. Ph.D. Thesis, China University of Mining & Technology, Beijing, China, 2020. [Google Scholar]
- Mander, J.; Priestley, M. Theoretical stress-strain model for confined concrete. Aus. J. of Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Menegotto, M.; Pinto, P. Method of analysis for cyclically loaded reinforced concrete plane frames including changes in geometry and non-elastic behavior of elements under combined normal force and bending. In Proceedings of the Conference on Resistance and Ultimate Deformability of Structures Acted on by Well Defined Repeated Loads, IABSE Reports Volume 13, Lisbon, Protugal, 13 September 1973; pp. 15–22. [Google Scholar]
- GB/T 50010-2010; Code for Design of Concrete Structures. China National Standards: Beijing, China, 2010.
- Baltay, P.; Gjelsvik, A. Coefficient of friction for steel on concrete at high normal stress. J. Mater. Civ. Eng. 1990, 2, 46–49. [Google Scholar] [CrossRef]
- Wang, D. Research of Seismic Performance and Reinforcement Performance of Precast Prestressed Concrete Connections with Unbonded Post-Tensioned Tendons. Ph.D. Thesis, Beijing University of Technology, Beijing, China, 2008. [Google Scholar]
- Yang, S. Research of Finite Element Modeling Method and Seismic Performance of Large-Span Hybrid Connection Frame Joints. Master’s Thesis, Chongqing University, Chongqing, China, 2023. [Google Scholar]
- Girard, C.; Bastien, J. Finite-element bond-slip model for concrete columns under cyclic loads. Aus. J. Struct. Eng. 2002, 128, 1502–1510. [Google Scholar] [CrossRef]
- Lowes, L. Finite Element Modeling of Reinforced Concrete Beam-Column Bridge Connections; University of California: Berkeley, CA, USA, 1999. [Google Scholar]
- Priestley, M.; Tao, J. Precast frames connected with unbonded prestressing tendons (PRESSS). PCI J. 1993, 38, 58–69. [Google Scholar] [CrossRef]
- GB 50292-2015; Reliability Appraisal Standard for Civil Building. China National Standards: Beijing, China, 2015.
| Contact Area | Contact Properties | Explanation of Contact | The Type Selections and Parameter Values of Sub-Property |
|---|---|---|---|
| The bonded section of the mild steel | Behavior of normal direction | Hard contact | No need to take a value |
| Behavior of tangential direction | Penalized friction | Friction coefficient | |
| Viscous behavior | Specified stiffness friction | ||
| The damage initiation | Maximum nominal tensile stress criterion | ||
| The interface between fiber cement grouting and prefabricated beam end face | Behavior of normal direction | Hard contact | No need to take a value |
| Behavior of tangential direction | Penalized friction | Friction coefficient | |
| Viscous behavior | Specified stiffness friction | ||
| The damage initiation | Maximum nominal tensile stress criterion |
| Specimens | (%) | (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Test | CZM Method | Method 1 | Method 2 | Method 3 | CZM Method | Method 1 | Method 2 | Method 3 | |
| EHJ | 25.5/35.4 | 25.0/29.3 | 21.1/17.4 | 20.9/14.9 | 22.9/23.6 | −2.1/−17.3 | −17.1/−50.8 | −18/−57.8 | −10.3/−33.3 |
| IHJ | 28.3/22.9 | 25.3/23.3 | 22.4/27.2 | 17.3/16.9 | 23.8/25.3 | −10.6/1.6 | −21.1/19 | −39.1/−26.1 | −15.9/10.5 |
| M-P-Z4 | 15.4/10.5 | 14.4/9.6 | 9.5/6.9 | 10.9/7.7 | 11.6/8.4 | −6.3/−8.5 | −38.1/−34.6 | −29.1/−26.1 | −24.9/−20.3 |
| N-P-Z4 | 11.5/12.5 | 16.3/17.0 | 9.5/10.2 | 10.6/11.0 | 10.9/11.8 | 41.5/29.7 | −17.8/−18.2 | −7.8/−11.6 | −5.6/−5.0 |
| O-P-Z4 | 41.2/37.3 | 35.3/33.7 | 21.8/17.3 | 24.5/15.5 | 27.5/21.7 | −14.2/−9.5 | −47/−53.4 | −40.4/−58.3 | −33.1/−41.8 |
| HCB1 | 6.8/33.9 | 6.5/6.7 | 26.2/26.8 | 21.5/19.5 | 12.6/14.3 | −4.1/−80.1 | 284.3/−20.7 | 214.9/−42.5 | 85.1/−57.9 |
| HCB2 | 5.0/11.7 | 4.9/6.9 | 7.8/8.1 | 7.2/8.7 | 6.2/6.4 | −2.5/−40.8 | 55.9/−30.5 | 44.0/−25.8 | 23.4/−45.5 |
| HCB3 | 2.9/12.5 | 2.4/5.1 | 10.5/14 | 9.8/13.4 | 3.8/8.8 | −18.0/−59.3 | 266.5/12.2 | 242.1/7.9 | 31.9/−29.9 |
| Specimens | (%) | (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Test | CZM Method | Method 1 | Method 2 | Method 3 | CZM Method | Method 1 | Method 2 | Method 3 | |
| EHJ | 17.05 | 17.44 | 13.9 | 14.9 | 18.2 | −2.23 | −20.2 | −14.9 | 4.51 |
| IHJ | 15.72 | 16.50 | 12.2 | 13.4 | 17.8 | −4.75 | −26.0 | −18.8 | 7.82 |
| M-P-Z4 | 12.81 | 14.97 | 11.6 | 11.9 | 12.2 | −14.4 | −22.8 | −20.9 | −18.78 |
| N-P-Z4 | 13.69 | 10.90 | 13.5 | 13.2 | 14.6 | 25.61 | 23.9 | 21.2 | 34.02 |
| O-P-Z4 | 17.95 | 19.41 | 13.3 | 14.2 | 16.7 | −7.52 | −31.5 | −26.7 | −13.74 |
| HCB1 | 14.68 | 18.48 | 13.1 | 13.9 | 16.0 | −20.55 | −29.0 | −24.9 | −13.42 |
| HCB2 | 11.39 | 12.48 | 9.3 | 10.3 | 10.7 | −8.74 | −25.9 | −17.5 | −14.58 |
| HCB3 | 10.99 | 12.23 | 8.4 | 8.7 | 10.3 | −10.13 | −31.1 | −28.7 | −15.43 |
| Reinforcement | (MPa) | (MPa) | (MPa) | (MPa) |
|---|---|---|---|---|
| HPB300 | 300 | 420 | 351 | 492 |
| HRB400E | 400 | 540 | 443 | 599 |
| HRB500E | 500 | 630 | 554 | 699 |
| HRB600E | 600 | 750 | 665 | 812 |
| 1860-degree tendon | 1581 | 1860 | 1751 | 2060 |
| (MPa) | (MPa) | (MPa) | (MPa) |
|---|---|---|---|
| 2.39 | 26.8 | 3.2 | 36.1 |
| Class | Examples | Lups | Grade | Lu (mm) | As (mm2) | Ap (mm2) | |||
|---|---|---|---|---|---|---|---|---|---|
| Basic | LHJ | 0.5 | 0.6 fptk | 0 | L/2 | HRB400E | 450 | 2018 | 2216 |
| LHJ-SL | |||||||||
| A | LHJ-40C | 0.5 | 0.6 fptk | 0 | L/2 | HRB400E | 450 | 2624 | 1558 |
| LHJ-55C | 0.55 | 1737 | 2647 | ||||||
| LHJ-60C | 0.6 | 1490 | 3270 | ||||||
| B | LHJ-5PE | 0.5 | 0.5 fptk | 0 | L/2 | HRB400E | 450 | 2025 | 2607 |
| LHJ-7PE | 0.7 fptk | 2013 | 1928 | ||||||
| C | LHJ-24E | 0.5 | 0.6 fptk | h/24 | L/2 | HRB400E | 450 | 2154 | 1754 |
| LHJ-12E | h/12 | 2272 | 1468 | ||||||
| LHJ-6E | h/6 | 2648 | 1114 | ||||||
| D | LHJ-1UP | 0.5 | 0.6 fptk | 0 | L | HRB400E | 450 | 1974 | 2277 |
| LHJ-3UP | L/3 | 2028 | 2086 | ||||||
| E | LHJ-50G | 0.5 | 0.6 fptk | 0 | L/2 | HRB500E | 450 | 1719 | 2184 |
| LHJ-60G | HRB600E | 1443 | 2176 | ||||||
| F | LHJ-30U | 0.5 | 0.6 fptk | 0 | L/2 | HRB400E | 300 | 1999 | 2242 |
| LHJ-60U | 600 | 2039 | 2191 |
| Loading Level | (mm) | Explanation | |
|---|---|---|---|
| 1 | 0.25% | 11.25 | / |
| 2 | 0.68% | 30.60 | The calculated value of under a large earthquake |
| 3 | 1.00% | 45.00 | / |
| 4 | 1.50% | 67.50 | / |
| 5 | 2.00% | 90.00 | Large earthquake limit value in the Seismic Code |
| 6 | 2.75% | 123.75 | / |
| 7 | 3.50% | 157.50 | displacement limit value in the Prestressed Seismic Code |
| Examples | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| LHJ/LHJ-SL | 0.60 fptk | 0.62 fptk | 0.02 fptk | 0.74 fptk | 0.14 fptk | 0.79 fptk | 0.19 fptk | 0.82 fptk | 0.22 fptk | 0.62 fptk |
| LHJ-40C | 0.60 fptk | 0.66 fptk | 0.06 fptk | 0.75 fptk | 0.15 fptk | 0.82 fptk | 0.22 fptk | 0.88 fptk | 0.28 fptk | 0.64 fptk |
| LHJ-55C | 0.60 fptk | 0.63 fptk | 0.03 fptk | 0.71 fptk | 0.11 fptk | 0.76 fptk | 0.16 fptk | 0.80 fptk | 0.20 fptk | 0.63 fptk |
| LHJ-60C | 0.60 fptk | 0.61 fptk | 0.01 fptk | 0.68 fptk | 0.08 fptk | 0.72 fptk | 0.12 fptk | 0.72 fptk | 0.12 fptk | 0.62 fptk |
| LHJ-5PE | 0.50 fptk | 0.52 fptk | 0.02 fptk | 0.63 fptk | 0.13 fptk | 0.68 fptk | 0.18 fptk | 0.71 fptk | 0.21 fptk | 0.52 fptk |
| LHJ-7PE | 0.70 fptk | 0.72 fptk | 0.02 fptk | 0.83 fptk | 0.13 fptk | 0.88 fptk | 0.18 fptk | 0.92 fptk | 0.22 fptk | 0.72 fptk |
| LHJ-24E | 0.60 fptk | 0.63 fptk | 0.03 fptk | 0.75 fptk | 0.15 fptk | 0.81 fptk | 0.21 fptk | 0.85 fptk | 0.25 fptk | 0.63 fptk |
| LHJ-12E | 0.60 fptk | 0.63 fptk | 0.03 fptk | 0.76 fptk | 0.16 fptk | 0.83 fptk | 0.23 fptk | 0.89 fptk | 0.29 fptk | 0.64 fptk |
| LHJ-6E | 0.60 fptk | 0.64 fptk | 0.04 fptk | 0.77 fptk | 0.17 fptk | 0.84 fptk | 0.24 fptk | 0.92 fptk | 0.32 fptk | 0.65 fptk |
| LHJ-1UP | 0.60 fptk | 0.61 fptk | 0.01 fptk | 0.69 fptk | 0.09 fptk | 0.73 fptk | 0.13 fptk | 0.76 fptk | 0.16 fptk | 0.61 fptk |
| LHJ-3UP | 0.60 fptk | 0.64 fptk | 0.04 fptk | 0.81 fptk | 0.21 fptk | 0.89 fptk | 0.29 fptk | 0.94 fptk | 0.34 fptk | 0.62 fptk |
| Examples | (mm) | (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| LHJ | 3.75/0.60 | 11.10/8.56 | 18.16/16.60 | 35.31/34.70 | 12.31/1.98 | 12.34/9.51 | 14.68/13.44 | 22.42/22.08 |
| LHJ-SL | 3.81/0.44 | 10.08/7.52 | 16.67/14.08 | 32.81/35.27 | 12.45/1.43 | 11.20/8.36 | 13.47/11.37 | 20.83/22.40 |
| LHJ-40C | 3.87/0.70 | 29.86/28.6 | 44.71/43.77 | 64.43/60.45 | 12.64/2.29 | 33.18/31.78 | 36.13/35.37 | 40.91/38.38 |
| LHJ-55C | 3.77/0.60 | 10.61/7.55 | 17.67/15.63 | 34.32/32.84 | 12.31/1.98 | 11.78/8.39 | 14.28/12.63 | 21.79/20.85 |
| LHJ-60C | 3.72/0.66 | 11.22/9.84 | 25.55/26.52 | 55.37/55.85 | 12.15/2.16 | 12.47/10.93 | 20.64/21.43 | 35.16/35.46 |
| LHJ-24E | 3.74/0.61 | 14.66/11.06 | 23.73/22.16 | 45.92/44.85 | 12.23/1.99 | 16.29/12.29 | 19.18/17.90 | 29.16/28.47 |
| LHJ-12E | 3.73/0.78 | 25.43/21.86 | 36.49/35.44 | 54.10/52.54 | 12.21/2.56 | 28.25/24.29 | 29.49/28.64 | 34.35/33.36 |
| LHJ-6E | 3.67/1.00 | 44.04/43.49 | 70.70/71.66 | 100.38/95.8 | 11.99/3.26 | 48.93/48.32 | 57.13/57.90 | 63.73/60.83 |
| LHJ-1UP | 3.90/0.51 | 11.12/9.05 | 17.68/16.61 | 34.82/37.29 | 12.74/1.65 | 12.36/10.06 | 14.28/13.43 | 22.11/23.68 |
| LHJ-3UP | 3.96/0.62 | 11.15/9.32 | 19.49/17.92 | 39.22/41.17 | 12.94/2.03 | 12.39/10.36 | 15.75/14.48 | 24.90/26.14 |
| Examples | |||||||
|---|---|---|---|---|---|---|---|
| LHJ | 0.00121 | 0.0185 | 0.0300 | 0.0395 | 0.0425 | 39.23% | −7.06% |
| LHJ-40C | 0.00166 | 0.0214 | 0.0343 | 0.0447 | 0.0474 | 31.23% | −5.70% |
| LHJ-55C | 0.000917 | 0.0166 | 0.0274 | 0.0379 | 0.0397 | 41.69% | −4.53% |
| LHJ-60C | 0.000606 | 0.0118 | 0.0216 | 0.0261 | 0.0358 | 59.84% | −27.37% |
| LHJ-50G | 0.00115 | 0.0156 | 0.0283 | 0.0383 | 0.0417 | 41.08% | −8.15% |
| LHJ-60G | 0.00106 | 0.0131 | 0.0266 | 0.0365 | 0.0432 | 43.85% | −15.51% |
| LHJ-30U | 0.00132 | 0.0231 | 0.0380 | 0.0505 | 0.0577 | 22.31% | −12.48% |
| LHJ-60U | 0.00108 | 0.0139 | 0.0239 | 0.0331 | 0.0338 | 49.08% | −2.07% |
| LHJ-30U-SE | 0.00218 | 0.0223 | 0.0365 | 0.0483 | / | / | / |
| Examples | (kN·m) | (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| LHJ | 4.41 | 65.74 | 117.27 | 164.22 | 2.57 | 11.47 | 14.29 | 16.02 |
| LHJ-40C | 4.21 | 81.12 | 142.41 | 213.41 | 2.48 | 14.85 | 18.35 | 20.45 |
| LHJ-55C | 4.68 | 56.42 | 98.95 | 150.27 | 2.65 | 10.11 | 12.11 | 14.40 |
| LHJ-60C | 4.73 | 47.68 | 90.45 | 132.68 | 2.52 | 7.80 | 10.73 | 12.04 |
| LHJ-50G | 4.05 | 58.37 | 111.02 | 157.61 | 2.44 | 10.17 | 13.55 | 15.50 |
| LHJ-60G | 3.78 | 50.94 | 102.04 | 151.06 | 2.26 | 8.86 | 12.54 | 15.05 |
| LHJ-30U | 4.76 | 70.32 | 113.73 | 167.03 | 2.75 | 12.06 | 13.89 | 15.96 |
| LHJ-60U | 4.14 | 61.43 | 115.89 | 169.22 | 2.39 | 10.79 | 14.30 | 16.40 |
| LHJ-30U-SE | 1.26 | 63.63 | 103.15 | 159.24 | 1.39 | 11.09 | 13.32 | 15.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jian, B.; Chen, X.; Yang, S.; Li, P. Study on Finite Element Modeling Method and Seismic Performance of Hybrid Connection Joints of Large-Span Frames. Buildings 2025, 15, 2992. https://doi.org/10.3390/buildings15172992
Jian B, Chen X, Yang S, Li P. Study on Finite Element Modeling Method and Seismic Performance of Hybrid Connection Joints of Large-Span Frames. Buildings. 2025; 15(17):2992. https://doi.org/10.3390/buildings15172992
Chicago/Turabian StyleJian, Bin, Xiang Chen, Shuai Yang, and Pengcheng Li. 2025. "Study on Finite Element Modeling Method and Seismic Performance of Hybrid Connection Joints of Large-Span Frames" Buildings 15, no. 17: 2992. https://doi.org/10.3390/buildings15172992
APA StyleJian, B., Chen, X., Yang, S., & Li, P. (2025). Study on Finite Element Modeling Method and Seismic Performance of Hybrid Connection Joints of Large-Span Frames. Buildings, 15(17), 2992. https://doi.org/10.3390/buildings15172992






