Abstract
Thermal effects critically influence the design and construction of steel-concrete composite cable-stayed bridges, where material thermal mismatch complicates structural responses. Current code-specified temperature gradient models inadequately address long-span bridges. This study employs in-situ monitoring of the Chibi Yangtze River Bridge to propose a refined vertical temperature gradient model, utilizing an exponential function for the concrete deck and a linear function for the steel web. Finite element analysis across six construction stages reveals: (1) Under negative temperature gradients, the concrete deck develops tensile stresses (2.439–2.591 MPa), approximately 30% lower than code-predicted values (3.613–3.715 MPa), highlighting risks of longitudinal cracking. (2) At the maximum double-cantilever stage, transverse stress distributions show pronounced shear lag effects, positive shear lag in deck sections connected to crossbeams and negative shear lag in non-connected sections. The proposed model reduces tensile stress conservatism in codes by 30–33%, enhancing prediction accuracy for composite girders. This work provides critical insights for thermal effect management in long-span bridge construction.
1. Introduction
Cable-stayed bridges with steel-concrete composite girders effectively address two key limitations: the restricted span capacity of concrete cable-stayed bridges due to their excessive self-weight, and the fatigue susceptibility of orthotropic steel decks in all-steel cable-stayed bridges. This dual advantage has led to their increasingly widespread application in bridge engineering practice, particularly for projects requiring both long spans and durable deck systems [1,2]. However, a core scientific challenge in optimizing life-cycle performance for long-span bridges involves the rigorous assessment of operational environmental exposures and their corresponding structural performance characteristics. This challenge becomes particularly pronounced given their typical deployment across extreme geographical settings-including deep gorges and major river crossings-where complex microclimate conditions produce severe vertical temperature gradients in structural members.
Steel exhibits high thermal conductivity, enabling rapid heat transfer that allows its temperature to quickly equilibrate with ambient conditions during sudden temperature fluctuations [3]. In contrast, concrete’s thermal conductivity is approximately 1/50th that of steel, resulting in significantly slower response to environmental temperature variations. This fundamental material mismatch generates substantial interfacial thermal stresses that must be carefully considered in design. Early research on the temperature field of composite bridges dates back to Zuk’s pioneering work in 1965 [4]. Subsequent studies by Dilger [5], Kennedy [6], and Fu [7] employed both theoretical and experimental approaches to analyze temperature distributions and induced stresses in composite bridges. Their work established critical parameters, including maximum/minimum temperature differentials and stress characteristics in composite I-beams and box girders.
Beyond the service stage, researchers such as Bertagnoli [8] and Gara [9] investigated thermal effects on concrete during construction phases. Their studies focused on temperature-induced stresses and cracking mechanisms, enabling the prediction of time-dependent spatial stress distributions and informing crack mitigation strategies in composite bridge construction. More recently, Liu [10] investigated the influence of air temperature on the annual and diurnal strain behaviors of the deck, pylon, and cable elements in the newly constructed Kömürhan cable-stayed bridge in Turkey (2021). By analyzing one year of monitoring data (January–December 2021), including a detailed examination of July 3, the day with the highest recorded temperature, the study revealed that air temperature plays a significant role in the daily and yearly strain responses of the steel deck. In contrast, the strain in the concrete pylon exhibited only a weak correlation with temperature. Additionally, cable forces in both the main span and the back span anchorage block tended to increase with higher temperatures. The findings highlight thermal effects as the dominant factor shaping the strain behaviors of cable-stayed bridges under normal operational conditions. Zhou [11] and Ji [12] performed comprehensive temperature monitoring and numerical analyses on three representative bridge types. Their findings established critical reference data for temperature load specifications across different geographical regions and bridge configurations in China [13].
As thermal effects in bridge structures correlate directly with meteorological parameters-including solar radiation, wind speed, and air temperature, extensive research has quantified temperature distributions using meteorological data [14,15]. Huang [16] developed a generalized numerical model for solar-induced temperature fields. Notably, seasonal extremes and their thermal impacts have been systematically investigated [17,18,19]. Tomé [20] introduced an optimized framework for simulating large cable-stayed bridges’ behavior under daily/seasonal temperature variations.
To investigate temperature distribution and thermal effects in steel-concrete composite beams, Wang [21] conducted both experimental modeling and numerical simulations of temperature gradient effects in composite bridge decks. The study demonstrated that vertical temperature distributions in composite bridge decks exhibit nonlinear characteristics, which align with the gradient trends specified in design codes. Through long-term monitoring of a composite beam test model, Zhang [22] statistically derived the distribution patterns and characteristic values of the most critical temperature gradients. Fan [23] developed a vertical discrete, dimensionality-reduced model for rapid temperature load calculation in steel-concrete composite bridges. The study proposed a MATLAB-based state equation solver to implement an efficient one-dimensional numerical model. Validation through an outdoor sunshine experiment confirmed the model’s accuracy against refined simulations, revealing a computational efficiency improvement of nearly 1000 times. This streamlined thermal model significantly accelerates temperature field analysis and design temperature load computations, offering a robust and practical tool for advancing research in composite bridge engineering.
Extensive theoretical and experimental investigations on thermal effects in steel-concrete composite beams have been conducted worldwide through model tests, numerical simulations, and in-situ bridge measurements, yielding numerous valuable findings. However, current research remains limited regarding temperature fields and thermal effects during construction stages of long-span composite cable-stayed bridges. China’s highway design specifications lack unified criteria for regional parameter selection, potentially rendering code-based thermal effect assessments inaccurate. This study employs comprehensive in-situ temperature monitoring of the Chibi Yangtze River Bridge to develop a refined thermal gradient model. Field measurements of environmental parameters and structural temperature distributions were directly integrated into finite element simulations for stress calculation and model validation. Such instrumentation is not only feasible but increasingly essential for large-scale infrastructure projects.
2. Basic Theory
Under normal operating conditions, bridges experience continuous thermal cycling on both annual and daily timescales. Bearings and expansion joints effectively accommodate seasonal expansion and contraction from annual temperature variations, preventing excessive thermal stresses. The daily temperature cycle—driven principally by solar radiation and diurnal temperature changes (Figure 1)—causes progressive bridge heating after sunrise. This creates a thermal gradient between the warmer deck surface and cooler underside, inducing cross-sectional stress. Following sunset, the bridge surface cools through thermal radiation and convection, gradually equilibrating with ambient air temperatures.
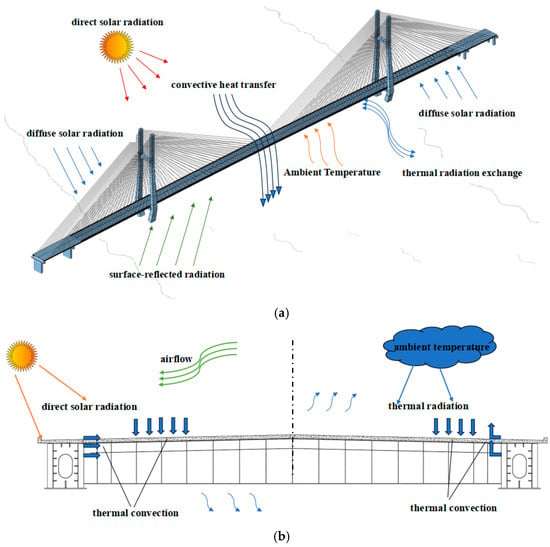
Figure 1.
Diurnal temperature cycle diagram for bridges, (a). Overview of the bridge; (b). Cross-section view.
Bridge structural responses to thermal loading include longitudinal, vertical, and lateral deformations, with nonlinear temperature gradients inducing additional self-balancing sectional stresses. When subjected to a nonlinear thermal gradient across its cross-section (Figure 2), a structural girder exhibits decomposable thermal responses comprising three distinct components (Figure 2): a uniform temperature component Tu, a linear temperature gradient component Tv, and a nonlinear residual temperature component TR. The uniform component Tu exclusively induces axial deformation without generating sectional curvature. The linear gradient component Tv, which produces pure bending about the neutral axis, governs flexural deformation. The residual component, mathematically expressed as TR(y) = T(y) − Tv(y) − Tu, creates differential thermal expansion across the girder depth. The unrestrained thermal strain profile would inherently violate the Bernoulli-Euler plane-section hypothesis. To reconcile this kinematic incompatibility, the cross-section mobilizes internal restraint forces, generating a compensatory stress field. These self-balancing thermal stresses critically influence fatigue and serviceability assessments in modern bridge codes.

Figure 2.
Temperature action decomposition for composite beams.
In the case of composite girders, the relative slippage effect should be accounted for, with its analytical model illustrated in Figure 3.
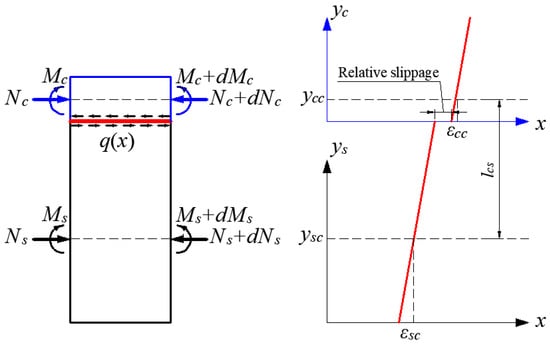
Figure 3.
Analytical model for composite girder with relative slippage consideration.
When considering interface slip behavior, the following fundamental assumptions are adopted:
- (1)
- The composite girder operates within the elastic deformation range;
- (2)
- Full curvature compatibility exists between the concrete slab and steel girder, with no vertical separation occurring at their interface;
- (3)
- The shear force transferred through discrete shear connectors is idealized as a continuously distributed load along the girder’s longitudinal axis.
Based on the above assumptions, the thermal stresses in the steel girder (σₛ) and concrete slab (σc) can be calculated using Equation (1):
where Es and Ec denote the Young’s modulus of steel and concrete, respectively εs(x,ys); and εc(x,yc) represent the longitudinal strains in the steel girder and concrete slab at their respective depths; αs and αc are the coefficients of thermal expansion of steel and concrete; and T(y) is the corresponding temperature.
The combined longitudinal stress and moment for both the steel girder and concrete slab are given by the integrals of thermal stress, presented in Equation (2):
where Ns and Nc are the axial force induced by thermal stress for steel and concrete, respectively; Ms and Mc are the bending moment induced by thermal stress for steel and concrete, respectively; Ac and As denote the cross-sectional areas of the steel girder and concrete slab, respectively; bs(ys) and bc(yc) represent the width functions of the steel girder and concrete slab, respectively, evaluated at their corresponding section heights ys and yc; φ is the curvature of the girder; Ic and Is represent the moments of inertia for the steel girder and concrete slab, respectively.
When modeling the concrete slab and steel girder as discrete free-body diagrams, the resultant longitudinal forces comprise three components: axial force in the steel girder (Ns), the axial force in the concrete slab (Nc), and the interfacial shear force (Q(x)). These force components are governed by the equilibrium condition formulated in Equation (3):
Based on moment equilibrium considerations at the concrete-steel interface, the governing relationship can be expressed as Equation (4):
The thermal stress can be calculated by solving the second-order ordinary differential equation of Q(x). Because of force balance of the micro-section, the strain at the neutral axis of concrete slab and steel girder can be obtained as Equation (5):
Through combination of governing Equations (2) and (3) with equilibrium condition (4), the composite girder curvature φ is derived as defined by Equation (6):
where lcs represents the neutral-axis separation distance between the concrete slab and steel girder.
The interfacial shear force can be determined through the constitutive relationship between relative slip displacement and equivalent shear stiffness, as mathematically formulated in Equation (7):
where K denotes the equivalent shear slip stiffness determined from the mechanical properties of shear connectors; D(x) represents the cumulative interfacial slip displacement, and binterface defines the characteristic width of the shear transfer interface.
The thermal stress distributions in the steel girder and concrete slab components of simply supported composite girders can be quantified through the analytical solutions presented in Equations (8) and (9), respectively.
3. Field Temperature Monitoring
3.1. Bridge Overview and Layout of Measuring Points on the Main Girder
The main bridge of the Chibi Yangtze River Bridge is a steel-concrete composite girder cable-stayed bridge with double pylons and double cable planes. The main bridge has a span arrangement of (90 + 240 + 720 + 240 + 90) m, with the main span of 720 m being the longest in the world among bridges of this type. The deck is 36.5 m wide, and the main girder adopts the form of a twin-box section, which consists of a steel box girder and a precast concrete deck, with thicknesses of 3.181 m and 26 cm in a standard segment, respectively, that are connected by shear connectors arranged on the longitudinal beams, transverse beams, and small longitudinal beams.
In order to grasp the real-time temperature in the concrete deck and steel girder during the construction of the bridge’s main girder, temperature test section S2 was established. As illustrated in Figure 4, section S2 is located in girder segment #6, 78 m from the tower center-line. Temperature sensors were deployed at 26 locations (10 concrete/16 steel per girder), with vertical distribution detailed in Figure 5.

Figure 4.
Test girder segments and test sections (unit: m).
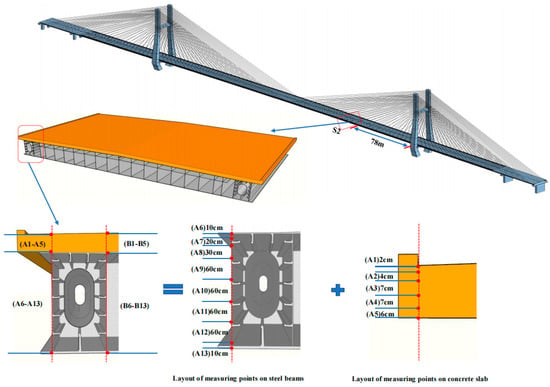
Figure 5.
Temperature sensors layout.
3.2. Temperature Distribution of Composite Girder
According to the construction progress of the main girder on site, temperature measurements were conducted from June 2020, to May 2021, with data collected at two-hour intervals. Analysis revealed that the temperature at each vertical measuring point of the cross-section exhibited distinct periodic variations over time. Figure 6 shows the temperature variation and the daily maximum and minimum air temperature over the test period. For bridge structures exposed to solar radiation and atmospheric temperature variations, the most unfavorable positive vertical temperature difference can occur during intense solar radiation in summer, while the most unfavorable negative vertical temperature difference can arise from sudden atmospheric cooling in winter. To investigate the dynamic characteristics of temperature changes within individual cycles, test results from three complete 24-h thermal cycles were selected for detailed analysis. Representative measurement days—30 August 2020; 23 October 2020; and 22 December 2020—were chosen, and the vertical temperature distribution across the cross-section on these days is illustrated in Figure 7, Figure 8 and Figure 9. Table 1 summarizes environmental parameters from reference monitoring days.

Figure 6.
Temperature variation over the test period.

Figure 7.
Temperature change on August 30th, (a). Side A; (b). Side B.

Figure 8.
Temperature change on October 23rd, (a). Side A; (b). Side B.

Figure 9.
Temperature change on December 22nd, (a). Side A; (b). Side B.

Table 1.
Environmental parameters for reference monitoring days.
As can be seen from Figure 7, Figure 8 and Figure 9, the temperature variation curves in Section A and Section B exhibited high consistency across the three selected measurement days, confirming the uniform distribution of temperature within the cross-section. However, significant temperature differences were observed among vertical measurement points, clearly indicating the presence of a thermal gradient along the height of the section.
The highest temperature peaks were recorded at the top surface of the concrete deck slab, where temperature fluctuations were also the most pronounced. This phenomenon is primarily attributed to direct solar radiation exposure, leading to rapid heat accumulation and temperature rise. Due to the relatively low thermal conductivity of concrete, temperatures decreased sharply in regions farther from the top surface.
From the top slab to the bottom of the girder, temperatures exhibited a gradual but nonlinear decline, closely following an exponential decay pattern. Notably, while thermal gradients were present, the steel web plates showed minimal temperature variation among measurement points. Moreover, the temperature trends remained consistent across all three observation days, suggesting stable thermal behavior in the steel web region, with negligible impact on the overall structural response.
Figure 10 shows the temperature time-history curves for the top and bottom slab of the composite girder at the measurement section. As observed, the top slab exhibits significant diurnal temperature variation due to solar radiation exposure, while the bottom slab–being sheltered from direct solar radiation–experiences substantially less temperature fluctuation throughout the day compared to the top slab.

Figure 10.
Time-history curve of temperature at the top and bottom slab.
4. Thermal Behavior Analysis of the Main Bridge During Construction of Chibi Yangtze River Highway Bridge
4.1. Code-Specified Temperature Gradient Models and Design Values
The temperature gradient models from JTG D60-2015 [24], AASHTO [25], and Eurocode [26] were selected for comparison; details are shown in Figure 11. Table 2 presents the temperature base values specified in these codes for determining the vertical temperature gradient in steel-concrete composite girders. It reveals that code differences lie in both the form of temperature curves and the factors considered when determining temperature base values. Primary factors influencing vertical temperature distribution include material properties, deck slab thickness, solar radiation intensity, ambient temperature, and the type/thickness of the wearing surface. Solar radiation intensity and ambient temperature are predominantly determined by the bridge’s geographical location. Notably, the temperature base values in JTG D60-2015 omit deck slab thickness and geographical location. The AASHTO specifications exclude deck slab thickness and wearing surface considerations. Eurocode provides two calculation models (conventional and simplified) but does not incorporate geographical location effects on temperature base values.

Figure 11.
Temperature gradient models in cirrentt specifications, (a). Composite girder section; (b). JTG (PTG); (c). AASHTO (PTG); (d). Eurocode (e). Simplified Eurocode.

Table 2.
The specified value of the vertical temperature gradient in the code.
4.2. Vertical Temperature Gradient Profile
The measured temperature field, owing to its high accuracy, can effectively capture the nuanced characteristics of temperature distribution in composite girder cross-sections. However, the distribution curves of measured temperature fields typically exhibit significant complexity and dynamic variability, which inevitably complicates the precise calculation and analysis of thermal differential effects. Direct utilization of measured data for thermal effect assessment is often constrained by computational complexity, making it challenging to efficiently and accurately apply in practical engineering scenarios.
Moreover, this intricate variability not only increases analytical difficulty but also limits the widespread adoption of measured temperature fields in engineering practice. Due to the absence of concise and effective computational methods, engineers often struggle to fully leverage measured temperature data for guiding design and construction.
To address these challenges while maintaining computational accuracy, this study proposes a simplified mathematical model based on the characteristics of measured temperature distributions, with reference to relevant international codes and literature. Specifically, analysis of the measured vertical temperature field reveals that the temperature distribution in the concrete deck exhibits a nonlinear pattern, which aligns closely with the characteristics of an exponential function. Consequently, an exponential function was selected to model the vertical temperature gradient in the concrete deck. This approach not only simplifies calculations but also more accurately represents the actual thermal behavior of the concrete slab.
For the temperature distribution in steel webs, a linear function was adopted to describe the thermal gradient, as it effectively captures the fundamental variation trend while remaining practical for engineering applications. By employing these two distinct functional forms, the complex measured temperature distribution curves were simplified, resulting in the proposed vertical temperature gradient model for composite girders, as illustrated in Figure 12.

Figure 12.
Modeling approach for vertical temperature gradients in composite girders. (hc = thickness of concrete deck slab, H = girder height).
The temperature gradient mathematical model was derived through curve fitting, as expressed by the following Equation (10):
Figure 13 presents the temperature gradient distributions generated by both the proposed model in this study and the thermal load models specified in current design codes (AASHTO, Eurocode, and JTG D60-2015). To validate the accuracy of the proposed model, the temperature gradient distribution corresponding to the recorded thermal load on 30 August 2020 is also displayed. As shown in the figure, both the proposed model and the temperature base values specified in current specifications deviate from measured temperature data. However, for the concrete slab, the proposed models yield temperature gradient distributions closely aligned with field measurements. This demonstrates that the proposed thermal models exhibit significantly improved agreement with actual thermal actions compared to existing design specifications.

Figure 13.
Comparison of temperature gradient distribution.
5. Finite Element Analysis
5.1. Global Modeling with Midas Civil
A comprehensive bridge analysis model was developed using beam elements in Midas Civil (Figure 14). By monitoring the structural, boundary, and load variations at each construction stage, the global internal force distribution of the bridge across different construction phases was determined.

Figure 14.
Global beam element analysis model of the 1/2 Cable-Stayed Bridge (Maximum balanced cantilever construction stage).
5.2. Local Modeling with ABAQUS
A detailed spatial local computational solid model (Figure 15) for each construction stage of the Chibi Yangtze River Bridge was developed using ABAQUS. The concrete deck slab and anchor plates were modeled using three-dimensional eight-node solid elements with reduced integration (C3D8R). The main steel girder, which includes longitudinal beams, transverse beams, and small longitudinal beam, was represented using four-node shell elements with reduced integration (S4R). To ensure computational accuracy, nine Simpson’s integration points were employed across the thickness of the shell elements. Furthermore, to simulate the slip effect between the steel main girder and the bridge deck, spring elements were utilized to model the connection behavior of the shear studs. This approach considered only the longitudinal slip direction while neglecting transverse displacements and any potential uplift of the concrete deck.

Figure 15.
Finite element model, (a). Overall model of the full bridge; (b). Local spatial FE model (Boundary conditions); (c). Local spatial FE model (Connection detail between main girder and transverse beam).
During the construction of the three segments at the top of the main girder and pier, temporary three-way fixation measures (in the longitudinal, transverse, and vertical directions) were implemented at the construction site to secure the connection between the main girder and the main tower. These measures were essential to ensure the structural stability and safety throughout the construction process. To accurately reflect the actual engineering conditions, the boundary conditions of the main girder in the tower area were modeled as fixed (Figure 15b). The cable forces for the stay cables were derived from the overall bar system model (as illustrated in Figure 15a), corresponding to the specific requirements of each construction stage.
Six cross-sections (designated as Ⅰ-Ⅰ to Ⅵ-Ⅵ, Figure 16) spaced at 2-m intervals were selected within the standard main steel girder segment, as illustrated in Figure 16. Section VI-VI represents the intermediate section between two stay cables. Sections I-I, III-III, and V-V are directly connected to the transverse beams, whereas sections II-II, IV-IV, and VI-VI are situated at the midpoints between adjacent transverse beams.

Figure 16.
Schematic diagram of six sections in the bridge transverse direction in the standard segment.
5.3. Temperature Effect Analysis
As a representative case study, the maximum double-cantilever construction stage was selected for detailed investigation. Finite element analysis was performed using ABAQUS to evaluate temperature-induced stresses in the deck slabs of six cross-sections of girder segments #1, #6, and #16. Two distinct thermal gradient models were compared: (1) the fitted gradient model developed in this study, and (2) the vertical temperature gradient model specified in JTG D60-2015. The resulting stress distributions are presented in Figure 17 and Figure 18.

Figure 17.
Stress in bridge deck slab under positive temperature gradient (CC6), (a). Segment #1 (Proposed gradient model); (b). Segment #1 (JTG D60-2015); (c). Segment #6 (Proposed gradient model); (d). Segment #6 (JTG D60-2015); (e). Segment #16 (Proposed gradient model); (f). Segment #16 (JTG D60-2015).

Figure 18.
Stress in bridge deck slab under negative temperature gradient (CC6), (a). Segment #1 (Proposed gradient model); (b). Segment #1 (JTG D60-2015); (c). Segment #6 (Proposed gradient model); (d). Segment #6 (JTG D60-2015); (e). Segment #16 (Proposed gradient model); (f). Segment #16 (JTG D60-2015).
Key findings reveal that both thermal gradient models produced fundamentally similar transverse stress distribution patterns across all composite girder sections in the concrete deck. Crucially, pronounced positive shear lag occurred in deck sections connected to cross-beams (Sections I-I, III-III, and V-V), and distinct negative shear lag manifested in non-connected sections (Sections II-II, IV-IV, and VI-VI). Comparative stress analysis (Table 3) demonstrates the proposed model’s significant reduction in predicted stresses versus conventional methods (JTG D60-2015).

Table 3.
Peak stress comparison under thermal gradients (Unit: MPa).
The significantly lower tensile strength of concrete compared to its compressive strength highlights the critical importance of considering thermal gradient effects in deck design. Compared to specification-based thermal gradients (JTG D60-2015), the proposed model demonstrates significantly stronger agreement with measured thermal effects. The reduced tensile stresses predicted by the proposed model (approximately 30–34% lower than code specifications) suggest that current design approaches may be overly conservative regarding thermal-induced cracking potential.
6. Conclusions
This study investigated thermal effects on composite girders during the construction of the Chibi Yangtze River Bridge. The key findings are as follows:
- (4)
- A refined vertical temperature gradient model, combining an exponential function for the concrete deck and a linear function for the steel web, was developed based on field monitoring. This model reduces tensile stress predictions in the concrete deck by 30–33% compared to code-specified models under negative temperature gradients, mitigating over-conservatism in cracking risk assessment.
- (5)
- During the maximum cantilever stage, crossbeam connectivity induces distinct shear lag effects: positive shear lag (stress concentration) occurs at connected sections and negative shear lag (stress reduction) at non-connected sections. This necessitates differentiated design considerations for deck slabs.
- (6)
- The concrete deck develops critical tensile stresses under negative temperature gradients due to concrete’s low tensile strength, highlighting the imperative for thermal gradient considerations in design to prevent longitudinal cracking.
This work provides practical guidelines for thermal effect management in long-span composite cable-stayed bridge construction.
Author Contributions
Conceptualization, H.L. and Q.S.; methodology, H.L. and B.L.; software, W.W.; validation, C.Y.; investigation, Y.P.; writing—original draft preparation, H.L. and W.W.; writing—review and editing, B.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was financially supported by the Natural Science Foundation of Hunan Province, China (Grant Nos. 2025JJ70253, and 2025JJ70276), the Program of Hunan Province Education Department (Grant Nos. 23A0496 and 23B06245), the Hunan Province Degree and Graduate Education Reform Research Project (Grant No. 2024JGZD060), the Teaching Reform Research Project of Hunan Institute of Science and Technology (Grant No. 2024A02), and the College Students’ Innovation and Entrepreneurship Training Program, China (Grant Nos. S202512658011, and S202512658012).
Data Availability Statement
For inquiries related to the availability of the original data, please contact the corresponding author.
Acknowledgments
The authors would like to thank the investigation team for supporting the research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Luo, H.; Feng, J.; She, Q.; Li, B.; Wu, C.; Zeng, Y. Analysis of Shear Lag Effect of Steel-Concrete Composite Box Girders with Straight Steel Webs. IAENG Int. J. Appl. Math. 2024, 54, 507–517. [Google Scholar]
- Luo, H.; Feng, J.; She, Q.; Li, B.; Wu, C.; Pan, M.; Zeng, Y. Analysis for Effective Flange Width Considering Slip Effect for Main Girder of Composite Cable stayed Bridges during Construction Phase. Eng. Lett. 2025, 33, 2465–2477. [Google Scholar]
- Giussani, F. The effects of temperature variations on the long-term behaviour of composite steel-concrete beams. Eng. Struct. 2009, 31, 2392–2406. [Google Scholar] [CrossRef]
- Zuk, W. Thermal Behavior of Composite Bridges-Insulated and Uninsulated. Highw. Res. Rec. 1965, 76, 231–253. [Google Scholar]
- Dilger, W.H.; Ghali, A.; Chan, M.; Cheung, M.S.; Maes, M.A. Temperature stresses in composite box girder bridges. J. Struct. Eng. 1983, 109, 1460–1478. [Google Scholar] [CrossRef]
- Kennedy, J.B.; Soliman, M.H. Temperature distribution in composite bridges. J. Struct. Eng. 1987, 113, 475–482. [Google Scholar] [CrossRef]
- Fu, H.; Ng, S.; Cheung, M.S. Thermal behavior of composite bridges. J. Struct. Eng. 1990, 116, 3302–3323. [Google Scholar] [CrossRef]
- Bertagnoli, G.; Gino, D.; Martinelli, E. A simplified method for predicting early-age stresses in slabs of steel-concrete composite beams in partial interaction. Eng. Struct. 2017, 140, 286–297. [Google Scholar] [CrossRef]
- Gara, F.; Leoni, G.; Dezi, L. Slab cracking control in continuous steel-concrete bridge decks. J. Bridge Eng. 2013, 18, 1319–1327. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Y.; Jiang, L.; Zhang, N. Long-term field test of temperature gradients on the composite girder of a long-span cable-stayed bridge. Adv. Struct. Eng. 2019, 22, 2785–2798. [Google Scholar] [CrossRef]
- Zhou, Y.C.; Hu, S.N.; Song, L.; Li, Z.Q. Effect analysis of steel-concrete composite beam caused by sudden change of temperature. Jiaotong Yunshu Gongcheng Xuebao 2013, 13, 20–26. (In Chinese) [Google Scholar]
- Ji, D.J.; Liu, J.; Zhang, Z.F. Temperature effect analysis of steel-concrete composite girder cable-stayed bridge in arctic-alpine region. J. Archit. Civ. Eng. 2016, 33, 113–119. (In Chinese) [Google Scholar]
- Fan, J.S.; Liu, C.; Liu, Y.F. Review of Temperature Distribution and Temperature Effects of Steel-concrete Composite Girder Bridges in China. China J. Highw. Transp. 2020, 33, 1–13. (In Chinese) [Google Scholar]
- Sheng, X.; Lin, C.; Zheng, W.; Li, Y.; Chen, Z. The solar radiation induced spatiotemporal temperature distribution and time-varying temperature effect in long-span ballastless track continuous beam-arch bridge. Adv. Struct. Eng. 2025, 28, 1233–1255. [Google Scholar] [CrossRef]
- Liao, Y.; Han, Y.; Zhang, R.; Zong, Z.; Sun, H. A data-driven approach for modeling stochastic structural temperature field of a long-span cable-stayed bridge. Eng. Struct. 2025, 335, 120267. [Google Scholar] [CrossRef]
- Huang, M.S.; Zhang, J.W.; Luo, J. Construction and Experimental Verification of an Efficient Numerical Model of One-Dimensional Temperature Field for Large-Span Cable-Stayed Bridge with Steel-Concrete Composite Girders. Eng. Mech. 2024, 41, 197–205. (In Chinese) [Google Scholar]
- Gong, B.; Feng, L.; Liu, J.; Liu, S.; Wang, Z.; Liu, Y. Finite-Element Analysis of Temperature Field and Effect on Steel-Concrete Composite Pylon of Cable-Stayed Bridge without Backstays. Buildings 2024, 14, 1731. [Google Scholar] [CrossRef]
- Jian, S.F.; Yu, F.L.; Cheng, L. Experiment study and refined modeling of temperature field of steel-concrete composite beam bridges. Eng. Struct. 2021, 240, 112350. [Google Scholar] [CrossRef]
- Shan, Y.; Li, L.; Xia, Q.; Gao, W.; Jing, Q.; Xia, Y. Temperature behavior of cable-stayed bridges. Part I—Global 3D temperature distribution by integrating heat-transfer analysis and field monitoring data. Adv. Struct. Eng. 2023, 26, 1579–1599. [Google Scholar] [CrossRef]
- Tomé, S.E.; Pimentel, M.; Figueiras, J. Structural response of a concrete cable-stayed bridge under thermal loads. Eng. Struct. 2018, 176, 652–672. [Google Scholar] [CrossRef]
- Wang, D.; Tan, B.; Wang, X.; Zhang, Z. Experimental study and numerical simulation of temperature gradient effect for steel-concrete composite bridge deck. Meas. Control 2021, 54, 681–691. [Google Scholar] [CrossRef]
- Zhang, P.J.; Wang, C.S.; Wu, G.S.; Wang, Y. Temperature gradient models of steel-concrete composite girder based on long-term monitoring data. J. Constr. Steel Res. 2022, 194, 107309. [Google Scholar] [CrossRef]
- Fan, J.S.; Li, B.L.; Liu, C.; Liu, Y.F. An efficient model for simulation of temperature field of steel-concrete composite beam bridges. Structures 2022, 43, 1868–1880. [Google Scholar] [CrossRef]
- JTG D60-2015; General Code for Design of Highway Bridges and Culverts. Ministry of Transport of the People’s Republic of China: Beijing, China, 2015.
- AASHTO-LRFD; Bridge Design Specifications (10th ed). American Association of State Highway and Transportation Officials: Washington, DC, USA, 2024.
- EN 1991-1-5; Actions on Structures. Part 1.5: General Actions-Thermal Actions. European Committee for Standardization, Eurocode: Brussels, Belgium, 2003.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).