Experimental Study on Improving the Strength and Ductility of Prefabricated Concrete Bridge Piers Using GFRP Tube Confinement

Abstract

The application of precast assembled pier systems in high-seismicity regions is often constrained by their seismic performance limitations. To validate the optimization effect of GFRP confinement on the hysteretic performance of bridge piers, this study first conducted axial compression tests on 54 glass fiber-reinforced polymer (GFRP)-confined concrete cylindrical specimens. The investigation focused on the effects of fiber layers (6 and 10), orientation angles ($\pm 45°$, $\pm 60°$, $\pm 80°$), slenderness ratios (2 and 4), and compression section configurations (fully loaded vs. core concrete loading only) on confinement efficacy. The experimental results demonstrate that specimens with $\pm 60°$ fiber angles achieved an optimal balance between strength and ductility, exhibiting an average strength enhancement of 298.0% and a maximum axial strain of 2.7% compared to unconfined concrete. Subsequently, two GFRP tube-confined concrete bridge piers with varying fiber layers (PRCG1: 6 layers; PRCG2: 10 layers) and one unconfined reference pier (PRC) were designed and fabricated. All specimens employed grout-filled sleeves to connect caps and piers. Pseudo-static tests revealed that GFRP confinement effectively mitigated damage in plastic hinge zones and enhanced seismic performance. Compared to the PRC, PRCG1 and PRCG2 exhibited increases in ultimate displacement by 19.50% and 28.57%, in ductility coefficients by 18.56% and 27.84%, and in cumulative hysteretic energy dissipation by 13.90% and 26.43%, respectively. At the 5% drift ratio, their load capacities increased by 26.74% and 23.25%, stiffnesses improved by 28.91% and 25.51%, and residual displacements decreased by 20.89% and 11.17%. The accuracy and applicability of the GFRP tube-confined bridge pier model, developed based on the Lam–Teng model, were validated through numerical simulations using the OpenSees fiber element approach.

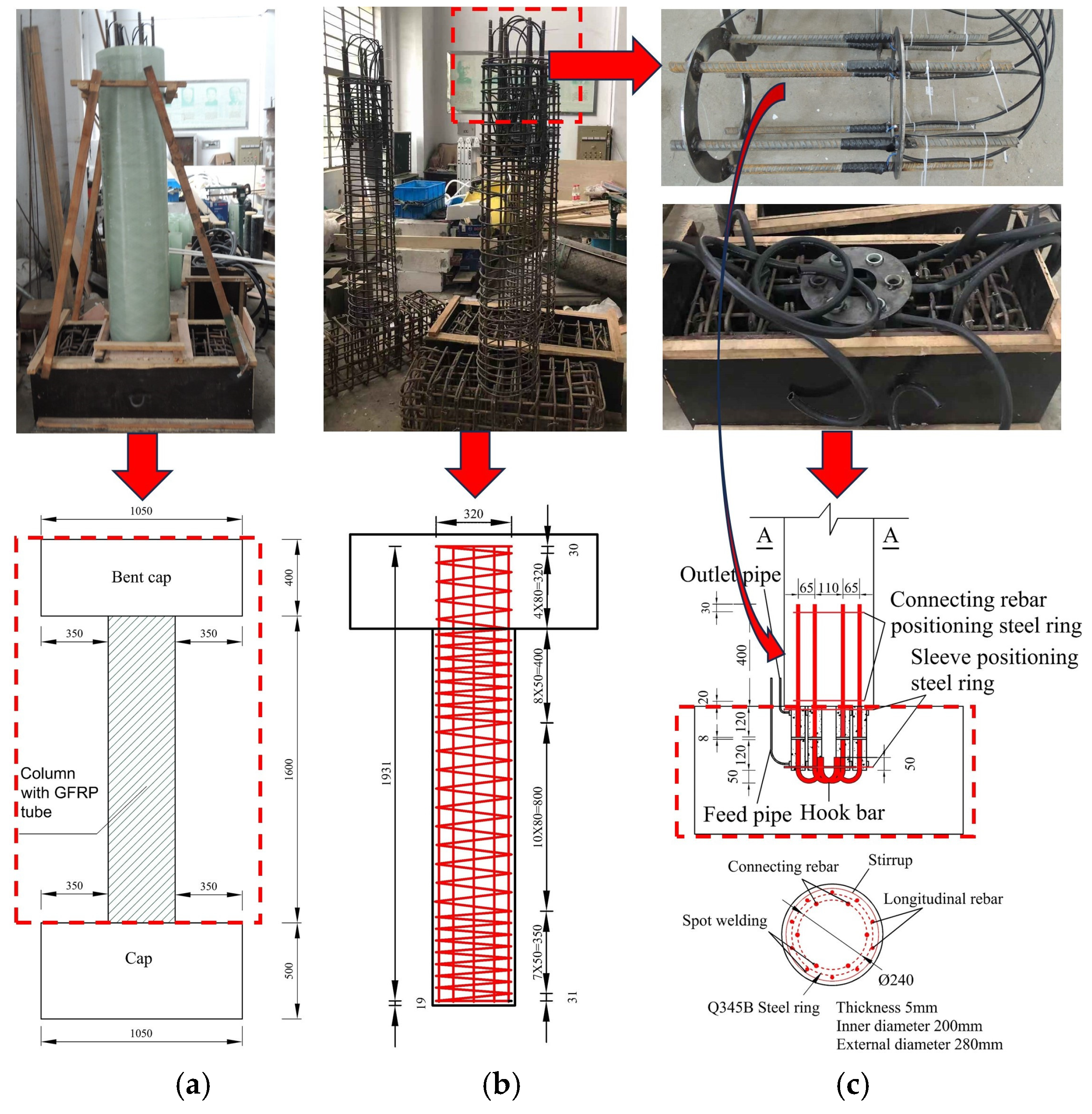
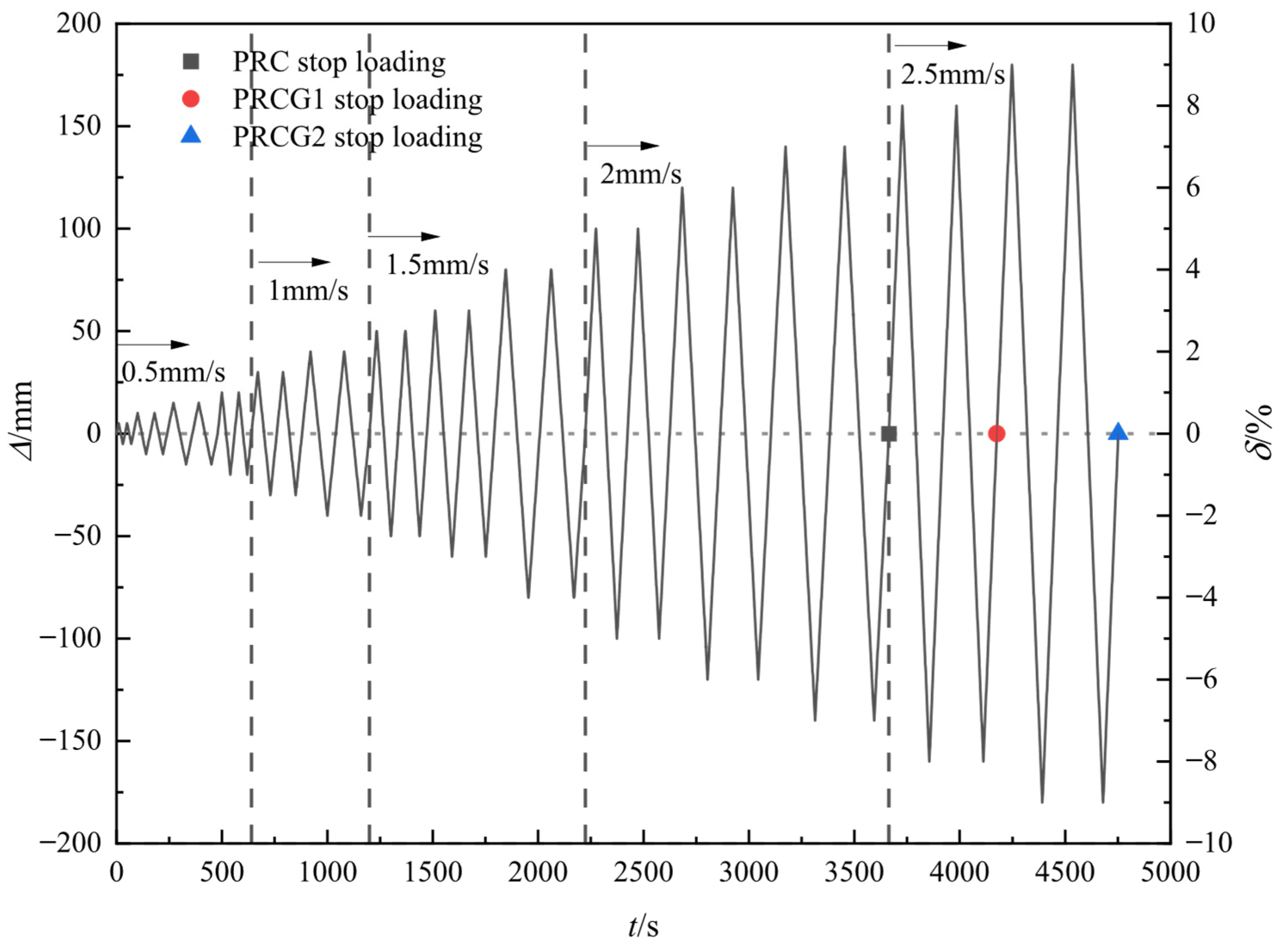
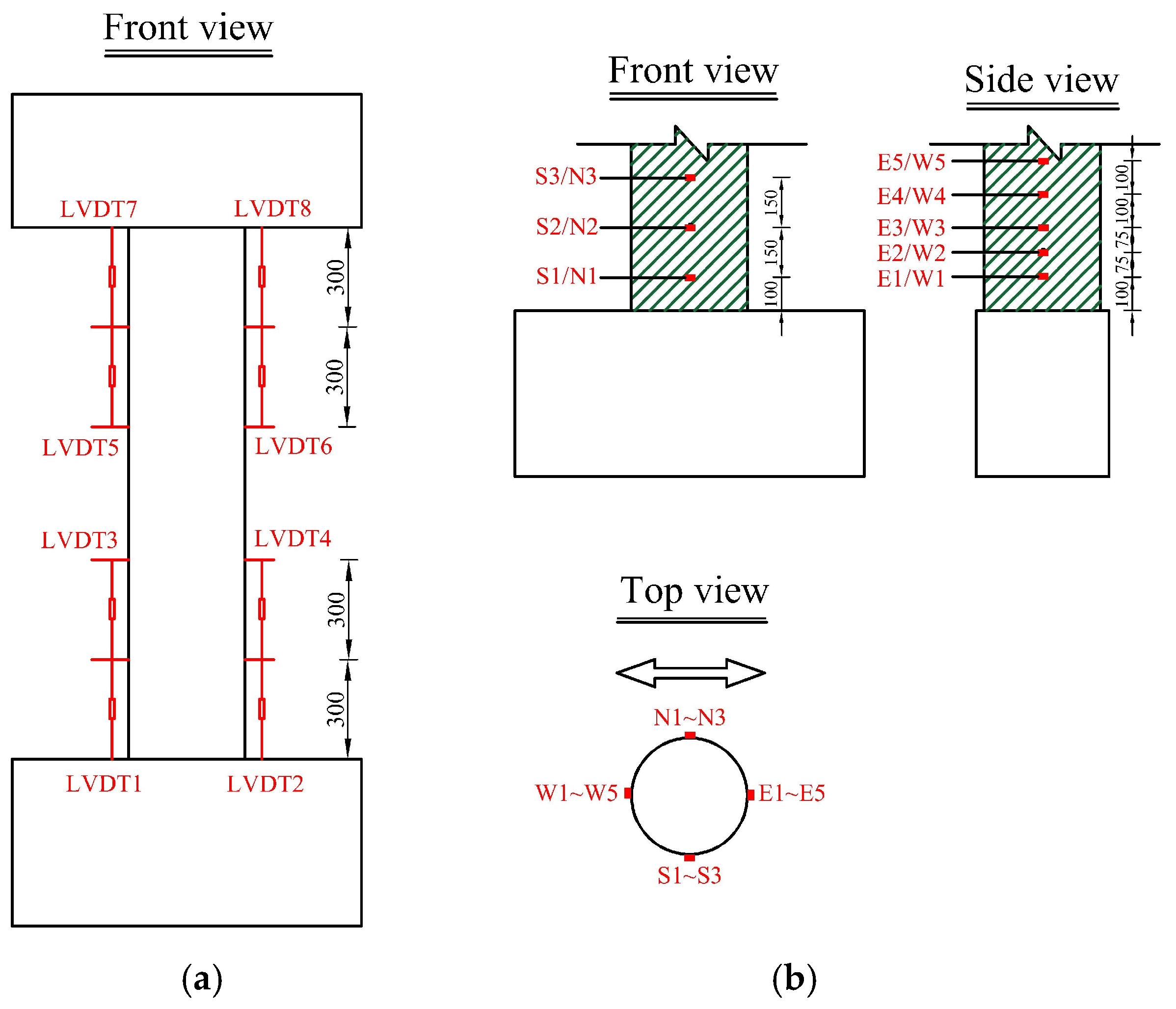
1. Introduction

Fiber-Reinforced Polymer (FRP) possesses exceptional properties, including lightweight characteristics, a high strength-to-weight ratio, and corrosion resistance. In civil engineering, it is predominantly employed for retrofitting or strengthening existing concrete structures [1]. Two primary application methods exist:

(1)

Confinement by FRP sheets: Wrapping FRP sheets around concrete columns to form externally bonded FRP-confined concrete members;

(2)

Concrete-filled FRP tubes: Casting concrete into prefabricated FRP tubes to create integral FRP–concrete composite columns.

When utilizing FRP sheets for concrete confinement, the fiber orientation is exclusively aligned in the hoop direction. In contrast, FRP tubes can be engineered with diverse lamination sequences, necessitating the simultaneous optimization of both hoop and axial mechanical properties [2]. Glass-fiber-reinforced polymer (GFRP) not only serves as confinement sheets for structural components but also enables the design and fabrication of multifunctional GFRP tubes with customizable configurations [3].

Numerous researchers have conducted extensive investigations into the seismic performance of conventional reinforced concrete bridge piers strengthened with FRP. Existing studies demonstrate that FRP confinement significantly enhances the ductility and energy dissipation capacity of piers, while altering their failure modes—for instance, transforming brittle shear failure into ductile flexural failure, or mitigating lap-splice failure through improved fatigue resistance. Furthermore, FRP effectively increases the lateral deformation capacity but exhibits limited influence on the maximum lateral load-carrying capacity and negligible effects on flexural stiffness [4,5,6].

Tan et al. [7] investigated the seismic behavior of GFRP-confined ultra-high performance concrete (UHPC) composite columns through quasi-static cyclic tests. Their study characterized the structural skeleton curves, developed a finite element (FE) model for the composite columns, and quantitatively evaluated the effects of key parameters—including the GFRP tube diameter-to-thickness ratio, circular elastic modulus of GFRP, and concrete tensile strength—on seismic performance. Wang et al. [8] explored the enhancement of seismic capacity in GFRP-UHPC columns by integrating H-shaped steel cores under quasi-static loading. Considering six design variables (steel section dimensions, steel yield strength, GFRP thickness, axial load ratio, shear connector configuration, and UHPC steel fiber content), they fabricated 14 specimens to analyze load–displacement hysteresis behavior and component strain evolution.

Although extensive research exists on the seismic performance of cast-in-place bridge piers incorporating various FRP types, concrete strength grades, or internal structural designs, experimental studies investigating GFRP tube-confined prefabricated assembled bridge piers remain limited in scope. This knowledge gap leads to significant constraints on deploying precast pier systems in moderate-to-high seismic regions, where achieving ductile failure modes and low residual displacements is critical for seismic resilience [9,10]. Sadeghian et al. [11,12] developed a novel moment-resisting connection by embedding concrete-filled GFRP tubes directly into concrete foundations or pile caps. Through parametric analysis, they characterized the effects of the tube diameter-to-thickness ratio, wall thickness, fiber architecture, and embedment depth on seismic performance. Their study demonstrates that a simplified design model can accurately predict failure modes, including bonding failure at the interface or bending failure of the GFRP tube, under cyclic loading conditions. Zhu et al. [13] proposed a structural form with concrete-filled GFRP tubes embedded in pile caps; these piers exhibited excellent seismic behavior under low-cycle reversed loading.

Other studies primarily focus on post-tensioned precast segmental piers. Hassanli et al. [14] employed FRP confinement at the base segments of unbonded post-tensioned prestressed concrete columns. Quasi-static tests revealed FRP fracture in all specimens at drift ratios exceeding 9%. A single-layer FRP confinement significantly enhanced the columns’ peak load (32% increase on average), ultimate drift capacity (69% improvement), and post-peak stiffness, with confined concrete achieving ultimate compressive strains up to 0.0056 under equivalent initial post-tensioning. Motaref et al. [15] conducted shake table tests on 1:3-scale segmented piers constructed with varied materials. The results demonstrated that FRP confinement improves pier strength, ductility, and effectively mitigates joint damage. Zhang et al. [16] utilized CFRP composites to repair earthquake-damaged prefabricated segmental piers. The repaired specimens exhibited higher energy dissipation and greater residual displacements than original specimens, with inter-segment sliding identified as the primary failure mode.

ElGawady et al. [17,18] evaluated the seismic performance of GFRP tube-confined post-tensioned precast piers via quasi-static tests, revealing that confined piers only had 25–50% of the residual displacement of RC piers but lower hysteretic energy dissipation. Moustaf and ElGawady [19] designed a precast hollow pier with dual walls (GFRP tube + steel tube) filled internally with concrete; shake table tests demonstrated its capacity to withstand high accelerations without severe damage and superior self-centering capabilities. Dawood and ElGawady [20] conducted finite element analysis on 84 FRP-confined self-centering post-tensioned prefabricated bridge piers with varied design parameters. They derived empirical equations based on idealized bilinear skeleton curves and validated their attainment of target performance levels across different seismic zones through a dedicated design procedure. Xue et al. [21] and Ma et al. [22] examined the effects of CFRP external reinforcement at the base segment on the seismic behavior of bridge piers via finite element modeling. The results indicated that CFRP reinforcement significantly increased the global stiffness and lateral load capacity, while reducing residual displacements substantially. The concrete at segment joints was identified as the critical failure zone, though the number of CFRP layers exhibited a negligible influence on seismic performance metrics.

As a primary connection method for precast assembled piers, the grouted sleeve splicing of rebars demonstrates mature technical specifications. Haber et al. [23] performed low-cycle reversed loading tests on five half-scale bridge column specimens. Four novel column–foundation moment connection types—including head joints and grouted sleeve connections—were implemented. All prefabricated models simulated traditional cast-in-place structural behavior, demonstrating a comparable global mechanical response, damage patterns, and energy dissipation capacity to cast-in-place columns. Given that grouted sleeves may alter plastic hinge zone performance, Haber et al. [24] further conducted low-cycle cyclic tests on 0.42-scale columns with dual-sleeve connections. By utilizing transition splices and high-strength rebars in foundations, the plastic hinge relocated above the sleeve region, effectively enhancing the piers’ plastic rotation capacity and ductility. Xu et al. [25] established, through finite element analysis, that an increased sleeve diameter and length in grouted-sleeve connected piers proportionally amplified the pier body curvature and rebar strain at joints compared to sleeve-free cases. When sleeves are embedded within pile caps, piers exhibit plastic hinge behavior comparable to cast-in situ piers, with seismic performance meeting or exceeding that of conventional construction, thus satisfying prescribed seismic requirements [26].

The existing literature indicates that seismic-induced damage in precast assembled piers primarily localizes at segment joints, manifesting as longitudinal reinforcement buckling or fracture. While GFRP tube confinement effectively mitigates this phenomenon, the extent of its enhancement on seismic performance metrics (e.g., load-bearing capacity, deformation, ductility, stiffness, hysteretic energy dissipation, and residual displacement) remains unexplored for “cast-in-place-equivalent” precast piers with grouted sleeve connections. To address this research gap, this study designed and fabricated 18 groups (54 specimens) of GFRP tube-confined concrete cylinders. Axial compression tests were conducted to investigate failure modes, bearing capacities, and stress–strain relationships. By optimizing the GFRP tube thickness and fiber orientation angles, a novel prefabricated pier system was developed: factory-precast GFRP tubes serve as concrete casting molds to form composite structures, which are assembled via connecting rebars embedded in grouted sleeves within caps. This design eliminates intermediate column joints, thereby circumventing adverse seismic effects. The system utilizes GFRP to provide circumferential confinement for core concrete while retaining longitudinal reinforcement to ensure flexural strength, achieving a strength–ductility balance. Quasi-static tests validated its seismic performance. In summary, this research integrates material–structure–design innovations based on the synergistic mechanism of GFRP confinement and grouted sleeve connections, concurrently enhancing bridge seismic safety and construction efficiency. It provides a reference for applying Accelerated Bridge Construction (ABC) technology in high-seismicity regions.

2. Materials and Methods

2.1. GFRP Tube-Confined Concrete Specimens Design and Fabrication

The filament-wound GFRP tubes employed in this study were factory-prefabricated, with customizable dimensions (height and diameter) tailored to experimental requirements. These tubes were manufactured via a reciprocating cross-winding process. The mechanical property testing of GFRP tubes is typically performed by manufacturers. Axial tensile properties are evaluated in accordance with GB/T 5349-2005 [27], while circumferential tensile performance is assessed using the split-disk test method specified in ISO 8521:2020 [28] and ASTM D2290-19a [29]. The key mechanical properties of the GFRP tubes are summarized in

Table 1. Performance parameters of fiber wound GFRP tubes.

	${\mathit{E}}_{\mathbf{i}\mathbf{a}}$ 1/GPa	${\mathit{E}}_{\mathbf{p}\mathbf{a}}$ 2/GPa	${\mathit{E}}_{\mathbf{i}\mathbf{h}}$ 3/GPa	${\mathit{E}}_{\mathbf{p}\mathbf{h}}$ 4/GPa	${\mathit{f}}_{\mathbf{c}\mathbf{t}}$ 5/MPa	${\mathit{f}}_{\mathbf{l}\mathbf{t}}$ 6/MPa	${\mathit{\epsilon }}_{\mathbf{c}\mathbf{t}}$ 7/%	${\mathit{\epsilon }}_{\mathbf{l}\mathbf{t}}$ 8/%	$\mathit{\upsilon }$ 9
$\pm 45°$	29.0	29.0	18.0	3.7	112.3	111.8	0.39	3.01	0.30
$\pm 60°$	18.0	12.4	29.4	23.4	102.6	410.2	0.83	1.75	0.26
$\pm 80°$	16.5	9.7	35.1	35.1	94.4	578.6	0.97	1.65	0.21

¹ Initial axial stiffness; ² Secant stiffness at peak axial stress; ³ Initial hoop stiffness; ⁴ Secant stiffness at peak hoop stress; ⁵ Peak axial stress; ⁶ Peak hoop stress; ⁷ Peak axial strain; ⁸ Peak hoop strain; ⁹ Poisson ratio.

, where $E_{\mathrm{i}\mathrm{a}}$ and $E_{\mathrm{i}\mathrm{h}}$ denote the elastic moduli, and $E_{\mathrm{p}\mathrm{a}}$ and $E_{\mathrm{p}\mathrm{h}}$ represent the secant moduli at peak load. The relevant calculations are defined as follows:

$$E_{\mathrm{i}\mathrm{a}}={\displaystyle \frac{{\sigma }_{\mathrm{a}}}{{\epsilon }_{\mathrm{a}}}}$$

(1)

$$E_{\mathrm{i}\mathrm{h}}={\displaystyle \frac{{\sigma }_{\mathrm{h}}}{{\epsilon }_{\mathrm{h}}}}$$

(2)

$$E_{\mathrm{p}\mathrm{a}}={\displaystyle \frac{f_{\mathrm{c}\mathrm{t}}}{{\epsilon }_{\mathrm{c}\mathrm{t}}}}={\displaystyle \frac{P_{\mathrm{u}\mathrm{a}}}{{A\epsilon }_{\mathrm{c}\mathrm{t}}}}$$

(3)

$$E_{\mathrm{p}\mathrm{h}}={\displaystyle \frac{f_{\mathrm{l}\mathrm{t}}}{{\epsilon }_{\mathrm{l}\mathrm{t}}}}={\displaystyle \frac{P_{\mathrm{u}\mathrm{h}}\left(d-t\right)}{{2A\epsilon }_{\mathrm{l}\mathrm{t}}}}$$

(4)

where ${\sigma }_{\mathrm{a}}$ and ${\sigma }_{\mathrm{h}}$ denote the axial stress and hoop stress of the GFRP tube in the elastic stage, respectively; ${\epsilon }_{\mathrm{a}}$ and ${\epsilon }_{\mathrm{h}}$ represent the axial strain and hoop strain in the elastic stage; $P_{\mathrm{u}\mathrm{a}}$ and $P_{\mathrm{u}\mathrm{h}}$ are the ultimate axial load and ultimate hoop load, respectively; $d$ is the outer diameter; $t$ denotes the wall thickness; and $A$ refers to the cross-sectional area. Definitions of additional symbols are provided in the footnotes to

Table 2. Geometric and material properties of GFRP tube-confined concrete specimens.

Group	Diameter × High/mm	Compression Section	$\mathit{\theta }$/(°)	$\mathit{n}$	Number
A	150 × 300	Full section	$\pm 45$	6	A45-6
				10	A45-10
			$\pm 60$	6	A60-6
				10	A60-10
			$\pm 80$	6	A80-6
				10	A80-10
B	150 × 600	Full section	$\pm 45$	6	B45-6
				10	B45-10
			$\pm 60$	6	B60-6
				10	B60-10
			$\pm 80$	6	B80-6
				10	B80-10
C	150 × 300	Core concrete	$\pm 45$	6	C45-6
				10	C45-10
			$\pm 60$	6	C60-6
				10	C60-10
			$\pm 80$	6	C80-6
				10	C80-10

.

A total of 54 GFRP tube-confined concrete cylinders were fabricated, organized into 3 primary groups and 18 subgroups (3 specimens per subgroup). The experimental variables included the number of fiber layers $n$ (6, 10), fiber winding angles $\theta$ ($\pm 45°$, $\pm 60°$, $\pm 80°$), and slenderness ratio (height/diameter) $\lambda$ (2, 4). Additionally, two compression methods were applied: full cross-section compression and core-concrete-only compression (details in Table 2). Specimen nomenclature: Numerals 45/60/80 denote $\theta$, letters A/B/C indicate specimen dimensions and loading type, and numerals 6/10 specify $n$.

All specimens were fabricated using filament-wound GFRP tubes as permanent formwork. Commercial concrete of identical specifications and batch was cast into the tubes to form GFRP-confined concrete cylindrical specimens. The concrete mix proportions are detailed in

Table 3. Concrete mix proportion.

	Cement [PO42.5]	Flyash [F-III]	Mineral Powder [S95]	Sand	Water	Rubble [10–25 mm]	Rubble [5–10 mm]	Water Reducer	Unit Weight
Proportioning dosage/(kg $·$ m−3) 4/5000 Proportioning dosage	241	134	66	748	163	826	207	4.2	2389.2
Mix proportion	1			1.696	0.370	1.873	0.469	0.010	-

. The average compressive strength of the concrete, measured from three 150 mm cubic specimens, was 41.6 MPa. For benchmark comparison, three unconfined plain concrete cylinders (diameter: 150 mm; heights: 300 mm and 600 mm) were prepared. The measured average axial compressive strengths were 34.8 MPa for the 300 mm high cylinders and 23.2 MPa for the 600 mm high cylinders. Correspondingly, the average peak compressive strains were 0.20% and 0.10%. Figure 1 illustrates the specimens before and after concrete casting.

2.2. Design and Fabrication of Bridge Pier Specimens

The specimens comprise three pier types: PRC is prefabricated reinforced concrete piers; PRCG1 and PRCG2 are prefabricated GFRP tube-confined reinforced concrete piers with 6-layer and 10-layer GFRP confinement, respectively. All specimens share identical cross-sectional dimensions (inner diameter = 350 mm, height = 1600 mm) and structural configuration. The fiber winding angle was optimized to $\pm 58°$ to balance strength enhancement and deformability, leveraging the anisotropic mechanical properties of GFRP composites for optimal confinement efficacy.

The pier column and bent cap were constructed as monolithic cast-in-place structures. The longitudinal reinforcement comprised ten Φ12 HRB400 rebars, with spiral reinforcement spaced at 50/80 mm using Φ8 HRB400 stirrups. The foundation was cast separately and assembled post-curing, ensuring sufficient strength development in each component. Integration between the column and cap was achieved via grouted sleeve splicing with OVM GT16 ductile cast iron sleeves embedded in the cap. These sleeves connected to six Φ16 HRB400 hooked rebars, utilizing BY(s)-YJ85 high-strength grout with an average compressive strength of 104.5 MPa (tested on six 100 mm cubes). The precast assembly configuration is detailed in Figure 2.

2.3. Axial Compression Test Loading and Measurement Point Layout

Axial compression tests on GFRP-confined concrete specimens were performed using a YE-5000kN four-column hydraulic testing machine (Changchun New Testing Machine Co., Ltd., Changchun, China) under monotonic static loading. The loading procedure comprised the following: 1. Lowering the crossbeam to accommodate the specimen height; 2. Adjusting the upper platen to contact the specimen surface with zero initial force; 3. Applying displacement-controlled loading via the upward movement of the lower platen.

For full cross-section loading, a steel plate was positioned atop the specimen, followed by a calibrated load cell to record axial forces. Conversely, the core-concrete-only loading configuration utilized a circular steel pad (Ø140 mm × 20 mm) placed on the specimen surface, with a steel plate and load cell sequentially stacked above it.

Linear Variable Differential Transformers (LVDTs, YHD-50 type) were mounted at 180° symmetrical positions on opposing sides of each specimen to quantify global axial deformation. At the mid-height section, eight strain gauges were circumferentially affixed: four aligned longitudinally to capture axial strain, and four transversely to measure hoop strain. Synchronized data acquisition employed 1 Hz timed sampling, with the testing machine’s load-cell readings providing real-time force validation for strain measurements.

Loading ceased when any of the following occurred: 1. Specimen failure (visual crushing/GFRP fracture); 2. Instrumentation failure: >50% of strain gauges damaged or signal loss in >50% channels; 3. Load decay to <80% of peak load. Figure 3 illustrates the axial compression loading configuration, test setup, and strain gauge layout, where H denotes the specimen height and S represents the cross-sectional circumference.

2.4. Quasi-Static Test Loading and Measurement Point Layout

The test system comprised horizontal and vertical loading units, a computerized control system, a data acquisition module, and a reaction platform. Prior to testing, the pier cap was rigidly fixed to the I-beam reaction platform via ground anchor bolts, while the bent cap was secured to the load-bearing crossbeam using two L-shaped steel plates and horizontal anchor bolts, establishing the loading interface. During testing, a 100-ton hydraulic jack applied and maintained a constant axial compression ratio of 0.2: PRC and PRCG2 underwent concentric axial compression; PRCG1 was subjected to eccentric compression. Subsequently, a 25-ton MTS actuator imposed horizontal reciprocating cyclic loads through a transverse steel frame, inducing controlled lateral displacements at the pier top. The MTS system recorded horizontal force and displacement at a sampling rate of 0.5 Hz. The quasi-static test configuration is illustrated in Figure 4.

The test employed displacement-controlled loading with two full cycles per displacement increment. Loading rates were regulated by the target displacement amplitude at each stage. To investigate the seismic behavior under ultimate conditions and monitor GFRP tube strain evolution, loading continued beyond peak load capacity. For structural integrity preservation, the maximum drift ratios were capped at 7% for PRC, 8% for PRCG1, and 9% for PRCG2 (Figure 5), where $t$ denotes loading time, $∆$ represents lateral displacement, and $\delta$ signifies drift ratio.

To monitor deformation development in bridge pier specimens and quantify the constraint effect of GFRP tubes, YHD-50 LVDTs were vertically distributed along the pier height, while BX120-20AA circumferential strain gauges were bonded to the GFRP tube surfaces. All sensors were connected to a dynamic strain acquisition system operating at 0.5 Hz. Identical instrumentation layouts were applied across specimens. For PRCG1 and PRCG2, the strain gauge arrangements were geometrically consistent but distinguished by nomenclature (e.g., G1S1 for PRCG1 vs. G2S1 for PRCG2), as detailed in Figure 6.

3. Axial Compression Test Results

3.1. Specimen Failure Phenomenon

The representative failure modes of GFRP-confined concrete specimens are illustrated in Figure 7. When the number of fiber layers $n=6$, the thinner GFRP tube wall underwent longitudinal splitting due to concrete expansion pressure, with cracks propagating from the ends toward the midspan until full penetration. For $n=10$, the thicker tube wall exhibited multi-stage failure: initial localized fiber fracture occurred, followed by strain accumulation leading to the delamination or fracture of the wall, accompanied by significant plastic deformation prior to ultimate failure.

Although all specimens failed through material fracture without instability-induced collapse, specimens with a slenderness ratio ($\lambda$) of 4 displayed measurable lateral deflection at mid-height. Specimens with a lower $\lambda$ of 2 demonstrated more effective lateral confinement compared to those with higher ratios, resulting in more uniform strain distribution across the section.

For specimens under full-section compression, failure manifested as coupled fracture of the GFRP tube and crushing of the concrete core. The GFRP tube directly carried axial loads, thereby weakening its hoop confinement capacity. In contrast, for specimens with only the concrete core under compression, the GFRP tube solely provided lateral confinement. Concrete crushing was more localized, and cracks in the GFRP tube primarily propagated from the midspan without preferential cracking induced by stress concentration at the ends. These specimens exhibited superior axial–hoop strain compatibility.

Crucially, the fiber failure direction aligned with the $\theta$ orientation, indicating that $\theta$ dominates the failure mechanism compared to the $n$, $\lambda$, or compression section configuration.

(1)

$\theta$ = $\pm 80°$. At approximately 50% of the peak strength, opacification (whitening) initiated on the GFRP surface and propagated along the fiber orientation, accompanied by audible fiber fracturing. Upon reaching peak load, catastrophic brittle failure occurred due to excessive tensile stress, resulting in instantaneous structural collapse. Simultaneously, hoop fracture of the GFRP tube coupled with concrete crushing was observed: Hoop fracture bands initiated at the tube midspan, while the confined concrete exhibited shear slip or conical crushing.

(2)

$\theta$ = $\pm 60°$. Similar opacification and fiber fracturing phenomena were observed. Failure was governed by combined through-thickness tensile and interlaminar shear stresses, manifesting as longitudinal splits along the specimen height. This transitional failure mode exhibited minor bulging deformation prior to collapse, yet retained predominantly brittle characteristics.

(3)

$\theta$ = $\pm 45°$. Post-peak, localized fiber whitening occurred without immediate rupture. The specimen underwent progressive damage degradation: bearing capacity decayed gradually, accompanied by the delamination of outer-layer fibers, widespread discoloration propagation, and pronounced lateral bulging due to insufficient confinement efficiency. No catastrophic hoop fracture was observed, and concrete crushing zones exhibited a dispersed distribution pattern.

3.2. Specimen Bearing Capacity

The axial stress $f_{\mathrm{c}}$ is calculated as the axial force (measured by the load cell) divided by the compressive cross-sectional area. The axial strain ${\epsilon }_{\mathrm{c}}$ and circumferential strain ${\epsilon }_{\mathrm{l}}$ are derived from the averaged measurements of four longitudinal and transverse strain gauges, respectively, with LVDT data serving as the displacement reference. The test results for each specimen group are summarized in

Table 4. Axial compression test results for GFRP tube-confined concrete.

Number	${\mathit{f}}_{\mathbf{c}\mathbf{c}}^{\mathbf{\prime }}$ 1			${\mathit{\epsilon }}_{\mathbf{c}\mathbf{c}}$ 2			${\mathit{\epsilon }}_{\mathbf{f}\mathbf{e}}$ 3			${\mathit{f}}_{\mathbf{l}}$ 4/MPa	${\mathit{f}}_{\mathbf{c}\mathbf{c}}^{\mathbf{\prime }}/{\mathit{f}}_{\mathbf{c}\mathbf{o}}^{\mathbf{\prime }}$ 5	${\mathit{f}}_{\mathbf{l}}/{\mathit{f}}_{\mathbf{c}\mathbf{o}}^{\mathbf{\prime }}$
	$\mathit{\mu }$ 6/MPa	$\mathit{\sigma }$ 7/MPa	${\mathit{C}}_{\mathbf{v}}$ 8	$\mathit{\mu }$/%	$\mathit{\sigma }$/%	${\mathit{C}}_{\mathbf{v}}$	$\mathit{\mu }$/%	$\mathit{\sigma }$/%	${\mathit{C}}_{\mathbf{v}}$
A45-6	44.1	1.84	0.042	0.4	0.02	0.061	/			5.5	1.27	0.16
A45-10	49.3	0.99	0.020	0.9	0.04	0.040	/			8.9	1.42	0.26
A60-6	102.4	3.19	0.031	2.6	0.11	0.042	1.4	0.08	0.058	15.5	2.94	0.44
A60-10	124.1	2.52	0.020	2.7	0.07	0.026	1.5	0.08	0.052	27.9	3.57	0.80
A80-6	127.5	4.40	0.035	2.2	0.11	0.049	1.2	0.07	0.062	16.4	3.66	0.47
A80-10	157.7	4.84	0.031	2.5	0.10	0.041	1.2	0.06	0.048	21.6	4.53	0.62
B45-6	39.9	0.42	0.011	0.5	0.01	0.028	/			5.4	1.72	0.23
B45-10	44.2	0.50	0.011	0.4	0.01	0.020	/			9.2	1.91	0.40
B60-6	89.9	3.35	0.037	1.9	0.10	0.051	1.7	0.10	0.061	18.5	3.88	0.80
B60-10	120.7	3.26	0.027	2.3	0.11	0.050	1.7	0.11	0.064	31.4	5.20	1.35
B80-6	117.4	3.90	0.033	2.2	0.12	0.055	1.5	0.10	0.063	21.6	5.06	0.93
B80-10	146.1	3.99	0.027	2.2	0.08	0.039	1.5	0.09	0.060	26.7	6.30	1.15
C45-6	57.1	2.09	0.037	0.5	0.03	0.057	/			5.6	1.64	0.16
C45-10	64.8	1.40	0.022	0.5	0.03	0.051	/			9.7	1.86	0.28
C60-6	122.8	2.16	0.018	2.3	0.12	0.053	1.6	0.09	0.057	17.6	3.53	0.50
C60-10	165.8	3.71	0.022	2.6	0.14	0.054	1.6	0.07	0.043	29.3	4.76	0.84
C80-6	155.3	1.85	0.012	2.2	0.08	0.037	1.4	0.05	0.038	19.4	4.46	0.56
C80-10	183.5	5.28	0.029	2.6	0.17	0.064	1.4	0.10	0.069	25.2	5.27	0.72

¹ Peak compressive strength of confined concrete; ² Peak axial strain; ³ Effective confinement hoop strain; ⁴ Effective confinement strength; ⁵ Unconfined concrete compressive strength; ⁶ Mean; ⁷ Standard deviation; ⁸ Coefficient of variation.

. A comparative analysis of the peak strength ($f_{\mathrm{c}\mathrm{c}}^{\prime }$) across specimen groups is presented in Figure 8. The effective confinement strength ($f_{\mathrm{l}}$) was calculated as follows [30]:

$$f_{\mathrm{l}}={\displaystyle \frac{2E_{\mathrm{f}}n{t}_{\mathrm{f}}{\epsilon }_{\mathrm{f}\mathrm{e}}}{D}}$$

(5)

where $E_{\mathrm{f}}$ is the hoop tensile secant modulus of GFRP; $n$ is the fiber layers; $t_{\mathrm{f}}$ is the laminate thickness of GFRP tube; ${\epsilon }_{\mathrm{f}\mathrm{e}}$ is the effective confinement hoop strain; and $D$ is the diameter of concrete cylinder.

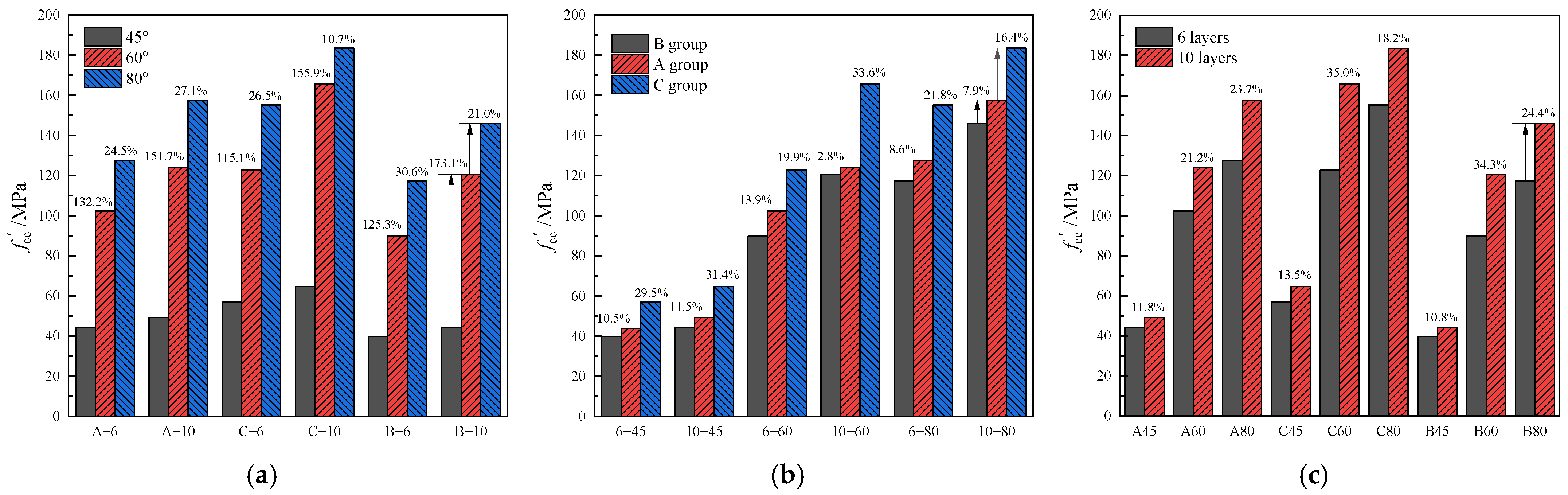
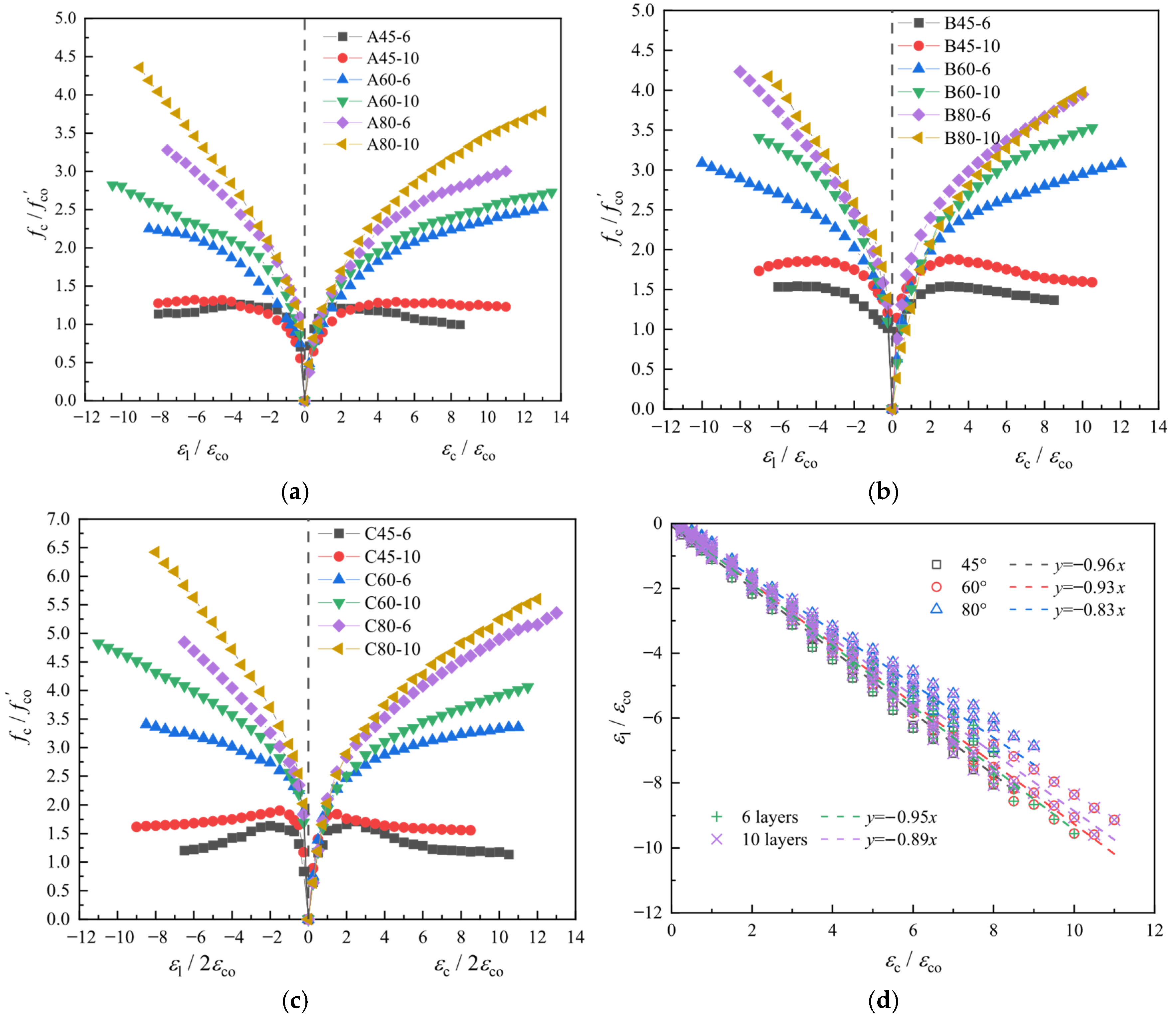
When the $\theta$ increased from $\pm 45°$ to $\pm 60°$, the $f_{\mathrm{c}\mathrm{c}}^{\prime }$ increased by 115.1–173.1% (relative) and 50.0–101.0 MPa (absolute). Further increasing $\theta$ to $\pm 80°$ yielded smaller gains of 10.7–27.1% (relative) and 17.7–33.6 MPa (absolute). Increasing the $n$ from 6 to 10 enhanced $f_{\mathrm{c}\mathrm{c}}^{\prime }$ by 10.8–35.0% (relative) and 4.3–43.0 MPa (absolute). Specimens with a $\lambda$ of 2 exhibited a 2.8–13.9% higher relative strength and a 3.4–12.5 MPa higher absolute strength than those with $\lambda =4$. Compared to full-section compression, core-concrete-loaded specimens showed significantly higher $f_{\mathrm{c}\mathrm{c}}^{\prime }$ (16.4–33.6% relative increase; 13.0–41.7 MPa absolute increase). Relative to the unconfined concrete strength $f_{\mathrm{c}\mathrm{o}}^{\prime }$, (1) Group A/B/C specimens achieved 189.8%, 301.2%, and 258.7% mean $f_{\mathrm{c}\mathrm{c}}^{\prime }$ enhancement, respectively; (2) specimens with $\theta =\pm 45°$, $\pm 60°$, and $\pm 80°$ exhibited mean $f_{\mathrm{c}\mathrm{c}}^{\prime }$ increases of 63.7%, 298.0%, and 388.0%, respectively; and (3) specimens with $n=6$ and $n=10$ showed mean $f_{\mathrm{c}\mathrm{c}}^{\prime }$ improvements of 212.9% and 286.9%, respectively.

3.3. Stress–Strain Analysis

The normalized stress–strain curves for each specimen group are shown in Figure 9, where ${\epsilon }_{\mathrm{c}\mathrm{o}}$ denotes the peak strain of unconfined concrete corresponding to $f_{\mathrm{c}\mathrm{o}}^{\prime }$. Notably, the surface cracking of GFRP tubes during loading damaged strain gauges prior to specimen failure, necessitating reliance on peak stress data from Table 4.

Figure 9 indicates that all GFRP-confined specimens exhibit near-linear stress–strain responses in the initial loading phase. As $f_{\mathrm{c}}$ approaches $f_{\mathrm{c}\mathrm{o}}^{\prime }$, the GFRP confinement mechanism activates, inducing nonlinear curvature in the curves. Subsequent increases in ${\epsilon }_{\mathrm{c}}$ reduce tangent slope magnitudes, with significant variations observed across specimens—attributable primarily to GFRP confinement effectiveness.

The $f_{\mathrm{c}\mathrm{c}}^{\prime }$ of GFRP-confined specimens increased by up to 530%, while the ${\epsilon }_{\mathrm{c}\mathrm{c}}$ exhibited a maximum enhancement of 1600%. Although ${\epsilon }_{\mathrm{c}}$ growth consistently outpaced ${\epsilon }_{\mathrm{l}}$ during loading, specimens with higher $\theta$ and $n$ demonstrated an enhanced axial deformation capacity but reduced circumferential deformation performance. Critically, ${\epsilon }_{\mathrm{c}}$ and ${\epsilon }_{\mathrm{l}}$ maintained a near-linear correlation throughout the loading process.

For GFRP-confined concrete short columns, the $f_{\mathrm{c}\mathrm{c}}^{\prime }$ and ${\epsilon }_{\mathrm{c}\mathrm{c}}$ of Group A and B specimens exhibit minimal differences. However, since the $f_{\mathrm{c}\mathrm{o}}^{\prime }$ of Group A is 50.0% higher than that of Group B, the normalized strength ratio ($f_{\mathrm{c}\mathrm{c}}^{\prime }/f_{\mathrm{c}\mathrm{o}}^{\prime }$) of Group B is significantly larger, demonstrating the enhanced confinement efficacy of GFRP tubes for specimens with higher $\lambda$.

After converting $f_{\mathrm{c}\mathrm{c}}^{\prime }$ to the ultimate bearing capacity (accounting for differing compressive areas), Group A and C specimens show $\pm 9.1\mathrm{\%}$ variation in load-carrying capacity, indicating close agreement. In contrast, the ${\epsilon }_{\mathrm{f}\mathrm{e}}$ differs by 6.3–14.3%. This implies that compressing GFRP tubes with confined concrete (vs. core-concrete-only loading) minimally impacts axial performance but weakens the circumferential deformation capacity, particularly in specimens with a larger $\theta$.

The stress–strain response exhibits a triphasic profile comprising an initial linear segment, a transitional phase, and a subsequent linear segment. Prior to $f_{\mathrm{c}}$ reaching 0.8–0.9$f_{\mathrm{c}\mathrm{o}}^{\prime }$, specimens remain in the linear elastic regime with the negligible activation of GFRP confinement. During the elastoplastic transition, curves diverge significantly across specimens, characterized by a reduced tangent slope, rapid microcrack proliferation, and substantial core concrete expansion, which progressively activates the GFRP tube’s passive confinement mechanism. In the plastic stage, (1) for $\theta =\pm 60°$ and $\pm 80°$, $f_{\mathrm{c}}$ increases with ${\epsilon }_{\mathrm{c}}$, culminating in $f_{\mathrm{c}\mathrm{c}}^{\prime }$, where $f_{\mathrm{c}\mathrm{c}}^{\prime }{=f}_{\mathrm{c}\mathrm{u}}^{\prime }$ (indicating synchronized strength–failure). At this point, the measured ${\epsilon }_{\mathrm{c}\mathrm{c}}$ substantially exceeds values from the GFRP material tests, whereas the ${\epsilon }_{\mathrm{f}\mathrm{e}}$ is marginally lower; (2) for $\theta =\pm 45°$, $f_{\mathrm{c}}$ plateaus or declines, resulting in $f_{\mathrm{c}\mathrm{u}}^{\prime }<f_{\mathrm{c}\mathrm{c}}^{\prime }$ and ${\epsilon }_{\mathrm{c}\mathrm{u}}\gg {\epsilon }_{\mathrm{c}\mathrm{c}}$, signifying a significant residual deformation capacity.

The stress–strain curves of 6-layer $\pm 80°$ specimens consistently demonstrate a superior mechanical performance compared to 10-layer $\pm 60°$ specimens across all groups. This indicates that $\theta$ exerts a dominant influence over $n$ on specimen properties under the given parameters. Specifically, $\pm 45°$ GFRP tubes provide relatively weak confinement, yielding minimal strength enhancement despite significantly improved ductility and clear ductile failure patterns; both $\pm 60°$ and $\pm 80°$ configurations effectively enhance strength and ductility through distinct axial–circumferential strain coupling mechanisms. Optimal selection should therefore prioritize $\theta$ based on the specific engineering requirements for strength–ductility balance.

4. Quasi-Static Test Results

4.1. Specimen Failure Mode and Structural Performance Levels

As illustrated in Figure 10, the failure modes of each bridge pier specimen are characterized as follows:

For the PRC specimen with grouted sleeve connectors embedded in caps, initial horizontal cracks (width < 0.2 mm) emerged in the pier shaft above the bottom joint at drift ratios ($\delta$ < 1%). During the development phase ($\delta$ = 1–2%), these cracks propagated diagonally, forming flexural–shear cracks. At $\delta$ > 2.5%, concrete cover spalling occurred in wedge-shaped or circular patterns, with a significantly lower damage height in the bottom region compared to the top cast-in-place section. Concurrently, extensive concrete spalling and reinforcement exposure were observed at the top. When $\delta$ > 4%, longitudinal bars in the loading direction yielded and buckled first, followed by adjacent bars perpendicular to loading. Stirrups exhibited outward bending, and ultimate failure was triggered by the fracture of sleeve-exposed rebars rather than sleeve connector failure.

PRCG1 and PRCG2 exhibited similar damage evolution. At $\delta$ < 3%, GFRP tubes effectively suppressed crack propagation through circumferential confinement, minimizing joint opening. Continuous increases in hoop tensile stress/strain within the plastic hinge zone (above the joint) significantly inhibited concrete dilation. At drift ratios > 5%, localized fiber whitening and delamination occurred on GFRP surfaces—particularly near caps—yet without circumferential rupture (distinct from the brittle fracture of traditional CFRP wraps). This demonstrates GFRP’s ductility advantage in:

(1)

Blocking the “concrete-splitting-to-rebar-buckling” chain failure;

(2)

Retarding concrete strength degradation;

(3)

Validating the “confinement precedes reinforcement” design philosophy.

The allowable drift ratio $\delta$ (defined as the ratio of pier-top horizontal displacement $\mathsf{\Delta }$ to pier height $H$) is a critical performance indicator in seismic design. Its limits vary with failure modes, performance objectives, and code requirements. According to the JTG/T 2231-2020 [31] and experimental studies herein, bridge piers must remain elastic under the E1 earthquake (frequent-level earthquake) and prevent collapse under the E2 earthquake (rare-level earthquake), with performance thresholds categorized into five levels as listed in

Table 5. Seismic performance level classification for bridge piers.

Hierarchical Performance Levels	$\mathit{\delta }$/%			Description of the Damage Condition
	Conventional Cast-in-Place Piers	Precast Assembly Piers	GFRP Tube-Confined Precast Assembly Piers
Fully operational	≤0.2–0.5	≤0.2–0.5	≤0.5–1	The structure exhibits no visible cracks, with full maintenance of structural functionality; concurrently, the GFRP tube demonstrates negligible visual degradation or deformation
Temporary use	≤0.67	≤1	≤1.5	Minor concrete cracking is observed with crack widths ≤ 0.1 mm, while the GFRP tube shows no structural compromise and maintains visually unaltered surface characteristics.
Post-repair use	≤1.25	≤2	≤2.5	Crack propagation initiates with concurrent minor joint opening below 2 mm, activating the GFRP constraint mechanism and inducing localized resin whitening.
Life safety	≤1.67–2	≤2–2.5	≤3–3.5	Concrete spalling occurs concurrently with yielding of longitudinal reinforcement and joint opening of 2–5 mm, accompanied by a progressive increase in GFRP confining stress and significant fiber whitening.
Collapse prevention	≤2.5–3.0	≤3.5–4	≤4.5–5	Advanced concrete crushing occurs with transverse reinforcement exposure and fracture of longitudinal bars, while the GFRP tube base initiates delamination and causes fiber rupture.

.

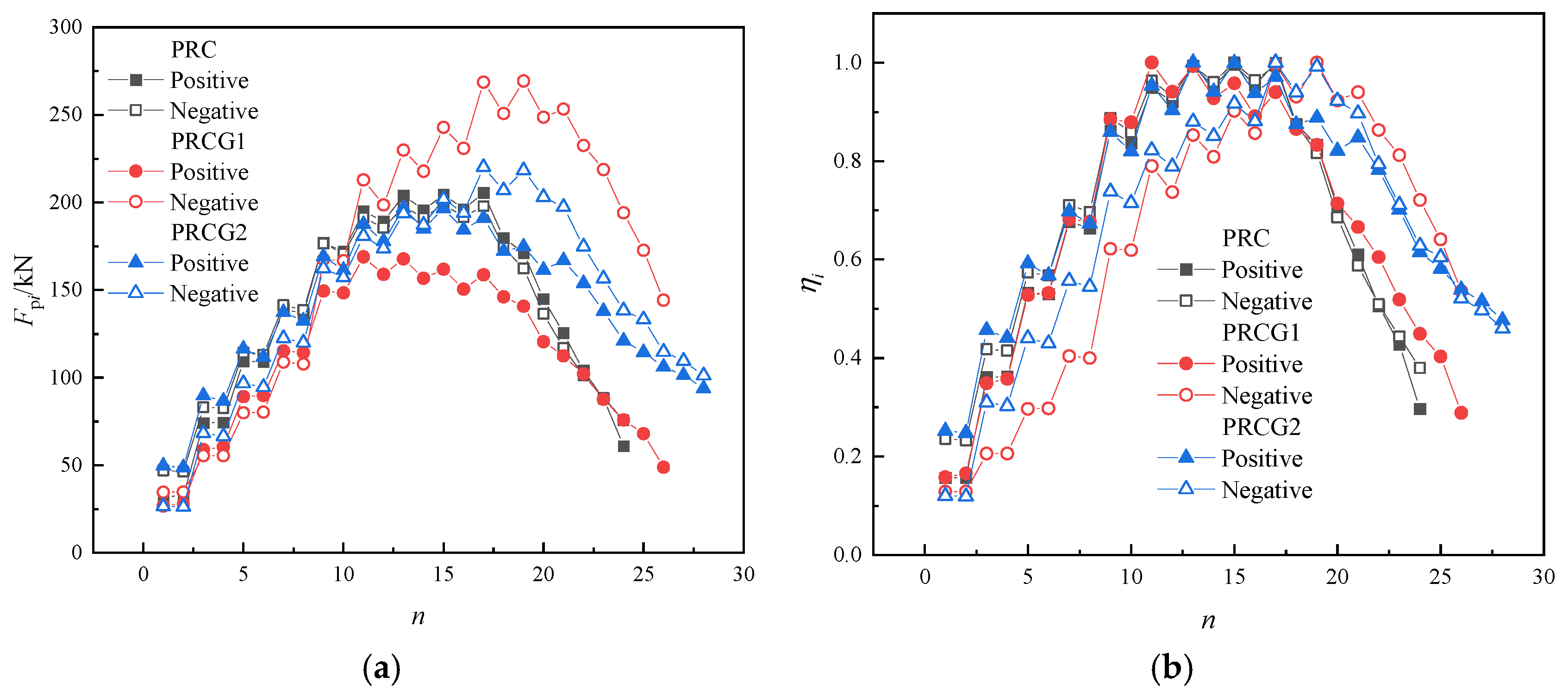
4.2. Hysteresis Performance

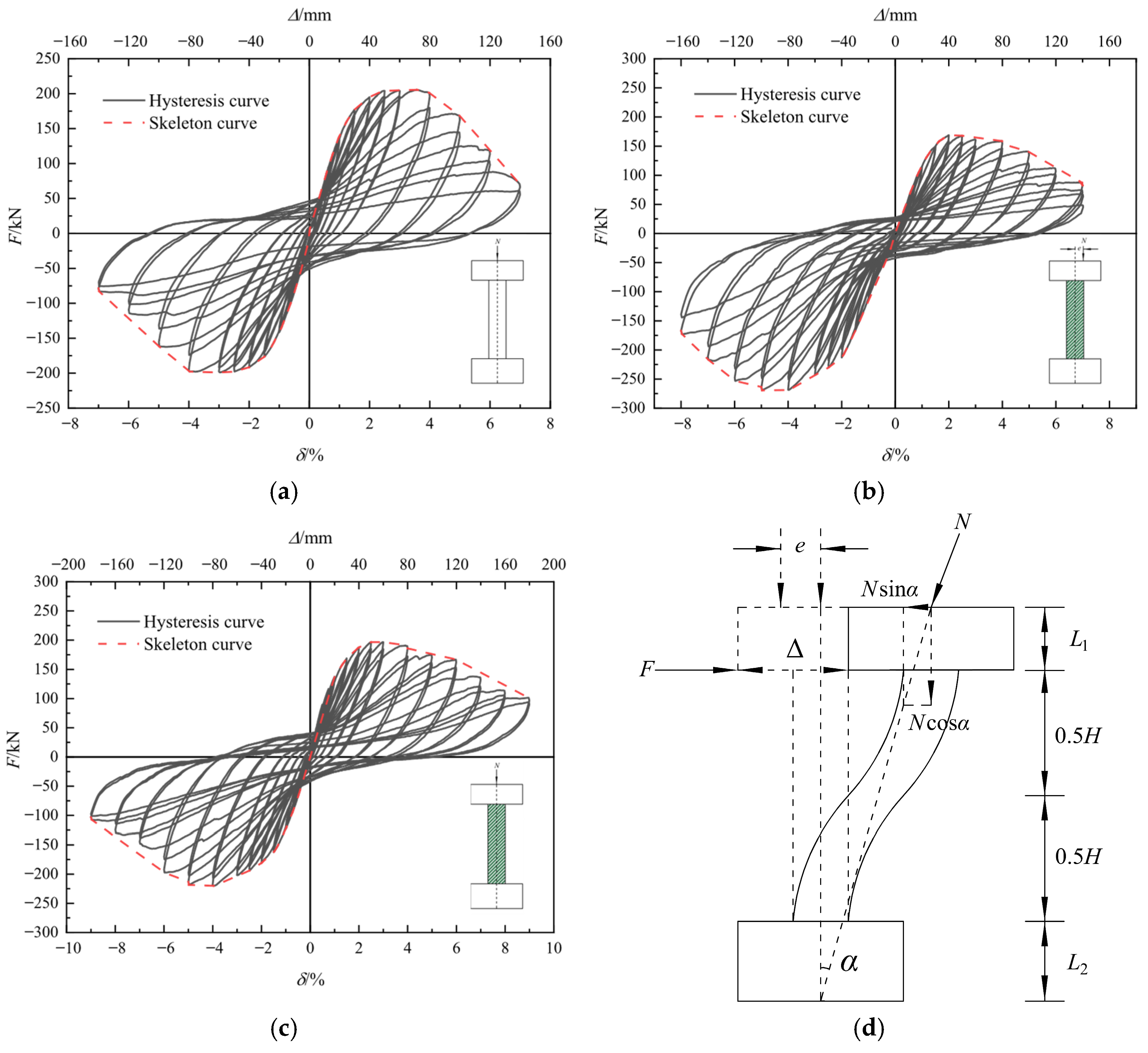
The hysteretic responses and skeleton curves of all specimens under quasi-static testing are presented in Figure 11. The skeleton curve was derived by constructing a tangent to the outermost points of each hysteresis loop. For double-curvature columns (i.e., columns fixed at both ends with lateral displacement applied horizontally), the inflection point of the pier column can be approximated at mid-height. Figure 11d defines the key parameters: $F$ denotes the lateral load, $N$ is axial force, $\alpha$ represents the inclination angle between the axial force and vertical direction, $e$ indicates eccentricity, $H$ is column height, $L_1$ and $L_2$ are the bent cap and cap heights, respectively.

The hysteretic responses of all specimens exhibited predominantly fusiform to inverted S-shaped loops, characteristic of flexural failure mechanisms. During initial loading, hysteresis loops approached linear elasticity, whereas subsequent cycles demonstrated progressive fullness with minor pinching, accompanied by stiffness degradation and strength deterioration. The loading–unloading stiffness progressively declined, and the hysteretic energy dissipation (quantified by loop area) initially increased before diminishing. While PRC and PRCG2 displayed symmetric hysteresis in both loading directions, PRCG1 exhibited marked asymmetry due to the eccentric axial force ($e\approx +100\mathrm{m}\mathrm{m}$) applied at the column top. This eccentricity induced differential stress states—compressive on one side and tensile on the opposite side—thereby offsetting adverse bidirectional force interactions. Consequently, averaging seismic performance indices across both directions remains methodologically valid for comparative analysis.

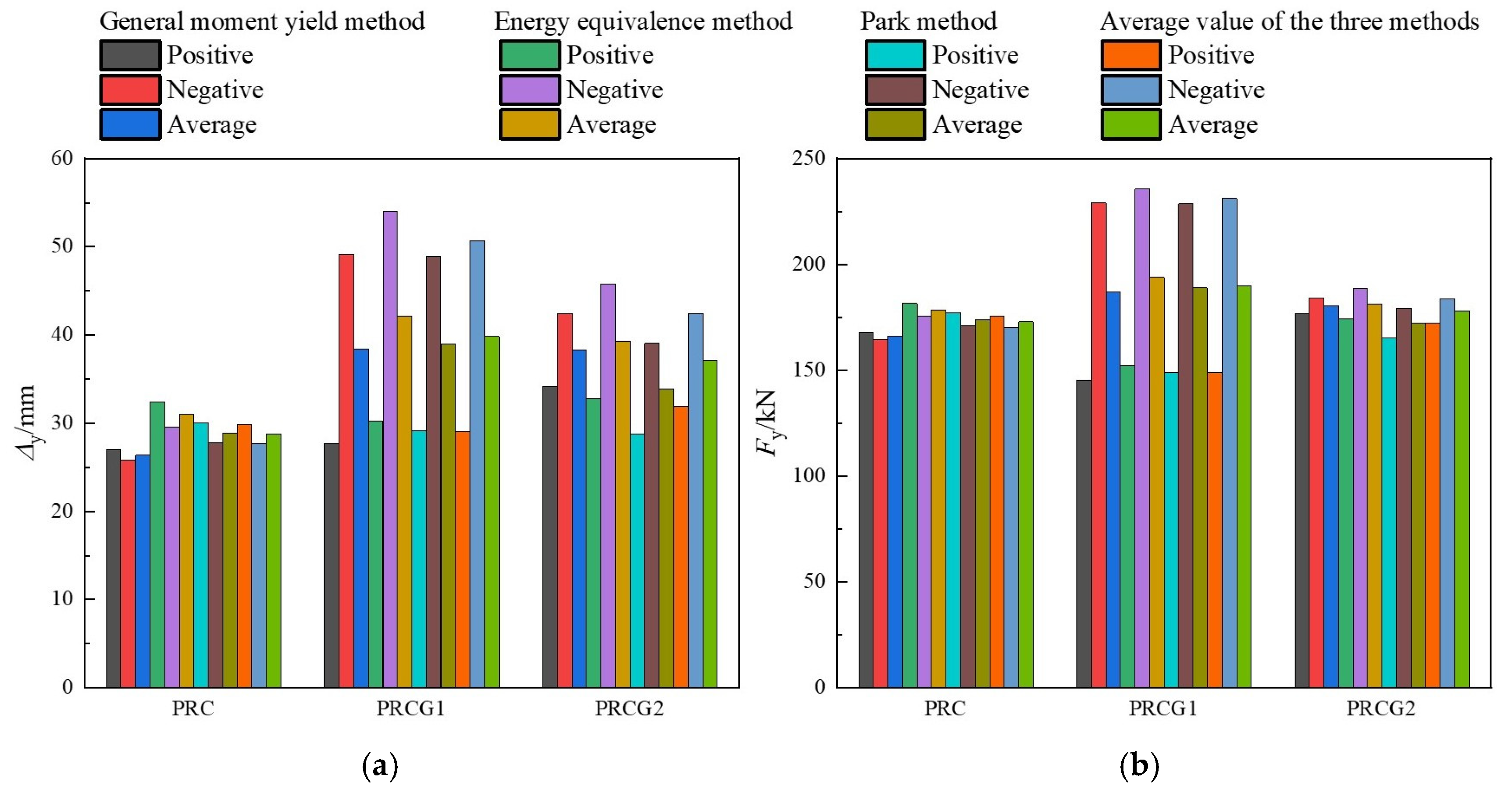
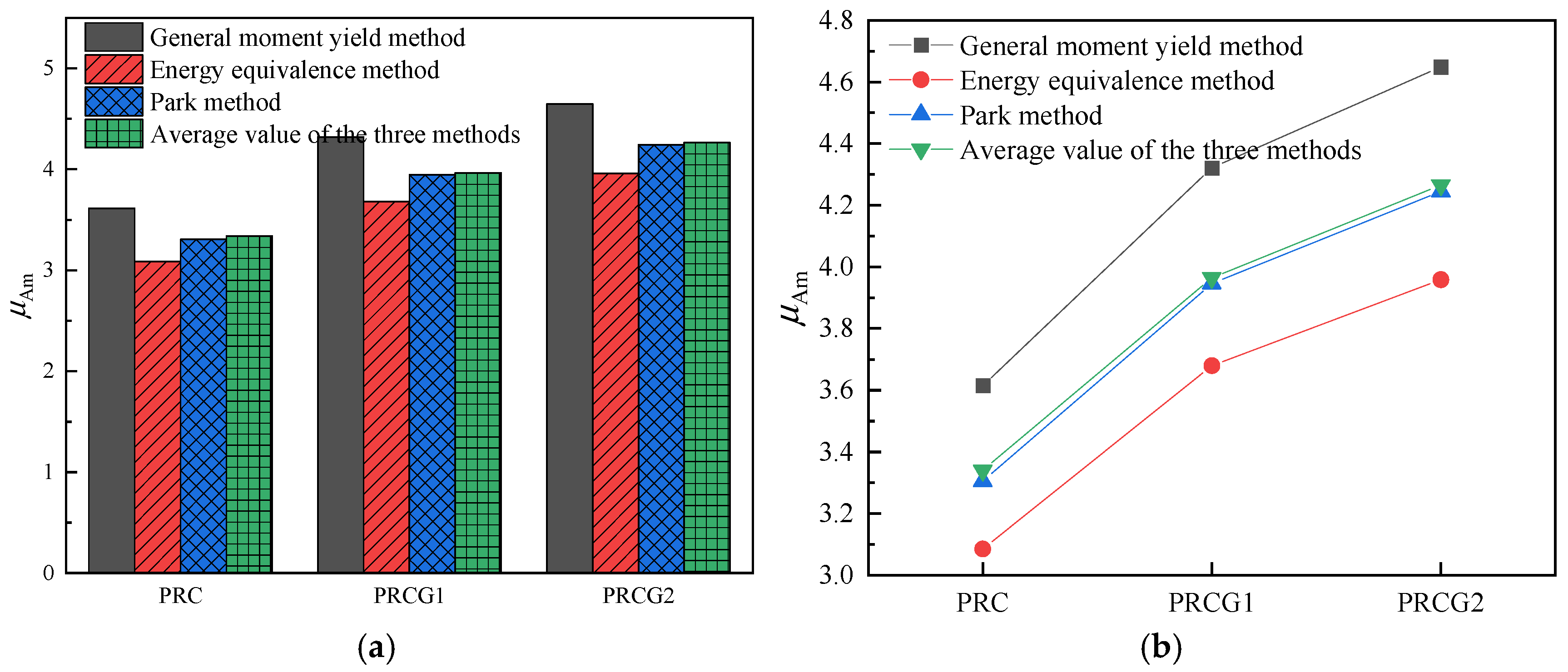
In this study, the equivalent yield force ($F_{\mathrm{y}}$) and equivalent yield displacement (${∆}_{\mathrm{y}}$) were derived from three methodologies: the generalized moment yield method, energy equivalence method, and Park method [32]. With the Park method parameter set to 0.7, the results are illustrated in Figure 12. The energy equivalence method yielded the maximum values for both $F_{\mathrm{y}}$ and ${∆}_{\mathrm{y}}$, while the generalized moment yield and Park methods produced comparable results. Averaged across both loading directions, the analysis demonstrates that PRCG1 and PRCG2 exhibited $F_{\mathrm{y}}$ increases of 9.86% and 2.98%, respectively, and ${∆}_{\mathrm{y}}$ increases of 38.61% and 29.22%, respectively, relative to the PRC specimen.

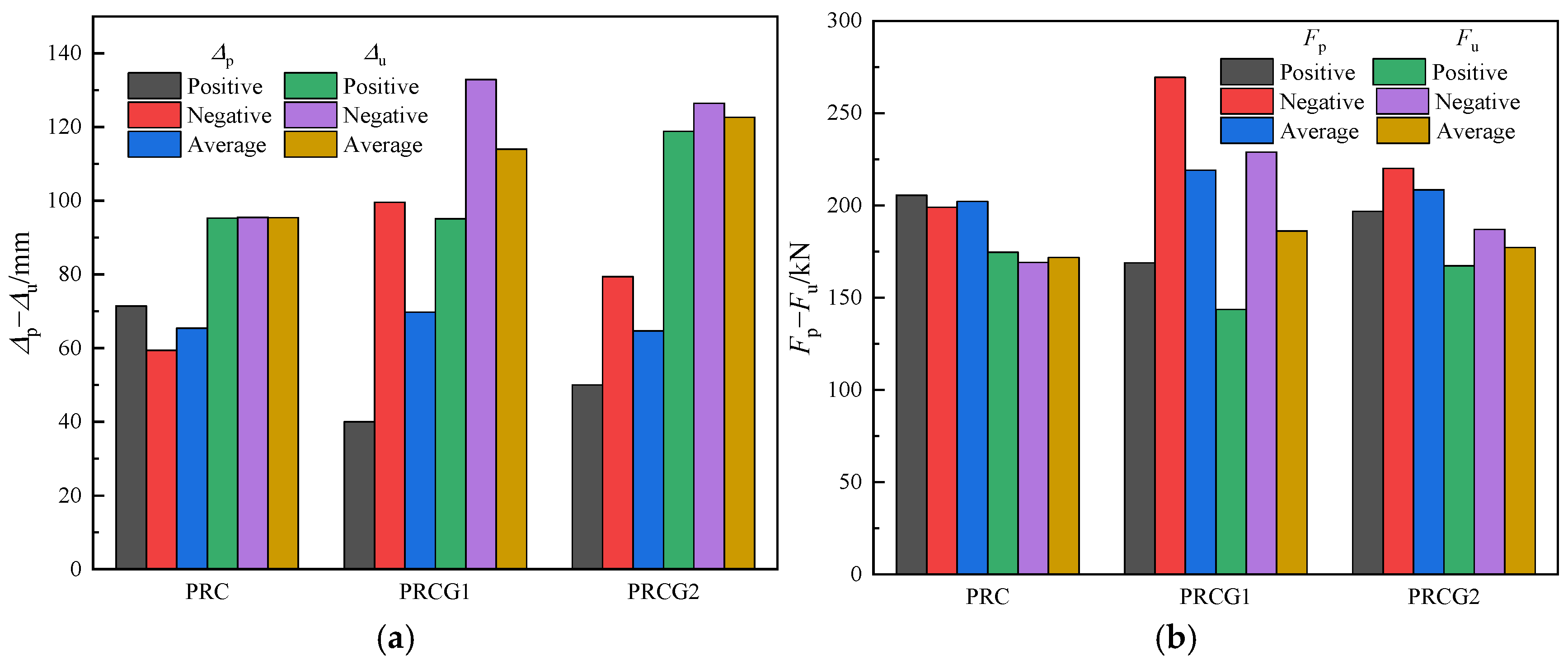
The peak force ($F_{\mathrm{p}}$) and corresponding peak displacement (${∆}_{\mathrm{p}}$) were determined experimentally. The ultimate bearing capacity ($F_{\mathrm{u}}$) was defined as the load at which the force dropped to 85% of $F_{\mathrm{p}}$ (ultimate strength coefficient = 0.85), with the associated displacement denoted as ${∆}_{\mathrm{u}}$ (Figure 13). The analysis reveals minimal variation in ${∆}_{\mathrm{p}}$ across specimens, whereas $F_{\mathrm{p}}$ and $F_{\mathrm{u}}$ increased in GFRP tube-confined piers. Post-peak displacement amplification activated the GFRP confinement mechanism, effectively suppressing concrete lateral expansion, preventing protective layer spalling, and delaying rebar buckling. Consequently, while the PRC specimen exhibited rapid post-peak strength degradation, PRCG1 and PRCG2 demonstrated gradual strength deterioration, resulting in substantially higher ${∆}_{\mathrm{u}}$. Bidirectional averaging shows that PRCG1 and PRCG2 achieved $F_{\mathrm{u}}$ increases of 8.36% and 3.07%, respectively, and ${∆}_{\mathrm{u}}$ increases of 19.50% and 28.57%, relative to PRC.

The ductility coefficient ${\mu }_{\mathrm{m}}$ of the unconfined prefabricated reinforced concrete pier is defined as follows:

$${\mu }_{\mathrm{m}}={\displaystyle \frac{{∆}_{\mathrm{u},\mathrm{P}\mathrm{R}\mathrm{C}}}{{∆}_{\mathrm{y},\mathrm{P}\mathrm{R}\mathrm{C}}}}$$

(6)

where ${∆}_{\mathrm{u},\mathrm{P}\mathrm{R}\mathrm{C}}$ and ${∆}_{\mathrm{y},\mathrm{P}\mathrm{R}\mathrm{C}}$ denote the ultimate displacement and yield displacement of PRC, respectively.

For GFRP-confined prefabricated piers, the confinement effect significantly delays initial rebar yielding. Direct calculation of the conventional ductility coefficient ${\mu }_{\mathrm{m}}$ would underestimate the actual enhancement by 20–40% due to the artificially increased denominator (${∆}_{\mathrm{y},\mathrm{P}\mathrm{R}\mathrm{C}\mathrm{G}}$ > ${∆}_{\mathrm{y},\mathrm{P}\mathrm{R}\mathrm{C}}$, ${∆}_{\mathrm{y},\mathrm{P}\mathrm{R}\mathrm{C}\mathrm{G}}$ is the yield displacement of PRCG1/PRCG2). Consequently, a modified ductility coefficient (${\mu }_{\mathrm{A}\mathrm{m}}$) is proposed to isolate the pure confinement-induced ductility gain:

$${\mu }_{\mathrm{A}\mathrm{m}}={\displaystyle \frac{{∆}_{\mathrm{u},\mathrm{P}\mathrm{R}\mathrm{C}\mathrm{G}}}{{∆}_{\mathrm{y},\mathrm{P}\mathrm{R}\mathrm{C}}}}$$

(7)

where ${∆}_{\mathrm{u},\mathrm{P}\mathrm{R}\mathrm{C}\mathrm{G}}$ is the ultimate displacement of the GFRP tube-confined pier (PRCG1/PRCG2).

A comparative analysis of ductility coefficients (Figure 14) reveals that the generalized moment yield method yielded the highest ${\mu }_{\mathrm{A}\mathrm{m}}$ value, while the energy equivalence method produced the lowest; the Park method generated intermediate results, closely aligning with the tri-method average. Loading direction averaging demonstrates that PRCG1 and PRCG2 achieved ${\mu }_{\mathrm{A}\mathrm{m}}$ increases of 18.56% and 27.84%, respectively, relative to PRC.

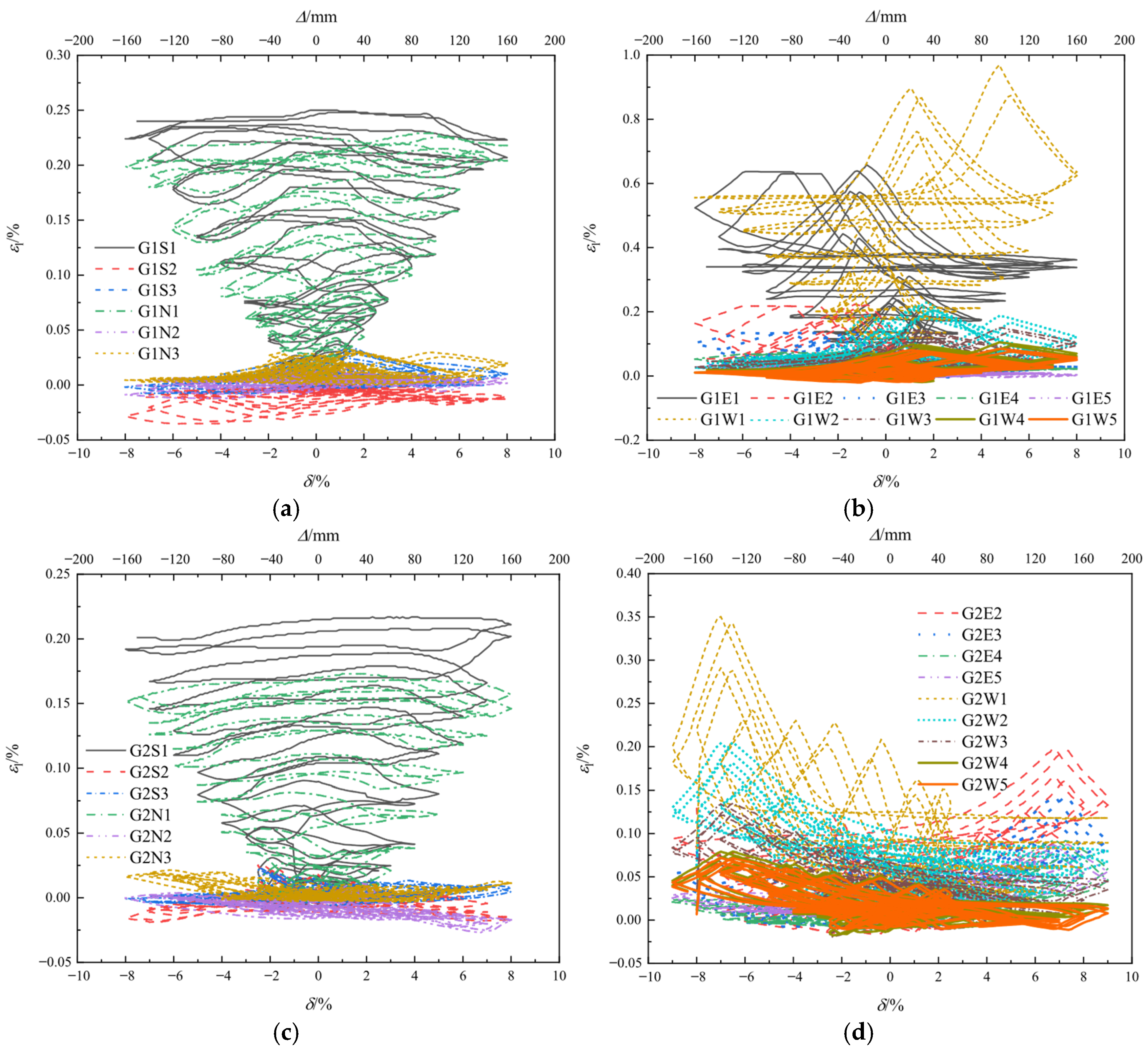
4.3. Strain Analysis of GFRP Tubes

The circumferential strain evolution of GFRP tubes in specimens PRCG1 and PRCG2 is presented in Figure 15, with tensile strain values designated as positive and compressive strains as negative. The strain data in Figure 16 correspond to the maximum displacement during each stage of cyclic loading, measured at 100 mm above the pile cap. The notation “−1” and “−2” denotes the first and second cycles of the displacement stage, respectively. Due to the pre-loading damage of strain gauge G2E1, its data in Figure 16d are substituted by G2E2.

Debonding inspection was performed by striking the GFRP tube surface with a rubber hammer at the start of every loading cycle. The consistent occurrence of dull acoustic signatures—contrasting with the hollow tones characteristic of delaminated zones—confirmed interfacial integrity throughout testing. The results indicate that the hoop strain perpendicular to the loading direction in GFRP tubes peaks at each cycle’s maximum displacement, exhibiting an approximately linear strain–displacement relationship at low magnitudes. PRCG1 and PRCG2 demonstrate comparable strain distributions, with localized elevation at the 100 mm height above the pier base—reaching maxima of 0.25% and 0.22%, respectively. Notably, the maximum hoop strain in the loading direction occurred prior to peak displacement. Critical strain measurements revealed values of 0.96% at 100 mm and 0.23% at 175 mm for PRCG1, compared to 0.35% and 0.20% for PRCG2 at corresponding heights. This strain localization indicates concrete damage concentration within the basal 100 mm zone, with rapid attenuation above 175 mm height, where concrete damage becomes negligible. While the ultimate circumferential strain of $\pm 60°$ GFRP tubes reaches 1.75% in material tests (Table 1), the effective circumferential strains observed in confined concrete specimens range from 1.4% to 1.7% (Table 4). This discrepancy arises because strain gauges capture localized deformations, and the combined effects of limited sample sizes and stress concentration phenomena introduce measurement variability. Consequently, maintaining a deformation reserve is critical to mitigate the risk of brittle fracture.

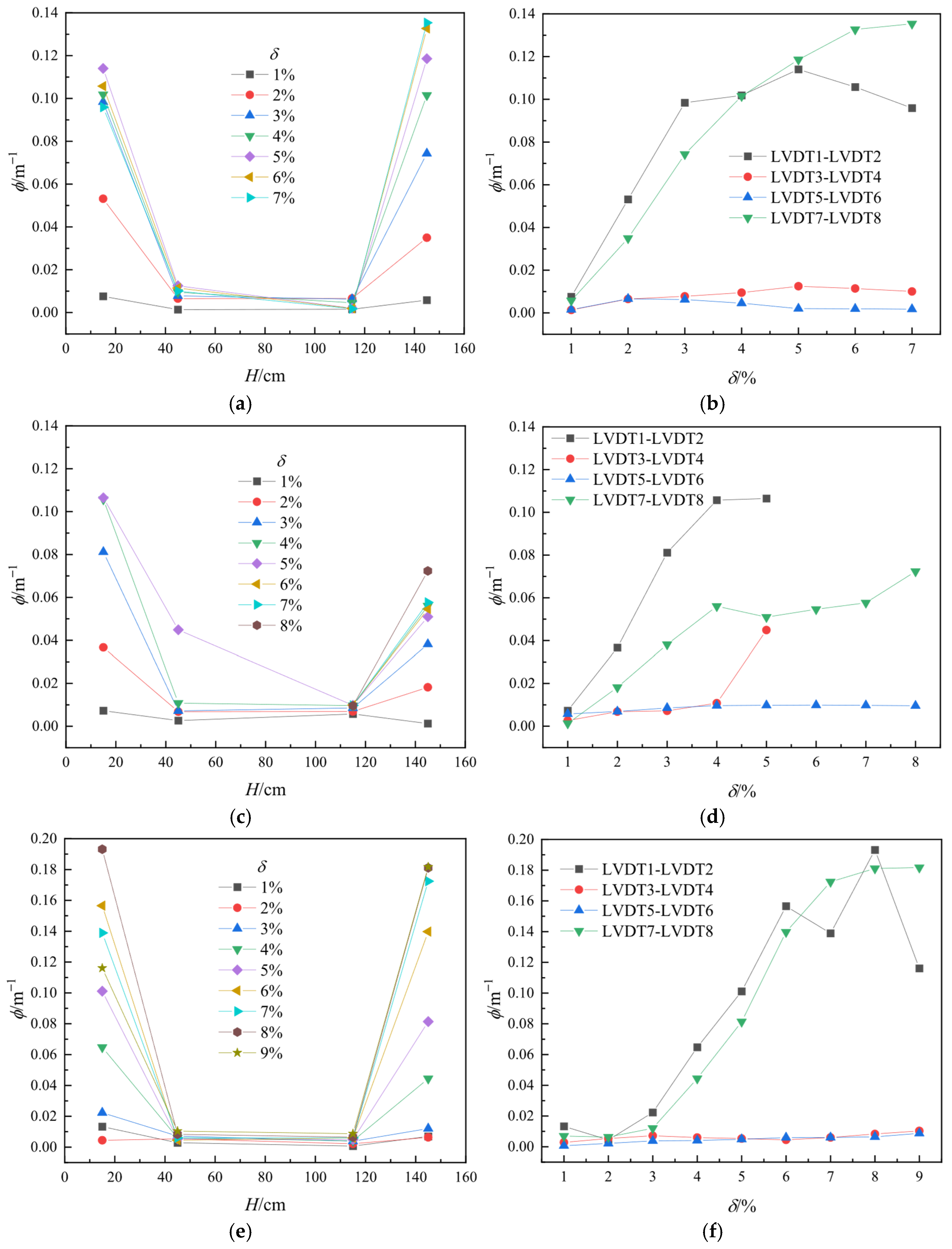
4.4. Analysis of Bridge Pier Curvature

The curvature $\varphi$ of each layer of the specimen can be calculated based on the relative displacement difference $L_{\mathrm{r}}$ between layers measured by the displacement meters on both sides of the specimen loading direction:

$$\varphi ={\displaystyle \frac{L_{\mathrm{r}}}{L_{\mathrm{h}}{L}_{\mathrm{v}}}}$$

(8)

where $L_{\mathrm{h}}$ denotes the horizontal spacing between gauges and $L_{\mathrm{v}}$ represents the vertical measurement height of the gauges.

Figure 17 illustrates the distribution of $\varphi$ along the column height at varying displacement levels, along with the $\varphi –\delta$ correlation (Note: data for LVDT1–LVDT2 and LVDT3–LVDT4 of PRCG1 are unavailable when $\delta >5\%$). The curvature exhibits approximate symmetry about the mid-span section, with peak values localized within the plastic hinge zones at the pier base and top, attenuating toward the mid-span region. At initial loading stages, the curvature differences among specimens were negligible. However, at $\delta =2\%$ and 3%, the base curvature of the PRC pier reached 1.92 and 1.95 times that of PRCG1, and 5.50 and 6.17 times that of PRCG2, respectively. Subsequently, the curvature disparity between PRCG2 and PRC diminished. At $\delta =4\%$ and 5%, the PRC base curvature was 1.81 and 2.33 times that of PRCG1, and 2.28 and 1.46 times that of PRCG2. Progressive displacement amplification induced a transition from near-linear to nonlinear $\varphi$–$\delta$ correlation. Crucially, at higher displacements, the base curvature of PRCG2 exceeded that of PRC due to severe damage-induced deformation degradation in PRC, whereas PRCG2 retained a partial deformation capacity. Collectively, GFRP-tube-confined piers (PRCG1/PRCG2) demonstrated significantly lower curvature than PRC at most $\delta$ levels, confirming superior flexural performance.

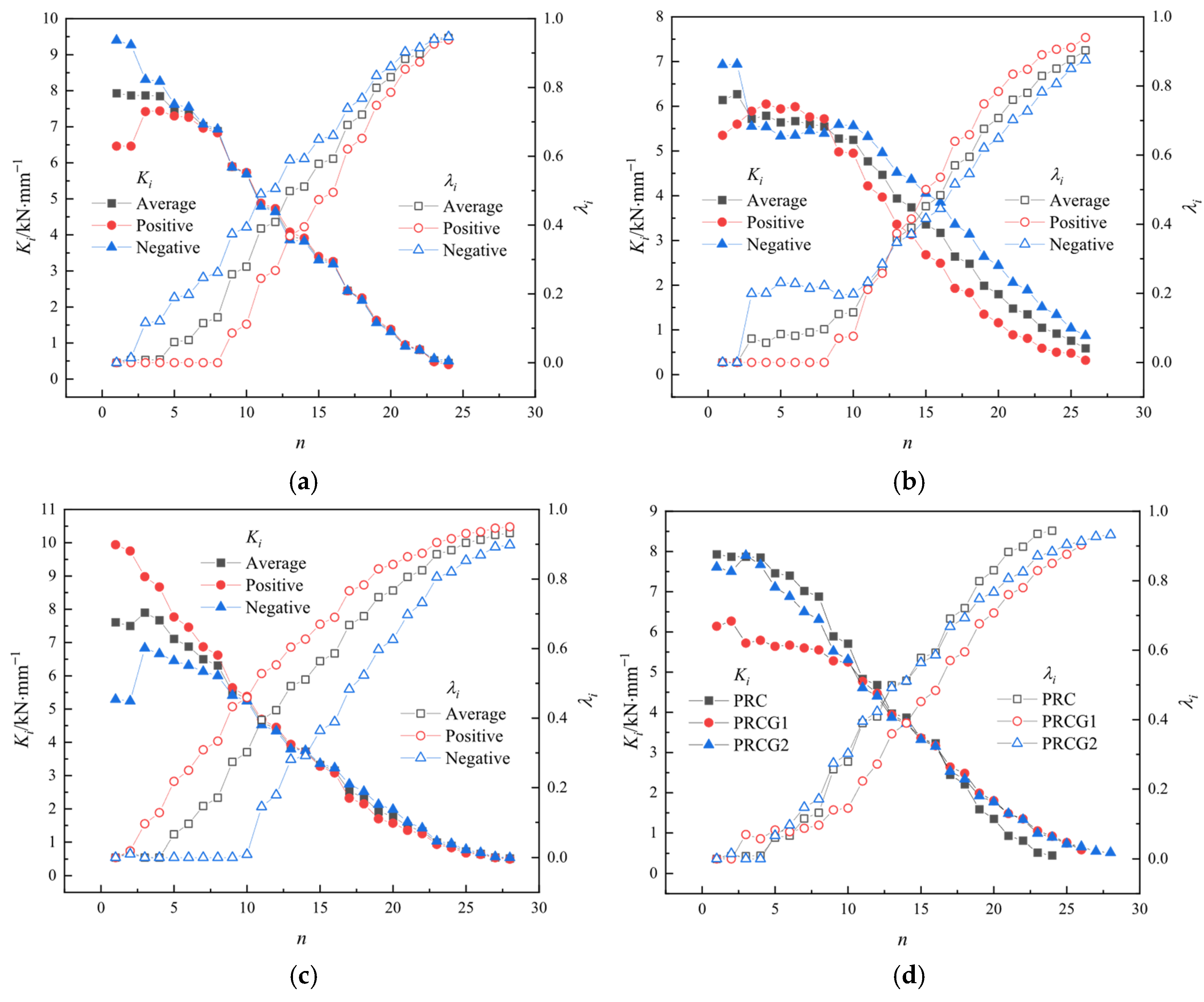
4.5. Strength Variation and Stiffness Degradation

To compare the bearing capacity of distinct specimens at identical displacement levels, the hysteretic curves were decomposed to extract the first and second hysteresis loops per loading cycle. The peak bearing capacity ($F_{\mathrm{p}i}$) of each loop was quantified, and the corresponding bearing capacity coefficient (${\eta }_i$) was derived, as depicted in Figure 18. Here, $n$ denotes the hysteresis loop index, and ${\eta }_i$ is calculated using the following:

$${\eta }_i={\displaystyle \frac{F_{\mathrm{p}i}}{F_{\mathrm{p}}}}$$

(9)

GFRP tube-confined specimens exhibit superior lateral resistance and enhanced safety reserves under large displacements. After averaging the positive/negative loading directions and first/second cycles, the bearing capacity of PRCG1 and PRCG2 increased by 26.74% and 23.25% (vs. PRC) at hysteresis loops 19–20 ($\delta =5\%$), 56.46% and 54.84% at loops 21–22 ($\delta =6\%$), and 84.05% and 76.91% at loops 23–24 ($\delta =7\%$), respectively. Concurrently, the ${\eta }_i$ for PRC were 0.76, 0.56, and 0.39 at $\delta =5\%$, $6\%$, and $7\%$, significantly lower than PRCG1 (0.87, 0.77, 0.63) and PRCG2 (0.91, 0.83, 0.67). This demonstrates that GFRP confinement effectively mitigates strength degradation in bridge piers under seismic action and ensures residual load-carrying capacity.

During quasi-static testing, the specimen exhibits progressive stiffness degradation due to accumulated damage mechanisms, including concrete cracking/crushing, steel-concrete bond slip, and reinforcement buckling. The stiffness $K_i$ at each loading cycle is defined as follows:

$$K_i={\displaystyle \frac{F_{\mathrm{p}i}}{{\mathsf{\Delta }}_{\mathrm{p}i}}}$$

(10)

where ${\mathsf{\Delta }}_{\mathrm{p}i}$ denotes the peak displacement per hysteresis loop.

The stiffness degradation coefficient ${\lambda }_i$ is calculated by the following:

$${\lambda }_i={\displaystyle \frac{K_{\mathrm{I}}-K_i}{K_{\mathrm{I}}}}$$

(11)

where $K_{\mathrm{I}}$ represents the initial undamaged stiffness.

Under small-to-medium displacement amplitudes, the GFRP tube exhibits negligible effects on specimen stiffness ($K_i$), as shown in Figure 19. This is attributed to the concrete’s elastic deformation phase, wherein restrained transverse dilation fails to mobilize the tube’s tensile properties. With the GFRP tube contributing insignificantly to structural rigidity, axial compression is primarily resisted by concrete and internal steel reinforcement, which govern the initial stiffness response. However, under large displacements, GFRP confinement significantly enhances $K_i$ and suppresses the stiffness degradation coefficient (${\lambda }_i$). Initially, PRC and PRCG2 display asymmetric $K_i$ in positive/negative loading directions, but this anisotropy diminishes in mid-to-late loading stages. The directional discrepancy in ${\lambda }_i$ is pronounced early but converges progressively with loading progression. For PRCG1, load eccentricity induces persistently higher $K_i$ in the negative direction. At $\delta =3\%$, the direction-averaged $K_i$ of all specimens converges to comparable levels. Beyond this threshold, PRCG1 and PRCG2 exhibit higher $K_i$ than PRC. Specifically, at $\delta =\left\{4\%,5\%,6\%,7\%\right\}$, the $K_i$ of the reference specimen PRC decreased progressively to 2.33 kN/mm, 1.47 kN/mm, 0.87 kN/mm, and 0.49 kN/mm, respectively, reflecting severe mechanical degradation under cyclic loading. In contrast, GFRP tube confinement significantly enhanced structural integrity: PRCG1 exhibited stiffness increases of 9.87%, 28.91%, 64.88%, and 103.09% versus PRC, while PRCG2 showed increases of 4.51%, 25.51%, 61.49%, and 93.81% at the same $\delta$ levels.

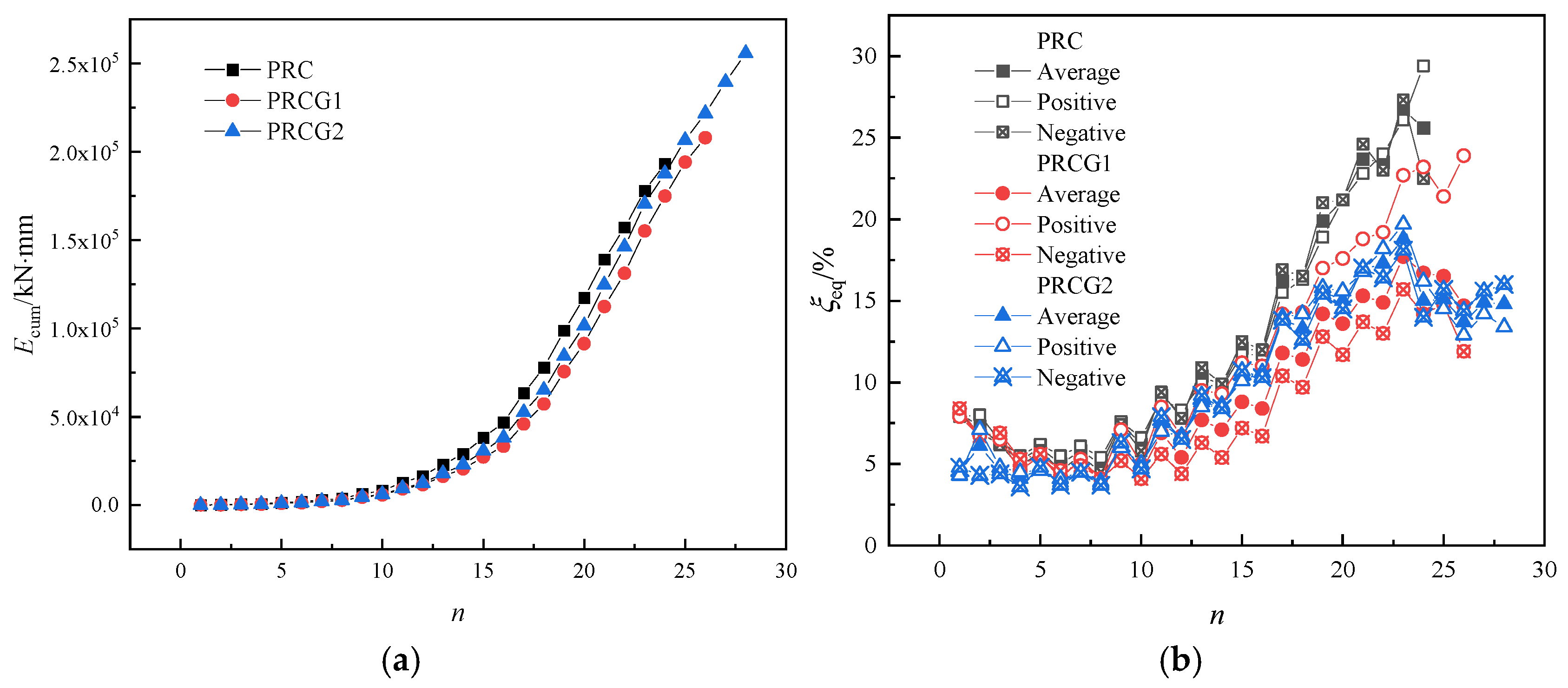
4.6. Dissipation Capacity and Residual Displacement

Figure 20 presents the cumulative hysteretic energy dissipation capacity ($E_{\mathrm{c}\mathrm{u}\mathrm{m}}$) and equivalent viscous damping ratio (${\xi }_{\mathrm{e}\mathrm{q}}$) of the specimen under incrementally increased cyclic loading. The equivalent viscous damping ratio ${\xi }_{\mathrm{e}\mathrm{q}}$ is calculated as follows:

$${\xi }_{\mathrm{e}\mathrm{q}}={\displaystyle \frac{1}{2\pi }}{\displaystyle \frac{S_{\mathrm{A}\mathrm{B}\mathrm{C}}}{S_{\mathrm{O}\mathrm{B}\mathrm{D}}}}$$

(12)

where $S_{\mathrm{A}\mathrm{B}\mathrm{C}}$ denotes the hysteresis loop area (representing cumulative energy dissipation per cycle), and $S_{\mathrm{O}\mathrm{B}\mathrm{D}}$ is the triangular area under the equivalent elastic deformation envelope (quantifying recoverable elastic strain energy).

Within the displacement range of $\delta$ = 0–7%, the $E_{\mathrm{c}\mathrm{u}\mathrm{m}}$ follows the order PRC > PRCG2 > PRCG1. Notably, the energy dissipation disparity between PRC and GFRP-confined specimens (PRCG1/PRCG2) exhibits a non-monotonic trend: initially increasing, peaking near $\delta =5\%$ (indicating severe damage in PRC primarily through plastic hinge zone failure), then progressively decreasing. At their respective ultimate bearing capacities, PRCG1 and PRCG2 achieve 13.90% and 26.43% higher $E_{\mathrm{c}\mathrm{u}\mathrm{m}}$ than PRC, demonstrating GFRP’s efficacy in enhancing energy absorption. For the ${\xi }_{\mathrm{e}\mathrm{q}}$, the relationship PRC > PRCG2 > PRCG1 persists across $\delta$ = 1.5–7%, with the gap widening as displacement increases. Beyond $\delta$ = 7%, ${\xi }_{\mathrm{e}\mathrm{q}}$ declines due to the accelerated growth of elastic deformation energy relative to hysteretic dissipation. These findings demonstrate that GFRP tubes promote structural energy dissipation, correlating with improved ductility and reduced damage severity.

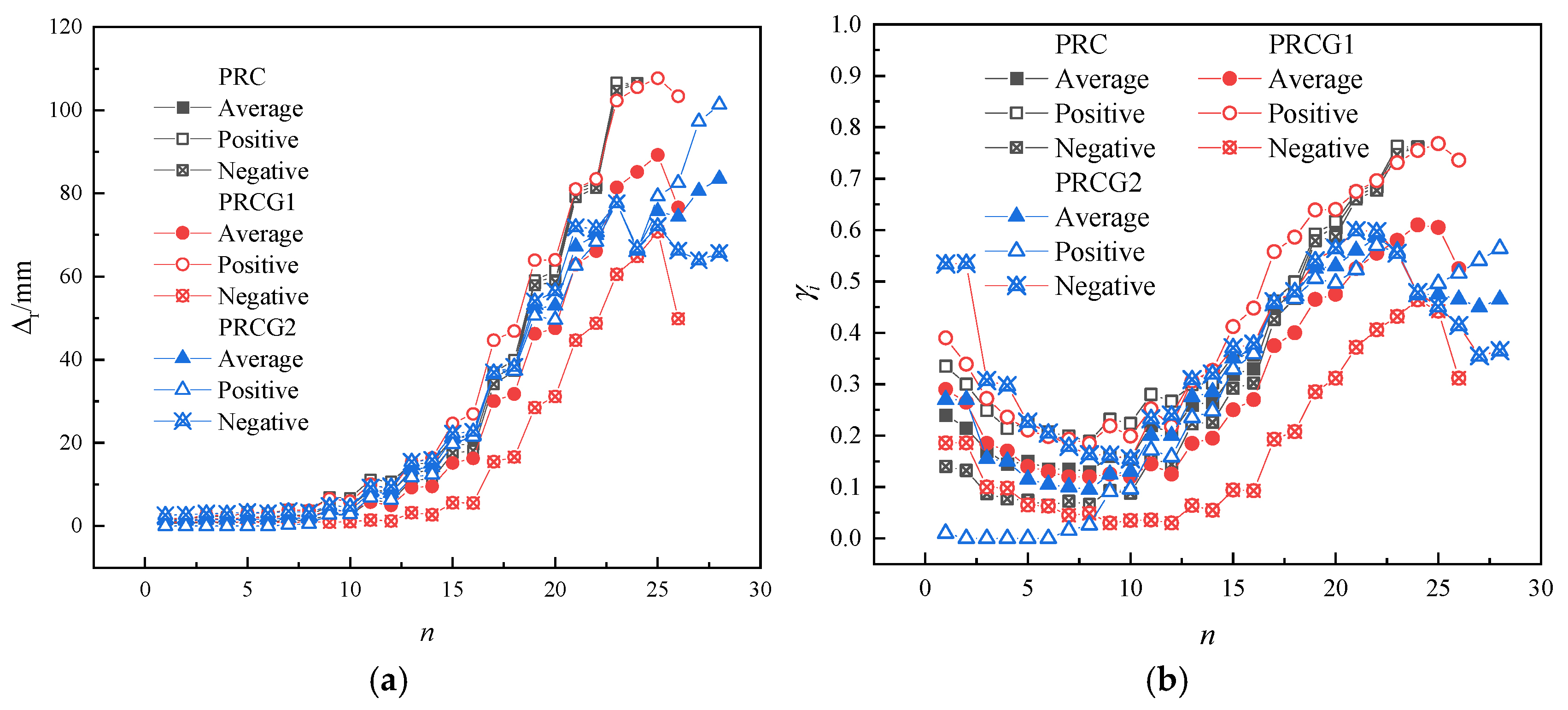
Residual displacement (denoted as ${\mathsf{\Delta }}_{\mathrm{r}}$) is defined as the intercept of the unloading path on the hysteresis loop with the displacement axis (X-axis), representing the irrecoverable plastic deformation of the structure after seismic excitation. This parameter serves as a critical indicator for evaluating structural seismic resilience, as smaller ${\mathsf{\Delta }}_{\mathrm{r}}$ values correlate with lower post-earthquake repair costs and a reduced probability of secondary disasters. The residual deformation proportion (${\gamma }_i$), as illustrated in Figure 21, is quantified by the following equation:

$${\gamma }_i={\displaystyle \frac{{\mathsf{\Delta }}_{\mathrm{r}}}{{\mathsf{\Delta }}_{\mathrm{p}i}}}$$

(13)

During the initial loading stage, the ${\mathsf{\Delta }}_{\mathrm{r}}$ exhibited minimal variation across specimens. PRC showed symmetric ${\mathsf{\Delta }}_{\mathrm{r}}$ in positive and negative directions, whereas PRCG2 displayed slight asymmetry, and PRCG1 demonstrated significantly larger directional discrepancies. As the displacement amplitude increased, ${\mathsf{\Delta }}_{\mathrm{r}}$ accumulated progressively, while the ${\gamma }_i$ initially decreased before rising. Notably, the second loading cycle at each $\delta$ level yielded higher ${\mathsf{\Delta }}_{\mathrm{r}}$ and ${\gamma }_i$ than the first cycle. Beyond $\delta$ = 4%, PRC exhibited accelerated ${\mathsf{\Delta }}_{\mathrm{r}}$ growth, surpassing both GFRP-confined specimens (PRCG1 and PRCG2). At $\delta$ = 5%, the ${\mathsf{\Delta }}_{\mathrm{r}}$ of PRCG1 and PRCG2 was 12.39 mm and 6.62 mm lower than PRC, respectively; at $\delta$ = 6%, these differences increased to 16.51 mm and 12.39 mm. At $\delta$ = 7%, ${\mathsf{\Delta }}_{\mathrm{r}}$ reached 106.03 mm (PRC), 83.30 mm (PRCG1), and 72.12 mm (PRCG2), corresponding to ${\gamma }_i$ values of 0.76, 0.60, and 0.52. Compared to PRC, GFRP confinement reduced ${\mathsf{\Delta }}_{\mathrm{r}}$ by 21.44% (PRCG1) and 31.98% (PRCG2), and ${\gamma }_i$ by 21.05% and 31.58%, respectively. This confirms that GFRP tube confinement enhances the self-centering capacity of bridge piers by constraining concrete dilation, thereby significantly mitigating post-seismic residual displacements.

4.7. GFRP Tube-Confined Concrete Model and Numerical Simulation

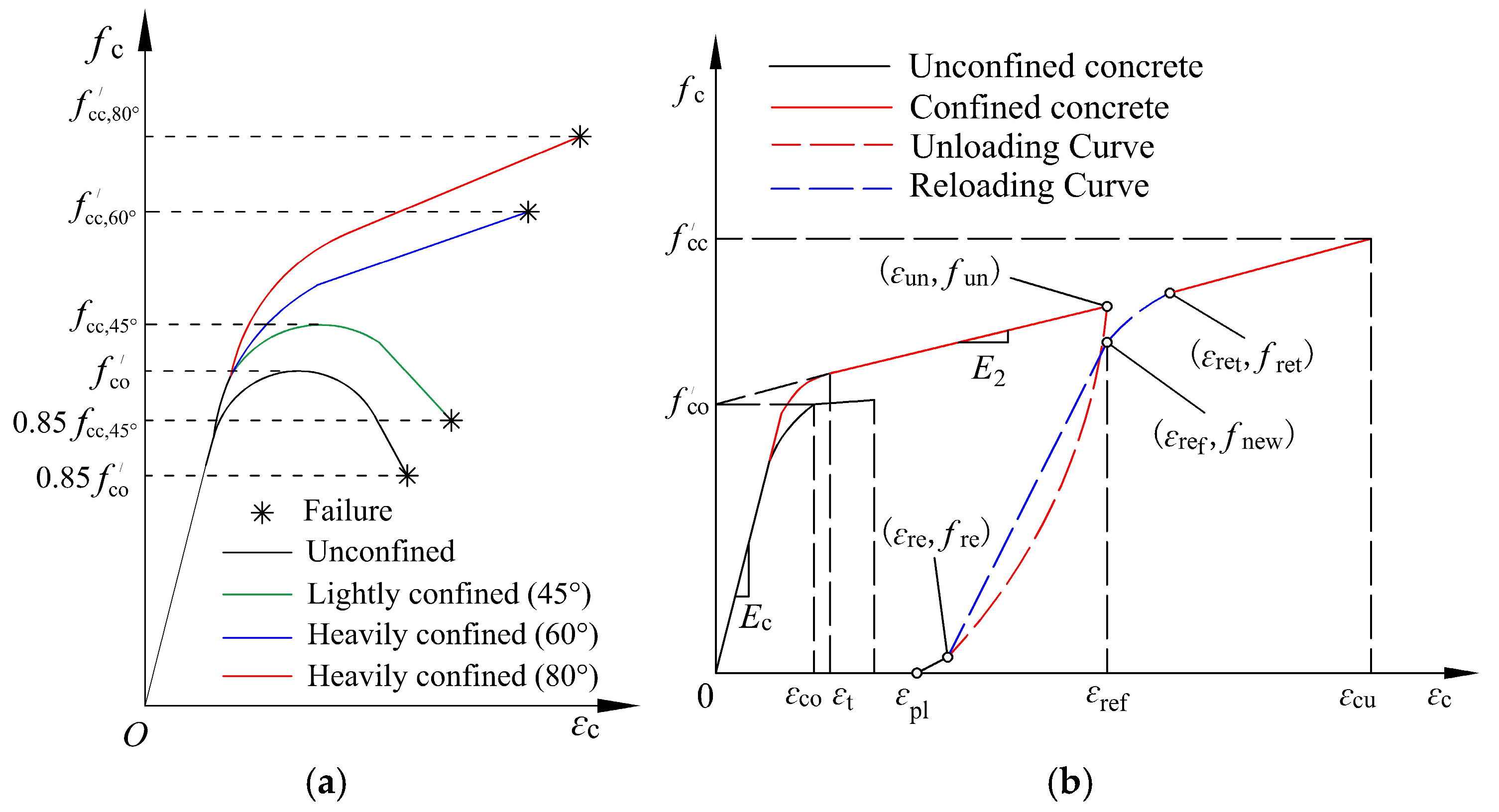
Depending on the confinement level provided by GFRP tubes, the uniaxial stress–strain behavior can be characterized by one of the curves in Figure 22a. Notably, $\pm 45°$ GFRP tubes exhibit ineffective hoop confinement with limited strength enhancement, which should be avoided in practical engineering applications. Figure 22b schematically illustrates the loading–unloading rules for GFRP-confined concrete under cyclic loading under strong confinement conditions, where

• The stress and strain at the unloading initiation point are defined as unloading stress ($f_{\mathrm{u}\mathrm{n}}$) and unloading strain (${\epsilon }_{\mathrm{u}\mathrm{n}}$), respectively;
• The strain at the intersection of the unloading curve and the strain axis is termed plastic strain (${\epsilon }_{\mathrm{p}\mathrm{l}}$);
• The stress and strain at the reloading initiation point are designated as reloading stress ($f_{\mathrm{r}\mathrm{e}}$) and reloading strain (${\epsilon }_{\mathrm{r}\mathrm{e}}$), respectively;
• The stress and strain at the intersection of the reloading curve and the envelope curve are identified as return stress ($f_{\mathrm{r}\mathrm{e}\mathrm{t}}$) and return strain (${\epsilon }_{\mathrm{r}\mathrm{e}\mathrm{t}}$), respectively;
• The reference strain (${\epsilon }_{\mathrm{r}\mathrm{e}\mathrm{f}}$) corresponds to the previous unloading strain (${\epsilon }_{\mathrm{u}\mathrm{n}}$) projected onto the reloading curve, with the stress at this point ($f_{\mathrm{n}\mathrm{e}\mathrm{w}}$) serving as the key parameter for quantifying stress degradation.

The proposed constitutive model for GFRP tube-confined concrete, developed based on Lam and Teng’s theory [33,34], characterizes the uniaxial stress–strain relationship as follows:

$$f_{\mathrm{c}}=\left\{\begin{array}{c}{E}_{\mathrm{c}}{\epsilon }_{\mathrm{c}}-{\displaystyle \frac{{\left(E_{\mathrm{c}}-E_2\right)}^2}{4f_{\mathrm{c}\mathrm{o}}^{\prime }}}0\le {\epsilon }_{\mathrm{c}}\le {\epsilon }_{\mathrm{t}}\\ f_{\mathrm{c}\mathrm{o}}^{\prime }+E_2{\epsilon }_{\mathrm{c}}{\epsilon }_{\mathrm{t}}\le {\epsilon }_{\mathrm{c}}\le {\epsilon }_{\mathrm{c}\mathrm{u}}\le 0.01\end{array}\right.$$

(14)

$$E_2={\displaystyle \frac{f_{\mathrm{c}\mathrm{c}}^{\prime }-f_{\mathrm{c}\mathrm{o}}^{\prime }}{{\epsilon }_{\mathrm{c}\mathrm{u}}}}$$

(15)

$${\epsilon }_{\mathrm{t}}={\displaystyle \frac{2f_{\mathrm{c}\mathrm{o}}^{\prime }}{E_{\mathrm{c}}-E_2}}$$

(16)

$${\epsilon }_{\mathrm{c}\mathrm{u}}={\epsilon }_{\mathrm{c}\mathrm{o}}\left[1.50+12{\displaystyle \frac{f_{\mathrm{l}}}{f_{\mathrm{c}\mathrm{o}}^{\prime }}}{\left({\displaystyle \frac{{\epsilon }_{\mathrm{f}\mathrm{e}}}{{\epsilon }_{\mathrm{c}\mathrm{o}}}}\right)}^{0.45}\right]$$

(17)

where $E_{\mathrm{c}}$ denotes the elastic modulus of unconfined concrete; ${\epsilon }_{\mathrm{c}\mathrm{u}}$ represents the limiting axial compressive strain of confined concrete; ${\epsilon }_{\mathrm{t}}$ is the transitional strain at the intersection of the parabolic and linear segments of the stress–strain curve; and $E_2$ defines the slope of the second linear branch post-transitional strain.

The unloading and reloading rules follow the Lam and Teng models [35]. The reloading curve of this model comprises two distinct segments: a linear phase and a parabolic phase. The unloading curve employs a polynomial formulation, demonstrating higher accuracy than alternative models [36,37,38], expressed as follows:

$$f_{\mathrm{c}}=\left\{\begin{array}{c}{f}_{\mathrm{r}\mathrm{e}}+E_{\mathrm{r}\mathrm{e}}\left({\epsilon }_{\mathrm{c}}-{\epsilon }_{\mathrm{r}\mathrm{e}}\right){\epsilon }_{\mathrm{r}\mathrm{e}}\le {\epsilon }_{\mathrm{c}}\le {\epsilon }_{\mathrm{r}\mathrm{e}\mathrm{f}}\\ A{\epsilon }_{\mathrm{c}}^2+B{\epsilon }_{\mathrm{c}}+C{\epsilon }_{\mathrm{r}\mathrm{e}\mathrm{f}}\le {\epsilon }_{\mathrm{c}}\le {\epsilon }_{\mathrm{r}\mathrm{e}\mathrm{t}}\end{array}\right.$$

(18)

$$E_{\mathrm{r}\mathrm{e}}={\displaystyle \frac{{f_{\mathrm{n}\mathrm{e}\mathrm{w}}-f}_{\mathrm{r}\mathrm{e}}}{{\epsilon }_{\mathrm{r}\mathrm{e}\mathrm{f}}-{\epsilon }_{\mathrm{r}\mathrm{e}}}}$$

(19)

$$f_{\mathrm{c}}=a{\epsilon }_c^{\eta }+b{\epsilon }_c+c$$

(20)

where $E_{\mathrm{r}\mathrm{e}}$ denotes the slope of the linear segment on the reloading curve. The specific coefficients $A$, $B$, $C$, $a$, $b$, $c$, and $\eta$ are defined in reference [35] and are not reiterated here.

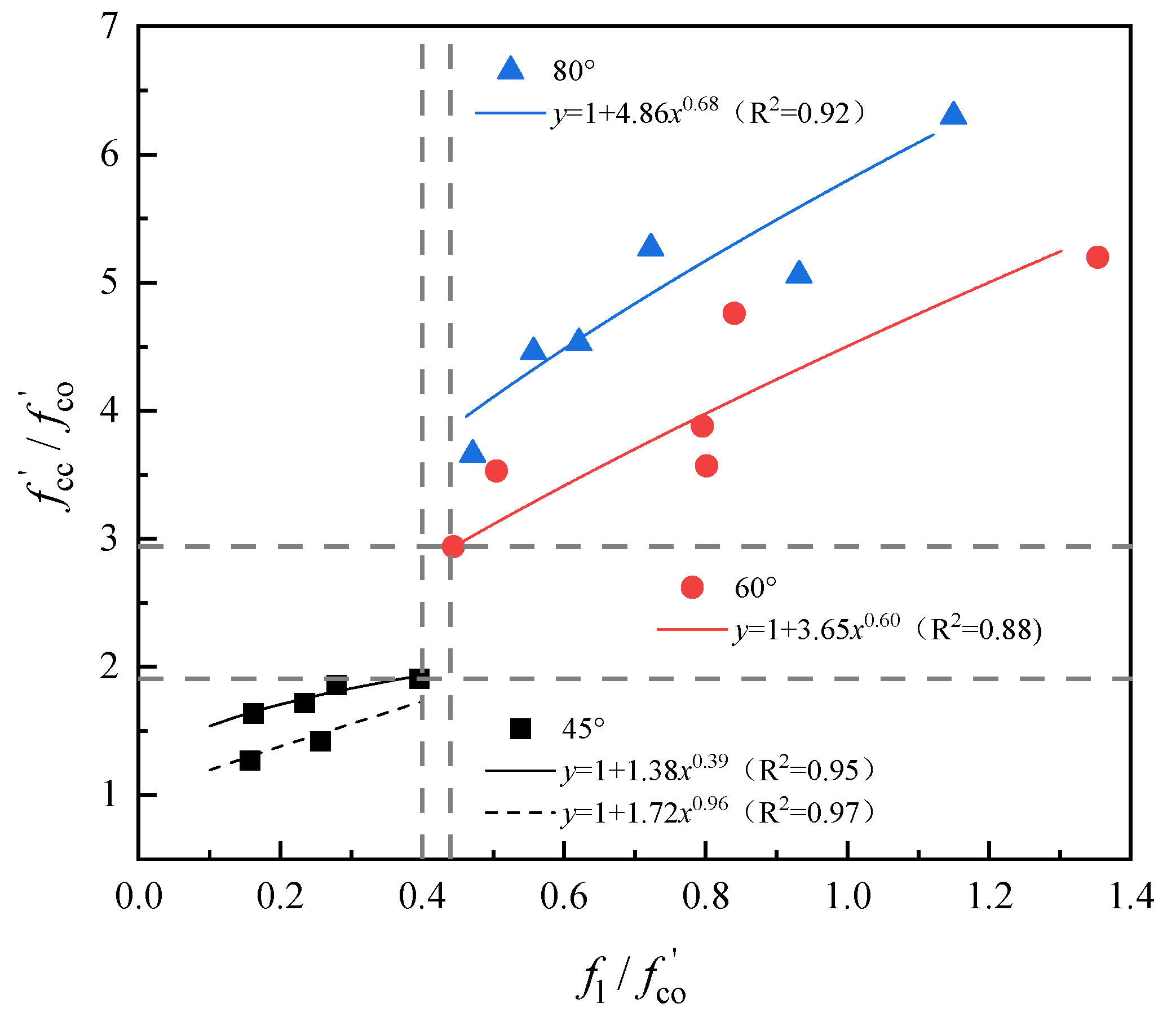
Regression analysis was performed on the experimental data from 54 specimens in this study, categorized by fiber orientation. The results are presented in Figure 23, where the coefficient of determination ($R^2$) is calculated as follows:

$$R^2=1-{\displaystyle \frac{{\sum }_i{\left(y_i^{\prime }-y_i\right)}^2}{{\sum }_i{\left(y_i-\overline{y}\right)}^2}}$$

(21)

where $y_i^{\prime }$ denotes the predicted value;$y_i$ represents the measured value; and $\overline{y}$ is the mean of all measured values.

The predictive formula for the confined compressive strength ($f_{\mathrm{c}\mathrm{c}}^{\prime }$) of GFRP tube-confined specimens with varying fiber angles is derived as follows:

$$\pm 45°:f_{\mathrm{c}\mathrm{c}}^{\prime }=\left\{\begin{array}{c}{f}_{\mathrm{c}\mathrm{o}}^{\prime }+1.38{f_{\mathrm{c}\mathrm{o}}^{\prime }\left({\displaystyle \frac{f_{\mathrm{l}}}{f_{\mathrm{c}\mathrm{o}}^{\prime }}}\right)}^{0.39}\ge 1.5,\left(R^2=0.95\right)\\ f_{\mathrm{c}\mathrm{o}}^{\prime }+1.72f_{\mathrm{c}\mathrm{o}}^{\prime }{\left({\displaystyle \frac{f_{\mathrm{l}}}{f_{\mathrm{c}\mathrm{o}}^{\prime }}}\right)}^{0.96}<1.5,\left(R^2=0.97\right)\end{array}\right.$$

(22)

$$\pm 60°:f_{\mathrm{c}\mathrm{c}}^{\prime }=f_{\mathrm{c}\mathrm{o}}^{\prime }+3.65f_{\mathrm{c}\mathrm{o}}^{\prime }{\left({\displaystyle \frac{f_{\mathrm{l}}}{f_{\mathrm{c}\mathrm{o}}^{\prime }}}\right)}^{0.60},\left(R^2=0.88\right)$$

(23)

$$\pm 80°:f_{\mathrm{c}\mathrm{c}}^{\prime }=f_{\mathrm{c}\mathrm{o}}^{\prime }+4.86f_{\mathrm{c}\mathrm{o}}^{\prime }{\left({\displaystyle \frac{f_{\mathrm{l}}}{f_{\mathrm{c}\mathrm{o}}^{\prime }}}\right)}^{0.68},\left(R^2=0.92\right)$$

(24)

Equations (22)–(24) represent statistically averaged results derived from specimens with identical fiber angles (dominant influencing factor), considering two kinds of layer counts (6, 10), slenderness ratios (2, 4), and distinct loading protocols. These formulas can guide rapid preliminary design when parameters fall within the sufficiently representative ranges.

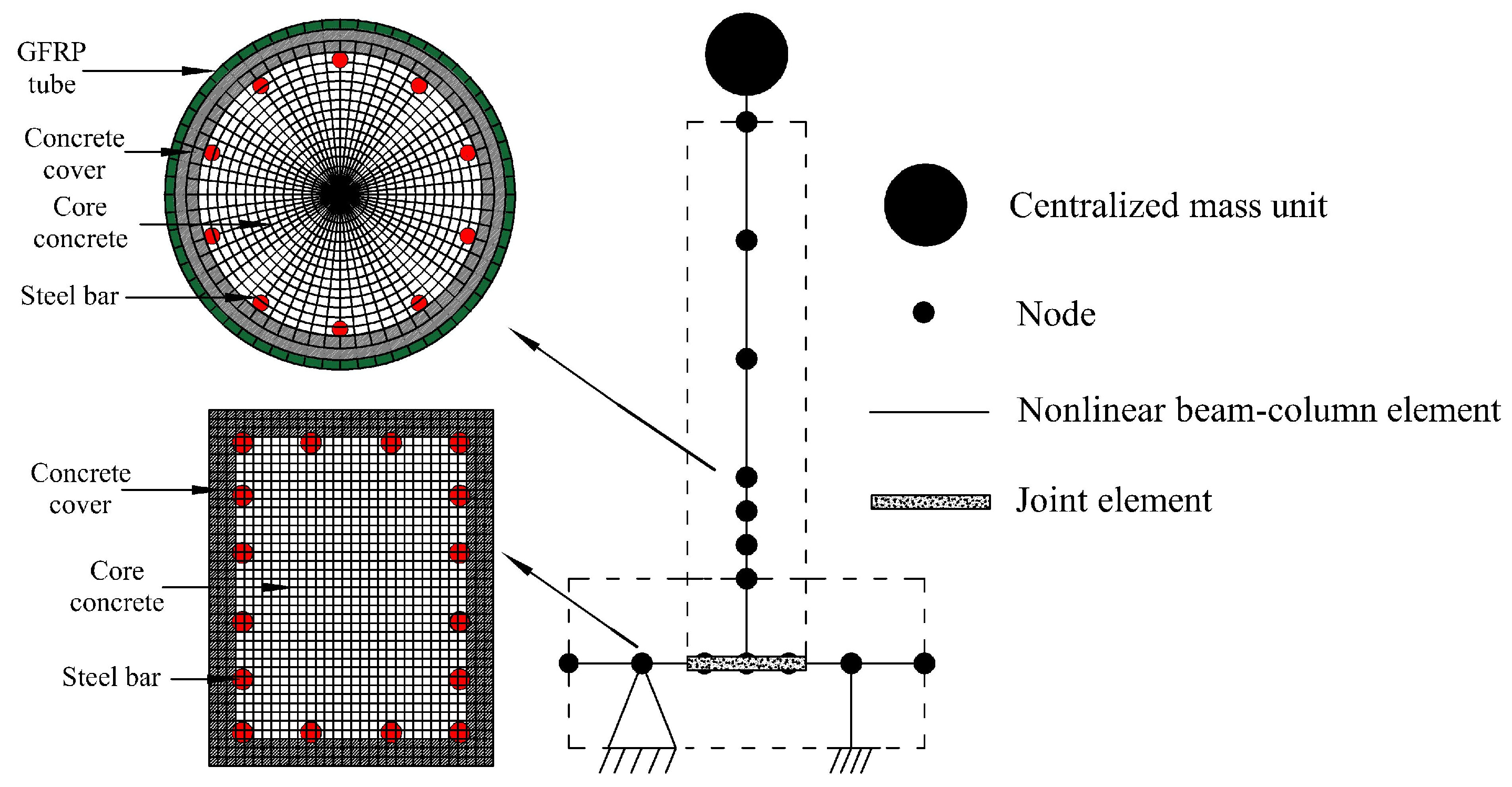
Furthermore, by embedding the proposed constitutive model for GFRP-confined concrete into the OpenSees (v3.1.0) material library via custom development, the numerical simulation of quasi-static testing on bridge piers can be implemented.

The specimen was modeled in OpenSees using nonlinear beam-column elements. Based on the actual geometric dimensions, the element was discretized with 15 integration points, locally refined near the joint interface. The pier cross-section was divided into 1000 fiber elements (50 circumferential × 20 radial). The column-footing joint was simulated with high-strength grout material matching the joint height, concentrating deformation at the interface. A fixed-end constraint was applied at the base, while rotational restraints were imposed at the top. The sustained dead load at the pier top was modeled as a centralized mass element. Displacement-controlled loading was adopted throughout the test. The specimen model schematics are illustrated in Figure 24.

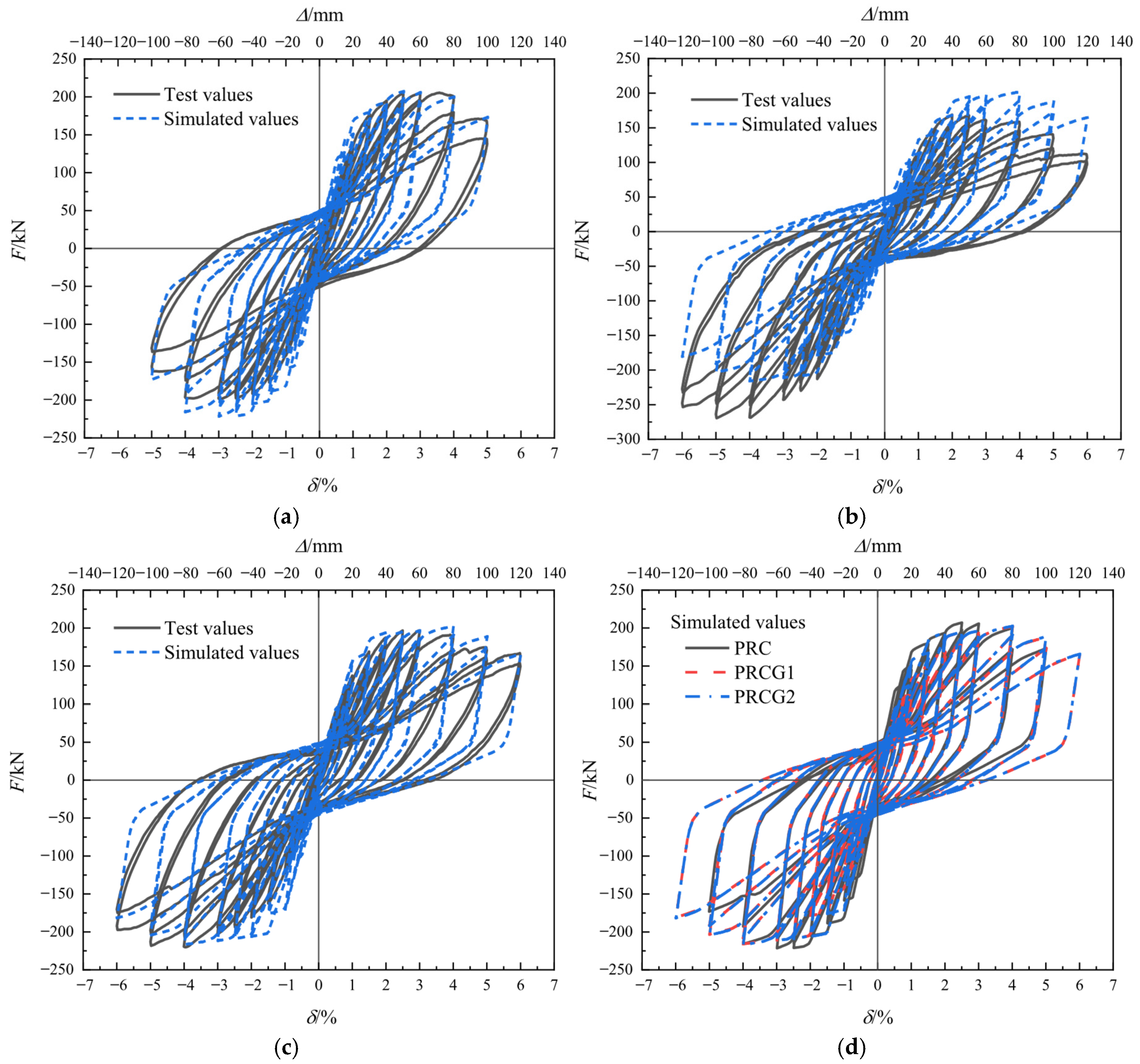
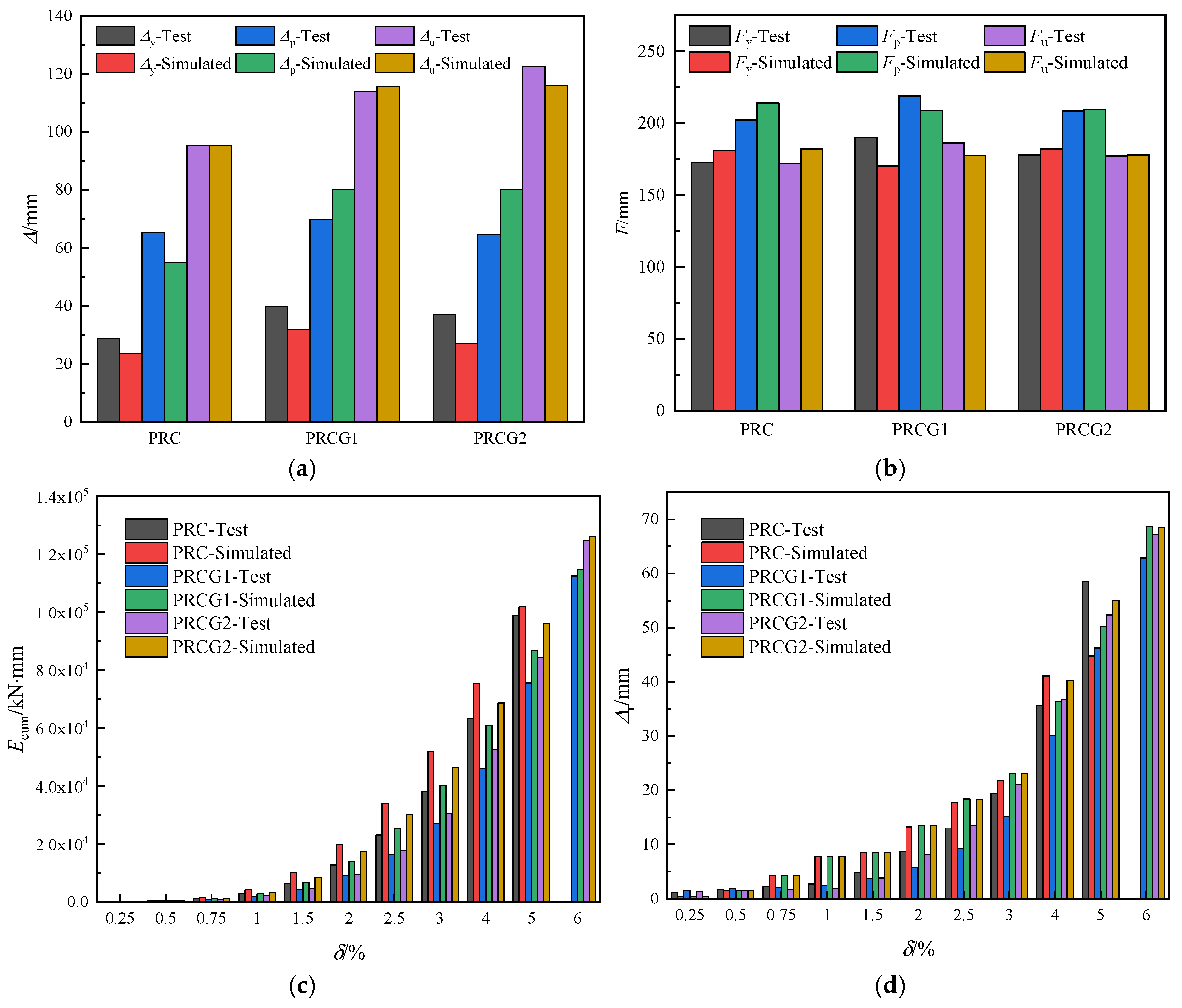
Given severe damage progression in later loading stages, numerical simulations were terminated at a 5% drift ratio for the PRC specimen and 6% drift ratio for PRCG1/PRCG2 to ensure convergence. As illustrated in Figure 25, the simulated hysteretic responses demonstrate close alignment with the experimental results, accurately replicating the strength degradation and stiffness deterioration caused by sequential steel fracture and concrete crushing under low-cycle cyclic loading. Crucially, PRCG1 and PRCG2 exhibit near-identical hysteretic behavior when axial force eccentricity is neglected, confirming that the 6-ply GFRP tube thickness delivers adequate confinement for the prefabricated bridge piers examined in this study.

Figure 26 demonstrates that the simulated ultimate displacements (${∆}_{\mathrm{u}}$), averaged across positive/negative loading directions, exhibit the closest agreement with experimental values, with absolute deviations ranging from −6.6 to 1.7 mm (−5.7% to 1.5% relative error). The peak displacements (${∆}_{\mathrm{p}}$) show larger discrepancies, with simulation-experiment differences of −10.4 to 15.3 mm (−18.9% to 19.1%). In contrast, the simulated yield displacements $({∆}_{\mathrm{y}}$) are consistently lower than the experimental results (mean of three calculation methods), with absolute deviations of −10.2 to −5.3 mm (−22.5% to −38.0%). For the PRC, PRCG1, and PRCG2 specimens, the differences in yield force ($F_{\mathrm{y}}$) between simulation and experiment are 8.2 kN (+4.6%), −19.5 kN (−11.4%), and 3.9 kN (+2.1%), respectively. Similarly, the discrepancies in the peak/ultimate load capacities ($F_{\mathrm{p}}$/$F_{\mathrm{u}}$) are 12.1 kN/10.3 kN (+5.6%), −10.4 kN/−8.8 kN (−5.0%), and 1.1 kN/0.9 kN (+0.5%).

Comparisons of the simulated versus experimental hysteretic energy dissipation ($E_{\mathrm{c}\mathrm{u}\mathrm{m}}$) (based on the first cycle at each loading level) indicate that the numerical model accurately estimates the total $E_{\mathrm{c}\mathrm{u}\mathrm{m}}$. However, it overestimates the energy dissipation in intermediate loading cycles while underestimating the energy increment near failure. For specimens PRC, PRCG1, and PRCG2, the simulation-to-test discrepancy evolves as follows: from −4.9% (initial) to +37.5% (peak), then declines to +3.1%; from +5.8% to +35.3%, then declines to +1.9%; and from +13.3% to +45.3%, then declines to +1.1%, respectively. The residual displacements (${\mathsf{\Delta }}_{\mathrm{r}}$) in PRC simulations are overestimated by 2.1–5.6 mm (3.9–13.7% relative to the peak displacement per hysteresis loop, ${\gamma }_i$) prior to failure. For PRCG1 and PRCG2, ${\mathsf{\Delta }}_{\mathrm{r}}$ values are consistently overestimated by 2.2–9.1 mm (3.9–19.4%) and 1.3–5.8 mm (1.0–15.9%), respectively.

5. Conclusions

This study established a methodologically grounded experimental program comprising axial compression tests on 54 GFRP tube-confined concrete specimens (organized into 18 test groups) to systematically investigate the effects of the fiber layer count, winding angle, slenderness ratio, and cross-sectional confinement configuration on compressive behavior and stress–strain responses. Building upon this foundation, quasi-static cyclic tests were conducted on two precast assembled bridge piers with GFRP confinement (PRCG1 and PRCG2, differing in tube thickness) and one unconfined reference pier (PRC), revealing that GFRP confinement significantly enhances seismic performance. The key findings are as follows:

(1)

Axial compression testing revealed that specimens with $\pm 45°$ fiber winding angles demonstrated ductile failure behavior, contrasting with the brittle failure observed in specimens with $\pm 60°$ and $\pm 80°$ fiber winding angles. Peak stress exhibited a positive correlation with both increased fiber winding angle and a greater number of fiber layers, with the fiber winding angle exerting a comparatively stronger influence. For constrained concrete short columns, compressive strength enhancement proved more pronounced in specimens characterized by higher slenderness ratios. Owing to the Poisson’s ratio mismatch between GFRP tubes and concrete, the confinement effect in fully loaded specimens exhibits delayed activation, requiring higher axial strain for full mobilization. Nevertheless, the ultimate bearing capacity demonstrates negligible disparity compared to specimens subjected to core concrete loading only.

(2)

(Both the cast-in-place column top and precast assembled column bottom in the PRC specimens developed sufficient plastic hinge zones, culminating in bending–shear failure. Localized cracking of the GFRP tubes was confined to regions near the joints in specimens PRCG1 and PRCG2, which subsequently exhibited bending failure. The GFRP tubes effectively confined the development and lateral expansion of shear diagonal cracks within the concrete, prevented the spalling of the concrete protective layer, and delayed the yield and fracture of the reinforcing bars.

(3)

The measured average curvature distribution for each specimen exhibited the deformation characteristics associated with double-curvature bending, with the GFRP tube-confined specimens demonstrating lower curvature and superior bending resistance. For specimens PRCG1 and PRCG2, the hoop strain of the GFRP tubes increases with the growth of maximum lateral displacement. The recorded maximum hoop strains are 0.96% and 0.35%, respectively, which are significantly lower than the material’s ultimate strain of 1.75% and below the effective hoop strain range (1.4–1.7%) measured in axially compressed concrete specimens confined by GFRP tubes.

(4)

GFRP tube confinement significantly enhances the strength and deformation capacity of precast assembled concrete bridge piers. Under small eccentric axial loading, its impact on the averaged seismic performance indices is negligible. Relative to the PRC control specimen, specimens PRCG1 and PRCG2 exhibit notable performance improvements: ultimate displacement increases of 19.50% and 28.57%, ductility coefficient increases of 18.56% and 27.84%, and cumulative hysteresis energy dissipation enhancements of 13.90% and 26.43% at ultimate bearing capacity, respectively. At drift rates of 5%, 6%, and 7%, PRCG1 demonstrates bearing capacity gains of 26.74%, 56.46%, and 84.05%, stiffness increases of 28.91%, 64.88%, and 103.09%, and residual displacement decreases of 20.89%, 20.38%, and 21.44% relative to PRC. Similarly, PRCG2 shows respective bearing capacity increases of 23.25%, 54.84%, and 76.91%; stiffness gains of 25.51%, 61.49%, and 93.81%; and residual displacement reductions of 11.17%, 15.29%, and 31.98%.

(5)

An analytical model for GFRP tube-confined bridge piers with varying fiber angles was established based on the Lam–Teng model. The peak strength values determined from experimental results provide critical references for practical engineering design and application. Quasi-static testing of bridge piers was simulated using the OpenSees fiber model, validating the effectiveness of the proposed model. As the primary failure modes of the GFRP-confined pier specimens in this study involve buckling and fracture of longitudinal reinforcement, the full mechanical potential of the GFRP tubes remains underutilized. To further enhance seismic performance, the adoption of high-ductility high-strength steel bars or FRP reinforcement is recommended, thereby balancing the mechanical properties between the GFRP-confined concrete and longitudinal reinforcement.