Temperature–Load Stress Analysis of Ultra-Long Pool Structures Based on Distributed Fiber Optic Sensing and Finite Element Analysis
Abstract
1. Introduction
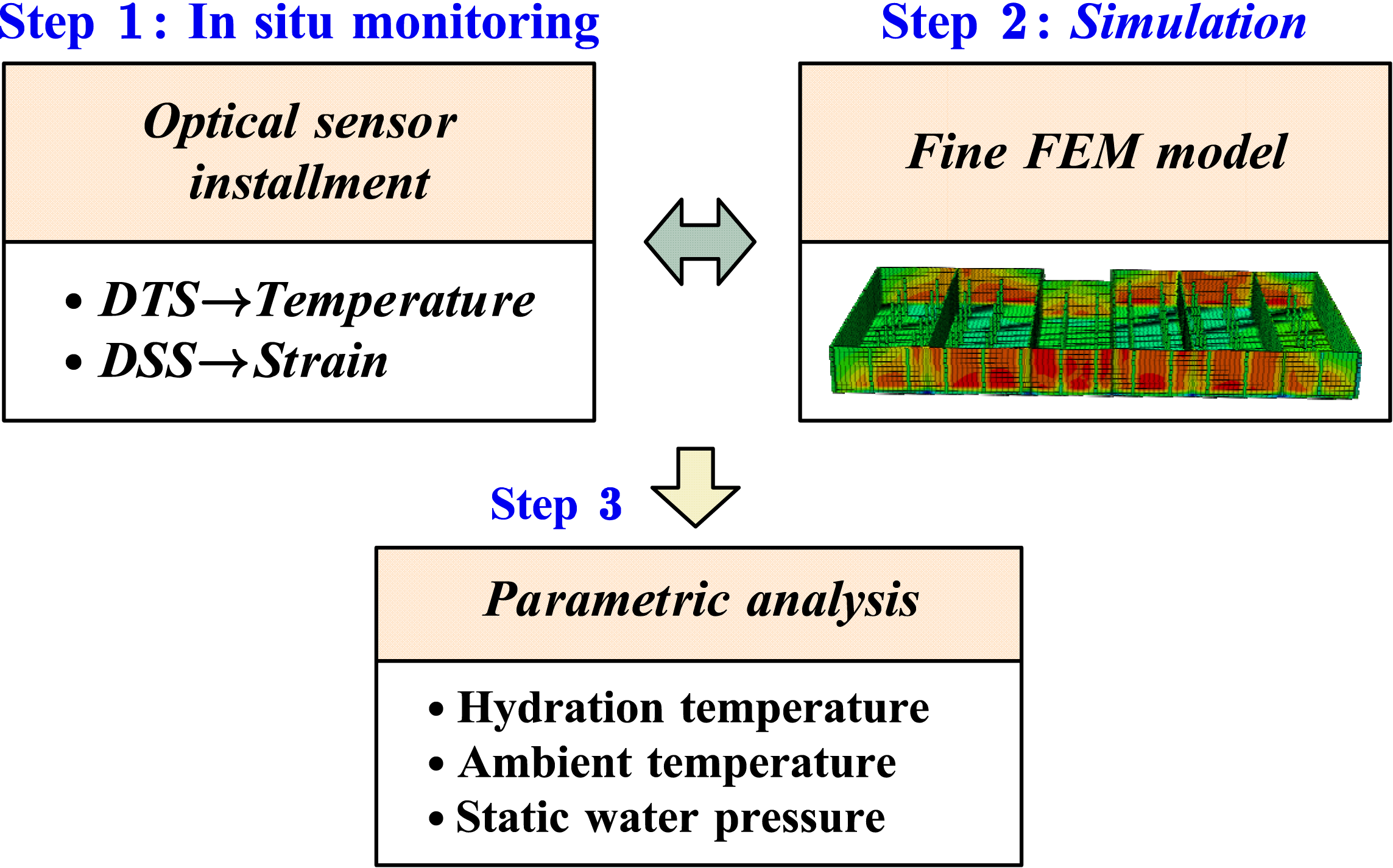
2. Methodology
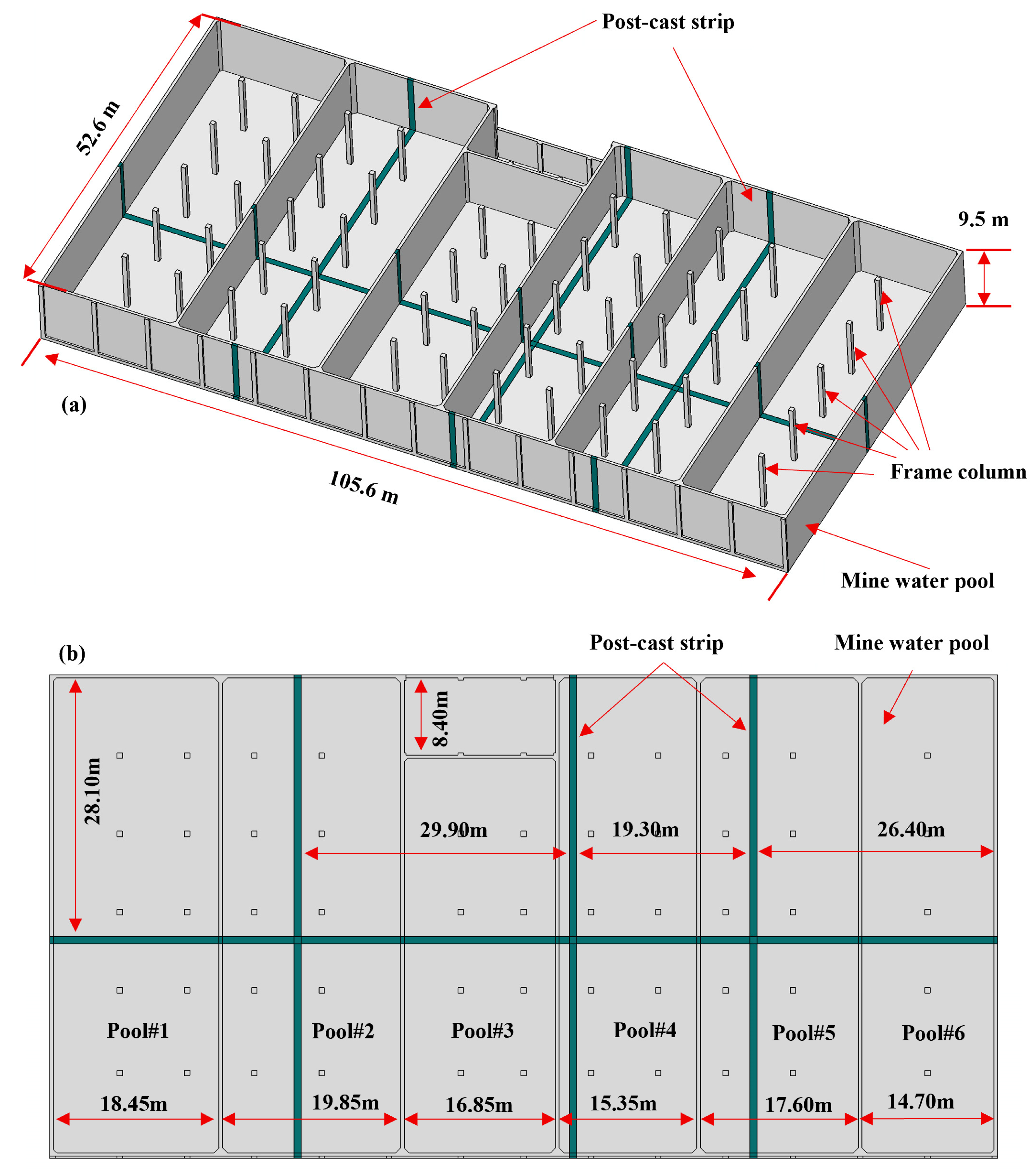
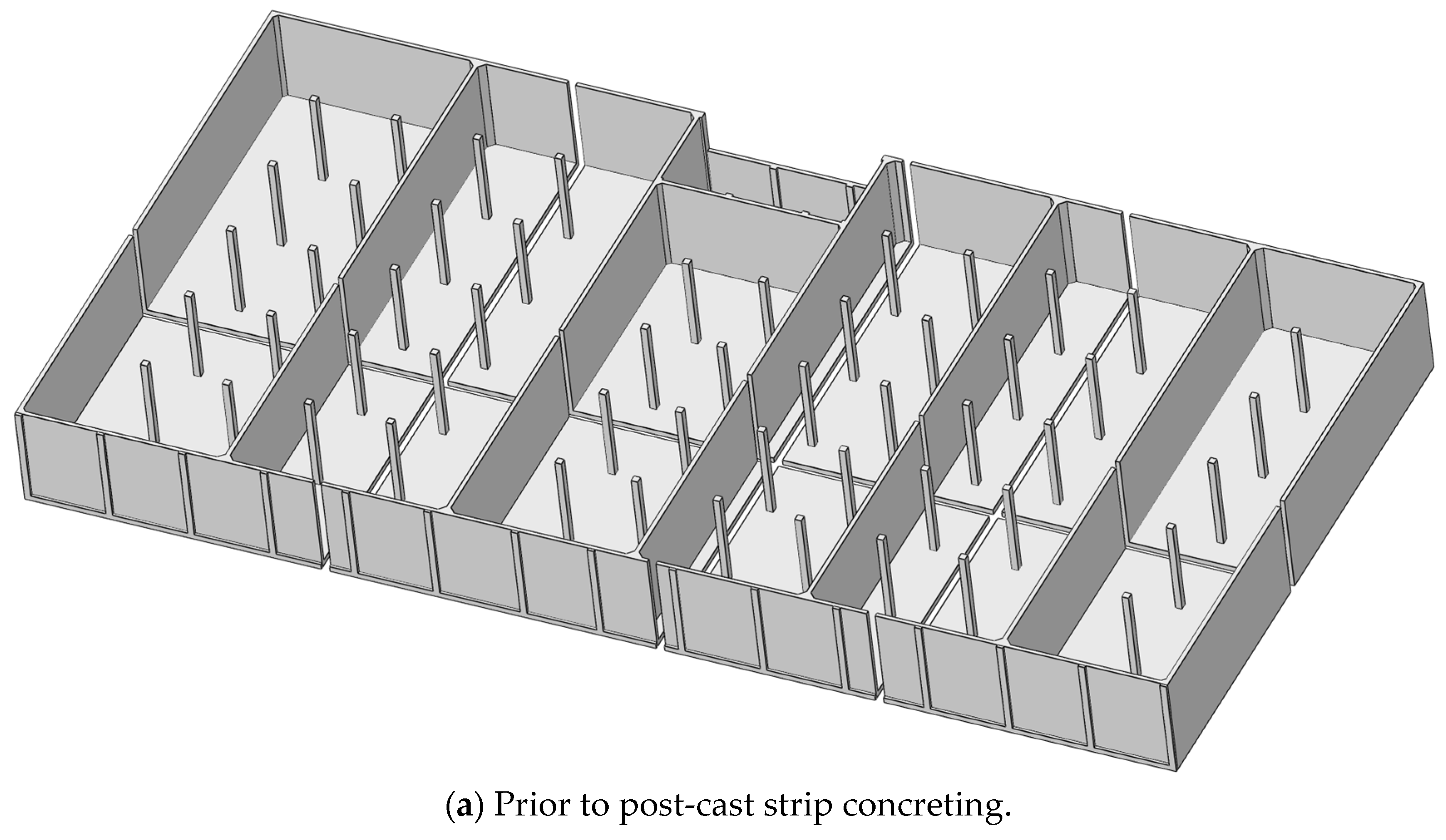
2.1. Overview of Ultra-Long Pool Structure
2.2. Distributed Fiber Optic Sensing
2.3. Material Properties
2.3.1. Material Experiments
2.3.2. Concrete Constitutive Laws
2.3.3. Steel Reinforcement Constitutive Laws
2.4. Numerical Modeling
2.5. Considered Conditions
3. Hydration Temperature Effects
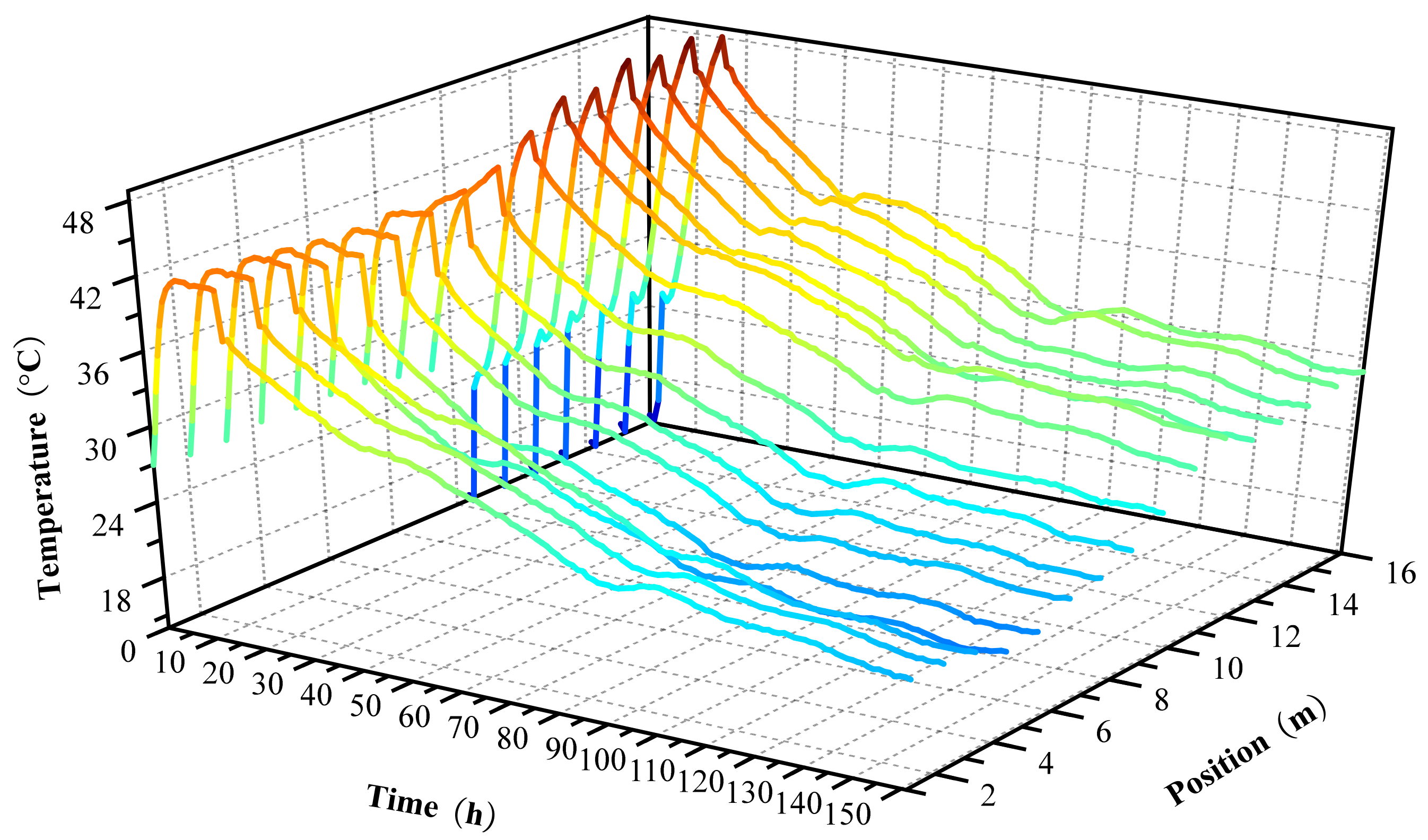
3.1. Verification of the FEM Model
3.2. Effect of Initial Casting Temperature
3.3. Effect of Peak Hydration Temperature
3.4. Effect of Ambient Temperature
3.5. Tensile Damage Assessment and Cracking Risk
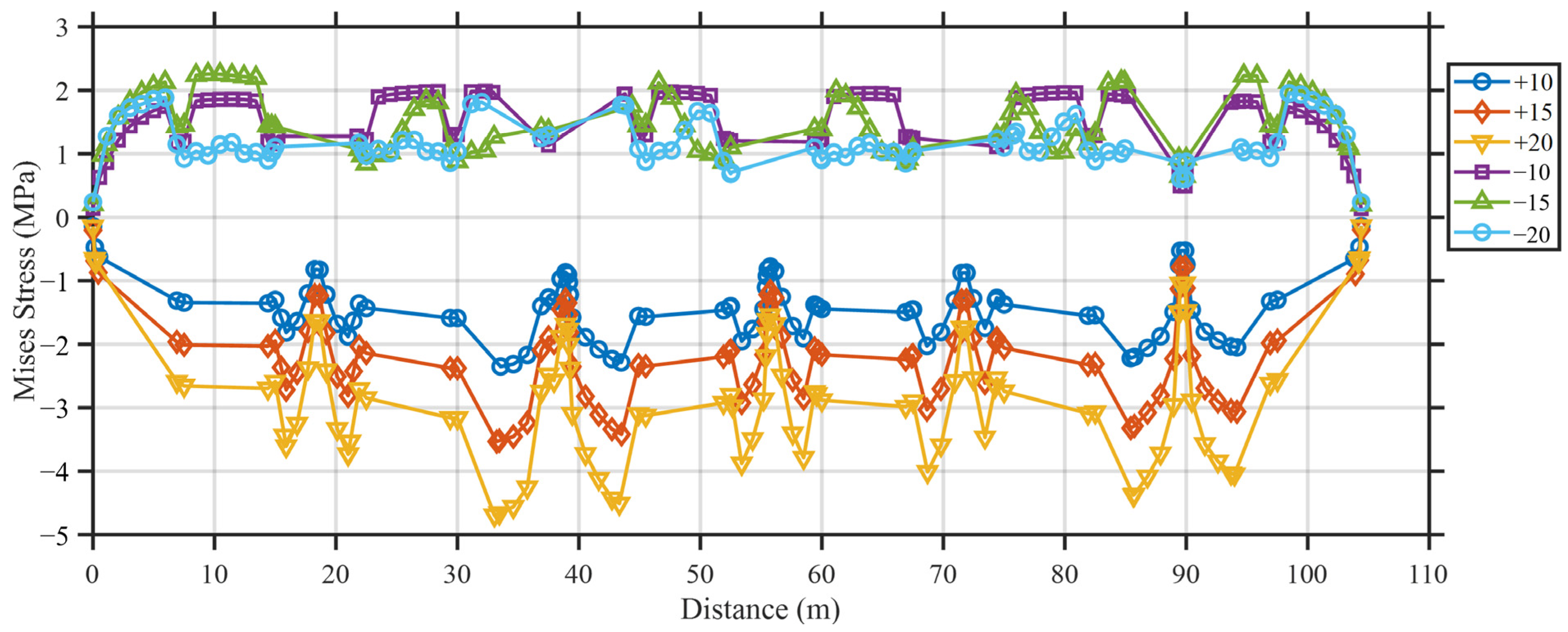
3.6. Stress Distribution Along the Longitudinal Pool Wall
3.7. Recommendations for Crack Control
4. Influence of Ambient Temperature Variations
4.1. Stress Response Under Heating Scenarios
4.2. Stress Response Under Cooling Scenarios
4.3. Heating Scenarios Versus Cooling Scenarios
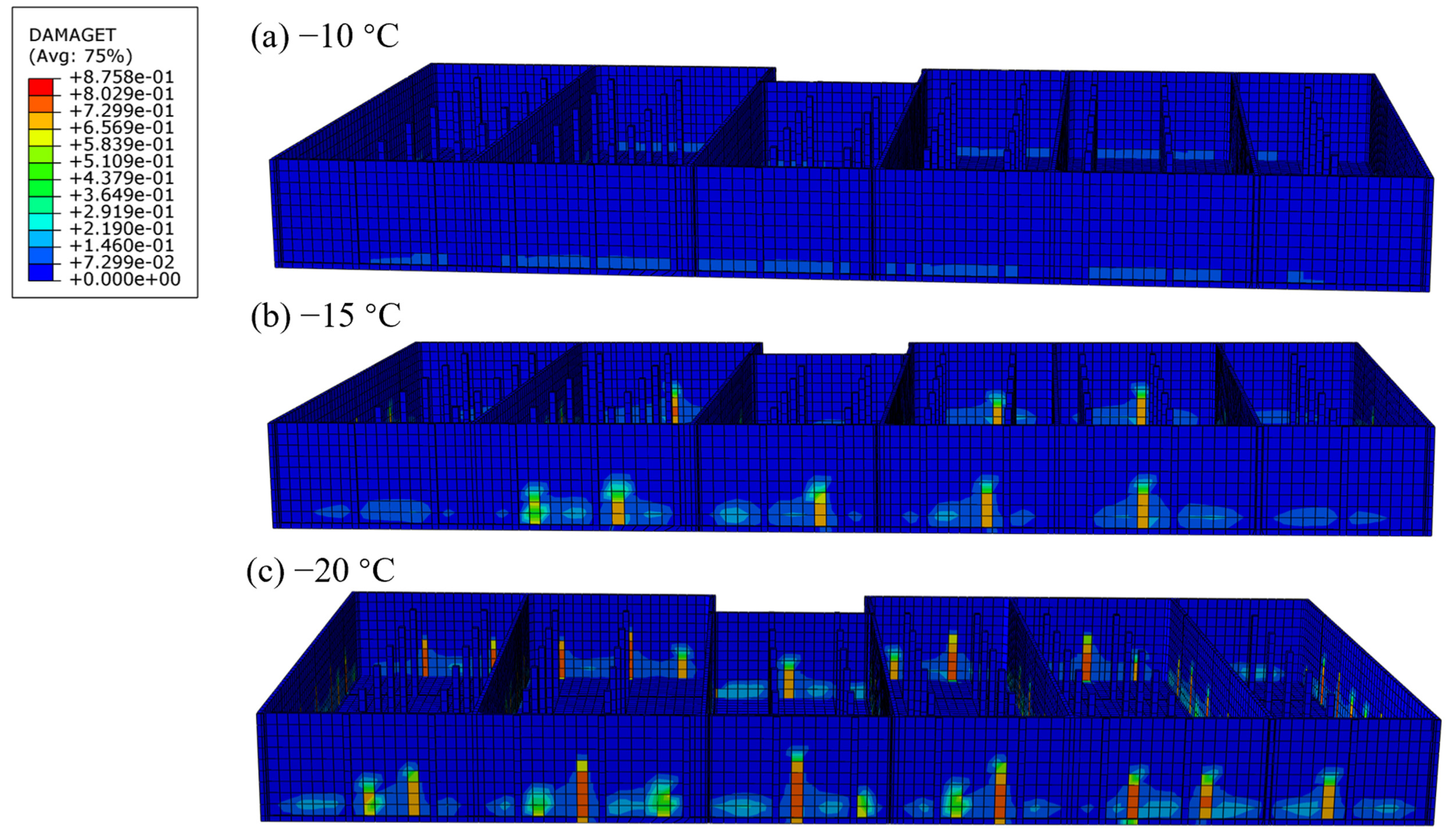
4.4. Concrete Damage Observation
5. Water Loading
5.1. Structural Response Under Single Sub-Pool Loading
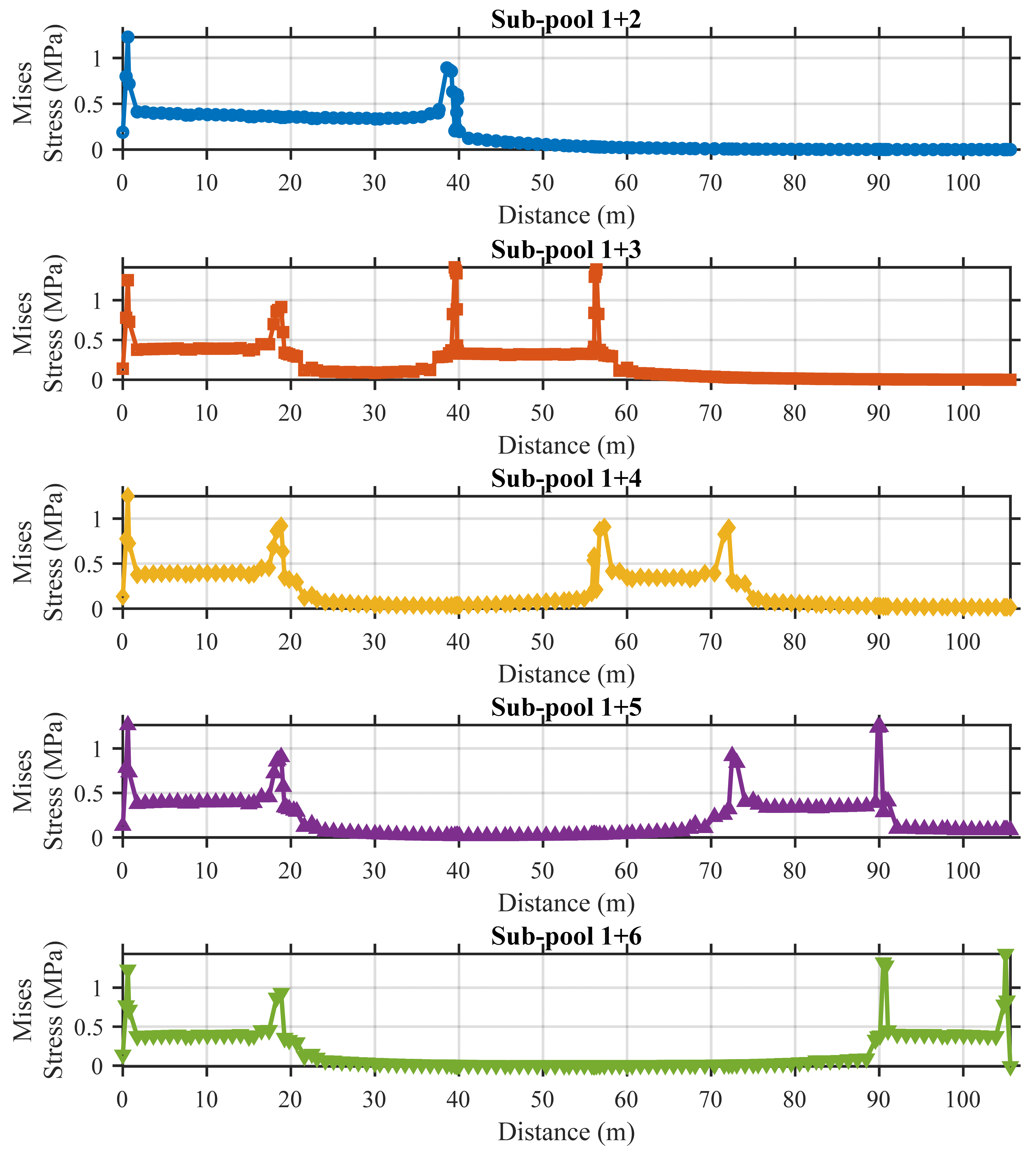
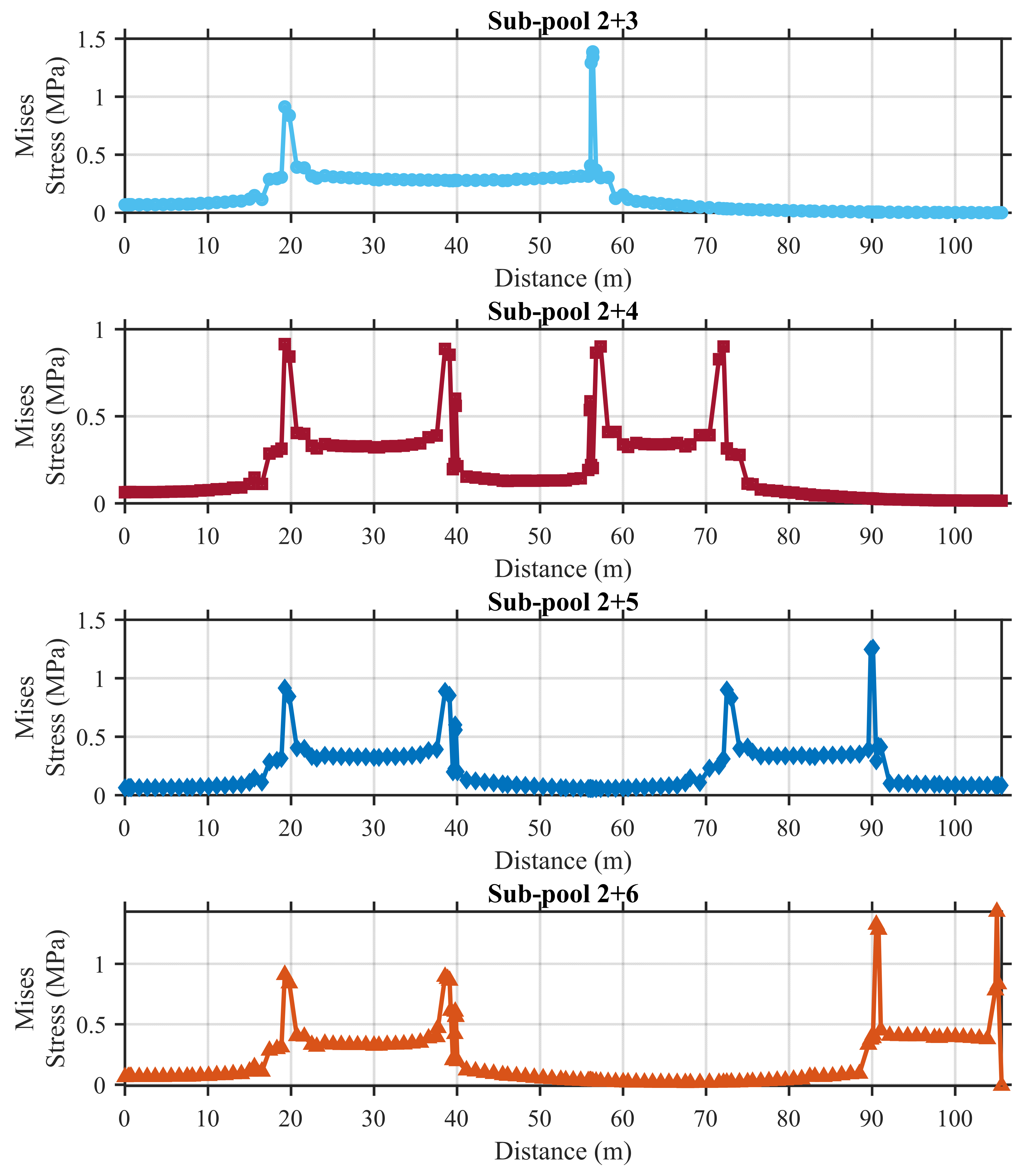
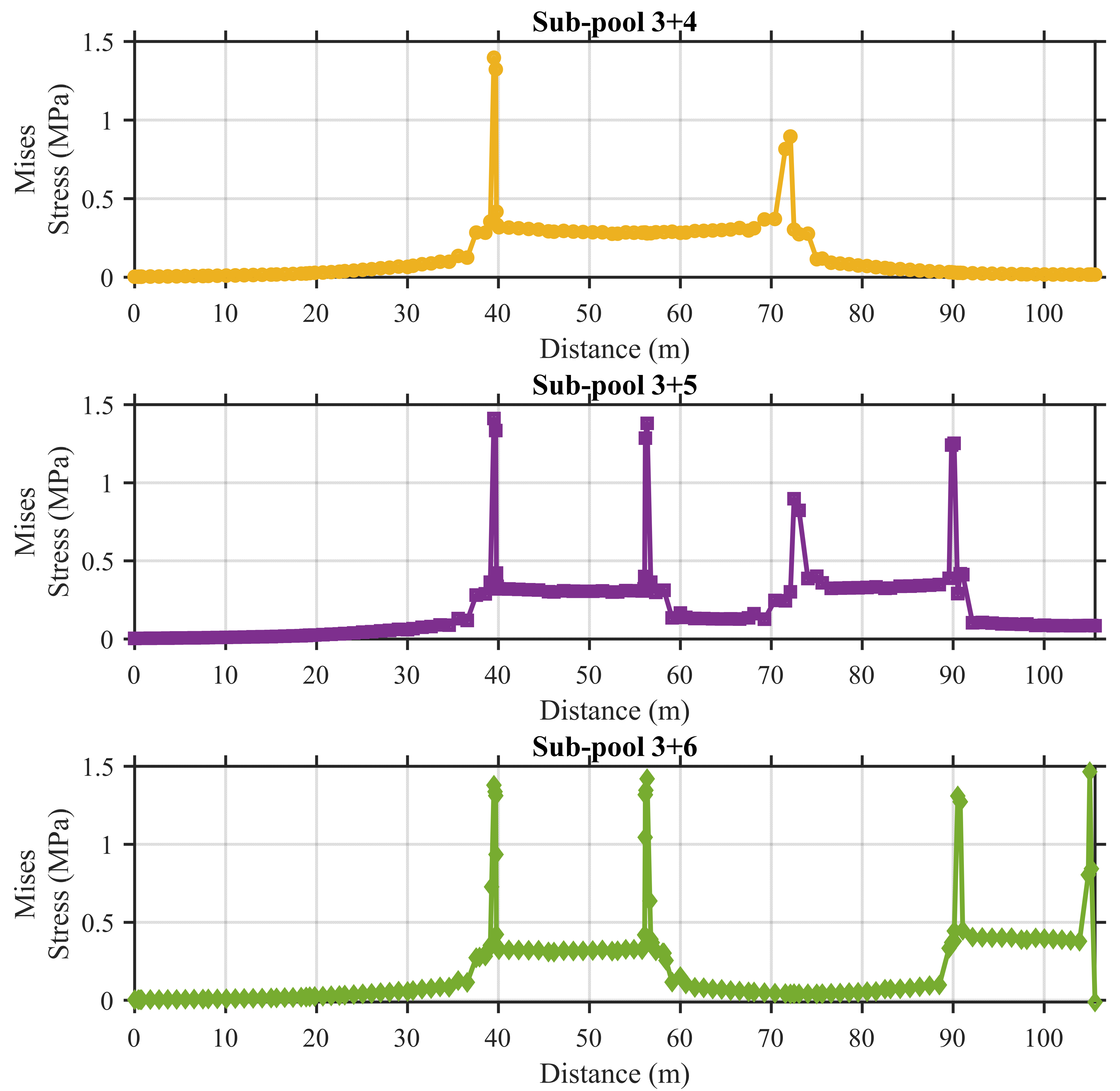
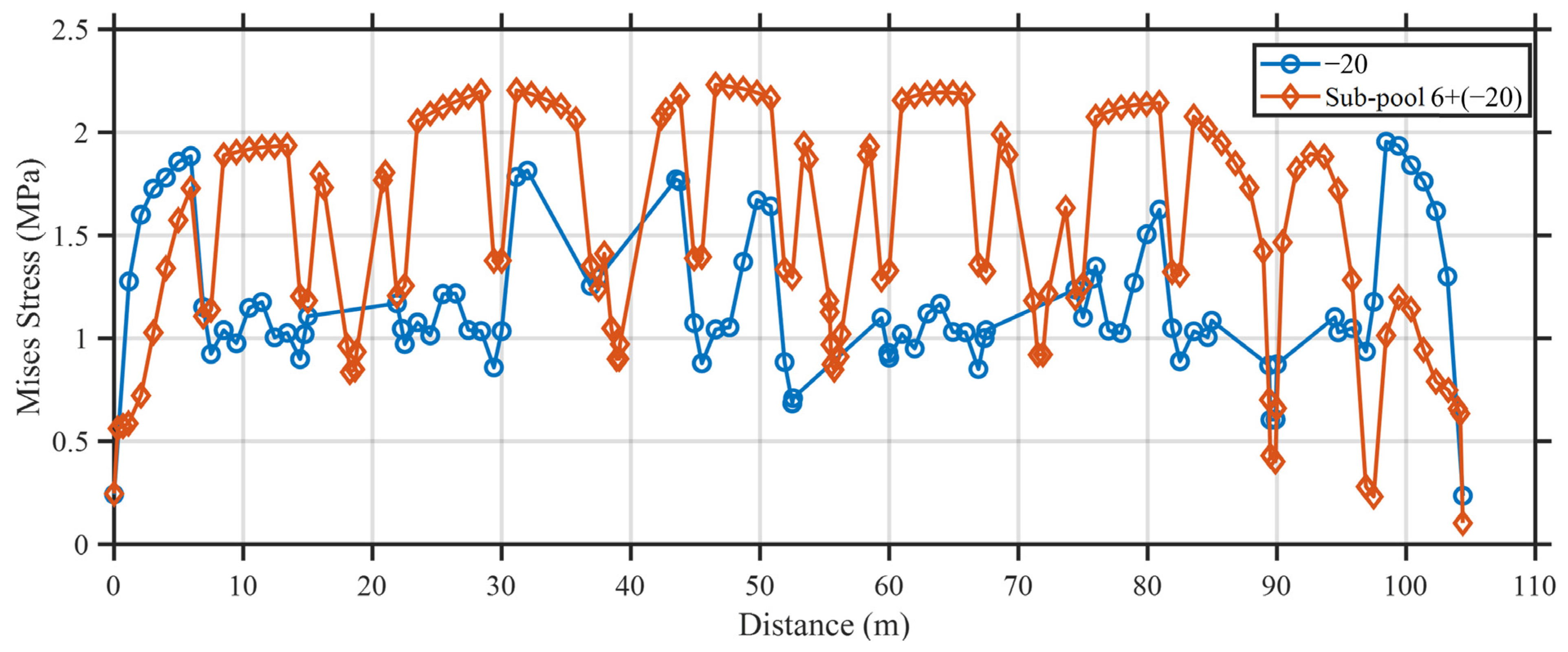
5.2. Structural Response Under Dual Sub-Pool Loading
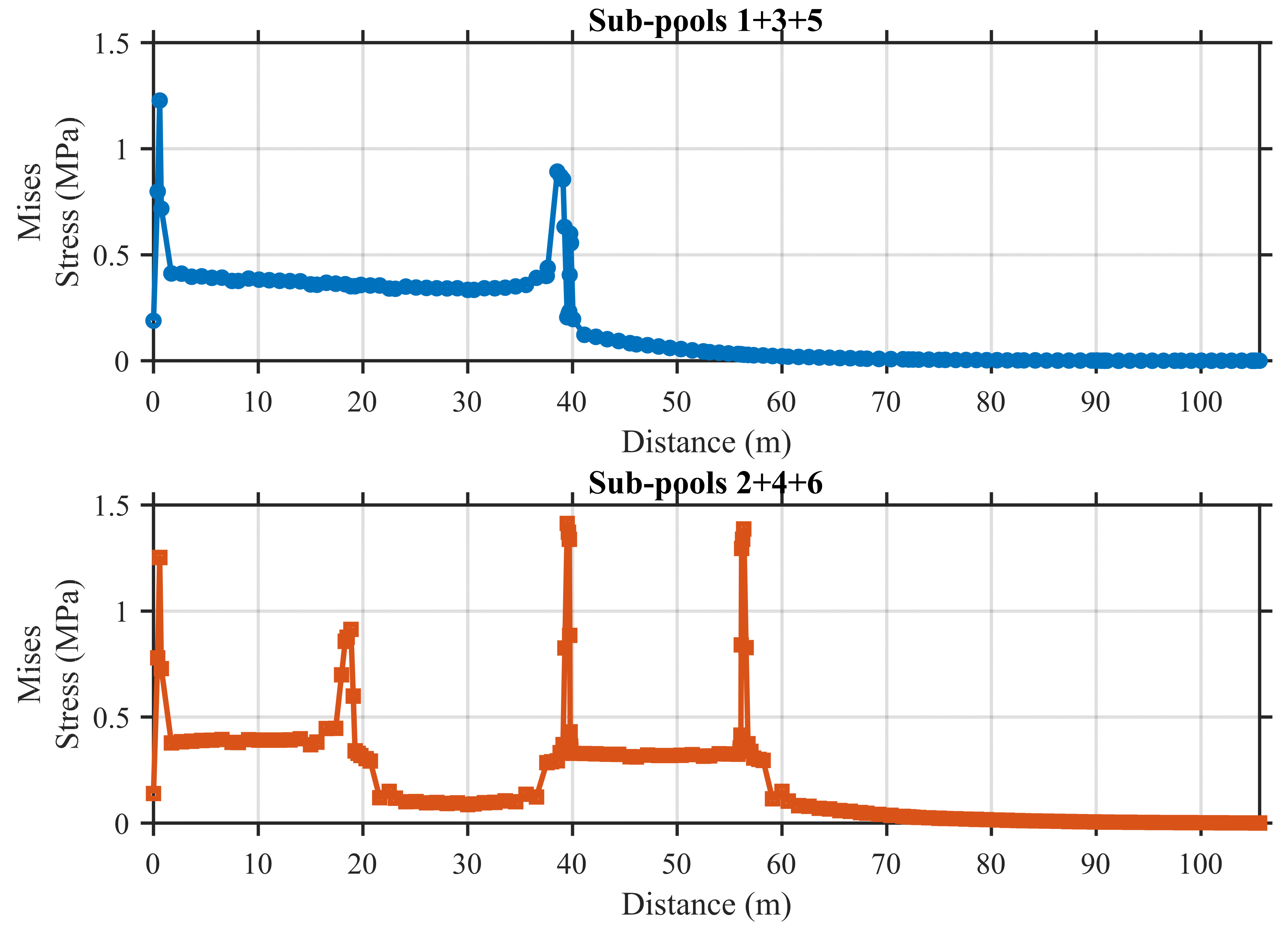
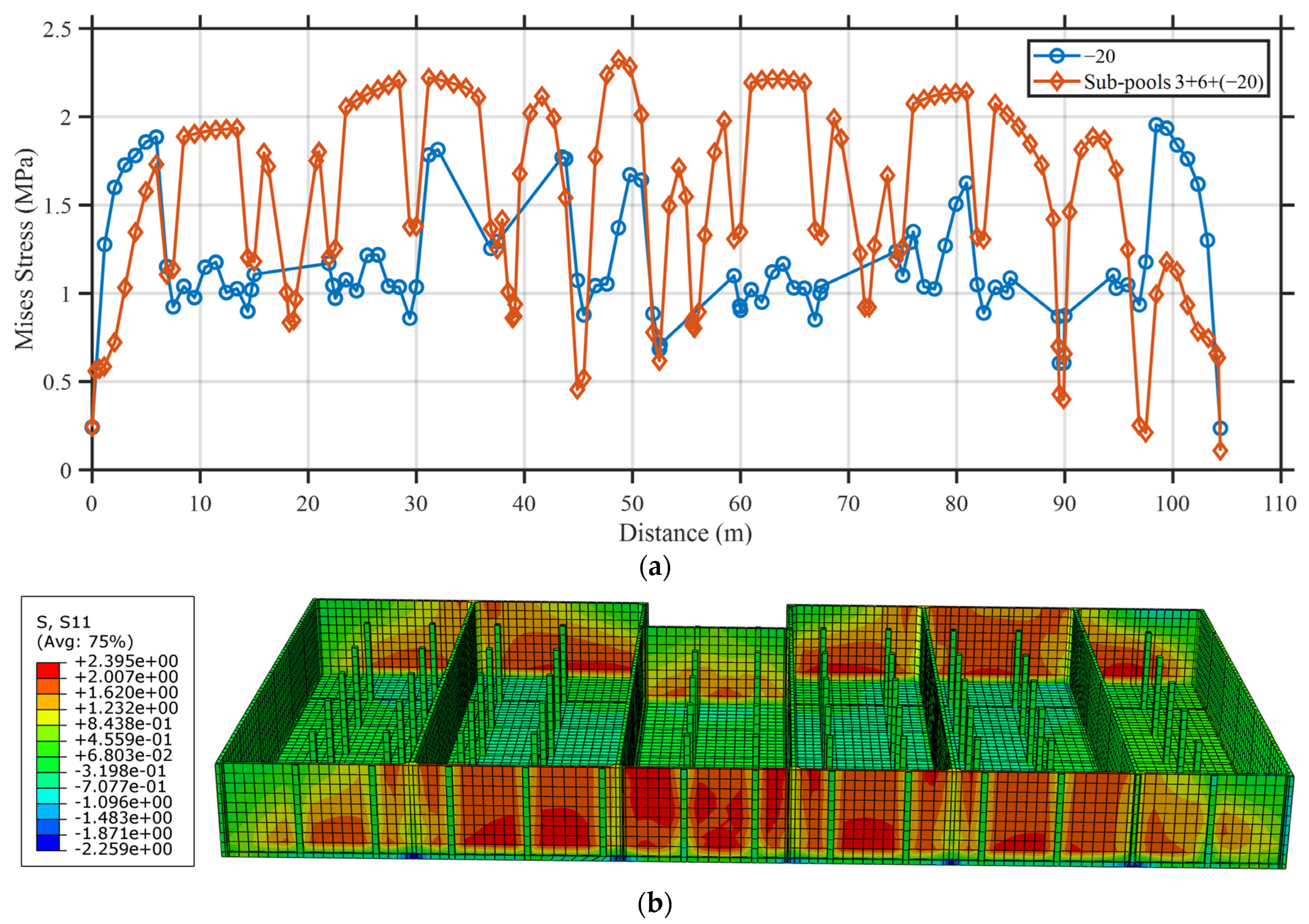
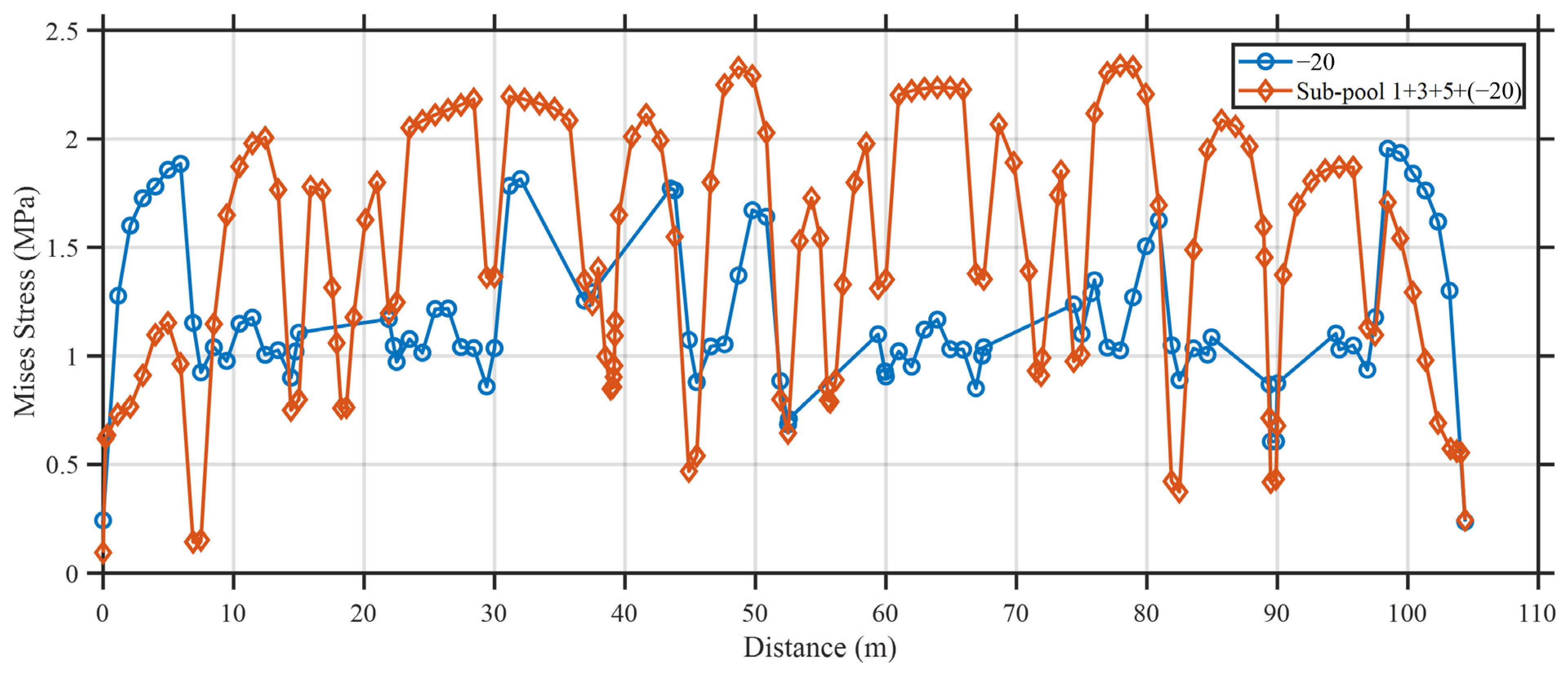
5.3. Structural Response Under Triple Sub-Pool Loading
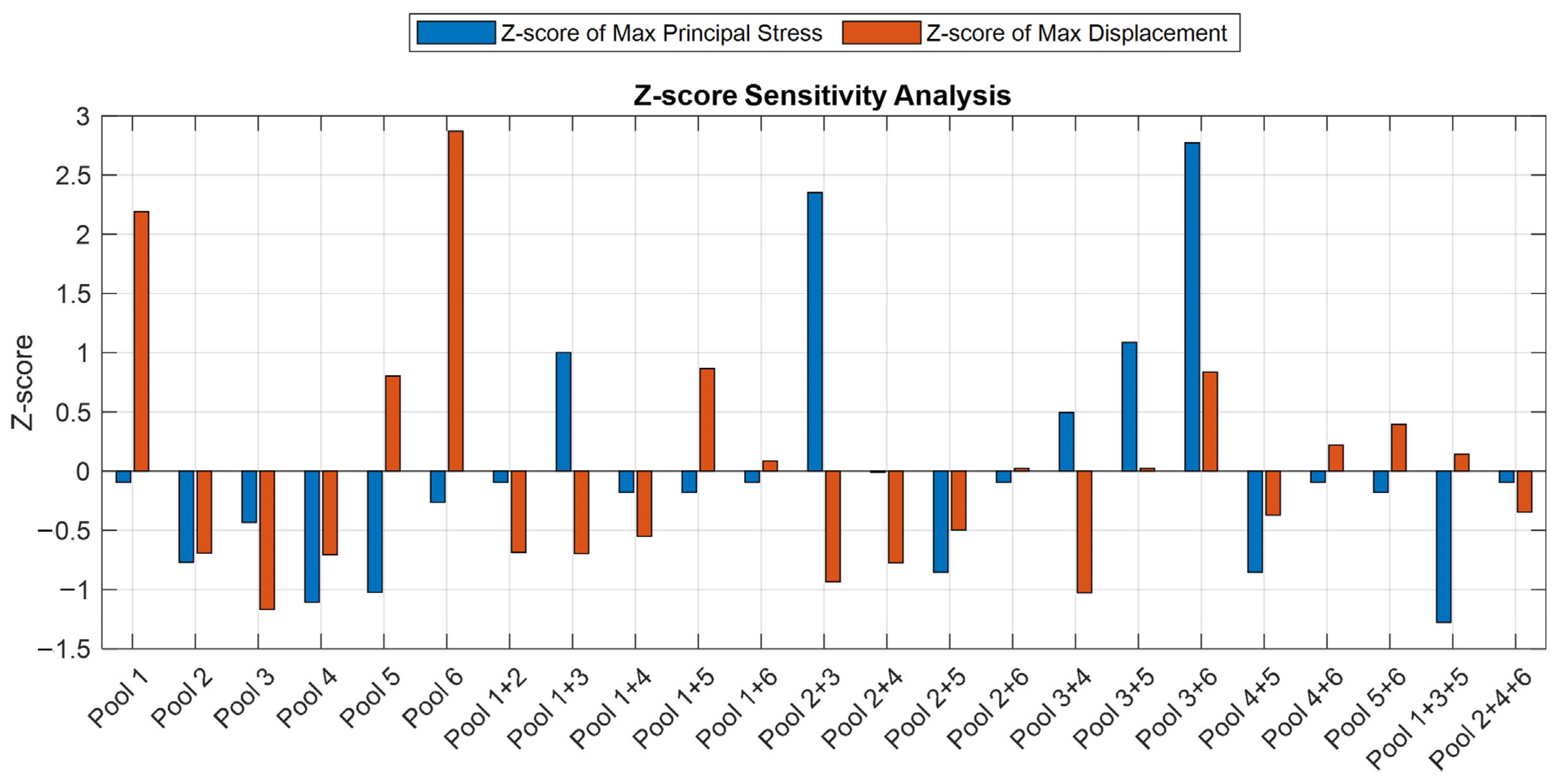
5.4. Sensitive Analysis
5.5. Coupling Effects Under Load and Temperature
6. Conclusions
- (1)
- A finite element model was developed and validated using DFOS monitoring data. The comparison showed an average error within 9% between the simulated and measured peak thermal strain values, confirming the model’s reliability in reproducing the structural response under thermal and mechanical effects.
- (2)
- Based on the validated model, parametric studies revealed that a temperature drop of −20 °C combined with staged loading in sub-pool 3+6 and sub-pool 1+3+5 leads to the most severe tensile stress conditions, increasing stress levels by up to 30%. These findings indicate that localized cracking is most likely to occur under extreme thermal gradients and asymmetric loading scenarios.
- (3)
- Simulation results revealed that tensile stress distribution is highly sensitive to both the temperature history during curing and the subsequent loading scheme. Stress concentrations tend to develop near construction joints and wall intersections, which are vulnerable regions for crack initiation under service conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chattopadhyay, S.; Chattopadhyay, D. Coal and other mining operations: Role of sustainability. In Fossil Energy; Springer: New York, NY, USA, 2020; pp. 333–356. [Google Scholar]
- Yuan, S.; Sui, W.; Han, G.; Duan, W. An optimized combination of mine water control, treatment, utilization, and reinjection for environmentally sustainable mining: A case study. Mine Water Environ. 2022, 41, 828–839. [Google Scholar] [CrossRef]
- Xu, Z.; Sun, Y. Mine water safety and environment: Chinese experience. Water 2024, 16, 2833. [Google Scholar] [CrossRef]
- de Lima, J.P.M.; Amaral, M.C.S.; de Lima, S.C.R.B. Sustainable water management in the mining industry: Paving the way for the future. J. Water Process Eng. 2025, 71, 107239. [Google Scholar] [CrossRef]
- Wang, D.B.; Song, X.B.; Nie, H.Y. Cracking analysis of massive concrete with large-diameter pipes during construction. Constr. Build. Mater. 2022, 338, 127636. [Google Scholar] [CrossRef]
- Fairbairn, E.M.; Azenha, M. Thermal cracking of massive concrete structures. In State of Art Report of the RILEM TC; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Li, K.; Li, L. Crack-altered durability properties and performance of structural concretes. Cem. Concr. Res. 2019, 124, 105811. [Google Scholar] [CrossRef]
- Zhou, G.D.; Yi, T.H. Thermal load in large-scale bridges: A state-of-the-art review. Int. J. Distrib. Sens. Netw. 2013, 9, 217983. [Google Scholar] [CrossRef]
- Schrefler, B.A.; Majorana, C.E.; Khoury, G.A.; Gawin, D. Thermo-hydro-mechanical modelling of high performance concrete at high temperatures. Eng. Comput. 2002, 19, 787–819. [Google Scholar] [CrossRef]
- de Borst, R.; Peeters, P.P. Analysis of concrete structures under thermal loading. Comput. Methods Appl. Mech. Eng. 1989, 77, 293–310. [Google Scholar] [CrossRef]
- Hooshmand, A.; Kianoush, R.; Siad, H.; Lachemi, M.; Moslemi, M. Investigation of leakage and self-healing of direct tension cracks under sustained loading and high-water pressure. Constr. Build. Mater. 2021, 267, 120879. [Google Scholar] [CrossRef]
- Jahandari, S.; Tao, Z.; Alim, M.A.; Li, W. Integral waterproof concrete: A comprehensive review. J. Build. Eng. 2023, 78, 107718. [Google Scholar] [CrossRef]
- Stoiber, N.; Kromoser, B. Topology optimization in concrete construction: A systematic review on numerical and experimental investigations. Struct. Multidiscip. Optim. 2021, 64, 1725–1749. [Google Scholar] [CrossRef]
- Ji, J.; Li, Z.; Ma, T.; Wang, H.; Li, J.; Wang, J. Evaluation on the Crack Resistance of Cement-Stabilized Macadam Mixture with Crack-Resistant Interlocking Gap Gradation and Rubber Powder. J. Mater. Civ. Eng. 2024, 36, 04024269. [Google Scholar] [CrossRef]
- Fang, L.; Fu, D.; Yuan, Q.; Xu, S.; Zhang, D.; Cai, H.; Zeng, X.; Wang, Y.; Zhou, J. Combined effects of low-heat cement, expansive agent and shrinkage-reducing admixture on drying shrinkage and cracking of concrete. Case Stud. Constr. Mater. 2025, 22, e04344. [Google Scholar] [CrossRef]
- Liu, K.; Wang, X.; Luo, Z. Pre-tension-free distributed UW-FBG detection method for two-dimensional bearing capacity of super-long bored piles. J. Mod. Opt. 2025, 72, 382–390. [Google Scholar] [CrossRef]
- Xu, K.; Wang, F.; Wang, Y.; Dai, P.; Wang, J.; Liu, Y.; Fan, Y.; Sun, Z.; Wang, Y.; Zhao, W.; et al. Large-capacity interrogation for ultra-weak fiber Bragg grating array with a DFB Laser Array Chip. J. Light. Technol. 2025, 43, 8467–8473. [Google Scholar] [CrossRef]
- GB 175-2023; Common Portland Cement. China Architecture and Building Press: Beijing, China, 2023.
- JGJ 52-2006; Standard for Technical Requirements and Test Method of Sand and Crushed Stone (or Gravel) for Ordinary Concrete. China Architecture and Building Press: Beijing, China, 2006.
- GB/T 50081-2019; Standard for Test Methods of Concrete Physical and Mechanical Properties. China Architecture and Building Press: Beijing, China, 2019.
- Wu, Z.; Zhang, J.; Yu, H.; Wu, Q.; Da, B. Computer-aided investigation of the tensile behavior of concrete: Relationship between direct and splitting tensile strength. In Structures; Elsevier: Amsterdam, The Netherlands, 2023; Volume 55, pp. 453–467. [Google Scholar]
- Simulia. ABAQUS User’s Manual, Version 6.14; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2014.
- GB50010-2010; Code for Design of Concrete Structures. China Architecture and Building Press: Beijing, China, 2010.
- Xing, G.; Al-Dhabyani, M.A.; Al-Shakhada, N.A.; Li, X. Experimental and numerical investigations on the behavior and failure mechanism of RC beams strengthened with near-surface mounted high-strength aluminum alloy bars. J. Struct. Eng. 2021, 147, 04021208. [Google Scholar] [CrossRef]

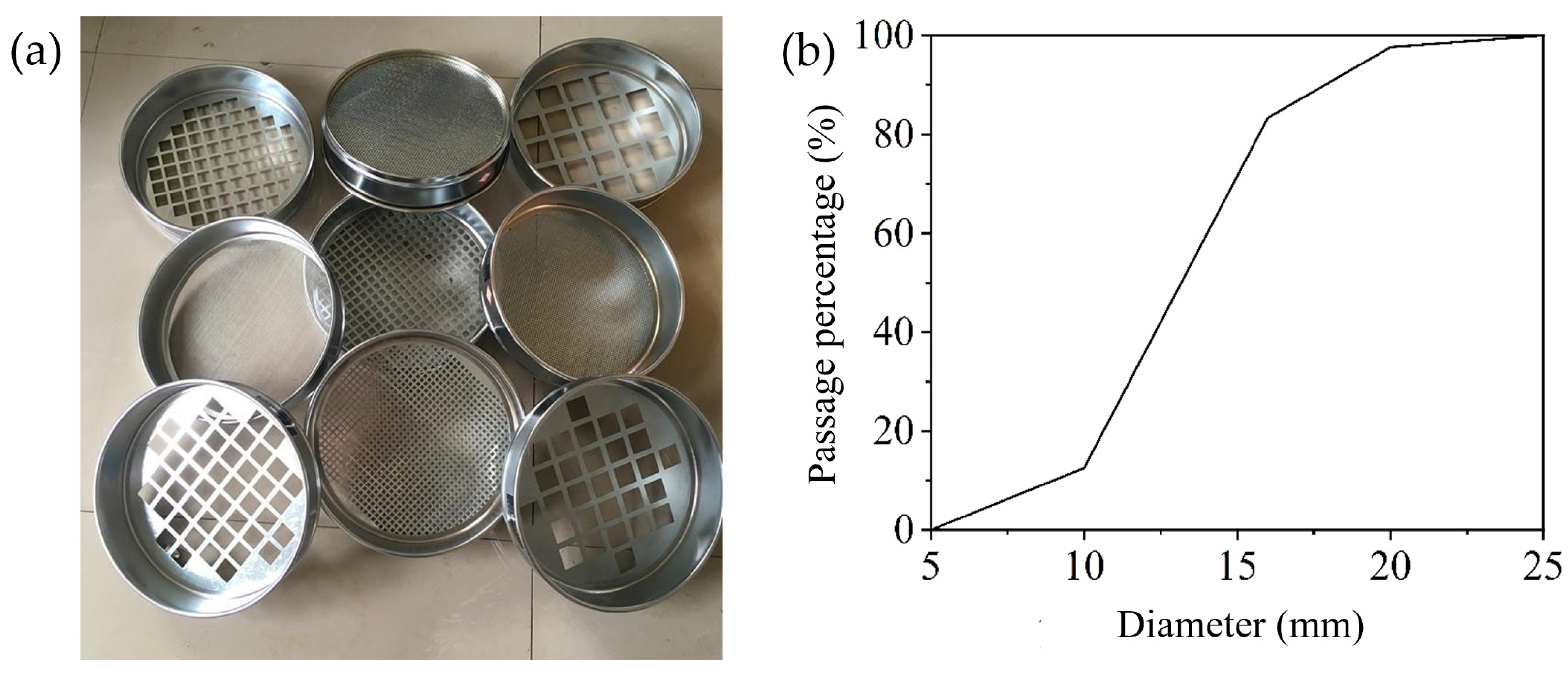
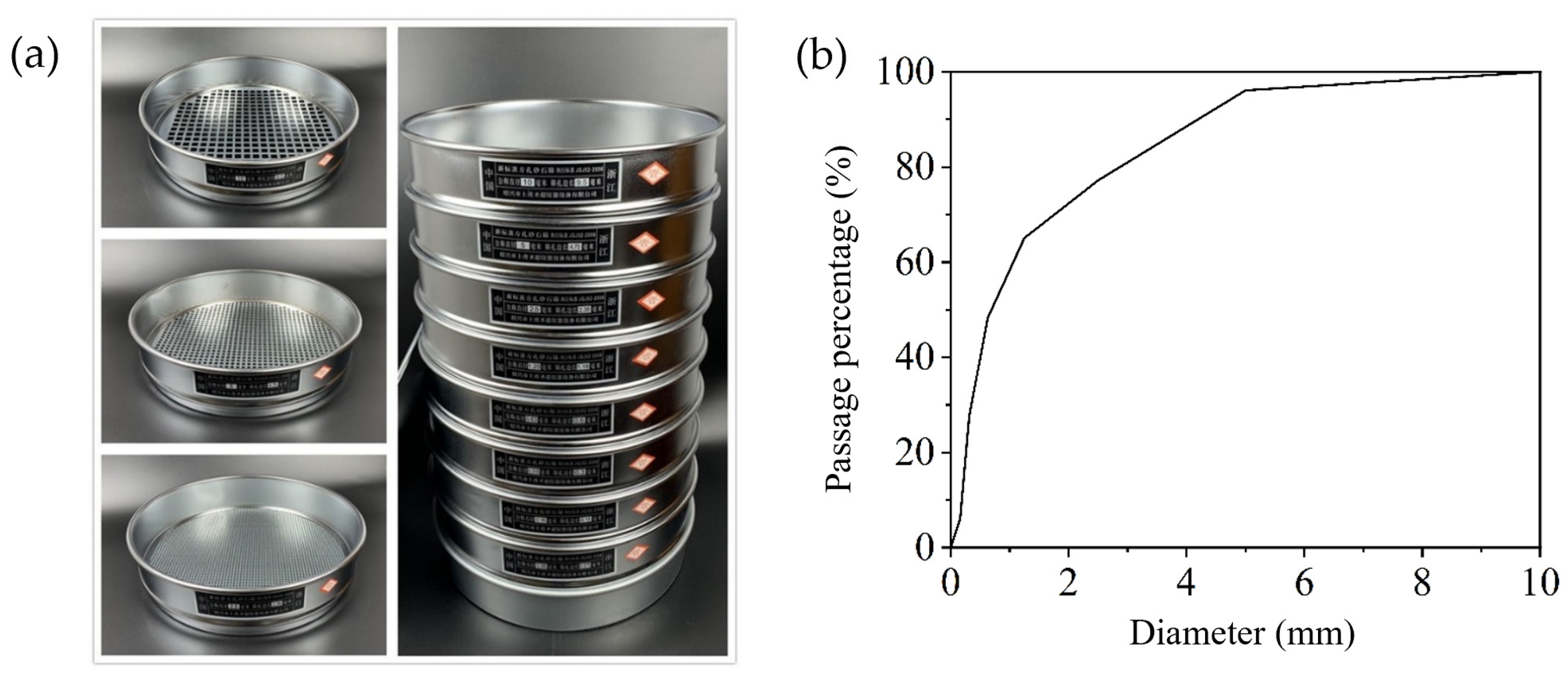












| SiO2 | Al2O3 | CaO | Fe2O3 | MgO | Na2O | K2O | SO3 | TiO2 | |
|---|---|---|---|---|---|---|---|---|---|
| Cement | 19.49 | 5.54 | 65.01 | 3.22 | 2.75 | 0.31 | 1.07 | 2.32 | 0.29 |
| Fly ash | 48.22 | 40.87 | 3.83 | 2.65 | 0.53 | 0.30 | 0.59 | 0.86 | 1.63 |
| Averaged Value (kg/m3) | |
|---|---|
| Apparent density | 2580 |
| Bulk density | 1530 |
| Compacted bulk density | 1660 |
| Averaged Value (kg/m3) | |
|---|---|
| Apparent density | 2660 |
| Bulk density | 1590 |
| Compacted bulk density | 1820 |
| Cement | Fly Ash | Sand | Gravel | Water | Sp | (MPa) | (MPa) | |
| Specimen | 295 | 110 | 724 | 1053 | 158 | 9.68 | 45.0 ± 2.0 | 2.53 ± 0.36 |
| Parameter | Dilation Angle, ψ | Plastic Potential Eccentricity, ε | Stress Ratio σbo/σco | Yielding Surface Shape Factor, k | Viscosity Parameter, μ |
|---|---|---|---|---|---|
| Value | 30 | 0.1 | 1.16 | 0.6667 | 0.0001 |
| No. | Description | Value(s) | Type/Notes |
| 1 | Hydration heat | Casting temperature: 15/20/25 °C Peak temperature: 45/50/55 °C | Thermal |
| 2 | Seasonal temperature increases | +10/+15/+20 °C | Thermal |
| 3 | Seasonal temperature decreases | −10/−15/−20 °C | Thermal |
| 4 | Static water loading | Only one sub-pool filled (6 cases) | Loading |
| Two sub-pools filled (15 cases) 1-2/1-3/1-4/1-5/1-6/2-3/2-4/2-5/2-6 3-4/3-5/3-6/4-5/4-6/5-6 | |||
| -Sub-pools 1, 3, and 5 filled | |||
| -Sub-pools 2, 4, and 6 filled |
| Peak Mises Stress (MPa) | Stabilized Mises Stress | Tensile Damage | |
|---|---|---|---|
| 15-45-15 | 4.26 | 2.94 | None |
| 15-50-15 | 4.97 | 3.00 | None |
| 15-55-15 | 5.68 | 2.80 | Minor Damage |
| 20-45-15 | 3.55 | 2.95 | None |
| 20-50-15 | 4.26 | 3.43 | None |
| 20-55-15 | 4.98 | 3.50 | None |
| 20-60-20 | 5.68 | 3.09 | Minor Damage |
| 25-45-15 | 2.84 | 1.42 | None |
| 25-50-15 | 3.55 | 3.38 | None |
| 25-55-15 | 4.26 | 3.88 | None |
| 25-60-25 | 4.98 | 3.01 | None |
| 30-60-25 | 4.26 | 3.43 | None |
| Cases | Mean Stress (MPa) | Max Stress (MPa) | Min Stress (MPa) | Std. |
|---|---|---|---|---|
| +10 °C | −1.392542 | −0.137349 | −2.351090 | 0.491334 |
| +15 °C | −2.067914 | −0.196965 | −3.531970 | 0.742718 |
| +20 °C | −2.722492 | −0.139204 | −4.694190 | 1.057008 |
| −10 °C | 1.537784 | 1.984240 | 0.138476 | 0.442215 |
| −15 °C | 1.498055 | 2.254750 | 0.196443 | 0.500747 |
| −20 °C | 1.181225 | 1.954480 | 0.235292 | 0.354571 |
| Max Principal Stress (MPa) | Max Displacement (mm) | Tensile Damage | |
|---|---|---|---|
| Sub-pool 1 | 2.54 | 58.51 | Minor damage |
| Sub-pool 2 | 2.46 | 52.57 | Minor damage |
| Sub-pool 3 | 2.50 | 51.59 | Minor damage |
| Sub-pool 4 | 2.42 | 52.54 | Minor damage |
| Sub-pool 5 | 2.43 | 55.65 | Minor damage |
| Sub-pool 6 | 2.52 | 59.91 | Minor damage |
| Max Principal Stress (MPa) | Max Displacement (mm) | Tensile Damage | |
|---|---|---|---|
| Sub-pool 1+2 | 2.54 | 52.58 | Minor damage |
| Sub-pool 1+3 | 2.67 | 52.56 | Minor damage |
| Sub-pool 1+4 | 2.53 | 52.86 | Minor damage |
| Sub-pool 1+5 | 2.53 | 55.78 | Minor damage |
| Sub-pool 1+6 | 2.54 | 54.17 | Minor damage |
| Sub-pool 2+3 | 2.83 | 52.07 | Minor damage |
| Sub-pool 2+4 | 2.55 | 52.40 | Minor damage |
| Sub-pool 2+5 | 2.45 | 52.97 | Minor damage |
| Sub-pool 2+6 | 2.54 | 54.04 | Minor damage |
| Sub-pool 3+4 | 2.61 | 51.88 | Minor damage |
| Sub-pool 3+5 | 2.68 | 54.04 | Minor damage |
| Sub-pool 3+6 | 2.88 | 55.72 | Minor damage |
| Sub-pool 4+5 | 2.45 | 53.23 | Minor damage |
| Sub-pool 4+6 | 2.54 | 54.45 | Minor damage |
| Sub-pool 5+6 | 2.53 | 54.81 | Minor damage |
| Max Stress (MPa) | Max Displacement (mm) | Tensile Damage | |
|---|---|---|---|
| Sub-pool 1+3+5 | 2.40 | 54.29 | Minor damage |
| Sub-pool 2+4+6 | 2.54 | 53.28 | Minor damage |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Han, X.; Zhang, D.; Li, J.; Miao, P.; Wang, W. Temperature–Load Stress Analysis of Ultra-Long Pool Structures Based on Distributed Fiber Optic Sensing and Finite Element Analysis. Buildings 2025, 15, 2961. https://doi.org/10.3390/buildings15162961
Li Y, Han X, Zhang D, Li J, Miao P, Wang W. Temperature–Load Stress Analysis of Ultra-Long Pool Structures Based on Distributed Fiber Optic Sensing and Finite Element Analysis. Buildings. 2025; 15(16):2961. https://doi.org/10.3390/buildings15162961
Chicago/Turabian StyleLi, Yongxing, Xinyang Han, Dajian Zhang, Jianrong Li, Pengyong Miao, and Wenrui Wang. 2025. "Temperature–Load Stress Analysis of Ultra-Long Pool Structures Based on Distributed Fiber Optic Sensing and Finite Element Analysis" Buildings 15, no. 16: 2961. https://doi.org/10.3390/buildings15162961
APA StyleLi, Y., Han, X., Zhang, D., Li, J., Miao, P., & Wang, W. (2025). Temperature–Load Stress Analysis of Ultra-Long Pool Structures Based on Distributed Fiber Optic Sensing and Finite Element Analysis. Buildings, 15(16), 2961. https://doi.org/10.3390/buildings15162961





