Mechanical Performance of Square Box-Type Core Mold Hollow Floor Slabs Based on Field Tests and Numerical Simulation
Abstract
1. Introduction
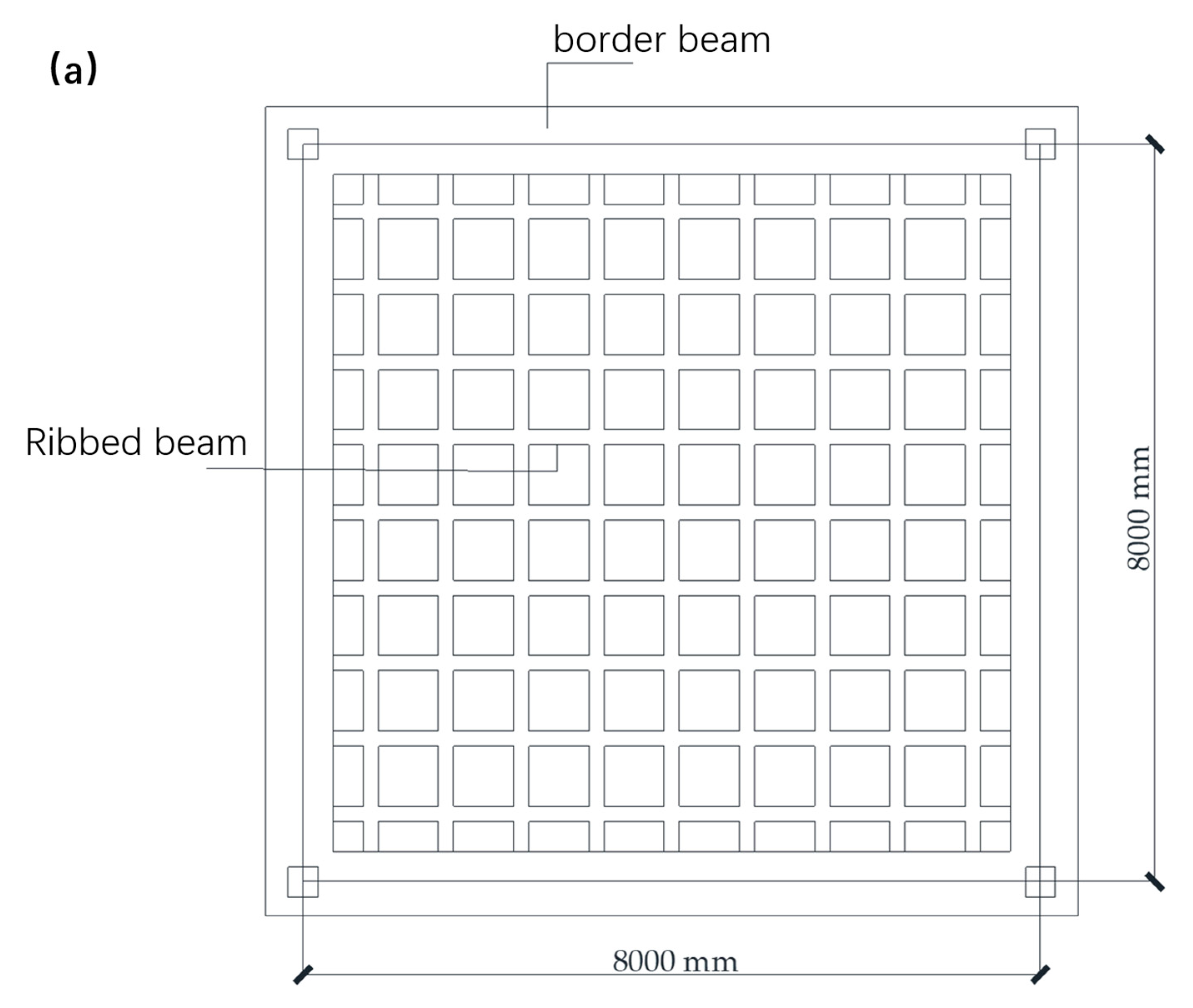
2. Project Overview
3. In Situ Experiment of the Box-Shaped Hollow Floor Slab
3.1. Experiment Plan
3.1.1. Overview of Experimental Instruments and Equipment
3.1.2. Mechanical Properties of Engineering Materials
3.2. Experimental Methods
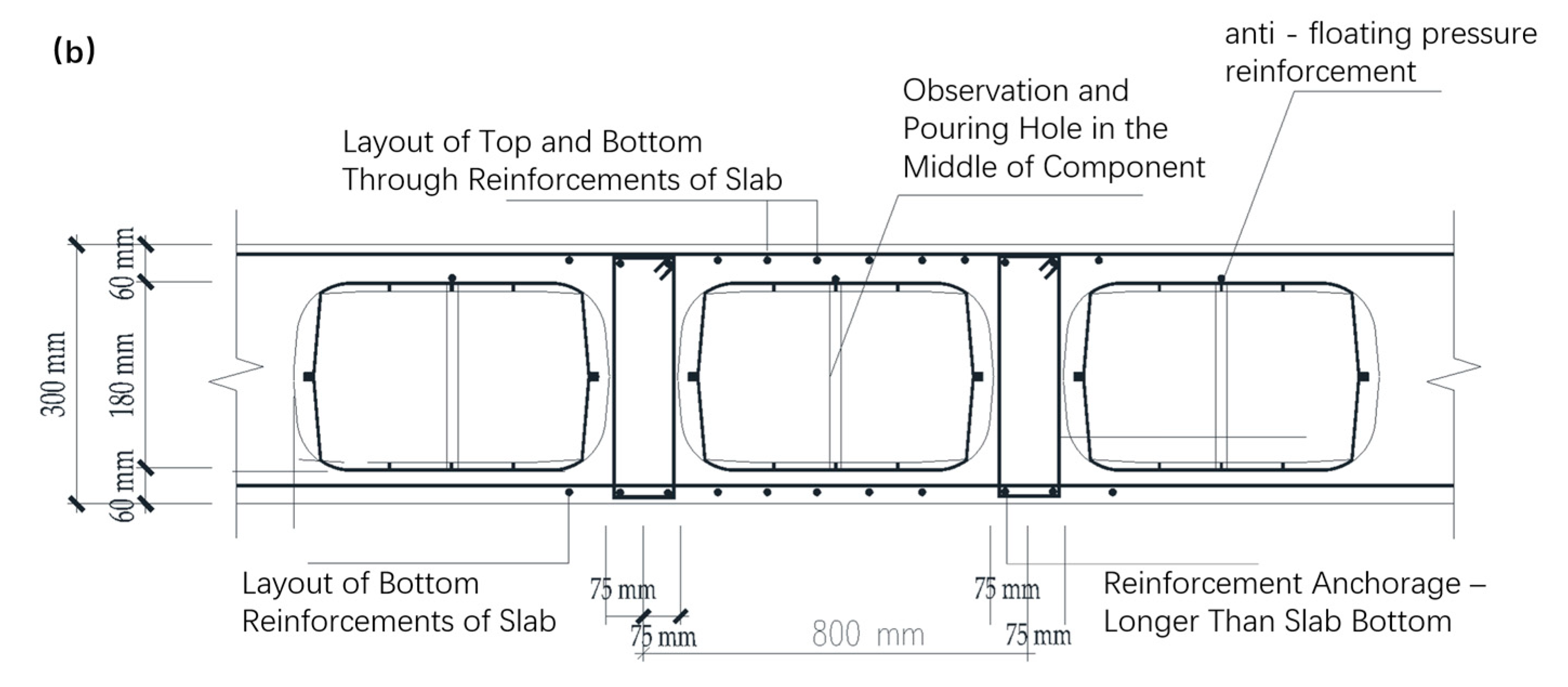
3.2.1. Monitoring System Installation
3.2.2. Implementation of Graded Loading
3.2.3. Structural Response Monitoring
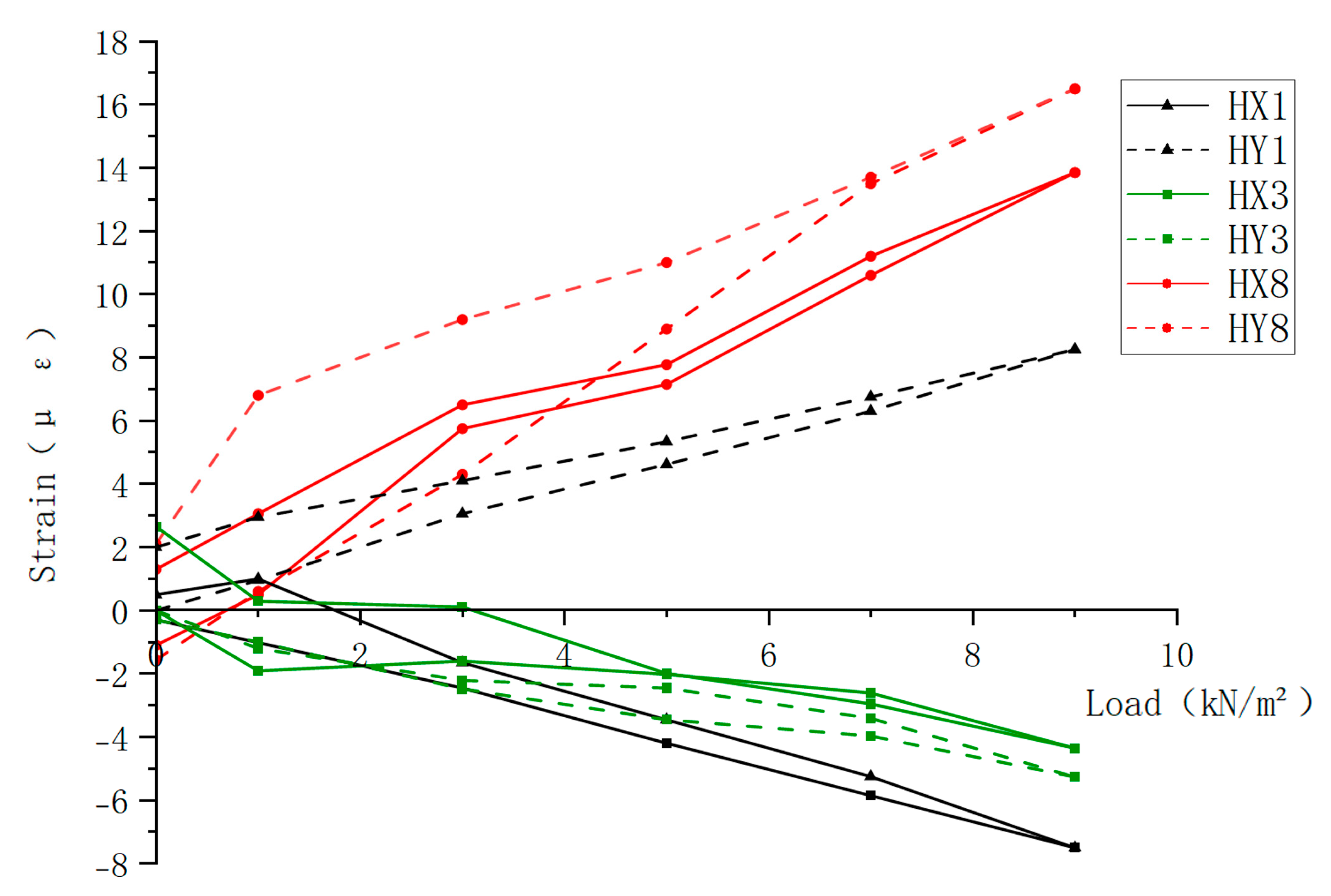
3.3. Experimental Results and Analysis
- E—Elastic Modulus,
- σ—Stress,
- ε—Strain

4. Numerical Calculation Analysis of the Box-Shaped Hollow Floor Slab
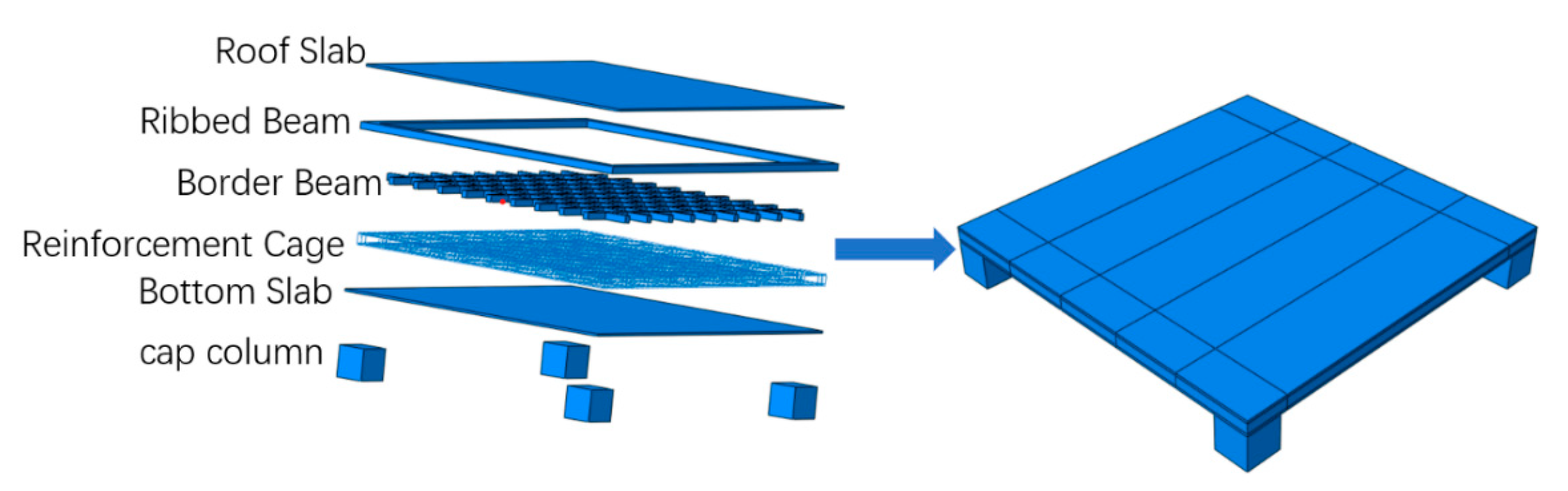
4.1. Model Construction
4.1.1. Material Constitutive Relationship
4.1.2. Model Establishment
4.2. Simulation Results and Analysis
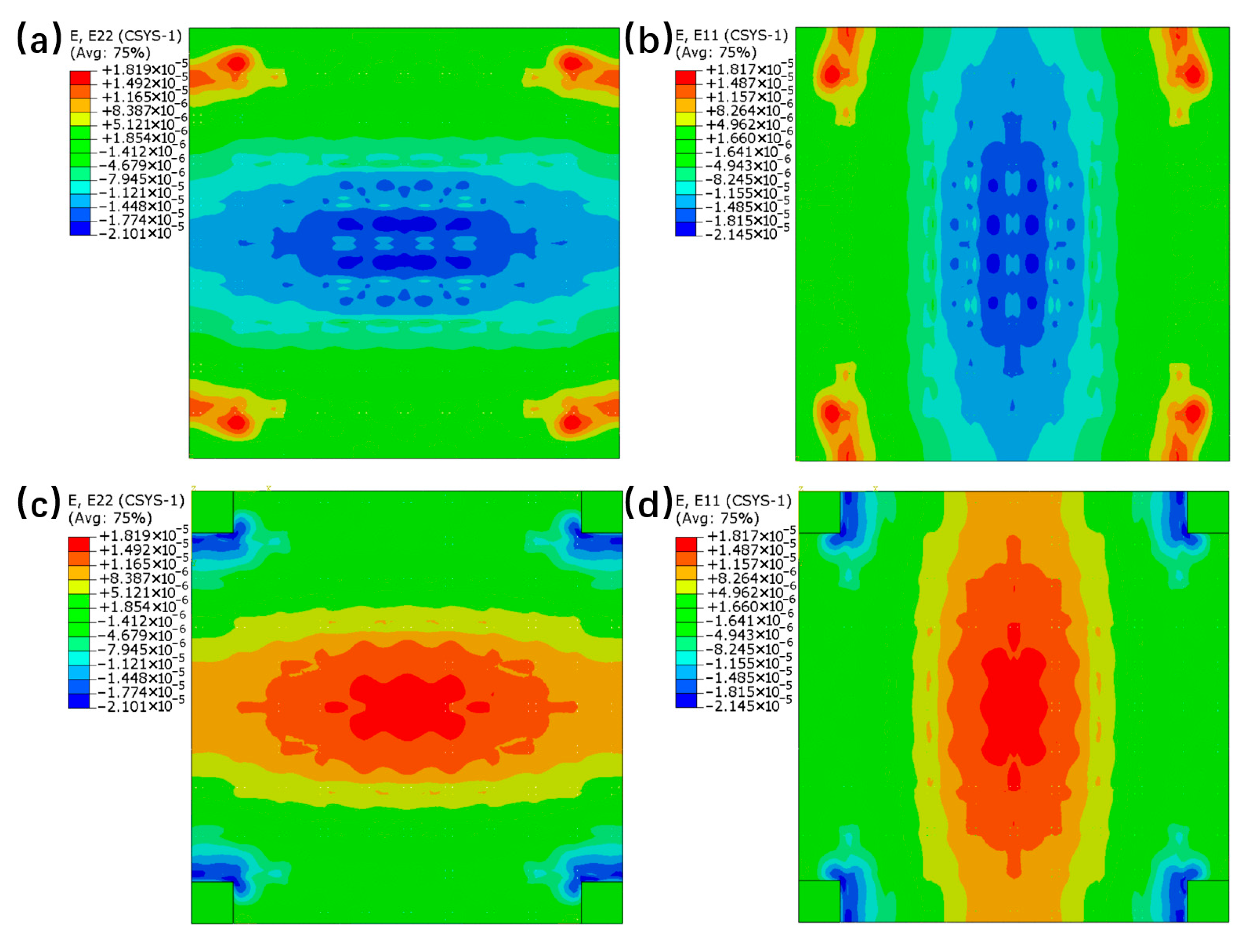
4.2.1. Rebar Strain Analysis
4.2.2. Concrete Strain Analysis
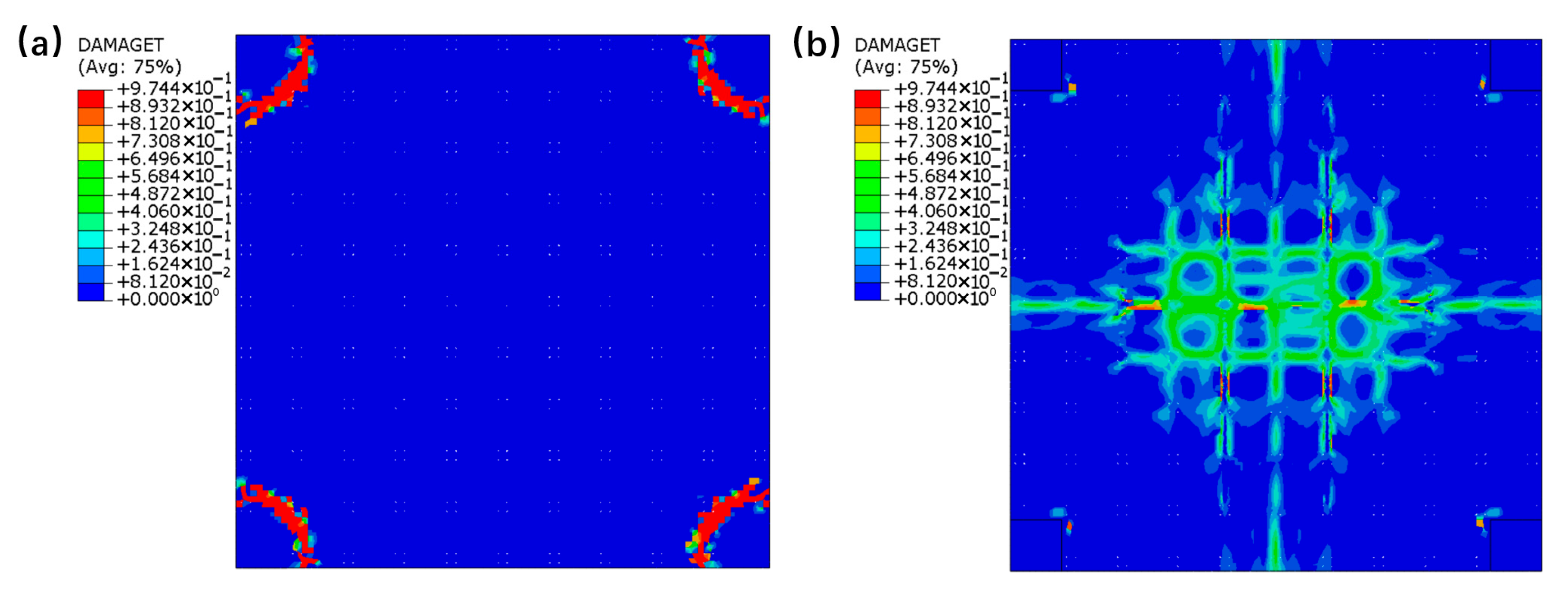
4.2.3. Ultimate Load Capacity Analysis of the Hollow Floor Slab
4.3. Comparison Analysis of Experiments and Finite Element Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, X.; Yu, J.; Wang, S.; Chen, L.; Zhang, Q. Research and application of active hollow core slabs in building systems for utilizing low energy sources. Appl. Energy 2014, 116, 424–435. [Google Scholar] [CrossRef]
- Zhu, G.; Wang, X.; Wang, W.; Wang, J.; Yang, Y. Research on the Flexural Behavior of Profiled Steel Sheet–Hollow Concrete Composite Floor Slab. Buildings 2025, 15, 2140. [Google Scholar] [CrossRef]
- Al-Kheetan, M.J. Properties of Lightweight Pedestrian Paving Blocks Incorporating Wheat Straw: Micro-to Macro-Scale Investigation. Results Eng. 2022, 16, 100758. [Google Scholar] [CrossRef]
- Mahdi, A.A.; Ismael, M.A. Structural Behavior of Hollow-Core One-Way Slabs of High Strength Self-Compacting Concrete. Int. J. Eng. 2021, 34, 39–45. [Google Scholar] [CrossRef]
- Eisa, A.; Aboul-Nour, L.A.; El-Ghamry, A.; Katunský, D. Flexural Behavior of Two-Layer Reinforced Concrete Slab with Hollow Cores. Adv. Mech. Eng. 2024, 16, 16878132231224940. [Google Scholar] [CrossRef]
- Sahoo, S.; Veerendar, C.; Prakash, S.S. Experimental and Numerical Studies on Flexural Behaviour of Lightweight and Sustainable Precast Fibre Reinforced Hollow Core Slabs. Constr. Build. Mater. 2023, 377, 131072. [Google Scholar] [CrossRef]
- Meng, X.; Cheng, S.; El Ragaby, A. Shear Strengthening of Prestressed Concrete Hollow-Core Slabs Using Externally Bonded Carbon-Fiber-Reinforced Polymer Sheets. PCI J. 2019, 64, 77–94. [Google Scholar] [CrossRef]
- Rasskazov, A.O.; Sokolovskaya, I.I.; Shul’ga, N.A. Equilibrium equations of multilayer hollow shells and plates. Sov. Appl. Mech. 1980, 16, 395–399. [Google Scholar] [CrossRef]
- Tan, K.H.; Zheng, L.X.; Paramasivam, P. Designing hollow-core slabs for continuity. PCI J. 1996, 41, 82–91. [Google Scholar] [CrossRef]
- Mostafa, M.; Hogan, L.; Elwood, K.J. Seismic Performance of Precast Hollow-Core Floors with Modern Detailing: A Case Study. SESOC J. 2022, 35, 86–100. [Google Scholar]
- Al-Azzawi, A.A.; Al-Aziz, B.M.A. Behavior of reinforced lightweight aggregate concrete hollow-core slabs. Comput. Concr. 2018, 21, 117–126. [Google Scholar] [CrossRef]
- Ahmed, S.M.; Avudaiappan, S.; Sheet, I.S.; Saavedra Flores, E.I.; Pina, J.C.; Yanez, S.J.; Guzmán, C.F. Prediction of Longitudinal Shear Resistance of Steel-Concrete Composite Slabs. Eng. Struct. 2019, 193, 295–300. [Google Scholar] [CrossRef]
- Gul, A.; Shahzada, K.; Alam, B.; Badrashi, Y.I.; Khan, S.W.; Khan, F.A.; Rehman, Z.U. Experimental Study on the Structural Behavior of Cast In-Situ Hollow Core Concrete Slabs. Civ. Eng. J. 2020, 6, 1983–1991. [Google Scholar] [CrossRef]
- Lyu, J.; Wang, Y.; Van Coile, R.; Huang, Z.; Zhaohui, H. Experimental Investigation on the Fire Resistance of Cast-in-Situ Hollow Core Concrete Slabs Constructed Using Filler Boxes and an Assembly Box System. Struct. Concr. 2018, 20, 144–163. [Google Scholar] [CrossRef]
- Ghamry, A.; Esia, A.; Aboul-Nour, L. Structural behavior of Lightweight and High strength Layered Hollow Core Slabs. Fract. Struct. Integr. 2022, 17, 134–152. [Google Scholar] [CrossRef]
- Sayhood, E.K.; Mohammed, N.S.; Hilo, S.J.; Salih, S.S. Comprehensive Empirical Modeling of Shear Strength Prediction in Reinforced Concrete Deep Beams. Infrastructures 2024, 9, 67. [Google Scholar] [CrossRef]
- Sagadevan, R.; Rao, B.N. Flexural Behavior of Reinforced Concrete Biaxial Voided Square Slabs. ACI Struct. J. 2020, 117, 3–14. [Google Scholar] [CrossRef]
- Mahboob, A.; Hassanshahi, O.; Hakimi, A.; Moradi, M. Evaluating the performance of hollow core slabs (HCS)-concrete and simplifying their implementation. Recent Prog. Mater. 2023, 5, 1–15. [Google Scholar] [CrossRef]
- Firouzranjbar, S.; Schultz, A. Numerical Investigation of Modified Punching Shear Behavior in Precast Prestressed Hollow Core Slabs Under Concentrated Loads. SSRN. 2023. Available online: https://ssrn.com/abstract=5076557 (accessed on 23 July 2025). [CrossRef]
- Prakashan, L.V.; George, J.; Edayadiyil, J.B.; George, J.M. Experimental Study on the Flexural Behavior of Hollow Core Concrete Slabs. Appl. Mech. Mater. 2017, 857, 107–112. [Google Scholar] [CrossRef]
- Frăţilă, E.; Kiss, Z. Finite Element Analysis of Hollow-Core Slabs. J. Appl. Eng. Sci. 2016, 6, 29–33. [Google Scholar] [CrossRef]
- Zeng, X.; Feng, Y.; Ruan, S.; Xu, M.; Gong, L. Experimental and Numerical Study on Flexural Behavior of a Full-Scale Assembled Integral Two-Way Multi-Ribbed Composite Floor System. Buildings 2023, 13, 2517. [Google Scholar] [CrossRef]
- Jin, J.; Hu, W.; Zheng, F.; Wu, B. Experimental and Numerical Studies on the Mechanical Behavior of a Novel Bidirectional, Prestressed, Prefabricated, Composite Hollow-Core Slab. Buildings 2025, 15, 232. [Google Scholar] [CrossRef]
- Li, X.; Wu, G.; Popal, M.S.; Jiang, J. Experimental and Numerical Study of Hollow Core Slabs Strengthened with Mounted Steel Bars and Prestressed Steel Wire Ropes. Constr. Build. Mater. 2018, 188, 456–469. [Google Scholar] [CrossRef]
- GB/T 50152-2012; Standard for Test Method of Concrete Structures. China Architecture & Building Press: Beijing, China, 2012.
- JGJ/T 268-2012; Echnical Specification for Cast-in-situ Concrete Hollow Floor Structure. China Architecture & Building Press: Beijing, China, 2012.
- GB 50010-2010; Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2017.
- Safar, A.; Lou, K.B. A study of the action of the beam and beamless (flush) floor slabs of the multistorey buildings. Erciyes Univ. Fen Bilim. Enstitüsü Fen Bilim. Derg. 2007, 23, 127–135. [Google Scholar]
- Gong, L.; Chen, Z.; Feng, Y.; Ruan, S.; Tu, L. Experimental Study on an Innovative Hollow Concrete Floor System Assembled with Precast Panels and Self-Thermal-Insulation Infills. Adv. Civ. Eng. 2021, 2021, 6663412. [Google Scholar] [CrossRef]







| No. | Cube Size (mm) | Applied Load (KN) | Compressive Strength (MPa) | Average Strength (MPa) |
|---|---|---|---|---|
| 1 | 150 × 150 × 150 | 900.93 | 34.53 | 34.66 |
| 2 | 150 × 150 × 150 | 908.75 | 34.79 |
| No. | Yield Strength (MPa) | Tensile Strength (MPa) | Maximum Load (KN) |
|---|---|---|---|
| 1 | 416 | 550 | 184.16 |
| 2 | 435 | 572 | 186.23 |
| Material | Grade | Density (kN/m3) | Elastic Modulus (GPa) | Poisson’s Ratio |
|---|---|---|---|---|
| Concrete | C30 | 24 | 30 | 0.2 |
| rebar | HRB400 | 78 | 200 | 0.3 |
| Expansion Angle (mm) | Eccentricity | fb0/fc0 | K | Viscous Coefficient |
|---|---|---|---|---|
| 30 | 0.1 | 1.16 | 2/3 | 0.005 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Chen, F.; Yu, W.; Sheng, J.; Wei, L.; Hu, A. Mechanical Performance of Square Box-Type Core Mold Hollow Floor Slabs Based on Field Tests and Numerical Simulation. Buildings 2025, 15, 2948. https://doi.org/10.3390/buildings15162948
Zhang Z, Chen F, Yu W, Sheng J, Wei L, Hu A. Mechanical Performance of Square Box-Type Core Mold Hollow Floor Slabs Based on Field Tests and Numerical Simulation. Buildings. 2025; 15(16):2948. https://doi.org/10.3390/buildings15162948
Chicago/Turabian StyleZhang, Ziguang, Fengyu Chen, Wenjun Yu, Jie Sheng, Lin Wei, and Ankang Hu. 2025. "Mechanical Performance of Square Box-Type Core Mold Hollow Floor Slabs Based on Field Tests and Numerical Simulation" Buildings 15, no. 16: 2948. https://doi.org/10.3390/buildings15162948
APA StyleZhang, Z., Chen, F., Yu, W., Sheng, J., Wei, L., & Hu, A. (2025). Mechanical Performance of Square Box-Type Core Mold Hollow Floor Slabs Based on Field Tests and Numerical Simulation. Buildings, 15(16), 2948. https://doi.org/10.3390/buildings15162948







